HMPA: an innovative hybrid multi-population algorithm based on artificial ecosystem-based and Harris Hawks optimization algorithms for engineering problems

Abstract

Optimization algorithms have made considerable advancements in solving complex problems with the ability to be applied to innumerable real-world problems. Nevertheless, they are passed through several challenges comprising of equilibrium between exploration and exploitation capabilities, and departure from local optimums. Portioning the population into several sub-populations is a robust technique to enhance the dispersion of the solution in the problem space. Consequently, the exploration would be increased, and the local optimums can be avoided. Furthermore, improving the exploration and exploitation capabilities is a way of increasing the authority of optimization algorithms that various researches have been considered, and numerous methods have been proposed. In this paper, a novel hybrid multi-population algorithm called HMPA is presented. First, a new portioning method is introduced to divide the population into several sub-populations. The sub-populations dynamically exchange solutions aiming at balancing the exploration and exploitation capabilities. Afterthought, artificial ecosystem-based optimization (AEO) and Harris Hawks optimization (HHO) algorithms are hybridized. Subsequently, levy-flight strategy, local search mechanism, quasi-oppositional learning, and chaos theory are utilized in a splendid way to maximize the efficiency of the HMPA. Next, HMPA is evaluated on fifty unimodal, multimodal, fix-dimension, shifted rotated, hybrid, and composite test functions. In addition, the results of HMPA is compared with similar state-of-the-art algorithms using five well-known statistical metrics, box plot, convergence rate, execution time, and Wilcoxon’s signed-rank test. Finally, the performance of the HMPA is investigated on seven constrained/unconstrained real-life engineering problems. The results demonstrate that the HMPA is outperformed the other competitor algorithms significantly.

1 Introduction

Optimization algorithms are the most efficient approaches for solving time-consuming and complex real-world scientific, medical, engineering, and other NP-complete problems [1]. In the optimization process, the value of a target function is minimized or maximized [2, 3]. Meta-heuristic algorithms provide new techniques in discovering optimal or near-optimal solutions in a reasonable amount of time [4]. In recent years, researchers have increasingly focused on these algorithms, and they developed numerous algorithms inspired by various phenomena. For instance, Smart Flower Optimization Algorithm (SFOA) [5], Group Teaching Optimization Algorithm (GTOA) [6], Locust Swarm Optimization (LSO) [7], Manta Ray Foraging Optimization (MRFO) [8], Supply–Demand-Based Optimization (SDO) [9], Artificial Electric Field Algorithm (AEFA) [10], Equilibrium Optimizer (EO) [11], Sooty Tern Optimization Algorithm (STOA) [12], Henry Gas Solubility Optimization (HGSO) [13], Fitness Dependent Optimizer (FDO) [14], Parasitism-Predation algorithm (PPA) [15], Emperor Penguin Optimizer (EPO) [16], Multi-Objective Spotted Hyena Optimizer (MOSHO) [17], Seagull Optimization Algorithm (SOA) [18], Spotted Hyena Optimizer (SHO) [19, 20], and Marine Predators Algorithm (MPA) [21] are among the most recently published meta-heuristic algorithms. These algorithms are widely used in complex problems such as time series [22,23,24], industrial applications [25], non-linear applications [26,27,28,29], clustering and feature selection [30].

Considering the inspiring phenomenon, meta-heuristic algorithms can be divided into different categories. Figure 1 illustrates a possible classification of the meta-heuristic algorithms and provides some representative algorithms for each category.

Fig. 1

Classification of meta-heuristic algorithms

Artificial Ecosystem-based Optimization (AEO) [31], and Harris Hawks Optimization (HHO) [32] algorithms are two influential and potent population-based meta-heuristic algorithms, which are inspired by the flow of energy in the ecosystem of the Earth, and intelligence cooperative behavior of Harris’ hawks in nature, respectively. These algorithms, like other optimization algorithms, start with a randomly generated set of solutions within the problem space [33, 34]. Then, the solutions are updated according to the historical data and the other solutions’ information in the limited iteration [35]. In this gradual process, the quality of the solutions is increased, and further optimal solutions are found for the given problem. These algorithms were applied to various problems, and tested on abundant test functions, attaining promising results.

However, they have several deficiencies. For example, the convergence rate of them is scant in some high-dimensional and complex problems, and they do not have full confidence in finding an optimal solution in a reasonable time. In addition, the AEO algorithm has insufficient exploration capability and has inadequate performance on multimodal problems. Besides, they fall into local optimums easily. Once a solution gets stuck on a local optimum, it cannot search other areas of the problem space with more iterations. This observation is exceptionally unfavorable for real-world NP-Hard applications.

To compensate for the above-mentioned and other shortcomings, the notable creation and successful development of new optimization algorithms is still a challenging task. Researchers have provided various techniques to overcome these weaknesses (e.g., taking advantage of the chaos theory [36,37,38], hybridizing supplementary algorithms [39,40,41,42,43,44], using the memory in solutions [45,46,47,48], applying greedy or hill climbing selection methods [49,50,51,52], dividing the population into several sub-populations [53,54,55,56], utilizing of orthogonal learning [57,58,59], using quantum-based strategy [60,61,62], employing oppositional learning [63,64,65], taking benefits of information sharing mechanisms [66,67,68], etc.).

In this paper, the following strides have been taken to overcome the stated deficiencies of the AEO and HHO algorithms.

Initially, a multi-population technique has been introduced to enhance the population diversity. The Multi-population technique significantly increases the exploration capability by scattering the solutions over the entire search space. This dispersion allows solutions to search for more areas of problem space and find promising areas. With this technique, the population is divided into several sub-populations, and each sub-population searches independently. Nonetheless, the number of solutions in the sub-populations are changed dynamically.

Next, the quasi-oppositional mechanism is utilized to increase exploration capability further. The quasi-oppositional mechanism is an expansion of opposite position-based learning that many papers have considered the phenomenon [69,70,71].

Afterwards, a chaotic-based local search (CLS) approach is adopted in the proposed algorithm to increase the exploitation capability of it. The CLS, using the advantages of the chaotic maps, probes around a solution to find better ones. This behavior dramatically increases the exploitation ability [72, 73]. Furthermore, for improving the exploitation as much as possible, the levy-flight random walk has also been exploited. According to the obtained results of the levy-flight based optimization algorithms, it can be concluded that levy-flight is an efficient technique to improve efficiency [74,75,76].

Next, the greedy selection strategy has been introduced to accelerate the convergence speed. The greedy selection mechanism can mitigate excessive differentiation and preserve the excellent characteristics of the solution [57]. Additionally, this strategy can also achieve further targeted search process. However, it can cause solutions to get stuck in local optimums and prevent them from jumping out. Hence, a mechanism is required to take solutions out of local optimums.

Finally, a mechanism is introduced to bring the trapped solution out. The effectiveness of the mechanism has been evidenced in our previous work [1].

The resulting multi-population hybrid algorithm is extensively evaluated over forty-five unconstrainted single-objective test functions from different categories. The evaluations are conducted with statistically comparing the resulting algorithm with numerous similar meta-heuristic algorithms. Moreover, the Wilcoxon signed-rank test is used to investigate the possible significant difference between the proposed algorithm and the competitor algorithms. In the end, the superiority of the proposed multi-population algorithm is tested on seven widely-used constrained and unconstrained engineering problems.

The key contributions of this paper can be summarized as follow:

• AEO algorithm has been hybridized with HHO in an innovative way.

• A novel multi-population model has been introduced to the resulting algorithm.

• A new levy-flight based function has been presented.

• Two neoteric local search algorithms have been provided.

• The quasi-oppositional learning technique has been used.

• The proposed algorithm has been tested on fifty classical and CEC 2017 test functions.

• The proposed algorithm has been applied on several real-life applications.

• The proposed algorithm has been compared with state-of-the-art algorithm statistically and visually.

• The obtained results have been proved by Wilcoxon signed-rank test.

The rest of the paper is organized as follows. Section 2 reviews some of the multi-population and multi-swarm algorithms. Sections 3 and 4 present a concise description of artificial ecosystem-based optimization, and Harris Hawks optimization algorithms, respectively. Section 5 provides the mathematical details and different parts of the proposed algorithm. In Sect. 6, the experimental results of the algorithms are provided on the test functions. Section 7 gives the results of real-world problems experiments, and finally, Sect. 8 propounds the conclusion and future perspectives.

2 Literature review

This section aims at giving a brief review of the presented multi-population algorithms. Many pieces of research attempted to improve the performance of meta-heuristic algorithms using multi-swarming or multi-populating techniques. For instance, in [77], Qiu proposed a novel multi-swarm particle swarm optimization algorithm. In the proposed algorithm, the population is divided into several sub-swarms, and the particles of each sub-swarm update their positions according to the corresponding best particle of the swarm.

Besides, Rao et al. suggested an adaptive multi-team perturbation Jaya algorithm in [53]. In the suggested schema, the multiple teams of the population are used to explore search scopes efficiently, and the teams have the same size with different perturbation or movement equations. The supremacy of the solutions of the teams are investigated based on the fitness value and boundary violations.

Furthermore, in [55], Rao and Pawar presented self-adaptive multi-population Rao algorithms for solving engineering design problems. In this study, the initial population of Rao algorithms is divided into several sub-population to keep the diversity of the population. In addition, the number and members of sub-populations are changed over time. The resulting algorithms are evaluated on 25 test functions and several constrained engineering problems.

Additionally, in [78], the authors propounded a multi-swarm multi-objective hybrid algorithm called MSMO/2D. In MSMO/2D, the particle swarm optimization algorithm is integrated with decomposition and dominance strategies. This algorithm has been proposed to reduce the gap between solutions in the Pareto Front, and maximize the solutions’ diversity.

Moreover, a new multi-swarm hybrid optimization algorithm has been presented in [79] by Nie, and Xu for solving dynamic optimization problems. In the presented multi-swarm algorithm, the particle swarm algorithm is combined with the simulated annealing algorithm and a prediction strategy. Afterwards, the resulting algorithm has been applied to the CEC 2009 test functions. These changes enhanced the adaptability of individual evolution and balanced exploration and exploitation.

Similarly, in [80], Li et al. proposed a multi-swarm cuckoo search algorithm named MP-QL-CS, which is enhanced by the Q-learning strategy. In Q-Learning, the optimal action is learned by selecting the action of enlarging the accumulative benefits with a discount. Additionally, to evaluate the multi-stepping evolution effect and learn the optimal step size, Q function value used a step size control in the proposed algorithm. The Q function is defined as diminished, the maximum expected, and cumulative reward.

In addition, in [81], the authors developed a novel multi-population differential evolution algorithm. In the proposed algorithm, the diversity of the population increases while the simplicity is preserved. The diversity is achieved by dividing the population into independent subpopulations, which each subpopulation has the different mutation and update equations. A new mutation strategy, which utilizes information on the best solution or a randomly selected one, is used as another contribution to balance exploration and exploitation by generating better individuals. Moreover, in the proposed algorithm, function evaluations are divided into epochs. At the end of each epoch, solutions of the sub-populations are exchanged.

In a similar study, Biswas et al. proposed a new multi-swarm artificial bee colony algorithm for global searching [82]. In this study, the swarm of bees is divided into multiple sub-swarms, which are characterized using different and unique perturbation mechanisms. Also, the reinitializing operator has been replaced with a set of criteria for detecting impotent sub-swarms. Whenever an impotent bee is detected in a sub-swarm, the foragers mitigation strategy is performed considering the minimum member constraint.

Likewise, in [83], Di Carlo et al. provided a novel multi-population adaptive inflationary differential evolution algorithm. In the inflationary differential evolution algorithm, some of the restart, and local search techniques of monotonic basin hopping have been used. In addition, in the proposed adaptive differential evolution algorithm, the CR, and F parameters are adopting with each other automatically with the size of local restart bubble, and the number of local restarts of monotonic basin hopping. The multi-swarming technique in the proposed algorithm avoids trapping in the local optimums.

Withal, Xiang and Zhou offered a multi-colony artificial bee colony algorithm in [84]. In the offered algorithm, a multi-deme model and a dynamic information technique are used to handle multi-objective problems. The colonies in the algorithm search the problem space independently by exchanging useful information. The colonies have the same number of employed and onlooker bees, and the bees search the space by neighboring information and use the greedy mechanism to keep better solutions.

Correspondingly, in [85], the authors propounded a new hybrid multi-swarm particle swarm optimization and shuffled frog leaping algorithm to improve particle communications and enhance their searching ability. Accompanying the multi-swarming, and updating along with a cooperating strategy have been proposed in the propounded algorithm. The particles of the sub-swarms update their positions using the equations morphed from the shuffled frog leaping algorithm.

In addition, Wu et al. proposed a multi-population differential evolution algorithm with different mutation strategies [86]. The mutation strategies are current particle to best particle, current particle to random particle, and random mutation. In the proposed algorithm, four sub-populations are used: three sub-populations with a smaller size and one with a larger size. After a specified number of rounds, the best mutation strategy can be determined using the fitness improvements and consumed functions evaluated. Subsequently, the reward sub-population will dynamically be allocated to the determined best performing mutation strategy.

3 Artificial ecosystem-based optimization

The artificial ecosystem-based optimization (AEO) is a novel nature-inspired meta-heuristic algorithm, which is presented in [31] by Zhao et al. AEO is a population-based algorithm inspired from the energy flow in the ecosystem of Earth, and has three main operators: production, consumption, and decomposition. The details of the AEO algorithm, along with the exposition of its operators, have been presented in the [31]. However, a brief overview of the operator’s head with its equations is presented here.

3.1 Production

The first operator of the AEO algorithm is production. Through using this operator, a new individual is produced using Eq. (1) between the best individual and a randomly selected individual from the current population.

$$ {\text{New}}X_{1}^{{{\text{It}} + 1}} = \left( {1 - a} \right) \cdot {\text{Best}}X + a \cdot X_{r}^{\text{It}} $$

(1)

$$ a = \left( {1 - \frac{\text{It}}{{{\text{Max}}\_{\text{it}}}}} \right) \cdot r_{1} $$

(2)

$$ X_{r}^{\text{It}} = {\text{Lb}} + r \cdot \left( {{\text{Ub}} - {\text{Lb}}} \right) $$

(3)

where ${\text{Best}}X$ is the best individual found so far, ${\text{It}}$ is the current iteration, $r$ and $r_{1}$ are random number vectors within (0,1) whose sizes are ${\text{Dim}}$ and one, respectively. Furthermore, ${\text{Dim}}$ is the dimension of the problem, ${\text{Lb}}$ and ${\text{Ub}}$ are the lower and upper bounds of problem space, respectively. The $a$ is a coefficient, which decreases linearly over time and specifies the exploration or exploitation of the ${\text{New}}X_{1}^{{{\text{It}} + 1}}$.

3.2 Consumption

The second operator of the AEO is the consumption operator. The consumer individuals are divided into three species: Herbivore, Carnivore, and Omnivore, and are updated by Eqs. (4)–(6), respectively.

$$ {\text{New}}X_{i}^{{{\text{It}} + 1}} = X_{i}^{\text{It}} + C \cdot \left( {X_{i}^{\text{It}} - {\text{New}}X_{1}^{{{\text{It}} + 1}} } \right) $$

(4)

$$ {\text{New}}X_{i}^{{{\text{It}} + 1}} = X_{i}^{\text{It}} + C \cdot \left( {X_{i}^{\text{It}} - X_{j}^{\text{It}} } \right) $$

(5)

$$ {\text{New}}X_{i}^{{{\text{It}} + 1}} = X_{i}^{\text{It}} + C \cdot r_{2} \cdot \left( {X_{i}^{\text{It}} - {\text{New}}X_{1}^{{{\text{It}} + 1}} } \right) + \left( {1 - r_{2} } \right)\left( {X_{i}^{\text{It}} - X_{j}^{\text{It}} } \right) $$

(6)

where $r_{2}$ is a random number in range (0,1), $X_{j}^{ }$ is a randomly chosen solution from the current population, and $C$ can be obtained as below:

$$ C = \frac{1}{2}.\frac{u}{v} $$

(7)

where $u$ and $v$ are normally distributed random numbers. It is worth mentioning that the second-best individual is in the Herbivore category.

3.3 Decomposition

The last operator of the AEO is a decomposition operator, which models the decomposition process in ecosystems. This process is formulated as Eq. (8). In other words, the individuals in this phase are updated by Eq. (8).

$$ {\text{New}}X_{i}^{{{\text{It}} + 1}} = X_{N}^{\text{It}} + D \cdot \left( {e \cdot X_{N}^{\text{It}} - h \cdot X_{i}^{\text{It}} } \right) $$

(8)

where $X_{N}^{\text{It}}$ is the best individual in the current iteration, $D$, $e$, and $h$ are calculated using Eqs. (9)–(11), respectively.

$$ D = 3u $$

(9)

$$ e = r_{3} \cdot {\text{rand}}i\left( {\left[ {1 2} \right]} \right) - 1 $$

(10)

$$ h = 2 \cdot r_{3} - 1 $$

(11)

where $u$ is a normally distributed random numbers, and $r_{3}$ is a random number in (0,1). The flowchart of the AEO has been illustrated in Fig. 2.

Fig. 2

Flowchart of the basic AEO

4 Harris Hawks optimization

Harris Hawks optimization (HHO) algorithm is another powerful population-based meta-heuristic algorithm, which is motivated by the behavior of Harris’ hawks in nature [32]. As with the previous algorithm, a summary of the HHO algorithm is given with its update equations (for more details, refer to [32]). HHO models the intelligence cooperative behavior and chasing style of Harris hawks mathematically. The HHO consists of two main phases: exploration and exploitation, which are characterized in the next subsections. In addition, these phases are selected by parameter E, which can be obtained by Eq. (12).

$$ E = 2E_{0} \left( {1 - \frac{\text{It}}{{{\text{Max}}\_{\text{it}}}}} \right) $$

(12)

where $E_{0}$ is the initial energy of the prey, ${\text{It}}$ and ${\text{Max\_it}}$ are the current, and maximum number of iterations, respectively. Whenever $\left| E \right| \ge 1$, the exploration phase is selected, and when $\left| E \right| < 1$, the exploitation phase is going to be selected.

4.1 Exploration phase

The current phase presents the exploration mechanism of HHO. In this phase, the solutions are updated by the perching strategy of Harris hawks that is simulated by Eq. (13).

$$ {\text{New}}X_{i}^{{{\text{It}} + 1}} = \left\{ {\begin{array}{*{20}l} {X_{r}^{\text{It}} - r_{1} \left| {X_{r}^{\text{It}} - 2r_{2} X_{i}^{\text{It}} } \right|} & {q \ge 0.5} \\ {\left( {{\text{Best}}X - X_{m}^{\text{It}} } \right) - r_{3} \left( {{\text{Lb}} + r_{4} \left( {{\text{Ub}} - {\text{Lb}}} \right)} \right)} & {q < 0.5} \\ \end{array} } \right. $$

(13)

In Eq. (13), $X_{i}^{\text{It}}$ is the current position of $i{\text{th}}$ solution in iteration ${\text{It}}$, ${\text{New}}X_{i}^{{{\text{It}} + 1}}$ is the updated position of $i{\text{th}}$, $X_{r}^{\text{It}}$ is a randomly chosen solution from the population, $r_{1}$, $r_{2}$, $r_{3}$, $r_{4}$, and q are random numbers in (0,1), ${\text{Best}}X$ is the best solution found so far, ${\text{Lb}}$ and ${\text{Ub}}$ are the lower and upper bounds of problem space, and $X_{m}^{\text{It}}$ is the average of the solutions in the current population, and can be calculated using Eq. (14).

$$ X_{m}^{\text{It}} = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} X_{i}^{\text{It}} $$

(14)

where N is the number of solutions in the population.

4.2 Exploitation phase

This phase models the surprising pounce of the Harris hawks. Given that the preys try to escape from the menacing situation, the Harris hawks use different chasing styles for hunting. In this phase, four possible strategies are suggested to simulate the attacking behaviors: soft besiege, hard besiege, soft besiege with progressive rapid dives, and hard besiege with progressive rapid dive, which are briefly described in the next subsections. Two parameters are used in HHO to choose one of these four strategies. First parameter is $r$, which is a random number inside (0,1), and the second one is E, which is calculated using Eq. (12).

4.2.1 Soft besiege

When $r \ge 0.5$ and $\left| E \right| \ge 0.5$, the soft besiege phase is selected, and the solution is updated by Eq. (15).

$$ X_{i}^{{{\text{It}} + 1}} = \Delta X^{\text{It}} - E\left| {J \cdot {\text{Best}}X - X_{i}^{\text{It}} } \right| $$

(15)

$$ \Delta X^{\text{It}} = {\text{Best}}X - X_{i}^{\text{It}} $$

(16)

$$ J = 2\left( {1 - r_{5} } \right) $$

(17)

where $r_{5}$ is a random number between $\left[ {0,1} \right]$.

4.2.2 Hard besiege

When $r \ge 0.5$ and $\left| E \right| < 0.5$, the hard besiege phase is used, and the solution is updated by Eq. (18).

$$ X_{i}^{{{\text{It}} + 1}} = {\text{Best}}X - E\left| {\Delta X^{\text{It}} } \right| $$

(18)

4.2.3 Soft besiege with progressive rapid dives

When $r < 0.5$ and $\left| E \right| \ge 0.5$, the third strategy is selected, and the solution is updated using Eq. (19).

$$ X_{i}^{{{\text{It}} + 1}} = \left\{ {\begin{array}{*{20}l} Y & {F\left( Y \right) < F\left( {X_{i}^{\text{It}} } \right)} \\ Z & {F\left( Z \right) < F\left( {X_{i}^{\text{It}} } \right)} \\ \end{array} } \right. $$

(19)

$$ Y = {\text{Best}}X - E\left| {J \cdot {\text{Best}}X - X_{i}^{\text{It}} } \right| $$

(20)

$$ Z = Y + S \times L $$

(21)

$$ LF\left( x \right) = 0.01 \times \frac{u \times \sigma }{{\left| v \right|^{{\frac{1 }{\beta }}} }} $$

(22)

$$ \sigma = \left( {\frac{{ \varGamma \left( {1 + \beta } \right) \times \sin \left( { \frac{\pi \beta }{2} } \right)}}{{\varGamma \left( { \frac{1 + \beta }{2} } \right) \times \beta \times 2\left( {\frac{ \beta - 1 }{2} } \right)}}} \right)^{{\frac{1 }{\beta }}} $$

(23)

where $F$ is the fitness of the given solution, $S$ is a random vector, $L$ is the levy-flight function, $u$ and $v$ are random values in (0,1), and $\beta$ is a constant value of 1.5.

4.2.4 Hard besiege with progressive rapid dives

When $r < 0.5$ and $\left| E \right| < 0.5$, the solution is updated using the last phase, which is modeled by Eq. (24).

$$ X_{i}^{{{\text{It}} + 1}} = \left\{ {\begin{array}{*{20}l} Y & {F\left( Y \right) < F\left( {X_{i}^{\text{It}} } \right)} \\ Z & {F\left( Z \right) < F\left( {X_{i}^{\text{It}} } \right)} \\ \end{array} } \right. $$

(24)

$$ Y = {\text{Best}}X - E\left| {J \cdot {\text{Best}}X - X_{m}^{\text{It}} } \right| $$

(25)

$$ Z = Y + S \times L $$

(26)

where $X_{m}^{\text{It}}$, and $L$ are calculated using Eqs. (14) and (22), respectively. The flowchart of the HHO algorithm is represented in Fig. 3.

Fig. 3

Flowchart of the basic HHO

5 Proposed hybrid multi-population algorithm (HMPA)

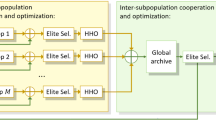
As mention earlier, the main challenge of the meta-heuristic algorithms is enhancing the exploration and exploitation capabilities and balancing them. In addition, providing an approach to avoid or jump out of local optimums is another challenge relevant to the so-called algorithms. In the proposed hybrid multi-population algorithm (HMPA), the whole list of these issues is considered, and a solution is provided for each of them, which are described below in detail. Figure 4 outlines the schematic view of the HMPA.

Fig. 4

Flowchart of HMPA

5.1 Proposed multi-population technique

First, a novel multi-population technique has been utilized to propagate the diversity of solutions. This technique helps to make the solutions more scattered and search for more space of the problem. For this intension, three sub-populations are considered in the proposed method, which exchanges the solutions dynamically. The first sub-population is responsible for independently searching the entire space of the problem, which initially includes 60% of the solutions. This process improves exploration significantly. The solutions in the first sub-population update their position using Eq. (27). Additionally, this equation is used in the initialization phase to initialize the solutions.

$$ {\text{new}}X_{i}^{\text{It}} = {\text{Lb}} + {\text{rand}}\left( {0,1} \right) \times \left( {{\text{Ub}} - {\text{Lb}}} \right) $$

(27)

To make this random search process more efficient, the new solution that is being produced will replace the previous solution only if it has better fitness. The greedy selection mechanism dramatically increases efficiency. Figure 5 presents the pseudo-code of the greedy selection mechanism that is used in HMPA.

Fig. 5

Pseudo-code of the greedy selection mechanism

Moreover, in each $H$ iterations, the best solution of the first sub-population is selected and added to one of the second or third sub-populations. Thenceforth, the selected solution will be eliminated from the first sub-population. In this way, the number of solutions in the first sub-population is reduced, and the solutions for the next two sub-populations increased over time. This makes the algorithm more searchable in the initial iterations and more exploitable in the final iterations.

Afterwards, the remained 40% of initial solutions are divided into two sub-populations equally. The solutions of each sub-population update their positions according to the best solution (local best of the sub-population) and other solutions of the corresponding sub-population. Consequently, the solutions are converged to two different areas, instead of converging only to one point. Besides, there is a counter in the solutions of second and third sub-populations, which counts the unsuccessful updates of the solutions. With this parameter, the trapped solutions in the local optimal points can be detected. The details of this parameter and its effectiveness are entirely stated in our previous work [1]. Similarly, in each $H$ iterations, if the counter of a solution exceeds a threshold (${\text{Thr}}$), and the members of the sub-population (${\text{NM}}$) were more than specified minimum numbers (${\text{MNM}}$), the solution will be transmitted into the first sub-population to reinitialize. Maintaining the minimum number of solutions in the sub-populations are for retaining the successful functioning of the sub-populations. As it is vividly apparent, the size of the sub-populations is changed dynamically, and they can exchange the solutions. Figure 6 illustrates the exchange mechanism between sub-populations.

Fig. 6

Solution exchange mechanism between sub-populations

The solutions of the second and third sub-populations are updated either with AEO or HHO algorithm.

5.2 Quasi-oppositional learning

The quasi-oppositional position technique (QOPP) is used in the HMPA to enhance the searching ability. The QOPP is a learning-based technique, which can improve the searching ability by generating the symmetrical position of a solution [87]. In HMPA, the QOPP has been used only in the autonomous solutions of the first sub-population. The pseudo-code of the QOPP is presented in Fig. 7.

Fig. 7

Pseudo-code of the QOPP

In pseudo-code of Fig. 7, $D$ is the dimension of the problem, and ${\text{QOp}}X_{i}^{\text{It}}$ is the quasi-opposite position of $X_{i}^{\text{It}}$. In addition, as shown in Fig. 4, after generating new solutions using the QOPP, the greedy selection mechanism is used yet again.

5.3 Chaotic local search strategy

Chaotic local search (CLS) strategy explores the nearby of a solution to discover promising areas [69]. Therefore, this strategy enhances exploitation capability. Besides, taking advantages of chaos theory increases the potency of the strategy. In HMPA, the CLS strategy is just applied to the local best of the sub-populations. In this way, only around the best solutions will be explored, and the execution time will be reduced. In the CLS, a new local best solution can be calculated using Eq. (28).

$$ {\text{newBest}}X = {\text{Best}}X + \left( {{\text{CV}}^{k + 1} - 0.5} \right) \times \left( {X_{r1}^{\text{It}} - X_{r2}^{\text{It}} } \right) $$

(28)

where $X_{r1}^{\text{It}}$ and $X_{r2}^{\text{It}}$ are two randomly selected solutions from the corresponding sub-population, and ${\text{CV}}^{k + 1}$ is the chaotic value generated by the chaotic map. In the HMPA, the piecewise map has been selected as the chaotic map, which is a well-known chaotic map and generates random numbers between (0,1). The piecewise chaotic map is modeled mathematically as below:

$$ {\text{CV}}^{k + 1} = \left\{ {\begin{array}{*{20}l} {\frac{{{\text{CV}}^{k} }}{P}} & {0 \le {\text{CV}}^{k} \le P} \\ {\frac{{{\text{CV}}^{k} - P}}{0.5 - P}} & {P \le {\text{CV}}^{k} < 0.5} \\ {\frac{{1 - P - {\text{CV}}^{k} }}{0.5 - P}} & {0.5 \le {\text{CV}}^{k} < 1 - P} \\ {\frac{{1 - {\text{CV}}^{k} }}{P}} & {1 - P \le {\text{CV}}^{k} < 1} \\ \end{array} } \right. $$

(29)

P = 0.4

Figure 8 shows the distribution of the piecewise map over time.

Fig. 8

Distribution of the piecewise map over time

Similarly, the pseudo-code of the CLS strategy is provided in Fig. 9.

Fig. 9

Pseudo-code of the CLS strategy

After producing a new local best using the proposed CLS strategy, the greedy selection mechanism is used to increase profitability.

5.4 Proposed levy-flight function (PLF)

The levy-flight random walk function has been introduced earlier in Sect. 4 in the HHO algorithm. The levy-flight random walk is an advantageous approach to enhance the performance of the algorithms by increasing exploitation. This approach has been used in the state-of-the-art algorithms in various ways. In HMPA, this approach is used in a novel way, as illustrated in Fig. 10.

Fig. 10

Proposed levy-flight function (PLF)

In the PLF, the first command can speed up the convergence, and the second command improves the exploitation capability. Additionally, ${\text{LF}}$ is the value obtained by the Eq. (22).

5.5 Proposed local search mechanism (PLS)

To increase the searching strength of the HMPA, a local search mechanism denoted as PLS is also proposed, which searches the space between solutions of the sub-population more accurately to discover better solutions. In PLS, a new solution is generated using Eq. (30).

$$ X_{i}^{{{\text{It}} + 1}} = \left\{ {\begin{array}{*{20}l} {X_{i}^{\text{It}} + \mu \cdot \left( {X_{i}^{\text{It}} - X_{j}^{\text{It}} } \right)} & {\delta < {\text{CP}}2} \\ {X_{i}^{\text{It}} + \mu \cdot \left( {{\text{Best}}X - NX} \right)} & {\text{otherwise}} \\ \end{array} } \right. $$

(30)

where $\mu$ is coefficient between $\left( { - L, + L} \right)$, $L$ and $\delta$ are random numbers in (0,1), $X_{j}^{\text{It}}$ is a randomly chosen solution from the sub-population, ${\text{CP}}2$ is a control parameter with a value of 0.5, and $NX$ is a solution vector produced by Eq. (27). The pseudo-code of the PLS is provided in Fig. 11.

Fig. 11

Proposed local search mechanism (PLS)

5.6 Computational complexity

In this subsection, the computational complexity of HMPA is discussed in terms of time complexity on three main process of the algorithm: initialization, fitness evaluation, and updating phase.

The complexity of the initialization phase is $O\left( N \right)$, where $N$ is the total number of solutions. The evaluating fitness of solutions requires $O\left( {T \times \left( {N \times N + 3 \times K} \right)} \right)$ time, since the fitness of each solution is evaluated twice in each iteration, and three local best solutions are evaluated $K$ times in each iteration. The $T$ is the maximum number of iterations.

The updating phase of the proposed algorithm is consisting of three branches; therefore, the complexity of the updating phase is discussed for each branch.

The complexity of the first branch is $O\left( {T \times \left( {N_{1} + D \times N_{1} + K} \right)} \right),$ which $N_{1}$ is the number of solutions in the first sub-population, and $D$ indicates the dimension of the problem.

For the second and third branches the approximate complexity must be expressed, since the ${\text{AEO}}$ or ${\text{HHO}}$, and ${\text{PLS}}$ or ${\text{PLF}}$ algorithms are selected randomly in each iteration. The approximate complexity of the second and third branches are $O\left( {T \times (N_{2} \times (A_{1} + A_{2} } \right) + K))$ and $O\left( {T \times (N_{3} \times (A_{1} + A_{2} } \right) + K))$, respectively. Where, $A_{1}$ is the average complexity of ${\text{HHO}}$ and ${\text{AEO}}$ algorithms, $A_{2}$ is the average complexity of ${\text{PLS}}$ and ${\text{PLF}}$ methods, $N_{2}$ and $N_{3}$ are the number of solutions in the second and third sub-populations, respectively. The complexity of ${\text{PLS}}$ is $O\left( {N_{n} } \right)$, ${\text{PLF}}$ is $O\left( 1 \right)$, ${\text{HHO}}$ is $O\left( {N \times \left( {T + T \times D + 1} \right)} \right)$, and ${\text{AEO}}$ is $O\left( {T \times N \times N} \right)$. It is worth to mention that $\mathop \sum \limits_{n = 1}^{3} N_{n} = N$.

6 Experimental results

To substantiate the superiority of the proposed HMPA, the performance of HMPA is evaluated on fifty widely-used test functions comprising unimodal, multimodal, fix-dimension, shifted rotated, hybrid, and composite functions. The results of the HMPA is compared with several state-of-the-art meta-heuristic algorithms in terms of the best, worst, median, average, standard deviation, average execution time (AET) in second, and box plot metrics over the results of 30 independent executions. Furthermore, the convergence speed of the algorithms is compared graphically. Moreover, the Wilcoxon signed-rank test is used to prove the supremacy of HMPA. The R column in the tables of Wilcoxon signed-rank test presents the result of the test, which ‘ + ’, ‘− show the HMPA is significantly is better, or worse than the competitor algorithm, respectively. When the results of the algorithms are equal or very close to each other, the difference between algorithms cannot be determined using this test (The ‘ = ’ sign in R column).

Harris hawks optimization (HHO) [32], artificial ecosystem-based optimization (AEO) [31], spotted hyena optimizer (SHO) [88], farmland fertility algorithm (FFA) [89], Salp swarm algorithm (SSA) [90], moth-flame optimization (MFO) [91], and antlion optimizer (ALO) [92] have been selected as competitor algorithms. The number of solutions in the algorithms is set to 50, and stopping criteria in them is considered to reach 1000 rounds of iteration. The values of other parameters of these algorithms are presented in Table 1, which are the default values proposed by the authors in the original papers.

Table 1 Parameter values of the algorithms

The specifications of the system by which the experiments are conducted are shown in Table 2.

Table 2 Running platform specifications

6.1 Experiments on unimodal test functions

In this subsection, the performance of the HMPA is evaluated on a set of standard unimodal test functions illustrated in Table 3. These test functions challenge the exploitation capability of the algorithms and categorized into separable and non-separable functions. The statistical results of the algorithms on unimodal test functions are specified in Table 4.

Table 3 Details of the unimodal test functions

Table 4 Statistical results obtained by the algorithms on the unimodal test functions

According to Table 4, the proposed HMPA has achieved better results on all unimodal test functions. To further evaluate the obtained results, the box plot metric is used, and the graphical results are provided in Fig. 12.

Fig. 12

Box plots of the obtained results from the algorithms on the unimodal test functions

According to Table 4, the proposed HMPA has achieved better results on all unimodal test functions. To further evaluate the obtained results, the box plot metric is used, and the graphical results are provided in Fig. 12.

Figure 12 states that the HMPA has reached better and more coherent results in the independent runs. The convergence rate of algorithms is also significant in evaluating the efficiency of optimization algorithms. Figure 13 represents the convergence rates comparison of the algorithms visually.

Fig. 13

Convergence graphs of the algorithms on the unimodal test functions

Figure 13 expresses the HMPA started with better solutions and converged quickly in the early iterations. Moreover, the Wilcoxon signed-rank test is performed on the HMPA versus other competitor algorithms, and the results are provided in Table 5 for investigating the significant differences among the algorithms.

Table 5 Wilcoxon signed-rank test results of the HMPA versus the competitor algorithms with 5% significance level on the unimodal test functions

The p-values presented in Table 5 declare that the HMPA has a significant difference with other algorithms on all test functions, except on TF1-TF4 with SHO, and TF1-TF2 with AEO algorithms.

6.2 Experiments on multimodal test functions

This subsection evaluates the performance of the HMPA on six widely used standard multimodal test functions. The multimodal test functions are demonstrated in Table 6.

Table 6 Details of the multimodal test functions

These test functions have a lot of local optima points and challenge the exploration capability of the algorithm. The statistical results of the algorithms on multimodal test functions are presented in Table 7.

Table 7 Statistical results obtained by the algorithms on the multimodal test functions

As it is evident from the results of Table 7, the HMPA attained better results in all test functions. For further in-depth scrutinizing the obtained results of the algorithms on multimodal test functions, the box plot graphs are plotted and shown in Fig. 14.

Fig. 14

Box plots of the obtained results from the algorithms on the multimodal test functions

As depicted in the diagrams of Fig. 14, unlike other algorithms that have diverse results in each execution, the obtained results in the proposed algorithm are closer to each other. In addition, the comparisons of the convergence rate of the algorithms are provided in Fig. 15.

Fig. 15

Convergence graphs of the algorithms on the multimodal test functions

The graphs of Fig. 15 represent that the HMPA is converged with more agility than other competitor algorithms in all multimodal test functions. Besides, the results of algorithms are further investigated statistically by the nonparametric Wilcoxon signed-rank test, and the consequence is presented in Table 8.

Table 8 Wilcoxon signed-rank test results of the HMPA versus the competitor algorithms with 5% significance level on the multimodal test functions

As it is evident from Table 8, the HMPA has a significant difference from other algorithms, except in TF9-TF11 from HHO, SHO, and AEO algorithms. Although the results of the algorithms are similar, considering the convergence rate of the algorithms, it can be inferred that the HMPA is premier than the other algorithms in all multimodal test functions.

6.3 Experiments on fix-dimension test functions

Fix-dimension test functions are kind of standard test functions with constant and unchangeable dimensions. This subsection presents the results of experiments on ten well-known fix-dimension test functions. The details of the test functions are provided in Table 9.

Table 9 Details of the fixed-dimension test functions

Similarly, the statistics of the obtained results by the algorithms on these test functions are presented in Table 10.

Table 10 Statistical results obtained by the algorithms on the fix-dimension test functions

The statistical results presented in Table 10 indicate that the HMPA algorithm outperforms the competitor algorithms. Additionally, the box plot graphs of the algorithms on fix-dimension test functions are depicted in Fig. 16.

Fig. 16

Box plots of the obtained results from the algorithms on the fix-dimension test functions

The box plots of Fig. 16 affirm the authenticity of the statistical results of the algorithms. Moreover, the convergence speeds of the algorithms are examined on fix-dimension test functions, and the results are illustrated in Fig. 17. Likewise, the non-parametric Wilcoxon signed-rank test results are provided in Table 11 to investigate the possible superiority of the HMPA with further confidence.

Fig. 17

Convergence graphs of the algorithms on the fix-dimension test functions

Table 11 Wilcoxon signed-rank test results of the HMPA versus the competitor algorithms with 5% significance level on the fix-dimension test functions

6.4 Experiments on CEC 2017 test functions

These test functions are the most complicated test functions, which comprise three categories: shifted and rotated hybrid, and composite. Shifted and rotated test functions are the result of rotating the optimal points around a particular axis, which complicates the optimization process. Hybrid and composite test functions are the results of combining several test functions. To achieve satisfactory results in these test functions, the algorithms must have superior exploitation and exploration capabilities along with local optima avoidance ability. CEC 2017 includes twenty-nine single-objective test functions, which the second and twenty-second test functions have been removed in the recent update [93]. The brief description of CEC 2017 test functions is presented in Table 12. Similar to the previous subsections, the statistical results of the algorithms are provided in Table 13.

Table 12 Brief description of CEC 2017 test functions

Table 13 Statistical results obtained by the algorithms on CEC 2017 test functions

In line with the statistics presented in Table 13, the HMPA found better solutions for all CEC 2017 test functions. The box plot graphs are depicted in Fig. 18 for additional examination.

Fig. 18

Box plots of the obtained results from the algorithms on CEC 2017 test functions

The box plots of Fig. 18 confirm the statistical results of Table 13 and expose the superiority of the HMPA. Besides, Box charts show that the HMPA is less dependent on the initial solutions, and it demonstrated better achievements than the rest of the algorithms. Likewise, the convergence speeds of the algorithms are compared, and the results are established in Fig. 19.

Fig. 19

Convergence graphs of the algorithms on CEC 2017 test functions

The graphs of Fig. 19 indicate that the HMPA outperforms the other comparative algorithms in terms of convergence rate, in all CEC 2017 test functions except TF32. In addition, it can be inferred that HMPA has the ability to go out of the local optimum points. Besides, the results of the Wilcoxon signed-rank test on these test functions are disclosed in Table 14.

Table 14 Wilcoxon signed-rank test results of the HMPA versus the competitor algorithms with 5% significance level on CEC 2017 test functions

Drawing on the results of Figs. 18, 19, and Tables 13, 14, it can be concluded that the HMPA could find optimal or near-optimal solutions for CEC 2017 test functions, and have a significant difference from other representative algorithms.

According to the results of experiments on the vast set of test functions, it can be concluded that the HMPA outperforms in all test functions.

7 Real-world engineering applications

To further investigate the superiority of the HMPA, in this section, the algorithms have been utilized to solve real-life engineering problems. For this purpose, the algorithms are applied to seven constrained and unconstrained real-world engineering problems of minimization and maximization nature. Besides, the results of HMPA is compared statistically with the results of the algorithms used in Sect. 6, as well as Tree Seed Algorithm (TSA) [95], Manta Ray Foraging Optimization (MRFO) [8], Sine Cosine Algorithm (SCA) [96], and Whale Optimization Algorithm (WOA) [97]. The values of the parameters of the algorithms are provided in Table 1. It is worth mentioning that, in the constrained engineering problems, the death penalty mechanism is utilized as a constraint handling method, in which a considerable positive/negative number is added to the objective value as a penalty. As a result, the infeasible solutions would be rejected.

7.1 Welded beam design problem

The welded beam design problem is a constrained optimization problem, the objective of which is to minimize the fabrication cost of welding. The constraints are shear stress (τ) and bending stress (θ) in the beam, buckling load ($P_{\text{c}}$) on the bar, and deflection (δ) of the beam. Additionally, the thickness of the weld (h), length of the clamped bar (l), height of the bar (t), and thickness of the bar (b) are the design variables of the problem. The welded beam design problem is illustrated in Fig. 20.

Fig. 20

Welded beam design problem

Below is outlined the problem’s constraints as well as mathematical formulation.Consider:

$$ \vec{v} = \left[ {v_{1} v_{2} v_{3} v_{4} } \right] = \left[ {h l t b} \right], $$

Minimize:

$$ f\left( {\vec{v}} \right) = 1.10471v_{1}^{2} v_{2} + 0.04811v_{3} v_{4} \left( {14.0 + v_{2} } \right), $$

Subject to:

$$ c_{1} \left( {\vec{v}} \right) = \tau \left( {\vec{v}} \right) - \tau_{ \hbox{max} } \le 0, $$

$$ c_{2} \left( {\vec{v}} \right) = \sigma \left( {\vec{v}} \right) - \sigma_{ \hbox{max} } \le 0, $$

$$ c_{3} \left( {\vec{v}} \right)v = \delta \left( v \right) - \delta_{ \hbox{max} } \le 0, $$

$$ c_{4} \left( {\vec{v}} \right) = v_{1} - v_{4} \le 0, $$

$$ c_{5} \left( {\vec{v}} \right) = P - P_{\text{c}} \left( {\vec{v}} \right) \le 0, $$

$$ c_{6} \left( {\vec{v}} \right) = 0.125 - v_{1} \le 0, $$

$$ c_{7} \left( {\vec{v}} \right) = 1.10471v_{1}^{2} + 0.04811v_{3} v_{4} \left( {14.0 + v_{2} } \right) - 5.0 \le 0, $$

where $0.1 \le v_{1} \le 2$, $0.1 \le v_{2} \le 10$, $0.1 \le v_{3} \le 10$, $0.1 \le v_{4} \le 2$,

$$ \tau \left( {\vec{v}} \right) = \sqrt {\left( {\tau^{\prime}} \right)^{2} + 2\tau^{\prime}\tau^{\prime\prime}\frac{{v_{2} }}{2R} + \left( {\tau^{\prime\prime}} \right)^{2} } , $$

(31)

$$ \tau^{\prime} = \frac{P}{{\sqrt 2 v_{1} v_{2} }}, $$

$$ \tau^{\prime\prime} = \frac{\text{MR}}{J}, $$

$$ M = P\left( {L + \frac{{v_{2} }}{2}} \right), $$

$$ R = \sqrt {\frac{{v_{2}^{2} }}{4} + \left( {\frac{{v_{1} + v_{3} }}{2}} \right)^{2} } , $$

$$ J = 2\left\{ {\sqrt 2 v_{1} v_{2} \left[ {\frac{{v_{2}^{2} }}{4} + \left( {\frac{{v_{1} + v_{3} }}{2}} \right)^{2} } \right]} \right\}, $$

$$ \sigma \left( {\vec{v}} \right) = \frac{6PL}{{v_{4} v_{3}^{2} }}, $$

$$ \delta \left( {\vec{v}} \right) = \frac{{6PL^{3} }}{{Ev_{3}^{3} v_{4} }}, $$

$$ P_{\text{c}} \left( {\vec{v}} \right) = \frac{{4.013E\sqrt {\frac{{v_{3}^{2} v_{4}^{6} }}{36}} }}{{L^{2} }} \left( {1 - \frac{{v_{3} }}{2L}\sqrt {\frac{E}{4G}} } \right),\;\;P = 6000\;{\text{lb}}., $$

$L = 14$ inch, $E = 30 \times 10^{6}$ psi, $G = 12 \times 10^{6}$ psi, $\delta_{ \hbox{max} } = 0.25$ inch, $\tau_{ \hbox{max} } = 13,600$ psi, $\sigma_{ \hbox{max} } = 30,000$ psi.

In Table 15, the statistical analysis of the algorithms is conveyed. Moreover, the best points and their corresponding fitness values obtained by the algorithms on this problem are provided in Table 16.

Table 15 Statistical results of the algorithms on the welded beam design problem

Table 16 The best-obtained results on the welded beam design problem

For further comparison of the algorithms, the convergence rates of the algorithms are plotted in Fig. 21.

Fig. 21

Convergence graphs of the algorithms on the welded beam design problem

In view of the attained outcomes, HMPA outstrips other competitor algorithms.

7.2 Speed reducer design problem

This subsection describes the speed reducer design problem with the objective of minimizing the weight of reducer. The speed reducer design problem is a constrained mixed-integer optimization problem and has seven design variables: face width (b), the module of teeth (m), number of teeth in the pinion (z), length of the first shaft between bearings ($l_{1}$), length of the second shaft between bearings ($l_{2}$), the diameter of first shafts ($d_{1}$), and the diameter of the second shafts ($d_{2}$). The constraints of this problem are bending stress of the gear teeth, surface stress, transverse deflections of the shafts, and stresses in the shafts. The schematic view of this problem is represented in Fig. 22.

Fig. 22

Speed reducer design problem

The constraints and the mathematical formulation of the problem are as follows:

Consider:

$$ \vec{v} = \left[ {v_{1} ,v_{2} ,v_{3} ,v_{4} ,v_{5} ,v_{6} ,v_{7} } \right] = \left[ {b,m,z,l_{1} ,l_{2} ,d_{1} ,d_{2} } \right], $$

Minimize:

$$ \begin{aligned} f\left( {\vec{V}} \right) = & 0.7854v_{1} v_{2}^{2} (3.3333v_{3}^{2} + 14.9334v_{3} - 43.0934) \\ & - 1.508v_{1} \left( {v_{6}^{2} + v_{7}^{2} } \right) + 7.4777\left( {v_{6}^{3} + v_{7}^{3} } \right) + 0.7854\left( {v_{4} v_{6}^{2} + v_{5} v_{7}^{2} } \right), \\ \end{aligned} $$

Subject to:

$$ c_{21} \left( {\vec{v}} \right) = \frac{27}{{v_{1} v_{2}^{2} v_{3} }} - 1 \le 0, $$

$$ c_{2} \left( {\vec{v}} \right) = \frac{397.5}{{v_{1} v_{2}^{2} v_{3}^{3} }} - 1 \le 0, $$

$$ c_{3} \left( {\vec{v}} \right) = \frac{{1.93v_{4}^{3} }}{{v_{2} v_{6}^{4} v_{3} }} - 1 \le 0, $$

$$ c_{4} \left( {\vec{v}} \right) = \frac{{1.93v_{5}^{3} }}{{v_{2} v_{7}^{4} v_{3} }} - 1 \le 0, $$

$$ c_{5} \left( {\vec{v}} \right) = \frac{{\left[ {\left( {745\left( {v_{4} /v_{2} v_{3} } \right)} \right)^{2} + 16.9 \times 10^{6} } \right]^{0.5} }}{{110v_{6}^{3} }} - 1 \le 0, $$

$$ c_{6} \left( {\vec{v}} \right) = \frac{{\left[ {\left( {745\left( {v_{5} /v_{2} v_{3} } \right)} \right)^{2} + 1575 \times 10^{5} } \right]^{0.5} }}{{110v_{7}^{3} }} - 1 \le 0, $$

$$ c_{7} \left( {\vec{v}} \right) = \frac{{v_{2} v_{3} }}{40} - 1 \le 0, $$

$$ c_{8} \left( {\vec{v}} \right) = \frac{{5v_{2} }}{{v_{1} }} - 1 \le 0, $$

$$ c_{9} \left( {\vec{v}} \right) = \frac{{v_{1} }}{{12v_{2} }} - 1 \le 0, $$

$$ c_{10} \left( {\vec{v}} \right) = \frac{{1.5v_{6} + 1.9}}{{v_{4} }} - 1 \le 0, $$

$$ c_{11} \left( {\vec{v}} \right) = \frac{{1.1v_{7} + 1.9}}{{v_{5} }} - 1 \le 0, $$

(32)

where $2.6 \le v_{1} \le 3.6$, $7.3 \le v_{5} \le 8.3$, $0.7 \le v_{2} \le 0.8$, $2.9 \le v_{6} \le 3.9$, $17 \le v_{3} \le 28$, $5.0 \le v_{7} \le 5.5$, $7.3 \le v_{4} \le 8.3$.

The statistical results of the algorithms on the speed reducer design problem are presented in Table 17. Besides, the best-obtained points are represented in Table 18, and the convergence graphs of the algorithms are illustrated in Fig. 23.

Table 17 Statistical results of the algorithms on the speed reducer design problem

Table 18 The best-obtained results of the algorithms on the speed reducer design problem

Fig. 23

Convergence graphs of the algorithms on the speed reducer design problem

As reported in Tables 17, 18, and Fig. 23, the HMPA algorithm outdid the other algorithms.

7.3 Pressure vessel design problem

The third constrained problem is the pressure vessel design problem, which tries to minimize the costs of material, forming, and welding of a cylindrical vessel. The design variables of this problem are: the thickness of the shell ($T_{\text{s}}$), the thickness of the head ($T_{\text{h}}$), inner radius ($R$), and length of the cylindrical section without the head ($L$). The pressure vessel, along with the design variables, has been presented in Fig. 24.

Fig. 24

Pressure vessel design problem

The constraints and the mathematical formulation of the problem are as follows:Consider:

$$ \vec{v} = \left[ {v_{1} ,v_{2} ,v_{3} ,v_{4} } \right] = \left[ {T_{s} ,T_{h} ,R,L} \right], $$

Minimize:

$$ f\left( {\vec{v}} \right) = 0.6224v_{1} v_{3} v_{4} + 1.7781v_{2} v_{3}^{2} + 3.1661v_{1}^{2} v_{4} + 19.84v_{1}^{2} v_{3} , $$

Subject to:

$$ c_{1} \left( {\vec{v}} \right) = - v_{1} + 0.0193v_{3} \le 0, $$

$$ c_{2} \left( {\vec{v}} \right) = - v_{3} + 0.00954v_{3} \le 0, $$

$$ c_{3} \left( {\vec{v}} \right) = - \pi v_{3}^{2} v_{4} - \frac{4}{3}\pi v_{3}^{3} + 1,296,000 \le 0, $$

$$ c_{4} \left( {\vec{v}} \right) = v_{4} - 240 \le 0, $$

(33)

where $0 \le v_{1} \le 99$, $0 \le v_{2} \le 99$, $10 \le v_{3} \le 200$, $10 \le v_{4} \le 200$.

The obtained results on this problem are presented statistically in Table 19, and the best solutions found by the algorithms are provided in Table 20. Besides, the convergence graphs of the algorithms are shown in Fig. 25.

Table 19 Statistical results of the algorithms on the pressure vessel design problem

Table 20 The best-obtained results on the pressure vessel design problem

Fig. 25

Convergence graphs of the algorithms on the speed reducer design problem

The results show that the HMPA algorithm obtained better results, and converged more quickly in comparison with other algorithms.

7.4 Tension/compression spring design problem

The tension/compression spring design problem is another constrained engineering problem to minimize tension/compression spring weight. There are three design variables in this problem: wire diameter (d), mean coil diameter (D), and the number of active coils (P), which have been shown in Fig. 26.

Fig. 26

Tension/compression spring design problem

The constraints and the mathematical formulation of the problem are as below:Consider:

$$ \vec{v} = \left[ {v_{1} ,v_{2} ,v_{3} } \right] = \left[ {d,D,P} \right], $$

Minimize:

$$ f\left( {\vec{v}} \right) = \left( {v_{3} + 2} \right)v_{2} v_{1}^{2} , $$

Subject to:

$$ c_{1} \left( {\vec{v}} \right) = 1 - \frac{{v_{2}^{3} v_{3} }}{{71785v_{1}^{4} }} \le 0, $$

$$ c_{2} \left( {\vec{v}} \right) = \frac{{4v_{2}^{2} - v_{1} v_{2} }}{{12,566\left( {v_{2} v_{1}^{3} - v_{1}^{4} } \right)}} + \frac{1}{{5108v_{1}^{2} }} \le 0, $$

$$ c_{3} \left( {\vec{v}} \right) = 1 - \frac{{140.45v_{1} }}{{v_{2}^{2} v_{3} }} \le 0, $$

$$ c_{4} \left( {\vec{v}} \right) = \frac{{v_{1} + v_{2} }}{1.5} - 1 \le 0, $$

(34)

where $0.05 \le v_{1} \le 2.0$, $0.25 \le v_{2} \le 1.3$, $2.0 \le v_{3} \le 15.0$.

Tables 21 and 22 give the statistical results and the best points obtained by the algorithms, respectively. Furthermore, Fig. 27 depicts the convergence graphs of the algorithms.

Table 21 Statistical results of the algorithms on the tension/compression spring design problem

Table 22 The best-obtained results of the algorithms on the tension/compression spring design problem

Fig. 27

Convergence graphs of the algorithms on the tension/compression spring design problem

The results state that HMPA is the preeminent algorithm among the competitor algorithms.

7.5 Gear train design problem

Gear train design problem is an unconstrained real-life engineering problem with the aim of finding the optimal number of teeth in the gears between the driver and driveshafts. As depicted in Fig. 28, this problem has four gears:$T_{\text{d}}$, $T_{\text{b}}$, $T_{\text{a}}$, and $T_{\text{f}}$. It is evident that the number of teeth in the gears must be an integer.

Fig. 28

Gear train design problem

The objective and mathematical formulation of this problem are as follows:Consider:

$$ \vec{v} = \left[ {v_{1} ,v_{2} ,v_{3} ,v_{4} } \right] = \left[ {T_{\text{d}} , T_{\text{b}} , T_{\text{a}} , T_{\text{f}} } \right], $$

Objective is to minimize:

$$ f\left( {\vec{v}} \right) = \left[ {\frac{1}{6.931} - \frac{{v_{1} v_{2} }}{{v_{3} v_{4} }}} \right]^{2} , $$

(35)

where $12 \le v_{1} \le 60$, $12 \le v_{2} \le 60$, $12 \le v_{3} \le 60$, $12 \le v_{4} \le 60$.

The statistical results of the algorithms and the best solutions are expressed in Table 23 and Table 24, respectively. In addition, the result of convergence evaluation is illustrated in Fig. 29.

Table 23 Statistical results of the algorithms on the gear train design problem

Table 24 The best obtained results of the algorithms on the gear train design problem

Fig. 29

Convergence graphs of the algorithms on the gear train design problem

The results demonstrate that the HMPA has been more triumphant in solving gear train design problem.

7.6 Spread spectrum radar poly-phase design problem

Spread spectrum radar poly-phase design problem is a complex continuous optimization problem to minimize the envelope module of the compressed radar pulse at the receiver output. The objective and the mathematical formulation of this problem are as below:Objective is to minimize:

$$ F\left( {\vec{v}} \right) = { \hbox{max} }\left\{ {f_{1} \left( {\vec{v}} \right), f_{2} \left( {\vec{v}} \right), \ldots ,f_{2m} \left( {\vec{v}} \right)} \right\}, $$

(36)

where $N = 10$, $m = 2N - 1$, $\vec{v} = \left( {v_{1} ,v_{2} , \ldots ,v_{N} } \right) \in R^{N} | 0 \le v_{i} \le 2\pi , i = 1,2, \ldots ,N$, $f_{2i - 1} \left( {\vec{v}} \right) = \mathop \sum \limits_{j = i}^{N} \cos \mathop \sum \limits_{{k = \left| {2i - j - 1} \right| + 1}}^{j} v_{k} , i = 1,2, \ldots ,N$, $f_{2i} \left( {\vec{v}} \right) = 0.5\mathop \sum \limits_{j = i + 1}^{N} \cos \mathop \sum \limits_{{k = \left| {2i - j} \right| + 1}}^{j} v_{k}$, $i = 1,2, \ldots ,N - 1$, $f_{m + i} \left( {\vec{v}} \right) = - f_{i} \left( {\vec{v}} \right) ,\;\; i = 1,2, \ldots ,m$.

Tables 25 and 26 represent the statistical results, and the solutions found by the algorithms, respectively. Figure 30 presents the convergence rates of the algorithms on this problem.

Table 25 Statistical results of the algorithms on the spread spectrum radar poly-phase code design problem

Table 26 The best-obtained results of the algorithms on spread spectrum radar poly-phase code design problem

Fig. 30

Convergence graphs of the algorithms on the spread spectrum radar poly-phase code design problem

It can be inferred from the statistical results of Tables 25 and 26 that the HMPA obtained better results, and considering the graphs of Fig. 30, the HMPA converged prier competitor algorithms.

7.7 Optimal thermo-hydraulic performance of an artificially roughened air heater problem

In this subsection, the performance of the algorithms is tested on a maximization problem, contrariwise, other subsections that deal with minimization issues. Optimal thermo-hydraulic performance of an artificially roughened air heater problem is a maximization design problem intended to maximize the heat transfer rate and maintaining the slightest amount of frictions losses. This problem consists of three variables: relative roughness pitch (p/e), relative roughness height (e/D), and Reynolds number (Re) that have been illustrated in Fig. 31.

Fig. 31

Optimal thermo-hydraulic performance of an artificially roughened air heater problem

The objective and the mathematical formulation of this problem are as below:Consider:

$$ \vec{v} = \left[ {v_{1} ,v_{2} ,v_{3} } \right] = \left[ {e/D, p/e, {\text{Re}}} \right], $$

Objective is to maximize:

$$ \eta = 2.51 \ln (e^{ + } ) + 5.5 - 0.1R_{\text{M}} - G_{\text{H}} , $$

where $R_{\text{M}} = 0.95v_{2}^{0.53}$, $G_{\text{H}} = 4.5\left( {e^{ + } } \right)^{0.28} \left( {0.7} \right)^{0.57}$, $e^{ + } = v_{1} v_{3} \sqrt {\frac{{\overline{f} }}{2}}$, $\overline{f} = \frac{{f_{\text{s}} + f_{\text{r}} }}{2}$, $f_{\text{s}} = 0.079v_{3}^{ - 0.25}$, $f_{\text{r}} = \frac{2}{{\left( {0.95v_{3}^{0.53} + 2.5 \ln \left( {\frac{1}{2}v_{1} } \right)^{2} - 3.75} \right)^{2} }}$, $0.02 \le v_{1} \le 0.8$, $10 \le v_{2} \le 40$, $3000 \le v_{3} \le 20000$.

Analogously, the statistical results are written in Table 27, and the best-obtained solutions are provided in Table 28. Furthermore, the convergence graphs are illustrated in Fig. 32.

Table 27 Statistical results of the algorithms on optimal thermo-hydraulic performance of an artificially roughened air heater problem

Table 28 The best-obtained results of the algorithms on optimal thermo-hydraulic performance of an artificially roughened air heater problem

Fig. 32

Convergence graphs of the algorithms on the optimal thermo-hydraulic performance of an artificially roughened air heater problem

According to the statistical results, it can be subsumed that most of the algorithms obtained optimal solution of the problem, and their results are close to each other. Similarly, given Fig. 32, the convergence rate of HMPA is relatively frail than several competitor algorithms.

8 Conclusion and future perspectives

This paper presents an innovative hybrid multi-population algorithm called HMPA. In HMPA, the initial population is portioned into three sub-population. The sub-populations use an information exchange method to trade the solutions according to the

predefined principles. Furthermore, artificial ecosystem-based optimization (AEO), and Harris Hawks optimization (HHO) algorithms, which are the most recently developed powerful population-based optimization algorithms, are utilized in a hybrid model. Afterwards, some enhancement techniques are appended to the proposed framework to increase the potencies of the different aspects of the algorithm. In each round, solutions of the sub-populations are updated by only two techniques.

The HMPA is tested on fifty test functions, and the results are compared statistically and visually with well-known state-of-the-art algorithms. The experimental results reveal that the HMPA has extraordinary exploitation, exploration, and local optima departure capabilities. Moreover, the obtained results are inferentially corroborated using a nonparametric test called the Wilcoxon signed-rank test to investigate the conjectured dominance of the HMPA. The test divulges that the HMPA has a significant difference with the competitor algorithms.

In addition, HMPA is applied to seven constrained and unconstrained real-world engineering problems for further investigation of HMPA’s performance. The results demonstrated that HMPA could solve real-life problems more efficiently.

It is a question of future research to investigate the discretization and binarization of the HMPA. Besides, the HMPA can be extended to solve multi-objective problems.