The parameterized level set method for structural topology optimization with shape sensitivity constraint factor

Abstract

In recent years, the parameterized level set method (PLSM) has attracted widespread attention for its good stability, high efficiency and the smooth result of topology optimization compared with the conventional level set method. In the PLSM, the radial basis functions (RBFs) are often used to perform interpolation fitting for the conventional level set equation, thereby transforming the iteratively updating partial differential equation (PDE) into ordinary differential equations (ODEs). Hence, the RBFs play a key role in improving efficiency, accuracy and stability of the numerical computation in the PLSM for structural topology optimization, which can describe the structural topology and its change in the optimization process. In particular, the compactly supported radial basis function (CS-RBF) has been widely used in the PLSM for structural topology optimization because it enjoys considerable advantages. In this work, based on the CS-RBF, we propose a PLSM for structural topology optimization by adding the shape sensitivity constraint factor to control the step length in the iterations while updating the design variables with the method of moving asymptote (MMA). With the shape sensitivity constraint factor, the updating step length is changeable and controllable in the iterative process of MMA algorithm so as to increase the optimization speed. Therefore, the efficiency and stability of structural topology optimization can be improved by this method. The feasibility and effectiveness of this method are demonstrated by several typical numerical examples involving topology optimization of single-material and multi-material structures.

1 Introduction

As an effective and powerful design tool, structural topology optimization is to find the optimal material distribution within a certain design domain by minimizing or maximizing the objective function and satisfying the prescribed constraint and boundary conditions. Since the homogenization method for the topology optimization of linearly elastic structures was proposed by Bendsøe and Kikuchi in 1988 [1], the theory on topology optimization of continuum structure has developed rapidly. A number of methods for structural topology optimization have been proposed correspondingly and grown in popularity thereupon. For the topology optimization of continuum structure, the methods can be mainly divided into the following categories: the homogenization method [1]; the density-based method [2,3,4]; the level set method [5,6,7,8]; the phase-field method [9]; the evolutionary optimization method [10] and so on. Among them, the level set method can well deal with relatively complex structural boundaries, thereby becoming a hot research spot in recent years.

The level set method was first applied to topology optimization design by Osher and Sethian in 1988 [11], and then Allaire et al. proposed the level set method combined with shape derivative to solve the shape and topology optimization problem in 2004 [6]. In the level set topology optimization algorithm, representation of the level set equation and the filtering scheme of sensitivity plays a decisive role in the optimization effectiveness. Thus, selecting an appropriate representation of the level set equation and the corresponding scheme of sensitivity filtering has been becoming a hot research direction in recent years. In the conventional level set strategy for dealing with topology optimization, the level set function needs reinitializing frequently to maintain a signed distance function, which gives the shortest distance to the nearest point on the interface, using a PDE(partial differential equation)-based method [12] or a fast marching method [13], [14]. The re-initialization is an important process in the conventional level set method to keep the gradient norm of level set function constant and make the evolution process stable.

Another issue of the conventional level set method is lack of the capacity to create new holes inside the material design domain, which makes it relatively easy to get stuck at a local minimum. A general way to overcome this weakness is to put a sufficient number of holes in the initial design to keep the complexity of the structural topology since the level set method has no difficulty in handling topology change by merging holes [6], [8]. After that, some alternative level set methods have been developed with nucleation capacity to alleviate the dependency of the final solution on the initial design [15,16,17,18,19]. Among these alternative level set methods, a couple of ones have shown excellent capability of nucleating new hole inside the two-dimensional domains [16], [17].

To improve the numerical efficiency, several level set methods for structural topology optimization have been put forward successively. Xia et al. [20] proposed a semi-Lagrange method in 2006 to solve the problem of structural topology optimization based on level set method. The semi-Lagrange method can get rid of the limitation of iterative step size and improved optimization efficiency. Luo et al. [21] proposed a semi-implicit scheme in 2008 to remove the restraint of the Courant-Friedrichs-Lewy (CFL) condition of the explicit schemes when the level set method is used in structural shape and topology optimization. Luo et al. [22] proposed a meshless Galerkin level set method in 2012 to deal with the numerical calculation, which is difficult in conventional level set method.

In addition to the above-mentioned methods, a parameterized level set equation was proposed in 2004 by Wang et al. [23], which made a significant advancement in the level set method. In the parameterized level set method (PLSM), the radial basis functions (RBFs) are often used to perform interpolation fitting for the conventional level-set equation, thereby transforming the iteratively updating partial differential equation (PDE) into ordinary differential equations (ODEs). In general, there are two types of RBFs used in the PLSM: one is the globally supported radial basis function (GS-RBF), and the other is the compactly supported radial basis function (CS-RBF). In 2008, Luo et al. [16] proposed a level set-based parameterization method for structural shape and topology optimization, where the CS-RBF is employed to describe the implicit representation of a desired smoothness and accuracy. Hence the mathematically more difficult PDE-driven optimization problem is transformed into an easier parametric optimization, leading to an efficient updating scheme that is directly derived from the stationary optimality criteria conditions. Compared with the conventional level set method by directly solving either a Hamilton–Jacobi equation [24] or a reaction-diffusion equation [25], the PLSM evolves boundaries by updating a set of parameterized coefficients at grid points [16], [23]. The PLSM has a number of advantages. First, it is capable of avoiding some numerical manipulations caused by solving the Hamilton–Jacobi equation with a finite difference scheme. Second, an approximate re-initialization scheme can be applied to the method, to improve the gradient of the level set function around the interface as well as to preserve the ability of nucleation of internal holes. Third, smooth boundaries can be obtained without implementing any filter or additional smoothing schemes. Furthermore, the method can be used for optimization of irregular design domains of unstructured meshes without difficulty [26].

In the PLSM with GS-RBF and CS-RBF, there is actually a huge difference with relevance to “global support” and “compact support”, which is described as follows. The CS-RBF not only significantly contributes high computational efficiency, but also helps change the original Hamilton–Jacobi PDE into a system of ODEs and finally to a set of algebraic equations (AEs). It thoroughly parameterizes the original Hamilton–Jacobi PDE. Correspondingly, the original topology optimization problem is changed to a “size” optimization problem, to which a lot of highly efficient and mature optimization algorithms in structural optimization, such as optimality criteria (OC), sequential linear programming (SLP), sequential quadratic programming (SQP), and sequential convex programming-method of moving asymptotes (SCP-MMA), can be readily applied. The original CFL condition has been completely removed thus. Sometimes, the “size” optimization problem with CS-RBF can be regarded as a generalized SIMP method, with the expansion coefficients as the design variables rather than the elemental densities as design variables. In this setting, it can be considered that the PLSM with CS-RBF is essentially a SIMP method, as the expansion coefficients are bounded rather than unbounded [27]. However, the GS-RBF limits the application scope of PLSM in practice: it can only handle small size of two-dimensional (2D) problems and is hard to deal with three-dimensional (3D) examples. Furthermore, the GS-RBF can only transform the original PDE into a system of ODEs. The current dominant numerical methods for solving ODEs are the finite difference methods (FDMs), such as Up-wind scheme and Runge–Kutta method. Hence, the GS-RBF only partially releases the hurdles of the CFL condition, but the time step limitation is still exciting in ODEs. In this way, the numerical methods for solving ODEs still need to be followed up to solve the structural optimization problems, since the algorithms of OC, SLP, SQP, and SCP-MMA are difficult to directly apply. Moreover, the shape parameter of the GS-RBF has an obvious influence on the accuracy of interpolation, but there is still lack of an effective scheme to determine the optimal value of the shape parameter. Hence, to overcome the unfavorable features related to the global support, the CS-RBF is well accepted due to its strictly positive definiteness and sparsity of the collection matrices [28,29,30]. One of the most important papers to detail the features and benefits of the PLSM with CS-RBF was published in 2007 [27], and the unified structural optimization model was described by the PLSM that applies CS-RBF with favorable smoothness and accuracy for interpolation 7 years later [31]. Compared with the GS-RBF, although the CS-RBF has a slightly reduced accuracy of interpolation, the improvement of optimization speed can cover such a weak influence. It is noteworthy that: the bounds for the design variables in the PLSM can be easily determined; and the moving limit for the design variables can also be easily settled with a few numerical skills to stabilize the optimization procedure [16]. However, this is not a shortcoming of the PLSM, but the numerical requirement when MMA or other optimization methods are used. Moreover, it is easy to understand that: the re-initializations are to resurrect a signed-distance function behavior of the level-set surface; and Up-wind differencing in the conventional level set methods may make the function lose shapes in the under-resolved regions owing to unwanted front energy dissipation, when marching the shape on finite-difference grid [32]. It should be emphasized that the solution of PLSM after the CS-RBF parameterization has nothing to do with the numerical process of the PDE.

In some applications, it is observed that the level set method does not lead to enough topological changes, and in particular the level set methods presented above cannot reconstruct inner contours like a ring-type structure in an automatic way. Many shape optimization problems, in particular those arising from inverse obstacle problems, are ill-posed, i.e. either there exists no solution and/or they do not depend on the data in a stable way. To solve the problems, a level set approach by including the topological derivative was generalized for shape optimization and reconstruction, which is related to changes in the objective functional corresponding to the introduction of (infinitesimally) small holes [33]. The approach was applied for a simple model problem in shape reconstruction, where the topological derivative can be computed without additional effort. Numerical tests related to the model problem demonstrated that the generalized method based on shape and topological derivative successfully reconstructs obstacles in situations where the conventional level set approach fails.

Subsequently, Ho et al. [34] proposed a dynamic node optimization algorithm based on RBF to simplify the solution of parametric level set equations in 2013. Then, a level set topology optimization method with cubic spline curve as the RBF [35] greatly enriched the research on the PLSM and the corresponding theory. In 2017, Zhang et al. [36] introduced a closed B-spline curve to solve shape and topology optimization of the holes in the complex design domain. Also in 2017, Jahangiry and Tavakkoli [37] used the non-uniform rational B-spline (NURBS) basis function to approximate the level set equation, so that the sensitivity analysis can be directly derived from the objective function. Recently, Wang et al. [38] developed a level set modeling technique for designing and optimization of solid/cellular structures, called cellular level set in B-splines (CLIBS), which is highly scalable, potentially leading to high definition modeling and optimization applications on a large-scale computing platform.

Topology optimization has benefited considerably from three decades of development and been already applied in many areas. With the in-depth study of topology optimization theory, multi-material topology optimization methods [39], [40] and 3D structural topology optimization methods [41], [42] make the established optimization model closer to the practical working conditions. To obtain the optimized shell and infill simultaneously, a multi-scale level set topology optimization method has been used to design shell-infill structures [43]. In addition, some topology optimization methods that deal with dynamic constraints [44] and random uncertainties [45] have also come into being. Furthermore, the level set method has also been applied to topology optimization of frequency-dependent viscoelastic structures [46].

With the development of computer simulation analysis software (such as ANSYS and MATLAB) and high-performance computers as well as other electronic devices, structural topology optimization has developed rapidly in theory and methodology. At present, the level set method for structural topology optimization has many advantages, such as high optimization speed, no filtering steps required, no gray-scale element generated and clear boundary of optimization results. Nevertheless, the existing level set method also has certain deficiencies. Because structural boundary is implicitly represented with a PDE by the level set method, a large computational cost is often required to solve the PDE for topology optimization. In the process of solving the PDE by the level set method, the evolution of structural boundary to an extent has dependence on the initialization of structural boundary, and the mesh-dependence phenomenon sometimes occurs. This can easily make the obtained structural boundary not smooth, and even cause the numerical instability in the topology optimization process. To overcome the deficiencies, by adding shape sensitivity constraint factor, we propose an improved PLSM based on CS-RBF for structural topology optimization with relatively high speed, good stability and reasonable results.

In this work, a PLSM with shape sensitivity constraint factor is proposed to solve structural topology optimization. In this method, the CS-RBF interpolation is employed to transform the PDE into the ODEs, thus avoiding directly calculating the relatively complex PDE. In addition, this method adopts the gradient-based mathematical programming algorithm MMA to update the design variables, so the stability of optimization process and the accuracy of optimization results are guaranteed. With the shape sensitivity constraint factor, the updating step length is changeable and controllable in the iterative process of MMA algorithm so as to increase the optimization speed. The derivation of shape function and sensitivity analysis effectively avoids tedious computational steps of initializing the level set function, so that the optimization result is less dependent on the initial design and can form new holes. Compared with the conventional level set method and the PLSM based on GS-RBF interpolation, the proposed method can greatly enhance the optimization efficiency on the premise of ensuring the accuracy of optimization results. Furthermore, the proposed method exhibits relatively good stability for topology optimization problems. At the same time, the parameterized scheme makes the optimization step size no longer limited by the CFL condition, thereby improving the solving efficiency.

The rest of the paper is arranged as follows. The mathematical model and principle of the PLSM based on CS-RBF are introduced in Sect. 2. The PLSM based on CS-RBF by adding shape sensitivity constraint factor is proposed in Sect. 3, where the sensitivity analysis and the optimization process are described as well. The model for topology optimization of multi-material structure is described by the proposed method in Sect. 4. In Sect. 5, several typical numerical examples are presented to demonstrate the feasibility and effectiveness of the proposed method. Finally, the conclusions are given in Sect. 6.

2 Parameterization of level set functions

2.1 The level set method for structural topology optimization

In structural topology optimization via the conventional level set method, design boundary of the structure is implicitly represented by the zero-value curve of a higher-dimensional level set equation. By numerically solving the Hamilton–Jacobi equation, the normal velocity of the level set equation is obtained. By calculating the normal velocity field, the zero-value curve of the level set equation is gradually moved to achieve the result of boundary evolution. Therefore, the motion of zero-value curve of higher-dimensional level set equation is controlled by a set of numerical solutions of the Hamilton–Jacobi PDEs to which are set the initial values.

Taking the 2D structure as an example, its structural boundary is implicitly represented by the zero-value curve of a 3D level set equation defined in the design domain $D \subset R^{2}$. The material distribution of the structure is shown in Fig. 1, and the relationship between the value of the level set equation and the material distribution is expressed as follows.

$$\left\{ \begin{aligned} &\varPhi (x,t) > 0 \Leftrightarrow x \in \varOmega \hfill \\& \varPhi (x,t) = 0 \Leftrightarrow x \in \partial \varOmega \hfill \\ &\varPhi (x,t) < 0 \Leftrightarrow x \in D\backslash \varOmega \hfill \\ \end{aligned} \right.$$

(1)

Fig. 1

Relationship between the level set equation and the material distribution of design domain. (a In 3D coordinates; b In 2D coordinates)

In Eq. (1), $D$ denotes the design domain; $\varOmega$ denotes the solid part with material to be designed; $\partial \varOmega$ denotes boundary of the design domain, namely the zero-value curve described by level set equation; and $x$ denotes a point in the design domain. To achieve the evolution of structural boundary, a dynamic virtual time factor $t$ is introduced to describe the dynamic change of the zero-value curve of level set equation, and the Hamilton–Jacobi PDE [47] is expressed as follows.

$$\frac{\partial \varPhi (x,t)}{\partial t} - V_{n} \left| {\nabla \varPhi (x,t)} \right| = 0$$

(2)

In Eq. (2), $V_{n} = V \bullet ({{\nabla \varPhi (x,t)} \mathord{\left/ {\vphantom {{\nabla \varPhi (x,t)} {\left| {\nabla \varPhi (x,t)} \right|}}} \right. \kern-0pt} {\left| {\nabla \varPhi (x,t)} \right|}})$ represents the normal velocity field. Where, $V = {{{\text{d}}x} \mathord{\left/ {\vphantom {{{\text{d}}x} {{\text{d}}t}}} \right. \kern-0pt} {{\text{d}}t}}$ is the velocity field; $\varPhi (x,t)$ represents the value of level set equation at the point $x$; $x$ is the design variable; and $t$ is a virtual time factor. Therefore, the solution of the PDE moving along the normal direction is the boundary of the level set equation curve.

Based on the boundary representation by the level set method above, the structural topology optimization problem with the minimal average compliance can be formulated as:

$${ \hbox{min} }:J({\mathbf{u}}) = \int_{D} {\varepsilon_{ij} ({\mathbf{u}})E_{ijkl} \varepsilon_{kl} ({\mathbf{u}})H(\varPhi ){\text{d}}\varOmega }$$

$${\text{s}}.{\text{t}}:a({\mathbf{u}},{\mathbf{v}}) = L({\mathbf{v}}),\forall {\mathbf{v}} \in U,\left. {\mathbf{u}} \right|_{{\partial D_{{\mathbf{u}}} }} = {\mathbf{u}}_{0}$$

$$\int_{D} {H(\varPhi )} d\varOmega < V_{\hbox{max} }$$

(3)

In Eq. (3), $J({\mathbf{u}})$ is the overall compliance value of the structure; $E_{ijkl}$ is the elastic modulus of the material; $\varepsilon$ is the strain tensor; $H(\varPhi )$ is the Heaviside smoothing equation; $\varPhi$ is the value of level set equation; ${\mathbf{u}}$ is the allowable displacement in the displacement field $U$; ${\mathbf{v}}$ is virtual displacement; ${\mathbf{u}}_{0}$ is a fixed displacement constraint; $\partial D_{{\mathbf{u}}}$ represents a fixed boundary of the structure; $V_{\hbox{max} }$ is the maximum allowable volume of the material; $a({\mathbf{u}},{\mathbf{v}}) = L({\mathbf{v}})$ is the weak form of the material elastic equilibrium equation; $a({\mathbf{u}},{\mathbf{v}})$ and $L({\mathbf{v}})$ are, respectively, expressed as follows.

$$a({\mathbf{u}},{\mathbf{v}}) = \int_{D} {\varepsilon_{ij} ({\mathbf{u}})E_{ijkl} \varepsilon_{kl} ({\mathbf{v}})d\varOmega }$$

(4)

$$L({\mathbf{v}}) = \int_{D} {p{\mathbf{v}}d\varOmega } + \int_{\varGamma } {\tau {\mathbf{v}}d\varGamma }$$

(5)

where $p$ is a body force of the material and $\tau$ is the boundary load; $\varepsilon_{kl} ({\mathbf{v}})$ is the strain tensor on the virtual displacement; $\varGamma$ is the boundary condition.

In the optimization problem under static load equilibrium state, the virtual displacement ${\mathbf{v}}$ is equal to the actual displacement ${\mathbf{u}}$, so Eqs. (4) and (5) meet the constraint requirements. At this time, the mathematical model of Eq. (3) is transformed into a minimum problem with only one volume constraint, as shown below.

$${ \hbox{min} }:J({\mathbf{u}}) = \int_{D} {\varepsilon_{ij} ({\mathbf{u}})E_{ijkl} \varepsilon_{kl} ({\mathbf{u}})H(\varPhi )d\varOmega }$$

$${\text{s}}.{\text{t}}:\int_{D} {H(\varPhi )} d\varOmega - V_{\hbox{max} } < 0$$

(3a)

It can be seen from Eq. (3a) that structural topology optimization problem via the level set method is transformed into a minimum problem with a volume constraint. For this problem, the gradient-based method [7] is employed to solve the objective function. By combining the constraint conditions with the objective function, the Lagrange equation is established as follows.

$$L({\mathbf{u}},\varPhi ) = \int_{D} {\varepsilon_{ij} ({\mathbf{u}})E_{ijkl} \varepsilon_{kl} ({\mathbf{u}})H(\varPhi )d\varOmega } + \lambda \left( {\int_{D} {H(\varPhi )d\varOmega } - V_{\hbox{max} } } \right)$$

(6)

where, $\lambda$ is the Lagrange multiplier, whose value is always positive; $\lambda \left( {\int_{D} {H(\varPhi )d\varOmega } - V_{\hbox{max} } } \right)$ is the term involving volume constraint of structural topology optimization. As the volume constraint changes continuously, the multiplier is constantly updated by a simple scheme named bi-section algorithm [48]. According to References [8] and [33], the topological derivative of the Lagrange equation with respect to the virtual time $t$ is established as follows.

$$\frac{{\partial L({\mathbf{u}},\varPhi )}}{\partial t} = \int_{D} {(\lambda - \varepsilon_{ij} ({\mathbf{u}})E_{ijkl} \varepsilon_{kl} ({\mathbf{u}}))V_{n} ds}$$

(7)

2.2 Parameterization process of level set equation

In the conventional level set method for structural topology optimization, the level set equation is expressed by an implicit PDE, and its explicitly analytical expression is unknown. Therefore, in the process of topology optimization via the level set method, the level set equation must be discretized by distance transformation. In the Eulerian method, the numerical procedure for solving the Hamilton–Jacobi PDE is inevitable. The numerical procedure requires the selection of appropriate Up-wind scheme [11], [49], normal velocity field and re-initialization algorithm to solve the equation, and these steps may restrict the actual effect of the level set method. For example, the step of re-initialization for the level set equation will hinder the generation of new holes in the material. In the numerically solving process, the discretization itself will also adversely affect the optimization results of the level set method. Therefore, a parameterization approach is used to interpolate the level set equation in this section, which avoids the defects of the conventional level set method in the discretization process.

With the interpolation scheme and optimization model based on the RBF, a globally smoother level set equation can be obtained, which effectively improves the numerical accuracy and stability of the level set method. The RBF, a radial symmetry function centered on a specific point [16], can be expressed as follows.

$$\varphi_{i} ({\mathbf{x}}) = \varphi (\left\| {{\mathbf{x}} - x_{i} } \right\|)\begin{array}{*{20}c} , & {x_{i} \in D} \\ \end{array}$$

(8)

where $\left\| \bullet \right\|$ represents the Euclidean distance in the design domain and ${\mathbf{x}}$ represents the geometric position of a particular point; and a series of uncorrelated basis functions are formed using only one fixed equation form $\varphi (\left\| {{\mathbf{x}} - x_{i} } \right\|)$. According to the scope of action, the RBFs can be divided into GS-RBF and CS-RBF. Since the interpolation function generated by GS-RBF is related to the nodes in the entire design domain, it takes a lot of computational cost using GS-RBF in interpolation calculation. Compared with the GS-RBF, the CS-RBF is only affected by the nodes within the supported radius $r$. Therefore, the CS-RBF function matrix is a sparse matrix, which can save a lot of computational cost in the interpolation calculation, and meanwhile keep a similar accuracy of the calculation results. In addition, the CS-RBF at one node is a radial symmetric matrix, so strictly positive definiteness can be guaranteed when related matrix operations are performed. To ensure a certain smoothness of the curve, the second-order continuous CS-RBF is used for curve interpolation.

$$\varphi (r) = \hbox{max} \left\{ {0,(1 - r)^{4} } \right\}(4r + 1)$$

(9)

where

$$r = \frac{{\sqrt {(x - x_{i}^{c} )^{2} + (y - y_{i}^{c} )^{2} } }}{{d_{\hbox{min} } }}$$

(10)

where r represents the influence coefficient between the finite element node ${\mathbf{x}}$ with the coordinates $(x,y)$ and the reference point $x_{{}}^{c}$ with the coordinates $(x_{i}^{c} ,y_{i}^{c} )$, which is determined by the search radius $d_{\hbox{min} }$ and the Euclidean distance from ${\mathbf{x}}$ to $x_{{}}^{c}$. To simplify the calculation, it is generally preferred to take 2 to 4 times the node size. The level set equation can be fitted with $m$ different center-point-interpolation functions as follows.

$$\varPhi ({\mathbf{x}},t) = \sum\limits_{i = 1}^{m} {\alpha_{i} (t)\varphi_{i} ({\mathbf{x}})}$$

(11)

In Eq. (11), $\alpha_{i} (t)$ denotes the coefficient of the $i$ th CS-RBF interpolation, which is the design variable of the level set function. $\varphi_{i} ({\mathbf{x}})$ is the $i$ th CS-RBF mentioned above. By substituting Eq. (11) into Eq. (2), the Hamilton–Jacobi PDE is transformed into:

$$\sum\limits_{i = 1}^{m} {\mathop \alpha \limits^{ \bullet }_{i} (t)\varphi_{i} ({\mathbf{x}})} - V_{n} \left| {\nabla \varPhi } \right| = 0$$

(12)

Then, the normal velocity $V_{n}$ in Eq. (12) can be formulated as:

$$V_{n} = \frac{1}{{\left| {\nabla \varPhi } \right|}}\sum\limits_{i = 1}^{m} {\mathop \alpha \limits^{ \bullet }_{i} (t)\varphi_{i} ({\mathbf{x}})}$$

(13)

Substituting Eq. (13) into Eq. (7), the derivative of Lagrange equation to the virtual time factor is expressed as:

$$\frac{dL}{dt} = \sum\limits_{i = 1}^{m} {\mathop \alpha \limits^{ \bullet }_{i} (t)} \int_{\varGamma } {(\lambda - \varepsilon_{ij} ({\mathbf{u}})E_{ijkl} \varepsilon_{kl} ({\mathbf{u}}))\frac{1}{{\left| {\nabla \varPhi } \right|}}\varphi_{i} ({\mathbf{x}})ds}$$

(14)

By applying the chain rule, Eq. (14) can be written as:

$$\frac{dL}{dt} = \sum\limits_{i = 1}^{m} {\frac{\partial J}{{\partial \alpha_{i} }}\mathop \alpha \limits^{ \bullet }_{i} (t)} + \lambda \sum\limits_{i = 1}^{m} {\frac{\partial V}{{\partial \alpha_{i} }}\mathop \alpha \limits^{ \bullet }_{i} (t)}$$

(15)

In Eq. (15), $\frac{\partial J}{{\partial \alpha_{i} }}$ is the sensitivity of objective function, and $\frac{\partial V}{{\partial \alpha_{i} }}$ is the shape derivative or shape sensitivity.

3 Optimization algorithm of adding shape sensitivity constraint factor

3.1 Shape sensitivity constraint factor

As is known from Eq. (15), in the case of parameterization, the level set equations of structural boundary have been transformed from PDE to ODEs. According to Eq. (11), the value of the level set equation $\varPhi ({\mathbf{x}},t)$ changes with the expansion coefficients $\alpha_{i} (t)$ of the respective RBFs. For solving the ODEs, the gradient-based optimization algorithm can be used to numerically solve the equation, including the OC method [3] and the MMA method [50]. Since the MMA algorithm has a rigorous theoretical and mathematical derivation basis, it is often used to update the design variables to achieve the goal of updating the level set equation values at the nodes.

In this work, to enhance the computational efficiency of structural topology optimization, a shape sensitivity constraint factor is introduced to control the input variable of the MMA algorithm. Then, the constrained shape derivative or shape sensitivity is written as:

$$\overline{{\frac{\partial V}{{\partial \alpha_{i} }}}} = \zeta \cdot \frac{\partial V}{{\partial \alpha_{i} }}$$

(16)

where $\zeta$ is the shape sensitivity constraint factor.

Substituting Eq. (16) into Eq. (15), then the derivative of Lagrange equation to the virtual time factor is described as:

$$\frac{{{\text{d}}L}}{{{\text{d}}t}} = \sum\limits_{i = 1}^{m} {\frac{\partial J}{{\partial \alpha_{i} }}\mathop \alpha \limits^{ \bullet }_{i} (t)} + \lambda \sum\limits_{i = 1}^{m} {\zeta \cdot \frac{\partial V}{{\partial \alpha_{i} }}\mathop \alpha \limits^{ \bullet }_{i} (t)}$$

(17)

where the sensitivity of objective function $\frac{\partial J}{{\partial \alpha_{i} }}$ and shape derivative or shape sensitivity $\frac{\partial V}{{\partial \alpha_{i} }}$ are, respectively, formulated as follows.

$$\frac{\partial J}{{\partial \alpha_{i} }} = - \int_{\varGamma } {\varepsilon_{ij} ({\mathbf{u}})E_{ijkl} \varepsilon_{kl} ({\mathbf{u}})\frac{1}{{\left| {\nabla \varPhi } \right|}}\varphi_{i} ({\mathbf{x}})ds}$$

(18)

$$\frac{\partial V}{{\partial \alpha_{i} }} = \int_{\varGamma } {\zeta \cdot \frac{1}{{\left| {\nabla \varPhi } \right|}}\varphi_{i} ({\mathbf{x}})ds}$$

(19)

For the simplicity of numerical solution, the Dirac function can be used to transform the boundary integral into the integral of the entire design domain, as is shown below.

$$ds = \delta (\varPhi )\left| {\nabla \varPhi } \right|d\varOmega$$

(20)

where, $\delta (\varPhi )$ denotes the Dirac function, which is the derivative of the Heaviside function $H(\varPhi )$.

3.2 Selection of shape sensitivity constraint factor value

In this section, the cantilever beam structure is chosen as an example to study the effect of different values of shape sensitivity constraint factor on the results via the parameterized level set topology optimization method based on CS-RBF proposed in this paper. Figure 2 shows the design domain and boundary conditions of the cantilever beam structure. The ratio of the length and width of the design domain is 2:1, where the left side is fixed and a downward force $F = 1$ is applied at the midpoint of the right side. The design domain is divided into $80 \times 40$ quadrilateral meshes. The Young’s modulus of the solid material is set to $E_{0} = 1$. To avoid the singularity of the calculation results, the Young’s modulus of the void material is set to $E_{\hbox{min} } = 10^{ - 9}$. The Poisson’s ratio is set to $\gamma = 0.3$, and the volume fraction constraint is set to 0.4. The Lagrange multiplier $\lambda$ is set to 1. Then, the convergence process of objective function and volume constraint is analyzed with different values of the shape sensitivity constraint factor $\zeta$. Figures 3 and 4 show the convergence curves of objective function and volume fraction for topology optimization of cantilever beam with different values of shape sensitivity constraint factor $\zeta = 0.005$, $\zeta = 0.01$, $\zeta = 0.02$, $\zeta = 0.05$ and $\zeta = 0.1$, respectively.

Fig. 2

Design domain and boundary conditions of cantilever beam structure

Fig. 3

Curves of objective function for topology optimization of cantilever beam structure with different values of shape sensitivity constraint factor

Fig. 4

Curves of volume fraction for topology optimization of cantilever beam structure with different values of shape sensitivity constraint factor

From Figs. 3 and 4, it can be found that in the topology optimization process of single-material cantilever beam: when the value of $\zeta$ is 0.005, the values of objective function (structural compliance) and volume fraction remain stable after just 20 iterations or so, but the stable value of structural compliance is relatively large, which indicates the convergence condition is relatively quickly reached while the optimal result is not achieved in this case; when the value of $\zeta$ is greater than 0.01 and less than 0.05, although the optimization iteration process also remains relatively stable, the convergence speed of the optimization iteration decreases gradually with the continuous increase value of $\zeta$; when the value of $\zeta$ is greater than 0.05, the objective function (structural compliance) and volume fraction fail to reach their respective stable values even after 200 iterations. This means that numerical oscillation is likely to occur in the optimization iteration process if the value of $\zeta$ is set somewhat large. Therefore, under the condition that the value of $\zeta$ is small enough, reasonably selecting the value of $\zeta$ can lead to both good stability and high efficiency of topology optimization by this method.

3.3 Description of the numerical algorithm

The flow chart describing the implementing process of the optimization aelastic moduli of materiallgorithm in this work is shown in Fig. 5.

Fig. 5

Flow chart showing parameterized level set topology optimization process with shape sensitivity constraint factor

The implementation process of the optimization algorithm shown in Fig. 5 can also be described as the following iterative steps:

• 1 Initialize Φ₀, ϕ_i, calculate the values of design variables $\alpha_{i}$ and then generate meshes;

• 2 Start iteration, and set the iterative number n = 1: 200;

• 3 Implement Finite element analysis, calculation of displacement matrix U, global stiffness matrix K and value of structural compliance C;

• 4 Calculate the values of the objective function sensitivity $\frac{\partial J}{{\partial \alpha_{i} }}$ and the shape derivative or shape sensitivity $\frac{\partial V}{{\partial \alpha_{i} }}$ according to Eqs. (18) and (19) respectively;

• 5 Apply the MMA algorithm to update the values of design variables $\alpha_{i}$;

• 6 Update the value of the corresponding level set equation according to Eq. (11);

• 7 Check whether or not the convergence condition $\left| {J({\mathbf{u}})^{n + 1} - J({\mathbf{u}})^{n} } \right| \le Tolerance$ is met: If the convergence condition is not met repeat steps 3–6. If the convergence condition is met, stop the iteration and output the data such as the iterative curves of structural compliance and volume fractions

4 Topology optimization of multi-material structure by this method

In the above two sections, the PLSM based on CS-RBF with shape sensitivity constraint factor is proposed for topology optimization of single-material structure. To further demonstrate the effectiveness of the proposed method, this method is applied to topology optimization of multi-material structure. The model for topology optimization of multi-material structure by this method is described in this section.

For the linearly elastic problem with minimum compliance as an objective function, the model for topology optimization of multi-material structure here refers to the multi-material mathematical model with the level set method in Ref. [40], so the elastic modulus $E^{3} ({\mathbf{x}},\varPhi_{k} )$ (for the sake of simplicity, topology optimization of three-material structure is taken as an example) in the multi-material structural design domain is formulated as:

$$E^{3} ({\mathbf{x}},\varPhi_{k} ) = H(\varPhi_{1} )H(\varPhi_{2} )E_{1} + H(\varPhi_{1} )(1 - H(\varPhi_{2} ))H(\varPhi_{3} )E_{2} + H(\varPhi_{1} )(1 - H(\varPhi_{2} ))(1 - H(\varPhi_{3} ))E_{3}$$

(21)

where, $\varPhi_{k}$ represents the $k$ th level set function; $E_{1}$, $E_{2}$ and $E_{3}$ indicate the elastic moduli of material 1, material 2 and material 3, respectively. The volume fractions of three materials can be written as follows.

$$\begin{aligned} &V^{1} = \int_{\varOmega } {H(\varPhi_{1} )d\varOmega } \hfill \\ &V^{2} = \int_{\varOmega } {H(\varPhi_{1} )(1 - H(\varPhi_{2} ))d\varOmega } \hfill \\ &V^{3} = \int_{\varOmega } {H(\varPhi_{1} )(1 - H(\varPhi_{2} ))(1 - H(\varPhi_{3} ))d\varOmega } \hfill \\ \end{aligned}$$

(22)

where, $V^{1}$ denotes total volume fraction of material 1, material 2 and material 3; $V^{2}$ denotes total volume fraction of material 2 and material 3; $V^{3}$ denotes the volume fraction of material 3.

Referring to the multi-material level set topology optimization method in Ref. [51], the derivative of the objective function to the design variables $\alpha_{i}^{k} ,(k = 1,2,3)$ are expressed as:$\frac{dJ}{{\partial \alpha_{i}^{k} }} = - \sum\nolimits_{i = 1}^{m} {\int_{\varGamma } {\varepsilon_{ij} ({\mathbf{u}})\frac{{\partial E^{3} ({\mathbf{x}},\varPhi_{k} )}}{{\partial \alpha_{i}^{k} }}\varepsilon_{kl} ({\mathbf{u}})d\varOmega } }$, $(k = 1,2,3)$ (23)

According to Eq. (21), the derivation of the elastic modulus to the design variables are formulated as follows.

$$\begin{aligned} \frac{{\partial E^{3} ({\mathbf{x}},\varPhi_{i} )}}{{\partial \alpha_{i}^{1} }} &= \delta (\varPhi_{1} )\varphi_{i} ({\mathbf{x}})\left( {H(\varPhi_{2} )E_{1} + (1 - H(\varPhi_{2} ))}\right.\\&\quad\times \left.{H(\varPhi_{3} )E_{2} + (1 - H(\varPhi_{2} ))(1 - H(\varPhi_{3} ))E_{3} } \right) \hfill \\ \frac{{\partial E^{3} ({\mathbf{x}},\varPhi_{i} )}}{{\partial \alpha_{i}^{2} }} &= \delta (\varPhi_{2} )\varphi_{i} ({\mathbf{x}})H(\varPhi_{1} )\left( {E_{1} - \left( {H(\varPhi_{3} )E_{2} }\right.}\right.\\&\quad \left.{\left.{+ (1 - H(\varPhi_{3} ))E_{3} } \right)} \right) \hfill \\ \frac{{\partial E^{3} ({\mathbf{x}},\varPhi_{i} )}}{{\partial \alpha_{i}^{3} }} &= \delta (\varPhi_{3} )\varphi_{i} ({\mathbf{x}})H(\varPhi_{1} )(1 - H(\varPhi_{2} ))\left( {E_{2} - E_{3} } \right) \hfill \\ \end{aligned}$$

(24)

where, $\delta (\varPhi_{k} ),(k = 1,2,3)$ indicate the Dirac functions; $\varphi_{i} ({\mathbf{x}})$ indicates the $i$ th CS-RBF at point ${\mathbf{x}}$. Similarly, according to the expressions of volume fractions in Eq. (22), the shape derivatives of the volume fractions to the design variables $\alpha_{i}^{k} ,(k = 1,2,3)$ can be calculated, and when the shape sensitivity constraint factor $\zeta$ is added, the corresponding formulas for calculating shape sensitivity by this method are expressed as follows.

$$\begin{aligned} \frac{{\partial V^{1} }}{{\partial \alpha_{i}^{1} }} &= \int_{\varOmega } {\zeta \cdot \delta (\varPhi_{1} )\varphi_{i} ({\mathbf{x}})d\varOmega } \hfill \\ \frac{{\partial V^{2} }}{{\partial \alpha_{i}^{2} }} &= - \int_{\varOmega } {\zeta \cdot H(\varPhi_{1} )\delta (\varPhi_{2} )\varphi_{i} ({\mathbf{x}})d\varOmega } \hfill \\ \frac{{\partial V^{3} }}{{\partial \alpha_{i}^{3} }} &= - \int_{\varOmega } {\zeta \cdot H(\varPhi_{1} )(1 - H(\varPhi_{2} ))\delta (\varPhi_{3} )\varphi_{i} ({\mathbf{x}})d\varOmega } \hfill \\ \end{aligned}$$

(25)

According to Eqs. (24) and (25), the MMA algorithm can be used to update the design variables $\alpha_{i}^{k} ,(k = 1,2,3)$ by the recursive method.

5 Numerical examples

In this section, three typical numerical examples of structural topology optimization are presented to demonstrate the feasibility and effectiveness of the proposed method. Each individual numerical example comprises two cases which involve topology optimization of single-material and multi-material structures, respectively. In these examples, the proposed method is used to perform structural topology optimization with the minimum compliance as the objective function and the volume fractions as the constraints. Then, the topology optimization results obtained by this method are analyzed or compared with those obtained by other methods, to highlight the efficiency and advantage of the proposed method.

5.1 Cantilever beam

For the cantilever beam structure in this example, the design domain and boundary conditions are also shown in Fig. 2. The ratio of the length and width of the design domain is 2:1, the left side is fixed, and a downward force $F = 1$ is applied at the midpoint of the right side. The design domain is also divided into $80 \times 40$ quadrilateral meshes. This example consists of two cases. The first case of this example involves topology optimization of single-material cantilever beam structure, which is used to verify the relatively high efficiency of the proposed PLSM based on CS-RBF compared with the PLSM based on GS-RBF. In this case, the parameter settings are provided below this paragraph. The Young’s modulus of the solid material is set to $E_{0} = 1$. To avoid the singularity of the calculation results, the Young’s modulus of the void material is set to $E_{\hbox{min} } = 10^{ - 9}$. The Poisson’s ratio is set to $\gamma = 0.3$, and the volume fraction constraint is set to 0.4. The shape sensitivity constraint factor is set to $\zeta = 0.01$, and the Lagrange multiplier $\lambda$ is set to 1.

Figure 6 (a–d) show the topology optimization process of single-material cantilever beam structure by the proposed PLSM based on CS-RBF, where black color represents the solid material and white color represents the void. Figure 7 shows the final topology optimization results of single-material cantilever beam structure obtained by the proposed PLSM based on CS-RBF and the PLSM based on GS-RBF in Ref. [52]. Figures 8 and 9 show the objective function iteration curves and volume fraction iteration curves for topology optimization of single-material cantilever beam structure by the two methods, respectively. In Figs. 8 and 9, the red lines represent the curves of objective function and volume fraction in the optimization process by the proposed PLSM based on CS-RBF, and the blue lines represent the curves of objective function and volume fraction in the optimization process by the PLSM based on GS-RBF in Ref. [52]. As shown in Figs. 8 and 9: the convergence condition is satisfied by the proposed PLSM based on CS-RBF after 106 iterations, and the compliance of 74.0453 and the volume fraction of 0.4004 are reached in the meanwhile; the convergence condition is satisfied by the PLSM based on GS-RBF in Ref. [52] after 127 iterations, and meanwhile the compliance of 72.0189 and the volume fraction of 0.4001 are reached. It can be concluded that the convergence rate of objective function by the proposed PLSM based on CS-RBF is higher than that by the PLSM based on GS-RBF.

Fig. 6

Topology optimization process of single-material cantilever beam structure by the proposed PLSM based on CS-RBF. (a Optimization result after 20 iterations; b Optimization result after 40 iterations; c Optimization result after 60 iterations; d Optimization result after 60 iterations, namely the optimal topology result)

Fig. 7

Optimal topology results of single-material cantilever beam structure. (a Optimal topology result obtained by the proposed PLSM based on CS-RBF; b Optimal topology result obtained by the PLSM based on GS-RBF in Ref. [52])

Fig. 8

Curves of objective function in topology optimization of single-material cantilever beam structure by two different methods. (Red line represents the change of compliance obtained by the proposed PLSM based on CS-RBF; and blue line represents the change of compliance obtained by the PLSM based on GS-RBF in Ref. [52])

Fig. 9

Curves of volume fraction in topology optimization of single-material cantilever beam structure by two different methods. (Red line represents the change of volume fraction obtained by the proposed PLSM based on CS-RBF; and blue line represents the change of volume fraction obtained by the PLSM based on GS-RBF in Ref. [52])

Due to large difference in the computational amount of interpolation between the CS-RBF and the GS-RBF per iteration, the two factors of iteration number and objective function value cannot clearly approach a conclusion that the speed of the proposed PLSM based on CS-RBF is higher than that of the PLSM based on GS-RBF. Therefore, a computer whose configuration with Intel Core i5-3450 CPU@3.2 GHz and 16 GB of memory is chosen to calculate the time consumed by the proposed PLSM based on CS-RBF and the PLSM based on GS-RBF in Ref. [52], respectively, where the same convergence and initial design conditions are set. The comparative analysis data are listed in Table 1.

Table 1 Comparison of time cost, iteration numbers and optimal value of compliance for topology optimization of single-material cantilever beam structure by two different methods

Table 1 shows that: for the proposed PLSM based on CS-RBF, the time consumed in a single iteration is only 0.0485 s, the number of iterations is 106, and the total time consumed from the initial design to the optimal result is 5.478 s; while for the PLSM based on GS-RBF in Ref. [52], the time consumed in a single iteration is 0.1723 s, the number of iterations is 127, and the total time consumed from the initial design to the optimal result is 22.17 s. It can be found from Table 1 that: the time spent per iteration by the proposed PLSM based on CS-RBF in this paper is 71.85% lower than that by the PLSM based on GS-RBF; and the total time spent in the optimization process by the proposed PLSM based on CS-RBF in this paper is 75.29% lower than that by the PLSM based on GS-RBF.

From Table 1 and Fig. 8, it can be concluded that the optimization speed is greatly improved at the cost of a small amount of compliance (2.8%). Therefore, the proposed method can effectively enhance the optimization efficiency and reduce design cost in engineering practice.

The second case of this example involves topology optimization of three-material cantilever beam structure, which is used to further demonstrate the effectiveness of the proposed method. In this case, the design domain and boundary conditions are the same as those in the first case of this example. The design domain is also divided into $80 \times 40$ quadrilateral meshes. The parameter settings in this case are provided below this paragraph. The porous structure shown in Fig. 10 represents the initial material distribution of three-material cantilever beam structure, where the red part represents material 1, the green part represents material 2, and the blue part represents material 3. The corresponding elasticity moduli of the three materials are set to $E_{1} = 1$, $E_{2} = 3$ and $E_{3} = 9$, respectively. The volume fraction constraints of the three materials are set to $Vol_{1} = 0.1$, $Vol_{2} = 0.1$ and $Vol_{3} = 0.3$, respectively.

Fig. 10

Initial material distribution of three-material cantilever beam structure

Topology optimization of three-material cantilever beam structure is carried out by the proposed method and the multi-material level set method in Ref. [40]. Figure 11 represents the final topology optimization results of three-material cantilever beam structure obtained by the two above-mentioned methods. From Fig. 11, it can be seen that the boundary of topology optimization result obtained by the proposed method is clearer than that by the multi-material level set method in Ref. [40]. Figures 12 and 13 represent the convergence curves of objective function and volume fraction in topology optimization of three-material cantilever beam structure by the two above-mentioned methods, respectively. It can be found from Figs. 12 and 13 that: when topology optimization iteration stops at 116 steps by the proposed method, the value of objective function is 9.937, and meanwhile volume fractions of the three materials are $Vol_{1} = 0.1001$, $Vol_{2} = 0.0999$ and $Vol_{3} = 0.3000$, respectively; when topology optimization iteration stops at 150 steps by the multi-material level set method in Ref. [40], the value of objective function is 10.105, and meanwhile volume fractions of the three materials are $Vol_{1} = 0.1063$, $Vol_{2} = 0.0944$ and $Vol_{3} = 0.3038$, respectively.

Fig. 11

Final topology optimization results of three-material cantilever beam structure obtained by two different methods. (a Optimal topological structure by the proposed method; b Optimal topological structure by the multi-material level set method in Ref. [40])

Fig. 12

Curves of objective function and volume fraction in topology optimization of three-material cantilever beam structure by the proposed method. (The legends ‘Vol1’, ‘Vol2’ and ‘Vol3’ represent the volume fractions of material 1, material 2, and material 3, respectively)

Fig. 13

Curves of objective function and volume fraction in topology optimization of three-material cantilever beam structure by the multi-material level set method in Ref. [40]. (The legends ‘Vol1’, ‘Vol2’ and ‘Vol3’ represent the volume fractions of material 1, material 2, and material 3, respectively)

In this case, it can be concluded that compliance of the final topology optimization result obtained by the proposed method is lower than that obtained by the multi-material level set method in Ref. [40], and the number of iteration steps by this method is less than that by the multi-material level set method in Ref. [40] in the optimization process. In other words, this method greatly improves the effect and speed in topology optimization of three-material cantilever beam structure.

5.2 Two-bar bracket

Figure 14 shows the design domains and boundary conditions of two-bar bracket structure, where the ratio of the length and width of the design domain is 2:1. The left side is fixed and a downward force $F = 1$ is applied at the midpoint of the right side. The design domains are divided into $50{\kern 1pt} \times {\kern 1pt} 100$ quadrilateral meshes. In Fig. 14, (a) represents the design domain of solid material and its boundary conditions, (b) represents the design domain of solid material with a circular hole whose radius equals 15 times the size of the divided meshes and its boundary conditions, and (c) represents the design domain of porous material and its boundary conditions. This example consists of two cases. The first case of this example involves topology optimization of single-material two-bar bracket structure with different design domains, which is used to verify the stability of the proposed method. In this case, the parameter settings are provided below this paragraph. The Young’s modulus of the solid material is set to $E_{0} = 1$. To avoid the singularity of the calculation results, the Young’s modulus of the void material is set to $E_{\hbox{min} } = 10^{ - 9}$. The Poisson’s ratio is set to $\gamma = 0.3$, and the volume fraction constraint is set to 0.3. The shape sensitivity constraint factor is set to $\zeta = 0.01$, and the Lagrange multiplier $\lambda$ is set to 1.

Fig. 14

Design domains and boundary conditions of two-bar bracket structure. (a design domain of solid material; b design domain of solid material with a circular hole whose radius equals 15 times the size of the divided meshes; c design domain of porous material)

Figure 15 shows the topology optimization results of single-material two-bar bracket structure with three different initial design domains by the proposed method. Figure 16 shows the curves of objective function in the topology optimization of single-material two-bar bracket structure with three different initial design domains by the proposed method. As shown in Fig. 15, the distribution of material is almost the same as one another for the final topology optimization results of single-material two-bar bracket structure with three different initial design domains by the proposed method. As shown in Fig. 16, the compliance values are 8.0879, 8.0968, and 8.0846 corresponding to the final topology optimization results of single-material two-bar bracket structure with initial design domains of solid material, solid material with a circular hole, and porous material, respectively.

Fig. 15

Final topology optimization results of single-material two-bar bracket structure with three different initial design domains. ((a), (b) and (c) represent optimal topology results of single-material two-bar bracket structure with initial design domains of solid material, solid material with a circular hole whose radius equals 15 times the size of the divided meshes and porous material, respectively)

Fig. 16

Curves of objective function in topology optimization of single-material two-bar bracket structure with three different initial design domains. (The legends ‘a’, ‘b’ and ‘c’ represent the compliance values of single-material two-bar bracket structure with initial design domains of solid material, solid material with a circular hole whose radius equals 15 times the size of the divided meshes and porous material, respectively)

From this case, it can be found that: when the proposed method is used under the same constraints, the topology optimization results of single-material two-bar bracket structure are not affected by the initial design domains. It proves that the proposed method in this paper has good stability for structural topology optimization.

The second case of this example involves topology optimization of three-material two-bar bracket structure, which is used to further demonstrate the effectiveness of the proposed method. In this case, the design domain and boundary conditions are the same as those illustrated in Fig. 14a. The parameter settings in this case are provided below this paragraph. Figure 17a shows the initial material distribution of three-material two-bar bracket structure, where the red part represents material 1, the green part represents material 2, and the blue part represents material 3. The corresponding elasticity moduli of the three materials are set to $E_{1} = 1$, $E_{2} = 3$ and $E_{3} = 9$, respectively. The volume fraction constraints of the three materials are set to $Vol_{1} = 0.1$, $Vol_{2} = 0.1$ and $Vol_{3} = 0.3$, respectively. The design domain is also divided into $50 \times 100$ quadrilateral meshes.

Fig. 17

Initial material distribution and final topology optimization result of three-material two-bar bracket structure. (a Initial material distribution of three-material two-bar bracket structure; b Optimal topology of three-material two-bar bracket structure by the proposed method)

Figure 17b illustrates the optimal topology result of three-material two-bar bracket structure obtained by the proposed method after 64 iterations, and the corresponding compliance value is 0.81051. It can be found from the optimal result that: the strong material (material 3) is distributed in the main portion of the optimized structure to bear most of the stress induced by the external force, the volume fraction of which is large; the volume fraction of the intermediate strength material (material 2) and the weak material (material 1) are small, which are distributed in the form of auxiliary materials to consolidate the overall performance of the structure.

Figure 18 shows the iterative curves of the objective function and volume fraction in topology optimization of three-material two-bar bracket structure by this method. From Fig. 18, it can be found that: after only 20 iterations, the values of objective function and volume fraction gradually become stable, indicating that this method has the advantages of high speed and stable process, no numerical oscillation, and no other adverse effects when applied to topology optimization of multi-material two-bar bracket structure.

Fig. 18

Curves of objective function and volume fraction in topology optimization of three-material two-bar bracket structure by the proposed method. (The legends ‘Vol1’, ‘Vol2’ and ‘Vol3’ represent the volume fractions of material 1, material 2, and material 3, respectively)

From this case, it can be concluded that this method can maintain high efficiency of the optimization process and good stability of the optimization results in the topology optimization of relatively complex multi-material structure.

5.3 Three-point-load bridge

The design domain of the three-point-load bridge is shown in Fig. 19, where the ratio of length and width is 8:3. The lower-left corner of the design domain is fixed and the lower-right corner of the design domain is simply supported. Two downward forces of $F = 1$ are applied at the one-fourth point and the three-fourth point of the lower side, and meanwhile a downward force of $F = 2$ is applied at the midpoint of the lower side. This example consists of two cases. The first case of this example involves topology optimization of single-material three-point-load bridge, which is presented to highlight the effectiveness and advantage of the proposed method. In this case, the parameter settings are provided below this paragraph. The design domain is divided into $80 \times 30$ quadrilateral meshes, the Young’s modulus of the solid material is set to $E_{0} = 1$. To avoid the singularity of the calculation results, the Young’s modulus of the void material is set to $E_{\hbox{min} } = 10^{ - 9}$. The Poisson’s ratio is set to $\gamma = 0.3$, and the volume fraction constraint is set to 0.4. The shape sensitivity constraint factor is set to $\zeta = 0.02$, and the Lagrange multiplier $\lambda$ is set to 1. To make the optimization process quick, a porous structure is also used in this case. Thus, the radius of the hole in the design domain is set to $r = 3$.

Fig. 19

Initial design domain of three-point-load bridge

In this case, the SIMP interpolation method, the conventional level set method and the proposed method are used for solving the same structural topology optimization design problem, and then the final topology optimization results obtained by the three methods are compared to highlight the effectiveness and advantage of the proposed method.

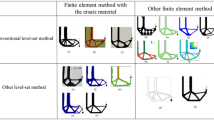
The final topology optimization results of single-material three-point-load bridge obtained by the proposed method, the conventional level set method, and the SIMP interpolation method are shown in Figs. 20, 21, and 22, respectively. From Figs. 20, 21, and 22, it can be found that the proposed method is the most satisfactory in terms of the smoothness.

Fig. 20

Final topology optimization result of single-material three-point-load bridge by the proposed method

Fig. 21

Final topology optimization result of single-material three-point-load bridge by the conventional level set method

Fig. 22

Final topology optimization result of single-material three-point-load bridge by the SIMP interpolation method

Figures 23 and 24 show the iterative curves of objective function and volume fraction in the topology optimization of single-material three-point-load bridge by the three different methods, respectively. In Figs. 23 and 24, the red lines represent the topology optimization process via the proposed method, the compliance value of the final optimization result is 239.2, and the corresponding volume fraction is 0.3999; the blue lines represent the topology optimization process via the conventional level set method, the compliance value of the final optimization result is 273.0, and the corresponding volume fraction is 0.4001; the green lines represent the topology optimization process via the SIMP interpolation method, and the optimization process has a final compliance value of 290.9 and a volume fraction of 0.4000. From Figs. 23 and 24, it can be found that: among the three methods, the proposed method has resulted in the smallest compliance value of optimal result (239.2 < 273.0 < 290.9) in the case of almost identical volume fractions.

Fig. 23

Curves of objective function in the topology optimization of single-material three-point-load bridge by three different methods. (Red, blue, and green lines represent the values of compliance obtained by the proposed method, the conventional level set method, and the SIMP interpolation method, respectively)

Fig. 24

Curves of volume fraction in the topology optimization of single-material three-point-load bridge by three different methods. (Red, blue, and green lines represent the values of volume fraction obtained by the proposed method, the conventional level set method, and the SIMP interpolation method, respectively)

The second case of this example involves topology optimization of three-material three-point-load bridge, which is used to further demonstrate the effectiveness and advantage of the proposed method. In this case, the design domain and boundary conditions are the same as those in the first case of this example. The parameter settings in this case are provided below this paragraph. Figure 25a indicates the initial material distribution of three-material three-point-load bridge, where the red part represents material 1, the green part represents material 2, and the blue part represents material 3. The corresponding elasticity moduli of the three materials are set to $E_{1} = 1$, $E_{2} = 3$ and $E_{3} = 9$, respectively. The volume fraction of the three materials are set to $Vol_{1} = 0.1$, $Vol_{2} = 0.1$ and $Vol_{3} = 0.3$, respectively.

Fig. 25

Initial material distribution and final topology optimization result of three-material three-point-load bridge. (a Initial material distribution of three-material three-point-load bridge; b Optimal topology of three-material three-point-load bridge by the proposed method)

Figure 25b shows the optimal topology result of three-material three-point-load bridge by the proposed method after 177 iterations, and the corresponding compliance value is 24.975. It can also be found from the optimal result that: the strong material (material 3) is distributed in the main portion of the optimized structure to bear most of the stress induced by the external force, the volume fraction of which is large; the volume fraction of the intermediate strength material (material 2) and the weak material (material 1) are small, which are distributed in the form of auxiliary materials to consolidate the overall performance of the structure.

Figure 26 shows the iterative curves of the objective function and volume fraction in the topology optimization of three-material three-point-load bridge by this method. From Fig. 26, it can also be found that: after only 20 iterations, the values of objective function and volume fraction gradually become stable, indicating that the proposed method has the advantages of high speed and stable process, no numerical oscillation, and no other adverse effects when applied to topology optimization of multi-material multi-point-load bridge.

Fig. 26

Curves of objective function and volume fraction in the topology optimization of three-material three-point-load bridge by the proposed method. (The legends ‘Vol1’, ‘Vol2’ and ‘Vol3’ represent the volume fractions of material 1, material 2, and material 3, respectively)

From this case, it can also be concluded that this method can maintain high efficiency of the optimization process and good stability of the optimization results in the topology optimization of relatively complex multi-material structure.

6 Conclusions

In this contribution, a PLSM based on CS-RBF with shape sensitivity constraint factor is proposed for structural topology optimization. The parameterized level set topology optimization method based on CS-RBF has good numerical stability, by which the optimal design results with smooth boundary can be obtained. Inheriting the advantages mentioned above, the proposed method controls the objective function by adding shape sensitivity constraint factor in the process of updating the design variables via the MMA algorithm. With the shape sensitivity constraint factor, the step length is changeable and controllable in the updating iterative process of MMA algorithm so as to increase the speed of the proposed method. The balance of convergence speed and numerical stability can be reached by the values of sensitivity and shape derivative. Under the condition that the optimized design result has enough accuracy, the computational cost is greatly reduced and the convergence speed is also increased. Several typical single-material and multi-material numerical examples are presented to demonstrate the effectiveness and feasibility of the proposed method. Numerical simulation results show that: besides greatly reducing the computational cost, this method has the following advantages. (1) This method has good numerical stability, by which the optimization results with smooth boundary can be obtained. (2) The optimization results have little dependence on the initial designs when new holes are generated. (3) With the help of shape sensitivity constraint factor, it is no longer necessary for this method to initialize the level set equation, so the stability of the optimization process is greatly enhanced. (4) Since the gradient-based MMA algorithm with rigorous theoretical derivation is used to update the design variables, this method is suitable for the complex optimization design system with multiple constraints.

In this work, the proposed method has already been demonstrated by the examples involving topology optimization of 2D structures. As stated in the introduction above, the PLSM based on CS-RBF is essentially a SIMP method. The SIMP method has already been applied to addressing 3D topology optimization problems. Therefore, it is certain that the proposed method can also be extended to dealing with topology optimization of 3D structures. Nevertheless, achieving this goal currently is quite challenging for us due to some technical difficulties. Accordingly, we intend to pursue this goal by tackling these technical difficulties in future work.