1 Introduction

When the energy within a rock mass reaches a certain threshold value, microcracks occur. This process is accompanied by the release of elastic waves. The release of elastic waves is called micro-seismicity [24, 31]. Since the 1930s, the location of such micro-seismicity has been a problem, and the search for micro-seismic phenomena has gained increasing attention. Microseismic monitoring has been successfully applied in practical engineering, such as South Africa’s Integrated Seismic System, Canada’s Engineering Seismology Group, and Poland’s Seismological Observation System [8, 13, 14, 26]. This technique plays an important role in the early warning and prediction of geological hazards including landslide [15, 16, 27, 28, 32]. This technology has been widely used in fields such as mining, underground, and tunnel engineering [4, 7, 22, 23]. Compared with traditional deformation monitoring, micro-seismic monitoring technology shows remarkable three-dimensional space and real-time advantages and is not limited to point measurements. However, source location is a fundamental problem for micro-seismic monitoring. Hence, effective source localization algorithms are vital in developing micro-seismic monitoring technology [9, 19].

Source localization is a hot research topic that involves geophysics, geotechnical engineering, and information science. Early localization algorithms included the Geiger method [11], joint inversion method [6], and relative positioning method [25]. Recently, some new methods to locate seismic sources have been developed from engineering applications [5, 9, 17, 19, 21]. Based on the mathematical transformation of the arrival time, Dong and Li [5] proposed a source localization method that does not incorporate the wave velocity. Li et al. [17] improved the method of Dong and Li [5] to provide a simple iterative source search model without considering the velocity. Feng et al. [9] proposed a piecewise velocity model and determined the seismic source position using a particle swarm algorithm. Li et al. [19, 20] used the simplex algorithm to capture the micro-seismic source location, with an L1 norm objective function improving the accuracy of source location. In practice, the accuracy of locating the micro-seismic source is affected by many factors, such as signal observation, the velocity model, the objective function, and the layout of the geophone. These factors are interrelated, and inaccuracies in any one of them may lead to an increase in the source location error. Therefore, the influence of various factors should be minimized to improve the accuracy of source localization.

In engineering, a uniform velocity model is usually used for convenience [12]. Some researchers have gradually established a multi-directional velocity model [4]; however, this requires a large quantity of wave velocity measurement data, which is difficult for complex rock formations. The positioning method is improved from the objective function, and the mathematical processing is convenient [18].

According to the objective function of the factors influencing micro-seismic source localization, the characteristics of the wave velocity and the effect of the objective function on positioning accuracy are analysed. Based on an improved objective function, a new method of micro-seismic source location is developed.

2 General model of micro-seismic source location

2.1 Mathematical model of micro-seismic source location

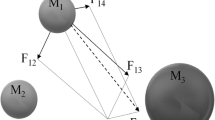
In practical engineering, micro-seismic monitoring obtains useful information by analysing signals from rock fractures, which can provide a scientific basis for evaluating rock mass stability [29, 30]. A number of geophones are arranged in a monitoring area around the seismic source. If micro-seismic events occur in the region, the signal is captured by the signal geophone and converted into a voltage or charge. Multi-point synchronous data acquisition from each geophone observation enables the position and velocity to be determined in the location equation. As a result, the space–time parameters of the micro-seismic source can be obtained, and the source localization can be realized. In practical applications, the P-wave is typically used for localization because of difficulties in measuring the S-wave. In Fig. 1, point O is the source, and A–J are the geophones. The P-wave signal generated by the source propagates in all directions, and the actual P-wave velocity is not isotropic. However, for convenience of the mathematical description, the P-wave velocity is usually assumed to be the same in all directions [5, 17, 19, 20].

Fig. 1
figure 1

Sketch of the micro-seismic source location

Full size image

The ideal mathematical model of micro-seismic positioning is written as follows:

$$ \sqrt {(x_{i} - x_{\text{o}} )^{2} + (y_{i} - y_{\text{o}} )^{2} + (z_{i} - z_{\text{o}} )^{2} } = v_{\text{p}} (t_{i} - t_{0} ), $$
(1)

where (xi, yi, zi) are the coordinates of geophone i (i = 1, 2,…, n), vp is the P-wave velocity, ti is the observed time of the geophone i, t0 is the shock time, and (xo, yo, zo) are the source coordinates. The parameters (xo, yo, zo), vp, and t0 are unknown.

2.2 Method of determining the micro-seismic source

Optimization techniques such as genetic algorithms (GA) and particle swarm optimization (PSO) have been used to solve Eq. (1). When an optimization algorithm is employed, the objective function can be specified. By transforming Eq. (1), the trigger times (TT) and time difference (TD) methods, which are widely used for actual micro-seismic source location, are developed.

The TT method is described as follows [5, 17]:

$$ \hbox{min} \,{\text{fun}} = \sum\limits_{i = 1}^{n} {\left( {t_{i} - \frac{{\sqrt {(x_{i} - x_{\text{o}}^{'} )^{2} + (y_{i} - y_{\text{o}}^{'} )^{2} + (z_{i} - z_{\text{o}}^{'} )^{2} } }}{{v_{\text{p}}^{'} }} - t_{0}^{'} } \right)}^{2} , $$
(2)

where the source location \( (x_{\text{o}}^{'} , \, y_{\text{o}}^{'} , \, z_{\text{o}}^{'} ) \), P-wave velocity \( v_{\text{p}}^{'} \) obtained from inversion and seismic time \( t_{0}^{'} \) are unknown.

The TD method is written as [5, 17, 19] follows:

$$ \hbox{min} {\text{ fun}} = \sum\limits_{i = 1}^{n - 1} {\left( {t_{i + 1} - t_{i} - \frac{{\left( {\sqrt {(x_{i + 1} - x_{\text{o}}^{'} )^{2} + (y_{i + 1} - y_{\text{o}}^{'} )^{2} + (z_{i + 1} - z_{\text{o}}^{'} )^{2} } - \sqrt {(x_{i} - x_{\text{o}}^{'} )^{2} + (y_{i} - y_{\text{o}}^{'} )^{2} + (z_{i} - z_{\text{o}}^{'} )^{2} } } \right)}}{{v_{\text{p}}^{'} }}} \right)^{2} } , $$
(3)

where the source location \( (x_{\text{o}}^{'} , \, y_{\text{o}}^{'} , \, z_{\text{o}}^{'} ) \) and P-wave velocity (\( v_{\text{p}}^{'} \)) are unknown.

Equation (2) or (3) is solved by an optimization method, and the minimum value of the objective function is taken as the inverse solution of the seismic source.

3 Error analysis of source localization

Micro-seismic localization contains many types of errors related to the spatial coordinates of the geophone, anisotropy of the wave velocity, and observed time. Errors are produced by known parameters in the micro-seismic location, and it is difficult to obtain an accurate solution. Therefore, it is very important to select an approximate solution that satisfies the engineering requirements. Spatial coordinate errors and arrival time errors can be corrected by improving instrument observations. This section is mainly concerned with the effects of velocity errors and the objective function on the source localization.

Micro-seismic source location techniques have been widely applied in engineering because methods based on a uniform velocity are easy to implement. However, the actual wave velocity is not uniform. The error caused by the uniform velocity model has gained increasing attention. To illustrate the non-uniformity of the wave velocity, the velocity is calculated using data (see Table 1) from a previous project [10]; the positional arrangement of the geophones is shown in Fig. 2, and the calculated results are shown in Fig. 3. Figure 3a describes the velocity of the seismic source to each geophone calculated by the TT method. The velocity in Fig. 3b was calculated using the TD method, that is, by comparing the velocity at each pair of geophones. As there are 11 geophones, there are \( C_{11}^{2} = 55 \) sets of velocities. In Fig. 3, the velocity difference at each geophone is remarkable. According to the principle of the arrival time difference, the velocity calculated by each pair of geophones is different.

Table 1 The monitoring data [10]
Full size table
Fig. 2
figure 2

Positional arrangement of the geophones

Full size image
Fig. 3
figure 3

Velocity calculations: a TT method and b TD method

Full size image

The objective function of micro-seismic source location has an important influence on the positioning result. An objective function combining P-wave and S-wave arrival times has been proposed [18]. However, its equilibrium coefficient needs to be determined empirically. The current method is to minimize the objective function to obtain the positioning results. The known parameters of micro-seismic location produce errors; thus, the localization results from minimizing the objective function are inconsistent with the actual conditions. Figure 4 compares the objective function [f, see Eqs. (2) and (3)] and the positioning accuracy (d), which is the Euclidean distance between the estimated and actual locations in the search region (confined by boundary conditions for algorithm settings). Actual source positions of \( \pm \) 10 m, \( \pm \) 100 m, and \( \pm \) 1000 m correspond to small, medium, and large scales, respectively.

Fig. 4
figure 4

Comparison of the objective function value and location accuracy: a1 small scale (TT), a2 small scale (TD), b1 medium scale (TT), b2 medium scale (TD), c1 large scale (TT), and c2 large scale (TD)

Full size image

In Fig. 4, for each scale, the objective function of the micro-seismic location problem has many extreme points. Therefore, the source search is a complex multi-extremum optimization problem. At different scales, the source coordinates of the global minimum of the objective function are not equal to those of the minimum distance function. The error of the micro-seismic positioning system is difficult to eliminate. Enlarging the search area increases number of minimum points of the objective function; thus, searching becomes more difficult. It is necessary to determine the boundary conditions according to the actual conditions to reduce difficulties in searching the micro-seismic location.

In summary, the velocity model and the objective function have a significant effect on micro-seismic source location. In the next section, a micro-seismic source localization algorithm is proposed to improve the accuracy of micro-seismic source location.

4 Improvement of the micro-seismic source location method

4.1 Modification of the objective function

As it is difficult to locate the micro-seismic source accurately with a single source location, a combined objective function for micro-seismic source localization was introduced by Li et al. [18]. However, the method of combining P-wave and S-wave arrival times increases the technical difficulty. Although the velocity model and the objective function are the factors affecting the location error of the micro-seismic source, it is difficult to modify the velocity model, while the correction of the objective function becomes much easier. Therefore, the following objective function is proposed:

$$ \hbox{min} \,{\text{fun}} = \alpha \sum\limits_{i = 1}^{n} {\left( {t_{i} - \frac{{\sqrt {(x_{i} - x_{\text{o}}^{'} )^{2} + (y_{i} - y_{\text{o}}^{'} )^{2} + (z_{i} - z_{\text{o}}^{'} )^{2} } }}{{v_{\text{p}}^{'} }} - t_{0}^{'} } \right)}^{2} + \beta D\left( {\left( {t_{i} - \frac{{\sqrt {(x_{i} - x_{\text{o}}^{'} )^{2} + (y_{i} - y_{\text{o}}^{'} )^{2} + (z_{i} - z_{\text{o}}^{'} )^{2} } }}{{v_{\text{p}}^{'} }} - t_{0}^{'} } \right)^{2}_{{_{i = 1, \ldots ,n} }} } \right)$$
(4)

where D is the variance function (\( D(w_{i} )_{i = 1,2, \ldots ,n} = {{\sum\nolimits_{i = 1}^{n} {\left( {w_{i} - \left( {\sum\nolimits_{i = 1}^{n} {w_{i} } } \right)/n} \right)} } \mathord{\left/ {\vphantom {{\sum\nolimits_{i = 1}^{n} {\left( {w_{i} - \left( {\sum\nolimits_{i = 1}^{n} {w_{i} } } \right)/n} \right)} } n}} \right. \kern-0pt} n}, \)), which can be calculated according to probability theory; and \( \alpha \), and \( \beta \) are the weight coefficients (\( 0 \le \alpha ,\beta \le 1 \), generally, \( \alpha = \beta \)). The first term in Eq. (4) can be considered the L2-norm (compared with the L1-norm, the L2-norm is more holistic, while the L1-norm is sparse), which is used to evaluate the accuracy of the positioning results. The second term is used to characterize the stability of the overall results. The variance function is used to evaluate the positioning accuracy of each geophone. The smaller the variance is, the more stable the data becomes, which can be used to characterize the information utilization ratio of each detector. Based on the TD method, another improved objective function can also be given by

$$ \begin{aligned} \hbox{min} {\text{ fun}} & = \alpha \sum\limits_{i = 1}^{n - 1} {\left( {t_{i + 1} - t_{i} - \frac{{\left( {\sqrt {(x_{i + 1} - x_{\text{o}}^{'} )^{2} + (y_{i + 1} - y_{\text{o}}^{'} )^{2} + (z_{i + 1} - z_{\text{o}}^{'} )^{2} } - \sqrt {(x_{i} - x_{\text{o}}^{'} )^{2} + (y_{i} - y_{\text{o}}^{'} )^{2} + (z_{i} - z_{\text{o}}^{'} )^{2} } } \right)}}{{v_{\text{p}}^{'} }}} \right)^{2} } \\ & \quad + \beta D\left( {\left( {t_{i + 1} - t_{i} - \frac{{\left( {\sqrt {(x_{i + 1} - x_{\text{o}}^{'} )^{2} + (y_{i + 1} - y_{\text{o}}^{'} )^{2} + (z_{i + 1} - z_{\text{o}}^{'} )^{2} } - \sqrt {(x_{i} - x_{\text{o}}^{'} )^{2} + (y_{i} - y_{\text{o}}^{'} )^{2} + (z_{i} - z_{\text{o}}^{'} )^{2} } } \right)}}{{v_{\text{p}}^{'} }}} \right)_{i = 1,2, \ldots ,n - 1} } \right) \\ \end{aligned} $$
(5)

4.2 Particle swarm optimization

PSO [1] is one of the most representative intelligent optimization algorithms. Unlike traditional optimization methods, PSO does not need a derivative function and is easy to implement with fast convergence. The complexity of the PSO algorithm is obviously lower than that of other intelligent optimization algorithms [2], such as the GA, artificial fish swarm algorithm, and artificial bee colony algorithm. The advantages of PSO have been seen in many engineering fields. In this algorithm, the solution of the problem is represented by the particle position x.

To realize local and global optimization, the current velocity v and particle position x are iterated until they satisfy some preset conditions. The key equation of the PSO algorithm is expressed as follows:

$$ v_{i}^{k + 1} = wv_{i}^{k} + c_{1} r_{1} (p_{i}^{k} - x_{i}^{k} ) + c_{2} r_{2} (g_{i}^{k} - x_{i}^{k} ), $$
(6)
$$ x_{i}^{k + 1} = x_{i}^{k} + v_{i}^{k + 1} , $$
(7)

where \( v_{i}^{k} \), and \( x_{i}^{k} \) are the particle velocity and position after k iterations, respectively; \( p_{i}^{k} \) is the local optimal position of the particles; \( g_{i}^{k} \) is the global best position of the particles, and c1, and c2 are the learning factor and the step adjustment parameter, respectively. The inertia weight w is an important parameter in the PSO algorithm that balances the effectiveness of global and local searches. The value of w generally decreases with each iteration according to

$$ w_{i} = w_{\text{max} } - \frac{i}{N}(w_{\text{max} } - w_{\text{min} } ), $$
(8)

where wmax= 0.9, wmin= 0.4 and i/N is the ratio of the iteration number to the total (maximum) number of iterations. By linearly decreasing the inertia coefficient, the global search performed at the initial stage of the algorithm gradually becomes a local search in the later stages of the algorithm.

In this paper, the PSO algorithm is employed to search the source location. If Eq. (4) is the objective function, then the number of the optimization variable is 5. If Eq. (5) is the objective function, then the number of the optimization variable is 4. The flow chart of the improved method is given in Fig. 5. In addition to the PSO algorithm, the other optimization algorithms can also be employed. The PSO algorithm is mainly considered in this paper because it is easy to perform. Among the optimization algorithms, genetic algorithm and particle swarm optimization are the two most common algorithms. Compared with genetic algorithms, the implementation steps of particle swarm optimization are much more concise (the genetic algorithm includes three processes of inheritance, hybridization and mutation). Particle swarm optimization is the most concise optimization one until now.

Fig. 5
figure 5

The flow chart of the improved method

Full size image

5 Engineering example

5.1 Case 1

Data for the observation of each event by the geophones are presented in Table 2 [10]. The source location of the event is located by the method proposed in this paper. The proposed method (method 1, Eq. (4) is used to describe the objective function) is compared with a localization method based on the arrival time (method 2). Because the proposed method mainly focuses on an improved objective function, specific search algorithms such as GA and PSO are not compared. Therefore, based on the two methods, PSO is used for the search process, which is computed by MATLAB.

Table 2 Geophone coordinates and observations [10]
Full size table

The same two-parameter set (population number of 50, evolution algebra of 2000) was applied in each method, and the results are presented in Table 3. The source location given by method 1 is (67,429.98 m, 52,080.40 m, 430.26 m), and that given by method 2 is (67,430.70 m, 52126.32 m, 478.74 m). The actual source location is (67,464.76 m, 52,109.28 m, 441.29 m).

Table 3 Results calculated by the two methods
Full size table

An improved positioning accuracy is defined as:

$$ p = \frac{{d_{2} - d_{1} }}{{d_{2} }} \times 100\% , $$
(9)

where d1 is the positioning error (the Euclidean distance between the actual source and method 1) of method 1 and d2 is the positioning error of method 2 (the Euclidean distance between the actual source and method 2). Both methods can show relatively accurate source locations. The calculated results indicate that the accuracy of method 1 is about 14% better than that of method 2.

5.2 Case 2

The geophone layout scheme [3] shown in Fig. 6 consists of eight geophones. The two methods used in case 2 were used to locate the source of the event.

Fig. 6
figure 6

Positional arrangement of the geophones for case 2

Full size image

The parameters for each method were as described above (population number of 50, evolutionary algebra of 1000). The results are presented in Table 3. The localization result given by method 1 is (6515.50 m, 8674.40 m, 534.30 m), whereas that given by method 2 is (6494.90 m, 8633.30 m, 564.40 m). The actual source location in this event is (6597.50 m, 8704.10 m, 534.80 m). The localization results of method 1 are more than 32% better than those of method 2 in Table 4.

Table 4 Error analysis of the two methods
Full size table

6 Conclusions

  1. 1.

    The actual wave velocity is anisotropic. Using the time of arrival or the time difference method, the wave velocity is anisotropic. Therefore, it is difficult to ignore the effect of the velocity error on positioning.

  2. 2.

    A new inverse objective function has been proposed by combining the advantages of the L2 norm function and the variance function. The effectiveness of the proposed method was verified by two case studies. This objective function can assess the accuracy and ensure the stability of the positioning results. Deviations in the accuracy at different geophone positions can be prevented.