1 Introduction

Overhanging rock failure is a geological problem in mountainous regions worldwide and can cause sudden and severe disasters. A large number of macro- and micro-cracks are produced in overhanging rock under the influence of geological structures, excavation, long-term weathering, precipitation, and other factors. Because of stress concentrations at crack tips, rock failure is essentially crack-initiated followed by the eventual propagation of macro- and micro-cracks through the rock (Atkinson 1987; Chen et al. 2006).

Fracture mechanics (FM) focuses on a mechanical description of cracks in brittle materials and is developing rapidly in the field of geological disasters. Tharp and Coffin (1985) demonstrated that simplified FM methods are consistent with observed slope stability conditions and that joints behave as predicted. Kemeny (2003, 2005) presented a time-dependent model of rock joint cohesion reduction and factor of safety based on FM using both a deterministic and probabilistic technique. Chen and Tang (2013) developed analysis methods for various types of perilous rock based on FM.

There are three basic fracture modes, differentiated by the applied stress experienced by cracks: Mode I (tensile opening), Mode II (shear sliding), and Mode III (shear tearing) (Anderson 2005). Possible failure mechanisms of the overhanging rock can be divided into three categories: falling (tensile–shear fracture), toppling (tensile–shear fracture), and sliding (compression–shear fracture) (Chen and Tang 2013). For toppling overhanging rock subjected to tensile–shear fracture, the propagation of the controlling crack is a fundamental cause of its instability (Braathen et al. 2004; Chen et al. 2006; Chen and Tang 2007; Wu et al. 2016; Huang et al. 2017). Investigation of crack initiation and propagation using FM is therefore of great significance for defining the mechanism of toppling overhanging rock instability.

However, additional factors influencing overhanging rock, including the geometry of the controlling crack and loading conditions, have effects on stability that increase the difficulty of studying rock failure mechanisms. For example, the failure of overhanging rock on steep slopes or cliffs is quite difficult to simulate using large in situ tests, so laboratory fracture models of overhanging rock subjected to tensile–shear stresses are an effective way to analyze the mechanical mechanism of crack initiation and propagation under different conditions. Nevertheless, few studies on overhanging rock fracture models have been published (Huang et al. 2017).

Simulations of rock crack propagation have long been a hotspot in the numerical analysis of rock mechanics. Mature analytical methods include the finite element method (FEM) (Bouchard et al. 2000), extended finite element method (XFEM) (Belytschko and Black 1999), discrete element method (Ergenzinger et al. 2011), numerical manifold method (Zhang et al. 2010), and meshless method (Belytschko et al. 1995). XFEM is an efficient numerical method for solving the discontinuous problem of crack propagation (Belytschko and Black 1999), because it overcomes the problem of high-density meshing in areas where stress and deformation are concentrated and does not require remeshing during crack propagation. Owing to this advantage, XFEM is generally acknowledged as the preferred method for analyzing discontinuous problems (Chessa et al. 2002; Areias and Belytschko 2005; Lecampion 2009; Pathak et al. 2013).

To study the influence of a controlling crack on overhanging rock under gravity or external load, this paper describes tensile–shear fracture tests of overhanging rock models with prefabricated sandstone, analyzes the evolution of load–displacement curves and model failure modes, and discusses the effects of crack parameters and load distance on the mechanical properties of overhanging rock. Maximum circumferential stress theory is used as the fracture criterion of mixed mode I–II fractures to calculate the stress intensity factor (SIF) at the crack tips and theoretical failure loads using different crack and load parameters. The propagation paths of cracks at different load distances are simulated by XFEM, and the evolution process of the equivalent stress at crack tips is analyzed.

2 Fracture Mode of Toppling Overhanging Rock

2.1 Mixed Mode I–II Fractures of Toppling Overhanging Rock

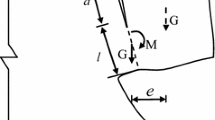
In actual overhanging rock, the inclination angle of the controlling crack is generally larger than that of the rock layer, which is mostly located in the tensile structural plane generated by unloading. The center of gravity of the overhanging rock mass lies in the outer side of the controlling rock, which is the key to overhanging rock toppling. Overhanging rock is usually destroyed under load action by rotating and toppling around the bottom surface. A mechanical model for overhanging rock is shown in Fig. 1, where T is the vertical load on the overhanging rock, G is the weight of the overhanging rock, a0 is the length of the controlling crack, b is the locking section length of the overhanging rock, H is the thickness of the overhanging rock, β is the inclination angle of the controlling crack, and x1 and x2 are the horizontal distances from the center of the applied loads to the controlling crack. In this model, there is a displacement constraint on the left side of the overhanging rock and an external load applied on the right side of the rock.

Fig. 1
figure 1

Idealized diagram of a mechanical model for overhanging rock

Full size image

For the overhanging rock, T and G generate shear stress at the crack tip and also a bending moment M by the eccentric action of the load. The stress state of the crack tip can thus be equivalently decomposed into pure shear and pure bending moment. Figure 2 shows the different fracture modes of overhanging rock under two kinds of stress. Shear stress causes a mode II fracture and the equivalent bending moment causes a mode I fracture; thus, a mixed mode I–II fracture is generated at the crack tip in the overhanging rock.

Fig. 2
figure 2

Diagrammatic sketches illustrating fracture control modes for an overhanging rock: a pure shear; b pure bending moment

Full size image

2.2 Fracture Criteria of Mixed Mode I–II Crack

The stresses acting around a mixed mode I–II crack are plotted in two dimensions in Fig. 3, and the stress components at the crack tip in polar coordinates can be written as (Lawn and Wilshaw 1975):

Fig. 3
figure 3

Force diagram of a mixed mode I–II crack

Full size image
$$\begin{gathered} {\sigma _{{\text{rr}}}}=\frac{1}{{2\sqrt {2\pi r} }}\left[ {{K_{\text{I}}}\left( {3 - \cos \theta } \right) \cdot \cos \frac{\theta }{2}+{K_{{\text{II}}}}\left( {3\cos \theta - 1} \right) \cdot \sin \frac{\theta }{2}} \right], \hfill \\ {\sigma _{\theta \theta }}=\frac{1}{{2\sqrt {2\pi r} }}\cos \frac{\theta }{2}\left[ {{K_{\text{I}}}\left( {1+\cos \theta } \right) - 3{K_{{\text{II}}}}\sin \theta } \right], \hfill \\ {\tau _{{\text{r}}\theta }}=\frac{1}{{2\sqrt {2\pi r} }}\cos \frac{\theta }{2}\left[ {{K_{\text{I}}}\sin \theta +{K_{{\text{II}}}}\left( {3\cos \theta - 1} \right)} \right], \hfill \\ \end{gathered}$$
(1)

where σrr, σθθ, and τrθ are the radial stress, circumferential tensile stress, and shear stress at the crack tip, respectively, θ is the crack deviation angle (positive counterclockwise, negative clockwise), and r is the distance from the crack tip. The expressions \({K_{\text{I}}}={\sigma ^\infty }\sqrt {\pi a}\) and \({K_{{\text{II}}}}={\tau ^\infty }\sqrt {\pi a}\) are the mixed mode I and mode II stress intensity factors of an infinite plate with a central crack, where a is the crack half-length, and σ∞ and τ∞ are the far-field tensile stress and the far-field shear stress, respectively.

According to the Stress Intensity Factors Handbook and the calculation of SIF for a controlling crack (Murakami 1987; Chen and Tang 2007), the SIF at the crack tip under the pure bending moment M produced in Fig. 2b can be expressed as:

$${K_{{\text{IM}}}}=F\frac{{6M}}{{t{H^2}}}\sqrt {\pi {a_0}} ,$$
(2)

in which:

$$M=T({x_1} - {a_0}\cos \beta )+G{x_2},$$
(3)

where t is the thickness of the model and F is the boundary correction factor. The boundary used in the Handbook deviates from that of the test model, and crack parameters and load distance also influence the effective model boundary. It is necessary to calibrate F. F of the test model is calibrated by the J-integral method (Rice and Rosengren 1968). The revised F can be given by:

$$F=1.01 - 1.68\frac{{{a_0}{x_1}}}{{{H^2}}}+65.08{\left( {\frac{{{a_0}{x_1}}}{{{H^2}}}} \right)^2}+85.68{\left( {\frac{{{a_0}{x_1}}}{{{H^2}}}} \right)^3} - 128.16{\left( {\frac{{{a_0}{x_1}}}{{{H^2}}}} \right)^4}.$$
(4)

In Fig. 2a, SIF at the crack tip under pure shear stress can be written as (Murakami 1987):

$${K_{{\text{II}}\tau }}=1.12\tau \sqrt {\pi {a_0}} ,$$
(5)

in which:

$$\tau =\frac{{T+G}}{{tH}}.$$
(6)

Erdogan and Sih (1963) proposed a composite criterion of maximum circumferential stress. This criterion holds that a mixed mode I–II crack propagates along the corresponding direction of maximum tensile stress and that the fracture direction should satisfy the following equation:

$$\frac{{\partial {\sigma _\theta }}}{{\partial \theta }}=0,\quad \frac{{{\partial ^2}{\sigma _\theta }}}{{\partial {\theta ^2}}}<0.$$
(7)

Equation (8) can be obtained from Eqs. (1) and (7):

$${\theta _0}=\arctan \frac{{ - 3{K_{\text{I}}}{K_{{\text{II}}}}+\sqrt {9K_{{\text{I}}}^{2}K_{{{\text{II}}}}^{2} - 8K_{{{\text{II}}}}^{2}\left( {K_{{\text{I}}}^{2} - K_{{{\text{II}}}}^{2}} \right)} }}{{K_{{\text{I}}}^{2} - K_{{{\text{II}}}}^{2}}}.$$
(8)

The equivalent stress intensity factor Ke, corresponding to the maximum circumferential tensile stress, is expressed as:

$${K_e}=\frac{1}{2}\cos \frac{{{\theta _0}}}{2}\left[ {{K_{\text{I}}}\left( {1+\cos {\theta _0}} \right) - 3{K_{{\text{II}}}}\sin {\theta _0}} \right].$$
(9)

when Ke > KIC (KIC denoting fracture toughness), fracture propagation of the crack in the overhanging rock will occur.

3 Experimental Scheme of Tensile–Shear Fracture

3.1 Sandstone Rock Material

Sandstone samples used in the tests were obtained from Sichuan, China. The sandstone is fine-grained, well-cemented, and exhibits brittle fracture. The basic physical and mechanical parameters obtained by uniaxial and triaxial compression tests of a Φ50 × 100 mm sample are listed in Table 1. The fracture toughness KIC of the sandstone sample was obtained by the cracked chevron-notched Brazilian disk (CCNBD) test (ISRM 1995).

Table 1 Basic physical and mechanical parameters of sandstone sample
Full size table

3.2 Testing Apparatus and Procedures

The sandstone samples used for testing were cubic blocks with edge lengths of 80 mm (± 1%). The rock sample surface was ground flat to ensure load uniformity during testing. Pre-cut slits (cracks) in each sample were made with a milling machine. We investigated the effects of crack length, crack angle, and distance between the crack tip and the load, as well as the failure mode. The samples were divided into three groups: A, B, and C, corresponding to different crack lengths a0, crack angles β, and load distances x1. Detailed parameters for each sample group are listed in Table 2.

Table 2 Testing condition for each group of samples
Full size table

Tests were performed using an MTS815 rock mechanics test system (MTS Systems Corporation, Eden Prairie, MN, USA). A purpose-built auxiliary steel framework was used to fix the rock sample on one side of the crack and a linear loading shaft to apply a linear load on the other side (Fig. 4). The displacement control mode of the test system was used during the tests at an advance rate of 0.1 mm min−1. A radial displacement sensor was placed on the upper half of the sample to measure horizontal displacement. A vertical displacement sensor was used to measure the vertical compressive displacement of the rock samples.

Fig. 4
figure 4

Photograph of the overhanging rock test apparatus

Full size image

3.3 Displacement–Load Relationship Analysis

Figure 5 presents the displacement–load curves under different crack lengths with a crack angle of 90° and load distance of 20 mm. The curves show that loads increase steadily in the early stage and decrease rapidly after the peak point. As crack length increases, the peak load decreases from about 14.12 to 6.75 kN (Fig. 5a). The peak loads of 30 and 40 mm are 57.65 and 47.54% for the 20-mm crack length, respectively. As crack length increases from 20 to 30 mm, the peak load decreases by 42.35%. As crack length increases from 30 to 40 mm, the peak load decreases by 17.08%. Although the peak load decreases with increase in the crack length, the reduction trend slows.

Fig. 5
figure 5

Displacement–load curves for samples under three different crack lengths: a vertical displacement–load curves; b horizontal displacement–load curves

Full size image

The horizontal displacement–load curve can reflect the initiation and growth process of micro-cracks. Because the appearance of micro-cracks is difficult to observe, it is effective to select the load corresponding to the rapid increase of horizontal displacement as the initiation load. Considering test accuracy and curve characteristics, the load at a horizontal displacement of 0.005 mm was used as the initiation load (Fig. 5b). For the 30-mm crack length, micro-cracks begin to occur and continue developing from initiation load to peak load. When the vertical load increases to 8.14 kN, macroscopic secondary cracks appear at the crack tip and rapidly propagate. At this time, the vertical load drops precipitously and the corresponding horizontal displacement increases substantially. Compared with crack lengths of 40 mm, the horizontal displacement for the crack length of 20 mm has a larger growth rate, and the gap between the initiation and peak loads is small. When the crack length is smaller, the sample is subjected to a larger load; however, the time between micro-crack generation and sample failure is shorter. Samples with smaller crack lengths therefore show stronger brittle characteristics.

Figure 6 shows the displacement–load changes with different load distances for a crack length of 30 mm and crack angle of 90°. Figure 6 demonstrates that the closer the load position is to the crack, the greater the peak load and vertical displacement. The maximum load can reach 15.74 kN, the minimum is 3.32 kN, and the peak load at a 30-mm load distance is only 21.09% of the peak load at a 10-mm load distance (Fig. 6a). When the load distance increases from 10 to 20 mm, the peak load decreases by 48.35%. When the load distance increases from 20 to 30 mm, the peak load decreases by 59.16%. The decreasing amplitude of load gradually increases with increasing load distance.

Fig. 6
figure 6

Displacement–load curves for samples at three different load distances: a vertical displacement–load curves; b horizontal displacement–load curves

Full size image

The load corresponding to the same horizontal displacement decreases with increasing load distance (Fig. 6b). The larger the load distance, the easier it is to produce micro-tension cracks. For samples with smaller load distance (e.g., 10 mm), the growth trend of the horizontal displacement in the early stage is relatively mild, and micro-cracks caused by the bending moment begin to occur with the gradual accumulation of tensile stress. Following an initiation load of 10.42 kN, horizontal displacement increases rapidly, and the accumulation of micro-cracks intensifies until macroscopic secondary cracks occur. It can be concluded from changes in the horizontal displacement–load curve that the sample undergoes gradual damage. For samples with larger load distance (e.g., 30 mm), horizontal displacement increases sharply upon initiation and no additional gradual growth transition is observed. Micro-cracks rapidly tear and expand under a larger bending moment, and the sample is destroyed. The difference between initiation and peak loads at a load distance of 30 mm is only 0.89 kN. Therefore, with increasing load distance, failure progresses from gradual damage, to destruction, to sudden destruction.

Figure 7 shows the displacement–load curves for different crack angles with a crack length of 30 mm and load distance of 20 mm. When the crack angles are 80° and 90°, the vertical displacement–load curves almost overlap in the early stage, but the latter has a relatively large peak load (Fig. 7a). The load with a 90° angle is larger compared to loads corresponding to the same horizontal displacement (Fig. 7b). The shear bearing capacity from tests using the two angles are similar, and the tensile bearing capacity at the 80° crack angle is smaller. When the crack angle is 70°, there are two peak points in the vertical displacement–load curve, and the corresponding horizontal displacement–load curve exhibits two inflection points (Fig. 7b). The peak load of the 90° angle is the maximum, and a double peak load appears at the 70° crack angle.

Fig. 7
figure 7

Displacement–load curves for samples with three different crack angles: a vertical displacement–load curves; b horizontal displacement–load curves

Full size image

3.4 Failure Mode Analysis

Figure 8 show failure modes of samples with different crack lengths. At a crack length of 30 mm, the fracture angle at the crack tip is about 42°. The fracture angle at a crack length of 40 mm is about 67°. Analysis of the propagation path of the secondary crack indicates that the longer the crack length, the more the secondary crack will extend toward the right side of the test model. Crack length therefore has a significant influence on the secondary crack propagation path of the overhanging rock model.

Fig. 8
figure 8

Failure modes of samples under different crack lengths with a crack angle of 90° and load distance of 20 mm: a a0 = 20 mm; b a0 = 30 mm; c a0 = 40 mm. The peak loads corresponding to panels a, b, and c are 14.12, 8.14, and 6.75 kN, respectively

Full size image

The failure modes of samples with different load distances are shown in Fig. 9. When the load distance is 10 mm, micro-cracks caused by the bending moment begin to occur as tensile stress that gradually accumulates. After the load reaches about 12.7 kN, horizontal displacement starts to increase rapidly, and accumulation of micro-cracks intensifies until macroscopic secondary cracks occur. When the load distance is 30 mm, the rock sample splits longitudinally, and the tensile force generated by the bending moment is at a maximum.

Fig. 9
figure 9

Failure modes of samples at different load distances for a crack length of 30 mm and crack angle of 90°: a x1 = 10 mm; b x1 = 20 mm; c x1 = 30 mm. The peak loads corresponding to panels a, b, and c are 15.74, 8.14, and 3.32 kN, respectively

Full size image

Figure 10 shows failure modes of samples at different crack angles. When the crack angle is 70°, the pre-crack tip breaks at the first peak point of the displacement–load curve, which compacts the gap between the crack surfaces, and a secondary split crack occurs at the loading point. Another secondary split crack appears at the second peak point and extends toward the pre-crack tip. Repetition of the loading test under this angle yields similar results. The reason for this phenomenon is that the distance between the crack tip and load distance is small, and the region between those two points forms a larger tensile stress concentration area. That is to say, differences in the failure modes operate in samples with different crack angles. When the crack angle is reduced from 90° to 70°, the failure mode of the sample converts from tensile shear to longitudinal splitting.

Fig. 10
figure 10

Failure modes of samples with different crack angles for a crack length of 30 mm and load distance of 20 mm: a β = 70°; b β = 80°; c β = 90°. The peak loads corresponding to panels a–c are 5.99, 6.59, and 8.14 kN, respectively

Full size image

4 Numerical Simulation of Crack Propagation

4.1 Numerical Calculation Model

A geometric model for simulating crack propagation based on the test model is shown in Fig. 11. The calculated model is a cube with 80-mm edge lengths and a crack length of 30 mm. The upper and lower boundaries (lines A–B and C–D) and the left boundary (line B–C) are constrained. The parameters for calculation analysis are consistent with those of the test model in Table 1. The simulation involves the following steps: establish the geometric model, input material parameters, divide the finite element mesh, and, finally, apply a load to the right side of the crack. A plane strain model is employed. The calculation becomes more complex with increasing crack propagation length. Crack propagation is therefore calculated in several steps.

Fig. 11
figure 11

Geometric model for simulating crack propagation

Full size image

4.2 Numerical Analysis

Numerical simulations of crack propagation under different load distances were performed. Remeshing is a complicated and time-consuming operation during simulated crack propagation; however, the XFEM solves this problem. Based on the partition of unity method, the XFEM adds discontinuous enhancement functions to reflect the singularity of the crack tip and ensures mutual independence between the computed grid and internal geometry. The XFEM has unique advantages for solving discontinuous problems caused by material or geometric factors, especially when the problem involves the evolution of discontinuous boundaries. In the numerical model, the failure loads for three load distances were 13.61, 7.95, and 4.42 kN, respectively. To better analyze the crack propagation process, the loads applied in the numerical models for different load distances were 13.7, 8.0, and 4.5 kN, respectively. Figure 12 displays the horizontal displacement at different load distances.

Fig. 12
figure 12

Contours of horizontal displacement at different load distances: a x1 = 10 mm; b x1 = 20 mm; c x1 = 30 mm. The corresponding load values of panels a–c are 13.7, 8.0, and 4.5 kN, respectively

Full size image

The equivalent (von Mises) stress contours at different load distances are shown in Fig. 13. The number of calculation steps for each model is 13. The crack propagation paths are in agreement with the failure patterns of samples shown in Fig. 9. The model has clear stress concentrations at the load point, crack tip, and bottom constraint boundary point. The stress concentration at the crack tip becomes more marked with increasing load distance. When the load distance is 30 mm, the equivalent stress at the crack tip is significantly greater than that of the load point, which also indicates that crack propagation is rapid under larger tensile stress.

Fig. 13
figure 13

Contours of equivalent stress at different load distances: a x1 = 10 mm; b x1 = 20 mm; c x1 = 30 mm. The corresponding load values of panels a–c are 13.7, 8.0, and 4.5 kN, respectively

Full size image

The variation of equivalent stress with propagation steps using a 20-mm load distance is shown in Fig. 14. Under the action of tensile–shear stress, crack initiation begins at about 40° to the right side of the model, and then extends to the bottom boundary. In the early stages of propagation (before step 5), the equivalent stress at the crack tip is still relatively small and the stress concentration is mainly at the load point. In later stages (steps 5–10), the center of gravity of the model begins to move outward and the equivalent stress at the crack tip increases rapidly. At step 13, the equivalent stress of the crack tip reaches the maximum, which is about 3.9 times the equivalent stress at crack initiation. The equivalent stress increases slowly at first but then more rapidly, indicating that the rock fracture is sudden. In tests of the overhanging rock model, the vertical load also shows a rapid release after reaching the failure load.

Fig. 14
figure 14

Variation of crack propagation path and equivalent stress with calculation step at a load distance of 20 mm: a Step 1; b Step 5; c Step 10; and d Step 13

Full size image

5 Investigation Results and Analysis

5.1 Displacement–Load Curves and Failure Modes from the Tests

We analyzed the displacement–load curves and failure modes of each test group. Table 3 lists the results of samples tested under different conditions. The vertical displacement, initiation load, and peak load for the rock model with a 20-mm crack length and 10-mm load distance are greater than those of other conditions. The difference between the initiation and peak load using a 20-mm crack length is less than that for the 10-mm load distance. Compared with the 10-mm load distance, the overhanging rock model with a 20-mm crack length is more prone to brittle fracture than gradual damage. A comparison of the horizontal displacement–load curves of different crack lengths and load distances indicates that a small crack length can promote the development of brittle failure, while a small load distance can give rise to gradual damage. Horizontal displacement is the largest using a load distance of 30 mm, while the initiation and peak loads are minimum. Increasing load distance exerts the greatest influence on overhanging rock stability. For the failure mode, only the model with a 70° crack angle splits through between the load point and pre-crack tip; the other states exhibit tensile–shear failure. In tensile–shear failure, the initiation angle is largest for a crack length of 40 mm. Overall, load distance and crack length are significant factors affecting overhanging rock stability. Crack length and crack angle greatly influence the failure type of overhanging rock.

Table 3 Test results of sample under different conditions
Full size table

5.2 Comparison and Analysis of the Model Fractures

Equations (2)–(6) and (9) are used to calculate SIFs at the crack tip to compare stress field variations. Table 4 compares peak load and SIF between the experimental and theoretical results. The calculated SIF and theoretical failure load corresponding to Ke (= KIC) are listed in Table 4 for cases of a 90° crack angle. Compared with the theoretical failure load, the test peak load at a crack length of 20 mm and load distance of 10 mm are slightly larger, while the test peak load at a 30-mm load distance is smaller. There is a gap between the measured and theoretical value, which is related to the discreteness of the sample. Compared with the crack length, the theoretical failure load decreases more with increasing load distance, which is consistent with the results obtained from the experiments.

Table 4 Comparison of the load and stress intensity factor (SIF) between tests and theory
Full size table

Except for the load distance of 10 mm, KI is mostly greater than KII, indicating that the failure mode of toppling overhanging rock is closely related to tensile failure. Changes in KI and KII, as calculated from experiment and theory, become smaller with increasing crack length. The variation between KI and KII due to different load distances is greater than those due to crack length and crack angle, and for the load distance of 30 mm, KI is much larger than KII, which indicates that the external load distance has a significant impact on overhanging rock instability. When dealing with overhanging rock, it is therefore very important to prevent bottom excavation and to increase bottom support to improve overhanging rock stability.

Figure 15 compares numerical and experimental results. The crack initiation angles for three different load distances are about 34°, 40°, and 15°, respectively. The failure load for the 10-mm load distance is smaller than that obtained from the physical tests. The growth rate of the vertical displacement–load curve is essentially the same as that in the tests, but the vertical displacement corresponding to failure load is smaller. The horizontal displacement corresponding to the same load is larger in the early stage, in which the difference is more obvious at a load of 10 kN. When the load distance is 20 mm, the horizontal displacement corresponding to the same load in the model test is slightly smaller than the numerical simulation in the initial loading stage, but this gap gradually decreases and starts to exceed the numerical results after 6 kN. For a load distance of 30 mm, the vertical displacement–load curve in the numerical results has a large growth rate and a greater failure load. Compared with the numerical simulation, the horizontal displacement in the physical test increases sharply, showing a more significant brittle failure characteristic. The experimental and numerical results are listed in Table 5.

Fig. 15
figure 15

Comparison between numerical simulation results and physical tests

Full size image
Table 5 Comparison between numerical simulation results and physical test data
Full size table

6 Conclusions

We investigated the evolution of displacement–load curves and failure modes of samples with different crack lengths, crack angles, and load distances based on fracture tests of toppling overhanging rock models. Maximum circumferential stress theory is used to calculate the SIF and theoretical failure load, and changes in the equivalent stress of the numerical model at different load distances were analyzed by XFEM. Through comparisons between physical tests, theoretical calculations, and numerical simulations, the rationality of the obtained analysis results is verified.

  1. (1)

    The initiation load and peak load decrease with increasing crack length, but the decreasing trend slows down. The smaller the crack length, the more brittleness the overhanging rock model exhibits.

  2. (2)

    The peak load decreases with increasing load distance. With increasing load distance, the overhanging rock failure evolves from gradual damage to sudden destruction.

  3. (3)

    There are differences in the failure mode of overhanging rock models at different crack angles. When the crack angle is reduced from 90° to 70°, the failure mode of overhanging rock models is converted from tensile–shear failure to longitudinal splitting.

  4. (4)

    Load distance and crack length are the main factors affecting the stability of overhanging rock. Crack length and crack angle greatly influence the failure type of overhanging rock.