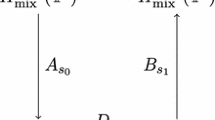Approximation and Entropy Numbers of Embeddings Between Approximation Spaces

Abstract

We consider general linear approximation spaces $X^b_q$ based on a quasi-Banach space X, and we analyze the degree of compactness of the embedding $X^b_q \hookrightarrow X$. Applications are given to periodic Besov spaces on the d-torus, including spaces of generalized and logarithmic smoothness. In particular, we obtain the exact asymptotic behavior of approximation and entropy numbers of embeddings of such Besov spaces in Lebesgue spaces and in Besov spaces of logarithmic smoothness.

1 Introduction

The problem of compactness of embeddings between function spaces on bounded domains $\varOmega$ in ${{\mathbb {R}}}^d$ is a classical question with a long history. Many authors have studied this problem by using a variety of techniques, some of them based upon piecewise-polynomial approximation, more refined spline approximations, the Fourier-analytical approach, or wavelet bases. See, for example, the books by Triebel [48, 4.10], König [29, 3.C], Edmunds and Triebel [22, 3.3] and the references given there; see also the papers by Leopold [36] and Cobos and Kühn [14]. The related question of embeddings between weighted function spaces on ${\mathbb {R}}^d$ has also been extensively studied, as can be seen in the papers by Haroske and Triebel [28], Kühn, Leopold, Sickel and Skrzypczak [33,34,35], Kühn [31, 32] and Haroske and Skrzypczak [26, 27]. The outcome is the description of the degree of compactness of the embeddings $\text {id}$ in terms of the asymptotic behavior of entropy numbers $(e_n(\text {id}))$ and of approximation numbers $(a_n(\text {id}))$. For the case where $\varOmega$ is a bounded domain in ${\mathbb {R}}^d$ with $C^\infty$ boundary, $1<p<\infty , 0 < q \le \infty , s > 0$, and we consider the embedding operator $\text {id}$ from the Besov space $B^s_{p,q}(\varOmega )$ into the Lebesgue space $L_p(\varOmega )$, it turns out that $a_n(\text {id})$ and $e_n(\text {id})$ behave asymptotically as $n^{-s/d}$ (see [22, Theorems 3.3.3/2 and 3.3.4]). The space $B^s_{p,q}({\mathbb {R}}^d)$ is defined by using the Fourier transform, and $B^s_{p,q}(\varOmega )$ is the restriction of $B^s_{p,q}({\mathbb {R}}^d)$ to $\varOmega$.

In this paper, we deal with periodic spaces of functions on the d-torus ${\mathbb {T}}^d$, defined by using the modulus of smoothness. Besides Besov spaces $\mathbf B ^s_{p,q}$, we also consider Besov spaces of generalized smoothness $\mathbf B ^{s, \psi }_{p,q}$, where $s \ge 0$ and $\psi$ is a slowly varying function, paying special attention to the case when $s=0$ and $\psi (t) = (1 + |\log t|)^\gamma$ that we denote by $\mathbf B ^{0,\gamma }_{p,q}$ (see, for example, the papers by DeVore, Riemenschneider, and Sharpley [20]; Caetano, Gogatishvili and Opic [6]; or Cobos and Domínguez [9, 10]). Spaces $\mathbf B ^{0,\gamma }_{p,q}$ have only logarithmic smoothness.

Let $1< p < \infty$. For the embedding $\text {id} : \mathbf B ^{s,\psi }_{p,q} \hookrightarrow L_p$ with $s>0$, we show that the approximation and entropy numbers behave as $n^{-s/d}/\psi (n^{1/d})$. If $s=0$ and $\psi (t) = (1 + |\log t|)^\gamma$, then the behavior is as $(\log n)^{-(\gamma + 1/q)}$ if $\gamma + 1/q > 0$, while in the limit case $\gamma = -1/q$ and $0< q < \infty$, we derive that they behave asymptotically as $(\log \log n)^{-1/q}$. Note that when $s=0$, the estimates do not depend on the dimension d. We also establish sharp results on approximation and entropy numbers of embeddings $\mathbf B ^{s,\psi }_{p,u} \hookrightarrow \mathbf B ^{0,\gamma }_{p,q}$.

To establish all these estimates, we follow a new approach based on the structure of $\mathbf B ^{s,\psi }_{p,q}$ as approximation space modeled on $L_p$. In fact, given an abstract approximation scheme $(X;A_n)$, we consider the approximation spaces $X^b_q$, where b is a certain sequence of positive numbers, and we analyze the degree of compactness of the embedding $X^b_q \hookrightarrow X$ in terms of approximation and entropy numbers.

We work with sufficiently general sequences b, so that spaces $X^b_q$ include as special cases the classical approximation spaces $X^\alpha _q$ (see [4, 5, 18, 19, 39, 41]), the more general spaces $X^{(\alpha ,\psi )}_q$ (see [10, 43]), as well as limiting approximation spaces $X^{(0,\gamma )}_q$ (see [15, 16, 23]) and $X^{[\alpha ,\psi ;r]}_q$ (see [24, 44]). Almira and Luther [1, 2] have also studied an extension of spaces $X^\alpha _q$, but our conditions on the parameters are different.

In Sect. 2, we introduce the spaces $X^b_q$, show an equivalent quasi-norm in $X^b_q$, and prove a representation theorem, which allows us to describe any element $f \in X^b_q$ as the sum of a series $f = \sum _{j=0}^\infty g_j$ with $g_j \in A_{n(j)}$ for a certain sequence (n(j)). This result comprises several others in the literature, namely, the representation theorems established by Pietsch [41, Theorem 3.1] for $X^\alpha _q$, Cobos and Resina [16, 17] and Fehér and Grässler [23, Theorem 1] for $X^{(0,\gamma )}_q$ with $\gamma > -1/q$, Pustylnik [43, Theorem 3.3] for $X^{(\alpha ,\psi )}_q$, and Pustylnik [44, Theorem 3.2] and Fernández-Martínez and Signes [24, Theorem 5.4] for $X^{[\alpha ,\psi ;r]}_q$. In addition, it gives new information for $X^{(0,-1/q)}_q$, the extreme case where $\gamma = -1/q$ and $0< q < \infty$ which shows another jump in the scale.

In Sect. 3, we develop a procedure that shows how one can relate limiting spaces with classical approximation spaces by selecting an appropiate subsequence of the approximation sets $A_n$. As a consequence, we derive the reiteration theorem and the interpolation theorem for limiting spaces $X^{(0,\gamma )}_q$ with $\gamma > -1/q$ established in [23, Theorems 2 and 5] from the corresponding results for spaces $X^\alpha _q$ given in [41, Theorem 3.2], [38] and [5, Korollar 2.3.1]. This technique yields a new result in the extreme case $\gamma =-1/q$. We also use this approach to derive interpolation properties of limiting spaces from the properties of spaces $X^\alpha _q$.

Then, in Sect. 4, we work with linear approximation schemes $(X;A_n)$, that is, we suppose that $A_n = P_n(X)$, where $(P_n)$ is a sequence of uniformly bounded projections in X. We consider the embedding $\text {id} : X^b_q \hookrightarrow X$ and we show an upper estimate for approximation numbers and a lower estimate for entropy numbers. When $X^b_q$ equals $X^{(\alpha ,\psi )}_q$ and $\alpha > 0$, we determine the exact asymptotic behavior of entropy and approximation numbers of the embedding. We also cover the case $X^b_q = X^{(0,\gamma )}_q$ for $\gamma \ge -1/q$, as well as some other embeddings including $\text {id}: X^{(\alpha ,\psi )}_u \hookrightarrow X^{(0,\gamma )}_q$.

In the final Sect. 5, we apply the previous results to embeddings $\mathbf B ^{s,\psi }_{p,q} \hookrightarrow L_p, \mathbf B ^{0,\gamma }_{p,q} \hookrightarrow L_p$ and $\mathbf B ^{s,\psi }_{p,u} \hookrightarrow \mathbf B ^{0,\gamma }_{p,q}$ establishing the results already stated for approximation numbers and entropy numbers.

Working with Besov spaces given by the modulus of smoothness, usually the cases of positive smoothness and logarithmic smoothness require different tools. See, for example, [12, 13, 20]. However, our approach allows us to cover both cases simultaneously. Other applications of the abstract results are possible. In particular, they can be used to derive similar results for Besov sequence spaces.

2 Approximation Spaces

Hereafter, given two sequences $(u_n), (v_n)$ of nonnegative real numbers, we write $u_n \lesssim v_n$ if there is a constant $c > 0$ such that $u_n \le c \,v_n$ for all $n \in {\mathbb {N}}$. The notation $u_n \sim v_n$ means $u_n \lesssim v_n$ and $v_n \lesssim u_n$. A similar notation is used for quasi-norms.

Let $(X, \Vert \cdot \Vert _X)$ be a quasi-Banach space, and let $(A_n)_{n \in {\mathbb {N}}_0}$ be a sequence of subsets of X satisfying the following conditions:

$$\begin{aligned}&A_0 = \{0\} \subseteq A_1 \subseteq \ldots \subseteq A_n \subseteq \ldots \subseteq X, \\&\lambda A_n \subseteq A_n \text { for any scalar } \lambda \text { and any } n \in {\mathbb {N}}_0 = {\mathbb {N}} \cup \{0\}, \\&A_n + A_m \subseteq A_{n + m} \text { for any } n, m \in {\mathbb {N}}_0. \end{aligned}$$

Given any $f \in X$, we put $E_0(f) = \Vert f\Vert _X$ and

$$\begin{aligned} E_n(f) = E_n(f)_X = \inf \{\Vert f - g\Vert _X : g \in A_n\}, n \in {\mathbb {N}}. \end{aligned}$$

Let $b = (b_n)$ be a sequence of positive numbers with $b_1=1$, and let $0 < q \le \infty$. We assume that

$$\begin{aligned} \sum _{n=1}^\infty b_n^q n^{-1} = \infty \text { if } q < \infty \, \text { and }\, \sup _{n \ge 1} \,\{b_n\} = \infty \text { if } q=\infty . \end{aligned}$$

(2.1)

The approximation space $X^b_q = (X;A_n)^b_q$ consists of all $f \in X$ that have a finite quasi-norm

$$\begin{aligned} \Vert f\Vert _{X^b_q} = {\left\{ \begin{array}{ll} &{} \left( \sum \limits _{n=1}^\infty (b_n E_{n-1}(f))^q n^{-1}\right) ^{1/q}\quad \text { if } \,0< q < \infty , \\ &{} \sup _{n \ge 1} \,\{b_n E_{n-1}(f)\}\quad \text { if }\, q=\infty . \end{array}\right. } \end{aligned}$$

It is easy to check that if (2.1) does not hold, then we are in the trivial case where $X = X^b_q$ with equivalence of quasi-norms.

Clearly, $X^b_q \hookrightarrow X$, where $\hookrightarrow$ means continuous embedding. Moreover, if $b_n \sim h_n$, then $X^b_q = X^h_q$ with equivalence of quasi-norms.

Next we give some examples.

Example 2.1

Let $b_n = n^\alpha$, where $\alpha > 0$. The approximation spaces $X^\alpha _q$ generated by $b=(b_n)$ are the classical approximation spaces considered in [5, 18, 19, 39, 41]. It is shown in [41, Proposition 2] that

$$\begin{aligned} \Vert f\Vert _{X^\alpha _q} \sim \Vert f\Vert _{X^\alpha _q}^\diamond = \left( \Vert f\Vert ^q _X + \sum _{j=1}^\infty 2^{j \alpha q} E_{2^j }(f)^q\right) ^{1/q}. \end{aligned}$$

This equivalent quasi-norm is very useful for developing the theory of spaces $X^\alpha _q$. It involves the sequences $(\varphi (j))=(2^{j\alpha })$ and $(n(j))=(2^j)$, which have the following connection with the sequence $(b_n) = (n^\alpha )$: If $q=\infty$, we have

$$\begin{aligned} \max \{b_k : n(j) + 1 \le k \le n(j+1)\}&=\max \left\{ k^\alpha : 2^j + 1 \le k \le 2^{j+1}\right\} = 2^{(j+1)\alpha }\\&\sim \varphi (j)\,, \end{aligned}$$

and if $0< q < \infty$, we obtain

$$\begin{aligned} \sum _{k=n(j)+1}^{n(j+1)} \frac{b_k^q}{k} \sim \int _{2^j}^{2^{j+1}} x^{\alpha q}\, \frac{dx}{x} \sim 2^{j \alpha q} = \varphi (j)^q. \end{aligned}$$

Note also that $1 = n(0)< n (1)< \cdots< n (j) < \cdots$, $1 = \varphi (0)< \varphi (1)< \cdots< \varphi (j) < \cdots$, and that $1<\varphi (j+1)/\varphi (j)= 2^\alpha$, $j\in {\mathbb {N}}_0$. Furthermore,

$$\begin{aligned} \sum _{j=0} ^{r-1} n(j) =\sum _{j=0} ^{r-1} 2^j \le 2^{r}= n(r)\,. \end{aligned}$$

In a more general way, if $\psi$ is a slowly varying function (see [21, pp. 108–109] and also [3]), we designate by $X^{(\alpha ,\psi )}_q$ the approximation space generated by $b=(b_n)=(n^\alpha \psi (n))$ (see [10, 43]). Without loss of generality, we may assume that $(b_n)$ is an increasing sequence. If we take this time $(\varphi (j))=(2^{j\alpha } \psi (2^j))$ and $(n(j))=(2^j)$, then we have similar relationships as above between $(b_n)$ and $(\varphi (j)), (n(j))$. Indeed, if $0< q < \infty$, by [21, Proposition 3.4.33], we get

$$\begin{aligned} \sum _{k=n(j)+1}^{n(j+1)} \frac{b_k^q}{k} \sim \int _{2^j}^{2^{j+1}} (x^\alpha \psi (x))^q \frac{dx}{x} \sim 2^{j \alpha q} \psi (2^{j})^q = \varphi (j)^q. \end{aligned}$$

Moreover, using [3, Theorem 1.5.6], we obtain that there are $N\in {\mathbb {N}}$ and constants $1<K_1 < K_2$ such that

$$\begin{aligned}\ K_1 \le \frac{\varphi (j+1)}{\varphi (j)} \le K_2\,, \quad j\ge N. \end{aligned}$$

Example 2.2

Let $b_n = (1 + \log n)^\gamma$ with $\gamma \ge -1/q$ if $0< q < \infty$ and $\gamma > 0$ if $q=\infty$. We write $X^{(0,\gamma )}_q$ for the approximation spaces generated by the sequence $b = (b_n)$. These kinds of approximation spaces have been studied in [15,16,17, 23].

If $\gamma >-1/q$, according to [23, Lemma 1], we have

$$\begin{aligned} \Vert f\Vert _{X^{(0,\gamma )}_q} \sim \Vert f\Vert _{X^{(0,\gamma )}_q}^\diamond = \left( \Vert f\Vert _X^q + \sum _{j=1}^\infty \big (2^{j (\gamma + 1/q)} E_{\mu _j }(f)\big )^q\right) ^{1/q}\,, \end{aligned}$$

where $\mu _j = 2^{2^j}$. So, the companion sequences of $(b_n)$ are now $(n(j))=(\mu _j)$ and $(\varphi (j))=(2^{j(\gamma + 1/q)})$. We have again

$$\begin{aligned} \sum _{k=n(j)+1} ^{n(j+1)} \frac{b_k ^q}{k}&= \sum _{k=\mu _j + 1} ^{\mu _{j+1}} \frac{(1 + \log k)^{\gamma q}}{k} \sim \int _{\mu _j}^{\mu _{j+1}} (1 + \log x)^{\gamma q} \frac{dx}{x} \\&\sim 2^{j(\gamma q + 1)} = \varphi (j)^q\,, \end{aligned}$$

with

$$\begin{aligned}1<\frac{\varphi (j+1)}{\varphi (j)} = 2^{\gamma +1/q}\,, \quad j\in {\mathbb {N}}_0\,,\end{aligned}$$

and

$$\begin{aligned}\sum _{j=0} ^{r-1} n(j)= \sum _{j=0} ^{r-1} 2^{2^j} \le 2^{2^r} = n(r)\,.\end{aligned}$$

If $\gamma = -1/q$ and $0< q < \infty$, let $\rho _j = 2^{\mu _j} = 2^{2^{2^j}}$. The choice $n(j) = \rho _j$ and $\varphi (j) = 2^{j/q}$ yields sequences satisfying similar relationships as above.

Extracting the common features from these examples, in what follows we work with approximation spaces $X^b _q$ satisfying that there is a sequence of positive integers $1 = n(0)< n (1)< \cdots< n (j) < \cdots$ and another sequence of positive numbers $(\varphi (j))_{j\in {\mathbb {N}}_0}$ such that $1=\varphi (0)$ and

$$\begin{aligned} \left\{ \begin{array}{lcl} \sum \limits _{k = n(j) + 1}^{n(j+1)} b_k^q k^{-1} \sim \varphi (j)^q &{}\quad \text { if } &{} q < \infty , \\ &{} &{} \\ \max \limits _{n(j) + 1 \le k \le n(j+1)} b_k \sim \varphi (j) &{}\quad \text { if } &{} q= \infty . \end{array} \right. \end{aligned}$$

(2.2)

We also suppose that there are an integer $N \in {\mathbb {N}}$ and real constants $1< K_1 < K_2$ such that

$$\begin{aligned} K_1 \le \frac{\varphi (j+1)}{\varphi (j)} \le K_2,\, j \ge N. \end{aligned}$$

(2.3)

In particular, the sequence $(\varphi (j))$ is increasing with $\varphi (j) \sim \varphi (j+1)$ and $\lim _{j \rightarrow \infty } \varphi (j) = \infty$. In addition, we also assume that

$$\begin{aligned} \left\{ \begin{array}{lcl} \sum \limits _{j=0}^{r-1} n(j) \le n(r) \text { for all } r \in {\mathbb {N}}, &{} \\ \qquad \qquad \text { or } \\ A_n \text { is a linear subspace of } X \text { for all } n \in {\mathbb {N}}. \end{array} \right. \end{aligned}$$

(2.4)

Next we show an equivalent quasi-norm in $X^b_q$.

Lemma 2.1

Under the assumptions (2.1), (2.2), and (2.3), the quasi-norm of $X^b_q$ is equivalent to

$$\begin{aligned} \Vert f\Vert _{X^b_q}^\diamond = \left( \Vert f\Vert ^q _X + \sum _{j=1}^\infty \varphi (j)^q E_{n(j)}(f)^q\right) ^{1/q} \end{aligned}$$

(the sum should be replaced by the supremum if $q=\infty$).

Proof

Suppose $0< q < \infty$. According to (2.2), our assumption on $(\varphi (j))$, and the fact that $(E_n(f))$ is nonincreasing, we obtain

$$\begin{aligned} \Vert f\Vert _{X^b_q}&= \left( \Vert f\Vert ^q _X + \sum _{j=0}^\infty \sum _{k=n(j)+1}^{n(j+1)} \frac{(b_k E_{k-1}(f))^q}{k}\right) ^{1/q} \\&\le \left( \Vert f\Vert ^q _X + \sum _{j=0}^\infty E_{n(j)}(f)^q \sum _{k=n(j)+1}^{n(j+1)} \frac{b_k^q}{k}\right) ^{1/q} \\&\lesssim \left( \Vert f\Vert ^q _X + \sum _{j=1}^\infty \varphi (j)^q E_{n(j)}(f)^q \right) ^{1/q} \\&= \Vert f\Vert _{X^b_q}^\diamond . \end{aligned}$$

Conversely, using (2.2), we derive

$$\begin{aligned} \Vert f\Vert _{X^b_q}&= \left( \Vert f\Vert _X^q + \sum _{j=0}^\infty \sum _{k=n(j)+1}^{n(j+1)} \frac{(b_k E_{k-1}(f))^q}{k}\right) ^{1/q} \\&\gtrsim \left( \Vert f\Vert _X^q + \sum _{j=0}^\infty E_{n(j+1)-1}(f)^q \varphi (j)^q\right) ^{1/q} \\&\sim \Vert f\Vert _{X^b_q}^\diamond . \end{aligned}$$

The case $q=\infty$ is similar. $\square$

Writing down Lemma 2.1 for the case $b_n = n^\alpha \psi (n)$ (Example 2.1), we recover a result contained in [43, Theorem 3.2]. In the special case $\psi (t)=1$ for all $t > 0$, that is, in the case of classical approximation spaces, we obtain [41, Proposition 2].

If $b_n = (1 + \log n)^\gamma$ with $\gamma >-1/q$ (Example 2.2), we recover [23, Lemma 1]. For the case $\gamma =-1/q$ and $0<q<\infty$, Lemma 2.1 gives that

$$\begin{aligned} \Vert f\Vert _{X^{(0,-1/q)}_q} \sim \Vert f\Vert _{X^{(0,-1/q)}_q}^\diamond = \left( \Vert f\Vert _X^q + \sum _{j=1}^\infty (2^{j/q} E_{\rho _j}(f))^q\right) ^{1/q}\,. \end{aligned}$$

The following result provides a characterization for elements of $X^b_q$ as sums of series with terms in the sets $A_{n(j)}$. Recall that we may assume without loss of generality that $\Vert \cdot \Vert _X$ is a p-norm with $0< p < q$ (see [30, 15.10] or [29, Proposition 1.c.5]).

Theorem 2.1

Assume that (2.1), (2.2), (2.3), and (2.4) hold. Let $f \in X$. Then $f \in X^b_q$ if, and only if, there is a representation $f = \sum _{j=0}^\infty g_j$ (convergence in X) with $g_j \in A_{n(j)}$ and $(\varphi (j) \Vert g_j\Vert _X) \in \ell _q$. Furthermore,

$$\begin{aligned} \Vert f\Vert _{X^b_q}^*= \inf \left\{ \left( \sum _{j=0}^\infty (\varphi (j) \Vert g_j\Vert _X)^q\right) ^{1/q} : g_j \in A_{n(j)} \text { and } f = \sum _{j=0}^\infty g_j\right\} \end{aligned}$$

is an equivalent quasi-norm on $X^b_q$.

Proof

Suppose $0< q < \infty$, and let $f \in X^b_q$. Take any $\varepsilon > 0$, and for each $j \in {\mathbb {N}}_0$, select $f_j \in A_{n(j)}$ such that $\Vert f-f_j\Vert _X \le (1 + \varepsilon ) E_{n(j)}(f)$. Put $f_{-1} = 0$ and $g_j = f_j - f_{j-1}, j \in {\mathbb {N}}_0$. Since $f \in X^b_q$ and (2.1) holds, we have that $E_n(f) \rightarrow 0$ as $n \rightarrow \infty$. This yields that

$$\begin{aligned} \Big \Vert f - \sum _{j=0}^k g_j\Big \Vert _X = \Vert f - f_k\Vert _X \le (1 + \varepsilon ) E_{n(k)}(f) \rightarrow 0 \text { as } k \rightarrow \infty . \end{aligned}$$

Hence $f=\sum _{j=0}^\infty g_j$ with convergence in X. Moreover,

$$\begin{aligned} \Vert g_j\Vert _X \le c_X (\Vert f-f_j\Vert _X + \Vert f-f_{j-1}\Vert _X) \le 2 (1 + \varepsilon ) c_X E_{n(j-1)}(f), j \in {\mathbb {N}}, \end{aligned}$$

and

$$\begin{aligned} \Vert g_0\Vert _X \le c_X (\Vert f\Vert _X + \Vert f-f_0\Vert _X) \le 2 (1 + \varepsilon ) c_X \Vert f\Vert _X. \end{aligned}$$

Here $c_X$ is the constant in the quasi-triangle inequality in X, whence, using (2.3) and Lemma 2.1, we get

$$\begin{aligned} \Vert f\Vert _{X^b_q}^*&\le \left( \sum _{j=0}^\infty (\varphi (j) \Vert g_j\Vert _X)^q\right) ^{1/q} \\&\lesssim \left( \Vert f\Vert ^q _X + \sum _{j=1}^\infty \varphi (j-1)^q E_{n(j-1)}(f)^q\right) ^{1/q} \lesssim \Vert f\Vert _{X^b_q}. \end{aligned}$$

Next we check the converse inequality. As we pointed out before, we may assume that $\Vert \cdot \Vert _X$ is a p-norm with $0< p < q$. Let $s > 0$ such that $1/p = 1/q + 1/s$. Given any representation $f = \sum _{j=0}^\infty g_j$ (convergence in X) with $g_j \in A_{n(j)}$ and $(\varphi (j) \Vert g_j\Vert _X) \in \ell _q$, we have by (2.4) that $\sum _{j=0}^r g_j \in A_{n(r+1)}, r \in {\mathbb {N}}$. Take any $1< D < K_1$. We have

$$\begin{aligned} E_{n(r+1)}(f)&\le \Big \Vert f - \sum _{j=0}^r g_j\Big \Vert _X = \left( \Big \Vert \sum _{j=r+1}^\infty g_j\Big \Vert _X^p\right) ^{1/p} \\&\le \left( \sum _{j=r+1}^\infty \Vert g_j\Vert _X^p\right) ^{1/p} = \left( \sum _{j=r+1}^\infty (D^j \Vert g_j\Vert _X)^p D^{-j p}\right) ^{1/p} \\&\le \left( \sum _{j=r+1}^\infty (D^j \Vert g_j\Vert _X)^q\right) ^{1/q} \left( \sum _{j=r+1}^\infty D^{-j s}\right) ^{1/s} \\&= \frac{D^{-(r+1)}}{(1 - D^{-s})^{1/s}} \left( \sum _{j=r+1}^\infty (D^j \Vert g_j\Vert _X)^q\right) ^{1/q}. \end{aligned}$$

Therefore, using Lemma 2.1 and (2.3), we obtain

$$\begin{aligned} \Vert f\Vert _{X^b_q}&\sim \left( \Vert f\Vert ^q _X + \sum _{j=1}^\infty \varphi (j)^q E_{n(j)}(f)^q\right) ^{1/q} \\&\lesssim \left( \Vert f\Vert _X^q + \sum _{j=1}^\infty (\varphi (j) D^{-j})^q \sum _{k=j}^\infty (D^k \Vert g_k\Vert _X)^q\right) ^{1/q} \\&= \left( \Vert f\Vert _X^q + \sum _{k=1}^\infty (D^k \Vert g_k\Vert _X)^q \sum _{j=1}^k (\varphi (j) D^{-j})^q\right) ^{1/q}. \end{aligned}$$

On the other hand, since $D/K_1 < 1$, (2.3) also implies that $(\varphi (k) D^{-k})_{k \ge N}$ is increasing because

$$\begin{aligned} \frac{\varphi (k)}{D^k} \le \frac{\varphi (k+1)}{D^{k+1}} \frac{D}{K_1} < \frac{\varphi (k+1)}{D^{k+1}},\, k \ge N. \end{aligned}$$

Moreover,

$$\begin{aligned} \varphi (j) \le K_1^{j-k} \varphi (k) \text { for } N \le j \le k. \end{aligned}$$

Therefore,

$$\begin{aligned} \sum _{j=1}^k (\varphi (j) D^{-j})^q&\le \sum _{j=1}^{N-1} (\varphi (j) D^{-j})^q + (\varphi (k) K_1^{-k})^q \sum _{j=N}^k (K_1/D)^{j q} \\&\lesssim \sum _{j=1}^{N-1} (\varphi (j) D^{-j})^q + (\varphi (k) D^{-k})^q \\&\lesssim (\varphi (k) D^{-k})^q. \end{aligned}$$

Consequently, we derive that

$$\begin{aligned} \Vert f\Vert _{X^b_q} \lesssim \left( \Vert f\Vert _X^q + \sum _{k=1}^\infty (\varphi (k) \Vert g_k\Vert _X)^q\right) ^{1/q}. \end{aligned}$$

Finally, since

$$\begin{aligned} 1 = \varphi (0) < \varphi (N) \le \frac{\varphi (j)}{K_1^{j-N}} \text { for } j \ge N, \end{aligned}$$

using Hölder’s inequality, we obtain

$$\begin{aligned} \Vert f\Vert _X&\le \left( \sum _{j=0}^\infty \Vert g_j\Vert _X^p\right) ^{1/p} \lesssim \left( \sum _{j=0}^\infty (\varphi (j) \Vert g_j\Vert _X)^q\right) ^{1/q} \left( \sum _{j=0}^\infty K_1^{-s j}\right) ^{1/s} \\&\lesssim \left( \sum _{j=0}^\infty (\varphi (j) \Vert g_j\Vert _X)^q\right) ^{1/q}, \end{aligned}$$

and we conclude that $\Vert f\Vert _{X^b_q} \lesssim \Vert f\Vert _{X^b_q}^*$.

The case $q=\infty$ can be treated analogously. $\square$

When $b_n=n^\alpha \psi (n)$ (Example 2.1), Theorem 2.1 gives [43, Theorem 3.3] for $\ell _q$ spaces. The case $\psi (t)=1$ for all $t > 0$ corresponds to [41, Theorem 3.1]. Applying Theorem 2.1 in the case $b_n = (1+ \log n)^\gamma$ with $\gamma >-1/q$ (Example 2.2), we recover the representation theorem for spaces $X^{(0,\gamma )} _q$ established in [16, Theorem 1.2], [17, Theorem 2], and [23, Theorem 1]. For the case $\gamma = -1/q$ and $0< q < \infty$, Theorem 2.1 produces the following result which covers a case left open in [16] and [23].

Theorem 2.2

Let $0< q < \infty$. An element $f \in X$ belongs to $X^{ (0,-1/q)}_q$ if, and only if, there exists $g_j \in A_{\rho _j}$ such that $f = \sum _{j=0}^\infty g_j$ (convergence in X) with $(2^{j/q} \Vert g_j\Vert _X) \in \ell _q$. Moreover,

$$\begin{aligned} \Vert f\Vert _{X^{(0,-1/q)}_q}^*= \inf \left\{ \left( \sum _{j=0}^\infty (2^{j/q} \Vert g_j\Vert _X)^q\right) ^{1/q} : g_j \in A_{\rho _j}, f = \sum _{j=0}^\infty g_j\right\} \end{aligned}$$

is an equivalent quasi-norm on $X^{(0,-1/q)}_q$.

In Examples 2.1 and 2.2 and Theorem 2.2, the powers of 2 can be replaced by powers of e (see [42, Sect. 3] for more general results in the case of spaces $X^\alpha _q$). We close this section with another concrete case of approximation space, involving now iterated logarithms and exponentials. We put

$$\begin{aligned} \texttt {L}_1(t) = \log t\,, \,\texttt {L}_r (t)= \log (\texttt {L}_{r-1}(t))\,,\,\texttt {E}_1 (t) =e^t \,,\, \texttt {E}_r (t) =e^{\texttt {E}_{r-1} (t)}\,,\, r>1. \end{aligned}$$

Example 2.3

Let $0<q\le \infty , \alpha >0, r\in {\mathbb {N}}$, and let $\psi$ be a slowly varying function. Put

$$\begin{aligned} b_1 =1\,,\quad b_n= \texttt {L}_r (n)^\alpha \psi \big (\texttt {L}_r (n) \big ) \prod _{j=1} ^r \texttt {L}_j (n)^{-1/q}\,,\quad n>1\,. \end{aligned}$$

Clearly, $(b_n)$ satisfies (2.1). Take

$$\begin{aligned} n(j) = \texttt {E}_{r+1} (j) \quad \text {and} \quad \varphi (j)= \texttt {L}_r \big (n(j) \big )^\alpha \psi \big (\texttt {L}_r \big (n(j) \big ) \big ) = e^{j\alpha } \psi (e^j)\,. \end{aligned}$$

Then we have

$$\begin{aligned} \sum _{k=n(j)+1} ^{n(j+1)} b_k ^q k^{-1}&= \sum _{k=\texttt {E}_{r+1} (j)+1} ^{\texttt {E}_{r+1} (j+1)} \texttt {L}_r (k)^{\alpha q} \psi \big ( \texttt {L}_r (k) \big )^q \frac{1}{k \prod _{j=1}^r \texttt {L}_j (k)}\\&\sim e^{j\alpha q} \psi (e^j )^q \int _{\texttt {E}_{r+1} (j)} ^{\texttt {E}_{r+1} (j+1)} \frac{dx}{x\prod _{j=1}^r \texttt {L}_j (x)}\\&=\varphi (j)^q \,. \end{aligned}$$

This shows that (2.2) holds. Using [3, Theorem 1.5.6], we can find $1<K_1 < K_2$ and $N\in {\mathbb {N}}$ such that

$$\begin{aligned} K_1 \le \frac{\varphi (j+1)}{\varphi (j)}= e^\alpha \frac{\psi (e^{j+1})}{\psi (e^j)} \le K_2 \,. \end{aligned}$$

So, (2.3) is also satisfied. Moreover,

$$\begin{aligned} \sum _{j=0} ^{m-1} n(j) \le m \texttt {E}_{r+1} (m-1) \le \texttt {E}_{r+1} (m)= n(m) \,. \end{aligned}$$

We put $X^{[\alpha , \psi ;r]} _q$ for the approximation space generated by the sequence $(b_n)$ defined above. Notice that if $r=1$ and $\psi (t) =1$ for all $t>0$, then $X^{[\alpha , 1;1]} _q$ coincides with the space $X^{(0, \alpha -1/q)} _q$ in Example 2.2. Moreover, $X^{[1/q, 1;2]} _q$ is the space $X^{(0, -1/q)} _q$.

It follows from Lemma 2.1 that

$$\begin{aligned} \Vert f\Vert _{X^{[\alpha , \psi ;r]} _q} \sim \Big ( \Vert f\Vert ^q _X + \sum _{j=1} ^\infty \big ( e^{j\alpha } \psi (e^j) E_{\texttt {E}_{r+1} (j)}(f)\big )^q\Big )^{1/q}\,. \end{aligned}$$

(2.5)

Writing down Theorem 2.1 for spaces $X^{[\alpha , \psi ;r]} _q$, we obtain the following result.

Theorem 2.3

Let $0<q\le \infty , \alpha >0, r\in {\mathbb {N}}$, and let $\psi$ be a slowly varying function. Then $f\in X^{[\alpha , \psi ;r]} _q$ if, and only if, there is a representation $f=\sum _{j=0} ^\infty g_j$ (convergence in X) with $g_j \in A_{\texttt {E}_{r+1} (j)}$ and $\big ( e^{j\alpha } \psi (e^j) \Vert g_j\Vert _X\big )\in \ell _q$. Furthermore,

$$\begin{aligned} \Vert f\Vert ^*_{X^{[\alpha , \psi ;r]} _q}= \inf \left\{ \left( \sum _{j=0} ^\infty \big ( e^{j\alpha } \psi (e^j) \Vert g_j\Vert _X \big )^q \right) ^{1/q} : g_j \in A _{\texttt {E}_{r+1} (j)} \, \text {and}\, f=\sum _{j=0} ^\infty g_j\right\} \end{aligned}$$

is an equivalent quasi-norm on $X^{[\alpha , \psi ;r]} _q$.

When $r=1$ (respectively $r>1$), Theorem 2.3 gives back a result contained in [44, Theorem 3.2] (respectively, [24, Theorem 5.4]).

3 Relationships Between Approximation Spaces Generated by Different Approximation Families

Let X and $(A_n)_{n \in {\mathbb {N}}_0}$ be as in the previous section. Let again $\mu _j = 2^{2^j}$ and $\rho _j = 2^{\mu _j}$.

Theorem 3.1

Consider the new approximation families defined by

$$\begin{aligned} B_n = A_{2^n} \text { if } n \in {\mathbb {N}} \text { with } B_0 = \{0\} \end{aligned}$$

and

$$\begin{aligned} D_n = A_{\mu _n} \text { if } n \in {\mathbb {N}} \text { with } D_0 = \{0\}. \end{aligned}$$

• (a) If $\,0<q\le \infty$ and $\gamma >-1/q$, then

  $$\begin{aligned} X^{(0,\gamma )}_q = (X;B_n)^{\gamma + 1/q}_q. \end{aligned}$$

  (3.1)

• (b) If $\,0<q<\infty$ and $\gamma = -1/q$, then

  $$\begin{aligned} X^{(0,-1/q)}_q = (X;D_n)^{ 1/q}_q. \end{aligned}$$

  (3.2)

Proof

According to Example 2.2, Lemma 2.1, and Example 2.1, we obtain

$$\begin{aligned} X^{(0,\gamma )}_q&= (X;A_n)^{(0,\gamma )}_q \\&= \left\{ f \in X : \Vert f\Vert _{X^{(0,\gamma )}_q}^\diamond = \left( \Vert f\Vert _X^q + \sum _{j=1}^\infty (2^{j(\gamma + 1/q)} E_{\mu _j}(f))^q\right) ^{1/q} < \infty \right\} \\&= (X;B_n)^{\gamma + 1/q}_q. \end{aligned}$$

This establishes (a). Concerning (b), we get

$$\begin{aligned} X^{(0,-1/q)}_q&= (X;A_n)^{(0,-1/q)}_q \\&= \left\{ f \in X : \Vert f\Vert _{X^{(0,-1/q)}_q}^\diamond = \left( \Vert f\Vert _X^q + \sum _{j=1}^\infty (2^{j/q} E_{\rho _j}(f))^q\right) ^{1/q} < \infty \right\} \\&= (X;D_n)^{1/q}_q. \end{aligned}$$

$\square$

As a consequence of Theorem 3.1, certain results on limiting spaces $X^{(0,\gamma )}_q$ that have direct proofs in the literature can be derived from the known results for the classical approximation spaces $X^\alpha _q$. This is the case of the reiteration formula. It was shown by Pietsch [41, Theorem 3.2] that

$$\begin{aligned} \left( X^\alpha _q\right) ^\beta _r = X^{\alpha + \beta }_r \text { provided that } 0< \alpha , \beta< \infty \text { and } 0 < q, r \le \infty . \end{aligned}$$

(3.3)

For limiting spaces, Fehér and Grässler [23, Theorem 2] proved that

$$\begin{aligned} \left( X^{(0,\gamma )}_q\right) ^{(0,\delta )}_r = X^{(0,\gamma + \delta + 1/q)}_r \text { for } 0 < q, r \le \infty , \gamma> -1/q \text { and } \delta > -1/r. \end{aligned}$$

(3.4)

Formula (3.4) follows from (3.3) using (3.1). Namely,

$$\begin{aligned} \left( X^{(0,\gamma )}_q\right) ^{(0,\delta )}_r&= \left( (X;B_n)^{\gamma + 1/q}_q ; B_n\right) ^{\delta + 1/r}_r \\&= (X;B_n)^{\gamma + 1/q + \delta + 1/r}_r \\&= X^{(0,\gamma + 1/q+ \delta )}_r. \end{aligned}$$

This method allows us to treat the extreme case $\gamma = -1/q, \delta = -1/r$, which was not covered in [23, Theorem 2].

Theorem 3.2

Let $0< q , r < \infty$. Then

$$\begin{aligned}&\left( X^{(0,-1/q)}_q\right) ^{(0,-1/r)}_r \\&\quad = \left\{ f \in X : \Vert f\Vert = \left( \Vert f\Vert _X^r + \sum _{n=1}^\infty \big ((1 + \log n)^{1/q} E_{2^n}(f)\big )^r \frac{1}{n}\right) ^{1/r} < \infty \right\} . \end{aligned}$$

Proof

By (3.2), (3.3), and (3.1), we derive

$$\begin{aligned}&\left( X^{(0,-1/q)}_q\right) ^{(0,-1/r)}_r = \left( (X;D_n)^{1/q}_q ; D_n\right) ^{1/r}_r \\&\quad = (X;D_n)^{1/q + 1/r}_r = (X;B_n)^{(0,1/q)}_r \\&\quad = \left\{ f \in X : \Vert f\Vert = \left( \Vert f\Vert _X^r + \sum _{n=1}^\infty \big ((1 + \log n)^{1/q} E_{2^n}(f)\big )^r \frac{1}{n}\right) ^{1/r} < \infty \right\} . \end{aligned}$$

$\square$

The case $(X^{(0,-1/q)}_q)^{(0,\delta )}_r$ with $\delta >-1/r$ can be treated with similar ideas.

Theorem 3.3

Let $0< q< \infty , 0<r\le \infty$, and $\delta >-1/r$. Then

$$\begin{aligned}&\left( X^{(0,-1/q)}_q\right) ^{(0,\delta )}_r \\&\quad = \left\{ f \in X : \Vert f\Vert = \left( \Vert f\Vert _X ^r + \sum _{n=1}^\infty \big (n^{\delta + 1/r}(1 + \log n)^{1/q} E_{2^n }(f)\big )^r \frac{1}{n}\right) ^{1/r} < \infty \right\} . \end{aligned}$$

Proof

We claim that $X^{(0,-1/q)} _q =(X;B_n)^{(0,0)} _q$. Indeed, for all $k\in {\mathbb {N}}$, we have

$$\begin{aligned} \sum _{n=2^k -1} ^{2^{k+1}} \frac{1}{n (1+\log n)} \sim \int _{2^k} ^{2^{k+1}}\frac{dx}{x \log x} = \log \left( 1+\frac{1}{k}\right) \sim \frac{1}{k} \,. \end{aligned}$$

Hence,

$$\begin{aligned} \Vert f\Vert _{X^{(0, -1/q)} _q}&=\Big (\Vert f\Vert _X ^q + \sum _{k=1} ^\infty \, \sum _{n=2^k -1} ^{2^{k+1}} E_{n} (f)^q \frac{1}{n(1+\log n)}\Big )^{1/q}\\&\quad \sim \Big (\Vert f\Vert _X ^q + \sum _{k=1} ^\infty E_{2^k } (f)^q \frac{1}{k}\Big )^{1/q} = \Vert f\Vert _{(X;B_n)^{(0,0)} _q}, \end{aligned}$$

which establishes our claim. Therefore, applying [10, Theorem 3.2] with $\psi (t)=(1+ \log t)^{1/q}$, we obtain

$$\begin{aligned}&\left( X^{(0,-1/q)}_q\right) ^{(0,\delta )}_r = \left( (X;B_n)^{(0,0)} _q ; B_n\right) ^{\delta + 1/r} _r = (X;B_n)^{(\delta + 1/r, \psi )} _r \\&\quad =\left\{ f \in X : \Vert f\Vert = \left( \Vert f\Vert _X ^r + \sum _{n=1}^\infty \big (n^{\delta + 1/r}(1 + \log n)^{1/q} \,E_{2^n }(f)\big )^r \frac{1}{n}\right) ^{1/r} < \infty \right\} . \end{aligned}$$

$\square$

This approach is also useful to establish interpolation formulae. Let $(A_0,A_1)$ be a pair of quasi-Banach spaces, that is to say, two quasi-Banach spaces $A_i$ that are continuously embedded in the same Hausdorff topological vector space. Peetre’s K -functional is defined for $a \in A_0 + A_1$ by

$$\begin{aligned} K(t,a) = \inf \{\Vert a_0\Vert _{A_0} + t \Vert a_1\Vert _{A_1} : a = a_0 + a_1, a_i \in A_i\}, t > 0. \end{aligned}$$

For $0 < q \le \infty$ and $0< \theta < 1$, the real interpolation space $(A_0,A_1)_{\theta ,q}$ is formed by all those $a \in A_0 + A_1$ having a finite quasi-norm

$$\begin{aligned} \Vert a\Vert _{(A_0,A_1)_{\theta ,q}} = \left( \int _0^\infty (t^{-\theta } K(t,a))^q \frac{dt}{t}\right) ^{1/q} \end{aligned}$$

(the integral should be replaced by the supremum if $q=\infty$).

According to a result of Peetre and Sparr [38] (see also [5, Korollar 2.3.1]), for $0< \alpha _0 \ne \alpha _1< \infty , 0 < r_0, r_1, q \le \infty$, and $0< \theta < 1$, we have

$$\begin{aligned} \left( X^{\alpha _0}_{r_0}, X^{\alpha _1}_{r_1}\right) _{\theta ,q} = X^\alpha _q, \end{aligned}$$

(3.5)

where $\alpha = (1 - \theta ) \alpha _0 + \theta \alpha _1$.

If $0 < q, q_0, q_1 \le \infty , \gamma _j > -1/q_j, j = 0,1, \gamma _0 + 1/q_0 \ne \gamma _1 + 1/q_1$, and $0< \theta < 1$, Fehér and Grässler [23, Theorem 5] proved that

$$\begin{aligned} \left( X^{(0,\gamma _0)}_{q_0}, X^{(0,\gamma _1)}_{q_1}\right) _{\theta ,q} = X^{(0,\gamma )}_q, \end{aligned}$$

(3.6)

where $\gamma = \gamma _\theta + 1/q_\theta - 1/q, 1/q_\theta = (1-\theta )/q_0 + \theta /q_1$, and $\gamma _\theta = (1-\theta ) \gamma _0 + \theta \gamma _1$.

We can recover (3.6) from (3.5) by using (3.1):

$$\begin{aligned} \left( X^{(0,\gamma _0)}_{q_0}, X^{(0,\gamma _1)}_{q_1}\right) _{\theta ,q}&= \left( (X;B_n)^{\gamma _0 + 1/q_0}_{q_0}, (X;B_n)^{\gamma _1 + 1/q_1}_{q_1}\right) _{\theta ,q} \\&= (X;B_n)^{\gamma _\theta + 1/q_\theta -1/q + 1/q}_q \\&= X^{(0,\gamma )}_q. \end{aligned}$$

For the extreme case $\gamma _j = -1/q_j$, we derive the following new interpolation formulae.

Theorem 3.4

Let $0< q_0, q_1< \infty , 0< \theta < 1$, and $1/q_\theta = (1-\theta )/q_0 + \theta /q_1$. Then

$$\begin{aligned} \left( X^{(0,-1/q_0)}_{q_0}, X^{(0,-1/q_1)}_{q_1}\right) _{\theta ,q_\theta } = X^{(0,-1/q_\theta )}_{q_\theta }. \end{aligned}$$

Furthermore, if $0 < r \ne q_\theta$, then

$$\begin{aligned}&\left( X^{(0,-1/q_0)}_{q_0}, X^{(0,-1/q_1)}_{q_1}\right) _{\theta ,r} \\&\quad = \left\{ f \in X : \Vert f\Vert = \left( \Vert f\Vert _X^r + \sum _{n=1}^\infty ((1 + \log n)^{1/q_\theta - 1/r} E_{2^n}(f))^r \frac{1}{n}\right) ^{1/r} < \infty \right\} . \end{aligned}$$

Proof

According to (3.2) and (3.5), we get

$$\begin{aligned} \left( X^{(0,-1/q_0)}_{q_0}, X^{(0,-1/q_1)}_{q_1}\right) _{\theta ,q_\theta }&= \left( (X;D_n)^{1/q_0}_{q_0}, (X;D_n)^{1/q_1}_{q_1}\right) _{\theta , q_\theta } = (X;D_n)^{1/q_\theta }_{q_\theta } \\&= X^{(0,-1/q_\theta )}_{q_\theta }. \end{aligned}$$

Similarly, if $r \ne q_\theta$, we obtain

$$\begin{aligned}&\left( X^{(0,-1/q_0)}_{q_0}, X^{(0,-1/q_1)}_{q_1}\right) _{\theta ,r} = (X;D_n)^{1/q_\theta }_r = (X;B_n)^{(0,1/q_\theta - 1/r)}_r \\&\quad = \left\{ f \in X : \Vert f\Vert = \left( \Vert f\Vert _X^r + \sum _{n=1}^\infty ((1 + \log n)^{1/q_\theta - 1/r} E_{2^n}(f))^r \frac{1}{n}\right) ^{1/r} < \infty \right\} . \end{aligned}$$

$\square$

Next we consider interpolation of approximation spaces generated by different quasi-Banach spaces. Let $X_0, X_1$ be quasi-Banach spaces with $X_1 \hookrightarrow X_0, A_n \subseteq X_1$ for $n \in {\mathbb {N}}$, and suppose that the following assumption holds.

Assumption ${\mathcal {A}}$. There exist a second approximation family $(\tilde{A}_n)_{n \in {\mathbb {N}}_0}$ in $X_1$ and a sequence of linear operators $L_n : \tilde{A}_n \longrightarrow A_n, n \in {\mathbb {N}}_0,$ with the following property: If there are a positive constant M and a sequence $(g_n)_{n \in {\mathbb {N}}_0}, g_n \in \tilde{A}_n,$ such that

$$\begin{aligned} \Vert f - g_n\Vert _{X_0} \le M \tilde{E}_n(f)_{X_0}, \end{aligned}$$

where $\tilde{E}_n(f)_{X_0}$ is the best approximation error of $f \in X_0$ with respect to $\tilde{A}_n$, then

$$\begin{aligned} \Vert f - L_n g_n\Vert _{X_j} \le C_j E_n(f)_{X_j}, j = 0, 1. \end{aligned}$$

Here the constants $C_j$ depend only on M and $X_j$.

Under Assumption ${\mathcal {A}}$, DeVore and Popov [19, Theorem 2] proved that

$$\begin{aligned} \left( (X_0)^{\alpha _0}_{q_0}, (X_1)^{\alpha _1}_{q_1}\right) _{\theta , q_\theta } = \left( (X_0, X_1)_{\theta , q_\theta }\right) ^{\alpha _\theta }_{q_\theta } \end{aligned}$$

(3.7)

provided that $0< \alpha _0, \alpha _1< \infty , 0< q_0, q_1 \le \infty , 0< \theta < 1, \alpha _\theta =(1-\theta )\alpha _0 + \theta \alpha _1$, and $1/q_\theta = (1 - \theta )/q_0 + \theta / q_1$. We can complement (3.7) with the following formulae for limiting approximation spaces.

Theorem 3.5

Let $X_0, X_1$ be quasi-Banach spaces such that $X_1 \hookrightarrow X_0, A_n \subseteq X_1$ for $n \in {\mathbb {N}}$, and Assumption ${\mathcal {A}}$ holds. Let $0< \theta < 1$.

• (a) If $0 < q_0, q_1 \le \infty , \gamma _j > -1/q_j$ for $j=0,1, \gamma _\theta = (1 - \theta ) \gamma _0 + \theta \gamma _1$, and $1/q_\theta = (1-\theta )/q_0 + \theta /q_1,$ then

  $$\begin{aligned} \left( (X_0)^{(0,\gamma _0)}_{q_0}, (X_1)^{(0,\gamma _1)}_{q_1}\right) _{\theta , q_\theta } = \left( (X_0,X_1)_{\theta ,q_\theta }\right) ^{(0,\gamma _\theta )}_{q_\theta }. \end{aligned}$$

• (b) If $0< q_0, q_1 < \infty ,$ then

  $$\begin{aligned} \left( (X_0)^{(0,-1/q_0)}_{q_0}, (X_1)^{(0,-1/q_1)}_{q_1}\right) _{\theta ,q_\theta } = \left( (X_0,X_1)_{\theta , q_\theta }\right) ^{(0,-1/q_\theta )}_{q_\theta }. \end{aligned}$$

Proof

It is not hard to check that Assumption ${\mathcal {A}}$ also holds for the approximation schemes $(X_0;B_n), (X_1;B_n)$, whence (3.1) and (3.7) yield

$$\begin{aligned} \left( (X_0)^{(0,\gamma _0)}_{q_0}, (X_1)^{(0,\gamma _1)}_{q_1}\right) _{\theta , q_\theta }&= \left( (X_0;B_n)^{\gamma _0 + 1/q_0}_{q_0}, (X_1;B_n)^{\gamma _1 + 1/q_1}_{q_1}\right) _{\theta , q_\theta } \\&= \left( (X_0,X_1)_{\theta , q_\theta };B_n\right) ^{\gamma _\theta + 1/q_\theta }_{q_\theta } = \left( (X_0,X_1)_{\theta ,q_\theta }\right) ^{(0,\gamma _\theta )}_{q_\theta }. \end{aligned}$$

The proof of (b) is similar but using (3.2). $\square$

Now we turn our attention to spaces $X^{[\alpha , \psi ;r]} _q$ introduced in Example 2.3. As we show in the next result, spaces $X^{[\alpha , \psi ;r]} _q$ are related to spaces $X^{(\alpha , \psi )} _q$ of Example 2.1 if we make a suitable selection of the approximation sets $A_n$.

Theorem 3.6

Given $r\in {\mathbb {N}}$, consider the approximation family

$$\begin{aligned} G ^{(r)} _n = A_{\texttt {E}_{r+1} (n)} \text { if } n \in {\mathbb {N}} \text { and } G^{(r)} _0 = \{0\}\,. \end{aligned}$$

If $0<q\le \infty , \alpha >0$, and $\psi$ is a slowly varying function, then

$$\begin{aligned} X^{[\alpha , \psi ;r]} _q = (X;G ^{(r)} _n )^{(\alpha , \psi )} _q \,. \end{aligned}$$

Proof

This follows from (2.5). $\square$

Let $0<\alpha _0 , \alpha _1<\infty , 1\le q_0 , q_1 \le \infty$, and let $\psi _0 , \psi _1$ be slowly varying functions. By [43, Theorem 4.2], the following holds:

$$\begin{aligned} \big ( X^{(\alpha _0, \psi _0)} _{q_0} \big )^{(\alpha _1, \psi _1)} _{q_1} = X^{(\alpha _0 + \alpha _1 , \psi _0 \psi _1)} _{q_1}\,. \end{aligned}$$

(3.8)

Combining Theorem 3.6 with (3.8), we obtain the following reiteration formula:

$$\begin{aligned} \big ( X^{[\alpha _0, \psi _0 ; r]} _{q_0} \big )^{[\alpha _1, \psi _1 ;r]} _{q_1} = X^{[\alpha _0 + \alpha _1 , \psi _0 \psi _1 ;r]} _{q_1}, \end{aligned}$$

which is a special case of [44, Theorem 3.5] if $r=1$ and [24, Theorem 5.6] if $r>1$.

As for interpolation formulae, it follows from [43, Corollary 5.4] that

$$\begin{aligned} \big ( X^{(\alpha _0 , \psi _0)} _{q_0} , X^{(\alpha _1 , \psi _1)} _{q_1}\big )_{\theta ,q} = X_q ^{\left( (1-\theta )\alpha _0 + \theta \alpha _1 , \psi _0 ^{1-\theta } \psi _1 ^\theta \right) } \end{aligned}$$

provided that $0< \alpha _0 \ne \alpha _1<\infty , 0<\theta <1, 1 \le q_0, q_1 , q \le \infty$, and $\psi _0 , \psi _1$ are slowly varying functions. Hence, for any $r\in {\mathbb {N}}$, using Theorem 3.6, we derive

$$\begin{aligned} \big ( X^{[\alpha _0 , \psi _0 ;r]} _{q_0} , X^{[\alpha _1 , \psi _1;r]} _{q_1}\big )_{\theta ,q} = X_q ^{\left[ (1-\theta )\alpha _0 + \theta \alpha _1 , \psi _0 ^{1-\theta } \psi _1 ^\theta ;r\right] }\,. \end{aligned}$$

4 Approximation and Entropy Numbers of Embeddings

Let $T \in {\mathfrak {L}}(V,W)$ be a bounded linear operator between the quasi-Banach spaces V, W. For $k \in {\mathbb {N}}$, the k-th approximation number $a_k(T)$ of T is given by

$$\begin{aligned} a_k(T) = \inf \{\Vert T-R\Vert _{V,W} : R \in {\mathfrak {L}}(V,W) \text { with rank } R < k \}, \end{aligned}$$

where $\text {rank } R$ is the dimension of the range of R. The k-th (dyadic) entropy number $e_k(T) = e_k(T:V \longrightarrow W)$ of T is defined as the infimum of all $\varepsilon > 0$ such that there are $w_1, \ldots , w_{2^{k-1}} \in W$ with

$$\begin{aligned} T(U_V) \subseteq \bigcup _{j=1}^{2^{k-1}} (w_j + \varepsilon \,U_W). \end{aligned}$$

Here $U_V, U_W$ are the closed unit balls of V, W,  respectively (see [8, 22, 40]).

Note that T is compact if and only if $\lim _{k \rightarrow \infty } e_k(T) = 0$. On the other hand, if $\lim _{k \rightarrow \infty } a_k(T) = 0$, then T is compact, but there are compact operators T such that $\lim _{k \rightarrow \infty } a_k(T) > 0$ (see [22]). The asymptotic decay of the sequences $(e_k(T)), (a_k(T))$ can be considered as a measure of the degree of compactness of the operator T.

It follows from the definitions that

$$\begin{aligned} \Vert T\Vert _{V,W} = a_1(T) \ge a_2(T) \ge \cdots \ge 0 \text { and } \Vert T\Vert _{V,W} \ge e_1(T) \ge e_2(T) \ge \cdots \ge 0. \end{aligned}$$

Moreover, entropy and approximation numbers are multiplicative; that is, for all $k , l \in {\mathbb {N}}$,

$$\begin{aligned} a_{k + l -1}(S \circ T) \le a_k(S) a_l(T),\quad e_{k + l -1}(S \circ T) \le e_k(S) e_l(T). \end{aligned}$$

In this section, we determine the exact asymptotic behavior of the approximation and entropy numbers of embeddings involving approximation spaces.

In what follows, we assume that $(X;A_n)$ is a linear approximation scheme. This means that there is a uniformly bounded sequence of linear projections $P_n$ mapping X onto $A_n$. Then

$$\begin{aligned} \Vert f - P_n f\Vert _X \le c \, E_n(f), f \in X, n \in {\mathbb {N}}, \end{aligned}$$

(4.1)

where $c = c_X [1 + \sup \{\Vert P_n\Vert _{X,X} : n \in {\mathbb {N}}\}]$. Note that (2.4) holds. We also have the following stability property.

Lemma 4.1

Let $0<q\le \infty$, and assume that (2.1), (2.2), and (2.3) hold and that $(X;A_n)$ is a linear approximation scheme. Then $(X^b_q;A_n)$ is a linear approximation scheme as well.

Proof

Suppose that $0<q<\infty$. The case $q=\infty$ can be treated in the same way. Let $(P_n)$ be the sequence of linear projections on X with $\Vert P_n\Vert _{X,X} \le M$ for all $n \in {\mathbb {N}}$. We are going to show that these projections are also uniformly bounded in $X^b_q$. We may assume that X is p-normed with $0< p < q$. Put $1/s = 1/p - 1/q$.

Given any $n \in {\mathbb {N}}$, let $j_0 \in {\mathbb {N}}_0$ be such that $n(j_0) \le n < n(j_0 + 1)$. Take any $f \in X^b_q$. We can find a representation $f = \sum _{j=0}^\infty g_j$ with $g_j \in A_{n(j)}$ and

$$\begin{aligned} \left( \sum _{j=0}^\infty (\varphi (j) \Vert g_j\Vert _X)^q\right) ^{1/q} \le 2 \, \Vert f\Vert _{X^b_q}^*\le c \, \Vert f\Vert _{X^b_q}. \end{aligned}$$

Since

$$\begin{aligned} P_n f = \sum _{j=0}^{j_0} g_j + P_n \Big ( \sum _{j=j_0 + 1}^\infty g_j\Big )\,, \end{aligned}$$

applying Theorem 2.1 and Hölder’s inequality, we obtain

$$\begin{aligned} \Vert P_n f\Vert ^q_{X^b_q}&\lesssim \sum _{j=0}^{j_0} \varphi (j)^q \Vert g_j\Vert _X^q + \varphi (j_0 + 1)^q \Big \Vert P_n \Big ( \sum _{j=j_0 + 1}^\infty g_j\Big )\Big \Vert _X^q \\&\le \sum _{j=0}^{j_0} \varphi (j)^q \Vert g_j\Vert _X^q + \varphi (j_0 + 1)^q \left( \sum _{j=j_0 + 1}^\infty \Vert P_n g_j\Vert _X^p \right) ^{q/p} \\&\le \sum _{j=0}^{j_0} \varphi (j)^q \Vert g_j\Vert _X^q + M^q \, \varphi (j_0 + 1)^q \left( \sum _{j=j_0 + 1}^\infty \Vert g_j\Vert _X^p \right) ^{q/p} \\&\le \sum _{j=0}^{j_0} \varphi (j)^q \Vert g_j\Vert _X^q \\&\quad + M^q \, \varphi (j_0 + 1)^q \sum _{j=j_0 + 1}^\infty \varphi (j)^q \Vert g_j\Vert _X^q \left( \sum _{j=j_0 + 1}^\infty \varphi (j)^{-s} \right) ^{q/s}\,. \end{aligned}$$

Now using (2.3), we derive that

$$\begin{aligned} \Vert P_n f\Vert ^q_{X^b_q}&\lesssim \sum _{j=0}^{j_0} \varphi (j)^q \Vert g_j\Vert _X^q + M^q (1 - K_1^{-s})^{-q/s} \sum _{j=j_0 + 1}^\infty \varphi (j)^q \Vert g_j\Vert _X^q \\&\le (1 + M^q (1 - K_1^{-s})^{-q/s} ) \, c^q \, \Vert f\Vert ^q_{X^b_q}. \end{aligned}$$

This proves that $(P_n)$ is uniformly bounded on $X^b_q$. $\square$

Working with a linear approximation scheme $(X;A_n)$ with projections $(P_n)$, let

$$\begin{aligned} Q_0 = P_1 \text { and } Q_j = P_{n(j)} - P_{n(j-1)} \text { for } j \in {\mathbb {N}}. \end{aligned}$$

For any $f \in X^b_q$, we have by (2.1) that $(E_n(f)) \rightarrow 0$. Then (4.1) yields that $(P_n f) \rightarrow f$ in X and therefore $f = \sum _{j=0}^\infty Q_j f$ in X.

The following result can be proved by using (4.1) with the same arguments as in Theorem 2.1.

Theorem 4.1

Let $0<q\le \infty$, and assume that (2.1), (2.2), and (2.3) hold and that $(X;A_n)$ is a linear approximation scheme. Let $f \in X$. Then $f \in X^b_q$ if and only if $f = \sum _{j=0}^\infty Q_j f$ (convergence in X) with $(\varphi (j) \Vert Q_j f\Vert _X) \in \ell _q$. Moreover,

$$\begin{aligned} \Vert f\Vert _{X^b_q}^{\triangle } = \Vert (\varphi (j) \Vert Q_j f\Vert _X)\Vert _{\ell _q} \end{aligned}$$

is an equivalent quasi-norm in $X^b_q$.

Now we can establish the following estimates.

Theorem 4.2

Let $0<q\le \infty$, and assume that (2.1), (2.2), and (2.3) hold and that $(X;A_n)$ is a linear approximation scheme with $m(j) = dim A_{n(j)}, j \in {\mathbb {N}}_0$. We have for embedding $id : X^b_q \hookrightarrow X$,

$$\begin{aligned} a_{m(j) + 1} (id ) \lesssim \frac{1}{\varphi (j)} \lesssim e_{m(j) + 1}(id ). \end{aligned}$$

Proof

We know that $\text {id } = \sum _{k=0}^\infty Q_k$. Moreover,

$$\begin{aligned} \text {rank } \sum _{k=0}^j Q_k = \text {rank } P_{n(j)} = \text {dim } A_{n(j)} = m(j). \end{aligned}$$

Since we can assume without loss of generality that $\Vert \cdot \Vert _X$ is a p-norm, we get

$$\begin{aligned} a_{m(j) + 1} (\text {id})&\le \Big \Vert \text {id} - \sum _{k=0}^j Q_k\Big \Vert _{X^b_q,X} = \Big \Vert \sum _{k=j+1}^\infty Q_k\Big \Vert _{X^b_q,X} \\&\le \left( \sum _{k=j+1}^\infty \Vert Q_k\Vert _{X^b_q,X}^p\right) ^{1/p}. \end{aligned}$$

Theorem 4.1 implies that $\Vert Q_k\Vert _{X^b_q,X} \le c/\varphi (k), k \in {\mathbb {N}}_0$. Therefore, using (2.3), we obtain for $j \ge N$,

$$\begin{aligned} a_{m(j) + 1} (\text {id})&\le c \left( \sum _{k=j+1}^\infty \varphi (k)^{-p}\right) ^{1/p} \le c \,\frac{1}{\varphi (j+1)} \left( \sum _{k=j+1}^\infty K_1^{(j+1-k) p}\right) ^{1/p} \\&\lesssim \frac{1}{\varphi (j+1)}. \end{aligned}$$

This yields that $a_{m(j) + 1} (\text {id}) \lesssim 1/\varphi (j)$.

Next we establish the lower estimate for entropy numbers. Since $m(j) = \text {dim } A_{n(j)}$, volume arguments (see [8, (1.1.10), p. 9]) show that

$$\begin{aligned} e_{m(j)+1} (\text {id} : A_{n(j)} \longrightarrow A_{n(j)}) \sim 1. \end{aligned}$$

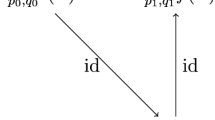
Consider the following commutative diagram:

We have

$$\begin{aligned} 1&\lesssim e_{m(j) + 1} (\text {id} : A_{n(j)} \longrightarrow A_{n(j)}) \le 2 \, e_{m(j) + 1} (\text {id} : A_{n(j)} \longrightarrow X) \\&\le 2 \, \Vert \text {id}\Vert _{A_{n(j)}, X^b_q} \, e_{m(j) + 1} (\text {id} : X^b_q \longrightarrow X). \end{aligned}$$

In order to estimate $\Vert \text {id}\Vert _{A_{n(j)}, X^b_q}$, note that if f belongs to $A_{n(j)}$, then f is already a series representation as in Theorem 2.1. Hence,

$$\begin{aligned} \Vert f\Vert _{X^b_q} \lesssim \Vert f\Vert _{X^b_q}^*\le \varphi (j) \Vert f\Vert _X. \end{aligned}$$

Consequently,

$$\begin{aligned} e_{m(j) + 1} (\text {id} : X^b_q \longrightarrow X) \gtrsim 1 / \varphi (j). \end{aligned}$$

$\square$

The estimates in Theorem 4.2 can be improved in the important concrete cases that we discuss below, where we give the precise asymptotic behavior for entropy and approximation numbers.

Hereafter, we suppose that there is $0 < \lambda \in {\mathbb {R}}$ such that

$$\begin{aligned} m(j) = \text {dim } A_{n(j)} \sim n(j)^\lambda . \end{aligned}$$

(4.2)

We write $[\cdot ]$ for the greatest integer function.

Corollary 4.1

Let $b_n = n^\alpha \psi (n)$, where $\alpha > 0$ and $\psi$ is a slowly varying function. Assume that $(X;A_n)$ is a linear approximation scheme satisfying (4.2) and that $0 < q \le \infty$. Then for the embedding $id : X^b_q \hookrightarrow X$, we have

$$\begin{aligned} a_n(id ) \sim e_n(id ) \sim \frac{1}{n^{\alpha /\lambda } \,\psi (n^{1/\lambda })}. \end{aligned}$$

Proof

As we have seen in Example 2.1, in this case $\varphi (j) = 2^{j \alpha }\, \psi (2^j)$ and $n(j) = 2^j$. According to Theorem 4.2, we derive

$$\begin{aligned} a_{[2^{j \lambda }] + 1} (\text {id}) \lesssim \frac{1}{2^{j \alpha } \,\psi (2^j)} \lesssim e_{[2^{j \lambda }] + 1} (\text {id}). \end{aligned}$$

This yields that

$$\begin{aligned} a_n(\text {id}) \lesssim \frac{1}{n^{\alpha /\lambda } \, \psi (n^{1/\lambda })} \lesssim e_n(\text {id}). \end{aligned}$$

Now using [14, Theorem 3.3], we conclude the desired result. $\square$

Corollary 4.2

Assume that $(X;A_n)$ is a linear approximation scheme satisfying (4.2), and let $0< \alpha _1 < \alpha _0$ and $0 < q_0, q_1 \le \infty$. Then for the embedding $id : X^{\alpha _0}_{q_0} \hookrightarrow X^{\alpha _1}_{q_1}$, we have

$$\begin{aligned} a_n(id ) \sim e_n(id ) \sim n^{-(\alpha _0 - \alpha _1)/\lambda }. \end{aligned}$$

Proof

According to (3.3), we have that

$$\begin{aligned} X^{\alpha _0}_{q_0} = (X^{\alpha _1}_{q_1})^{\alpha _0 - \alpha _1}_{q_0}\,, \end{aligned}$$

and, by Lemma 4.1, the approximation scheme $(X^{\alpha _1}_{q_1};A_n)$ is also linear. Hence, the result follows from Corollary 4.1. $\square$

Since $(X^{(0,\gamma )}_q)^\alpha _p = X^{(\alpha ,\gamma +1/q)}_p$ if $\gamma > -1/q$ (see [10, Theorem 3.2]), we can also derive the following.

Corollary 4.3

Assume that $(X;A_n)$ is a linear approximation scheme satisfying (4.2), and let $\alpha > 0, 0 < q_0, q_1 \le \infty$ and $\gamma _1 > -1/q_1$. Then for the embedding $id : X^{(\alpha , \gamma _1 + 1/q_1)}_{q_0} \hookrightarrow X^{(0,\gamma _1)}_{q_1}$, we have

$$\begin{aligned} a_n(id ) \sim e_n(id ) \sim n^{-\alpha /\lambda }. \end{aligned}$$

Corollary 4.4

Let $0 < q \le \infty , \gamma \ge -1/q$, and assume that $(X;A_n)$ is a linear approximation scheme satisfying (4.2). Then for the embedding $id : X^{(0,\gamma )}_q \hookrightarrow X$, we have:

• (a) If $\gamma > -1/q$, then

  $$\begin{aligned} a_n(id ) \sim e_n(id ) \sim (\log n)^{-(\gamma + 1/q)}. \end{aligned}$$

• (b) If $\gamma = -1/q$ and $0< q < \infty$, then

  $$\begin{aligned} a_n(id ) \sim e_n(id ) \sim (\log \log n)^{-1/q}. \end{aligned}$$

Proof

Suppose first that $\gamma > -1/q$. By Example 2.2, we have $\varphi (j) = 2^{j(\gamma + 1/q)}$ and $n(j) = \mu _j = 2^{2^j}$. Applying Theorem 4.2, we get

$$\begin{aligned} a_{[\mu _j^\lambda ] + 1}(\text {id}) \lesssim (\log \mu _j)^{-(\gamma + 1/q)} \lesssim e_{[\mu _j^\lambda ] + 1}(\text {id}). \end{aligned}$$

It follows that

$$\begin{aligned} a_n(\text {id}) \lesssim (\log n)^{-(\gamma + 1/q)} \lesssim e_n(\text {id}). \end{aligned}$$

Then [14, Theorem 3.3] yields the estimate (a).

If $\gamma = -1/q$ and $0< q < \infty$, then $\varphi (j) = 2^{j/q}$ and $n(j) = \rho _j = 2^{\mu _j}$. By Theorem 4.2, we obtain

$$\begin{aligned} a_{[\rho _j^\lambda ] + 1} (\text {id}) \lesssim (\log \log \rho _j)^{-1/q} \lesssim e_{[\rho _j^\lambda ]+1}(\text {id}). \end{aligned}$$

This yields that

$$\begin{aligned} a_n(\text {id}) \lesssim (\log \log n)^{-1/q} \lesssim e_n(\text {id}), \end{aligned}$$

and so, applying again [14, Theorem 3.3], we derive that

$$\begin{aligned} a_n(\text {id}) \sim e_n(\text {id}) \sim (\log \log n)^{-1/q}. \end{aligned}$$

$\square$

Having in mind Lemma 4.1, we can combine Corollary 4.4 with the reiteration formula (3.4) to obtain the following result.

Corollary 4.5

Let $0 < q_0, q_1 \le \infty$ and $\gamma _0, \gamma _1 \in {\mathbb {R}}$ with $\gamma _0 + 1/q_0> \gamma _1 + 1/q_1 > 0$. If $(X;A_n)$ is a linear approximation scheme satisfying (4.2), then for the embedding $id : X^{(0,\gamma _0)}_{q_0} \hookrightarrow X^{(0,\gamma _1)}_{q_1}$, we have

$$\begin{aligned} a_n(id ) \sim e_n(id ) \sim (\log n)^{-(\gamma _0 - \gamma _1 + 1/q_0 - 1/q_1)}. \end{aligned}$$

Remark 4.1

Note that the estimates in Corollaries 4.4 and 4.5 do not depend on the exponent $\lambda$ in (4.2).

Next we analyze the degree of compactness of the embeddings from spaces $X^{(\alpha ,\psi )}_u$ with $\alpha >0$ into limiting approximation spaces. The proofs are more involved due to the jumps in the scale and the lack of relationships among the parameters.

Theorem 4.3

Let $0< \alpha< \infty , 0 < u, q \le \infty , \gamma + 1/q > 0$, and $\psi$ be a slowly varying function. Assume that $(X;A_n)$ is a linear approximation scheme satisfying (4.2). Then for the embedding $id : X^{(\alpha ,\psi )}_u \hookrightarrow X^{(0,\gamma )}_q$, we get

$$\begin{aligned} a_n(id ) \sim e_n(id ) \sim n^{-\alpha /\lambda } (\log n)^{\gamma + 1/q}\psi (n^{1/\lambda })^{-1}. \end{aligned}$$

Proof

Assume $0< u, q < \infty$. According to Example 2.1, for the space $X^{(\alpha ,\psi )}_u$, we have $n(j)=2^j$. Let $Q_0 = P_1$ and $Q_j = P_{2^j}-P_{2^{j-1}}, j \in {\mathbb {N}}$. Write also $n_\gamma (j) = \mu _j$ and $R_j = P_{n_\gamma (j)} - P_{n_\gamma (j-1)}, j \in {\mathbb {N}}$, with $R_0 = P_2$. Take $j , r \in {\mathbb {N}}$ with

$$\begin{aligned} 2^{r-2} < j \le 2^{r-1}, \text { so } \log j \sim r. \end{aligned}$$

(4.3)

As $m(j) \sim n(j)^\lambda = 2^{j \lambda }$, there are positive numbers $c_1, c_2$ such that $c_1 2^{j \lambda } \le m(j) \le c_2 2^{j \lambda }$. We have

$$\begin{aligned} a_{[c_2 2^{j \lambda }] + 1}(\text {id})&\le \Vert \text {id} - P_{n(j)}\Vert _{X^{(\alpha , \psi )}_u, X^{(0,\gamma )}_q} = \Big \Vert \text {id} - \sum _{k=0}^j Q_k\Big \Vert _{X^{(\alpha ,\psi )}_u, X^{(0,\gamma )}_q} \\&= \Big \Vert \sum _{k=j+1}^{2^r} Q_k + \sum _{k> r} R_k\Big \Vert _{X^{(\alpha ,\psi )}_u, X^{(0,\gamma )}_q}\\&\le c \left( \Big \Vert \sum _{k=j+1}^{2^r} Q_k\Big \Vert _{X^{(\alpha ,\psi )}_u, X^{(0,\gamma )}_q} + \Big \Vert \sum _{k > r} R_k\Big \Vert _{X^{(\alpha ,\psi )}_u, X^{(0,\gamma )}_q}\right) . \end{aligned}$$

We proceed to estimate the norm of these operators. Given any $f \in X^{(\alpha ,\psi )}_u$, since $\sum _{k=j+1}^{2^r} Q_k f \in A_{\mu _r},$ applying Theorem 2.1 to $X^{(0,\gamma )}_q$, where $\varphi (j) = 2^{j(\gamma + 1/q)}$, we get that

$$\begin{aligned} \Big \Vert \sum _{k=j+1}^{2^r} Q_k f\Big \Vert _{X^{(0,\gamma )}_q} \lesssim 2^{(\gamma + 1/q) r} \Big \Vert \sum _{k=j+1}^{2^r} Q_k f\Big \Vert _X. \end{aligned}$$

In order to estimate the last term, we may assume without loss of generality that $\Vert \cdot \Vert _X$ is a p-norm with $0< p < u$. Put $1/s = 1/p -1/u$. We obtain

$$\begin{aligned} \Big \Vert \sum _{k=j+1}^{2^r} Q_k f\Big \Vert _X&\le \left( \sum _{k=j+1}^{2^r} \Vert Q_k f\Vert _X^p\right) ^{1/p} \\&\le \left( \sum _{k=j+1}^{2^r} (2^{k \alpha } \psi (2^k) \Vert Q_k f\Vert _X)^{u}\right) ^{1/u} \left( \sum _{k=j+1}^{2^r} 2^{-k \alpha s} \psi (2^k)^{-s}\right) ^{1/s} \\&\lesssim 2^{- j \alpha } \psi (2^j)^{-1} \left( \sum _{k=j+1}^{2^r} (2^{k \alpha } \psi (2^k) \Vert Q_k f\Vert _X)^{u}\right) ^{1/u} \\&\lesssim 2^{- j \alpha } \psi (2^j)^{-1} \Vert f\Vert _{X^{(\alpha ,\psi )}_u}. \end{aligned}$$

Therefore,

$$\begin{aligned} \Big \Vert \sum _{k=j+1}^{2^r} Q_k \Big \Vert _{X^{(\alpha ,\psi )}_u, X^{(0,\gamma )}_q} \lesssim 2^{(\gamma + 1/q) r} 2^{-j \alpha } \psi (2^j)^{-1} \sim j^{\gamma + 1/q} 2^{-j \alpha } \psi (2^j)^{-1}. \end{aligned}$$

As for the norm of the other operator, first we notice that

$$\begin{aligned} \Vert R_k f\Vert _X&= \Big \Vert \sum _{\nu = 2^{k-1} + 1}^{2^k} Q_\nu f\Big \Vert _X \le \left( \sum _{\nu =2^{k-1} + 1}^{2^k} \Vert Q_\nu f\Vert _X^p\right) ^{1/p} \\&\le \left( \sum _{\nu = 2^{k-1} + 1}^{2^k} (2^{\nu \alpha } \psi (2^\nu ) \Vert Q_\nu f\Vert _X)^{u}\right) ^{1/u} \left( \sum _{\nu =2^{k-1} + 1}^{2^k} 2^{-\nu \alpha s} \psi (2^\nu )^{-s}\right) ^{1/s} \\&\lesssim 2^{- \alpha 2^{k-1}} \psi (2^{2^{k-1}})^{-1} \left( \sum _{\nu = 2^{k-1} + 1}^{2^k} (2^{\nu \alpha } \psi (2^\nu ) \Vert Q_\nu f\Vert _X)^{u}\right) ^{1/u}. \end{aligned}$$

Therefore, if $u \le q$, we have

$$\begin{aligned}&\Big \Vert \sum _{k> r} R_k f\Big \Vert _{X^{(0,\gamma )}_q} \lesssim \left( \sum _{k> r} (2^{k (\gamma + 1/q)} \Vert R_k f\Vert _X)^q\right) ^{1/q} \le \left( \sum _{k> r} (2^{k (\gamma + 1/q)} \Vert R_k f\Vert _X)^u\right) ^{1/u} \\&\quad \lesssim \left( \sum _{k> r} 2^{k (\gamma + 1/q) u} 2^{- \alpha u 2^{k-1}} \psi (2^{2^{k-1}})^{-u} \sum _{\nu = 2^{k-1} + 1}^{2^k} (2^{\nu \alpha } \psi (2^\nu ) \Vert Q_\nu f\Vert _X)^{u}\right) ^{1/u} \\&\quad \lesssim 2^{r (\gamma + 1/q)} 2^{-\alpha 2^{r-1}} \psi (2^{2^{r-1}})^{-1} \left( \sum _{k > r} \sum _{\nu = 2^{k-1} + 1}^{2^k} (2^{\nu \alpha } \psi (2^\nu ) \Vert Q_\nu f\Vert _X)^{u}\right) ^{1/u}\,. \end{aligned}$$

Now using (4.3) and Theorem 4.1, we conclude that $\Big \Vert \sum _{k > r} R_k f\Big \Vert _{{X^{(0,\gamma )}_q}, {X^{(\alpha ,\psi )}_u}}\lesssim j^{\gamma + 1/q} 2^{-j \alpha } \psi (2^j)^{-1}$.

If $q < u$, then $\rho = u/q > 1$. Let $1/\rho + 1/\rho ' = 1$. By Hölder’s inequality, we obtain

$$\begin{aligned}&\Big \Vert \sum _{k>r} R_k f\Big \Vert _{X^{(0,\gamma )}_q} \lesssim \left( \sum _{k> r} (2^{k (\gamma + 1/q)} \Vert R_k f\Vert _X)^q\right) ^{1/q} \\&\quad \lesssim \left( \sum _{k> r} \left( 2^{k(\gamma + 1/q) u} 2^{-\alpha 2^{k-1} u} \psi (2^{2^{k-1}})^{-u} \sum _{\nu = 2^{k-1} + 1}^{2^k} (2^{\nu \alpha } \psi (2^\nu ) \Vert Q_\nu f\Vert _X)^{u} \right) ^{q/u}\right) ^{1/q} \\&\quad \le \left( \sum _{k> r} \, \sum _{\nu = 2^{k-1} + 1}^{2^k} (2^{\nu \alpha } \psi (2^\nu ) \Vert Q_\nu f\Vert _X)^{u}\right) ^{1/u} \\&\qquad \times \left( \sum _{k > r} \left( 2^{k (\gamma + 1/q)} 2^{-\alpha 2^{k-1}} \psi (2^{2^{k-1}})^{-1}\right) ^{q \rho '}\right) ^{1/q \rho '}\,. \end{aligned}$$

Hence

$$\begin{aligned} \Big \Vert \sum _{k>r} R_k f\Big \Vert _{X^{(0,\gamma )}_q}&\lesssim 2^{r(\gamma + 1/q)} 2^{-\alpha 2^{r-1}} \psi (2^{2^{r-1}})^{-1} \Vert f\Vert _{X^{(\alpha ,\psi )}_u} \\&\lesssim j^{\gamma + 1/q} 2^{-j \alpha } \psi (2^j)^{-1} \Vert f\Vert _{X^{(\alpha ,\psi )}_u}. \end{aligned}$$

Consequently, for any $0< q, u < \infty$, it follows that $a_{[c_2 2^{j \lambda }]+1}(\text {id}) \lesssim j^{\gamma + 1/q} 2^{-j \alpha } \psi (2^j)^{-1}$, which yields that

$$\begin{aligned} a_n(\text {id}) \lesssim n^{-\alpha /\lambda } (\log n)^{\gamma + 1/q} \psi (n^{1/\lambda })^{-1}. \end{aligned}$$

(4.4)

Next we establish the lower estimate for entropy numbers. Let $k_0 \in {\mathbb {N}}$ with $c_1 2^{k_0 \lambda } - c_2 > 0$. Take any $r \in {\mathbb {N}}$, and let $j \in {\mathbb {N}}$ be such that

$$\begin{aligned} j = 2^r + k_0. \end{aligned}$$

(4.5)

Let $Y = \{g \in A_{2^j} : P_{\mu _r} g = 0\} = \ker (P_{\mu _r} : A_{2^j} \longrightarrow A_{2^j})$. Since

$$\begin{aligned} A_{\mu _r} = P_{\mu _r} A_{\mu _r} \subseteq P_{\mu _r} A_{2^j} \subseteq P_{\mu _r} X = A_{\mu _r}, \end{aligned}$$

we have that $P_{\mu _r} : A_{2^j} \longrightarrow A_{2^j}$ has rank equal to $\text {dim } A_{\mu _r}$. Hence,

$$\begin{aligned} \text {dim } A_{2^j}&= \text {dim } [\,\ker (P_{\mu _r} : A_{2^j} \longrightarrow A_{2^j})] + \text {rank } [\,P_{\mu _r}: A_{2^j} \longrightarrow A_{2^j}] \\&= \text {dim } Y + \text {dim } A_{\mu _r}. \end{aligned}$$

Using (4.5), we get

$$\begin{aligned} \text {dim } Y \ge c_1 2^{j \lambda } - c_2 \mu _r^\lambda = 2^{(j-k_0)\lambda } \left( c_1 2^{k_0 \lambda } - c_2\right) \sim 2^{j \lambda }. \end{aligned}$$

By volume arguments (see [8, (1.1.10), p. 9]), we derive

$$\begin{aligned} 1 \lesssim 2^{([2^{j \lambda }] - 1)/\text {dim } Y} \, e_{[2^{j \lambda }]} (\text {id }: Y \longrightarrow Y) \lesssim e_{[2^{j \lambda }]} (\text {id }: Y \longrightarrow Y). \end{aligned}$$

Moreover, since $(\text {id } - P_{\mu _r}) g = g$ for any $g \in Y$, the following commutative diagram holds

It follows that

$$\begin{aligned} 1 \lesssim \Vert \text {id}\Vert _{Y, X^{(\alpha ,\psi )}_u} e_{[2^{j \lambda }]} \left( \text {id }: X^{(\alpha ,\psi )}_u \hookrightarrow X^{(0,\gamma )}_q\right) \Vert \text {id } - P_{\mu _r}\Vert _{X^{(0,\gamma )}_q, Y}. \end{aligned}$$

We now proceed to estimate the norms of the two operators. By Theorem 2.1, given any $f \in Y \subseteq A_{2^j}$, we obtain

$$\begin{aligned} \Vert f\Vert _{X^{(\alpha ,\psi )}_u} \lesssim \Vert f\Vert _{X^{(\alpha ,\psi )}_u}^*\le 2^{j \alpha } \psi (2^j) \Vert f\Vert _X, \end{aligned}$$

whence $\Vert \text {id}\Vert _{Y, X^{(\alpha ,\psi )}_u} \lesssim 2^{j \alpha } \psi (2^j)$. As for the other operator, given any $f \in X^{(0,\gamma )}_q$, using that $\Vert \cdot \Vert _X$ is a p-norm with $1/p = 1/q + 1/s$ and Theorem 4.1, we obtain

$$\begin{aligned} \Vert (\text {id } - P_{\mu _r}) f\Vert _X&= \Big \Vert \Big (\text {id } - \sum _{k=0}^r R_k\Big ) f\Big \Vert _X = \Big \Vert \sum _{k=r+1}^\infty R_k f\Big \Vert _X \\&\le \left( \sum _{k=r+1}^\infty (2^{(\gamma + 1/q) k} \Vert R_k f\Vert _X)^q\right) ^{1/q} \left( \sum _{k=r+1}^\infty 2^{-(\gamma + 1/q) s k}\right) ^{1/s} \\&\lesssim 2^{-(\gamma + 1/q) r} \Vert f\Vert _{X^{(0,\gamma )}_q} \\&\lesssim j^{-(\gamma + 1/q)} \Vert f\Vert _{X^{(0,\gamma )}_q}. \end{aligned}$$

So, $\Vert \text {id } - P_{\mu _r}\Vert _{X^{(0,\gamma )}_q, X} \lesssim j^{-(\gamma + 1/q)}$. This yields that

$$\begin{aligned} e_{[2^{j \lambda }]}(\text {id}) \gtrsim 2^{-j \alpha } \psi (2^j)^{-1} j^{\gamma + 1/q}, \end{aligned}$$

and therefore

$$\begin{aligned} e_n(\text {id}) \gtrsim n^{-\alpha /\lambda } \psi (n^{1/\lambda })^{-1} (\log n)^{\gamma + 1/q}. \end{aligned}$$

(4.6)

Finally, by (4.4), (4.6), and [14, Theorem 3.3], we conclude that

$$\begin{aligned} a_n (\text {id}) \sim e_n(\text {id}) \sim n^{-\alpha /\lambda } \psi (n^{1/\lambda })^{-1} (\log n)^{\gamma + 1/q}. \end{aligned}$$

The cases $q=\infty$ and/or $u=\infty$ can be treated similarly. $\square$

Remark 4.2

In the particular case $\psi (t) = (1 + |\log t|)^{\gamma + 1/q}, t > 0,$ of Theorem 4.3, we recover Corollary 4.3.

The techniques used in the proof of Theorem 4.3 can be modified to deal with the limit case $\gamma = -1/q$, where there is another jump in the scale. Instead of $R_j$, we work with $S_j = P_{\rho _j} - P_{\rho _{j-1}}$, and the space Y is defined as the collection of all $g \in A_{2^j}$ such that $P_{\rho _r} g=0$. The result reads as follows.

Theorem 4.4

Let $0< \alpha< \infty , 0< u \le \infty , 0< q < \infty$, and let $\psi$ be a slowly varying function. Assume that $(X;A_n)$ is a linear approximation scheme satisfying (4.2). Then for the embedding $id : X^{(\alpha ,\psi )}_u \hookrightarrow X^{(0,-1/q)}_q$, we have

$$\begin{aligned} a_n(id ) \sim e_n(id ) \sim n^{-\alpha /\lambda } (\log \log n)^{1/q} \psi (n^{1/\lambda })^{-1}. \end{aligned}$$

To complete this section, we establish a result on spaces $X^{[\alpha , \psi ;r]} _q$ (Example 2.3).

Theorem 4.5

Let $0< \alpha< \infty , r\in {\mathbb {N}}, 0 < q \le \infty$, and let $\psi$ be a slowly varying function. Assume that $(X;A_n)$ is a linear approximation scheme satisfying (4.2). Then for the embedding $id : X^{[\alpha ,\psi ;r]}_q \hookrightarrow X$, we have

$$\begin{aligned} a_n(id ) \sim e_n(id ) \sim \texttt {L}_r (n )^{-\alpha } \psi \big (\texttt {L}_r (n ) \big )^{-1} \,. \end{aligned}$$

Proof

This time $\varphi (j)=e^{j\alpha } \psi (e^j)$ and $n(j)=\texttt {E}_{r +1}(j)$. Theorem 4.2 yields

$$\begin{aligned} a_{[\texttt {E}_{r +1}(j)^\lambda ]+1}(\text {id}) \lesssim \texttt {L}_{r}\big ( \texttt {E}_{r +1}(j)\big )^{-\alpha } \psi \big ( \texttt {L}_{r}\big ( \texttt {E}_{r+1}(j)\big ) \big )^{-1} \lesssim e_{[\texttt {E}_{r +1}(j)^\lambda ]+1} (\text {id}), \end{aligned}$$

and so

$$\begin{aligned} a_n (\text {id}) \lesssim \texttt {L}_{r} (n^{1 /\lambda })^{-\alpha } \psi \big ( \texttt {L}_{r}(n^{1/\lambda })\big )^{-1} \lesssim e_n (\text {id})\,. \end{aligned}$$

Besides,

$$\begin{aligned} \texttt {L}_{r} (n^{1 /\lambda })^{\alpha } \psi \big ( \texttt {L}_{r}(n^{1/\lambda })\big ) \sim \texttt {L}_{r} (n)^{\alpha } \psi \big ( \texttt {L}_{r}(n)\big )\,. \end{aligned}$$

Then the result follows by using [14, Theorem 3.3]. $\square$

5 Applications to Besov Spaces

Let $d \in {\mathbb {N}}$, and let ${\mathbb {T}}^d$ be the d-torus

$$\begin{aligned} {\mathbb {T}}^d = \{x=(x_1,\ldots ,x_d) \in {\mathbb {R}}^d : |x_j| \le \pi \text { for } j=1,\ldots ,d\}. \end{aligned}$$

We identify points x, y if $x - y = 2 k \pi$ for any $k \in {\mathbb {Z}}^d$.

For $1< p < \infty ,$ let $L_p = L_p({\mathbb {T}}^d)$ be the usual Lebesgue space on ${\mathbb {T}}^d$. For $s \ge 0, 0 < q \le \infty$, and $\psi$ a slowly varying function, $\mathbf B ^{s,\psi }_{p,q}$ stands for the Besov space formed by all $f \in L_p$ having a finite quasi-norm

$$\begin{aligned} \Vert f\Vert _\mathbf{B ^{s,\psi }_{p,q}} = \Vert f\Vert _{L_p} + \left( \int _0^1 (t^{-s} \psi (t) \omega _k(f,t)_p)^q \frac{dt}{t}\right) ^{1/q} \end{aligned}$$

(with the usual modification if $q=\infty$). Here $s < k \in {\mathbb {N}}$, and $\omega _k(f,t)_p$ is the k-th order modulus of smoothness of f, given by

$$\begin{aligned} \omega _k(f,t)_p = \sup _{|h| \le t} \Vert \varDelta ^k_h f\Vert _{L_p},\quad t > 0, \end{aligned}$$

where

$$\begin{aligned} \varDelta ^1_h f(x) = f(x+h)-f(x) \text { and } \varDelta ^{k+1}_h f (x) = \varDelta ^1_h (\varDelta ^k_h f) (x). \end{aligned}$$

Note that for all $k\in {\mathbb {N}}$ with $k>s$, all these quasi-norms are equivalent. The case $\psi (t) = 1$ and $s > 0$ corresponds to the classical periodic Besov spaces $\mathbf B ^s_{p,q}$ defined by differences. If $s=0$ and $\psi (t) = (1 + |\log t|)^\gamma$, we simply write $\mathbf B ^{0,\gamma }_{p,q}$.

Let $T_0 = \{0\}$, and for $n \in {\mathbb {N}}$, let

$$\begin{aligned} T_n = \left\{ \sum _{\sum _{j=1}^d |k_j| \le n} c_k e^{i k \cdot x} : c_k \in {\mathbb {C}}, k = (k_1,\ldots ,k_d) \in {\mathbb {Z}}^d\right\} \end{aligned}$$

be the linear space of all trigonometric polynomials of (triangular) degree less than or equal to n. Here $k \cdot x = k_1 x_1 + \cdots + k_d x_d$. Consider also the sets of all trigonometric polynomials of cubic (respectively, spherical) degree less than or equal to n given by

$$\begin{aligned} R_n = \left\{ \sum _{\max _{j=1,\ldots ,d} |k_j| \le n} c_k e^{i k \cdot x} : c_k \in {\mathbb {C}}, k = (k_1,\ldots ,k_d) \in {\mathbb {Z}}^d\right\} \end{aligned}$$

and

$$\begin{aligned} S_n = \left\{ \sum _{\left( \sum _{j=1}^d |k_j|^2\right) ^{1/2} \le n} c_k e^{i k \cdot x} : c_k \in {\mathbb {C}}, k = (k_1,\ldots ,k_d) \in {\mathbb {Z}}^d\right\} . \end{aligned}$$

Put also $R_0 = S_0 = \{0\}$. It is clear that if $d=1$, then $T_n = R_n = S_n$.

In multivariate approximation, the set from which the frequencies of the approximating polynomials are taken plays an important role, because some results depend on the particular choice of this set (see, for example, [25] and [49]). However, as we show below, the families $(T_n),(R_n)$, and $(S_n)$ yield the same approximation spaces.

We have

$$\begin{aligned} T_n \subseteq R_n \subseteq T_{d n},\quad T_n \subseteq S_n \subseteq T_{d n}. \end{aligned}$$

For $J_n = T_n, R_n, S_n$, put

$$\begin{aligned} E_n^J(f) = \inf \{\Vert f-g\Vert _{L_p} : g \in J_n\}. \end{aligned}$$

Let $k_0 \in {\mathbb {N}}$ such that $d < 2^{k_0}$. We have $E^T_{2^{j+k_0}}(f) \le E^R_{2^j}(f) \le E^T_{2^j}(f)$ and $E^T_{2^{j+k_0}}(f) \le E^S_{2^j}(f) \le E^T_{2^j}(f)$. Therefore, if $s > 0$, we get

$$\begin{aligned} \Vert f\Vert _{(L_p;R_n)^{(s,\psi )}_q}^\diamond&= \left( \Vert f\Vert ^q _{L_p}+ \sum _{j=1}^\infty (2^{j s} \psi (2^j) E^R_{2^j }(f))^q\right) ^{1/q} \\&\le \Vert f\Vert _{(L_p;T_n)^{(s,\psi )}_q}^\diamond \\&\lesssim \left( \Vert f\Vert _{L_p}^q + \sum _{j=1}^\infty (2^{j s} \psi (2^j) E^T_{2^{j+k_0}} (f))^q\right) ^{1/q} \\&\lesssim \Vert f\Vert _{(L_p;R_n)^{(s,\psi )}_q}^\diamond . \end{aligned}$$

Similarly, $(L_p;T_n)^{(s,\psi )}_q = (L_p;S_n)^{(s,\psi )}_q$ and $(L_p;T_n)^{(0,\gamma )}_q = (L_p;R_n)^{(0,\gamma )}_q = (L_p;S_n)^{(0,\gamma )}_q$.

Note also that $(L_p;R_n)$ is a linear approximation scheme with

$$\begin{aligned} (P_n f) (x) = \sum _{\max _{j=1,\ldots ,d} |k_j| \le n} \widehat{f}(k) \,e^{i k \cdot x} \end{aligned}$$

and

$$\begin{aligned} \widehat{f}(k) = (2 \pi )^{-d} \int _{{\mathbb {T}}^d} f(x)\, e^{-i k \cdot x} d x,\quad k \in {\mathbb {Z}}^d, \end{aligned}$$

(see [25, Corollary 3.5.2 and Theorem 3.5.7]). Moreover, $\text {dim } R_n = (2n+1)^d$, so (4.2) is satisfied.

When $\psi (t)=1$ and $s > 0$, it is known that $\mathbf B ^s_{p,q} = (L_p;R_n)^s_q$ (see [37, 5.3] and also [46, Corollary 3.7.1]). On the other hand, if $d=1$ and $\psi (t) = (1 + |\log t|)^\gamma$, it is shown in [20, Corollary 7.1/(i)] that $\mathbf B ^{0,\gamma }_{p,q} = (L_p;R_n)^{(0,\gamma )}_q$. In fact, using Jackson and Bernstein inequalities (see [37, 47]) and a convenient form of Hardy’s inequality, for $d \in {\mathbb {N}}$, if $s > 0$ and $\psi$ is a slowly varying function, then $\mathbf B ^{s,\psi }_{p,q}=(L_p;R_n)^b_q$, where $b = (n^s \psi (n))$, and if $\gamma \ge -1/q$, then $\mathbf B ^{0,\gamma }_{p,q} = (L_p;R_n)^{(0,\gamma )}_q$ (see [45]; see also [9, Lemma 2.1]). Therefore, as a direct consequence of Corollaries 4.1 to 4.5, we derive the following results.

Corollary 5.1

Let $1< p< \infty , 0 < q \le \infty , s > 0$, and let $\psi$ be a slowly varying function. Then for the embedding $id : \mathbf B ^{s,\psi }_{p,q} \hookrightarrow L_p$, we have

$$\begin{aligned} a_n(id ) \sim e_n(id ) \sim \frac{1}{n^{s/d} \psi (n^{1/d})}. \end{aligned}$$

Corollary 5.2

Let $1< p< \infty , 0 < q_0, q_1 \le \infty$, and $0< s_1 < s_0$. Then for the embedding $id : \mathbf B ^{s_0}_{p,q_0} \hookrightarrow \mathbf B ^{s_1}_{p,q_1}$, we have

$$\begin{aligned} a_n(id ) \sim e_n(id ) \sim n^{-(s_0 - s_1)/d}. \end{aligned}$$

Corollary 5.3

Let $1< p< \infty , 0 < q \le \infty$, and $\gamma \ge -1/q$. Then for the embedding $id : \mathbf B ^{0,\gamma }_{p,q} \hookrightarrow L_p$, we have:

• (a) If $\gamma > -1/q$, then

  $$\begin{aligned} a_n (id ) \sim e_n(id ) \sim (\log n)^{-(\gamma + 1/q)}. \end{aligned}$$

• (a) If $\gamma = -1/q$ and $0< q < \infty$, then

  $$\begin{aligned} a_n(id ) \sim e_n(id ) \sim (\log \log n)^{-1/q}. \end{aligned}$$

Corollary 5.4

Let $1< p< \infty , 0 < q_0, q_1 \le \infty$, and $\gamma _0, \gamma _1 \in {\mathbb {R}}$ with $\gamma _0 + 1/q_0> \gamma _1 + 1/q_1 > 0$. Then for the embedding $id : \mathbf B ^{0,\gamma _0}_{p,q_0} \hookrightarrow \mathbf B ^{0,\gamma _1}_{p,q_1}$, we have

$$\begin{aligned} a_n(id ) \sim e_n(id ) \sim (\log n)^{-(\gamma _0 - \gamma _1 + 1/q_0 -1/q_1)}. \end{aligned}$$

Remark 5.1

It should be noticed that the asymptotic behaviors described in Corollaries 5.3 and 5.4 are independent of the dimension d. Moreover, the fine index q is involved in the estimates, which is not the case in Corollaries 5.1 and 5.2.

Corollary 5.5

Let $1< p< \infty , s > 0, 0 < q_0, q_1 \le \infty$, and $\gamma > -1/q_1$. Then for the embedding $id : \mathbf B ^{s, \gamma + 1/q_1}_{p,q_0} \hookrightarrow \mathbf B ^{0,\gamma }_{p,q_1}$, we have

$$\begin{aligned} a_n(id ) \sim e_n(id ) \sim n^{-s/d}. \end{aligned}$$

The following result is a consequence of Theorems 4.3 and 4.4. It shows the degree of compactness of embeddings when we replace in Corollary 5.5 the function $(1+|\log t|)^{\gamma +1/q_1}$ by any other slowly varying function $\psi$. It also allows $\gamma$ to take the extreme value $-1/{q_1}$.

Corollary 5.6

Let $1< p< \infty , s > 0, 0 < u, q \le \infty , \gamma \ge -1/q$, and let $\psi$ be a slowly varying function. Then for the embedding $id : \mathbf B ^{s,\psi }_{p,u} \hookrightarrow \mathbf B ^{0,\gamma }_{p,q}$, we obtain:

• (a) If $\gamma > -1/q$, then

  $$\begin{aligned} a_n(id ) \sim e_n(id ) \sim n^{-s/d} (\log n)^{\gamma + 1/q} \psi (n^{1/d})^{-1}\quad . \end{aligned}$$

• (b) If $\gamma = -1/q$ and $0< q < \infty$, then

  $$\begin{aligned} a_n(id ) \sim e_n(id ) \sim n^{-s/d} (\log \log n)^{1/q} \psi (n^{1/d})^{-1}\quad . \end{aligned}$$

Remark 5.2

In several recent papers (see [11,12,13]), dealing with Besov spaces with smoothness close to zero, it has been pointed out that in this case there are important differences between spaces defined by the modulus of smoothness and spaces defined via the Fourier transform. Corollary 5.3 can also be used to illustrate this fact. Indeed, if we assume that $1<p<\infty , 0<q\le \min (2,p)$, and $\gamma >0$, it follows from Corollary 5.3 that

$$\begin{aligned} a_n \left( \text {id} : \mathbf B ^{0,\gamma }_{p,q} \hookrightarrow L_p\right) \sim e_n\left( \text {id} : \mathbf B ^{0,\gamma }_{p,q} \hookrightarrow L_p\right) \sim (\log n)^{-(\gamma + 1/q)}\,. \end{aligned}$$

(5.1)

However, for spaces defined by the Fourier transform, approximation and entropy numbers have a worse behavior. In fact, let $\varOmega$ be a bounded Lipschitz domain in ${\mathbb {R}}^d$ and define $B^{0, \gamma } _{p,q}(\varOmega )$ by restriction from $B^{0, \gamma } _{p,q}({\mathbb {R}}^d)$, the Besov space on ${\mathbb {R}}^d$ of logarithmic smoothness given by the Fourier transform. According to [7, Theorem 4.3], under our assumptions on $p,q,\gamma$, we have that $B^{0, \gamma } _{p,q}({\mathbb {R}}^d)$ is formed by regular distributions. Hence $B^{0, \gamma } _{p,q}(\varOmega ) \hookrightarrow L_p$. Using [14, Corollary 4.6], one can show that

$$\begin{aligned} a_n \left( \text {id} : B^{0,\gamma }_{p,q} (\varOmega ) \hookrightarrow L_p\right) \sim e_n\left( \text {id} : B^{0,\gamma }_{p,q} (\varOmega ) \hookrightarrow L_p\right) \sim (\log n)^{-\gamma }\,. \end{aligned}$$

Note that the exponent of the logarithm in this formula is worse than in (5.1).