Universal Lower Bounds for Potential Energy of Spherical Codes

Abstract

We derive and investigate lower bounds for the potential energy of finite spherical point sets (spherical codes). Our bounds are optimal in the following sense—they cannot be improved by employing polynomials of the same or lower degrees in the Delsarte–Yudin method. However, improvements are sometimes possible, and we provide a necessary and sufficient condition for the existence of such better bounds. All our bounds can be obtained in a unified manner that does not depend on the potential function, provided the potential is given by an absolutely monotone function of the inner product between pairs of points, and this is the reason we call them universal. We also establish a criterion for a given code of dimension n and cardinality N not to be LP-universally optimal; e.g., we show that two codes conjectured by Ballinger et al. to be universally optimal are not LP-universally optimal.

1 Introduction

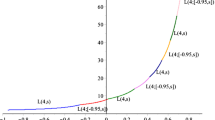
Minimal energy configurations, maximal codes, and spherical designs have wide ranging applications in various fields of science, such as crystallography, nanotechnology, material science, information theory, wireless communications, etc. In this article, we shall derive lower bounds on the potential energy of such configurations via a unified method working for a large class of potential interaction functions. A fundamental connection between our lower bounds and the classical Delsarte–Goethals–Seidel bounds on spherical designs and Levenshtein’s bounds on maximal codes is presented. For a fixed dimension and code cardinality, the Delsarte–Goethals–Seidel bounds serve to localize the analysis, and then, as illustrated in Fig. 2, the zeros of the Levenshtein optimal polynomials for maximal codes determine the optimal polynomials for a large class of potentials.

Following Levenshtein’s terminology (see [27]) we call the lower bounds that we obtain universal. This choice of this term is also consistent with its use by Cohn and Kumar in their study [14] of universally optimal energy configurations, since our bounds likewise work for all absolutely monotone potential functions of the inner product. Furthermore, our lower bounds are attained for all sharp configurations as defined in [14].

Let $\mathbb {S}^{n-1}$ denote the unit sphere in $\mathbb {R}^n$. We refer to a finite set $C \subset \mathbb {S}^{n-1}$ as a spherical code, and, for a given (extended real-valued) function $h(t):[-1,1] \rightarrow [0,+\infty ]$, we define the h -energy of a spherical code C by

$$\begin{aligned} E(C;h):=\sum _{x, y \in C, x \ne y} h(\langle x,y \rangle ), \end{aligned}$$

where $\langle x,y \rangle$ denotes the inner product of x and y. Note that for $x, y \in {\mathbb {S}}^{n-1}$, we have $|x-y|^2=2-2\langle x,y \rangle$.

A commonly arising problem is to minimize the potential energy provided the cardinality |C| of C is fixed, that is, to determine

$$\begin{aligned} {\mathcal {E}}(n,N;h):=\inf \left\{ E(C;h):|C|=N, \, C\subset S^{n-1}\right\} , \end{aligned}$$

the minimum possible h-energy of a spherical code of cardinality N (see [20, 31]). Although the theorems in Sect. 2 hold for general potentials h, we will be especially concerned with functions h(t) that are absolutely monotone (strictly absolutely monotone); that is, $h^{(i)}(t)\ge 0$, $i=0,1,\dots$ ($h^{(i)}(t)> 0$, $i=0,1,\dots$). Some examples of absolutely monotone potentials include the Riesz $\alpha$ -potential $h(t)=[2(1-t)]^{-\alpha /2}$, $\alpha >0$, and in particular the Newton potential (when $\alpha =n-2$); the Gauss potential $h(t)=e^{2t-2}$; and the Korevaar potential $h(t)=(1+r^2-2rt)^{-(n-2)/2}$, $0<r<1$. Although the logarithmic potential $h(t)=-(1/2)\ln {(2-2t)}$ is not positive on $[-1,0]$, all its derivatives are positive, and the results in this article apply to this potential as well. The situation is similar for the Fejes–Tóth potential $h(t)=-[2(1-t)]^{\alpha /2}$, $0<\alpha <2$, which includes the important particular case in discrete geometry of $\alpha =1$, namely of finding configurations that maximize the sum of all mutual distances.

A general technique (referred to here as the Delsarte–Yudin method) for obtaining lower bounds for the h-energy of arbitrary spherical codes was developed by Yudin [35] using Delsarte’s linear programming method [17, 18, 21] and was further applied by Kolushov and Yudin [22], Andreev [1], and Cohn and Kumar [14]. These bounds depend on the choice of polynomials satisfying certain constraints. Here we provide explicit solutions to Delsarte’s linear program based upon Levenshtein’s work on maximal codes [26, 27], which allows us to establish universal lower bounds on potential energy for a large class of potential functions h.

In Sect. 2, we describe in a unified manner results from Delsarte et al. [18] and Levenshtein [25–27] that are instrumental in defining our bounds. Theorems 2.3 and 2.6 explain the importance of special type quadrature rules in determining lower bounds on energy and investigation of their optimality. Theorem 3.1 is one of the main results in this paper. It gives lower bounds that are optimal in the following sense – they cannot be improved by polynomials of the same or lower degree that satisfy the standard linear programming constraints specified in Theorem 2.2. On the other hand, the bounds of Theorem 3.1 can be further improved in some cases, and Theorem 4.1 gives necessary and sufficient conditions for existence of such improvements via the so-called test functions, which were first introduced and investigated for analysis of the Levenshtein bounds for maximal codes in 1996 by Boyvalenkov et al. [11]. We derive a quantitative version of [11, Theorem 5.2] in Theorem 4.11, which provides a criterion for disproving that certain codes are LP-universally optimal. As an application, we prove that the two codes conjectured to be universally optimal in [2] are not LP-universally optimal; namely, their universal optimality may not be established by an ad-hoc approach similar to the 600-cell approach given in [14, 15].

2 Linear Programming Framework and 1 / N-Quadrature Rules

2.1 Gegenbauer Polynomials and the Delsarte–Yudin Linear Programming Framework

For fixed dimension n, the Gegenbauer polynomials [33] are defined by $P_0^{(n)}=1$, $P_1^{(n)}=t$ and the three-term recurrence relation

$$\begin{aligned} (i+n-2)P_{i+1}^{(n)}(t)=(2i+n-2)tP_i^{(n)}(t)-iP_{i-1}^{(n)}(t) \text{ for } i \ge 1. \end{aligned}$$

(1)

We note that $\{P_i^{(n)}(t)\}$ are orthogonal in $[-1,1]$ with respect to the weight $(1-t^2)^{(n-3)/2}$ and that $P_i^{(n)}(1)=1$. In standard Jacobi polynomial notation (see [33, Chapter 4]), we have that

$$\begin{aligned} P_i^{(n)}(t)=\frac{P_i^{((n-3)/2, (n-3)/2)}(t)}{P_i^{((n-3)/2, (n-3)/2)}(1)}. \end{aligned}$$

Denote the space of real polynomials of degree at most k by ${\mathcal {P}}_k$. Any $f\in {\mathcal {P}}_k$ can be uniquely expanded in terms of the Gegenbauer polynomials as $f(t) = \sum _{i=0}^k f_iP_i^{(n)}(t)$. The coefficients $f_i$ given by

$$\begin{aligned} f_i=\frac{\int _{-1}^1f(t)P_i^{(n)}(t)(1-t^2)^{(n-3)/2}\, \hbox {d}t}{\int _{-1}^1 \left[ P_i^{(n)}(t)\right] ^2(1-t^2)^{(n-3)/2}\, \hbox {d}t},\qquad i=0,1,\ldots ,k, \end{aligned}$$

play an important role in linear programming theorems.

Let $\{Y_{k\ell }(x) : \ell =1,2,\ldots ,r_k\}$ be an orthonormal basis of the space $\mathrm {Harm}(k)$ of homogeneous harmonic polynomials in n variables of degree k restricted to $\mathbb {S}^{n-1}$, where

$$\begin{aligned} r_k:=\dim \,\mathrm {Harm}(k)=\left( {\begin{array}{c}n+k-3\\ n-2\end{array}}\right) \frac{2k+n-2}{k}=\left( {\begin{array}{c}n+k-1\\ n-1\end{array}}\right) -\left( {\begin{array}{c}n+k-3\\ n-1\end{array}}\right) \, \end{aligned}$$

(2)

and orthonormality is with respect to integration over the sphere utilizing $\sigma _n$, the normalized $(n-1)$-dimensional Hausdorff measure restricted to $\mathbb {S}^{n-1}$. The functions $\{Y_{k\ell }$, $\ell =1,2,\ldots ,r_k\}$ are known as spherical harmonics of degree k. The Gegenbauer polynomials and spherical harmonics are related through the well-known addition formula (see [23]):

$$\begin{aligned} \frac{1}{r_k}\sum _{\ell =1}^{r_k}Y_{k\ell }(x)Y_{k\ell }(y) = P_k^{(n)}(\langle x, y \rangle ),\ \ \ x,y\in \mathbb {S}^{n-1}; \end{aligned}$$

(3)

that is, the Gegenbauer polynomial $P_k^{(n)}(t)$ is, up to a normalization, the kernel for the orthogonal projection onto $\mathrm {Harm}(k)$.

If f is a function integrable on $[-1,1]$ with respect to the weight function $(1-t^2)^{(n-3)/2}$ and y is any fixed point on $\mathbb {S}^{n-1}$, then the following relation (a particular/special case of the Funk–Hecke formula, see [29, Theorem 6]) holds:

$$\begin{aligned} \int _{S^{n-1}}f(\langle x, y \rangle )d\sigma _n (x)=\gamma _n\int \limits _{-1}^{1}f(t)(1-t^2)^{(n-3)/2}\hbox {d}t, \end{aligned}$$

where

$$\begin{aligned} \gamma _n:= \frac{\Gamma \left( \frac{n}{2}\right) }{\sqrt{\pi } \Gamma \left( \frac{n-1}{2}\right) }. \end{aligned}$$

If $C=\{x_1,\ldots ,x_N\}$ is a spherical code of N points on $\mathbb {S}^{n-1}$, then it follows from (3) that:

$$\begin{aligned} \sum _{i,j=1}^{N}P_k^{(n)}(\langle x_i, x_j \rangle )=\frac{1}{r_k} \sum _{\ell =1}^{r_k}\sum _{i,j=1}^{N}Y_{k \ell }(x_i)Y_{k \ell }(x_j)= \frac{1}{r_k}\sum _{\ell =1}^{r_k}\left( \sum _{i=1}^{N}Y_{k \ell }(x_i)\right) ^2\ge 0. \end{aligned}$$

(4)

We define the k-th moment of C by

$$\begin{aligned} M_k(C):=\sum _{i,j=1}^N P^{(n)}_k(\langle x_i , x_j\rangle ). \end{aligned}$$

From (4), we have $M_k(C)=0$ if and only if $\sum _{i=1 }^N Y(x_i)=0$ for all spherical harmonics $Y\in \mathrm {Harm}(k)$. If $M_k(C)=0$ for $1\le k\le \tau$, then C is called a spherical $\tau$ -design. Equivalently, C is a spherical $\tau$-design if and only if

$$\begin{aligned} \int _{{\mathbb {S}}^{n-1}} p(x) d\sigma _n(x)= \frac{1}{|C|} \sum _{x \in C} p(x) \end{aligned}$$

($\sigma _n$ is the normalized $(n-1)$-dimensional Hausdorff measure) holds for all polynomials $p(x) = p(x_1,x_2,\ldots ,x_n)$ of degree at most $\tau$. The set

$$\begin{aligned} {\mathcal {I}}(C):=\{k\in {\mathbb {N}}:M_k(C)=0\} \end{aligned}$$

(5)

is called the index set of C. Hence, C is a spherical $\tau$-design if and only if $\{1, 2, \ldots , \tau \}\subset {\mathcal {I}}(C)$.

Suppose $f:[-1,1]\rightarrow \mathbb {R}$ is of the form

$$\begin{aligned} f(t)=\sum _{k=0}^\infty f_k P_k^{(n)}(t),\qquad f_k\ge 0 \text { for all } k\ge 1, \end{aligned}$$

(6)

where we remark that $f(1)=\sum _{k=0}^\infty f_k<\infty$. Since $|P_k^{(n)}(t)|\le 1$, it follows that the right-hand side of (6) converges uniformly on $[-1,1]$. We then obtain the following relations, which form the basis for many packing and energy bounds for spherical codes $C=\{x_i\}_{i=1}^N$ of cardinality N (see [6, 14, 21, 35]):

$$\begin{aligned} E(C;f)= & {} \sum _{i,j=1}^N f(\langle x_i, x_j \rangle )-f(1)N \nonumber \\= & {} \sum _{k=0}^\infty f_k \sum _{i,j=1}^{N}P_k^{(n)}(\langle x_i, x_j \rangle )-f(1)N \nonumber \\= & {} \sum _{k=0}^\infty f_kM_k(C)-f(1)N \nonumber \\\ge & {} f_0N^2-f(1)N. \end{aligned}$$

(7)

Since $M_k(C)=0$ for $k=1,\ldots , \tau$ when C is a $\tau$-design, the following result immediately follows from (7).

Theorem 2.1

(Delsarte et al. [18]) Suppose C is a spherical $\tau$-design on $\mathbb {S}^{n-1}$ and f(t) is a polynomial of degree at most $\tau$ such that $f(t)\ge 0$ on $[-1,1]$ and $f_0=\gamma _n \int _{-1}^1 f(t)(1-t^2)^{(n-3)/2}\, \hbox {d}t>0$. Then

$$\begin{aligned} |C|\ge \frac{f(1)}{f_0}. \end{aligned}$$

(8)

Maximizing the right-hand side of (8) over polynomials satisfying the above hypotheses, Delsarte et al. [18] obtain a lower bound on

$$\begin{aligned} B(n,\tau ):=\min \{|C|: C \subset {\mathbb {S}}^{n-1} \text{ is } \text{ a } \text{ spherical } \tau \hbox {-design}\} \end{aligned}$$

Specifically, they show

$$\begin{aligned} B(n,\tau ) \ge D(n,\tau ) := \left\{ \begin{array}{ll} \displaystyle { 2{n+k-2 \atopwithdelims ()n-1}} &{}\quad \text{ if } \tau =2k-1, \\ &{} \\ \displaystyle {{n+k-1 \atopwithdelims ()n-1}+{n+k-2 \atopwithdelims ()n-1}} &{}\quad \text{ if } \tau =2k. \end{array} \right. \end{aligned}$$

(9)

We refer to $D(n,\tau )$ as the Delsarte–Goethals–Seidel bound for spherical $\tau$-designs.

Another application of (7) is Yudin’s lower bound on energy.

Theorem 2.2

(Yudin [35]) Suppose $f:[-1,1]\rightarrow \mathbb {R}$ is of the form (6) with $f_k\ge 0$ for all $k\ge 1$. Then, for $N\ge 2$,

$$\begin{aligned} {\mathcal {E}}(n,N;f)\ge f_0 N^2-f(1) N. \end{aligned}$$

Consequently, if $h:[-1,1]\rightarrow [0,\infty ]$ satisfies $h(t)\ge f(t)$, $t\in [-1,1]$, we have

$$\begin{aligned} {\mathcal {E}}(n,N;h)\ge f_0N^2-f(1)N. \end{aligned}$$

(10)

Furthermore, C is an optimal (energy minimizing) code for h, and equality holds in (10) if and only if both of the following conditions hold:

• (a) $f(t)=h(t)$ for all $t\in \{ \langle x, y \rangle : x\ne y, \ x,y \in C \};$

• (b) for all $k\ge 1$, either $f_k=0$ or $M_k (C)=0$.

For a given $h:[-1,1]\rightarrow [0,\infty ]$, we denote by $A_{n,h}$ the set of functions $f\le h$ satisfying the conditions (6). Recall that for such f, the coefficient sequence $(f_0,f_1,\ldots ) \in \ell _1$. The problem of maximizing the lower bound $f_0 N^2- f(1)N$ arising in Theorem 2.2 can then be expressed in terms of an infinite linear program:

$$\begin{aligned}&\text {maximize} \quad F(f_0,f_1,\ldots ) := N\left( f_0(N-1)-\sum _{k= 1}^\infty f_k \right) , \nonumber \\&\text {subject to } \, \sum _{k=0}^\infty f_kP_k^{(n)}(t)\le h(t), t\in [-1,1]\, \text { and } f_k\ge 0, \text { for all } k\ge 1. \end{aligned}$$

(11)

In the following, we shall consider the above linear program restricted to a subspace $\Lambda$ (usually finite-dimensional) of the linear space $C([-1,1])$ of real-valued functions continuous on $[-1,1]$. For such a $\Lambda$, we define

$$\begin{aligned} {\mathcal {W}}(n,N,\Lambda ;h):= \sup _{f \in \Lambda \cap A_{n,h}} N^2(f_0 -f(1)/N). \end{aligned}$$

(12)

In general, it can be a difficult problem to find the value of ${\mathcal {W}}(n,N,\Lambda ;h)$. We consider sufficient conditions that allow us to solve for ${\mathcal {W}}(n,N,\Lambda ;h)$. In particular, we explicitly find the solutions of the truncated linear program (11) and thus find (12) when $\Lambda ={\mathcal {P}}_k$, for all $k\le \tau (n,N)$, for some $\tau (n,N)$ (as defined in equation (19) below). In the particular case when $m=\tau (n,N)$, we derive the universal lower bound (ULB) for potential energy of spherical codes.

2.2 1 / N-Quadrature Rules and Lower Bounds for Energy

We refer to a finite sequence of ordered pairs $\{(\alpha _i, \rho _i)\}_{i=1}^{k}$ as a 1 / N -quadrature rule if $-1 \le \alpha _1 < \alpha _2 < \cdots <\alpha _{k} < 1$ and $\rho _i>0$ for $i=1,2,\ldots ,k$, and say that $\{(\alpha _i, \rho _i)\}_{i=1}^{k}$ is exact for a subspace $\Lambda \subset C([-1,1])$ if

$$\begin{aligned} f_0:=\gamma _n\int _{-1}^1f(t)(1-t^2)^{(n-3)/2}\hbox {d}t= \frac{f(1)}{N}+ \sum _{i=1}^{k} \rho _i f(\alpha _i) \end{aligned}$$

(13)

for all $f\in \Lambda$.

Theorem 2.3

Let $\{(\alpha _i, \rho _i)\}_{i=1}^{k}$ be a 1 / N-quadrature rule that is exact for a subspace $\Lambda \subset C([-1,1])$.

• (a) If $f\in \Lambda \cap A_{n,h}$, then

  $$\begin{aligned} {\mathcal {E}}(n,N;h)\ge N^2\sum _{i=1}^{k} \rho _i f(\alpha _i). \end{aligned}$$

• (b) We have

  $$\begin{aligned} {\mathcal {W}}(n,N,\Lambda ;h)\le N^2\sum _{i=1}^{k} \rho _i h(\alpha _i). \end{aligned}$$

  (14)

If there is some $f\in \Lambda \cap A_{n,h}$ such that $f(\alpha _i)=h(\alpha _i)$ for $i=1,\ldots , k$, then equality holds in (14), which yields the universal lower bound

$$\begin{aligned} {\mathcal {E}}(n,N;h)\ge N^2\sum _{i=1}^{k} \rho _i h(\alpha _i). \end{aligned}$$

(15)

Proof

If $f\in \Lambda$, then (13) holds, and so, from Theorem 2.2, we obtain

$$\begin{aligned} {\mathcal {E}}(n,N;h)\ge N^2(f_0- {f(1)}/{N})=N^2\sum _{i=1}^{k} \rho _i f(\alpha _i), \end{aligned}$$

showing that (a) holds.

For (b), using (13), we obtain

$$\begin{aligned} {\mathcal {W}}(n,N,\Lambda ;h)= & {} \sup _{f \in \Lambda \cap A_{n,h}} N^2(f_0 -f(1)/N) \\= & {} \sup _{f \in \Lambda \cap A_{n,h}}N^2\sum _{i=1}^{k} \rho _i f(\alpha _i)\le N^2\sum _{i=1}^{k} \rho _i h(\alpha _i). \end{aligned}$$

Clearly equality holds if there is some $f\in \Lambda \cap A_{n,h}$ such that $f(\alpha _i)=h(\alpha _i)$ for $i=1,\ldots , k$. $\square$

As we describe next, a spherical code $C=\{x_1,\ldots , x_N\}\subset \mathbb {S}^{n-1}$ provides a quadrature rule that is exact on the subspace

$$\begin{aligned} \Lambda _C:= \left\{ f(t)=f_0+\sum _{\ell \in {\mathcal {I}}(C)} f_\ell P_\ell ^{(n)}(t):\sum _{\ell \in {\mathcal {I}}(C)} |f_\ell |<\infty \right\} , \end{aligned}$$

with ${\mathcal {I}}(C)$ as defined in (5). Let

$$\begin{aligned} \left\{ \langle x_i, x_j\rangle :x_i\ne x_j \in C\right\} =:\{-1\le \alpha _1<\alpha _2<\cdots <\alpha _{k}<1\}, \end{aligned}$$

and let $\{q_\ell \}$ denote the inner product distribution; i.e.,

$$\begin{aligned} q_\ell :=\frac{\big |\left\{ (i,j) :\langle x_i,x_j\rangle =\alpha _\ell \right\} \big |}{N^2}, \qquad \ell =1,\ldots , k. \end{aligned}$$

If $f\in \Lambda _C$, then $f_\ell =0$ for all $\ell \not \in {\mathcal {I}}(C)$ (unless $\ell =0$) and equality holds in (7). Hence, for such f, we obtain

$$\begin{aligned} f_0=\frac{1}{N^2}\big (E(C;f)+Nf(1)\big )= \frac{f(1)}{N}+\sum _{\ell =1}^{k}q_\ell f(\alpha _\ell ); \end{aligned}$$

(16)

that is, $\{(\alpha _\ell , q_\ell )\}_{\ell =1}^{k}$ is a 1 / N-quadrature rule exact for $\Lambda _C$.

Example 2.4

As an example, we consider the 600-cell C consisting of 120 points in $\mathbb {S}^3$. Each $x\in C$ has 12 nearest neighbors forming an icosahedron (the Voronoi cells are dodecahedra), and there are 8 inner products $-1=\alpha _1<\alpha _2<\cdots < \alpha _8<1$ between distinct points in C. If $f(t)\le h(t)$ on $[-1,1]$ and $f(\alpha _k)=h(\alpha _k)$ and for all $\alpha _k>-1$, then we must also have $f'(\alpha _k)=h'(\alpha _k)$, resulting in $2\cdot 7+1=15$ interpolation conditions. If C were a 14-design, then this would suggest we search for $f\in A_{4,h} \cap \Lambda$ with $\Lambda ={\mathcal {P}}_{14}$. However, C is only an 11-design (i.e., $M_{12}(C)\ne 0$), although $M_{13}(C)=\cdots = M_{19}(C)=0$, so C is almost a 19-design. This suggests we choose $\Lambda$ to be a 15-dimensional subspace of ${\mathcal {P}}_{19}\cap \{P_{12}^{(4)}\}^\perp$. In fact, Cohn and Kumar [14, Section 7] show that for any absolutely monotone potential h on $[-1,1]$, there is a unique $f\in A_{4,h}\cap \Lambda$ for $\Lambda :=\{ f \in {\mathcal {P}}_{17}:f_{11}=f_{12}=f_{13}=0\}$ that proves the optimality of C.

Example 2.5

Another example is provided by the so-called sharp configurations [14], namely, configurations with k distinct inner products that are spherical designs of strength $2k-1$. In this case, $\Lambda ={\mathcal {P}}_{2k-1}$, and the existence of the 1 / N-quadrature is provided by the configuration quadrature (16) and the design property. We shall return to this example in Remark 3.3 following Theorem 3.1.

The two examples above cover all currently known universally optimal configurations. The next theorem provides sufficient conditions for optimality of (15) even in a larger subspace.

Theorem 2.6

Let $\{(\alpha _i, \rho _i)\}_{i=1}^{k}$ be a 1 / N-quadrature rule that is exact for a subspace $\Lambda \subset C([-1,1])$ and such that equality holds in (14). Suppose $\Lambda '=\Lambda \bigoplus \text {span }\{P_j^{(n)} :j\in {\mathcal {I}}\}$ for some index set ${\mathcal {I}}\subset {\mathbb N}$. If $Q_j^{(n)}:= \frac{1}{N}+\sum _{i=1}^{k}\rho _i P_j^{(n)}(\alpha _i) \ge 0$ for $j\in {\mathcal {I}}$, then

$$\begin{aligned} {\mathcal {W}}(n,N,\Lambda ';h) = {\mathcal {W}}(n,N,\Lambda ;h) = N^2\sum _{i=1}^{k}\rho _i h(\alpha _i). \end{aligned}$$

Proof

Suppose $f(t) \in A_{n,h}\cap \Lambda '$. Then we may write the decomposition of f as

$$\begin{aligned} f(t)= g(t)+\sum _{j\in {\mathcal {I}}} f_j P_j^{(n)}(t) \end{aligned}$$

for some $g\in \Lambda$ and $f_j\ge 0$, for $j\in {\mathcal {I}}$. Note that $f_0=g_0$, since $0\not \in {\mathcal {I}}$. Furthermore, since the quadrature rule $\{(\alpha _i, \rho _i)\}_{i=1}^{k}$ is exact for $g\in \Lambda$, we have

$$\begin{aligned} f_0- f(1)N^{-1}= & {} g_0 - f(1)N^{-1} = \frac{g(1)}{N}+\sum _{i=1}^{k} \rho _i g(\alpha _i) -\left( g(1)+\sum _{j\in {\mathcal {I}}} f_j \right) N^{-1} \\= & {} \sum _{i=1}^{k} \rho _i \left( f(\alpha _i)-\sum _{j\in {\mathcal {I}}} f_j P_j^{(n)}(\alpha _i)\right) -\left( \sum _{j\in {\mathcal {I}}} f_j \right) N^{-1}\\= & {} \sum _{i=1}^{k} \rho _i f(\alpha _i)-\sum _{j\in {\mathcal {I}}} f_j \left( \frac{1}{N}+ \sum _{i=1}^{k}\rho _i P_j^{(n)}(\alpha _i) \right) \\= & {} \sum _{i=1}^{k} \rho _i f(\alpha _i)-\sum _{j\in {\mathcal {I}}}f_jQ_j^{(n)} \le \sum _{i=1}^{k} \rho _i h(\alpha _i)=\frac{1}{N^2}{\mathcal {W}}(n,N,\Lambda ;h), \end{aligned}$$

where, for the last inequality, we used $f(t) \in A_{n,h}$ and $Q_j^{(n)} \ge 0$. $\square$

2.3 Levenshtein Bounds for Spherical Codes

Let

$$\begin{aligned} A(n,s):=\max \left\{ |C| :C \subset {\mathbb {S}}^{n-1}, \langle x,y \rangle \le s, \, x\ne y \in C\right\} \end{aligned}$$

denote the maximal possible cardinality of a spherical code on ${\mathbb {S}}^{n-1}$ of prescribed maximal inner product s.

For $a,b \in \{0,1\}$ and $i \ge 1$, let $t_i^{a,b}$ denote the greatest zero of the adjacent Jacobi polynomial $P_i^{(a+\frac{n-3}{2},b+\frac{n-3}{2})}(t)$, and also define $t_0^{1,1}=-1$. For $\tau \in {\mathbb {N}}$, let $I_\tau$ denote the interval

$$\begin{aligned} I_\tau := \left\{ \begin{array}{ll} \left[ t_{k-1}^{1,1},t_k^{1,0} \right] &{}\quad \text{ if } \tau =2k-1, \\ &{} \ \\ \left[ t_k^{1,0},t_k^{1,1} \right] &{}\quad \text{ if } \tau =2k. \\ \end{array}\right. \end{aligned}$$

The collection of intervals is well defined from the interlacing properties $t_{k-1}^{1,1}<t_k^{1,0}<t_k^{1,1}$, see [27, Lemmas 5.29, 5.30]. Note also that it partitions $I=[-1,1)$ into countably many subintervals with nonoverlapping interiors.

For every $s \in I_\tau$, using linear programming bounds for special polynomials $f_\tau ^{(n,s)}(t)$ of degree $\tau$ (see [27, Equations (5.81) and (5.82)]), Levenshtein proved that (see [27, Equation (6.12)])

$$\begin{aligned} A(n,s) \le \left\{ \begin{array}{ll} L_{2k-1}(n,s) = {k+n-3 \atopwithdelims ()k-1} \left[ \frac{2k+n-3}{n-1} - \frac{P_{k-1}^{(n)}(s)-P_k^{(n)}(s)}{(1-s)P_k^{(n)}(s)} \right] &{}\quad \text{ if } s\in I_{2k-1} \\ &{} \\ L_{2k}(n,s) = {k+n-2 \atopwithdelims ()k} \left[ \frac{2k+n-1}{n-1} - \frac{(1+s)( P_k^{(n)}(s)-P_{k+1}^{(n)}(s))}{(1-s)(P_k^{(n)}(s)+P_{k+1}^{(n)}(s))} \right] &{}\quad \text{ if } s\in I_{2k}. \\ \end{array}\right. \end{aligned}$$

(17)

For every fixed dimension n, each bound $L_\tau (n,s)$ is smooth with respect to s. The function

$$\begin{aligned} L(n,s) = \left\{ \begin{array}{ll} L_{2k-1}(n,s) &{} \text{ if } s \in I_{2k-1}, \\ \\ L_{2k}(n,s) &{} \text{ if } s \in I_{2k} \\ \end{array}\right. \end{aligned}$$

is continuous in s. The connection between the Delsarte–Goethals–Seidel bound (9) and the Levenshtein bounds (17) is given by the equalities

$$\begin{aligned} L_{2k-2}\left( n,t_{k-1}^{1,1}\right)= & {} L_{2k-1}\left( n,t_{k-1}^{1,1}\right) = D\left( n,2k-1\right) , \nonumber \\ L_{2k-1}\left( n,t_k^{1,0}\right)= & {} L_{2k}\left( n,t_k^{1,0}\right) = D(n,2k), \end{aligned}$$

(18)

at the ends of intervals $I_\tau$ (Fig. 1).

Fig. 1

The Levenshtein function L(4, s) on $I_{\tau }$, $1\le \tau \le 6$

2.4 Levenshtein’s 1 / N-Quadrature Rule

Levenshtein’s method for obtaining his bounds on cardinality of maximal spherical codes utilizes orthogonal polynomials theory and Gauss-type quadrature rules that we now briefly review. The location of the cardinality N relative to the Delsarte–Goethals–Seidel numbers $D(n,\tau )$ is an important step in determining our universal lower bounds. The monotonicity of the bounds $D(n,\tau )$ with respect to $\tau$ (see (9)) implies that for every fixed dimension n and cardinality N, there is unique

$$\begin{aligned} \tau :=\tau (n,N) \quad \text {such that} \quad N \in (D(n,\tau ),D(n,\tau +1)]. \end{aligned}$$

(19)

For the so found $\tau$, define $k:= \left\lceil \frac{\tau +1}{2} \right\rceil$, and let $\alpha _k=s$ be the unique solution of (see (18))

$$\begin{aligned} N=L_{\tau }(n,s), \quad s \in I_\tau . \end{aligned}$$

(20)

Then as described by Levenshtein in [27, Section 5] (see also [9, 26]), there exist uniquely determined quadrature nodes and nonnegative weights

$$\begin{aligned} -1 \le \alpha _1 < \cdots <\alpha _k < 1,\quad \rho _1,\ldots ,\rho _k \in {\mathbb {R}}^+,\quad i=1,\ldots ,k \end{aligned}$$

(21)

such that the Radau/Lobatto 1 / N-quadrature (see [5, 16]) holds:

$$\begin{aligned} f_0= \frac{f(1)}{N}+\sum _{i=1}^{k} \rho _i f(\alpha _i) \ \ \text{ for } \text{ all }\ f\in {\mathcal {P}}_{\tau }. \end{aligned}$$

(22)

When $\tau =2k-2$ is even, then $\alpha _1=-1$ and (22) is Lobatto quadrature. The numbers $\alpha _i$, $i=2,\ldots ,k$, are the roots of the equation

$$\begin{aligned} P_{k-1}(t)P_{k-2}(\alpha _k) - P_{k-1}(\alpha _{k})P_{k-2}(t)=0, \end{aligned}$$

(23)

where $P_i(t)=P_i^{(\frac{n-1}{2},\frac{n-1}{2})}(t)$. When $\tau =2k-1$ is odd, then $\alpha _1>-1$ and (22) becomes Radau quadrature. The numbers $\alpha _i$, $i=1\ldots ,k$, are the roots of the equation

$$\begin{aligned} P_k(t)P_{k-1}(\alpha _k) - P_k(\alpha _{k})P_{k-1}(t)=0, \end{aligned}$$

(24)

where $P_i(t)=P_i^{(\frac{n-1}{2},\frac{n-3}{2})}(t)$. In fact, $\{\alpha _i\}$ are roots of the Levenshtein’s polynomials $f_{\tau }^{(n,\alpha _{k})}(t)$ (see [27, Equations (5.81) and (5.82)]).

The dynamical behavior of the quadrature nodes $\{\alpha _i\}$ is the following. When $N\in (D(n,2k-2), D(n,2k-1))$, then $\alpha _1 =-1$ and the quadrature (22) is Lobatto. The solution $\alpha _k$ of (20) belongs to the interval $(t_{k-1}^{1,0},t_{k-1}^{1,1})$, and all $\{\alpha _i\}_{i=2}^{k}$ strictly increase with N. We have that

$$\begin{aligned} 1=|\alpha _1|>|\alpha _2|>|\alpha _k|>|\alpha _3|>|\alpha _{k-1} |>\cdots . \end{aligned}$$

At the transition point $N=D(n,2k-1)$, $\alpha _1 =-1$ and $\alpha _k =t_{k-1}^{1,1}$. The equation (23) becomes $P_{k-1}^{(n+2)} (t)=0$, which implies that

$$\begin{aligned} 1=|\alpha _1|>|\alpha _2|=|\alpha _k|>|\alpha _3|=|\alpha _{k-1}| >\cdots . \end{aligned}$$

As N increases from $D(n,2k-1)$ to D(n, 2k), $\alpha _k$ strictly increases from $t_{k-1}^{1,1}$ to $t_k^{1,0}$, as do the rest of the nodes $\{\alpha _i\}_{i=1}^{k-1}$. In particular, $\alpha _1>-1$ and (22) defines Radau quadrature, and

$$\begin{aligned} 1>|\alpha _1|>|\alpha _k|>|\alpha _2|>|\alpha _{k-1} |>\cdots . \end{aligned}$$

More details on the nodes $\{\alpha _i\}$ can be found in [12, Appendix], [10, Corollary 3.9], and [7, Section 2.6].

3 Universal Lower Bounds

3.1 Optimal Polynomials for Lower Bounds

The optimal polynomials of degrees one and two to be applied in Theorem 2.2 can be found by direct computations and manipulations with the corresponding derivatives. These polynomials suggest a general form of polynomials which are optimal in the following sense—they give lower bounds that cannot be improved by utilizing other polynomials of the same or lower degree in Theorem 2.2.

Our choice of polynomials for Theorem 2.2 can be viewed as an extension of the ideas of Levenshtein [26, 27], who uses suitable quadrature formulas (Subsection 2.4) to explain the bounds (17) and their optimality in the same sense as above. This similarity should not seem unusual; the maximal code problem is an infinite version of the Riesz energy problem. In fact, Cohn and Kumar [14] use a similar idea to deal with universally optimal configurations. Thus, our paper can be viewed as a natural extension of the works [14, 26, 27]. Recall that given a fixed dimension n and a code cardinality N, we can associate $\tau =\tau (n,N)$ and $s \in I_\tau$ such that $L_\tau (n,s)=N$ (see (19) and (20)). Depending on the parity of $\tau$, we distinguish two cases:

Case (i): $\tau =2k-2$ and $\alpha _k=s\in \left( t_{k-1}^{1,0},t_{k-1}^{1,1}\right]$. Then we choose f(t) as the Hermite interpolation polynomial of degree $2k-2$ defined by (recall that $\alpha _1=-1$ in this case)

$$\begin{aligned} f(-1)=h(-1), \ f(\alpha _i)=h(\alpha _i), \ f^\prime (\alpha _i)=h^\prime (\alpha _i), \ i=2,\ldots ,k. \end{aligned}$$

(25)

Case (ii): $\tau =2k-1$ and $\alpha _k=s\in \left( t_{k-1}^{1,1},t_k^{1,0}\right]$. Then f(t) is the Hermite interpolation polynomial of degree $2k-1$ defined by

$$\begin{aligned} f(\alpha _i)=h(\alpha _i), \ f^\prime (\alpha _i)=h^\prime (\alpha _i), \ i=1,2,\ldots ,k; \end{aligned}$$

(26)

In the notation of Cohn–Kumar’s paper [14, p. 110], our polynomials are

$$\begin{aligned} f (t)=H(h; (t-s)f_{\tau }^{(n,s)} (t)). \end{aligned}$$

(27)

3.2 Main Theorem

The equations (25) and (26) define a Hermite interpolation problem for f(t) to intersect and touch the graph of the potential function h(t) (see [22, Theorems 2 and 3], [14, Section 5]). This implies as in [14, Sections 3 and 5] that $f\in A_{n,h}$ and we could use f(t) for bounding ${\mathcal E}(n,N;h)$ from below. Observe that the nodes (21) are independent of the potential function h; hence we call our bound on ${\mathcal E}(n,N;h)$ a universal lower bound (ULB).

Next, we state our main theorem. We note that here is the first time we impose the condition that the potential function h(t) is absolutely monotone and that none of the preceding results has required this property.

Theorem 3.1

Let n, N be fixed and h(t) be an absolutely monotone potential. Suppose that $\tau =\tau (n,N)$ is as in (19), and choose $k= \left\lceil \frac{\tau +1}{2} \right\rceil$. Associate the quadrature nodes and weights $\alpha _i$ and $\rho _i$, $i=1,\ldots ,k$, as in (22). Then

$$\begin{aligned} {\mathcal E}(n,N;h) \ge R_{\tau }(n,N;h):=N^2\sum _{i=1}^{k} \rho _i h(\alpha _i) . \end{aligned}$$

(28)

Moreover, the polynomials f(t) defined by (26), respectively by (25), provide the unique optimal solution of the linear program (12) for the subspace $\Lambda ={\mathcal {P}}_\tau$, and consequently,

$$\begin{aligned} {\mathcal {W}}(n,N, {\mathcal {P}}_\tau ;h)=R_{\tau }(n,N;h). \end{aligned}$$

(29)

Remark 3.2

The optimality of the Hermite interpolants (27) is analogous to the optimality of the Levenshtein polynomials $f_\tau ^{(n,s)} (t)$ (proved first by Sidelnikov [32]), and emphasizes the universality of our bound.

Remark 3.3

As noted in Example 2.5, the sharp configurations (see [14]) define 1 / N-quadrature. Moreover, the k inner products coincide with $\{\alpha _i\}$. Consequently, the bounds (28) are attained by all sharp configurations.

Proof of Theorem 3.1

We first consider the odd case (ii); that is, $\tau =2k-1$. The conditions in (ii) define Hermite interpolation at the points $\alpha _i$, $i=1,2,\ldots ,k$, and give a unique polynomial f of degree $2k-1$ with positive leading coefficient. The absolute monotonicity of h(t) implies that $f(t)\le h(t)$.

Next we derive that f satisfies condition (6) as well. From (24) we have that the quadrature nodes $\{\alpha _1,\dots ,\alpha _{k}\}$ are zeros of a polynomial of the type $P_k (t)+cP_{k-1}(t)$, where $\{P_i\}$ are the Jacobi orthogonal polynomials $\{P_i^{(\frac{n-1}{2},\frac{n-3}{2})}\}$. From the interlacing properties of the orthogonal polynomials we obtain that the constant $c=-P_k (s)/P_{k-1}(s)$ is nonnegative. Indeed, the largest roots of the Jacobi polynomials $t_{k-1}^{1,0}$ of $P_{k-1}$ satisfy $t_{k-1}^{1,0}<t_{k-1}^{1,1}$ (see [26]). Since the last but largest root of $P_k$ is smaller than $t_{k-1}^{1,0}$ (by the interlacing property), we obtain that the ratio $P_k (t)/P_{k-1}(t)$ doesn’t change sign in $[t_{k-1}^{1,1},t_k^{1,0})$. Moreover, from [7, Lemma 3.1.3(a)] (see also [8, Lemma 1.5.8]),

$$\begin{aligned} \displaystyle {-\frac{P_k (t_{k-1}^{1,1})}{P_{k-1} (t_{k-1}^{1,1})} = \frac{n+2k-3}{n+2k-1}}>0; \end{aligned}$$

(30)

hence $c\ge 0$. Utilizing the approach of [14, Sections 3 and 5], we conclude that the Hermite interpolant f has nonnegative Gegenbauer expansion. Therefore, $f \in A_{n,h}$.

We now use (22) to derive the universal bound of f. We have

$$\begin{aligned} f_0= & {} \frac{f(1)}{N}+ \sum _{i=1}^{k} \rho _i f(\alpha _i) \iff N(f_0N-f(1))=N^2\sum _{i=1}^{k} \rho _i f(\alpha _i)\\= & {} N^2\sum _{i=1}^{k} \rho _i h(\alpha _i), \end{aligned}$$

which means that ${\mathcal E}(n,N;h) \ge N^2\sum _{i=1}^{k} \rho _i h(\alpha _i)=R_{2k-1}(n,N;h)$.

Furthermore, for any polynomial $u =\sum _{i=0}^{2k-1} u_i P_i^{(n)}(t) \in A_{n,h}$ of degree at most $2k-1$, we have

$$\begin{aligned} N(f_0N-f(1))=N^2\sum _{i=1}^{k} \rho _i h(\alpha _i) \ge N^2\sum _{i=1}^{k} \rho _i u(\alpha _i)=N(u_0N-u(1)), \end{aligned}$$

(31)

i.e., $N(u_0N-u(1)) \le R_{2k-1}(n,N;h)$, and u(t) does not improve (28).

Should equality hold in (31) for some $u \in A_{n,h}\cap {\mathcal {P}}_{2k-1}$, we observe that $u(\alpha _i )=h(\alpha _i)$ for $i=1,2,\dots , k$. Additionally, the condition $u(t)\le h(t)$ implies that $u^\prime (\alpha _i)=h^\prime (\alpha _i)$ for all $\alpha _i\in (-1,1)$. Hence, u satisfies the Hermite interpolation data (26), and by the uniqueness of the Hermite interpolant, $u\equiv f$. Therefore, f is the unique optimal solution to the linear programming problem (11) in the class $A_{n,h}\cap {\mathcal {P}}_{2k-1}$, and (29) holds.

In the even case (i), we proceed analogously, where we only modify the proof of the nonnegativity of the Gegenbauer expansion. In this case, we utilize [15, Lemma 10]. $\square$

Fig. 2

The optimal polynomials (Hermite interpolants) that provide the ULB for Gauss, Korevaar, and Newton potentials (in ascending order), along with the corresponding Levenshtein polynomial for $n=4$, $N=24$

3.3 Discussion and Examples

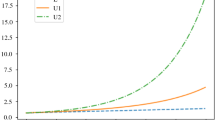
The bounds (28) are easy for computation and investigation. Moreover, the approach by which they were derived doesn’t depend on the potential function, and in this sense they are universal. This universality is illustrated in Fig. 2, where we consider $n=4$, $N=24$ and plot the Gauss, Korevaar, and Newton potential functions, together with the corresponding optimal Hermite interpolants of degree $\tau =5$, that solve the linear program (11) in the class ${\mathcal {P}}_5$. We also overlay the Levenshtein polynomial $f_5^{(4,s)}(t)$, whose zeros are the solutions of (24), where s satisfies $L_5 (4,s)=24$. These zeros of the Levenshtein polynomial also serve as quadrature nodes for the universal lower bound (28) and as Hermite interpolation nodes for the optimal LP polynomials.

In [2] the authors have done an extensive experimental investigation of energy-minimizing point configurations; in particular, they provide the computational minimizers for the Newton potential energy ($h(t)=[2(1-t)]^{-(n-2)/2}$) when $n=1,2,\dots ,32$ and $N=1,2,\dots ,64$. Table 1 compares the Newton energy from [2] and our universal lower bound (ULB) when $n=4$ and $N=5,6,\dots ,64$.

Table 1 Newtonian (harmonic) energy comparison (see [2]) with ULB for $n=4$, $N=5, \dots ,64$

Utilizing the same Newton energy-minimizing configurations provided in [2] in Table 2, we compare our universal lower bound (ULB) with the Gauss potential ($h(t)=e^{2t-2}$) energies of these configurations, which in general provide upper bounds on the minimal Gauss energy for the same choice of $n=4$ and $N=5,6,\dots ,64$. We note that the error dramatically improves, which is to be expected, as the Hermite interpolants of analytic potential functions are excellent approximants. Observe that for $N=5$ and $N=8$, the bounds are exact. Both cases are universally optimal.

Table 2 Gauss energy of the harmonic optimal configurations (as provided in [2]) compared with ULB for $n=4$, $N=5,\dots , 64$

In the next result, we describe the explicit solution of the linear program (12) for $\Lambda ={\mathcal {P}}_m$ for all $m\le \tau (n,N)$.

Theorem 3.4

Let $m\le \tau (n,N)$. Then the solution of the linear program (12) for $\Lambda ={\mathcal {P}}_m$ is given by the Hermite interpolants at the Levenshtein nodes determined by $N=L_m (n,s)$.

Proof

To derive the theorem, we need to modify the proof of Theorem 3.1 as follows (we consider the odd case (ii) $m=2k-1$, the even being similar). We determine $\alpha _k:=s$ as the solution of $L_{2k-1} (n,s)=N$ that is in the interval $[t_{k-1}^{1,1},t_k)$ and the nodes $\alpha _1,\dots ,\alpha _{k-1}$ as the solutions of (24). Here $t_k=t_k^{0,0}$ denotes the largest root of the Gegenbauer polynomial $P_k^{(n)}$ (observe that (17) shows that $t_k$ is a pole of $L_{2k-1} (n,s)$). If $m<\tau (n,N)$, then $s\in (t_k^{1,0},t_k)$ and the constant $c=-P_k (s)/P_{k-1} (s)<0$, so the argument of Theorem 3.1 doesn’t apply. However, [15, Lemma 10] with the multi-set $\{\alpha _1,\alpha _1,\alpha _2,\alpha _2,\dots ,\alpha _k,\alpha _k\}$ implies that the Hermite interpolant with these nodes is a linear combination with nonnegative coefficients of the polynomials $\{1,(t-\alpha _1) , (t-\alpha _1)^2 , (t-\alpha _1)^2 (t-\alpha _2) , \dots , (t-\alpha _1)^2 (t-\alpha _2)^2 \cdot \dots \cdot (t-\alpha _k) \}$. The positive definiteness of all these polynomials except for the last one can be derived by utilizing [14, Theorem 3.1 and Lemma 5.3] (for the application of which the sign of c is irrelevant), while the positive definiteness of the last polynomial for $s\in (t_k^{1,0},t_k)$ is noted in the proof of [26, Theorem 5.2]. $\square$

Example 3.5

Here we present the LP solutions for $n=4$, $N=24$, the Newtonian potential $h(t)=(2-2t)^{-1}$, and $\Lambda ={\mathcal {P}}_m$ for $m=1,\ldots , 5$. Note that in this case $\tau (n,N)=5$. For $m=1,\dots ,5$, we solve $24=L_m(4,s)$ to determine quadrature points and weights (cf. Fig. 1). The corresponding optimal polynomials from Theorem 3.4 given in terms of Gegenbauer expansions (up to three digits) are:

$$\begin{aligned} g_1 (t)= & {} .499P_0^{(4)}(t)+.229P_1^{(4)}(t), \\ g_2 (t)= & {} .581P_0^{(4)}(t)+.305P_1^{(4)}(t)+0.093P_2^{(4)}(t), \\ g_3(t)= & {} .658P_0^{(4)}(t)+.395P_1^{(4)}(t)+.183P_2^{(4)}(t) + 0.069P_3^{(4)}(t), \\ g_4(t)= & {} .69P_0^{(4)}(t)+.43P_1^{(4)}(t)+.23P_2^{(4)}(t) + .10P_3^{(4)}(t)+0.027P_4^{(4)}(t), \\ g_5(t)= & {} .71P_0^{(4)}(t)+.46P_1^{(4)}(t)+.26P_2^{(4)}(t) + .13P_3^{(4)}(t)+0.05P_4^{(4)}(t)\\&+\,0.01^{(4)}P_5(t). \end{aligned}$$

A natural question is whether linear programming bounds can be improved if we consider polynomials of higher than $\tau (n,N)$ degree. The next section investigates this topic. As one would expect from our results thus far presented, the analogy with the situation for maximal spherical codes is quite close.

4 Necessary and Sufficient Conditions for Optimality of the Universal Lower Bounds

4.1 Test Functions

Let n and N be fixed, $\tau =\tau (n,N)$ and $L_\tau (n,s)=N$ be as in (19) and (20), and j be a positive integer. We introduce the following functions¹ in n and $s=\alpha _k$:

$$\begin{aligned} Q_j(n,s):=\frac{1}{N}+\sum _{i=1}^{k} \rho _i P_j^{(n)}(\alpha _i) \quad \text {for } s \in I_\tau . \end{aligned}$$

(32)

It follows that $Q_j(n,s)=0$ for $1 \le j \le \tau$ and $s \in I_\tau$ (since this is the coefficient $f_0=0$ in the Gegenbauer expansion of $P_j^{(n)}(t)$). Thus the functions $Q_j(n,s)$ are not interesting for these cases, and so we assume below that $j \ge \tau +1$ when $s \in I_\tau$.

The next theorem shows that the functions $Q_j(n,s)$ give necessary and sufficient conditions for existence of improving polynomials of higher degrees.

Theorem 4.1

The bounds (28) can be improved by a polynomial from $A_{n,h}$ of degree at least $\tau +1$ if and only if $Q_j(n,s) < 0$ for some $j \ge \tau +1$. Furthermore, if h is strictly absolutely monotone and $Q_j(n,s)<0$ for some $j \ge \tau +1$, then (28) can be improved by a polynomial from $A_{n,h}$ of degree exactly j.

Proof

We give a proof for $\tau =2k-1$.

(Necessity) The necessity follows from Theorem 2.6 for ${\mathcal {I}}=\{2k,2k+1,\dots \}$.

(Sufficiency) Conversely, assume that h is strictly absolutely monotone, and suppose that $Q_j(n,s) <0$ for some $j \ge 2k$.

We shall improve the bound (28) by using the polynomial

$$\begin{aligned} f(t)=\epsilon P_j^{(n)}(t)+g(t), \end{aligned}$$

where $\epsilon >0$ and $g(t)\in {\mathcal {P}}_{2k-1}$ will be properly chosen. Set $\tilde{h}(t):= h(t)-\epsilon P_j^{(n)}(t)$, and select $\epsilon$ such that $\tilde{h}^{(i)}(t) \ge 0$ on $[-1,1]$ for all $i=0,1,\dots ,j$. Observe that for this choice of $\epsilon$, the function $\tilde{h}(t)$ is absolutely monotone. The polynomial g(t) is chosen as the Hermite interpolant of $\tilde{h}$ at the nodes $\{ \alpha _i\}$; i.e.,

$$\begin{aligned} g(\alpha _i)=\tilde{h}(\alpha _i), \ g^\prime (\alpha _i)=\tilde{h}^\prime (\alpha _i), \ i=1,2,\ldots ,k. \end{aligned}$$

Since $\tilde{h}(t)$ is an absolutely monotone function, we infer as in Theorem 3.1 that $g \in A_{n,\tilde{h}}$, implying that $f\in A_{n,h}$.

Let $g(t)=\sum _{\ell =0}^{2k-1} g_\ell P_\ell ^{(n)}(t)$. Note that $f_0=g_0$ and $f(1)=g(1)+\epsilon$. We next prove that the bound given by f(t) is better than $R_{2k-1}(n,N;h)$. To this end, we multiply by $\rho _i$ and sum up the first interpolation equalities:

$$\begin{aligned} \sum _{i=1}^{k} \rho _i g(\alpha _i) = \sum _{i=1}^{k} \rho _i h(\alpha _i)-\epsilon \sum _{i=1}^{k} \rho _i P_j^{(n)}(\alpha _i). \end{aligned}$$

Since

$$\begin{aligned} \sum _{i=1}^{k} \rho _i g(\alpha _i)=g_0-\frac{g(1)}{N} \end{aligned}$$

by (22) and

$$\begin{aligned} \sum _{i=1}^{k} \rho _i P_j^{(n)}(\alpha _i)=Q_j(n,s)-\frac{1}{N} \end{aligned}$$

by the definition of the test functions (32), we obtain

$$\begin{aligned} g_0-\frac{g(1)}{N}=\frac{R_{2k-1}(n,N;h)}{N^2} + \frac{\epsilon }{N}-\epsilon Q_j(n,s), \end{aligned}$$

which is equivalent to

$$\begin{aligned} N(Ng_0-(g(1)+\epsilon ))=R_{2k-1}(n,N;h)-\epsilon N^2Q_j(n,s). \end{aligned}$$

Therefore $N(Nf_0-f(1))=R_{2k-1}(n,N;h)-\epsilon N^2Q_j(n,s)>R_{2k-1}(n,N;h)$; i.e., the polynomial f(t) gives better bound indeed. We also obtained a new bound

$$\begin{aligned} W(n,N;h) \ge R_{2k-1}(n,N;h)-\epsilon N^2Q_j(n,s). \end{aligned}$$

(33)

$\square$

Theorem 4.1 provides a sufficient condition for solving the infinite linear program (11).

Corollary 4.2

If $Q_j(n,s) \ge 0$ for all $j>\tau (n,N)$, then $f_{\tau (n,N)}^h (t)$ solves the linear program (11).

4.2 Investigation of the Test Functions

The test functions (32) coincide with the functions with the same name that were introduced and investigated in 1996 by Boyvalenkov et al. [11]. More details and all proofs are given in the dissertations [7, 8]. We cite some results from [7, 8, 11] with reformulations for energy bounds.

Theorem 4.3

([7, 8, 11]) The bounds $R_\tau (n,N;h)$ cannot be improved by using polynomials of degrees $\tau +1$ and $\tau +2$.

Set $k_1(n):=\sqrt{n-2}$, and let $k_2(n) \ge 9$ be such that

$$\begin{aligned} 4n \le k_2(n)^2-4k_2(n)+5+\sqrt{k_2(n)^4-8k_2(n)^3-6k_2(n)^2+24k_2(n)+25}. \end{aligned}$$

Then we have the following theorems.

Theorem 4.4

(a) [11, Theorem 4.9] If $n \ge 3$ and $k \ge k_1(n)$, then all bounds $R_{2k}(n,N;h)$ corresponding to s in the interior of the interval $I_{2k}$ can be improved by polynomials of degree $2k+3$.

(b) [7, Theorem 3.5.9], [8, Theorem 3.4.14] If $n \ge 3$ and $k \ge k_2(n)$, then all bounds $R_{2k-1}(n,N;h)$ corresponding to s in the interior of the interval $I_{2k-1}$ can be improved by polynomials of degree $2k+3$.

Remark 4.5

To make the paper self-contained, we include a proof of Theorem 4.4(b) in the Appendix.

Theorem 4.6

(a) If $n \ge 3$ and $k \ge k_1(n)$, then

$$\begin{aligned} {\mathcal {E}} (n,N;h) \ge R_{2k-1}(n,N;h)-\epsilon N^2Q_{2k+3}(n,s) \end{aligned}$$

for every $N \in (D(n,2k-1),D(n,2k))$, where $\epsilon$ is chosen as in Theorem 4.1.

(b) If $n \ge 3$ and $k \ge k_2(n)$, then

$$\begin{aligned} {\mathcal {E}} (n,N;h) \ge R_{2k}(n,N;h)-\epsilon N^2Q_{2k+3}(n,s) \end{aligned}$$

for every $N \in (D(n,2k),D(n,2k+1))$, where $\epsilon$ is chosen as in Theorem 4.1.

Proof

This follows from (33) and the fact that Theorem 4.4 is based on the inequality $Q_{2k+3}(n,s)<0$, which holds true for the mentioned values of n and $\tau$. $\square$

Another application of Theorem 4.4 concerns the sharp configurations. Recall from Remark 3.3 that the h-energy for any sharp configuration attains the ULB in (28) for any absolutely monotone potential h, in particular, for Riesz $\alpha$-potentials. Thus, a sharp configuration is also a maximal spherical $(n,L_{2k-1}(n,s),s)$ =(dimension, cardinality, maximal cosine) code, i.e., a code that attains the odd Levenshtein bound $L_{2k-1}(n,s)$ (cf. [26]). In fact, the next corollary is implicit in [12] and follows from the main result of [28] as well.

Corollary 4.7

For any fixed dimension $n \ge 3$, there are only finitely many values of N for which there is a sharp configuration of cardinality N.

Proof

Theorem  4.4 implies that in every fixed dimension $n \ge 3$, every Levenshtein bound $L_{2k-1}(n,s)$ can be improved in the whole open interval $\left( t_k^{1,0}, t_k^{1,1} \right)$ provided k is large enough. The remaining end points correspond to tight spherical designs, which means (among many other things) that $k \le 6$ [3, 4]. This leaves only finitely many possible intervals $I_{2k-1}$ where the Levenshtein bound $L_{2k-1}(n,s)$ can be attained. Every such interval contains finitely many s, corresponding to cardinalities N, which completes the proof. $\square$

We complete the subsection with the following conjecture, based on the above results and numerous investigations of the test functions as related to maximal spherical codes.

Conjecture 4.8

If $Q_j (n,s)\ge 0$ for $j=\tau (n,N)+3$ and $\tau (n,N)+4$, then $Q_j (n,s)\ge 0$ for all $j>\tau (n,N)$.

4.3 Test Functions and LP Universality

We now apply the test functions to the study of universal configurations.

Definition 4.9

A spherical code $C\subset {\mathbb {S}}^{n-1}$ of cardinality $|C|=N$ is called LP-universally optimal if

$$\begin{aligned} E(C;h)={\mathcal {W}}(n,N,{\mathcal {P}};h) \quad \hbox {for all absolutely monotone } h, \end{aligned}$$

where ${\mathcal {P}}$ is the subspace of polynomials.

Remark 4.10

Observe that from (10) and (12), one infers that LP-universally optimal codes are in fact universally optimal. If the conjecture in Ballinger et al. [2] is true, then Theorem 4.12 below implies that the converse does not hold.

We derive a criterion for positivity of test functions of large enough j that can be used for proving that certain spherical codes of given dimension n and cardinality N are not LP-universally optimal. We utilize (n, N) to denote² codes $C \subset {\mathbb {R}}^n$ with cardinality $| C |=N$. As examples, the cases $(n,N)=(10,40)$, (14, 64), and (15, 128) are analyzed.

Sharp estimations for Gegenbauer polynomials can be derived from [19] (see also [24]). In [19, Theorem 1], the following inequality is given:

$$\begin{aligned} \max _{t\in [-1,1]}\sqrt{1-t^2}w(t)p_j^2 (t)\le \frac{2e \left( 2+\sqrt{\alpha ^2+\beta ^2}\right) }{\pi }, \end{aligned}$$

(34)

where $\{ p_j (t)\}$ are the orthonormal Jacobi polynomials with weight $w(t)=(1-t)^\alpha (1+t)^\beta$. Utilizing $\alpha =\beta =\frac{n-3}{2}$ to get Gegenbauer polynomials and the normalization $P_j^{(n)}(1)=1$, we rewrite (34) as

$$\begin{aligned} |P_j^{(n)} (t)| \le \frac{\Gamma \left( \frac{n-1}{2} \right) }{(1-t^2)^{(n-2)/4}} \sqrt{\frac{2^{n-2} e(4+(n-3)\sqrt{2})\, j!}{\pi (2j+n-2)\, (j+n-3)!}}, \end{aligned}$$

(35)

where $\Gamma (x)$ is the Gamma function [34]. Note that for every fixed $n\ge 3$ and $t\in (-1,1)$, the right-hand side of (35) is strictly monotone decreasing in j.

Let k, $\alpha _1$, $\alpha _2$, and $\rho _1$ be as in Theorem 3.1. Denote by $j_0(n,N)$ the smallest degree $j>\tau (n,N)$ such that the right-hand side of (35) is less than $\frac{1}{N-1}$ when

$$\begin{aligned} t={\left\{ \begin{array}{ll} \alpha _1 &{} \text {if } \alpha _1>-1,\\ \alpha _2 &{} \text {if } \alpha _1=-1 \text { and } \rho _1<\frac{1}{N}, \end{array}\right. } \end{aligned}$$

(36)

or less than $\frac{2}{N-2}$ when $t=\alpha _2$ if $\alpha _1=-1$ and $\rho _1=1/N$.

Theorem 4.11

Let $n\ge 3$, $N\ge 2$, and let k, $\alpha _1$, $\alpha _2$, and $\rho _1$ be as in Theorem 3.1. Then $Q_j(n,\alpha _k)\ge 0$ for all $j\ge j_0(n,N)$.

Proof

As the comments on the dynamical behavior of the quadrature nodes $\{\alpha _i\}$ at the end of Sect. 2 indicate, we have $|\alpha _1| \ge |\alpha _i|$ for $i=2, \ldots , k$, and in the case $\alpha _1=-1$, we further have $|\alpha _2|\ge |\alpha _i|$ for $i=3, \ldots , k$.

We first consider the case $|\alpha _1|<1$; i.e., $\alpha _1>-1$. If $j\ge j_0(n,N)$, then we have

$$\begin{aligned} Q_j(n,s) \ge \frac{1}{N}-\sum _{i=1}^k\rho _i |P_j^{(n)}(\alpha _i)| \ge \frac{1}{N}-\left( 1-\frac{1}{N}\right) \cdot \frac{1}{N-1}=0 \end{aligned}$$

(we used $N\sum _{i=1}^k \rho _i=N-1$ following from (13) for $f(t)=1$). The case $\alpha _1=-1$ and $\rho _1<1/N$ is handled similarly using (35) as suggested by the second line of (36).

For the final special case $\alpha _1=-1$ and $\rho _1=1/N$, it is clear (cf. [12]) that $Q_j(n,s)=0$ for odd j. The case of even j follows similarly as above using the facts that $P_j^{(n)}(-1)=1$ and that $|\alpha _i|\le |\alpha _2|$ for $i= 3,\ldots , k$. $\square$

Theorem 4.11 gives a useful tool for disproving LP-universal optimality. For given n and N and numerics suggesting that Corollary 4.2 may hold, one finds explicitly $j_0(n,N)$ and calculates the remaining test functions $Q_j(n,s)$ for every $j \in \{\tau (n,N) + 3,\tau (n,N) + 4,\ldots ,j_0(n,N)-1\}$. This will be applied in the next subsection for some codes from [2].

4.4 Examples

Table 3 lists the first twenty test functions for some interesting configurations with negative values in bold. We utilize (n, N) to denote codes $C \subset {\mathbb {R}}^n$ with cardinality $| C |=N$.

Table 3 Test functions for some special (n, N) spherical codes

Judging by the behavior of the test functions, the linear programming method will provide improvements on our ULB for (4, 24) and (7, 182), but it is unlikely to give a solution similar to the case with the 600-cell (4, 120), where a polynomial in ${\mathcal {P}}_{17}$ served as an exact lower bound. Indeed, the fact that the test functions $Q_{14}, Q_{15}$, and $Q_{17}$ are negative provides additional insight on the unique status of the 600-cell as the only universally optimal code known that is not a sharp configuration.

The first configuration (4, 24) is the $D_4$ root system, or the so-called kissing number configuration in ${\mathbb {R}}^4$ (see [30]), which was shown by Cohn et al. (see [13]) not to be universal. The negative test functions $Q_8(4,s)$ and $Q_9(4,s)$, $s=\alpha _2 \approx 0.4749504897$, suggest searching for a polynomial $f(t)=\sum _{i=0}^9 f_i P_i^{(4)}(t)$ with $f_6=f_7=0$ and four touching points of the graphs of f(t) and the potential h(t). We have developed a numerical algorithm for handling such situations. For example, if $h(t)=\frac{1}{2(1-t)}$ is the Newton potential, our numerical calculations led to the polynomial

$$\begin{aligned} f(t)= & {} 0.4987 + 0.4852t + 0.4535t^2 + 0.5546t^3 + 0.9401t^4 + 0.8425t^5 \\&-\,0.3305t^6 - 0.7479t^7 + 0.1889t^8 + 0.37394t^9 \\= & {} 0.0073P_9^{(4)}(t)+ 0.0066P_8^{(4)}(t)+0.0659P_5^{(4)}(t)+ 0.2384P_4^{(4)}(t) \\&+\, 0.5116P_3^{(4)}(t) + \,0.7915P_2^{(4)}(t)+ 0.9236P_1^{(4)}(t)+ 0.7142P_0^{(4)}(t). \end{aligned}$$

The Hermite interpolation points are approximately $-0.860297$, $-0.489872$, $-0.195724$, and 0.47850. The bound obtained from f(t) is 333.1575, while the universal lower bound (28) gives $R_5(4,24;1/(2(1-t))=333$ and the energy of the $D_4$ root system is 334. Theoretical and computational aspects of the aforementioned algorithm for improvements (when possible) of our ULB and their nature will be discussed elsewhere.

Theorem 4.12

The spherical codes $(n,N)=(10,40)$, (14, 64), and (15, 128) are not LP-universally optimal.

Remark 4.13

The codes (10, 40) and (14, 64) were conjectured by Ballinger et al. in [2] to be universally optimal.

Proof

It follows from Theorem 4.11 and numerical calculations as explained in the end of the last subsection that the codes listed in the theorem are not LP-universally optimal. Indeed, we have $\tau (10,40)=3$ (so $\alpha _1>-1$), $j_0(10,40)=10$, and the second column in Table 3 shows that this code is not LP-universally optimal. Similarly, $\tau (14,64)=3$, $j_0(14,64)=8$, and the inspection of the third column of Table 3 suffices. The code (15, 128) was not conjectured to be universally optimal (but not eliminated) in [2] and we see that it is not LP-universally optimal because of $\tau (15,128)=3$, $j_0(14,64)=9$, and the fourth column in Table 3. $\square$

Appendix

In this appendix, we give the proof of Theorem 4.4(b), which has appeared so far only in the dissertation of Boumova [7]. We set $P_i^{(\frac{n-1}{2}, \frac{n-3}{2})}(t) := P_i^{1,0}(t)$ for short and use the Christoffel–Darboux formula (see [27, Equation (5.65)])

$$\begin{aligned} P_i^{1,0}(t)\sum _{j=0}^i r_j=\sum _{j=0}^i r_jP_j^{(n)}(t)={n+i-2 \atopwithdelims ()i}\frac{P_i^{(n)}(t)-P_{i+1}^{(n)}(t)}{1-t}. \end{aligned}$$

(37)

We also set $P_i^{(n)}(t)=\sum _{j=0}^i a_{i,j}t^j$.

For the proof of Theorem 4.4(b), we show for each $n\ge 3$ and s in the interior of $I_{2k-1}$ that $Q_{2k+3}(n,s)<0$ for k sufficiently large, and thus, by Theorem 4.1, the bound $R_{2k-1}(n,N;h)$ can be improved. For this purpose, we present several lemmas.

Lemma 4.14

Let $n \ge 3$, $s \in \left( t_{k-1}^{1,1},t_k^{1,0}\right)$, and $\alpha _i=\alpha _i(s)$, $i=1,\ldots , k$ be the associated Levenshtein quadrature nodes, see (22). Then $Q_{2k+3}(n,s)<0$ if and only if

$$\begin{aligned} \sum _{i=1}^{k} \alpha _i^2 < \frac{2k^2+k+1-n}{n+4k+2}. \end{aligned}$$

Proof

This is Corollary 4.4(a) from [11]. $\square$

To find the sum $\sum _{i=1}^{k} \alpha _i^2$ appearing in Lemma 4.14, we express the sums $\sum _{i=1}^{k} \alpha _i$ and $\sum _{1 \le i< j\le k} \alpha _i\alpha _j$ as functions of n, k, and s.

Lemma 4.15

For every $s \in I_{2k-1}$, $k \ge 2$, the numbers $\alpha _1,\alpha _2,\ldots ,\alpha _k$ satisfy the equalities

$$\begin{aligned} \sum _{i=1}^{k} \alpha _i= & {} -\frac{k}{n+2k-2} X , \end{aligned}$$

(38)

$$\begin{aligned} \sum _{1 \le i< j \le k} \alpha _i\alpha _j= & {} - \frac{k^2-k}{2(n+2k-4)} + \frac{k(k-1)}{(n+2k-2)(n+2k-4)} X, \end{aligned}$$

(39)

where

$$\begin{aligned} X = 1 - \frac{(n+2k-1)(n+k-2)}{k(n+2k-3)} \cdot \frac{P_k^{1,0}(s)}{P_{k-1}^{1,0}(s)}. \end{aligned}$$

Proof

The numbers $\alpha _1,\alpha _2,\ldots ,\alpha _{k}$ are the roots of the equation (24)

$$\begin{aligned} q(t) = P_k^{1,0}(t)P_{k-1}^{1,0}(s) - P_k^{1,0}(s)P_{k-1}^{1,0}(t)=0. \end{aligned}$$

Comparing the coefficients in (37), we obtain

$$\begin{aligned} q(t)= & {} \frac{a_{k,k} r_k P_{k-1}^{1,0}(s)}{\sum _{i=0}^k r_i} t^k \\&+ ~a_{k-1,k-1} r_{k-1} \left( \frac{P_{k-1}^{1,0}(s)}{\sum _{i=0}^k r_i} - \frac{P_k^{1,0}(s)}{\sum _{i=0}^{k-1} r_i} \right) t^{k-1}\\&+ ~\left[ \frac{( a_{k,k-2} r_k + a_{k-2,k-2} r_{k-2}) P_{k-1}^{1,0}(s)}{\sum _{i=0}^k r_i} - \frac{ a_{k-2,k-2} r_{k-2} P_k^{1,0}(s)}{\sum _{i=0}^{k-1} r_i} \right] t^{k-2}+\cdots \end{aligned}$$

Therefore, we have

$$\begin{aligned} \sum _{i=1}^{k} \alpha _i= & {} -~\frac{a_{k-1,k-1} r_{k-1} \left( \frac{P_{k-1}^{1,0}(s)}{\sum _{i=0}^k r_i} - \frac{P_k^{1,0}(s)}{\sum _{i=0}^{k-1} r_i} \right) }{\frac{a_{k,k} r_k P_{k-1}^{1,0}(s)}{\sum _{i=0}^k r_i}} \\= & {} -~\frac{a_{k-1,k-1}r_{k-1} }{a_{k,k}r_k} \left( 1 - \frac{\sum _{i=0}^k r_i}{\sum _{i=0}^{k-1} r_i} \cdot \frac{P_k^{1,0}(s)}{P_{k-1}^{1,0}(s)} \right) \\= & {} -\frac{k}{n+2k-2} \left( 1 - \frac{(n+2k-1)(n+k-2)}{k(n+2k-3)} \cdot \frac{P_k^{1,0}(s)}{P_{k-1}^{1,0}(s)} \right) . \end{aligned}$$

Here, we used that

$$\begin{aligned} \frac{a_{k-1,k-1}}{a_{k,k}}=\frac{n+k-3}{n+2k-4} \end{aligned}$$

from (1), the constants $r_i$ as in (2), and $\sum _{i=0}^j r_i$, which is equal to the Delsarte–Goethals–Seidel bound D(n, 2j) (this is for $j=k$ and $j=k-1$).

Similarly, we obtain

$$\begin{aligned} \sum _{1 \le i< j \le k} \alpha _i\alpha _j= & {} \frac{\frac{( a_{k,k-2} r_k + a_{k-2,k-2} r_{k-2}) P_{k-1}^{1,0}(s)}{\sum _{i=0}^k r_i} - \frac{ a_{k-2,k-2} r_{k-2} P_k^{1,0}(s)}{\sum _{i=0}^{k-1} r_i} }{\frac{a_{k,k} r_k P_{k-1}^{1,0}(s)}{\sum _{i=0}^k r_i}}\\= & {} \frac{ a_{k,k-2}}{a_{k,k} } + \frac{ a_{k-2,k-2} r_{k-2}}{a_{k,k} r_k} \left( 1 - \frac{\sum _{i=0}^k r_i}{\sum _{i=0}^{k-1} r_i} \frac{P_k^{1,0}(s)}{P_{k-1}^{1,0}(s)} \right) \\= & {} - \frac{k^2-k}{2(n+2k-4)} + \frac{k(k-1)}{(n+2k-2)(n+2k-4)} \\&\times \left( 1 - \frac{(n+2k-1)(n+k-2)}{k(n+2k-3)} \frac{P_k^{1,0}(s)}{P_{k-1}^{1,0}(s)} \right) . \end{aligned}$$

$\square$

It follows from Lemma 4.14 and equalities (38) and (39) that we have to investigate the sign of the function

$$\begin{aligned} G(n,k,s)= & {} \sum _{i=1}^{k} \alpha _i^2 - \frac{2k^2+k+1-n}{n+4k+2}\\= & {} \left( \sum _{i=1}^{k} \alpha _i \right) ^2 - 2\sum _{1 \le i< j \le k} \alpha _i\alpha _j - \frac{2k^2+k+1-n}{n+4k+2} \\= & {} \frac{k^2}{(n+2k-2)^2}X^2 - \frac{2k(k-1)}{(n+2k-2)(n+2k-4)}X \\&+ \frac{k(k-1)}{n+2k-4} - \frac{2k^2+k+1-n}{n+4k+2}, \end{aligned}$$

where X is as in Lemma 4.15 and $s \in I_{2k-1}=\left[ t_{k-1}^{1,1},t_k^{1,0}\right]$.

Lemma 4.16

For fixed n and k, the function G(n, k, s) is decreasing for $s \in I_{2k-1}$.

Proof

The function G(n, k, s) is quadratic with respect to X. Since $s \in \left[ t_{k-1}^{1,1},t_k^{1,0}\right] \subset \left( t_{k-1}^{1,0},t_k^{1,0}\right]$, the ratio $P_k^{1,0}(s)/P_{k-1}^{1,0}(s)$ increases in $I_{2k-1}$ (see [26, Corollary 2.1]). Therefore X decreases in s in the same interval, and we need to determine the numbers

$$\begin{aligned} X_1= & {} 1 - \frac{(n+2k-1)(n+k-2)}{k(n+2k-3)} \cdot \frac{P_k^{1,0}\left( t_{k-1}^{1,1}\right) }{P_{k-1}^{1,0}\left( t_{k-1}^{1,1}\right) } \end{aligned}$$

and

$$\begin{aligned} X_2= & {} 1 - \frac{(n+2k-1)(n+k-2)}{k(n+2k-3)} \cdot \frac{P_k^{1,0}\left( t_k^{1,0}\right) }{P_{k-1}^{1,0}\left( t_k^{1,0}\right) } \end{aligned}$$

(the end points of the interval of variation of X). We obtain

$$\begin{aligned} X_1 = 1 + \frac{(n+2k-1)(n+k-2)(n+2k-3)}{k(n+2k-3)(n+2k-1)}= \frac{n+2k-2}{k} \end{aligned}$$

using (30) and

$$\begin{aligned} X_2 = 1, \end{aligned}$$

because $P_k^{1,0}\left( t_k^{1,0}\right) = 0$.

We can already locate the numbers $X_1$ and $X_2$ with respect to the minimum of the graph of the quadratic function

$$\begin{aligned} g(X)= & {} G(n,k,s) \\= & {} \frac{k^2}{(n+2k-2)^2}X^2~ -~\frac{2k(k-1)}{(n+2k-2) (n+2k-4)}X\\&~ + ~\frac{k(k-1)}{n+2k-4}~-~\frac{2k^2+k-n+1}{n+4k+2}. \end{aligned}$$

The minimum of g(X) is attained at the point

$$\begin{aligned} X_0 = \frac{(k-1)(n+2k-2)}{k(n+2k-4)}. \end{aligned}$$

We have

$$\begin{aligned} X_0 - X_2 = X_0-1= -\frac{n-2}{k(n+2k-4)} < 0 \end{aligned}$$

for every $n \ge 3$ and $k \ge 2$. This shows that $X_0 < 1 = X_2 < X_1$; i.e., $X_2$ and $X_1$ lie on the left side of $X_0$. Hence g(X) decreases from $g(X_1)$ to $g(X_2)$ when X decreases from $X_1$ to $X_2$. This means that G(n, k, s) decreases in s in the whole interval $I_{2k-1}$. This completes the proof. $\square$

Thus we need to consider the sign of the function G(n, k, s) in the end points of the interval $I_{2k-1}=[t_{k-1}^{1,1},t_k^{1,0}]$. Define the functions

$$\begin{aligned} \varphi _1(n,k) = G\left( n,k,t_{k-1}^{1,1}\right) =g(X_1) \end{aligned}$$

and

$$\begin{aligned} \varphi _2(n,k) = G\left( n,k,t_k^{1,0}\right) =g(X_2). \end{aligned}$$

From the above, we have

$$\begin{aligned} \varphi _1(n,k) > G(n,k,s) > \varphi _2(n,k) \end{aligned}$$

for all $s \in \left( t_{k-1}^{1,1},t_k^{1,0}\right)$. We calculate $\varphi _1(n,k)$ and $\varphi _2(n,k)$.

Lemma 4.17

For every $n \ge 3$ and $k \ge 2$, we have

$$\begin{aligned} \varphi _1(n,k)= & {} \frac{ (4-n)k^2 + 4(n-2)k + 2n^2-5n}{(n+2k-4)(n+4k+2)}, \nonumber \\ \varphi _2(n,k)= & {} \frac{(n-2)(n+2k-1)(n-k^2-2)}{(n+4k+2) (n+2k-2)^2}. \end{aligned}$$

(40)

Proof

Plug $X_1 = \frac{n+2k-2}{k}$ and $X_2=1$ into g(X). $\square$

Theorem 4.18

Let $n\ge 3$ and $k \ge 9$ satisfy

$$\begin{aligned} n \le \frac{k^2-4k+5 + \sqrt{k^4-8k^3-6k^2+24k+25}}{4}. \end{aligned}$$

Then $Q_{2k+3}(n,s)<0$ for all $s \in \left( t_{k-1}^{1,1},t_k^{1,0} \right)$.

Proof

For $k \ge 9$, all values of n such that

$$\begin{aligned} 3 \le n \le \frac{k^2-4k+5 + \sqrt{k^4-8k^3-6k^2+24k+25}}{4} \end{aligned}$$

are solutions of the inequality $\varphi _1(n,k)<0$ (see (40)). Therefore $G(n,k,s)<0$ for all $s \in \left( t_k^{1,0},t_k^{1,1}\right)$ in this case. This means that $Q_{2k+3}(n,s)<0$ for $s \in \left( t_{k-1}^{1,1}, t_k^{1,0} \right)$. $\square$