1 Introduction

We are interested in estimating the following partially linear regression model (PLRM):

$$\begin{aligned} y_{i}={{\mathbf {x}}}_{i}'{\varvec{\beta }}+f\left( t_{i}\right) +\varepsilon _{i},\ \ \ i=1,\ldots ,n, \end{aligned}$$
(1)

where \(y_{i}\)’s are observed values of response variable, \({{\mathbf {x}}}'_{i}=\left( x_{i1},\ldots ,x_{ip}\right) \) is the ith observed vector of explanatory variables including \(p-\)dimensional vector with \(p \le n \), \(t_{i}\)’s are values of an extra univariate variable satisfying \(t_{1}\le \cdots \le t_{n}\), \({\varvec{\beta }}=\left( \beta _{1},\ldots ,\beta _{p}\right) '\) is an unknown \(p-\)dimensional vector of regression coefficients, \(f\left( \cdot \right) \) is an unknown smooth function, and \(\varepsilon _{i}\)’s are random disturbances assumed to be as \(\mathcal {N}\left( 0,\sigma ^{2}\right) \). Also, the vector \({\varvec{\beta }}\) is the parametric part of the model, and \(f\left( \cdot \right) \) is the nonparametric part of the model. The model (1) also called a semi-parametric model, and in vector–matrix form is written as

$$\begin{aligned} {{\mathbf {y}}}={{\mathbf {X}}}{\varvec{\beta }}+\varvec{f}+\varvec{\varepsilon }, \end{aligned}$$
(2)

where \({{\mathbf {y}}}=\left( y_{1},\ldots ,y_{n}\right) '\), \( {{\mathbf {X}}}=\left( {{\mathbf {x}}}_{1},\ldots ,{{\mathbf {x}}}_{n}\right) '\), \(\varvec{f}=\left( f\left( t_{1}\right) ,\ldots ,f\left( t_{n}\right) \right) '\), and \(\varvec{ \varepsilon }=\left( \varepsilon _{1},\ldots ,\varepsilon _{n}\right) '\) is random vector with \(\text {E}\,\left( \varvec{\varepsilon }\right) =\varvec{0}\) and \(\text {Var}\,\left( \varvec{\varepsilon }\right) =\sigma ^{2}{{\mathbf {I}}}_{n}\).

The PLRM generalizes both parametric linear regression and nonparametric regression models which correspond to the cases \({\varvec{\beta }}= \varvec{0}\) and \(\varvec{f}=\varvec{0}\), respectively. The key idea is to estimate the parameter vector \(\varvec{\beta }\), the function \(\varvec{f}\) and the mean vector \({{\mathbf {X}}}{\varvec{\beta }}+\varvec{f}\).

PLRMs have many applications. These models were originally studied by Engle et al. (1986) to determine the effect of weather on the electricity sales. In the following, several authors have investigated the PLRM, including Speckman (1988), Eubank et al. (1998), Schimek (2000), Liang (2006), Ahmed (2014), Aydın (2014) and Wu and Asar (2016), among others. The most popular approach for the PLRM is based on the fact that the cubic spline is a linear estimator for the nonparametric regression problem. Hence, the nonparametric procedure can be naturally extended to handle the PLRM.

In the using linear least squares regression, it is often encountered the problem of multicollinearity. In order to solve this issue, ridge regression has been proposed by Hoerl and Kennard (1970). It is well known that ridge estimator provides a slight improvement on the estimations of partial regression coefficients when the column vectors of the matrix in a linear model \({{\mathbf {y}}}={{\mathbf {X}}}{\varvec{\beta }}+\varvec{ \varepsilon }\) are highly correlated. In recent years a number of authors have proposed the use of the ridge type (biased) estimate approach to solve the problem of multicollinearity on estimating the parameters of the PLRMs, see Roozbeh and Arashi (2013), Arashi and Valizadeh (2015) and Yüzbaşı and Ahmed (2016). Contrary to these studies, we combine the idea of Speckman’s smoothing spline with the Ridge type-estimation in a optimal way in order to controlling bias parameter because of several reasons. Here are two of them: (1-) The principle of adding a penalty term to a sum of squares or more generally to a log-likelihood applies to a wide variety of linear and non-linear problems. (2-) The researchers, especially Shiller (1984), Green et al. (1985) and Eubank (1986), think that this method simply seems to work well.

For PLRMs, Ahmed et al. (2007) considered a profile least squares approach based on using kernel estimates of \(f\left( \cdot \right) \) to construct absolute penalty, shrinkage, and pretest estimators of \({\varvec{\beta }}\) in the case where \({\varvec{\beta }}\)\(=\)\(\left( {\varvec{\beta }}_{1}',{\varvec{\beta }}_{2}'\right) '.\) Similarly, for PLRMs, the suitability of estimating the nonparametric component based on the B-spline basis function is explored by Raheem et al. (2012).

In this paper, we introduce estimations techniques based on ridge regression when the matrix \({{\mathbf {X}}}'{{\mathbf {X}}}\) appears to be ill-conditioned in the PLRM using smoothing splines. Also, we consider that the coefficients \({\varvec{\beta }}\) can be partitioned as \(\left( {\varvec{\beta }}_{1},{\varvec{\beta }}_{2}\right) \) where \({\varvec{\beta }}_{1}\) is the coefficient vector for main effects, and \({\varvec{\beta }}_{2}\) is the vector for nuisance effects. We are essentially interested in the estimation of \(\varvec{ \beta }_{1}\) when it is reasonable that \({\varvec{\beta }}_{2}\) is close to zero. We suggest pretest ridge regression, shrinkage ridge regression and positive shrinkage ridge regression estimators for PLRMs. In the empirical applications, shrinkage estimators have been not paid attention to much due to the computational load till recently. However, with improvements in computing capability, this situation has changed. For example, as our real data example in Sect. 6, the annual salary of a baseball player may or may or not be effected by a number of situations (co-variates). A real baseball coach’s opinion, experience, and knowledge often give precise information regarding certain parameter values in an annual salary of a baseball player model. Furthermore, some variable selections techniques give an idea about important co-variates. Hence, researchers may take into consideration this auxiliary information and choose either the full model or the candidate sub-model for following work. The Stein-rule and pretest estimation procedures has received considerable attention from researchers since these methods can be obtained by shrinking the full model estimates in the direction of the subspace leads to more efficient estimators when the shrinkage is adaptive and based on the estimated distance between the subspace and the full space, for more information.

The organization of this study is given as following: the full and sub-model estimators are given in Sect. 2. The pretest, shrinkage estimators and some penalized estimations, namely the least absolute shrinkage and selection operator (Lasso), the adaptive Lasso (aLasso) and the smoothly clipped absolute deviation (SCAD) are also presented in Sect. 3. The asymptotic investigations of listed estimators are given in Sect. 4. In order to demonstrate the relative performance with our suggested estimators, a Monte Carlo simulation study is conducted in Sect. 5. A real data example is presented to illustrate the usefulness of the suggested estimators in Sect. 6. Finally, the conclusions and remarks are given in Sect. 7.

2 Full model estimation

Generally, the back-fitting algorithm is considered for the estimation of the model (2) . In this paper, we consider Speckman approach based on penalized residual sum of squares method for estimation purpose. We estimate \(\varvec{\beta }\) and \(\varvec{f}\) by minimizing the following penalized sum of squares equation

$$\begin{aligned} SS\left( {\varvec{\beta }},f\right)= & {} \sum \limits _{i=1}^{n}\left( y_{i}- {{\mathbf {x}}}_{i}'{\varvec{\beta }}-f\left( t_{i}\right) \right) ^{2}+\lambda \int \limits _{a}^{b}\left( f^{\prime \prime }\left( t\right) \right) ^{2}dt \nonumber \\= & {} \left( {{\mathbf {y}}}-{{\mathbf {X}}}{\varvec{\beta }}-\varvec{f}\right) '\left( {{\mathbf {y}}}-{{\mathbf {X}}}{\varvec{\beta }}-\varvec{f}\right) +\lambda \varvec{f}'{{\mathbf {K}}}\varvec{f}, \end{aligned}$$
(3)

where \({{\mathbf {K}}}\) is positive definite penalty matrix with solution,

$$\begin{aligned} \varvec{\widehat{f}}={{\mathbf {S}}}_{\lambda }{{\mathbf {y}}}, \end{aligned}$$

where \({{\mathbf {S}}}_{\lambda }=\left( {{\mathbf {I}}}_n-\lambda {{\mathbf {K}}}\right) ^{-1}\) is a well-known positive-definite (symmetrical) smoother matrix which depends on fixed smoothing parameter \(\lambda >0\) and the knot points \(t_{1},\ldots ,t_{n}\). The smoother matrix \({{\mathbf {S}}}_{\lambda }\) is obtained from univariate cubic spline smoothing (i.e. from penalized sum of squares equation (3) without parametric terms \({{\mathbf {X}}}{\varvec{\beta }}\)). Function \(\widehat{f}_{\lambda },\) the estimator of function f,  is obtained by cubic spline interpolation that rests on condition \(\widehat{f} \left( t_{i}\right) =\left( \widehat{f}\right) _{i},\)\(i=1,\ldots ,n.\) The penalty \({{\mathbf {K}}}\) matrix in (3) is obtained by means of the knot points, and defined as following way:

$$\begin{aligned} {{\mathbf {K}}}={{\mathbf {U}}}'{{\mathbf {R}}}^{-1}{{\mathbf {U}}}, \end{aligned}$$

where \(h_{j}=t_{j+1}-t_{j}\), \(j=1,2,\ldots ,n-1,\)\({{\mathbf {U}}}\) is tri-diagonal \(\left( n-2\right) \times n\) matrix with \({{\mathbf {U}}}_{jj}=1/h_{j},~{{\mathbf {U}}}_{j,j+1}=-\left( 1/h_{j}+1/h_{j+1}\right) ,\)\({{\mathbf {U}}}_{j,j+2}=1/h_{j+1}\) and \( {{\mathbf {R}}}\) is symmetric tri-diagonal matrix of order \(\left( n-2\right) \) with \({{\mathbf {R}}}_{j-1,j}={{\mathbf {R}}}_{j,j-1}=h_{j}/6\) and \( {{\mathbf {R}}}_{jj}=\left( h_{j}+h_{j+1}\right) /3.\)

The first term in the Eq. (3) denotes the residual sum of the squares and it penalizes the lack of fit. The second term in the same equation denotes the roughness penalty and it penalizes the curvature of the function. The amount of penalty is controlled by a smoothing parameter \(\lambda >0\). In general, large values of \(\lambda \) produce smoother estimators while smaller values produce more wiggly estimators. Thus, the \(\lambda \) plays a key role in controlling the trade-off between the goodness of fit represented by \(\left( {{\mathbf {y}}}-{{\mathbf {X}}}{\varvec{\beta }}-\varvec{f}\right) '\left( {{\mathbf {y}}}-{{\mathbf {X}}}{\varvec{\beta }}-\varvec{f}\right) \) and smoothness of the estimate measured by \(\lambda \varvec{f}'{{\mathbf {K}}}\varvec{f}\).

In this paper we have discussed the partially linear model with a univariate nonparametric predictor t given in model (1). If \(t > 1\), then a single smooth function in model (1) is replaced by two or more unspecified smooth functions. In this case, the fitted model is of the form

$$\begin{aligned} y_{i}={{\mathbf {x}}}_{i}'\varvec{\beta }+\sum _{j=1}^{p} f_j\left( t_{ij}\right) +\varepsilon _{i},\ \ \ i=1,2,\ldots ,n, \end{aligned}$$
(4)

The model (4) is also called as the partially linear additive model.

As stated previously, the main idea in PLRM is to estimate the vector \(\varvec{\beta }\) and \({\varvec{f}}\) by minimizing the penalized residual sum of squares criterion (3). We carry this idea a step further for the partially linear additive model (4). In this context, the optimization problem is to minimize

$$\begin{aligned} (\widehat{\varvec{\beta }};\varvec{\widehat{f}})=\underset{\varvec{\beta ,f}}{\arg \min }\left\{ \sum \nolimits _{i=1}^{n}\left( {\tilde{y}}_{i}-{\tilde{{{\mathbf {x}}}}}_{i}'\varvec{\beta }-\sum _{j=1}^{p} f_j\left( t_{ij}\right) \right) ^{2}+ \sum _{j=1}^{p}\lambda _j \int \limits _{a}^{b}\left( f_j^{\prime \prime }\left( t\right) \right) ^{2}dt \right\} ,\nonumber \\ \end{aligned}$$
(5)

over all twice differentiable functions \(f_j\) defined on [a, b]. In here \(f_j\) is a unspecified univariate function and \(\lambda _j\)’s are separate smoothing parameters for each smooth functions \(f_j\). As in the case with a single smooth function, if the \(\lambda _j\)’s are all zero, we get a smooth system that interpolates the data. Also, when each \(\lambda _j\) goes to \(\infty \), we obtain a standard least squares fit.

In the partially linear additive regression models, the functions \(\lambda _j\) can be estimated by a single smoothing spline manner. Using a straightforward extension of the arguments used in a univariate smoothing spline, the solution to Eq. (5) can be obtained by minimizing the matrix–vector form of Eq. (5), given by

$$\begin{aligned} (\widehat{\varvec{\beta }};\varvec{\widehat{f}})=\underset{\varvec{\beta ,f }}{\arg \min }\left\{ \left( {{\mathbf {y}}}-{{\mathbf {X}}}\varvec{\beta }-\sum _{j=1}^{p} \varvec{f_j}\right) ' \left( {{\mathbf {y}}}-{{\mathbf {X}}}\varvec{\beta }-\sum _{j=1}^{p} \varvec{f_j}\right) + \sum _{j=1}^{p}\lambda _j \varvec{f_j}'{{\mathbf {K}}}_j \varvec{f_j} \right\} , \end{aligned}$$

where \({{\mathbf {K}}}_j\)’s are the penalty matrices for each predictor, similarly to the \({{\mathbf {K}}}\) for a univariate predictor given in Eq. (3), see Hastie and Tibshirani (1990) for additive models.

The resulting estimator is called as partial spline, see Wahba (1990). On the other hand, Eq. (3) is also known as the roughness penalty approach Green and Silverman (1994). This estimation concept is based on iterative solution of the normal equations Rice (1986) indicated that partial spline estimator is asymptotically biased for the optimal choice as the components \({{\mathbf {X}}}\) depend on t. Applying results due to Speckman (1988), this bias can be substantially reduced. In the following section, we present full model semi-parametric estimation based on ridge regression.

2.1 Full model and sub-model semi-parametric ridge strategies

For a pre-specified value of \(\lambda \) the corresponding estimators \({\varvec{\beta }}\) and \(\varvec{f}\) for based on model (2) can be obtained by

$$\begin{aligned} \varvec{\widehat{\beta }=}\left( {{\tilde{{{\mathbf {X}}}}}}' {\tilde{{{\mathbf {X}}}}}\right) ^{-1}{\tilde{{{\mathbf {X}}}}}'{\tilde{{{\mathbf {y}}}}} \text { and }\,\varvec{\widehat{f}}={{\mathbf {S}}}_{\lambda }\left( {{\mathbf {y}}}-{{\mathbf {X}}}\widehat{\varvec{\beta }}\right) , \end{aligned}$$

where \({\tilde{{{\mathbf {X}}}}}=\left( {{\mathbf {I}}}_n-{{\mathbf {S}}}_{\lambda }\right) {{\mathbf {X}}}\) and \({\tilde{{{\mathbf {y}}}}}=\left( {{\mathbf {I}}}_n- {{\mathbf {S}}}_{\lambda }\right) {{\mathbf {y}}}\), respectively.

By multiplying both sides of model (2) with \(\left( {{\mathbf {I}}}_n-{{\mathbf {S}}}_{\lambda }\right) \),

$$\begin{aligned} {\tilde{{{\mathbf {y}}}}}={\tilde{{{\mathbf {X}}}}}{\varvec{\beta }}+\tilde{\varvec{\varepsilon }}, \end{aligned}$$
(6)

where \(\varvec{{\tilde{f}}}=\left( {{\mathbf {I}}}_n-{{\mathbf {S}}}_{\lambda }\right) \varvec{f}\), \(\tilde{\varvec{\varepsilon }}=\varvec{{\tilde{f}}}+\varvec{ \varepsilon }^{*}\) and \(\varvec{\varepsilon }^{*}=\left( {{\mathbf {I}}}_n-{{\mathbf {S}}}_{\lambda }\right) \varvec{\varepsilon }\).

Therefore, model (6) is transformed into an optimal problem to estimate semi-parametric estimator. We now consider model (6) with ridge penalty to estimate semi-parametric ridge estimator. We formulate this as follows:

$$\begin{aligned} \underset{{\varvec{\beta }}}{\arg \min }\left( {\tilde{{{\mathbf {y}}}}}- {\tilde{{{\mathbf {X}}}}}{\varvec{\beta }}\right) '\left( {\tilde{{{\mathbf {y}}}}}- {\tilde{{{\mathbf {X}}}}}{\varvec{\beta }}\right) +k{\varvec{\beta }}' {\varvec{\beta }}, \end{aligned}$$
(7)

where \(k\ge 0\) is the tuning parameter. By solving (7), we get full model semi-parametric ridge regression estimator of \(\varvec{\beta }\) as follows:

$$\begin{aligned} \widehat{\varvec{\beta }}^\text {Ridge}\,=\left( {\tilde{{{\mathbf {X}}}}}'{\tilde{{{\mathbf {X}}}}}+k{{\mathbf {I}}}_{p}\right) ^{-1} {\tilde{{{\mathbf {X}}}}}'{\tilde{{{\mathbf {y}}}}}\text {.}\, \end{aligned}$$

Let \(\widehat{\varvec{\beta }}_{1}^{\mathrm{FM}}\) be the semi-parametric unrestricted or full model ridge estimator of \({\varvec{\beta }}_{1}.\) From model (7), the semi-parametric full model ridge estimator \(\varvec{\widehat{ \beta }}_{1}^{\mathrm{FM}}\) of \({\varvec{\beta }}_{1}\) is

$$\begin{aligned} \widehat{\varvec{\beta }}_{1}^{\mathrm{FM}}=\left( {\tilde{{{\mathbf {X}}}}} _{1}'\tilde{\mathbf{M }}_{2}^\text {R}\,{\tilde{{{\mathbf {X}}}}}_{1}+k{{\mathbf {I}}}_{p_{1}}\right) ^{-1}{\tilde{{{\mathbf {X}}}}}_{1}' \tilde{\mathbf{M }}_{2}^\text {R}\,{\tilde{{{\mathbf {y}}}}}, \end{aligned}$$

where \(\tilde{\mathbf{M }}_{2}^\text {R}\,={{\mathbf {I}}}_{n}-{\tilde{{{\mathbf {X}}}}}_{2}\left( {\tilde{{{\mathbf {X}}}}}_{2}'{\tilde{{{\mathbf {X}}}}} _{2}+k{{\mathbf {I}}}_{p_{2}}\right) ^{-1}{\tilde{{{\mathbf {X}}}}} _{2}'\) and \({\tilde{{{\mathbf {X}}}}}_{i}=\left( {{\mathbf {I}}}_{n}- {{\mathbf {S}}}_{\lambda }\right) {{\mathbf {X}}}_{i}\), \(i=1,2.\)

Now, consider \({\varvec{\beta }}_{2}\varvec{=0}\), and add ridge penalty function on model (1) ,

$$\begin{aligned} y_{i}={{\mathbf {x}}}_{i}'{\varvec{\beta }}+f\left( t_{i}\right) +\varepsilon _{i}\;\;\text {subject to }\,{\varvec{\beta }}' {\varvec{\beta }}\varvec{\le }\phi ^{2}\text { and }\,{\varvec{\beta }}_{2}\varvec{=0}. \end{aligned}$$

Hence we have the following partially linear sub-model

$$\begin{aligned} {{\mathbf {y}}}={{\mathbf {X}}}_{1}{\varvec{\beta }}_{1}+\varvec{f}+\varvec{\varepsilon }\;\;\text {subject to }\, {\varvec{\beta }}_{1}'\varvec{ \beta }_{1}\varvec{\le }\phi ^2. \end{aligned}$$
(8)

Let us denote \(\widehat{\varvec{\beta }}_{1}^{\mathrm{SM}}\) the semi-parametric sub-model or restricted ridge estimator of \({\varvec{\beta }}_{1}\) as defined subsequently. Generally speaking, \(\widehat{\varvec{\beta }}_{1}^{\mathrm{SM}}\) performs better than \(\widehat{\varvec{\beta }}_{1}^{\mathrm{FM}}\) when \(\varvec{ \beta }_{2}\) close to \(\varvec{0}\). However, for \({\varvec{\beta }}_{2}\) away from the origin \(\varvec{0}\), \(\widehat{\varvec{\beta }}_{1}^{\mathrm{SM}}\) can be inefficient. From model (8), the semi-parametric sub-model ridge estimator \(\varvec{\widehat{\beta } }_{1}^{\mathrm{SM}}\) of \({\varvec{\beta }}_{1}\) has the form

$$\begin{aligned} \widehat{\varvec{\beta }}_{1}^{\mathrm{SM}}=\left( {\tilde{{{\mathbf {X}}}}} _{1}'{\tilde{{{\mathbf {X}}}}}_{1}+k{{\mathbf {I}}}_{p_{1}}\right) ^{-1}{\tilde{{{\mathbf {X}}}}}_{1}'{\tilde{{{\mathbf {y}}}}} \text {.}\, \end{aligned}$$

3 Pretest, shrinkage and some penalty estimation strategies

The pretest estimator is a combination of \(\widehat{\varvec{\beta }}_{1}^{\mathrm{FM}}\) and \(\widehat{\varvec{\beta }}_{1}^{\mathrm{SM}}\) via an indicator function \( \text {I}\,\left( \mathcal {T}_{n}\le c_{n,\alpha }\right) ,\) where \(\mathcal {T}_{n}\) is an appropriate test statistic to test \(\text {H}\,_{0}:{\varvec{\beta }}_{2}= \varvec{0}\) versus \(\text {H}\,_{A}:{\varvec{\beta }}_{2}\ne \varvec{0.}\) Moreover, \(c_{n,\alpha }\) is an \(\alpha -\)level critical value using the distribution of \(\mathcal {T}_{n}.\)

We define test statistics for testing null hypothesis \(\text {H}\,_0:{\varvec{\beta }}_{2}\varvec{ =0}\) as follows:

$$\begin{aligned} \mathcal {T}_{n}=\frac{n}{\widehat{\sigma }^{2}} \varvec{ \widehat{\beta }}_{2}'\left( {\tilde{{{\mathbf {X}}}}} _{2}'\tilde{\mathbf{M }}_{1}{\tilde{{{\mathbf {X}}}}}_{2}\right) \widehat{\varvec{\beta }}_{2}, \end{aligned}$$

where

$$\begin{aligned} \widehat{\sigma }^{2}=\frac{1}{n}.\frac{\left\| \left( {{\mathbf {I}}}_{n}-\mathbf H _{\lambda }\right) {\tilde{{{\mathbf {y}}}}}\right\| ^{2} }{\text {tr}\,\left( {{\mathbf {I}}}_{n}-\mathbf H _{\lambda }\right) '\left( {{\mathbf {I}}}_{n}-\mathbf H _{\lambda }\right) }, \end{aligned}$$

and

$$\begin{aligned} \widehat{\varvec{\beta }}_{2}^{}=\left( {\tilde{{{\mathbf {X}}}}} _{2}'\tilde{\mathbf{M }}_{1}{\tilde{{{\mathbf {X}}}}}_{2}\right) ^{-1} {\tilde{{{\mathbf {X}}}}}_{2}'\tilde{\mathbf{M }}_{1}{\tilde{{{\mathbf {y}}}}}, \end{aligned}$$

with \(\tilde{\mathbf{M }}_{1}={{\mathbf {I}}}_{n}-{\tilde{{{\mathbf {X}}}}} _{1}\left( {\tilde{{{\mathbf {X}}}}}_{1}'{\tilde{{{\mathbf {X}}}}} _{1}\right) ^{-1}{\tilde{{{\mathbf {X}}}}}_{1}'\) and \(\mathbf H _{\lambda }\) is called as smoother matrix for the model (1).

The \(\mathbf H _{\lambda }\) matrix is obtained as follows:

$$\begin{aligned} \widehat{{{\mathbf {y}}}}= & {} {{\mathbf {X}}}\widehat{\varvec{\beta }}^{\mathrm{FM}}+\varvec{\widehat{f}} \\= & {} {{\mathbf {X}}}\left( {\tilde{{{\mathbf {X}}}}}'{\tilde{{{\mathbf {X}}}}} +k{{\mathbf {I}}}_{p}\right) ^{-1}{\tilde{{{\mathbf {X}}}}}' {\tilde{{{\mathbf {y}}}}}+\varvec{S}_{\lambda }\left( {{\mathbf {y}}}-{{\mathbf {X}}}\left( {\tilde{{{\mathbf {X}}}}}'{\tilde{{{\mathbf {X}}}}}+k {{\mathbf {I}}}_{p}\right) ^{-1}{\tilde{{{\mathbf {X}}}}}'{\tilde{{{\mathbf {y}}}}}\right) \\= & {} {{\mathbf {X}}}\left( {{\mathbf {I}}}-{{\mathbf {S}}}_{\lambda }\right) \left( {\tilde{{{\mathbf {X}}}}}'{\tilde{{{\mathbf {X}}}}}+k {{\mathbf {I}}}_{p}\right) ^{-1}{\tilde{{{\mathbf {X}}}}}'{{\mathbf {y}}}\\&+\,{{\mathbf {S}}}_{\lambda }\left( {{\mathbf {y}}}-{{\mathbf {X}}}\left( {{\mathbf {I}}}-{{\mathbf {S}}}_{\lambda }\right) \left( {\tilde{{{\mathbf {X}}}}} '{\tilde{{{\mathbf {X}}}}}+k{{\mathbf {I}}}_{p}\right) ^{-1} {\tilde{{{\mathbf {X}}}}}'{{\mathbf {y}}}\right) \\= & {} {\tilde{{{\mathbf {X}}}}}\left( {\tilde{{{\mathbf {X}}}}}'{\tilde{{{\mathbf {X}}}}}+k{{\mathbf {I}}}_{p}\right) ^{-1}{\tilde{{{\mathbf {X}}}}} '{{\mathbf {y}}}+{{\mathbf {S}}}_{\lambda }\left( {{\mathbf {y}}}- {\tilde{{{\mathbf {X}}}}}\left( {\tilde{{{\mathbf {X}}}}}'{\tilde{{{\mathbf {X}}}}}+k{{\mathbf {I}}}_{p}\right) ^{-1}{\tilde{{{\mathbf {X}}}}} '{{\mathbf {y}}}\right) \\= & {} \mathbf H {{\mathbf {y}}}+{{\mathbf {S}}}_{\lambda }{{\mathbf {y}}}-\varvec{S}_{\lambda } \mathbf H {{\mathbf {y}}}\\= & {} \left( {{\mathbf {S}}}_{\lambda }+\left( {{\mathbf {I}}}_{n}-{{\mathbf {S}}}_{\lambda }\right) \mathbf H \right) {{\mathbf {y}}}\\= & {} \mathbf H _{\lambda }{{\mathbf {y}}}, \end{aligned}$$

where \(\mathbf H ={\tilde{{{\mathbf {X}}}}}\left( {\tilde{{{\mathbf {X}}}}} '{\tilde{{{\mathbf {X}}}}}+k{{\mathbf {I}}}_{p}\right) ^{-1} {\tilde{{{\mathbf {X}}}}}'.\) Thus, the mentioned smoother matrix is

$$\begin{aligned} \mathbf H _{\lambda }= {{\mathbf {S}}}_{\lambda }+\left( {{\mathbf {I}}}_{n}-{{\mathbf {S}}}_{\lambda }\right) \mathbf H . \end{aligned}$$

Under \(\text {H}\,_{0}\), the test statistic \(\mathcal {T}_{n}\) follows chi-square distribution with \(p_{2}\) degrees of freedom for large n values. Then, we can choose an \(\alpha -\)level critical value \(c_{n,\alpha }.\)

The semi-parametric ridge pretest estimator \(\widehat{\varvec{\beta }}_{1}^{\mathrm{PT}}\) of \({\varvec{\beta }}_{1}\) is defined by

$$\begin{aligned} \widehat{\varvec{\beta }}_{1}^{\mathrm{PT}}=\widehat{\varvec{\beta }}_{1}^{\mathrm{FM}}-\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{FM}}-\varvec{ \widehat{\beta }}_{1}^{\mathrm{SM}}\right) \text {I}\,\left( \mathcal {T}_{n}\le c_{n,\alpha }\right) . \end{aligned}$$

The shrinkage estimator for a PLRM was introduced by Ahmed et al. (2007). This shrinkage estimator is a smooth function of the test statistic.

The semi-parametric ridge shrinkage or Stein-type estimator \(\widehat{\varvec{\beta }}_{1}^{\mathrm{S}}\) of \(\varvec{ \beta }_{1}\) is defined by

$$\begin{aligned} \widehat{\varvec{\beta }}_{1}^{\mathrm{S}}=\widehat{\varvec{\beta }}_{1}^{\mathrm{SM}}+\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{FM}}-\varvec{ \widehat{\beta }}_{1}^{\mathrm{SM}}\right) \left( 1-(p_{2}-2)\mathcal {T} _{n}^{-1}\right) , p_{2}\ge 3. \end{aligned}$$

The positive part of the semi-parametric ridge shrinkage estimator \(\varvec{\widehat{ \beta }}_{1}^{\mathrm{PS}}\) of \( {\varvec{\beta }}_{1}\) defined by

$$\begin{aligned} \widehat{\varvec{\beta }}_{1}^{\mathrm{PS}}=\widehat{\varvec{\beta }}_{1}^{\mathrm{SM}}+\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{FM}}-\varvec{ \widehat{\beta }}_{1}^{\mathrm{SM}}\right) \left( 1-(p_{2}-2)\mathcal {T} _{n}^{-1}\right) ^{+}, \end{aligned}$$

where \(z^{+}=max\left( 0,z\right) \)

3.1 Some penalty estimation strategies

Now, we suggest the semi-parametric penalty estimators by using the smoothing spline method. For a given penalty function \(\pi \left( \cdot \right) \) and regularization parameter \(\lambda \), the general form of the objective function of semi-parametric penalty estimators can be written as

$$\begin{aligned} \sum \nolimits _{i=1}^{n}\left( {\tilde{y}}_{i}-{\tilde{{{\mathbf {x}}}}}_{i}'{\varvec{\beta }}\right) ^{2}+\lambda \pi \left( \cdot \right) , \end{aligned}$$

where \({\tilde{y}}_{i}\) is the ith observation of \({\tilde{{{\mathbf {y}}}}}\), \({\tilde{{{\mathbf {x}}}}}_{i}'\) is the i th row of \({\tilde{{{\mathbf {X}}}}}\) and \(\pi \left( \cdot \right) =\sum \nolimits _{i=1}^{p}\left| \beta _{i}\right| ^{\iota }\), \(\iota >0.\)

If \(\iota =2,\) then the ridge regression estimator can be written

$$\begin{aligned} \widehat{\varvec{\beta }}^\text {Ridge}\,=\underset{{\varvec{\beta }}}{\arg \min }\left\{ \sum \nolimits _{i=1}^{n}\left( {\tilde{y}}_{i}-{\tilde{{{\mathbf {x}}}}}_{i}'{\varvec{\beta }}\right) ^{2}+\lambda \sum _{j=1}^{p}\left| \beta _{j}\right| ^{2}\right\} . \end{aligned}$$

For \(\iota =1\), it is related to the Lasso, that is,

$$\begin{aligned} \widehat{\varvec{\beta }}^\text {Lasso}\,=\underset{{\varvec{\beta }}}{\arg \min }\left\{ \sum \nolimits _{i=1}^{n}\left( {\tilde{y}}_{i}-{\tilde{{{\mathbf {x}}}}}_{i}'{\varvec{\beta }}\right) ^{2}+\lambda \sum _{j=1}^{p}\left| \beta _{j}\right| \right\} . \end{aligned}$$

The aLasso estimator \({\varvec{\beta }}^\text {aLasso}\,\) is defined as

$$\begin{aligned} \widehat{\varvec{\beta }}^\text {aLasso}\,\underset{{\varvec{\beta }}}{=\arg \min }\left\{ \sum \nolimits _{i=1}^{n}\left( {\tilde{y}}_{i}-{\tilde{{{\mathbf {x}}}}}_{i}'{\varvec{\beta }}\right) ^{2}+\lambda \sum _{j=1}^{p} \widehat{\zeta }_{j}\left| \beta _{j}\right| \right\} , \end{aligned}$$

where the weight function is

$$\begin{aligned} \widehat{\zeta }_j = \frac{1}{|\widehat{\beta }^*_j|^\iota }; \quad \iota >0, \end{aligned}$$

and \(\widehat{\beta }_j^*\) is a root-n consistent estimator of \(\beta \).

The SCAD estimator \(\widehat{\varvec{\beta }}^\text {SCAD}\,\) is defined as

$$\begin{aligned} \widehat{\varvec{\beta }}^\text {SCAD}\,\underset{{\varvec{\beta }}}{=\arg \min }\left\{ \sum \nolimits _{i=1}^{n}\left( {\tilde{y}}_{i}-{\tilde{{{\mathbf {x}}}}}_{i}'{\varvec{\beta }}\right) ^{2}+ \sum _{j=1}^{p}J_{\alpha ,\lambda }\left( \beta _{j}\right) \right\} , \end{aligned}$$

where

$$\begin{aligned} J_{\alpha ,\lambda }\left( x\right) =\lambda \left\{ \text {I}\,\left( \left| x\right| \le \lambda \right) +\frac{\left( \alpha \lambda -\left| x\right| \right) _{+}}{\left( \alpha -1\right) \lambda }\text {I}\,\left( \left| x\right| >\lambda \right) \right\} ,\;x\ge 0. \end{aligned}$$

In order to select the optimal regularization parameter \(\lambda \), we used glmnet and ncvreg packages in R for Lasso and SCAD, respectively. Also, the aLasso is obtained by 10 fold cross-validation with weights from the 10 fold cross-validated Lasso.

4 Asymptotic analysis

In this section, we define expressions for asymptotic distributional biases (ADBs), asymptotic covariance matrices and asymptotic distributional risks (ADRs) of the pretest and shrinkage along with full model and sub-model estimators. For this purpose we consider a sequence \(\left\{ K_n\right\} \) is given by

$$\begin{aligned} K_{n}:{\varvec{\beta }}_{2}={\varvec{\beta }}_{2\left( n\right) }=\frac{ \varvec{w}}{\sqrt{n}},\;\varvec{w}=\left( w_{1},\ldots ,w_{p_{2}}\right) '\in {\mathbb {R}}^{p_{2}}. \end{aligned}$$

Now, we define a quadratic loss function using a positive definite matrix (p.d.m) \(\mathbf W \), by

$$\begin{aligned} L\left( {\varvec{\beta }}_{1}^{*}\right) =n\left( {\varvec{\beta }}_{1}^{*}-{\varvec{\beta }}_{1}\right) '{} \mathbf W \left( {\varvec{\beta }}_{1}^{*}-\varvec{ \beta }_{1}\right) , \end{aligned}$$

where \({\varvec{\beta }}_{1}^{*}\) is anyone of suggested estimators. Now, under \(\left\{ K_{n}\right\} ,\) we can write the asymptotic distribution function of \({\varvec{\beta }}_{1}^{*}\) as

$$\begin{aligned} F\left( {{\mathbf {x}}}\right) =\underset{n\rightarrow \infty }{\lim }P\left( \sqrt{n}\left( {\varvec{\beta }}_{1}^{*}-{\varvec{\beta }}_{1}\right) \le {{\mathbf {x}}}|K_{n}\right) , \end{aligned}$$

where \(F\left( {{\mathbf {x}}}\right) \) is non degenerate. Then ADR of \( {\varvec{\beta }}_{1}^{*}\) is defined as follows:

$$\begin{aligned} \text {ADR}\,\left( {\varvec{\beta }}_{1}^{*}\right) =\text {tr}\,\left( \mathbf W \int _{{\mathbb {R}}^{p_{1}}}\int {{\mathbf {x}}}{{\mathbf {x}}}'dF\left( {{\mathbf {x}}}\right) \right) =\text {tr}\,\left( \mathbf WV \right) , \end{aligned}$$

where \(\mathbf V \) is the dispersion matrix for the distribution \( F\left( {{\mathbf {x}}}\right) .\)

Asymptotic distributional bias of an estimator \({\varvec{\beta }}_{1}^{*}\) is defined as

$$\begin{aligned} \text {ADB}\,\left( {\varvec{\beta }}_{1}^{*}\right) =\text {E}\,\left\{ \underset{ n\rightarrow \infty }{\lim }\sqrt{n}\left( {\varvec{\beta }}_{1}^{*}- {\varvec{\beta }}_{1}\right) \right\} . \end{aligned}$$

We make the following two regularity conditions:

  1. (i)

    \(\quad \frac{1}{n}\underset{1\le i\le n}{\max } {\tilde{{{\mathbf {x}}}}}_{i}'({\tilde{{{\mathbf {X}}}}}'{\tilde{{{\mathbf {X}}}}})^{-1}{\tilde{{{\mathbf {x}}}}}_{i}\rightarrow 0\) as \(n\rightarrow \infty ,\) where \({\tilde{{{\mathbf {x}}}}}_{i}'\) is the ith row of \( {\tilde{{{\mathbf {X}}}}}\),

  2. (ii)

    \(\frac{1}{n}\sum \nolimits _{i=1}^{n}{\tilde{{{\mathbf {X}}}}}' {\tilde{{{\mathbf {X}}}}}\rightarrow \varvec{{\tilde{Q}}}\), where \(\varvec{{\tilde{Q}}}\) is a finite positive-definite matrix.

By virtue of Lemma 1, which is defined at appendix, assumed regularity conditions, and local alternatives, the ADBs of the estimators are:

Theorem 1

$$\begin{aligned} \text {ADB}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{FM}}\right)= & {} -\varvec{ \eta }_{11.2}, \\ \text {ADB}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{SM}}\right)= & {} -\varvec{ \varvec{\xi }}, \\ \text {ADB}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{PT}}\right)= & {} -\varvec{ \eta }_{11.2}-\varvec{\delta }\text {H}\,_{p_{2}+2}\left( \chi _{p_{2},\alpha }^{2};{\varDelta } \right) , \\ \text {ADB}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{S}}\right)= & {} -\varvec{ \eta }_{11.2}-(p_{2}-2)\varvec{\delta }\text {E}\,\left( \chi _{p_{2}+2 }^{-2}\left( {\varDelta } \right) \right) , \\ \text {ADB}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{PS}}\right)= & {} -\varvec{ \eta }_{11.2}-\varvec{\delta }\text {H}\,_{p_{2}+2}\left( \chi _{p_{2},\alpha }^{2};{\varDelta } \right) , \\&-(p_{2}-2)\varvec{\delta }\text {E}\,\left\{ \chi _{p_{2}+2}^{-2}\left( {\varDelta } \right) \text {I}\,\left( \chi _{p_{2}+2}^{2}\left( {\varDelta } \right) >p_{2}-2\right) \right\} , \end{aligned}$$

where \(\varvec{{\tilde{Q}}}\) = \(\left( \begin{array}{cc} \varvec{{\tilde{Q}}}_{11} &{} \varvec{{\tilde{Q}}}_{12} \\ \varvec{{\tilde{Q}}}_{21} &{} \varvec{{\tilde{Q}}}_{22} \end{array} \right) \), \({\varDelta } =\left( \varvec{w}^{\varvec{\intercal }}\varvec{ {\tilde{Q}}}_{22.1}^{-1}\varvec{w}\right) \sigma ^{-2}\), \(\varvec{ {\tilde{Q}}}_{22.1}=\varvec{{\tilde{Q}}}_{22}-\varvec{{\tilde{Q}}}_{21} \varvec{{\tilde{Q}}}_{11}^{-1}\varvec{{\tilde{Q}}}_{12}\), \(\varvec{\eta }\) = \(\left( \begin{array}{c} \varvec{\eta }_{1} \\ \varvec{\eta }_{2} \end{array} \right) \) =\(-\lambda _{0}\varvec{{\tilde{Q}}}^{-1}{\varvec{\beta }}\), \(\varvec{\eta }_{11.2}=\varvec{\eta }_{1}-\varvec{ {\tilde{Q}}}_{12}\varvec{{\tilde{Q}}}_{22}^{-1}\left( \left( \varvec{ \beta }_{2}-\varvec{w}\right) -\varvec{\eta }_{2}\right) \), \( \varvec{\xi }=\varvec{\eta }_{11.2}-\varvec{\delta }\), \(\varvec{\delta }\)\(=\varvec{{\tilde{Q}}}_{11}^{-1}\varvec{{\tilde{Q}} }_{12}\varvec{\omega }\) and \(\text {H}\,_{v}\left( x,{\varDelta } \right) \) be the cumulative distribution function of the non-central chi-squared distribution with non-centrality parameter \({\varDelta } \) and v degree of freedom, and

$$\begin{aligned} \text {E}\,\left( \chi _{v}^{-2j}\left( {\varDelta } \right) \right) =\int \nolimits _{0}^{\infty }x^{-2j}d\text {H}\,_{v}\left( x,{\varDelta } \right) . \end{aligned}$$

Proof

See Appendix. \(\square \)

Since the bias expressions for all the estimators are not in scaler form, we also convert them to quadratic forms. Thus, we define the asymptotic quadratic distributional bias (AQDB) of an estimator \( {\varvec{\beta }}_{1}^{*}\) is

$$\begin{aligned} {\text {AQDB}\,\left( {\varvec{\beta }}_{1}^{*}\right) =\left( \text {ADB}\,\left( {\varvec{\beta }}_{1}^{*}\right) \right) '\varvec{{\tilde{Q}}} _{11.2}\left( \text {ADB}\,\left( {\varvec{\beta }}_{1}^{*}\right) \right) , } \end{aligned}$$
(9)

where \(\varvec{{\tilde{Q}}}_{11.2}=\varvec{{\tilde{Q}}}_{11}-\varvec{ {\tilde{Q}}}_{12}\varvec{{\tilde{Q}}}_{22}^{-1}\varvec{{\tilde{Q}}}_{21}\).

Considering Eq. (9), we present the AQDBs of the estimators as follows:

$$\begin{aligned} \text {AQDB}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{FM}}\right)= & {} \varvec{ \eta }_{11.2}'\varvec{{\tilde{Q}}}_{11.2}\varvec{\eta }_{11.2}, \\ \text {AQDB}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{SM}}\right)= & {} \varvec{ \varvec{\xi }}'\varvec{{\tilde{Q}}}_{11.2}\varvec{ \varvec{\xi }}, \\ \text {AQDB}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{PT}}\right)= & {} \varvec{ \eta }_{11.2}'\varvec{{\tilde{Q}}}_{11.2}\varvec{\eta }_{11.2}+ \varvec{\eta }_{11.2}'\varvec{{\tilde{Q}}}_{11.2}\varvec{ \delta }\text {H}\,_{p_{2}+2}\left( \chi _{p_{2},\alpha }^{2};{\varDelta } \right) \\&+\,\varvec{\delta }'\varvec{{\tilde{Q}}}_{11.2}\varvec{\eta } _{11.2}\text {H}\,_{p_{2}+2}\left( \chi _{p_{2},\alpha }^{2};{\varDelta } \right) \\&+\,\varvec{\delta }'\varvec{{\tilde{Q}}}_{11.2}\varvec{ \delta }\text {H}\,_{p_{2}+2}^{2}\left( \chi _{p_{2},\alpha }^{2};{\varDelta } \right) , \\ \text {AQDB}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{S}}\right)= & {} \varvec{ \eta }_{11.2}'\varvec{{\tilde{Q}}}_{11.2}\varvec{\eta } _{11.2}+(p_{2}-2)\varvec{\eta }_{11.2}'\varvec{{\tilde{Q}}} _{11.2}\varvec{\delta }\text {E}\,\left( \chi _{p_{2}+2}^{-2}\left( {\varDelta } \right) \right) \\&+(p_{2}-2)\varvec{\delta }'\varvec{{\tilde{Q}}}_{11.2} \varvec{\eta }_{11.2}\text {E}\,\left( \chi _{p_{2}+2}^{-2}\left( {\varDelta } \right) \right) \\&+(p_{2}-2)^{2}\varvec{\delta }'\varvec{{\tilde{Q}}}_{11.2} \varvec{\delta }\left( \text {E}\,\left( \chi _{p_{2}+2}^{-2}\left( {\varDelta } \right) \right) \right) ^{2}, \\ \text {AQDB}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{PS}}\right)= & {} \varvec{ \eta }_{11.2}'\varvec{{\tilde{Q}}}_{11.2}\varvec{\eta } _{11.2}+\left( \varvec{\delta }'\varvec{{\tilde{Q}}}_{11.2} \varvec{\eta }_{11.2}+\varvec{\eta }_{11.2}'\varvec{\tilde{Q }}_{11.2}\varvec{\delta }\right) \\&\times \left[ \text {H}\,_{p_{2}+2}\left( (p_{2}-2);{\varDelta } \right) \right. \\&\left. +(p_{2}-2)\text {E}\,\left\{ \chi _{p_{2}+2}^{-2}\left( {\varDelta } \right) \text {I}\,\left( \chi _{p_{2}+2}^{-2}\left( {\varDelta } \right)>p_{2}-2\right) \right\} \right] \\&+\,\varvec{\delta }'\varvec{{\tilde{Q}}}_{11.2}\varvec{ \delta }\left[ \text {H}\,_{p_{2}+2}\left( (p_{2}-2);{\varDelta } \right) \right. \\&\left. +\,(p_{2}-2)\text {E}\,\left\{ \chi _{p_{2}+2}^{-2}\left( {\varDelta } \right) \text {I}\,\left( \chi _{p_{2}+2}^{-2}\left( {\varDelta } \right) >p_{2}-2\right) \right\} \right] ^{2}. \end{aligned}$$

Assuming that \(\varvec{{\tilde{Q}}} _{12}\ne \varvec{0}\), then

  1. (i)

    The AQDB of \(\widehat{\varvec{\beta }}_{1}^{\mathrm{FM}}\) is an constant with \(\varvec{\eta }_{11.2}'\varvec{ {\tilde{Q}}}_{11.2}\varvec{\eta }_{11.2}\).

  2. (ii)

    The AQDB of \(\widehat{\varvec{\beta }}_{1}^{\mathrm{SM}}\) is an unbounded function of \(\varvec{\varvec{\xi }}' \varvec{{\tilde{Q}}}_{11.2}\varvec{\varvec{\xi }}\).

  3. (iii)

    The AQDB of \(\widehat{\varvec{\beta }}_{1}^{\mathrm{PT}}\) begins from \(\varvec{\eta }_{11.2}'\varvec{{\tilde{Q}}}_{11.2} \varvec{\eta }_{11.2}\) at \({\varDelta } =0\). For \({\varDelta } >0\), it increases to a maximum and then decreases towards 0.

  4. (iv)

    Similarly, the AQDB of \(\widehat{\varvec{\beta }}_{1}^{\mathrm{S}}\) starts from \(\varvec{\eta }_{11.2}'\varvec{\tilde{Q }}_{11.2}\varvec{\eta }_{11.2}\) at \({\varDelta } =0\), and it increases to a point and then decreases towards zero for non-zero \({\varDelta } \) values because of \(\text {E}\,\left( \chi _{p_{2}+2}^{-2}\left( {\varDelta } \right) \right) \) being a non increasing log convex function of \({\varDelta } \). Lastly, for all \( {\varDelta } \) values, the behaviour of the AQDB of \(\varvec{\widehat{\beta } }_{1}^{\mathrm{PS}}\) is almost the same \(\widehat{\varvec{\beta }}_{1}^{\mathrm{S}}\), but the quadratic bias curve of \(\widehat{\varvec{\beta }}_{1}^{\mathrm{PS}}\) remains on below the curve of \(\widehat{\varvec{\beta }}_{1}^{\mathrm{S}}\).

Now, we present the asymptotic covariance matrices of the proposed estimators which are given by as follows:

Theorem 2

$$\begin{aligned} \text {Cov}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{FM}}\right)= & {} \sigma ^{2}\varvec{{\tilde{Q}}}_{11.2}^{-1}+\varvec{\eta }_{11.2} \varvec{\eta }_{11.2}', \\ \text {Cov}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{SM}}\right)= & {} \sigma ^{2}\varvec{{\tilde{Q}}}_{11}^{-1}+\varvec{\varvec{ \xi }\varvec{\xi }}', \\ \text {Cov}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{PT}}\right)= & {} \sigma ^{2}\varvec{{\tilde{Q}}}_{11.2}^{-1}+\varvec{\eta }_{11.2} \varvec{\eta }_{11.2}'+2\varvec{\eta }_{11.2}' \varvec{\delta }\text {H}\,_{p_{2}+2}\left( \chi _{p_{2},\alpha }^{2};{\varDelta } \right) \\&+\,\sigma ^{2}\left( \varvec{{\tilde{Q}}}_{11.2}^{-1}- \varvec{{\tilde{Q}}}_{11}^{-1}\right) \text {H}\,_{p_{2}+2}\left( \chi _{p_{2},\alpha }^{2}; {\varDelta } \right) \\&+\,\varvec{\delta \delta }'\left[ 2\text {H}\,_{p_{2}+2}\left( \chi _{p_{2},\alpha }^{2};{\varDelta } \right) -\text {H}\,_{p_{2}+4}\left( \chi _{p_{2},\alpha }^{2};{\varDelta } \right) \right] ,\\ \text {Cov}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{S}}\right)= & {} \sigma ^{2}\varvec{{\tilde{Q}}}_{11.2}^{-1}+\varvec{\eta }_{11.2} \varvec{\eta }_{11.2}'+2(p_{2}-2)\varvec{\delta \eta } _{11.2}'\text {E}\,\left( \chi _{p_{2}+2}^{-2}\left( {\varDelta } \right) \right) \\&-\,(p_{2}-2)\sigma ^{2}\varvec{{\tilde{Q}}}_{11}^{-1}\varvec{{\tilde{Q}}} _{12}\varvec{{\tilde{Q}}}_{22.1}^{-1}\varvec{{\tilde{Q}}}_{21} \varvec{{\tilde{Q}}}_{11}^{-1}\left\{ 2\text {E}\,\left( \chi _{p_{2}+2 }^{-2}\left( {\varDelta } \right) \right) \right. \\&\left. -\,(p_{2}-2)\text {E}\,\left( \chi _{p_{2}+2}^{-4}\left( {\varDelta } \right) \right) \right\} \\&+\,(p_{2}-2)\varvec{\delta \delta }'\left\{ 2\text {E}\,\left( \chi _{p_{2}+2}^{-2}\left( {\varDelta } \right) \right) \right. \\&\left. -\,2\text {E}\,\left( \chi _{p_{2}+4}^{-2}\left( {\varDelta } \right) \right) -(p_{2}-2)\text {E}\,\left( \chi _{p_{2}+4}^{-4}\left( {\varDelta } \right) \right) \right\} , \\ \text {Cov}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{PS}}\right)= & {} \text {Cov}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{S}}\right) \\&-\,2\varvec{\delta \eta }_{11.2}'\text {E}\,\left( \left\{ 1-(p_{2}-2)\chi _{p_{2}+2}^{-2}\left( {\varDelta } \right) \right\} \text {I}\,\left( \chi _{p_{2}+2}^{2}\left( {\varDelta } \right) \le p_{2}-2\right) \right) \\&+\,(p_{2}-2)\sigma ^{2}\varvec{{\tilde{Q}}}_{11}^{-1}\varvec{{\tilde{Q}}} _{12}\varvec{{\tilde{Q}}}_{22.1}^{-1}\varvec{{\tilde{Q}}}_{21} \varvec{{\tilde{Q}}}_{11}^{-1} \\&\times \left[ 2\text {E}\,\left( \chi _{p_{2}+2}^{-2}\left( {\varDelta } \right) \text {I}\,\left( \chi _{p_{2}+2}^{2}\left( {\varDelta } \right) \le p_{2}-2\right) \right) \right. \\&\left. -\,(p_{2}-2)\text {E}\,\left( \chi _{p_{2}+2}^{-4}\left( {\varDelta } \right) \text {I}\,\left( \chi _{p_{2}+2}^{2}\left( {\varDelta } \right) \le p_{2}-2\right) \right) \right] \\&-\,\sigma ^{2}\varvec{{\tilde{Q}}}_{11}^{-1}\varvec{{\tilde{Q}}}_{12} \varvec{{\tilde{Q}}}_{22.1}^{-1}\varvec{{\tilde{Q}}}_{21}\varvec{ {\tilde{Q}}}_{11}^{-1}\text {H}\,_{p_{2}+2}\left( (p_{2}-2);{\varDelta } \right) \\&+\,\varvec{\delta \delta }'\left[ 2\text {H}\,_{p_{2}+2}\left( (p_{2}-2);{\varDelta } \right) -\text {H}\,_{p_{2}+4}\left( (p_{2}-2);{\varDelta } \right) \right] \\&-\,(p_{2}-2)\varvec{\delta \delta }'\left[ 2\text {E}\,\left( \chi _{p_{2}+2}^{-2}\left( {\varDelta } \right) \text {I}\,\left( \chi _{p_{2}+2 }^{2}\left( {\varDelta } \right) \le p_{2}-2\right) \right) \right. \\&-\,2\text {E}\,\left( \chi _{p_{2}+4}^{-2}\left( {\varDelta } \right) \text {I}\,\left( \chi _{p_{2}+4}^{2}\left( {\varDelta } \right) \le p_{2}-2\right) \right) \\&\left. +\,(p_{2}-2)\text {E}\,\left( \chi _{p_{2}+2}^{-4}\left( {\varDelta } \right) \text {I}\,\left( \chi _{p_{2}+2}^{2}\left( {\varDelta } \right) \le p_{2}-2\right) \right) \right] . \end{aligned}$$

Proof

See Appendix. \(\square \)

Finally, we obtain the ADRs of the estimators under \(\left\{ K_{n}\right\} \) given as:

Theorem 3

$$\begin{aligned} \text {ADR}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{FM}}\right)= & {} \sigma ^{2}\text {tr}\,\left( \mathbf W \varvec{{\tilde{Q}}}_{11.2}^{-1}\right) +\varvec{\eta } _{11.2}'{} \mathbf W \varvec{\eta }_{11.2}, \\ \text {ADR}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{SM}}\right)= & {} \sigma ^{2}\text { tr}\,\left( \mathbf W \varvec{{\tilde{Q}}}_{11}^{-1}\right) +\varvec{\varvec{ \xi }}'\varvec{\varvec{W\xi }}, \\ \text {ADR}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{PT}}\right)= & {} \text {ADR}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{FM}}\right) -2\varvec{\eta } _{11.2}'{} \mathbf W \varvec{\delta }\text {H}\,_{p_{2}+2}\left( \chi _{p_{2},\alpha }^{2};{\varDelta } \right) \\&-\,\sigma ^{2}\text {tr}\,\left( \mathbf W \varvec{{\tilde{Q}}}_{11.2}^{-1}- \mathbf W \varvec{{\tilde{Q}}}_{11}^{-1}\right) \text {H}\,_{p_{2}+2}\left( \chi _{p_{2},\alpha }^{2};{\varDelta } \right) \\&+\,\varvec{\delta }'{} \mathbf W \varvec{\delta }\left\{ 2\text {H}\,_{p_{2}+2}\left( \chi _{p_{2},\alpha }^{2};{\varDelta } \right) -\text {H}\,_{p_{2}+4}\left( \chi _{p_{2},\alpha }^{2};{\varDelta } \right) \right\} ,\\ \text {ADR}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{S}}\right)= & {} \text {ADR}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{FM}}\right) +2(p_{2}-2)\varvec{\eta } _{11.2}'{} \mathbf W \varvec{\delta }\text {E}\,\left( \chi _{p_{2}+2 }^{-2}\left( {\varDelta } \right) \right) \\&\,-(p_{2}-2)\sigma ^{2}\text {tr}\,\left( \varvec{{\tilde{Q}}}_{21} \varvec{{\tilde{Q}}}_{11}^{-1}{} \mathbf W \varvec{{\tilde{Q}}}_{11}^{-1}\varvec{ {\tilde{Q}}}_{12}\varvec{{\tilde{Q}}}_{22.1}^{-1}\right) \left\{ 2\text {E}\,\left( \chi _{p_{2}+2}^{-2}\left( {\varDelta } \right) \right) \right. \\&\left. -(p_{2}-2)\text {E}\,\left( \chi _{p_{2}+2}^{-4}\left( {\varDelta } \right) \right) \right\} \\&+\,(p_{2}-2)\varvec{\delta }'{} \mathbf W \varvec{\delta }\left\{ 2\text {E}\,\left( \chi _{p_{2}+2}^{-2}\left( {\varDelta } \right) \right) \right. \\&\left. -2\text {E}\,\left( \chi _{p_{2}+4}^{-2}\left( {\varDelta } \right) \right) -(p_{2}-2)\text {E}\,\left( \chi _{p_{2}+4}^{-4}\left( {\varDelta } \right) \right) \right\} ,\\ \text {ADR}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{PS}}\right)= & {} \text {ADR}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{S}}\right) \\&-\,2\varvec{\eta }_{11.2}'{} \mathbf W \varvec{\delta }\text {E}\,\left( \left\{ 1-(p_{2}-2)\chi _{p_{2}+2}^{-2}\left( {\varDelta } \right) \right\} \text {I}\,\left( \chi _{p_{2}+2}^{2}\left( {\varDelta } \right) \le p_{2}-2\right) \right) \\&+\,(p_{2}-2)\sigma ^{2}\text {tr}\,\left( \varvec{{\tilde{Q}}}_{21} \varvec{{\tilde{Q}}}_{11}^{-1}{} \mathbf W \varvec{{\tilde{Q}}}_{11}^{-1}\varvec{ {\tilde{Q}}}_{12}\varvec{{\tilde{Q}}}_{22.1}^{-1}\right) \\&\times \left[ 2\text {E}\,\left( \chi _{p_{2}+2}^{-2}\left( {\varDelta } \right) \text {I}\,\left( \chi _{p_{2}+2}^{2}\left( {\varDelta } \right) \le p_{2}-2\right) \right) \right. \\&\left. -(p_{2}-2)\text {E}\,\left( \chi _{p_{2}+2}^{-4}\left( {\varDelta } \right) \text {I}\,\left( \chi _{p_{2}+2}^{2}\left( {\varDelta } \right) \le p_{2}-2\right) \right) \right] \\&-\,\sigma ^{2}\text {tr}\,\left( \varvec{{\tilde{Q}}}_{21}\varvec{\tilde{Q }}_{11}^{-1}{} \mathbf W \varvec{{\tilde{Q}}}_{11}^{-1}\varvec{{\tilde{Q}}}_{12} \varvec{{\tilde{Q}}}_{22.1}^{-1}\right) \text {H}\,_{p_{2}+2}\left( (p_{2}-2);{\varDelta } \right) \\&+\,\varvec{\delta }'{} \mathbf W \varvec{\delta }\left[ 2\text {H}\,_{p_{2}+2}\left( (p_{2}-2);{\varDelta } \right) -\text {H}\,_{p_{2}+4}\left( (p_{2}-2);{\varDelta } \right) \right] \\&-\,(p_{2}-2)\varvec{\delta }'{} \mathbf W \varvec{\delta }\left[ 2\text {E}\,\left( \chi _{p_{2}+2}^{-2}\left( {\varDelta } \right) \text {I}\,\left( \chi _{p_{2}+2}^{2}\left( {\varDelta } \right) \le p_{2}-2\right) \right) \right. \\&-\,2\text {E}\,\left( \chi _{p_{2}+4}^{-2}\left( {\varDelta } \right) \text {I}\,\left( \chi _{p_{2}+4}^{2}\left( {\varDelta } \right) \le p_{2}-2\right) \right) \\&\left. +(p_{2}-2)\text {E}\,\left( \chi _{p_{2}+2}^{-4}\left( {\varDelta } \right) \text {I}\,\left( \chi _{p_{2}+2}^{2}\left( {\varDelta } \right) \le p_{2}-2\right) \right) \right] . \end{aligned}$$

Proof

See Appendix. \(\square \)

If \(\varvec{{\tilde{Q}}}_{12}=\varvec{0}\), then \(\varvec{\delta }=\varvec{0}\), \(\varvec{\xi }=\varvec{\eta }_{11.2} \) and \(\varvec{{\tilde{Q}}}_{11.2}=\varvec{{\tilde{Q}}}_{11}\), all the ADRs reduce to common value \(\sigma ^{2}\text {tr}\,\left( \mathbf W \varvec{{\tilde{Q}}} _{11}^{-1}\right) +\varvec{\eta }_{11.2}'{} \mathbf W \varvec{\eta }_{11.2}\) for all \(\varvec{\omega }\). On the other hand, assuming \( \varvec{{\tilde{Q}}}_{12}\ne 0\), then

  1. (i)

    As \({\varDelta } \) moves away from 0, the \(\text {ADR}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{SM}}\right) \) becomes unbounded. Furthermore, the \(\text {ADR}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{PT}}\right) \) perform better than \(\text {ADR}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{FM}}\right) \) for all values of \({\varDelta } \ge 0\), that is \( \text {ADR}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{PT}}\right) \le \text {ADR}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{FM}}\right) \).

  2. (ii)

    For all \(\mathbf W \) and \(\varvec{\omega }\), \(\text {ADR}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{S}}\right) \le \text {ADR}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{FM}}\right) \), if

    $$\begin{aligned} \frac{\text {tr}\,\left( \varvec{{\tilde{Q}}}_{21}\varvec{{\tilde{Q}}} _{11}^{-1}{} \mathbf W \varvec{{\tilde{Q}}}_{11}^{-1}\varvec{{\tilde{Q}}}_{12} \varvec{{\tilde{Q}}}_{22.1}^{-1}\right) }{ch_{max}\left( \varvec{ {\tilde{Q}}}_{21}\varvec{{\tilde{Q}}}_{11}^{-1}{} \mathbf W \varvec{{\tilde{Q}}} _{11}^{-1}\varvec{{\tilde{Q}}}_{12}\varvec{{\tilde{Q}}} _{22.1}^{-1}\right) }\ge \frac{p_{2}+2}{2}, \end{aligned}$$

    where \(ch_{max}(\cdot )\) is the maximum characteristic root.

  3. (iii)

    To compare \(\widehat{\varvec{\beta }}_{1}^{\mathrm{PS}}\) and \(\widehat{\varvec{\beta }}_{1} ^{\mathrm{S}}\), we observe that the \(\text {ADR}\,\left( \widehat{\varvec{\beta }}_{1} ^{\mathrm{PS}}\right) \) overshadows \(\text {ADR}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{S}}\right) \) for all the values of \( \varvec{\omega }\). Moreover, with result \(\left( \text {ii}\,\right) \), we have \(\text {ADR}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{PS}}\right) \le \text {ADR}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{S}}\right) \le \text {ADR}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{FM}}\right) \) all \(\mathbf W \) and \(\varvec{\omega }\).

5 Simulation studies

In this section, we consider a Monte Carlo simulation to evaluate the relative quadratic risk performance of the listed estimators. All calculations were carried out in R Development Core Team (2010). We simulate the response from the following model:

$$\begin{aligned} y_{i}=x_{1i}\beta _{1}+x_{2i}\beta _{2}+\cdots +x_{pi}\beta _{p}+f\left( t_{i}\right) +\varepsilon _{i\text { }\,},\ i=1,\ldots ,n, \end{aligned}$$
(10)

where \({{\mathbf {x}}}_{i}\sim \mathcal {N}\left( \varvec{0}, \varvec{{\varSigma } }_{x}\right) \) and \(\varepsilon _{i}\) are i.i.d. \( \mathcal {N}\left( 0,1\right) \). We also define \(\varvec{{\varSigma } }_{x}\) that is positive definite covariance matrix. The off-diagonal elements of the covariance matrix \(\varvec{{\varSigma } }_{x}\) are considered to be equal to \(\rho \) with \(\rho =0.25,0.5,0.75\). The condition number (CN) is used to test the multicollinearity, which is defined as the ratio of the largest eigenvalue to the smallest eigenvalue of matrix \({{\mathbf {X}}}'{{\mathbf {X}}}\). If CN is larger than 30, then it implies the existence of multicollinearity in the data set, Belsley (1991). We also get \(\alpha =0.05\) and \(t_{i}=\left( i-0.5\right) /n.\) Furthermore, we consider the hypothesis \(\text {H}\,_{0}:\beta _{j}=0,\) for \( j=p_{1}+1,p_{1}+2,\ldots ,p,\) with \(p=p_{1}+p_{2}.\) Hence, we partition the regression coefficients as \({\varvec{\beta }}=\left( {\varvec{\beta }}_{1},{\varvec{\beta }}_{2}\right) =\left( {\varvec{\beta }}_{1}, \varvec{0}\right) \) with \({\varvec{\beta }}_{1}=\left( 1,1,1,1,1\right) \). In (10), we consider two different the nonparametric functions \( f_{1}\left( t_{i}\right) =\sqrt{t_{i}\left( 1-t_{i}\right) }\sin \left( \frac{ 2.1\pi }{t_{i}+0.05}\right) \) and \(f_{2}\left( t_{i}\right) =0.5\sin \left( 4\pi t_{i}\right) \) to generate response \(y_{i}.\)

In literature, there are a number of studies about bandwidth selection for a PLRM. Some recent studies are: Li et al. (2011) provide a theoretical justification for the earlier empirical observations of an optimal zone of bandwidths. Further, Li and Palta (2009) introduced a bandwidth selection for semi-parametric varying-coefficient. In our study, we use generalized cross-validation (GCV) to select the optimal \(\lambda \) value for given k. By Wahba (1990), the GCV score function can be procured by

$$\begin{aligned} \text {GCV}\,\left( \lambda , k \right) =\frac{n\left\| {{\mathbf {y}}}-\widehat{{{\mathbf {y}}}} \right\| ^{2}}{\left\{ \text {tr}\,\left( {{\mathbf {I}}}_{n}-\mathbf H _{\lambda }\right) \right\} ^{2}}. \end{aligned}$$

For further information about selection of the optimal ridge parameter and the optimal bandwidth, we refer to Amini and Roozbeh (2015) and Roozbeh (2015).

Each realization was repeated 5000 times. We define \({\varDelta } ^{*}=\left\| \varvec{\beta -\beta }_{0}\right\| ,\) where \(\varvec{ \beta }_{0}=\left( {\varvec{\beta }}_{1},\varvec{0}\right) ,\) and \( \left\| \cdot \right\| \) is the Euclidean norm. In order to investigate of the behaviour of the estimators for \({\varDelta } ^{*}>0,\) further datasets were generated from those distributions under local alternative hypothesis.

The performance of an estimator was evaluated by using mean squared error (MSE). In order to easy comparison, we also calculate the relative mean squared efficiency (RMSE) of the \({\varvec{\beta }}_{1}^{\blacktriangledown }\) to the \( \widehat{\varvec{\beta }}_{1}^{\mathrm{FM}}\) is given by

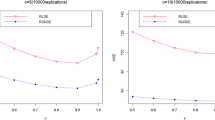
$$\begin{aligned} \text {RMSE}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{FM}}:{\varvec{\beta }}_{1}^{\blacktriangledown }\right) =\frac{\text {MSE}\,\left( \widehat{\varvec{\beta }}_{1}^{\mathrm{FM}}\right) }{\text {MSE}\,\left( {\varvec{\beta }}_{1}^{\blacktriangledown }\right) }, \end{aligned}$$

where \({\varvec{\beta }}_{1}^{\blacktriangledown }\) is one of the suggested estimators. If the RMSE of an estimator is larger than one, it is superior to the full model estimator. Results are reported briefly in Table 1, and plotted to easier comparison in Figs. 1 and 2.

Table 1 RMSEs for \(n=50\), \({p}_1=5\), \({p}_2=10\) and \(\rho =0.25\)
Full size table
Fig. 1
figure 1

Relative efficiency of the estimators as a function of \({\varDelta }^{*}\) for \(n=50\)

Full size image
Fig. 2
figure 2

Relative efficiency of the estimators as a function of \({\varDelta }^{*}\) for \(n=100\)

Full size image

We summary the results as follows:

  1. (i)

    When \({\varDelta } ^{*}=0\), SM outperforms all the other estimators. On the other hand, after the small interval near \({\varDelta } ^{*}=0\), the RMSE of \(\widehat{\varvec{\beta }}_{1}^{\mathrm{SM}}\) decreases and goes to zero.

  2. (ii)

    The ordinary least squares (OLS) estimator \(\widehat{\varvec{\beta }}_{1}^{}\) performs much worse than ridge-type suggested estimators when \(\rho \) is large.

  3. (iii)

    For large \(p_{2}\), the CN increases, whereas the RMSE of \(\varvec{\widehat{\beta }}_{1}^{\mathrm{FM}}\) decreases, the RMSE of \(\widehat{\varvec{\beta }}_{1}^{\mathrm{SM}} \) increases.

  4. (iv)

    The PT outperforms shrinkage ridge regression estimators at \({\varDelta } ^{*}=0\) when \(p_{1}\) and \(p_{2}\) close to each other. But, for large \(p_{2}\) values, \(\widehat{\varvec{\beta }}_{1}^{\mathrm{PS}}\) has biggest RMSE. As \({\varDelta } ^{*}\) increases, the RMSE of \(\widehat{\varvec{\beta }}_{1}^{\mathrm{PT}}\) decreases, and it remains on below 1, and then it increases and approaches one.

  5. (v)

    It is seen that the RMSE of \( \widehat{\varvec{\beta }}_{1}^{\mathrm{S}}\) is smaller than the RMSE of \( \widehat{\varvec{\beta }}_{1}^{\mathrm{PS}}\) for all \({\varDelta } ^{*}\) values.

  6. (vi)

    Overall, our results are consistent with the studies of Ahmed et al. (2007); Raheem et al. (2012).

In Table 2, we show the results the comparison the suggested estimators with penalty estimators. From the simulation results, the SM outperforms all other estimators. We observe that ridge pretest and ridge shrinkage estimators perform better than penalty estimators when both \(\rho \) and \(p_{2}\) are large. Especially, when \(\rho \) is large, performance of penalty estimators decrease, whereas the performance of ridge pretest and ridge shrinkage estimators increase. Therefore, the OLS performs much worse than ridge-type suggested estimators, since covariates are designed to be correlated.

In Fig. 3, we plotted estimations of the nonparametric functions \(f_1\) and \(f_2\). The curves estimated by smoothing spline denoted a similar behaviours to real functions especially for larger sample size.

6 Application

We implement proposed strategies to the Baseball data which is analyzed by Friendly (2002). The data contains 322 rows and 22 variables. We also omit missing values and four covariates which are not scaler. Hence, we have 263 sample and 17 covariates, and Table 3 lists the detailed descriptions of both the dependent variable and covariates.

Table 2 CNs and RMSEs for \({\varDelta }^{*} = 0\)
Full size table
Fig. 3
figure 3

Estimation of non-parametric functions for \(p_{1}=5\) and \(p_{2}=10\)

Full size image
Table 3 List of Variable
Full size table

We calculated the CN value is 5830 which implies the existence of multicollinearity in the data set.

The chosen variables via BIC and AIC are shown in Table 4, and AIC selects a model with more variables than BIC. So, in Table 5, the full- and sub- models are given. As it can be seen in Table 5, we omit the intercept term in this analysis since this term was very close to zero in calculations.

Table 4 Candidate sub-models
Full size table

In Table 5, as stated previously, f denotes a smooth function. To select the covariate which can be modelled non-parametrically, we used White Neural Network test (see tseries package in R) for nonlinearity of each of the covariates. According to the results of this test, we have found that the Years has a significant nonlinear relationship with the response lnSal.

Table 5 Fitting models
Full size table

To evaluate the performance of each method, we obtain prediction errors by using 10-fold cross validation following 999 resampled bootstrap samples. Further, we also calculate the Relative Prediction Error (RPE) of each method with respect to the full model estimator. If the RPE of any estimator is larger than one, then this indicates the superiority of that method over the full model estimator. The results are shown in Table 6. According to these results, not surprisingly the SM has maximum RPE since this estimator is computed based on the true model. Further, shrinkage methods outperform penalty estimators although pretest method may less efficient. Finally, we may suggest to use BIC method to construct suggested techniques.

Table 6 Relative prediction errors
Full size table

In Table 7, we present the coefficients of parametric part of model. Moreover, the curve estimated by smoothing spline which the smoothing parameter is selected by GCV is shown in Fig. 4.

Table 7 Estimation of parametric coefficients
Full size table

7 Conclusion

In this paper, we suggest pretest, shrinkage and penalty estimation for PLRMs. The parametric components is estimated by using ridge regression approach, the nonparametric component is estimated by using Speckman approach based on penalized residual sum of squares method. The advantages of listed estimators are studied both theoretically and numerically. Our results show that the sub-model estimator outperforms shrinkage and penalty estimators when the null hypothesis is true, i.e., \({\varDelta }^{*}=0\). Moreover, the pretest and shrinkage estimators performs better than the full model estimator. On the other hand, as the restriction moves away from \({\varDelta }^{*}=0\), i.e., the assumption of null hypothesis is violated, the efficiency of sub-model estimator gradually decreases even worse than full model estimator. Also, the pretest estimation may not perform well for little violations of null hypothesis while the performance of it act like full model when the violations of null hypothesis is large. Finally, shrinkage estimation outperforms the full model estimator in every case. We also compare listed estimators with penalty estimators through Monte Carlo simulation. Our asymptotic theory is well supported by numerical analysis. In summary, construction estimators outshine penalty estimators when \(p_2\) is large, and these estimators much more consistent than penalty estimators in the presence of multicollinearity.

Fig. 4
figure 4

Graph of the estimation of nonparametric function

Full size image