1 Introduction

Shrinkage estimators, hierarchical models and empirical Bayes methods, dating back to the groundbreaking works of [24] and [21], have profound impacts in statistics and in scientific and engineering applications. They provide effective tools to pool information from (scientifically) related populations for simultaneous inference—the data on each population alone often do not lead to the most effective estimation, but by pooling information from the related populations together (for example, by shrinking toward their consensus “center”), one could often obtain more accurate estimate for each individual population. Ever since the seminal works of [24] and [10], an impressive list of articles has been devoted to the study of shrinkage estimators in normal models, including [1, 2, 4–6, 8, 12, 14, 16, 22, 25], among others.

In this article, we consider shrinkage estimation in the presence of linear predictors. In particular, we study optimal shrinkage estimators for heteroscedastic data under linear models. Our study is motivated by three main considerations. First, in many practical problems, one often encounters heteroscedastic (unequal variance) data; for example, the sample sizes for different groups are not all equal. Second, in many statistical applications, in addition to the heteroscedastic response variable, one often has predictors. For example, the predictors could represent longitudinal patterns [7, 9, 27], exam scores [22], characteristics of hospital patients [18], etc. Third, in applying shrinkage estimators to real data, it is quite natural to ask for the optimal way of shrinkage.

The (risk) optimality is not addressed by the conventional estimators, such as the empirical Bayes ones. One might wonder if such an optimal shrinkage estimator exists in the first place. We shall see shortly that in fact (asymptotically) optimal shrinkage estimators do exist and that the optimal estimators are not empirical Bayes ones but are characterized by an unbiased risk estimate (URE).

The study of optimal shrinkage estimators under the heteroscedastic normal model was first considered in [29], where the (asymptotic) optimal shrinkage estimator was identified for both the parametric and semiparametric cases. Xie et al. [30] extends the (asymptotic) optimal shrinkage estimators to exponential families and heteroscedastic location-scale families. The current article can be viewed as an extension of the idea of optimal shrinkage estimators to heteroscedastic linear models.

We want to emphasize that this article works on a theoretical setting somewhat different from [30] but can still cover its main results. Our theoretical results show that the optimality of the proposed URE shrinkage estimators does not rely on normality nor on the tail behavior of the sampling distribution. What we require here are the symmetry and the existence of the fourth moment for the standardized variable.

This article is organized as follows. We first formulate the heteroscedastic linear models in Sect. 2. Interestingly, there are two parallel ways to do so, and both are natural extensions of the heteroscedastic normal model. After reviewing the conventional empirical Bayes methods, we introduce the construction of our optimal shrinkage estimators for heteroscedastic linear models in Sect. 3. The optimal shrinkage estimators are based on an unbiased risk estimate (URE). We show in Sect. 4 that the URE shrinkage estimators are asymptotically optimal in risk. In Sect. 5 we extend the shrinkage estimators to a semiparametric family. Simulation studies are conducted in Sect. 6. We apply the URE shrinkage estimators in Sect. 7 to the baseball data set of [2] and observe quite interesting and encouraging results. We conclude in Sect. 8 with some discussion and extension. The appendix details the proofs and derivations for the theoretical results.

2 Heteroscedastic Hierarchical Linear Models

Consider the heteroscedastic estimation problem

$$\displaystyle{ Y _{i}\vert \boldsymbol{\theta }\mathop{\sim }\limits^{\text{indep.}}\mathcal{N}\left (\theta _{i},A_{i}\right ),\ \ \ \ i = 1,\ldots,p, }$$
(1)

where \(\boldsymbol{\theta }= \left (\theta _{1},\ldots,\theta _{p}\right )^{T}\) is the unknown mean vector, which is to be estimated, and the variances A i  > 0 are unequal, which are assumed to be known. In many statistical applications, in addition to the heteroscedastic \(\boldsymbol{Y } = \left (Y _{1},\ldots,Y _{p}\right )^{T}\), one often has predictors \(\boldsymbol{X}\). A natural question is to consider a heteroscedastic linear model that incorporates these covariates. Notation-wise, let \(\{Y _{i},\boldsymbol{X}_{i}\}_{i=1}^{p}\) denote the p independent statistical units, where Y i is the response variable of the i-th unit, and \(\boldsymbol{X}_{i} = (X_{1i},\ldots,X_{ki})^{T}\) is a k-dimensional column vector that corresponds to the k covariates of the i-th unit. The k × p matrix

$$\displaystyle{\boldsymbol{X} = \left [\boldsymbol{X}_{1}\vert \cdots \vert \boldsymbol{X}_{p}\right ],\ \ \ \ \boldsymbol{X}_{1},..,\boldsymbol{X}_{p} \in \mathbb{R}^{k},}$$

where \(\boldsymbol{X}_{i}\) is the i-th column of \(\boldsymbol{X}\), then contains the covariates for all the units. Throughout this article we assume that \(\boldsymbol{X}\) has full rank, i.e., \(\mathrm{rank}(\boldsymbol{X}) = k\).

To include the predictors, we note that, interestingly, there are two different ways to build up a heteroscedastic hierarchical linear model, which lead to different structure for shrinkage estimation.

Model I: Hierarchical linear model.:

On top of (1), the θ i ’s are \(\theta _{i}\mathop{ \sim }\limits^{\text{indep.}}\mathcal{N}\left (\boldsymbol{X}_{i}^{T}\boldsymbol{\beta },\lambda \right )\), where \(\boldsymbol{\beta }\) and λ are both unknown hyper-parameters. Model I has been suggested as early as [26]. See [16] and [17] for more discussions. The special case of no covariates (i.e., k = 1 and \(\boldsymbol{X} = \left [1\vert \cdots \vert 1\right ]\)) is studied in depth in [29].

Model II: Bayesian linear regression model.:

Together with (1), one assumes \(\boldsymbol{\theta }=\boldsymbol{ X}^{T}\boldsymbol{\beta }\) with \(\boldsymbol{\beta }\) following a conjugate prior distribution \(\boldsymbol{\beta }\sim \mathcal{N}_{k}\left (\boldsymbol{\beta }_{0},\lambda \boldsymbol{W}\right )\), where \(\boldsymbol{W}\) is a known k × k positive definite matrix and \(\boldsymbol{\beta }_{0}\) and λ are unknown hyper-parameters. Model II has been considered in [3, 15, 20] among others; it includes ridge regression as a special case when \(\boldsymbol{\beta }_{0} =\boldsymbol{ 0}_{k}\) and \(\boldsymbol{W} =\boldsymbol{ I}_{k}\).

Figure 1 illustrates these two hierarchical linear models. Under Model I, the posterior mean of \(\boldsymbol{\theta }\) is \(\hat{\theta }_{i}^{\lambda,\boldsymbol{\beta }} =\lambda \left (\lambda +A_{i}\right )^{-1}Y _{i} + A_{i}\left (\lambda +A_{i}\right )^{-1}\boldsymbol{X}_{i}^{T}\boldsymbol{\beta }\) for i = 1, …, p, so the shrinkage estimation is formed by directly shrinking the raw observation Y i toward a linear combination of the k covariates \(\boldsymbol{X}_{i}\). If we denote \(\mu _{i} =\boldsymbol{ X}_{i}^{T}\boldsymbol{\beta }\), and \(\boldsymbol{\mu }= \left (\mu _{1},\ldots,\mu _{p}\right )^{T} \in \mathcal{L}_{\mathrm{row}}\left (\boldsymbol{X}\right )\), the row space of \(\boldsymbol{X}\), then we can rewrite the posterior mean of \(\boldsymbol{\theta }\) under Model I as

$$\displaystyle{ \hat{\theta }^{\lambda,\boldsymbol{\mu }} = \dfrac{\lambda } {\lambda +A_{i}}Y _{i} + \dfrac{A_{i}} {\lambda +A_{i}}\mu _{i},\ \ \ \ \text{with }\boldsymbol{\mu } \in \mathcal{L}_{\mathrm{row}}\left (\boldsymbol{X}\right ). }$$
(2)
Fig. 1
figure 1

Graphical illustration of the two heteroscedastic hierarchical linear models

Full size image

Under Model II, the posterior mean of \(\boldsymbol{\theta }\) is

$$\displaystyle{ \boldsymbol{\hat{\theta }}^{\lambda,\boldsymbol{\beta }_{0} } =\boldsymbol{ X}^{T}\boldsymbol{\hat{\beta }}^{\lambda,\boldsymbol{\beta }_{0} },\ \ \ \text{with }\boldsymbol{\hat{\beta }}^{\lambda,\boldsymbol{\beta }_{0} } =\lambda \boldsymbol{ W}(\lambda \boldsymbol{W} +\boldsymbol{ V })^{-1}\boldsymbol{\hat{\beta }}^{\mathrm{WLS}} +\boldsymbol{ V }\left (\lambda \boldsymbol{W} +\boldsymbol{ V }\right )^{-1}\boldsymbol{\beta }_{ 0}, }$$
(3)

where \(\boldsymbol{\hat{\beta }}^{\mathrm{WLS}} = \left (\boldsymbol{XA}^{-1}\boldsymbol{X}^{T}\right )^{-1}\boldsymbol{XA}^{-1}\boldsymbol{Y }\) is the weighted least squares estimate of the regression coefficient, \(\boldsymbol{A}\) is the diagonal matrix \(\boldsymbol{A} =\mathrm{ diag}\left (A_{1},\ldots,A_{p}\right )\), and \(\boldsymbol{V } = (\boldsymbol{XA}^{-1}\boldsymbol{X}^{T})^{-1}\). Thus, the estimate for θ i is linear in \(\boldsymbol{X}_{i}\), and the “shrinkage” is achieved by shrinking the regression coefficient from the weighted least squares estimate \(\boldsymbol{\hat{\beta }}^{\mathrm{WLS}}\) toward the prior coefficient \(\boldsymbol{\beta }_{0}\).

As both Models I and II are natural generalizations of the heteroscedastic normal model (1), we want to investigate if there is an optimal choice of the hyper-parameters in each case. Specifically, we want to investigate the best empirical choice of the hyper-parameters in each case under the mean squared error loss

$$\displaystyle{ l_{p}(\boldsymbol{\theta },\boldsymbol{\hat{\theta }}) = \dfrac{1} {p}\left \Vert \boldsymbol{\theta }-\boldsymbol{\hat{\theta }}\right \Vert ^{2} = \dfrac{1} {p}\sum _{i=1}^{p}\left (\theta _{ i} -\hat{\theta }_{i}\right )^{2} }$$
(4)

with the associated risk of \(\boldsymbol{\hat{\theta }}\) defined by

$$\displaystyle{R_{p}(\boldsymbol{\theta },\boldsymbol{\hat{\theta }}) = \mathbb{E}_{\boldsymbol{Y }\vert \boldsymbol{\theta }}\left (l_{p}(\boldsymbol{\theta },\boldsymbol{\hat{\theta }})\right ),}$$

where the expectation is taken with respect to \(\boldsymbol{Y }\) given \(\boldsymbol{\theta }\).

Remark 1

Even though we start from the Bayesian setting to motivate the form of shrinkage estimators, our discussion will be all based on the frequentist setting. Hence all probabilities and expectations throughout this article are fixed at the unknown true \(\boldsymbol{\theta }\), which is free in \(\mathbb{R}^{p}\) for Model I and confined in \(\mathcal{L}_{\mathrm{row}}\left (\boldsymbol{X}\right )\) for Model II.

Remark 2

The diagonal assumption of \(\boldsymbol{A}\) is quite important for Model I but not so for Model II, as in Model II we can always apply some linear transformations to obtain a diagonal covariance matrix. Without loss of generality, we will keep the diagonal assumption for \(\boldsymbol{A}\) in Model II.

For the ease of exposition, we will next overview the conventional empirical Bayes estimates in a general two-level hierarchical model, which includes both Models I and II:

$$\displaystyle{ \boldsymbol{Y }\vert \boldsymbol{\theta }\sim \mathcal{N}_{p}(\boldsymbol{\theta },\boldsymbol{A})\text{ and }\boldsymbol{\theta } \sim \mathcal{N}_{p}(\boldsymbol{\mu },\boldsymbol{B}), }$$
(5)

where \(\boldsymbol{B}\) is a non-negative definite symmetric matrix that is restricted in an allowable set \(\mathcal{B}\), and \(\boldsymbol{\mu }\) is in the row space \(\mathcal{L}_{\mathrm{row}}(\boldsymbol{X})\) of \(\boldsymbol{X}\).

Remark 3

Under Model I, \(\boldsymbol{\mu }\) and \(\boldsymbol{B}\) take the form of \(\boldsymbol{\mu }=\boldsymbol{ X}^{T}\boldsymbol{\beta }\) and \(\boldsymbol{B} \in \mathcal{B} = \left \{\lambda \boldsymbol{I}_{p}:\lambda > 0\right \}\), whereas under Model II, \(\boldsymbol{\mu }\) and \(\boldsymbol{B}\) take the form of \(\boldsymbol{\mu }=\boldsymbol{ X}^{T}\boldsymbol{\beta }_{0}\) and \(\boldsymbol{B} \in \mathcal{B} = \left \{\lambda \boldsymbol{X}^{T}\boldsymbol{WX}:\lambda > 0\right \}\). It is interesting to observe that in Model I, \(\boldsymbol{B}\) is of full rank, while in Model II, \(\boldsymbol{B}\) is of rank k. As we shall see, this distinction will have interesting theoretical implications for the optimal shrinkage estimators.

Lemma 1

Under the two-level hierarchical model (5), the posterior distribution is

$$\displaystyle{\boldsymbol{\theta }\vert \boldsymbol{Y } \sim \mathcal{N}_{p}\left (\boldsymbol{B}(\boldsymbol{A} +\boldsymbol{ B})^{-1}\boldsymbol{Y } +\boldsymbol{ A}(\boldsymbol{A} +\boldsymbol{ B})^{-1}\boldsymbol{\mu },\boldsymbol{A}(\boldsymbol{A} +\boldsymbol{ B})^{-1}\boldsymbol{B}\right ),}$$

and the marginal distribution of \(\boldsymbol{Y }\) is \(\boldsymbol{Y } \sim \mathcal{N}_{p}\left (\boldsymbol{\mu },\boldsymbol{A} +\boldsymbol{ B}\right )\) .

For given values of \(\boldsymbol{B}\) and \(\boldsymbol{\mu }\), the posterior mean of the parameter \(\boldsymbol{\theta }\) leads to the Bayes estimate

$$\displaystyle{ \boldsymbol{\hat{\theta }}^{\boldsymbol{B},\boldsymbol{\mu }} =\boldsymbol{ B}(\boldsymbol{A} +\boldsymbol{ B})^{-1}\boldsymbol{Y } +\boldsymbol{ A}(\boldsymbol{A} +\boldsymbol{ B})^{-1}\boldsymbol{\mu }. }$$
(6)

To use the Bayes estimate in practice, one has to specify the hyper-parameters in \(\boldsymbol{B}\) and \(\boldsymbol{\mu }\). The conventional empirical Bayes method uses the marginal distribution of \(\boldsymbol{Y }\) to estimate the hyper-parameters. For instance, the empirical Bayes maximum likelihood estimates (EBMLE) \(\boldsymbol{\hat{B} }^{\mathrm{EBMLE}}\) and \(\boldsymbol{\hat{\mu }}^{\mathrm{EBMLE}}\) are obtained by maximizing the marginal likelihood of \(\boldsymbol{Y }\):

$$\displaystyle{\left (\boldsymbol{\hat{B} }^{\mathrm{EBMLE}},\boldsymbol{\hat{\mu }}^{\mathrm{EBMLE}}\right ) =\mathop{ \mathrm{argmax}}\nolimits \limits _{ \begin{array}{c}\boldsymbol{B}\in \mathcal{B}\\ \boldsymbol{\mu }\in \mathcal{L}_{\mathrm{ row}}\left (\boldsymbol{X}\right )\end{array}} -\left (\boldsymbol{Y }-\boldsymbol{\mu }\right )^{T}\left (\boldsymbol{A} +\boldsymbol{ B}\right )^{-1}\left (\boldsymbol{Y }-\boldsymbol{\mu }\right ) -\log \left (\det \left (\boldsymbol{A} +\boldsymbol{ B}\right )\right ).}$$

Alternatively, the empirical Bayes method-of-moment estimates (EBMOM) \(\boldsymbol{\hat{B}}^{\mathrm{EBMOM}}\) and \(\boldsymbol{\hat{\mu }}^{\mathrm{EBMOM}}\) are obtained by solving the following moment equations for \(\boldsymbol{B} \in \mathcal{B}\) and \(\boldsymbol{\mu }\in \mathcal{L}_{\mathrm{row}}\left (\boldsymbol{X}\right )\):

$$\displaystyle\begin{array}{rcl} \boldsymbol{\mu }& =& \boldsymbol{X}^{T}\left (\boldsymbol{X}\left (\boldsymbol{A} +\boldsymbol{ B}\right )^{-1}\boldsymbol{X}^{T}\right )^{-1}\boldsymbol{X}\left (\boldsymbol{A} +\boldsymbol{ B}\right )^{-1}\boldsymbol{Y }, {}\\ \boldsymbol{B}& =& \left (\boldsymbol{Y }-\boldsymbol{\mu }\right )\left (\boldsymbol{Y }-\boldsymbol{\mu }\right )^{T} -\boldsymbol{ A}. {}\\ \end{array}$$

If no solutions of \(\boldsymbol{B}\) can be found in \(\mathcal{B}\), we then set \(\boldsymbol{\hat{B}}^{\mathrm{EBMOM}} =\boldsymbol{ 0}_{p\times p}\). Adjustment for the loss of k degrees of freedom from the estimation of \(\boldsymbol{\mu }\) might be applicable for \(\boldsymbol{B} =\lambda \boldsymbol{ C}\) (\(\boldsymbol{C} =\boldsymbol{ I}_{p}\) for Model I and \(\boldsymbol{X}^{T}\boldsymbol{WX}\) for Model II): we can replace the second moment equation by

$$\displaystyle{\lambda = \left ( \dfrac{p} {p - k} \dfrac{\left \Vert \boldsymbol{Y }-\boldsymbol{\mu }\right \Vert ^{2}} {\mathrm{tr}\left (\boldsymbol{C}\right )} -\dfrac{\mathrm{tr}\left (\boldsymbol{A}\right )} {\mathrm{tr}\left (\boldsymbol{C}\right )}\right )^{+}.}$$

The corresponding empirical Bayes shrinkage estimator \(\boldsymbol{\hat{\theta }}^{\mathrm{EBMLE}}\) or \(\boldsymbol{\hat{\theta }}^{\mathrm{EBMOM}}\) is then formed by plugging \((\boldsymbol{\hat{B} }^{\mathrm{EBMLE}},\boldsymbol{\hat{\mu }}^{\mathrm{EBMLE}})\) or \((\boldsymbol{\hat{B} }^{\mathrm{EBMOM}},\boldsymbol{\hat{\mu }}^{\mathrm{EBMOM}})\) into Eq. (6).

3 URE Estimates

The formulation of the empirical Bayes estimates raises a natural question: which one is preferred \(\boldsymbol{\hat{\theta }}^{\mathrm{EBMLE}}\) or \(\boldsymbol{\hat{\theta }}^{\mathrm{EBMOM}}\)? More generally, is there an optimal way to choose the hyper-parameters? It turns out that neither \(\boldsymbol{\hat{\theta }}^{\mathrm{EBMLE}}\) nor \(\boldsymbol{\hat{\theta }}^{\mathrm{EBMOM}}\) is optimal. The (asymptotically) optimal estimate, instead of relying on the marginal distribution of \(\boldsymbol{Y }\), is characterized by an unbiased risk estimate (URE). The idea of forming a shrinkage estimate through URE for heteroscedastic models is first suggested in [29]. We shall see that in our context of hierarchical linear models (both Models I and II) the URE estimators that we are about to introduce have (asymptotically) optimal risk properties.

The basic idea behind URE estimators is the following. Ideally we want to find the hyper-parameters that give the smallest risk. However, since the risk function depends on the unknown \(\boldsymbol{\theta }\), we cannot directly minimize the risk function in practice. If we can find a good estimate of the risk function instead, then minimizing this proxy of the risk will lead to a competitive estimator.

To formally introduce the URE estimators, we start from the observation that, under the mean squared error loss (4), the risk of the Bayes estimator \(\boldsymbol{\hat{\theta }}^{\boldsymbol{B},\boldsymbol{\mu }}\) for fixed \(\boldsymbol{B}\) and \(\boldsymbol{\mu }\) is

$$\displaystyle{ R_{p}(\boldsymbol{\theta },\boldsymbol{\hat{\theta }}^{\boldsymbol{B},\boldsymbol{\mu }}) = \dfrac{1} {p}\left \Vert \boldsymbol{A}\left (\boldsymbol{A} +\boldsymbol{ B}\right )^{-1}\left (\boldsymbol{\mu }-\boldsymbol{\theta }\right )\right \Vert ^{2} + \dfrac{1} {p}\mathrm{tr}\left (\boldsymbol{B}\left (\boldsymbol{A} +\boldsymbol{ B}\right )^{-1}\boldsymbol{A}\left (\boldsymbol{A} +\boldsymbol{ B}\right )^{-1}\boldsymbol{B}\right ), }$$
(7)

which can be easily shown using the bias-variance decomposition of the mean squared error. As the risk function involves the unknown \(\boldsymbol{\theta }\), we cannot directly minimize it. However, an unbiased estimate of the risk is available:

$$\displaystyle{ \mathrm{URE}\left (\boldsymbol{B},\boldsymbol{\mu }\right ) = \dfrac{1} {p}\left \Vert \boldsymbol{A}\left (\boldsymbol{A} +\boldsymbol{ B}\right )^{-1}\left (\boldsymbol{Y }-\boldsymbol{\mu }\right )\right \Vert ^{2} + \dfrac{1} {p}\mathrm{tr}\left (\boldsymbol{A} - 2\boldsymbol{A}\left (\boldsymbol{A} +\boldsymbol{ B}\right )^{-1}\boldsymbol{A}\right ), }$$
(8)

which again can be easily shown using the bias-variance decomposition of the mean squared error. Intuitively, if \(\mathrm{URE}\left (\boldsymbol{B},\boldsymbol{\mu }\right )\) is a good approximation of the actual risk, then we would expect the estimator obtained by minimizing the URE to have good properties. This leads to the URE estimator \(\boldsymbol{\hat{\theta }}^{\mathrm{URE}}\), defined by

$$\displaystyle{ \boldsymbol{\hat{\theta }}^{\mathrm{URE}} =\boldsymbol{ \hat{B} }^{\mathrm{URE}}(\boldsymbol{A} +\boldsymbol{ \hat{B} }^{\mathrm{URE}})^{-1}\boldsymbol{Y } +\boldsymbol{ A}(\boldsymbol{A} +\boldsymbol{ \hat{B} }^{\mathrm{URE}})^{-1}\boldsymbol{\hat{\mu }}^{\mathrm{URE}}\mathbf{,} }$$
(9)

where

$$\displaystyle{\left (\boldsymbol{\hat{B} }^{\mathrm{URE}},\boldsymbol{\hat{\mu }}^{\mathrm{URE}}\right ) =\mathop{ \mathrm{argmin}}\nolimits \limits _{ B\in \mathcal{B},\ \boldsymbol{\mu }\in \mathcal{L}_{\mathrm{row}}\left (\boldsymbol{X}\right )}\mathrm{URE}\left (\boldsymbol{B},\boldsymbol{\mu }\right ).}$$

It is worth noting that the value of \(\boldsymbol{\mu }\) that minimizes (8) for a given \(\boldsymbol{B}\) is neither the ordinary least squares (OLS) nor the weighted least squares (WLS) regression estimate, echoing similar observation as in [29].

In the URE estimator (9), \(\boldsymbol{\hat{B} }^{\mathrm{URE}}\) and \(\boldsymbol{\hat{\mu }}^{\mathrm{URE}}\) are jointly determined by minimizing the URE. When the number of independent statistical units p is small or moderate, joint minimization of \(\boldsymbol{B}\) and the vector \(\boldsymbol{\mu }\), however, may be too ambitious. In this setting, it might be beneficial to set \(\boldsymbol{\mu }\) by a predetermined rule and only optimize \(\boldsymbol{B}\), as it might reduce the variability of the resulting estimate. In particular, we can consider shrinking toward a generalized least squares (GLS) regression estimate

$$\displaystyle{\boldsymbol{\hat{\mu }}^{\boldsymbol{M}} =\boldsymbol{ X}^{T}\left (\boldsymbol{XMX}^{T}\right )^{-1}\boldsymbol{XMY } =\boldsymbol{ P}_{\boldsymbol{ M},\boldsymbol{X}}\boldsymbol{Y },}$$

where \(\boldsymbol{M}\) is a prespecified symmetric positive definite matrix. This use of \(\boldsymbol{\hat{\mu }}^{\boldsymbol{M}}\) gives the shrinkage estimate \(\boldsymbol{\hat{\theta }}^{\boldsymbol{B},\boldsymbol{\hat{\mu }}^{\boldsymbol{M}} } =\boldsymbol{ B}(\boldsymbol{A} +\boldsymbol{ B})^{-1}\boldsymbol{Y } +\boldsymbol{ A}(\boldsymbol{A} +\boldsymbol{ B})^{-1}\boldsymbol{\hat{\mu }}^{\boldsymbol{M}}\), where one only needs to determine \(\boldsymbol{B}\). We can construct another URE estimate for this purpose. Similar to the previous construction, we note that \(\boldsymbol{\hat{\theta }}^{\boldsymbol{B},\boldsymbol{\hat{\mu }}^{\boldsymbol{M}} }\) has risk

$$\displaystyle\begin{array}{rcl} R_{p}(\boldsymbol{\theta },\boldsymbol{\hat{\theta }}^{\boldsymbol{B},\boldsymbol{\hat{\mu }}^{\boldsymbol{M}} })& =& \dfrac{1} {p}\left \Vert \boldsymbol{A}\left (\boldsymbol{A} +\boldsymbol{ B}\right )^{-1}\left (\boldsymbol{I}_{ p} -\boldsymbol{ P}_{\boldsymbol{M},\boldsymbol{X}}\right )\boldsymbol{\theta }\right \Vert ^{2} \\ & & +\dfrac{1} {p}\mathrm{tr}\left (\left (\boldsymbol{I}_{p} -\boldsymbol{ A}\left (\boldsymbol{A} +\boldsymbol{ B}\right )^{-1}\left (\boldsymbol{I}_{ p} -\boldsymbol{ P}_{\boldsymbol{M},\boldsymbol{X}}\right )\right )\boldsymbol{A}\right. \\ & & \quad \times \left.\left (\boldsymbol{I}_{p} -\boldsymbol{ A}\left (\boldsymbol{A} +\boldsymbol{ B}\right )^{-1}\left (\boldsymbol{I}_{ p} -\boldsymbol{ P}_{\boldsymbol{M},\boldsymbol{X}}\right )\right )^{T}\right ).{}\end{array}$$
(10)

An unbiased risk estimate of it is

$$\displaystyle{ \mathrm{URE}_{\boldsymbol{M}}\left (\boldsymbol{B}\right ) = \dfrac{1} {p}\left \Vert \boldsymbol{A}\left (\boldsymbol{A} +\boldsymbol{ B}\right )^{-1}\left (\boldsymbol{Y } -\boldsymbol{\hat{\mu }}^{\boldsymbol{M}}\right )\right \Vert ^{2}+\dfrac{1} {p}\mathrm{tr}\left (\boldsymbol{A} - 2\boldsymbol{A}\left (\boldsymbol{A} +\boldsymbol{ B}\right )^{-1}\left (\boldsymbol{I}_{ p} -\boldsymbol{ P}_{\boldsymbol{M},\boldsymbol{X}}\right )\boldsymbol{A}\right ). }$$
(11)

Both (10) and (11) can be easily proved by the bias-variance decomposition of mean squared error. Minimizing \(\mathrm{URE}_{\boldsymbol{M}}\left (\boldsymbol{B}\right )\) over \(\boldsymbol{B}\) gives the URE GLS shrinkage estimator (which shrinks toward \(\boldsymbol{\hat{\mu }}^{\boldsymbol{M}}\)):

$$\displaystyle{ \boldsymbol{\hat{\theta }}_{\boldsymbol{M}}^{\mathrm{URE}} =\boldsymbol{ \hat{B} }_{\boldsymbol{ M}}^{\mathrm{URE}}\left (\boldsymbol{A} +\boldsymbol{ \hat{B} }_{\boldsymbol{ M}}^{\mathrm{URE}}\right )^{-1}\boldsymbol{Y } +\boldsymbol{ A}\left (\boldsymbol{A} +\boldsymbol{ \hat{B} }_{\boldsymbol{ M}}^{\mathrm{URE}}\right )^{-1}\boldsymbol{\hat{\mu }}^{\boldsymbol{M}}\mathbf{,} }$$
(12)

where

$$\displaystyle{\boldsymbol{\hat{B} }_{\boldsymbol{M}}^{\mathrm{URE}}\boldsymbol{ =}\mathop{ \mathrm{argmin}}\nolimits \limits _{\boldsymbol{ B}\in \mathcal{B}}\mathrm{URE}_{\boldsymbol{M}}\left (\boldsymbol{B}\right ).}$$

Remark 4

When \(\boldsymbol{M} =\boldsymbol{ I}_{p}\), clearly \(\boldsymbol{\hat{\mu }}^{\boldsymbol{M}} =\boldsymbol{\hat{\mu }} ^{\mathrm{OLS}}\), the ordinary least squares regression estimate. When \(\boldsymbol{M} =\boldsymbol{ A}^{-1}\), then \(\boldsymbol{\hat{\mu }}^{\boldsymbol{M}} =\boldsymbol{\hat{\mu }} ^{\mathrm{WLS}}\), the weighted least squares regression estimate.

Remark 5

Tan [28] briefly discussed the URE minimization approach for Model I without the covariates in [29] in relation to [11], where Model I is assumed but an unbiased estimate of the mean prediction error (rather than the mean squared error) is used to form a predictor (rather than an estimator).

Remark 6

In the homoscedastic case, (12) reduces to standard shrinkage toward a subspace \(\mathcal{L}_{\mathrm{row}}\left (\boldsymbol{X}\right )\), as discussed, for instance, in [23] and [19].

4 Theoretical Properties of URE Estimates

This section is devoted to the risk properties of the URE estimators. Our core theoretical result is to show that the risk estimate URE is not only unbiased for the risk but, more importantly, uniformly close to the actual loss. We therefore expect that minimizing URE would lead to an estimate with competitive risk properties.

4.1 Uniform Convergence of URE

To present our theoretical result, we first define \(\mathcal{L}\) to be a subset of \(\mathcal{L}_{\mathrm{row}}\left (\boldsymbol{X}\right )\):

$$\displaystyle{\mathcal{L} =\{\boldsymbol{\mu }\in \mathcal{L}_{\mathrm{row}}\left (\boldsymbol{X}\right ): \left \Vert \boldsymbol{\mu }\right \Vert \leq Mp^{\kappa }\left \Vert \boldsymbol{Y }\right \Vert \},}$$

where M is a large and fixed constant and κ ∈ [0, 1∕2) is a constant. Next, we introduce the following regularity conditions:

(A) \(\sum _{i=1}^{p}A_{i}^{2} = O\left (p\right )\); (B) \(\sum _{i=1}^{p}A_{i}\theta _{i}^{2} = O\left (p\right )\); (C) \(\sum _{i=1}^{p}\theta _{i}^{2} = O\left (p\right )\);

(D) \(p^{-1}\boldsymbol{XAX}^{T} \rightarrow \boldsymbol{\varOmega }_{D}\); (E) \(p^{-1}\boldsymbol{XX}^{T} \rightarrow \boldsymbol{\varOmega }_{\boldsymbol{E}} > 0\);

(F) \(p^{-1}\boldsymbol{XA}^{-1}\boldsymbol{X}^{T} \rightarrow \boldsymbol{\varOmega }_{F} > 0\); (G) \(p^{-1}\boldsymbol{XA}^{-2}\boldsymbol{X}^{T} \rightarrow \boldsymbol{\varOmega }_{G}\).

The theorem below shows that \(\mathrm{URE}\left (\boldsymbol{B},\boldsymbol{\mu }\right )\) not only unbiasedly estimates the risk but also is (asymptotically) uniformly close to the actual loss.

Theorem 1

Assume conditions (A)–(E) for Model I or assume conditions (A) and (D)–(G) for Model II. In either case, we have

$$\displaystyle{\sup \limits _{\boldsymbol{B}\in \mathcal{B},\ \boldsymbol{\mu }\in \mathcal{L}}\left \vert \mathrm{URE}\left (\boldsymbol{B},\boldsymbol{\mu }\right ) - l_{p}\left (\boldsymbol{\theta },\boldsymbol{\hat{\theta }}^{\boldsymbol{B},\boldsymbol{\mu }}\right )\right \vert \rightarrow 0\text{ in }L^{1},\text{ as }p \rightarrow \infty.}$$

We want to remark here that the set \(\mathcal{L}\) gives the allowable range of \(\boldsymbol{\mu }\): the norm of \(\boldsymbol{\mu }\) is up to an \(o\left (p^{1/2}\right )\) multiple of the norm of \(\boldsymbol{Y }\). This choice of \(\mathcal{L}\) does not lead to any difficulty in practice because, given a large enough constant M, it will cover the shrinkage location of any sensible shrinkage estimator. We note that it is possible to define the range of sensible shrinkage locations in other ways (e.g., one might want to define it by ∞-norm in \(\mathbb{R}^{p}\)), but we find our setting more theoretically appealing and easy to work with. In particular, our assumption of the exponent κ < 1∕2 is flexible enough to cover most interesting cases, including \(\boldsymbol{\hat{\mu }}^{\mathrm{OLS}}\), the ordinary least squares regression estimate, and \(\boldsymbol{\hat{\mu }}^{\mathrm{WLS}}\), the weighted least squares regression estimate (as in Remark 4) as shown in the following lemma.

Lemma 2

(i) \(\boldsymbol{\hat{\mu }}^{\mathrm{OLS}} \in \mathcal{L}\) . (ii) Assume \(\left (\mathrm{A}\right )\) and \(\left (\mathrm{A}^{{\prime}}\right )\ \sum _{i=1}^{p}A_{i}^{-2-\delta } = O\left (p\right )\) for some δ > 0; then \(\boldsymbol{\hat{\mu }}^{\mathrm{WLS}} \in \mathcal{L}\) for \(\kappa = 4^{-1} + \left (4 + 2\delta \right )^{-1}\) and a large enough M.

Remark 7

We want to mention here that Theorem 1 in the case of Model I covers Theorem 5.1 of [29] (which is the special case of k = 1 and \(\boldsymbol{X} = \left [1\vert 1\vert \ldots \vert 1\right ]\)) because the restriction of \(\left \vert \mu \right \vert \leq \max \limits _{1\leq i\leq p}\left \vert Y _{i}\right \vert\) in [29] is contained in \(\mathcal{L}\) as

$$\displaystyle{\max \limits _{1\leq i\leq p}\left \vert Y _{i}\right \vert = (\max \limits _{1\leq i\leq p}Y _{i}^{2})^{1/2} \leq (\sum _{ i=1}^{p}Y _{ i}^{2})^{1/2} = \left \Vert \boldsymbol{Y }\right \Vert.}$$

Furthermore, we do not require the stronger assumption of \(\sum _{i=1}^{p}\left \vert \theta _{i}\right \vert ^{2+\delta } = O\left (p\right )\) for some δ > 0 made in [29]. Note that in this case (k = 1 and \(\boldsymbol{X} = \left [1\vert 1\vert \ldots \vert 1\right ]\)) we do not even require conditions \(\left (\mathrm{D}\right )\) and \(\left (\mathrm{E}\right )\), as condition \(\left (\mathrm{A}\right )\) directly implies \(\mathrm{tr}(\left (\boldsymbol{X}\boldsymbol{X}^{T}\right )^{-1}\boldsymbol{X}\boldsymbol{A}\boldsymbol{X}^{T}) = O\left (1\right )\), the result we need in the proof of Theorem 1 for Model I.

Remark 8

In the proof of Theorem 1, the sampling distribution of \(\boldsymbol{Y }\) is involved only through the moment calculations, such as \(\mathbb{E}(\mathrm{tr}(\boldsymbol{Y Y }^{T} -\boldsymbol{ A} -\boldsymbol{\theta \theta }^{T})^{2})\) and \(\mathbb{E}(\left \Vert \boldsymbol{Y }\right \Vert ^{2})\). It is therefore straightforward to generalize Theorem 1 to the case of

$$\displaystyle{Y _{i} =\theta _{i} + \sqrt{A_{i}}Z_{i},}$$

where Z i follows any distribution with mean 0, variance 1, \(\mathbb{E}\left (Z_{i}^{3}\right ) = 0\), and \(\mathbb{E}\left (Z_{i}^{4}\right ) < \infty \). This is noteworthy as our result also covers that of [30] but the methodology we employ here does not require to control the tail behavior of Z i as in [29, 30].

4.2 Risk Optimality

In this section, we consider the risk properties of the URE estimators. We will show that, under the hierarchical linear models, the URE estimators have (asymptotically) optimal risk, whereas it is not necessarily so for other shrinkage estimators such as the empirical Bayes ones.

A direct consequence of the uniform convergence of URE is that the URE estimator has a loss/risk that is asymptotically no larger than that of any other shrinkage estimators. Furthermore, the URE estimator is asymptotically as good as the oracle loss estimator. To be precise, let \(\boldsymbol{\tilde{\theta }}^{\mathrm{OL}}\) be the oracle loss (OL) estimator defined by plugging

$$\displaystyle\begin{array}{rcl} \left (\boldsymbol{\tilde{B}}^{\mathrm{OL}},\boldsymbol{\tilde{\mu }}^{\mathrm{OL}}\right )& =& \mathop{\mathrm{argmin}}\nolimits \limits _{ B\in \mathcal{B},\ \boldsymbol{\mu }\in \mathcal{L}}l_{p}\left (\boldsymbol{\theta },\boldsymbol{\hat{\theta }}^{\boldsymbol{B},\boldsymbol{\mu }}\right ) {}\\ & =& \mathop{\mathrm{argmin}}\nolimits \limits _{B\in \mathcal{B},\ \boldsymbol{\mu }\in \mathcal{L}}\left \Vert \boldsymbol{B}(\boldsymbol{A} +\boldsymbol{ B})^{-1}\boldsymbol{Y } +\boldsymbol{ A}(\boldsymbol{A} +\boldsymbol{ B})^{-1}\boldsymbol{\mu }-\boldsymbol{\theta }\right \Vert ^{2} {}\\ \end{array}$$

into (6). Of course, \(\boldsymbol{\tilde{\theta }}^{\mathrm{OL}}\) is not really an estimator, since it depends on the unknown \(\boldsymbol{\theta }\) (hence we use the notation \(\boldsymbol{\tilde{\theta }}^{\mathrm{OL}}\) rather than \(\boldsymbol{\hat{\theta }}^{\mathrm{OL}}\)). Although not obtainable in practice, \(\boldsymbol{\tilde{\theta }}^{\mathrm{OL}}\) lays down the theoretical limit that one can ever hope to reach. The next theorem shows that the URE estimator \(\boldsymbol{\hat{\theta }}^{\mathrm{URE}}\) is asymptotically as good as the oracle loss estimator, and, consequently, it is asymptotically at least as good as any other shrinkage estimator.

Theorem 2

Assume the conditions of Theorem  1 and that \(\boldsymbol{\hat{\mu }}^{\mathrm{URE}} \in \mathcal{L}\) . Then

$$\displaystyle\begin{array}{rcl} \lim \limits _{p\rightarrow \infty }\mathbb{P}\left (l_{p}\left (\boldsymbol{\theta },\boldsymbol{\hat{\theta }}^{\mathrm{URE}}\right ) \geq l_{ p}\left (\boldsymbol{\theta },\boldsymbol{\tilde{\theta }}^{\mathrm{OL}}\right )+\epsilon \right )& =& 0\ \ \ \ \forall \epsilon > 0, {}\\ \limsup \limits _{p\rightarrow \infty }\left (R_{p}\left (\boldsymbol{\theta },\boldsymbol{\hat{\theta }}^{\mathrm{URE}}\right ) - R_{ p}\left (\boldsymbol{\theta },\boldsymbol{\tilde{\theta }}^{\mathrm{OL}}\right )\right )& =& 0. {}\\ \end{array}$$

Corollary 1

Assume the conditions of Theorem  1 and that \(\boldsymbol{\hat{\mu }}^{\mathrm{URE}} \in \mathcal{L}\) . Then for any estimator \(\boldsymbol{\hat{\theta }}^{\boldsymbol{\hat{B} }_{p},\boldsymbol{\hat{\mu }}_{p}} =\boldsymbol{ \hat{B} }_{p}\left (\boldsymbol{A} +\boldsymbol{ \hat{B} }_{p}\right )^{-1}\boldsymbol{Y } +\boldsymbol{ A}\left (\boldsymbol{A} +\boldsymbol{ \hat{B} }_{p}\right )^{-1}\boldsymbol{\hat{\mu }}_{p}\) with \(\boldsymbol{\hat{B} }_{p} \in \mathcal{B}\) and \(\boldsymbol{\hat{\mu }}_{p} \in \mathcal{L}\) , we always have

$$\displaystyle\begin{array}{rcl} \lim \limits _{p\rightarrow \infty }\mathbb{P}\left (l_{p}\left (\boldsymbol{\theta },\boldsymbol{\hat{\theta }}^{\mathrm{URE}}\right ) \geq l_{ p}\left (\boldsymbol{\theta },\boldsymbol{\hat{\theta }}^{\boldsymbol{\hat{B}}_{p},\boldsymbol{\hat{\mu }}_{p} }\right )+\epsilon \right )& =& 0\ \ \ \ \forall \epsilon > 0, {}\\ \limsup \limits _{p\rightarrow \infty }\left (R_{p}\left (\boldsymbol{\theta },\boldsymbol{\hat{\theta }}^{\mathrm{URE}}\right ) - R_{ p}\left (\boldsymbol{\theta },\boldsymbol{\hat{\theta }}^{\boldsymbol{\hat{B} }_{p},\boldsymbol{\hat{\mu }}_{p} }\right )\right )& \leq & 0. {}\\ \end{array}$$

Corollary 1 tells us that the URE estimator in either Model I or II is asymptotically optimal: it has (asymptotically) the smallest loss and risk among all shrinkage estimators of the form (6).

4.3 Shrinkage Toward the Generalized Least Squares Estimate

The risk optimality also holds when we consider the URE estimator \(\boldsymbol{\hat{\theta }}_{\boldsymbol{M}}^{\mathrm{URE}}\) that shrinks toward the GLS regression estimate \(\boldsymbol{\hat{\mu }}^{\boldsymbol{M}} =\boldsymbol{ P}_{\boldsymbol{M},\boldsymbol{X}}\boldsymbol{Y }\) as introduced in Sect. 3.

Theorem 3

Assume the conditions of Theorem  1 , \(\boldsymbol{\hat{\mu }}^{\boldsymbol{M}} \in \mathcal{L}\) , and

$$\displaystyle{ p^{-1}\boldsymbol{XMX}^{T} \rightarrow \boldsymbol{\varOmega }_{ 1} > 0,\ \ \ \ p^{-1}\boldsymbol{XAMX}^{T} \rightarrow \boldsymbol{\varOmega }_{ 2},\ \ \ \ p^{-1}\boldsymbol{XMA}^{2}\boldsymbol{MX}^{T} \rightarrow \boldsymbol{\varOmega }_{ 3}, }$$
(13)

where only the first and third conditions above are assumed for Model I and only the first and the second are assumed for Model II. Then we have

$$\displaystyle{ \sup \limits _{\boldsymbol{B}\in \mathcal{B}}\left \vert \mathrm{URE}_{\boldsymbol{M}}\left (\boldsymbol{B}\right ) - l_{p}\left (\boldsymbol{\theta },\boldsymbol{\hat{\theta }}^{\boldsymbol{B},\boldsymbol{\hat{\mu }}^{\boldsymbol{M}} }\right )\right \vert \rightarrow 0\text{ in }L^{1}\text{ as }p \rightarrow \infty. }$$
(14)

As a corollary, for any estimator \(\boldsymbol{\hat{\theta }}^{\boldsymbol{\hat{B} }_{p},\boldsymbol{\hat{\mu }}^{\boldsymbol{M}} } =\boldsymbol{ \hat{B} }_{p}\left (\boldsymbol{A} +\boldsymbol{ \hat{B} }_{p}\right )^{-1}\boldsymbol{Y } +\boldsymbol{ A}\left (\boldsymbol{A} +\boldsymbol{ \hat{B} }_{p}\right )^{-1}\boldsymbol{\hat{\mu }}^{\boldsymbol{M}}\) with \(\boldsymbol{\hat{B} }_{p} \in \mathcal{B}\) , we always have

$$\displaystyle\begin{array}{rcl} \lim \limits _{p\rightarrow \infty }\mathbb{P}\left (l_{p}\left (\boldsymbol{\theta },\boldsymbol{\hat{\theta }}_{\boldsymbol{M}}^{\mathrm{URE}}\right ) \geq l_{ p}\left (\boldsymbol{\theta },\boldsymbol{\hat{\theta }}^{\boldsymbol{\hat{B} }_{p},\boldsymbol{\hat{\mu }}^{\boldsymbol{M}} }\right )+\epsilon \right )& =& 0\ \ \ \ \forall \epsilon > 0, {}\\ \limsup \limits _{p\rightarrow \infty }\left (R_{p}\left (\boldsymbol{\theta },\boldsymbol{\hat{\theta }}_{\boldsymbol{M}}^{\mathrm{URE}}\right ) - R_{ p}\left (\boldsymbol{\theta },\boldsymbol{\hat{\theta }}^{\boldsymbol{\hat{B} }_{p},\boldsymbol{\hat{\mu }}^{\boldsymbol{M}} }\right )\right )& \leq & 0. {}\\ \end{array}$$

Remark 9

For shrinking toward \(\boldsymbol{\hat{\mu }}^{\mathrm{OLS}}\), where \(\boldsymbol{M} =\boldsymbol{ I}_{p}\), we know from Lemma 2 that \(\boldsymbol{\hat{\mu }}^{\mathrm{OLS}}\) is automatically in \(\mathcal{L}\), so we only need one more condition \(p^{-1}\boldsymbol{XA}^{2}\boldsymbol{X}^{T} \rightarrow \boldsymbol{\varOmega }_{3}\) for Model I. For shrinking toward \(\boldsymbol{\hat{\mu }}^{\mathrm{WLS}}\), where \(\boldsymbol{M} =\boldsymbol{ A}^{-1}\), (13) is the same as the conditions (E) and (F) of Theorem 1, so additionally we only need to assume (A′) of Lemma 2 and (F) for Model I.

5 Semiparametric URE Estimators

We have established the (asymptotic) optimality of the URE estimators \(\boldsymbol{\hat{\theta }}^{\mathrm{URE}}\) and \(\boldsymbol{\hat{\theta }}_{\boldsymbol{M}}^{\mathrm{URE}}\) in the previous section. One limitation of the result is that the class over which the URE estimators are optimal is specified by a parametric form: \(\boldsymbol{B} =\lambda \boldsymbol{ C}\) (0 ≤ λ ≤ ∞) in Eq. (6), where \(\boldsymbol{C} =\boldsymbol{ I}_{p}\) for Model I and \(\boldsymbol{C} =\boldsymbol{ X}^{T}\boldsymbol{WX}\) for Model II. Aiming to provide a more flexible and, at the same time, efficient estimation procedure, we consider in this section a class of semiparametric shrinkage estimators. Our consideration is inspired by Xie et al. [29].

5.1 Semiparametric URE Estimator Under Model I

To motivate the semiparametric shrinkage estimators, let us first revisit the Bayes estimator \(\boldsymbol{\hat{\theta }}^{\lambda,\boldsymbol{\mu }}\) under Model I, as given in (2). It is seen that the Bayes estimate of each mean parameter θ i is obtained by shrinking Y i toward the linear estimate \(\mu _{i} =\boldsymbol{ X}_{i}^{T}\boldsymbol{\beta }\), and that the amount of shrinkage is governed by A i , the variance: the larger the variance, the stronger is the shrinkage. This feature makes intuitive sense.

With this observation in mind, we consider the following shrinkage estimators under Model I:

$$\displaystyle{\hat{\theta }_{i}^{\boldsymbol{b},\boldsymbol{\mu }} = \left (1 - b_{ i}\right )Y _{i} + b_{i}\mu _{i},\ \ \ \ \text{with }\boldsymbol{\mu } \in \mathcal{L}_{\mathrm{row}}\left (\boldsymbol{X}\right ),}$$

where \(\boldsymbol{b}\) satisfies the monotonic constraint

$$\displaystyle{\mathrm{MON}\left (\boldsymbol{A}\right ): b_{i} \in \left [0,1\right ],\ b_{i} \leq b_{j}\text{ whenever }A_{i} \leq A_{j}.}$$

\(\mathrm{MON}\left (\boldsymbol{A}\right )\) asks the estimator to shrink more for an observation with a larger variance. Since other than this intuitive requirement, we do not post any parametric restriction on b i , this class of estimators is semiparametric in nature.

Following the optimality result for the parametric case, we want to investigate, for such a general estimator \(\boldsymbol{\hat{\theta }}^{\boldsymbol{b},\boldsymbol{\mu }}\) with \(\boldsymbol{b} \in \mathrm{ MON}\left (\boldsymbol{A}\right )\) and \(\boldsymbol{\mu }\in \mathcal{L}_{\mathrm{row}}\left (\boldsymbol{X}\right )\), whether there exists an optimal choice of \(\boldsymbol{b}\) and \(\boldsymbol{\mu }\). In fact, we will see shortly that such an optimal choice exists, and this asymptotically optimal choice is again characterized by an unbiased risk estimate (URE). For a general estimator \(\boldsymbol{\hat{\theta }}^{\boldsymbol{b},\boldsymbol{\mu }}\) with fixed \(\boldsymbol{b}\) and \(\boldsymbol{\mu }\in \mathcal{L}_{\mathrm{row}}\left (\boldsymbol{X}\right )\), an unbiased estimate of its risk \(R_{p}(\boldsymbol{\theta },\boldsymbol{\hat{\theta }}^{\boldsymbol{b},\boldsymbol{\mu }})\) is

$$\displaystyle{\mathrm{URE}^{SP}\left (\boldsymbol{b},\boldsymbol{\mu }\right ) = \dfrac{1} {p}\left \Vert \mathrm{diag}\left (\boldsymbol{b}\right )\left (\boldsymbol{Y }-\boldsymbol{\mu }\right )\right \Vert ^{2} + \dfrac{1} {p}\mathrm{tr}\left (\boldsymbol{A} - 2\mathrm{diag}\left (\boldsymbol{b}\right )\boldsymbol{A}\right ),}$$

which can be easily seen by taking \(\boldsymbol{B = A}(\mathrm{diag}\left (\boldsymbol{b}\right )^{-1} -\boldsymbol{ I}_{p})\) in (8). Note that we use the superscript “SP” (semiparametric) to denote it. Minimizing over \(\boldsymbol{b}\) and \(\boldsymbol{\mu }\) leads to the semiparametric URE estimator \(\boldsymbol{\hat{\theta }}_{SP}^{\mathrm{URE}}\), defined by

$$\displaystyle{ \boldsymbol{\hat{\theta }}_{SP}^{\mathrm{URE}} = (\boldsymbol{I}_{ p} -\mathrm{ diag}(\boldsymbol{\hat{b}}_{SP}^{\mathrm{URE}}))\boldsymbol{Y } +\mathrm{ diag}(\boldsymbol{\hat{b}}_{ SP}^{\mathrm{URE}})\boldsymbol{\hat{\mu }}_{ SP}^{\mathrm{URE}}\mathbf{,} }$$
(15)

where

$$\displaystyle{\left (\boldsymbol{\hat{b}}_{SP}^{\mathrm{URE}},\boldsymbol{\hat{\mu }}_{ SP}^{\mathrm{URE}}\right ) =\mathop{ \mathrm{argmin}}\nolimits \limits _{\boldsymbol{ b}\in \mathrm{MON}\left (\boldsymbol{A}\right ),\ \boldsymbol{\mu }\in \mathcal{L}_{\mathrm{row}}\left (\boldsymbol{X}\right )}\mathrm{URE}^{SP}\left (\boldsymbol{b},\boldsymbol{\mu }\right ).}$$

Theorem 4

Assume conditions (A)–(E). Then under Model I we have

$$\displaystyle{\sup \limits _{\boldsymbol{b}\in \mathrm{MON}\left (\boldsymbol{A}\right ),\;\boldsymbol{\mu }\in \mathcal{L}}\left \vert \mathrm{URE}^{SP}\left (\boldsymbol{b},\boldsymbol{\mu }\right ) - l_{ p}\left (\boldsymbol{\theta },\boldsymbol{\hat{\theta }}^{\boldsymbol{b},\boldsymbol{\mu }}\right )\right \vert \rightarrow 0\text{ in }L^{1}\text{ as }p \rightarrow \infty.}$$

As a corollary, for any estimator \(\boldsymbol{\hat{\theta }}^{\boldsymbol{\hat{b}_{p}},\boldsymbol{\hat{\mu }}_{p}} = (\boldsymbol{I}_{p} -\mathrm{ diag}(\boldsymbol{\hat{b}}_{p}))\boldsymbol{Y } +\mathrm{ diag}(\boldsymbol{\hat{b}}_{p})\boldsymbol{\hat{\mu }}_{p}\) with \(\boldsymbol{\hat{b}}_{p} \in \mathrm{ MON}\left (\boldsymbol{A}\right )\) and \(\boldsymbol{\hat{\mu }}_{p} \in \mathcal{L}\) , we always have

$$\displaystyle\begin{array}{rcl} \lim \limits _{p\rightarrow \infty }\mathbb{P}\left (l_{p}\left (\boldsymbol{\theta },\boldsymbol{\hat{\theta }}_{SP}^{\mathrm{URE}}\right ) \geq l_{ p}\left (\boldsymbol{\theta },\boldsymbol{\hat{\theta }}^{\boldsymbol{\hat{b}}_{p},\boldsymbol{\hat{\mu }}_{p} }\right )+\epsilon \right )& =& 0\ \ \ \ \forall \epsilon > 0, {}\\ \limsup \limits _{p\rightarrow \infty }\left (R_{p}\left (\boldsymbol{\theta },\boldsymbol{\hat{\theta }}_{SP}^{\mathrm{URE}}\right ) - R_{ p}\left (\boldsymbol{\theta },\boldsymbol{\hat{\theta }}^{\boldsymbol{\hat{b}}_{p},\boldsymbol{\hat{\mu }}_{p} }\right )\right )& \leq & 0. {}\\ \end{array}$$

The proof is the same as the proofs of Theorem 1 and Corollary 1 for the case of Model I except that we replace each term of A i ∕(λ + A i ) by b i .

5.2 Semiparametric URE Estimator Under Model II

We saw in Sect. 2 that, under Model II, shrinkage is achieved by shrinking the regression coefficient from the weighted least squares estimate \(\boldsymbol{\hat{\beta }}^{\mathrm{WLS}}\) toward the prior coefficient \(\boldsymbol{\beta }_{0}\). This suggests us to formulate the semiparametric estimators through the regression coefficient. The Bayes estimate of the regression coefficient is

$$\displaystyle{\boldsymbol{\hat{\beta }}^{\lambda,\boldsymbol{\beta }_{0} } =\lambda \boldsymbol{ W}(\lambda \boldsymbol{W} +\boldsymbol{ V })^{-1}\boldsymbol{\hat{\beta }}^{\mathrm{WLS}} +\boldsymbol{ V }\left (\lambda \boldsymbol{W} +\boldsymbol{ V }\right )^{-1}\boldsymbol{\beta }_{ 0},\ \ \ \ \text{with }\boldsymbol{V } = (\boldsymbol{XA}^{-1}\boldsymbol{X}^{T})^{-1}}$$

as shown in (3). Applying the spectral decomposition on \(\boldsymbol{W}^{-1/2}\boldsymbol{V W}^{-1/2}\) gives \(\boldsymbol{W}^{-1/2}\boldsymbol{V W}^{-1/2} =\boldsymbol{ U\varLambda }\boldsymbol{U}^{T}\), where \(\boldsymbol{\varLambda }=\mathrm{ diag}\left (d_{1},\ldots,d_{k}\right )\) with d 1 ≤ ⋯ ≤ d k . Using this decomposition, we can rewrite the regression coefficient as

$$\displaystyle{\boldsymbol{\hat{\beta }}^{\lambda,\boldsymbol{\beta }_{0} } =\lambda \boldsymbol{ W}^{1/2}\boldsymbol{U}\left (\lambda \boldsymbol{I}_{ k}+\boldsymbol{\varLambda }\right )^{-1}\boldsymbol{U}^{T}\boldsymbol{W}^{-1/2}\boldsymbol{\hat{\beta }}^{\mathrm{WLS}} +\boldsymbol{ W}^{1/2}\boldsymbol{U\varLambda }\left (\lambda \boldsymbol{I}_{ k}+\boldsymbol{\varLambda }\right )^{-1}\boldsymbol{U}^{T}\boldsymbol{W}^{-1/2}\boldsymbol{\beta }_{ 0}.}$$

If we denote \(\boldsymbol{Z} =\boldsymbol{ U}^{T}\boldsymbol{W}^{1/2}\boldsymbol{X}\) as the transformed covariate matrix, the estimate \(\boldsymbol{\hat{\theta }}^{\lambda,\boldsymbol{\beta }_{0}} =\boldsymbol{ X}^{T}\boldsymbol{\hat{\beta }}^{\lambda,\boldsymbol{\beta }_{0}}\) of \(\boldsymbol{\theta }\) can be rewritten as

$$\displaystyle{\boldsymbol{\hat{\theta }}^{\lambda,\boldsymbol{\beta }_{0} } =\boldsymbol{ Z}^{T}\left (\lambda \left (\lambda \boldsymbol{I}_{ k}+\boldsymbol{\varLambda }\right )^{-1}\boldsymbol{U}^{T}\boldsymbol{W}^{-1/2}\boldsymbol{\hat{\beta }}^{\mathrm{WLS}} +\boldsymbol{\varLambda } \left (\lambda \boldsymbol{I}_{ k}+\boldsymbol{\varLambda }\right )^{-1}\boldsymbol{U}^{T}\boldsymbol{W}^{-1/2}\boldsymbol{\beta }_{ 0}\right ).}$$

Now we see that \(\lambda \left (\lambda \boldsymbol{I}_{k}+\boldsymbol{\varLambda }\right )^{-1} =\mathrm{ diag}(\lambda /\left (\lambda +d_{i}\right ))\) plays the role as the shrinkage factor. The larger the value of d i , the smaller \(\lambda /\left (\lambda +d_{i}\right )\), i.e., the stronger the shrinkage toward \(\boldsymbol{\beta }_{0}\). Thus, d i can be viewed as the effective “variance” component for the i-th regression coefficient (under the transformation). This observation motivates us to consider semiparametric shrinkage estimators of the following form

$$\displaystyle\begin{array}{rcl} \boldsymbol{\hat{\theta }}^{\boldsymbol{b},\boldsymbol{\beta }_{0} }& =& \boldsymbol{Z}^{T}\left (\left (\boldsymbol{I}_{ k} -\mathrm{ diag}\left (\boldsymbol{b}\right )\right )\boldsymbol{U}^{T}\boldsymbol{W}^{-1/2}\boldsymbol{\hat{\beta }}^{\mathrm{WLS}} +\mathrm{ diag}\left (\boldsymbol{b}\right )\boldsymbol{U}^{T}\boldsymbol{W}^{-1/2}\boldsymbol{\beta }_{ 0}\right ) \\ & =& \boldsymbol{Z}^{T}\left (\left (\boldsymbol{I}_{ k} -\mathrm{ diag}\left (\boldsymbol{b}\right )\right )\boldsymbol{\varLambda ZA}^{-1}\boldsymbol{Y } +\mathrm{ diag}\left (\boldsymbol{b}\right )\boldsymbol{U}^{T}\boldsymbol{W}^{-1/2}\boldsymbol{\beta }_{ 0}\right ), {}\end{array}$$
(16)

where \(\boldsymbol{b}\) satisfies the following monotonic constraint

$$\displaystyle{\mathrm{MON}\left (\boldsymbol{D}\right ): b_{i} \in \left [0,1\right ],\ b_{i} \leq b_{j}\text{ whenever }d_{i} \leq d_{j}.}$$

This constraint captures the intuition that, the larger the effective variance, the stronger is the shrinkage.

For fixed \(\boldsymbol{b}\) and \(\boldsymbol{\beta }_{0}\), an unbiased estimate of the risk \(R_{p}(\boldsymbol{\theta },\boldsymbol{\hat{\theta }}^{\boldsymbol{b},\boldsymbol{\beta }_{0}})\) is

$$\displaystyle\begin{array}{rcl} \mathrm{URE}^{SP}\left (\boldsymbol{b},\boldsymbol{\beta }_{ 0}\right )& =& \dfrac{1} {p}\left \Vert \boldsymbol{Z}^{T}\left (\boldsymbol{I}_{ k} -\mathrm{ diag}\left (\boldsymbol{b}\right )\right )\boldsymbol{\varLambda ZA}^{-1}\boldsymbol{Y } +\boldsymbol{ Z}^{T}\mathrm{diag}\left (\boldsymbol{b}\right )\boldsymbol{U}^{T}\boldsymbol{W}^{-1/2}\boldsymbol{\beta }_{ 0} -\boldsymbol{ Y }\right \Vert ^{2} {}\\ & +& \dfrac{1} {p}\mathrm{tr}\left (2\boldsymbol{Z}^{T}\left (\boldsymbol{I}_{ k} -\mathrm{ diag}\left (\boldsymbol{b}\right )\right )\boldsymbol{\varLambda Z} -\boldsymbol{ A}\right ), {}\\ \end{array}$$

which can be shown using the bias-variance decomposition of the mean squared error. Minimizing it gives the URE estimate of \(\left (\boldsymbol{b},\boldsymbol{\beta }_{0}\right )\):

$$\displaystyle{\left (\boldsymbol{\hat{b}}_{SP}^{\mathrm{URE}},\left (\boldsymbol{\hat{\beta }}_{ 0}\right )_{SP}^{\mathrm{URE}}\right ) =\mathop{ \mathrm{argmin}}\nolimits \limits _{\boldsymbol{ b}\in \mathrm{MON}\left (\boldsymbol{D}\right ),\ \boldsymbol{\beta }_{0}\in \mathbb{R}^{k}}\mathrm{URE}^{SP}\left (\boldsymbol{b},\boldsymbol{\beta }_{ 0}\right ),}$$

which upon plugging into (16) yields the semiparametric URE estimator \(\boldsymbol{\hat{\theta }}_{SP}^{\mathrm{URE}}\) under Model II.

Theorem 5

Assume conditions (A), (D)–(G). Then under Model II we have

$$\displaystyle{\sup \limits _{\boldsymbol{b}\in \mathrm{MON}\left (\boldsymbol{D}\right ),\;\boldsymbol{X}^{T}\boldsymbol{\beta }_{0}\in \mathcal{L}}\left \vert \mathrm{URE}^{SP}\left (\boldsymbol{b},\boldsymbol{\beta }_{ 0}\right ) - l_{p}\left (\boldsymbol{\theta },\boldsymbol{\hat{\theta }}^{\boldsymbol{b},\boldsymbol{\beta }_{0} }\right )\right \vert \rightarrow 0\text{ in }L^{1}\text{ as }p \rightarrow \infty.}$$

As a corollary, for any estimator \(\boldsymbol{\hat{\theta }}^{\boldsymbol{\hat{b}_{p}},\boldsymbol{\hat{\beta }}_{0,p}}\) obtained from (16) with \(\boldsymbol{\hat{b}}_{p} \in \mathrm{ MON}\left (\boldsymbol{D}\right )\) and \(\boldsymbol{X}^{T}\boldsymbol{\hat{\beta }}_{0} \in \mathcal{L}\) , we always have

$$\displaystyle\begin{array}{rcl} \lim \limits _{p\rightarrow \infty }\mathbb{P}\left (l_{p}\left (\boldsymbol{\theta },\boldsymbol{\hat{\theta }}_{SP}^{\mathrm{URE}}\right ) \geq l_{ p}\left (\boldsymbol{\theta },\boldsymbol{\hat{\theta }}^{\boldsymbol{\hat{b}}_{p},\boldsymbol{\hat{\beta }}_{0,p} }\right )+\epsilon \right )& =& 0\ \ \ \ \forall \epsilon > 0, {}\\ \limsup \limits _{p\rightarrow \infty }\left (R_{p}\left (\boldsymbol{\theta },\boldsymbol{\hat{\theta }}_{SP}^{\mathrm{URE}}\right ) - R_{ p}\left (\boldsymbol{\theta },\boldsymbol{\hat{\theta }}^{\boldsymbol{\hat{b}}_{p},\boldsymbol{\hat{\beta }}_{0,p} }\right )\right )& \leq & 0. {}\\ \end{array}$$

The proof of the theorem is essentially identical to those of Theorem 1 and Corollary 1 for the case of Model II except that we replace each d i ∕(λ + d i ) by b i .

6 Simulation Study

In this section, we conduct simulations to study the performance of the URE estimators. For the sake of space, we will focus on Model I. The four URE estimators are the parametric \(\boldsymbol{\hat{\theta }}^{\mathrm{URE}}\) of Eq. (9), the parametric \(\boldsymbol{\hat{\theta }}_{\boldsymbol{M}}^{\mathrm{URE}}\) of Eq. (12) that shrinks toward the OLS estimate \(\boldsymbol{\hat{\mu }}^{\mathrm{OLS}}\) (i.e., the matrix \(\boldsymbol{M} =\boldsymbol{ I}_{p}\)), the semiparametric \(\boldsymbol{\hat{\theta }}_{SP}^{\mathrm{URE}}\) of Eq. (15), and the semiparametric \(\boldsymbol{\hat{\theta }}_{SP}^{\mathrm{URE},\,\mathrm{OLS}}\) that shrinks toward \(\boldsymbol{\hat{\mu }}^{\mathrm{OLS}}\), which is formed similarly to \(\boldsymbol{\hat{\theta }}_{\boldsymbol{M}}^{\mathrm{URE}}\) by replacing A i ∕(λ + A i ) with a sequence \(\boldsymbol{b} \in \mathrm{ MON}\left (\boldsymbol{A}\right )\). The competitors here are the two empirical Bayes estimators \(\boldsymbol{\hat{\theta }}^{\mathrm{EBMLE}}\) and \(\boldsymbol{\hat{\theta }}^{\mathrm{EBMOM}}\), and the positive part James-Stein estimator \(\boldsymbol{\hat{\theta }}^{\mathrm{JS}+}\) as described in [2, 17]:

$$\displaystyle{\hat{\theta }_{i}^{\mathrm{JS+}} =\hat{\mu }_{ i}^{\mathrm{WLS}} + \left (1 - \frac{p - k - 2} {\sum _{i=1}^{p}\left (Y _{i} -\hat{\mu }_{i}^{\mathrm{WLS}}\right )^{2}/A_{i}}\right )^{+}\left (Y _{ i} -\hat{\mu }_{i}^{\mathrm{WLS}}\right ).}$$

As a reference, we also compare these shrinkage estimators with \(\boldsymbol{\tilde{\theta }}^{\mathrm{OR}}\), the parametric oracle risk (OR) estimator, defined as plugging \(\tilde{\lambda }^{\mathrm{OR}}\boldsymbol{I}_{p}\) and \(\boldsymbol{\tilde{\mu }}^{\mathrm{OR}}\) into Eq. (6), where

$$\displaystyle{\left (\tilde{\lambda }^{\mathrm{OR}},\boldsymbol{\tilde{\mu }}^{\mathrm{OR}}\right ) =\mathop{ \mathrm{argmin}}\nolimits \limits _{ 0\leq \lambda \leq \infty,\;\boldsymbol{\mu }\in \mathcal{L}_{\mathrm{row}}\left (\boldsymbol{X}\right )}R_{p}\left (\boldsymbol{\theta },\boldsymbol{\hat{\theta }}^{\lambda,\boldsymbol{\mu }}\right )}$$

and the expression of \(R_{p}(\boldsymbol{\theta },\boldsymbol{\hat{\theta }}^{\lambda,\boldsymbol{\mu }})\) is given in (7) with \(\boldsymbol{B} =\lambda \boldsymbol{ I}_{p}\). The oracle risk estimator \(\boldsymbol{\tilde{\theta }}^{\mathrm{OR}}\) cannot be used without the knowledge of \(\boldsymbol{\theta }\), but it does provide a sensible lower bound of the risk achievable by any shrinkage estimator with the given parametric form.

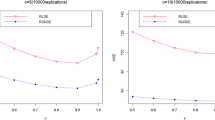
For each simulation, we draw \(\left (A_{i},\theta _{i}\right )\) (i = 1, 2, …, p) independently from a distribution \(\pi \left (A_{i},\theta _{i}\vert \boldsymbol{X}_{i},\boldsymbol{\beta }\right )\) and then draw Y i given \(\left (A_{i},\theta _{i}\right )\). The shrinkage estimators are then applied to the generated data. This process is repeated 5000 times. The sample size p is chosen to vary from 20 to 500 with an increment of length 20. In the simulation, we fix a true but unknown \(\boldsymbol{\beta }= \left (-1.5,4,-3\right )^{T}\) and a known covariates \(\boldsymbol{X}\), whose each element is randomly generated from \(\mathrm{Unif}\left (-10,10\right )\). The risk performance of the different shrinkage estimators is given in Fig. 2.

Fig. 2
figure 2

Comparison of the risks of different shrinkage estimators for the two simulation examples

Full size image

Example 1

The setting in this example is chosen in such a way that it reflects grouping in the data:

$$\displaystyle\begin{array}{rcl} A_{i}& \sim & 0.5 \cdot 1_{\left \{A_{i}=0.1\right \}} + 0.5 \cdot 1_{\left \{A_{i}=0.5\right \}};\ {}\\ \theta _{i}\vert A_{i}& \sim & N\left (2 \cdot 1_{\left \{A_{i}=0.1\right \}} +\boldsymbol{ X}_{i}^{T}\boldsymbol{\beta },0.5^{2}\right );\ Y _{ i} \sim N\left (\theta _{i},A_{i}\right ). {}\\ \end{array}$$

Here the normality for the sampling distribution of Y i ’s is asserted. We can see that the four URE estimators perform much better than the two empirical Bayes ones and the James-Stein estimator. Also notice that both of the two (parametric and semiparametric) URE estimators that shrink towards \(\boldsymbol{\hat{\mu }}^{\mathrm{OLS}}\) is almost as good as the other two with general data-driven shrinkage location—largely due to the existence of covariate information. We note that this is quite different from the case of [29], where without the covariate information the estimator that shrinks toward the grand mean of the data performs significantly worse than the URE estimator with general data-driven shrinkage location.

Example 2

In this example, we allow Y i to depart from the normal distribution to illustrate that the performance of those URE estimators does not rely on the normality assumption:

$$\displaystyle\begin{array}{rcl} A_{i}& \sim & \mathrm{Unif}\left (0.1,1\right );\ \theta _{i} = A_{i} +\boldsymbol{ X}_{i}^{T}\boldsymbol{\beta }; {}\\ Y _{i}& \sim & \mathrm{Unif}(\theta _{i} -\sqrt{3}A_{i},\theta _{i} + \sqrt{3}A_{i}). {}\\ \end{array}$$

As expected, the four URE estimators perform better or at least as good as the empirical Bayes estimators. The EBMLE estimator performs the worst due to its sensitivity on the normality assumption. We notice that the EBMOM estimator in this example has comparable performance with the two parametric URE estimators, which makes sense as moment estimates are more robust to the sampling distribution. An interesting feature that we find in this example is that the positive part James-Stein estimator can beat the parametric oracle risk estimator and perform better than all the other shrinkage estimators for small or moderate p, even though the semiparametric URE estimators will eventually surpass the James-Stein estimator, as dictated by the asymptotic theory for large p. This feature of the James-Stein estimate is again quite different from the non-regression setting discussed in [29], where the James-Stein estimate performs the worst throughout all of their examples. In both of our examples only the semiparametric URE estimators are robust to the different levels of heteroscedasticity.

We can conclude from these two simulation examples that the semiparametric URE estimators give competitive performance and are robust to the misspecification of the sampling distribution and the different levels of the heteroscedasticity. They thus could be useful tools in analyzing large-scale data for applied researchers.

7 Empirical Analysis

In this section, we study the baseball data set of [2]. This data set consists of the batting records for all the Major League Baseball players in the 2005 season. As in [2] and [29], we build a given shrinkage estimator based on the data in the first half season and use it to predict the second half season, which can then be checked against the true record of the second half season. For each player, let the number of at-bats be N and the successful number of batting be H, then we have H ij  ∼ Binomial(N ij , p j ), where i = 1, 2 is the season indicator and j = 1, ⋯ , p is the player indicator. We use the following variance-stabilizing transformation [2] before applying the shrinkage estimators

$$\displaystyle{Y _{ij} =\arcsin \sqrt{\frac{H_{ij } + 1/4} {N_{ij} + 1/2}},}$$

which gives \(Y _{ij}\dot{ \sim } N(\theta _{j},(4N_{ij})^{-1})\), \(\theta _{j} =\arcsin \sqrt{p_{j}}\). We use

$$\displaystyle{\mathrm{TSE}(\boldsymbol{\hat{\theta }}) =\sum _{j}(Y _{2j} -\hat{\theta }_{j})^{2} -\sum \limits _{ j} \frac{1} {4N_{2j}}.}$$

as the error measurement for the prediction [2].

7.1 Shrinkage Estimation with Covariates

As indicated in [29], there exists a significant positive correlation between the player’s batting ability and his total number of at-bats. Intuitively, a better player will be called for batting more frequently; thus, the total number of at-bats will serve as the main covariate in our analysis. The other covariate in the data set is the categorical variable of a player being a pitcher or not.

Table 1 summarizes the result, where the shrinkage estimators are applied three times—to all the players, the pitchers only, and the non-pitchers only. We use all the covariate information (number of at-bats in the first half season and being a pitcher or not) in the first analysis, whereas in the second and the third analyses we only use the number of at-bats as the covariate. The values reported are ratios of the error of a given estimator to that of the benchmark naive estimator, which simply uses the first half season Y 1j to predict the second half Y 2j . Note that in Table 1, if no covariate is involved (i.e., when \(\boldsymbol{X} = \left [1\vert \cdots \vert 1\right ]\)), the OLS reduces to the grand mean of the training data as in [29].

Table 1 Prediction errors of batting averages using different shrinkage estimators
Full size table

7.2 Discussion of the Numerical Result

There are several interesting observations from Table 1.

  1. 1.

    A quick glimpse shows that including the covariate information improves the performance of essentially all shrinkage estimators. This suggests that in practice incorporating good covariates would significantly improve the estimation and prediction.

  2. 2.

    In general, shrinking towards WLS provides much better performance than shrinking toward OLS or a general data-driven location. This indicates the importance of a good choice of the shrinkage location in a practical problem. An improperly chosen shrinkage location might even negatively impact the performance. The reason that shrinking towards a general data-driven location is not as good as shrinking toward WLS is probably due to that the sample size is not large enough for the asymptotics to take effect.

  3. 3.

    Table 1 also shows the advantage of semiparametric URE estimates. For each fixed shrinkage location type (toward OLS, WLS, or general), the semiparametric URE estimator performs almost always better than their parametric counterparts. The only one exception is in the non-pitchers only case with the general data-driven location, but even there the performance difference is ignorable.

  4. 4.

    The best performance in all three cases (all the players, the pitchers only, and the non-pitchers only) comes from the semiparametric URE estimator that shrinks toward WLS.

  5. 5.

    The James-Stein estimator with covariates performs quite well except in the pitchers only case, which is in sharp contrast with the performance of the James-Stein estimator without covariates. This again highlights the importance of covariate information. In the pitchers only case, the James-Stein performs the worst no matter one includes the covariates or not. This can be attributed to the fact that the covariate information (the total number of at-bats) is very weak for the pitchers only case; in the case of weak covariate information, how to properly estimate the shrinkage factors becomes the dominating issue, and the fact that the James-Stein estimator has only one uniform shrinkage factor makes it not competitive.

7.3 Shrinkage Factors

Figure 3 shows the shrinkage factors of all the shrinkage estimators with or without the covariates for the all-players case of Table 1. We see that the shrinkage factors are all reduced after including the covariates. This makes intuitive sense because the shrinkage location now contains the covariate information, and each shrinkage estimator uses this information by shrinking more toward it, resulting in smaller shrinkage factors.

Fig. 3
figure 3

Plot of the shrinkage factors \(\hat{\lambda }/\left (\hat{\lambda }+A_{i}\right )\) or \(1 -\hat{ b}_{i}\) of all the shrinkage estimators for the case of all players

Full size image

8 Conclusion and Discussion

Inspired by the idea of unbiased risk estimate (URE) proposed in [29], we extend the URE framework to multivariate heteroscedastic linear models, which are more realistic in practical applications, especially for regression data that exhibits heteroscedasticity. Several parallel URE shrinkage estimators in the regression case are proposed, and these URE shrinkage estimators are all asymptotically optimal in risk compared to other shrinkage estimators, including the classical empirical Bayes ones. We also propose semiparametric estimators and conduct simulation to assess their performance under both normal and non-normal data. For data sets that exhibit a good linear relationship between the covariates and the response, a semiparametric URE estimator is expected to provide good estimation result, as we saw in the baseball data. It is also worth emphasizing that the risk optimality for the parametric and semiparametric URE estimators does not depend on the normality assumption of the sampling distribution of Y i . Possible future work includes extending this URE minimization approach to simultaneous estimation in generalized linear models (GLMs) with canonical or more general link functions.

We conclude this article by extending the main results to the case of weighted mean squared error loss.

Weighted Mean Squared Error Loss One might want to consider the more general weighted mean squared error as the loss function:

$$\displaystyle{l_{p}\left (\boldsymbol{\theta },\boldsymbol{\hat{\theta }};\boldsymbol{\psi }\right ) = \dfrac{1} {p}\sum _{i=1}^{p}\psi _{ i}\left (\theta _{i} -\hat{\theta }_{i}\right )^{2},}$$

where ψ i  > 0 are known weights such that ∑ i = 1 p ψ i  = p. The framework proposed in this article is straightforward to generalize to this case.

For Model II, we only need to study the equivalent problem by the following transformation

$$\displaystyle{ Y _{i} \rightarrow \sqrt{\psi _{i}}Y _{i},\ \theta _{i} \rightarrow \sqrt{\psi _{i}}\theta _{i},\ \boldsymbol{X}_{i} \rightarrow \sqrt{\psi _{i}}\boldsymbol{X}_{i},\ A_{i} \rightarrow \psi _{i}A_{i}, }$$
(17)

and restate the corresponding regularity conditions in Theorem 1 by the transformed data and parameters. We then reduce the weighted mean square error problem back to the same setting we study in this article under the classical loss function (4).

Model I is more sophisticated than Model II to generalize. In addition to the transformation in Eq. (17), we also need λ → ψ i λ in every term related to the individual unit i. Thus,

$$\displaystyle{\sqrt{\psi _{i}}\theta _{i}\vert \boldsymbol{X},\boldsymbol{\beta },\lambda \mathop{\sim }\limits^{\text{indep.}}N\left (\sqrt{\psi _{i}}\boldsymbol{X}_{i}^{T}\boldsymbol{\beta },\lambda \psi _{ i}\right ),}$$

so these transformed parameters \(\sqrt{\psi _{i}}\theta _{i}\) are also heteroscedastic in the sense that they have different weights, while the setting we study before assumes all the weights on the θ i are one. However, if we carefully examine the proof of Theorem 1 for the case of Model I, we can see that actually we do not much require the equal weights on the θ i ’s. What is important in the proof is that the shrinkage factor for unit i is always of the form \(A_{i}/\left (A_{i}+\lambda \right )\), which is invariant under the transformation A i  → ψ i A i and λ → ψ i λ. Thus, after reformulating the regularity conditions in Theorem 1 by the transformed data and parameters, we can still follow the same proof to conclude the risk optimality of URE estimators (parametric or semiparametric) even under the consideration of weighted mean squared error loss.

For completeness, here we state the most general result under the semiparametric setting for Model I. Let

$$\displaystyle\begin{array}{rcl} \boldsymbol{\hat{\theta }}_{SP,\boldsymbol{\psi }}^{\mathrm{URE}}& =& \left (\boldsymbol{I}_{ p} -\mathrm{ diag}\left (\boldsymbol{\hat{b}}_{\boldsymbol{\psi }}^{\mathrm{URE}}\right )\right )\boldsymbol{Y } +\mathrm{ diag}\left (\boldsymbol{\hat{b}}_{\boldsymbol{\psi }}^{\mathrm{URE}}\right )\boldsymbol{\hat{\mu }}_{\boldsymbol{\psi }}^{\mathrm{URE}}, {}\\ \mathrm{URE}\left (\boldsymbol{b},\boldsymbol{\mu };\boldsymbol{\psi }\right )& =& \dfrac{1} {p}\sum _{i=1}^{p}\psi _{ i}\left (b_{i}^{2}\left (Y _{ i} -\mu _{i}\right )^{2} + \left (1 - 2b_{ i}\right )A_{i}\right ), {}\\ \left (\boldsymbol{\hat{b}}_{\boldsymbol{\psi }}^{\mathrm{URE}},\boldsymbol{\hat{\mu }}_{\boldsymbol{\psi }}^{\mathrm{URE}}\right )& =& \mathop{\mathrm{argmin}}\nolimits \limits _{\boldsymbol{ b}\in \mathrm{MON}\left (\boldsymbol{A}\right ),\;\boldsymbol{\mu }\in \mathcal{L}_{\mathrm{row}}\left (\boldsymbol{X}\right )}\mathrm{URE}\left (\boldsymbol{b},\boldsymbol{\mu };\boldsymbol{\psi }\right ). {}\\ \end{array}$$

Theorem 6

Assume the following five conditions \(\left (\psi \text{-}\mathrm{A}\right )\) \(\sum _{i=1}^{p}\psi _{i}^{2}A_{i}^{2} = O\left (p\right )\) , \(\left (\psi \text{-}\mathrm{B}\right )\ \sum _{i=1}^{p}\psi _{i}^{2}A_{i}\theta _{i}^{2} = O\left (p\right )\) , \(\left (\psi \text{-}\mathrm{C}\right )\) \(\sum _{i=1}^{p}\psi _{i}\theta _{i}^{2} = O\left (p\right )\) , \(\left (\psi \text{-}\mathrm{D}\right )\ p^{-1}\sum _{i=1}^{p}\psi _{i}^{2}A_{i}\boldsymbol{X}_{i}\boldsymbol{X}_{i}^{T}\) converges, and \(\left (\psi \text{-}\mathrm{E}\right )\ p^{-1}\sum _{i=1}^{p}\psi _{i}\boldsymbol{X}_{i}\boldsymbol{X}_{i}^{T} \rightarrow \boldsymbol{\varOmega }_{\boldsymbol{\psi }} > 0\) . Then we have

$$\displaystyle{\sup \limits _{\boldsymbol{b}\in \mathrm{MON}\left (\boldsymbol{A}\right ),\;\boldsymbol{\mu }\in \mathcal{L}_{\boldsymbol{\psi }}}\left \vert \mathrm{URE}\left (\boldsymbol{b},\boldsymbol{\mu };\boldsymbol{\psi }\right ) - l_{p}\left (\boldsymbol{\theta },\boldsymbol{\hat{\theta }}^{\boldsymbol{b},\boldsymbol{\mu }};\boldsymbol{\psi }\right )\right \vert \mathop{ \rightarrow }\limits_{ p \rightarrow \infty }0\text{ in }L^{1}\text{,}}$$

where \(\boldsymbol{\mu }\in \mathcal{L}_{\boldsymbol{\psi }}\) if and only if \(\boldsymbol{\mu }\in \mathcal{L}_{\mathrm{row}}\left (\boldsymbol{X}\right )\) and

$$\displaystyle{\sum _{i=1}^{p}\psi _{ i}\mu _{i}^{2} \leq Mp^{\kappa }\sum _{ i=1}^{p}\psi _{ i}Y _{i}^{2}}$$

for a large and fixed constant M and a fixed exponent \(\kappa \in \left [0,1/2\right )\) . As a corollary, for any estimator \(\boldsymbol{\hat{\theta }}^{\boldsymbol{\hat{b}}_{p},\boldsymbol{\hat{\mu }}_{p}} = (\boldsymbol{I}_{p} -\mathrm{ diag}(\boldsymbol{\hat{b}}_{p}))\boldsymbol{Y } +\mathrm{ diag}(\boldsymbol{\hat{b}}_{p})\boldsymbol{\hat{\mu }}_{p}\) with \(\boldsymbol{\hat{b}}_{p} \in \mathrm{ MON}\left (\boldsymbol{A}\right )\) and \(\boldsymbol{\hat{\mu }}_{p} \in \mathcal{L}_{\boldsymbol{\psi }}\) , we have

$$\displaystyle\begin{array}{rcl} \lim \limits _{p\rightarrow \infty }\mathbb{P}\left (l_{p}\left (\boldsymbol{\theta },\boldsymbol{\hat{\theta }}_{SP,\boldsymbol{\psi }}^{\mathrm{URE}}\right ) \geq l_{ p}\left (\boldsymbol{\theta },\boldsymbol{\hat{\theta }}^{\boldsymbol{\hat{b}}_{p},\boldsymbol{\hat{\mu }}_{p} }\right )+\epsilon \right )& =& 0\ \ \ \ \forall \epsilon > 0, {}\\ \limsup \limits _{p\rightarrow \infty }\left (R_{p}\left (\boldsymbol{\theta },\boldsymbol{\hat{\theta }}_{SP,\boldsymbol{\psi }}^{\mathrm{URE}}\right ) - R_{ p}\left (\boldsymbol{\theta },\boldsymbol{\hat{\theta }}^{\boldsymbol{\hat{b}}_{p},\boldsymbol{\hat{\mu }}_{p} }\right )\right )& \leq & 0. {}\\ \end{array}$$