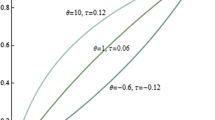1 Introduction

One of the most popular parametric families of copulas is the FGM family defined by

$$\begin{aligned} C_\alpha (u,v)=uv+\alpha \cdot u(1-u)v(1-v),\quad (u,v)\in {[0,1]}^{2},\quad \alpha \in [-1,1], \end{aligned}$$

and studied in Farlie (1960), Gumbel (1960) and Morgenstern (1956) (see also Eyraud (1938)). A survey of properties, generalizations and applications of the FGM copula is found in Balakrishnan and Lai (2009), Sect. 2.2 (see also Joe 2015, Sect. 4.29). A main drawback of this family is its limited range of correlation \([-1/3,1/3]\). Several FGM extensions have been proposed by Sarmanov (1966), Huang and Kotz (1984, 1999), Lai and Xie (2000), Bairamov et al. (2001), Bairamov and Kotz (2003), Rodrìguez-Lallena and Úbeda-Flores (2004), Kim and Sungur (2004), etc. Among them, only a few become close to a comprehensive family. Amblard and Girard (2002, 2011) extend the range of variation of Spearman’s rho to the interval \([-3/4,3/4]\) while Amblard and Girard (2009) extend it to \([-3/4,1]\). Replacing parameters by matrices, Amblard et al. (2013) reach values of Spearman’s rho arbitrarily close to 1 without a singular component. For fixed correlation as close to \(\pm \)1 as desired, it is also possible to construct absolutely continuous copulas with the prescribed correlation, as shown by Ferguson (1995). However, the obtained class of copulas is not parametric and does not include the FGM copula. In the present paper, we solve the comprehensive FGM extension problem in a simple new way.

Let \(M(u,v)=\min (u,v)\) and \(W(u,v)=\max (u+v-1,0)\) be the Hoeffding-Fréchet bounds. We claim that the truncated bivariate functions defined by

$$\begin{aligned} \begin{array}{l} C_\alpha (u,v)=\min \{M(u,v),uv+\alpha \cdot u(1-u)v(1-v)\},\quad \alpha \in [0,\infty ), \\ C_\alpha (u,v)=\max \{W(u,v),uv+\alpha \cdot u(1-u)v(1-v)\},\quad \alpha \in (-\infty ,0], \\ \end{array} \end{aligned}$$

yield a comprehensive family of copulas. Its Spearman rho and Kendall tau are odd functions of the parameter and takes values in \([-1,1]\). A short account of the content follows.

Section 2 is about anti-symmetric copulas. A family of copulas \(C_\alpha (u,v)\) is called anti-symmetric if its complement function for independence, defined by \(C_\alpha ^\bot (u,v)=C_\alpha (u,v)-uv\), is anti-symmetric in at least one of two ways. Flipped copulas generate anti-symmetric copulas with odd Spearman and Kendall tau dependence measures, as shown in Theorem 2.1 and Corollary 2.1. We show that the linear Spearman copula, studied by the author (see Hürlimann 2012 and references therein), is anti-symmetric. Several additional examples illustrate this construction. In particular, the copula by Cuadras and Augé (1981) and the Chogosov copula, studied by Peyre (2013), are extended herewith to comprehensive families. In Sect. 3, we show that the above truncated FGM functions define a comprehensive and anti-symmetric copula, called Hoeffding-Fréchet extended FGM (HF-FGM) copula. Moreover, we obtain the analytical representation of the copula, including its absolutely continuous and singular components. The Sects. 4 and 5 derive formulas for its Spearman rho and Kendall’s tau dependence functions.

2 Anti-symmetric copulas with odd Spearman rho and Kendall tau dependence functions

To fix ideas, we consider one-parametric families of copulas \(C_\alpha (u,v),\;(u,v)\in I^2\), \(I={[0,1]}\), indexed by a parameter \(\alpha \) with values in a symmetric range \([-c,-\alpha _0 ]\cup [\alpha _0 ,c]\), \(\alpha _0 \ge 0,\;{0}<c\le \infty \). By abuse of notation, if \(c=\infty \) then \(\alpha \in (-\infty ,-\alpha _0 ]\cup [\alpha _0 ,\infty )\). The convenient notation \(\bar{x}=1-x\) is used throughout. The independent copula is denoted by \(\Pi (u,v)=uv\). The Hoeffding-Fréchet upper bound is \(M(u,v)=\min (u,v)\) and the Hoeffding-Fréchet lower bound is \(W(u,v)=\max (u+v-1,0)\). Up to a sign change, the following notion is also used in Sungur et al. (2007), Definition 2.1.

Definition 2.1

Let C(u, v) be any copula. The complement function of the copula C for the independent copula, here called complement function for independence, denoted by \(C^\bot (u,v)\), is the signed distance between the copula and the independent copula defined by

$$\begin{aligned} C^\bot (u,v)=C(u,v)-uv. \end{aligned}$$
(2.1)

We are interested in copulas with odd Spearman rho and Kendall tau dependence functions.

Definition 2.2

The one-parametric family of copulas \(C_\alpha (u,v)\) is called an anti-symmetric family if the complement function for independence satisfies one of the following two properties:

$$\begin{aligned} (AS1) \quad C_{-\alpha }^\bot (u,v)= & {} -C_\alpha ^\bot (u,\bar{v}),\quad \forall \;\alpha \in [-c,-\alpha _0 ]\cup [\alpha _0 ,c]\\ (AS2) \quad C_{-\alpha }^\bot (u,v)= & {} -C_\alpha ^\bot (\bar{u},v),\quad \forall \;\alpha \in [-c,-\alpha _0 ]\cup [\alpha _0 ,c] \end{aligned}$$

The complement function for independence can be used to extend a family of copulas \(C_\alpha (u,v)\) with a given parameter range to an anti-symmetric family of copulas with wider parameter range.

Theorem 2.1

Let \(C_\alpha (u,v)\) be a copula with parameter range \(\alpha \in [\alpha _0 ,c],\;\alpha _0 \ge 0\). The extensions to the parameter range \([-c,-\alpha _0 ]\) defined by \(C_{-\alpha }^{(1)} (u,v)=u-C_\alpha (u,\bar{v})\) and \(C_{-\alpha }^{(2)} (u,v)=v-C_\alpha (\bar{u},v)\) generate anti-symmetric families of copulas.

Proof

Given a random vector (X, Y) with copula C(u, v) it is well-known that \(C^{(1)}(u,v)=u-C(u,\bar{v})\) and \(C^{(2)}(u,v)=v-C(\bar{u},v)\) are the copulas of \((X,-Y)\) and \((-X,Y)\). These copulas satisfy the properties (AS1) and (AS2) of anti-symmetric copulas. \(\square \)

The extended copulas \(C_{-\alpha }^{(i)} (u,v)\) are sometimes called flipped copulas (see De Baets et al. 2009; Klement et al. 2014; Nelsen 2006, Exercise 2.6, Theorem 2.4.4 and Exercise 6.9). \(\square \)

Corollary 2.1

Spearman’s rho and Kendall’s tau of anti-symmetric families of copulas are odd functions such that \(\rho _S^{(i)} (-\alpha )=-\rho _S (\alpha ) \quad \tau _K^{(i)} (-\alpha )=-\tau _K (\alpha ),\;i=1,2\), \(\alpha \in [\alpha _0 ,c],\;\alpha _0 \ge 0\).

Proof

By Theorem 5.1.9 in Nelsen (2006), Spearman’s rho and Kendall’s tau of a random vector (X, Y) are concordance measures and satisfy \(\rho _S (X,-Y)=\rho _S (-X,Y)=-\rho _S (X,Y)\) and \(\tau _K (X,-Y)=\tau _K (-X,Y)=-\tau _K (X,Y)\). The result follows from the proof of Theorem 2.1. \(\square \)

Example 2.1

linear Spearman copula

Let \(C_\theta (u,v)=(1-\theta )\cdot \Pi (u,v)+\theta \cdot M(u,v),\;\theta \in {[0,1]}\), be the Fréchet copula (e.g. Nelsen 2006, Exercise 2.4, Example 5.6, Joe 1997, family (B11), Joe 2015, Sect. 4.30). Its complement function for independence equals \(C_\theta ^\bot (u,v)=\theta \cdot I(u,v)\) with

$$\begin{aligned} I(u,v)=\left\{ \begin{array}{l} \bar{u}v,\quad u\ge v \\ u\bar{v},\quad u\le v \\ \end{array}\right. \end{aligned}$$
(2.2)

Theorem 2.1 implies that

$$\begin{aligned} \begin{aligned} C_{-\theta }^{(1)} (u,v)&=uv-C_\alpha ^\bot (u,\bar{v})=uv-\theta \cdot I(u,\bar{v})\\&=(1-\theta )\cdot \Pi (u,v)+\theta \cdot W(u,v),\;\theta \in {[0,1]},\\ C_{-\theta }^{(2)} (u,v)&=uv-C_\alpha ^\bot (\bar{u},v)=uv-\theta \cdot I(\bar{u},v)\\&=(1-\theta )\cdot \Pi (u,v)+\theta \cdot W(u,v),\;\theta \in {[0,1]}. \end{aligned} \end{aligned}$$

One has \(C_{-\theta }^{(1)} (u,v)=C_{-\theta }^{(2)} (u,v)\), but this must not be true in general (see Example 2.2). The extended one-parametric family \(C_\theta (u,v),\;\theta \in [-1{,1],}\) is an anti-symmetric comprehensive family of copulas, called linear Spearman copula. It has been studied extensively by the author (see Hürlimann 2012 and references therein).

Example 2.2

Comprehensive anti-symmetric extension of the Cuadras-Augé copula

Cuadras-Auge (1981) consider the weighted geometric mean of the copulas M(u, v) and \(\Pi (u,v)\) to define for \(\theta \in {[0,1]}\) the copula (e.g. Nelsen 2006, Exercise 2.5)

$$\begin{aligned} C_\theta (u,v)=M(u,v)^\theta \cdot \Pi (u,v)^{1-\theta }=\left\{ {{\begin{array}{*{20}c} \\ \\ \end{array} }} \right. \begin{array}{l} u^{1-\theta }v,\quad u\ge v \\ uv^{1-\theta },\quad u\le v \\ \end{array} \end{aligned}$$
(2.3)

From Theorem 2.1 one gets

$$\begin{aligned} C_{-\theta }^{(1)} (u,v)=\left\{ \begin{array}{l} u(1-u^{-\theta }\bar{v}),\quad u\ge \bar{v} \\ u(1-\bar{v}^{1-\theta }),\quad u\le \bar{v} \\ \end{array}\right. , \quad C_{-\theta }^{(2)} (u,v)=\left\{ \begin{array}{l} v(1-v^{-\theta }\bar{u}),\quad v\ge \bar{u} \\ v(1-\bar{u}^{1-\theta }),\quad v\le \bar{u} \\ \end{array}\right. \end{aligned}$$

Since \(C_{-\theta }^{(2)} (u,v)=C_{-\theta }^{(1)} (v,u)\ne C_{-\theta }^{(1)} (u,v)\) the anti-symmetric construction yields here two non-symmetric copula extensions (see Nelsen 2006, p. 38, for the notion of symmetric copula). Moreover, one knows that \(\rho _S (\theta )=3\theta /(4-\theta )\) and \(\tau _K (\theta )=\theta /(2-\theta )\) both with values in [0, 1] (e.g. Nelsen 2006, Examples 5.5 and 5.7). It follows that the anti-symmetric extensions are comprehensive families. Note that the Cuadras-Augé copula is a special case of the important two-parameter family by Marshall and Olkin (1967) (see Nelsen 2006, Sect. 3.1.1).

Example 2.3

a comprehensive anti-symmetric extended copula of Hoeffding-Fréchet type

Durante (2006), Chapter 4, proposes the following interesting family of copulas

$$\begin{aligned} C_f (u,v)=M(u,v)\cdot f(\max (u,v)), \end{aligned}$$

where the function f is a differentiable function (up to finitely many points) from I to I. This function defines a copula under the necessary and sufficient conditions stated in Theorem 4.1.1 of Durante (2006). A simple member of this family is Example 4.1.3 there, namely

$$\begin{aligned} C_\alpha (u,v)=\min \{M(u,v),\alpha uv\},\quad \alpha \in [1,\infty ). \end{aligned}$$
(2.4)

With (2.2) one has \(M(u,v)=uv+I(u,v)\), \(C_\alpha (u,v)=uv+\min \{I(u,v),(\alpha -1)uv\}\), and the complement function for independence reads \(C_\alpha ^\bot (u,v)=\min \{I(u,v),(\alpha {-}1)uv\}\). Through application of Theorem 2.1 one obtains the anti-symmetric copula extension, valid for \(\alpha \ge 1\):

$$\begin{aligned} \begin{aligned} C_{-\alpha }^{(1)} (u,v)&=uv-C_\alpha ^\bot (u,\bar{v})=uv-\min \{I(u,\bar{v}),(\alpha -1)u\bar{v}\} \\&=\max \{uv-I(u,\bar{v}),u(1-\alpha \bar{v})\}=\max \{W(u,v),u(1-\alpha +\alpha v)\}. \end{aligned} \end{aligned}$$
(2.5)

From (2.4) and (2.5) one sees that the function \(\alpha uv\), respectively \(u(1-\alpha +\alpha v)\), has been truncated from above, respectively below, in order to satisfy automatically the Hoeffding-Fréchet bounds, which are necessary conditions for a genuine copula. One observes that \(C_1 =C_{-1} =\Pi \), \(C_\infty =M,\;C_{-\infty } =W\), and this type of Hoeffding-Fréchet extended copula is a comprehensive anti-symmetric family. Moreover, through direct calculation, one obtains its Spearman rho as \(\rho _S (\alpha )=1-\alpha ^{-3}(12\alpha -6\alpha ^2-5),\;\alpha \ge 1\), and clearly \(\rho _S (-\alpha )=-\rho _S (\alpha )\) on \((-\infty ,-1]\cup [1,\infty )\).

Example 2.4

Hoeffding-Fréchet comprehensive extension of Chogosov’s copula

Consider the bivariate function from \(I^2\) to I defined by

$$\begin{aligned} C_\theta (u,v)=\min \{M(u,v),uv+\theta \sqrt{(u\bar{u})(v\bar{v})} \},\quad \theta \in {[0,1]}. \end{aligned}$$
(2.6)

This so-called Chogosov law is indeed a copula, as shown in Peyre (2013), Proposition 3.5 (see also Peyre 2010a, b). The complement function for independence is given by \(C_\theta ^\bot (u,v)=\min \{I(u,v),\theta \sqrt{(u\bar{u})(v\bar{v})} \}\). Again, the Hoeffding-Fréchet extended Chogosov copula is obtained from Theorem 2.1 and reads

$$\begin{aligned} C_{-\theta }^{(1)} (u,v)=uv-C_\alpha ^\bot (u,\bar{v})=\max \{W(u,v),uv-\theta \sqrt{(u\bar{u})(v\bar{v})} \},\quad \theta \in {[0,1]}. \end{aligned}$$
(2.7)

Since \(I(\bar{u},v)=I(u,\bar{v})\) one sees furthermore that \(C_{-\theta }^{(1)} (u,v)=C_{-\theta }^{(2)} (u,v)\) and this anti-symmetric family is uniquely determined. Moreover, one knows that \(C_0 =\Pi ,\;C_1 =M,\;C_{-1} =W\). Therefore, the extended Chogosov copula is an anti-symmetric comprehensive family.

3 Hoeffding-Fréchet comprehensive extension of the FGM copula

We apply the recipe in the last two examples to obtain a comprehensive extension of the FGM copula. Consider the following general pattern to generate anti-symmetric families of copulas. Let \(f_\alpha (u,v),\;g_\alpha (u,v)\) be two non-negative real functions defined on \(I^2\) with parameter \(\alpha \in [\alpha _0 ,c],\;\alpha _0 \ge 0\). We are interested in those \(f_\alpha ,\;g_\alpha \), for which the following functions

$$\begin{aligned} \begin{aligned} C_\alpha (u,v)&=\min \{M(u,v),f_\alpha (u,v)\}, \\ C_{-\alpha } (u,v)&=\max \{W(u,v),g_\alpha (u,v)\},\quad \alpha \in [\alpha _0 ,c]. \\ \end{aligned} \end{aligned}$$
(3.1)

define an anti-symmetric comprehensive family of copulas. Example 2.3 is generated by the functions \(f_\alpha (u,v)=\alpha uv,\;g_\alpha (u,v)=u(1-\alpha +\alpha v)\). Since \(f_1 (u,v)=g_1 (u,v)=uv\) yields the independent copula, Example 2.3 can be viewed as a Hoeffding-Fréchet extended independent copula, abbreviated HF-\(\Pi \). Similarly, the Hoeffding-Fréchet extended Chogosov copula from Example 2.4 can be abbreviated as HF-Chogosov. Without any attempt to characterize the class (3.1) completely, we undertake a first analysis of the family generated by the “FGM functions” \(f_\alpha ^{FGM} (u,v)=uv+\alpha (u\bar{u})(v\bar{v})\), \(g_\alpha (u,v)=f_{-\alpha }^{FGM} (u,v),\;\alpha \in [0,\infty )\).

For ease of notation, the Hoeffding-Fréchet extended FGM copula is abbreviated HF-FGM. Its upper part for \(\alpha \in [0,\infty )\) is abbreviated HFU-FGM and its lower part for \(\alpha \in (-\infty ,0]\) is abbreviated HFL-FGM. In the next results, we derive explicit representations of these copulas and show that the HF-FGM family is a comprehensive family of copulas. Clearly, it suffices to focus on \(\left| \alpha \right| \ge 1\) because \(C_\alpha (u,v)=uv+\alpha (u\bar{u})(v\bar{v}),\;\alpha \in [-1,1]\), coincides with the FGM copula.

Lemma 3.1

Let \(\alpha \in [1,\infty )\) and set \(\alpha ^\pm =\textstyle {1 \over 2}(1\pm \sqrt{1-4\alpha ^{-1}} )\) in case \(\alpha \ge 4\). The function \(h(x)=\alpha ^{-1}-x\bar{x},\;x\in I\) satisfies the following properties:

(P1)   If \(\quad \alpha \in [1,4]\) then \(h(x)\ge 0,\;\forall \;x\in I\)

(P2)   If \(\quad \alpha \ge 4\) then \(h(x)\ge 0,\;\forall \;x\in {[0},\alpha ^-]\cup [\alpha ^+,1]\)

(P2)   If \(\quad \alpha \ge 4\) then \(h(x)\le 0,\;\forall \;x\in [\alpha ^-,\alpha ^+]\)

Proof

This elementary exercise is left to the reader. \(\square \)

Next, depending on \(\alpha \in [1,\infty )\), it will be useful to partition the unit square \(I^2\) into six (two by two symmetric) domains (the dependence upon \(\alpha \) is omitted). For \(\alpha \in [1,4]\) the domains are

$$\begin{aligned}&D_1 =\{v\in {[0},1-\alpha ^{-1}],\;u\in [(\alpha \bar{v})^{-1},1{]\}}, D_2 = \{v\in {[0,}1-\alpha ^{-1}],\nonumber \\&\quad \;u\in [v,(\alpha \bar{v})^{-1}{]\}},\\ \end{aligned}$$
$$\begin{aligned}&D_3 = \{v\in [1-\alpha ^{-1}{,1],}\;u\in [v,1{]\}}, {\text {and for }} \alpha \in [4,\infty )\, {\text {they are}} \\&D_1 =\{v\in {[0},\alpha ^-]\cup [\alpha ^+,1-\alpha ^{-1}],\;u\in [(\alpha \bar{v})^{-1},1{]\}}\cup \{v\in [\alpha ^-,\alpha ^+],\;u\in [v,1{]\}},\\&D_2 =\{v\in {[0},\alpha ^-]\cup [\alpha ^+,1-\alpha ^{-1}],\;u\in [v{,}(\alpha \bar{v})^{-1}{]\}}, \\&D_3 =\{v\in [1-\alpha ^{-1}{,1],}\;u\in [v,1{]\}}. \end{aligned}$$

Furthermore, in both cases set \(\bar{D}_i =\{(u,v)\;:\;(v,u)\in D_i {\},}\quad {i}={1,2,3}\). For each \(\alpha \in [1,\infty )\) one has \(D_1 \cup D_2 \cup D_3 \cup \bar{D}_1 \cup \bar{D}_2 \cup \bar{D}_3 =I^2\). Figure 1 illustrates for a special case. \(\square \)

Proposition 3.1

For \(\alpha \in [1,\infty )\) the HFU-FGM and HFL-FGM functions are given by

$$\begin{aligned} C_\alpha (u,v)= & {} \left\{ \begin{array}{l} v,\quad (u,v)\in D_1 \\ u,\quad (u,v)\in \bar{D}_1 , \\ uv+\alpha (u\bar{u})(v\bar{v}),\quad (u,v)\in D_2 \cup D_3 \cup \bar{D}_2 \cup \bar{D}_3 . \\ \end{array}\right. \\ C_{-\alpha } (u,v)= & {} \left\{ \begin{array}{l} u-\bar{v},\quad (u,v)\in D_1 \\ 0,\quad (u,v)\in \bar{D}_1 , \\ uv-\alpha (u\bar{u})(v\bar{v}),\quad (u,v)\in D_2 \cup D_3 \cup \bar{D}_2 \cup \bar{D}_3 . \\ \end{array}\right. \end{aligned}$$

\(\square \)

Fig. 1
figure 1

Domains \(D_1 \) and \(D_2 \cup D_3 \) for the special case \(\alpha =2\)

Full size image

Proof

Consider the HFU-FGM function. By symmetry of u, v, it suffices to show the result for the domains \(D_1 \) and \(D_2 \cup D_3 \). First, assume that \(\alpha \in [1,4]\) and \(u\ge v\). The equality \(C_\alpha (u,v)=v\) holds if, and only if, one has \(v\le uv+\alpha (u\bar{u})(v\bar{v})\), that is \(\alpha u\bar{v}\ge 1\), or equivalently \(u\in [(\alpha \bar{v})^{-1},1]\). A necessary condition for this is \(v\in {[0},1-\alpha ^{-1}]\). Since \({max\{}v,(\alpha \bar{v})^{-1}\}=(\alpha \bar{v})^{-1}\) by the property (P1) of Lemma 3.1, one sees that \(C_\alpha (u,v)=v\;\Leftrightarrow (u,v)\in D_1 \). It follows that on the complement \(D_2 \cup D_3 \) of \(D_1 \) in the part \(\{v\le u\}\) below the diagonal \(\{v=u\}\) one must have \(f_\alpha ^{FGM} (u,v)\le v=M(u,v)\), which implies that \(C_\alpha (u,v)=uv+\alpha (u\bar{u})(v\bar{v})\) on \(D_2 \cup D_3 \). Now, let \(\alpha \in [4,\infty )\) and \(u\ge v\). Similarly to the above one has \(C_\alpha (u,v)=v\) if, and only if, one has \(u\in {[max\{}v,(\alpha \bar{v})^{-1}\},1]\). Again, one must have \(v\in {[0},1-\alpha ^{-1}]\). The property (P2) of Lemma 3.1 shows that \(v\le (\alpha \bar{v})^{-1}\) occurs if, and only if, one has \(v\in {[0},\alpha ^-]\cup [\alpha ^+,1-\alpha ^{-1}]\). This shows that \(C_\alpha (u,v)=v\) if \(v\in {[0},\alpha ^-]\cup [\alpha ^+,1-\alpha ^{-1}],\;u\in [(\alpha \bar{v})^{-1},1]\). The reverse inequality \(v\ge (\alpha \bar{v})^{-1}\) holds by property (P3) of Lemma 3.1 if, and only if, one has \(v\in [\alpha ^-,\alpha ^+]\). Since necessarily \(\alpha ^+\le 1-\alpha ^{-1}\) one has also \(C_\alpha (u,v)=v\) if \(v\in [\alpha ^-,\alpha ^+],\quad u\in [v,1]\). Together, one gets \(C_\alpha (u,v)=v\;\Leftrightarrow (u,v)\in D_1 \). In virtue of the same argument as above one concludes that \(C_\alpha (u,v)=uv+\alpha (u\bar{u})(v\bar{v})\) on \(D_2 \cup D_3 \). The proof for the HFL-FGM function is similar. \(\square \)

Theorem 3.1

(Hoeffding-Fréchet extended FGM copula). The Hoeffding-Fréchet extension of the FGM function defines the following copula:

$$\begin{aligned} \begin{array}{l} C_\alpha (u,v)=\min \{M(u,v),f_\alpha ^{FGM} (u,v)\},\quad \alpha \in [0,\infty ), \\ C_\alpha (u,v)=\max \{W(u,v),f_\alpha ^{FGM} (u,v)\},\quad \alpha \in (-\infty ,0]. \\ \end{array} \end{aligned}$$
(3.2)

Proof

For \(\alpha \in [0,\infty )\) the function \(C_{-\alpha } (u,v)\) is the anti-symmetric extension of \(C_\alpha (u,v)\). With Theorem 2.1 it suffices to show that \(C_\alpha (u,v)\) is a copula, where one can assume that \(\alpha \in [1,\infty )\). The proof is similar to Peyre (2013), Sect. 3.3, who shows that the Chogosov law (2.6) is a copula. With Proposition 3.1 the HFU-FGM function has a non-vanishing absolutely continuous joint density on the support \(\{D_2 \cup D_3 \cup \bar{D}_2 \cup \bar{D}_3 \}^\circ \) (the notation \(D^\circ \) stands for the inner of the domain D), which is given by

$$\begin{aligned} c_\alpha (x,y):=\partial ^2C_\alpha (x,y)/\partial x\partial y=1+\alpha (\bar{x}-x)(\bar{y}-y). \end{aligned}$$
(3.3)

The mass of the singular component is concentrated on the boundary \(\partial D_1 \) between the domains \(D_1 \) and \(D_2 \cup D_3 \), and the boundary \(\partial \bar{D}_1 \) between \(\bar{D}_1 \) and \(\bar{D}_2 \cup \bar{D}_3 \) (cf. Fig. 1). Let \(\partial D_1 (t),\;\partial \bar{D}_1 (t)\), denote curve parameterizations of the boundaries and let \(\varepsilon _1 (t),\;\bar{\varepsilon }_1 (t)\), describe the jump sizes of \(C_\alpha ^x (v):=\partial C_\alpha (x,v)/\partial x\) at the boundaries. Then, the formula \(C_\alpha (u,v)=\int \limits _0^u {C_\alpha ^x (v)dx} \) implies the decomposition \(C_\alpha (u,v)=A_C (u,v)+S_C (u,v)\) into the absolutely continuous component

$$\begin{aligned} A_C (u,v)=\iint \limits _{(D_2 \cup D_3 \cup \bar{D}_2 \cup \bar{D}_3 )\cap [0,u]x[0,v]}{c_\alpha (x,y)dxdy} \end{aligned}$$

and the singular component

$$\begin{aligned} S_C (u,v)=\int \limits _{\partial D_1 (t)\cap [0,u]x[0,v]} {\varepsilon _1 (t)dt} +\int \limits _{\partial \bar{D}_1 (t)\cap [0,u]x[0,v]} {\bar{\varepsilon }_1 (t)dt} . \end{aligned}$$

To show that \(C_\alpha (u,v)\) generates a copula one must verify that the density is positive wherever defined and that the jumps are non-negative. This is done in two parts. Example 3.1 works out the necessary steps in a special case.

Part I: The density is positive

One must show that \(c_\alpha (u,v)=1+\alpha (\bar{u}-u)(\bar{v}-v)\ge 0\) on \(\{D_2 \cup D_3 \cup \bar{D}_2 \cup \bar{D}_3 \}^\circ \). We begin with the case \(\alpha \in [1,4]\). Obviously, if \(u\le \textstyle {1 \over 2},v\le \textstyle {1 \over 2}\) or \(u\ge \textstyle {1 \over 2},v\ge \textstyle {1 \over 2}\), then \((\bar{u}-u)(\bar{v}-v)\ge 0\) and \(c_\alpha (u,v)\ge 0\) is trivially fulfilled. There remains the two cases \(v\ge \textstyle {1 \over 2}\ge u\) and \(u\ge \textstyle {1 \over 2}\ge v\). In the first case, one has \((u,v)\in \{\bar{D}_2 \cup \bar{D}_3 \}^\circ \) and distinguishes between two sub-cases.

Sub-case (a): \((u,v)\in \bar{D}_3 ^\circ \)

One uses the inequalities \(v\le 1\) and \(u\ge 1-\alpha ^{-1}\) to get the affirmation as follows:

$$\begin{aligned} c_\alpha (u,v)=1+\alpha (1-2u)(1-2v)\ge 1-\alpha +2\alpha u\ge 1-\alpha +2\alpha (1-\alpha ^{-1})=\alpha -1\ge 0. \end{aligned}$$

Sub-case (b): \((u,v)\in \bar{D}_2 ^\circ \)

Since \(v\le (\alpha \bar{u})^{-1}\), one has \(-v\ge -(\alpha \bar{u})^{-1}\), hence \(c_\alpha (u,v)\ge 1+(1-2u)(\alpha -\alpha u-2)\bar{u}^{-1}\). First, let \(\alpha \in [2,4]\). If \(u\le 1-2\alpha ^{-1}\), one gets \(\alpha -\alpha u-2\ge \alpha -\alpha (2\alpha ^{-1}-1)-2=2(\alpha -2)\ge 0\), and \(c_\alpha (u,v)\ge 0\) follows. If \(u\ge 1-2\alpha ^{-1}\), then \(c_\alpha (u,v)\ge 0\) if, and only, if one has \((1-2u)(\alpha -\alpha u-2)\le 1-u\), which is equivalent with \(q(u)=u^2-\textstyle {3 \over 2}(1-\alpha ^{-1})u+\textstyle {1 \over 2}(1-\alpha ^{-1})\ge 0\). Since the discriminant of the latter quadratic equation is negative, the condition holds. Now, let \(\alpha \in {[1,}2]\). Since \(\alpha -\alpha u-2\le \alpha -2\le 0\) the requirement \(c_\alpha (u,v)\ge 0\) is again equivalent with \(q(u)\ge 0\) and holds because its discriminant is negative.

The remaining case \(u\ge \textstyle {1 \over 2}\ge v\) follows similarly (symmetry in the variables u, v). The assertion for \(\alpha \in [1,4]\) is shown. Now, let \(\alpha \in [4,\infty )\). Again, only the two cases \(v\ge \textstyle {1 \over 2}\ge u\) and \(u\ge \textstyle {1 \over 2}\ge v\) are relevant. In the first case, one has \((u,v)\in \{\bar{D}_2 \cup \bar{D}_3 \}^\circ \). If \((u,v)\in \bar{D}_3 ^\circ \) the same proof as under the Sub-case (a) above holds. Let now \((u,v)\in \bar{D}_2 ^\circ \). One has \(u\le \alpha ^-\), or \(\alpha ^+\le u\le 1-\alpha ^{-1}\), and \(u\le v\le (\alpha \bar{u})^{-1}\). If \(u\le \alpha ^-\), then also \(u\le \alpha ^-\le 1-2\alpha ^{-1}\) because \(\alpha \ge 4\). In this situation, the inequality \(-u\ge 2\alpha ^{-1}-1\) implies that \(\alpha -\alpha u-2\ge \alpha -\alpha (2\alpha ^{-1}-1)-2=2(\alpha -2)\ge 0\), hence \(c_\alpha (u,v)\ge 0\). Since the inequality \(\alpha ^+\le u\le \textstyle {1 \over 2}\le 1-\alpha ^{-1}\) is impossible for \(\alpha >4\), the case \(v\ge \textstyle {1 \over 2}\ge u\) is done. The remaining case \(u\ge \textstyle {1 \over 2}\ge v\) follows similarly.

Part II: The singular component is non-negative

In virtue of the given formula for the singular component, it suffices to show that the jump sizes of \(C_\alpha ^u (v)=\partial C_\alpha (u,v)/\partial u\) located on \(\partial D_1 \cap [0,u]x[0,v]\) and \(\partial \bar{D}_1 \cap [0,u]x[0,v]\) are non-negative. Consider first the case \(\alpha \in [1,4]\). One notes that \(\partial D_1 ]\) corresponds to the condition \(\alpha u\bar{v}=1\) while \(\partial \bar{D}_1 \) corresponds to \(\alpha \bar{u}v=1\). These boundaries are the graphs of the functions

$$\begin{aligned} \begin{array}{ll} v=v_1 (u)=1-(\alpha u)^{-1},&{}\quad u\in [\alpha ^{-1}{,1],} \\ v=\bar{v}_1 (u)=(\alpha \bar{u})^{-1},&{}\quad u\in {[0,1}-\alpha ^{-1}]. \\ \end{array} \end{aligned}$$
(3.4)

From Proposition 3.1 one obtains

$$\begin{aligned} \partial C_\alpha (u,v)/\partial u{=}\left\{ \begin{array}{l} 0,\quad (u,v)\in D_1^\circ , \\ v+\alpha (\bar{u}-u)(v\bar{v}),\quad (u,v)\in \{D_2 \cup D_3 \}^\circ \cup \{\bar{D}_2 \cup \bar{D}_3 \}^\circ , \\ 1,\quad (u,v)\in \bar{D}_1^\circ \,. \\ \end{array}\right. \end{aligned}$$
(3.5)

Located on the segments \(\partial D_1 (t)\cap [0,u]x[0,v]\) and \(\partial \bar{D}_1 (t)\cap [0,u]x[0,v]\) of (3.4) the jumps have the following non-negative sizes:

$$\begin{aligned} \begin{array}{l} \varepsilon _1 (t)=v_1 (t)+\alpha (\bar{t}-t)v_1 (t)\bar{v}_1 (t)=v_1 (t)\bar{t}t^{-1}\ge 0, \\ \bar{\varepsilon }_1 (t)=\bar{\bar{v}}_1 (t)-\alpha (\bar{t}-t)\bar{v}_1 (t)\bar{\bar{v}}_1 (t)=\bar{\bar{v}}_1 (t)t\bar{t}^{-1}\ge {0.} \\ \end{array} \end{aligned}$$
(3.6)

Now, consider the case \(\alpha \in [4,\infty )\). The boundaries are the graphs of the functions

$$\begin{aligned} \begin{array}{l} v=v_1 (u)=\left\{ {\begin{array}{l} 1-(\alpha u)^{-1},\quad u\in [\alpha ^{-1}{,}\alpha ^{-1}(1-\alpha ^-)^{-1}], \\ u,\quad u\in [\alpha ^{-1}{,}\alpha ^{-1}(1-\alpha ^-)^{-1}{,}\alpha ^+], \\ 1-(\alpha u)^{-1},\quad u\in [\alpha ^+{,1].} \\ \end{array}} \right. \\ v=\bar{v}_1 (u)=\left\{ {\begin{array}{l} (\alpha \bar{u})^{-1},\quad u\in {[0,}\alpha ^-], \\ u,\quad u\in [\alpha ^-{,}\alpha ^+], \\ (\alpha \bar{u})^{-1},\quad u\in [\alpha ^+{,1}-\alpha ^{-1}]. \\ \end{array}} \right. \\ \end{array} \end{aligned}$$
(3.7)

Since the jump sizes are of the same form (3.6) with changed values, the resulting singular component is non-negative. The proof of Theorem 3.1 is complete. \(\square \) \(\square \)

Example 3.1

Absolutely continuous and singular components of the HFU-FGM copula

To illustrate the proof of Theorem 3.1 consider the case \(\alpha ={2}\) and fix a point in the unit square, say \((u,v)=(0.75,0.25)\in D_1 \). With the parameteriztion \(\partial D_1 (t)=\{(t,1-1/2t)\;:\;t\in [0.5,1]\}\) and the jump size \(\varepsilon _1 (t)=(1-1/2t)(1-t)/t,\;t\in [0.5,1]\), one obtains from the fact that \(\partial D_1 (t)\cap [0,u]x[0,v]=\{(t,1-1/2t)\;:\;t\in [0.5,2/3]\}\) the singular and absolutely components as

$$\begin{aligned} S_C (u,v)&=\int \limits _{0.5}^{2/3} {\varepsilon _1 (t)dt} =0.01486,\quad A_C (u,v)=\int \limits _0^{0.5} {\int \limits _0^{0.25} {c_\alpha (x,y)dydx} }\\&\quad +\int \limits _{0.5}^{2/3} {\int \limits _{1-1/2x}^{0.25} {c_\alpha (x,y)dydx} } =0.23514, \end{aligned}$$

which shows that \(C_\alpha (u,v)=A_C (u,v)+S_C (u,v)=v=0.25\) as should be because \((u,v)\in D_1 \).

Finally, we show that the HF-FGM family is a comprehensive anti-symmetric family with Sperman’s rho and Kendall’s tau attaining the whole range of values \([-1{,1]}\).

Theorem 3.2

Spearman’s rho and Kendall’s tau of the HF-FGM copula are monotone increasing functions satisfying the limiting property \(\mathop {\lim }\nolimits _{\alpha \rightarrow \pm \infty } \rho _S (\alpha )=\mathop {\lim }\nolimits _{\alpha \rightarrow \pm \infty } \tau _K (\alpha )=\pm 1\). Therefore, the HF-FGM copula is an anti-symmetric comprehensive family.

Proof

If \(0\le \alpha \le \beta \) the property \(\rho _S (\alpha )\le \rho _S (\beta )\) follows from the representation \(\rho _S (\alpha )=12\cdot \int \nolimits _{I^2} {\int {C_\alpha (u,v)dudv} } -3\), the fact that \(C_\alpha (u,v)\le C_\beta (u,v)\), and Corollary 2.1. To show that \(\mathop {\lim }\nolimits _{\alpha \rightarrow \infty } \rho _S (\alpha )=1\), write \(I^2=D_+ \cup D{ }_-\) with \(D_+ =\{u\ge v\}\) and \(D_- =\{u<v\}\). Then one has \(\rho _S (\alpha )=12\cdot (J_+ (\alpha )+J_- (\alpha ))-3\) with \(J_\pm (\alpha )={\iint \limits _{D_\pm }{ {C_\alpha (u,v)dudv}}} \) and \(J_+ (\alpha )=J_- (\alpha )\) by symmetry of the copula. For \(\alpha \ge 4\) use Proposition 3.1 to decompose the double integral \(J_+ (\alpha )\) into three parts \(J_+ (\alpha )=I_1 (\alpha )+I_2 (\alpha )+I_3 (\alpha )\) such that

$$\begin{aligned} I_1 (\alpha )=\int \limits _0^{\alpha ^-} {\int \limits _{(\alpha \bar{v})^{-1}}^1 {vdu} dv} +\int \limits _{\alpha ^+}^{1-\alpha ^{-1}} {\int \limits _{(\alpha \bar{v})^{-1}}^1 {vdu} dv} +\int \limits _{\alpha ^-}^{\alpha ^+} {\int \limits _v^1 {vdu} dv} , \end{aligned}$$
(3.8)
$$\begin{aligned} I_2 (\alpha )=\int \limits _0^{\alpha ^-} {\int \limits _v^{(\alpha \bar{v})^{-1}} {\{uv+\alpha (u\bar{u})(v\bar{v})\}du} dv} +\int \limits _{\alpha ^+}^{1-\alpha ^{-1}} {\int \limits _v^{(\alpha \bar{v})^{-1}} {\{uv+\alpha (u\bar{u})(v\bar{v})\}du} dv} , \end{aligned}$$
(3.9)
$$\begin{aligned} I_3 (\alpha )=\int \limits _{1-\alpha ^{-1}}^1 {\int \limits _v^1 {\{uv+\alpha (u\bar{u})(v\bar{v})\}du} dv} , \end{aligned}$$
(3.10)

Now, if \(\alpha \rightarrow \infty \) one has \(\alpha ^-\rightarrow 0,\;\alpha ^+\rightarrow 1\), and one sees that \(\mathop {\lim }\limits _{\alpha \rightarrow \infty } I_1 (\alpha )=\int \limits _0^1 {\int \limits _v^1 {vdu} dv} =\frac{1}{6},\) and \(\mathop {\lim }\limits _{\alpha \rightarrow \infty } I_2 (\alpha )=\mathop {\lim }\limits _{\alpha \rightarrow \infty } I_3 (\alpha )=0\), hence \(\mathop {\lim }\limits _{\alpha \rightarrow \infty } \rho _S (\alpha )=24\cdot \mathop {\lim }\limits _{\alpha \rightarrow \infty } J_+ (\alpha )-3=1\). It follows that the HF-FGM copula is comprehensive. Invoking now Theorem 5.1.9 of Nelsen (2006) implies the statement about Kendall’s tau. The result is shown. \(\square \)

4 Spearman’s rho for the HF-FGM copula

For \(\alpha \ge 0\) Spearman’s rho can be expressed as a piecewise continuous function

$$\begin{aligned} \rho _S (\alpha )=\left\{ \begin{array}{l} \rho _1 (\alpha ),\quad \alpha \in {[0,1],} \\ \rho _2 (\alpha ),\quad \alpha \in {[1,4],} \\ \rho _3 (\alpha ),\quad \alpha \in [4,\infty ). \\ \end{array}\right. \end{aligned}$$
(4.1)

Table 1 displays some typical values. A graphical comparison with Kendall’s tau follows later in Fig. 2. One notes that the first two pieces already yield the improved range of variation \(\rho _S (\alpha )\in {[0,0.95288]}\) compared to \(\rho _S (\alpha )\in {[0,1/3]}\) for the FGM copula.

Table 1 Values of Spearman’s rho for the HFU-FGM copula
Full size table
Fig. 2
figure 2

Kendall’s tau versus Spearman’s rho

Full size image

Theorem 4.1

(Analytical formula for Spearman’s rho). The functions \(\rho _j (\alpha ),\;j=1,2,3\), are given by \(\rho _1 (\alpha )=\textstyle {1 \over 3}\alpha \) (FGM copula) and

$$\begin{aligned} \rho _2 (\alpha )= & {} \rho _1 (\alpha )+\textstyle {4 \over 3}\alpha \left( \textstyle {{\alpha -1} \over \alpha }\right) ^3+2(3-\alpha )\left( \textstyle {{\alpha -1} \over \alpha }\right) ^2+\textstyle {{16} \over \alpha }\left( \textstyle {{\alpha -1} \over \alpha }\right) -\textstyle {4 \over \alpha }\left( \textstyle {{3\alpha +1} \over \alpha }\right) \ln \alpha ,\\ \rho _3 (\alpha )= & {} \rho _2 (\alpha )+8\left( (1-\alpha ^+)^3-(\alpha ^+)^3\right) -3(1+\alpha )\left( (1-\alpha ^+)^4-(\alpha ^+)^4\right) \\&+\,4\alpha \left( (1-\alpha ^+)^5-(\alpha ^+)^5\right) -\textstyle {4 \over 3}\alpha \left( (1-\alpha ^+)^6-(\alpha ^+)^6\right) \\&-12\alpha ^{-1}\left\{ 2\alpha ^+-1-\ln (\textstyle {{\alpha ^+} \over {1-\alpha ^+}})\right\} +4\alpha ^{-2}\left\{ \textstyle {{1-2\alpha ^+} \over {\alpha ^+(1-\alpha ^+)}}+\ln (\textstyle {{\alpha ^+} \over {1-\alpha ^+}})\right\} . \end{aligned}$$

Remark 4.1

The piecewise continuous property is immediately verified. It is trivial that \(\rho _2 (1)=\rho _1 (1)\), and one has \(\rho _3 (4)=\rho _2 (4)\) because \(\alpha ^+=1-\alpha ^+=\textstyle {1 \over 2}\) in case \(\alpha =4\). The representation has been chosen this way to control and validate the derivation of the formulas.

Proof

It suffices to show the cases \(j=2,3\). As shown in the proof of Theorem 3.2, one can write \(\rho _j (\alpha )=24\cdot J_+ (\alpha )-3\), with \(J_+ (\alpha )=\sum \limits _{i=1}^3 {I_i (\alpha )} ,\;I_i (\alpha )=\int \limits _{D_i } {\int {C_\alpha (u,v)dudv} } ,\;j=2,3\). It is convenient to use the following definite integral notations:

$$\begin{aligned} F_k (x)&=\int \limits _0^{\bar{x}} {v^kdv} =\bar{x}^{k+1}/(k+1),\;k=1,2,\ldots ,5,\nonumber \\ G_k (x)= & {} \int \limits _0^{\bar{x}} {v(\bar{v})^{-k}dv} =\left\{ \begin{array}{l} x-1-\ln x,\;k=1, \\ x^{-1}-1+\ln x,\;k=2. \\ \end{array}\right. \end{aligned}$$
(4.2)

The defined functions are normalized such that \(F_k (1)=0,\;k=1,2,\ldots ,5,\) and \(G_k (1)=0,\;k=1,2\). Furthermore, we set \(\Delta _k^F (\alpha )=F_k (\alpha ^+)-F_k (\alpha ^-),\;k=2,\ldots ,5,\quad \Delta _k^G (\alpha )=G_k (\alpha ^+)-G_k (\alpha ^-),\;k=1,2\).

For \(j=2\) rearrangement of integrals yields \(J_+ (\alpha )=I_1 (\alpha )+K_2 (\alpha )-K_3 (\alpha )\) with

$$\begin{aligned} I_1 (\alpha )&=\int \limits _0^{1-\alpha ^{-1}} {\int \limits _{(\alpha \bar{v})^{-1}}^1 {vdu} dv} =\int \limits _0^{1-\alpha ^{-1}} {v\{1-(\alpha \bar{v})^{-1}\}dv} = F_1 (\alpha ^{-1})-\alpha ^{-1}G_1 (\alpha ^{-1}),\\ K_2 (\alpha )&=\int \limits _0^1 {\int \limits _v^1 {\{uv+\alpha (u\bar{u})(v\bar{v})\}du} dv} =\textstyle {1 \over 8}(1+\textstyle {\alpha \over 9}),\\ K_3 (\alpha )&=\int \limits _0^{1-\alpha ^{-1}} \int \limits _{(\alpha \bar{v})^{-1}}^1 \left\{ uv+\alpha (u\bar{u})(v\bar{v})\right\} du dv =\int \limits _0^{1-\alpha ^{-1}} {\textstyle {1 \over 2}\left\{ 1-(\alpha \bar{v})^{-1}\right\} vdv} \\&\quad +\,\alpha \cdot \int \limits _0^{1-\alpha ^{-1}} {\left\{ \textstyle {1 \over 6}(v-v^2-\textstyle {1 \over 2}\alpha ^{-2}v(\bar{v})^{-1}+\textstyle {1 \over 3}\alpha ^{-3}v(\bar{v})^{-2}\right\} dv}\\&=\textstyle {1 \over 2}F_1 (\alpha ^{-1})-\textstyle {1 \over 2}\alpha ^{-1}G_2 (\alpha ^{-1}) \\&\quad +\,\alpha \cdot \left\{ \textstyle {1 \over 6}F_1 (\alpha ^{-1})-\textstyle {1 \over 6}F_2 (\alpha ^{-1})-\textstyle {1 \over 2}\alpha ^{-2}G_1 (\alpha ^{-1})+\textstyle {1 \over 3}\alpha ^{-3}G_2 (\alpha ^{-1})\right\} . \end{aligned}$$

Inserted into \(\rho _2 (\alpha )=24\left\{ I_1 (\alpha )+K_2 (\alpha )-K_3 (\alpha )\right\} -3\) one obtains

$$\begin{aligned} \rho _2 (\alpha )=\rho _1 (\alpha )+4(3-\alpha )F_1 (\alpha ^{-1})+4\alpha F_2 (\alpha ^{-1})-12\alpha ^{-1}G_1 (\alpha ^{-1})+4\alpha ^{-2}G_2 (\alpha ^{-1}), \end{aligned}$$

which implies the desired expression for \(\rho _2 (\alpha )\) taking into account the notations. For \(j=3\) rearrange the equations (3.8)–(3.10) to get \(J_+ (\alpha )=I_1 (\alpha )+K_1 (\alpha )+K_2 (\alpha )-K_3 (\alpha )\) with

$$\begin{aligned} I_1 (\alpha )= & {} \int \limits _0^{1-\alpha ^+} {\int \limits _{(\alpha \bar{v})^{-1}}^1 {vdu} dv} +\int \limits _{1-\alpha ^-}^{1-\alpha ^{-1}} {\int \limits _{(\alpha \bar{v})^{-1}}^1 {vdu} dv} +\int \limits _{1-\alpha ^+}^{1-\alpha ^-} {\int \limits _v^1 {vdu} dv}\\= & {} \left[ {F_1 (v)-\alpha ^{-1}G_1 (v)} \right] _0^{\alpha ^+} +\left[ {F_1 (v)-\alpha ^{-1}G_1 (v)} \right] _{\alpha ^-}^{\alpha ^{-1}} \\&+\,\left[ {F_1 (v)-F_2 (v)} \right] _{\alpha ^+}^{\alpha ^-} =F_1 (\alpha ^{-1})+\Delta _2^F (\alpha )-\alpha ^{-1}G_1 (\alpha ^{-1})-\alpha ^{-1}\Delta _1^G (\alpha )\,, \\ K_1 (\alpha )= & {} \int \limits _0^{\alpha ^-} {\int \limits _v^{(\alpha \bar{v})^{-1}} {\left\{ uv+\alpha (u\bar{u})(v\bar{v})\right\} du} dv} =\int \limits _0^{1-\alpha ^+} {\textstyle {1 \over 2}\left\{ (\alpha \bar{v})^{-2}-v^2\right\} vdv} \\&+\,\alpha \cdot \left\{ \int \limits _0^{1-\alpha ^+} {\left\{ \textstyle {1 \over 2}\alpha ^{-2}v(\bar{v})^{-1}-\textstyle {1 \over 3}\alpha ^{-3}v(\bar{v})^{-2}-\textstyle {1 \over 2}v^3+\textstyle {5 \over 6}v^4-\textstyle {1 \over 3}v^5\right\} dv} \right\} \\= & {} \textstyle {1 \over 2}\alpha ^{-2}G_2 (\alpha ^+)-\textstyle {1 \over 2}F_3 (\alpha ^+) \\&+\,\alpha \cdot \left\{ \textstyle {1 \over 2}\alpha ^{-2}G_1 (\alpha ^+)-\textstyle {1 \over 3}\alpha ^{-3}G_2 (\alpha ^+)-\textstyle {1 \over 2}F_3 (\alpha ^+)+\textstyle {5 \over 6}F_4 (\alpha ^+)-\textstyle {1 \over 3}F_5 (\alpha ^+)\,\right\} , \end{aligned}$$
$$\begin{aligned} K_2 (\alpha )= & {} \int \limits _{\alpha ^+}^1 {\int \limits _v^1 {\left\{ uv+\alpha (u\bar{u})(v\bar{v})\right\} du} dv} =\int \limits _{1-\alpha ^-}^1 {\textstyle {1 \over 2}(v-v^3)dv}\\&+\,\alpha \cdot \left\{ \int \limits _{1-\alpha ^-}^1 {(\textstyle {1 \over 6}v-\textstyle {1 \over 6}v^2-\textstyle {1 \over 2}v^3+\textstyle {5 \over 6}v^4-\textstyle {1 \over 3}v^5)dv} \right\} \\= & {} \textstyle {1 \over 8}-\textstyle {1 \over 2}F_1 (\alpha ^-)+\textstyle {1 \over 2}F_3 (\alpha ^-)+\alpha \cdot \left\{ \textstyle {1 \over {72}}-\textstyle {1 \over 6}F_1 (\alpha ^-)+\textstyle {1 \over 6}F_2 (\alpha ^-)+\textstyle {1 \over 2}F_3 (\alpha ^-)\right. \\&\left. -\,\textstyle {5 \over 6}F_4 (\alpha ^-)+\textstyle {1 \over 3}F_5 (\alpha ^-)\right\} , \\ K_3 (\alpha )= & {} \int \limits _{\alpha ^+}^{1-\alpha ^{-1}} {\int \limits _{(\alpha \bar{v})^{-1}}^1 {\left\{ uv+\alpha (u\bar{u})(v\bar{v})\right\} du} dv} =\int \limits _{1-\alpha ^-}^{1-\alpha ^{-1}} {\textstyle {1 \over 2}\left\{ 1-(\alpha \bar{v})^{-2}\right\} vdv} \\&+\,\alpha \cdot \left\{ \int \limits _{1-\alpha ^-}^{1-\alpha ^{-1}} {(\textstyle {1 \over 6}v-\textstyle {1 \over 6}v^2-\textstyle {1 \over 2}\alpha ^{-2}v(\bar{v})^{-1}+\textstyle {1 \over 3}\alpha ^{-3}v(\bar{v})^{-2})dv} \right\} \\= & {} \textstyle {1 \over 2}\left\{ F_1 (\alpha ^{-1})-F_1 (\alpha ^-)\right\} \\&-\,\textstyle {1 \over 2}\alpha ^{-2}\left\{ G_2 (\alpha ^{-1})-G_2 (\alpha ^-)\right\} +\alpha \cdot \Big \{\textstyle {1 \over 6}\left\{ F_1 (\alpha ^{-1})-F_1 (\alpha ^-)\right\} \\&-\textstyle {1 \over 6}\left\{ F_2 (\alpha ^{-1})-F_2 (\alpha ^-)\right\} \\&-\,\textstyle {1 \over 2}\alpha ^{-2}\left\{ G_1 (\alpha ^{-1})-G_1 (\alpha ^-)\right\} +\textstyle {1 \over 3}\alpha ^{-3}\left\{ G_2 (\alpha ^{-1})-G_2 (\alpha ^-)\right\} . \end{aligned}$$

Gathering all terms together, one obtains the expression

$$\begin{aligned} J_+ (\alpha )&=I_1 (\alpha )+K_1 (\alpha )+K_2 (\alpha )-K_3 (\alpha )=\left( \textstyle {1 \over 8}+\textstyle {\alpha \over {72}}\right) +\textstyle {1 \over 2}\left( 1-\textstyle {\alpha \over 3}\right) F_1 \left( \alpha ^{-1}\right) \\&\quad +\textstyle {\alpha \over 6}F_2 (\alpha ^{-1})+\Delta _2^F (\alpha ) \\&\quad -\textstyle {1 \over 2}(1+\alpha )\Delta _3^F (\alpha )+\textstyle {{5\alpha } \over 6}\Delta _4^F (\alpha )-\textstyle {\alpha \over 3}\Delta _5^F (\alpha )-\textstyle {1 \over 2}\alpha ^{-1}\left\{ G_1 (\alpha ^{-1})+\Delta _1^G (\alpha )\right\} \\&\quad +\textstyle {1 \over 6}\alpha ^{-2}\left\{ G_2 (\alpha ^{-1})+\Delta _2^G (\alpha )\right\} . \end{aligned}$$

Inserting into the equation \(\rho _3 (\alpha )=24\cdot J_+ (\alpha )-3\) and making use of the above expression for \(\rho _2 (\alpha )\), one obtains the formula

$$\begin{aligned} \rho _3 (\alpha )&=\rho _2 (\alpha )+24\Delta _2^F (\alpha )-12(1+\alpha )\Delta _3^F (\alpha )+20\alpha \Delta _4^F (\alpha )-8\alpha \Delta _5^F (\alpha )\\&\quad -12\alpha ^{-1}\Delta _1^G (\alpha )+4\alpha ^{-2}\Delta _2^G (\alpha ). \end{aligned}$$

Finally, taking into account the notations one obtains the stated expression. \(\square \)

Table 2 Values of Kendall’s tau for the HFU-FGM copula
Full size table

5 Kendall’s tau for the HF-FGM copula

For \(\alpha \ge 0\) Kendall’s tau can be expressed as (see Table 2 and Fig. 2 for illustration)

$$\begin{aligned} \tau _K (\alpha )=\left\{ \begin{array}{l} \tau _1 (\alpha ),\quad \alpha \in {[0,1],} \\ \tau _2 (\alpha ),\quad \alpha \in {[1,4],} \\ \tau _3 (\alpha ),\quad \alpha \in [4,\infty ). \end{array}\right. \end{aligned}$$
(5.1)

Theorem 5.1

(Analytical formula for Kendall’s tau). The functions \(\tau _j (\alpha ),\;j=1,2,3\), are given by \(\tau _1 (\alpha )=\textstyle {2 \over 9}\alpha \) (FGM copula) and

$$\begin{aligned} \tau _2 (\alpha )= & {} \tau _1 (\alpha )-\textstyle {4 \over 9}\alpha (\textstyle {{\alpha -1} \over \alpha })^3-2(\textstyle {{\alpha -1} \over \alpha })^2-2(2+\textstyle {{5\alpha +9} \over {3\alpha }})(\textstyle {{\alpha -1} \over \alpha })+4(1+\textstyle {2 \over \alpha }+\textstyle {1 \over {3\alpha ^2}})\ln (\alpha ),\\ \tau _3 (\alpha )= & {} \tau _2 (\alpha )-2((1-\alpha ^+)^2-(\alpha ^+)^2)+(1+\alpha )^2((1-\alpha ^+)^4-(\alpha ^+)^4)\\&-\,4\alpha (1+\alpha )((1-\alpha ^+)^5-(\alpha ^+)^5) \\&+\,\textstyle {2 \over 9}\alpha (8+27\alpha )((1-\alpha ^+)^6-(\alpha ^+)^6)-4\alpha ^2((1-\alpha ^+)^7-(\alpha ^+)^7)\\&+\,\alpha ^2((1-\alpha ^+)^8-(\alpha ^+)^8) \\&4\left\{ 2\alpha ^+-1-\textstyle {1 \over 2}((1-\alpha ^+)^2-(\alpha ^+)^2)-\ln (\textstyle {{\alpha ^+} \over {1-\alpha ^+}})\right\} -4\alpha ^{-1}\left\{ \textstyle {{1-2\alpha ^+} \over {\alpha ^+(1-\alpha ^+)}}\right. \\&\left. -\,2\alpha ^++1+2\ln (\textstyle {{\alpha ^+} \over {1-\alpha ^+}})\right\} \\&+\,\textstyle {4 \over 3}\alpha ^{-2}\left\{ \textstyle {1 \over 2}\textstyle {{(1-\alpha ^+)^2-(\alpha ^+)^2} \over {(\alpha ^+)^2(1-\alpha ^+)^2}}-2\textstyle {{1-2\alpha ^+} \over {\alpha ^+(1-\alpha ^+)}}-\ln (\textstyle {{\alpha ^+} \over {1-\alpha ^+}})\right\} . \end{aligned}$$

Proof

With Nelsen (2006), formula 5.1.12, and Proposition 3.1, one has (symmetry in \(u,\;v)\) \(\tau _j (\alpha )=1-4\cdot \int \int \limits _{I^2} {\textstyle {{\partial C_\alpha (u,v)} \over {\partial u}}\textstyle {{\partial C_\alpha (u,v)} \over {\partial v}}dudv} =1-8\cdot \int \int \limits _{D_2 \cup D_3 } \left\{ u+\alpha (u\bar{u})(\bar{v}-v)\right\} \left\{ v+\alpha (\bar{u}-u)(v\bar{v})\right\} dudv.\)

Write \(\tau _j (\alpha )=1-8\cdot (J_2 +J_3 ),\) with \(J_2 ,\;J_3 \), the integrals over the domains \(D_2 ,\;D_3 \). It suffices to show the cases \(j=2,3\). Similarly to the proof of Theorem 4.1, consider the notations

$$\begin{aligned} F_k (x)= & {} \int \limits _0^{\bar{x}} {v^kdv} =\bar{x}^{k+1}/(k+1),\;k=1,2,\ldots ,7, \nonumber \\ G_k^i (x)= & {} \int \limits _0^{\bar{x}} {v^i(\bar{v})^{-k}dv} ,\;i=1,2,\;k=1,2,3. \end{aligned}$$
(5.2)

The defined functions are normalized such that for all indices, one has \(F_k (1)=0\) and \(G_k^i (1)=0\). Comparing with (4.2) one sees that \(G_k^1 (x)=G_k (x),\;k=1,2\). Furthermore, we set \(\Delta _k^F (\alpha )=F_k (\alpha ^+)-F_k (\alpha ^-),\;k=1,\ldots ,7,\quad \Delta _k^{2,G} (\alpha )=G_k^2 (\alpha ^+)-G_k^2 (\alpha ^-),\;k=1,2,3\), and \(G_1^2 (x)=x-1-\textstyle {1 \over 2}\bar{x}^2-\ln x,\quad G_2^2 (x)=x^{-1}-x+2\cdot \ln x, G_3^2 (x)=\textstyle {1 \over 2}x^{-2}-2x^{-1}+\textstyle {3 \over 2}-\ln x.\)

For \(j=2\) rearrangement of integrals yields \(J_2 +J_3 =K_2 (\alpha )-K_3 (\alpha )\), with

$$\begin{aligned} K_2 (\alpha )= & {} \int \limits _0^1 {\int \limits _v^1 {uvdudv} } +\alpha \cdot \int \limits _0^1 {\int \limits _v^1 {\left\{ (2u-3u^2)(v\bar{v})-(u-u^2)v^2\right\} dudv} }\\&+\,\alpha ^2\cdot \int \limits _0^1 {\int \limits _v^1 {(u-3u^2+2u^3)(v\bar{v}^2-v^2\bar{v})dudv} } =\int \limits _0^1 {\textstyle {1 \over 2}(v-v^3)dv}\\&+\, \alpha \cdot \int \limits _0^1 {(-\textstyle {1 \over 6}v^2-v^3+\textstyle {5 \over 2}v^4-\textstyle {4 \over 3}v^5)dv} -\textstyle {1 \over 2}\alpha ^2\\&\quad \cdot \int \limits _0^1 {v^3(1-5v+9v^2-7v^3+2v^4)dv}\\= & {} \textstyle {1 \over 8}-\textstyle {1 \over {36}}\alpha , \end{aligned}$$
$$\begin{aligned} K_3 (\alpha )= & {} \int \limits _0^{1-\alpha ^{-1}} {\int \limits _{(\alpha \bar{v})^{-1}}^1 {uvdudv} } +\alpha \cdot \int \limits _0^{1-\alpha ^{-1}} {\int \limits _{(\alpha \bar{v})^{-1}}^1 {\left\{ (2u-3u^2)(v\bar{v})-(u-u^2)v^2\right\} dudv} } \\&+\, \alpha ^2\cdot \int \limits _0^{1-\alpha ^{-1}} {\int \limits _{(\alpha \bar{v})^{-1}}^1 {(u-3u^2+2u^3)(v\bar{v}^2-v^2\bar{v})dudv} }\\= & {} \int \limits _0^{1-\alpha ^{-1}} {\textstyle {1 \over 2}\left\{ v-\alpha ^{-2}v(\bar{v})^{-2}\right\} dv} \\&+\, \alpha \cdot \left\{ \int \limits _0^{1-\alpha ^{-1}} {\left\{ -\alpha ^{-2}v(\bar{v})^{-1}+\alpha ^{-3}v(\bar{v})^{-2}\right\} dv}\right. \end{aligned}$$
$$\begin{aligned}&\quad \left. \int \limits _0^{1-\alpha ^{-1}} {\left\{ \textstyle {1 \over 6}v^2-\textstyle {1 \over 2}\alpha ^{-2}v^2(\bar{v})^{-2}+\textstyle {1 \over 3}\alpha ^{-3}v^2(\bar{v})^{-3}\right\} dv} \right\} \\&+\, \alpha ^2\cdot \left\{ {\int \limits _0^{1-\alpha ^{-1}} {\begin{array}{l} \{-\textstyle {1 \over 2}\alpha ^{-2}v+\alpha ^{-3}v(\bar{v})^{-1}-\textstyle {1 \over 2}\alpha ^{-4}v(\bar{v})^{-2} \\ +\textstyle {1 \over 2}\alpha ^{-2}v^2(\bar{v})^{-1}-\alpha ^{-3}v^2(\bar{v})^{-2}+\textstyle {1 \over 2}\alpha ^{-4}v^2(\bar{v})^{-3}\}dv \\ \end{array}} } \right\} \\= & {} \textstyle {1 \over 2}F_1 (\alpha ^{-1})-\textstyle {1 \over 2}\alpha ^{-2}G_2^1 (\alpha ^{-1}) \\&+\,\alpha \cdot \left\{ -\textstyle {1 \over 6}F_2 (\alpha ^{-1})-\alpha ^{-2}G_1^1 (\alpha ^{-1})+\alpha ^{-3}G_2^1 (\alpha ^{-1})\right. \\&\left. +\,\textstyle {1 \over 2}\alpha ^{-2}G_2^2 (\alpha ^{-1})-\textstyle {1 \over 3}\alpha ^{-2}G_3^2 (\alpha ^{-1}) \right\} \\&+\, \alpha ^2\cdot \left\{ \begin{array}{l} -\textstyle {1 \over 2}\alpha ^{-2}F_1 (\alpha ^{-1})+\alpha ^{-3}G_1^1 (\alpha ^{-1})-\textstyle {1 \over 2}\alpha ^{-4}G_2^1 (\alpha ^{-1})\\ +\textstyle {1 \over 2}\alpha ^{-2}G_1^2 (\alpha ^{-1})-\alpha ^{-3}G_2^2 (\alpha ^{-1})+\textstyle {1 \over 2}\alpha ^{-4}G_3^2 (\alpha ^{-1}) \\ \end{array} \right\} . \end{aligned}$$

Inserted into \(\tau _2 (\alpha )=1-8\cdot \left\{ K_2 (\alpha )-K_3 (\alpha )\right\} ,\) one obtains

$$\begin{aligned} \tau _2 (\alpha )=\tau _1 (\alpha )-\textstyle {4 \over 3}\alpha F_2 (\alpha ^{-1})+4G_1^2 (\alpha ^{-1})-4\alpha ^{-1}G_2^2 (\alpha ^{-1})+\textstyle {4 \over 3}\alpha ^{-2}G_3^2 (\alpha ^{-1}), \end{aligned}$$

which implies the desired expression for \(\tau _2 (\alpha )\) taking into account the notations. For \(j=3\) rearrange the equations to get \(J_2 +J_3 =K_1 (\alpha )+K_2 (\alpha )-K_3 (\alpha )\) with

$$\begin{aligned} K_1 (\alpha )= & {} \int \limits _0^{\alpha ^-} {\int \limits _v^{(\alpha \bar{v})^{-1}} {uvdu} dv} +\alpha \cdot \int \limits _0^{\alpha ^-} {\int \limits _v^{(\alpha \bar{v})^{-1}} {\left\{ (2u-3u^2)(v\bar{v})-(u-u^2)v^2\right\} du} dv} \\&+\, \alpha ^2\cdot \int \limits _0^{\alpha ^-} {\int \limits _v^{(\alpha \bar{v})^{-1}} {(u-3u^2+2u^3)(v\bar{v}^2-v^2\bar{v})du} dv} =\int \limits _0^{1-\alpha ^+} {\textstyle {1 \over 2}\left\{ (\alpha \bar{v})^{-2}-v^2\right\} vdv} \\&+\, \alpha \cdot \left\{ \int \limits _0^{1-\alpha ^+} \Big \{\alpha ^{-2}v(\bar{v})^{-1}-\alpha ^{-3}v(\bar{v})^{-2}-v^3+2v^4-v^5-\left( \textstyle {1 \over 2}(\alpha \bar{v})^{-2}\right. \right. \\&\left. \left. -\textstyle {1 \over 3}(\alpha \bar{v})^{-3} -\textstyle {1 \over 2}v^2+\textstyle {1 \over 3}v^3\right) v^2\Big \}dv \right\} \\&+\,\alpha ^2\cdot \left\{ {\int \limits _0^{1-\alpha ^+} {\begin{array}{l} \{\textstyle {1 \over 2}\alpha ^{-2}v-\textstyle {1 \over 2}\alpha ^{-2}v^2(\bar{v})^{-1}-\alpha ^{-3}v(\bar{v})^{-1}+\alpha ^{-3}v^2(\bar{v})^{-2}+\textstyle {1 \over 2}\alpha ^{-4}v(\bar{v})^{-2}\\ -\textstyle {1 \over 2}\alpha ^{-4}v^2(\bar{v})^{-3} \\ -\textstyle {1 \over 2}v^3(1-5v+9v^2-7v^3+2v^4)\}dv \\ \end{array}} } \right\} \\&=\,\textstyle {1 \over 2}\alpha ^{-2}G_2^1 (\alpha ^+)-\textstyle {1 \over 2}F_3 (\alpha ^+)+\alpha \cdot \left\{ {\begin{array}{l} \alpha ^{-2}G_1^1 (\alpha ^+)-\alpha ^{-3}G_2^1 (\alpha ^+)-F_3 (\alpha ^+)\\ \quad +2F_4 (\alpha ^+)-F_5 (\alpha ^+) \\ \quad -\textstyle {1 \over 2}\alpha ^{-2}G_2^2 (\alpha ^+)+\textstyle {1 \over 3}\alpha ^{-3}G_3^2 (\alpha ^+)\\ \quad +\textstyle {1 \over 2}F_4 (\alpha ^+)-\textstyle {1 \over 3}F_5 (\alpha ^+) \\ \end{array}} \right\} \\&+\,\alpha ^2\cdot \left\{ {\begin{array}{l} \textstyle {1 \over 2}\alpha ^{-2}F_1 (\alpha ^+)-\textstyle {1 \over 2}\alpha ^{-2}G_1^2 (\alpha ^+)-\alpha ^{-3}G_1^1 (\alpha ^+)+\alpha ^{-3}G_2^2 (\alpha ^+)+\textstyle {1 \over 2}\alpha ^{-4}G_2^1 (\alpha ^+) \\ -\textstyle {1 \over 2}\alpha ^{-4}G_3^2 (\alpha ^+)-\textstyle {1 \over 2}\left\{ F_3 (\alpha ^+)-5F_4 (\alpha ^+)+9F_5 (\alpha ^+)-7F_6 (\alpha ^+)+2F_7 (\alpha ^+)\right\} \\ \end{array}} \right\} , \end{aligned}$$
$$\begin{aligned} K_2 (\alpha )= & {} \int \limits _{\alpha ^+}^1 {\int \limits _v^1 {uvdu} dv} +\alpha \cdot \int \limits _{\alpha ^+}^1 {\int \limits _v^1 {\left\{ (2u-3u^2)(v\bar{v})-(u-u^2)v^2\right\} du} dv} \\&+\,\alpha ^2\cdot \int \limits _{\alpha ^+}^1 {\int \limits _v^1 {(u-3u^2+2u^3)(v\bar{v}^2-v^2\bar{v})du} dv} =\int \limits _{1-\alpha ^-}^1 {\textstyle {1 \over 2}(v-v^3)dv} \\&+\,\alpha \cdot \int \limits _{1-\alpha ^-}^1 {(-\textstyle {1 \over 6}v^2-v^3+\textstyle {5 \over 2}v^4-\textstyle {4 \over 3}v^5)dv} -\textstyle {1 \over 2}\alpha ^2\cdot \int \limits _{1-\alpha ^-}^1 {v^3(1-5v+9v^2-7v^3+2v^4)dv} \\= & {} \textstyle {1 \over 8}-\textstyle {1 \over 2}F_1 (\alpha ^-)+\textstyle {1 \over 2}F_3 (\alpha ^-)+\alpha \cdot \left\{ {-\textstyle {1 \over {36}}+\textstyle {1 \over 6}F_2 (\alpha ^-)+F_3 (\alpha ^-)-\textstyle {5 \over 2}F_4 (\alpha ^-)+\textstyle {4 \over 3}F_5 (\alpha ^-)} \right\} \\&+\,\textstyle {1 \over 2}\alpha ^2\cdot \left\{ {F_3 (\alpha ^-)-5F_4 (\alpha ^-)+9F_5 (\alpha ^-)-7F_6 (\alpha ^-)+2F_7 (\alpha ^-)} \right\} , \end{aligned}$$
$$\begin{aligned} K_3 (\alpha )= & {} \int \limits _{\alpha ^+}^{1-\alpha ^{-1}} {\int \limits _{(\alpha \bar{v})^{-1}}^1 {uvdu} dv} +\alpha \cdot \int \limits _{\alpha ^+}^{1-\alpha ^{-1}} {\int \limits _{(\alpha \bar{v})^{-1}}^1 {\left\{ (2u-3u^2)(v\bar{v})-(u-u^2)v^2\right\} du} dv} \\&+\,\alpha ^2\cdot \int \limits _{\alpha ^+}^{1-\alpha ^{-1}} {\int \limits _{(\alpha \bar{v})^{-1}}^1 {(u-3u^2+2u^3)(v\bar{v}^2-v^2\bar{v})du} dv} =\int \limits _{1-\alpha ^-}^{1-\alpha ^{-1}} {\textstyle {1 \over 2}\left\{ v-\alpha ^{-2}v(\bar{v})^{-2}\right\} dv} \\&+\,\alpha \cdot \left\{ {\int \limits _{1-\alpha ^-}^{1-\alpha ^{-1}} {\left\{ (-\alpha ^{-2}v(\bar{v})^{-1}+\alpha ^{-3}v(\bar{v})^{-2})-\left( \textstyle {1 \over 6}v^2-\textstyle {1 \over 2}\alpha ^{-2}v^2(\bar{v})^{-2}+\textstyle {1 \over 3}\alpha ^{-3}v^2(\bar{v})^{-3}\right) \right\} dv} } \right\} \\&+\alpha ^2\cdot \left\{ {\int \limits _{1-\alpha ^-}^{1-\alpha ^{-1}} {\begin{array}{l} \{-\textstyle {1 \over 2}\alpha ^{-2}v+\textstyle {1 \over 2}\alpha ^{-2}v^2(\bar{v})^{-1}+\alpha ^{-3}v(\bar{v})^{-1} \\ -\alpha ^{-3}v^2(\bar{v})^{-2}-\textstyle {1 \over 2}\alpha ^{-4}v(\bar{v})^{-2}+\textstyle {1 \over 2}\alpha ^{-4}v^2(\bar{v})^{-3}\}dv \\ \end{array}} } \right\} \\= & {} \textstyle {1 \over 2}\cdot \{ {F_1 (\alpha ^{-1})-F_1 (\alpha ^-)\}-\textstyle {1 \over 2}\alpha ^{-2}\{G_2^1 (\alpha ^{-1})-G_2^1 (\alpha ^-)} \} \\&+\,\alpha \cdot \left\{ {\begin{array}{l} -\alpha ^{-2}\left\{ G_1^1 (\alpha ^{-1})-G_1^1 (\alpha ^-)\right\} +\alpha ^{-3}\left\{ G_2^1 (\alpha ^{-1})-G_2^1 (\alpha ^-)\right\} -\textstyle {1 \over 6}\left\{ F_2 (\alpha ^{-1})-F_2 (\alpha ^-)\right\} \\ +\textstyle {1 \over 2}\alpha ^{-2}\left\{ G_2^2 (\alpha ^{-1})-G_2^2 (\alpha ^-)\right\} -\textstyle {1 \over 3}\alpha ^{-3}\left\{ G_3^2 (\alpha ^{-1})-G_3^2 (\alpha ^-)\right\} \\ \end{array}} \right\} \\&+\,\alpha ^2\cdot \left\{ {\begin{array}{l} -\textstyle {1 \over 2}\alpha ^{-2}\left\{ F_1 (\alpha ^{-1})-F_1 (\alpha ^-)-G_1^2 (\alpha ^{-1})+G_1^2 (\alpha ^-)\right\} +\alpha ^{-3}\{G_1^1 (\alpha ^{-1})-G_1^1 (\alpha ^-) \\ -G_2^2 (\alpha ^{-1})+G_2^2 (\alpha ^-)\}-\textstyle {1 \over 2}\alpha ^{-4}\left\{ G_2^1 (\alpha ^{-1})-G_2^1 (\alpha ^-)-G_3^2 (\alpha ^{-1})+G_3^2 (\alpha ^-)\right\} \\ \end{array}} \right\} . \\ \end{aligned}$$

Inserting the above into the equation \(\tau _3 (\alpha )=1-8\cdot \left\{ K_1 (\alpha )+K_2 (\alpha )-K_3 (\alpha )\right\} \), rearranging terms, and using the expression for \(\tau _2 (\alpha )\), one obtains the formula

$$\begin{aligned} \tau _3 (\alpha )= & {} \tau _2 (\alpha )-4\Delta _1^F (\alpha )+4(1+\alpha )^2\Delta _3^F (\alpha )-20\alpha (1+\alpha )\Delta _4^F (\alpha )\\&+\,\textstyle {4 \over 3}\alpha (8+27\alpha )\Delta _5^F (\alpha )-28\alpha ^2\Delta _6^F (\alpha ) \\&+\,8\alpha ^2\Delta _7^F (\alpha )+4\Delta _1^{2,G} (\alpha )-4\alpha ^{-1}\Delta _2^{2,G} (\alpha )+\textstyle {4 \over 3}\alpha ^{-2}\Delta _3^{2,G} (\alpha ). \\ \end{aligned}$$

Finally, taking into account the notations one obtains the stated expression. \(\square \)

Let us conclude with a brief outlook on the used methodology and its relationship with current developments. In the literature, various notions of bivariate symmetry play an important role, e.g. marginal, radial and joint symmetry, as well as exchangeability, are quite common (e.g. Nelsen 2006, Sect. 2.7). For example, two random variables are exchangeable if, and only if, its copula is symmetric. Our construction relies on the specific anti-symmetry of Definition 2.2. One can ask whether and how bivariate anti-symmetry might be defined and used for more general bivariate copulas. One might relate such a notion to various concepts of bivariate asymmetry and non-exchangeability (e.g. Joe 2015, Sect. 2.15) as reflected in recent papers by Klement and Mesiar (2006), Nelsen (2007), Durante (2009), Durante et al. (2010), Genest et al. (2012), Dehgani et al. (2013), Rosco and Joe (2013), and Genest and Nešlehová (2014).