Accurate Bayesian Data Classification Without Hyperparameter Cross-Validation

Abstract

We extend the standard Bayesian multivariate Gaussian generative data classifier by considering a generalization of the conjugate, normal-Wishart prior distribution, and by deriving the hyperparameters analytically via evidence maximization. The behaviour of the optimal hyperparameters is explored in the high-dimensional data regime. The classification accuracy of the resulting generalized model is competitive with state-of-the art Bayesian discriminant analysis methods, but without the usual computational burden of cross-validation.

1 Introduction

In the conventional formulation of classification problems, one aims to map data samples x ∈ ℝ^d correctly into discrete classes y ∈ {1, … C}, by inferring the underlying statistical regularities from a given training set $\mathscr{D}=\{(\boldsymbol {x}_{1},y_{1}),\ldots ,(\boldsymbol {x}_{n},y_{n})\}$ of i.i.d. samples and corresponding classes. The standard approach to this task is to define a suitable parametrization p(x, y|θ) of the multivariate distribution from which the samples in $\mathscr{D}$ were drawn. If the number of samples n is large compared to the data dimensionality d, computing point estimates of the unknown parameters θ by maximum likelihood (ML) or maximum a posteriori probability (MAP) methods is accurate and usually sufficient. On the other hand, if the ratio d/n is not small, point estimation–based methods are prone to overfitting. This is the ‘curse of dimensionality’. Unfortunately, the regime of finite d/n is quite relevant for medical applications, where clinical data-sets often report on relatively few patients but contain many measurements per patient.¹

In generative classification models, a crucial role is played by the class-specific sample covariance matrices that capture the correlations between the components of x. These will have to be inferred, either explicitly or implicitly. While the sample covariance matrix Σ is a consistent estimator for the population covariance matrix Σ₀ in the limit d/n → 0, for finite d/n, the empirical covariance eigenvalue distribution ϱ(ξ) is a poor estimator for its population counterpart ϱ₀(λ). This becomes more pronounced as d/n increases.² In addition to the clear bias in covariance estimation induced by high ratios of d/n, the geometry of high-dimensional spaces produces further extreme and often counterintuitive values of probability masses and densities (MacKay 1999).

The overfitting problem has been known for many decades, and many strategies have been proposed to combat its impact on multivariate point estimation inferences. Regularization methods add a penalty term to the ML loss function. The penalty strength acts as a hyperparameter, and is to be estimated. The penalty terms punish, e.g. increasing values of the sum of absolute parameter values (LASSO) or squared parameter values (ridge regression), or a linear combination of these (elastic net) (Zou and Hastie 2005). They appear naturally upon introducing prior probabilities in Bayesian inference, followed by MAP point estimation. Feature selection methods seek to identify a subset of ‘informative’ components of the sample vectors. They range from linear methods such as principal component analysis (Hotelling 1933) to non-linear approaches such as auto-encoders (Hinton and Salakhutdinov 2006). They can guide experimental work, by suggesting which data features to examine. Most of these techniques use heuristics to determine the number of features to select. Early work by Stein et al. (1956) introduced the concept of shrinking a traditional estimator toward a ‘grand average’. In the univariate case, this was an average of averages (Efron and Morris 1977). For the multivariate case, the James-Stein estimator is an admissible estimator of the population covariance matrix (James and Stein 1961). This idea was further developed by Ledoit and Wolf (2004) and Haff (1980). More recent approaches use mathematical tools from theoretical physics to predict (and correct for) the overfitting bias in ML regression analytically (Coolen et al. 2017).

Any sensible generative model for classifying vectors in ℝ^d will have at least ${\mathcal O}(d)$ parameters. The fundamental cause of overfitting is the fact that in high-dimensional spaces, where d/n is finite even if n is large, the posterior parameter distribution $p(\boldsymbol {\theta }|\mathscr{D})$ (in a Bayesian sense) will be extremely sparse. Replacing this posterior by a delta-peak, which is what point estimation implies, is always a very poor approximation, irrespective of which protocol is used for estimating the location of this peak. It follows that by avoiding point estimation altogether, i.e. by retaining the full posterior distribution and doing all integrations over model parameters analytically, one should reduce overfitting effects, potentially allowing for high-dimensional data-sets to be classified reliably. Moreover, only hyperparameters will then have to be estimated (whose dimensionality is normally small, and independent of d), so one avoids the prohibitive computational demands of sampling high-dimensional spaces. The need to do all parameter integrals analytically limits us in practice to parametric generative models with class-specific multivariate Gaussian distributions. Here, the model parameters to be integrated over are the class means in ℝ^d and class-specific d × d covariance matrices, and with carefully chosen priors, one can indeed obtain analytical results. The Wishart distribution is the canonical prior for the covariance matrices. Analytically tractable choices for the class means are the conjugate (Keehn 1965; Geisser 1964) or the non-informative priors (Brown et al. 1999; Srivastava and Gupta 2006).

As the data dimensionality increases, so does the role of Bayesian priors and their associated hyperparameters, and the method used for computing hyperparameters impacts more on the performance of otherwise identical models. The most commonly used route for hyperparameter estimation appears to be cross-validation. This requires re-training one’s model k times for k-fold cross-validation; for leave-one-out cross-validation, the model will need to be re-trained n times.

In this paper, we generalize the family of prior distributions for parametric generative models with class-specific multivariate Gaussian distributions, without loss of analytical tractability, and we compute hyperparameters via evidence maximization, rather than cross-validation. This allows us to derive closed-form expressions for the predictive probabilities of two special model instances. The numerical complexity of our approach does not increase significantly with d since all integrals whose dimensions scale with d are solved analytically.

In Section 2, we first define our generative Bayesian classifier and derive the relevant integrals. Special analytically solvable cases of these integrals, leading to two models (A and B), are described in Section 3 along with the evidence maximization estimation of hyperparameters. Closed-form expressions for the predictive probabilities corresponding to these two models are obtained in Section 3.4. We then examine the behaviour of the hyperparameters in Section 4.1 and carry out comparative classification performance tests on synthetic and real data-sets in Section 5. We conclude our paper with a discussion of the main results.

2 Definitions

2.1 Model and Objectives

We have data $\mathscr{D}=\{(\boldsymbol {x}_{1},y_{1}),\ldots ,(\boldsymbol {x}_{n},y_{n})\}$ consisting of n samples of pairs (x, y), where x ∈ ℝ^d is a vector of covariates, and y ∈ {1, … , C} a discrete outcome label. We seek to predict the outcome y₀ associated with a new covariate vector x₀, given the data $\mathscr{D}$. So we want to compute

$$ \begin{array}{@{}rcl@{}} p(y_{0}|\boldsymbol{x}_{0},\mathscr{D})&=& \frac{p(y_{0},\boldsymbol{x}_{0}|\mathscr{D})} {{\sum}_{y = 1}^{C} p(y,\boldsymbol{x}_{0}|\mathscr{D})} = \frac{p(y_{0},\boldsymbol{x}_{0}|\boldsymbol{x}_{1},\ldots,\boldsymbol{x}_{n};y_{1},\ldots,y_{n})} {{\sum}_{y = 1}^{C} p(y,\boldsymbol{x}_{0}|\boldsymbol{x}_{1},\ldots,\boldsymbol{x}_{n};y_{1},\ldots,y_{n})} \\ &=& \frac{p(\boldsymbol{x}_{0},\ldots,\boldsymbol{x}_{n};y_{0},\ldots,y_{n})} {{\sum}_{y = 1}^{C} p(\boldsymbol{x}_{0},\ldots,\boldsymbol{x}_{n};y,y_{1},\ldots,y_{n})} \end{array} $$

(1)

We next need an expression for the joint distribution p(x₀, … , x_n;y₀, … , y_n). We assume that all pairs (x_i, y_i) are drawn independently from a parametrized distribution p(x, y|θ) whose parameters θ we do not know. Using de Finetti’s representation theorem and the fact that exchangeability is a weaker condition than i.i.d, we can write the joint distribution of $\{ (\boldsymbol {x}_{i},y_{i}) \}_{i = 0}^{n}$ as

$$ \begin{array}{@{}rcl@{}} p(\boldsymbol{x}_{0},\ldots,\boldsymbol{x}_{n};y_{0},\ldots,y_{n})&=& \int\!\mathrm{d}\boldsymbol{\theta} p(\boldsymbol{\theta})\prod\limits_{i = 0}^{n} p(\boldsymbol{x}_{i},y_{i}|\boldsymbol{\theta}) \end{array} $$

(2)

It now follows that

$$ \begin{array}{@{}rcl@{}} p(y_{0}|\boldsymbol{x}_{0},\mathscr{D})&=& \frac{ \int\!\mathrm{d}\boldsymbol{\theta} p(\boldsymbol{\theta}){\prod}_{i = 0}^{n} p(\boldsymbol{x}_{i},y_{i}|\boldsymbol{\theta})} {{\sum}_{y = 1}^{C} \int\!\mathrm{d}\boldsymbol{\theta} p(\boldsymbol{\theta})p(\boldsymbol{x}_{0},y|\boldsymbol{\theta}){\prod}_{i = 1}^{n} p(\boldsymbol{x}_{i},y_{i}|\boldsymbol{\theta})} \end{array} $$

(3)

We regard all model parameters with dimensionality that scales with the covariate dimension d as micro-parameters, over which we need to integrate (in the sense of θ above). Parameters with d-independent dimensionality are regarded as hyperparameters. The hyperparameter values will be called a ‘model’ H. Our equations will now acquire a label H:

$$ \begin{array}{@{}rcl@{}} p(y_{0}|\boldsymbol{x}_{0},\mathscr{D},H)&=& \frac{ \int\!\mathrm{d}\boldsymbol{\theta} p(\boldsymbol{\theta}|H){\prod}_{i = 0}^{n} p(\boldsymbol{x}_{i},y_{i}|\boldsymbol{\theta},H)} {{\sum}_{y = 1}^{C} \int\!\mathrm{d}\boldsymbol{\theta} p(\boldsymbol{\theta}|H)p(\boldsymbol{x}_{0},y|\boldsymbol{\theta},H){\prod}_{i = 1}^{n} p(\boldsymbol{x}_{i},y_{i}|\boldsymbol{\theta},H)} \end{array} $$

(4)

The Bayes-optimal hyperparameters H are those that maximize the evidence, i.e.

$$ \begin{array}{@{}rcl@{}} \hat{H}&=& \text{argmax}_{H} p(H|\mathscr{D}) = \text{argmax}_{H} \log\left\{\frac{p(\mathscr{D}|H)p(H)}{{\sum}_{H^{\prime}}p(\mathscr{D}|H^{\prime})p(H^{\prime})}\right\} \\&=&\text{argmax}_{H} \left\{ \log \int\!\mathrm{d}\boldsymbol{\theta} p(\boldsymbol{\theta}|H)\prod\limits_{i = 1}^{n} p(\boldsymbol{x}_{i},y_{i}|\boldsymbol{\theta},H)+\log p(H)\right\} \end{array} $$

(5)

What is left is to specify the parametrization p(x, y|θ) of the joint statistics of covariates x and y in the population from which our samples are drawn. This choice is constrained by our desire to do all integrations over θ analytically, to avoid approximations and overfitting problems caused by point estimation. One is then naturally led to class-specific Gaussian covariate distributions:

$$ \begin{array}{@{}rcl@{}} p(\boldsymbol{x},y|\boldsymbol{\theta})= p(y)p(\boldsymbol{x}|y,\boldsymbol{\theta}), p(\boldsymbol{x}|y,\boldsymbol{\theta})=\frac{\mathrm{e}^{-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu}_{y})^{T} {\boldsymbol{\Lambda}}_{y}(\boldsymbol{x}-\boldsymbol{\mu}_{y})}}{\sqrt{(2\pi)^{d}/\text{Det}{\boldsymbol{\Lambda}}_{y}}} \end{array} $$

(6)

Thus, the parameters to be integrated over are θ = {μ_y, Λ_y, y = 1, … , C}, i.e. the class-specific means and precision matrices.

2.2 Integrals to be Computed

In both the inference formula $p(y_{0}|\boldsymbol {x}_{0},\mathscr{D},H)$ (4) and in the expression for $\hat {H}$ (5), the relevant integral we need to do analytically is the one in

$$ \begin{array}{@{}rcl@{}} {\Omega}(H,n,\mathscr{D})&=& -\log \int\!\mathrm{d}\boldsymbol{\theta} p(\boldsymbol{\theta}|H)\prod\limits_{i = 1}^{n} p(\boldsymbol{x}_{i},y_{i}|\boldsymbol{\theta},H) \end{array} $$

(7)

In the case where we require ${\Omega }(H,n + 1,\mathscr{D})$, when evaluating the numerator and the denominator of Eq. 4, we simply replace ${\prod }_{i = 1}^{n}$ by ${\prod }_{i = 0}^{n}$, so that

$$ \begin{array}{@{}rcl@{}} p(y_{0}|\boldsymbol{x}_{0},\mathscr{D})= \frac{\mathrm{e}^{-{\Omega}(H,n + 1,\mathscr{D})}}{{\sum}_{z = 1}^{C} \mathrm{e}^{-{\Omega}(H,n + 1,\mathscr{D})}|_{y_{0}=z}} \hat{H}= \text{argmin}_{H} {\Omega}(H,n,\mathscr{D}) \end{array} $$

(8)

Working out ${\Omega }(H,n,\mathscr{D})$ for the parametrization (6) gives:

$$ \begin{array}{@{}rcl@{}} {\Omega}(H,n,\mathscr{D})&=& \frac{1}{2}nd\log(2\pi)-\sum\limits_{i = 1}^{n} \log p_{y_{i}} \\ && -\log \int\!\left[\prod\limits_{z = 1}^{C} \mathrm{d}\boldsymbol{\mu}_{z}\mathrm{d}{\boldsymbol{\Lambda}}_{z} p_{z}(\boldsymbol{\mu}_{z},{\boldsymbol{\Lambda}}_{z})\!\right] \!\left[\prod\limits_{i = 1}^{n} (\text{Det}{\boldsymbol{\Lambda}}_{y_{i}})^{\frac{1}{2}}\!\right] \mathrm{e}^{-\frac{1}{2}{\sum}_{i = 1}^{n} (\boldsymbol{x}_{i}-\boldsymbol{\mu}_{y_{i}})^{T} {\boldsymbol{\Lambda}}_{y_{i}}(\boldsymbol{x}_{i}-\boldsymbol{\mu}_{y_{i}})}\\ \end{array} $$

(9)

where $p(y_{i}) = p_{y_{i}}$ is the prior probability of a sample belonging to class y_i. For generative models, this is typically equal to the empirical proportion of samples in that specific class. To simplify this expression, we define the data-dependent index sets I_z = {i|y_i = z}, each of size $n_{z}=|I_{z}|={\sum }_{i = 1}^{n} \delta _{z,y_{i}}$. We also introduce empirical covariate averages and correlations, with x_i = (x_i1, … , x_id):

$$ \begin{array}{@{}rcl@{}} \hat{X}^{z}_{\mu}=\frac{1}{n_{z}}\sum\limits_{i\in I_{z}} x_{i\mu}, \qquad \hat{C}^{z}_{\mu\nu}=\frac{1}{n_{z}}\sum\limits_{i\in I_{z}} (x_{i\mu}-\hat{X}^{z}_{\mu}) (x_{i\nu}-\hat{X}^{z}_{\nu}) \end{array} $$

(10)

Upon defining the vector $\hat {\boldsymbol {X}}_{z}=(\hat {X}^{z}_{1},\ldots ,\hat {X}^{z}_{d}$), and the d × d matrix $\hat {\boldsymbol {C}}_{\!z}=\{\hat {C}^{z}_{\mu \nu }\}$, we can then write the relevant integrals after some simple rearrangements in the form

$$ \begin{array}{@{}rcl@{}} {\Omega}(H,n,\mathscr{D}) &=& \frac{1}{2}nd\log(2\pi)-\sum\limits_{z = 1}^{C} n_{z} \log p_{z} \\ &&-\log \int\left[\prod\limits_{z = 1}^{C} \mathrm{d}\boldsymbol{\mu}_{z}\mathrm{d}{\boldsymbol{\Lambda}}_{z} p_{z}(\boldsymbol{\mu}_{z},{\boldsymbol{\Lambda}}_{z})(\text{Det}{\boldsymbol{\Lambda}}_{z})^{\frac{n_{z}}{2}} \mathrm{e}^{-\frac{1}{2} n_{z} {\boldsymbol{\mu}_{z}^{T}} {\boldsymbol{\Lambda}}_{z}\boldsymbol{\mu}_{z}}\right] \\&&\times \mathrm{e}^{{\sum}_{z = 1}^{C} \boldsymbol{\mu}_{z}\cdot{\boldsymbol{\Lambda}}_{z}{\sum}_{i\in I_{z}}\boldsymbol{x}_{i}-\frac{1}{2}{\sum}_{z = 1}^{C} {\sum}_{i\in I_{z}} {\boldsymbol{x}_{i}^{T}} {\boldsymbol{\Lambda}}_{z}\boldsymbol{x}_{i}} \\ &=& \frac{1}{2}nd\log(2\pi)-\sum\limits_{z = 1}^{C} n_{z} \log p_{z} \\&&-\sum\limits_{z = 1}^{C} \log \!\int\!\mathrm{d}\boldsymbol{\mu}\mathrm{d}{\boldsymbol{\Lambda}} p_{z}(\boldsymbol{\mu}+\hat{\boldsymbol{X}}_{z},{\boldsymbol{\Lambda}})(\text{Det}{\boldsymbol{\Lambda}})^{\frac{1}{2}n_{z}} \mathrm{e}^{-\frac{1}{2} n_{z}\boldsymbol{\mu}^{T} {\boldsymbol{\Lambda}} \boldsymbol{\mu} -\frac{1}{2} n_{z}\text{Tr}(\hat{\boldsymbol{C}}_{z}{\boldsymbol{\Lambda}})} \end{array} $$

(11)

To proceed, it is essential that we compute ${\Omega }(H,n,\mathscr{D})$ analytically, for arbitrary $\hat {\boldsymbol {X}}\in \text {I\!R}^{d}$ and arbitrary positive definite symmetric matrices $\hat {\boldsymbol {C}}$. This will constrain the choice of our priors p_z(μ, Λ) for the covariate averages and correlations in outcome class z. All required integrals are of the following form, with Λ limited to the subset Ξ^d of symmetric positive definite matrices:

$$ {\Psi}_{z}(H,n,\mathscr{D})= {\int}_{\text{I\!R}^{d}}\!\mathrm{d}\boldsymbol{\mu}{\int}_{{\Xi}^{d}}\!\mathrm{d}{\boldsymbol{\Lambda}} p_{z}(\boldsymbol{\mu}+\hat{\boldsymbol{X}}_{z}|{\boldsymbol{\Lambda}})p_{z}({\boldsymbol{\Lambda}})(\text{Det}{\boldsymbol{\Lambda}})^{\frac{1}{2}n_{z}} \mathrm{e}^{-\frac{1}{2} n_{z}\boldsymbol{\mu}^{T} {\boldsymbol{\Lambda}} \boldsymbol{\mu} -\frac{1}{2} n_{z}\text{Tr}(\hat{\boldsymbol{C}}_{z}{\boldsymbol{\Lambda}}) } $$

(12)

We will drop the indications of the sets over which the integrals are done, when these are clear from the context. The tricky integral is that over the inverse covariance matrices Λ. The choice in Shalabi et al. (2016) corresponded to $p_{z}(\boldsymbol {\mu },{\boldsymbol {\Lambda }})\propto \mathrm {e}^{-\frac {1}{2}\boldsymbol {\mu }^{2}/{\beta _{z}^{2}}}\delta [{\boldsymbol {\Lambda }}-1\!\!\mathrm {I}/{\alpha _{z}^{2}}]$, which implied assuming uncorrelated covariates within each class. Here we want to allow for arbitrary class-specific covariate correlations.

2.3 Priors for Class-Specific Means and Covariance Matrices

The integrals over μ and Λ can be done in either order. We start with the integral over μ. In contrast to most studies, we replace the conjugate prior for the unknown mean vector by a multivariate Gaussian with an as yet arbitrary precision matrix A. This should allow us to cover a larger parameter space than the conjugate prior (which has Λ_z^− 1 as its covariance matrix):

$$ \begin{array}{@{}rcl@{}} p_{z}(\boldsymbol{\mu}|\boldsymbol{A})&=& (2\pi)^{-\frac{d}{2}}\sqrt{\text{Det}\boldsymbol{A}_{z}} \mathrm{e}^{-\frac{1}{2}\boldsymbol{\mu}^{T} \boldsymbol{A}_{z}\boldsymbol{\mu}} \end{array} $$

(13)

Insertion into Eq. 12 gives

$$ \begin{array}{@{}rcl@{}} {\Psi}_{z}&=&(2\pi)^{-\frac{d}{2}}\!\! \int\!\mathrm{d}{\boldsymbol{\Lambda}} p_{z}({\boldsymbol{\Lambda}})\mathrm{e}^{-\frac{1}{2} n_{z}\text{Tr}(\hat{\boldsymbol{C}}_{z}{\boldsymbol{\Lambda}})-\frac{1}{2}\hat{\boldsymbol{X}}_{z}^{T} \boldsymbol{A}_{z}\hat{\boldsymbol{X}}_{z}} \left[ \text{Det}({\boldsymbol{\Lambda}}^{n_{z}}) \text{Det}\boldsymbol{A}_{z}\right]^{\frac{1}{2}} \\ && \times \int\!\mathrm{d}\boldsymbol{\mu} \mathrm{e}^{-\frac{1}{2} \boldsymbol{\mu}^{T} (n_{z}{\boldsymbol{\Lambda}}+\boldsymbol{A}_{z}) \boldsymbol{\mu} -\boldsymbol{\mu}^{T} \boldsymbol{A}_{z}\hat{\boldsymbol{X}}_{z}} \\ &=& \int\!\mathrm{d}{\boldsymbol{\Lambda}} p_{z}({\boldsymbol{\Lambda}})\mathrm{e}^{-\frac{1}{2} n_{z}\text{Tr}(\hat{\boldsymbol{C}}_{z}{\boldsymbol{\Lambda}})} \left[ \frac{\text{Det}({\boldsymbol{\Lambda}}^{n_{z}}) \text{Det}\boldsymbol{A}_{z}}{\text{Det}(n_{z}{\boldsymbol{\Lambda}}+\boldsymbol{A}_{z})}\right]^{\frac{1}{2}} \mathrm{e}^{\frac{1}{2}\boldsymbol{X}^{T} \boldsymbol{A}_{z} (n_{z}{\boldsymbol{\Lambda}}+\boldsymbol{A}_{z})^{-1}\boldsymbol{A}_{z}\hat{\boldsymbol{X}}_{z}-\frac{1}{2}\hat{\boldsymbol{X}}_{z}^{T} \boldsymbol{A}_{z}\hat{\boldsymbol{X}}_{z}} \\ &=& \int\!\mathrm{d}{\boldsymbol{\Lambda}} p_{z}({\boldsymbol{\Lambda}})\mathrm{e}^{-\frac{1}{2} n_{z}\text{Tr}(\hat{\boldsymbol{C}}_{z}{\boldsymbol{\Lambda}})} \!\left[\text{Det}(n_{z}{\boldsymbol{\Lambda}}^{1-n_{z}}\boldsymbol{A}_{z}^{-1}+{\boldsymbol{\Lambda}}^{-n_{z}}) \right]^{-\frac{1}{2}} \mathrm{e}^{-\frac{1}{2}\hat{\boldsymbol{X}}^{T} [(n_{z}{\boldsymbol{\Lambda}})^{-1}+(\boldsymbol{A}_{z})^{-1}]^{-1}\hat{\boldsymbol{X}}_{z}} \\ \end{array} $$

(14)

Our present more general assumptions lead to calculations that differ from the earlier work of, e.g. Keehn (1965), Brown et al. (1999), and Srivastava et al. (2007). Alternative analytically tractable priors are the transformation-invariant Jeffrey’s or Reference priors, which are derived from information-theoretic arguments (Berger et al. 1992). There, the calculation of the predictive probability is simpler, but the sample covariance matrix is not regularized. This causes problems when n < d, where the sample covariance matrices would become singular and the predictive probability would cease to be well defined. Our next question is for which choice(s) of A_z we can do also the integrals over Λ in Eq. 14 analytically. Expression (14), in line with Keehn (1965), Brown et al. (1999), and Srivastava et al. (2007), suggests using for the measure p_z(Λ) over all positive definite matrices Λ ∈ Ξ^d a Wishart distribution, which is of the form

$$ \begin{array}{@{}rcl@{}} p({\boldsymbol{\Lambda}})&=& \frac{(\text{Det}{\boldsymbol{\Lambda}})^{(r-d-1)/2}}{2^{rd/2}{\Gamma}_{d}(\frac{r}{2})(\text{Det}\boldsymbol{S})^{r/2}}\mathrm{e}^{-\frac{1}{2}\text{Tr}({\boldsymbol{S}}^{-1}{\boldsymbol{\Lambda}})} \end{array} $$

(15)

Here, r > d − 1, S is a positive definite and symmetric d × d matrix, and Γ_p(x) is the multivariate gamma function which is expressed in terms of the ordinary gamma function via:

$$ \begin{array}{@{}rcl@{}} {\Gamma}_{p}\left( \frac{r}{2} \right)&=& \pi^{p(p-1)/4}\prod\limits_{j = 1}^{p} {\Gamma} \left( \frac{r}{2}-\frac{j-1}{2} \right) \end{array} $$

(16)

The choice Eq. 15 is motivated solely by analytic tractability. However, since the prior domain is the space of all positive definite matrices, we are assured that upon using Eq. 15, our posterior will be consistent. Distribution (15) implies stating that Λ is the empirical precision matrix of a set of r i.i.d. random zero-average Gaussian vectors, with covariance matrix S. Since Eq. 15 is normalized, for any S, we can use it to do all integrals of the following form analytically:

$$ \begin{array}{@{}rcl@{}} {\int}_{{\Xi}^{d}}\mathrm{d}{\boldsymbol{\Lambda}} (\text{Det}{\boldsymbol{\Lambda}})^{(r-d-1)/2} \mathrm{e}^{-\frac{1}{2}\text{Tr}({\boldsymbol{S}}^{-1}{\boldsymbol{\Lambda}})} &=& 2^{rd/2}{\Gamma}_{d} \left( \frac{r}{2} \right)(\text{Det}\boldsymbol{S})^{r/2} \end{array} $$

(17)

In order for Eq. 14 to acquire the form (17), we need a choice for A_z such that the following holds, for some γ₀, γ₁ ∈ ℝ: [(n_zΛ)^− 1 + (A_z)^− 1]^− 1 = γ_1zΛ + γ_0z1 I. Rewriting this condition gives:

$$ \begin{array}{@{}rcl@{}} \boldsymbol{A}_{z}(\gamma_{0z},\gamma_{1})&=&[(\gamma_{1z}{\boldsymbol{\Lambda}}+\gamma_{0z}1\!\!\mathrm{I})^{-1}- (n_{z}{\boldsymbol{\Lambda}})^{-1}]^{-1} \end{array} $$

(18)

Conditions to ensure A_z is positive definite are considered in the supplementary material. Upon making the choice (18) and using Eq. 17, we obtain for the integral (14):

$$ \begin{array}{@{}rcl@{}} {\Psi}_{z} &=& \mathrm{e}^{-\frac{1}{2}\gamma_{0z}\hat{\boldsymbol{X}}_{z}^{2}}\int\!\mathrm{d}{\boldsymbol{\Lambda}} p_{z}({\boldsymbol{\Lambda}}) \frac{\mathrm{e}^{-\frac{1}{2} n_{z}\text{Tr}(\hat{\boldsymbol{C}}_{z}{\boldsymbol{\Lambda}})-\frac{1}{2}\gamma_{1z}\hat{\boldsymbol{X}}_{z}^{T} {\boldsymbol{\Lambda}}\hat{\boldsymbol{X}}_{z}}}{ \sqrt{\text{Det}[n_{z}{\boldsymbol{\Lambda}}^{1-n_{z}}(\gamma_{1z}{\boldsymbol{\Lambda}}+\gamma_{0z}1\!\!\mathrm{I})^{-1}]}} \end{array} $$

(19)

We conclude that we can evaluate (19) analytically, using Eq. 17, provided we choose for p_z(Λ) the Wishart measure, and with either γ_0z → 0 and γ_1z ∈ (0, n_z) or with γ_1z → 0 and γ_0z ∈ (0, n_zλ_min). Alternative choices for (γ_0z, γ_1z) would lead to more complicated integrals than the Wishart one.

The two remaining analytically integrable candidate model branches imply the following choices for the inverse correlation matrix A_z of the prior p_z(μ|A_z) for the class centres:

$$ \begin{array}{@{}rcl@{}} \gamma_{0z}= 0: \boldsymbol{A}_{z}=\frac{n_{z}\gamma_{1z}}{n_{z}-\gamma_{1z}}{\boldsymbol{\Lambda}},\qquad \gamma_{1z}= 0: \boldsymbol{A}_{z}=\left[\gamma_{0z}^{-1}1\!\!\mathrm{I}-(n_{z}{\boldsymbol{\Lambda}})^{-1}\right]^{-1} \end{array} $$

(20)

Note that the case A_z → 0, a non-informative prior for class means as in Brown et al. (1999), corresponds to (γ_0z, γ_1z) = (0, 0). However, the two limits γ_0z → 0 and γ_1z → 0 will generally not commute, which can be inferred from working out (19) for the two special cases γ_0z = 0 and γ_1z = 0:

$$ \begin{array}{@{}rcl@{}} \gamma_{0z}= 0: &&{\Psi}_{z} =\left( \frac{\gamma_{1z}}{n_{z}}\right)^{\!\frac{d}{2}} \int\!\mathrm{d}{\boldsymbol{\Lambda}} p_{z}({\boldsymbol{\Lambda}})[\text{Det}({\boldsymbol{\Lambda}})]^{\frac{n_{z}}{2}} \mathrm{e}^{-\frac{1}{2} n_{z}\text{Tr}(\hat{\boldsymbol{C}}_{z}{\boldsymbol{\Lambda}})-\frac{1}{2}\gamma_{1z}\hat{\boldsymbol{X}}_{z}^{T} {\boldsymbol{\Lambda}}\hat{\boldsymbol{X}}_{z}} \end{array} $$

(21)

$$ \begin{array}{@{}rcl@{}} \gamma_{1z}= 0: && {\Psi}_{z} = \left( \frac{\gamma_{0z}}{n_{z}}\right)^{\!\frac{d}{2}} \mathrm{e}^{-\frac{1}{2}\gamma_{0z}\hat{\boldsymbol{X}}_{z}^{2}}\int\!\mathrm{d}{\boldsymbol{\Lambda}} p_{z}({\boldsymbol{\Lambda}}) [\text{Det}({\boldsymbol{\Lambda}})]^{\frac{n_{z}-1}{2}} \mathrm{e}^{-\frac{1}{2} n_{z}\text{Tr}(\hat{\boldsymbol{C}}_{z}{\boldsymbol{\Lambda}})} \end{array} $$

(22)

This non-uniqueness of the limit A_z → 0 is a consequence of having done the integral over Λ first.

3 The Integrable Model Branches

3.1 The Case γ_0z = 0: Model A

We now choose γ_0z = 0, and substitute for each z = 1 … C the Wishart distribution Eq. 15 into Eq. 19, with seed matrix S = k_z1 I. This choice is named Quadratic Bayes in Brown et al. (1999). We also define the p × p matrix $\hat {\boldsymbol {M}}_{z}$ with entries $\hat {M}^{z}_{\mu \nu }=X^{z}_{\mu } X^{z}_{\nu }$. The result of working out (19) is, using Eq. 17:

$$ \begin{array}{@{}rcl@{}} {\Psi}_{z} &=&\left( \frac{2^{n_{z}}\gamma_{1z}}{n_{z} k_{z}^{r_{z}}}\right)^{\!\frac{d}{2}}\frac{{\Gamma}_{d}\left( \frac{r_{z}+n_{z}}{2}\right)}{{\Gamma}_{d} \left( \frac{r_{z}}{2}\right)} [\text{Det}(n_{z}\hat{\boldsymbol{C}}_{z}+\gamma_{1z}\hat{\boldsymbol{M}}_{z}+k_{z}^{-1}1\!\!\mathrm{I})]^{-(r_{z}+n_{z})/2} \end{array} $$

(23)

This, in turn, allows us to evaluate (11):

$$ \begin{array}{@{}rcl@{}} {\Omega}(H,n,\mathscr{D})&=& \frac{1}{2}nd\log(\pi)-\sum\limits_{z = 1}^{C} n_{z} \log p_{z} -\frac{1}{2}d\sum\limits_{z = 1}^{C} \left[\log(\gamma_{1z}/n_{z})-r_{z}\log k_{z}\right] \\ &&-\sum\limits_{z = 1}^{C} \log \left[\frac{{\Gamma}_{d}\left( \frac{r_{z}+n_{z}}{2}\right)}{{\Gamma}_{d}\left( \frac{r_{z}}{2}\right)}\right] \\&&+ \frac{1}{2}\sum\limits_{z = 1}^{C} (r_{z}+n_{z})\log \text{Det}(n_{z}\hat{\boldsymbol{C}}_{z}+\gamma_{1z}\hat{\boldsymbol{M}}_{z}+k_{z}^{-1}1\!\!\mathrm{I}) \end{array} $$

(24)

The hyperparameters of our problem are {p_z, γ_1z, r_z, k_z}, for z = 1 … C. If we choose flat hyper-priors, to close the Bayesian inference hierarchy, their optimal values are obtained by minimizing (24), subject to the constraints ${\sum }_{z = 1}^{C} p_{z}= 1$, p_z ≥ 0, r_z ≥ d, γ_1z ∈ [0, n_z], and k_z > 0. We now work out the relevant extremization equations, using the general identity ∂_x log DetQ = Tr(Q^− 1∂_xQ):

• Minimization over p_z: p_z = n_z/n.

• Minimization over k_z:

  $$ \begin{array}{@{}rcl@{}} k_{z}= 0& \text{or} & r_{z}=n_{z}\left[\frac{dk_{z}}{\text{Tr}[ (n_{z}\hat{\boldsymbol{C}}_{z}+\gamma_{1z}\hat{\boldsymbol{M}}_{z}+k_{z}^{-1}1\!\!\mathrm{I})^{-1}}-1\right]^{-1} \end{array} $$

  (25)

• Minimization over r_z, using the digamma function $\psi (x)=\frac {\mathrm {d}}{\mathrm {d} x}\log {\Gamma }(x)$:

  $$ \begin{array}{@{}rcl@{}} r_{z}=d & \text{or} & \log k_{z} =\frac{1}{d}\sum\limits_{j = 1}^{d} \left[ \psi\left( \frac{r_{z}+n_{z}-j + 1}{2}\right) -\psi\left( \frac{r_{z}-j + 1}{2}\right)\right] \\ &&\left.-\frac{1}{d}\log \text{Det}(n_{z}\hat{\boldsymbol{C}}_{z}+\gamma_{1z}\hat{\boldsymbol{M}}_{z}+k_{z}^{-1}1\!\!\mathrm{I}) \right] \\&& \end{array} $$

  (26)

• Minimization over γ_1z:

  $$ \begin{array}{@{}rcl@{}} \gamma_{1z}\in\{0,n_{z}\} & \text{or} &\gamma_{1z} =\frac{1} {r_{z}+n_{z}}\left[\frac{1}{d}\text{Tr}[ (n_{z}\hat{\boldsymbol{C}}_{z}+\gamma_{1z}\hat{\boldsymbol{M}}_{z}+k_{z}^{-1}1\!\!\mathrm{I})^{-1}\hat{\boldsymbol{M}}_{z}]\right]^{-1} \end{array} $$

  (27)

In addition, we still need to satisfy the inequalities r_z ≥ d, γ_1z ∈ [0, n_z], and k_z > 0.

We observe in the above results that, unless we choose γ_1z ∈ {0, n_z}, i.e. A = 0 or A^− 1 = 0, we would during any iterative algorithmic solution of our order parameter equations have to diagonalize a d × d matrix at each iteration step. This would be prohibitively slow, even with the most efficient numerical diagonalization methods. Since γ_1z = n_z implies that the prior p_z(μ|A) forces all class centres to be in the origin, we will be left for the current model branch only with the option γ_1z → 0, corresponding to a flat prior for the class centres. We thereby arrive at the Quadratic Bayes model of Brown et al. (1999), with hyperparameter formulae based on evidence maximization.

3.2 The Case γ_1z = 0: Model B

We next inspect the alternative model branch by choosing γ_1z = 0, again substituting for each z = 1…C the Wishart distribution (15) into Eq. 19 with seed matrix S = k_z1 I. The result is:

$$ \begin{array}{@{}rcl@{}} {\Psi}_{z} &=&\left( \frac{2^{n_{z}-1}\gamma_{0z}}{n_{z} k_{z}^{r_{z}}}\right)^{\!\frac{d}{2}}\frac{{\Gamma}_{d}\left( \frac{r_{z}+n_{z}-1}{2}\right)}{{\Gamma}_{d}(\frac{r_{z}}{2})} [\text{Det}(n_{z}\hat{\boldsymbol{C}}_{z}+k_{z}^{-1}1\!\!\mathrm{I})]^{-(r_{z}+n_{z}-1)/2} \mathrm{e}^{-\frac{1}{2}\gamma_{0z}\hat{\boldsymbol{X}}^{2}_{z}} \end{array} $$

(28)

For the quantity (11), we thereby find:

$$ \begin{array}{@{}rcl@{}} {\Omega}(H,n,\mathscr{D})&=& \frac{1}{2}nd\log(\pi)+\frac{1}{2}dC\log 2-\sum\limits_{z = 1}^{C} n_{z} \log p_{z} -\frac{1}{2}d\sum\limits_{z = 1}^{C} \left[\!\log\!\left( \frac{\gamma_{0z}}{n_{z}}\right)-r_{z}\log k_{z}\right] \\&&-\sum\limits_{z = 1}^{C} \log \left[\frac{{\Gamma}_{d}\left( \frac{r_{z}+n_{z}-1}{2}\right)}{{\Gamma}_{d}\left( \frac{r_{z}}{2}\right)}\right] +\frac{1}{2}\sum\limits_{z = 1}^{C} \gamma_{0z}\hat{\boldsymbol{X}}^{2}_{z} \\ &&+ \frac{1}{2}\sum\limits_{z = 1}^{C} (r_{z}+n_{z}-1)\log \text{Det}(n_{z}\hat{\boldsymbol{C}}_{z}+k_{z}^{-1}1\!\!\mathrm{I}) \end{array} $$

(29)

If as before we choose flat hyper-priors, the Bayes-optimal hyperparameters {p_z, γ_1z, r_z, k_z}, for z = 1…C are found by maximizing the evidence (29), subject to the constraints ${\sum }_{z = 1}^{C} p_{z}= 1$, p_z ≥ 0, r_z ≥ d, γ_0z ≥ 0, and k_z > 0. For the present model branch B, differentiation gives:

• Minimization over p_z: p_z = n_z/n.

• Minimization over k_z:

  $$ \begin{array}{@{}rcl@{}} k_{z}= 0& \text{or} & r_{z}=(n_{z}-1)\left[\frac{dk_{z}}{\text{Tr}[ (n_{z}\hat{\boldsymbol{C}}_{z}+k_{z}^{-1}1\!\!\mathrm{I})^{-1}}-1\right]^{-1} \end{array} $$

  (30)

• Minimization over r_z:

  $$ \begin{array}{@{}rcl@{}} r_{z}=d & \text{or} & \log k_{z} =\frac{1}{d}\sum\limits_{j = 1}^{d} \left[ \psi\left( \!\frac{r_{z}+n_{z}-j}{2}\right)\! -\psi\!\left( \!\frac{r_{z}-j + 1}{2}\!\right)\right] -\frac{1}{d}\log \text{Det}(n_{z}\hat{\boldsymbol{C}}_{z}+k_{z}^{-1}1\!\!\mathrm{I})\\ \end{array} $$

  (31)

• Minimization over γ_0z: $\gamma _{0z}=d/\hat {\boldsymbol {X}}^{2}_{z}$.

In addition, we still need to satisfy the inequalities r_z ≥ d and k_z > 0. In contrast to the first integrable model branch A, here we are able to optimize over γ_0z without problems, and the resulting model B is distinct from the Quadratic Bayes classifier of Brown et al. (1999).

3.3 Comparison of the Two Integrable Model Branches

Our initial family of models was parametrized by (γ_0z, γ_1z). We then found that the following two branches are analytically integrable, using Wishart priors for class-specific precision matrices:

$$ \begin{array}{@{}rcl@{}} \mathrm{A}: && (\gamma_{0z},\gamma_{1z})=(0,\hat{\gamma}_{1z})~~\text{with}~~ \hat{\gamma}_{1z}\to 0 \end{array} $$

(32)

$$ \begin{array}{@{}rcl@{}} \mathrm{B}: && (\gamma_{0z},\gamma_{1z})=(\hat{\gamma}_{0z},0)~~ \text{with~~} \hat{\gamma}_{0z}\to d/\hat{\boldsymbol{X}}_{z}^{2} \end{array} $$

(33)

Where conventional methods tend to determine hyperparameters via cross-validation, which is computationally expensive, here we optimize hyperparameters via evidence maximization. As expected, both models give p_z = n_z/n. The hyperparameters (k_z, r_z) are to be solved from the following equations, in which ϱ_z(ξ) denotes the eigenvalue distribution of $\hat {\boldsymbol {C}}_{z}$:

$$ \begin{array}{@{}rcl@{}} \mathrm{A}: && k_{z}= 0 \text{ or } r_{z}=n_{z}\left[\frac{1}{\int\!\mathrm{d}\xi \rho_{z}(\xi) (n_{z}k_{z}\xi+ 1)^{-1}}-1\right]^{-1} \end{array} $$

(34)

$$ \begin{array}{@{}rcl@{}} && r_{z}=d \text{ or } \frac{1}{d}\sum\limits_{j = 1}^{d} \left[ \psi\left( \frac{r_{z}+n_{z}-j + 1}{2}\right) {-}\psi\left( \frac{r_{z}-j + 1}{2}\right)\right] =\int\!\mathrm{d}\xi \rho_{z}(\xi)\log(n_{z}k_{z}\xi+ 1)\\ \end{array} $$

(35)

$$ \begin{array}{@{}rcl@{}} \mathrm{B}: && k_{z}= 0 \text{ or } r_{z}=(n_{z}-1)\left[\frac{1}{\int\!\mathrm{d}\xi \rho_{z}(\xi) (n_{z}k_{z}\xi+ 1)^{-1}}-1\right]^{-1} \end{array} $$

(36)

$$ \begin{array}{@{}rcl@{}} && r_{z}=d \text{ or } \frac{1}{d}\sum\limits_{j = 1}^{d} \left[ \psi\left( \frac{r_{z}+n_{z}-j}{2}\right) -\psi\left( \frac{r_{z}-j + 1}{2}\right)\right] =\int\!\mathrm{d}\xi \rho_{z}(\xi)\log (n_{z}k_{z}\xi+ 1)\\ \end{array} $$

(37)

We see that the equations for (k_z, r_z) of models A and B differ only in having the replacement n_z → n_z − 1 in certain places. Hence, we will have $\left ({k_{z}^{A}},{r_{z}^{A}}\right )=\left ({k_{z}^{B}},{r_{z}^{B}}\right )+{\mathcal O}(n_{z}^{-1})$.

3.4 Expressions for the Predictive Probability

Starting from Eq. 8, we derive an expression for the predictive probability for both models (see supplementary material). The predictive probability for model B:

$$ \begin{array}{@{}rcl@{}} p(y_{0}|\boldsymbol{x}_{0},\mathscr{D})\!\!&=&\!\! \frac{W_{y_{0}} \mathrm{e}^{- \frac{\gamma_{0 y_{0}}}{2(n_{y_{0}}+ 1)}\!\left[ 2\hat{\boldsymbol{X}}_{y_{0}} \cdot(\boldsymbol{x}_{0}-\hat{\boldsymbol{X}}_{y_{0}} ) +\frac{1}{n_{y_{0}}+ 1}(\boldsymbol{x}_{0}-\hat{\boldsymbol{X}}_{y_{0}} )^{2} \right]} \!\!\left( \!1\!+\frac{n_{y_{0}}}{n_{y_{0}}+ 1}(\boldsymbol{x}_{0}-\!\hat{\boldsymbol{X}}_{y_{0}})\!\cdot\! \boldsymbol{\Xi}_{y_{0}}^{-1}(\boldsymbol{x}_{0}-\!\hat{\boldsymbol{X}}_{y_{0}})\!\right)^{\!-\frac{1}{2} (r_{y_{0}}\!+n_{y_{0}})}} {{\sum}_{z = 1}^{C} W_{z} \mathrm{e}^{-\frac{ \gamma_{0 z}}{2(n_{z}+ 1)}\left[ 2\hat{\boldsymbol{X}}_{z} \cdot(\boldsymbol{x}_{0}-\hat{\boldsymbol{X}}_{z} ) +\frac{1}{n_{z}+ 1}(\boldsymbol{x}_{0}-\hat{\boldsymbol{X}}_{z} )^{2} \right]} \!\left( \!1+\frac{n_{z}}{n_{z}+ 1}(\boldsymbol{x}_{0}-\hat{\boldsymbol{X}}_{z})\cdot\boldsymbol{\Xi}_{y_{0}}^{-1}(\boldsymbol{x}_{0}-\hat{\boldsymbol{X}}_{z})\right)^{-\frac{1}{2} (r_{z}\!+n_{z})}} \\ \end{array} $$

(38)

with p_z = n_z/n, and

$$ \begin{array}{@{}rcl@{}} W_{z}= p_{z}\left( \frac{n_{z}}{n_{z}+ 1}\right)^{\frac{d}{2}}\frac{{\Gamma}\left( \frac{r_{z}+n_{z}}{2}\right)} {{\Gamma}\left( \frac{r_{z}+n_{z}-d}{2}\right)}[\text{Det}\boldsymbol{\Xi}_{z}]^{-\frac{1}{2}}, \quad \gamma_{0z}=d/\hat{\boldsymbol{X}}^{2}_{z},\quad {\Xi}_{z}=n_{z}\hat{\boldsymbol{C}}_{z}\!+k_{z}^{-1}1\!\!\mathrm{I}\\ \end{array} $$

(39)

Upon repeating the same calculations for model A, one finds that its predictive probability is obtained from expression (38) simply by setting $\gamma _{0 y_{0}}$ to zero (keeping in mind that for model A, we would also insert into this formula distinct values for the optimal hyperparameters k_z and r_z).

4 Phenomenology of the Classifiers

4.1 Hyperparameters: LOOCV Versus Evidence Maximization

The most commonly used measure for classification performance is the percentage of samples correctly predicted on unseen data (equivalently, the trace of the confusion matrix), and most Bayesian classification methods also use this measure as the optimization target for hyperparameters, via cross-validation. Instead, our method of hyperparameter optimization maximizes the evidence term in the Bayesian inference. In k-fold cross-validation, one needs to diagonalize for each outcome class a d × d matrix k times, whereas using the evidence maximization route, one needs to diagonalize such matrices only once, giving a factor k reduction in what for large d is the dominant contribution to the numerical demands. Moreover, cross-validation introduces fluctuations into the hyperparameter computation (via the random separations into training and validation sets), whereas evidence maximization is strictly deterministic.

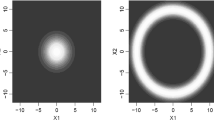
The two routes, cross-validation versus evidence maximization, need not necessarily lead to coincident hyperparameter estimates. In order to investigate such possible differences, we generated synthetic data-sets with equal class sizes n₁ = n₂ = 50, and with input vectors of dimension d = 50. Using a 100 × 100 grid of values for the hyperparameters k₁ and k₂, with k_z ∈ [0, k_{max, z}], we calculated the leave-one-out cross-validation (LOOCV) estimator of the classification accuracy for unseen cases, for a single data realization. The values of (r₁, r₂) were determined via evidence maximization, using formula (35) (i.e. following model branch A, with the non-informative prior for the class means). The value k_{max, z} is either the upper limit defined by the condition r_z > d − 1 (if such a limit exists, dependent on the data realization), otherwise set numerically to a fixed large value. The location of the maximum of the resulting surface determines the LOOCV estimate of the optimal hyperparameters (k₁, k₂), which can be compared to the optimized hyperparameters (k₁, k₂) of the evidence maximization method.

Figure 1 shows the resulting surface for uncorrelated data, i.e. $\mathbf {\Sigma }_{1}=\mathbf {\Sigma }_{2}=\mathbb {I}_d$. The comparison points from our evidence-based optimal hyperparameters (k₁, k₂) are shown in Table 1. The small values for (k₁, k₂) imply that the model correctly infers that the components of x in each class are most likely uncorrelated. The same protocol was subsequently repeated for correlated data, using a Toeplitz covariance matrix, the results of which are shown in Fig. 2 and Table 1. The larger values for (k₁, k₂) imply that here the model correctly infers that the components of x in each class are correlated. In both cases, the differences between optimal hyperparameter values defined via LOOCV as opposed to evidence maximization are seen to be minor (Table 2).

Fig. 1

LOOCV classification accuracy in (k₁, k₂) space for uncorrelated synthetic data, with class means μ₁ = (0, 0, … , 0) and μ₂ = (2.5, 0, … , 0), population covariance matrices $\mathbf {\Sigma }_{1}=\mathbf {\Sigma }_{2}=\mathbb {I}_d$, and covariate dimension d = 50. The hyperparameters (r₁, r₂) for models A and B were determined via Eq. 35. The results are based on a single data realization

Fig. 2

LOOCV classification accuracy in (k₁, k₂) space for correlated synthetic data, with class means μ₁ = (0, 0, … , 0) and μ₂ = (2.5, 0, … , 0), population covariance matrices Σ₁ = Σ₂ = Σ of symmetric Toeplitz form with first row (d, d − 1, … , 2, 1), and covariate dimension d = 50. The hyperparameters (r₁, r₂) for models A and B were determined via Eq. 35. The results are based on a single data realization

Table 1 Comparison of hyperparameter estimation using cross-validation and evidence maximization for correlated and uncorrelated data

Table 2 Comparison of classification accuracy using cross-validation and evidence maximization methods for estimating hyperparameters using the same data as Figs. 1 and 2

4.2 Overfitting

Next, we illustrate the degree of overfitting for models A and B, using examples of both correlated and uncorrelated synthetic data-sets. We sampled from the data described in Table 3, using case 1 (uncorrelated) and case 8 (correlated). In all cases, we chose C = 3 classes of n_z = 13 samples each, for a broad range of data dimensions d. See the caption of Table 3 for a full description of the statistical features of these synthetic data-sets. Measuring training and validation classification performance via LOOCV on these data resulted in Fig. 3, where each data-point is an average over 250 simulation experiments. The degree of divergence between the training and validation curves (solid versus dashed) is a direct measure of the degree of overfitting. We observe that model B overfits less for uncorrelated data, and model A overfits less for correlated data. This pattern is also seen more generally in Table 4, for a broader range of synthetic data-sets. However, we note that all models still perform significantly above the random guess level on unseen data, even when d ≫ n_z. For instance, for d = 150 (corresponding to d/n_z ≈ 11.5), the Bayesian models can still classify some 80% of the unseen data correctly.

Fig. 3

Overfitting in models A and B as measured via LOOCV. Top—uncorrelated data (case 1 in Table 3). Bottom—correlated data (case 8 in Table 3). In all cases, n_z = 13 for each of the three classes. Solid lines—classification accuracy on training samples; dashed lines—classification accuracy on validation samples. Horizontal dotted line—baseline performance of a random guess classifier

Table 3 Description of synthetic data-sets

Table 4 Classification performance for synthetic data-sets

We thank the reviewers for pointing out other measurements of agreement between true and predicted values in particular the adjusted Rand Index (Morey and Agresti 1984; Hubert and Arabie 1985) which neatly corrects for chance prediction results.

5 Classification Accuracy

We compare the classification accuracy of our Bayesian models A and B, with hyperparameters optimized by evidence maximization, to other successful state-of-the-art generative classifiers from Srivastava et al. (2007). These include the distribution-based Bayesian classifier (BDA7), the Quadratic Bayes (QB) classifier (Brown et al. 1999), and a non-Bayesian method, the so-called eigenvalue decomposition discriminant analysis (EDDA) as described in Bensmail and Celeux (1996). All three use cross-validation for model selection and hyperparameter estimation. The classifiers (our models A and B and the three benchmark methods from Srivastava et al. (2007)) are all tested on the same synthetic and real data-sets, and following the definitions and protocols described in Srivastava et al. (2007), for a fair comparison. Model A differs from Quadratic Bayes (Brown et al. 1999) only in that our hyperparameters have been estimated using evidence maximization, as described in Section 3, rather than via cross-validation. Model A is seen in Table 4 to have lower error rates than Quadratic Bayes in the majority of the synthetic data-sets. In contrast, model B is mathematically different from both model A and Quadratric Bayes.

5.1 Implementation

The classifier was implemented in MATLAB.³ The leave-one-out cross-validation pseudo-code is displayed below.

The rate-limiting step in the algorithm is calculation of sample eigenvalues (approximately $\mathcal {O}(d^{3})$). Figure 4 shows the relationship between algorithm time and data dimension for binary classification with 100 data samples.⁴

Fig. 4

Processing time in seconds for binary classification on synthetic data (50 samples in each class). Both models had similar timings so only model A is plotted. Note the logarithmic scale

5.2 Synthetic Data

The study of Srivastava et al. (2007) used a set of ten synthetic data-sets, all with Gaussian multivariate covariate distributions and a range of choices for class-specific means and covariance matrices. In the present study, we generated data with exactly the same statistical features. The first six of these choices were also used in Friedman (1989) and involve diagonal covariance matrices. The remaining four represent correlated data. Each data-set has C = 3 outcome classes and is separated into a training set, with n_z = 13 samples in each class, and a validation set, with n_z = 33 samples in each class. In terms of the balance n_z/d, this allows for a direct comparison with the dimensions used in Srivastava et al. (2007). The results shown in Table 4 are all averages over 100 synthetic data runs. The data dimensions are chosen from d ∈ {10, 50, 100}. Since all these synthetic data-sets involve multivariate Gaussian covariate distributions, there is no model mismatch with any of the models being compared.

The means and covariance matrices of the synthetic data-sets are given in Table 3. The covariance matrices for the correlated data-sets are defined in terms of auxiliary random d × d matrices R_z, with i.i.d. entries sampled from the uniform distribution on the interval [0,1], according to either $\mathbf {\Sigma }_{z}=\mathbf {R}_{z}^{T} \mathbf {R}_{z}$ or $\mathbf {\Sigma }_{z}=\mathbf {R}_{z}^{T} \mathbf {R}_{z} \mathbf {R}_{z}^{T} \mathbf {R}_{z}$. These covariance matrices have a single dominant eigenvalue, and further non-dominant eigenvalues that are closer to zero for data-sets 9-10. Data-sets 7 and 9 have all class means at the origin, whereas each element of the class mean vectors from data-sets 8 and 10 is independently sampled from a standard normal distribution.

Table 4 shows the classification error rates, as percentages of misclassified samples over the validation set. The variability of these for results for the models BDA7, QB, and EDDA, i.e. the error bars in the classification scores, is not reported in Srivastava et al. (2007) (where only the best classifier was determined using a signed ranked test). For completeness, we have included in this study the standard deviation of the error rate over the 100 synthetic data runs for our models A and B. Given that all experiments involved the same dimensions of data-sets and similar average error rates, the error bars for the Srivastava et al. (2007) results are expected to be similar to those of models A and B. We conclude from Table 4 that our models A and B perform on average quite similarly to the benchmark classifiers BDA7, QB, and EDDA. On some data-sets, model A and/or B outperform the benchmarks, on others they are outperformed. However, models A and B achieve this competitive level of classification accuracy without cross-validation, i.e. at a much lower computational cost.

5.3 Real Data

Next, we test the classification accuracy of our models against the real data-sets used in Srivastava et al. (2007), which are publicly available from the UCI machine learning repository.⁵ Three data-sets were left out due to problems with matching the formats: Image segmentation (different number of samples than Srivastava et al. (2007)), Cover type (different format of training/validation/test), and Pen digits (different format of training/validation/test). Before classification, we looked for identifying characteristics which could allow for retrospective interpretation of the results, e.g. occurrence of discrete covariate values, covariance matrix entropies, or class imbalances. None were found to be informative. No scaling or pre-processing was done to the data before classification.

We duplicated exactly the protocol of Srivastava et al. (2007), whereby only a randomly chosen 5% or 10% of the samples from each class of each data-set are used for training, leaving the bulk of the data (95% or 90%) to serve as validation (or test) set. The resulting small training sample sizes lead to n_z ≪ d for a number of data-sets, providing a rigorous test for classifiers in overfitting-prone conditions. For example, the set Ionosphere, with d = 34, has original class sizes of 225 and 126 samples leading in the 5% training scenario to training sets with n₁ = 12 and n₂ = 7. We have used the convention of rounding up any non-integer number of training samples (rounding down the number of samples had only a minimal effect on most error rates). The baseline column gives the classification error that would be obtained if the majority class is predicted every time.

We conclude from the classification results shown in Tables 5 and 6 (which are to be interpreted as having non-negligible error bars) that also for the real data, models A and B are competitive with the other Bayesian classifiers. The exceptions are Ionosphere (where models A and B outperform the benchmark methods, in both tables) and the data-sets Thyroid and Wine (where in Table 6, our model A is being outperformed). Note that in Table 6, Thyroid and Wine have only 2 or 3 data samples in some classes of the training set. This results in nearly degenerate class-specific covariance matrices, which hampers the optimization of hyperparameters via evidence maximization. Model B behaves well even in these tricky cases, presumably due to the impact of its additional hyperparameter $\gamma _{0z}=d/\hat {\boldsymbol {X}}^{2}_{z}$. As expected, upon testing classification performance using leave-one-out cross-validation (details not shown here) rather than the 5% or 10% training set methods above, all error rates are significantly lower.

Table 5 Average error rate using randomly selected 10% of training samples in each class

Table 6 Average error rate using randomly selected 5% of training samples in each class

Examining the results from Sections 5.2 and 5.3 does not lead us to conclusions on when one specific model outperforms the other. We are currently pursuing two approaches to this problem: (1) finding analytical expressions for the probability of misclassification similar to Raudys and Young (2004) but with the true data-generating distribution different from model assumptions and (2) numerical work generating synthetic data from a multivariate t-distribution with varying degrees of freedom.

6 Discussion

In this paper, we considered generative models for supervised Bayesian classification in high-dimensional spaces. Our aim was to derive expressions for the optimal hyperparameters and predictive probabilities in closed form. Since the dominant cause of overfitting in the classification of high-dimensional data is using point estimates for high-dimensional parameter vectors, we believe that by carefully choosing Bayesian models for which parameter integrals are analytically tractable, we will need point estimates only at hyperparameter level, reducing overfitting.

We showed that the standard priors of Bayesian classifiers that are based on class-specific multivariate Gaussian covariate distributions can be generalized, from which we derive two special model cases (A and B) for which predictive probabilities can be derived analytically in fully explicit form. Model A is known in the literature as Quadratic Bayes (Brown et al. 1999), whereas model B is novel and has not yet appeared in the literature. In contrast to common practice for most Bayesian classifiers, we use evidence maximization (MacKay 1999) to find analytical expressions for our hyperparameters in both models. This allows us to find their optimal values without needing to resort to computationally expensive cross-validation protocols.

We found that the alternative (but significantly faster) hyperparameter determination by evidence maximization leads to hyperparameters that are generally very similar to those obtained via cross-validation, and that the classification performance of our models A and B degrades only gracefully in the ‘dangerous’ regime n ≪ d where we would expect extreme overfitting. We compared the classification performance of our models on the extensive synthetic and real data-sets that have been used earlier as performance benchmarks in Srivastava and Gupta (2006) and Srivastava et al. (2007). Interestingly, the performance of our models A and B turned out to be competitive with state-of-the-art Bayesian models that use cross-validation, despite the large reduction in computational expense. This will enable users in practice to classify high-dimensional data-sets quicker, without compromising on accuracy.

This paper shows that the analytical approach merits further investigation. Calculating the predictive probability for arbitrary γ_0z, γ_1z values remains to be done. The main obstacle being the resulting symbolic integration. We believe this could lead to interesting analytically tractable classification models.