Egalitarianism, utilitarianism, and the Nash bargaining solution

Abstract

A bargaining solution satisfies egalitarian–utilitarian monotonicity (EUM) if the following holds under feasible-set-expansion: a decrease in the value of the Rawlsian (resp. utilitarian) objective is accompanied by an increase in the value of the utilitarian (resp. Rawlsian) objective. A bargaining solution is welfarist if it maximizes a symmetric and strictly concave social welfare function. Every 2-person welfarist solution satisfies EUM, but for $n\ge 3$ every n-person welfarist solution violates it. In the presence of other standard axioms, EUM characterizes the Nash solution in the 2-person case, but leads to impossibility in the n-person case.

1 Introduction

Egalitarianism and utilitarianism are key concepts of distributive justice, and the tension between them is the subject of vibrant debates between the supporters of these opposing schools of thought (see, e.g., the book by Fleurbaey et al. 2008). Given this tension, it is natural to look for a “golden path”: a criterion that respects, simultaneously, a minimal degree of both utilitarianism and egalitarianism. In the present paper I investigate one possible “golden path” in the context of Nash’s (1950) bargaining theory.

In Nash’s bargaining model a generic problem is denoted by S, and it consists of non-negative utility vectors from which a single vector needs to be selected.¹ A bargaining solution assigns a unique point for every problem, $f(S)\in S$. Let $U(x)\equiv \sum x_i$ and $R(x)\equiv \text {min}_ix_i$. The utilitarian solution maximizes U on every problem and the egalitarian solution selects for every problem the maximal feasible point whose coordinates are equal to one another; under standard assumptions on the structure of the problem, this equal-coordinates point maximizes R.²

Typically, $\text {argmax}_{s\in S}U(s)\cap \text {argmax}_{s\in S}R(s)=\emptyset$. If one finds merits in both U and R, then the question arises of how to create a compromise between them. Any solution which is designed to create such a compromise should, I believe, adhere to the following requirement: For all $S\subset T$:

• $R(f(T))<R(f(S))\Rightarrow U(f(T))>U(f(S))$;

  and

• $U(f(T))<U(f(S))\Rightarrow R(f(T))>R(f(S))$.

That is, when opportunities expand, a decrease in the value of the objective-function of one criterion (utilitarianism or egalitarianism) must be accompanied by an increase in the value of the objective-function of the other criterion. Say that a solution satisfies egalitarian–utilitarian monotonicity (EUM) if it meets this requirement.

The justification for EUM is that if one recognizes the validity of the positions of both utilitarians and egalitarians, and if no consideration justifies hurting both utilitarians and egalitarians simultaneously, then it would not be desirable to use a solution that, upon an enlargement of the feasible set, makes both constituencies unhappy. If one makes the utilitarians unhappy, there should be a benefit to the egalitarians, and vice versa.

Though EUM’s building blocks are utilitarianism and egalitarianism—two specific welfarist criteria—in the 2-person case it has the following general aspect: every bargaining solution which is the maximizer of some symmetric and strictly concave social welfare function—hereafter, a welfarist solution—satisfies EUM. By contrast, if there are more than two players, every welfarist solution violates EUM. Another distinction between the 2-person case and the n-person case is that once EUM is combined with other standard axioms, a characterization of the Nash solution is obtained in the 2-person case, but in the n-person case this combination results in impossibility.³$^,$⁴

The connections among egalitarianism, utilitarianism, and the Nash bargaining solution have been studied ever since the pioneering work of Shapley (1969), who showed that the Nash solution is the only solution that maximizes the utilitarian and Rawlsian objectives simultaneously for an appropriate rescaling of the individual utilities.⁵ Mariotti (1999) showed that the Nash solution is characterized by scale covariance and Suppes-Sen dominance (SSD). A vector xSuppes-Sen dominates (SS-dominates) another vector y if there is a permutation of x such that the permuted vector, call it $x'$, Pareto-dominates y; namely, $x'>y$.⁶ SSD requires that the solution point not be SS-dominated by any other feasible point. SSD expresses the view that it does not matter which person enjoys what payoff, it only matters what payoffs are being distributed; clearly, it is a weakening of both utilitarianism and egalitarianism. Anbarci and Sun (2011b) showed that Mariotti’s result can be improved by weakening SSD to an axiom called weak SSD, which requires that there be no feasible point that dominates the solution point both in the SS-sense and in an additional sense, called equity dominance. The present paper contributes to this literature by providing a further ethical foundation for the 2-person Nash bargaining solution.

The rest of the paper is organized as follows. Definitions and axioms are presented in Sect. 2. The connection between EUM and welfarism is studied in Sect. 3. In Sect. 4 I show how the combination of EUM with other standard axioms results in a characterization of the Nash solution in the 2-person case, and in impossibility in the n-person case. Both egalitarianism and utilitarianism are based on the idea that utilities of different individuals are comparable; hence, EUM is also based on that assumption. This may seem inconsistent with the Nash solution, which is typically thought of as precluding such comparisons. In Sect. 5 I address this issue and argue that the discrepancy can be settled. There, I also address the issue of symmetry, and highlight the important role it has in my analysis. In Sect. 6 I conclude.

2 Definitions and axioms

A problem is a compact and convex set $S\subset {\mathbb {R}}_+^n$ that contains the origin $\mathbf{0 }\equiv (0,\ldots ,0)$, contains a vector with all coordinates strictly positive, and is comprehensive. Comprehensiveness means that if $x\in S$ then $y\in S$, for every y that satisfies $\mathbf{0 }\le y\le x$.⁷

Let $\Delta _r\equiv \{x\in {\mathbb {R}}_+^n:\sum x_j\le r\}$. The bargaining domain in this paper is:

$$\begin{aligned} \{S:|\text {argmax}_{s\in S}U(S)|=1\}\cup \{\Delta _r: r>0\}. \end{aligned}$$

That is, the bargaining domain consists of problems for which one of the following applies: (1) the utilitarian point is unique, or (2) the problem is a simplex.

The weak Pareto frontier ofS is $WP(S)\equiv \{x\in S: y>x\Rightarrow y\notin S\}$ and its strong Pareto frontier is $P(S)\equiv \{x\in S: y\gneqq x\Rightarrow y\notin S\}$. The best that player i can hope for in S—his ideal payoff in S—is $a_i(S)\equiv \text {max}\{s_i: s\in S\}$. The point $a(S)\equiv (a_1(S),\ldots ,a_n(S))$ is called the ideal point of S.

A solution is a map f that assigns a unique point for every problem, $f(S)\in S$. The following are important solutions. The Nash solutionN (Nash 1950) maximizes $\Pi _is_i$ over $s\in S$ for every S. The egalitarian solutionE (Kalai 1977) assigns for every S the maximal feasible point of the form $(\lambda ,\lambda ,\ldots ,\lambda )$. The utilitarian solution, u, assigns for every S the maximizer of U(s) over $s\in S$; on a simplex $\Delta _r$, for which the utility-sum-maximizer is not unique, this solution is defined to select $(\frac{r}{n},\ldots ,\frac{r}{n})$. The Kalai–Smorodinsky solutionKS (Kalai and Smorodinsky 1975) assigns for every S the point $\lambda a(S)$, where $\lambda$ is the maximum possible. The i-th dictatorial solution, $D^i$, assigns for every S the vector whose i-th coordinate is $a_i(S)$ and every other coordinate is zero. The disagreement solution, D, assigns for every problem the origin. The midpoint solution assigns for each S the point $m(S)\equiv \frac{1}{n}a(S).$

The following are axioms a solution may satisfy. In their statements, S and T are arbitrary problems. Since the axioms are well-known, I skip a discussion thereof.

Pareto optimality (PO): $f(S)\in P(S)$.

Weak Pareto optimality (WPO): $f(S)\in WP(S)$.

Symmetry (SY): If $S=\pi S$ for every permutation $\pi$, then $f_1(S)=\cdots =f_n(S)$.⁸

Suppes-Sen dominance (SSD): There does not exist an $s\in S$ and a permutation $\pi$, such that $\pi s>f(S)$.

Scale covariance (S.COV): $f(l\circ S)=l(f(S))$, for every vector of positive linear transformation $l=(l_1,\ldots ,l_n)$.

Conflict-freeness (CF): $a(S)\in S\Rightarrow f(S)=a(S)$.

Independence of irrelevant alternatives (IIA): $[f(T)\in S\subset T]\Rightarrow f(S)=f(T)$.

Restricted Independence of irrelevant alternatives (RIIA): $[f(T)\in S\subset T] \& [\exists r\le 1 s.t a(S)=ra(T)]\Rightarrow f(S)=f(T)$.

3 Welfarism

A symmetric, strictly concave and non-decreasing function $W:{\mathbb {R}}_+^n\rightarrow {\mathbb {R}}$ is called a social welfare function (SWF).⁹ A solution f is welfarist if there exists a SWF W such that $f(S)\equiv \text {argmax}_{s\in S}W(s)$. A solution which is not welfarist is called non-welfarist.

Proposition 1

Let $n=2$. Let f be a welfarist solution. Then f satisfies egalitarian–utilitarian monotonicity.

Proof

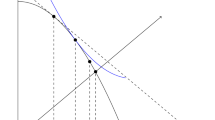
Let $n=2$, let f be a welfarist solution whose underlying SWF is W and let $S\subset T$. Let $A\equiv f(S)$. Suppose first that A is off the $45^\circ$ line; wlog, to its north–west.

Case 1: $A>\mathbf{0 }$. Let I be W’s indifference curve that passes through A. Let $B=\pi A$, were $\pi$ is the non-identity permutation. Note that the line that passes through A and B has slope $-1$ and it intersects I at A and at B. If $f_1(T)\in (A_1,B_1)$, we are done, since this implies that $R(f(T))>R(f(S))$. If not, then $U(f(T))>U(f(S))$.

Case 2: $A_i=0$ for some i. If $f(T)>\mathbf{0 }$, then $R(f(T))>R(f(S))$. If not, then $U(f(T))>U(f(S))$.

If A is on the $45^\circ$-line then the hyperplane through A with slope $-1$ separates S and the upper contour set of I; this implies that EUM’s requirement must hold as one moves from S to T (Fig. 1).$\square$

Fig. 1

Illustration of Case 1 in Proposition 1’s proof

The converse of Proposition 1 is not true. Moreover, even in the class of solutions that satisfy PO and SY (of which the welfarist solutions are a sub-class), there are non-welfarist EUM-satisfying solutions.¹⁰

Proposition 2

Let $n=2$. Then there exists a non-welfarist solution that satisfies Pareto optimality, symmetry, and egalitarian–utilitarian monotonicity.

Proof

Let ${\hat{f}}$ be the solution that assigns to each S the maximizer of $(\frac{A(S)}{1+A(S)})ab+(\frac{1}{1+A(S)})(a+b)$ over $(a,b)\in S$, where A(S) is the area of S. Clearly this solution satisfies PO and SY. I will now prove that it satisfies EUM. Let $S\subset T$, let $x={\hat{f}}(S)$ and $y={\hat{f}}(T)$. Assume by contradiction that $(R(y),U(y))\lneqq (R(x),U(x))$. Clearly, $y_1y_2>x_1x_2$. Assume, wlog, that $y_1\ge y_2$.

Suppose first that $x_1\ge x_2$. In this case $x_2\ge y_2$ and $y_1>x_1$. Also, $x_2=y_2$ is impossible, as it would imply $y_1+y_2>x_1+x_2$. Therefore $x_2>y_2$. Now, $x_1+x_2\ge y_1+y_2$ implies $(x_1+x_2)^2\ge (y_1+y_2)^2$, or $x_1^2+2x_1x_2+x_2^2\ge y_1^2+2y_1y_2+y_2^2$. Since $y_1y_2>x_1x_2$ it follows that $x_1^2-2x_1x_2+x_2^2\ge y_1^2-2y_1y_2+y_2^2$, or $x_1-x_2>y_1-y_2$. Since $y_1>x_1$ it follows that $y_2>x_2$—a contradiction. The case $x_2\ge x_1$ is treated similarly. Therefore, EUM is satisfied.

Finally, it is easy to see that ${\hat{f}}$ violates IIA; hence, it is non-welfarist. $\square$

Proposition 1 does not generalize to the n-person case. Moreover, with more than two players there does not exist any welfarist solution that satisfies EUM.

Proposition 3

Let $n\ge 3$. Let f be a welfarist solution. Then f violates egalitarian–utilitarian monotonicity.

To prove Proposition 3, I make use of the following lemma.

Lemma 1

Let $n\ge 3$. Let $S=\text {conv}\{x\in {\mathbb {R}}_+^n:\sum _{i=1}^n\alpha _ix_i\le 1\}$, where $0<\alpha _1<\cdots <\alpha _n$. Let $x\in S\cap {\mathbb {R}}^n_{++}$ be such that $|\{j:x_j=\text {min}_ix_i\}|=1$. Then there exists $y\in S$ such that $U(y)>U(x)$ and $R(y)\ge R(x)$.

Proof

Consider first $n=3$. Let then $S=\text {conv}\{(a,b,c)\in {\mathbb {R}}_+^3:\alpha a+\beta b+\gamma c\le 1\}$, where $0<\alpha<\beta <\gamma$, and let $x\in S\cap {\mathbb {R}}_{++}^3$ be a point whose minimum-value coordinate is unique. Clearly it can be assumed that $x\in P(S)$. Note that the ideal point of S is $a(S)=(\frac{1}{\alpha },\frac{1}{\beta },\frac{1}{\gamma })$ and that $x=(\frac{\lambda _1}{\alpha },\frac{\lambda _2}{\beta },\frac{1-\lambda _1-\lambda _2}{\gamma })$, where $(\lambda _1,\lambda _2,1-\lambda _1-\lambda _2)\in {\mathbb {R}}_{++}^3$ are convex weights.

Case 1: $\text {min}_ix_i=\frac{\lambda _1}{\alpha }$. Let $y(\epsilon )\equiv (\frac{\lambda _1+\epsilon }{\alpha },\frac{\lambda _2-\epsilon }{\beta },\frac{1-\lambda _1-\lambda _2}{\gamma })$. For a sufficiently small $\epsilon$, $y(\epsilon )\in S$ and it satisfies $U(y(\epsilon ))>U(x)$ and $R(y(\epsilon ))>R(x)$.

Case 2: $\text {min}_ix_i\ne \frac{\lambda _1}{\alpha }$. Wlog, suppose that $\text {min}_ix_i=\frac{\lambda _2}{\beta }$. In this case, define $y(\epsilon )\equiv (\frac{\lambda _1+\epsilon }{\alpha },\frac{\lambda _2}{\beta },\frac{1-\lambda _1-\lambda _2-\epsilon }{\gamma })$. For a sufficiently small $\epsilon$, $y(\epsilon )\in S$ and it satisfies $U(y(\epsilon ))>U(x)$ and $R(y(\epsilon ))=R(x)$.

Now consider $n>3$. Let $\{j,k,l\}$ be three coordinates one of which is the minimum-value coordinate. Applying the above arguments to these coordinates completes the proof. $\square$

Proof of Proposition 3:

Let $n\ge 3$. Assume by contradiction that f is a welfarist solution that satisfies EUM. For such a solution there exists a problem S such that the assumptions of Lemma 1 are satisfied for S and x, where $x=f(S)$. By that lemma, there is a $y\in S$ such that $U(y)>U(x)$ and $R(y)\ge R(x)$. Let $V\equiv \text {comp}(\{y\})$. Clearly, $f(V)=y$. This contradicts EUM, since $V\subset S$. $\square$

4 Characterizations and impossibilities

Continuing the theme from the previous section, the following result describes a further difference between the 2-person case and the n-person case.

Theorem 1

Let f be a solution that satisfies scale covariance and conflict-freeness. Then:

• If $n=2$ then f satisfies egalitarian–utilitarian monotonicity if and only if it is the Nash solution;

• If $n\ge 3$ then f violates egalitarian–utilitarian monotonicity.

To prove Theorem 1, I make use of the following lemma.

Lemma 2

Let f satisfy conflict-freeness and egalitarian–utilitarian monotonicity. Then f satisfies Suppes-Sen dominance.

Proof

Let f satisfy CF and EUM. Assume by contradiction that it violates SSD. Then there is an S such that $x=f(S)$ is SS-dominated by some $s^*$, where $s^*=\pi s$ for some $s\in S$ and permutation $\pi$. That is, $s^*>x$. Note that $U(s^*)=U(s)$ and $R(s^*)=R(s)$. Let $V\equiv \text {comp}(\{s\})$. Note that $V\subset S$. By CF, $f(V)=s$. Since $s^*>x$ it follows that $U(s^*)>U(x)$, hence $U(s)>U(x)$. Therefore, by EUM, it has to be that as one moves from V to S the value of the Rawlsian objective increases, namely $R(x)>R(s)$. Therefore $R(x)>R(s^*)$ and so $x_i=R(x)>R(s^*)=s^*_j$, where i and j are coordinates in which the respective minima are obtained. This implies $x_j\ge s^*_j$, in contradiction to $s^*>x$. $\square$

Proof of Theorem 1:

Let f be a solution that satisfies the axioms. By Lemma 2, it satisfies SSD. By Mariotti (1999), since f satisfies SSD and S.COV, $f=N$. By Proposition 3, $n=2$. $\square$

The axioms in the 2-person part of Theorem 1 are independent: u satisfies all of them but S.COV, KS satisfies all but EUM, and D satisfies all but CF. Nash (1950) characterized N on the basis of WPO, SY, S.COV, and IIA.¹¹ Since WPO&SY&S.COV imply CF, the 2-person part of Theorem 1 implies that EUM can replace IIA in the 2-person version of Nash’s theorem. It should be noted, however, that none of $\{\text {IIA, EUM}\}$ implies the other. As we saw in Proposition 2, EUM does not imply IIA. In the other direction, note that the solution that assigns to each S the unique point of $P(S)\cap \{s\in S: s\ge D^1(S)\}$ satisfies IIA, but not EUM.¹²

The n-person part of Theorem 1 describes an impossibility result. The following theorem stresses this theme further, and shows that in the presence of other plausible axioms and $n\ge 3$, EUM leaves no room for an economically-meaningful solution.

Theorem 2

Let $n\ge 3$. A solution satisfies egalitarian–utilitarian monotonicity, symmetry, scale covariance, and restricted independence of irrelevant alternatives if and only if it is the disagreement solution.

Proof

It is straightforward that D satisfies the axioms, hence I omit the details. Conversely, let f be a solution that satisfies them. First, I argue that there exists a rectangle R such that $f(R)\ne a(R)$; otherwise, f would satisfy CF, in contradiction to Theorem 1. By S.COV, it can be assumed that R is symmetric. By SY, $f(R)=\theta a(R)$ for some $\theta <1$. By RIIA and S.COV, $\theta =0$. Therefore, by S.COV, $f(R')=\mathbf{0 }$ for every rectangle $R'$. Since every problem can be included in a sufficiently large rectangle, EUM implies $f=D$. $\square$

The axioms in Theorem 2 are independent: N satisfies all of them but EUM, any $D^i$ satisfies all of them but SY, E satisfies all of them but S.COV, and m satisfies all of them but RIIA. Theorem 2 does not have a counterpart in the 2-person case: besides D, the 2-person N also satisfies the axioms. Moreover, these are the only such 2-person solutions.

Theorem 3

Let $n=2$. A solution satisfies egalitarian–utilitarian monotonicity, symmetry, scale covariance, and restricted independence of irrelevant alternatives if and only if it is either the Nash solution or the disagreement solution.¹³

Proof

Clearly both N and D satisfy the axioms.¹⁴ Conversely, let f be a solution that satisfies them. If f does not satisfy CF, then the arguments from the proof of Theorem 2 apply, and $f=D$. If f does satisfy CF, then by Theorem 1$f=N$. $\square$

The axioms in Theorem 3 are independent: KS satisfies all of them but EUM, each $D^i$ satisfies all of them but SY, E satisfies all of them but S.COV, and m satisfies all of them but RIIA.

5 Further remarks

5.1 Interpersonal comparisons

The starting point of my analysis was (the tension between) egalitarianism and utilitarianism—two concepts that assume interpersonal utility comparisons. The Nash solution, on the other hand, satisfies S.COV, an axiom which is often understood as precluding such comparisons. This discrepancy can be settled by viewing S.COV as precluding interpersonal comparisons only in practice, not in principle.¹⁵

5.2 Symmetry

Throughout the analysis I have assumed symmetry; in particular, EUM is defined on the basis of the symmetric versions of egalitarianism and utilitarianism, and a social welfare function, per the definition of Sect. 3, is symmetric. In principle, symmetry can be relaxed, as follows.

Let $n = 2$. Given $p\in (0,1)$, let $U^p(x)\equiv px_1+(1-p)x_2$ and $R^p(x)\equiv \text {min}\{(1-p)x_1,px_2\}$.¹⁶ The parameter p expresses the importance of individual 1 over that of individual 2. EUM is then generalized as follows: a 2-person solution f satisfies p-EUM if whenever the feasible set expands, a decrease of $U^p$’s value (resp. $R^p$’s value) is accompanied by an increase of $R^p$’s value (resp. $U^p$’s value). A 2-person solution f is a general welfarist solution if $f(S)\equiv \text {argmax}_{s\in S}W(s)$, where $W:{\mathbb {R}}_+^2\rightarrow {\mathbb {R}}$ is a strictly concave and non-decreasing function (that may or may not be symmetric). The following question presents itself: does every general welfarist 2-person solution satisfy p-EUM for some p? The result below answers this question in the negative.

Proposition 4

There exists a general welfarist 2-person solution that does not satisfy p-EUM for any $p\in (0,1)$.

Proof

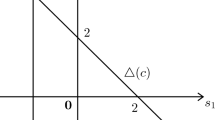
Consider the general welfarist solution corresponding to $W(x_1,x_2)=x_1+ln(1+x_2)$. I argue that it does not satisfy p-EUM for any p. To see this, fix a $p\in (0,1)$. Let l be the line whose equation is $x_2=(\frac{1-p}{p})x_1$. Given a constant $k>0$, let $l^k$ be the line whose equation is $x_2=-(\frac{p}{1-p})x_1+k$. Note that $l^k$ is orthogonal to l and $l^k_+\equiv l^k\cap {\mathbb {R}}_+^2=\text {conv}\{(k(\frac{1-p}{p}),0),(0,k)\}$. Let $x^k$ be the unique point of $l\cap l^k$.

Let $S^{k,a}$ be the problem whose Pareto frontier is $\text {conv}\{(k(\frac{1-p}{p}),0),(0,k+a)\}$. Thus, for $a=0$ the frontier is given by $l^k_+$. Momentarily I will consider positive, but arbitrarily small a.

Note that, in any problem, f selects a point which is either on the horizontal axis or in the relative interior of the frontier; when f selects a point in the relative interior of $S^{k,0}$’s frontier, the associated tangency condition is $1+x_2=\frac{p}{1-p}$, therefore $x_2=\frac{2p-1}{1-p}$ and $x_1=\frac{k(1-p)+1-2p}{p}$.

Fig. 2

Illustration of Proposition 4’s proof

Let $x\equiv f(S^{k,0})$. I argue that for a large enough k, $x_1>x_1^k$. This is clear if $x=(x_1,0)$; I will now prove that this is also true when x is given by the aforementioned tangency condition. That is, the claim is:

$$\begin{aligned} \frac{k(1-p)+1-2p}{p}>k\left[ \frac{p(1-p)}{p^2+(1-p)^2}\right] . \end{aligned}$$

Multiplying both sides by $\frac{p}{1-p}$ gives:

$$\begin{aligned} k+\frac{1-2p}{p}>k\left[ \frac{p^2}{p^2+(1-p)^2}\right] . \end{aligned}$$

(1)

It is clear that (1) holds for all sufficiently large k’s. Fix such a k and consider $S^{k,a}$, where $a>0$ is a small number. Let $x^a$ be the unique point of $P(S^{k,a})\cap l$. Let $V^a\equiv \text {comp}(\{x^a\})$. Note that $f(V^a)=x^a$, that $V^a\subset S^{k,a}$, and that $f(S^{k,a})\sim x$. In the move $V^a\mapsto S^{k,a}$ both the $U^p$-value and the $R^p$-value of the solution point decrease. Hence, f does not satisfy p-EUM (Fig. 2). $\square$

6 Conclusion

I have presented a new axiom, egalitarian–utilitarian monotonicity (EUM), that offers a compromise between utilitarianism and egalitarianism in the Nash bargaining framework. In the 2-person case EUM is a weakening of (a particular sense of) welfarism, but with more than two players it is inconsistent with welfarism. With more than two players it is impossible to reconcile EUM with other standard requirements, whereas in the 2-person case the combination of EUM and other standard axioms pins down the Nash solution.

The following table summarizes the solutions I have considered and the various axioms;¹⁷ for each solution and axiom, it is indicated whether the axiom is satisfied by the 2-person version of the solution. For $n\ge 3$ the same table applies, except that EUM is violated by N.

Solution$\backslash$axiom	EUM	PO	WPO	SY	S.COV	IIA	RIIA	SSD
N	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$
KS	−	$\surd$	$\surd$	$\surd$	$\surd$	−	$\surd$	−
E	$\surd$	−	$\surd$	$\surd$	−	$\surd$	$\surd$	$\surd$
u	$\surd$	$\surd$	$\surd$	$\surd$	−	$\surd$	$\surd$	$\surd$
$D^i$	$\surd$	−	$\surd$	−	$\surd$	$\surd$	$\surd$	−
D	$\surd$	−	−	$\surd$	$\surd$	$\surd$	$\surd$	−
m	$\surd$	−	−	$\surd$	$\surd$	−	−	−