Liquid film flow rate from measurements of disturbance wave characteristics for applications in thin film flow

Abstract

This paper discusses the extension of an optical liquid film thickness measurement technique to characterize liquid film flow rate in wavy thin liquid film flow. The technique, based on laser refractometry, is used to measure wave height, shape, frequency, and velocity. A two-zone model to process the measured wave characteristics is used to estimate the liquid film flow rate. The method is validated in a falling film facility where easy optical access allows comparisons of the wave velocity measurements with high-speed videos and where the calculated liquid film mass flow rate can be compared with actual measurements. The paper provides a framework for analyzing time-resolved film thickness data using multizone models in more complex liquid film flows, such as in two-phase annular flow.

1 Introduction

Liquid film flows consist of a thin film of liquid flowing along a solid substrate. The surface of the film is open to a vapor, and in many cases, waves are observed at the liquid/vapor interface. This type of flow is found in many industrial processes that take advantage of the large surface area available for heat and mass transfer. Examples include falling film absorbers (Killion and Garimella 2001) and heat exchangers (Collier and Thome 1994). There are two major categories of liquid film flows. Falling film flows are driven entirely by gravity and, typically, they exhibit no shear at the liquid–vapor interface. In contrast, in two-phase annular flow, the flow consists of a turbulent vapor core surrounded by a thin liquid film. The liquid film flow is driven mainly by the shear exerted by a vapor core at the liquid–vapor interface. Annular flows are complex, with droplets being sheared off the film into the vapor core and, conversely, droplets in suspension in the vapor core impinging onto the liquid film. In both situations, knowing the liquid film flow rate is important as it has a direct impact on heat transfer (Chen 1966). The liquid film flow rate is, however, very difficult to measure directly in annular flows.

Under most flow conditions of practical interest, waves appear at the surface of liquid film flows. These waves result from the instability of the liquid–vapor interface. Two main types of waves are observed: ripple waves, which are small, short-lived capillary waves (Zhou and Prosperetti 2020), and larger, long-lasting waves, traditionally called disturbance waves in two-phase annular flow (Hewitt et al. 1990). These larger waves carry a large fraction of the liquid mass and play a major role in the physics of liquid film flow (Hall Taylor et al. 2014).

Anyone who has looked at a two-phase flow textbook quickly realizes that most models of these flows rely on empirical correlations, e.g., Ghiaasiaan (2017). Often, the liquid film flow is modeled using correlations based on time-averaged characteristics, e.g., Whalley (1977); Hewitt and Govan (1990); Zhang and Hewitt (2017). A better approach consists in treating the “base film,” which is the stable liquid film between waves, and larger waves as separate “zones,” e.g., Hurlburt et al. (2006); Schubring and Shedd (2011); Le Corre (2022). These multizone models are still empirical, but their more detailed description of the liquid film flow makes them more generally applicable. More detailed modeling can be achieved with Computational Fluid Dynamics (CFD) simulations. Karmakar and Acharya (2020) review existing CFD work on falling films. Annular flows are more complex, and fewer CFD works are available, e.g., Fukano and Inatomi (2003); Rodriguez (2009); Saxena and Prasser (2020). However, because of the high computational cost of CFD simulations, multizone models are often the most advanced available option for design purposes.

The multizone models discussed above require characteristics of the waves such as amplitude, shape, frequency, and velocity as inputs. Historically, a lot of information about waves in falling films has been obtained from visualizations and film thickness measurements. For example, in a recent paper, Ambrosini et al. (2002) observed the transition between wavy laminar flow (a regime to which most measurements discussed in the present paper belong) and turbulent flow at higher Reynolds numbers using conductance probes. The most advanced measurements in falling films include detailed characterization of the velocity profiles (Adomeit and Renz 2000; Charogiannis et al. 2017) and heat transfer (Markides et al. 2016) inside the wavy film. These authors found that while the velocity distribution under the base film is close to that predicted by the Nusselt analytical solution derived for a smooth laminar film, the velocity profile under waves differs significantly (Adomeit and Renz 2000; Charogiannis et al. 2017) in wavy laminar flow. This results in increased mixing and heat transfer under the waves (Markides et al. 2016).

A few groups were able to measure velocity profiles in two-phase annular flow (Zadrazil and Markides 2014; Ashwood et al. 2015). For example, Shedd (2013) demonstrated that the Universal Velocity Profile applies in the base film and within individual waves. However, most of the work has focused on measuring wave characteristics using a variety of film thickness measurement techniques, high-speed videos, or both. The review by Moreira et al. (2020) discusses many of these works that were performed with single fluids, where the liquid and vapor are of the same species. Examples of how these results can be used directly as inputs to multizone models are provided in Le Corre (2022) or Morse et al. (2024).

The ultimate goal of this work is to develop a method for measuring the liquid film flow rate in annular flow. As a first step, we are validating the approach in a falling film facility where optical access is easier and where the liquid film flow rate can be measured accurately and independently for comparison. In Sect. 2, we review existing liquid film thickness measurement methods and present the optical method that was used in this work. Section 3 introduces the experimental setup and validation process. Section 4 presents the analysis of time-resolved film thickness measurements and calculations of large wave characteristics for a range of flow rates and conditions. Finally, Sect. 5 presents the results obtained using a two-layer physical framework to analyze the wave characteristics. Similar to the two-layer approach taken by Le Corre (2022), the two-layer characterization framework for the large waves in this work splits the wavy liquid film into a wave layer and a base film layer. It provides a method for calculating the liquid film flow rate carried by the base film and waves, given time-resolved liquid film thickness measurements.

2 Film thickness measurement methods

A wide array of liquid film thickness measurement techniques with different capabilities have been developed over the years. A comprehensive review of these methods has been presented by Clark (2002) and Tibiriçá et al. (2010). Some of the earliest work used needle contact probes (Neal and Bankoff 1963) for point measurements and conductance probes (Collier and Hewitt 1964) for localized measurements. The needle contact probe measures film thickness by physically measuring the distance at which a needle tip contacts the film surface (Fujita et al. 1986; Nosoko et al. 1996). It requires access to physical space above the film surface and is suitable for external flows. Several drawbacks of this method include poor time resolution, potential of probe bending during calibration (Hewitt et al. 1962), and film distortion due to physical contact. This technique is limited to point measurements.

Conductance probes are some of the most widely used film measurement techniques (Clark 2002). Electrodes are arranged in and around the flow to measure the electrical conductance of liquid in a certain region. Depending on the electrode arrangement, the film thickness within a certain range can be linearly correlated with the measured electrical conductance. With an appropriately designed electrode configuration, the ease of implementation and near-instantaneous response (Pearlman 1963) are contributing factors to their wide adoption. These probes, however, require physical contact with the flow and can potentially disrupt the liquid film. Even in the case of flush-mounted electrodes, where the electrodes are flush with the flow channel wall, the film can be disrupted by the change in wall material. Moreover, these measurement techniques are limited to being implemented in electrically conductive working fluids. Capacitance probes operate similarly (Clark 2002).

Optical methods are often used to measure refrigerant films as refrigerants tend to be dielectric (Ubara et al. 2022; Fehring 2018). Interferometry (Jonsson and Höglund 1993; Morales-Espejel et al. 2015) is a commonly used optical thin film measurement technique, where the optical interference pattern caused by monochromatic light passing through a thin film correlates precisely with the film thickness. Fluorescence (Schubring et al. 2010) is another technique in which the intensity of the light emitted by a fluorescent dye mixed with the working fluid is proportional to the film thickness. The introduction of the dye can be problematic as it may alter the working fluid properties, and may leave deposits if the liquid film dries out. Confocal chromatic displacement sensors (Ubara et al. 2022) take advantage of controlled chromatic aberration to determine the distance between a target surface and a polychromatic light sensor. As with optical methods in general, implementing these measurement techniques requires careful calibration and specialized optics, light sources or materials.

2.1 Technique used in this work

The optical film thickness measurement technique used in this work was adapted from the method introduced by Hurlburt and Newell (1996) and refined by Shedd and Newell (1998) and Moreira et al. (2020). It relies on the total internal reflection of light past the critical angle of refraction at the liquid–vapor interface. The beam path of a laser ray through various layers is shown in Fig. 1. A collimated beam is directed perpendicular to the exterior glass surface. A translucent white tape is attached to this interface to diffuse the incident beam into the glass. Diffused rays then propagate into the liquid before reaching the liquid–vapor interface. Since the refractive index of vapor is lower than the liquid, a critical angle, $\theta _{\text {c}}$, exists that satisfies Snell’s law for total internal reflection at this interface. Incident rays propagating at an angle lower than $\theta _{\text {c}}$ will mostly refract through the interface, whereas rays propagating at and above $\theta _{\text {c}}$ will reflect completely. The reflected light forms a circular shape resembling a light ring. The position of the reflected beam on the white tape, where an image is taken, depends on the liquid thickness, $\delta$, at the point of total internal reflection. By setting the initial incident beam location as a reference, the radii around the light ring are measured and the associated liquid thicknesses inferred. The process of analyzing the reflected light ring images is described in Sect. 4.

Fig. 1

Optical schematic of the film thickness measurement technique

3 Experimental setup and instrumentation

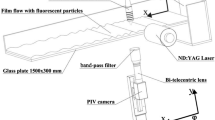
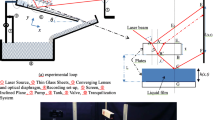
The validation of the optical film thickness measurement technique used in this work is performed on a falling film facility with de-ionized water as the working fluid. The facility shown in Fig. 2 features an inclined glass pane as the flow channel. The clear glass pane is 1500 mm long, 430 mm wide, 0.7 mm thick, and allows optical measurements of the film thickness. The schematic of the facility is shown in Fig. 3. Water is pumped from the lower tank to the upper tank using a rotary vane pump (Fluid O-Tech PA411) driven by a permanent magnet DC motor (Dayton 2M167D). The pump provides a maximum volumetric flow rate of 2 L/min. The mass flow rate is controlled using a motor control module and measured by a Coriolis flow meter (Micro Motion 2700). The incline angle, $\theta$, can be changed from 0° to 60° from horizontal.

Fig. 2

Photograph of the falling film facility

Fig. 3

Schematic of the falling film facility

3.1 Optical setup

A rendering of the optical setup is shown in Fig. 4. The setup includes a polarized 5 mW HeNe laser, a beamsplitter, and a high-speed camera. An aluminum optical breadboard was used to hold all of the optical components. Starting from the laser source (632.8 nm, ThorLabs HNL050LB), a laser beam propagates through the 0.5-inch lens tube (ThorLabs SM05L10) to the silver turning mirror (ThorLabs CCM5-P01). The laser module is housed inside a 66-mm optical rail segment (ThorLabs XT66RL2) that also supports the high-speed camera.

Following the laser beam path in Fig. 4, the laser beam is directed to a beamsplitter where the reflected light is absorbed by a beam block. The transmitted light propagates to the glass pane. The laser reflections from the glass–water interface projects a light ring onto a white diffusing tape. The high-speed camera (Phantom VEO 640) is mounted directly over and parallel to the laser so that it can collect images of the reflected image in the beamsplitter.

Fig. 4

a Rendering and b optical setup for the film thickness measurement system

3.2 Parametric study

Two sets of parametric studies were conducted using the falling film facility in which the mass flow rate and incline angle are the independent parameters. The first study was carried out following the test matrix provided in Appendix (Table 1), using 2000 frames per second (fps) image sampling frequency. Each data set was 5 s long and included approximately 20 disturbance waves. Mass flow rates were chosen such that wave features moved slowly enough that the captured images of both the ring and the film could be used to clearly discern wave structures. Incline angles were limited by the capabilities of the facility to 60° from horizontal.

After analyzing images captured in the first study, a second study was conducted to fill in missing data. The first study was used to examine the variations among disturbance waves in each flow condition. By lowering the imaging frequency to 1000 fps in the second study, twice as many waves were recorded for each experiment, but with less time resolution for each wave. The list of tests in the second study is provided in Table 2 of Appendix.

4 Results

A time series of light ring images, one of which is shown in Fig. 5, are first fit to ellipses. The ellipses are defined by two orthogonal radii ($R_1$ and $R_2$), a rotation ($\theta _{\text {rot}}$) about the horizontal (x) axis, and center positions for which the corresponding local thickness can be calculated (Hurlburt and Newell 1996; Schubring et al. 2010; Fehring 2018). Hurlburt and Newell (1996) used the cross-correlated lag times of two independent film thickness sensors to calculate disturbance wave velocities in the flow. The sensors were a fixed distance apart and aligned in the flow direction. In this experiment, the light ring captured from a single film thickness sensor is used by bisecting the ring into two halves (the upstream (top) and downstream (bottom) halves). The two radii are related to the upstream and downstream film thicknesses and can be cross-correlated in time to provide wave velocity. The physical distance in the flow direction between the two film thickness measurement locations is half of one ring radius, or approximately 0.005 m.

Fig. 5

a Sample light ring image with liquid flowing downward. b Illustration of ring detection parameters and key variables. The green line is the fitted ellipse, the red lines are the radii and rotation that defines the ellipse, and the blue lines are the two radii converted into film thickness values

The two light ring radii, $(R_{\text {up}}, R_{\text {down}})$, are calculated through several steps. First, a reference center point ($x_c, z_c$) is defined using the center of a ring obtained from a dry calibration image. Since there is no liquid in a dry image, the center reflects the fixed point at which the laser beam is incident with the glass pane. Next, a line passing the reference center point is drawn in the flow direction. The coordinates ($x_c$, z) of the intersection between the fitted ellipse and the vertical line are calculated:

$$\begin{aligned}&\left( \frac{x_c\cdot \cos (\theta _{\text {rot}})+z\cdot \sin (\theta _{\text {rot}})}{R_1}\right) ^2\nonumber \\&\quad +\left( \frac{x_c\cdot \sin (\theta _{\text {rot}})-z\cdot \cos (\theta _{\text {rot}})}{R_2}\right) ^2=1. \end{aligned}$$

(1)

Then, the distance from each intersection to the center point is recorded as the upstream and downstream radii. Finally, the corresponding film thicknesses, $\delta$, are calculated:

$$\begin{aligned} \delta =\frac{(R-R_{\text {dry}})}{2\tan (\theta _{\text {crit}})} c_{\text {pixel}} \end{aligned}$$

where $\theta _{\text {crit}}$ is the critical angle of light between water and air, and $c_{\text {pixel}}$ is the pixel size, and R is the light ring radius. The resulting film thickness time traces calculated from the upstream and downstream radii of a light ring are shown in Fig. 6.

Fig. 6

Time trace pair of film thicknesses, upstream and downstream. The raw data (shown as scatter points) are overlaid with smooth curves using a moving median filter with a filter size of 0.02 s. ${\bar{\Gamma }}$ = 0.19 kg/m-s, $\theta$ = 30$^\circ$

The unfiltered data are smoothed using a moving median filter with a size that contains 0.02 s of data. Figure 7 shows the effect of the filter size on the time-averaged wave velocity (${\bar{w}}_{\text {wave}}$), wave mass flow rate (${\bar{\Gamma }}_{\text {wave}}$), and base mass flow rate (${\bar{\Gamma }}_{\text {base}}$). Between 0.02 and 0.06 s, the measured average film characteristics are unaffected by the filter size. In the following, a filter size of 0.02 s was chosen as it provides the best time resolution and captures the shape of the waves. See Sect. 5 for how the base film and wave flow rates are calculated.

Fig. 7

Effects of the moving median filter size on $w_{\text {wave}}$, $\Gamma _{\text {wave}}$, and $\Gamma _{\text {base}}$. ${\bar{\Gamma }}$ = 0.10 kg/m-s, $\theta$ = 40$^\circ$

4.1 Wave recognition

The wave recognition and velocity calculation process is based on the work by Moreira et al. (2020) and Su (2018). Figure 8 shows the film thickness time trace associated with three waves. The sudden increase in film thickness delineates one wave from another. These delineations are identified through an automated algorithm. The start of each wave is defined as a local minima on a rising edge in the upstream (top) thickness time trace. This rising edge traverses from a trough to a peak and passes through specified thickness values ($\pm \sigma$) above and below the overall mean wave thickness, as shown by the horizontal lines in Fig. 8. These $\pm \sigma$ values are arbitrary thresholds that were chosen iteratively to ensure that the detection algorithm captures all the large-scale waves but ignores small-scale ripples. We verified that the wave detection is not sensitive to small changes in these threshold values. The boundaries between waves that are identified using this criterion are shown in Fig. 8. Small ripples may create local peaks and troughs in the data, but due to their small amplitudes they do not satisfy the recognition criteria and therefore are not identified as individual disturbance waves. Assuming that the waves are traveling at constant speed across the small distance between the top and bottom of the light ring and that their structure stays the same during this short travel, the cross-sectional profiles of the waves in the $z\textit{-}y$ plane can be measured by transforming the wave film thickness in the time domain (as seen in Fig. 6), to the spatial domain. Individual wave cross-sectional profiles (the lines) are shown in Fig. 9a overlaid with the corresponding unfiltered film thickness data (the shaded regions) for total mass flow rate, $\Gamma _{\text {total}}=0.19$ kg/m-s, and $\theta =30^\circ$, and measured with a sampling frequency of 2000 Hz. Each of the 11 waves is extracted from the time-domain signal in Fig. 6 and transformed into the spatial domain using the respective velocity. The overlaid unfiltered data show that the filter rounds out (decreases) the peak of some waves. Moreover, for the same mass flow rate, in Fig. 9b, waves at a $60^\circ$ incline angle tend to coalesce with each other. We also observe that their amplitude tends to be smaller than the amplitude of waves at a $30^\circ$ incline angle. Figure 10 shows the same wave cross sections aligned at their peaks. Most of the waves overlap to a distinct shape, suggesting one representative shape can be used for modeling waves.

Fig. 8

a Start of each wave is defined as a point on the rising edge in the thickness data that travels from a trough to a peak and passes through specified values ($\pm \sigma$) above and below the overall mean wave thickness. b Full plot showing the calculated wave velocities. ${\bar{\Gamma }}$ = 0.19 kg/m-s, $\theta$ = 30$^\circ$

Fig. 9

Thickness profiles of 20 individual waves for a $\theta = 30^\circ$ and b $\theta =60^\circ$. A moving median filter of 0.02 s is applied to the signal to reduce noise. The wave profiles are constructed using the process described in Sect. 4.1. ${\bar{\Gamma }}$ = 0.19 kg/m-s

Fig. 10

Cross section of the waves aligned by wave peaks. Note that there are some outliers, but the waves are generally extremely similar in both shape and size. ${\bar{\Gamma }}$ = 0.19 kg/m-s, $\theta$ = 30$^\circ$

4.2 Wave velocity measurement

The velocity of each wave is calculated using the most probable phase lag found by cross-correlating the top and bottom film thickness data, as shown in Fig. 11a. Figure 11b shows the cross-correlation for different phase shifts. The phase shift corresponding to the highest cross-correlation indicates the most probable time required for the wave to travel across the light ring. The time resolution of the cross-correlation vs. phase shift data is dependent on the sampling frequency of the film thickness data. In order to improve the time resolution, a smoothing spline is fitted to the cross-correlation curve in the region near the approximate maximum value. The maximum of the fitted curve is used as the most probably phase shift to calculate the wave velocity. This phase shift is applied to the bottom wave curve in Fig 11a, as shown by the dashed line, to verify that the shifted curve closely matches the top wave curve.

Fig. 11

Phase shift associated with the maximum cross-correlation (b) between the top and bottom wave FT signals (a) is the time estimate of a wave to travel across a known small distance

4.3 Validation of wave velocity measurements

The accuracy of the wave velocities calculated using the cross-correlation method was verified by comparing them with manually calculated wave velocities based on high-speed video taken from above the film. The manually calculated wave velocities were calculated by measuring the time each wave took to travel a known distance in a series of wave images taken from the side. These high-speed images were taken synchronously with the light ring images used for film thickness. Figure 12 shows a sample side view image with a known distance reference. The velocities calculated using the automated versus manual methods are compared in Fig. 13. 82% and 71% of automatically calculated velocity values are within 25% and 15% of the manually calculated values, respectively.

Fig. 12

Sample photograph of the wavy flow imaged from above the incline wall and viewed from the side at an angle. The dashed lines indicated the wave fronts. The 10-mm reference mark is used to measure the time for wave 1 to travel a set distance, which is used to measure its velocity

Fig. 13

Comparison between automated versus manually measured ring velocity with a 15% margin of error

5 Two-layer characterization framework

The experimentally observed falling liquid film suggests that the film is composed of large intermittent waves superimposed on a base film layer, as illustrated in Fig. 14. Further data analysis can be performed using the two-layer framework. The total mass flow rate per unit width into the page at any instant in time, $\Gamma _{{\text {total}},i}$, for each segment of the flow is the sum of $\Gamma _{b,i}$ associated with the base film and $\Gamma _{w,i}$ associated with the waves:

$$\begin{aligned} \Gamma _{{\text {total}},i} = \Gamma _{b,i} + \Gamma _{w,i}. \end{aligned}$$

(2)

Time averaging Eq. (2), we obtain:

$$\begin{aligned} {\overline{\Gamma }}_{{\text {total}}} = {\overline{\Gamma }}_{b} + {\overline{\Gamma }}_{w}. \end{aligned}$$

(3)

Fig. 14

Illustration of the base wave liquid film model for a falling liquid film on an inclined plane. The incline angle is $\theta$ with respect to horizontal. $\delta$ and $\Gamma$ represent the film thickness and mass flow per span-wise width of the flow channel (into the page), respectively. Subscripts w and b are used to denote wave and base film quantities, respectively. $L_w$ is the stream-wise distance between waves

In this work, the base film is defined as the underlying liquid layer with an associated $\Gamma _{b,i}$ given by:

$$\begin{aligned} \Gamma _{b,i} = \rho _l {\overline{w}}_{b} \delta _{b} \end{aligned}$$

(4)

where $\rho _l$ is the liquid density, ${\overline{w}}_{b}$ is the time-averaged base film velocity, and $\delta _{b}$ is the base film thickness. The base film layer in the falling film facility is assumed to be a wave-less, gravity-driven, fully developed laminar flow, with no shear at the liquid–vapor interface. The mean velocity of such a flow is given by:

$$\begin{aligned} {\overline{w}}_{b} = \frac{ \Delta \rho \,g\,\delta _{b}^2\,\sin (\theta )}{3 \mu _{l}} \end{aligned}$$

(5)

where $\Delta \rho$ is the difference in density at the vapor–liquid interface, g is the gravitational acceleration in the downwards direction, and $\mu _l$ is the liquid viscosity (Carey 1992). Here, the base film flow rate is assumed to be constant with time. Therefore, the time-averaged base film flow is the same as the instantaneous value:

$$\begin{aligned} {\overline{\Gamma }}_{b} = \rho _l \frac{ \Delta \rho g \sin (\theta ) }{3 \mu _{l} } \delta _{b}^3. \end{aligned}$$

(6)

${\overline{\Gamma }}_w$ is the average $\Gamma _{w}$ associated with many (n) waves observed experimentally

$$\begin{aligned} {\overline{\Gamma }}_{w}&= \sum _{i=1}^n \Bigg [ \frac{ \int _{0}^{L_{w,i}} \delta _{w,i} \; {\text {d}}z }{t_{i}} \Bigg ] \frac{\rho _l}{n} \nonumber \\&= \sum _{i=1}^n \Bigg [ \frac{ \int _{0}^{L_{w,i}} \left( \delta _{i} - \delta _{b}\right) \; {\text {d}}z }{t_{i}} \Bigg ] \frac{\rho _l}{n} \nonumber \\&= \sum _{i=1}^n \Bigg [ \frac{ \int _{0}^{L_{w,i}} \left( \delta _{i} \right) \; dz }{t_{i}} \Bigg ] \frac{\rho _l}{n} - \overbrace{\sum _{i=1}^n \Bigg [ \frac{ \int _{0}^{L_{w,i}} \; {\text {d}}z }{t_{i}} \Bigg ] \frac{\rho _l}{n} \delta _{b}}^{= \; {\overline{\Gamma }}_b} \end{aligned}$$

(7)

where $t_i$ represents the duration of time required for wave i to travel $L_{w,i}$ (the distance between two waves); $t_i$ includes any intermittency between waves (during which $\delta _{w,i}\approx 0$). Here, the wave shape is assumed to be 2-D and constant across the width of the flow channel. Further, there is no velocity gradient within each wave. Substituting Eqs. (4) and (7) into Eq. (3) leads to:

$$\begin{aligned} \begin{aligned} {\overline{\Gamma }}_{\text {total}}&= \rho _l \frac{ \Delta \rho g \sin (\theta ) }{3 \mu _{l} } \delta _{b}^3 + \sum _{i=1}^n \Bigg [ \frac{ \int _{0}^{L_{w,i}} \left( \delta _{w,i} \right) \; {\text {d}}z }{t_{i}} \Bigg ] \frac{\rho _l}{n} \\&\quad - \sum _{i=1}^n \Bigg [ \frac{ \int _{0}^{L_{w,i}} \; {\text {d}}z }{t_{i}} \Bigg ] \frac{\rho _l}{n} \delta _{b}. \end{aligned} \end{aligned}$$

(8)

Equation (8) represents ${\overline{\Gamma }}_{\text {total}}$ as a function of $\delta _b$, the only unknown (or unmeasured) variable. All other variables are known from experimental measurements. Rearranging Eq. (8) leads to:

$$\begin{aligned} \begin{aligned}&\left( \rho _l \frac{ \Delta \rho g \sin (\theta ) }{3 \mu _{l} }\right) \delta _{b}^3 - \left( \sum _{i=1}^n \Bigg [ \frac{ \int _{0}^{L_{w,i}} \; {\text {d}}z }{t_{i}} \Bigg ] \frac{\rho _l}{n} \right) \delta _{b} \\&\quad + \left( \sum _{i=1}^n \Bigg [ \frac{ \int _{0}^{L_{w,i}} \left( \delta _{w,i} \right) \; {\text {d}}z }{t_{i}} \Bigg ] \frac{\rho _l}{n} - {\overline{\Gamma }}_{total} \right) = 0. \end{aligned} \end{aligned}$$

(9)

Equation (9) shows that the base film thickness satisfying the two-layer wave equation is the solution to a cubic polynomial. The following sections validate this approach and describe an estimation of the base film thickness obtained from experimental data. Using the estimation, other variables in Eq. (9) can be solved.

5.1 Validation of the two-layer framework

The performance of the two-layer framework is validated using independently measured liquid film flow rate and liquid film thickness values. Figure 15 shows that 78% of the estimated base film thickness values, obtained from Eq. (9) using the total mass flow rate and wave characteristics, agree within 25% of the measured values for Kapitza number, $\text{Ka}{}>3900$. The base film thickness is obtained from Eq. (9) using the total mass flow rate and wave characteristics. $\text{Ka}{}$ is the ratio of surface tension force to gravitational force:

$$\begin{aligned} Ka=\frac{\sigma _l}{\rho _l(g\sin {\theta })^{\frac{1}{3}}\nu _l^{\frac{4}{3}}}, \end{aligned}$$

(10)

where $\sigma _l$ is the liquid surface tension and $\nu _l$ is the liquid kinematic viscosity. The measured base film thickness is defined as the median of the first quartile of the measured film thickness, which is related to the film thickness that exists, on average, between waves. The data points are categorized by $\text{Ka}{}$. Given a liquid film flow rate, the framework accurately predicts the base film thickness. Alternatively, given an average base film thickness, it predicts the corresponding liquid film flow rate, as shown in Fig. 16. The framework tends to estimate both variables more poorly when $\text{Ka}{}<3900$. At these low $\text{Ka}{}$ numbers, when the incline angle is steep, waves are traveling so close to one another that it is difficult to measure the base film accurately. Consequently, the measured base film is overestimated and predictions are not accurate.

Fig. 15

Two-layer framework generally predicts the base film thickness well when compared to the observed base film thickness for $Ka>3900$

Fig. 16

Two-layer framework predicts the liquid film flow rate well given the base film thickness

5.2 Analysis using two-layer framework

The wave and base film liquid flow rates can be estimated separately using the two-layer framework. As shown in Fig. 17, most of the liquid mass is transported by the waves. The base film flow rate increases with the film Reynolds number, $\textit{Re}_{\textit{f}}{}$, albeit at a slower rate than the wave flow rate. $\textit{Re}_{\textit{f}}{}$ is defined as (Bergman et al. 2011),

$$\begin{aligned} \textit{Re}_{\textit{f}}{}=\frac{4\Gamma _{\text {total}}}{\mu}. \end{aligned}$$

(11)

Fig. 17

Estimated liquid flow rate in the base film and the waves as a function of $\textit{Re}_{\textit{f}}{}$ and $\text{Ka}{}$

The measurements showed several trends in the wave characteristics with respect to the film Reynolds number. The characteristics are presented in wall units to be more generally comparable with other data. Figure 18 shows that the wave velocity (in wall units) increases with $\textit{Re}_{\textit{f}}{}$ to approximately 1/3 power:

$$\begin{aligned} w^+_{w}=2.44\textit{Re}_{\textit{f}}{}^{0.31}\qquad (r^2=0.87), \end{aligned}$$

(12)

The wave velocity in wall units is defined as:

$$\begin{aligned} w^+_{w}=\frac{{\bar{w}}_w}{{\bar{w}}_{\tau ,w}}, \end{aligned}$$

(13)

where ${\bar{w}}_{\tau ,w}$ is the friction velocity of the wave represented in terms of a characteristic wall shear stress, $\tau _{{\text {wall}},w}=\rho g {\bar{\delta }}_{w}\sin {\theta }$, and is estimated as:

$$\begin{aligned} \begin{aligned} w_{\tau ,w}&= \sqrt{\frac{\tau _{{\text {wall}},w}}{\rho }} \\&= \sqrt{g{\bar{\delta }}_{w}\sin {\theta }}, \end{aligned} \end{aligned}$$

(14)

where ${\bar{\delta }}_{w}$ is the time-averaged film thickness. Note that the true wall shear stress is expected to be greater than the characteristic value we are using (e.g., Fulford (1964); Moran et al. (2002)).

Fig. 18

Wave velocity in wall units as a function of $\textit{Re}_{\textit{f}}{}$

Wave frequency as a function of the film Reynolds number, $\textit{Re}_{\textit{f}}{}$, and categorized by the Kapitza number, $\text{Ka}{}$, is shown in Fig. 19. The wave frequency is defined as the inverse of the wave period, or time between waves, as illustrated in Fig. 8. Box plots are used to present the distribution of wave frequency for each flow condition. The results show that the median wave frequency is not a strong function of $\textit{Re}_{\textit{f}}{}$ and increases slightly with $\text{Ka}{}$. As $\text{Ka}{}$ increases, the spread of wave frequency tends to decrease.

Fig. 19

Wave frequency statistics as a function of $\textit{Re}_{\textit{f}}{}$.The boxes represent the 2nd and 3rd quartiles, which are separated by the median. The whiskers of the box plot represent the 1st and 4th quartiles. The crosses represent outliers that are defined as values greater than 1.5 times the interquartile range away from the bottom or top of the box

Figure 20 shows that for $\text{Ka}{}>3900$ the wave amplitude in wall units increases linearly with $\textit{Re}_{\textit{f}}{}$:

$$\begin{aligned} \delta ^+_{w}=0.03\textit{Re}_{\textit{f}}{}\qquad \left( r^2=0.53\right) . \end{aligned}$$

(15)

The wave amplitude in wall units is defined as:

$$\begin{aligned} \delta ^+_{w}=\frac{{\bar{\delta }}_{w}{\bar{w}}_{\tau ,w}}{\nu _l} \end{aligned}$$

(16)

where $\nu _l$ is the liquid kinematic viscosity.

Fig. 20

Wave amplitude in wall units as a function of $\textit{Re}_{\textit{f}}{}$

Henstock and Hanratty (1976) presented similar analysis for disturbance waves in vertical annular flows and developed an empirical fit of time-averaged film thickness (in wall units) to the film Reynold’s number:

$$\begin{aligned} \delta ^+_{\text {avg}} = \left[ \left( 0.707 \textit{Re}_{\textit{f}}{}^{0.5}\right) ^{2.5}+\left( 0.0379\textit{Re}_{\textit{f}}{}^{0.90}\right) ^{2.5}\right] ^{0.40}, \end{aligned}$$

(17)

where $\delta ^+_{\text {avg}}$ is defined as:

$$\begin{aligned} \delta ^+_{\text {avg}} = \frac{{\bar{\delta }}_{f}w_{\tau ,{\text {avg}}}}{\nu _l}. \end{aligned}$$

(18)

The characteristics of the liquid film in annular flow are similar to those of a falling film, although the liquid vapor interface is sheared in annular flow. Results from this work are well predicted by the Henstock and Hanratty (1976) correlation, as shown in Fig. 21. Ambrosini et al. (2002) also found good agreement with the Henstock and Hanratty correlation. This suggests that the current framework may also apply to other types of liquid film flows such as vertical annular flow, although a more elaborate model (such as the one by Le Corre (2022)) will be needed due to the inherent complexity of two-phase flow.

Fig. 21

Results from the current work agree with published correlations by Henstock and Hanratty (1976)

6 Conclusion

The development and validation of the two-layer framework for a free falling film were presented. Using a non-intrusive optical technique, the time-resolved film thickness of a falling water film on an inclined wall was measured. Applying this framework to analyze the film thickness resulted in estimations of the liquid film mass flow rate associated with the base film and the wave. These estimations were then compared against an independently measured mass flow rate, validating the analysis method. The estimations also show an increasing wave mass flow rate with $\text{Re}_{{f}}{}$. The base film flow rate increases with $\text{Re}_{{f}}{}$ for $\text{Ka}{}\ge 4200$.

Improving upon the wave velocity calculation methods introduced by Moreira et al. (2020) and Su (2018), wave amplitude, velocity, and frequency were inferred from the time-resolved film thickness measurements. Wave amplitude and velocity in wall units increase linearly with $\textit{Re}_{\textit{f}}{}$ until $\textit{Re}_{\textit{f}}{}$ reaches 225, after which they taper off. Median values of wave frequencies ranged from approximately 5.5 to 9.5 [Hz] for $\textit{Re}_{\textit{f}}{}$ ranging from 200 to 1100 and $\text{Ka}{}$ ranging from 3800 to 5200.

The potential applicability of applying the two-layer analysis framework in experimental data of annular flow was realized by comparing results with established correlation. The ability to estimate base film and wave mass flow rates separately using a non-intrusive and instantaneous optical film thickness measurement technique allows more detailed investigations of the film structures and the associated mass transfer.

Appendices

Appendix 1: Experimental test conditions

See Tables 1 and 2.

Table 1 Test conditions for 2000 fps sampling rate

Table 2 Test conditions for 1000 fps sampling rate

Appendix 2: Uncertainty in film thickness measurement

Several sources of uncertainty in the optic-based film thickness measurements are described by Hurlburt and Newell (1996), Moreira (2021), and Moreira et al. (2020). Here, we will discuss the effects of the wavy liquid–vapor interface on the measurement results. Figure 22 illustrates the beam path reflecting from a liquid–vapor interface that is parallel to the wall versus one that is at an angle, or distorted. In the case of a parallel interface, for a given wall geometry and set of fluid and material properties, the ring radius is a function of the liquid film thickness, $\delta$. When the liquid–vapor interface is at an angle, $\omega$, with respect to the wall surface, the ring radius is a function of both $\omega$ and $\delta$. $\theta _c$ represents the critical angle at the liquid–vapor interface. Subscripts i and r denote the incident and reflected critical angle with respect to the wall normal direction.

Fig. 22

Illustration of parallel versus distorted liquid–vapor interface

For wavy films with steep liquid–vapor interface angles, such as those in annular flow, the interface angle causes an error in film thickness that needs to be accounted for. Figure 23 shows the same uncertainty analysis for water-air interface angles ($\omega$) from 0° to 9° for film thicknesses ranging from 500 to 1300 μm. Under these conditions, the uncertainty in film thickness is within 20%.

Fig. 23

Uncertainty in film thickness measurement versus liquid–vapor (water-air) interface angle

For quantifying the uncertainty in film thickness of this falling film work, one of the waves in Fig. 10 is used to represent a wavy film. This is shown in Fig. 24a by the solid red curve. The local angle, $\omega$, versus the stream-wise position is shown in Fig. 24b, with a maximum of no more than 3E−3°. In comparison, the uncertainty in critical angle is much greater at approximately 0.40°. This is estimated assuming an uncertainty in refractive index of 0.005. $\theta _{c,i}$ and $\theta _{c,r}$ are then calculated and shown in Fig. 24c. The expected light ring radius is shown in Fig. 24d. The error in calculated film thickness compared to the simulated film thickness is shown by the black dashed curve in Fig. 24e. Effectively, there is negligible error in the calculated film thickness in this falling film work that is due to the wavy liquid–vapor interface.

Fig. 24

Simulated wavy film thickness calculation results