1 Introduction

Tip vortices have long been of deep interest and concerns owing to their adverse effects in a wide range of engineering applications. For an aircraft in flight, undesirable consequences caused by tip vortices, such as wake encounter (Gerz et al. 2002) and induced drag (Birch et al. 2004), are recognized to have negative influences on the commercial benefits and even the flight safety. For devices handling liquids, more deleterious problems are caused by tip vortices. Due to the local low pressure in vortices, tip vortices emanating from the blade tip of marine propeller or turbomachine tend to induce cavitation which poses hazards to the structural safety of blades (Arndt 1981) and radiates additional noise (Higuchi et al. 1989). This cavitation is known as the tip vortex cavitation (TVC) and has been found to be closely associated with the tip vortex flow (Arndt 2002). Therefore, it is necessary to study the flow properties of tip vortices in details for a better understanding of vortex-induced cavitation mechanism.

A single streamwise vortex generated by the elliptical hydrofoil is a simplified model for tip vortices from blades of propeller. Early investigations on the tip vortex of an elliptical hydrofoil mainly concentrated on the TVC-related vortex properties. The TVC inception was considered to be most associated with the minimum pressure coefficient \(C_{p_{\min }}\) which seems to depend on the vortex core radius scaled with the Reynolds number (McCormick Jr 1962). Based on the axisymmetric vortex approximation, the pressure field of the tip vortex was found to be significantly correlated to the tangential velocity (Batchelor 1964). It is possible to estimate \(C_{p_{\min }}\) with measured tangential velocity field (Arndt et al. 1991; Arndt and Keller 1992). In addition, \(C_{p_{\min }}\) in a vortex can also be effectively estimated from a theoretical vortex model (Franc and Michel 2005) that is characterized by the vortex strength and viscous core radius (Boulon et al. 1999).

With the development of flow measurement and numerical simulation, investigations on the tip vortex are no longer restricted to the vortex properties related to TVC. The tip vortex evolution has received more attention, which would be conductive to comprehensively understanding the tip vortex flow and TVC mechanism. By flow visualization and laser velocimetry, several studies revealed that the tip vortex formation and development are subject to the boundary-layer behaviors on the hydrofoil, which are determined by the Reynolds number, the incident angle and the shape of hydrofoil (Higuchi et al. 1987; Pauchet and Briangon-Marjollet 1993; Fruman et al. 1995a; Astolfi et al. 1999). Since TVC usually occurs in the vicinity of the hydrofoil tip (Zhang et al. 2015), the tip vortex flow in this region has remained a subject of intense research. It was found that the local flow is fully three-dimensional and turbulent under the interaction between the tip vortex and boundary layers, and the in-core flow unsteadiness may be responsible for the local large pressure fluctuation (Stinebring et al. 1991; Maines and Arndt 1997). Peng et al. (2017, 2019) further launched stereo particle image velocimetry (SPIV) experiments which shed light on the tip vortex evolution in the near field of hydrofoil. They found that the vortex circulation peaks in the near field, and the TVC inception occurs exactly at the position of peak vortex circulation, which reveals the connection between TVC and the local vortex circulation. The method predicting \(C_{p_{\min }}\) by a theoretical vortex model was also validated by their work. Unfortunately, owing to the limitations of SPIV, detailed streamwise development of the tip vortex and the mechanism of the circulation evolution were not further elucidated. Corresponding numerical studies on the three-dimensional tip vortex could be found in Asnaghi et al. (2019, 2020a). The tip flow and the vortex formation were qualitatively illustrated in their work.

Additionally, several investigations on the tip vortex have been further extended to the flow control for TVC mitigation. For the hydrofoil with winglet, the maximum tangential velocity of the tip vortex is halved and the vortex core size increases significantly, leading to delayed TVC inception (Amini et al. 2019; Maeda et al. 2021). Artificial roughness applied to the tip region can make the local boundary layers more turbulent, resulting in a weaker and more dispersed vortex that can hardly induce cavitation (Asnaghi et al. 2020b; Svennberg et al. 2020). By the active mass injection of polymer solution in the tip region, the in-core flow unsteadiness is signally reduced and the viscous core is enlarged, which is also practical for alleviating TVC (Fruman et al. 1995b; Yakushiji 2009; Chang et al. 2011). Although these control methods have achieved certain effects, the efficiency still needs to be further optimized, which is not only relevant to the control strategy itself, but also to the in-depth study on tip vortex flow.

Many previous experimental investigations revealed significant features and properties of the tip vortex in certain cross sections, i.e., from a two-dimensional point of view. As the tip vortex travels downstream, the streamwise variation might bring significant influence on the vortex characteristics, such as vortex trajectory, circulation evolution and vorticity transport. Thus, three-dimensional studies for the tip vortex are urgently needed, especially experimental studies. In recent years, with the development of a novel multi-view PIV system: tomographic particle image velocimetry (TPIV) (Elsinga et al. 2006), the volumetric measurement of the three-component (3C) velocity field has become feasible. As a mature technique for three-dimensional flow measurement, TPIV has been successfully applied in various flow problems (Scarano 2012; Gao et al. 2013), such as vortex breakdown over a non-slender delta wing (Wang et al. 2016a), unsteady vortices on a flapping wing (Ehlers et al. 2016) and wake structures of a zigzagging bubble (She et al. 2021). The TPIV technique is also rather practicable for researches in the field of hydrodynamics. Adhikari and Longmire (2012) applied the infrared TPIV system to the measurement of volumetric velocity fields during aquatic predator–prey interactions. Tu et al. (2022) utilized TPIV to study wake flows of a live fish. Felli et al. (2015) conducted a pioneering application of TPIV for the hydrodynamic and hydroacoustic analysis of a marine propeller. Therefore, to capture the three-dimensional structure of the tip vortex and quantitatively investigate the corresponding hydrodynamics, TPIV is taken as an appropriate solution for the current experimental measurement.

In the current work, TPIV measurement is applied to the non-cavitating tip vortex of an elliptical hydrofoil. By collecting fully three-dimensional flow field, this study is aimed at clarifying the tip vortex evolution in the near field where TVC is more to prone to incept. It is of great significance for understanding the flow mechanism of TVC inception. Firstly, the wandering motion of the near-field tip vortex is studied, and an available post-processing method is applied to filtering out the wandering smoothing effects. The inherent driving mechanism of the near-field wandering motion is further revealed. Then, the three-dimensional propagating trajectory and flow properties, especially the vortex circulation, of the tip vortex are investigated based on the time-averaged flow field. According to the flow topology and circulation evolution, the development stages of the tip vortex are analyzed in detail, strengthening the understanding of the vortex evolution in the near field. The impact of hydrofoil configuration on the vortex evolution is interpreted from the aspect of vorticity transport, which partly complements the previous researches on the hydrofoil configuration and might be informative for the hydrofoil design.

2 Experimental apparatus and methods

2.1 Test model and experimental setup

The experiments were carried out in the high-speed cavitation tunnel of Zhejiang University, China, with a test section of 1000 mm (length) \(\times\) 200 mm (width) \(\times\) 200 mm (height). The freestream velocity in the cavitation tunnel can be continuously adjusted in the range of 0.2–10 m/s with the turbulence level below 1%. The Reynolds number \({\text {Re}}_c\) in the current study is defined based on the root-chord length c of the tested hydrofoil as follows:

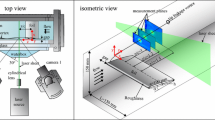
$$\begin{aligned} {{\text {Re}}_c = U_{\infty }c/\nu }\, \end{aligned}$$
(1)

where \(U_\infty\) is the freestream velocity and \(\nu\) is the kinematic viscosity of the fluid. The test elliptical hydrofoil is made from aviation aluminum alloy, with the cross-sectional profile of NACA 66\(_2\)-415, the half span length b of 100 mm and the root-chord length c of 83.66 mm. The TPIV measurement volume and its location relative to the hydrofoil are shown in Fig. 1a. The flow field results are presented in the Cartesian coordinate system with the origin at the hydrofoil tip. The x, y and z axes are aligned with the streamwise, vertical and transverse (spanwise direction of the hydrofoil) directions of the cavitation tunnel reference frame, respectively. The normalized streamwise distance x/c is utilized to illustrate the development area of the tip vortex. The near field in the current work is defined as the area of \(x/c<1\), and the far field is typically defined as the area \(x/c \gg 1\). These definitions are cited from the lifespan stages of the airplane wake vortices (Breitsamter 2011). The hydrofoil was mounted on a turnplate with integrated angular encoder and stepper motor, ensuring the hydrofoil tip being at the center line of the test section and allowing the change of incident angle \(\alpha\). Since the laser sheet was from the bottom of the test section, a small part of the laser sheet was blocked by the test model, resulting in a shadow on the suction side. Thus, a mirror was set on the top of test section which can reflect the remaining part of the laser sheet to illuminate this shadow. In our cases, the shadow area caused by the model obstruction is quite limited, and the intensity of the supplementary light from the mirror is strong enough. Therefore, enough particles on the suction side were clearly captured, which was robust for the reconstruction of the local tip vortex flow. Six cases for different incident angles and Reynolds numbers were investigated in the current study (Table 1).

Fig. 1
figure 1

Schematics of a the elliptical hydrofoil with the coordinate system and b the experimental setup of TPIV system

Full size image
Table 1 Tested cases for different incident angles \(\alpha\) and Reynolds numbers \(\textrm{Re}_c\) in the current study
Full size table

The TPIV system was employed for measuring the cavitation-free velocity field of the tip vortex. The TPIV experimental setup is shown in Fig. 1b. Four Photron FASTCAM high-speed cameras (two SA4 200K M3 and two Mini AX100) were used to record particle images from one side of the cavitation tunnel. Each camera with a resolution of \(1024\times 1024\) pixels was equipped with a Nikon Micro 200 mm focal-length macro-objective lens at \(f_{\#} = 22\). A 18-mm-thick laser sheet was generated by a Vlite-Hi-527-50 laser generator (Nd:YLF, 50 mJ per pulse at 1 kHz, from Beamtech Optronics Co., Ltd.) to illuminate the measurement volume. The sampling frequency for the entire system was 1 kHz. The recording cameras and the laser generator were synchronized by a Micropulse 725 Synchronizer (from MicroVec, Inc.). To minimize the laser reflection from the hydrofoil surface, fluorescent particles (Rhodamine B-labelled poly particles, from MicroVec, Inc.) with a mean diameter of 35 \(\mu\)m were uniformly seeded in the cavitation tunnel as tracers. The particle seeding density was approximately 0.025 particles per pixel, which was calculated by counting intensity peaks in the images. These particles can be excited by the laser at a wavelength of 527 nm and emit 584 nm light. All recording cameras were equipped with long-pass filters to eliminate light with a wavelength shorter than 560 nm.

2.2 Analysis methodologies

2.2.1 TPIV post-processing

The TPIV data were processed in the MicroVec4 v1.2 software (from MicroVec, Inc.) to deduce the velocity field of the tip vortex. The 3D particle field was reconstructed by employing the intensity-enhanced multiplicative algebraic reconstruction technique (IntE-MART) (Wang et al. 2016b). The size of measurement volume is 35 mm \(\times\) 20 mm \(\times\) 18 mm in x (streamwise), y (vertical) and z (spanwise) directions of the lab frame, respectively. The magnification is 0.043 mm per voxel, resulting in a volume with 814 \(\times\) 465 \(\times\) 418 voxels. The multigrid volumetric cross-correlation analysis with window deformation (Scarano 2001) was also applied to improve the accuracy of resolving the local velocity gradient. The initial interrogation window is 48 \(\times\) 48 \(\times\) 48 voxels and the final one is 32 \(\times\) 32 \(\times\) 32 voxels with an overlap rate of 75%, which leads to a spatial resolution of 1.38 mm. There are about 6.6 particles in the initial interrogation window and 1.9 particles in the final one. Finally, a velocity field with 101 \(\times\) 58 \(\times\) 52 vectors is acquired, in which the vector interval is 8 voxels (0.344 mm).

As for the vortex flow, it is very important to accurately resolve the high velocity gradient in the vortex core which is mainly from the local in-plane velocities (v and w), namely the in-core velocity gradients \(\partial v/\partial z\) and \(\partial w/\partial y\). In the current work, the uncertainty of the in-plane velocities in the vortex core is \(\varepsilon _v/U_\infty =0.71\%\), \(\varepsilon _w/U_\infty =0.75\%\), and the uncertainty of corresponding velocity gradients is \(\varepsilon _{\partial v/\partial z}c/U_\infty =0.91\), \(\varepsilon _{\partial w/\partial y}c/U_\infty =0.96\). The uncertainties are estimated following Sciacchitano and Wieneke (2016). According to the magnification (0.043 mm per pixel) and the vector interval (8 voxels, 0.344mm), there are about 11 vectors along the radial direction of the vortex core (the core radius is about 2 mm), which is sufficient to resolve the velocity gradient in the vortex core. Moreover, the in-core velocity distribution measured in the current work is further compared with those of the vortex models, such as the Rankine vortex (Lamb 1924) and the Vatistas vortex(Vatistas et al. 1991), to validate the accuracy of TPIV measurement. It is found that the measured in-core velocity distribution well conforms to those of the vortex models, indicating that TPIV measurement applied in the current study can accurately resolve the high velocity gradient in the tip vortex flow.

2.2.2 Identification of tip vortex parameters and wandering correction

\(\lambda _{ci}\)-criterion is a vortex identification method, by which vortices can be effectively identified from complex flows (Zhou et al. 1999). This method is based on the fact that the velocity gradient tensor \(\nabla {{{{\varvec{u}}}}}\) in Cartesian coordinates can be decomposed into the form with a conjugate pair of the complex eigenvalues with complex eigenvectors. The decomposition is as follows:

$$\begin{aligned} \nabla {{{{\varvec{u}}}}}=\begin{bmatrix} {{\varvec{v}}}_r&{{\varvec{v}}}_{cr}&{{\varvec{v}}}_{ci} \end{bmatrix} \begin{bmatrix} \lambda _r &{}0 &{} 0 \\ 0&{}\lambda _{cr} &{} \lambda _{ci} \\ 0&{} -\lambda _{ci} &{} \lambda _{cr} \end{bmatrix} \begin{bmatrix} {{\varvec{v}}}_r&{{\varvec{v}}}_{cr}&{{\varvec{v}}}_{ci} \end{bmatrix} ^{-1}, \end{aligned}$$
(2)

where \(\lambda _r\) is the real eigenvalue with a corresponding real eigenvector \({{\varvec{v}}}_{r}\), and \(\lambda _{cr} \pm \lambda _{ci}{} i\) are the conjugate pair of the complex eigenvalues with complex eigenvectors \({{\varvec{v}}}_{cr} \pm {{\varvec{v}}}_{ci}{} i\). The local flow is either stretched or compressed along the axis \({{\varvec{v}}}_{r}\). On the plane spanned by the vectors \({{\varvec{v}}}_{cr}\) and \({{\varvec{v}}}_{ci}\), the flow is swirling and the strength of the local swirling motion is quantified by \(\lambda _{ci}\) (Gao et al. 2011). In the current work, since the tip vortex is basically along the freestream direction, the streamwise or axial components of \(\lambda _{ci}\) and vorticity, i.e., \(\lambda _{ci,x}\) and \(\omega _x\), are utilized to identify the tip vortex. Note that the anticlockwise rotating tip vortex results in negative \(\lambda _{ci,x}\) and \(\omega _x\). The streamwise vorticity \(\omega _x\) is defined as

$$\begin{aligned} \omega _x = \frac{\partial w}{\partial y}-\frac{\partial v}{\partial z}\, \end{aligned}$$
(3)

where v and w are the local vertical and spanwise velocities, respectively.

The center of the weighted \(\lambda _{ci,x}\) in each cross section of the measurement volume is considered as the tip vortex center, which is defined as

$$\begin{aligned} y_c = \frac{\iint y\lambda _{ci,x} \textrm{d}y\textrm{d}z}{\iint \lambda _{ci,x} \textrm{d}y\textrm{d}z}\ ,\ z_c = \frac{\iint z\lambda _{ci,x} \textrm{d}y\textrm{d}z}{\iint \lambda _{ci,x} \textrm{d}y\textrm{d}z}\ . \end{aligned}$$
(4)

\(y_c\) and \(z_c\) are the coordinates of vortex center in a certain cross section. Applying this method, the adverse effect of the inherent peak value locations at discrete grid nodes on the vortex center detection can be mitigated (Cheng et al. 2019). As for the vortex core identification, the core periphery could be delineated by finding discrete positions with peak tangential velocity (Pennings et al. 2015; Dreyer 2015; Xie et al. 2021). In the present work, an enclosed area bounded by a continuous line with an appropriate threshold, the \(\lambda _{ci,x}\) contour with the threshold \(\mid \lambda _{ci,x} \mid /\mid \lambda _{ci,x} \mid _{\max } = 0.125\), is used to determine the core periphery. It is found the local peak tangential velocities are basically located on this contour line, which ensures the effectiveness of the detected vortex periphery. The normalized core circulation is calculated by

$$\begin{aligned} {\varGamma _x}^*=\frac{\varGamma _x}{U_\infty r_e}=\frac{1}{U_\infty r_e}\iint \limits _{S} \omega _x \textrm{d}s\, \end{aligned}$$
(5)

where \(U_\infty\) is the freestream velocity, S is the integral domain, \(\omega _x\) is the streamwise vorticity. \(r_e\) is the equivalent radius of the core defined as

$$\begin{aligned} r_e = \sqrt{S_c/\pi }\, \end{aligned}$$
(6)

where \(S_c\) is the area bounded by the \(\lambda _{ci,x}\) contour with a threshold of \(\mid \lambda _{ci,x} \mid /\mid \lambda _{ci,x} \mid _{\max } = 0.125\), namely the area of the integral domain S (the vortex core area).

The tip vortex measurement, especially static measuring techniques, has long suffered from an unique uncertainty caused by a random oscillation of the vortex axis (Bhagwat and Ramasamy 2012). This oscillation is known as the vortex wandering. Without taking into account the wandering motion, the expected time-averaged process is actually a weighted average in both time and space (Iungo et al. 2009). Consequently, a smoothed vortex, with overestimated diameter and underestimated peak tangential velocity, is usually acquired and appears to be more diffuse than in reality, which is called the smoothing effect of wandering motion (Devenport et al. 1996). In order to obtain more accurate tip vortex properties, an effective and convenient “re-centered” method (Heyes et al. 2004; Beresh et al. 2010; Bhagwat and Ramasamy 2012; Dreyer et al. 2014; Cheng et al. 2019) is applied to obtaining wandering-free data in the current work. The principle is to perform the time-averaged process in the reference frame moving with the wandering vortex. The reference point is the vortex center calculated by the weighted \(\lambda _{ci,x}\).

3 Results

3.1 The near-field wandering motion

To quantitatively characterize the wandering motion, the wandering amplitude \(\sigma _r\) at a certain streamwise position is defined as follows:

$$\begin{aligned} {\sigma _r=\sqrt{\frac{\sum \nolimits _{i=0}^N{\sigma ^2_{r,t_i}}}{N}}=\sqrt{\frac{\sum \nolimits _{i=0}^N\left( {\sigma ^2_{y,t_i}}+{\sigma ^2_{z,t_i}}\right) }{N}}\, } \end{aligned}$$
(7)

where \(\sigma _{y,t_i}\) and \(\sigma _{z,t_i}\) are the vertical and spanwise displacements of the vortex center relative to the mean center position at moment \(t_i\), respectively. \(\sigma _{r,t_i}\) is considered as a resultant offset fluctuating with time, and its root mean square is utilized to represent the wandering amplitude \(\sigma _r\).

Fig. 2
figure 2

Streamwise evolution of the wandering amplitude \(\sigma _r\) for a different incident angles \(\alpha\) \((\textrm{Re}_c = 3.31\times 10^5)\) and b different Reynolds numbers \(\textrm{Re}_c\) \((\alpha = 10^\circ )\)

Full size image

The streamwise development of wandering amplitude \(\sigma _r\) is shown in Fig. 2. As observed, the development processes of \(\sigma _r\) under different flow conditions are quite similar. In the very near-tip field (\(x/c<0.15\)), the wandering amplitude \(\sigma _r\) is at a relatively high level, about \(1\%\) of the root chord c, indicating that the local wandering motion is intense. With the tip vortex propagating downstream, the wandering amplitude is halved and reaches a relatively constant state in the field of \(x/c=0.15{-}0.25\). For further downstream (\(x/c>0.25\)), a discernible growth trend of \(\sigma _r\) can be observed under all flow conditions. It is noted that the wandering amplitude appears to be insensitive to both \(\alpha\) and \(\textrm{Re}_c\). Only as the incident angle increases to an unduly high level (\(\alpha =15^\circ\)), the corresponding wandering amplitude increases notably, while its streamwise variation still follows the same trend as those under other flow conditions. However, previous researches mainly concentrated on the wingtip vortex in the far field (\(x/c\gg 1\)) and have concluded that the wandering amplitude decreases with increasing incident angle but increases with increasing freestream velocity (Devenport et al. 1996; Heyes et al. 2004; Beresh et al. 2010; Xiang et al. 2021). Obviously, the near-field wandering motion does not follow such rules, which might suggest that the driving mechanism of the near-field wandering motion is quite different from that in the far field. The dominant factor influencing the streamwise evolution of \(\sigma _r\) will be discussed subsequently.

Fig. 3
figure 3

Instantaneous 3D flow structures of the tip vortex and contours of the turbulence intensity I at \(x/c=0,\,0.075,\,0.15,\,0.225\) for \(\textrm{Re}_c = 3.31\times 10^5\) with a \(\alpha = 5^\circ\) and b \(\alpha =15^\circ\) (gray iso-surface: \(\mid \lambda _{ci,x} \mid /\mid \lambda _{ci,x} \mid _{\max } = 0.15\); blue: \(\mid \lambda _{ci,x} \mid /\mid \lambda _{ci,x} \mid _{\max } = 0.35\); red: \(\mid \lambda _{ci,x} \mid /\mid \lambda _{ci,x} \mid _{\max } = 0.55\)); c streamwise variations of the wandering amplitude \(\sigma _r\) and the spatial average turbulence intensity \(\langle \ I\ \rangle\) for \(\textrm{Re}_c = 3.31\times 10^5\) at different incident angles

Full size image

Two typical cases (\(\textrm{Re}_c=3.31\times 10^5\), \(\alpha =5^\circ ,\,15^\circ\)) are presented in Fig. 3a and b. The instantaneous three-dimensional description of the tip vortex is given by the iso-surfaces of \(\lambda _{ci,x}\) with three thresholds (\(\mid \lambda _{ci,x} \mid /\mid \lambda _{ci,x} \mid _{\max }=0.15,\,0.35,\,0.55\)). The turbulence intensity I, shown by contours at different streamwise positions (\(x/c=0,\,0.075,\,0.15,\,0.225\)), is used to evaluate the extent of local flow unsteadiness. The dimensionless turbulence intensity I is defined as

$$\begin{aligned} I = \sqrt{\frac{\overline{u'^2}+\overline{v'^2}+\overline{w'^2}}{3U^2_\infty }}\, \end{aligned}$$
(8)

where \(u'\), \(v'\) and \(w'\) are the fluctuating components in the x, y and z directions, respectively. Note that all these three fluctuating components \(u'\), \(v'\) and \(w'\) are extracted from the wandering-free data (original data processed by the re-centered method). The tip vortex is generated upstream of the hydrofoil tip and propagates downstream. Around \(x/c=0\), the tip vortex is at the roll-up stage, where the vortex structure is not fully shaped. As shown by the \(\lambda _{ci,x}\) iso-surfaces, the tip region flow is dominated by small coherent structures, which were also observed in numerical simulations by Asnaghi et al. (2020a). These small coherent structures might consist of shear layers and small-scale secondary vortices induced during tip vortex roll-up. Further according to the contours of I, the local turbulence intensity is at a rather high level in the tip region with abundant small structures, and decreases markedly downstream along with the dissipation of these small structures (the flow around the tip vortex tends to be steady at \(x/c=0.15\)). It indicates that local small structures may contribute high three-dimensionality and unsteadiness to the tip region flow. As the incident angle increases to \(15^\circ\), the tip flow becomes extremely unsteady and the local turbulence intensity is up to \(0.4{-}0.5\) as shown by the first contour in Fig. 3b, which is attributed to the more violent roll-up process at an unduly high incident angle.

Figure 3c displays the streamwise variations of the wandering amplitude and the turbulence intensity which are marked by hollow circle and dashed line, respectively. \(\langle \ I\ \rangle\) is the spatial average of the turbulence intensity I and utilized to quantitatively characterize the flow unsteadiness at each streamwise position. The streamwise evolution of the wandering amplitude \(\sigma _r\) agrees well with that of the spatial-averaged turbulence intensity \(\langle \ I\ \rangle\) within the entire measured area, indicating that the wandering motion is highly correlated with the local turbulence. This phenomenon is consistent with previous observations that the wandering motion is sensitive to the external turbulence and the wandering amplitude increases with increasing local turbulence intensity (Heyes et al. 2004; Bailey and Tavoularis 2008; Miloud et al. 2020). Another phenomenon is that the incident angle of hydrofoil and the Reynolds number have a weaker effect on the wandering motion in the near field. By contrast, in the far field (\(x/c\gg 1\)), since the vortex is fully formed and thus the influence of external turbulence is rather restricted, the wandering motion is believed to be subject to a vortex instability(Edstrand et al. 2016), which is more sensitive to the incident angle and the Reynolds number. Therefore, it can be concluded that the driving mechanism of the near-field vortex wandering is indeed quite different from that of the far-field vortex wandering by previous researches, and the strong wandering motion in the near field is mainly attributed to the local turbulence intensity rather than a vortex instability.

Fig. 4
figure 4

Tangential velocity \(u_{\theta }\) and streamwise vorticity \(\omega _x\) profiles from the CT and RT data at a, b \(x/c=0.05\) and c, d \(x/c=0.2\) (\(\textrm{Re}_c=3.31\times 10^5\))

Full size image

To illustrate wandering smoothing effects on the time-averaged tip vortex flow in detail, the tangential velocity \(u_\theta\) and the streamwise vorticity \(\omega _x\) from the conventional time-averaged (CT, without re-centered process) data are compared with those from the re-centered time-averaged (RT) data (Fig. 4). Note that the RT data in the current work are consider as the true and accurate measurements of the tip vortex flow. The tangential velocity \(u_\theta\) of the tip vortex is defined as

$$\begin{aligned} u_\theta = v \textrm{sin}\theta -w\textrm{cos}\theta \, \end{aligned}$$
(9)

where \(\theta\) is the local angular coordinate measured in the \(y-z\) plane. \(u_\theta\) and \(\omega _x\) are plotted as a function of y/c, and the vortex center is located at \(y/c=0\). The vortex core region is simply defined as the region between the vortex center and the location of peak \(u_\theta\), and the flow field outside the vortex core is termed as the outer region. For the CT data, it is obvious that the tangential velocity and streamwise vorticity of the tip vortex are underestimated due to the smoothing effects of the wandering motion. The size of vortex core is larger than that in reality (longer distance from the vortex center to the location of peak \(u_\theta\)). The smoothing effects are non-negligible particularly in the very near-tip field (\(x/c<0.15\)), where the wandering motion is intense as shown in Fig. 2. For example at \(x/c=0.05\) (Fig. 4a and b), the underestimations of peak \(u_\theta\) and peak \(\omega _x\) are up to \(2.99\%\) and \(9.22\%\), respectively, and the core size is overestimated by \(17.4\%\). For further downstream (Fig. 4c and d), the discrepancies between the CT and RT flow fields are less conspicuous due to the weaker wandering motion. The underestimations of peak \(u_\theta\) and peak \(\omega _x\) are less than \(3\%\), and the overestimation of core size is about \(13.6\%\). In addition, it is worth noting that the smoothing effects are more noticeable in the vortex core, whereas they are negligible in the outer region. This phenomenon might be attributed to that the in-core radial gradients of vortex parameters, such as \(u_{\theta }\) and \(\omega _x\), are much higher than those in the outer region, and the weighted-average effect introduced by the wandering motion is thus far more pronounced in the core region.

In a word, unlike in the far field, the wandering motion in the near field is mainly subject to the local flow unsteadiness with weaker dependence on both the incident angle and Reynolds number. The smoothing effects caused by the wandering motion have a non-negligible impact on mean-flow patterns, bringing extra deviations to the measurement results. As a result, the correction of smoothing effects is essential for the investigation of near-field tip vortex. With the aid of re-centered process, the wandering smoothing effects are effectively filtered out, and more accurate vortex properties are obtained. In the following sections, quantitative analyses on tip vortex properties are based on the re-centered time-averaged data.

3.2 Structure of the near-field tip vortex

Due to the similarity of the flow topology, as well as the formation and development processes under different flow conditions, the case \(\textrm{Re}_c=3.31\times 10^5\), \(\alpha =10^\circ\) is taken as an example to give a general sense of the three-dimensional tip vortex structure and relevant properties. As aforementioned, corresponding results are from the RT data. Figure 5 shows \(\lambda _{ci,x}\) iso-surfaces of the tip vortex and trajectory of the vortex center. The trajectory is fitted by the third-order polynomial and highlighted with the black solid line. As seen in Fig. 5a, the tip vortex emanates from the leading edge and is mainly formed on the suction side, with its swirling strength and size gradually increasing along the streamwise direction.

Fig. 5
figure 5

Mean flow field of the tip vortex for \(\textrm{Re}_c=3.31\times 10^5\), \(\alpha =10^\circ\). a 3D flow field, tip vortex in b \(x{-}y\) plane and c \(x{-}z\) plane. Gray iso-surface: \(\mid \lambda _{ci,x} \mid /\mid \lambda _{ci,x} \mid _{\max } = 0.15\); blue: \(\mid \lambda _{ci,x} \mid /\mid \lambda _{ci,x} \mid _{\max } = 0.35\); red: \(\mid \lambda _{ci,x} \mid /\mid \lambda _{ci,x} \mid _{\max } = 0.55\). The black solid line represents the trajectory of the vortex center

Full size image

The tip vortex has a typical columnar shape, since small-scale structures around the hydrofoil tip and the twisted vortex tube caused by flow unsteadiness are filtered out under the time-averaged perspective. To further exhibit the propagating orientation of the tip vortex during its formation process, the vortex center trajectory in the \(x{-}y\) plane is displayed in Fig. 5b. This trajectory resembles a flat parabola with its vertex at about \(x/c=0.1\). Downstream from the vertex, the tip vortex lifts off the upper surface of hydrofoil. In the \(x{-}z\) plane (Fig. 5c), it is clear to see that the tip vortex initiates at about \(x/c = -0.07\), and the vortex travels along the elliptical outline of the hydrofoil in the region close to the tip, covering \(x/c=-0.07{-}0.1\). Downstream from \(x/c=0.16\), the propagating path in the \(x{-}z\) plane deflects and tends to be aligned with the streamwise direction. In other words, a turning point of the vortex trajectory occurs. It might suggest that the tip vortex leaves the trailing edge and enters the wake region in the vicinity of \(x/c=0.16\). Therefore, the main effective region for the tip vortex formation covers about \(x/c=-0.07{-}0.16\), where the tip vortex is formed by the shear layers rolling up along the elliptical outline of hydrofoil tip. Previous numerical research (Asnaghi et al. 2020b) found similar distribution of the main effective region. Consequently, the vorticity or momentum transport from the shear layers to the tip vortex is important for the vortex formation process, which will be discussed subsequently.

Fig. 6
figure 6

Trajectories of the tip vortex center under different flow conditions. a, b Different incident angles \(\alpha\) (\(\textrm{Re}_c = 3.31\times 10^5\)) and c, d different Reynolds numbers \(\textrm{Re}_c\) (\(\alpha = 10^\circ\)). The turning points on vortex trajectories are marked with colored solid dots

Full size image

Detailed illustrations about the vortex center trajectory and the corresponding turning point under different flow conditions are displayed in Fig. 6. The hydrofoil sketch in Fig. 6 is at an incident angle of \(10^\circ\) for simplicity and better presentation of the relative position between the tip vortex and the hydrofoil. Figure 6a presents that the vortex center trajectory in the \(x{-}y\) plane is subject to the incident angle \(\alpha\). Specifically, since the tip vortex is attached to the hydrofoil and propagates along its upper surface profile, the location of the trajectory is lowered in the vertical direction with increasing incident angle. This phenomenon, the flow tendency of staying attached to the convex surface (the upper surface of hydrofoil), might be due to the Coanda effect (Wille and Fernholz 1965). Conversely, the vortex center trajectory in the \(x{-}z\) plane (Fig. 6b) is weakly dependent on \(\alpha\), which is basically along the elliptical outline of hydrofoil in the tip region. From the observations in \(x{-}y\) and \(x{-}z\) planes, it might be concluded that the vortex center trajectory mainly depends on the spatial position and shape of the hydrofoil. Since the hydrofoil is at a fixed spatial position (\(\alpha =10^\circ\)) under different Reynolds numbers and its elliptical shape is invariant, vortex center trajectories for different \(\textrm{Re}_c\) (Fig. 6c and d) perfectly collapse. In addition, it is interesting that in the \(x{-}z\) plane, the turning point of the vortex center trajectory can always be detected at about \(x/c=0.16\) for different \(\alpha\) and \(\textrm{Re}_c\). In other words, despite the effect of the solid boundary (hydrofoil), the position of the turning point is nearly invariable under different flow conditions. Since the vortex trajectory is highly related to the formation and evolution progress of the tip vortex, the insensitive of the turning point to the flow condition may imply significant characteristics and properties of the tip vortex.

Back to the representative case (\(\textrm{Re}_c=3.31\times 10^5\), \(\alpha =10^\circ\)), the local slope \(k_t\) (\(k_t={\partial {z^*}}/{\partial {x^*}}\)) of the vortex center trajectory in the \(x{-}z\) plane reaches its minimum at \(x/c=0.167\), as shown by the carmine dashed line in Fig. 7a. This quantitatively indicates that the streamwise variation trend of \(k_t\) is changed and the vortex center trajectory is deflected at this position. When a streamwise vortex encounters the solid wall, the lateral displacement of the vortex is typically observed, and its propagation direction is thus deflected. This phenomenon arises from image effects and the associated mutual induction (Bodstein et al. 1996; Rockwell 1998). Likewise, when the vortex has just left the influence area of the solid wall, its path may also change (Seath and Wilson 1986). Combining the geometry of vortex center trajectory and the distribution of \(\lambda _{ci,x}\) iso-surface in Fig. 7a, it is reasonable to infer that the turning point in the \(x{-}z\) plane is the position where the tip vortex completely leaves the trailing edge of the hydrofoil and enters the wake region.

Fig. 7
figure 7

Case \(\textrm{Re}_c=3.31\times 10^5\), \(\alpha =10^\circ\). a Vortex center trajectory (the black solid line) in the \(x{-}z\) plane and its slope \(k_t\) (the black dashed line). The carmine dashed line and dot represent the location where \(k_t\) reaches its minimum. Contour maps with in-plane (\(y-z\) plane) velocity vectors of b streamwise vorticity \(\omega _x\) and c crossflow velocity \(u_{cf}\) at \(x/c=0,\,0.08,\,0.16,\,0.24\). The gray iso-surface with a threshold of \(\mid \lambda _{ci,x} \mid /\mid \lambda _{ci,x} \mid _{\max } = 0.125\) depicts the vortex core periphery which is highlighted with the black solid line in each slice

Full size image

The formation and development processes of the vortical structure are further exhibited in Fig. 7b, indicated by the distribution of the streamwise vorticity \(\omega _x\) from the tip region to the wake region. During the early growth stage, the tip vortex with low in-core vorticity is attached to the suction side. As the tip vortex develops downstream, it continuously gains strength, and the in-core vorticity gradually increases. Downstream from the turning point (\(x/c\ge 0.16\)), the tip vortex has already entered the wake region, and the streamwise vorticity contour map exhibits two distinct regions: the core region and the hydrofoil wake. The vortex core contains the majority of vorticity, whereas the wake sheet, typically composed of shedding boundary layers, has less vorticity and wraps around the vortex core. Moreover, the core is basically formed at \(x/c=0.16\). For further downstream, the in-core vorticity remains at a relatively stable level, implying that the vorticity conveyed to the core starts to be restricted. It can be concluded that the external vorticity supply of the vortex core tends to be limited when the tip vortex enters the wake region. In other words, the restricted external supply of the vortex core is another evidence that the tip vortex completely leaves the trailing edge and enters the wake region.

As a supplement, Fig. 7c further depicts the mass flux transport during the tip vortex evolution from the perspective of crossflow velocity \(u_{cf}\). The crossflow velocity \(u_{cf}\) is defined as the resultant of v and w components:

$$\begin{aligned} u_{cf} = \sqrt{v^2+w^2}\ . \end{aligned}$$
(10)

At \(x/c=0\), the tip vortex is at the early stage of formation, where the vortex is not shaped and only the roll-up process of the separated shear layers with relatively high \(u_{cf}\) can be observed, as shown by the first contour in Fig. 7c. As the tip vortex travels downstream, the boundary layers with low \(u_{cf}\) on the suction side are entrained and wrapped by the separated shear layers. Thus, the low-velocity vortex core is formed. In the region of \(x/c=0.08{-}0.16\), the vortex core is directly connected to the shedding boundary layers. A passage with low \(u_{cf}\) between the core and shedding boundary layers can be observed, indicating that there is mass transport between them. In the wake region (\(x/c>0.16\)), the core periphery with high \(u_{cf}\) is formed as shown by the velocity vectors in the fourth contour, obstructing the direct connection between the vortex core and the external (wake sheet). Coinciding with the evolution of \(\omega _x\), the mass flux transported to the core is restricted in the wake region. This consistency again confirms that the vortex leaves the trailing edge at the turning point of vortex center trajectory.

The above results reveal the evolution process of the near-field tip vortex from the perspectives of three-dimensional topological structure and flow properties. The position that the tip vortex leaves the hydrofoil and enters the wake region is quantitatively located. Interestingly, this position appears to be independent of the flow condition. In terms of the vortex topology, this position appears as a turning point of the vortex center trajectory. According to the local flow properties, the mass and energy transport from the external to the vortex core starts to be restricted at this position. In the next section, this special position will be further clarified from the point view of the vortex circulation. The flow mechanisms of the circulation evolution and local vorticity transport will be discussed in detail.

3.3 Circulation evolution

The vortex circulation is a significant parameter to evaluate the vortex strength and is believed to be closely associated with the inner pressure of the vortex. In this section, the circulation evolution of the tip vortex is utilized to characterize the vortex formation and development processes. The tip vortex circulation is approximated with the circulation of the identified vortex core. The streamwise component of vorticity is dominant in the tip vortex flow. Thus, \(\omega _x\) is used to calculate the normalized core circulation \({\varGamma _x}^*\) defined by Eq.(5). The vortex core radius \(r_c\) is estimated by the equivalent core radius \(r_e\), and the corresponding calculating process has been illustrated in Sect. 2.2.2.

Fig. 8
figure 8

Normalized core circulation \({\varGamma _x}^*\) for a different incident angles \(\alpha\) (\(\textrm{Re}_c = 3.31\times 10^5\)) and b different Reynolds numbers \(\textrm{Re}_c\) (\(\alpha = 10^\circ\)). The carmine dashed line represents the streamwise position of the peak core circulation discovered by Peng et al. (2017) (\(\alpha = 7^\circ , \textrm{Re}_c = 4.66\times 10^5,\,1.21\times 10^6\)) and the shaded bands represent the position where \({\varGamma _x}^*\) firstly reaches a relatively constant value under different flow conditions

Full size image

Two plots of normalized core circulation \({\varGamma _x}^*\) against the dimensionless streamwise distance x/c are provided in Fig. 8. It is shown that pronounced variations in vortex circulation are observed within the parameter space. For cases at different incident angles (Fig. 8a), the magnitude of \({\varGamma _x}^*\) is positively correlated with the incident angle \(\alpha\). It is noted that there are two distinguishable stages during the circulation evolution: \({\varGamma _x}^*\) grows dramatically (the growth stage) and then reaches a relatively constant value (the plateau stage). The streamwise position where \({\varGamma _x}^*\) reaches the asymptotic value seems to be independent of the incident angle, as shown by the narrow shaded band in Fig. 8a. For cases with different Reynolds numbers (Fig. 8b), collapse in the core circulation data is observed across the entire experimental Reynolds-number range. Since the tip vortex initiates upstream of the hydrofoil tip as previously presented in Fig. 5, the core circulation is not zero at \(x/c=0\). At the growth stage, the core circulation grows to about twice the magnitude of that at \(x/c=0\), suggesting that the growth stage is quite significant for the tip vortex development. When the tip vortex enters the plateau stage, the core circulation firstly grows to its maximum. According to the general estimation formula for vortex pressure (Dreyer et al. 2014), this indicates that the vortex center pressure firstly reaches its minimum. Thus, it can be reasonably inferred that the near-field tip vortex cavitation is more prone to incept at this position. Peng et al. (2017) examined the vortex circulation in several cross sections utilizing SPIV and found that the peak core circulation is located at \(x/c=0.16\) as shown by the carmine dashed line in Fig. 8, which is in agreement with the current results. It suggests that the quantitative results of tip vortex circulation using TPIV is rather convincing and accurate. They also observed that TVC does incept at the position of peak circulation, which partly validates the current inference about the position of TVC inception. With the help of TPIV, the current results provide the continuous streamwise variation of the tip vortex circulation rather than vortex circulations at several streamwise positions by Peng et al. (2017). Therefore, the streamwise variation of the vortex circulation can be further analyzed in detail to interpret the near-field tip vortex evolution.

Table 2 Comparison between the position \({\varGamma _x}^*\) firstly reaching a constant value and the position of the turning point of the vortex center trajectory at different incident angles \(\alpha\)
Full size table

As illustrated in Sect. 3.2, the tip vortex leaves the trailing edge and enters the wake region at the turning point of the vortex center trajectory. The in-core vorticity remains at a relatively stable level in the wake region. Therefore, it is further speculated that the turning point is also the position of \({\varGamma _x}^*\) firstly reaching a constant value. Comparison between these two positions is given in Table 2. It is shown that these two positions are highly consistent for all operating conditions, suggesting that the stabilization of core circulation is another quantitative manifestation that the tip vortex completely leaves the trailing edge and enters the wake region. Interestingly, a similar phenomenon that the vortex circulation tends to reach an asymptotic state was also found in free vortex ring. This phenomenon is termed as the “pinch-off” process and indicates that the formation of vortex ring has been completed (Gharib et al. 1998). Considering the similarity between the tip-vortex and vortex-ring circulation evolution, the position that the tip vortex circulation firstly reaches a constant value is also called the pinch-off position in the current study. Note that, the inherent mechanisms of the circulation pinch-off for a free vortex ring and a tip vortex are quite different. During the formation process of a vortex ring, the vorticity carried by the vortex ring tends to be saturated and vorticity from the shear layer region is no longer entrained into the vortex ring, triggering the circulation pinch-off. The whole formation process is completed spontaneously. By contrast, the tip vortex initiates on the suction side and develops downstream with attached to the hydrofoil. When the tip vortex propagates to the trailing edge, the circulation pinch-off is triggered with the absence of the hydrofoil. It can be considered that the formation process of the tip vortex is forced to be terminated, and the tip vortex travels further downstream in a self-sustaining state, i.e., its core circulation is at a constant level.

Fig. 9
figure 9

a Streamwise growth rate of \({\varGamma _x}^*\) for \(\textrm{Re}_c=3.31\times 10^5\) at different incident angles. For the case \(\textrm{Re}_c=3.31\times 10^5\), \(\alpha =10^\circ\), b streamwise evolution of three circulation components \({\varGamma _x}^*\), \({\varGamma _y}^*\) and \({\varGamma _z}^*\); c streamwise growth rates of \({\varGamma _x}^*\), \({\varGamma _y}^*\) and \({\varGamma _z}^*\). The position where \({\partial {{\mid \varGamma _x}^* \mid }}/{\partial {x^*}}\) reaches its maximum is highlighted with the dashed line and the pinch-off position is highlighted with the dash-dotted line

Full size image

The streamwise growth rate of the core circulation \({\partial {{\mid \varGamma _x}^* \mid }}/{\partial {x^*}}\) is further given in Fig. 9a. Since the core circulation is the integral of in-core vorticity in essence, \({\partial {{\mid \varGamma _x}^* \mid }}/{\partial {x^*}}\) can be considered as the streamwise variation of vorticity transport. The shear layers roll up more violently and supply more streamwise vorticity to the vortex with increasing incident angle. Thus, one can observe that \({\partial {{\mid \varGamma _x}^* \mid }}/{\partial {x^*}}\) is positively correlated with the incident angle of hydrofoil. In addition, the peak \({\partial {{\mid \varGamma _x}^* \mid }}/{\partial {x^*}}\) is observed in the region of \(x/c=0.046{-}0.066\) as shown by the dashed lines, while for the case \(\alpha =15^\circ\), \({\partial {{\mid \varGamma _x}^* \mid }}/{\partial {x^*}}\) decreases monotonically. After the growth rate peaks, it gradually decreases along the streamwise direction and approximates zero when the tip vortex reaches the pinch-off position. During the decrease in the circulation growth rate, the in-core vorticity is still directly fed by shear layers. It is speculated that there might be vorticity transport in other directions, leading to the decrease in streamwise vorticity transport.

Take the case \(\textrm{Re}_c=3.31\times 10^5\), \(\alpha =10^\circ\) as an example once more, circulation components in different directions are provided in Fig. 9b. Variations in other two circulation components, the vertical one \({\varGamma _y}^*\) and the spanwise one \({\varGamma _z}^*\), are observed. The vertical component \({\varGamma _y}^*\) decreases to a relatively low level at \(x/c=0.1\) and then levels off for further downstream. In the region of \(x/c=0{-}0.1\), the tip vortex is attached to the suction side of hydrofoil with a certain incident angle, resulting in the inclined vortex path. The tip vortex thus has the vertical vorticity component in this region, and \({\varGamma _y}^*\) is non-zero. As illustrated in Fig. 5c, the vortex center trajectory in the \(x{-}y\) plane resembles a flat parabola with its vertex at \(x/c=0.1\), indicating that the vortex propagating path tends to align with the freestream in the region of \(x/c=0{-}0.1\). Consequently, \({\varGamma _y}^*\) resulted from the inclined vortex path continuously decreases in this region. Since the tip vortex lifts off the hydrofoil and travels further downstream (\(x/c>0.1\)) along the freestream direction, \({\varGamma _y}^*\) remains at a relatively low level. By contrast, the spanwise component \({\varGamma _z}^*\) presents a similar trend to the streamwise one. \({\varGamma _z}^*\) starts to grow at about \(x/c=0.07\), where the growth rate of the streamwise component \({\partial {{\mid \varGamma _x}^* \mid }}/{\partial {x^*}}\) peaks as shown by the blue dashed line in Fig. 9a. With the tip vortex traveling to the pinch-off position, \({\varGamma _z}^*\) also grows to a constant level, i.e., the pinch-off for \({\varGamma _z}^*\) is triggered. These results indicate that the deteriorating efficiency of the streamwise vorticity transport is mainly relevant to the growth of spanwise circulation component \({\varGamma _z}^*\).

To further examine the claim that the streamwise vorticity transport decreases with growing spanwise circulation component, the streamwise growth rates of \({\varGamma _x}^*\), \({\varGamma _y}^*\) and \({\varGamma _z}^*\) are plotted as a function of the dimensionless distance x/c in Fig. 9c. As the tip vortex travels from the hydrofoil tip to the pinch-off position, the variation trends of \({\partial {{\mid \varGamma _x}^* \mid }}/{\partial {x^*}}\) and \({\partial {\mid \varGamma _z}^* \mid }/{\partial x^*}\) appear to be contrary. \({\partial {{\mid \varGamma _x}^* \mid }}/{\partial {x^*}}\) decreases rapidly from its maximum, while \({\partial {\mid \varGamma _z}^* \mid }/{\partial x^*}\) starts to grow from zero, implying that the direction of local vorticity transport has started to change and the proportion of spanwise vorticity transport to the total has increased. For the vertical direction, \({\partial {\mid \varGamma _y}^* \mid }/{\partial x^*}\) is negative in the region of \(x/c=0{-}0.1\), suggesting that the vertical circulation component \({\varGamma _y}^*\) continuously decreases in this region. At \(x/c=0.1\), since the vortex propagating path in the \(x{-}y\) plane is basically aligned with the freestream, \({\partial {\mid \varGamma _y}^* \mid }/{\partial x^*}\) approximates zero. In the whole near field, \({\partial {\mid \varGamma _y}^* \mid }/{\partial x^*}\) is not much greater than zero, and \({\varGamma _y}^*\) is at a relatively low level. Thus, it is believed that the transport of vertical vorticity has no significant effect on that of streamwise vorticity.

Fig. 10
figure 10

Schematic diagram of the formation and development mechanism of the near-field tip vortex

Full size image

So far, the formation and development of the near-field tip vortex have been comprehensively presented. It is found that the entire development process of the tip vortex can be divided into several stages based on local flow characteristics. According to the vortex topology (Fig. 7) and circulation evolution (Fig. 8), two main stages can be determined. The tip vortex grows rapidly in strength at the initial stage, Stage-1, and then is completely detached from the hydrofoil in a self-sustaining state at the second stage, Stage-2. Moreover, Stage-1 can be further divided into two sub-stages based on the local vorticity transport. A schematic is provided in Fig. 10 to visually illustrate corresponding flow phenomena and mechanisms at each stage.


Stage-1.1 (vortex-attached stage, \(0< x/c\le 0.06\)): The core circulation of the tip vortex \(\mid {\varGamma _x}^* \mid\) increases significantly and monotonically at Stage-1 (Fig. 8), while its streamwise growth rate \({\partial {{\mid \varGamma _x}^* \mid }}/{\partial {x^*}}\) firstly grows to the maximum and then decreases to zero (Fig. 9a). As mentioned previously, \({\partial {{\mid \varGamma _i}^* \mid }}/{\partial {x^*}}\) can be considered as the streamwise variation of the to-core vorticity transport. Thus, according to the trend of \({\partial {{\mid \varGamma _x}^* \mid }}/{\partial {x^*}}\), Stage-1 can be further divided into two sub-stages, and the position of maximum \({\partial {{\mid \varGamma _x}^* \mid }}/{\partial {x^*}}\) (\(x/c\approx 0.06\)) is taken as their division. Stage\(-\)1.1 is the first sub-stage and covers \(x/c=0{-}0.06\) where the tip vortex is attached to the suction side and directly fed by the shear-layer vorticity from the pressure side. It can be considered that the shear layers typically roll up along the tangent of the elliptical hydrofoil outline to transport vorticity to the tip vortex. In the vicinity of the hydrofoil tip (\(x/c=0\)), the tangent of the hydrofoil outline is basically parallel to the freestream, resulting in that the shear-layer vorticity \(\omega\) is mainly contributed from its streamwise component \(\omega _x\) rather than its spanwise component \(\omega _z\), as shown by the first plot of the right part in Fig. 10. Thus, during this stage, \(\mid {\varGamma _x}^* \mid\) grows with an increasing growth rate, while both \(\mid {\varGamma _z}^* \mid\) and \({\partial {{\mid \varGamma _z}^* \mid }}/{\partial {x^*}}\) approximate zero, as shown by Fig. 9b and c.


Stage-1.2 (vortex-lifting stage, \(0.06< x/c\le 0.16\)): Stage\(-\)1.2 is the second sub-stage where the tip vortex gradually lifts from the suction side and propagates along the elliptical outline of the hydrofoil, as presented by the vortex trajectory in Fig. 6. The left boundary of this stage is the maximum of \({\partial {{\mid \varGamma _x}^* \mid }}/{\partial {x^*}}\) (\(x/c\approx 0.06\)) as illustrated in Stage\(-\)1.1, and the right boundary is the position of the tip vortex completely leaving the trailing edge of the hydrofoil (\(x/c\approx 0.16\)), namely the position of the turning point on the vortex trajectory (Fig. 7a) or the circulation pinch-off position (Fig. 8). Although the shear layers still transport vorticity to the tip vortex at this stage, the direction of the shear-layer vorticity \(\omega\) is changed. With the tip vortex approaching the trailing edge, \(\omega\) gradually deviates from the freestream direction due to the increased angle between the tangent of the hydrofoil outline and the freestream, as shown by the second plot of the right part in Fig. 10. As a result, the shear-layer vorticity \(\omega\) is no longer only contributed from its streamwise component \(\omega _x\), and its spanwise component \(\omega _z\) is enhanced. Since the total to-core vorticity transport is limited, an increase in the proportion of the spanwise component results in a decrease in the proportion of the streamwise component. Therefore, during this stage, the spanwise circulation component \(\mid \varGamma _z^* \mid\) starts to grow from zero with a positive growth rate \({\partial {{\mid \varGamma _z}^* \mid }}/{\partial {x^*}}\), whereas \(\mid \varGamma _x^* \mid\) continues to increase monotonically but with a decreasing growth rate, as shown by Fig. 9b and c.


Stage-2 (vortex-detached stage, \(x/c>0.16\)): At this stage, the tip vortex is detached from the hydrofoil and enters the wake region. At the position where the tip vortex just leaves the trailing edge (\(x/c\approx 0.16\)), the vortex trajectory is deflected and tends to be aligned with the freestream (Fig. 7a). Since the shear layers rolling up along the hydrofoil can no longer directly transport vorticity to the detached tip vortex, the tip vortex travels further downstream in a self-sustaining state, i.e., its core circulation is at a constant level with corresponding circulation growth rate closed to zero (for all three circulation components, Fig. 9). Interestingly, the circulation pinch-off is always triggered at the same position in the current work. A wide range of the incident angle \(\alpha\) has been investigated, even including an unduly high incident angle (\(\alpha =15^\circ\)), while the pinch-off position seems irrelevant to \(\alpha\) (Fig. 8a). Similar phenomenon that the roll-up region of the tip vortex and the location of the minimum pressure are weakly dependent on the incident angle for a skewed-back blade was also found by Reclari et al. (2019). Besides, the pinch-off position also appears to be independent of the freestream within the range of current experimental \(\textrm{Re}_c\) (Fig. 8b). A question comes to our minds: what is the pinch-off position subject to? In other words, what does the circulation evolution of the tip vortex depend on?

By examining the work of Peng et al. (2017), it is found that the cross profile (NACA 66\(_2\)-415) and aspect ratio (\(\varLambda =b/c=1.19\)) of the hydrofoil utilized by them are the same as those of the test model in the present study (NACA 66\(_2\)-415, \(\varLambda =1.19\)), but under different flow conditions (\(\alpha = 7^\circ ,\,Re_c = 4.66\times 10^5,\,1.21\times 10^6\) in the work of Peng et al.). The position of peak circulation observed by them is consistent with that in current results, indicating the similarity of pinch-off positions for hydrofoils with a similar configuration. In addition, the outline of the trailing edge has been shown to have an impact on the process of the to-core vorticity transport, as discussed in the vortex development stages (Fig. 10). Thus, it is natural to speculate that the hydrofoil configuration might play a critical role in the circulation evolution of a tip vortex. Fruman et al. (1995a) experimentally tested three typical hydrofoils having the same cross profile but different shapes (elliptical one, straight trailing edge and straight leading edge). They observed that the development processes of vortex circulation were quite dissimilar for different hydrofoil shapes, while such difference in circulation was not fully explained. Combined with the current observation that the vortex evolution is strongly related to the shape of trailing edge, it might be further explained that the process of the to-core vorticity transport is altered due to the difference in hydrofoil configuration (the shape of trailing edge), thus leading to the variation in circulation evolution.

In summary, we can conclude that the tip vortex evolution is closely related to the hydrofoil configuration, especially the geometric feature of the trailing edge. The outline of the trailing edge has an impact on the circulation evolution of the tip vortex by altering the local process of the to-core vorticity transport. Moreover, for a single hydrofoil configuration, the circulation evolution seems irrelevant to the flow condition (the incident angle and Reynolds number). According the circulation evolution and local vorticity transport, the development process of the near-field tip vortex can be divided into three stages: vortex-attached stage, vortex-lifting stage and vortex-detached stage. At the vortex-attached stage, the tip vortex is attached to the hydrofoil surface. The streamwise circulation component grows dramatically, while the vertical component continuously decreases accompanied with the change of vortex trajectory. At the vortex-lifting stage, the tip vortex gradually lifts off the hydrofoil. Owing to the growth of the spanwise circulation component, the streamwise component grows at a decreasing growth rate. The vertical component decreases to a relatively low value and levels off. As the tip vortex enters the vortex-detached stage, the tip vortex completely leaves the hydrofoil and enters the wake region. At the position where the tip vortex just leaves the hydrofoil, the circulation pinch-off is triggered, and the vortex trajectory is deflected. The tip vortex travels further downstream in a self-sustaining state, i.e., its circulation remains at a constant level.

4 Conclusions

In the current study, a non-cavitating tip vortex in the near field of an elliptical hydrofoil is experimentally investigated utilizing TPIV. Benefiting from this volumetric measurement system with high temporal resolution, the formation and development of the near-field tip vortex under different flow conditions are completely captured. From the aspects of wandering motion and flow properties, the three-dimensional evolution of near-field tip vortex is analyzed in detail. Besides, the experimental database of the fully three-dimensional tip vortex formed in the current work can be used for the comparison and validation of corresponding numerical simulation.

Unlike in the far field, the near-field wandering motion is weakly dependent on both the Reynolds number and incident angle. The near-field wandering motion is mainly attributed to the local flow unsteadiness. Several small coherent structures are observed around the hydrofoil tip, which consists of shear layers and small-scale secondary vortices induced during the roll-up process of the tip vortex. As a result, the local flow is highly unsteady and corresponding wandering motion is rather intensive. During data post-processing, smoothing effects resulted from such wandering motion might be introduced, leading to extra deviations. To filter out the wandering smoothing effects, a simple and effective method, the re-centered process, is applied. By this method, more accurate vortex properties can be obtained. All quantitative analyses in the current study were based on the wandering-free data.

The \(\lambda _{ci,x}\) iso-surfaces demonstrate that the tip vortex emanates from the leading edge of the hydrofoil and is mainly formed on the suction side. A turning point of the vortex center trajectory can always be detected, and its position appears to be independent of the flow condition. According to the \(\lambda _{ci,x}\) iso-surfaces combined with contour maps of streamwise vorticity and crossflow velocity, it is found that the tip vortex completely leaves the trailing edge and enters the wake region at this turning point. Moreover, the external supply to the vortex core starts to be restricted and the pinch-off of vortex circulation is triggered, i.e., the vortex circulation grows to a constant level, at this turning point. Further analysis of local flow properties hints that the tip vortex evolution can be divided into three stages, vortex-attached stage, vortex-lifting stage and vortex-detached stage, which are mainly attributed to the hydrofoil configuration, such as the shape and trailing edge outline, rather than the flow condition.