1 Introduction

Studying the unsteady aerodynamics of wings interacting with various types of gusts is motivated by a desire for performance and reliability improvements across applications such as high-performance aircraft, unmanned aerial systems, micro aerial vehicles, helicopters, and high-efficiency wind turbines. In particular, an understanding of the underlying flow physics is crucial for aerodynamic applications including lift enhancement, active flow control, gust alleviation, or control-embedded design optimization.

A starting point for such investigations which still receives considerable contemporary attention is the study of a nominally two-dimensional airfoil encountering unsteady effects, caused by airfoil motion and/or a time-varying freestream velocity. Classical unsteady aerodynamic theories, based on potential flow, trace back to the early 20th century, such as Theodorsen’s theory for airfoils undertaking periodic motions (Theodorsen 1935), and Wagner’s indicial response function (Wagner 1925; Walker 1931). In a similar vane, Küssner’s function (Küssner 1936) gives the response of a thin airfoil to a sharp-edged transverse gust, while Sears (1941) and Greenberg (1947) describe harmonic gusts in the transverse and streamwise direction, respectively. More recently, as reviewed in Jones (2020) and Jones and Cetiner (2021), transverse (Corkery et al. 2018; Chowdhury et al. 2019; Sedky et al. 2020), vortical (Medina et al. 2018; Eldredge and Jones 2019; Rockwood and Medina 2020; Le Provost and Eldredge 2021), and streamwise (Dunne and McKeon 2015; Leung et al. 2018; He and Williams 2020c, 2020) gusts have received attention through both computational and experimental investigations. On the experimental side, Greenblatt (2016) reviewed earlier and more recent gust/unsteady flow generation approaches that are used in low-speed unsteady wind tunnels. Louver mechanisms at the upstream/downstream end of the test section are widely used in simulating large-scale turbulence (Makita 1991), surging flows (Farnsworth et al. 2020), and periodic oscillating flows (Wei et al. 2019). Meanwhile, active grids are utilized to produce atmospheric turbulence that has smaller length scales (Roadman and Mohseni 2009; Sytsma and Ukeiley 2011; Knebel et al. 2011).

For cross-flow/transverse gusts, while some of the two-dimensional velocity profiles can be simulated by forced motions of the test objects, e.g., pitching (He and Williams 2020b) and/or plunging motions (Perrotta and Jones 2018), perturbations in the flows enable richer characterization of such unsteady flows, and closer-to-real conditions to be generated in the test facilities. In particular, direct jet and towing (Corkery et al. 2018; Biler et al. 2021), jet-vortex-generator arrays (Olson et al. 2021), and perturbations on the wall (Fernandez et al. 2021) are some of the recent advances in efforts to generate transverse or cross-flow gusts in wind/water tunnels. However, the realization of traveling cross flows is still less seen in previous studies, nor is there a trivial solution to create controlled velocity gradients in selected directions (He and Williams 2020c; Gloutak et al. 2022).

In this paper, we present a suction-driven approach to produce controlled, transverse gusts as traveling waves in the Andrew Fejer Unsteady Wind Tunnel (AFUWT) at the Illinois Institute of Technology. The AFUWT is a closed-circuit wind tunnel with unsteady flow capability that is controlled by louver mechanisms. It was one of the earliest university wind tunnels to produce unsteady fluctuations in the freestream (Miller and Fejer 1964). Rennie et al. (2019) developed a low-dimensional model through the method of characteristics for the wind tunnel to produce longitudinal (streamwise) von Kármán spectrum gusts with open-loop control of the louvers. Further, He and Williams (2020) improved the wind tunnel’s capability and performance of controlling streamwise fluctuations in selected frequency ranges, replicating the von Kármán and Dryden spectra in the gusts with different length scales and intensities, by introducing a spectral feedback loop to establish closed-loop control for the wind tunnel. Recent modifications to the AFUWT installed a suction duct on the top of the test section so the flow had a bypass passage, which will be shown in Sect. 2.1. The suction effect that was generated by the bypass created a secondary (vertical) velocity component for the test-section flow. In the meantime, an additional set of louver mechanisms that had similar configurations with what was used in Pfeiffer and King (2018) was instrumented in the suction duct, where the louvers were controlled individually to distribute the suction in the streamwise direction. Thus, the unsteady test capability of the AFUWT was extended to temporal and spatial (two-dimensional) cross-flow perturbations, in addition to the streamwise disturbances.

In addition to the wind tunnel engineering and experiments, we developed theoretical models relevant to these cross-flow capabilities, including a lumped element model for the flow rates (described in Sect. 2.3) and potential flow solutions for the flow field (Sect. 2.4). These theoretical models can provide preliminary guidelines for experimental settings, such as the flow rate allocation between the test section and the suction duct, the spatial suction distributions on the top of the test section, and predictions of the flowfield within the test section in the presence of traveling wave gusts. Furthermore, these models allow us to analyze the suction-driven configuration more generally, which could enable further refinements to the design process for future unsteady wind tunnel upgrades.

Experimental results characterizing the modified AFUWT are shown in Sect. 3. The flow measurements and visualizations demonstrate that the suction-driven approach is able to generate both steady and traveling transverse flows. While we were able to create velocity gradients (\({\mathrm {d}} u/{\mathrm {d}} x\) and \({\mathrm {d}} v/{\mathrm {d}} x\)) in the test section, the velocity profiles, the waveforms, and the spectra of the gusts were not finely adjusted, since those were beyond the scope of this paper. Both the amplitudes and wavelengths that were used in the early-stage traveling wave tests resulted in large scale gusts, where the gust ratio (the ratio of the magnitude of the transverse velocity component to the mean streamwise flow speed) was \(\mathcal {O}(0.1)\) and the ratio of the wavelength to the test-section length was \(\mathcal {O}(1)\). A recent study in an active-grid-controlled wind tunnel with a slightly larger test section (\(0.8\,\mathrm{m}\times 1.0\,\mathrm{m}\times 2.6\,\mathrm{m}\)) (Wester et al. 2022) also reported gust ratios on the same order of magnitude, with a transverse velocity component ranging between 0.03 and 0.1 of the mean streamwise flow speed.

The main objective of this paper is to demonstrate the feasibility of the suction-driven transverse gusts in the wind tunnel. Subsequently, the influence of the traveling-wave gusts on velocity profile and flow angle of attack was documented.

2 Wind tunnel modification and theoretical models

2.1 Modification of the Andrew Fejer Unsteady Wind Tunnel

The original AFUWT incorporated a set of 4 louvers at the downstream end of the test section to enable control of the freestream flow speed, and generate longitudinal velocity fluctuations with desired velocity profiles or gust spectra (details are described in Rennie et al. 2019 and He and Williams 2020). The latest upgrade of the wind tunnel includes the construction of a suction duct onto the top of the test section. The diffuser and the main fan were modified or exchanged to meet the new working requirement, including the structure of the diffuser, flow rate capacity of the fan, as well as fan blade pitch function which allows the blade pitch angle to be adjusted to adapt to low or high flow speed conditions.

Figure 1 shows a schematic diagram of the modified sections of the AFUWT. The features relevant to the main flow passing through the test section were retained from the previous configuration, including the downstream louvers, and the breather (which was always closed in the experiments presented in this paper) to the diffuser. The breather is located in between the downstream louvers and the diffuser, which is also the exit of the test section. We use downstream louvers to refer to the test section exit in the rest of this paper since they are most responsible for determining the streamwise flow rate. The ceiling of the test section was replaced by a sealed duct that covers the entire top of the test section with 10 sub-channels at the inlet, angled at \(45^\circ\) to the horizontal. Each channel consists of a louver mechanism, which through its rotation is able to change the blockage of the channel from completely blocked to fully open (these louvers are referred to as top louvers in the rest of this paper). The suction duct returns to the diffuser through a straight channel and a curved exhaust. By sharing a pressure drop that was generated by the main fan, the duct created a certain amount of suction from the top of the test section, hence a vertical velocity component (cross flow) is generated in the test section in addition to the streamwise flow, the principles of which are discussed in Sect. 2.2. The flow that diverge between the test section and suction duct merge in the diffuser and return to the fan to complete the wind tunnel circuit.

Fig. 1
figure 1

Modified sections of the Andrew Fejer Unsteady Wind Tunnel

Full size image
Fig. 2
figure 2

Test section details

Full size image

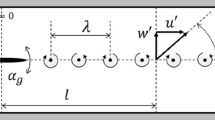
The detailed configuration of the test section and the suction duct is shown in Fig. 2. The test section had a length of \(L_{\mathrm{TS}}=2.1\,\mathrm{m}\) and cross-section dimensions of \(0.61\mathrm {m}\times 0.61 \mathrm {m}\). The coordinates are defined such that the \(x-\)axis is in the streamwise (horizontal) direction and the \(y-\)axis is in the vertical direction orientated at the bottom left corner of the test section. The distances in \(x-\) and \(y-\) directions are normalized by test-section length \(L_\mathrm {TS}\) and height \(H_\mathrm {TS}\) respectively. A layer of honeycomb is placed in between the test section and the inlet of the suction duct to reduce the turbulent disturbances from the suction. Each top louver is individually driven by a Nanotec® PD4-C6018L4204-E-01 servo motor, which allows for independent control of the blockage area in each sub-channel. As a louver rotates from \(0^\circ\) (parallel to sub-channel walls) to \(90^\circ\) (perpendicular to sub-channel walls), the blockage ratio in its sub-channel varies from 0 to 1. The motors are controlled through a dSPACE® DS1104 control box with a sampling rate of \(F_\mathrm {s}=1000\,\mathrm {samples/s}\). Despite the potential coupling between the test section and the suction duct (as they share the same pressure source), the downstream louvers mainly control the mean flow \(u_0\) and the longitudinal velocity fluctuation \(u'\), while the top louvers mainly enable temporal and spatial variance of the vertical velocity fluctuation \(v'\). In the results presented in this paper, the velocity quantities are normalized by the mean flow speed \(u_0\) such that \(u^*=u/u_0\) and \(v^*=v/u_0\), the \(z-\)vorticity is normalized by the test-section length and mean flow speed where \(\omega _z^*=\omega _z L_\mathrm {TS}/u_0\), and time is scaled based on the convective time \(t_c=L_\mathrm {TS}/u_0\).

The velocity components in the test section were measured by a Dantec Dynamics® MiniCTA 54T42 \(x\)-wire anemometer as well as an Aeroprobe® Air Data Probe (5 holes). Time-resolved particle image velocimetry (PIV) was performed to visualize the flow fields at the center part of the test section. The PIV vector grid is \(160\times 136\) on a \(504\,\mathrm {mm}\times 427\,\mathrm {mm}\) domain, thus, the spatial resolution is \(3.15\,\mathrm {mm}\) (\(0.0015L_\mathrm {TS}\)). The velocity vector fields are processed by the LaVision DaVis software with a 32 pixels by 32 pixels interrogation window with a 50% overlap. The data acquisition and louver control utilized a dSPACE® MicroLabBox® system. The dSPACE system was operated at a sampling frequency of \(F_\mathrm {s}=1000\,\mathrm {samples/s}\) and the time-resolved PIV data were acquired at a rate of 100 image pairs per second. A low-pass filter at a cut-off frequency of 20 Hz was applied to the measured data.

2.2 Cross flow generation

The vertical velocity fluctuation \(v'\) in the test section is created by the suction from the suction duct. As the main fan runs, it creates a pressure drop \(\Delta p\) between the inlet of the test section and the diffuser. This pressure drop moves the air in the tunnel from the test-section inlet to the diffuser exhaust. When the breather is closed, the flow rate \(Q_\mathrm {in}\) at the inlet of the test section equals the flow rate \(Q_\mathrm {out}\) where the two branches of flows merge in the diffuser. Since the suction duct constructs a parallel flow path to the test section, the total flow rate \(Q_\mathrm {in}\) is shared by the test section (\(Q_\mathrm {TS}\)) and the suction duct (\(Q_\mathrm {SD}\)), where \(Q_\mathrm {in}=Q_\mathrm {TS}+Q_\mathrm {SD}\) (see Fig. 2b for parameter locations). While the drop in the test-section flow rate slows the flow speed in the longitudinal direction, the suction generated by the flow that goes into the suction duct drives the flow to move vertically in the test section, in addition to the horizontal movement. As a result, the cross-flow feature of the wind tunnel is achieved by creating a vertical velocity component to the flow velocity. Note that the vertical velocity fluctuation is one-sided, since the suction on the top can only create positive velocity in the \(y-\)direction.

The major factor that affects the values of \(Q_\mathrm {TS}\) and \(Q_\mathrm {SD}\) is the fluid resistance of the test section \(R_\mathrm {TS}\) and the suction duct \(R_\mathrm {SD}\), as well as the variable fluid resistance of the downstream louvers \(R_\mathrm {LT}\) and the top louvers \(R_\mathrm {LS}\). Once the resistance is determined, the flow rates in these two sections are fixed in principle. On the other hand, downstream louvers and top louvers enables us to change the ratio of the resistance \(\frac{R_\mathrm {TS}+R_\mathrm {LT}}{R_\mathrm {SD}+R_\mathrm {LS}}\) by changing the blockage areas. As the resistance ratio changes, \(Q_\mathrm {TS}\) and \(Q_\mathrm {SD}\) change accordingly and can be controlled in designated manners within the system limits. Consequently, the u and v velocity components in the test section are controlled.

Since each louver is independently driven by a servo motor, this allows for individual control of the louver blockage. For example, the top louvers can rotate nonuniformly as a function of the \(x\)-coordinate. In other words, the suction/flow rate can be spatially distributed along the suction-duct inlet (the top of the test section) in the streamwise direction as \(\tilde{Q}_\mathrm {SD}|_{H_\mathrm {TS}}(t,x)\), where \(\int _0^{L_\mathrm {TS}} \tilde{Q}_\mathrm {SD}|_{y=H_\mathrm {TS}} {\mathrm {d}} x = Q_\mathrm {SD}\). The distributed flow rate leads to a nonuniform suction for the flow in the test section from the top; therefore, the vertical velocity fluctuation in the test section \(v'\) varies as a function of both \(t\) and \(x\). If we enforce a traveling-wave function to the louver motions (flow rate distribution), the propagated cross-flow fluctuation can be written in the form of \(v'(g(x-c_\mathrm {w}t))\), in which g is the waveform and \(c_\mathrm {w}\) is the wave speed. Further, when a sinusoidal waveform is applied, the one-sided \(v'\) is expressed as

$$\begin{aligned} v' = \frac{1}{2}v_{\max }\left[ 1-\cos \left( \frac{2\pi f_\mathrm {w}}{c_\mathrm {w}}x - 2\pi f_\mathrm {w}t\right) \right] , \end{aligned}$$
(1)

where \(f_\mathrm {w}\) is the wave frequency. Letting \(c_\mathrm {w} = u_0\), the cross-flow becomes a sinusoidal traveling wave.

2.3 Flow rate characterization through lumped element method

The method of characteristics that was used in Rennie et al. (2019) can continue to be applied for the modified AFUWT to give a preliminary approximation of the flow rates in the test section and the suction duct. Through a lumped element model, the influence of the fluid resistance and the flow inertia in the two branches, the test section and the suction duct, are taken into account to obtain estimates of the overall flow rate distributions in these two branches when a determined total flow rate is given at a fixed fan speed.

The test section and the suction duct are modeled as a parallel circuit as shown in Fig. 3. The basic assumption is the same as mentioned in Sect. 2.2; namely, the pressure drop \(\Delta p\) is determined by the fan speed only and does not change with the resistance. This allows for setting an artificial \(Q_\mathrm {in}\) without knowing the exact \(\Delta p\) value. For instance, a typical test-section inlet flow speed \(V_\mathrm {in}=6\,\mathrm {m/s}\) gives \(Q_\mathrm {in}=2.23\,\mathrm {m^3/s}\). A simplification of the wind tunnel configuration also applies here that the inlets and the exhausts of the test section and the suction duct are considered to be merged, respectively, so that the two sections start at the same location and intersect with each other at their ends. Use of the lumped element circuit in Fig. 3 to represent the wind tunnel branches automatically assumes a linear fluid resistance in the model. While the realistic resistance may not be fully linear due to suction-duct geometry, flow speed variations, louver rotations, etc., these influences are minimal in steady-state cases. Therefore, we keep this assumption for steady-state flow rate estimations.

Fig. 3
figure 3

Lumped element model for the test section and the suction duct

Full size image

With the given assumptions and the simplifications, Kirchhoff’s current law (continuity) gives

$$\begin{aligned} 0 = Q_\mathrm {in} - Q_\mathrm {TS} - Q_\mathrm {SD}. \end{aligned}$$
(2)

And Kirchhoff’s voltage law (momentum equation) gives

$$\begin{aligned} 0 =&~ (R_\mathrm {TS}+R_\mathrm {LT})Q_\mathrm {TS} + I_\mathrm {TS}\frac{{\mathrm {d}} Q_\mathrm {TS}}{{\mathrm {d}} t} \nonumber \\&- (R_\mathrm {SD}+R_\mathrm {LS})Q_\mathrm {SD} - I_\mathrm {SD}\frac{{\mathrm {d}} Q_\mathrm {SD}}{{\mathrm {d}} t}, \end{aligned}$$
(3)

in which \(I_\mathrm {TS} = \rho L_\mathrm {TS}/A_\mathrm {TS}\) and \(I_\mathrm {SD} = \rho L_\mathrm {SD}/A_\mathrm {SD}\) are the flow inertia (appears as the flow inertance) terms. The flow inertance of the suction duct is approximated by dividing the suction duct into the upward suction part (taking flow from the test section) and the horizontally flowing part (returning to the diffuser). The flow resistance \(R_\mathrm {TS}+R_\mathrm {LT}\) (flow resistance of the test section and the downstream louvers) and \(R_\mathrm {SD}+R_\mathrm {LS}\) (flow resistance of the suction duct and the top louvers) in Eq. 3 are estimated based on the measurements from Feroz (2017) and Rennie et al. (2019), where \(R_\mathrm {SD}\) takes the corners into account. Combining Eqs. 2 and 3 while letting \(R_1=R_\mathrm {TS}+R_\mathrm {LT}\) and \(R_2=R_\mathrm {SD}+R_\mathrm {LS}\), we write

$$\begin{aligned} \frac{{\mathrm {d}} Q_\mathrm {TS}}{{\mathrm {d}} t} + \frac{R_1+R_2}{I_\mathrm {TS}+I_\mathrm {SD}}Q_\mathrm {TS} = \frac{R_2}{I_\mathrm {TS}+I_\mathrm {SD}}Q_\mathrm {in}. \end{aligned}$$
(4)

Solving for \(Q_\mathrm {TS}\) in Eq. 4, we obtain the volume flow rates in the test section

$$\begin{aligned} Q_\mathrm {TS}(t) =&\left[ Q_\mathrm {TS}(t_0) - \frac{R_2}{R_1+R_2}Q_\mathrm {in}\right] \exp \left( -\frac{R_1+R_2}{I_\mathrm {TS}+I_\mathrm {SD}}t\right) \nonumber \\&+ \frac{R_2}{R_1+R_2}Q_\mathrm {in}, \end{aligned}$$
(5)

thus, in the suction duct

$$\begin{aligned} Q_\mathrm {SD}(t) = Q_\mathrm {in} - Q_\mathrm {TS}(t), \end{aligned}$$
(6)

where we define the initial condition as \(Q_\mathrm {TS}(t_0) = Q_\mathrm {in}\), which also simulates step opening of the top louvers.

The ODE solutions for \(Q_\mathrm {TS}\) and \(Q_\mathrm {SD}\) from Eqs. 5 and 6 reflect the fact that the steady-state flow rates are affected by the resistance ratio only, and we can change the weights of the flow rates by varying the resistance of the louvers.

An example result where \(V_\mathrm {in}=6\,\mathrm {m/s}\) (thus, \(Q_\mathrm {in}=2.23\,\mathrm {m^3/s}\)) and the top louvers are fully opened while the downstream louvers are half opened is shown in Fig. 4. When the flow reaches steady state, the flow rates are \(Q_\mathrm {TS}=1.50\,\mathrm {m^3/s}\) and \(Q_\mathrm {SD}=0.73\,\mathrm {m^3/s}\). If we use the cross-section area of the test section and the inlet area of the suction duct to calculate the magnitudes of the horizontal and vertical velocity components, respectively, we have \(u_0=0.67V_\mathrm {in}\) and \(v_0=0.10V_\mathrm {in}\). The lumped element calculation of the velocity components assumes a uniform velocity profile in the \(y-\)direction, which is not physically realistic. However, the model is still valuable since it gives preliminary predictions of the key parameters to be expected from the suction-driven architecture and these parameters can guide the adjustment of the potential flow model to enable quantitatively accurate predictions, which will be discussed in Sect. 2.4. The lumped element model also gives a general prediction of the average flow angle in the test section due to the vertical velocity component. For example, for the case considered in Fig. 4, the flow angle of attack is predicted to be \(8.1^\circ\) in the steady-state solution. Lastly, the lumped element model also predicts the existence of a time constant that governs how quickly the system responds to a change in parameters (e.g. changing the resistance by adjusting louver positions). Consequently, this suggests that the importance of the transient effects predicted by Eq. 6 would depend on the timescales involved with the gust (e.g. the speed of a traveling gust).

Fig. 4
figure 4

Lumped element model estimation of the transient response of test-section velocity components

Full size image

2.4 Potential flow solutions

The flow field in the test section can be modeled as a superposition of a uniform flow in the horizontal direction and a distribution of sinks on the top in a channel. Using a methodology similar to that proposed in Greengard (1990), the boundary conditions of the channel can be enforced through the use of an infinite number of image sources/sinks above and below the actual cross flow location. Figure 5 shows this formulation with 10 sinks and some of their images, showing the transverse gust velocity field without a background freestream. Working in the complex plane (with complex variable \(\tilde{z}\)), we consider a channel with lower and upper walls at \(\tilde{z} = 0\) and \(\tilde{z} = i H_{\mathrm {TS}}\) respectively. A source/sink at a location \(\tilde{z}_\mathrm {sk}\) induces a complex velocity

$$\begin{aligned} w = \frac{\tilde{Q}_{\mathrm {sk}}}{2\pi \left( \tilde{z}-\tilde{z}_\mathrm {sk}\right) }. \end{aligned}$$
(7)

We wish to place a row of sinks along the top surface of the channel at location \(\tilde{z}_{\mathrm {sk},j} = x_j + iH_{\mathrm {TS}}\), with each sink having strength \(\tilde{Q}_{\mathrm {sk},j}\). To enforce a no penetration boundary condition at the lower surface, we place image sinks at \(\tilde{z}_{\mathrm {sk},j} \pm i 2 k H_{\mathrm {TS}}\), for all integers \(k\). This gives a total complex velocity induced by these sinks of

$$\begin{aligned} w = \sum _{j=1}^n\frac{\tilde{Q}_{\mathrm {sk},j}}{2\pi } \sum _{k=-\infty }^\infty \frac{1}{z-z_\mathrm {sk}+i 2 k H_{\mathrm {TS}}}. \end{aligned}$$
(8)

As discussed in Greengard (1990), the inner sum can be viewed as the Laurent series expansion of a coth function. Adding in the freestream velocity \(u_0\), this gives the total complex velocity within the channel as

$$w = u_0 + \frac{1}{4 H_{\mathrm {TS}}} \sum _{j=1}^n\tilde{Q}_{\mathrm {sk},j} \coth \left( \frac{\pi }{2 H_{\mathrm {TS}}}(\tilde{z}-\tilde{z}_{\mathrm {sk},j})\right) ,$$
(9)

where again \(\tilde{Q}_{\mathrm {sk},j}\) is the strength (flow flux per unit length) of the sink at \(\tilde{z}_{\mathrm {sk},j}\). Note also that in the limit of a continuous distribution of sinks, the sum in Eq. 9 can be replaced by an integral. The potential flow solutions in this paper use 105 discrete sinks and their images, which gives a velocity field that closely matches that from a continuous sink distribution.

Fig. 5
figure 5

Physical and image sinks in the potential flow model

Full size image

Figure 6 shows the test section flow field given by this analytical solution steady conditions, in which \(u_0 = 4.03\,\mathrm {m/s}\) and \(\int _0^{L_\mathrm {TS}}\tilde{Q}{\mathrm {d}} x = Q_\mathrm {SD}/\mathrm {[m]}=0.73\,\mathrm {m^2/s}\) (from the ODE solutions in Sect. 2.3). The top subplot shows the top louver opening ratio and the flow angle of attack extracted from the potential flow solution. The top louvers are fully opened in this case (the opening ratio is 1 for all \(x\)-locations), thus \(\tilde{Q}\) is uniformly distributed along the top boundary. The mean flow angle of attack at half test-section height is \(\bar{\alpha }_\mathrm {TS}|_{y=\frac{1}{2}H_\mathrm {TS}}=8.45^\circ\), which is comparable to that was obtained from the solution of the lumped element model. The \(u_0\)-normalized velocity components \(u^*\) and \(v^*\) are shown in contours. The spatial deceleration in \(u^*\) (as seen in the middle subplot) causes the flow angle of attack to increase throughout the test section, which is expected since more flow goes into the suction duct as x increases. The \(v^*\) contour at the bottom shows that the vertical velocity gradient \({\mathrm {d}} v^*/{\mathrm {d}} x\) is approximately zero, away from the streamwise inlet and outlet regions. Note that the potential flow model may not be accurate near these boundaries, as it does not account for features of the wind tunnel such as the louvers downstream of the test section.

Fig. 6
figure 6

Potential flow solution for \(V_\mathrm {in}=6\,\mathrm {m/s}\) and louvers fully opened

Full size image

To simulate the traveling-wave flow field with the potential flow model, the flow flux distribution on the top boundary is allowed to vary with respect to both the time and position based on Eq. 1. Assuming that the vertical velocity at the test-section ceiling/suction-duct inlet is proportional to the local flow flux of the sinks, the traveling cross flow can be determined by appropriately defining the flow flux distribution \(\tilde{Q}(t,x)\) based on the blockages of each of the sub-channels in the suction duct. This allows for time-varying solutions for the flow field to be determined for given wave speeds and frequencies. We emphasize that this method assumes that the flow response to changing louver positions is immediate, and thus that the flow field at a given time is only a function of the instantaneous louver position. Section 3.4 will show how this approach can be modified to incorporate the transient effects predicted by the lumped element model (Eq. 5), with an empirically-determined time constant.

Two snapshots of the solution at a wave speed of \(6\,\mathrm {m/s}\) and a wave frequency of \(1.5\,\mathrm {Hz}\) are shown in Fig. 7. Note that the inlet flow speed of the test section \(V_\mathrm {in}\) and the total flow flux \(\int _0^{L_\mathrm {TS}}\tilde{Q}{\mathrm {d}} x\) at the suction-duct inlet are different from those in the fully-opened solution in Fig. 6. The wave speed and frequency chosen here to match subsequent experiments, which consider a mean flow speed of \(u_0=6\,\mathrm {m/s}\) and a highest wave frequency of \(f_\mathrm {w}=1.5\,\mathrm {Hz}\) (see Sect. 3.6). From the left (\(t=0.6T\), where \(T\) is the period) to right columns (\(t=0.9T\)), the snapshots visually show how traveling characteristics are realized by a spatiotemporally-varying sink distribution on the top boundary. The louver, opening ratio shown in the top plots demonstrates the sinusoidal form of the sink distribution. Although the correlation between the suction strength and the louver opening ratio may not be fully linear in reality, it is reasonable to assume a linear relation between them in this simplified theoretical analysis (comprehensive studies on the dynamic control of the tunnel could be the subject of future research). At \(t = 0.6T\), the zero opening ratio is at \(x=0.67L_\mathrm {TS}\) while the full opening point has not moved into the test-section domain (the half wavelength in this case \(\frac{1}{2}\lambda _\mathrm {w}=2\,\mathrm {m}\) is close to the test-section length since we specified the wave speed to be the same as the mean flow speed). The effect of the spatial suction distribution is visualized in the velocity field contours, especially, the \(v-\)component contours show the influence of neighboring suction concentrations as one of them is moving out of the test-section exit to the right and the second peak is entering the test-section inlet from the left. When the time comes to \(0.9T\), the first peak is completely out of the domain and the second peak has traveled into and dominated the test section. The flow angle of attack also “travels” with the mean flow as a result of the varying suction effect.

Fig. 7
figure 7

Snapshots of potential flow solution for traveling wave at \(c_\mathrm {w}=u_0=6\,\mathrm {m/s}\) and \(f_\mathrm {w}=1.5\,\mathrm {Hz}\). The top row shows the spatial distribution of the louver opening ratio and flow angle in the middle of the test section, while the remaining subplots show the predicted instantaneous velocity fields

Full size image

Through the flow rates from the lumped element model and the flow field from the potential flow solutions, the theoretical analysis provides some knowledge of what to expect from the suction-driven approach. It also gives preliminary guidance on how to operate the wind tunnel in experiments, which are discussed in the next section. However, we are aware that these theoretical models are simplified descriptions of the wind tunnel, so one should not expect a full replication of the flow parameters or the flow field from the models. Nevertheless, the potential flow model has a good potential to include more comprehensive configurations, e.g., modeling an airfoil encountering traveling waves, taking advantage of the experimental discovery of this paper that the transverse gusts generated are nominally irrotational as a benefit of the low-vorticity flow field created by the suction-driven approach (see Sect. 3.5).

3 Experimental results and discussions

The test-section flow field is measured using point hot wire/x wire measurements, 5-hole aeroprobe measurements, as well as particle image velocimetry (PIV) in baseline, steady suction, step input, and traveling wave tests. For the baseline tests, the downstream louvers are fully open and the top louvers are fully closed, while the breather remains fully closed. The calibration is obtained through the 5-hole aeroprobe and the single-wire hot wire measurements. The overall flow speed uncertainty is \(\pm 0.08\,\mathrm {m/s}\) for the minimum fan blade pitch case and is \(\pm 0.13\,\mathrm {m/s}\) for the maximum fan blade pitch. The calibration gives the operational envelope of the flow speed to be \(0.3-18.0\,\mathrm {m/s}~(50-1000\,\mathrm {rpm})\) and \(0.6-28.3\,\mathrm {m/s}~(50-1200\,\mathrm {rpm})\) for the minimum and maximum fan blade pitch angles, respectively.

3.1 Baseline flow field

Figure 8 shows an example baseline flow field at \(u_0=3.3\,\mathrm {m/s}\) that is measured by PIV within a sampling window \(0.38L_\mathrm {TS} \leqslant x \leqslant 0.62L_\mathrm {TS}\) longitudinally and \(0.15H_\mathrm {TS} \leqslant z \leqslant 0.85H_\mathrm {TS}\) vertically in the test section.

Fig. 8
figure 8

PIV measurement of mid-test-section baseline flow at \(u_0=3.3\,\mathrm {m/s}\)

Full size image

Figure 8a gives the normalized mean field (averaged over 5 s) of \(u^*-\), \(v^*-\)component, and \(z-\)vorticity \(\omega _z^*\) from top to bottom. The relatively small color map scales make the spatial variations in the velocity and vorticity visible, however, the variations are in fact very small if we examine the absolute values and the corresponding standard deviations which are shown in Fig. 8b. High standard deviation values at the corners of the PIV window indicate that most of the uncertainty comes from the PIV measurement noise at these locations, which raises the overall \(\sigma\) values. As we sort out where the noise comes from, the standard deviation values (in both space and time) in the center region of the test section are \(\sigma _{u^*}=0.0098\), \(\sigma _{v^*}=0.0094\), and \(\sigma _{\omega _z^*}=2.08\). Note that these \(\sigma\) values are the mean values among the entire PIV window which includes the noisy boundaries and corners. If we solely consider the inner region (\(0.4L_\mathrm {TS} \leqslant x \leqslant 0.6L_\mathrm {TS}\), \(0.25H_\mathrm {TS} \leqslant y \leqslant 0.75H_\mathrm {TS}\)), \(\sigma _{\omega _z^*}\) varies between 1.22 and 1.65, for instance. Therefore, the inner region appears near-white due to both the high \(\sigma\) values at the corners that extend the overall color scale and the small \(\sigma\) values (relative to the noise caused by PIV measurement) calculated in the inner region itself. Nevertheless, the spatial variations of \(\sigma\) in the inner region are still observable on logarithmic color scales. For the \(z-\)vorticity, particularly, the mean value is \(\omega _z^*=-0.003\), which gives that \(95.5\%\) (\(2\sigma\) range) of the variation of \(\omega _z^*\) is within \(-0.003\pm 4.16\) with the PIV measurement noise being taken into account. This background noise level becomes important when we compare the vorticity variations in the cross-flow cases later in Sect. 3.5. On the other hand, spatial distributions of the standard deviation carry the information about how stable the low-vorticity condition is maintained in the test section, which cannot be obtained through time-averaged data in steady cases or instantaneous snapshots in dynamic cases.

3.2 Steady suction

In all transverse flow experiments, the downstream louvers are half open in order to properly distribute the total flow rate between the test section and the suction duct. By fully opening louvers 5 and 6 at the center of the ceiling while keeping the rest of the louvers fully closed, the suction duct generates steady suction from \(0.4L_\mathrm {TS}\) to \(0.6L_\mathrm {TS}\) as shown by the louver opening ratio in Fig. 9a, which deflects the flow upward in the test section. The actual flow field (averaged over 5 s) in the PIV window (Fig. 9b) is comparable to the potential flow field in the same window (Fig. 9a). As a result, the experimentally-measured velocity components extracted along the horizontal center line agree with the potential flow predictions (top subplot of Fig. 9b). The spatial distribution the of flow angle of attack at the center line also agrees with the potential flow prediction (top subplot of Fig. 9a), reaching a peak of \(\alpha _{\mathrm {TS}_{\max }}|_{y=\frac{1}{2}H_\mathrm {TS}}\approx 9^\circ\). We conclude that the steady suction configuration gives a flow field that is consistent with the potential flow model with appropriately-defined flow rates.

Fig. 9
figure 9

Steady suction test results at \(u_0=2.0\,\mathrm {m/s}\), comparing experimental measurements with potential flow model predictions

Full size image

3.3 Transient response

Understanding the transient response of the flow field to the louver input is essential for precise control of the transient cross-flow velocity that is generated. Figure 10 shows the snapshots of the flow field in the transient process, in which the \(0.4L_\mathrm {TS}\) to \(0.6L_\mathrm {TS}\) top louvers are opened or closed by step inputs. The repeated step inputs keep the louvers open for 4 s and then closed for 4 s in sequence. From top to bottom, each row shows the \(u^*\), \(v^*\), and \(\omega _z^*\) contours from left to right at a certain moment in dimensional time. Flow field at each time correspond to the louver status which changes from the beginning of the step opening (\(t=0.4\,\mathrm {s}\)), during the transient response to opening (\(t=0.6\,\mathrm {s}\)), approaching a steady state at maximum opening (\(t=4\,\mathrm {s}\)), in the transient related to step closing (\(t=4.47\,\mathrm {s}\)), and to after closing (\(t=4.6\,\mathrm {s}\)). The results show that both \(u^*\) and \(v^*\) contribute to the evolution of the flow field as the louvers rotate. It is worth noting that the vorticity value in the test section remains at a very low level regardless of the operating status of the louvers/flow conditions (again, the color maps are magnified by the small scale), which will be discussed more in Sect. 3.5.

Fig. 10
figure 10

Snapshots of transient response of cross flow at \(u_0=3.3\,\mathrm {m/s}\)

Full size image

Point velocity results of the transient response are obtained by measuring the vertical velocity component at the center of the test section (\(x=0.5L_\mathrm {TS}\), \(y=0.5H_\mathrm {TS}\), and the lateral location is at the middle of the test-section span). The vertical velocity measured by the \(x\) wire and PIV are shown in Fig. 11. The top plot shows the phase-averaged \(x\)-wire measurements of \(v^*\) with \(u_0=2.2\,\mathrm {m/s}\) over 25 tests and the bottom plot shows the phase-averaged \(v^*\) extracted from PIV measurements with \(u_0=3.3\,\mathrm {m/s}\) over 10 cycles. Both sets of data demonstrate good repeatability of the transient gusts. The non-zero mean \(v^*\) value that appears during the louver-closed phase is due to the small amount of leakage which generates low-level suction on the top. While this definitely needs to be compensated in wing/model tests (e.g., through effective angle of attack offset), on the other hand, it also shows how sensitive the test-section flow is to the suction effect. With these data, the time constants of the opening stage \(\tau _\mathrm {open}\) and the closing stage \(\tau _\mathrm {close}\) are found for the two cases above, where \(\tau _\mathrm {open}=0.41\,\mathrm {s}\) and \(\tau _\mathrm {close}=0.11\,\mathrm {s}\) in the \(u_0=2.2\,\mathrm {m/s}\) case, and \(\tau _\mathrm {open}=0.46\,\mathrm {s}\) and \(\tau _\mathrm {close}=0.10\,\mathrm {s}\) for the \(u_0=3.3\,\mathrm {m/s}\) case. The time constants are comparable between the two cases with a slight difference associated with the mean flow speed.

Fig. 11
figure 11

Point velocity measurements in the center of the test section for transient response to louver opening and closing

Full size image

Although the louvers open and close at the maximum rotational rate when a step input is given (in practice, the louvers take approximately \(0.03\,\mathrm {s}\) to rotate \(90^\circ\) when responding to the step input from minimum to maximum), the flow responds asymmetrically to the two-step inputs. Such asymmetry is also found in Neuhaus et al. (2021) where the gust is controlled by an upstream active grid. There, the rising and falling times in the velocity step tests are reported to have dependency upon the step amplitude, with the rising time increasing with step amplitude, and the falling time having the opposite trend. In addition, Neuhaus et al. (2021) reports oscillations in the velocity response that are most apparent for the large-amplitude step-down cases. In the present work (which utilizes the largest step amplitude possible for the setup), the rising time \(\tau _\mathrm {open}\) is significantly longer than the falling time \(\tau _\mathrm {close}\). This is because a longer time is required for the suction effect to develop due to the fluid inertance in the suction duct, which echos the ODE solutions from Sect. 2.3. In contrast, when the louvers close, the suction is shut down directly without much interaction with the suction duct, so that \(\tau _\mathrm {close}\) reflects the much shorter time that is required for the mean flow to remove the suction effect. The streamwise velocity will experience a temporary influence due to the coupling in the flow rates and the suction effect. The \(u^*\) contours clearly show the acceleration and deceleration regions that are divided by the sink/suction center. Therefore, the rising phase is not a strict “step” in terms of the aerodynamic input to wings/models in the test section. Nevertheless, it does shift the flow condition from one steady state to another in less than half of a \(L_\mathrm {TS}\)-based convective time (\(\tau _\mathrm {open}<0.5t_c\)) or, in terms of the typical wing/model scale, less than 5 chord-based convective times. We, therefore, expect to observe substantial transient effects during this process.

3.4 Traveling gusts

To perform experimental validation of traveling transverse gusts, we first consider isolated, single-peak gusts. The test wave frequency is fixed at \(f_\mathrm {w}=1\,\mathrm {Hz}\), while the wave speed has two values; one equal to the mean horizontal flow speed \(c_\mathrm {w}=u_0\) and one that is half of the flow speed \(c_\mathrm {w}=0.5u_0\). Figure 12a and b show snapshots of these two cases respectively, as the gusts travel through the test section with a mean flow speed of \(u_0=2.84\,\mathrm {m/s}\). Note that the PIV results shown in this section are for non-phase-averaged data, showing the real-time flow field response to the traveling-suction gust. From left to right the snapshots at several points in time are shown as the gusts travel in the streamwise direction. The top rows show the spatial suction distribution on the test-section ceiling via the louver opening ratio (note that the discontinuity due to the finite louver size in the real cases is not represented here) and the model-predicted and the PIV-measured flow angles of attack along the \(x\)-direction. The middle rows show the \(v^*\) contours of the potential flow simulated flow fields and the bottom rows are the \(v^*\) contours of the PIV-measured flow fields. By comparing the two cases, the flow angle of attack shows dependency upon the traveling wave speed. The PIV-measured flow angle of attack does not reach the value that is predicted by the potential flow model when the wave speed is the same as the mean flow speed in the given experimental configuration. Instead, the measured and predicted flow angles of attack have better agreement in the half wave speed (\(c_\mathrm {w}=0.5u_0\)) case. The difference is also shown by the doubled vertical velocity magnitude in the half wave speed case (note the different color map scales). This phenomenon may relate to (1) the transient behavior of the test-section velocity responding to the louver motions that was discussed in Sect. 3.3; (2) the split of flow rates in the dynamic cases does not exactly follow the quasi-steady model predictions, of which the limitation was mentioned earlier. On the other hand, we do observe that the velocity gradients \({\mathrm {d}} v^*/{\mathrm {d}} x\) and \({\mathrm {d}} u^*/{\mathrm {d}} x\) (not shown in the plots) are generated and carried by the traveling gusts in experiments regardless of the wave speed. For instance, the elliptical contour lines in the PIV-measured \(v^*\) fields are well replicated by the potential flow model, which indicates similar velocity gradient patterns between the model predicted and the experimental results.

Fig. 12
figure 12

Traveling gust results at three instances of time, comparing flow angle and velocity field measurements with potential flow model predictions

Full size image

To improve the accuracy of the potential flow model predictions in dynamic cases, we could implement the transient response of the flow responding to the louver input into the potential flow model. As an initial attempt, the exponential behavior of the vertical velocity component in Fig. 11 during the step-open stage can be approximated by a first-order linear dynamical system of the sink strength responding to the louver input, which has a normalized step response \(h(t)\) of the form

$$\begin{aligned} h(t) = 1- \exp \left( -\tau _\mathrm {open} t\right) \end{aligned}$$
(10)

which is of the same general form as given by the lumped element model, Eq. 5. Hence, the flow field response is no longer a function of the instantaneous louver opening ratio, but also depends on its time history. In particular, if the original potential flow model gives a sink strength of \(\tilde{Q}_{\mathrm {input}}(t)\), the transient correction for each sink is given by

$$\begin{aligned} \tilde{Q}_{\mathrm {output}}(t) = \int _{\tau = 0}^t \tilde{Q}_{\mathrm {input}}(\tau ) h (t-\tau ) d \tau , \end{aligned}$$
(11)

where the time constant \(\tau _\mathrm {open}\) in the step response \(h(t)\) is determined according to the measurements in Fig. 11. To account for the different mean flow speed, here the value of \(\tau _\mathrm {open}\) is interpolated from the measurements so we have \(\tau _\mathrm {open}=0.44\mathrm {s}\) at \(u_0=2.84\mathrm {m/s}\). In addition, a DC gain of 0.8 is implemented in the correction to obtain the correct step amplitude. Note that only \(\tau _\mathrm {open}\) is used to make the first-order correction, although two time constants exist in the experimental results. Figure 13 shows the effect that this modification has on the spatial sink strength distribution for the isolated gust traveling at \(c_\mathrm {w}=u_0\).

Fig. 13
figure 13

Spatial distributions of sink strength for an isolated transient gust with \(c_\mathrm {w}=u_0\), at three instances of time

Full size image

The potential flow fields modified by this transient correction are shown in Fig. 14, where we again compare the predicted flow angle of attack and \(v^*\) contours to the experimental results. The magnitudes of both the flow angle of attack and \(v^*\) (note the change of the color map scale) of the \(c_\mathrm {w}=u_0\) case (shown in Fig. 14a) are corrected since the modified sink strength does not have enough time to rise to the maximum value. Meanwhile, the \(c_\mathrm {w}=0.5u_0\) (shown in Fig. 14b) flowfield is comparatively unaffected by the transient-response modification (the gain and the time constant in the dynamical system are unchanged), which indicates that the transient effect of the flow responding to the louvers is less significant at this lower wave speed. However, we also notice that this initial modification of the potential flow model may not fully represent the transient behaviors of the wind tunnel. For instance, the louver-closing stage is not well modeled as the time constants \(\tau _\mathrm {open}\) and \(\tau _\mathrm {close}\) are indeed different according to the experimental measurements, however, here the first-order system only applies the \(\tau _\mathrm {open}\) time constant. Therefore, there could be further investigation combining the transient response and the potential flow model in future work.

Fig. 14
figure 14

Results for a traveling gust compared with predictions from the potential flow model with a transient response correction

Full size image

3.5 Irrotationality of the gusts

As mentioned in previous sections, low-vorticity conditions are maintained in the test section, both with and without transverse gusts. We will show, through quantitative comparison of the vorticity levels, that it is fair to state that we are able to generate nominally irrotational gusts in both steady and dynamic circumstances.

Fig. 15
figure 15

Time-series variation of test-section vorticity

Full size image

The average vorticity background noise is \(\omega ^*_{z_\mathrm {bgn}}=-0.003\pm 4.16\) (with a \(2\sigma\) confidence interval), as calculated in Sect. 3.1, of which the noise/high standard deviation values mainly come from the corners and the boundaries of the PIV window. This vorticity background noise and its uncertainty interval are plotted in gray shadow in Fig. 15. The phase-averaged vorticity fields of the transient and traveling gusts cases are plotted in thick colored lines with their \(2\sigma\) uncertainty boundaries are plotted in thin lines, where the uncertainty intervals are calculated with respect to both space and phase. We observe that the suction effect, which results in the transverse flow, has very small influence on the mean values of the vorticity in all cases, which fluctuate near zero between \(-0.14\) and \(0.11\). However, the suction effect does increase the uncertainty levels to some degree as the mean \(\sigma\) values are raised by \(17.3\%\), \(34.6\%\), and \(38.4\%\) for the three transverse gust cases, respectively, in comparison to the background noise uncertainty. The spatial standard deviation distributions of the vorticity in the transverse gust cases are mapped in Fig. 16, from which we confirm again that most of the uncertainty comes from the corners and boundaries of the PIV measurement window so we may conclude that the vorticity fluctuations in the data are largely due to this measurement uncertainty.

Fig. 16
figure 16

Spatial standard deviation map of test-section vorticity

Full size image

To give some context to the claim that the gusts generated are nominally irrotational, we compare the present results with flow fields that can be found in previous studies where the flows are typically rotational. For instance, the normalized vorticity values of the shear layers near airfoils vary within \(\omega _z^*=\pm 30\), \(\pm 50\), and \(\pm 40\) in steady flows (simulation) at \(Re=500\) (Asztalos et al. 2021), in surging flows (experimental) at \(Re=98,000\) (He and Williams 2020c), and under dynamic stall conditions (experimental) at \(Re=550,000\) (Deparday and Mulleners 2019), respectively. In contrast with these vorticity values, the net vorticity in the transverse gust tests is maintained at very low magnitudes (especially, the mean) near zero with uncertainties that are on the same order of the background noise uncertainty, which indicates that the flow in the test section is irrotational during the generation and diffusion of the gust. In addition, the irrotationality is well distributed in space at individual times as the standard deviation does not vary much spatially, except for the measurement errors near the boundaries that have been clarified to be noise.

3.6 Traveling waves in \(1-\cos\) form

By enforcing specific wave functions (Eq. 1), the wing is tested under single-sided sinusoidal transverse gusts, of which the propagated vertical disturbances are of the \(1-\cos\) form (FAA 2014). The control signals are given to each louver independently to enable the louvers open and close sinusoidally at the wave frequency, with phase delays between each louver signal applying the desired wave speed. For example, when we let \(c_\mathrm {w}=u_0=6\,\mathrm {m/s}\), the disturbances vary in space and “travel” with a phase speed that matches the mean flow speed. We observe that the vertical velocity profiles are not single-frequency sinusoidal waves in actual experiments, due to the presence of higher-frequency harmonics. This is because the transverse gusts are only controlled in an open-loop manner, with prescribed louver motions. However, this does not jeopardize the objectives of these traveling wave tests, since the transverse characteristics and the velocity variations are maintained and the results have good repeatability in all cases, as we will show by example velocity profiles and effective angles of attack in Fig. 17. Wave frequencies \(f_\mathrm {w}=0.5, 1.0\), and \(1.5\,\mathrm {Hz}\) are tested, corresponding to wavelengths of \(c_\mathrm {w}/f_\mathrm {w}=5.72L_\mathrm {TS}\), \(2.86L_\mathrm {TS}\), and \(1.90L_\mathrm {TS}\), respectively. The vertical disturbance amplitude varies between \(0.08u_0\) and \(0.1u_0\), which also gives the gust ratio. With reference to a typical chord length of a test object \(c=245\,\mathrm {mm}\) and a typical mean flow speed \(u_0=6\,\mathrm {m/s}\), the corresponding reduced frequencies, \(k = \frac{\pi f_\mathrm {w}c}{u_0}\), are \(k=\) 0.0641, 0.1282, and 0.1923. The example profiles (phase-averaged over 240, 120, or 80 cycles depending on the wave frequency) in Fig. 17 demonstrate how the wave frequency affects the actual velocity/flow angle of attack. In all cases, \(tu_0/L_\mathrm {TS}=0\) is referenced to the the moment when louver 5 is at \(0^\circ\) with a positive angular rate (in other words, when the louver crosses zero and starts to open). We observe phase shifts in the velocity profiles, so in the flow angle of attack, from lower to higher frequencies. If we use \(0.5\,\mathrm {Hz}\) case as a reference, the phase shifts \(0.120T\) in \(1.0\,\mathrm {Hz}\) case and \(0.246T\) in \(1.5\,\mathrm {Hz}\) case. It is worth noting that higher wave frequencies also reduce the harmonics of the main frequency in terms of power density, i.e., the energy of the harmonics decreases from \(61.6\%\) to \(32.9\%\) and \(21.9\%\) of the total energy within the \(0-10\,\mathrm {Hz}\) (mean removed) power spectra as the wave frequency increases.

Fig. 17
figure 17

\(1-\cos\) gust profiles, comparing the time evolution of the velocity and flow angle in the center of the test section

Full size image

4 Conclusions

We have presented a suction-driven approach to generate transverse gusts for steady cross flow, transient, and traveling wave conditions. The Andrew Fejer Unsteady Wind Tunnel was modified for this purpose, where an additional flow passage was added to the wind tunnel, through which a portion of the flow diverges from the main flow due to the suction that was generated. As the air flowed into two sections, the flow in the test section became two-dimensional. The suction duct covered and changed the original test-section ceiling into a series of louver mechanisms, while retaining the pre-existing louvers downstream of the test section. The louvers manipulated the resistance in the horizontal and vertical directions as they changed the blockage areas. The fluctuations of vertical velocity component could then be produced by properly distributing the flow rate to the louvers both in time and space.

Theoretical models were developed to make estimations of the suction effect in the wind tunnel, and to provide preliminary benchmarks for the experiments. Analytical potential flow solutions for the flow fields under the three transverse flow conditions were presented and compared with experimental results. The potential flow results agreed well with the PIV and x-wire measurements, although more details of the flow field were discovered from the results of the traveling waves, where the dependency of the flow angle of attack upon the gust wave speed was demonstrated. This dependency could not be predicted by the potential flow model, which assumes that the flow field is only a function of the instantaneous louver positions. However, by approximating the time history of the suction strength through a first-order linear dynamic system that represents the transient process, the potential model predictions can be improved and compared to experimental results of dynamic gust cases to a certain degree.

Transient responses of the flow to the suction input were documented so that later design of a complete gust control system becomes feasible. This could, for example, eventually enable accurate control of gust velocity profiles and/or spectra. In particular, we observed a substantial difference between the step open and close time constants. The significant rising time in the step open response was mostly due to the inertia of the flow in the suction duct. Therefore, one possible direction for improving the performance of future unsteady wind tunnels is to utilize a “running” suction duct in which the flow is constantly moving so it stands by to the demand from the test section. In the meantime, expanding the control capability of the tunnel to create more types of gusts (e.g. with different waveforms) could be another focus of future work.

The gusts generated by the wind tunnel have low turbulence levels and a high degree of repeatability. Besides the high-quality flow conditions in basic tests, the modified wind tunnel demonstrated promising potential for generating irrotational transverse gusts of different types. The fact that gusts are nominally irrotational allows for accurate potential flow predictions of the flow field. The vorticity in the test section was kept at background noise level regardless of the flow conditions (steady, transient, or traveling gusts). Given that classical unsteady aerodynamic theories were developed based on potential flow assumptions, the tunnel provides a convenient experimental environment to apply, validate, and extend these classical theories. For example, exploring the wing-gust interaction in low-vorticity gusts could be one of the immediate impacts of this feature. Further, one could more directly model certain gust conditions by starting with potential flow models and adding modifications to match experimental observations. For instance, one could consider a potential flow setup incorporating a 2-D wing in the test section, with a distribution of source/sink elements to model gusts. The inclusion of source/sink or doublet elements to model additional disturbances (Asztalos 2021) that could convect downstream over the wing in the test section (in additional to a traveling gust) is another example of a complex potential flow model that could be utilized.

From the PIV visualizations of the flow fields, we demonstrated that the wind tunnel could create velocity gradients, especially \({\mathrm {d}} v/{\mathrm {d}} x\), that could be carried by the traveling wave gusts. X-wire measurements of \(1-\cos\) form gust waves with different wave frequencies were generated to show the influence of the gusts which included the flow angle of attack and the velocity gradients. The wind tunnel’s transverse gust capability could be valuable in wing-gust studies that require the presence of traveling waves and spatial velocity gradients.