Assimilation and extension of particle image velocimetry data of turbulent Rayleigh–Bénard convection using direct numerical simulations

Abstract

A novel method for assimilating and extending measured turbulent Rayleigh–Bénard convection data is presented, which relies on the fractional step method also used to solve the incompressible Navier–Stokes equation in direct numerical simulations. Our approach is used to make measured tomographic particle image velocimetry (tomo PIV) fields divergence-free and to extract temperature fields. Comparing the time average of the extracted temperature fields with the temporally averaged temperature field, measured using particle image thermometry in a subdomain of the flow geometry, shows that extracted fields correlate well with measured fields with a correlation coefficient of $C_{T\tilde{T}}=0.84$. Additionally, extracted temperature fields as well as divergence-free velocity fields serve as initial fields for subsequent direct numerical simulations with and without feedback which generate small-scale turbulence initially absent in the experimental data. Although the tomo PIV data set was spatially under-resolved and did not include any information on the boundary layers, the here-proposed method successfully generates velocity and temperature fields featuring small-scale turbulence and thermal as well as kinetic boundary layers, without disturbing the large-scale circulation contained in the original experimental data significantly. The latter is underpinned by high vertical and horizontal velocity correlation coefficients—computed from velocity fields averaged in time and horizontal x-direction obtained from the measurement and from the simulation without feedback—of $C_{v\tilde{v}}=0.92$ and $C_{w\tilde{w}}=0.91$ representing the large-scale structure. For simulations with feedback, the generated velocity fields resemble the experimental data increasingly well for higher feedback gain values, whereas the temperature fluctuation intensity deviates noticeably from the values obtained from a direct numerical simulation without feedback for gain values $\alpha \ge 1$. Thus, a feedback gain of $\alpha =0.1$ was found optimal with correlation coefficients of $C_{v\tilde{v}}=0.96$ and $C_{w\tilde{w}}=0.95$ as well as a realistic temperature fluctuation intensity profile. The xt-averaged temperature fields obtained from the direct numerical simulations with and without feedback correlate somewhat less with the extracted temperature field ($C_{T\tilde{T}}\approx 0.6$), which is presumably caused by spatially under-resolved and temporally oscillating initial tomo PIV fields reflected by the extracted temperature field.

Graphical abstract

1 Introduction

Rayleigh–Bénard convection (RBC) is the buoyancy-driven flow of fluid between a heated bottom plate and a cooled top plate and serves as a canonical problem for the more complex thermal convection systems appearing in nature and engineering applications (Lohse and Xia 2010; Chillà and Schumacher 2012). This type of flow is usually characterised by the Prandtl number

$$\begin{aligned} \mathrm {Pr}=\frac{\hat{\nu }}{\hat{\kappa }}, \end{aligned}$$

(1)

reflecting the ratio of momentum diffusivity and thermal diffusivity, and the Rayleigh number

$$\begin{aligned} \mathrm {Ra}=\hat{\alpha }\hat{g}\hat{H}^3\frac{\Delta \hat{T}}{\hat{\nu }\hat{\kappa }}, \end{aligned}$$

(2)

representing the ratio of buoyancy and diffusive forces, with $\hat{\nu }$ the kinematic viscosity, $\hat{\kappa }$ thermal diffusivity, $\hat{\alpha }$ the thermal expansion coefficient, $\hat{g}$ the gravitational acceleration, $\hat{H}$ the convection cell height, and $\Delta \hat{T}$ the vertical temperature difference. Note that the dimensional quantities are denoted with circumflex and the dimensionless without. RBC can be investigated experimentally (Chavanne et al. 1997; du Puits et al. 2007; Schiepel et al. 2021) or numerically (Shishkina and Wagner 2008; Kaczorowski and Wagner 2009; Shishkina et al. 2010, 2013; Wagner and Shishkina 2013; Scheel et al. 2013; Stevens et al. 2018). Direct numerical simulations (DNS) provide temporally and spatially fully resolved velocity and temperature fields but are, due to computational limitations, restricted to moderate Rayleigh numbers and short observation times. Experiments, on the other hand, allow for high-Rayleigh number studies and long observation times, yet often lack parts of the data such as the boundary layers in measurements using particle image velocimetry (PIV) due to reflection of the laser light sheet and the lower tracer particle densities in the boundary layers. Further, turbulent small-scale structures are often filtered out since each velocity vector represents a surface- or volume-averaged representative obtained from a correlation step. However, highly resolved velocity fields can be measured accurately further away from the walls by means of PIV, whereas the temperature field is much more difficult to capture.

Being originally introduced in the field of meteorology, the assimilation of experimentally obtained data has become a significant instrument in the fluid dynamics community in general in recent years (Talagrand et al. 1987; Evensen 1994; Carrassi et al. 2018; Clark Di Leoni et al. 2020). A common approach is to generate a pressure field from a measured velocity field by solving the pressure Poisson equation (Fujisawa et al. 2005; van Oudheusden 2013; Pan et al. 2016; Schneiders et al. 2016; van Gent et al. 2017). Pan et al. (2016) estimate the error in assimilated pressure fields as well as its relation to the boundary condition, the dimension of the flow domain, and the flow type. In particular, Pan et al. (2016) point out that the error in the pressure calculation is dominated by the error inside the domain for large domains and by the error on the data boundary for small domains. Additionally, Gesemann et al. (2016) introduce the flow reconstruction tool FlowFit, where Cartesian velocity and pressure fields are reconstructed by minimising a cost function that accounts for the freedom of divergence in incompressible flows—as well as its derivative—and is applied to B-spline curves interpolated from particle tracking velocimetry data consisting of velocities and accelerations. Here, the minimisation problem—being a nonlinear, weighted least-square problem—is solved via the limited-memory Broyden–Fletcher–Goldfarb–Shanno algorithm described by Nocedal (1980). Evaluating their reconstruction method using synthetic data of forced isotropic turbulence provided by Li et al. (2008) by analysing vorticity iso-contours of the reconstructed fields and signal-to-noise ratios, Gesemann et al. (2016) show that their method improves with respect to simpler algorithms that penalise the divergence of velocity only or those that do not penalise divergence at all. Ehlers et al. (2020) further improve FlowFit by introducing additional virtual particles to the flow field between single-time particle measurements. Advecting these particles between the flow fields achieves temporal coupling and adds temporal constraints to the data. Comparing the resulting flow fields by means of DNS-based virtual experiments of forced isotropic turbulence and turbulent plane-channel flow, Ehlers et al. (2020) show that the reconstruction of the flow field improves significantly with respect to the original method by Gesemann et al. (2016).

By adapting a data assimilation scheme for Bénard convection from Farhat et al. (2016, 2020) present a data assimilation scheme for noisy temperature measurements of large to infinite Prandtl number RBC flows based on Newtonian relaxation. Evaluating their data assimilation scheme analytically and by means of two-dimensional direct numerical simulations of moderately turbulent flow, Farhat et al. (2020) establish that their scheme successfully assimilates temperature fields if the number of projected modes and the relaxation parameter relative to the Rayleigh number are large enough. More often than not, only the measured velocity fields are available, whereas pressure, temperature, or other scaler fields are also required to fully characterise the flow phenomenology. Assimilating three-dimensional velocity fields of homogeneous isotropic turbulence from scattered local velocity measurements of numerically generated data, Clark Di Leoni et al. (2020) present a so-called nudging algorithm where the right-hand sides of the Navier–Stokes equations are expanded by an additional forcing term that accounts for the difference between the actual flow field and the measured reference field. The full velocity field is obtained by integrating the modified equations in time by means of a DNS solver. A similar approach is introduced by Suzuki and Yamamoto (2015), where time-resolved particle tracking velocimetry (PTV) measurements of the planar-jet problem are assimilated by means of two-dimensional DNSs. Here, the additional feedback term is updated with PTV data at times PTV snapshots are available. Aiming at the assimilation of measured, spatially under-resolved, three-dimensional velocity fields from RBC, we present a novel approach that involves the additional numerical generation of the corresponding temperature fields as representatives of scalar fields. Our approach comprises the generation of small-scale fluctuations—initially lacking the measurement data—using a DNS solver with and without feedback term. Finally, the results obtained with the two methods are compared.

2 Experimental set-up

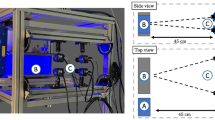
The experimental data is acquired in a rectangular RBC sample with dimensions $\hat{L}_x=250\,\mathrm{mm}$ and $\hat{L}_y=\hat{L}_z=\hat{H}=500\,\mathrm{mm}$, as presented in Fig. 1, where the heating and the cooling plates are indicated in red and blue, respectively. The measurement volume is highlighted with dashed white lines.

Fig. 1

Picture of the rectangular RBC cell. The heating and cooling plate are indicated in red and blue, respectively. The measurement volume is highlighted with dashed white lines.

The top and bottom of the experiment are embedded in an insulation mantle, indicated by (a) in Fig. 2. The temperature difference is generated by the cooling and heating elements, (b) and (f), whose temperatures are controlled by a water circuit and a resistive heating, respectively. The flow to be measured develops between two anodised black aluminium plates, (c) and (e), enclosing the sample. The four side walls (d) are made of 10 mm thick glass yielding high optical accessibility to the measurement volume. The set-up is supported by polyoxymethylene spacers, (g), installed within the insulation. These spacers are insulators good enough to avoid high heat fluxes, while simultaneously allowing for a horizontal alignment of the set-up within $0.01^\circ$ due to their high stability. Moreover, the spacers are fixed on the hardened aluminium ground plate (h) to ensure long-term stability.

Fig. 2

Schematic of the RBC sample along Z-direction. a marks the insulation layer, b and f indicate the cooling and heating elements, and c and e mark the anodised aluminium plates enclosing the sample. The glass cube, d the polyoxymethylene spacers, g and the hardened aluminium ground plate, h are labelled. The characteristic length of the sample is indicated by l

The heating and cooling plates are made of 1 cm aluminium. In order to minimise the heat loss through the side walls, the surrounding air temperature is controlled by an environmental control system to maintain the mean sample temperature within $\pm 0.5$ K. 45 Pt1000 resistance temperature detectors were used to monitor the temperatures in the heating and cooling plates as well as in the surroundings during the experiments. 16 of these sensors were installed in both the top and bottom plates with just 1 mm of aluminium between them and the fluid. These sensors exhibit a temperature standard deviation of 0.06 K, thus providing nearly isothermal boundary conditions for the heating and cooling plates.

The experimental data was acquired at an average sample temperature of $\hat{T}_0\,=\,18\,^\circ \mathrm{C}$ employing a water glycol-mixture with Pr = 18. Additionally, the temperature difference was regulated to $\Delta {\hat{T}}\,=\,4\,\mathrm{K}$, leading to a Rayleigh number of $\mathrm{Ra}\,=\,7.0\times 10^{9}$. For this parameter combination, the developing 3D-3C flow fields were measured using tomographic PIV (tomo PIV, Elsinga et al. 2006) and simultaneous 3D particle image thermometry (PIT, Dabiri and Gharib 1991; Schiepel et al. 2021) with the objective to investigate the velocity and temperature fields associated with the large-scale circulations (LSC). For the tomo PIV, four black-and-white (b/w) PCO1600 CCD cameras with a resolution of $1600 \times 1200$ pixels were utilised to monitor the convection sample from different perspectives. An additional PCO Pixelfly colour camera with a resolution of $1392 \times 1024$ was installed to record the colours of thermochromic liquid crystal particles reflecting the temperature. With these five cameras, the velocity fields were measured in the entire sample volume and the temperature fields in a subvolume with approximate height of 200 mm, width of 420 mm, and depth of 220 mm. For the latter, the observation volume was reduced due to the imaging limitations of the thermochromic liquid crystal particles which had to be imaged on multiple pixels of the Bayer-filter of the colour camera and with a sufficiently high intensity. All cameras were equipped with 21 mm Nikon lenses and tilted in accordance with the Scheimpflug condition. The sample was illuminated by an LED array consisting of $15\times 15$ LEDs of the type Osram Platinum Dragon LW W5SNA with a broad wavelength distribution covering the entire visible light spectrum. The LED array was triggered by a high-current power supply that provided defined light pulses. Focusing optics were positioned in front of the LEDs to decrease the divergence of the light, and thus, to generate a homogeneous intensity distribution within the measurement volume with light intensity fluctuations below 10%. This set-up allowed for a reliable image recording rate of 6.6 Hz.

The images from the four cameras were evaluated using a simultaneous algebraic reconstruction technique (Atkinson and Soria 2009) to determine 3D intensity maps employing $1000~\times ~1000~\times ~500$ voxels the volume in physical space. Afterwards, a cross-correlation algorithm with grid refinement was applied to determine the velocity fields. The interrogation windows started with a size of $144^3$ voxels and were refined to $50^3$ voxels with an additional overlap of 60% yielding $119\times 119\times 57$ vectors.

Using simultaneous tomo PIV-PIT, 1000 instantaneous velocity and temperature fields were determined. This number was chosen to obtain resolved velocity and temperature time series while assuring convergence of statistics. Assuming a circular path of the LSC within the volume and using the velocity magnitude of the time-averaged field, the measurement time frame corresponds to half a LSC turn-around or 26.55 free-fall times, respectively. Moreover, uncertainties of $\sigma _{\hat{v}} \le 0.66$ mm/s for the velocity and $\sigma _{\hat{T}} \le 0.095$ K for the temperature measurement were estimated (Schiepel et al. 2021).

The spatial and temporal resolution realised in the measurement are compared to the corresponding Kolmogorov scales so as to decide if the measurements are under or over-resolved. According to Ahlers et al. (2009), the Kolmogorov length scale can be estimated by

$$\begin{aligned} \hat{\eta }_K\approx \left( \frac{\hat{\nu }^3 \hat{H}}{\hat{v}^3_\mathrm{ref}}\right) ^4, \end{aligned}$$

(3)

with $\hat{\nu }$ the fluid kinematic viscosity and $\hat{v}_\mathrm{ref}$ the reference velocity. The reference velocity can be approximated with the maximum velocity of the mean velocity field $max\{(\langle \Vert \hat{\mathbf{u }}(t) \Vert \rangle _t)\}=0.0055$ m/s or the mean RMS velocity $\langle (\langle \hat{\mathbf{u }}^2(t) \rangle _t)^{1/2}\rangle _{xyz}=0.0033$ m/s, yielding flow Reynolds numbers of Re = 1228 or Re = 735, respectively. In agreement with Zürner et al. (2019), the Reynolds number based on the maximum mean velocity representing the LSC exceeds the Reynolds number based on the mean RMS velocity representing small-scale fluctuations. Since the former characteristic velocity is more restrictive for the estimation of the Kolmogorov scale as well as the boundary layer thickness, and thus, for the estimation of the computational grid in chapter 4, it will be used hereinafter. Furthermore, Ahlers et al. (2009) present the estimated Kolmogorov time scale as

$$\begin{aligned} \hat{\eta }_\tau \approx \sqrt{\frac{\hat{H}^4\mathrm {Pr}^2}{\hat{\nu }^2(\mathrm {Nu}-1)\mathrm {Ra}}}, \end{aligned}$$

(4)

where the Nusselt number is obtained by relations provided by Ahlers et al. (2009) based on the Grossmann–Lohse (GL) theory (Grossmann and Lohse 2000, 2001, 2002),

$$\begin{aligned} \mathrm {Nu}_{est} = 1 + \frac{\mathrm {Pr}^2}{\mathrm {Ra}}\left( \frac{c_1 \mathrm {Re}^2}{g} +c_2\mathrm {Re}^3 \right) , \end{aligned}$$

(5)

where

$$\begin{aligned} g= \sqrt{ \frac{\mathrm {Re}_c}{\mathrm {Re}}}\left[ 1+\left( \frac{\mathrm {Re}_c}{\mathrm {Re}}\right) ^2\right] ^{1/4}, \end{aligned}$$

(6)

with $\mathrm {Re}_c=3.4$, $c_1=8.05$, $c_2=1.38$ (Stevens et al. 2013), and the flow Reynolds number $\mathrm {Re}=\hat{v}_\mathrm{ref}\hat{H}/\hat{\nu }$. For the present tomo PIV data set, the Nusselt number is estimated as

$$\begin{aligned} \mathrm {Nu}_{est}= 129. \end{aligned}$$

(7)

The ratio of the estimated Kolmogorov scales and the spatial and temporal measurement resolution, $\Delta \hat{h}$ and $\Delta \hat{\tau }$, respectively, leads to

$$\begin{aligned} \hat{\eta }_K/\Delta \hat{h}= & {} 0.24\text { and} \end{aligned}$$

(8)

$$\begin{aligned} \hat{\eta }_\tau /\Delta \hat{\tau }= & {} 14. \end{aligned}$$

(9)

Thus, the measured velocity fields are spatially under- and temporally over-resolved. This and the fact that the boundary layers near the cooled and the heated plate are not captured in the tomo PIV are taken into account in the following analysis.

Regarding the orientation of the LSC, studies of RBC in cubic boxes, such as those of Bai et al. (2016), Foroozani et al. (2017), or Giannakis et al. (2018), report a meta-stable diagonal alignment of the LSC that switches the diagonal discretely. In the present case, the orientation of the LSC is evaluated via the resulting xy-planar velocity vector $\theta$ above the heated and below the cooled plate, as depicted in Fig. 3.

Fig. 3

Angle between the y-axis and the average planar velocity vector $\theta =\arctan {(\langle u \rangle _{xy} / \langle v \rangle _{xy})}$ at $z/H=0.1$ (a) and $z/H=0.9$ (b)

For the present case with $L_x/L_y=1/2$, a diagonal alignment would reflect in absolute angles of $| \theta | = 26.56 ^\circ$. In the measurement data, however, only angles up to $| \theta | \approx 9^\circ$ are captured. In the beginning of the measurement interval, the flow angle fluctuates between $-1^\circ$ and $4^\circ$ above the heated and between $-3^\circ$ and $1^\circ$ below the cooled plate. Around $\hat{t}\approx 60$ s, the angle above the heated plate shifts towards larger negative values and the angle below the cooled plate shifts towards positive value, which indicates a diagonal switching event. To further characterise the diagonal switching of the LSC—which is out of the scope of the present investigation—a longer measurement interval would be required.

3 Velocity field assimilation and temperature field generation

In order to assimilate the under-resolved, three-dimensional velocity field from the tomo PIV, a fractional step method is applied, which is described hereinafter. It is derived from the transport equations for mass, momentum, and temperature for an incompressible fluid and the Boussinesq approximation,

$$\begin{aligned} \frac{\partial \mathbf {u}}{\partial t} + \mathbf {u} \cdot \nabla \mathbf {u}= & {} -\nabla p +\sqrt{\mathrm {Pr}/\mathrm {Ra}}\nabla ^2 \mathbf {u} + T \mathbf {e}_z, \end{aligned}$$

(10)

$$\begin{aligned} \frac{\partial T}{\partial t} + \mathbf {u} \cdot \nabla T= & {} \sqrt{1/(\mathrm {Pr}\mathrm {Ra})}\nabla ^2 T, \end{aligned}$$

(11)

$$\begin{aligned} \nabla \cdot \mathbf {u}= & {} 0, \end{aligned}$$

(12)

with $\mathbf{u} =(u_x,u_y,u_z)$ the velocity, p the pressure, T the temperature, and $\mathbf {e}_z$ the unit vector in vertical direction. Note that bold symbols indicate vector quantities. Equations (10)–(12) govern the problem of RBC in a rectangular box with a heated bottom plate ($T=T_w$), a cooled top plate ($T=T_c$), and adiabatic side walls depicted in Fig. 4.

Fig. 4

RBC cell with volume $V=L_xL_yL_z$. All walls are no-slip boundaries; top and bottom walls are isothermal and side walls are adiabatic

Velocities have been non-dimensionalised with the free-fall velocity $\hat{u}_\mathrm{ref}=(\hat{\alpha }\hat{g}\Delta \hat{T}\hat{H}^3)^{1/2}$, spatial coordinates with the cell height $\hat{x}_\mathrm{ref}=\hat{H}$, the time coordinate with the corresponding reference time $\hat{t}_\mathrm{ref}=\hat{x}_\mathrm{ref}/\hat{u}_\mathrm{ref}$, and the pressure with the reference pressure $\hat{p}_\mathrm{ref}=\hat{\rho }\hat{u}^2_\mathrm{ref}$, where $\hat{\rho }$ is the fluid density. The temperature is non-dimensionalised by $T=(\hat{T}-\hat{T}_0)/\Delta \hat{T}$ with $\Delta \hat{T}=\hat{T}_w-\hat{T}_c$ and $\hat{T}_0=(\hat{T}_w-\hat{T}_c)/2$. At all walls, no-slip and impermeability boundary conditions are applied. In addition, the top and bottom plate are modelled isothermal, whereas the side walls are modelled adiabatic. In agreement with the experimental set-up (Sect. 2), the width of the box equals its height $L_y=L_z=H$, and the aspect ratio is set to $\Gamma =L_x/L_z=0.5$.

To solve the above problem numerically, Eq. (10) is discretised in time using equation (12), yielding for a Leapfrog time discretisation scheme (Wagner et al. 1994)

$$\begin{aligned}&\frac{1}{2\Delta t}(\mathbf {u}^{n+1}-\mathbf {u}^{n-1})+\mathbf {u}^n\cdot \nabla \mathbf {u}^n \nonumber \\&\quad = -\nabla p^n + \sqrt{\mathrm {Pr}/\mathrm {Ra}} \nabla ^2 \mathbf {u}^{n-1} + T^n\mathbf {e}_z, \end{aligned}$$

(13)

where n is the number of the time step, $\Delta t$ is the temporal increment between two time steps, and $\delta ^j_i$ is the Kronecker delta. To integrate Eq. (13) in time, in numerical flow simulation, a common approach is to apply a fractional step algorithm as the one introduced by Chorin (1967, 1968), the latter consisting of three steps. In the first step, an auxiliary velocity field $\mathbf{u} ^*$ is estimated from Eq. (13) neglecting the pressure term,

$$\begin{aligned}&\frac{1}{2\Delta t}(\mathbf {u}^{*}-\mathbf {u}^{n-1})+\mathbf {u}^n\cdot \nabla \mathbf {u}^n \nonumber \\&= \sqrt{\mathrm {Pr}/\mathrm {Ra}} \nabla ^2 \mathbf {u}^{n-1} + T^n \mathbf {e}_z. \end{aligned}$$

(14)

Subsequently, the following pressure Poisson equation is solved for the auxiliary field

$$\begin{aligned} \nabla ^2 \phi ^n = \nabla \cdot \mathbf {u}^*, \end{aligned}$$

(15)

with $\phi ^n = 2\Delta t p^n$ and the boundary condition ($\mathbf {n}\cdot \nabla \phi ^n)|_{\partial \gamma }=0$. Finally, the velocity at time step $n+1$ is updated as follows:

$$\begin{aligned} \mathbf {u}^{n+1} = \mathbf {u}^* - \nabla \phi ^n. \end{aligned}$$

(16)

In the present study, we enter the second step (15) directly with the measured velocity field as auxiliary field. Hence, we implement the Poisson solver to make the measured velocity fields divergence-free. Subsequently, temperature fields are extracted from the divergence-free velocity field using the discretised vertical momentum equation.

3.1 Velocity field assimilation

So as to obtain divergence-free velocity fields, first, the divergence is computed from the measured velocity fields, which are provided on an equidistant grid with dimensions $N_x \times N_y \times N_z = 57 \times 119 \times 119$. Then, a pseudo-pressure is computed from the velocity fields via the algorithm described in the following. Finally, the velocity field is corrected via the pseudo-pressure $\phi$. Here, we utilise the Poisson equation (15) with $\mathbf {u}^*$ being the experimentally obtained velocity field. The numerical solution of the Poisson equation requires the terms in Eq. (15) to be approximated by means of a second-order central finite-difference scheme on the equidistant measurement grid. In the following, the finite-difference approximation of the right-hand side of Eq. (15) in a grid cell centred around $(x_i,y_j,z_k)$ is denoted as $q_{ijk}$ and the corresponding discretised pseudo-pressure as $\phi _{ijk}$. Using the separation of variable approach, the three-dimensional discrete Poisson equation can be divided into $N_z$ two-dimensional problems as follows:

$$\begin{aligned} D_{xy}\phi _{ijk} + D_{z}\phi _{ijk} = q_{ijk}, \end{aligned}$$

(17)

with $D_i\phi _i=(\phi _{i+1}-2\phi _i+\phi _{i-1})/\Delta i^2$ and $D_{xy}=D_x+D_y$. Moreover, $D_z$ is subject to the eigenvalue problem,

$$\begin{aligned} D_{z}\mathbf {v}^l = \lambda _l\mathbf {v}^l,\text { }l=1,\dots ,N_z, \end{aligned}$$

(18)

with $N_z$ eigenvalues $\lambda _l$, and $N_z$ eigenvectors $\mathbf {v}^l$ = ($v_1^l$, $v_2^l$, ..., $v_{N_z}^l$). Then, the pseudo-pressure $\phi$ and the right-hand side of the Poisson equation are decomposed to

$$\begin{aligned} \phi _{ijk}= & {} \sum ^{N_z}_{l=1}\hat{\phi }^l_{ij}v_k^l, \end{aligned}$$

(19)

$$\begin{aligned} q_{ijk}= & {} \sum ^{N_z}_{l=1}\hat{q}^l_{ij}v_k^l. \end{aligned}$$

(20)

Substituting (19) and (20) back to equation (17) leads to

$$\begin{aligned} \sum ^{N_z}_{l=1}\left( D_{xy}\hat{\phi }^l_{ij}+\lambda _l\hat{\phi }_{ij}^l\right) \mathbf {v}^l = \sum ^{N_z}_{l=1} \hat{q}_{ij}^l\mathbf {v}^l. \end{aligned}$$

(21)

For $N_z$ linearly independent eigenvectors, a set of $N_z$ linearly independent, two-dimensional equations is obtained,

$$\begin{aligned} D_{xy}\hat{\phi }^l_{ij}+\lambda _l\hat{\phi }_{ij}^l = \hat{q}_{ij}^l,\text { }l=1,\dots ,N_z. \end{aligned}$$

(22)

The right-hand sides for the above equation are obtained from the three-dimensional, right-hand sides via

$$\begin{aligned} \hat{q}_{ij}^l=\left( \sum ^{N_z}_{k=1} \Delta z_k q_{ijk} v^l_k\right) \bigg /\left( \sum ^{N_z}_{k=1}\Delta z_k v^l_k v^l_k\right) . \end{aligned}$$

(23)

The algorithmic execution of the Poisson solver works as follows:

• 1. The eigenvectors $\mathbf {v}^l$ and eigenvalues $\lambda _l$ are computed a priori.

• 2. Then $\hat{q}^l_{ij}$ is computed (23).

• 3. $N_z$ independent systems of expression (22) are solved.

• 4. The $\phi _{ijk}$ field is recomposed (19).

The measured and the divergence-free v velocity component are compared in Fig. 5a, b. Furthermore, the divergence of the measured velocity field is presented in Fig. 5c.

Fig. 5

$\hat{v}$ velocity at $x/H=0.25$ before (a) and after (b) divergence has been removed. (c) Divergence of the measured velocity field

By applying the divergence-free condition to the measured velocity fields (Fig. 5a), local unphysical discontinuities have been removed, which results in the smoother velocity fields displayed in Fig. 5b. Discontinuities in the measured velocity field are reflected by strong local values—positive or negative—in the divergence field in Fig. 5c. The discontinuous structure in the v velocity field at ($y/H\approx 0.5$,$z/H\approx 0.95$) in Fig. 5a, for instance, leads to a high divergence at the same location (Fig. 5c), while in the divergence-free velocity field, the structure disappears (Fig. 5b).

The extraction of the temperature field from the momentum equation requires both spatial and temporal derivatives of the velocity field. As stated above, the measurement was spatially under- and temporally over-resolved. Therefore, the measured velocity signal—represented by the blue line in Fig. 6a showing the vertical velocity at $(x/H=0.25,y/H=0.5,z/H=0.5)$—exhibits temporal oscillations. The latter lead to strong artificial fluctuations in the finite-difference approximation of the temporal vertical velocity derivative. Consequently, temporal filtering is applied to the series of the divergence-free velocity fields using a filter length corresponding to the Kolmogorov time scale, the latter being one order of magnitude larger than the temporal measurement resolution (see Sect. 2). Thus, only unphysical scales, which are smaller than the Kolmogorov time scale, are cut off. A time series of the vertical velocity signal at $(x/H=0.25,y/H=0.5,z/H=0.5)$ after filtering (red line) corresponding to the unfiltered signal (blue line) is displayed in Fig. 6a.

Fig. 6

a Time series of the velocity components before and after filtering. b Box-averaged velocity spectra of the PIV data plotted against the frequency domain. Straight vertical line indicates the filter cut-off frequency.

Figure 6b illustrates box-averaged, frequency–velocity spectra of the measured PIV data. Here, the high-frequency region of the v- and w-spectra show an artificial oscillation caused by the above-mentioned resolution issues. These oscillations are below the frequency that corresponds to the estimated Kolmogorov time scale of $\eta _t=1.5$ s. Therefore, a sharp spectral cut-off filter with a filter length corresponding to the Kolmogorov time scale is applied to the raw velocity data (indicated by the straight line in Fig. 6).

3.2 Temperature field extraction

Finally, the temperature fields are extracted from the divergence-free velocity fields via a fourth-order central finite-difference approximation of the z-component of Eq. (13), i.e.

$$\begin{aligned}&T=\frac{w^{n+2}-8w^{n+1}+8w^{n-1}-w^{n-2} }{12\Delta t} + \mathbf {u}^n \cdot \nabla w^n\nonumber \\&+ \partial p^n /\partial z +\sqrt{\mathrm {Pr}/\mathrm {Ra}}\nabla ^2 w^n, \end{aligned}$$

(24)

for snapshot n with $\Delta t$ the time interval between two consecutive snapshots. In addition to the temporal discretisation, spatial derivatives in Eq. (24) are also discretised by means of a fourth-order approximation. Furthermore, the absence of velocity data near the boundaries in the experimental data set requires special treatment. At the solid boundaries, no-slip and impermeability boundary conditions are applied to the velocity field. For the temperature field, Dirichlet boundary conditions are applied to the top and bottom plate and Neumann boundary conditions to the sidewalls. Since both the kinetic and the thermal boundary layer are located within layers near the top and bottom plate where no experimental data is available, the thickness of these layers is estimated via the expressions

$$\begin{aligned} \delta _u/H\approx & {} 0.509\mathrm {Nu}^{-1}\mathrm {Pr}^{1/3} = 0.016\text {, for Pr}>3\text { and} \end{aligned}$$

(25)

$$\begin{aligned} \delta _\theta /H\approx & {} 0.5\mathrm {Nu}^{-1} = 0.0058\text {, for Pr}>3, \end{aligned}$$

(26)

with $\delta _u$ the kinetic and $\delta _\theta$ the thermal boundary layer, which have been derived by Shishkina et al. (2010) based on the Prandtl–Blasius equations for the fluid flow over a flat plate. Considering the kinetic boundary layer of the initial field, velocities are linearly interpolated along a wall-normal line from zero at the wall to the value of the first experimentally measured velocity point away from the wall. In terms of the thermal boundary layer, the boundary layer thickness is approximated using expression (26). Then, the temperature is set constant between the location of the first value of the extracted temperature field away from either the bottom or the top wall and the limit of the estimated boundary layer away from the wall, i.e. a wall distance of $\delta _\theta$. The temperature in the latter region is set to the value of the first grid point of the extracted temperature field away from the wall. Between a wall distance of $\delta _\theta$ and the boundaries, the temperature value is linearly interpolated with temperature boundaries being set to $T_1=-\,0.5$ and $T_{N_z}=0.5$. An extracted temperature field at measurement time $\hat{t}=15$ s including interpolated boundaries at $x/H=0.25$ is depicted in Fig. 7 together with the divergence-free velocity field.

Fig. 7

Extracted temperature field at $x/H=0.25$ as pseudo-colour image; Planar velocity (v, w) as vector plot.

According to the above-described procedure, temperature fields are calculated by solving Eq. (24) using 1000 consecutive tomo PIV velocity snapshots. To assess the quality of the extracted temperature fields, the average extracted temperature field is compared to the corresponding average temperature field obtained from PIT measurements that have been carried out simultaneously with the tomo PIV measurement (Schiepel et al. 2021). Figure 8 portrays a comparison of the average measured (a) and extracted temperature field (b) in a yz-plane at $x/H=0.25$.

Fig. 8

Average measured (a) and average extracted temperature field (b) at $x/H=0.25$ as pseudo-colour image.

Since the measurement is restricted to a subdomain of the flow geometry, only the corresponding cutout is shown. In order to perform the comparison, the corresponding spatio-temporal mean temperature has been subtracted from both fields which are then normalised by their root mean square temperature value. The resulting average temperature fields displayed in Fig. 8 show comparable structures with a positive temperature fluctuation in the bottom left and a negative temperature fluctuation in the top right of the depicted subdomain. Additionally, the extracted average temperature field is less smooth and appears to contain smaller scales than the measured one. To compare the coherence of the measured and the extracted temperature field qualitatively, we compute the correlation coefficient between the two fields as

$$\begin{aligned} C_{\psi \tilde{\psi }} = \frac{ COV(\psi ,\tilde{\psi })}{ RMS(\psi )RMS(\tilde{\psi })}, \end{aligned}$$

(27)

with

$$\begin{aligned}&COV(\psi ,\tilde{\psi }) =\int \limits _{y=0}^H\int \limits _{z=0}^H (\psi (y,z)-\langle \psi \rangle _{yz})(\tilde{\psi }(y,z)-\langle \tilde{\psi } \rangle _{yz}) \, \mathrm{d}y \, \mathrm{d}z, \end{aligned}$$

(28)

and

$$\begin{aligned} RMS(\psi ) = \sqrt{ \int \limits _{y=0}^H\int \limits _{z=0}^H (\psi (y,z)-\langle \psi \rangle _{yz})^2 \, \mathrm{d}y \, \mathrm{d}z}, \end{aligned}$$

(29)

where $\psi$ denotes the measured normalised temperature and $\tilde{\psi }$ denotes the extracted normalised temperature. Angled brackets indicate averaging with respect to the coordinates stated in the subscript. A correlation coefficient of 0.84 is obtained, reflecting that the extracted temperature field generally resembles the measured temperature field well, even though they somewhat differ in detail.

4 Direct numerical simulation

Extracted temperature fields and the divergence-free velocity fields serve as initial conditions for DNSs with and without feedback term as presented in Table 1. The governing equations are the transport equations for mass, momentum, and temperature for an incompressible fluid as well as the Boussinesq approximation (see Eqs. 12, 10, and 11). Following the approach of Suzuki and Yamamoto (2015) and Clark Di Leoni et al. (2020), the momentum equation is expanded by a feedback term that penalises the deviation of the computed velocity field from the experimentally obtained, divergence-free velocity field, yielding

$$\begin{aligned} \frac{\partial \mathbf {u}}{\partial t} + \mathbf {u} \cdot \nabla \mathbf {u} = -\nabla p +\sqrt{\mathrm {Pr}/\mathrm {Ra}}\nabla ^2 \mathbf {u} + T \mathbf {e}_z + \alpha (\mathbf {u}_\mathrm{ref}-\mathbf {u}), \end{aligned}$$

(30)

where $\alpha$ denotes the feedback gain and $\mathbf{u} _\mathrm{ref}$ is the experimentally obtained divergence-free velocity field (reference field). For $\alpha =0$, a conventional DNS without feedback is carried out, whereas for $\alpha \ne 0$, the feedback term is taken into account with the reference field being updated every time a PIV snapshot has been taken. In the following, numerical simulations with different $\alpha$ are evaluated and compared to the pure DNS case ($\alpha =0$). The DNSs of RBC require the full spatial resolution of the smallest velocity and temperature scales. These are the Kolmogorov and the Batchelor length scale

$$\begin{aligned} \eta _K= & {} \left( \frac{\nu ^3}{\varepsilon _u}\right) , \end{aligned}$$

(31)

$$\begin{aligned} \eta _B= & {} \left( \frac{\nu \kappa ^2}{\varepsilon _u}\right) =\eta _K\mathrm {Pr}^{-1/2}, \end{aligned}$$

(32)

where $\varepsilon _u=\nu \langle \partial u_i/\partial x_j \rangle$ is the kinetic dissipation rate. For the present case of $\mathrm {Pr}>1$, the Batchelor length scale is smaller than the Kolmogorov length scale, and thus, more restrictive with respect to the grid resolution. According to Grötzbach (1983), the minimum grid spacing in the bulk flow region can be estimated via the following approximation of the Batchelor scale

$$\begin{aligned} h^{bulk}/H\le \frac{\pi }{\Gamma }\frac{1}{((\mathrm {Nu}-1)\mathrm {Ra})^{1/4}} \text {, for Pr}>1. \end{aligned}$$

(33)

Additionally, for the minimum grid spacing in the thermal and viscous boundary layers, Shishkina et al. (2010) provide the following estimation based on the Prandtl–Blasius boundary layer theory

$$\begin{aligned} h^{BL}/H \le 2^{-3/2}a^{-1}E^{-3/2}\mathrm {Nu}^{-3/2}\text {, for Pr}>3, \end{aligned}$$

(34)

where $E \approx 0.982$ and $a\approx 0.482$. Moreover, Shishkina et al. (2010) recommend minimum numbers of nodes in the thermal and kinetic boundary layer of

$$\begin{aligned} N^\mathrm{min}_{\delta _\theta }= & {} \sqrt{2}a\mathrm {Nu}^{1/2}E^{3/2} \text {, for Pr}>3, \end{aligned}$$

(35)

$$\begin{aligned} N^\mathrm{min}_{\delta _u}= & {} \sqrt{2}a\mathrm {Nu}^{1/2}\mathrm {Pr}^{1/3}E^{1/2} \text {, for Pr}>3. \end{aligned}$$

(36)

Inserting the estimated Nusselt number from Eq. (7) in Eqs. (33) and (34) results in a minimum grid spacing of 0.0065 in the bulk flow region and $5.1\times 10^4$ in the boundary layers. Moreover, the minimum number of nodes in the boundary layers—Eqs. (35) and (35)—is estimated to $N^\mathrm{min}_{\delta _\theta }=8$ and $N^\mathrm{min}_{\delta _u}=20$ for the thermal and kinetic boundary layer, respectively. As shown in Table 1, the present simulation case fulfils the above-described grid requirements in the boundary layers as well as in the bulk flow.

Table 1 RBC simulation case

Based on the parameters above, DNSs initialised with extracted temperature and velocity fields with and without feedback were carried out. Starting with an under-resolved velocity field and the corresponding extracted temperature field, the DNS without feedback requires time to overcome an initial transient phase forming turbulent small scales. Figure 9 illustrates instantaneous temperature field realisations at $t=21.6$. Since the experimental data did not contain information on the boundary layers, spatially fine turbulent structures evolve in the temperature field during the simulations, particularly from the top and bottom boundaries (Fig. 9). These structures feature a higher temperature intensity than visible in the initial extracted temperature field (Fig.7). Furthermore, the initially sharp-edged-appearing structure of the temperature field has smoothened out after the integration of time.

Fig. 9

Instantaneous temperature field from DNS without feedback at $x/H=0.25$ and $t=21.6$ as pseudo-colour images.

When taking into account the feedback term, the structure of the simulated temperature field depends on the feedback gain $\alpha$. Since the measured velocity field lacks fine-scale turbulent structures, the temperature field structure in the bulk region becomes increasingly coarse as the feedback term increases (Fig. 10).

Fig. 10

Instantaneous temperature fields from DNS with feedback at $x/H=0.25$ and $t=21.6$ as pseudo-colour images. a $\alpha =0.01$; b $\alpha =0.1$; c $\alpha =1$.

Moreover, the temperature intensity outside the thermal boundary layer above the heated plate and below the cooled plate appears to be higher for large $\alpha$. To evaluate the simulated temperature and velocity fields for different $\alpha$, the flow quantities are statistically averaged hereinafter and compared to statistical averages of the measured velocity field as well as to statistical averages obtained from a DNS without feedback term. While the comparison of the mean velocity with the experiment assesses how well the simulated velocity field resembles the measured LSC of the flow, the comparison of RMS values with the DNS without feedback reveals how well small-scale fluctuations are captured in both the velocity and the temperature field. In order to detect when the DNSs have overcome the initial transient, the temporal evolution of the average Nusselt number at the heated and the cooled plate,

$$\begin{aligned} { \mathrm {Nu}_w = -\frac{1}{2}\left( \frac{\partial \langle T \rangle _{xy}}{\partial z}\Big |_{z/H=0}+\frac{\partial \langle T \rangle _{xy}}{\partial z}\Big |_{z/H=1}\right) , } \end{aligned}$$

(37)

representing the average vertical heat flux is depicted in Fig. 11.

Fig. 11

Temporal evolution of $\mathrm {Nu}_w$ representing the plane-averaged heat flux at the heated and the cooled plate for DNSs with different feedback gains α. Blue line, $\alpha =0$; red line, $\alpha =0.01$; green line, $\alpha =0.1$; orange line, $\alpha =1$; pink line, $\alpha =10$

According to Fig. 11, the DNS without feedback reaches a statistically stationary state at approximately $t_0=10$ with $\mathrm {Nu_w}\approx 120$ (blue line). While the heat flux time series obtained from the DNS with feedback collapses well with the one from the DNS without feedback for $\alpha = 0.01$ (red line), it differs only marginally from the DNS without feedback for $\alpha =0.1$ (green line). Deviating even more for $\alpha =1$ (yellow line), the estimated heat flux is still fluctuating around the expected value. For $\alpha =10$, however, Fig. 11 reflects heat flux values of $\partial \langle T \rangle _{xy}/\partial z < 100$, which are below the values obtained from the DNS without feedback. The deviation of the simulated velocity field $\mathbf{u}$ from the experimentally obtained reference field $\mathbf{u} _\mathrm{ref}$ is evaluated by means of the temporal evolution of the mean absolute difference between the simulated and the reference field, as depicted in Fig. 12.

Fig. 12

Mean absolute deviation of the simulated from the reference velocity field for different feedback gains. Blue line, $\alpha =0$; red line, $\alpha =0.01$; green line, $\alpha =0.1$; orange line, $\alpha =1$; pink line $\alpha =10$

For the DNS without feedback, the mean absolute difference between the simulated and the experimental velocity increases up to a value of approximately 0.024 at $t\approx 19$ where it saturates (blue line). For the DNS with feedback, the difference between the simulated and the experimental velocity field decreases as $\alpha$ increases. Using a feedback gain of $\alpha =10$, the mean absolute difference stays below a value of approximately $10^{-3}$ during the integration time (magenta line). In this case, the feedback term in Eq. (30) is so dominant that it effectively suppresses large deviations from the reference field. In the following, numerical statistical quantities are obtained by averaging over time from $t_0=10$ as follows:

$$\begin{aligned} { \langle \psi \rangle _t = \frac{1}{(t_1-t_0)}\int \limits _{t=t_0}^{t_1} \psi _l(t) \, \mathrm{d}t, } \end{aligned}$$

(38)

with $\psi$ the quantity of interest and $t_1$ the end time of the temporal averaging interval. Additionally, averaging over one or several of the spatial directions is defined as

$$\begin{aligned} \langle \psi \rangle _i = \frac{1}{L_i}\int \limits _{i=0}^{L_i} \psi (i) \, \mathrm{d}i,\quad i=x,y,z \end{aligned}$$

(39)

Applying the averaging operation (38) as well as an additional plane-average in x and y according to equation (39), the vertical profile of the v velocity is compared to the x-, y-, and t-average of the v velocity measured in the PIV data in Fig. 13.

Fig. 13

Comparison of spatio-temporally averaged velocity profiles $\langle v \rangle _{xyt}$ between PIV and DNS with different feedback gains. Blue line, $\alpha =0$; red line, $\alpha =0.01$; green line, $\alpha =0.1$; orange line, $\alpha =1$; pink line, $\alpha =10$;..., PIV data.

The averaged profiles show good general agreement although the DNS has generated small-scale turbulence that was initially lacking in the experimental data. On average, however, the LSC that was visible in the experimental data appears to sustain in the DNSs with and without feedback gain. As Fig. 13 indicates, the profile obtained from the simulation without feedback tends to shift the asymmetric experimental profile (dashed black line) towards a symmetric profile (blue line). Introducing the feedback term to the simulations leads to less deviation of the mean vertical v velocity profile from the experimentally measured profile. The best agreement between experimental and simulated mean velocity profiles is obtained for $\alpha = 1$. More precisely, the latter can be seen in the x- and t-averaged planar velocity depicted as vector plots in Fig. 14 for both PIV data (Fig. 14a) and DNS data (Fig. 14b–d).

Fig. 14

Spatio-temporally averaged velocity vector plots $\mathbf{u} _{yz} = \langle v \rangle _{xt} \mathbf{e} _y + \langle w \rangle _{xt} \mathbf{e} _z$ and temperature fields $\langle T \rangle _{xt}$ from PIV (a) and DNSs with and without feedback gain ($\alpha = 0$, b; $\alpha = 0.1$, c; $\alpha =1$, d).

In the PIV data (Fig. 14a) as well as in the DNS data with and without feedback (Fig. 14a), the LSC is clearly visible. The DNS without feedback, however, shows a LSC oriented around the centre of the cell ($y/H\approx 0.5$, $z/H\approx 0.5$, Fig. 14b), whereas for the PIV data as well as for DNSs with $\alpha \ge 0.1$ the LSC is oriented around $y/H \approx 0.55$ and $z/H\approx 0.6$ (Fig. 14a, c, d). Besides, the structure of the average extracted temperature field agrees reasonably well with the one integrated in time from the DNSs with and without feedback. The temperature levels are in the same order of magnitude in the extracted temperature field (Fig. 14a) and in the temperature field of the DNS without feedback (Fig. 14b). With increasing feedback gain $\alpha$, the average temperature field becomes more intense (Fig. 14c, d). In addition to the PIV data, the DNS data encompasses both the kinetic boundary layer, where velocities decay to zero near solid walls, and the thin thermal boundary layer near the heated bottom and the cooled top plate. In order to compare the coherence of the average flow structure between the tomo PIV measurement and the DNSs qualitatively, we compute the correlation coefficient between the flow field seen in Fig. 14a and each of the fields presented in Fig. 14b–d as well as the fields obtained from DNS with $\alpha =0.01$ and $\alpha =10$ (figure omitted). The correlation coefficient is defined as in Eq. (27) with $\psi$ denoting quantities obtained from the DNSs and $\tilde{\psi }$ denoting quantities obtained from the tomo PIV measurement. Accordingly, we obtain correlation coefficients of $C_{v\tilde{v}}={0.92}$ for the xt-averaged horizontal velocity component, $C_{w\tilde{w}}={0.91}$ for the xt-averaged vertical velocity component, and $C_{T\tilde{T}}={0.6}$ for the xt-averaged temperature when considering the DNS without feedback. Correlating the averaged PIV velocity field with the averaged velocity field obtained from DNS with feedback results in correlation coefficients that further increase with the feedback $\alpha$. For $\alpha =0.1$, we obtain $C_{v\tilde{v}}=0.96$ and $C_{w\tilde{w}}=0.95$; for $\alpha =1$, $C_{v\tilde{v}}=0.995$ and $C_{w\tilde{w}}=0.984$. The averaged extracted temperature field, on the other hand, remains less correlated with the averaged temperature field from DNSs involving feedback without a clear tendency. When increasing $\alpha$ from 0.1 to 1, the correlation coefficient increases from $C_{T\tilde{T}}=0.6$ to $C_{T\tilde{T}}=0.65$, before it drops to $C_{T\tilde{T}}=0.57$ when increasing the feedback gain further to $\alpha =10$. In summary, the average temperature field is less correlated between PIV and DNS data than the velocity field is. The temperature fields are extracted from measured velocity fields involving both temporal and spatial derivatives of the latter. Since the PIV velocity fields were spatially under-resolved and temporally treated with cut-off filtering because they showed temporal oscillations, the extracted temperature fields might be lacking information. During the DNSs, more intense temporal structures evolve, which is projected in the average temperature fields depicted in Fig. 14b–d that show somewhat less correlation with the PIV field (Fig. 14a) than the corresponding velocity fields do. To further evaluate the temperature field of the DNSs with and without feedback, RMS temperature profiles as depicted in Fig. 15 are taken into consideration.

Fig. 15

Comparison of spatio-temporally averaged RMS temperature profiles $T_\mathrm{rms}=\sqrt{\langle T'T' \rangle _{xyt}}$ between and DNSs with different feedback gains. Blue line, $\alpha =0$; red line, $\alpha =0.01$; green line, $\alpha =0.1$; orange line, $\alpha =1$; pink line $\alpha =10$.

As Fig. 15 indicates, the RMS temperature profiles exhibit peaks in the thermal boundary layers near the heated and cooled plate where $T_\mathrm{rms}\approx 0.09$, while their value in the bulk flow region remains on a much lower niveau ($T_\mathrm{rms}< 0.02$). The profile for the DNS without feedback collapses well with the one involving $\alpha =0.01$, and there is only little variation with respect to the case with a feedback gain of $\alpha =0.1$. The profile of $\alpha =1$ collapses well with those involving lower $\alpha$ near the heated and the cooled plate ($z/H \lesssim 0.05$ and $z/H\gtrsim 0.95$), whereas the temperature fluctuations are overestimated by approximately 40% elsewhere. For $\alpha =10$, the profile overestimates the temperature fluctuation intensity up to 94% around $z/h\approx 0.05$ and $z/H\approx 0.95$ with only little variation between $z/H\approx 0.3$ and $z/H \approx 0.7$. The overestimation of the temperature fluctuation intensity for $\alpha \ge 1$ corresponds to instantaneous observations of the temperature field depicted in Fig. 9, where more intense temperature structures mitigate from the thermal boundary layers.

In summary, the DNS with feedback results in an average velocity profile that resembles the experimental data well. However, introducing the feedback term to the momentum equation decreases the deviation of the velocity field from the experimental data further as the feedback gain increases, implying that high feedback gain values $\alpha$ are suitable. On the other hand, the temperature fluctuation intensity profiles deviate conspicuously from profiles of a DNS without feedback for $\alpha \ge 1$. For high $\alpha$, the feedback term in Eq. (30) becomes dominant with regard to the buoyancy term and effectively decouples the temperature from the momentum equation. Thus, the temperature field acts more like a passive scalar as its influence on the velocity field diminishes. Overall, a feedback gain of $\alpha =0.1$ has been proven to show good results, i.e. a high correlation of the simulated velocity field with the experimentally measured data as well as realistic temperature field fluctuations. Altogether, the good agreement between the LSC in the DNSs with and without feedback and in the PIV data confirms the validity of the present method of numerically extracting the temperature field from the measured data as well as using a DNS solver to generate the small-scale turbulence, which has been lacking in the experimental data set.

5 Conclusion

In the present work, we employ methods drawn from the DNS of RBC—i.e. the Poisson solver and the discretised momentum equation—to extract information out of the under-resolved measured velocity fields of RBC that are not directly accessible. With the aid of the Poisson solver, we managed to successfully remove discontinuities from the measured velocity data. Moreover, we extracted temperature fields from the velocity data by means of the discretised vertical momentum equation. Comparing the average extracted temperature field with measured temperature fields in a subdomain of the flow geometry, the high correlation coefficient $C_{T\tilde{T}}=0.84$) underlined that the extracted temperature field reflects the physics of this experiment.

Since the measured velocity fields were spatially under-resolved and did not contain any information at the boundaries, we used DNSs with and without feedback involving divergence-free velocity fields and corresponding extracted temperature fields as initial conditions to generate small-scale turbulence as well as thermal and kinetic boundary layers. After an initial transient, the DNS without feedback features small-scale temperature and velocity fluctuations while the LSC still agrees well with the initial experimental data, which is proven by large correlations between averaged flow fields from DNS and tomo PIV. Here, correlation coefficients of $C_{v\tilde{v}}=0.92$ and $C_{w\tilde{w}}=0.91$ are obtained for the vertical and horizontal velocity component averaged in time and in the horizontal x-direction, the latter components representing the LSC.

For simulations with feedback, the generated velocity fields resemble the experimental data increasingly well for higher values of $\alpha$, which reflects in correlation coefficients larger than $C_{v\tilde{v}}=0.995$ and $C_{w\tilde{w}}=0.98$ for $\alpha \ge 1$. Nonetheless, for $\alpha \ge 1$, the temperature fluctuation profile differs significantly from the one obtained from a DNS without feedback, which suggests that the governing equations—i.e. the temperature equation and the vertical momentum equation—decouple resulting in a temperature field acting like a passive scalar. Hence, a feedback gain of $\alpha =0.1$ is found to be optimal when considering the feedback term, since large correlation coefficients of $C_{v\tilde{v}}=0.96$ and $C_{w\tilde{w}}=0.95$ are achieved for the velocity field and the temperature fluctuation intensity profile matches the profile from a DNS without feedback well.

Note that the xt-averaged temperature field obtained from the DNS with and without feedback correlates somewhat less with the extracted temperature field ($C_{T\tilde{T}}\approx 0.6$), which is presumably caused by spatially under-resolved and temporally oscillating initial tomo PIV fields used to extract the temperature field.

In brief, the proposed method proved successful in extracting additional information out of an experimental RBC data set, even though the experimental data was under-resolved and lacked information at the boundaries.

In the future, the same approach can be applied to other flow problems like mixed convection (Mommert et al. 2020) or in cylindrical domains (Paolillo et al. 2018).