Design and qualification of an unsteady low-speed wind tunnel with an upstream louver system

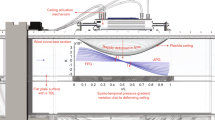
Abstract

The design and qualification of a longitudinal gust generator in a low-speed, blow-down, open-return wind tunnel was conducted. Flow-impeding louvers were used to rapidly change the blockage ratio at the inlet, effectively reducing test section flow speeds up to $60\%$ and $52\%$ for the closed and open test section configurations of the wind tunnel, respectively. The wind tunnel responds more quickly for higher fan speeds, shorter tunnel lengths, and during louver closing motions (deceleration). A mathematical model developed to predict the wind tunnel’s response shows these same trends and agrees with the experimental data to within 0.03 in amplitude ratio and $4.3^\circ$ in phase lag, for all cases studied. Comparison of the closed to open test section configurations reveals that flow disturbances propagate nearly instantaneously, or in a globally unsteady manner, within the closed configuration, while they convect at speeds similar to that of the mean flow when testing in the open configuration.

Graphic abstract

1 Introduction

A variety of facilities have been constructed and utilized to study the impact of unsteady flow phenomena on aerodynamic bodies. These facilities have evolved over the last 75 years, varying in both the method of introducing flow unsteadiness, as well as the type of unsteady flows generated. One classification focuses upon longitudinal velocity disturbances, or gusts. In this case, the velocity perturbation is aligned with the primary flow direction, resulting in a time-dependent variation of flow speed within the facility’s test section. The current study primarily focuses upon generating longitudinal gusts which propagate through a low-speed wind tunnel in a manner that is either (1) globally unsteady (i.e. purely time dependent) or (2) convectively unsteady (i.e. both time and space dependent). A brief literature survey of longitudinally unsteady wind tunnel facilities provides valuable context for the current work.

Carr (1981a, b), Al-Asmi and Castro (1993), and Greenblatt (2016) reviewed a variety of wind tunnel facilities capable of producing longitudinal gusts. Early studies in these facilities primarily focused on fundamental impacts of longitudinal oscillations of the free-stream on laminar boundary layers (Despard and Miller 1971; Patel 1975), transitional boundary layers (Miller and Fejer 1964; Obremski and Fejer 1967), and turbulent boundary layers (Karlsson 1959; Patel 1977; Pericleous 1978; Michel et al. 1981). In recent years, focus has shifted towards applications ranging from unsteady shock-wave motions (Szumowski and Meier 1996; Selerowicz and Szumowski 2002; Fernie and Babinsky 2002, 2003, 2004; Bruce and Babinsky 2008), to dynamic stall on two- and three-dimensional wings (Granlund et al. 2014; Strangfeld et al. 2016), and to other industrial applications (Kobayashi and Hatanaka 1992; Kobayashi et al. 1994; Navarro-Medina et al. 2011).

In all of these cases, longitudinal flow oscillations are imparted onto the primary flow through a time-varying oscillation of the cross-sectional flow area at some location within the facility. Typically, the cross-sectional area is regulated by counter-rotating vanes or louvers (Gompertz et al. 2011; Greenblatt 2016; Rennie et al. 2019) which can be actuated in either continuous rotation or periodic oscillation. In most of these facilities, the louvers are located immediately downstream of the test section within the wind tunnel circuit, which takes advantage of the largest flow velocity and smallest cross-sectional area within the circuit. This technique also eliminates the potential impact of louver wake disturbances, had the louvers been placed immediately upstream of the test section (Greenblatt 2016; Rennie et al. 2019). Still, downstream louvers generate pressure disturbances that propagate upstream within the facility, i.e. in the opposite direction of the primary flow, and also impart a significant fluctuation in both the static and stagnation pressures along the test section (Al-Asmi and Castro 1993).

Al-Asmi and Castro (1993) present several arguments for locating the louvers upstream of the test section. Doing so reduces static pressure fluctuations within the test section for the same velocity fluctuation amplitude and minimizes noise radiated through the test section and laboratory space. Another advantage is the test section can be easily reconfigured or removed entirely without impeding the operation of the louver system. This change from a closed to open test section fundamentally alters the development and propagation of longitudinal disturbances within the test section and represents the primary goal of the current study.

Most unsteady wind tunnel facilities are configured with closed test sections having solid walls. Pressure disturbances propagate through the solid walled ducts as one-dimensional planar waves at a speed of $c = a (1+M)$ downstream and $c = a (1-M)$ upstream (Morse and Ingard 1968, p. 715); where a is the speed of sound and M is the Mach number of the flow. For a low-speed, incompressible flow, this implies the disturbance propagation speed through the test section can be over an order of magnitude faster than the convective speed, thus approximating the gust as globally unsteady (Granlund et al. 2014; Greenblatt 2016).

In contrast, Patel and Hancock (1976) utilized a semi-open test section with a flexible nozzle extension. Oscillating this extension excited the shear layers that emanated from the nozzle’s free edges and rolled up into vortical structures. These vortical structures advected downstream at a speed commensurate with the primary flow, effectively producing a convectively unsteady gust. However, their facility was limited to small oscillation amplitudes below $10\%$ of the mean flow speed due to limitations with the nozzle extension and angular range of operation.

Fig. 1

A general schematic of the University of Colorado Boulder unsteady low-speed wind tunnel presenting both top (a) and side (b) views

The current work demonstrates the use of a louver system that imposes both globally and convectively unsteady velocity disturbances with large amplitudes solely by reconfiguring the wind tunnel test section. As part of this study, a mathematical model of the wind tunnel response was also developed to predict and better understand the operation of the unsteady, low-speed wind tunnel facility. The model presented in this paper draws upon the open-return and closed-return unsteady wind tunnel facility models, with louver systems installed downstream of the test section, recently published by Greenblatt (2016) and Rennie et al. (2019). Additionally it should be noted that preliminary findings from the current work were presented in Sinner et al. (2019), however significant improvements and modifications have been carried out, including the analysis of a third wind tunnel configuration in the current paper.

2 System design

Longitudinal gusts are generated by a custom louver system which was integrated onto the inlet of the low-speed wind tunnel within the Experimental Aerodynamics Laboratory at the University of Colorado Boulder. The wind tunnel itself is an open-return, blow-down facility, a basic schematic for which is provided in Fig. 1. Additional details about the facility are provided by Sinner et al. (2019), Sinner (2018), and Bateman (2017).

The modularity of the wind tunnel design allowed for testing in three configurations: (1) the standard closed test section configuration with the downstream diffuser installed, abbreviated CD configuration and pictured in Fig. 1; (2) the closed test section without the downstream diffuser (i.e. CT configuration); and (3) the open test section or free-jet configuration where both the test section and downstream diffuser are removed (i.e. OT configuration).

The louver system was installed at the fan inlet to ease access for installation and maintenance. Additionally, any unwanted flow irregularities generated by the louver vanes, such as their wakes, were expected to have a negligible impact on the flow quality within the test section; since both the fan and the flow conditioners are located downstream of the louver system. The louver system is composed of ten NACA 0015 airfoil vanes installed in five counter-rotating pairs, producing a maximum area reduction of $88\%$ from the fully open position. The test-section speed was limited to a maximum of 30 m/s when the louvers were in motion to mitigate excessive aerodynamic loading on the louver system.

The louvers are driven by a single Teknic M-3441 Hudson brushless motor with a 10 to 1 gearbox attached to the shaft of the center vane. With the 10 to 1 gearbox, the motor encoder provides 160, 000 counts per revolution of the louvers, providing a resolution of $\pm 0.00225^\circ$. For the current study the louvers were operated under continuous rotation to minimize motor following errors caused by the torque limit of the driving motor. Additionally, all angular positions presented represent the measured output positions from the motor encoder to help isolate the following errors from the analysis.

3 Theoretical model

To predict the dynamic response of the wind tunnel, a mathematical model was developed assuming one-dimensional, incompressible flow through a control volume defined by the wind tunnel walls. Incompressible flow was assumed because the test section speeds used in this study result in a maximum density variation of less than 0.5%. That said, neglecting compressibility effects could serve as a possible source of error in the theoretical model.

Changes in the wind tunnel boundary conditions, such as changes in applied forcing from the louvers, were assumed to propagate instantaneously throughout the control volume (i.e. speed of sound, $a = \infty$). Thus any phase lag associated with the propagation speed of disturbances at a finite speed of sound was also neglected. The implications of these assumptions are further discussed in Sec. 5.2; where the model response is compared with experimental measurements.

The mass flow rate, $\dot{m}$, volumetric flow rate, Q, and speed, U, at any station in the wind tunnel are given by Eqs. 1–3 as a result of the above assumptions and the conservation of mass. Here $\rho$ refers to density, A is area, and the subscript ts refers to the test section of the wind tunnel; the primary location of interest.

$$\begin{aligned}&\dot{m} = \rho U(x) A(x) = \rho U_{ts} A_{ts} \end{aligned}$$

(1)

$$\begin{aligned}&Q = U(x) A(x) = U_{ts} A_{ts} \end{aligned}$$

(2)

$$\begin{aligned}&U(x) = U_{ts} \frac{A_{ts}}{A(x)} \end{aligned}$$

(3)

The model construction follows a similar method outlined by Rennie et al. (2017, 2018, 2019), though significant modifications have been made for application to this facility. The model employs a control volume with boundaries placed just inside the wind tunnel walls, the inflow plane crossing exactly at the louvers, and outflow plane crossing at the exit. These stations are specifically denoted with subscripts in and ex, respectively. The conservation of momentum equation is then applied to this situation and is presented in a general form in Eq. 4.

$$\begin{aligned} \underbrace{\dfrac{\mathrm {d}}{\mathrm {d}t} \oint _V \rho \textit{\textbf{u}} \,dV}_{\textcircled {1}} + \underbrace{\oint _A \rho \textit{\textbf{u}} (\textit{\textbf{u}} \cdot \hat{\textit{\textbf{n}}}) \,dA}_{\textcircled {2}} = \underbrace{\oint _A \overline{\overline{\tau }} \cdot \hat{\textit{\textbf{n}}} \,dA}_{\textcircled {3}} + \underbrace{\oint _V \textit{\textbf{S}} \,dV}_{\textcircled {4}} \end{aligned}$$

(4)

Here, V and A are the volume and area of the control volume, $\textit{\textbf{u}}$ is the velocity vector, $\varvec{\hat{n}}$ is the unit outward normal vector along the control volume, $\overline{\overline{\tau }}$ is the stress tensor, and $\textit{\textbf{S}}$ represents any momentum sources or sinks within the control volume. Each of the primary terms in Eq. 4 are labeled to identify their physical meaning and to evaluate their relative magnitudes when the model is applied in the following sections of this paper. Note that due to the one-dimensional flow assumption only the x-component of the momentum equation is retained.

Term number $\textcircled {1}$ represents the time derivative of the total momentum within the system. By evaluating the volume integral under the one-dimensional, incompressible flow assumptions, and removing the x-dependence by considering continuity from Eq. 3, ${\textcircled {1}}$ is simplified as shown in Eq. 5. Note L is the overall length of the wind tunnel.

$$\begin{aligned} \begin{aligned} {\textcircled {1}} \Rightarrow \dfrac{\mathrm {d}}{\mathrm {d}t} \oint _V \rho \textit{\textbf{u}} \,dV&= \dfrac{\mathrm {d}}{\mathrm {d}t} \int _{x_{in}}^{x_{ex}} \rho U(x) A(x) \,dx\\&= \rho L A_{ts} \dfrac{\mathrm {d} U_{ts} }{\mathrm {d}t} \end{aligned} \end{aligned}$$

(5)

Term $\textcircled {2}$ captures the difference in momentum entering and leaving the control volume through the inlet and exit surfaces. Note that, once again, only x-components remain and by again utilizing continuity (Eq. 3) the inlet and exit terms can be reduced and rearranged as shown in Eq. 6.

$$\begin{aligned} \begin{aligned} {\textcircled {2}} \Rightarrow \oint _A \rho \textit{\textbf{u}} (\textit{\textbf{u}} \cdot \varvec{\hat{n}}) \,dA&= \rho U_{ex}^2 A_{ex} - \rho U_{in}^2 A_{in} \\&= \rho U_{ts}^2 A_{ts}^2 \left( \frac{1}{A_{ex}} - \frac{1}{A_{in}} \right) \end{aligned} \end{aligned}$$

(6)

Term $\textcircled {3}$ captures the forces on the control volume boundary. The surface stress tensor, $\overline{\overline{\tau }}$, can be split into isotropic, $-p \overline{\overline{\delta }}$, and deviatoric, $\overline{\overline{\sigma }}$, terms as shown in Eq. 7. The integration over the deviatoric stress tensor can be simplified to a frictional resisting force, $F_{\sigma }$, acting in the negative x-direction. While the remaining integration of the static pressure, p, can be broken into one integral of the absolute atmospheric pressure over the entire surface and another capturing the gauge pressure. Integration of the constant atmospheric pressure over the entire control volume is exactly zero. Additionally, the pressure at the exit of the tunnel, by standard outflow laws, matches atmospheric pressure, $p_{atm}$. This leaves only evaluation of the gauge pressure at the wind tunnel inlet for consideration as shown in Eq. 7.

Fig. 2

Normalized fan curve for the BAE-SWSI 600 centrifugal blower, from Twin City Fan & Blower used in the unsteady, low-speed wind tunnel

Assuming that the flow at the inlet is isentropic and that the inlet total pressure is equivalent to the atmospheric pressure, then the gauge pressure at the inlet is equivalent to the inlet dynamic pressure, $q_{in}$. These assumptions, along with continuity (Eq. 2), allow for further simplification of term $\textcircled {3}$, as shown in Eq. 7.

$$\begin{aligned} \begin{aligned} \textcircled {3} \Rightarrow \oint _A \overline{\overline{\tau }} \cdot \varvec{\hat{n}} \,dA&= \oint _A (-p \overline{\overline{\delta }} + \overline{\overline{\sigma }}) \cdot \varvec{\hat{n}} \,dA \\&= - \oint _A p \varvec{\hat{n}} \,dA - F_{\sigma } \varvec{\hat{i}} \\&= \oint _{A_{in}} (p_{in} - p_{atm}) \,dA - F_{\sigma }\\&= \oint _{A_{in}} (-q_{in}) \,dA - F_{\sigma }\\&= - \frac{\rho }{2} U_{ts}^2 \frac{A_{ts}^2}{A_{in}} - F_{\sigma } \end{aligned} \end{aligned}$$

(7)

Term $\textcircled {4}$ represents momentum sources and sinks within the system. The wind tunnel fan represents the sole momentum source. The momentum sinks come from momentum losses such as turbulence, non-isentropic expansions, etc. and can thus be reduced to a general loss term for momentum sinks, $F_{S}$. The momentum addition by the fan can be attributed to the pressure rise across the fan over the area that the fan acts as shown in Eq. 8.

$$\begin{aligned} \textcircled {4} \Rightarrow \oint _V \textit{\textbf{S}} \,dV = \varDelta p_{T,fan} A_{fan} - F_{S} \end{aligned}$$

(8)

These terms, $\textcircled {1}$ through $\textcircled {4}$, are recombined in Eq. 9.

$$\begin{aligned} \begin{aligned}&\underbrace{\rho L A_{ts} \dfrac{\mathrm {d} U_{ts} }{\mathrm {d}t}}_{{\textcircled {1}}} + \underbrace{\rho U_{ts}^2 A_{ts}^2 \left( \frac{1}{A_{ex}} - \frac{1}{A_{in}} \right) }_{{\textcircled {2}}} \\&= \underbrace{- \frac{\rho }{2} U_{ts}^2 \frac{A_{ts}^2}{A_{in}} - F_{\sigma }}_{{\textcircled {3}}} + \underbrace{\varDelta p_{T,fan} A_{fan} - F_{S}}_{{\textcircled {4}}} \end{aligned} \end{aligned}$$

(9)

The two loss terms, $F_{\sigma }$ and $F_S$, are combined into a single loss term, $F_{loss}$. This term captures the net total-pressure losses for the entire system and can be normalized by the test section conditions to provide an effective pressure loss coefficient, k, for the entire facility as shown in Eq. 10.

$$\begin{aligned} F_{loss} = F_{\sigma } + F_S = k q_{ts} A_{ts} = k \frac{\rho }{2} U_{ts}^2 A_{ts} \end{aligned}$$

(10)

The net total-pressure loss is then substituted into Eq. 9 which can then be rearranged as shown in Eq. 11.

$$\begin{aligned} \begin{aligned} \dfrac{\mathrm {d}U_{ts}}{\mathrm {d}t}&= \frac{U_{ts}^2 A_{ts}}{L} \left( \frac{1}{2 A_{in} \lbrace \theta \rbrace } - \frac{1}{A_{ex}}\right) \\&- \frac{U_{ts}^2}{2L} k \lbrace \theta , \varOmega _{fan} \rbrace + \frac{\varDelta p_{T,fan} \lbrace U_{ts}, \varOmega _{fan} \rbrace A_{fan}}{\rho L A_{ts}} \end{aligned} \end{aligned}$$

(11)

Figure 2 presents the normalized fan curve, from the manufacturer, which can be used to determine $\varDelta p_{T,fan}$. The manufacturer provides the results in terms of fan static pressure, FSP, versus volumetric flow rate, Q. Note that D represents the fan impeller diameter. An eighth order polynomial, also plotted in Fig. 2, was fit through the results and is defined as $FSP^* \lbrace {U_{ts}A_{ts}}/{\varOmega _{fan} D^3} \rbrace$. The fan total pressure rise is then found using Eq. 12.

$$\begin{aligned} \begin{aligned} \varDelta p_{T,fan}\lbrace U_{ts}, \varOmega _{fan} \rbrace&= \rho \varOmega _{fan}^2 D^2 FSP^* \lbrace \frac{U_{ts}A_{ts}}{\varOmega _{fan} D^3}\rbrace \\&+ \frac{\rho }{2} U_{ts}^2 \frac{A_{ts}^2}{A_{fan}^2} \end{aligned} \end{aligned}$$

(12)

Fig. 3

Loss coefficient, k (points), and empirical fits, $k \lbrace \theta \rbrace$ (lines), plotted against louver angle, $\theta$, at multiple fan speeds, $\varOmega _{fan}$, for all three wind tunnel configurations: closed test section with the exit diffuser, CD, (a); closed test section without the exit diffuser, CT (b); and open test section, OT (c)

The total mathematical model is rewritten in Eq. 13 with the fan total pressure terms incorporated and simplified. Also note that a common term has been factored from all of the contributions to the total acceleration to demonstrate the direct dependence of the wind tunnel time response with the square of the test section velocity, $U_{ts}^2$, and the inverse dependence with the overall length of the wind tunnel, L. Finally, an empirical correction factor, $C_{Corr}$, is included to scale all of the contributions to the wind tunnel acceleration. This term was empirically fit for each wind tunnel configuration and will be discussed in further detail in the following sections.

$$\begin{aligned} \begin{aligned} \underbrace{\dfrac{\mathrm {d}U_{ts}}{\mathrm {d}t}}_{Total}&= C_{Corr} \frac{U_{ts}^2}{L} \left[ \underbrace{\frac{A_{ts}}{2 A_{in} \lbrace \theta \rbrace }}_{Mom.~In} - \underbrace{\frac{A_{ts}}{A_{ex}}}_{Mom.~Out} - \underbrace{\frac{k \lbrace \theta , \varOmega _{fan} \rbrace }{2}}_{Losses} \right. \\&\left. + \underbrace{\frac{A_{ts}}{2 A_{fan}} + \frac{\varOmega _{fan}^2 D^2 A_{fan}}{U_{ts}^2 A_{ts}} FSP^* \lbrace \frac{U_{ts}A_{ts}}{\varOmega _{fan} D^3} \rbrace }_{Fan~Pressure} \right] \end{aligned} \end{aligned}$$

(13)

The dynamically varying area induced by the louvers at the inlet, $A_{in} \lbrace \theta \rbrace$, is analytically predicted based upon the louver angular position, $\theta$. This leaves the loss coefficient, $k \lbrace \theta \rbrace$, which can be estimated for steady conditions ($\mathrm {d}U_{ts} / \mathrm {d}t = 0$) as shown by Eq. 14. Static maps of the loss coefficients were empirically computed with steady-state measurements of the test section dynamic pressure for various combinations of fan speeds and louver angles. These results are presented in Fig. 3 for each of the three wind tunnel configurations studied.

$$\begin{aligned} \begin{aligned} k \lbrace \theta , \varOmega _{fan} \rbrace&= \frac{A_{ts}}{A_{in} \lbrace \theta \rbrace } - \frac{2 A_{ts}}{A_{ex}} + \frac{A_{ts}}{A_{fan}} \\&+ \frac{2 \varOmega _{fan}^2 D^2 A_{fan}}{U_{ts}^2 A_{ts}} FSP^* \lbrace \frac{U_{ts}A_{ts}}{\varOmega _{fan} D^3} \rbrace \end{aligned} \end{aligned}$$

(14)

The loss coefficient displays a similar dependence on $\theta$ and $\varOmega _{fan}$ for all three wind tunnel configurations. As a result, an empirical fit was found, $k \lbrace \theta , \varOmega _{fan} \rbrace$, for each configuration composed of a Fourier series dependence on louver angle and a second order polynomial dependence on fan speed, and are plotted in Fig. 3.

The variation in loss coefficient with louver angle was found to be approximately equal between all three configurations, as demonstrated in Fig. 3. The major difference between the configurations is that the losses are uniformly displaced higher for the configurations without the exit diffuser due to the increased speed, and reduced pressure recovery, at the exit of the wind tunnel. A first order estimate of this influence can also be provided by the second term in Eq. 14. Specifically, in both the CT (green) and OT (blue) configurations the exit cross-sectional area, $A_{ex}$, is equal to the test section area, $A_{ts}$, whereas the exit diffuser area ratio is 2.5 to 1 for the CD (red) configuration. This produces a first order estimate from the change in momentum out of the control volume alone of $\varDelta k_{model} = 1.2$, compared with the measured increase of $\varDelta k_{meas.} \approx 1.4$.

It should be noted that the total pressure or mechanical energy losses are typically estimated during wind tunnel design by summing up the local losses from each section within the wind tunnel circuit using basic theory and empirical estimates. This is done to predict the power required to drive the flow in the test section (Barlow et al. 1999, Chap. 3). This analysis was performed for each of the wind tunnel configurations for a louver deflection angle of $\theta = 0^\circ$ and the results agreed closely with the experimental data presented in Fig. 3 for each configuration. Additionally, the losses associated with the abrupt exit of the flow from the open-return wind tunnel duct accounted for 32%, 80%, and 85% of the total losses for the CD, CT, and OT configurations, respectively.

The solution of the ordinary differential equation (ODE), Eq. 13, was carried out numerically in Matlab using the ODE15s variable-step, variable-order solver to numerically integrate the solution from an initial guess of the test section velocity. The variation in louver angle with time, supplied to the solver, was prescribed in a periodic form such that the beginning and ending velocities in the cycle should be equal. This formed a boundary value problem, for which the numerical solution could be solved by iterating the forward integration with the ODE15s solver until the initial and final velocities within the periodic cycle converged to within $0.01\%$. Numerical results from this model are thoroughly discussed and compared to experimental measurements in Sect. 5 below.

3.1 Wind tunnel time constant

The total mathematical model (Eq. 13) was further analyzed to determine the wind tunnel time constant in a similar manner to that of Greenblatt (2016). Note that $U_{ts}$, $A_{in}$, and k all vary directly with $\theta$ which physically varies in time, t. Thus each of these terms represent time-varying components in Eq. 13. The governing equation was first reorganized to ensure that all time varying terms appear in the numerator, before they are each decomposed into mean and fluctuating components (e.g. $U_{ts}\lbrace t \rbrace = \overline{U}_{ts} + \widetilde{U}_{ts}\lbrace t \rbrace$, $A_{in}\lbrace t \rbrace = \overline{A}_{in} + \widetilde{A}_{in}\lbrace t \rbrace$, and $k\lbrace t \rbrace = \overline{k} + \widetilde{k}\lbrace t \rbrace$).

After expanding out each term in the equation, the higher order terms are neglected (e.g. $\widetilde{U}^2_{ts}$) and all of the mean terms cancel out of the equation because ${d\overline{U}_{ts}}/{dt} = 0$; leaving a linearized governing equation for the fluctuating velocity. The fluctuating velocity is then normalized by the mean velocity, as was done by Greenblatt (2016) , where $\varepsilon \lbrace t \rbrace = \widetilde{U}_{ts}\lbrace t \rbrace / \overline{U}_{ts}$. Lumping together like terms and factoring out the variables that fluctuate in time produces the first order ODE in Eq. 15.

$$\begin{aligned} \tau \frac{d \varepsilon \lbrace t \rbrace }{dt} + \varepsilon \lbrace t \rbrace = \tau B_A \widetilde{A}_{in}\lbrace t \rbrace + \tau B_k \widetilde{k} \lbrace t \rbrace \end{aligned}$$

(15)

The coefficients in Eq. 15 are defined in Eqs. 16–18. Additionally, note that $C_{FSP}$ represents the mean fan static pressure. The fluctuations in the fan static pressure rise were neglected as these variations were found to be negligibly small for the operational range used by the fan in the current study.

$$\begin{aligned}&\tau = \frac{L}{\overline{U}_{ts}} \left( \frac{2 A_{ts}}{A_{ex}} + \overline{k} - \frac{A_{ts}}{\overline{A_{in}}}-\frac{A_{ts}}{A_{fan}} \right) ^{-1} \end{aligned}$$

(16)

$$\begin{aligned}&B_A = \frac{\overline{U}_{ts}}{L \overline{A}_{in}} \left( C_{FSP} + \frac{A_{ts}}{2 A_{fan}} - \frac{\overline{k}}{2} - \frac{A_{ts}}{A_{ex}} \right) \end{aligned}$$

(17)

$$\begin{aligned}&B_k = - \frac{\overline{U}_{ts}}{2 L} \end{aligned}$$

(18)

$$\begin{aligned}&C_{FSP} = \frac{\varOmega _{fan}^2 D^2 A_{fan}}{\overline{U}_{ts}^2 A_{ts}} FSP^* \lbrace \frac{\overline{U}_{ts}A_{ts}}{\varOmega _{fan} D^3} \rbrace \end{aligned}$$

(19)

The wind tunnel time constant, $\tau$, in Eq. 16 is similar to that defined by Greenblatt (2016) in Eq. 29 of their paper. Specifically, this shows that the wind tunnel time response is mathematically proportional to the wind tunnel length, L. Note that L physically represents the inertia of the air mass within the wind tunnel system, which is a result of the one-dimensional incompressible flow assumption in the volume integral analysis (Eq. 5). Equation 16 also shows that the wind tunnel time response is inversely proportional to both the mean test section speed and the mean changes in total-pressure through the wind tunnel system for the chosen louver motion. When comparing the magnitudes of the terms within the brackets in Eq. 16, the mean loss coefficient, $\overline{k}$, is nearly an order of magnitude more dominant ($\overline{k} \approx 12$) than each of the other terms ($0.8 \lesssim {2 A_{ts}}/{A_{ex}} \lesssim 2$; ${A_{ts}}/{\overline{A}_{in}} \approx 0.4$; and ${A_{ts}}/{A_{fan}} \approx 0.3$) for the current facility depending upon the chosen louver motion. Thus $\tau$ is effectively a ratio of the fluid inertia to the total pressure losses or stiffness of the wind tunnel system. Furthermore, it can be argued that $\tau$ physically represents the disturbance time scale at which the tunnel response changes from being dominated by the losses (at low frequencies) to being dominated by the fluid inertia (at high frequencies) as demonstrated by the following analysis.

The first order, linear ODE presented in Eq. 15 can be evaluated under the limits of low and high sinusoidal louver driving frequencies, $\omega$, through assuming a particular solution of the normalized time-varying velocity, $\varepsilon \lbrace t \rbrace$, when the driving inputs follow a cosine variation as defined in Eq. 20 and 21. Note $\sigma _A$ and $\sigma _k$ are the amplitudes of $\widetilde{A}_{in}$ and $\widetilde{k}$, respectively.

$$\begin{aligned}&\widetilde{A}_{in} = \sigma _A cos(\omega t) \end{aligned}$$

(20)

$$\begin{aligned}&\widetilde{k} = \sigma _k cos(\omega t + \pi ) \end{aligned}$$

(21)

The resulting time-varying velocity and acceleration under the limiting assumption of low driving frequencies are presented in Eqs. 22 and  23, respectively.

$$\begin{aligned}&\varepsilon = {\tau B_A \sigma _A}\cos (\omega t) + {\tau B_k \sigma _k}\cos (\omega t + \pi ) \end{aligned}$$

(22)

$$\begin{aligned}&\frac{d \varepsilon }{dt} = - \omega {\tau B_A \sigma _A} \sin (\omega t) - \omega {\tau B_k \sigma _k} \sin (\omega t + \pi ) \end{aligned}$$

(23)

The fluctuating velocity amplitude remains unaffected, while the acceleration ${d \varepsilon }/{dt}$ approaches zero, as the driving frequency, $\omega$, is decreased. The above demonstrates that at low frequencies the unsteady test section velocity amplitude effectively results from a balance of the fan static pressure with the system losses.

$$\begin{aligned}&\varepsilon = \frac{1}{\omega }{B_k \sigma _k} \cos \left( \omega t + \pi /2 \right) \end{aligned}$$

(24)

$$\begin{aligned}&\frac{d \varepsilon }{dt} = - {B_k \sigma _k} \sin \left( \omega t + \pi /2 \right) \end{aligned}$$

(25)

In contrast, Eqs. 24 and  25 present the results for high driving frequencies. Under this limit, the acceleration, ${d \varepsilon \lbrace t \rbrace }/{dt}$, is driven by the amplitude of the unsteady wind tunnel losses ($\sigma _k$) but also inversely scales with wind tunnel inertia ($B_k = - \overline{U} / 2 L$). The unsteady test section velocity, $\varepsilon \lbrace t \rbrace$, approaches zero as the driving frequency, $\omega$, increases. Additionally, both $\varepsilon \lbrace t \rbrace$ and ${d \varepsilon \lbrace t \rbrace }/{dt}$ begin to lag their low frequency counterparts by $\pi /2$.

4 Experimental methods

Velocity measurements within the wind tunnel test section were made with two different systems: (1) a conventional pressure measurement system, and (2) a constant-temperature (hot-wire) anemometry system.

The pressure measurement system consisted of two static pressure rings, one on either side of the wind tunnel contraction. A T-Type thermocouple was used to measure the total temperature within the settling chamber, which is effectively equivalent to the test section static temperature for the low-speed flow studied. A differential pressure measurement, $\varDelta p$, was made between the static rings utilizing a MKS 220DD Baratron differential manometer. The test section static pressure was measured with a MKS 220DA Baratron absolute manometer. The temperature and static pressure measurements were used along with a relative humidity measurement in the laboratory to compute the static density within the wind tunnel test section. The data acquisition and conversion was carried out with a National Instruments cDAQ-9188 Compact DAQ Chassis along with two analog input modules: a NI 9222 analog voltage module and a NI 9212 thermocouple module. All of the data acquisition and control was handled through the programs written in the NI Labview programming environment.

Fig. 4

Locations of the constant temperature anemometer (hot-wire) probes for all wind tunnel configurations

Three constant temperature hot-wire probes were used within the wind tunnel test section to accurately quantify the time-varying performance of the unsteady wind tunnel facility. Two of these hot-wires, HW1 and HW2, were affixed at a height of ${0.18}{\hbox { m}}$ above the floor of the test section near its inlet, but spaced laterally apart at ${0.318}{\hbox { m}}$ spanning the wind tunnel centerline, as detailed in Fig. 4. This height ensured that the anemometer probes were placed well outside of the test section wall boundary layers. The third hot-wire, HW3, was mounted on a traverse system at the rear of the test section on the wind tunnel centerline ${2.77}{\hbox { m}}$ downstream from HW1 and HW2.

The purpose of the upstream hot-wire pair was to verify uniformity in flow across the test section, whereas comparison of the upstream and downstream hot-wire signals allowed for the determination of pressure disturbance propagation speeds within the wind tunnel. Similar locations were repeated for the open test section testing, however the upstream hot-wires were inverted and hung ${0.18}{\hbox { m}}$ downstream from the jet exit plane.

All of the hot-wire measurements were made using an A.A. Lab Systems AN-1003 Anemometer System with Dantec Dynamics ${5}{\mu \hbox {m}}$ miniature straight single-wire probes (model number 55P11) and corresponding probe supports. Note that the hot-wires were calibrated in place using the wind tunnel pressure measurement system under static operating conditions.

Fig. 5

The normalized velocity, $U^*$, versus static louver angles, $\theta$, at multiple fan speeds, $\varOmega _{fan}$, for each of the three configurations: CD (a), CT (b), and OT (c)

All of the phase or cycle averaged data presented comprise ensemble averages of 18 cycles for the periodic waveforms studied in this paper. Note that 22 cycles were collected, however the first three cycles and last cycle were all trimmed prior to ensemble averaging to isolate the transient dynamics from the frequency analysis carried out here. For the closed test section configurations, all hot-wires had a maximum standard deviation in velocity of ${{0.18}{\hbox { m/s}}}$ from the calibration, and ${{0.3}{\hbox { m/s}}}$ from the ensemble averages presented. For the open test section configuration, the upstream hot-wires had similar standard deviations in velocity to the closed configuration, however the downstream hot-wire had a maximum standard deviation in velocity of ${{2}{\hbox { m/s}}}$ from both the calibration and the ensemble averages presented. This higher standard deviation is primarily the result of vibrations in the hot-wire mount coupling with unsteadiness in the shear layer emanating from the free-jet.

5 Results and discussion

Results of both the static and dynamic response are presented for each of the three wind tunnel configurations presented earlier. Consistent colors are used for all data corresponding to each of these configurations, with ‘red’, ‘green’, and ‘blue’ corresponding to the CD, CT, and OT configurations respectively.

5.1 Static performance

The wind tunnel was initially operated under steady conditions, and the test section speeds were measured using the static pressure system to understand the wind tunnel’s static sensitivity to the louver system’s angular position. The normalized test section speed, $U^*$, is defined in Eq. 26 as the test section speed measured at a particular louver angle divided by the speed when the louvers are fully open, both of which are at the same fan RPM.

$$\begin{aligned} U^* = U_{ts}/U_{ts,\theta = 0} \end{aligned}$$

(26)

Plots of the normalized speed versus louver angle for a range of fan speeds are presented in Fig. 5. All of the wind tunnel configurations display a reduction in the test section speed as the louvers are closed, consistent with the results of Greenblatt (2016). The CD configuration displays the largest overall reduction, on the order of 60%, while the CT and OT configurations both display maximum reductions of 52%. This is consistent with the trends observed previously for the loss coefficient in Fig. 3.

The normalization, used in Fig. 5, effectively collapses the data, but a small fan speed dependence is still visible. Specifically, increasing the fan speed further reduces the normalized velocity for the same louver position for all wind tunnel configurations. An empirical relation was found to fit the steady speed response of the wind tunnel and is defined by Eq. 27 and plotted in the solid lines alongside the data points in Fig. 5. When discussing the dynamic motions in Sect. 5.2, this two-dimensional empirical fit is used to convert the commanded vane angle motions into a prescribed test section velocity (e.g. $U^*_{Prescribed}$) for each of the wind tunnel configurations.

$$\begin{aligned} U_{ts} \lbrace \theta , \varOmega _{fan} \rbrace = \sum _{m = 0}^{1} \sum _{n = 0}^{4} \left( C_{U_{ts}} \lbrace m, n \rbrace \varOmega _{fan}^m \right) \sin \left( 2 n \theta _r \right) \end{aligned}$$

(27)

5.2 Dynamic performance

Fig. 6

Normalized velocity, $U^*$, versus normalized time, $t^*$, for the CD configuration under sinusoidal dynamic motion for a fan speed of $\varOmega _{fan} = 150$ RPM. The measured louver angle, $\theta$, converted to a prescribed normalized velocity, $U^*_{Prescribed}$ is presented in (a), while the normalized measured wind speed, $U^*_{Measured}$, is presented in (b) and (c) versus $t^*$ and $t^*_{Shifted}$, respectively

After evaluating the wind tunnel’s performance under steady conditions, the louvers were dynamically rotated to produce a prescribed sinusoidal motion in velocity between fully open and fully closed louver positions. For each wind tunnel configuration, tests were carried out and are presented at multiple fan speeds to ascertain the wind tunnel’s time response and the propagation speed of disturbances within the facility. The theoretical model is used in Sect. 5.2.3 to further understand the wind tunnel’s performance by evaluating the response of each model component to an ideal square wave input in louver motion.

5.2.1 Closed test section configurations

Fig. 7

Amplitude ratio (a) and phase lag, $\phi$, (b) between measured and prescribed normalized speeds for the CD configuration undergoing sinusoidal oscillations for a range of normalized driving frequencies, $\omega \tau$, at two fan speeds, $\varOmega _{fan}$. Experimental data is plotted with the markers, the uncorrected model with the dashed line, and the corrected model with the solid line

Fig. 8

Amplitude ratio (a) and phase lag, $\phi$, (b) between measured and prescribed normalized speeds for the CT configuration undergoing sinusoidal oscillations for a range of normalized driving frequencies, $\omega \tau$, at two fan speeds, $\varOmega _{fan}$. Experimental data is plotted with the markers, the uncorrected model with the dashed line, and the corrected model with the solid line

Fig. 9

Normalized speed, $U^*$, measured by each of the three hot-wire probes for the CD configuration undergoing sinusoidal oscillations at frequencies of $f = 0.125$ (a), 0.25 (b), 0.5 (c), and 1 Hz (d) and a fan speed of $\varOmega _{fan} = 150$ RPM

The dynamic response of the velocity for the two closed test section configurations (CD and CT) are evaluated for periodic louver motions. Figure 6 presents the dynamic response of the CD configuration for the sinusoidal prescribed velocity fluctuations for a range of driving frequencies at a constant fan speed. The time-varying normalized velocity, $U^*$, includes the mean of the ensemble average of the two upstream hot-wires. Additionally, the time axis has been normalized by the driving frequency such that a consistent comparison can be made, where the normalized time, $t^* = t f$. As the frequency is increased, the amplitude of the oscillation in test section velocity is attenuated and the signal becomes further phase lagged from the ideal sine wave trajectory. It is also worth noting that the wind tunnel decelerates faster than it accelerates. This can be seen in Fig. 6c where each of the data sets has been individually shifted in normalized time to start at their peak values, yet minimum values always occur left of $t^* = 0.5$.

The wind tunnel’s response is further analyzed by considering the amplitude ratio and phase shift between the prescribed and measured sinusoidal motions. Bode plots of the values presented in Fig. 6 are plotted versus input driving frequencies normalized by the wind tunnel time constant, $\tau$, in Fig. 7 for the CD configuration. A similar analysis is presented in Fig. 8 for the CT configuration.

As highlighted by the model assumptions (Sect. 3), the theoretical model does not account for the physical propagation of pressure disturbances. As a result, the phase lag of the experimental data was shifted by the appropriate time lag to account for the propagation of disturbances from the wind tunnel inlet to the upstream hot-wire measurement location. This allowed for a more accurate comparison of the experimental data with the model.

Normalizing the driving frequency by the model predicted $\tau$ in Figs. 7 and  8 enables the data to collapse along a single curve for all of the tested fan speeds; as was previously shown by Greenblatt (2016). Per Eq. 16, $\tau$ decreases with an increase in test section speed, or an increase in the fan speed, for a set louver motion and wind tunnel configuration, as seen in Table 1. Additionally, a smaller $\tau$ allows for higher driving frequencies to be reached before the onset of phase lag and amplitude attenuation as shown in Figs. 7 and  8. Note that $\tau$ also decreases with decreasing length, and therefore the CT configuration has a faster time response than the CD configuration due to its increased fluid inertia. At high frequencies, the phase lag for both configurations tends towards $90^\circ$, or $\pi /2$, consistent with the theoretical model analysis described above as well as the prior work of Greenblatt (2016). Note that this phase lag is inherent in the modeled response, and therefore not a function of propagation speed.

Table 1 Summary of the average experimental time constants, $\tau$, for the three wind tunnel configurations at each of the tested fan speeds

The uncertainty in the amplitude ratio was calculated through propagating the standard deviation from the 18 cycle ensemble average of hot-wire data through the Bode plot analysis. The maximum standard deviation for the CD and CT configurations was found to be 0.0143 for the amplitude ratio, which is smaller than the symbol size used. As a result errorbars are not included in Figs. 7 and  8 for clarity.

Both the uncorrected and corrected responses from the wind tunnel model show similar trends to the experimental data in Figs. 7 and  8; including the perfect collapse of the frequency response through normalizing the driving frequency with $\tau$. It is clear from the figures that the uncorrected model (dashed line) significantly over predicts the wind tunnel’s frequency response for both the CD and CT configurations. While the magnitude of the frequency response is over predicted, the effective shape of the frequency response appears to be accurately captured by the uncorrected model. As a result, a simple constant of proportionality, $C_{Corr}$, was applied to the model as defined in Eq. 13. The correction factor was determined by minimizing the root mean square (RMS) error of the amplitude ratios and phase lags between the experimental data and the model for the frequencies and fan speeds tested. For the CD configuration, applying a correction factor of $C_{Corr}=0.465$ reduced the RMS error of the amplitude from 0.17 to 0.03, and that for the phase lag from $15.8^\circ$ to $4.3^\circ$. For the CT configuration, applying a correction factor of $C_{Corr}=0.500$ reduced the RMS error of the amplitude from 0.13 to 0.02, and that for the phase lag from $12.6^\circ$ to $2.7^\circ$.

The physical source of the error requiring correction is still unknown and requires further investigation at this time. The similarity between the CD and CT correction factors, and their moderate deviation from the OT configuration (discussed below), suggest that a large source of the error may be associated with the unsteady flow through the closed wind tunnel test section. As a result, the impact of the steady boundary layer growth along the test section walls was theoretically considered through applying an effective reduction in the cross-sectional area within the model caused by the boundary layer displacement thickness. However this had an insignificant impact on the modeled response, and thus is not considered the source of error at this time.

The fact that the current model does not account for the finite speed of sound (as discussed above) represents another potential source of error in the current model. Specifically, the existing model is unable to account for the influence of the finite disturbance propagation speed or partial reflections of the disturbances from the wind tunnel exit. This limitation could be overcome in future work by implementing an incompressible method of characteristics model, as demonstrated by Rennie et al. (2019).

Finally, the total wind tunnel losses were measured under steady wind tunnel conditions and do not capture potential dynamic losses in the system. If unsteady viscous effects such as time-varying flow separation or boundary layer thickening is occurring within the experimental facility, the model would have no means of accounting for it.

Fig. 10

Amplitude ratio (a) and phase lag, $\phi$, (b) between HW3 (downstream) and the average of HW1 + HW2 (upstream) for the CD configuration undergoing sinusoidal oscillations for a range of driving frequencies of the louver system, f, at two fan speeds, $\varOmega _{fan}$

The propagation speed of disturbances through the wind tunnel test section can be analyzed by comparing the HW1 and HW2 measurements to that made by HW3. Figure 9 presents a comparison of the response from all three hot-wire probes. This figure shows that all of the hot-wire measurements follow nearly identically in both amplitude and phase.

Bode plots are produced to assess the change in amplitude ratio and phase shift between the upstream and downstream measurements within the wind tunnel test section. Figure 10 presents these results for the CD wind tunnel configuration. A Fast Fourier Transform signal analysis method is again utilized, but the downstream hot-wire is instead compared to the mean of the ensemble average of the two upstream hot-wires. In this case, the phase shift is directly related to the propagation speed, c, of a disturbance between the two probes which is defined in Eq. 28, with $d = 2.77$ m representing the separation distance between the upstream and downstream probes, and f equal to the driving frequency.

$$\begin{aligned} c = \frac{-360^\circ }{\phi } f d \end{aligned}$$

(28)

The variation in amplitude ratio is extremely small with the downstream velocity attenuated at most by 6%, as can be seen in Fig. 10. The phase lag in the signals also have very small magnitudes with a maximum value of $\phi = -2.6^\circ$ for the CD configuration at all conditions tested. These small phase lags translate to very high propagation speeds on the order of 100 to 300 m/s for the data shown. In theory, disturbances should propagate downstream in the closed test section at a speed $c = a + U_{ts}$, or around ${352}{\hbox {m}/\hbox {s}}$ to ${362}{\hbox {m}/\hbox {s}}$ for the conditions tested. The measured propagation speeds were significantly slower than the theoretical propagation speeds and were also observed to vary more significantly with the mean flow speed than the above theoretical predictions. While the source of the variation from theory is not fully understood, the results presented in Fig. 10 are consistent with the results presented by Greenblatt (2016) in Fig. 14 of their paper.

The CT configuration had similar amplitude ratios and phase lags as that for the CD configuration and are not shown here for brevity. Still, the analysis drawn for the CD configuration also applies for the CT configuration as both have a closed test section configuration. Furthermore, the disturbances within the closed test section configurations propagate at a measured speed at least an order of magnitude faster than the convective speed of the flow. As a result, it is accurate to assume that flow accelerations imposed on a test article within the closed test section configurations will behave in a purely unsteady fashion. Thus, longitudinal gusts within a closed test section are globally unsteady.

5.2.2 Open test section configuration

The same dynamic sinusoidal velocity motion analysis was performed for the OT configuration, however not all of the figures will be repeated for brevity. Figure 11 presents the Bode plots which compare the prescribed sinusoidal velocity to the average of both upstream hot-wire measurements. Generally, the same trends with speed and frequency are observed for the OT configuration as for the CD and CT configurations. However, the shorter overall length, or smaller fluid inertia, of the OT tunnel configuration yields a smaller $\tau$, per Table 1, and therefore allows for a larger range of operable frequencies before the signal amplitude is attenuated and a phase lag develops, as seen in Fig. 11. The correction factor for the OT configuration was calculated in the same manner for the CD and CT configurations previously discussed. Specifically for the OT configuration, a correction factor of $C_{Corr}=0.705$ reduced the RMS error between the measured and model-predicted responses from 0.05 to 0.03 for the amplitude ratio and from $7.5^\circ$ to $3.4^\circ$ for the phase lag. The maximum standard deviation in the amplitude ratio was 0.0191 for the OT configuration, thus again errorbars were not included in Fig. 11 for clarity.

Fig. 11

Amplitude ratio (a) and phase lag, $\phi$, (b) between measured and prescribed normalized speeds for the OT configuration undergoing sinusoidal oscillations for a range of normalized driving frequencies, $\omega \tau$, at two fan speeds, $\varOmega _{fan}$. Experimental data is plotted with the markers, the uncorrected model with the dashed line, and the corrected model with the solid line

Fig. 12

Normalized speed, $U^*$, measured by each of the three hot-wire probes for the OT wind tunnel configuration undergoing sinusoidal oscillations at frequencies of $f = 0.125$ (a), 0.25 (b), 0.5 (c), and 1 Hz (d) and a fan speed of $\varOmega _{fan} = 150$ RPM

Fig. 13

Amplitude ratio (a), phase lag, $\phi$, (b), and propagation speed, c, (c) between HW3 (downstream) and the average of HW1 + HW2 (upstream) for the OT configuration undergoing sinusoidal oscillations for a range of driving frequencies, f, and fan speeds, $\varOmega _{fan}$. For comparison, the mean upstream wind tunnel speed is plotted (dashed line) for each fan speed in (c)

Figure 12 presents a comparison of all three hot-wires for the OT configuration at a fan speed of $\varOmega _{fan} = 150$ RPM to visually display the propagation speed of disturbances in the free jet. The most significant aspect of these plots is the way the phase averaged trace of the normalized velocity measured by HW3 drifts further to the right as the commanded frequency is progressively increased from $f = 0.125$ Hz (a) to $f = 1$ Hz (d). These plots also reveal a number of interesting points with the downstream hot-wire measurements.

First, while the amplitudes measured by the upstream hot-wires decay as the commanded frequency increases, the amplitude of HW3 does not. This appears to primarily influence the maximum velocity peak, because the minimum velocities remain at a similar value to their upstream counterparts. In addition to this downstream amplification the sinusoidal trajectory is also moderately distorted, with more time spent in the cycle while the velocity is at its minimum than its maximum. This stretching and steepening of the signal is likely due to the convective gradients in the flow as the faster velocity regions will move further than the slower velocity regions during the same period of time.

Second, significant noise is observed in the HW3 signal. This noise clearly demonstrates that the choice of 18 cycles in the ensemble average used in the current experiments is not sufficient to produce a smooth, stationary ensemble mean of the downstream open-test section data. The observed noise is related to two physical sources: (1) the turbulence in free-jet shear layers increase the flow unsteadiness encountered at this significant downstream position and (2) the structural vibrations in the downstream hot-wire probe support are amplified compared to the closed test section case due to the unsteadiness in the shear layer. In spite of these issues, valuable information, particularly regarding the phase shift and propagation speed, can still be garnered.

Figure 13 presents the amplitude ratio, phase shift, and propagation speed between the mean of the upstream hot-wires compared with downstream hot-wire for the OT configuration, as was done previously for the CD configuration in Fig. 10. The amplitude ratio data in Fig. 13a shows the growth of a resonant peak in the frequency response that is consistent with the time series data presented in Fig. 12. Note the significance of this peak appears to diminish with increasing wind tunnel fan speed. While the exact source of this resonant amplification is unknown, it is suspected to be resulting from the amplification of vortex paring in the free jet (Zaman and Hussain 1980; Hussain and Zaman 1980). The column mode in a free jet occurs at a Strouhal number of $St = f d_h / U = 0.85$ where $d_h = {0.80}{\hbox { m}}$ represents the hydraulic diameter of the jet orifice for the current facility. This correlates to frequencies of $f = 7.1$, 9.7, 12.4, and ${17.1}{\hbox { Hz}}$ for $\varOmega _{fan} = 150$, 200, 250, and ${350}{\hbox { RPM}}$, respectively. To confirm this hypothesis further investigations of the free-jet facility will be required at higher driving frequencies and with a focus on the shear layer development and evolution.

The phase shift data in Fig. 13b shows that the phase lag grows significantly between the upstream and downstream hot-wires as the driving frequency is increased. Note that the maximum measured phase lag is on the order of $\phi = -270^\circ$, compared to $\phi = -2.6^\circ$ for the closed test section configuration, demonstrating that the behavior of the velocity disturbances depends on test section configuration. This change in behavior is analyzed by directly considering the propagation speed computed from the phase lag as detailed in Eq. 28. Plots of these values for the OT configuration are included in Fig. 13c where an additional reference line is also included to highlight the mean flow speed at the exit of the free jet. From this figure, it is clear that the propagation speed of disturbances in the OT configuration closely matches the mean convective speed of the flow issuing from the free-jet. These results further show that velocity perturbations convect through the open test region at a speed on the order of the mean flow speed for the OT configuration.

5.2.3 Model decomposition

With the performance of the theoretical model bench-marked against experimental measurements, it can be used as a validated tool for decomposing each term within the unsteady control volume analysis. This process was undertaken to learn more about the tunnel response and to better identify the causes of the differences observed in acceleration and deceleration rates, previously identified in Fig. 6.

To facilitate this discussion, an ideal square wave from $\theta = 0^\circ$ to $90^\circ$ is prescribed to the louvers, as seen in Fig. 14a, and the change in test section speed, U, is calculated using the uncorrected model, seen in Fig. 14b. Under these conditions, the wind tunnel test section speed is varied between a maximum of $U = {11.04}{\hbox { m/s}}$, and a minimum of $U = {4.81}{\hbox { m/s}}$. Each of the acceleration components from the uncorrected theoretical model, Eq. 13, are presented in Fig. 14c, d, and e.

Fig. 14

Comparison of the terms within the theoretical model (Sect. 3) for the CD configuration at $\varOmega _{fan} = 150$ RPM undergoing an ideal square wave variation in louver angle (a). Additional plots display the predicted test section velocity (b), the contributions to the test section acceleration from momentum in and out of the control volume (c) and the momentum sources/sinks within the control volume (d), and the total acceleration within the test section (e). The vertical dashed line denotes the modeled time constant, $\tau$, while the gray regions indicate the acceleration and deceleration time constants

For the CD configuration at the chosen fan speed, the wind tunnel time constant is $\tau = {0.2962}{\hbox { s}}$ and is denoted by the elapsed time from the step change in the louver angle at $t = 0.5$ and 2 to the two respective vertical dashed lines in Fig. 14. The gray regions in the figure also denote the computed time constants for deceleration, $\tau _{decel.} = {0.146}{\hbox { s}}$ and acceleration, $\tau _{accel.} = {0.495}{\hbox { s}}$. These time constants were numerically estimated by identifying when the velocity crosses 63% of the change in velocity after the imposed step change in louver position. For all configurations tested, the deceleration time constant was consistently $\tau _{decel.} = 0.5 \tau$, while the acceleration time constant was $\tau _{accel.} = 1.7 \tau$. The discrepancy between the deceleration and acceleration time constants implies that the wind tunnel under these conditions is able to decelerate the flow approximately 3 times faster than it can accelerate the flow. Thus these differences are non-negligible and need to be accounted for if a symmetric variation in velocity is desired.

To better understand the physical source of these deviations, the time-varying contributions from each of the components in the control volume analysis are plotted in Fig. 14c and d where the blue lines denote positive (+) contributions to the acceleration and the red lines denote negative (-) contributions (i.e. decelerating components of the system). First, the fact that each of these terms is either always positive (i.e. Momentum In and Fan Pressure) or always negative (i.e. Momentum Out and Losses) demonstrates that independent operating parameters effectively control either the acceleration or deceleration of flow within the wind tunnel. Not surprisingly, the positive acceleration of flow within the test section is almost completely controlled by the pressure rise across the fan. The contribution from the fan pressure rise is nearly constant throughout the periodic cycle, only varying between ${8.2}{\hbox { m/s}^2}$ and ${11.5}{\hbox { m/s}^2}$. Additionally, note that all other components of acceleration experience their local minimums ($|dU / dt| < {1.3}{\hbox { m/s}^2}$) when the louvers open and the flow accelerates (i.e. $t = {2}{\hbox { s}}$).

In contrast, the flow deceleration is dominated by the losses within the wind tunnel, which are strongly dependent upon the louver angle, recall Fig. 3. In fact, the maximum negative accelerations achievable from completely closing the louvers significantly overpowers the positive acceleration provided by the fan by a factor of more than five for the case demonstrated here.

While the achievable positive acceleration rates can be improved by increasing the fan speed, which effectively increases the test section speed and static pressure rise across the fan, the maximum deceleration rate grows as a function of $U_{ts}^2$. As a result, the wind tunnel will always decelerate the flow more quickly than it can accelerate the flow for a given set of operating conditions.

6 Conclusions

The current work presents a summary of the design, modeling, and testing of an unsteady, low-speed wind tunnel capable of producing controlled large amplitude longitudinal velocity accelerations. As part of the system design, a basic predictive mathematical model was developed using a one-dimensional, incompressible control volume analysis to accurately capture the unsteady performance of the open-return wind tunnel facility.

The static loss coefficient empirical fit was implemented within the predictive model to design periodic louver motions that imposed a sinusoidally unsteady velocity within the wind tunnel test section under quasi-static conditions. From the analysis of these motions, it was shown that the wind tunnel response is characteristic of a low-pass filter. The time response was dramatically improved by shortening the overall length of the wind tunnel or by increasing the test section flow speed.

From the hot-wire probe measurements, the disturbance propagation speed was found to match the test section convective velocity for the OT configuration. In contrast, both of the closed test section configurations, CD and CT, demonstrated propagation speeds that were at least an order of magnitude faster than the convective speed of the flow and approached the speed of sound.

While the uncorrected model over predicted the wind tunnel acceleration for all of the configurations, applying a scalar correction factor reduced the rms error between the model and the experimental data. The error in the model is postulated to be the result of unaccounted for dynamic losses within the system and potentially the inability of the model to account for the finite speed of sound at which the physical disturbances propagate.

The flow deceleration rate is primarily controlled by the increase in the wind tunnel losses. In contrast, the acceleration rate is limited by the static pressure rise across the wind tunnel fan, and thus directly scales with the fan speed.

The derived model presented in this paper can be used to deterministically engineer louver motions that produce novel, unsteady test section speed profiles by accounting for the wind tunnel’s dynamic response. As a result, the modeling method outlined here could prove to be a versatile tool for future research in both gust interactions and unsteady aerodynamics.