Mechanical vs. phenomenological formulations to determine mean aerodynamic drag from stereo-PIV wake measurements

Abstract

The present work compares two different drag formulations based on a global balance of momentum (cf. for instance Rival and Van Oudheusden in Exp Fluids 58(3):20, 2017) fed with wake surveys of a finite-size wing. The traditional expression in terms of velocity and static pressure is considered, and compared to the phenomenological drag breakdown put forward by Méheut and Bailly (AIAA J 46(4):847–862, 2008) within the aerodynamic context. Both formulations require information on the velocity field, but also the static or stagnation pressure in the wake plane of the model of interest. In this paper, we focus on computing the results based on velocity data exclusively, acquired by stereo-PIV. These two methods are benchmarked experimentally on the wake of a SACCON model (Schütte et al. in J Aircraft 49(6):1638–1651, 2012) that has been measured in one of ONERA’s wind-tunnels, and their performance is evaluated by comparing their results to direct force balance measurements. It is shown that while both formulations perform similarly, with drag predictions lying within 10% of the balance measurements, the phenomenological approach can additionally inform on the physical origins of drag. The latter method may thus be valuable to aerodynamicists, by giving them valuable clues as to how to fine-tune the performances of a given airframe.

1 Introduction

In a world increasingly concerned with energy and cost savings, it has become critical for aerodynamicists to accurately measure and predict the effects of drag acting on air vehicles. This task is all the more difficult, as drag may result from drastically different physical phenomena, ranging from viscous skin friction to shock waves, via the mere presence of lift. The mandatory first step towards improving the efficiency of an airframe is thus to accurately describe and measure these various drag components. The direct measurement of total mean drag acting on a model using force balances has been tried and tested, and is nowadays customarily found on industrial and research experimental platforms. Though reliable, this method only gives a global assessment of drag, and makes it impossible to distinguish between its various sources.

This drawback may be bypassed by expressing the total aerodynamic force in terms of the surrounding flow’s properties, by means of a global balance of momentum. The main difficulty associated with the aforementioned method then comes from accurately evaluating the pressure and velocity fields throughout a control volume, which can sometimes be quite large. Within this context, particle image velocimetry (PIV) appears to be a measurement method particularly well suited for this task, as it can yield velocity fields throughout large domains. And indeed, Van Oudheusden et al. (2006, 2007) demonstrated that the control volume approach fed exclusively with planar PIV data was viable when considering the mean aerodynamic loads acting on a two-dimensional (2D) airfoil. Since then, the continuous improvements made to PIV whether in terms of accessing the out of plane velocity component, or increasing spatial and temporal resolutions have made it possible to infer ever more precisely the relationship between the forces acting on an object, and its surrounding flow. For instance, Ragni et al. (2009, 2011), computed the time and phase averaged loads acting on straightly flying and rotating airfoils, respectively. The lift was computed by integrating the pressure coefficient along the airfoil’s contour, which had been determined beforehand by integrating the Navier–Stokes equations fed with stereo-PIV data. Drag, on the other hand, was deduced from PIV measurements of the momentum deficit in the wake. These PIV based loads were reported to be within 10% of those measured using conventional methods (pressure taps and Pitot probes). Alternately, Unal et al. (1997), Kurtulus et al. (2007), David et al. (2009) and Villegas and Diez (2014) took advantage of time resolved planar PIV data to examine the relationship between the instantaneous loads acting on 2D profiles and the unsteady surrounding flow, and studied the drag in terms of convective, pressure and turbulent contributions. In particular, these studies enabled to associate periodic features of the loads to vortex shedding in the wake. More recently, Terra et al. (2017, 2019) have estimated the drag acting on bluff bodies, based on the investigation of their wakes with large-scale tomographic PIV. Notably, the former study investigates the drag acting on a sphere towed across quiescent air, and highlights the competition between the convective and pressure contributions to drag, as a function of the distance between the investigation plane and the model.

The control volume approach in the form discussed above still entangles the different drag components resulting from irreversible losses of energy (i.e., viscous, form and wave drag, which add up to profile drag), to those resulting from the presence of lift (i.e., induced drag). To illustrate this point, let us consider the wake vortices that typically appear at the edges of three-dimensional wings, which result from a sudden pressure discrepancy at the crossing of the wingtip. This sharp pressure gradient ultimately drives a strong cross-flow around the wingtip, whose magnitude can reach, in the present study, up to 20% of the streamwise velocity component. In the process of setting up wake vortices around its body, the airframe looses energy in the form of induced drag. It is however impossible to attribute the overall induced drag production to either inertia or pressure alone, since both effects contribute to the phenomenon. Within this context, the work of Jone’s (1936) can be seen as a first attempt to extract the profile drag resulting from viscous and form drag only, by considering the momentum deficit in the wake of two-dimensional (2D) airfoils flying through an incompressible fluid. This approach was further extended by Maskell (1972) and Cummings et al. (1996), who presented a way to determine lift induced drag. They did so by accounting for the presence of a transverse flow in the downstream plane, and showed that the induced drag in fact simply boiled down to the integration of the transverse kinetic energy at that same location. Finally, Destarac and Van Der Vooren (2004) and Kusunose et al. (1999) extended the latter methods to the compressible flow regime, where profile drag may also be generated by the emergence of shock waves upon the model. In such regimes, it is helpful to link profile drag to the production of entropy. In particular, the latter authors put forward a wave drag extraction method, based on the observation that the profile drag originating from viscous shear layers translates into a rotational wake (hence can be determined from Crocco’s theorem), whereas the profile drag resulting from shock waves can be associated to the irrotationnal region of the wake (hence wave drag can be calculated from the Rankine–Hugoniot shock jump formula).

The goal of the present work is to compare the performances of both approaches in an experimental context, where measurements stem from PIV. For the sake of simplicity, the framework adopted here will focus on the incompressible regime. We will start by reviewing the mechanical and phenomenological drag breakdown methods in Sect. 2. The experimental rig used for the present investigation will then be described in Sect. 3, while the implementation and robustness of both methods will be assessed in Sect. 4. Global drag results will eventually be presented and discussed in Sect. 5.

2 Theoretical background

2.1 Mechanical drag breakdown

Fig. 1

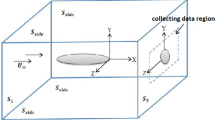
Control volume of interest. The region enclosed in the dashed loop is referred to as the wake w, which is a subset of the downstream plane ${\mathcal {S}}_1$. Outside of this region, the profile drag, induced drag and turbulent contributions have completely vanished, unlike those associated to the convective and pressure terms

Let us consider an aircraft model immersed in an upstream uniform flow $U_\infty \, \mathbf {e}_x$ of density $\rho$ and dynamic viscosity $\mu$. The cornerstone of the method consists in performing a global balance of momentum over the control volume ${\mathcal {V}}$ of contour $\partial {\mathcal {V}}$ and outwards pointing normal $\mathbf {n}$, which is fully encompassing a model of wing area $S_{\text {ref}}$ (cf. Fig. 1). Considering a steady mean flow and time averaged quantities, the mean aerodynamic load $\mathbf {F}$ acting on the model is traditionally found to be

$$\begin{aligned} \begin{aligned} \mathbf {F} \; = \;&- \int \limits _{\partial {\mathcal {V}}} \rho \left( \mathbf {U} \cdot \mathbf {n} \right) \mathbf {U} \, {\text {d}}S \, - \int \limits _{\partial {\mathcal {V}}} \rho \, \langle \mathbf {u}' \otimes \mathbf {u}' \rangle \cdot \mathbf {n} \, {\text {d}}S \\ \,&- \ \int \limits _{\partial {\mathcal {V}}} P \, \mathbf {n} \, {\text {d}}S \, + \, \mu \int \limits _{\partial {\mathcal {V}}}\left[ \nabla \mathbf {U} + \left( \nabla \mathbf {U} \right) ^T \right] \cdot \mathbf {n} \, {\text {d}}S, \end{aligned} \end{aligned}$$

(1)

where $\mathbf {U} = U \, \mathbf {e}_x + V \, \mathbf {e}_y + W \, \mathbf {e}_z$ and P, respectively represent the mean velocity and mean static pressure fields. The term $\langle \mathbf {u}' \otimes \mathbf {u}' \rangle$ refers to the Reynolds stress tensor, with $\mathbf {u}' = u' \, \mathbf {e}_x + v' \, \mathbf {e}_y + w' \, \mathbf {e}_z$ being the turbulent velocity fluctuation. The effects of viscous friction along $\partial {\mathcal {V}}$ are considerably smaller than any other term (about two orders of magnitude here), hence can be safely dropped. Assuming that the lateral boundaries are sufficiently far from the model, there is no flux of momentum across them, and the global balance simplifies to evaluating the difference of momentum between the up- and downstream planes of the control volume ${\mathcal {S}}_\infty$ and ${\mathcal {S}}_1,$ respectively. This assumption also implies that the turbulent stresses will be non negligible only in the downstream plane ${\mathcal {S}}_1$. Further invoking the conservation of mass, and the fact that integrating $P_\infty$ over the closed contour $\partial {\mathcal {V}}$ is zero, the total drag coefficient $C_D = 2 \, \mathbf {F} \cdot \mathbf {e}_x / \rho _\infty \, S_{\text {ref}} \, U_\infty ^2$ can be expressed in terms of a surface integral over the downstream plane ${\mathcal {S}}_1$ of the control volume, and reads

$$\begin{aligned} \begin{aligned} C_D \; =&\; \frac{2}{S_{\text {ref}}} \int \limits _{{\mathcal {S}}_1} \left[ \frac{\rho }{\rho _\infty } \frac{U}{U_\infty } \right. \left( 1 - \frac{U}{U_\infty } \right) \; + \; \frac{P_\infty - P}{\rho _\infty U_\infty ^2} \\&\left. - \; \frac{\rho }{\rho _\infty } \frac{\left\langle u' u' \right\rangle }{U_\infty ^2} \right] \, \mathrm {d}S. \end{aligned} \end{aligned}$$

(2)

In the above, subscript ‘$\infty$’ refers to the uniform free-stream quantities. Equation 2 gives a mechanical description of the production of drag, by associating it to the properties of the flow (namely convection, pressure and turbulent stresses), which concurrently take part in all the various drag sources. The mechanical drag breakdown $C_D^{\text {Mec}}$ ensues, and may be written as

$$\begin{aligned} C_D^{\text {Mec}} \; = \; C_D^{\text {Conv}} \; + \; C_D^{\text {Press}} \; + \; C_D^{\text {Turb}}, \end{aligned}$$

(3)

where

$$\begin{aligned} C_D^{\text {Conv}} \;= & {} \; \frac{2}{S_{\text {ref}}} \int \limits _{{\mathcal {S}}_1} \frac{\rho }{\rho _\infty } \frac{U}{U_\infty } \left( 1 - \frac{U}{U_\infty } \right) \mathrm {d}S, \end{aligned}$$

(4)

$$\begin{aligned} C_D^{\text {Press}} \;= & {} \; \frac{2}{S_{\text {ref}}} \int \limits _{{\mathcal {S}}_1} \frac{P_\infty - P}{\rho _\infty U_\infty ^2} \; \mathrm {d}S, \end{aligned}$$

(5)

and

$$\begin{aligned} C_D^{\text {Turb}} \; = \; - \frac{2}{S_{\text {ref}}} \int \limits _{{\mathcal {S}}_1} \frac{\rho }{\rho _\infty } \frac{\left\langle u' u' \right\rangle }{U_\infty ^2} \; \mathrm {d}S. \end{aligned}$$

(6)

According to this formulation, a sufficiently large plane $S_1$ must be considered, in order to compute a precise estimate of the total mean drag acting upon the model.

2.2 Phenomenological drag breakdown

Since the seminal work of Betz (1925), numerous phenomenological drag breakdown methods have been put forward, many of which are reviewed and compared in Méheut and Bailly (2008). We focus in this paper on the phenomenological drag breakdown put forward by the latter authors, which gives a complete drag breakdown, whose integration is reduced to the sole wake.

The cornerstone of Méheut and Bailly’s phenomenological drag breakdown is Eq. 2. Unlike them however, we keep the Reynolds stress term, which is fully accessible using stereo-PIV data. (Neglecting turbulent stresses was required when wake data was measured with five-hole and Pitot probes, which only gave access to mean velocity fields.) Eq. 2 is then specialized to the aerodynamic case by expressing the ratio of fluid densities using the perfect gas constitutive law, in which the stagnation pressure $P_i$ and temperature $T_i$ are introduced. The flow is supposed to be isenthalpic (i.e., there are no heat sources), such that the stagnation temperature remains constant and equal to its free-stream value everywhere. Finally, the downstream plane is assumed to be located sufficiently far away from the model, such that the quantities measured downstream differ only slightly from those upstream. Within this small perturbation framework, one can define $P_i = P_{i\infty } + \delta P_i$ ($P_{i\infty }$ being the free-stream stagnation pressure) and $\mathbf {U} = (U_\infty + \delta u) \, \mathbf {e}_x + \delta v \, \mathbf {e}_y + \delta w \, \mathbf {e}_z$, where the perturbations $\delta P_i / P_{i\infty }$, $\delta u / U_\infty$, $\delta v / U_\infty$ and $\delta w / U_\infty$ are all small compared to one. Owing to an asymptotic expansion up to second order, Méheut and Bailly showed that Eq. 2 could be re-written in the form

$$\begin{aligned} \begin{aligned} C_D \; =&\; \frac{1}{S_{\text {ref}}} \int \limits _w \left[ - \frac{2}{\gamma M_\infty ^2} \frac{\delta P_i}{P_{i\infty }} + \left( M_\infty ^2 - 1 \right) \frac{\delta u^2}{U_\infty ^2} \right] \mathrm {d}S \\&+ \; \frac{1}{S_{\text {ref}}} \int \limits _{{\mathcal {S}}_1} \frac{\delta v^2 + \delta w^2}{U_\infty ^2} \, \mathrm {d}S \\&- \frac{2}{S_{\text {ref}}} \int \limits _{{\mathcal {S}}_1} \frac{\rho }{\rho _\infty } \frac{\left\langle u' u' \right\rangle }{U_\infty ^2} \; \mathrm {d}S, \end{aligned} \end{aligned}$$

(7)

where $\gamma$ represents the heat capacity ratio, and $M\!a_\infty = U_\infty / \sqrt{\gamma r T_\infty }$ is the free-stream Mach number (r = 287 J/kg/K being the specific gas constant for air). The equation above now has a strong physical meaning. Indeed, the latter authors showed that the first integral on the right-hand side of Eq. 7 translated the irreversible losses of energy, and was thus attributable to profile drag. By contrast, the second integral on the right-hand side of Eq. 7 is proportional to the transverse kinetic energy that has emerged downstream of the model. As such, it is representative of the induced drag resulting from trailing vortices. In addition, the works of Maskell (1972) and Cummings et al. (1996) showed that the integration domain of this second integral could be reduced to the wake only, by rewriting the transverse kinetic energy in terms of the streamwise vorticity component $\omega = \left( \nabla \times \mathbf {U} \right) \cdot \mathbf {e}_x$, and the 2D mean streamfunction $\psi = - (\partial _{yy}^2 \, \omega + \partial _{zz}^2 \, \omega )$ according to

$$\begin{aligned} \int \limits _{S_1} \frac{\delta v^2 + \delta w^2}{U_\infty ^2} \, {\text {d}}S \; = \; \int \limits _{w} \frac{\psi \, \omega }{U_\infty ^2} \, \mathrm {d}S. \end{aligned}$$

(8)

As one may notice, the longitudinal velocity gradients must be negligible in the wake plane for Eq. 8 to be valid. As a result, the wake plane must be evaluated sufficiently far away from the model, in a location where the mean flow is dominated by longitudinal vorticity. In the case of trailing vortices behind NACA and cambered airfoils, this condition has been found to be reasonably achieved between 0.5 and 1 chord downstream the trailing edge (Birch et al. 2004). Finally, turbulent stresses naturally vanish outside of the wake since they originate from shear. It is therefore possible to reduce the integration domain of the third integral on the right-hand side of Eq. 7 to the wake only, as well. In the end, the phenomenological total drag breakdown $C_D^{\text {Phen}}$ reads

$$\begin{aligned} C_D^{\text {Phen}} \; = \; C_{D}^{\text {Prof}} \; + \; C_{D}^{\text {Ind}} \; + \; C_{D}^{\text {Turb}} , \end{aligned}$$

(9)

where

$$\begin{aligned} C_{D}^{\text {Prof}} \;= & {} \; \frac{1}{S_{\text {ref}}} \int \limits _w \left[ - \frac{2}{\gamma M_\infty ^2} \frac{\delta P_i}{P_{i\infty }} + \left( M_\infty ^2 - 1 \right) \frac{\delta u^2}{U_\infty ^2} \right] \mathrm {d}S, \end{aligned}$$

(10)

$$\begin{aligned} C_{D}^{\text {Ind}} \;= & {} \; \frac{1}{S_{\text {ref}}} \int \limits _{w} \frac{\psi \, \omega }{U_\infty ^2} \; \mathrm {d}S, \end{aligned}$$

(11)

and

$$\begin{aligned} C_D^{\text {Turb}} \; = \; - \frac{2}{S_{\text {ref}}} \int \limits _{w} \frac{\rho }{\rho _\infty } \frac{\left\langle u' u' \right\rangle }{U_\infty ^2} \; \mathrm {d}S. \end{aligned}$$

(12)

As already stated, the integration domain of the phenomenological breakdown (9) is reduced to the actual wake w, while the control volume approach (3) requires an integration over the entire downstream plane ${\mathcal {S}}_1$ (with the exception of $C_D^{\text {Turb}}$ being in fact the same in both formulations). This particular feature of the phenomenological method makes it quite appealing experimentally speaking, as it drastically reduces the span of the domain to capture. There is however a trade-off with reducing the integration domain to the wake. Indeed, doing so focuses all the information scattered throughout space in a much smaller region, and especially in the viscous cores of the wake vortices. As a result, though the phenomenological method allows for smaller measurements domains, it requires a fine spatial resolution to accurately capture sharper velocity gradients.

Fig. 2

Overview of the stereo-PIV setup: (i) Quantel Evergreen laser; (ii) laser sheet. In order to discretize the axial gradients present in Eq. (13), three PIV planes have been subsequently shone at locations $x = c_{\text {ref}}$ (solid line), and $x = c_{\text {ref}} \pm \varDelta x$ (dashed lines); (iii) $5.5 \, {\text {Mpixels}}$ LaVision Imager sCMOS cameras; (iv) wake plane split into four $480 \times 300 \, {\text {mm}}^2$ frames, with a 50 mm overlap

2.3 Pressure calculation method

Inspecting Eqs. 5 and 10 above shows that the knowledge of both the static and stagnation pressure in the wake plane is required in order to evaluate drag using the mechanical and phenomenological approaches. Computing the pressure field from PIV velocity data, under the constraint of an incompressible flow is a long standing issue, which has received considerable attention in the past years (Van Oudheusden 2013; Rival and Van Oudheusden 2017). Note that in the more true to life case of a compressible flow, one may still compute the pressure field from velocity data, by invoking isentropic and isenthalpic relations, as put forward by Van Oudheusden et al. (2007). Owing to the low value of the free-stream Mach number $Ma_\infty = 0.10$, this particular study is restricted to the incompressible framework.

The pressure calculation strategy adopted here is based on the work of Jeon et al. (2018), and relies on integrating the pressure gradient of the Navier–Stokes equations

$$\begin{aligned} - \nabla P \; = \; \rho \left[ \mathbf {U} \cdot \nabla \mathbf {U} + \nabla \cdot \langle \mathbf {u}' \otimes \mathbf {u}' \rangle \right] \, - \, \mu \varDelta \mathbf {U}. \end{aligned}$$

(13)

The different terms composing the pressure gradient are calculated from the PIV measurements by spatial second order schemes. The pressure field is then obtained by minimizing a functional built on the difference of the pressure gradient based on the PIV measurements and the estimated pressure gradient, which is equivalent to solving a Poisson equation. The field is generally divided in sub-domains, based on the amplitude of the pressure gradient. The sequential pressure reconstruction is initiated from the outer domain, where the highest measurement accuracy is expected, hence where a reliable pressure reference can be taken. The pressure field in the other sub-domains is then computed by imposing Dirichlet boundary conditions stemming from the previously computed outer domain.

Once the mean static pressure is reconstructed, the pressure integration constant $P_{{\text {BC}}}$ is adjusted so that the average of the reconstructed pressure computed along the contour of the PIV domain coincides with the average of the static pressure computed from the isentropic relation

$$\begin{aligned} P_{\text {BC}} \; = \; P_\infty \left[ 1 \, + \, M_\infty ^2 \, \frac{\gamma - 1}{2} \left( 1 - \frac{\Vert \mathbf {U}\Vert ^2}{U_\infty ^2} \right) \right] ^{\gamma /(\gamma - 1)} \end{aligned}$$

(14)

at the same location. The local stagnation pressure in the downstream plane eventually ensues from applying the local isentropic and isenthalpic relations to the previously determined local static pressure, following

$$\begin{aligned} P_i \; = \; P \left[ \frac{\displaystyle 1 \, + \, M_\infty ^2 \, \frac{\gamma - 1}{2} \left( 1 - \frac{\Vert \mathbf {U}\Vert ^2}{U_\infty ^2} \right) }{ \displaystyle 1 \, + \, M_\infty ^2 \, \frac{\gamma - 1}{2} } \right] ^{- \gamma /(\gamma -1)}. \end{aligned}$$

(15)

Fig. 3

Mean flow field in the reference plane $x = c_{\text {ref}}$ for $\alpha = 9^{\circ }$ (left) and $\alpha = 18^{\circ }$ (right). The colormap outlines the longitudinal velocity component $U = \mathbf {U} \cdot \mathbf {e}_x$, while the vectors represent the transverse flow in the wake plane $\mathbf {U}_\perp = V \mathbf {e}_y + W \mathbf {e}_z$. The mean ratio of the transverse to longitudinal velocity $\Vert \mathbf {U}_\perp \Vert / U$ computed throughout the wake is indicated in the boxes

Fig. 4

Magnitude of the normal turbulent stresses in the reference plane $x = c_{\text {ref}}$ for $\alpha = 9^{\circ }$ (left) and $\alpha = 18^{\circ }$ (right)

3 Experimental apparatus and instrumentation

3.1 Wind-tunnel setup

This study was conducted on a model of the SACCON geometry, a generic flying wing configuration that was introduced within the framework of aircraft control and stability analyses (Loeser et al. 2010; Vicroy et al. 2010). This particular configuration was chosen here as it is known to induce complex vortical patterns above its upper surface at medium and high angles of attack (Roosenboom et al. 2012; Schütte et al. 2012). It is therefore an excellent case study to try and test wake integral methods. The particular model used here has a wingspan $b = 1 \, {\text {m}}$, a reference chord $c_{\text {ref}}$ = 0.31 m and a reference area $S_{\text {ref}} = 0.3253 \, {\text {m}}^2$. It was placed inside the L1 wind-tunnel of Lille’s ONERA center, whose dodecagonal test-section is 2.4 m wide. The free-stream velocity was fixed at $U_\infty$ = 35 m/s throughout the campaign, which corresponds to a free-stream Reynolds number $Re_\infty = \rho \, c_{\text {ref}} \, U_{\infty } / \mu = 1.1 \, 10^6$, and a free-stream Mach number $M\!a_\infty = U_\infty / \sqrt{\gamma r T_\infty } = 0.10$. Three different angles of attack $\alpha = 9^{\circ }, 13^{\circ }$ and $18^{\circ }$ were investigated. The wake was measured one chord away from the model’s wingtips (cf. Fig. 2). The maximum blockage, which was encountered for $\alpha = 18^{\circ }$, did not exceed 2%, hence no particular correction was applied to the data.

3.2 Measurement protocol

The stereo-PIV setup revolved around a dual cavity Nd:YAG Quantel Evergreen laser, which emitted at wavelength 532 nm with an output energy of 200 mJ per laser head, and two LaVision Imager sCMOS cameras with a 5.5 Mpixels resolution. The PIV images were processed using 32 $\times$ 32 ${\text {pixels}}^2$ interrogation windows, with an overlap of 50%, which resulted in velocity fields with a spatial resolution of 3 mm. Time averages were performed over 5000 consecutive frames acquired at 5 Hz. This relatively low acquisition frequency was chosen in order to get statistically independent PIV snapshots, while still keeping a reasonable acquisition time (around 15 mn). The resulting dispersion on the mean flow was checked a posteriori for all cases, and was found to be of the order, or better than $0.1\%$ of $U_\infty$. Due to its large span, the wake was split into four $480 \times 300 \, {\text {mm}}^2$ overlapping PIV frames, with an overlap of 50 mm between adjacent frames. The cameras were fixed on a motor driven table that enabled a precise positioning of the different frames with respect to each other in space. In order to minimize the impact of edge effects when combining all frames together, the outer most frames were positioned such that they would contain the entire tip vortex. Finally, the longitudinal gradients present in Eq. 13 were discretized by considering two additional planes, respectively located at $x = c_{\text {ref}} \pm \varDelta x$, where $\varDelta x = 30 \, {\text {mm}}$.

Subsequently to stereo-PIV measurements, the left half of the model’s wake was surveyed using a five-hole probe. In order to reduce the acquisition time, the probe was mounted on a traversing system which swept across the wake at the constant speed of 5 mm/s. Data points were recorded every 2 mm, such that the characteristic traveling time $\tau _{\text {p}}$ of the probe between two measurements is $\tau _{\text {p}}$ = 0.4 s. By comparison, the characteristic time of the flow $\tau _{\text {u}}$ is reasonably associated to the turnover time of the tip vortex following $\tau _{\text {u}} = \ell / \Vert \mathbf {U_\perp } \Vert$, where $\ell$ is the size of the tip vortex, and $\Vert \mathbf {U}_\perp \Vert$ the magnitude of the cross-flow. Based on the data given in Fig. 3, $\tau _{\text {u}} \sim 0.03 \, {\text {s}}$, which is one order of magnitude smaller than $\tau _{\text {p}}$. As a result, the five-hole probe experiences many turnover times during its travel time from one measuring point to another. It is therefore reasonable to assume that it experiences a statistically steady flow despite its motion.

Alongside the stereo-PIV and five-hole probe measurements, the lift, drag and side forces, as well as the rolling, pitching and yawing moments were measured using an in-house force balance. The balance’s dynamic range for the lift and drag components was ± 5890 N and ± 1730 N respectively, with an uncertainty lower than 1/1000th of the balance's dynamic range.

3.3 General characterization of the wake

Figures 3 and 4 present the overall structure of the flow for $\alpha = 9^{\circ }$ and $18^{\circ },$ respectively. The mean flow is given in Fig. 3, in which the contour plot gives the mean streamwise velocity component, while the vectors illustrate the velocity field in the plane normal to the stream. Since the wake is slightly asymmetrical, all graphs have been evaluated on the left half of the model, for the sake of a fair comparison. The right plots of Figs. 3 and 4 are in fact mirror images of the actual flow.

For $\alpha =9^{\circ }$, the wake features a small vortex core, which forms at the very tip of the model around $\vert y \vert = 0.45 \, {\text {m}}$. This primary vortex is accompanied by a narrow vortex sheet, which develops as the flow smoothly passes around the body of the model. At this setting, the level of turbulent fluctuations is negligible, and reaches only a couple of percents in the very core of the tip vortex. By contrast, the wake for $\alpha = 18^{\circ }$, is dominated by a large vortex in the form of a kidney bean. This particular shape is typical of several unsteady vortices interacting with each other. As a matter of fact, Schütte et al. (2012) showed that for $\alpha = 18^{\circ }$, the tip vortex merges with a secondary vortex originating from the apex of the model. The unsteadiness of this process is confirmed by the maps of turbulent fluctuations displayed in Fig. 4, which shows a high level of normal turbulent stresses in the tip vortex region, reaching up to 10% of the free-stream kinetic energy.

In all cases, a strong cross-flow is induced in the vicinity of the tip vortices, whose intensity reaches, in average up to 10% for $\alpha = 9^{\circ }$ and 20% for $\alpha = 18^{\circ }$.

4 Experimental methods

4.1 Accuracy of the reconstructed pressure fields

The crux of the matter relies here in reconstructing the static and stagnation pressure fields in the downstream plane, from PIV measurements. In order to assess how reliable these reconstructed fields are, Figs. 5 and 6 compare streamwise profiles of PIV-reconstructed static and stagnation pressure to profiles stemming directly from five-hole probe wake measurements. In both figures, the profiles are plotted along the left side of the model, as five-hole probe measurements were available only there. Figures 5 and 6 strikingly show that the reconstructed static and stagnation pressure fields compare quite differently to their five-hole probe counterparts. Indeed, the reconstructed static pressure (Fig. 5) is systematically lower than the direct probe measurements, while the reconstructed stagnation pressure (Fig. 6) appears to be much closer to the probe measurements, except for $\alpha = 18^{\circ }$.

The discrepancy between the static and stagnation pressure reconstructed from PIV data, and their directly measured counterparts is better quantified by defining $C_{\text {p}}$ and $C_{\text {Pi}}$ as

$$\begin{aligned} C_{\text {P}} \; = \; \int \limits _{{\mathcal {S}}_1} \left( P_\infty - P\right) \, {\text {d}}y \, {\text {d}}z, \end{aligned}$$

(16)

and

$$\begin{aligned} C_{\text {Pi}} \; = \; \int \limits _{{\mathcal {S}}_1} \left( P_{i\infty } - P_i\right) \, {\text {d}}y \, {\text {d}}z, \end{aligned}$$

(17)

and subsequently the relative differences $\epsilon _P$ and $\epsilon _{\text {Pi}}$

$$\begin{aligned} \epsilon _{\text {P}} \; = \; \frac{\left| {C_{\text {P}}}^{\text {5HP}} \, - \, {C_{\text {P}}}^{\text {PIV}} \right| }{{C_{\text {P}}}^{\text {5HP}}}, \end{aligned}$$

(18)

and

$$\begin{aligned} \epsilon _{\text {Pi}} \; = \; \frac{\left| {C_{\text {Pi}}}^{\text {5HP}} \, - \, {C_{\text {Pi}}}^{\text {PIV}} \right| }{{C_{\text {Pi}}}^{\text {5HP}}}, \end{aligned}$$

(19)

where superscripts “5HP” and “PIV” refer to integrals evaluated with five-hole probe and PIV measurements, respectively.

Table 1 Relative differences between $C_{\text {P}}$ and $C_{\text {Pi}}$ computed with five-hole probe data and PIV measurements

Values of $\epsilon _{\text {P}}$ and $\epsilon _{P_i}$ are compared in Table 1 for all angles of attack investigated. According to this table, the reconstructed stagnation pressure is one order of magnitude more accurate than the static pressure at low angles of attack, despite the fact that its computation uses a rather crude estimate for the static pressure by virtue of Eq. 15. This observation suggests that underestimating the static pressure only weakly affects the stagnation pressure prediction.

This behavior is further investigated with Fig. 7, which compares two different methods of computing the stagnation pressure, based on Eq. 15. The first method consists in deducing $P_i$ from the static pressure, as done previously, while the second method consists in computing $P_i$ by imposing a uniform pressure throughout the wake plane. This figure shows that the global features of the stagnation pressure field can indeed be captured with the velocity field alone. However, in order to capture the stagnation pressure losses in the core of the tip vortex, it is preferable to compute $P_i$ from a prior computed, albeit coarse, static pressure field.

Fig. 5

Spanwise profiles of static pressure integrated vertically. Solid lines refer to direct pressure measurements with a five-Hole probe. Dashed lines refer to the reconstructed static pressure based on PIV measurements fed into Eq. 13

Fig. 6

Spanwise profiles of stagnation pressure integrated vertically. Solid lines refer to direct pressure measurements with a five-hole probe. Dashed lines refer to the reconstructed stagnation pressure based on PIV measurements fed into Eqs. 13 and 15

Fig. 7

Different options for the computation of the stagnation pressure. The solid line is associated to the direct five-hole probe measurements; The dashed line refers to $P_i$ computed from Eq. 15 fed with the prior computed static pressure P; the dash-dotted line shows the result of computing $P_i$ with Eq. 15 in which an isobar wake plane at $P_\infty$ is imposed

4.2 Wake identification

As accurate as the stagnation pressure estimate may be (whether directly measured or reconstructed), it still yields poor global results once integrated throughout the downstream plane, as stagnation pressure losses do not exactly vanish outside of the wake due to noise and uncertainties. It thus becomes necessary to extract the wake from its surrounding to enforce that stagnation pressure losses are confined there.

The wake is identified by investigating the stagnation pressure distribution function, which presents a sharp discontinuity. A threshold value on the maximum admissible stagnation pressure loss is then imposed based on the value at which this discontinuity occurs (cf. the dotted line in Fig. 8). Figure  9 shows the outer envelop of all the points lying beneath the aforementioned threshold, and confirms that the discontinuity in the stagnation pressure’s distribution function indeed coincides with the physical boundaries of the wake. From here on, the integration of the stagnation pressure is limited to this boundary. The procedure above is illustrated here for $\alpha = 13^{\circ }$, but works equally well at other angles of attack.

Fig. 8

Distribution function of $P_i/P_{i\infty }$ for $\alpha = 13^{\circ }$. The dotted line locates the discontinuity in the histogram, whose argument is taken as the threshold value between the actual wake and its surrounding

Fig. 9

Wake contour for $\alpha = 13^{\circ }$, as identified by the threshold value found in Fig. 8. This figure showcases the importance of cropping the wake’s surrounding before integration, as the latter introduces artificial stagnation pressure losses, which have no physical meaning

4.3 Sensitivity to spatial resolution

Tables 2 and 3 show the sensitivity of the mechanical and phenomenological methods to the spatial resolution of the PIV data, which is given by the size of the interrogation windows (WS). Unsurprisingly, the two drag contributions that appear to be the most sensitive to the spatial resolution are those involving the reconstructed pressure field, namely $C_D^{\text {Press}}$ and $C_D^{\text {Prof}}$, with a variation of forty to fifty drag counts between the highest and lowest resolutions (one drag count represents a $10^{-4}$ variation of the drag coefficient). Furthermore, decreasing the spatial resolution affects the turbulent and convective contributions by about 10 and 30 drag counts, respectively, as a result of $C_D^{\text {Turb}}$’s and $C_D^{\text {Conv}}$’s integrands missing the finer flow structures. Interestingly, the induced drag term is the least sensitive, and shows a variation of only 6 drag counts between the finest and coarsest cases, despite this term representing the velocity gradients in the plane perpendicular to the stream.

Table 2 Sensitivity of the mechanical decomposition to spatial resolution, for the $\alpha = 13^{\circ }$ case

Table 3 Sensitivity of the phenomenological decomposition to spatial resolution, for the $\alpha = 13^{\circ }$ case

4.4 Sensitivity to longitudinal discretization

Earlier work focused on reconstructing a pressure field from planar PIV highlighted the necessity to evaluate the derivatives in the out of plane direction (cf. for instance Van Oudheusden (2013)) in order to get the most accurate predictions. The purpose of the following test is to assess the impact of the streamwise gradients on the global drag predictions. To do so, we consider the three following schemes for the approximation of $\partial _x \mathbf {u}$ in Eq. 13, where for any function $\mathbf {u}(x,y,z)$:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial \mathbf {u}}{\partial x} \; = \; 0 \; + \; O(1) \\ \frac{\partial \mathbf {u}}{\partial x} \; = \; \frac{\mathbf {u}(c_{\text {ref}} + \varDelta x) - \mathbf {u}(c_{\text {ref}})}{\varDelta x} \; + \; O(\varDelta x)\\ \frac{\partial \mathbf {u}}{\partial x} \; = \; \frac{\mathbf {u}(c_{\text {ref}} + \varDelta x) - \mathbf {u}(c_{\text {ref}}-\varDelta x)}{2 \varDelta x} \; + \; O(\varDelta x^2) \end{array}\right. }. \end{aligned}$$

(20)

The first scheme is a shorthand for neglecting longitudinal velocity gradients altogether. In the following, an interrogation window of size $32 \times 32 \, {\text {pixels}}^2$ is used. Practically speaking, $\varDelta x$ = 30 mm is taken to be the spacing between adjacent PIV planes, while $x = c_{\text {ref}}$ refers to PIV measurements obtained in the middle plane located one chord away from the model’s wingtips (cf. Fig. 2).

Table 4 shows that in the case at hand, neglecting longitudinal velocity gradients in the pressure reconstruction algorithm has a somewhat larger effect on $C_D^{\text {Press}}$, than $C_D^{\text {Prof}}$, with a variation of up to thirteen drag counts for the former vs. four for the latter. This again seems to indicate that the stagnation pressure is a more robust quantity than the plain static pressure. In any case, the sensitivity of either $C_D^{\text {Press}}$ or $C_D^{\text {Prof}}$ to the discretization scheme appears to be marginal, when compared against their respective sensitivity to the spatial resolution of the data, which suggests that it is the latter that should be given priority when computing loads from wake data.

Table 4 Sensitivity of $C_D^{\text {Press}}$ and $C_D^{\text {Prof}}$ to the order of the discretization scheme used in Eq. (13), for the $\alpha = 13^{\circ }$ case. Results are obtained with PIV interrogation windows of size $32 \times 32 \, {\text {pixels}}^2$

5 Results and discussion

To begin with, Table 5 gives the global lift and drag coefficients measured by the force balance, which will be used as a reference throughout the remainder of the text. The relatively high measurement dispersion of 8% on the drag coefficient for $\alpha = 9^{\circ }$ comes from the low drag value occurring at this angle of attack, with respect to the balance’s dynamic range.

Table 5 Reference lift ($C_L^{\text {Bal}}$) and drag ($C_D^{\text {Bal}}$) coefficients measured using a force balance, for $\alpha = 9^{\circ }$, $13^{\circ }$ and $18^{\circ }$

Tables 6 and 7 display the global drag predictions and their breakdown, stemming from the mechanical (Eq. 3) and phenomenological (Eq. 9) approaches, as well as the relative difference between the global predictions and the balance measurements. According to these tables, the mechanical and phenomenological methods yield global drag predictions that all lie within 10% of the balance measurements. Furthermore, the mechanical breakdown tends to underestimate the balance measured drag coefficients. (The overshoot measured for $\alpha =9^{\circ }$ likely results from the large dispersion on the balance measurement.) In light of Fig. 5, this behavior probably comes from the inaccurate pressure reconstruction from PIV measurements, which tends to miss the amplitude of the depressions occurring inside the different flow structures found throughout the wake. By comparison, the drag coefficients computed using the phenomenological decomposition systematically overestimate those measured with the force balance.

Table 6 Total mean drag predictions and their breakdown, as given by the mechanical approach fed with PIV measurements. Computations are performed using the finest PIV resolution of 3 mm ($32 \times 32 \, {\text {pixels}}^2$ interrogation windows)

Table 7 Total mean drag predictions and their breakdown, as given by the phenomenological approach fed with PIV measurements

Table 8 Lower bound for the induced drag coefficient following from the lifting line theory applied to a finite wing whose aspect ratio is similar to that of the model at hand

The soundness of the induced drag coefficients given in Table 7 may be checked by comparing them to those deduced from the lifting line theory. While the latter does not strictly apply to the swept and twisted SACCON wing of this study, it can still be used to infer a lower bound for the induced drag coefficient. Indeed, according to the lifting line theory (c.f. for instance Anderson (1991)), the induced drag acting over a finite wing is minimum when it experiences an elliptical distribution of lift. The induced drag can then be expressed in terms of the total lift coefficient via

$$\begin{aligned} C_{D}^{\text {Ind}} \; = \; \frac{{C_L}^2 \, S_{\text {ref}}}{\pi \, b^2}. \end{aligned}$$

(21)

Table 8 provides the induced drag coefficient predicted using the lifting line theory (i.e., Eq. 21 and the balance data provided in Table 5). Comparing Tables 7 and 8 shows a reasonable agreement between the induced drag coefficients predicted by the lifting line theory and those measured by PIV. The maximum discrepancy is found to monotonically increase with the angle of attack (that is to say with the complexity and size of the wake), without exceeding 10% in the worst case ($\alpha = 18^{\circ }$). This behavior is sensible, given the fact that the lifting line theory assumes a wake originating from an aircraft’s trailing edge, while the swept SACCON geometry introduces secondary vortices originating from the leading edge of the model, which are bound to increase the total induced drag.

Table 7 sheds some light on the relative competition between the physical processes at play. In particular, the phenomenological breakdown displays a reversal in the competition between the induced and the profile drag, with the former dominating at low angles of attacks ($\alpha =9$ and $13^{\circ }$), and the latter at $\alpha = 18^{\circ }$. By contrast such a reversal does not transpire in the mechanical breakdown, for which the convective term always dominates. This observation may be physically interpreted in the light of Schütte et al.’s study Schütte et al. (2012), which shows that $\alpha =18^{\circ}$ coincides with the tip vortex being at the onset of bursting. From this point onward, the tip vortex progressively detaches from the upper surface of the model, therefore decreasing lift, hence also decreasing induced drag. Simultaneously, the resulting flow separation promotes pressure drag, which leads to an increase in profile drag. Such observations can prove quite valuable when optimizing an airframe for a particular flight regime, since tackling induced or profile drag requires radically different strategies. For instance, optimizing profile drag hints at reducing skin friction or delaying the flow separation, while reducing induced drag is usually tackled by preventing the formation of trailing vortices with wingtip devices. Inferring such strategies based on the mechanical decomposition alone would not be possible, since the competition between its different contributions may not automatically translate into physically interpretable drag sources.

The previous argument is illustrated with a more local point of view in Figs.  10 and 11, which present spanwise profiles of mechanical and phenomenological drag, obtained by, respectively, integrating Eqs. 3 and 9 along the z coordinate. Here, the cases $\alpha = 9$ and $18^{\circ }$ are considered. As before, all graphs are evaluated along the left half of the wing, the right parts of Figs. 10 and 11 being mirror images. For $\alpha = 9^{\circ }$, the phenomenological decomposition (Fig. 10, right) concentrates drag in a narrow region of the wake which coincides with the location of the tip vortex’s core. By contrast, the mechanical method (Fig. 10, left) associates drag for some part at the location of the tip vortex, but mostly along the model’s centerline, where a deficit in the longitudinal velocity component appears, as mean kinetic energy has been redistributed into the cross-flow. For $\alpha =18^ {\circ }$ however, the region of the wake mainly associated to the momentum deficit is clearly associated to the tip vortex. One must remain cautious when interpreting the wake in terms of drag production, since the latter only gives a picture of what the flow encountered along the model’s surface, where drag was actually produced via pressure and skin friction. It can nonetheless yield some insight, especially in the presence of dominating flow structures such as here.

Fig. 10

Spanwise profiles of drag contributions for $\alpha = 9^{\circ }$. (Left) mechanical decomposition: each black line represents a particular term of Eq. 3 integrated along z. (Right) phenomenological decomposition: each black line represents a particular term of Eq. 9 integrated along z. For both cases, the red line represents the cumulative integral of all terms: the reading at $y = 0$ gives the total drag produced on one half of the wing

Fig. 11

Spanwise profiles of drag contributions for $\alpha = 18^{\circ }$. (Left) mechanical decomposition: each black line represents a particular term of Eq. 3 integrated along z. (Right) phenomenological decomposition: each black line represents a particular term of Eq. 9 integrated along z. For both cases, the red line represents the cumulative integral of all terms: the reading at $y = 0$ gives the total drag produced on one half of the wing

Finally, Figs. 10 and 11 show the cumulative integral of all the different contributions to the mechanical and phenomenological breakdown, where the value read on the model’s centerline corresponds to the total drag produced by one half of the model. It should be observed that though the mechanical and the phenomenological methods translate in radically different spanwise profiles, they eventually integrate to similar values (within their respective accuracy), thus confirming that the two methods described in this paper are in fact two different points of view of the same phenomenon.

To put the current work in perspective with the existing literature, the global drag predictions obtained here (whether using the mechanical or phenomenological method) appear to be at par with those published in earlier studies dealing with the same issue. Indeed, as far as wake surveys using the phenomenological decomposition fed with five-hole probe measurements is concerned, Brune (1994) reports a relative difference better than 1% with respect to balance measurements on the drag prediction of a 1.80 m long rectangular wing, while Crowder et al. (1997) reports a 13% difference between balance measurements and the wake drag prediction of civil aircraft model flying at $Ma = 0.86$. In this case, the main source of error is attributed to the method not accounting for flow compressibility effects.

Regarding load evaluation using the mechanical approach fed with PIV data, Ragni et al. reports drag values that lie within 10% of those obtained using a Pitot wake rake behind a NACA0015 airfoil. In addition, De Kat and Bleischwitz (2016) measured drag coefficients from a wake survey behind a flat plate, and reported drag coefficients within 30% of direct force measurements. The latter authors computed the total mean drag based on Eq. (2) fed with a flow field reconstructed from PIV measurements of a sub-region of the wake. The flow in the entire downstream plane ${\mathcal {S}}_1$ was then inferred by invoking its symmetry with respect to the centerline, and its solenoidality. They thus attributed the relatively large discrepancies to the fact that they did not have access to the entire flow field. In that respect, the phenomenological method would perhaps be more suitable, as it naturally vanishes outside of the wake. Based on the present work however, another aspect that may have had an impact in their results might be their assumption of an exactly symmetrical wake. Though reasonable in a first approximation, Fig. 9, and the cumulative values of Figs. 10 and 11 which are systematically lower than half the total drag coefficient give evidence that this may not always be exactly true.

6 Conclusion

This paper benchmarks two different expressions of the control volume approach, using stereo-PIV data acquired in the complex wake of a finite-size wing: the phenomenological approach, written in terms of the stagnation pressure, and the mechanical approach, which uses the static pressure. The former method expresses drag in terms of profile and induced drag, while the latter expresses drag in terms of the surrounding flow’s properties. Until now, the phenomenological decomposition was numerically evaluated with five-hole probe measurements.

In the particular case at hand, we have shown that the mechanical and phenomenological methods perform similarly, as they yield integrated drag coefficients always within 10% of the balance measurements. Furthermore, we have illustrated how the phenomenological method can be used to physically interpret the drag sources at play, which can ultimately be used to optimize an airframe’s geometry for a particular flight regime. By contrast, the mechanical approach does not allow one to distinguish between the different physical origins of drag, as it entangles the convective and pressure effects together.

As far as the implementation of the methods is concerned, this study highlights by comparing the PIV-reconstructed static and stagnation pressure to direct five-hole probe measurements, that the latter is accessible with reasonable accuracy, although the reconstructed static pressure underestimates the depression associated to the flow features occurring throughout the wake. In that respect, the phenomenological method appears to be particularly well suited to the PIV investigation of aircraft wakes containing intense wake vortices, as it enables one to reduce the integration domain based on physical arguments alone.