Coupling temporal and spatial gradient information in high-density unstructured Lagrangian measurements

Abstract

Particle tracking velocimetry (PTV) produces high-quality temporal information that is often neglected when computing spatial gradients. A method is presented here to utilize this temporal information in order to improve the estimation of spatial gradients for spatially unstructured Lagrangian data sets. Starting with an initial guess, this method penalizes any gradient estimate where the substantial derivative of vorticity along a pathline is not equal to the local vortex stretching/tilting. Furthermore, given an initial guess, this method can proceed on an individual pathline without any further reference to neighbouring pathlines. The equivalence of the substantial derivative and vortex stretching/tilting is based on the vorticity transport equation, where viscous diffusion is neglected. By minimizing the residual of the vorticity-transport equation, the proposed method is first tested to reduce error and noise on a synthetic Taylor–Green vortex field dissipating in time. Furthermore, when the proposed method is applied to high-density experimental data collected with ‘Shake-the-Box’ PTV, noise within the spatial gradients is significantly reduced. In the particular test case investigated here of an accelerating circular plate captured during a single run, the method acts to delineate the shear layer and vortex core, as well as resolve the Kelvin-Helmholtz instabilities, which were previously unidentifiable without the use of ensemble averaging. The proposed method shows promise for improving PTV measurements that require robust spatial gradients while retaining the unstructured Lagrangian perspective.

1 Introduction

The development of aerodynamic or hydrodynamic systems requires a detailed understanding of the relationship between structural features on immersed bodies, such as profile shape or flexibility, and the resulting vortical flow field. Often these design features are used to manipulate highly-separated three-dimensional vortical flows, such as the unsteady vortex rings investigated by Shadden et al. (2006), similar to those found in jellyfish propulsion. In particular, it was found that Lagrangian analysis was much more effective at capturing the flow topology, especially at greater degrees of unsteadiness. Fully characterizing such flows not only requires determining velocity gradients familiar to Eulerian analysis, but also the transport of vorticity-containing mass over time, as shown in Fig. 1. Particle-tracking velocimetry (PTV) techniques, especially modern high-density methods such as Shake-the-Box (STB, a.k.a. 4D-PTV) described by Schanz et al. (2016), are ideally suited to capturing both the required velocity field, as well as the desired Lagrangian flow history. Several techniques exist to determine the velocity gradient, vorticity or pressure at a very high resolution from dense velocimetry data. These methods include FlowFit (see Gesemann et al. 2016) or VIC+ (see Schneiders and Scarano 2016). In both VIC+ and FlowFit, physical constraints on the system are used to improve the accuracy of velocity interpolation, such as through penalizing non-zero divergence in FlowFit. VIC+ in particular makes use of the vorticity transport equation as a physical constraint, and utilizes the high-quality substantial derivative available from PTV. This follows previous developments for particle image velocimetry (PIV) where physical constraints were able to leverage high spatial resolution to improve temporal resolution. This work is exemplified by Scarano and Moore (2012), where the spatial resolution of tomographic-PIV was used to estimate advection between velocity snapshots to super-sample data beyond the traditional Nyquist criterion. Alternatively, Jeon et al. (2014) demonstrated the use of high temporal resolution in time-resolved PIV to improve spatial resolution.

Fig. 1

a A vortex-pair forming on a flat plate is illustrated in the familiar Eulerian frame. b The same vortex-pair can be studied in a Lagrangian frame: at $t=t_1$ two control masses gain vorticity through the leading and trailing-edge shear layers, respectively, and are tracked forward in time into the vortex core at $t=t_2$. In this way the Lagrangian data can be used to determine the origin of vorticity-containing mass (by tracking structures backwards in time), or to study the evolution of mass gaining vorticity through time (by tracking mass through a shear layer)

The aerodynamic and hydrodynamic forces of highly-separated vortical flows are often analyzed with respect to the topology of the flow, for instance with Lagrangian coherent structures as demonstrated in Rockwood et al. (2016). PTV inherently provides this Lagrangian perspective on the development of the flow, as was illustrated above in Fig. 1. For instance, fluid that passes over a vorticity source like the leading-edge shear layer in Fig. 1 can be tracked forward along a pathline to study the evolution of that mass, in this case into a vortex. Meanwhile, the mass in this vortex can be tracked backwards in time to identify the source of this vorticity. Additionally, the high-quality substantial derivative determined from PTV dramatically improves the quality of pressure fields derived from the velocity field, as described by Neeteson and Rival (2015) and Neeteson et al. (2016). Wolf et al. (2013) also noted that conducting a Lagrangian-frame analysis alongside familiar Eulerian techniques yielded unique insight into vortex entrainment. However, most available high-resolution techniques for determining spatial gradients do so on the familiar Eulerian grid, while averaging techniques for Lagrangian data smooth away small-scale flow structures. Therefore, with the motivation of maintaining the intrinsic transport information of a pathline, the current study proposes a high-resolution method for determining derived properties natively on unstructured Lagrangian data, without resorting to averaging multiple runs.

In order to evaluate the robustness of the proposed methodology, it is applied to two test cases: First, a synthetic data set, for which true values of the velocity gradient tensor are known a priori, is used to verify that the method reduces gradient estimation error in the process of reducing noise. Second, an experimental 4D-PTV data set is used to evaluate the increase in fidelity and reduction in noise when the method is applied to real experimental data. The details of the vorticity-correction technique are presented next.

2 Background

By directly tracking individual particles, PTV does not experience the loss of fidelity that occurs when taking the average displacement across an interrogation window, as described by Kaehler et al. (2012). Furthermore, by collecting data along a pathline, high-quality temporal information is obtained, especially in the form of substantial derivatives. However, if one wishes to maintain the unstructured Lagrangian description of the flow, there are limited methods for computing spatial gradients. Among them there are regression-based methods that, for example, minimize the residual of an overdetermined set of directional derivatives, as discussed by Meyer et al. (2001). Alternatively, there are weighted-averaging techniques that calculate the gradient as a weighted-sum of local derivatives, as discussed by Correa et al. (2011).

In either of the above methods, individual outliers or poor spatial resolution can have a substantial effect on the value of gradients computed at any given point. The effect of individual outliers is mitigated from the Lagrangian nature of PTV measurements. Mitigating these effects of poor gradient estimations more generally can be accomplished by limiting how quickly such gradients can change (Lipschitz continuity), or by forcing the gradient to exist only within a certain bound (see Bunin et al. 2013). However, applying these constraints aggressively can reduce the fidelity of the computed gradient, especially if there is little a priori information about appropriate gradient magnitudes. Therefore, inspired by the use of physical constraints in the higher-order interpolation of Eulerian velocimetry data, we propose a method for filtering an initial gradient estimate on unstructured data by enforcing physical equations of motion. We propose the use of the vorticity-transport equation as a physical constraint, as it utilizes the high-quality temporal information along a pathline (the substantial derivative of vorticity). The transport equation is also a function of every component of the velocity gradient tensor, allowing the optimization of every component of the tensor simultaneously. The vorticity-transport equation takes the following form:

$$\begin{aligned} \dfrac{\text {D}\mathbf {\omega }}{\text {D}t}= (\mathbf {\omega }\cdot \nabla )\mathbf {U}+\nu \nabla ^2\mathbf {\omega } \ , \end{aligned}$$

(1)

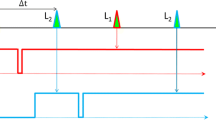
where the terms from left to right are the substantial derivative of vorticity $\omega$, vortex stretching/tilting, and the viscous diffusion of vorticity, respectively. In this study we will be neglecting viscous diffusion, under the assumption that the timescales of viscous diffusion are much greater than that of the measurement given a moderate Reynolds number. In order to cast Eq. (1) onto a set of unstructured Lagrangian data, we will introduce nomenclature described in Fig. 2. Here, N pathlines are enumerated by the counter p, while each pathline is tabulated in the vector $\mathbf {L}$, such that the number of frames in which a particle is observed is denoted $\mathbf {L}(p)$. At each timestep along a pathline, the position $\mathbf {X}$, velocity $\mathbf {U}$ and acceleration $\mathbf {a}$ of each particle are known for i timesteps. We will denote the components of these vectors with j.

Fig. 2

A schematic of one of N pathlines acquired within a PTV data set. The number of timesteps within each pathline are contained within the $1\times N$ vector array $\mathbf {L}$, while the pathlines themselves are enumerated by counter p. As such, the number of timesteps in which the current pathline is observed is given by $\mathbf {L}(p)$. The timesteps along pathline p are enumerated by the counter i, and at each timestep the three-dimensional position $\mathbf {X}(p,i)$, velocity $\mathbf {U}(p,i)$ and acceleration $\mathbf {a}(p,i)$ have been measured. With this data set, the velocity-gradient tensor $\nabla \mathbf {U}(p,i)$ is to be calculated

The vorticity-transport equation must have no residual at any point or time, and therefore we can estimate the quality of our gradient estimations by looking at the residual of the equation at any point:

$$\begin{aligned} R(p,i)=\sum _{j=1}^{3}\left( \dfrac{\text {D}{\omega }_j(p,i)}{\text {D}t}-(\mathbf {\omega }(p,i)\cdot \nabla ){u_j}(p,i)\right) ^2 \ . \end{aligned}$$

(2)

Rather than attempting to minimize this residual at each point individually, the maximum amount of temporal information can be transferred to the spatial gradient by minimizing this residual across an entire pathline simultaneously:

$$\begin{aligned} O=\sum \limits _{i=1}^{\mathbf {L}(p)}R(p,i)=\sum \limits _{i=1}^{\mathbf {L}(p)}\left[ \sum \limits _{j=1}^{3}\left( \dfrac{\text {D}{\omega }_j(p,i)}{\text {D}t}-(\mathbf {\omega }(p,i)\cdot \nabla ){u_j}(p,i)\right) ^2\right] \ . \end{aligned}$$

(3)

As an added practical benefit, this formulation operates pathline by pathline, resulting in a straightforward implementation. Recently, Schneiders et al. (2016) demonstrated a novel velocity interpolation technique that utilized full-particle trajectories in order to improve the fidelity of velocity field reconstructions at a single snapshot. In particular, increased information gleaned from long paths showed a clear improvement in velocity reconstruction fidelity. The current study also benefits from the use of long track information, as the optimization at any given point relies in part on the optimization both upstream and downstream of that point along a given pathline. In this way, a point with a poor initial velocity gradient estimate can benefit from better initial estimates at neighbouring points along the pathline. At this point we wish to find the velocity gradient $\nabla \mathbf {U}(p,i)$ along the entire pathline the minimizes O, given our initial guess. There are many ways to perform this optimization, but as a proof of concept we will use a simple gradient descent method. $\nabla O$ is determined with respect to all elements of $\mathbf {U}(p,i)$. O is then minimized by iteratively adjusting each individual element of $\nabla \mathbf {U}(p)$ along the direction $\nabla O$ by a step $\alpha$:

$$\begin{aligned} \nabla \mathbf {U}(p)_{k+1}=\nabla \mathbf {U}(p)_{k}-\alpha \nabla O \ . \end{aligned}$$

(4)

The individual components of velocity determined from particle tracking are unchanged. The above optimization scheme requires an initial estimate of the velocity gradient tensor to operate on. There are many methods to produce such an initial estimate. Here, we follow the method of Meyer et al. (2001), by minimizing the residual of an overdetermined set of directional derivatives.

The procedural order to implement this gradient optimization method varies slightly from the conceptual order described above. Given particle tracking data, implementing the above-described method would take the following order:

• 1. An initial estimate of the velocity gradient tensor is produced, across the entire set of particles at each timestep, using an established method, such as from an overdetermined set of directional derivatives (see: Meyer et al. 2001), weighted-averaging technique (see: Correa et al. 2011), or interpolation.

• 2. The data set is separated into pathlines, such that each pathline has $9\times \mathbf {L}(p)$ velocity gradient components to be adjusted.

• 3. These $9\times \mathbf {L}(p)$ velocity gradient components are evaluated based on the objective function in Eq. (3).

• 4. The gradient of this objective function is determined by making small adjustments to the $9\times \mathbf {L}(p)$ velocity gradient components.

• 5. New values of the velocity gradient components are determined using a steepest descent optimization following Eq. (4) until a local optimum of the objective function is found.

It is worth noting that, given an initial estimate is available, this optimization can be performed on any track individually without any reference to other particle tracks.

In the following section, the above methodology will be evaluated on a synthetic set of pathlines in order to have access to “true” reference values, and evaluate error reduction. Following this evaluation, the methodology will be implemented on experimental data to both evaluate noise reduction on real data, and to demonstrate Lagrangian analysis.

3 Numerical test case: dissipating Taylor–Green vortex

Since a physical measurement would not provide any insight into error reduction for the proposed methodology, the initial evaluation presented here utilizes a synthetic data set. A dissipating Taylor–Green vortex field in three dimensions is used for our test case (see Taylor and Green 1937). The data set for the Eulerian field was generated using a pseudo-spectral code whose formulation and validation is briefly described below. Simulated particles that perfectly follow the flow were advected through this domain, and Gaussian synthetic noise was added to the particle positions to simulate measurement error. Using the mean frame-to-frame displacement as a reference value, random displacements of between 0 and 3% were applied to each particle. This is comparable to the reconstruction quality of experimental techniques such as SMART (0.2 px error over 6 px frame-to-frame displacement; see Schanz et al. (2016). Particle positions were subsequently regularized using a five-snapshot, second-order polynomial fit. The error was subsequently evaluated both before and after applying the proposed methodology. The results for this synthetic test case described below, following a brief description of the computational method.

3.1 Computational methodology

For the dissipating Taylor–Green vortex, the following incompressible form of continuity and momentum equations are solved:

$$\begin{aligned} \frac{\partial u_i}{\partial x_i}= & {} \,0, \end{aligned}$$

(5)

$$\begin{aligned} \frac{\partial u_i}{\partial t} + \frac{\partial (u_i u_j)}{\partial x_j}= & {} -\frac{\partial p}{\partial x_i} + \frac{1}{Re_c} \frac{\partial ^2 u_i}{\partial x_j \partial x_j}, \end{aligned}$$

(6)

where $u_1,u_2,u_3$ are the velocity components in the $x_1,x_2,x_3$ directions, respectively. Note that the equations have become non-dimensionalized by a characteristic length-scale $L_c$ and velocity-scale $U_c$. Thus, the Reynolds number that appears in the viscous term is defined as $Re_c = U_c L_c/\nu$, where $\nu$ is the kinematic viscosity of the fluid.

Equations (5) and (6) are solved in spectral (Fourier) space using a pseudo-spectral method (see Orszag 1969, 1972). To remove the aliasing error, the 3/2 rule proposed by Orszag (1971) was adopted. Periodic boundary conditions are applied in all three directions with a domain size of $2\pi \times 2\pi \times 2 \pi$. The governing equations are integrated in time using fractional step method (see Kim and Moin 1985) with a second-order, three-step Runge-Kutta time-advancement scheme.

The three-dimensional dissipating Taylor–Green vortex is initialized following Canuto et al. (2007). The simulation was carried out at $Re_c = 100$ for which reference data was available from Brachet et al. (1983) and Canuto et al. (2007). The equations were integrated from $t=0$ to $t=16$ with grid resolution of $32 \times 32 \times 32$. This resolution was found to be appropriate for such a low Reynolds number flow based on a grid-convergence study and the above works in literature. Our data set is compared qualitatively and quantitatively against literature in Figs. 3 and 4. Iso-surfaces of u-component of velocity are shown in Fig. 3 for the current simulation and those of Brachet et al. (1983). Figure 3 (left) is the initial condition. Figure 3 (middle) is the current simulation at $t = 5.0$, which is the same as the results of Brachet et al. (1983), presented in Fig. 3 (right). In addition to this qualitative comparison, the dissipation rate, $\varepsilon = \nu \langle \frac{\partial u_i}{\partial x_j} \frac{\partial u_i}{\partial x_j} \rangle$ (where $\left<...\right>$ indicates volume averaging), is also compared with literature and is shown in Fig. 4. The result of the current simulation is in very good agreement with that of Brachet et al. (1983).

Fig. 3

Iso-surfaces of u-component of velocity with levels 0.25 (yellow) and −0.25 (blue) at $Re_c=100$. Left: initial flow field at $t=0$. Middle: current simulation at $t=5.0$. Right: Brachet et al. (1983) at $t=5.0$

Fig. 4

Dissipation rate for Taylor–Green vortex at $Re_c = 100$. Current study (solid); Brachet et al. (1983) (dashed)

3.2 Results: proposed method operating on the dissipating Taylor–Green vortex

Figure 5 shows snapshots of particles coloured by the root-mean-square (RMS) error of velocity-gradient components both before and after the vorticity-correction method was applied for high and low seeding densities. Here, the RMS error is computed across the individual elements of the velocity gradient tensor, instead of an ensemble of measurements:

$$\begin{aligned} \mathrm {Error}=\sqrt{\frac{1}{9}\sum _{i=1}^{3}\sum _{j=1}^{3} \partial _iu^2_j} \ . \end{aligned}$$

(7)

The before image is of the initial velocity gradient estimate produced utilizing the method of Meyer et al. (2001). The snapshots are taken at $t=5$, or approximately 1.5 convective times through the simulation. The RMS error of the velocity gradients range up to approximately 3% before correction, as expected given the magnitude of noise applied to the advected particles. Error is reduced by the vorticity-correction method throughout the domain for both seeding densities shown. These observations can be seen more clearly in the supplementary videos “taylor-green_low-density.mp4” and “taylor-green_high-density.mp4” This reduction in error was achieved at relatively low computational cost, with MATLAB-based implementation on a desktop-class computer optimizing approximately 25–100 pathlines per second, depending on seeding density.

Fig. 5

Particles were convected through the dissipating Taylor–Green vortex field with some artificial noise, and the resulting tracks were processed as if they were PTV data. The resulting RMS error in velocity-gradient components is shown for $t=5$. The upper row shows a high particle-density case ($N=25,000$) before (left) and after (right) the vorticity correction scheme was applied. The scatter plots on the second row shows a intermediate particle-density case ($N=6500$). In both cases, the vorticity correction scheme shows a reduction in RMS error. For each seeding density, the side-by-side comparison before and after correction can be viewed as a time sequence in the supplementary videos “taylor-green_low-density.mp4” and “taylor-green_high-density.mp4”

In addition to the error shown in Fig. 5, the vorticity field can also illustrate how the vorticity correction method is applied. Figure 6 shows the vorticity-magnitude sampled on a plane one half-wavelength from the centre of the computational domain ($z=\pi /2$). The time-step of this sample was chosen to be early in the simulation such that there were still large structures to identify, and the highest seeding density was used here. This vorticity field is shown interpolated onto an Eulerian grid as a contour plot. While the vorticity correction method does not recover the true gradients exactly, the alternating pattern of vorticity magnitude into nearly-circular structures is much more evident after correction than before.

Fig. 6

Vorticity magnitude is shown here for the plane $z=\pi /2$ for the high particle-density case. While the recovery if the vorticity pattern is not perfect, the alternating circular pattern is much more evident after the correction scheme is applied

Four seeding densities were evaluated following the same methodology. The average error was determined at each seeding density through the arithmetic average of RMS errors across the entire spatial and temporal domain, shown in Fig. 7. The initial cases, indicated with crosses, are the initial gradient estimates used as an input for the gradient optimization. While higher seeding densities presented lower error both before and after correction, the vorticity-correction methodology reduced mean error across all cases, with a maximum reduction in error of approximately 40%. It is speculated that the variation in converged error values with respect to seeding density is due to the simple gradient descent method uses here, which is only capable of determining local optima. As such, in its current implementation this gradient optimization technique is dependent on initial conditions. However, the larger error reduction (as a fraction of the initial error) observed at a particle count of 6000 is not expected to be an artefact of the random initialization as the particle positions were all confirmed to be uniform at their initialization. Moreover, this case still represents approximately $10^7$ individual gradient estimations, reducing the likelihood of random error. Figure 7 also shows the reduction in the objective function O as expressed in Eq. (3), as a function of iteration. The function quickly converges upon its final value within five to ten iterations, with an overall reduction of approximately 60% versus the initial value of the function.

Fig. 7

The per-particle RMS error averaged across the whole computational domain for four different seeding densities. The vorticity-correction method reduced error across all seeding densities. The reduction in the objective function is also shown here, as a function of iteration, for the highest seeding density (N = 25,000) (right)

4 Experimental test case: starting vortex on an accelerating circular plate

Given the reduction of error produced by the vorticity-correction method on synthetic data, as demonstrated in Fig. 5, we will now apply the method to experimental data derived from a single image sequence. The test case consists of the vortex wake behind a circular flat plate towed at a constant acceleration. The experimental setup is explained below.

4.1 Experimental apparatus and image-processing methodology

To test the gradient-evaluation method presented in Sect. 2, 4D-PTV (also known as Shake-the-Box) data was collected along the leeward side of a linearly accelerating circular plate. A schematic of the experimental apparatus is shown in Fig. 8. The experiments was performed in the 15 m-long, 1 m $\times$ 1 m cross-section optical towing tank at Queen’s University. Three-sided optical access is provided from the two side-walls and the bottom of the towing tank. An impulsively started circular plate of diameter D = 30 cm was accelerated normal to its path at a dimensionless acceleration of $a^*=aD^3/\nu ^2=1.07\times 10^{10}$, where a and $\nu$ represent dimensional acceleration and kinematic viscosity, respectively. The motion was achieved by a rack-and-pinion traverse above the towing tank. The sting holding the circular plate was 2D long, with a circular profile and a diameter of 0.1D, attaching to the plate on its suction side. The blockage ratio of the experiment is $7\%$. The sting assembly and optical setup are shown in Fig. 8b. Further documentation on this experiment can be found in Fernando and Rival (2016).

Fig. 8

Schematic of the experimental apparatus: a A $D=30$ cm circular plate was accelerated at at a non-dimensional rate of $a^*=aD^3/\nu ^2=1.1\times 10^{10}$ through a 15 m-long, 1 m $\times$1 m square cross-section optical towing tank; b particles were illuminated with a 40 mJ per-pulse laser and captured using four Photron SA-4 cameras

$55 \ \upmu \rm{m}$ polymer spheres were seeded in the flow to serve as tracer particles. The Stokes number of the particles was approximately $3\times 10^{-3}$, which ensured tracer-accuracy errors of $<1\%$ (see Raffel et al. 2007). The tracers were illuminated by a $527~\text {nm}$, 40mJ-per-pulse laser expanded into a $10\times 10\times 0.3~$cm${}^3$ volume. Four Photron SA4 high-speed cameras captured images of the tracers within this volume at a frame rate of 900 $\text {Hz}$. To minimize image distortions, water-filled prisms were fixed onto the glass pane of the tank such that all cameras were orthogonal to a prism face. The acquired images were then processed in DaVis 8.3.0 and using a 4D-PTV tracking algorithm; see Schanz et al. (2016) for details. Measurements were performed over a diameters-traveled domain of $0.1\le s/D \le 0.28$, which corresponds to circulation-based Reynolds numbers between $9\times 10^3\le {Re}_\Gamma \le 43\times 10^3$. Finally, the 4D-PTV pathlines were then extended forwards and backwards beyond their original lifespan via a pathline-extension method inspired by flow-map compilation techniques described in Brunton and Rowley (2010) and Raben et al. (2014).

4.2 High-fidelity measurements of the starting vortex growth

As direct estimates for gradient errors are no longer accessible, an instantaneous snapshot of the vorticity field is instead presented in Fig. 9 to demonstrate the increase in fidelity offered by the proposed vorticity-correction method. As in the numerical test case, the before image is of the initial velocity gradient estimate produced utilizing the method of Meyer et al. (2001). The noise of the starting vortex is reduced, allowing for the identification of structures not previously obvious, such as individual Kelvin-Helmholtz instabilities in the shear layer. These structures would also be obscured by ensemble-averaging, such that the ability to correct individual runs is critical. This noise reduction is more clearly shown in the supplementary video “circular_flat_plate.mp4”. The concentric circular vorticity levels also clearly identify the vortex core in the corrected vorticity field. Although the vorticity scale is saturated in Fig. 8a, it is worth noting that the small-scale structures remain obscured at all scaling levels. Furthermore, it should be noted that the vorticity correction method will often increase velocity gradient magnitudes, and does not simply smooth the gradient values. The computational cost of the proposed methodology did not significantly increase for the experimental data relative to the synthetic data, correcting pathlines on the order of 10 per second on a desktop-class computer.

Fig. 9

An instantaneous snapshot of the vorticity field captured from a single image sequence is shown here a before and b after vorticity-correction on flow-compiled PTV data. The correction scheme allows for the identification of individual instabilities in the shear layer, and the clear identification of the vortex core. This side-by-side comparison is available as a time sequence in the supplementary video “circular_flat_plate.mp4”

In order to give a rough estimate of both the computational cost and the reduction in the objective function, the objective function O as expressed in Eq. (3) is shown in Fig. 10. Despite the simple optimization method used in this study, the residual of most pathlines converged on its final value after five to ten iterations. However, it is worth noting that in the absence of an objective true value with which to compare to, no quantitative treatment of error reduction can be given here. The convergence on a local minimum, as opposed to zero, was seen as acceptable in order to avoid gradient estimations tending towards zero.

Fig. 10

The magnitude of the residual along an individual pathline is shown here as a function of iteration to visualize both the noise reduction observed and the computational speed. The 40% reduction in the objective is similar to the 40% reduction in error observed in synthetic data

We can demonstrate the utility of this high-fidelity result in Fig. 11. Here, we are now able to accurately identify key features in the flow due to the smooth, well-resolved vorticity field. Having identified a flow feature, the mass in that structure can then be tracked backwards in time along pathlines back to its source, as shown on the right in Fig. 11. Pathlines are coloured by time overlayed on a snapshot of vorticity from the later-most timestep of the dataset. In this way, we are able to identify where vorticity-containing mass originated. Alternatively, the left of Fig. 11 shows pathlines tracked forwards in time from a vorticity source. This forward and backward tracking together define the relationship between the resulting flow topology and vorticity source.

Fig. 11

Utilizing the pathline information can elucidate material transport within a flow. For instance, on the left a particles are tracked forward in time from the shear layer to a later time-step, shown here overlayed on the vorticity field at that later time-step. This shows the advection of material from a vorticity source. Alternatively, particles can be tracked from the vortex core backwards in time, shown in the right (b), to identify the origin of that vorticity-containing mass

5 Conclusions

The purpose of this study was to improve the estimation of spatial gradients on unstructured Lagrangian data without discarding any pathline information. Such robust gradient estimation can improve the understanding of vorticity transport through a flow for the purposes of aerodynamic or hydrodynamic optimization or flow control. Therefore, we proposed a gradient correction scheme based on the knowledge that the substantial derivative of vorticity through a flow must equal the vortex stretching/tilting through that flow. This constraint was realized by minimizing the residual of the vorticity-transport equation across all points of a pathline simultaneously.

The proposed method has been implemented on both synthetic and experimental data consisting of a decaying Taylor–Green vortex field and an accelerating circular plate, respectively. In the synthetic case, mean errors were shown to be consistently reduced by the proposed vorticity-correction method across all seeding densities, by up to 40%. However, as the method shown here is locally optimizing, the error reduction achieved is dependent on the spatial resolution of the initial gradient estimate. Meanwhile, the application of the proposed method to experimental data reduced the vorticity-transport residual by approximately 40%. The proposed method also provided access to small-scale flow structures such as the Kelvin-Helmholtz instabilities that were otherwise obscured. This retention of Lagrangian data was demonstrated with the direct investigation of material transport within a starting vortex. Small-scale flow structures could be identified in the post-processed data that were otherwise unavailable to the raw gradient outputs. By identifying those flow structures one could then track the vorticity-containing mass back to its origin. This experimental case demonstrates the value of retaining Lagrangian data for aerodynamic or hydrodynamic optimization, which could eventually lead to new insights when studying complex, vortical flows.