Effect of initial vortex core size on the coherent structures in the swirling jet near field

Abstract

This study investigates the sensitivity to initial conditions of swirling jets undergoing vortex breakdown. Emphasis is placed on the recirculation bubble and on the helical coherent structures that evolve in its periphery. It is proposed that the vortex core size of the incoming swirling jet is the critical parameter that determines the dynamics of these coherent structures. This proposition is assessed with Stereo Particle-Image-Velocimetry (PIV) measurements of the breakdown region of two swirling jet configurations with different vortex core sizes at very similar overall swirl intensities. The swirling jets were generated by radial vanes entering a mixing tube, and the vortex core size was adjusted by using different center-body geometries. The time-averaged flow fields in the breakdown region reveal substantial differences in the jet spreading and the size of the recirculation bubble. Proper Ortogonal Decomposition (POD) was applied to the anti-axisymmetric and axisymmetric velocity fluctuations, to reconstruct the dynamics of the helical instability and the breakdown bubble, respectively. We find that the mode shape of the helical instability is not affected by the vortex core size. The frequency is found to coincide with the vortex core rotation rate, which relates inversely to the core size. The shape and dynamics of the non-periodic breakdown bubble are significantly affected by a change in vortex core size. The POD reveals that the energy content of the dominant non-periodic structure is changed markedly with the vortex core size. The bubble dynamics are further investigated by tracking the upstream stagnation point from the PIV snapshots. It is shown that a larger vortex core promotes smooth fluctuations of the recirculation bubble, while a small initial vortex core is linked to bimodal fluctuations of the recirculation bubble. The conclusions drawn from this study are relevant for fundamental swirling jet studies, as well as for the design of swirl-stabilized combustors, where the investigated coherent structures influence combustion performance.

1 Introduction

Swirling jets have been thoroughly investigated throughout the last decades. They remain a topic of continued interest in both academia and industry. This can be attributed to the fact that swirling jets exhibit a rich variety of phenomena, such as vortex breakdown and the global mode associated with it. Changes in time-mean quantities of the swirling jet or the global mode were mostly investigated in relation to an increase in swirl number. The purpose of this study is to demonstrate that the near-field evolution of swirling jets undergoing vortex breakdown can exhibit substantial differences at comparable swirl intensities. We show that the size of the vortex core upstream of the breakdown region is the key parameter for the evolution of coherent structures in the near field.

The swirl intensity is usually characterized by a swirl number. Its definitions, and there are numerous, are always related to a ratio of axial to azimuthal momentum. The swirling jet far field seems to be well characterized by a swirl number, when appropriate scaling is applied (Shiri et al. 2008). However, the onset of vortex breakdown and associated coherent structures cannot be scaled by a universal number, and it is a matter of taste which one to use (Oberleithner et al. 2012, 2014; Toh et al. 2010; Billant et al. 1998; Liang and Maxworthy 2005; Chigier and Chervinsky 1967).

Swirling jets feature rich physical mechanisms, when sweeping from no swirl to very strong swirl. Oberleithner et al. (2012) investigated swirling jets at different swirl numbers. They found two important values of the swirl number, $S_{\mathrm{VB}}$ and $S_{\mathrm{crit}}$ with $S_{\mathrm{VB}} < S_{\mathrm{crit}}$. $S_{\mathrm{VB}}$ marks the swirl number above which a zone of recirculating fluid is permanently present in the flow. At values of the swirl number below $S_{\mathrm{VB}}$ either no recirculation zone or an intermittently occurring recirculation zone is present in the flow. At the second swirl number, $S_{\mathrm{crit}}$, the flow undergoes a supercritical Hopf bifurcation to a global mode. At swirl numbers larger than $S_{\mathrm{crit}}$ the flow was observed to oscillate on a limit cycle.

The global mode was identified as a helical coherent structure that winds around the recirculation zone and is observed to have an azimuthal wave number of one co-rotating with the base flow (Oberleithner et al. 2011; Ruith et al. 2003). Concerning the temporal dynamics, the global mode is known to oscillate at a well-defined frequency, similar to the von Karman vortex street. The global mode is consistently observed to dominate the dynamics of swirling flows undergoing vortex breakdown once it is present (Oberleithner et al. 2011; Ruith et al. 2003; Terhaar et al. 2014; Liang and Maxworthy 2005).

Broadly speaking, the research into swirling jets can be divided into two categories: in the first category, the flow domain in which vortex breakdown takes place is confined by walls. In the second category, the same domain is unconfined.

The importance of swirling jets in combustion applications has stimulated a large body of work on confined swirling jets (e.g., Escudier 1987; Syred et al. 1997; Paschereit et al. 1999). In the context of these studies, the confinement is due to the presence of combustor walls. A typical laboratory setup may consist of a swirler, a mixing tube with possibly a blunt center-body and an area expansion that is followed by the combustion chamber (Krüger et al. 2013; Reichel et al. 2015). The work of Stöhr et al. (2012) investigated the interaction of the global mode and a turbulent swirling flame. They found that the recirculation bubble is of particular importance, because the upstream stagnation point provided the instantaneous position of the flame root in their measurements. At this location, hot burnt gases frontally collide with the incoming fuel/air stream and ignite the fresh fuel. Recently, the benefits of axial air injection via a center-body on flashback safety were shown by Reichel et al. (2015). In this study, the flow in a generic swirl-stabilized combustor was studied. A 15 % air split was injected axially in the premixing tube before the area expansion of the combustion chamber. This study, however, did not investigate the influence of just the center-body on the downstream flow field.

On the other hand, there are numerous studies concerned with unconfined swirling flows. Panda and McLaughlin (1994), Liang and Maxworthy (2005), Oberleithner et al. (2011) and Oberleithner et al. (2014) investigated the large-scale structures in swirling jets. While each of these studies focused on the unconfined swirling jet, the respective experimental setup also included a confined part, in which the swirling flow was generated. A number of other studies delineated the importance of the initial conditions at the inlet of the unconfined flow for the downstream development of the swirling jet. Hallett and Toews (1987) investigated a setup similar to what can be found in combustion experiments. It did not contain a nozzle, but a sudden area jump from a pipe to a confined geometry. They focused on the effect of inlet conditions before the area jump and on the effect of the area jump itself on the onset of flow reversal. They found that a larger initial vortex core size leads to an increased amount of swirl that is necessary for the onset of vortex breakdown.

The study of Farokhi et al. (1989) considered the effect of the initial swirl distribution on the evolution of weakly swirling jets. Their setup consisted of a pipe, a converging nozzle and an unconfined part. Different distributions of azimuthal velocity were generated by three manifolds inside the confined part, which each had a different diameter. Thereby, the authors investigated two extreme cases: one, in which the swirl distribution was that of a vortex in solid body rotation, and a second configuration of a free vortex type flow. At the same mass flow rate and the same swirl number, the first distribution showed no sign of vortex breakdown, whereas the second distribution was on the verge of vortex breakdown. The authors concluded that the integrated swirl number is inadequate in describing the mean flow evolution of swirling jets. Rather, they suggested that the relative size of the vortex core in the nozzle exit plane is decisive in the further evolution of the swirling jet.

Toh et al. (2010) discuss many different swirl number definitions that are commonly used. In line with Farokhi et al. (1989), it is pointed out that any swirl number defined on the basis of some integral measure may be misleading, because swirling jets with very different initial swirl distributions can yield the same swirl number. However, the initial distribution of swirl is of paramount importance in the development of the weakly swirling jet.

Leclaire and Jacquin (2012) investigated the generation conditions of a swirling jet experiment, where vortex breakdown occurs in the unconfined flow. However, these authors directed their efforts more to the confined part of the flow and did not so much analyze the structures in the unconfined part of the flow. Their experiment used a rotating honeycomb to produce the swirling jet. As the authors state, some of the dynamics they observe are probably related to the presence of the rotating honeycomb.

The studies of Hallett and Toews (1987), Farokhi et al. (1989) and Toh et al. (2010) clearly show that the initial vortex core size is decisive for the downstream evolution of swirling jets. However, these studies investigated time-mean quantities of jets at swirl intensities below vortex breakdown. To our knowledge, no previous study has dealt with the influence of the initial conditions on the coherent structures of strongly swirling jets. In addition, the impact of the initial vortex core size on the instantaneous dynamics has not been investigated.

The use of center-bodies in combustion applications motivates us further to investigate how these center-bodies can be used as a means of passive flow control. We propose that a suitable center-body in the upstream, confined part of a swirling jet facility, can be used to modify the vortex core thickness in the nozzle exit plane. This in turn enables the modification of the free field dynamics.

This proposition is assessed with two different center-bodies.

The flow inside the mixing tube of the setup is measured with Laser-Doppler-Anemometry (LDA), whereas the unconfined part is captured with Particle-Image-Velocimetry (PIV). Proper Orthogonal Decomposition (POD) is used to extract the spatial structure and the energy of the coherent structures for each center-body configuration. A feature tracking approach is used to determine the dynamics of the recirculation bubble. Particularly, the work of Stöhr et al. (2012) draws our interest to the behavior of the upstream stagnation point. In light of the swirl number discussion by Toh et al. (2010), we will not specifically try to produce the same swirl number for each configuration, but instead target swirling jets that are similar in the properties of one large-scale feature. The flows considered will have the same time-mean upstream stagnation point.

The paper is outlined as follows: The experimental facility, the associated characteristic numbers, as well as the data acquisition and evaluation procedure are presented in Sect. 2. A discussion of PIV measurement uncertainties is included in this section. The POD and the feature tracking are introduced in Sect. 3. Section 4 shows the mean flow and the dynamical features of the two center-body configurations. The major findings are concluded in Sect. 5.

2 Experimental setup, measurement and data treatment

2.1 Swirling jet facility

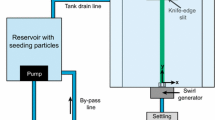
A turbulent free axisymmetric swirling jet was generated. A schematic of the experimental apparatus is shown in Fig. 1. The entire setup was centered inside a tent with a radius of 1.6 m and a height of 3.2 m. Air is fed into the swirler (zone I), where it radially passes eleven vanes. These vanes can be adjusted in angle simultaneously, to produce swirling jets of different intensity. The swirled air then passes into a 800-mm-long mixing tube (zone II) and moves downstream to a nozzle (zone III) with a diameter of 51 mm and an area contraction ratio of 9.1. After the nozzle, the air exits into the free field (zone IV) as a swirling jet. As indicated in Fig. 1, the facility admits space to mount a center-body on the bottom plate of the swirler. Note that air is supplied only through the swirler. No additional mass flow is injected through the center-body.

Figure 1 also shows the cartesian coordinate system that is used throughout this study. The origin is placed on the jet axis in the nozzle exit plane; x points in the axial direction, y in the cross-stream direction and z in the out-of-plane direction. In this coordinate system, the velocity vector $\mathbf {v}$ is defined. The components $v_{x}, v_{y}$ and $v_{z}$ are the contributions in the respective directions.

Additionally, a cylindrical coordinate system is introduced. The origin is the same as for the cartesian coordinate system. The radial coordinate r is aligned with the y-axis of the cartesian system at zero degrees of revolution. The axial direction is aligned with the x-axis and the angle $\theta$ is counted positive according to the right-hand rule. The velocity components in this system are denoted by $v_{x}, v_{r}$ and $v_{\theta }$.

Two center-bodies of different dimensions were used and the detailed measurements are listed in Table 1. Both center-bodies are sketched in Fig. 1. The solid line indicates C1, which is the center-body with the largest diameter and the largest height. The second configuration, C2, employs a center-body as long as C1, but markedly thinner. It is indicated by the dotted red line. Unlike the blunt body type center-bodies that are common in combustion research, the center-bodies used in this study consist of a pipe where the upper fifth is filled with a honeycomb element (cf. Fig. 1). For clarity of presentation, the honeycomb element is only sketched for C2. We remark that air can only enter and exit the center-body through the honeycomb.

The experimental apparatus is connected via a Bronkhorst EL-Flow mass flow controller to a pressurized air supply. The accuracy of the mass flow controller is ${\pm }0.8$ % of the readout value and ${\pm }0.2$ % of the total range. The relative reproduction error is less than ${\pm }0.1$ %.

Fig. 1

Experimental setup. All dimensions are in millimeters (not to scale)

2.2 Characteristic numbers

The flow is described in terms of two independent dimensionless numbers. The Reynolds number:

$$\begin{aligned} Re = \frac{v_\mathrm{bulk} D}{\nu } \quad \text{ with }\quad {v_{\mathrm{bulk}}} = \frac{Q}{\pi \cdot \left( D/2\right) ^{2}}. \end{aligned}$$

(1)

Q denotes the volumetric flow and D the nozzle diameter. The nozzle diameter D is taken as the characteristic length scale. The reference velocity $v_\mathrm{bulk}$ is 5.8 m/s throughout this study. We note that this choice of scaling is not unique. Shiri et al. (2008) introduced a length and velocity scale that leads to self-similar velocity profiles in the far field of swirling jets. However, we find that the advantages of the proposed scaling do not persist in the near field of swirling jets undergoing vortex breakdown. For example, the axial velocity profiles feature substantial differences in the breakdown region and cannot be collapsed in a self-similar manner.

As already pointed out, a swirl number based on an integral measure may disguise important differences in the initial conditions of the flow. In an attempt to overcome this, Billant et al. (1998) introduced a swirl number based on a velocity ratio. This swirl number is defined as

$$\begin{aligned} S_{\mathrm{B}} = \frac{2 \overline{v}_{\theta }(D/4,x_{0})}{\overline{v}_{x}(0,x_{0})}. \end{aligned}$$

(2)

$x_{0}$ denotes the axial location closest to the nozzle at which reliable measurements could be obtained, in this case 1.57 mm. Note that in the vicinity of the nozzle $\overline{v}_{\theta }(D/2,x_{0}) \approx \text {max}\left( \overline{v}_{\theta }(r,x_{0})\right)$. In addition to this, we give the swirl number of Chigier and Chervinsky (1967), $S_{\mathrm{CG}}$, since, in our perception, it is most commonly used in the literature.

$$\begin{aligned} S_{\mathrm{CG}} = \frac{\dot{G_{\theta }}}{D/2 \dot{G_{x}}} = \frac{2\pi \int \limits _{0}^{\infty }\rho \overline{v}_{x} \overline{v}_{\theta } r^{2} \mathrm {d}r}{D \pi \int \limits _{0}^{\infty }\rho \left( \overline{v_{x}^{2}}- \frac{\overline{v_{\theta }^{2}}}{2}\right) r \mathrm {d}r}. \end{aligned}$$

(3)

It quantifies the amount of swirl in the flow and is defined as the ratio between the axial flux of azimuthal momentum $\dot{G}_{\theta }$ and the axial flux of axial momentum $\dot{G}_{x}$. This swirl number is evaluated at the same axial position as $S_{\mathrm{B}}$. In deriving $S_{\mathrm{CG}}$ it was assumed that $\overline{{v_{x}^{'}}^{2}} \approx \overline{{v_{r}^{'}}^{2}} \approx \overline{{v_{\theta }^{'}}^{2}}$ and that the influence of the radial velocity can be neglected. In the vicinity of the nozzle, it can be expected that these assumptions are valid. A detailed discussion of the terms neglected in the derivation of $S_{\mathrm{CG}}$ is provided in Oberleithner et al. (2012). Swirl number definitions and their application to the near field of swirling jets are considered in Oberleithner et al. (2014).

The values of the Reynolds number, swirl number and the dimensions of the different center-body configurations are listed in Table 1. $l_{\mathrm{C}}$ and $d_{\mathrm{C}}$ refer to the length and diameter of the center-body, whereas $l_{\mathrm{P}}$ and $d_{\mathrm{P}}$ denote the length and diameter of the pipe, see Fig. 1.

Table 1 Overview of experimental parameters

2.3 Data acquisition

Stereo PIV was used to measure the flow field in zone IV. It consisted of a Quantel Dual-Nd:YAG laser at 532 nm wavelength with 170 mJ per pulse. Images were acquired with two pco 2000 cameras with a resolution of $2048\times 2048$ pixels. Each camera was equipped with a 50 mm Canon lense. Images were recorded at a frequency of 6 Hz.

The measurement plane was aligned with the x, y plane. In the cross-stream y-direction, the domain extended from $-2D$ to 2D, and in the axial x-direction, it extended from 0 to 4D. The cameras were positioned as such that the camera axis had a 45 angle to the $x,y$ plane. Figure 2 illustrates the setup. The angle $\theta$ equals $45^{\circ }$.

Fig. 2

Arrangement of the cameras in the PIV setup

The double images were processed using the commercial software PIVview (PIVTEC GmbH) using standard digital PIV processing (Willert and Gharib 1991). The data analysis employed iterative multigrid interrogation with image deformation (Scarano 2002). The final size of the interrogation window was $32\times 32$ pixel with an overlap of 50 %. Errors in the laser sheet alignment were minimized by the use of corrected mapping functions. The initial calibration datum marks were back projected onto the measurement plane by an optimized Tsai camera model (Soloff et al. 1997).

The LDA measurements in zone II were conducted with a Dantec two-component LDA system, operating in backscatter arrangement. The bursts produced by particles passing through the measurement volume were processed with Dantec burst spectrum analyzers. The system provides one beam pair at 514.5 nm and another at 488 nm wavelength. The LDA system was operated with a 600 mm focal length lens, a beam spacing of 38 mm and an expander ratio of 1.98. Based on these quantities, the measurement volume had a length of 1.4 mm and a width of 0.09 mm. Measurements were acquired in non-coincident mode to increase the data rate. Data processing was done with Dantecs FlowAnalyzer Software. The measurement domain extended from 0.58D downstream of the center-body to 0.58D upstream of the nozzle. In total, it spanned 11D, from $-4$ to $-15D$. The spacing between the measurement domain and the center-body, respectively, the nozzle was necessary to accommodate the beam spacing of the LDA. Furthermore, in the range from $-9$ to $-11\,x/D$ no data could be obtained because of the presence of a stabilizer bar in the experimental setup. For C1, the data in this range were linearly interpolated. For the C2, measurements were only taken in the domain ranging from $-15$ to $-11D$.

2.4 Measurement uncertainties and convergence of statistical quantities

Many factors can contribute to the overall uncertainty in Stereo PIV measurements. Some of these factors like optical aberration of the lenses or a misalignment of the laser sheet with the measurement plane pertain to the measurement setup, whereas other error sources stem from the evaluation process of the raw images. It can be assumed that with a state-of-the-art measurement setup and evaluation routine each of these error sources is of the same order of magnitude (Stanislas et al. 2008).

The absolute measurement uncertainty is therefore estimated in terms of the evaluation strategy as described in Sect. 2.3. With a typical particle image diameter of one pixel, Raffel et al. (1998) give an uncertainty of 0.1 pixel for the abovementioned evaluation strategy. This translates into an uncertainty of 4.2 % of the bulk velocity, with a pulse delay of $50\,{\upmu }$s and a magnification factor of seven pixel per millimeter. It is possible to reduce this error by using larger pulse delays. However, this was not feasible in the present study, because of the large out-of-plane swirl velocity.

It is worth noting that the measurement uncertainty is normally distributed. Its effect on the mean velocities should therefore average out, if a large enough sample is used for the calculation of the mean. However, it can be assumed that the uncertainty directly contaminates the measured values of fluctuating quantities.

In order to assess the sufficient amount of snapshots, we compute the standard error of the mean (SEM), as well as the upper and lower ($\pm b_{95}$) bound of the 95 % confidence interval for each velocity component and the fluctuating velocity components. The SEM is given as

$$\begin{aligned} \text {SEM} = \frac{\sqrt{\frac{1}{N-1}\sum \limits _{i = 1}^{N}{\left( \phi _{i} - \overline{\phi }\right) ^{2}}}}{\sqrt{N}}. \end{aligned}$$

(4)

The 95 % confidence interval is then calculated as

$$\begin{aligned}{}[-b_{95}, b_{95}] = \left[ \overline{\phi } - \widetilde{z}_{0.95} \text {SEM}, \overline{\phi } + \widetilde{z}_{0.95} \text {SEM} \right] . \end{aligned}$$

(5)

N denotes the number of samples, $\phi _{i}$ a random variable and $\overline{\phi }$ the average of that random variable. $\widetilde{z}_{0.95}$ is the value of the standard normal distribution at five percent probability of error.

Table 2 summarizes these quantities for a representative configuration at $y/D = 0$ and $x/D = 0.27$. At this position the worst convergence rates are observed. The values given in Table 2 are therefore an upper limit for the complete velocity field. Each quantity is given relative to the bulk velocity.

Table 2 SEM and bounds of the 95 % confidence interval

The computed boundaries are well within the estimated measurement uncertainty. We therefore conclude that a sufficient number of snapshots was recorded.

Under the measurement conditions of this study, the relative uncertainty of the provided mass flow amounts to ${\pm }0.05 \;kg/h$. This translates into a bulk velocity uncertainty of $\pm 0.0068 \;m/s$. This is considered as negligible.

For the LDA measurements, data were acquired for 30 s at each point. An average of 3000 and 98,000 samples were collected at each measurement point for the azimuthal and axial velocity component, respectively. On average, the confidence interval of the mean value at each measurement point is 8.5 and 2 % of the respective value for the azimuthal and the axial velocity component.

3 Methods for flow feature extraction from uncorrelated PIV snapshots

3.1 POD

POD is a suitable method for the analysis of coherent structures in turbulent flow. A general introduction to the method is given in Holmes et al. (1998). An example of POD applied to swirling jets undergoing vortex breakdown, with the goal of analyzing the properties of the global mode, is provided by Oberleithner et al. (2011).

The starting point of the POD is a decomposition of the velocity vector $\mathbf {v}$ into a mean $\overline{\mathbf {v}}$ and a fluctuating part $\mathbf {v}'$,

$$\begin{aligned} \mathbf {v}(\mathbf {x},t) = \overline{\mathbf {v}}(\mathbf {x}) + \mathbf {v}'(\mathbf {x},t). \end{aligned}$$

(6)

The idea of the POD is to represent the fluctuating part as a series, via

$$\begin{aligned} \mathbf {v}'(\mathbf x ,t) = \sum _{i=1}^{N}{a_{i}(t)\mathbf {\Psi }_{i}(\mathbf {x})}, \end{aligned}$$

(7)

where $\mathbf x$ denotes the coordinate vector and t the time. The decomposition consists of $a_{i}(t)$ temporal coefficients and $\mathbf {\Psi }_{i}$ spatial modes. The POD provides natural sorting of the spatial modes in terms of their turbulent kinetic energy. Furthermore, the POD is optimal in the sense that there is no other truncated series expansion of a data set that has a smaller mean square truncation error (Holmes et al. 1998)

In this study, we exploit the symmetry properties of the flow features that are to be extracted. Holmes et al. (1998) provide a thorough discussion of symmetries and the POD. We thus deviate from the standard POD formalism and seek a decomposition of the fluctuating velocity field in the form

$$\begin{aligned} \mathbf {v}^{'}= & {} \mathbf {v}_{\mathrm{sym}}^{'} + \mathbf {v}_{\mathrm{asym}}^{'} \nonumber \\= & {} \sum \limits _{i = 1}^{N} a_{i_{\mathrm{sym}}}\mathbf {\Psi }_{i_{\mathrm{sym}}} + \sum \limits _{i = 1}^{N} a_{i_{\mathrm{asym}}}\mathbf {\Psi }_{i_{\mathrm{asym}}}. \end{aligned}$$

(8)

That is, we decompose the velocity field of each PIV snapshot into a symmetric and an anti-symmetric part. The POD is then applied to each of the resulting velocity fields separately. In effect, the expected symmetry properties are enforced for each mode.

While there are a number of possibilities to compute the POD, we use the singular value decomposition to obtain the temporal coefficients, spatial modes and a measure of the turbulent kinetic energy of each mode. The velocity data from PIV measurements is arranged into a state matrix of size $3 \cdot M \times N$. The three velocity components at M spatial points result in $3 \cdot M$ rows of the state matrix and N PIV snapshots yield the number of columns in the state matrix. The singular value decomposition of the state matrix produces three matrices $U, {\varSigma }$ and $V'$. The columns of U contain the spatial modes, whereas the rows of ${\varSigma } V'$ contain the temporal coefficients of the respective mode. The squared elements of the diagonal matrix ${\varSigma }, \sigma ^2$, are a measure of the turbulent kinetic energy (TKE) of each mode. The total TKE is thus given as

$$\begin{aligned} \mathrm {TKE}_{\mathrm {total}} = 0.5 \sum _{i=1}^{N}{\sigma _{i}^{2}}. \end{aligned}$$

(9)

In turbulent flows, the large-scale structures of the flow usually contain a major part of the turbulent kinetic energy. Thus, the first few POD modes can be expected to provide a representation of the dominant coherent structures.

3.2 Symmetry properties

The POD analysis presented in this manuscript relies on the decomposition of the velocity field into a symmetric and an anti-symmetric part. Thus, a definition of these symmetry properties in polar and cartesian coordinates is given next. A symmetric structure has

$$\begin{aligned} v_{r}(r, \theta _{1}, x) = v_{r}(r, \theta _{2}, x). \end{aligned}$$

(10)

For the same structure,

$$\begin{aligned} v_{y}(x, y, z = 0) = v_{r}(r, \theta = 0, x) \end{aligned}$$

(11)

and

$$\begin{aligned} v_{y}(x, y, z = 0) = -v_{r}(r,\theta = \pi , x) \end{aligned}$$

(12)

for arbitrary $\theta _{1}$ and $\theta _{2}$. Hence, a symmetric structure in polar coordinates appears as anti-symmetric in cartesian coordinates. In the following, symmetry and anti-symmetry will always be in reference to a polar coordinate system.

To demonstrate the decomposition of the velocity field into symmetric and anti-symmetric parts, we consider an exemplary PIV data set. Consider first Fig. 3d, f. These two modes are the first and second modes of a POD applied only to the anti-symmetric part of the measured velocity fields. As will be discussed later on, these two are the prototypical representation of the helical global mode. In addition, Fig. 3b shows the first mode of the POD applied only to the symmetric part of the velocity fields. This structure will be identified subsequently as a non-periodic structure that is related to an axial shift of the recirculation bubble. Figure 3a, c, e displays the first three modes of a POD applied directly to the measured velocity fields. The helical mode is now represented by three POD modes instead of two. Figure 3a, c shows that two different phenomena have been merged into these three modes. This is most pronounced in Fig. 3a, which appears as a superposition of Fig. 3b, d.

Fig. 3

a, c, e The first three POD modes without a decomposition of the velocity field into symmetric and anti-symmetric part. b The first mode of POD applied only to the symmetric part of the velocity field. d, f The first and second mode of the POD applied only to the anti-symmetric part of the velocity field

3.3 Flow feature tracking (tracking the breakdown bubble dynamic)

This study focuses on two large-scale flow features of swirling jets undergoing vortex breakdown: (i) the global mode, which features large-scale periodic oscillations that can be readily analyzed via POD (Oberleithner et al. 2011; Stöhr et al. 2012) and (ii) the recirculation bubble that does not feature a periodic dynamic. To analyze the dynamic of the second, feature tracking is applied to a low-order reconstruction of the velocity field. We take the spatial fluctuations of the upstream end of the recirculation bubble as an indicator for the dynamics of the recirculation zone. In order to extract the location of the upstream stagnation point from the instantaneous velocity fields, we use the Q-criterion of Hunt et al. (1988), which is given as

$$\begin{aligned} Q = \frac{1}{2} \cdot \left( \left\| {\varOmega } \right\| ^{2} - \left\| S \right\| ^{2} \right) . \end{aligned}$$

(13)

S denotes the symmetric and ${\varOmega }$ the anti-symmetric part of the velocity gradient tensor $\nabla \mathbf {v}$. In its usual use, this criterion locates regions, in which the rotation is larger than the strain rate and therefore a vortex is identified when $Q > 0$. Considering a stagnation point, all velocity components reduce to zero. There, the sign of all velocity components changes across the stagnation point and the strain is larger than the rotation. Hence, the Q-criterion produces a negative value at a true point of flow stagnation.

To ease the discussion of the Q-criterion, the following terminology is introduced: First, a stagnation point of a velocity field can be described as a saddle point of a vector field. Second, a vortex with a rotatory motion is equivalent to a focus. Furthermore, in the context of vector field topology, features like saddles are termed critical points.

To aid in the further discussion, we write the Q-criterion for a two-dimensional flow in Cartesian coordinates:

$$\begin{aligned} Q = -\frac{1}{2}\left( \left( \frac{\partial v_{x}}{\partial x}\right) ^{2} + \left( \frac{\partial v_{y}}{\partial y}\right) ^{2}\right) - \frac{\partial v_{y}}{\partial x}\frac{\partial v_{x}}{\partial y} \end{aligned}$$

(14)

Fig. 4

Some prototypical topological structures of vector fields. a A saddle, b a focus, c the vector field of a Stuart vortex

For the identification of critical points, the Q-criterion is calculated from normalized velocities. Therefore, each velocity vector is divided by its magnitude $\left( \sqrt{v_x^2+v_y^2}\right)$, whereby only the directional information of the velocity field is retained. With this modification, the Q-criterion is more robust and its values lie only between minus one and one. The application of this criterion to some generic velocity fields will be given in the following. A saddle point is shown in Fig. 4a. In this case, the normal strain components contribute to the Q-criterion. The cross derivatives are identically zero. Therefore, the only overall contribution comes from the two normal strain components and the Q-criterion is negative. The ellipse shown in Fig. 4b is a representation of a vortical motion. In this case, the two normal strain components are zero and the only contribution to the Q-criterion stems from the cross-stream derivatives. While $\frac{\partial v_{y}}{\partial x}$ is negative, $\frac{\partial v_{x}}{\partial y}$ is positive and the overall value of the Q-criterion is positive. Finally, Fig. 4c shows the vector field of the Stuart vortex (Stuart 1967). It consists of two repelling foci and an interconnecting saddle. As is indicated by the colorbar, the value of the Q-criterion changes from positive to negative to positive values as the topology changes accordingly. We conclude that the Q-criterion is suitable to identify the structure we are interested in—the saddle points of instantaneous velocity fields.

We remark that other approaches exist to identify critical points in vector fields, the most classical being the calculation of the Poincaré–Hopf index (Foss 2004). The calculation of the Poincaré–Hopf index involves the identification of candidate critical points, as outlined in Depardon et al. (2006). The Poincaré–Hopf index is the integer number of rotations of a vector as a closed loop around the candidate critical points is traversed. In practice, a discretized circle is placed around each candidate point and the Poincaré–Hopf index is calculated via

$$\begin{aligned} I = \frac{\sum {\delta \theta }}{2 \pi }. \end{aligned}$$

(15)

$\delta \theta$ denotes the angular difference between successive vectors along the contour. If $I = -1$ the candidate point is a saddle, if it is 1, the candidate is a node or focus and if $I = 0$, the candidate point is not a critical point. However, with a given spatial resolution of the PIV grid only a few (around six, depending on the radius of the circle) vectors lie on the discretized circle. In this case, we found that the results of the Poincaré–Hopf index are comparable to the Q-criterion applied to a normalized velocity field. In fact, the focus on the angular information (normalization) in the Q-criterion is similar to the consideration of angular increments in the Poincaré–Hopf index. Both methods differ mainly where the velocity field shows sinks or sources, that is, where the flow becomes strongly three-dimensional and the in-plane continuity is violated. Additionally, the process of identifying candidate critical points and computing the Poincaré–Hopf index, as outlined in Depardon et al. (2006), took an order of magnitude more computational time than the identification of the saddle points via the Q-criterion.

Finally, it shall be noted that the Q-criterion as shown in Eq. 14 is valid only for strictly two-dimensional flows. The crucial point is that in a two-dimensional flow, the vortex axis is perpendicular to the vector field plane. However, the data that are analyzed here stem from a highly three-dimensional flow. This means that the axis of a given vortex may intersect the measurement plane at an arbitrary angle. This leads to the formation of degenerate saddle points that become increasingly elongated until only a stagnation line remains. This process is illustrated in Fig. 5. A pseudo three-dimensional vector field is obtained by extending a saddle point as in Fig. 4a in the z-direction. The resulting vector field is given for reference in Fig. 5a. If the vector field of Fig. 5 is sliced along the x, y plane, a two-dimensional saddle point is recovered. The corresponding value of the Q-criterion is indicated in Fig. 5b. As the plane of reference is rotated through the vector field, the saddle point becomes elongated along the x-direction. At the same time, the value of the Q-criterion is reduced, as shown in Fig. 5c. If the plane of reference is rotated to an angle of $90^{\circ }$ relative to its initial position, Fig. 5d, the saddle point visible in Fig. 5b has deformed into a stagnation line. The magnitude of the Q-criterion has reduced to half of its initial value at the location of the saddle point, since one of the in-plane velocity components has reduced to zero.

While the three-dimensional topology of the vector field of a swirling jet is more complex than the vector field shown in Fig. 5a, the trends observed for the pseudo three-dimensional vector field are expected to remain valid: If the topology of the vector field on the PIV plane is sufficiently two-dimensional, a clear saddle point forms. The value of the Q-criterion is close to $-1$, if the velocity vectors are appropriately normalized. The saddle-point structure on the PIV plane is distorted, if the normal to the saddle point is close to parallel to the PIV plane. In such a situation, the value of the Q-criterion will differ significantly from a value of $-1$.

Fig. 5

A pseudo three-dimensional vector field generated by extending a saddle as shown in Fig. 4a in the z-direction. a The resulting vector field is indicated by its streamlines. b–d The value of the Q-criterion on a plane that intersects the vector field at $0^{\circ }, 27^{\circ }$ and $90^{\circ }$ relative to the x-axis. The black solid line indicates the rotation axis of the plane

3.4 Outline of flow feature tracking from PIV data

The analysis of the PIV data is carried out according to the flowchart displayed in Fig. 6. In detail, the following steps are taken:

Fig. 6

Flowchart of the feature tracking process

• The fluctuating velocity component $\mathbf v '$ is extracted from each PIV snapshot.

• The fluctuating velocity component is decomposed into a symmetric, $\mathbf v '_{\mathrm{sym}}$, and an anti-symmetric part, $\mathbf v '_{\mathrm{asym}}$.

• A POD is computed for the symmetric and anti-symmetric part separately.

• A low-order reconstruction of the instantaneous velocity field is computed, employing only the first two symmetric and anti-symmetric POD modes $\mathbf{\Psi }_{1/2}$, see Fig. 12. The POD serves as a low-pass filter, rejecting small-scale fluctuations. Each velocity vector is normalized with its magnitude.

• The Q-criterion is computed via Eq. 14 and normalized with its smallest value. Saddle points are identified as the locations where the Q-criterion is above a certain threshold, typically 0.7. Thus, only incidences in which the local saddle point structure is sufficiently two-dimensional contribute to the stagnation point tracking.

4 Results

The presentation of the experimental results starts with the discussion of the time-averaged velocity measured in the mixing tube upstream of the contraction, followed by a presentation of the velocities in the nozzle exit plane and in the unconfined domain downstream. Thereafter, we characterize the global mode dynamics derived from the POD analysis. The results section terminates with a discussion of the recirculation bubble dynamics as it is derived from the Q-criterion-based approach.

4.1 The mean flow in the mixing tube

Fig. 7

a Sketch of the measurement planes. b Time-averaged axial and azimuthal velocity component for C1. c Time-averaged axial and azimuthal velocity component for C2. b, c Contour levels represent the axial velocity component. The contour line of zero axial velocity is indicated by the thin solid line. Profiles of the azimuthal velocity component are shown as thick black lines. The x, y coordinates of the corners of the center-bodies in a sectional view are marked as black dots

The two measurement planes in zone II are sketched in Fig. 7a for reference.

The contours of axial velocity shown in Fig. 7b reveal that the contraction affects the flow field in the entire mixing tube. The axial velocity accelerates markedly on the jet centerline toward the end of the mixing tube. At the same time pockets of recirculating fluid are present between the accelerating flow on the jet axis and the walls of the pipe. The contour line of zero axial velocity is marked by a solid black line in Fig. 7b. While the velocity increases above zero for $x/D > -8.5$, a velocity deficit remains in that part of the flow.

Comparing the axial velocity shown in Fig. 7b to the axial velocity fields of Leclaire and Jacquin (2012), we find that the acceleration due to the nozzle is present in both flows far upstream of the nozzle. However, we detect no trace of the wavy evolution of the axial velocity along the jet centerline that Leclaire and Jacquin (2012) report and which they attribute to standing Kelvin waves in their experimental setup. Rather, we observe a continuous increase in the magnitude of the axial velocity along the jet axis.

The profiles of the azimuthal velocity in Fig. 7b show the downstream evolution of this velocity component. From the center-body to the nozzle, the locations of the velocity extrema move inward, from approximately ${\pm }1.1D$ to ${\pm }0.3D$. The honeycomb element in the center-body functions as a flow-straightening device. While the axial velocity remains largely unchanged, the swirl velocity is strongly reduced after a short distance into the honeycomb (Barlow et al. 1999). Hence, a region of non-swirling fluid forms above the center-body, which is set back into rotation by the surrounding annular stream of rotating fluid. This is especially pronounced in Fig. 7b, where a plateau around $0\,$m/s is readily detectable in the profile of the azimuthal velocity in the vicinity of the honeycomb.

The contours of axial velocity and the profiles of the azimuthal component for C2 are given in Fig. 7c. The thinner center-body leads to larger recirculation zones, where the boundaries are again indicated by solid black lines. The magnitude of the axial velocity is strongly increased. The profiles of the azimuthal component retain their extrema at ${\pm }0.25D$ throughout the measurement domain. The magnitude of the azimuthal component is strongly increased compared to C1.

4.2 The mean flow in the nozzle exit plane

The velocity profiles in the nozzle exit plane play a special role in the present context, because they connect the internal with the external flow. In that sense, they set the inflow boundary condition for the unconfined flow.

Fig. 8

a Azimuthal velocity profiles in the nozzle exit plane. b Axial velocity profiles in the nozzle exit plane. Vertical lines in a indicate the vortex core radius. The respective swirl numbers are listed in Table 1

Figure 8a compares the profiles of the azimuthal velocity in the nozzle exit plane. C1 has a lower absolute velocity and the maximum of the velocity occurs at a larger radial distance from the jet axis. C2 exhibits a larger velocity at a smaller radial distance. This indicates that from C1 to C2 an increasingly concentrated vortex core enters the unconfined part of the flow. This is also reflected by the axial velocity (Fig. 8b). The overshoot in axial velocity increases as the maximum of the azimuthal velocity is shifted inwards. It is created by the rotating flow passing through a contraction (Batchelor 1999) and is found consistently in studies on swirling jets (Billant et al. 1998; Oberleithner et al. 2014). This indicates that the key difference between the two configurations is the formation of an increasingly concentrated vortex core that enters into the unconfined part of the flow. In line with the findings of Farokhi et al. (1989), we anticipate that the difference in the size of the vortex core critically influences the dynamics of the free field.

To quantify the difference of the vortex cores between the two configurations, Table 3 lists the normalized radius, $\delta _{\mathrm{VC}}$, of the respective vortex cores and their rotation rate at $r = \delta _{\mathrm{VC}}$. The vortex core size is defined by the first zero crossing of the axial vorticity, $\omega _{x}$, along the jet radius (Oberleithner et al. 2012). The rotation rate is computed via

$$\begin{aligned} {\varOmega }_{\mathrm{VC}} = \frac{\overline{v}_{\theta }\left( r = \delta _{\mathrm{VC}}\right) }{2 \pi \delta _{\mathrm{VC}}}. \end{aligned}$$

(16)

We find that the spatial and temporal scales of the vortex cores of C1 and C2 are distinctively different.

Table 3 $\delta _{\mathrm{VC}}$ for C1–C2

4.3 The unconfined mean flow

Fig. 9

a, b Contour of the time-averaged axial velocity of C1 and C2 superimposed with streamlines of the time-averaged velocity field. c The shape of the respective recirculation bubble, indicated by the contour line of zero axial velocity

Figure 9 displays the time-averaged axial velocity of the different center-body configurations. As was pointed out in the introduction, no attempt was made to produce two swirling jets with precisely the same swirl number. Rather, the similarity is observed in terms of the upstream location of the recirculation bubble. As can be inferred from Fig. 9c this was successful. Nevertheless, differences in the mean axial velocity are evident in Fig. 9. The extent of the recirculation region decreases from configuration $C_{1}$ to $C_{2}$. To allow for a better comparison, the contour line of zero axial velocity for each case is plotted in Fig. 9c.

To quantify the difference in the downstream evolution of the jets, the jet half width is presented in Fig. 10. It is defined as

$$\begin{aligned} r_{0.5} = y(\overline{v}_{x}/\overline{v}_{x \mathrm{max}} = 0.5) \end{aligned}$$

(17)

and represents the center of the outer shear layer. It encompasses the total jet spreading, as in Liang and Maxworthy (2005). C1, with a larger vortex core, clearly shows a larger jet spreading. It is difficult to put this observation into the context of previous studies. Among those studies that report quantitatively on the jet spreading (Liang and Maxworthy 2005; Toh et al. 2010; Chigier and Chervinsky 1967), only Liang and Maxworthy (2005) present two configurations where vortex breakdown is not occurring intermittently, but is present in the mean field. Two factors contribute to the spreading of a swirling jet: turbulent production and a displacement of the jet by the recirculation bubble. The contribution of the first effect is captured by the Reynolds number. Consistently, Liang and Maxworthy (2005) found that at the same Reynolds number the jet spreading increases with the swirl number. This observation was also made qualitatively by Oberleithner et al. (2012), who report that the size of the recirculation bubble grows as the swirl number is increased. This indicates that the dominant contribution to a difference in jet spreading stems from a different displacement of the jet. In this study the Reynolds number is equal for C1 and C2. We argue that the different jet spreading is caused by a different size of the recirculation bubble between C1 and C2 (Fig. 9c). In contrast to Liang and Maxworthy (2005) and Oberleithner et al. (2012), this difference is observed at the same swirl number $S_{\mathrm{B}}$.

Fig. 10

Half width of the jet in the outer shear layer for C1 and C2

4.4 The global mode in the unconfined flow: spatial structure and energy

Next, the properties of the global mode are analyzed by POD. The presentation starts with a discussion of the modal structures obtained from the symmetric and anti-symmetric POD, exemplified with the measurements of C1. In particular, this decomposition yields anti-symmetric structures that are related to the global mode and axisymmetric structures that are related to other phenomena. The resulting spatial modes are shown in Fig. 11. The corresponding POD spectra are presented in Fig. 12.

Fig. 11

a, b Transversal velocity component of the first two anti-symmetric POD modes of C1. c, d Transversal velocity component of the first two axisymmetric POD modes of C1

The first mode and second mode (Fig. 11a, b) correspond well with the first and second mode in Fig. 11 of Oberleithner et al. (2011). As Oberleithner et al. (2011) state, these two modes span the wave pattern of the global mode. Oberleithner et al. (2011) also present their third and fourth mode, which they state are structures uncorrelated with the global mode that describes a meandering motion of the recirculation bubble. Returning to Fig. 11d we observe that this mode has a similar structure. However, no structure similar to Fig. 11c was observed in Oberleithner et al. (2011).

Figure 12a, b shows the relative energy content of the first 100 POD modes computed from the symmetric and anti-symmetric POD approach. It is evident from Fig. 12a that the energy content of the first two modes is nearly equal which, according to Oberleithner et al. (2011), further corroborates that these two modes span a traveling wave. This observation is consistent with a periodic structure like the global mode. As Oberleithner et al. (2011) point out, the temporal behavior of the global mode can be elucidated by investigating the phase portrait of this structure. As we are considering states at which the vortex breakdown is present in the mean flow, the flow has undergone the supercritical bifurcation and the global mode oscillates on its limit cycle (Oberleithner et al. 2012). Thus, the phase portrait should indicate an oscillatory pattern.

Fig. 12

Relative energy content of the first 100 anti-symmetric (a) and symmetric (b) POD modes of C1

Fig. 13

Phase portrait of the first two anti-symmetric temporal coefficients. Each is normalized with the mean amplitude of the first two POD modes recorded during the measurement cycle of C1

Clearly, this is the case from the phase portrait of Fig. 13.

Returning to Fig. 11a, b, it is evident that the anti-symmetric mode pair has $v_{y}(0) \ne 0$. According to Oberleithner et al. (2014), only a mode with an azimuthal wave number of one can have this property. This, in addition to the close agreement of the phase portrait and the spatial structure of the first two anti-symmetric modes to Oberleithner et al. (2011), suggests that the first and second anti-symmetric modes represent the global mode.

Fig. 14

Superposition of one POD mode at largest (left column), respectively, smallest amplitude (right column) and the time-averaged axial velocity for C1. a, b Axial bubble mode; c, d bubble compression mode; e, f: 1st Global base mode; g, h 2nd Global base mode; the axes displayed in g apply to the entire figure. The dotted line in a–h indicates the contour of zero axial velocity in the mean field. The solid line indicates the contour of zero axial velocity in the superposed velocity field

Fig. 15

Caption is the same as for Fig. 14. The time-averaged axial velocity and the POD modes are taken from C2

4.5 The impact of the first POD modes on the time-averaged flow

We turn now to the role of the first and second symmetric POD modes of C1 and C2. To provide a more intuitive understanding of these structures, we consider them in conjunction with the time-averaged flow field. Figures 14 and 15 show the superposition of the mean axial velocity and the respective POD mode of C1 and C2, according to

$$\begin{aligned} v_{x} = \overline{v}_{x} + \mathbf{\Psi }_{i} \cdot a_{i}. \end{aligned}$$

(18)

The subscript i is either 1 or 2, depending on whether the first or second mode is considered. The superposed velocity fields were constructed for the symmetric and anti-symmetric POD modes. Figure 14a, b reveals that the first symmetric mode imposes an axial shift on the position of the upstream stagnation point relative to the time-mean position. At the same time a less pronounced transversal thickening or thinning of the recirculation bubble can be observed. While the downstream end of the recirculation bubble remains unaltered, the size of the recirculation bubble changes. Figure 14c, d shows that the second symmetric POD mode represents a movement of the recirculation bubble that is predominantly present in the downstream end of the recirculation bubble. The upstream end remains largely unchanged in axial position. As for the first symmetric POD mode, the second also represents a lateral elongation or compression of the recirculation bubble. However, the transversal displacement is more pronounced than that of the first symmetric mode. Thus, the first and second symmetric modes describe the change in axial and lateral extent of the recirculation bubble. Additionally, we find that the meandering motion of the recirculation bubble is captured by the first and second anti-symmetric modes. This is displayed in the two bottom rows of Fig. 14, where it is evident that the axial upstream and downstream position remains unaltered to a large extent. However, in particular the upstream end is displaced from left to right.

The first symmetric mode of C2, displayed in Fig. 15a, b also reflects an axial shift of the recirculation bubble. In contrast to C1, the entire recirculation bubble is shifted upstream and downstream around the time-mean position. The movement is not only restricted to the upstream stagnation point as is the case for C1, but also the downstream stagnation point is shifted by a considerable amount. The area of the recirculation bubble appears to change less than for C1. The effect of the second symmetric mode, Fig. 15c, d, is more pronounced for C2 than for C1. The upstream stagnation point shows as little movement as in C1. However, the compression or expansion of the recirculation bubble around the time-mean state is much more pronounced. The first and second anti-symmetric modes in Fig. 15e–h are equal in appearance to Fig. 14e–h. The global mode in C1 and C2 is equally represented by these two POD modes. The impact of these modes on the recirculation bubble is similar.

According to the changes in the flow structure that are captured by each mode, we term the first and second symmetric modes as axial bubble and axial compression modes, respectively. The first and second anti-symmetric modes are termed first and second global base modes.

Comparing these findings with Oberleithner et al. (2011), we find that the POD modes describing the global mode have been clearly identified for both configurations. In addition to measurements taken in a streamwise plane, Oberleithner et al. (2011) took measurements in a crosswise plane. In that plane they identified a POD mode that was interpreted as describing an axial shift in the position of the recirculation bubble. The same behavior is captured in the first and second symmetric modes of the data presented here. Hence, all the important large-scale dynamics are captured by the present analysis.

Table 4 Total fluctuation energy and the contribution of the first two symmetric and anti-symmetric POD modes

The POD analysis allows to extract the energy content of a given mode. This is used to measure the difference between the configurations C1 and C2. The first and second anti-symmetric modes in Table 4 have almost the same contribution to the total energy in both cases. Contrarily, the contribution of the symmetric modes changes significantly for each configuration. From C1 to C2, the absolute energy content of the first symmetric mode increases by approximately 10 %. The energy of the second symmetric mode is reduced by 47 % from C1 to C2. The most significant contribution to the large-scale dynamics stems from the axial bubble modes, which is evident from their energy contribution shown in Table 4. The contribution of the two global base modes ranks second and third. This is opposed to Oberleithner et al. (2011) who found these two modes to be dominant. This discrepancy may be related to the different experimental setup. The contribution of the bubble compression mode to the total fluctuating energy is for both configurations significantly smaller than that of the global base modes and the axial bubble mode. In particular for C2, Fig. 15c, d shows a large impact of this mode on the flow field. However, given its small energy contribution (Table 4) it represents rather extreme events that occur infrequently.

4.6 The correlation of the POD modes and the pressure in the vortex core

As shown in Fig. 13, the two anti-symmetric POD modes form a pair that describes the periodic oscillation of the global mode. This section addresses whether the two symmetric modes are correlated with the global mode or with the fluctuating pressure in the vortex core. It was demonstrated by Farokhi et al. (1989) that a smaller vortex core leads to a smaller mean static pressure in the center of the vortex core. Here, we are not primarily interested in time-mean quantities, but whether the fluctuations of the static pressure of the incoming vortex core are related to the dynamics of the recirculation bubble. To quantify the correlation, the linear correlation coefficient is calculated via

$$\begin{aligned} R(X,Y) = \frac{C(X,Y)}{\sqrt{C(X,Y)C(X,Y)}}, \end{aligned}$$

(19)

where C(X, Y) denotes the covariance matrix. X and Y are vectors of random variables. A value of $R = 0$ indicates that the two variables are uncorrelated, whereas a value of $R = \pm 1$ indicates that the two random variables are fully correlated. In this case, the random variables are the time coefficients of the different POD modes or the vector of the fluctuating pressure. Thus, the static pressure is computed for each PIV snapshot according to the radial equilibrium equation (Greitzer et al. 2004),

$$\begin{aligned} p(t) = \rho \int _{0}^{r_{max}}{\frac{v_{\theta }(t)^{2}}{r}}{\hbox {d}}r, \end{aligned}$$

(20)

which is integrated radially inward, assuming a steady inviscid symmetric vortex core with zero radial velocity. The assumption of zero radial velocity is a very strong assumption for strongly swirling jets. Additionally, the instantaneous velocity fields are in general not axisymmetric. Nevertheless, this assumption may be reasonable in the immediate vicinity of the nozzle. A more accurate representation of the pressure may be obtained by integrating the full radial momentum equation, neglecting the viscous terms. However, neither the temporal nor the out-of-plane gradient can be computed from the present data. Since we observe that an inclusion of the remaining gradient terms that stem from the convective acceleration in the momentum equation, into the pressure computation, does not qualitatively change the pressure distribution, we stick to the widely used radial equilibrium equation. The pressure signal is then extracted in the immediate vicinity of the nozzle and the jet axis, at $x = 0.03D$ and $y = 0$.

The correlation coefficients in the top four rows of Table 5 exhibit that the axial bubble and the bubble compression modes of C1 and C2 are not correlated to either of the global base modes. Nevertheless, it seems plausible that a change in the size or position of the recirculation bubble alters the amplitude of the global mode. A possible explanation for the lack of correlation may be different temporal scales of the symmetric modes and the global mode. Hosseini et al. (2015) investigated the wake of a pyramid and also found a POD mode pair that describes the vortex shedding and a dominant symmetric mode that describes an axial shift of the recirculation bubble. These authors used time-resolved PIV for their measurements and showed that the axial shift of the recirculation bubble occurs at a distinctively smaller frequency than the vortex shedding. If the situation were similar in this flow configuration, a shift of the recirculation bubble and a change of the global mode may be correlated, but with a time delay. In this case, the modal coefficients would appear as uncorrelated in the present study, even though both phenomena are correlated. However, this is only formulated as a speculation since the data in the present study are not sufficiently time-resolved to determine the frequencies at which the different phenomena occur.

The correlation coefficient $R(a_{1\mathrm{sym}},p)$ shows a significant correlation of the fluctuating pressure and the modal coefficient of the first symmetric mode. This correlation is especially pronounced for C2 with the smaller vortex core. While the radial equilibrium equation cannot be expected to describe the pressure evolution quantitatively correct, it shows one mechanism by which this correlation may occur. In its differential form,

$$\begin{aligned} \frac{\mathrm{d}p}{\mathrm{d}r} = \rho \frac{v_{\theta }^{2}}{r}, \end{aligned}$$

(21)

it indicates that a change in pressure is balanced by a change in the azimuthal velocity. Billant et al. (1998) derived a necessary criterion for vortex breakdown, stating that vortex breakdown occurs, if

$$\begin{aligned} \frac{\int _{0}^{\infty }{\frac{v_{\theta }^{2}(r,x_{0})}{r}{\hbox {d}}r}}{v_{x}^{2}(0,x_{0})}\ge 0.5, \end{aligned}$$

(22)

where $x_{0}$ is an axial station upstream of the stagnation point. Depending on the shape of the azimuthal velocity profile and the resulting overshoot in axial velocity on the jet axis, the values of this criterion may differ from snapshot to snapshot, which correlates to a more upstream or downstream position of vortex breakdown. An axial shift in the position of vortex breakdown necessarily changes the axial position of the recirculation bubble. This axial shift is described by the axial bubble mode. The remaining correlation coefficients indicate that no or only a very weak correlation prevails between the global base modes, the bubble compression mode and the pressure. Since the bubble compression mode is also uncorrelated with all other modes shown here, the compression of the bubble is driven by another mechanism that appears to be unrelated to the size of the incoming vortex core.

Table 5 Correlation coefficient of various POD modes and fluctuating pressure

4.7 Scaling of the global mode frequency

The PIV data analyzed so far are not sufficiently time-resolved to allow any insight into the temporal dynamics of each flow configuration. Thus, the analysis is complemented by hot wire measurements at $y = 0.53D$ and $x = 0.2D$. This position corresponds to the position of the outer shear layer in the vicinity of the nozzle. At this location, a good signal to noise ratio between the frequency peak of the global mode and broadband turbulent noise was obtained. The result of the hot wire measurements is presented in Table 6. The frequency of the global mode in C2 is 27 % higher than in C1. To provide a comparable quantity, the frequency of the global mode normalized with the rotation rate of the vortex core on the jet axis is listed in Table 6. The normalized frequency shows that the global mode frequency is determined by the rotation rate on the jet axis, which is basically the rate of the solid body rotation. The smaller vortex core implies higher rates, and thus, a higher global mode frequency.

Table 6 Global mode frequency, $f_{\mathrm{GM}}$, and the global mode frequency normalized with the rotation rate of the vortex core, ${\varOmega }_{\mathrm{VC}}$, on the jet axis for C1 and C2

4.8 The upstream stagnation point: spatial dynamics

We turn our attention now to the dynamics of the upstream stagnation point. Since only the large-scale dynamics are investigated in this study, instantaneous velocity fields are constructed from the mean flow and the axial bubble, bubble compression and the global base modes. The feature tracking outlined in Sect. 3.3 is then used to identify the instantaneous position of the upstream stagnation point.

Fig. 16

Reconstructed velocity field at four arbitrary phase angles of the global mode. a–d The phase angles are $36^{\circ }, 137^{\circ }, 73^{\circ }$ and $6^{\circ }$. Red dots mark the position of saddle points in the velocity field

The reconstructed velocity fields are shown at four arbitrary phase angles of the global mode in Fig. 16a–d. This figure illustrates the evolution of the recirculation bubble and the upstream stagnation point for C1. The location of the saddle points is marked by red dots. The feature tracking successfully identifies the saddle points in each velocity field. The predominantly two-dimensional structure of the saddle points is also visible in this figure. Typically, 20 % of the PIV snapshots were rejected, because the saddle point structure was found to be distorted by three-dimensional effects.

The results of the upstream stagnation point tracking are presented in the histograms of Fig. 17a, b. For C1, shown in Fig. 17a, the distribution of the position of the upstream stagnation point in the streamwise direction exhibits two maxima at circa $x = 0.3D$ and $x = 0.55D$. The position of the upstream stagnation point appears to be varying relatively continuously between these two extrema and around the time-mean location. The distribution of the upstream stagnation point of C2, Fig. 17b also shows two extrema at the approximately same position as C1. The location of the stagnation point is more concentrated around these extrema, when compared to C1. In the vicinity of the stagnation point relatively few occurrences of the upstream stagnation point are found. In this case, there appears to be a bimodal state, where the position of the upstream stagnation point jumps rather abruptly between two positions. A larger difference in the two histograms is evident from the lateral distribution of the upstream stagnation point. Here, C1 shows a stronger variation in the y coordinate of the stagnation point. This is in line with the discussion of the modal structure and the energy content of the POD modes. While the second symmetric mode of C2 showed a stronger compression or inflation of the recirculation bubble, the energy content of the mode indicated that these extreme events occur infrequently. This is recaptured by the distribution of the upstream stagnation point that varies stronger in the lateral direction for C1, where the second symmetric mode had a larger energy content than for C2. The difference in the axial position of the stagnation point is consistent with the difference in the first symmetric mode. This mode showed for C1 that the downstream stagnation point remains fixed. Only the upstream end of the recirculation bubble moved in position. For C2, the first symmetric mode represents an axial shift of the entire recirculation bubble, which is in line with a bimodal state.

Fig. 17

a, b Two-dimensional histogram of the position of the upstream stagnation point for C1, respectively C2. The time-mean position is marked by an ×

5 Conclusion

This study investigated the influence of the initial vortex core size on the near field of an unconfined swirling jet. Emphasis was placed on the dynamics of the breakdown bubble and the associated most energetic coherent structures.

The swirling jet was generated by a radial-inlet-type swirler and then guided through a mixing tube and released through a nozzle into the unconfined free field. LDA measurements were conducted inside the mixing tube, to analyze the swirl-generating mechanism. Stereo PIV measurements were conducted in the unconfined region shortly downstream of the contraction. Low-order representations of the dominant coherent structures in that region were developed based on POD and a feature tracking approach based on a critical-point-identification routine.

Measurements in the mixing tube show that center-bodies with a honeycomb element are suitable for passively controlling the tangential velocity profile in the mixing tube of the setup. In turn, the shape of the tangential velocity profile determines the size of the vortex core in the nozzle exit plane and thus controls the initial conditions of the unconfined swirling jet. It was demonstrated that the center-bodies of different diameters lead to different tangential velocity profiles by creating a region of non-rotating fluid that is of different size. This region of non-rotating fluid is set back into rotation by an annular stream of strongly swirling fluid. Depending on the extent of the non-rotating region, the tangential velocity profile that forms the vortex core in the nozzle exit plane has its extremum at larger or smaller radii.

PIV measurements of the unconfined flow were conducted for two different center-bodies and, respectively, two different initial velocity profiles. Both configurations shared the same swirl number in the immediate vicinity of the nozzle, but showed substantial differences in time-mean quantities, such as the jet spreading and the shape of the recirculation bubble. Exploiting the symmetry properties of the coherent structures, we can clearly identify a POD mode pair that spans the basis for the oscillating global mode. The spatial structure and energy content of this mode were insensitive to the vortex core sizes, whereas its oscillation frequency clearly correlates with the base flow rotation rate. We further identified two axisymmetric POD modes that exhibit a strong dependence of their energy content on the initial vortex core size. The more energetic is related to an axial shift of the recirculation bubble, whereas the less energetic mode represents a change of lateral extent. The temporal evolution of the most energetic mode was found to be correlated with pressure fluctuations inside the incoming vortex core. This suggests that the fluctuations of the breakdown bubble are related to fluctuations of the incoming azimuthal velocity profile, which drives pressure fluctuations. A smaller initial vortex core, and associated lower core pressure, results in stronger fluctuation intensities of the pressure and the bubble position.

The influence of the vortex core size on the bubble dynamics was investigated by tracking the upstream stagnation point from the Q-criterion of the PIV snapshots. Two-dimensional histograms of the saddle point locations revealed that a larger initial vortex core is linked to smooth fluctuations of the breakdown bubbles position around the time-mean position. The smaller initial vortex core led to discrete fluctuations of the instantaneous position that can be described as bimodal.

In successfully tracking the upstream stagnation, this study established that a vortex criterion-based approach may be a viable alternative to the identification of flow features in three-dimensional velocity fields via the Poincaré–Hopf index.

This study reveals the significance of the inflow profile for characteristics of the swirling jet dynamics and the insufficiency of a swirl number definition that does not account for the specific velocity profile. This study shows two main mechanisms that are determined by the vortex core size. For the same amount of swirl, a smaller vortex core size generates lower core pressures and thus stronger pressure fluctuations, which affect the stability of the breakdown bubble. A smaller vortex core size with the same amount of swirl also implies faster rotation rates of the vortex core, which affects the temporal dynamics of the helical global instability.