1 Introduction

Phononic crystals (PCs) are artificial periodic structures with remarkable frequency selectivity, that is, the PCs can shield the vibration in a specific band gap frequency range [1,2,3,4,5]. The superior property has great application prospects in the field of vibration isolation [6,7,8,9], acoustic filtering [10, 11]and energy harvesting [12, 13], etc.

At present, there are two dominant band gap generation mechanisms, namely Bragg scattering [14, 15] and local resonance [16, 17]. The hybridization phononic crystal [18, 19]that has attracted much attenuation in recent years is generated by the coupling effect of Bragg scattering and local resonance, so it is still reasonable to classify the existing band gap mechanisms into two categories. According to the corresponding mechanism, Bragg phononic crystal and locally resonant phononic crystal (LRPC) can be constructed, respectively. Thereinto, Bragg PCs generally have a high operating frequency and are not convenient for low-frequency vibration engineering application [20,21,22,23,24]. Unlike the strict periodicity and large size requirements of Bragg PCs, the local resonance mechanism proposed by Liu [25] can obtain low-frequency band gap using small size structure. However, the local resonance band gap (LRBP) obtained by conventional structure is still narrow, which poses a great challenge for the widespread application of LRPC.

To customize the wave attenuation region with a low-frequency broadband, many investigations have been carried out on the structural design of primitive cell. According to the material composition, the common local resonance structures can be divided into single-component and three-component LRPCs. The former generally require precision manufacturing or even 3D printing technology [26, 27], and have complex structures [28], low stiffness [29] and high manufacturing costs. This determines that they are more suitable for precision parts in the laboratory than actual engineering. Instead, the three-component structure was put forward along with the local resonance theory, which usually composed of heavy scatterer, soft coating layer and matrix. Generally, most engineering structures can be approximated as two-dimensional objects for research, such as row of piles [30, 31], foundations [32] and wave barriers [33]. Therefore, as long as the material and structure parameters are selected reasonably, the LRBP can be generated without complicated procedures. This determines that it is easy to implement and apply, so it still maintains tremendous vitality in the field of scientific research and engineering.

Previous investigations have mainly focused on the single primitive cell system, and the regulation of material [34,35,36] and geometric parameters [37, 38] on the band gap has been adequately discussed. Low frequency and broadband have always been the focus of researchers, but it is generally difficult to obtain them simultaneously by relying only on single cell. On the basis, multi-oscillator system is proposed to improve the attenuation efficiency by producing multiple band gaps. To obtain a wider band gap ranges in a limited two-dimensional plane, the hierarchical structure has been adequately investigated with abundant achievements [39,40,41,42,43,44]. Lee and Jeon [45] derived the power transmission coefficient of layered hierarchical structure based on transfer matrix method, which can open multiple band gaps in broadband frequency ranges. Wu et al. [46] proposed two-order hierarchical structure, and investigated the band gap properties based on spectral element method. The results indicate the micro-stop-bands and macro-stop-bands can be obtained simultaneously, which expand the Bragg band gap range and width. Mousanezhad et al. [47] investigated the band structures of hierarchical honeycombs architecture by finite element method (FEM), and found hierarchical design is able to generate new Bragg band gaps and shift the existing band gaps to lower frequencies. Miniaci et al. [48] designed a kind of hierarchical large-scale structure for seismic wave mitigation, which has a wider band gap than ordinary structure. For the local resonance band gap, the inward hierarchical structure is an effective way to expand the band gap. The usual operation is to set the primitive cell into a concentric ring structure, where the scatterer and coating layer are spaced apart, and then optimize the band gaps by adjusting the structure parameters. Zhou and Chen [49] discussed the band structure characteristics of locally resonant phononic crystal with periodic multilayered cylindrical electroactive polymer inclusions by FEM. The results shown that the two-layer structure can create two band gaps and the band gap boundaries can be regulated by applying electric field upon the electroactive layers. Zhou et al. [43] investigated the band structure and transmission spectra of multilayered LRPCs and found that the band gaps can be extended to multiple ranges by increasing the number of inclusion layers. Keeping the same filling fraction, Lei et al. [44] investigated the regulation law of concentric ring LRPCs using updated improved plane wave expansion method. As the number of layers of the concentric ring metamaterial increases, Chen et al. [41] pointed out that the structure produces strong coupling effect, which results in the negative effective mass density in multiple frequency ranges and generates more band gaps. Liu and Reina [50] simplified inward hierarchical structures into the mass-spring chains with different levels, and deduced the corresponding effective mass formula and dispersion relation. Xu et al. [51] also proposed one-dimensional hierarchical lumped mass-spring analytical model to investigate the dispersion relations of the inward hierarchical metamaterials, and tailored the band gaps with different frequency regions based on theoretical analysis achievements. An et al. [52] derived the general formula of hierarchical metamaterial with multilevel internal resonators based on effective mass density theory, the results indicate the total band width increases with the hierarchy.

However, we should also realize that the Bragg band gap is strictly dependent on the periodicity of the structure, and the band gap width decreases significantly when the structural periodicity is perturbed [53] and the scatterer symmetry is reduced [54]. Therefore, they have higher requirements on production technology and precision. Furthermore, the inward hierarchical structures need to guarantee strict concentric circle configuration to take advantage of the multiple band gap. With the increase of the number of layers, they give richer band gaps, but also divide heavy scatterer and the light coating layer into excessive smaller pieces, which increases the denser weak interface and reduces structural stability. Previous studies [35] have pointed out that significant property differences between the components underlie the formation of LRBP, and the contact interfaces are the relatively weak zone of the structure because of accumulative interfacial damages, local debonding and manufacturing defection [55]. Therefore, the inward hierarchical structures are actually difficult to fabricate, and may lead to stability and durability issues with the increasing number of inclusion layer, so they are currently limited to laboratory preparation and still have difficulties in practical applications.

Therefore, it is challenging to design structures that has low-frequency broadband properties and are easy to be constructed. In this paper, the two-dimensional three-component outward hierarchical locally resonant phononic crystals (OHLRPCs) are proposed and the band gap properties are investigated to obtain low-frequency broadband. This paper is structured as follows: the OHLRPC model with triple oscillator system is presented and the finite element method (FEM) for band gap calculation is exhibited. The band range and transmission properties of OHLRPC are calculated by dispersion analysis and frequency response function, respectively. The vibration mode properties are investigated to reveal the band gap mechanism. The band gap range determination equation based on effective mass theory is proposed to get quickly the band gap ranges, and then the parameter analysis is discussed to explore the development laws of band gaps. Furthermore, the OHLRPC with multiple cells are expanded and investigated in detail. Finally, the main conclusions are summarized. These valuable results can provide references for the design of local resonance structure in low-frequency vibration control field.

2 Model and methods

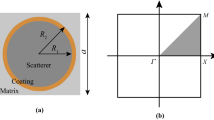
To investigate the band characteristics of OHLRPC, the single cell and irreducible Brillouin zone are first displayed in Fig. 1, which consists of a basalt scatterer, enveloped by expanded polystyrene and embedded in the cement mortar.

Fig. 1
figure 1

The primitive cell and irreducible Brillouin zone

Full size image

To facilitate the band gap properties analysis, a brief model with three types of primitive cells is used in this paper, as shown in Fig. 2. Among them, M refers to the matrix, and A, B and C refer to the three types of primitive cells, respectively. They have different scatterer radiuses, but the ratio of coating layer radius to scatterer radius is set to a constant value RO = 1.2, and the corresponding geometric parameters are demonstrated in Table 1. The lattice constants of primitive cell and supercell are marked as \(a_{0}\) = 0.15 m and \(A_{0}\) = 3 \(a_{0}\), respectively. The material parameters listed in Table 2 are the same as in reference [56].

Fig. 2
figure 2

Schematic illustration of OHLRPC primitive cell

Full size image
Table 1 The geometric parameters of OHLRPC
Full size table
Table 2 The material constant of OHLRPC
Full size table

The band structure calculation of OHLRPC is carried out by FEM, which can not only deal with complex primitive cell models and give high-precision results, but also carry out rich data mining and in-depth mechanism analysis. For the homogeneous isotropic medium, the governing equation of elastic wave propagation is expressed as

$$\rho {\mathbf{\ddot{u}}} = \rho {\mathbf{f}} + (\lambda + \mu )\nabla (\nabla \cdot {\mathbf{u}}) + \mu \nabla^{2} {\mathbf{u}},$$
(1)

where u is the displacement vector, r is the position vector, t is the time, ρ is the mass density, λ and μ are the Lamé constants, \(\nabla\) is the Hamilton differential operator, \(\cdot\) is the dot product. Due to the introduction of periodic boundary conditions in OHLRPC, the band structure can be obtained by analyzing the primitive cell based on the Bloch-Floquet theory, and the node displacement on the periodic boundary conditions should satisfy the following equation:

$${\varvec{u}}({\varvec{r}},t) = e^{{i({\varvec{kr}} - \omega t)}} {\varvec{u}}_{{\varvec{k}}} ({\varvec{r}}),$$
(2)
$${\varvec{u}}_{{\varvec{k}}} ({\varvec{r}}{ + }{\varvec{R}}){ = }{\varvec{u}}_{{\varvec{k}}} ({\varvec{r}})e^{{i{\mathbf{k}} \cdot {\mathbf{R}}}} ,$$
(3)

where k is wave vector, \({\varvec{u}}_{{\varvec{k}}} ({\varvec{r}})\) is the wave amplitude, R is lattice vector, ω is the angular frequency. Introducing the periodic boundary conditions of displacement, the dynamics equation is transformed into the eigenvalue problem:

$$({\varvec{K}} - \omega^{2} {\varvec{M}}){\varvec{U}} = 0,$$
(4)

where K is stiffness matrix of typical element; M is mass matrix; U is the displacement matrix of all nodes. The wave vectors are selected equidistantly along the irreducible Brillouin boundary (M–Г–X–M) presented in Fig. 1(b), and the relationship between the wave vector and the eigenfrequency \(k{ - }\omega\) is solved by Equ. (4), which is the band structure. The frequency range in which there is no dispersion curve in the band structure is the band gap. Due to the superiority of periodic boundary condition processing, the commercial software COMSOL is used to calculate the band structure of OHLRPC.

3 Results and discussion

3.1 Band gap mechanism analysis

Before analyzing the band gap of OHLRPC, the band structure of single cell with R1 = 0.04 m is calculated and presented in Fig. 3(a), and the LRBP interval is marked with a red-shaded area. The band gap range of single cell is 72.2–89.7 Hz, and the band gap width is 17.5 Hz, which shows the typical characteristics of local resonance represented by the flat lines.

Fig. 3
figure 3

The band structures of regular primitive cell and OHLRPC primitive cell

Full size image

Modal analysis plays a vital role in understanding the mechanism of band gap, so it is usually used to represent the characteristics of LRBP. The vibration modes of points (S1–S5) of flat line represented in Fig. 3 are exhibited in Fig. 4. The normalized vibration displacement is presented by the gradient fill colors, and the displacement amplitude gradually increases from blue to red. In addition, the arrows indicate the vibration direction at that point, and its magnitude is proportional to the displacement value. As shown in Fig. 4, the main displacement of primitive cell is concentrated in the scatterer even if the vibration directions are different, it means that different wave vectors correspond to the same eigen frequency in most wave vector directions, that is, different wave fields represent the similar vibration mode, which is the phenomenon of local resonance. Therefore, it is sufficient to select any point on the lower boundary when analyzing the mechanism of the band gap. For the sake of convenience, the point M of the band gap starting frequency and point Γ of the band gap ending frequency are uniformly selected in the subsequent analysis of the band gap mechanism.

Fig. 4
figure 4

The vibration modes at the flat lines of band gap starting frequency

Full size image

The vibration modes of band gap boundaries (point S1 and E1) are demonstrated in Fig. 5, for the starting frequency of band gap, the displacement is mainly concentrated in the scatterer in the form of translational vibration. This leads to a significant resultant force, and the strong coupling of resultant force and traveling wave in matrix opens the band gap. For the ending frequency of band gap, the scatterer and the matrix move in opposite directions, and the coupling effect of scatterer and matrix is weakened, which results in the closure of the band gap. The more detailed analysis of band gap mechanism for the single cell can refer to the literature [57].

Fig. 5
figure 5

The vibration modes of band gap boundaries

Full size image

In addition, this configuration possesses only single band gap in the studied frequency range, thus we can conveniently observe the interaction and effect of three primitive cells. For the convenience of comparison, the band structure of OHLRPC is demonstrated in Fig. 3(b). The band gap regions of outward hierarchical structure are 48.1–51.8 Hz, 57.8–64.6 Hz and 72.2–89.3 Hz, and the band gap width is 27.6 Hz. Obviously, the OHLRPC structure not only increases the two lower LRBPs, but also increases the band gap width by 57.7%.

To comprehend the band gap properties of OHLRPC, the vibration modes of each band gap boundary are demonstrated in Fig. 6. The meaning of the colors and arrow marks are the same as in Fig. 5. For the first band gap, the vibration modes of band gap boundaries (Points A1 and A2) marked in Fig. 3(b) are exhibited in Fig. 6(a) and (b). Obviously, the displacement is mainly concentrated on the type A scatterers for the starting frequency (Point A1) of first band gap. Even though their translational vibration directions are different, they exhibit a combined motion along the direction D1. Therefore, the interaction between scatterers A and matrix generates strong coupling effect, which opens the first band gap. In the ending frequency of first band gap (point A2), the scatterers A move in the opposite direction from all other cells and the matrix (Area B + C + M). To distinguish the vibration direction, the areas A are marked with white letters and area B + C + M is marked with black letters. Their relative motion has weakened the coupling effect, so the band gap is closed.

Fig. 6
figure 6

The vibration modes of OHLRPC in the band gap boundaries

Full size image

As shown in Fig. 6(c), the similar rules of vibration modes can be observed in the second band gap. For the starting frequency (Point B1) of second band gap, the type B scatterers present clear translational movement, which produces strong coupling effect and open the second band gap. Different from the ending frequency of first band gap, although the displacement at the ending frequency of second band gap is mainly concentrated in the scatterers B, the smaller displacement in the same direction can be still observed in the scatterers A. Therefore, the area (A + B) exhibits opposite movement to that of the zone (C + M), and the weakened coupling effect causes the close the second band gap.

Similarly, the translational vibration of scatterers C also produces significant coupling effect at 72.2 Hz, which leads to the third band gap, as shown in Fig. 6(e). For the ending frequency of third band gap, different details can also be observed. The displacement is mainly concentrated in scatterers C, and scatterers A and B also possess the larger displacements in the same direction. The coupling between the zone (A + B + C) and the matrix (M) is weakened, so the third band gap is no longer maintained.

To sum up, the increase of primitive cells produces more band gaps, and the corresponding vibration mode characteristics of starting frequencies indicate the band gap is determined by the translational vibration of specific cell. Each band gap is generated by the corresponding type of primitive cells, respectively. The number of band gaps is determined by the type of local resonance cell rather than the number. In other words, there is a one-to-one correspondence between the band gap and the cell type.

To further analyze the generation mechanism of band gap, the characteristics of band gap are discussed from the perspective of energy. The kinetic energy density distribution of band gap boundaries is shown in Fig. 7. In the starting frequency of each band gap, the kinetic energy is concentrated in the corresponding scatterer, respectively. This result is consistent with the vibration modes shown in Fig. 6. For the ending frequency of first band gap, the type A scatterers occupy the main kinetic energy, and the energy decreases continuously along A–B–C. On the contrary, the kinetic energy flows along A–B–C and gradually increases in the ending frequency of second band gap. For the ending frequency of third band gap, almost all kinetic energy flows to the scatterer C, followed by the matrix, and the scatterer A and B has almost no kinetic energy.

Fig. 7
figure 7

The kinetic energy density of OHLRPC in band gap boundaries

Full size image

In addition, the distribution of elastic strain energy density is demonstrated in Fig. 8 to support the analysis. For the starting frequency of each band gap, the elastic strain energy is mainly held by the coating layer of the corresponding primitive cell, because there is only the lateral vibration of the corresponding scatterer at this time. For the ending frequency, the elastic strain energy gradually flows from the scatterer A of the first band gap to the scatterer C of the third band gap. The difference is that there is no strain energy in the matrix for the ending frequency of third band gap, because the strain energy can only be generated by the coating layer.

Fig. 8
figure 8

The elastic strain energy density of OHLRPC in band gap boundaries

Full size image

Combing the energy distribution and vibration mode characteristics, we can find that OHLRPC can be equivalent to a distributed spring-mass system containing three groups of elements. Among them, the scatterer and coating layer can be regarded as mass and spring, respectively. This provides a theoretical basis for the subsequent parametric analysis and advanced design.

3.2 Attenuation properties analysis

The band structure only represents the theoretical shielding interval, the actual attenuation efficiency can be obtained by the frequency response function (FRF) test of practical finite structure. The FRF is generally defined as:

$$T = 20\log \frac{V}{{V_{0} }},$$
(5)

where T is FRF, dB; V and V0 are the displacement amplitude value of the receiving and excitation terminal, respectively. The analysis model with 5 cycles is shown in Fig. 9, the displacement excitation is applied on the left side of the model and the response values are extracted on the right side. The frequency is swept in steps of 0.1 Hz within 0–120 Hz in 0.1 Hz to ensure sufficient accuracy. In addition, three displacement extraction reference lines A, B and C are marked with red dotted lines along the long side of the model through the center of the scatterers in the figure. After completing the frequency response calculation by FEM, the displacement amplitude value can be extracted along the reference lines in post-processing for subsequent attenuation characteristic analysis. The transmission curve of OHLRPC is demonstrated in Fig. 10, and the shaded area where the value is less than 0 is the attenuation ranges. Compared with the band structure shown in Fig. 3(b), the attenuation zones are consistent with the band gaps.

Fig. 9
figure 9

The schematic representation of OHLRPC model used for FRF

Full size image
Fig. 10
figure 10

The frequency response function of OHLRPC

Full size image

To further comprehend the effects of band gap on vibration attenuation of OHLRPC, the displacement fields under different frequency excitation are discussed to represent the attenuation characteristics of OHLRPC, as shown in Fig. 11. In the displacement field of f = 50 Hz, since the frequency is in the first band gap, the main displacement is concentrated in the scatterer A, which indicate that the scatterers A absorb energy to prevent the propagation of elastic waves. Similarly, in the displacement fields of f = 60 Hz and f = 80 Hz, the scatterers B and C occupy the main displacements, respectively. The displacement distribution characteristics corresponds to the band gap mechanism described above. Instead, since f = 100 Hz is located in the passband interval, the main displacement is distributed in the matrix and the elastic wave can pass through the entire OHLRPC structure.

Fig. 11
figure 11

The displacement fields of OHLRPC under different frequency excitation

Full size image

Furthermore, the displacement of primitive cells is extracted along the reference line marked in Fig. 9 is shown in Fig. 12. For the displacement distribution at f = 50 Hz, the scatterer obviously has the largest displacement and the matrix has the smallest displacement, so the displacement curve drops sharply at the cell boundary, as shown in the enlarged view of Fig. 12(b). Then, from the excitation terminal to the receiving terminal, the displacement decays exponentially along the cell position in a serration pattern. Among them, the scatterer A has the most significant drop in amplitude. Besides, the cell B and C also show an exponential decrease, but the absolute amplitude is relatively smaller, which is not reflected in the previous vibration modes. Apparently, the similar patterns can be observed in the displacement distributions of f = 60 Hz and f = 80 Hz, they all show a significant exponentially decreasing trend with high coefficients of determination. The difference is that the amplitude of scatterer B is most pronounced at f = 60 Hz, while the value of scatterer C is dominant at f = 80 Hz. This again proves the one-to-one correspondence between the band gap and the primitive cell obtained in the Sect. 3.1. For the displacement distribution at pass band (f = 100 Hz), the matrix displacement and scatterer displacement are in the same order of magnitude, and even larger in cell B and C, as shown in Fig. 12(d). This indicates that the elastic waves at passband frequencies can pass through the OHLRPC without being affected by the shielding of the band gap.

Fig. 12
figure 12

The displacement distribution with the position of primitive cells

Full size image

3.3 Theoretical determination of band gap range

In the theoretical analysis of the band gap, the conventional LRPC primitive cell generally can be equivalent to a single spring-mass system [58] to facilitate the study, as shown in Fig. 13(a). According to the vibration modes and energy distribution characteristics of the scatterer and coating layer in the Sect. 3.1, there is a one-to-one correspondence between band gaps and primitive cells, so OHLRPC can be equivalent as a spring-mass system with three vibrators in series, as shown in Fig. 13(b).

Fig. 13
figure 13

The spring-mass model of regular and OHLRPC primitive cells

Full size image

Based on the effective mass theory [59,60,61], the spring-mass system of OHLRPC can be further equivalent to an effective mass model with three-freedom, as shown in Fig. 14. To investigate the propagation of elastic wave, an infinite mass-in-mass lattice structure is constructed and demonstrated in Fig. 15, which is connected by the unit cell with linear springs.

Fig. 14
figure 14

The spring-mass system and effective mass model of OHLRPC

Full size image
Fig. 15
figure 15

The infinite mass-in-mass lattice structure of OHLRPC

Full size image

For the mass-in-mass lattice structure of OHLRPC, the motion equations for the i-th unit cell can be written as:

$$m_{0}^{i} \ddot{u}_{0}^{i} + k_{0} (2u_{0}^{i} - u_{0}^{i - 1} - u_{0}^{i + 1} ) + k_{1} (u_{0}^{i} - u_{1}^{i} ) + k_{2} (u_{0}^{i} - u_{2}^{i} ) + k_{3} (u_{0}^{i} - u_{3}^{i} ) = 0,$$
(6)
$$m_{1} \ddot{u}_{1}^{i} + k_{1} (u_{1}^{i} - u_{0}^{i} ) = 0,$$
(7)
$$m_{2} \ddot{u}_{2}^{i} + k_{2} (u_{2}^{i} - u_{0}^{i} ) = 0,$$
(8)
$$m_{3} \ddot{u}_{3}^{i} + k_{3} (u_{3}^{i} - u_{0}^{i} ) = 0,$$
(9)

The motion equation can also be written in matrix form:

$$\varvec{M\ddot{U}} + {\varvec{KU}} = {\varvec{F}},$$
(10)
$${\varvec{M}} = \left[ {\begin{array}{*{20}c} {m_{0} } & 0 & 0 & 0 \\ 0 & {m_{1} } & 0 & 0 \\ 0 & 0 & {m_{2} } & 0 \\ 0 & 0 & 0 & {m_{3} } \\ \end{array} } \right],$$
(11)
$${\varvec{U}} = \left[ {\begin{array}{*{20}c} {u_{0} } & {u_{1} } & {u_{2} } & {u_{3} } \\ \end{array} } \right]^{T} ,$$
(12)
$${\varvec{F}} = \left[ {\begin{array}{*{20}c} F & 0 & 0 & 0 \\ \end{array} } \right]^{T} ,$$
(13)
$${\varvec{K}} = \left[ {\begin{array}{*{20}c} {k_{1} + k_{2} } & { - k_{1} } & { - k_{2} } & { - k_{3} } \\ { - k_{1} } & {k_{1} } & 0 & 0 \\ { - k_{2} } & 0 & {k_{2} } & 0 \\ { - k_{3} } & 0 & 0 & {k_{3} } \\ \end{array} } \right],$$
(14)

The following relation can be obtained by solving the above equations.

$$\left( {m_{0} + \sum\limits_{i = 1}^{n} {m_{i} \frac{{\omega_{i}^{2} }}{{\omega_{i}^{2} - \omega_{{}}^{2} }}} } \right)\;\omega_{{}}^{2} U_{0} + F_{0} = 0\;,n = 1,2,3,$$
(15)
$$\omega_{i} = \sqrt {k_{i} /m_{i} } ,$$
(16)
$$k_{i} = \frac{{\pi (R_{si} C_{11} + R_{ci} C_{44} )}}{{R_{ci} - R_{si} }}\;\;,\;i = 1,2,3,$$
(17)

where, n is the number of cell type; \(k_{i}\) is the equivalent stiffness of cell i; Rsi and Rci are the radius of scatterer and coating layer; C11 and C44 are elastic parameters of coating layer; \(\omega_{i}\) is the nature frequency of cell i; \(m_{i}\) is the equivalent mass; \(m_{eff}\) is the effective mass. To represent the same motion by a single effective mass, the following equation must be satisfied:

$$F_{0} = - m_{eff} \omega^{2} U_{0} ,$$
(18)

Combining formulas (15) and (18), the effective mass of OHLRPC with three type oscillators can be expressed as:

$$m_{eff} = m_{0} + \sum\limits_{i = 1}^{n} {m_{i} \frac{{\omega_{i}^{2} }}{{\omega_{i}^{2} - \omega_{{}}^{2} }}} \;\;,n = 1,2,3,$$
(19)
$$m_{st} = \sum\limits_{i = 0}^{n} {m_{i} } \;\;,n = 0,1,2,3,$$
(20)

where, \(m_{st}\) is the static mass of system. Solving the relationship of \(m_{eff} /m_{st} - \omega\) by sweeping the angular frequency within the target frequency range, and then the normalized effective mass curve can be obtained. As shown in Fig. 16, the effective mass meff is equal to static mass mst when the frequency f = 0, because local resonance effect is not manifested under static conditions. As the frequency increases, the effective mass first increases and then decreases to a negative value. The negative mass density intervals marked by shaded zone are the band gaps, and the color marking is same as Fig. 3. Comparing with the FEM results shown in Fig. 3(b), the band gap ranges obtained by effective mass method (EMM) are consistent with those of FEM. However, EMM does not need to build an entity physical model and has a great advantages in computation time.

Fig. 16
figure 16

The normalized effective mass curve of OLRPC

Full size image

To verify the accuracy of EMD, the comparison between FEM and EMM results for different configuration of OHLRPC are demonstrated in Fig. 17. The dotted line in the figure is a reference line with a slope k = 1, the closer the points representing the band gap boundary is to the line, the closer the FEM and EMM calculation results are. The deviation between the band gap boundaries calculated by the two methods is only 1.31% to 1.95%, so the accuracy of the band gap range determination based on EMM can be guaranteed.

Fig. 17
figure 17

The comparison result of FEM and EMM

Full size image

Applying the theoretical calculation formula derived on EMM, the band gap range can be obtained quickly, which will facilitate the rapid design and optimization of OHLRPC structure to meet different engineering application environments. When the structure increases to OHLRPC with n type oscillators, the form of effective mass expression keep constant, the above matrix only needs to be expanded to the following form:

$${\varvec{M}} = \left[ {\begin{array}{*{20}c} {m_{0} } & 0 & \cdots & 0 & 0 \\ 0 & {m_{1} } & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & {m_{n - 1} } & 0 \\ 0 & 0 & \cdots & {} & {m_{n} } \\ \end{array} } \right],$$
(21)
$${\varvec{U}} = \left[ {\begin{array}{*{20}c} {u_{0} } & {u_{1} } & \cdots & {u_{n - 1} } & {u_{n} } \\ \end{array} } \right]^{T} ,$$
(22)
$${\varvec{F}} = \left[ {\begin{array}{*{20}c} F & 0 & \cdots & 0 & 0 \\ \end{array} } \right]^{T} ,$$
(23)
$${\varvec{K}} = \left[ {\begin{array}{*{20}c} {k_{1} + k_{2} + \cdots + k_{n} } & { - k_{1} } & \cdots & { - k_{n - 1} } & {k_{n} } \\ { - k_{1} } & {k_{1} } & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ { - k_{n - 1} } & 0 & \cdots & {k_{n - 1} } & 0 \\ { - k_{n} } & 0 & \cdots & 0 & {k_{n} } \\ \end{array} } \right].$$
(24)

3.4 Parameter analysis of band gap regulation

To improve the attenuation efficiency of OHLRPC, the parameter analysis is carried out to discuss the band gap development law. In this section, the four geometric parameters are designated to investigate the band gap regulation, such as the primitive cell size, the lattice constant, the ratio of coating layer radius to scatterer radius and the random proportions of location. Since it has been proved that OHLRPC can be equivalent to a spring-mass system with three vibrators in series in the Sect. 3.3, we can refer to the research method of single vibrator system to theoretically analyze the regulation law of OHLRPC. For the single spring-mass system exhibited in Fig. 13(a), the starting and ending frequency of band gap are written as:

$$f_{{{\text{start}}}} = \frac{1}{2\pi }\sqrt {k/m_{1} } ,$$
(25)
$$f_{{{\text{end}}}} = \frac{1}{2\pi }\sqrt {k/m_{1} { + }k/m_{2} } ,$$
(26)
$$m_{1} = \rho_{{{\text{scatterer}}}} \pi R_{1}^{2} ,$$
(27)
$$m_{2} = \rho_{{{\text{matrix}}}} (a^{2} - \pi R_{2}^{2} ),$$
(28)
$$k = \frac{{4C_{11} R_{1} }}{{R_{2} - R_{1} }},$$
(29)
$$C_{11} = \lambda_{{{\text{coating}}}} + 2\mu_{{{\text{coating}}}} ,$$
(30)

where, \(f_{{{\text{start}}}}\) is the starting frequency of band gap, \(f_{{{\text{end}}}}\) is the ending frequency of band gap, \(m_{1}\) is the equivalent mass of oscillator, \(m_{2}\) is the equivalent mass of matrix, \(k\) is the equivalent stiffness of coating layer.

3.4.1 The primitive cell size

In terms of the size of the primitive cell, the radius of scatterer C is selected to represent the development law of band gap, and the influence of other cell size can be similarly deduced. As shown in the Fig. 18, as the radius of the type C scatterer increases, the initial frequency of the third band gap decreases gradually, while the initial frequency of first and second band gap remain unchanged. According to the previous modal analysis, the starting frequency is determined by the resonance frequency of the specific cell. Based on the formula (26), the increase in the radius of primitive cell C provides a larger equivalent mass \(m_{1}\), which results in a lower resonance frequency, so the third band gap gradually shifts to lower frequency. The equivalent stiffness and equivalent mass of the primitive cell B remain unchanged, so the starting frequency of second band gap keep constant. Based on the above reasons, the width of third band gap is increased and inevitably causes the compression of the second band gap, and finally merges into one band gap when R1 = 0.05 m. This is because the primitive cell C and B have the same structural parameters and resonance frequency at this time. This also proves the previous judgment that the number of band gaps is determined by the cell type rather than the number.

Fig. 18
figure 18

The effects of the radius of scatterer C on the band gaps

Full size image

3.4.2 The lattice constant

The effects of lattice constant on the band gaps are demonstrated in Fig. 19, and the abscissa axis represents the ratio of test value and the initial value of the lattice constant. Since the variation of the lattice constant does not affect the geometric parameters of the primitive cells, the starting frequencies of each band gap keep unchanged. However, with the decrease of lattice constant a, the ratio of scatterer to matrix is enhanced, thus both band gap width increase. From the equation (27), the reduction in the lattice constant causes a smaller equivalent mass of matrix \(m_{2}\), which leads to a larger \(f_{{{\text{end}}}}\) based on the formula (25). Especially, the third band gap increases substantially because it is not affected by the resonance of upper band gap. On the contrary, the width of the first and second band gap have limited increase due to the coupling effect of the resonance frequency of the upper band gap.

Fig. 19
figure 19

The effects of lattice constant on the band gaps

Full size image

3.4.3 The ratio of coating layer radius to scatterer radius

Keeping other conditions constant, the ratio of coating layer radius to scatterer radius Rsc is modified from 1.16 to 1.24 and the results are demonstrated in Fig. 20. With the increase of Rsc, all three band gaps move toward to lower frequency as a whole. Compared with Rsc = 1.16, the starting frequencies of the model with Rsc = 1.24 decreases by 9.1 Hz (17.0%), 10.9 Hz (17.0%) and 13.7 Hz (17.1%), respectively. Analyzing the reason, the increase of Rsc causes the increase of R2, which leads to the smaller equivalent stiffness k according to (28). Because the equivalent mass m1 keeps constant but the equivalent stiffness k decrease, the starting frequency reduce and the band gap width decrease slightly. Although the ratio of coating layer radius to scatterer radius Rsc has little effect on the band gap width, it can adjust significantly the distribution interval to obtain the lower frequency band gap.

Fig. 20
figure 20

The effects of the ratio of coating layer radius to scatterer radius on the band gaps

Full size image

3.4.4 The random proportions of location

Based on the COMSOL external program interface, the joint simulation of COMSOL and MATLAB can be carried out, which can achieve abundant functions. Call the random function of MATLAB, different calculation models with random rates RL between 5 and 20% can be generated, as demonstrated in Fig. 21. The calculation results are shown in the Fig. 22, and the results indicate that the band gap range and width keep constant with the increasing of random rate. Since the geometry and material parameters of primitive cell have not changed, thus their equivalent mass and spring stiffness keep constant, and the band gaps are unchanged. That is, the resonance properties of primitive cells are not affected by the arrangement position, which facilitates the manufacture and application of OHLRPC. Furthermore, utilizing the insensitivity of local resonance band gap to the positional arrangement, a geometric model of random distribution can be constructed to obtain a larger filling fraction and band gap width.

Fig. 21
figure 21

The OHLRPC model with different random rate of locations

Full size image
Fig. 22
figure 22

The effects of the random proportions of locations on band gaps

Full size image

4 Extension research of OHLRPC structure

According to the previous research results, the reasonable configuration and distribution are crucial to the wider band gap when the material parameters are determined. Therefore, the multi-frequency outward hierarchical local resonance phononic crystal (MOHLRPC) structure with multiple oscillators is constructed in this section, as shown in Fig. 23. In the calculation model, a combination of 5 types of primitive cells is selected, and their geometric parameters are demonstrated in Table 3. The lattice constant is determined as 0.2 m, and the material parameters are consistent with the previous case (Tables 4, 5).

Fig. 23
figure 23

The calculation model of MOHLRPC

Full size image
Table 3 The geometric parameters of MOHLRPC
Full size table
Table 4 The band ranges of MOHLRPC without Winkler Foundation
Full size table
Table 5 The band ranges of MOHLRPC with Winkler Foundation
Full size table

In practical engineering, there are many cases where the structure is subject to external constraints, such as highway pavement [62], beam foundation[63] and rock-socketed pile [64], etc. For the integrity of the analysis, the section investigates the vibration attenuation properties of MOHLRPC structure with external constraints, and the interaction of structure with external constraints is reduced to the classical Winkler foundation. The spring-mass theoretical model of MOHLRPC without and with Winkler foundation is demonstrated in Fig. 24, in which kf is the foundation reaction modulus, it is chosen as 2107 N/m3.

Fig. 24
figure 24

The spring-mass model of MOHLRPC

Full size image

For the convenience of comparison, the band gap interval statistics of the two configurations shown in Fig. 24 are demonstrated in Table 4 and Table 5, respectively. The band structure of MOHLRPC without Winkler foundation is demonstrated in Fig. 25(a), it has five band ranges and their intervals are 52.4–59.8 Hz, 72.2–82.2 Hz, 96.2–105.4 Hz, 115.4–130.8 Hz, 144.3–175.8 Hz, and the total band gap width is 73.5 Hz. Compared with the single cell, the band gap width is increased by 56.0 Hz and 3.20 times. When the Winkler foundation is considered, the structure exhibits 6 band gaps, the first of which is zero band gap. The intervals are 0–30.3 Hz, 52.4–61.4 Hz, 72.2–83.8 Hz, 96.2–106.3 Hz, 115.4–132.3 Hz, 144.3–182.3 Hz. The total band gap width is 115.9 Hz, which is increased by 98.4 Hz and 5.62 times. Actually, Zhang et al. [65] have derived the dispersion equation of phononic crystal Euler beam considering Winkler foundation by transfer matrix method. The results indicate that with the increase of foundation reaction modulus, the band width of zero-band gap and first band gap increase simultaneously. Obviously, for the MOHLRPC proposed in this manuscript, the confinement of Winkler foundation not only increases a band gap from zero, but also expand the width of each original band gap. For specific working conditions, the feature can be applied to obtain a wider shielding interval for the vibration control.

Fig. 25
figure 25

The band structure and FRF of MOHLPRC

Full size image

When calculating the FRF using three supercells, the results marked by the black line show the MOHLRPC without Winkler foundation has five obvious attenuation intervals, as shown in Fig. 26(a). The FRF curve drops sharply from the resonance frequency of primitive cell, and gradually rises as the frequency increases. Due to the effect of Fano resonance [66, 67], the attenuation amplitude is not uniform within the band gap. However, this phenomenon can be improved by increasing the number of supercells. So, we also calculated the FRF of MOHLRPC with 5 and 7 periodic supercells. As shown in the region Z1, with the increase of cell number, the attenuation inhomogeneity is gradually improved and shows a considerable efficiency in the whole band gap range. The more obvious development can be observed in other band gap ranges, especially the region Z2 in the fifth band gap. Meanwhile, the FRF of MOHLEPC with Winkler foundation shows the attenuation interval from zero and  a similar attenuation improvement law with the increase of the supercells, as shown in Fig. 26(b). From the economical point of view, the MOHLRPC with 5 supercells can already get better results, so it is necessary and useful to simulate the FRF of specific structure to determine the optimal design during practical engineering.

Fig. 26
figure 26

The transmission spectra of MOHLPRC

Full size image

For a more complete analysis of the band gap characteristics, the band gap mechanism of MOHLRPC with Winkler foundation is discussed. The vibration modes of band gap boundaries marked in Fig. 25(b) are represented in the Fig. 27. For the zero-band gap, both the scatterers and the matrix as a whole exhibit translational vibration due to the confinement of the foundation. The cutoff frequency of the zero-band gap is generally referred to as the critical frequency [68] or pivotal frequency [63], which is the function of the stiffness of Winkler springs and the mass of cell [68]. As the equivalent spring stiffness of Winkler foundation increases, the critical frequency gradually increases from zero, which leads to the emergence and extending of the zero-band gap. For the second band gap, the translational movement of cell A results in the strong coupling effect, which cause the open of first band gap. For the ending frequency, the cell A possesses relative movement with the generalized matrix (B + C + D + E + M), the coupling effect is weakened and the second band gap is closed. Similarly, the third to sixth band gaps basically exhibit similar characteristics. To express the control law more clearly, the scatterers that control the starting frequency are marked with white letters, and generalized matrix zones are marked with black letters. The result indicates that the MOHLRPC structure considering the mlti-oscillator coupling effect is effective in expanding the width of LRBP.

Fig. 27
figure 27

The displacement fields of multiple outward hierarchical structure

Full size image

To facilitate practical application for specific engineering conditions, it is necessary to demonstrate the process for active design of MOHLRPC. Based on the previous investigation, the design flow chart of MOHLRPC is presented in Fig. 28. First, the vibration subjects should be identified, which may contain multiple main frequency intervals. Besides, the expected vibration isolation targets should be determined. Second, appropriate material and physical parameters are selected by the band gap regulation obtained in the Sect. 3.4. After that, according to the application environment, the trail calculation of band gap ranges for MOHLRPC is conveniently performed using EMM, and the corresponding band gap of MOHLRPC with elastic foundation can be obtained by FEM. At this point, the band gap and target frequency range need to be judged, and the cell combination will be adjusted if the results do not meet the requirements. After achieving the band gap interval target, the FRF analysis of MOHLRPC is carried out, and the expected effect band be obtained by reasonably configurating the economical supercell number of MOHLRPC. Ultimately, the complete MOHLRPC design for the actual vibration environment and requirements is obtained.

Fig. 28
figure 28

The design flow chart of MOHLRPC

Full size image

Obviously, compared with the inward hierarchical locally resonant phononic crystal structure, the MOHLRPC proposed in this paper not only has better performance, but also is more operable for engineering application. For the inward hierarchical structure, more band gaps mean more thin layers and weak interfaces in a finite space. However, in the design and manufacture of outward hierarchical structure, the operation process is relatively simple. According to the design flow chart, the engineers calculated the related parameters of the specific cell combination, such as material parameters, structural size and cell number, etc. After that, the cell is fabricated and released into the matrix to establish MOHLRPC. Since the local resonance is not sensitive to the distribution position, the operation does not need too high precision, which greatly simplifies the operation difficulty. Furthermore, as the band gaps are realized through multiple independent primitive cells, the original dense weak interfaces are dispersed in the whole matrix, which can avoid the stress concentration and interfacial debonding issues. Actually, the MOHLRPC structure has been used to guide the research and development of polymer concrete material [69, 70], which has been prepared in batches as track bed slabs and has been successfully applied for low-frequency vibration control in subway engineering.

5 Conclusion

In conclusion, this paper investigated OHLRPC structure to discuss the band gap properties of multi-frequency vibration system. The band structure, band gap formation mechanism and frequency response function are applied to explain the subject. The effective mass method is applied to determine quickly the band gap range, and the parameter analysis is discussed to optimize the band gap. Furthermore, the MOHLRPC is proposed to expand the application. The major conclusions are summarized as follows:

  1. 1)

    The OHLRPC is able to obtain more and wider low-frequency band gaps, the elastic waves with frequencies in the band gap range are greatly attenuated, which is verified by frequency response functions and displacement field analysis.

  2. 2)

    The modal analysis indicates that the band gap number is positively correlated with the types of primitive cells rather than the cell number, and there is a one-to-one correspondence between the band gap and the oscillator type.

  3. 3)

    The results of frequency response analysis show that the displacement of the primitive cells decays exponentially when the frequency is within the band gap, and the main displacement is localized in the corresponding control primitive cells.

  4. 4)

    The band gap determination formula based on the effective mass method is derived to quickly obtain the band gap ranges of OHLRPC, and has been proved to have sufficient accuracy by comparison with FEM. The band gap can be expanded and optimized by regulating the primitive cell size, lattice constant, ratio of coating layer radius to scatterer radius, and the band gaps are not affected by the arrangement and position of primitive cells.

  5. 5)

    The MOHLRPC with multiple oscillator system is subsequently proposed, which exhibits the richer and wider band gap, and can give a zero-band gap when considering the confinement of elastic foundation. In addition, the design flow chart of MOHLRPC is given to facilitate the engineering application.

The MOHLRPC has simple structure and clear vibration attenuation mechanism, which is more operable and has great engineering application value for multi-frequency vibration control field.