Improved piezoelectric performance of 0.965 (K_0.48Na_0.52)(Nb_0.96Sb_0.04)O₃ − 0.035Bi_0.5Na_0.5Zr_0.15Hf_0.75O₃ piezocomposites using inherently auxetic polyethylene matrix

Abstract

Effective properties of a polyethylene matrix and $0.965\left({K}_{0.48}N{a}_{0.52}\right)\left(N{b}_{0.96}S{b}_{0.04}\right){O}_{3}-0.035B{i}_{0.5}N{a}_{0.5}Z{r}_{0.15}H{f}_{0.75}{O}_{3}$ (KNNS-BNZH) inclusion piezocomposite were calculated using finite element method. Auxetic [negative Poisson's ratio (NPR); $\nu =-0.32$] and non-auxetic (positive Poisson’s ratio $\nu =0.2$) polyethylene matrix was considered. Sensing, actuation, and energy harvesting performance of the piezocomposite are investigated at six different volume fractions using the effective properties. Performance was found to improve with an increase in volume fractions of the KNNS-BNZH piezoelectric inclusions in the polyethylene matrix. Significant improvement in voltage and harvested power was observed in the case of longitudinal mode when auxetic polyethylene matrix was used compared to non-auxetic. Poisson’s ratios effect was studied by varying it between $\nu =-0.9$ and $\nu =0.4$ at 30% piezoelectric inclusion by volume fraction. Sensing, actuation, and energy harvesting performance were studied at each Poisson’s ratio both in transverse and longitudinal modes. Auxetic piezocomposite at $\nu =-0.9$ performed better compared to non-auxetic at $\nu =0.4$. Voltage, actuation, and power all increased with the use of auxetic polyethylene matrix as compared to the non-auxetic one.

1 Introduction

Piezoelectric materials are special materials that demonstrate coupled electro-mechanical behaviors due to which they generate an electrical voltage in response to applied strain and vice versa [1]. These materials are often used for sensors, actuators, and energy harvester applications [2,3,4,5,6]. Bulk piezoelectric materials have several disadvantages and are therefore not very useful. Piezoelectric materials are mostly used in the form of piezoceramics or piezocomposites. Piezocomposites are manufactured easily and are flexible. This makes them a suitable choice to be used as sensors, actuators, and energy harvesters [7,8,9,10]. Different types of piezoelectric materials, both lead-based and lead-free, are reported by Priya et al. [11]. Lead-based piezoelectric materials were preferred due to their high piezoelectric coefficients. But due to their toxic nature, lead-free piezoelectric materials are gaining importance these days [12,13,14,15,16,17,18,19]. Several lead-free materials are reported in the literature like $\left(B{i}_{0.5}N{a}_{0.5}\right)Ti{O}_{3}$ [BNT], sodium potassium niobate $\left({K}_{0.5}N{a}_{0.5}\right)Nb{O}_{3}$ [KNN], bismuth potassium titanate $\left(B{i}_{0.5}{K}_{0.5}\right)Ti{O}_{3}$ [BKT], etc. [20]. KNN is a promising piezoelectric material, and several researchers have worked on KNN material[21,22,23,24,25]. Recently, Qiao et al.[26] fully characterized a promising lead-free KNN-based piezoelectric material $0.965\left({K}_{0.48}N{a}_{0.52}\right)\left(N{b}_{0.96}S{b}_{0.04}\right){O}_{3}-0.035B{i}_{0.5}N{a}_{0.5}Z{r}_{0.15}H{f}_{0.75}{O}_{3}$ (KNNS-BNZH) having high Curie temperature and high value of piezoelectric coefficient ${d}_{33}$. Various methods can be employed to enhance the performance of a piezoelectric material like imparting porosity to a solid piezoelectric material, controlling the sintering and calcination temperature, etc. [27,28,29].

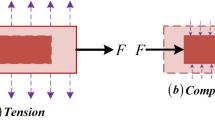
A different approach has been reported recently to enhance the piezoelectric performance of a piezocomposite using an auxetic polyethylene matrix [30]. Auxetic materials are unique materials that elongate in the transverse direction when subjected to tensile stress. On the contrary, they undergo contraction in the transverse direction when subjected to compressive load in the longitudinal direction [31]. The term “auxetic” is a Greek word that means that which tends to increase. Material can be made to behave like auxetic material using special types of structures like a honeycomb, circular auxetic structures, hexagonal and inverted hexagonal cells, etc. [32,33,34,35]. Inherently auxetic materials, having a negative Poisson’s ratio, are also reported in the literature [30, 36,37,38]. Krishnaswamy et al. [30] developed an inherently auxetic polyethylene material matrix and used it to develop a $BaTi{O}_{3}$-based piezocomposite. Auxetic matrix was found to enhance the effective piezoelectric properties.

Although much work has been done on auxetic structure-based piezoelectric materials, from the literature, it is confirmed that the studies on auxetic piezocomposites are sparse [32,33,34, 39, 40]. The present study is planned with this motivation. In the present work, piezocomposite material made of inherently auxetic and non-auxetic polymer-based matrix called polyethylene and KNNS-BNZH piezoelectric material was studied for sensing, actuation, and energy harvesting applications. Effective properties are calculated numerically at different volume fractions to study the sensing, actuation, and energy harvesting performance of the piezocomposite. Similar studies were conducted at a known volume fraction but for different Poisson’s ratios.

A micro-mechanical analysis approach has been adopted to calculate the effective properties of the piezocomposite. In this approach, a heterogeneous composite structure is replaced with a homogeneous medium. Several methods are available to calculate and predict the overall/effective electro-mechanical properties of the piezocomposite material. Chan [41] and Smith [42] reported basic analytical approaches to calculate effective properties of 1–3 piezocomposites. These basic analytical approaches however are not suitable for generalized loading conditions. The asymptotic homogenization approach is reported to take care of the arbitrary loading conditions [43, 44]. Li and Dunn [45] reported semi-analytical methods for theoretical studies generalizing Hashin–Shtrikman variational principles. Salavati et al. [46] used atomistic bond potential and equivalent mechanical energy approach to calculate effective properties in the nanoscale of boron nitride nanotubes. Level set methods are reported to optimize flexoelectric composite topologies, to detect material interfaces in piezoelectric structures, etc. [47, 48]. Mechanical mean-field-type methods have been reported capable of predicting the electro-elastic behavior [49,50,51,52]. However, this method does not account for local fluctuations of the field quantities. The above drawbacks have been overcome by the unit cell method which utilizes the periodic microfield approach. Various numerical methods can be used to calculate the field variables by the unit cell method. Several numerical techniques like the finite element method(FEM)[53], isogeometric analysis(IGA) [54,55,56], extended finite element method [48], etc., are available which can be used to calculate the effective properties. The finite element method has been used extensively to calculate piezoelectric fiber composite’s effective properties and has been widely reported in the literature [57,58,59,60,61,62]. In the present study also, the finite element method (FEM) has been used to calculate the effective elastic, piezoelectric and dielectric properties of the piezocomposite materials. Using this method, the linear response to complex loading condition involving mechanical and electrical load or a combination of both can be calculated.

2 Materials and methods

Auxetic materials are meta-materials that have a negative Poisson’s ratio due to which it undergoes lateral expansion when elongated. Such auxeticity can be imparted to the matrix geometrically by using structures manufactured by various 3D manufacturing and printing techniques. Auxeticity can also be imparted to materials, such as polymers by implementing specific processing steps [30] due to which the material possesses a negative Poisson’s ratio and is often referred to as inherently auxetic materials. In the present study, the performance of 0–3 piezocomposite made of polyethylene-based inherently auxetic and non-auxetic matrix material along with KNNS-BNZH piezoelectric ceramic inclusion is studied and compared. KNN-based piezoelectric materials are quite promising and popular among lead-free piezoelectric materials due to several factors like high piezoelectric coefficient, high Curie temperature, stability, etc [63,64,65,66]. The properties of the KNNS-BNZH piezoelectric material are given in Table 1 [26].

Table 1 Elastic and Piezoelectric properties of KNNS-BNZH material in strain charge form

Here, the compliance coefficients ${S}_{ij}$ are measured in ${10}^{-12} {m}^{2}/N$, and piezoelectric coefficients are measured in $pC/N$. ${\varepsilon }_{11}^{T}$ and ${\varepsilon }_{33}^{T}$ are relative permittivity in strain charge form and are dimensionless. Material can be inherently auxetic or it can be made to behave as an auxetic material using different types of auxetic structures[32,33,34,35]. In either case, Poisson’s ratio of such a material is negative, which physically means that when the material is elongated, its lateral dimension also increases and vice versa. In the present study, Poisson’s ratio of the auxetic and the non-auxetic material considered is ${\nu }_{a}=-0.32$ and ${\nu }_{\mathrm{na}}=0.2$. Polyethylene material can be made auxetic or non-auxetic depending upon the processing steps. The elastic modulus of the auxetic material is considered to be $E=100 MPa$. Effective properties of the piezocomposite were calculated at different volume fractions. The original 0–3 piezocomposite material is replaced by an equivalent homogeneous material. For sensing and energy harvesting purposes, the piezocomposite material is attached to a vibrating device. Commonly used vibrating structures are cymbal, stack, shell, cantilever beam, etc. [67]. In the present case, a cantilever beam made of structural steel, having Young’s modulus $E=200 GPa$ and density $\rho =7850 \mathrm{kg}/{\mathrm{m}}^{3}$ is used as a host structure. The piezocomposite is attached to one side of the cantilever beam host structure in unimorph configuration. The piezocomposite material is attached to the beam, beginning from the fixed end, to take advantage of the maximum bending stress developed at the fixed end of the beam. To reduce the natural frequency of vibration of the structure and bring it close to ambient vibration, a proof mass of ${m}_{p}=15 \mathrm{gm}$ is attached to the free end of the cantilever beam.

The structure is subjected to base excitation of $1\times g$ acceleration where $g$ is the acceleration due to gravity. Voltage and power responses are collected in the frequency domain.

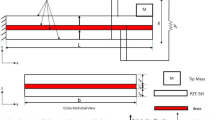
The performance of the actuator is measured in terms of the cantilever beam’s tip’s displacement. Both transverse and longitudinal modes are considered for the present study. Actuator displacement is measured in terms of the cantilever beams tip’s displacement. Cantilever beam-based energy harvester operating in transverse $\left({d}_{31}\right)$ mode and longitudinal $\left({d}_{33}\right)$ mode is shown in Figs. 1 and 2, respectively. Vibration led to the accumulation of charges in the electrodes. Sensing voltage is measured by the open-circuit voltage developed between the electrodes due to the accumulated charges.

Fig. 1

Cantilever beam-based piezoelectric energy harvester operating in transverse mode

Fig. 2

Cantilever beam-based piezoelectric energy harvester operating in longitudinal mode a Isometric view b Top view with dimensions

Power is harvested by connecting an external load resistance ${R}_{L}$ between the electrodes. Maximum power is harvested at an optimum resistance ${R}_{\mathrm{opt}}$ which depends upon the structure’s natural frequency of vibration and capacitance of the system and is given by Eq. (1):

$$ R_{{{\text{opt}}}} = \frac{1}{\omega C} $$

(1)

In Eq. (1), $\omega$ and $C$ are natural frequency of vibration of the structure and capacitance of the system.

3 Finite element model to calculate the effective properties

Several numerical and analytical methods are reported in the literature to calculate the effective elastic and piezoelectric coefficients of the 0–3 piezocomposites [53, 68,69,70]. Initial analytical methods were not sufficient [67, 71]. Berger et al. [58, 72] used both analytical and numerical methods to successfully evaluate the effective elastic and piezoelectric coefficients of a piezocomposite. The analytical solution was determined by the asymptotic homogenization method (AHM) [73, 74], and the finite element method (FEM) was used to determine the numerical solution. Numerical methods are more suitable compared to analytical methods when dealing with inclusions of complex shapes and are used by various researchers [53, 70, 75]. Numerical methods such as FEM are not applied over the entire material volume of the composite. Composite materials are generally considered to be made of a repetition of representative volume elements (RVE). Effective properties are then calculated by applying suitable boundary conditions to the RVE. Since effective elastic and piezoelectric properties depend only upon the volume fraction of the piezoelectric inclusions, it is possible to choose an RVE having unit dimensions. Such an RVE is often referred to as a unit cell. Effective properties calculated using RVE can be used to represent a homogeneous medium that can replace the original 0–3 composite, and the corresponding technique is called the homogenization technique [76]. Figure 3 shows a typical RVE whose opposite faces are designated as $A, B,$ and $C$. Boundary conditions are applied on these faces. The piezocomposite was poled along in the $z$ direction.

Fig. 3

A representative volume element containing piezoelectric inclusions

Piezoelectric materials when exposed to a mechanical strain give rise to a potential gradient. This phenomenon is often referred to as the direct piezoelectric effect. The opposite phenomenon in which a mechanical strain is observed when the piezoelectric material is exposed to a potential gradient is referred to as the converse piezoelectric effect. Problems dealing with the generation of potential gradients due to mechanical strain and vice versa are often referred to as coupled piezoelectric problems. The relationship between mechanical and electrical quantities of piezoelectric material is often characterized by piezoelectric coefficients. The constitutive Eq. relates the mechanical quantities stress to strain and the electrical quantities electric field to the electrical displacement. A coupled constitutive Eq. relating to these quantities is written in matrix form and is given by Eq. (2) [58]:

$$ \left\{ {\begin{array}{*{20}c} {\overline{T}_{11} } \\ {\overline{T}_{22} } \\ {\overline{T}_{33} } \\ {\overline{T}_{23} } \\ {\overline{T}_{31} } \\ {\overline{T}_{12} } \\ {\overline{D}_{1} } \\ {\overline{D}_{2} } \\ {\overline{D}_{3} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {C_{11}^{eff} } & {C_{12}^{eff} } & {C_{13}^{eff} } & 0 & 0 & 0 & 0 & 0 & { - e_{13}^{eff} } \\ {C_{12}^{eff} } & {C_{11}^{eff} } & {C_{13}^{eff} } & 0 & 0 & 0 & 0 & 0 & { - e_{13}^{eff} } \\ {C_{13}^{eff} } & {C_{13}^{eff} } & {C_{33}^{eff} } & 0 & 0 & 0 & 0 & 0 & { - e_{33}^{eff} } \\ 0 & 0 & 0 & {C_{44}^{eff} } & 0 & 0 & 0 & { - e_{15}^{eff} } & 0 \\ 0 & 0 & 0 & 0 & {C_{44}^{eff} } & 0 & { - e_{15}^{eff} } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {C_{66}^{eff} } & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {e_{15}^{eff} } & 0 & {\varepsilon_{11}^{eff} } & 0 & 0 \\ 0 & 0 & 0 & {e_{15}^{eff} } & 0 & 0 & 0 & {\varepsilon_{11}^{eff} } & 0 \\ {e_{13}^{eff} } & {e_{13}^{eff} } & {e_{33}^{eff} } & 0 & 0 & 0 & 0 & 0 & {\varepsilon_{33}^{eff} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\overline{S}_{11} } \\ {\overline{S}_{22} } \\ {\overline{S}_{33} } \\ {\overline{S}_{23} } \\ {\overline{S}_{31} } \\ {\overline{S}_{12} } \\ {\overline{E}_{1} } \\ {\overline{E}_{2} } \\ {\overline{E}_{3} } \\ \end{array} } \right\} $$

(2)

In Eq. (2), $\overline{T }$ and $\overline{S }$ are the average stress and strain, respectively. Similarly, $\overline{D }$ and $\overline{E }$ are the average value of the electrical displacement and electric field, respectively. $C, e,$ and $\varepsilon$ are the material parameters referred to as stiffness coefficients, piezoelectric coefficients, and relative permittivity, respectively. In tensor form, this can be written as:

$$ \left[ {\begin{array}{*{20}c} T \\ D \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} C & { - e^{t} } \\ e & \varepsilon \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} S \\ E \\ \end{array} } \right] $$

(3)

The symbols ${\varvec{T}},\boldsymbol{ }{\varvec{D}},\boldsymbol{ }{\varvec{S}},$ and ${\varvec{E}}$ are the stress $\left(\sigma \right)$, electrical displacement, strain $\left({\varepsilon }^{s}\right),$ and electrical field vectors. ${\varvec{C}},\boldsymbol{ }{\varvec{e}},$ and $\varepsilon$ are stiffness tensor, piezoelectric coupling tensor, and relative permittivity, respectively. It is assumed that the matrix and the piezoelectric inclusions are perfectly bonded to each other.

3.1 Implementation of boundary conditions

RVE’s can be arranged in a periodic array to get the actual composite material. Therefore, to simulate the responses, periodic boundary conditions are applied. Application of periodic boundary conditions ensures the same mode of deformation across the RVE without any interpenetration and separation at the boundary of the two RVEs. Expressed in terms of the Cartesian coordinate system, this can be written as given in Eq. (4) [62, 76]:

$$ u_{i} = \overline{S}_{ij} x_{i} + v_{i} $$

(4)

${where \overline{S} }_{ij}$ and ${v}_{i}$ are the average engineering strain and local fluctuations, respectively. The local fluctuations ${v}_{i}$ generally depend upon the applied global loads and is unknown. The periodic boundary conditions are specifically applied on the opposite faces of the RVE facing each other. The corresponding Equations of boundary conditions are given by Eqs. (5) and (6):

$$ u_{i}^{{K^{ + } }} = \overline{S}_{ij} x_{j}^{{K^{ + } }} + v_{i}^{{K^{ + } }} $$

(5)

$$ u_{i}^{{K^{ - } }} = \overline{S}_{ij} x_{j}^{{K^{ - } }} + v_{i}^{{K^{ - } }} $$

(6)

${where K}^{+}$ and ${K}^{-}$ denotes normal to the faces in the positive and negative directions, respectively. For equal values of local strains on the two faces facing each other, the macroscopic strain is given by Eq. (7):

$$ u_{i}^{{K^{ + } }} - u_{i}^{{K^{ - } }} = \overline{S}_{ij} \left( {x_{j}^{{K^{ + } }} - x_{j}^{{K^{ - } }} } \right) $$

(7)

The corresponding value for the electric potential is given by Eq (8):

$$ \Phi^{{K^{ + } }} - \Phi^{{K^{ - } }} = \overline{E}_{i} \left( {x_{i}^{{K^{ + } }} - x_{i}^{{K^{ - } }} } \right) $$

(8)

Volume average of the stress, strain, electric field and electrical displacement is calculated over the entire volume $V$ of the RVE using Eqs. (9) to (12), respectively:

$$ \overline{S}_{ij} = \frac{1}{V}\int_{V} {S_{ij} dV} $$

(9)

$$ \overline{T}_{ij} = \frac{1}{V}\int_{V} {T_{ij} dV} $$

(10)

$$ \overline{E}_{i} = \frac{1}{V}\int_{V} {E_{i} dV} $$

(11)

$$ \overline{D}_{i} = \frac{1}{V}\int_{V} {D_{i} dV} $$

(12)

Boundary conditions are applied by assigning zero values to all the strain fields except one. Effective properties are calculated using the average quantities calculated using Eqs. (9) to (12). Table 2 lists all the boundary conditions and the corresponding formulas required to calculate the effective mechanical and piezoelectric properties of the piezocomposite material. The boundary conditions are applied in the form ${u}_{i}/\varphi$, where ${u}_{i}$ means displacement boundary condition, whereas $\varphi$ means electrical boundary condition.

Table 2 Application of Boundary Conditions

4 Modeling of sensor, actuator, and energy harvester

The response of the piezoelectric material to the base vibration of the structure is modeled using the finite element method. The finite element method is a very common numerical scheme adopted to analyze and simulate the static and dynamic response of a piezoelectric structure [24, 77,78,79,80,81]. The piezoelectric material is attached to the cantilever beam beginning from the fixed end of the cantilever beam to exploit higher bending stress and bending moment at the fixed end of the cantilever beam. For simplification of analysis, the piezoelectric theory assumed here is a linear one. Electrodes connected to the piezoelectric material are connected to external resistance. Assuming linear behavior of piezoelectric material, the electromechanical constitutive Eq. for piezoelectric material is given by Eq. (3). The structure is discretized and the field variables within the structure can be written in terms of shape function and nodal variables as given in Eq. (13):

$$ \left\{ {\text{u}} \right\} = \left[ {\text{N}} \right]\left\{ {{\text{q}}^{e} } \right\} $$

(13)

where $\left\{{\varvec{u}}\right\}$ is the vector of field variables, $\left[{\varvec{N}}\right]$ is the shape function also referred to as polynomial interpolation function, and $\left\{{{\varvec{q}}}^{e}\right\}$ is a vector of the nodal variables. Since stress is related to strain and strain is related to displacement, strain–displacement relation, given in Eq. (14), is often used:

$$ \left\{ {\varepsilon^{s} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{\partial u}{{\partial x}}} \\ {\frac{\partial v}{{\partial y}}} \\ {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \\ {\frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial x}}} \\ {\frac{\partial v}{{\partial z}} + \frac{\partial w}{{\partial y}}} \\ \end{array} } \right\} $$

(14)

In tensor notation, this can be written as

$$ \left\{ {\varepsilon^{s} } \right\} = \left[ {\text{B}} \right]_{e} \left\{ {{\text{q}}^{e} } \right\} $$

(15)

where ${\varepsilon }^{s}$ is the strain vector, ${\left[\mathbf{B}\right]}_{e}$ is the matrix containing the derivatives of the polynomial functions w.r.t the material coordinates, and $\left\{{\mathbf{q}}^{\mathbf{e}}\right\}$ is a vector of the values of the field variables at the nodes. Similarly, the field variable of the electric field vector is related to the values of the potentials at the nodal coordinates by Eq.:

$$ \left\{ {\text{E}} \right\} = \left[ {{\text{B}}_{\phi } } \right]\left\{ \phi \right\} $$

(16)

Now applying Hamilton’s principle [55], we get:

$$ \delta \int\limits_{{t_{1} }}^{{t_{2} }} {\left( {K_{E} - H + W^{e} } \right) \times } dt = 0 $$

(17)

where ${K}_{E}$ is the kinetic energy, $H$ is the potential energy, and ${W}^{e}$ is the electrical energy stored due to piezoelectric material. The kinetic energy term can be written as:

$$ K_{e} = \frac{1}{2}\int\limits_{V} {\rho \left\{ {{\dot{\text{u}}}} \right\}^{T} \left\{ {{\dot{\text{u}}}} \right\}dV} $$

(18)

Using Eq. (13), Eq. (18) can be written as:

$$ K^{e} = \frac{1}{2}\left\{ {{\dot{\text{q}}}^{e} } \right\}^{T} \left[ {{\text{m}}_{{{\text{uu}}}}^{e} } \right]\left\{ {{\dot{\text{q}}}^{e} } \right\} $$

(19)

where

$$ \left[ {{\text{m}}^{e} } \right] = \int\limits_{V} {\rho \left[ {\text{N}} \right]^{T} \left[ {\text{N}} \right]dV} $$

(20)

The potential energy term can be written as:

$$ H = \int {\frac{1}{2}\left\{ {\varepsilon^{s} } \right\}^{T} \left\{ \sigma \right\}dV} $$

(21)

Stress $\sigma$ given in Eq. (21) can be written in terms of stiffness and piezoelectric coupling coefficient from Eq. (3) as:

$$ \left\{ \sigma \right\} = \left\{ {\left[ {\text{C}} \right]\left\{ {\varepsilon^{s} } \right\} - \left[ {e^{t} } \right]\left\{ {\text{E}} \right\}} \right\} $$

(22)

Substituting the mechanical strain vector and the electric field vector from Eqs. (15) and (16) into Eq. (22), we get

$$ H = \frac{1}{2}\left\{ {{\text{q}}^{e} } \right\}^{T} \left[ {{\text{k}}_{uu} } \right]\left\{ {{\text{q}}^{e} } \right\} + \frac{1}{2}\left\{ {{\text{q}}^{e} } \right\}^{T} \left[ {{\text{k}}_{\phi } } \right]\left\{ \phi \right\} $$

(23)

where we have

$$ \left[ {{\text{k}}_{uu} } \right] = \int\limits_{V} {\left[ {\text{B}} \right]^{T} \left[ {\text{C}} \right]\left[ {\text{B}} \right]dV} $$

(24)

and.

$$ \left[ {{\text{k}}_{u\phi } } \right] = \int\limits_{V} {\left[ {\text{B}} \right]\left[ e \right]\left[ {{\text{B}}_{\phi } } \right]dV} $$

(25)

The electrical energy produced by the piezoelectric material is given by.

$$ W^{e} = \frac{1}{2}\int\limits_{V} {\left\{ {\text{E}} \right\}^{T} \left\{ {\text{D}} \right\}dV} $$

(26)

Using the constitutive Eq., Eq. (26) can be rewritten as follows:

$$ W^{e} = - \frac{1}{2}\left\{ \phi \right\}^{T} \left[ {{\text{k}}_{{{\text{uf}}}} } \right]\left\{ {\text{q}} \right\} + \frac{1}{2}\left\{ \phi \right\}^{T} \left[ {{\text{k}}_{\phi \phi } } \right]\left\{ \phi \right\} $$

(27)

In Eq. (27), $\left[{\mathbf{k}}_{u{\varvec{\phi}}}\right]$ and $\left[{\mathbf{k}}_{\phi \phi }\right]$ are called piezoelectric coupling matrix and capacitance matrix. Substituting the above expressions in Hamilton’s Eq., considering damping of the material and simplifying, we get the elemental Eq. of motion of the beam given by Eqs. (28) and (29) [82]:

$$\left[ {m_{uu}^e} \right]\left\{ {{{\ddot u}^e}} \right\} + \left[ {C_{uu}^e} \right]\left\{ {{{\dot u}^e}} \right\} + \left[ {k_{uu}^e} \right]\left\{ {{u^e}} \right\} + \left[ {k_{u\varphi }^e} \right]\left\{ {{\varphi ^e}} \right\} = \left\{ {F_{ext}^e} \right\}$$

(28)

$$ \left[ {{\text{k}}_{\varphi u}^{e} } \right]\left\{ {u^{e} } \right\} + \left[ {{\text{k}}_{\varphi \varphi }^{e} } \right]\left\{ {\varphi^{e} } \right\} = \left\{ {{\text{Q}}^{e} } \right\} $$

(29)

$where\;m_{{uu}}^{e} ,C_{{uu}}^{e}$ and ${\mathrm{k}}_{uu}^{e}$ are the elemental mass, damping, and stiffness matrices. ${\mathrm{k}}_{u\varphi }^{e}$ and ${\mathrm{k}}_{\varphi u}^{e}$ are elemental direct and inverse piezoelectric coupling matrix, respectively. ${\mathrm{k}}_{\varphi \varphi }^{e}$ is the elemental dielectric stiffness matrix. Displacements and electric potential at the nodes are given by vectors $\left\{{u}^{e}\right\}$ and $\left\{{\varphi }^{e}\right\}$. Elemental force and charge vector are given by $\left\{{\mathrm{F}}_{ext}^{e}\right\}$ and $\left\{{\mathrm{Q}}^{e}\right\}$. Correspondingly, the stiffness matrix of the element is given by Eq. (30) as:

$${\left[ k \right]_e} = \left[ {\begin{array}{*{20}{c}}{k_{uu}^e}&{k_{u\varphi }^e}\\{k_{\varphi u}^e}&{k_{\varphi \varphi }^e}\end{array}} \right]$$

(30)

The elemental Equations are assembled to get the global Equations as given by Eqs. (31) and (32) as:

$$\left[ {{m_{uu}}} \right]\left\{ {\ddot u} \right\} + \left[ {{C_{uu}}} \right]\left\{ {\dot u} \right\} + \left[ {{k_{uu}}} \right]\left\{ u \right\} + \left[ {{k_{u\varphi }}} \right]\left\{ \varphi \right\} = \left\{ {{F_{ext}}} \right\} $$

(31)

$$\left[ {{k_{\varphi u}}} \right]\left\{ u \right\} + \left[ {{k_{\varphi \varphi }}} \right]\left\{ \varphi \right\} = \left\{ Q \right\}$$

(32)

In the global Equations of motion given by Eqs. (31) and (32), ${\mathrm{m}}_{uu}, {\mathrm{C}}_{uu}$ and ${k}_{\mathrm{uu}}$ are the global mass, damping and mechanical stiffness matrices, respectively. ${k}_{\mathrm{u\varphi }}$ and ${k}_{\mathrm{\varphi u}}$ are global direct and inverse piezoelectric coupling matrices, respectively. ${k}_{\mathrm{\varphi \varphi }}$ is the global dielectric stiffness matrix. The coupled Eq. of motion can be written as given by Eq. (33):

$$\left[ {\begin{array}{*{20}{c}}{{m_{uu}}}&0\\0&0 \end{array}} \right]\left\{ {\begin{array}{*{20}{c}}{\ddot u}\\{\ddot \varphi }\end{array}} \right\} + \left[ {\begin{array}{*{20}{c}}{{C_{uu}}}&0\\0&0 \end{array}} \right]\left\{ {\begin{array}{*{20}{c}}{\dot u}\\{\dot \varphi }\end{array}} \right\} + \left[ {\begin{array}{*{20}{c}}{{k_{uu}}}&{{k_{u\varphi }}}\\{{k_{\varphi u}}}&{{k_{\varphi \varphi }}}\end{array}} \right]\left\{ {\begin{array}{*{20}{c}}u\\\varphi \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}}{{F_{ext}}}\\Q \end{array}} \right\}$$

(33)

Boundary conditions are applied so that there is no displacement at the fixed end, i.e., $u=0$. Body load due to gravity acts throughout the length of the beam. Initial displacements and charges on the electrodes are considered to be zero. The entire system is subjected to base vibration, and voltage and power are recorded. Open-circuit voltage (OCV) gives the sensing voltage, and to harvest power, an external load resistance ${R}_{L}$ is attached between the electrodes. The sensing voltage is given by Eq. (34):

$$\left\{ \varphi \right\} = - {\left[ {{k_{\varphi \varphi }}} \right]^{ - 1}}\left[ {{k_{\varphi u}}} \right]\left\{ u \right\}$$

(34)

Current flowing through the circuit in terms of charge and voltage is given by

$$ i = - \frac{dQ}{{dt}} $$

(35)

$$ i = \frac{V}{{R_{L} }} $$

(36)

Using Eqs. (32) and (35), the current through the load resistance is given by.

$$i = - \frac{{dQ}}{{dt}} = - \frac{d}{{dt}}\left( {\left[ {{k_{\varphi u}}} \right]\left\{ u \right\} + \left[ {{k_{\varphi \varphi }}} \right]\left\{ \varphi \right\}} \right)$$

(37)

Using Eqs. (36) and (37), the voltage across the resistance is given by.

$$V = {R_L} \times - \frac{d}{{dt}}\left( {\left[ {{k_{\varphi u}}} \right]\left\{ u \right\} + \left[ {{k_{\varphi \varphi }}} \right]\left\{ \varphi \right\}} \right)$$

(38)

Harvested power can easily be calculated using the relation $P=Vi$ where $V$ and $i$ are calculated using Eqs. (37) and (38). respectively. To calculate the actuation response, the tip displacement of the cantilever beam was recorded in response to unit input voltage applied across the electrodes. During actuation, the initial displacement vector is zero, i.e., $\left\{u\right\}=0,$ and the initial charge vector on the electrodes is also zero, i.e., $\left\{\mathbf{Q}\right\}=0$. The potential vector $\left\{\varphi \right\}$ has zero values at the nodes on the ground electrodes and unity on the nodes on the other electrode at which unit voltage is applied. Initial values of the voltage in the remaining nodes are unknown and are to be determined. Substituting the above values, the potential distribution inside the piezoelectric material is calculated using Eq. $\left[{\mathbf{k}}_{\varphi \varphi }\right]\left\{\varphi \right\}=0$. Substituting this in Eq. (31) and solving for $\left\{u\right\}$, the actuation displacement due to unit voltage applied to one of the electrodes can be calculated.

5 Results and discussion

Effective properties of the piezocomposite made of KNNS-BNZH piezoelectric inclusions and polyethylene-based piezocomposite were calculated using homogenization technique for both auxetic and non-auxetic piezocomposite. The piezoelectric inclusions within the RVE are assumed to be dispersed randomly within the representative volume element (RVE). Figures 4 and 5 show the elastic and piezoelectric effective properties of the piezocomposite, respectively, at different volume fractions. The gradual increase in effective properties with volume fraction can be explained by a simple mixture rule. The effective properties, which were calculated using the homogenization technique, were used to investigate the sensing, actuation, and energy harvesting performance of the piezoelectric material attached to the host cantilever beam structure. Both transverse $\left({d}_{31}\right)$ and longitudinal $\left({d}_{33}\right)$ modes were considered. The schematic diagrams of the two modes of operations are shown in Figs. 1 and  5. Voltage and power responses are calculated in the frequency domain.

Open-circuit voltage developed in the electrodes in response to the applied strain gives rise to the sensing voltage. A load resistance ${R}_{L}$ is connected between the electrodes to harvest power. Harvested power is maximum at the optimum resistance; therefore, optimum resistance can be determined by plotting the power vs resistance curve as shown in Fig. 6. Figure 6 shows the power vs resistance plot for the auxetic piezocomposite operated in the transverse mode. Similar plots are also obtained for auxetic piezocomposite operated in the longitudinal mode and for non-auxetic piezocomposite operated both in transverse and longitudinal mode. Since the plots are similar, they are not shown here. Voltage and power in the frequency domain are shown in Fig. 7.

It can be observed that voltage and power increase with the increase in volume fraction of the piezoelectric material in the piezocomposite. It was also observed that the highest value of voltage and power at all the volume fractions were obtained within a closed range of natural frequency. This could be because the natural frequency of vibration depends upon the mass and stiffness properties of the entire structure, and in this case, the host steel beams mass and stiffness dominate over the piezocomposites mass and stiffness. Figure 8 shows the maximum voltage and power at different volume fractions for both auxetic and non-auxetic piezocomposites, and Fig. 9 shows the corresponding FOMs in the transverse and longitudinal modes. It can be observed that both voltage and harvested power increase with an increase in volume fraction of piezoelectric inclusions in the piezocomposite material. This can be explained by a simple mixture rule. It can be observed that voltage is higher in transverse mode compared to that in longitudinal mode, while power is more in transverse mode compared to that in longitudinal mode. In transverse mode, the electrodes are arranged in top–bottom configuration also referred to as TBE arrangement. In the longitudinal mode, interdigitated electrodes (IDE) are used. The capacitance of interdigitated electrodes (IDE) is always less than the capacitance of top–bottom electrodes (TBE).

This lower capacitance in IDE configuration compared to that of TBE configuration explains why higher voltage is obtained in longitudinal mode and higher power in transverse mode [83]. In the transverse mode of operation, better performance was observed in piezocomposite made of non-auxetic matrix compared to that made of the auxetic matrix. But in the longitudinal mode, the performance of piezocomposite made of the auxetic matrix was better than that made of the non-auxetic matrix. This could be explained by looking into the variation of elastic and piezoelectric properties with volume fraction as shown in Figs. 3 and 4. Sensing voltage depends upon both elastic properties and piezoelectric properties. It can be observed that both stiffness and piezoelectric coefficients increase with the increase in the volume fraction of the piezoelectric materials. While the increase in stiffness tends to reduce strain and hence voltage and power, an increase in piezoelectric coefficients, on the other hand, tends to increase the voltage and power. Depending upon which factor dominates the voltage and power may increase or decrease in the case of auxetic or non-auxetic cases.

Fig. 4

Effective elastic properties of the Piezocomposite at different volume fractions of KNNS-BNZH for a Non-Auxetic matrix b Auxetic matrix piezocomposite

Fig. 5

Piezoelectric Coefficients at different volume fractions of KNNS-BNZH piezoelectric inclusions in auxetic and non-auxetic polyethylene matrix

Fig. 6

Power vs resistance plot of auxetic piezoelectric composites at different volume fractions to find optimum resistance in the transverse $\left({d}_{31}\right)$ mode

Fig. 7

a Voltage and b Power versus frequency plot for auxetic piezocomposite at optimum resistance in transverse mode at different volume fractions of KNNS-BNZH

Fig. 8

Maximum voltage and harvested power at different volume fractions of KNNS-BNZH piezoelectric inclusions embedded in auxetic and non-auxetic polyethylene matrix (a), (c) in transverse $\left({d}_{31}\right)$ mode and (b), (d) in longitudinal $\left({d}_{33}\right)$ mode

Fig. 9

FOM at different volume fractions of KNNS-BNZH inclusions embedded in auxetic and non-auxetic polyethylene matrix in a Transverse $\left({d}_{31}\right)$ and b Longitudinal $\left({d}_{33}\right)$ mode

The opposite behavior of the auxetic and non-auxetic materials in transverse and longitudinal modes of operations can be understood by observing the piezoelectric coefficients of the auxetic and non-auxetic materials in transverse and longitudinal modes. For the present choice of Poisson’s ratio of the auxetic and non-auxetic materials (Auxetic $\nu =-0.32$ and Non-auxetic $\nu =0.2$), the piezoelectric coefficient in the transverse mode $\left({e}_{31}\right)$ of the non-auxetic material is always more than that of the auxetic material at all the volume fractions, while on the other hand, in the longitudinal mode, the piezoelectric coefficient ${e}_{33}$ of the auxetic material is always more than the non-auxetic one. This explains the opposite behaviors of sensing and energy harvesting performance of the auxetic and non-auxetic materials in the transverse and longitudinal modes of operation.

In transverse mode, no improvement was observed by using auxetic matrix compared to non-auxetic matrix. In transverse mode, the maximum voltage and maximum power dropped by about 9.4% and 20.2% in the case of auxetic piezocomposite compared to that of non-auxetic piezocomposite at a 30% volume fraction. In the case of longitudinal mode, however, a performance improvement was observed for piezocomposite made of auxetic matrix compared to non-auxetic matrix. Voltage increased by about 28% and harvested power by about 66% in the case of auxetic piezocomposite compared to the non-auxetic one at 30% volume fraction.

FOM calculated using Eq. (39) [84] is shown in Fig. 9. Plots of power and FOM against volume fractions show that they follow a similar pattern. This also explains the nature of power plots plotted with volume fractions.

$$ {\text{FOM = }}\frac{{e^{2} }}{{\varepsilon E_{y} }} $$

(39)

Physically, Eq. (39) means that both piezoelectric coefficient and stiffness increase, but in longitudinal mode, the piezoelectric coefficient increases at a faster rate compared to stiffness for auxetic material compared to non-auxetic material. In the case of transverse mode, stiffness increases at a faster rate compared to piezoelectric coefficients in the case of non-auxetic material compared to auxetic material. This is shown in Fig. 9 in the FOMs plotted against the volume fraction of the piezoelectric inclusions in the piezocomposite.

In the case of actuation, the cantilever beam’s tip deflection is recorded in response to a unit voltage applied across the electrodes. Figure 10a and b shows the deflection in the transverse and longitudinal mode for both auxetic and non-auxetic piezocomposite. In this case, also it was observed that non-auxetic piezocomposite performed better in transverse mode, while auxetic piezocomposite’s performance was better in longitudinal mode. In longitudinal mode, the deflection due to auxetic matrix improved by about 28% compared to non-auxetic matrix-based piezocomposite. The auxetic matrix in transverse mode did not show much improvement in actuation capabilities. The cantilever beam structures dimensions and piezocomposites properties affect the deflection of the cantilever beam’s tip deflection and are given by Eq. (40) [85]:

$$ \delta = \frac{{3L^{2} }}{2t} \times \frac{{2AB\left( {1 + B} \right)^{2} }}{{A^{2} B^{4} + 2A\left( {2B + 3B^{2} + 2B^{3} } \right) + 1}} \times d_{ij} E_{f} $$

(40)

Fig. 10

Cantilever tip deflection $\delta$ at different volume fractions of KNNS-BNZH piezoelectric inclusions in auxetic and non-auxetic polyethylene matrix both in a Transverse $\left({d}_{31}\right)$ mode and b Longitudinal $\left({d}_{33}\right)$ mode. Parameter ${\varphi }_{ij}$ c in transverse mode $\left({\varphi }_{31}\right)$ and d in longitudinal mode $\left({\varphi }_{33}\right)$

In the above Eq., $t$ and $L$ are the thickness and length of the beam. The beam thickness $t$ can be expressed as $t={t}_{p}+{t}_{m}$, where $t$ is the thickness of the beam, ${t}_{p}$ is the thickness of the piezoelectric material, and ${t}_{m}$ is the thickness of the host beam. The constants $A$ and $B$ are ratios of elastic modulus and thicknesses given by $A={E}_{m}/{E}_{p}$ and $B={t}_{m}/{t}_{p}$. ${E}_{m} and{E}_{p}$ are the elastic constants of the host and piezoelectric beam, respectively. ${d}_{ij}$ is the piezoelectric coefficient, and ${E}_{f}$ is the electric field.

The beam’s length and thickness do not vary; therefore, the tip deflection can be expressed as proportional to the following quantity given by Eq. (41):

$$ \delta \propto \frac{{2AB\left( {1 + B} \right)^{2} }}{{A^{2} B^{4} + 2A\left( {2B + 3B^{2} + 2B^{3} } \right) + 1}} \times d_{ij} E_{f} = \varphi_{ij} $$

(41)

The plots of ${\varphi }_{31}$ and ${\varphi }_{33}$ are shown in Fig. 10c and d. It can be observed that the tip deflection $\left(\delta \right)$ and the parameter ${\varphi }_{ij}$ vary with volume fraction in a similar manner in both transverse mode and longitudinal mode. This explains the nature of the actuation curve.

The effects of auxetic and non-auxetic matrix on the sensing, actuation, and energy harvesting performance are investigated further by changing Poisson’s ratio between -0.9 and 0 for auxetic material and between 0 and 0.4 for non-auxetic material. Material with negative Poisson’s ratio up to $\nu =-0.9$ has already been reported in the literature [38, 86]. Effective elastic and piezoelectric properties are calculated at 30% volume fraction at different Poisson’s ratios using homogenization technique as shown in Fig. 11. Figure 12a and b shows the maximum sensing voltage attained at different Poisson’s ratios. It can be observed that higher values of negative Poisson’s ratio enhance the sensing capabilities. Sensing capabilities of the auxetic matrix at $\nu =-0.9$ compared to the non-auxetic matrix at $\nu =0.4$ increased by about 2.46 times in transverse mode and by about 5.78 times in longitudinal mode. Similarly, Fig. 12c and d shows the plot of maximum power at different Poisson’s ratio. It can be observed that power increased by about 6.25 times in transverse mode and by about 34.2 times in longitudinal mode. Figure 13a and b shows the variation of FOM with Poisson’s ratio calculated using Eq. (39). Maximum power and FOM were found to vary with Poisson’s ratio in a similar pattern.

Fig. 11

Effective elastic properties at different Poisson's ratio a ${C}_{11},{C}_{33}$ b ${C}_{12}, {C}_{13}$ c ${C}_{44}, {C}_{66}$ and d ${e}_{31}, {e}_{33}$

Fig. 12

Sensing voltage at different Poisson's ratios in a Transverse mode b Longitudinal mode and harvested power at different Poisson’s ratios in c Transverse mode d Longitudinal mode

Fig. 13

Variation of FOM with Poisson's ratio in a Transverse mode and b Longitudinal mode

Actuation capabilities of the auxetic matrix at $\nu =-0.9$ increased by about 2.5 times in transverse mode and 5.7 times in longitudinal mode compared to the non-auxetic matrix at $\nu =0.4$ as shown in Fig. 14a and b. Actuation depends on material properties and geometrical properties given by the parameter ${\varphi }_{ij}$ in Eq. (41). Actuation tip displacement $\delta$ and the parameter ${\varphi }_{ij}$ vary in a similar pattern w.r.t the Poisson’s ratio $\nu$ as shown in Fig. 14. This explains the nature of the actuation curve shown in Fig. 14a and b.

Fig. 14

Actuation measured in terms of tip displacement of the cantilever beam in a Transverse mode and b Longitudinal mode; Actuation is proportional to c ${\varphi }_{31}$ in transverse mode and d ${\varphi }_{33}$ in longitudinal mode

Improvement in sensing, actuation, and energy harvesting capabilities of the auxetic piezocomposite compared to the non-auxetic one has been observed. This improvement can be attributed to the better mechanical coupling between the applied strain to the rigid KNNS-BNZH piezoelectric inclusions in the soft and flexible polyethylene matrix due to which the strain gets transferred to the piezoelectric inclusions in a much better way [30, 87].

6 Conclusion

Homogenization technique was used to calculate the effective elastic and piezoelectric properties of a KNNS-BNZH and polyethylene-based 0–3 piezocomposite using finite element method-based numerical technique. Two different types of polyethylene matrices were considered, viz. inherently auxetic matrix having negative Poisson’s ratio of $\nu =-0.32$ and non-auxetic matrix having positive Poisson’s ratio of $\nu =0.2$. A unit cell was used to calculate the effective elastic and piezoelectric properties at different volume fractions. The sensing, actuation, and energy harvesting performance of the piezoelectric material attached to the cantilever beam host structure was studied. For the chosen auxetic and non-auxetic materials, having Poisson’s ratio $\nu =-0.32$ and $\nu =0.2$, the auxetic piezocomposite mode did not show much improvement in performance in transverse mode compared to that in longitudinal mode. At 30% volume fraction, voltage and harvested power increased by about 28% and 66% in the longitudinal mode. Studies were also conducted at different Poisson’s ratios starting from $\nu =-0.9$ to $\nu =0.4$ at 30% volume fraction. At other Poisson’s ratios, in the range $\nu <-0.32$ in particular, the auxetic piezocomposite showed better performance compared to the non-auxetic one. Improved sensing, actuation, and harvested power performance were observed at negative Poisson’s ratio of $\nu =-0.9$ compared to the non-auxetic material having positive Poisson’s ratio of $\nu =0.4$. Sensing voltage increased by about 2.5 times in transverse mode and by about 5.8 times in longitudinal mode. Power increased by about 6 and 34 times in transverse and longitudinal modes, respectively. Actuation increased by about 2.5 and 5.7 times in transverse and longitudinal mode, respectively. Similarly in some other negative Poisson’s ratio zone of the auxetic matrix $\left(\nu >-0.32 \mathrm{and} \nu <0\right)$, non-auxetic piezocomposite demonstrated better performance compared to auxetic one. Therefore, choosing a proper value of the auxetic piezocomposite (when $\nu <0$) is quite important to ensure better performance of auxetic piezocomposite compared to the non-auxetic one in either mode of operation, transverse or longitudinal.

Appendix

See Figs. 15, 16, 17 and 18 and Table 3

The model used in the present study is validated by calculating and comparing the effective properties of a PZT-5 and a polymer-based piezocomposite calculated by Berger et al. [72] using finite element (FE) and asymptotic homogenization (AH) methods. The elastic, piezoelectric effective properties and the relative permittivity calculated using the present model and those used by Berger et al. are compared as shown in Fig. 

Fig. 15

Stiffness parameters of the present model compared with FEM and AHM model by Berger et al.[72]

15,

Fig. 16

Piezoelectric coefficient calculated by the present model compared with FEM and AHM model by Berger et al.[72]

16, and

Fig. 17

Relative permittivity calculated by present model and compared with FEM and AHM model by Berger et al.[72]

17.

It can be observed that the effective properties calculated by the present method and those calculated by Berger et al. [72] are in good agreement.

The energy harvester model is validated by comparing the voltage generated per unit base acceleration by the present method and by Erturk and Inman [88]. The parameters for the host beam and the piezoelectric material used for calculations and comparison are given in Table

Table 3 Piezoelectric material and Host beam material properties[88]

3.

The material properties ${C}_{11}^{E},{C}_{22}^{E}, {C}_{33}^{E}, \cdots , {C}_{66}^{E}$ are the elements of the stiffness matrix in stress charge form. ${e}_{31}^{E} and{e}_{32}^{E}$ are the piezoelectric coupling coefficient in the stress-charge form in transverse mode. ${e}_{33}^{E}$ is the coupling coefficient in longitudinal mode written in stress charge form. ${\epsilon }_{11}^{S} \mathrm{and} {\epsilon }_{33}^{S}$ are permittivity in stress-charge form. Voltage per unit base acceleration calculated at a load resistance of $R=1\times {10}^{6}\Omega$ by the present method and by Erturk and Inman [88] is compared and is shown in Fig. 

Fig. 18

Comparison of piezoelectric voltage calculated by the present method and by Erturk and Iman[88]

18. It can be observed that the voltages per unit base acceleration calculated by the two methods does not differ much which validates the present method. A minor difference between the two responses could be due to the discretization error.