1 Introduction

This work generates a liquid drop with the use of a vertical metal sheet. The question of the creation and dynamics of a single drop of liquid under the influence of gravity has focused primarily on the formation at room temperature conditions and can be experienced in typical activities of daily life. A “drop of water” [1, 2] can be observed, for example, by opening and closing a faucet. Inspiration in nature is found in raindrops (\(\sim 1\) mm) [3], in limestone stalactites growing from a single “mineral-laden drop of water” [4], and in Lord Kelvin’s 1862 estimate [5]- [9] of the age of Earth (\(> 10^7\) m). Knowledge gained is applied to developing inkjet printing technologies reviewed by Cummins and Desmulliez [10], measuring liquid properties such as surface tension [11]- [18], and dating the 500,000-year history of the Siberian permafrost [19].

Da Silva et al. have investigated the acceleration of metal drops in a laser beam [20], and Bowering et al. have studied the behavior of metal drops on silicon wafers [21]. Applications for the research are in a wide range of areas including applying laser drop generation currently used to produce liquid drops from metal wires and rods [20,21,22,23,24,25,26]. Additional applications are in laser welding [27], laser welding in the automotive industry [28], consumer goods such as refrigerators [29] and washing machine baskets [30], and defense applications [31,32,33,34,35].

More recent printing methods in additive manufacturing for metal droplet 3D printing have been developed by He et al. [36], Deng et al. [37], and Hou et al. [38]. He et al. [36] demonstrated droplet-based 3D printing with aluminum droplets. He et al. “establishes a specific droplet scanning strategy” [36] and directly fabricated aluminum tube structures with variable cross sections and with the use of dissolvable supports. Deng et al. [37] first quantified the size and toroid shape of gas pinholes formed following impact of molten droplets of an aluminum alloy on solid brass substrates. Using the fundamental studies of Deng et al. [37], researchers in additive manufacturing may be better able to predict defects arising from gas pinholes. Hou et al. [38] took into account for the first time the presence of solidified aluminum droplets in investigations of neighboring aluminum droplets during remelting and horizontal droplet deposition. Hou et al. [38] focused specifically on obstructions caused by ripples and solidification angles of the solidified aluminum droplets on remelting of molten droplets. Further, Hou et al. demonstrated that simulations of this process show good agreement with experiments [38].

The behavior of a water drop has been studied at least since 1508 beginning with the work of Leonardo da Vinci (“goccia d’acqua”), who mentioned the neck returning upwards after a water drop detached [39]- [42] Edmé Mariotte (“goutte d’eau”) in 1686 [43], Johann Segner in 1751 [44], Pierre-Simon Laplace and Thomas Young in 1805 [45, 46], Félix Savart in 1833 [47, 48], and T. Tate (“drop of Water”) in 1864 [49]. The formation of a liquid drop under the influence of gravity has been studied theoretically [52, 54, 56,57,58,59,60,61] and experimentally [50]- [55, 59, 61– 66] as, for example, in pendant drops [67] jets [68,69,70,71,72,73], and dripping faucets [74– 78].

The oscillation of a drop of liquid [79]- [90] has been studied since the 1880s by Horace Lamb [79], Lord Kelvin [80], and Lord Rayleigh [81, 82], who obtained an expression for the fundamental oscillation mode (Rayleigh frequency) of a spherical liquid drop given by [90] \(\omega _R = \sqrt{\frac{8 \sigma }{\rho R^3}}\), where \(\sigma ,\rho\) and R represent the surface tension, density, and mean radius of the drop, respectively [90]. Oscillations have also been studied in double droplet systems [91]- [93].

This work presents experimental observations of formation by laser heating of a single liquid drop, with no satellite drops, following the bursting of a thick vertical liquid film of molten steel in a vertical steel plate (in which the molten region was formed). “Between melting and freezing” [94] of the steel, the molten steel descends from a vertical liquid film, forming a liquid drop that is not in thermal equilibrium with ambient room temperature conditions. The flow of the liquid from the hole rim (referred to as the hoop herein) is more similar to the flow of liquid from one end of a horizontal pipe; the molten steel flows out the hoop toward the front of the steel plate (facing the high energy laser). Bursting occurs in the upper portion of the film, not in the center, as a dimple thins to zero thickness due to draining of fluid. The neck that produces the drop solidifies rapidly as it cools to room temperature. Specific application scenarios for this work are in the development of models to describe the interactions of high energy lasers with metal targets such as mortar rounds and UAVs [31,32,33,34,35].

The contributions of this paper are a description of the neck and drop formation process, tracking data of the neck and drop formation process as well as the falling drop, a rough estimate of the surface tension of molten steel from a falling oscillating drop, a proposed kinematic model of hole formation, and a discussion of the hole morphology including physical characteristics such as hole perimeter, hole area, hole circularity, and hole eccentricity.

2 Experimental

2.1 Materials and setup

The experiments are conducted with 1.5-mm-thick vertical cold rolled ASTM A1008 (6sh16) steel sheets. The steel sheets are imaged by an IDT Os7 high-speed camera operating at 3000 fps at room temperature (Fig. 1). Figure 2 shows the target geometry for a vertical target with thickness d and target at zero incidence angle. Figure 2a and b shows the target. The unit vectors are \(({\hat{x}}, {\hat{y}}, {\hat{z}})\), and the three-dimensional coordinate system \(\{x, y, z\}\) is also shown. The angle \(\theta\) is taken within the plane of the plate to take on positive values in the counterclockwise direction (Fig. 2).

Fig. 1
figure 1

Experimental setup [95] “Reproduced from Lanzerotti et al., Appl. Phys. Lett. vol. 115, (2019), with the permission of AIP Publishing.”

Full size image
Fig. 2
figure 2

Target geometry. Side view a and front view b of vertical target with c a US dime for size comparison. The laser propagates in the negative \({\hat{z}}\) direction

Full size image

2.2 Heating

The vertical film of molten steel is created by illuminating a 1.5-mm-thick vertical cold rolled ASTM A1008 (6sh16) steel sheet with a 1-kW, 1075-nm YLR-1000 infrared laser.

2.3 Samples

The steel sheet is cut in the machine shop with a size of approximately 6 inches x 3 inches to fit in the holder placed in front of the laser beam.

3 Results

3.1 Hole formation

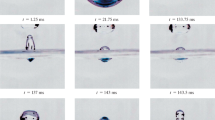
Table 1 and Fig. 3 present observations and photographs, respectively, of the hole, neck, and drop formation process. The laser was turned off at the right moment before the film burst so the film could be photographed. The photographs show that the film persists as a molten disk (Table 1, Step 1) after the laser is turned off (Table 1, Step 0) before the film ruptures (Table 1, Step 2). Gravity is responsible for the formation of a dimple and bulge in the liquid; there is an equilibrium between gravity and surface tension (Table 1, Step 1). If the front and back dimples become deep enough to meet, then a hole forms and rapidly expands (Table 1, Step 2). Fig. 3-1 shows a photograph of the frame just prior to (\(\frac{1}{3}\) ms) the first appearance of the hole in Fig. 3-2. Surface tension rapidly expands the hole (Table 1, Step 3).

Table 1 Formation of liquid drop
Full size table

Figure 3 shows a comparison of the initial position of the hole in Fig. 3-(2) with the final hole in Fig. 3-(7). The initial hole is located approximately 27 pixels (\(\approx 3.3\) mm) above the final hole center, as can be seen in the tracking data in Fig. 4a.

Fig. 3
figure 3

Photographs of formation of a liquid drop taken by a high-speed digital camera of the visible light emitted by the hot molten steel. Photographs 1-7 correspond to Steps 1-7 (Table 1), respectively, with (8) a US dime for size comparison. Photographs 1, 2, 3, 6 are “Reproduced from Lanzerotti et al., Appl. Phys. Lett. vol. 115, (2019), with the permission of AIP Publishing.” A comparison of the initial position of the hole in (2) with the final hole in (7) shows that the initial hole is off-center compared with the final hole. The off-center position of the initial hole is also shown in the tracking data at location (0,0), which is located approximately 27 pixels above the hole center, in Fig. 4

Full size image

Figure 4 shows the tracking positions of hole, neck, and falling drop, showing the position that the hole bursts in the thick molten film (Fig. 3-(2)) located at (0, 0) pixels (75 pixels per 9.53 mm). The off-center position of the initial hole is shown in the tracking data in position (0,0) that is approximately 27 pixels above the center of the final hole (Fig. 4a).These photographs show that the initial bursting location is off-center with respect to the final hole formed by the laser beam.

Fig. 4
figure 4

a Tracking positions of hole, neck, and falling drop, showing the position that the hole bursts in the thick molten film (Fig. 3-2) located at (0,0) pixels (75 pixels per 9.53 mm). This position is off center relative to the center of the hole, which is located approximately 27 pixels lower. b shows a US dime for size comparison

Full size image

3.2 Neck and drop formation

The molten liquid gathers into a spherical lump at the lower part of the hole (Table 1, Step 4a). Surface tension tends to make the liquid form into spheres; the lump is at the lower part of the hoop rim, since that is where the bulge was with the bulk of the liquid (Table 1, Step 4a). The liquid lump vibrates twice at the lower part of the hole (Table 1, Step 4b), as it settles into a sphere, before descending further as gravity has time to pull the liquid down to form a neck of molten steel between the hoop rim and the drop (Table 1, Step 5). The molten liquid drains preferentially at the front of the sheet (Figs. 6, 7a).

Tracking data obtained from photographs (Fig. 8) show that the neck width decreases (Fig. 5) and takes on its smallest value just prior to drop detachment. Photographs (Figs. 6, 7, 8) also show asymmetry in the neck in the front of the 9.88-mm-diameter hole (Fig. 7a) and hole rear (Fig. 7b) in the 1.5-mm-thick steel plate. A front view of the neck (at the front of the steel plate illuminated by the laser) is shown in Fig. 7a, and a rear view of the hole (the back of the steel plate) is shown in Fig. 7b. A comparison of Fig. 7a and b shows that the molten liquid drained preferentially at the front of the sheet.

The first appearance of the detached drop is shown in Fig. 3-(6) (Table 1, Step 6). The neck retracts upward slightly before freezing, with a small droplet that appears to form at the bottom of the neck (before the neck freezes) but does not detach (Table 1, Step 6; Fig. 3-(7)).

Fig. 5
figure 5

Neck width as a function of time after hole rupture (Table 1, Step 2). Drop detaches from neck at time \(t = 0.1700\) s (Table 1, Step 6)

Full size image
Fig. 6
figure 6

A photograph taken with a Canon PowerShot digital camera shows a front view of the neck below the rim of a 9.88-mm-diameter hole in a 1.5-mm-thick steel plate, showing molten liquid draining preferentially at the front face of the sheet. A US dime (10-cent coin) is included for size comparison

Full size image
Fig. 7
figure 7

Photographs taken with a Canon PowerShot digital camera from the right side of a 9.88-mm-diameter hole in a 1.5-mm-thick steel plate shows oblique views of a the front face of the sheet with the neck formed after molten liquid drained preferentially at the front of the sheet, and b the back face. A US dime (10-cent coin) is included for size comparison

Full size image

3.3 Falling drop

Photographs (Fig. 8) show that the drop then falls under gravity, and tracking data (Fig. 4) obtained from the photographs show that the drop shape oscillates (Figs. 8, 9) as the drop falls under gravity (Table 1, Step 7), with aspect ratio as high as \(\sim 1.5\) during the fall (Fig. 9d). The drop oscillates without appearing to hit the vertical steel plate. Images of the falling drop captured by the high-speed camera and tracking data from the trajectory of the center of the drop show that the position of the drop (Figs. 8, 9) is farther from the hole as time increases, as expected in gravity. The drop stops falling when it hits the mount surrounding the steel plate (Table 1, Step 8), after Fig. 8h, approximately one oscillation of the drop.

Fig. 8
figure 8

Photographs taken at 3000 fps by a high-speed camera of the visible light emitted by the hot molten steel showing a falling drop, with tracking using MotionStudio software. Time intervals between photographs are \(\varDelta t_{\text {ab}} = t_\text {a}- t_\text {b} \approx 5.33\) ms; \(\varDelta t_{\text {bc}} = t_\text {b} - t_\text {c} \approx 5.67\) ms; \(\varDelta t_{\text {cd}} = t_\text {c} - t_\text {d} \approx 6.33\) ms; \(\varDelta t_{\text {de}} = t_\text {d} - t_\text {e} \approx 7.67\) ms; \(\varDelta t_{\text {ef}} = t_\text {e} - t_\text {f} \approx 7.67\) ms; \(\varDelta t_{\text {fg}} = t_\text {f} - t_\text {g} \approx 3.67\) ms; \(\varDelta t_{\text {gh}} = t_\text {g} - t_\text {h} \approx 2.67\) ms. (i) shows a US dime for size comparison

Full size image
Fig. 9
figure 9

a Center, b width, c height, d aspect ratio of falling drop (Table 1, Step 7)

Full size image

A rough estimate of the surface tension \(\sigma \sim (150 \pm 20)\) \(\frac{{\text{mN}}}{{\text{m}}}\) is obtained (Table 2) from measurements of the mean radius R of the oscillating molten steel drop (Fig. 9), period T of drop oscillation (Fig. 9), with \(\sigma = \frac{\omega _R^2\rho _{\text {L}}R^3}{8}\) (Eqn. 1.1, Rayleigh frequency [90]). The density of liquid iron is estimated [96, 97] as \(\rho _{\text {L}} = 5810~\frac{\text {kg}}{\text {m}^3}\) by evaluating Nishizuka’s [96] expression cited by Morohoshi (Eq. 10 in  [97]) at 3134 K.

Table 2 Estimate of surface tension of molten steel obtained from measurements of oscillation frequency of falling drop (Table 1, Step 7) and mean radius of spherical drop (Table 1, Step 7)
Full size table

Scans of the deflection of the steel plate are acquired with a Chicago dial mechanical indicator CD1 with the steel plate mounted horizontally in a Haas TM-1 vertical milling machine. The data from the scans show minimal deflection after the plate cools to room temperature (Fig. 10).

Fig. 10
figure 10

Deflection out of the plane of the steel sheet with hole (Fig. 1b) measured by tracing a Chicago dial mechanical indicator CD1 (microns) across the surface of the steel plate. The steel plate is mounted horizontally in a Haas TM-1 milling machine. The black region shows where measurements were not taken (in the hole)

Full size image

4 Hole morphology

4.1 Kinematic model of hole formation

When the hole bursts at time \(t = t_\text {h}\), the initial speed \(v_{t_\text {h},\text {ellipse}}(\theta )\) of the hole perimeter is a function of the angle \(\theta\) relative to the horizontal (Fig. 2). In this situation, the angular dependence of the initial speed of the expanding hole may be written as,

$$\begin{aligned} v_{t_\text {h},\,\text {ellipse}}(\theta ) = \frac{v_\text {a, ellipse} v_\text {b, ellipse}}{\sqrt{v_\text {a, ellipse}^2 (\sin \theta )^2 + v_\text {b, ellipse}^2 (\cos \theta )^2} } \end{aligned}$$
(1)

where the terms \(v_\text {a,ellipse}\) and \(v_\text {b,ellipse}\) represent the initial speeds along the horizontal semi-major axis and vertical semi-minor axis, respectively.

The velocity vectors \(\mathbf {v}_{\text {ellipse}}(\theta , t)\) and position vectors \(\mathbf {r}_\text {ellipse}(\theta , t)\) for a proposed ellipse model of hole expansion as functions of time \(t \ge t_\text {h}\) can be written as,

$$\begin{aligned}&\mathbf {v}_\text {ellipse}(\theta , t) = v_{t_\text {h},\text {ellipse}} (\theta ) (\cos \theta ) {\hat{x}} \nonumber \\&\quad + \Big ( v_{t_\text {h},\text {ellipse}} (\theta ) (\sin \theta ) + a_{\text {y,ellipse}} t \Big ) {\hat{y}}, \nonumber \\&\mathbf {r}_\text {ellipse}(\theta , t) = \Big \{ x_{t_\text {h}} (\theta ) + v_{t_\text {h},\text {ellipse}} (\theta ) (\cos \theta ) t \Big \} {\hat{x}} \nonumber \\&\quad + \Big \{ y_{t_\text {h}}(\theta ) + v_{t_\text {h},\text {ellipse}} (\theta ) (\sin \theta ) t + \frac{1}{2} a_{\text {y,ellipse}} t^2 \Big \} {\hat{y}}. \end{aligned}$$
(2)

Least-squares linear fits to the measurement tracking data for the x-components of the position vector, \(\mathbf {r}_{\text {hole}}(\theta = 0^\circ , t)\) and \(\mathbf {r}_{\text {hole}}(\theta = 180^\circ ,t)\), and least-squares quadratic fits to the tracking data for the y-component of the position vector, \(\mathbf {r}_{\text {hole}}(\theta =90^\circ ,t)\) and \(\mathbf {r}_{\text {hole}}(\theta =270^\circ ,t)\), for \(t_\text {h} \le t \le (t_\text {h}+4)\) ms can be written with fit parameter estimates \(\{ {\tilde{v}}_{t_\text {h},x,0^\circ }\), \({\tilde{v}}_{t_\text {h},x,180^\circ }\), \({\tilde{v}}_{t_\text {h},y,90^\circ }\), \({\tilde{a}}_{t_\text {h},y,90^\circ }\), \({\tilde{v}}_{t_\text {h},y,270^\circ }\), \({\tilde{a}}_{t_\text {h},y,270^\circ } \}\) (Table 3), as

$$\begin{aligned} x_{\text {hole}}(\theta =0^\circ , t)= & {} \Big \{ ( 5,300 \pm 360 )~ \frac{{\text{pixels}}}{{\text {s}}} \Big \} t, \nonumber \\= & {} {\tilde{v}}_{t_\text {h},x,0^\circ } t, \end{aligned}$$
(3)
$$\begin{aligned} x_{\text {hole}}(\theta =180^\circ , t)= & {} \Big \{ -( 3,500 \pm 340 )~ \frac{{\text{pixels}}}{{\text {s}}} \Big \} t, \nonumber \\= & {} {\tilde{v}}_{t_\text {h},x,180^\circ } t, \end{aligned}$$
(4)
$$\begin{aligned} y_{\text {hole}}(\theta =90^\circ , t)= & {} \Big \{ ( 1,900 \pm 300 )~ \frac{{\text{pixels}}}{{\text{s}}} \Big \} t \nonumber \\&+ \Big \{ -( 240,000 \pm 89,000 ) \frac{{\text{pixels}}}{{\text{s}^2}} \Big \} t^2, \nonumber \\= & {} {\tilde{v}}_{t_\text {h},y,90^\circ } t + {\tilde{a}}_{t_\text {h},y,90^\circ } t^2, \end{aligned}$$
(5)
$$\begin{aligned} y_{\text {hole}}(\theta =270^\circ , t)= & {} \Big \{ -( 5,100 \pm 290 )~ \frac{{\text{pixels}}}{{\text{s}}} \Big \} t \nonumber \\&+ \Big \{ -( 530,000 \pm 85,000 ) \frac{{\text{pixels}}}{{\text{s}^2}} \Big \} t^2, \nonumber \\= & {} {\tilde{v}}_{t_\text {h},y,270^\circ } t + {\tilde{a}}_{t_\text {h},y,270^\circ } t^2. \end{aligned}$$
(6)

We assume constant initial speed of hole expansion along the semi-major axis and constant initial speed along the semi-minor axis (the two initial speeds may take on different values). We then calculate the average of the fit parameters obtained from least squares linear fits to the first five data points of the x-component of the tracking data with \(\theta = \{0^\circ , 180^\circ \}\) to obtain an estimate of the initial speed \({\tilde{v}}_{\text {a},\text {ellipse}}\) along the semi-major axis. Next, we calculate the average of the fit parameters of the linear term obtained from least squares quadratic fits to the first five data points of the y-component of the tracking data with \(\theta = \{90^\circ , 270^\circ \}\) to obtain an estimate of the initial speed \({\tilde{v}}_{\text {b},\text {ellipse}}\) along the semi-minor axis. These can be expressed as,

$$\begin{aligned} {\tilde{v}}_{\text {a},\text {ellipse}}= \,& {} \frac{1}{2}{( |{\tilde{v}}_{t_\text {h},x,0^\circ }| + |{\tilde{v}}_{t_\text {h},x,180^\circ }| )}, \\ \nonumber {\tilde{v}}_{\text {b},\text {ellipse}}=\, & {} \frac{1}{2}{( |{\tilde{v}}_{t_\text {h},y,90^\circ }| + |{\tilde{v}}_{t_\text {h},y,270^\circ }| )}, \end{aligned}$$
(7)

respectively.

Table 3 Table of parameters for ellipse model of hole formation
Full size table

We obtain an estimate of the acceleration in the y-direction \({\tilde{a}}_{t_{h},y,\text {ellipse}}\) by taking the average of the acceleration obtained from the fit to the position data vertically above the hole and below the hole, such that,

$$\begin{aligned} {\tilde{a}}_{y,\,\text {ellipse}} = \frac{1}{2}{({\tilde{a}}_{t_\text {h},y,90^\circ } + {\tilde{a}}_{t_{\text {h}},y,270^\circ } )}, \end{aligned}$$
(8)

where we assume that the vertical acceleration is constant at the points in time at the earliest stage of hole expansion. Substituting values for the fit parameters in Table 3 into Eqns. 7 and 8 , we obtain values for estimates \(\tilde{v}_{{a,ellipse}}\), \(\tilde{v}_{{b,ellipse}}\), and \(\tilde{a}_{{y,ellipse}}\), as

$$\tilde{v}_{{a,ellipse}} = {\mkern 1mu} {\text{ }}(4,400 \pm 1,300)~\frac{{\text{pixels}}}{\text{s}},$$
(9)
$$\tilde{v}_{{b,ellipse}} = (2,600 \pm 990)~\frac{{\text{pixels}}}{\text{s}},\,\tilde{a}_{{y,ellipse}} = - (390,000 \pm 200,000)~\frac{{\text{pixels}}}{{\text{s}^{2} }}.$$
(10)

These estimates can be used to obtain an estimate of the initial speed of the hole perimeter \({\tilde{v}}_{t_\text {h},\text {ellipse}}(\theta )\) according to

$$\begin{aligned} {\tilde{v}}_{t_\text {h},\text {ellipse}}(\theta ) = \frac{{\tilde{v}}_\text {a,ellipse} {\tilde{v}}_\text {b,ellipse}}{\sqrt{{\tilde{v}}_\text {a,ellipse}^2 (\sin \theta )^2 + {\tilde{v}}_\text {b,ellipse}^2 (\cos \theta )^2} }. \end{aligned}$$
(11)

Finally, equations of motion for the hole perimeter can be written for \(t_\text {h} \le t \le (t_\text {h} + 4)~\text {ms}\) as

$$\begin{aligned}&\mathbf {v}_{\text {ellipse}}(\theta , t) \nonumber \\&\quad = {\tilde{v}}_{t_\text {h},\text {ellipse}}(\theta ) (\cos \theta )~{\hat{x}} + {\tilde{v}}_{t_\text {h},\text {ellipse}}(\theta ) (\sin \theta )~{\hat{y}}, \nonumber \\&\mathbf {r}_{\text {ellipse}}(\theta , t) \nonumber \\&\quad = \{ x_{t_\text {h}}(\theta ) (\cos \theta ) + {\tilde{v}}_{t_\text {h},\text {ellipse}}(\theta ) (\cos \theta ) t\} {\hat{x}} \nonumber \\&\qquad + \{ y_{t_\text {h}}(\theta ) (\sin \theta ) + {\tilde{v}}_{t_\text {h},\text {ellipse}}(\theta ) (\sin \theta ) t + \frac{1}{2} {\tilde{a}}_{y,\text {ellipse}} t^2 \} {\hat{y}}. \end{aligned}$$
(12)

Figures 11 and 12 show horizontal and vertical tracking data of the hole perimeter for position vectors \(\{\mathbf {r}_{\text {hole}}(\theta = 45^\circ , t), \mathbf {r}_{\text {hole}}(\theta = 135^\circ , t), \mathbf {r}_{\text {hole}}(\theta = 225^\circ , t), \mathbf {r}_{\text {hole}}(\theta = 315^\circ ,t)\}\), respectively. The dashed lines represent results obtained using Eqn. 12 for the ellipse model of hole expansion. Figure 13 shows the height and width of the hole obtained from the position tracking data in Fig. 4.

Fig. 11
figure 11

Horizontal tracking data at hole perimeter for \(\theta ~=~\{0^\circ , 45^\circ , 90^\circ , 135^\circ , 180^\circ , 225^\circ , 270^\circ , 315^\circ \}\). Dashed lines represent predictions of ellipse model of hole expansion

Full size image
Fig. 12
figure 12

Vertical tracking data at hole perimeter for \(\theta ~=~\{0^\circ , 45^\circ , 90^\circ , 135^\circ , 180^\circ , 225^\circ , 270^\circ , 315^\circ \}\). Dashed lines represent predictions of ellipse model of hole expansion

Full size image
Fig. 13
figure 13

a Height and b width of hole obtained from measured tracking data (solid blue circles) and predictions of the ellipse model of hole expansion (green dashed lines)

Full size image

4.2 Hole eccentricity

We express the hole eccentricity, \(e_{\text {hole}}(t)\), as a function of hole height, \(h_{\text {hole}}(t)\), and hole width, \(h_{\text {width}}(t)\), as

$$\begin{aligned} e_{\text {hole}}(t)= \,& {} \sqrt{1 - \frac{h_{\text {hole}}^2 (t)}{w_{\text {hole}}^2(t)}}, \\ \nonumber= & {} \sqrt{1 - \frac{ \Big \{ y_{\text {hole}} (\theta = 270^\circ , t) - y_{\text {hole}} (\theta = 90^\circ , t) \Big \}^2 }{ \Big \{ x_{\text {hole}} (\theta = 180^\circ , t) - x_{\text {hole}} (\theta = 0^\circ ,t) \Big \}^2 }}. \end{aligned}$$
(13)

Table 4 shows measured values of the hole eccentricity, \(e_{\text {hole}}(t)\), obtained from the position tracking data and predictions obtained from the ellipse model of hole expansion in Fig. 13. Figure 14 and Table 4 show that the predictions show very good agreement with measurements calculated from the tracking data.

Fig. 14
figure 14

Eccentricity of hole obtained from measured tracking data (solid blue circles) and predictions of the ellipse model of hole expansion (green dashed lines)

Full size image
Table 4 Hole eccentricity \(e_{\text {hole}}(t)\) as a function of time
Full size table

4.3 Hole area

The area of the hole, \(A_{\text {hole}}(t)\), can be written as functions of the length of the semi-major axis, \(a_{\text {hole} }(t) = \frac{ w_{\text {hole} }(t) }{2}\), and length of the semi-minor axis, \(b_{\text {hole}} (t) = \frac{ h_{\text {hole}} (t) }{2}\), according to the expression,

$$\begin{aligned} A_{\text {hole}}(t)= & {} \pi a_{\text {hole} }(t) b_{\text {hole}} (t) , \end{aligned}$$
(14)
$$\begin{aligned}= & {} \pi \frac{ w_{\text {hole} }(t) }{2} \frac{ h_{\text {hole}} (t) }{2}, \end{aligned}$$
(15)
$$\begin{aligned}= & {} \frac{\pi }{4} \Big ( x_{\text {hole}} (\theta = 180^\circ , t) - x_{\text {hole}} (\theta = 0^\circ , t) \Big ) \nonumber \\&\Big ( y_{\text {hole}} (\theta = 270^\circ , t) - y_{\text {hole}} (\theta = 90^\circ , t) \Big ), \end{aligned}$$
(16)

where \(x_{\text {hole}} (\theta = 180^\circ , t)\) and \(x_{\text {hole}} (\theta = 0^\circ , t)\) represent x-coordinates of the hole width, and \(y_{\text {hole}} (\theta = 270^\circ , t)\) and \(y_{\text {hole}} (\theta = 90^\circ , t)\) represent y-coordinates of the hole height, respectively.

The standard deviation in the hole area, \(\sigma _{A_{\text {hole}}}(t)\), can be calculated from the variance, \(\sigma _{A_{\text {hole}}}^2(t)\), as

$$\begin{aligned} \sigma _{A_{\text {hole}}}(t)= & {} \sqrt{ \sigma _{A_{\text {hole}}}^2(t)}, \\ \nonumber= & {} \sqrt{ \sigma _{a_{\text {hole}}}^2 \left[ \frac{\partial A_{\text {hole}}(t)}{ \partial a_{\text {hole}}(t) } \right] ^2 + \sigma _{b_{\text {hole}}}^2 \left[ \frac{\partial A_{\text {hole}}(t)}{ \partial b_{\text {hole}}(t) } \right] ^2} , \\ \nonumber= & {} \sqrt{ \sigma _{a_{\text {hole}}}^2 \left[ \pi b_{\text {hole}} (t) \right] ^2 + \sigma _{b_{\text {hole}}}^2 \left[ \pi a_{\text {hole}} (t) \right] ^2}, \\ \nonumber= & {} \sqrt{ 2 \pi ^2 ( 4.0 b^2_{\text {hole}}(t) + 9.0 a^2_{\text {hole}}(t) ) }. \end{aligned}$$
(17)

where the uncertainty in the in the semi-major axis, \(a_{\text {hole}}= 2.0 \sqrt{2}\), and semi-minor axis, \(b_{\text {hole}} = 3.0 \sqrt{2}\), is estimated from the tracking data. Figure 15 shows the area of the hole (solid blue circles) as a function of time as obtained from measurement position tracking data. Predictions obtained from the ellipse model are shown as the dashed green line.

Fig. 15
figure 15

Hole area (solid blue circles) obtained from measurement position tracking measurement data and predictions obtained from ellipse model (dashed green line) with one-sigma error bars

Full size image

4.4 Hole perimeter

In 1914, Srinivasa Ramanujan [99]- [102] provided an approximation (I) for the perimeter of an ellipse, \(P_{\text {hole,1}} (t)\), as

$$\begin{aligned}&P_{\text {hole,1}} (t) = \pi \Big \{ 3[a_{\text {hole}}(t)+ b_{\text {hole}}(t) ] \nonumber \\&\quad - \sqrt{ \left[ 3a_{\text {hole}}(t) + b_{\text {hole}}(t) \right] \left[ a_{\text {hole}}(t) + 3b_{\text {hole}}(t) \right] } \Big \}. \end{aligned}$$
(18)

The standard deviation in the perimeter of the hole, \(\sigma _{P_{\text {hole,1}}}(t)\), for this approximation can be calculated from the variance, \(\sigma _{P_{\text {hole,1}}}^2(t)\),as

$$\begin{aligned} \sigma _{P_{\text {hole,1}}}(t)= & {} \sqrt{ \sigma _{P_{\text {hole,1}}}^2(t)}, \\ \nonumber= & {} \sqrt{ \sigma _{a_{\text {hole}}}^2(t) \left[ \frac{\partial P_{\text {hole,1}}(t)}{ \partial a_{\text {hole}}(t) } \right] ^2 + \sigma _{b_{\text {hole}}}^2(t) \left[ \frac{\partial P_{\text {hole,1}}(t)}{ \partial b_{\text {hole}}(t) } \right] ^2 }, \nonumber \end{aligned}$$
(19)

where the partial derivatives, \(\frac{\partial P_{\text {hole,1}}(t)}{ \partial a_{\text {hole}}(t) }\) and \(\frac{\partial P_{\text {hole,1}}(t)}{ \partial b_{\text {hole}}(t) }\), are given by,

$$\begin{aligned} \frac{\partial P_{\text{hole,1}}(t)}{\partial a_{\text{hole}}(t)} = {} 3\pi - \frac{\pi}{2} \Big \{ \frac{ 6a_{\text{hole}}(t) + 10b_{\text{hole}}(t) }{ \sqrt{3a^2_{\text{hole}} (t) + 10 a_{\text{hole}} (t) b_{\text{hole}}(t) + 3 b^2_{\text{hole}} (t) } } \Big \} , \\ \nonumber \frac{\partial P_{\text{hole,1}}(t)}{\partial b_{\text{hole}}(t)} = {} 3\pi - \frac{\pi}{2} \Big \{ \frac{ 6b_{\text{hole}} (t) + 10a_{\text{hole}}(t) }{ \sqrt{3a^2_{\text{hole}} (t) + 10 a_{\text{hole}} (t) b_{\text{hole}}(t) + 3 b^2_{\text{hole}} (t)} } \Big \}. \\ \nonumber \end{aligned}$$
(20)

Ramanujan [99]- [102] provided a second approximation (II) for the perimeter of the hole \(P_{\text {hole,2}} (t)\),

$$P_{{hole,2}} (t){\text{ }} = \pi [a_{{hole}} (t) + b_{{hole}} (t)]\left\{ {1 + \frac{{3h_{{hole}} (t)}}{{10 + \sqrt {4 - 3h_{{hole}} (t)} }}} \right\},$$
(21)

where the term, \(h_{\text {hole}}(t)\), is given by the expression,

$$\begin{aligned} h_{\text {hole}}(t) = \frac{[a_{\text {hole}}(t) - b_{\text {hole}}(t)]^2}{[a_{\text {hole}}(t) + b_{\text {hole}}(t) ]^2}. \end{aligned}$$
(22)

The standard deviation in the perimeter, \(\sigma _{P_{\text {hole,2}}}(t)\), for this approximation can be calculated from the variance, \(\sigma _{P_{\text {hole,2}}}^2(t)\), where

$$\begin{aligned} \sigma _{P_{\text {hole,2}}}(t)= & {} \sqrt{ \sigma _{P_{\text {hole,2}}}^2(t)}, \\ \nonumber= & {} \sqrt{ \sigma _{a_{\text {hole}}}^2(t) \left[ \frac{\partial P_{\text {hole,2}}(t)}{ \partial a_{\text {hole}}(t) } \right] ^2 + \sigma _{b_{\text {hole}}}^2(t) \left[ \frac{\partial P_{\text {hole,2}}(t)}{ \partial b_{\text {hole}}(t) } \right] ^2 }, \nonumber \end{aligned}$$
(23)

where the partial derivatives, \(\frac{\partial P_{\text {hole,2}}(t)}{ \partial a_{\text {hole}}(t) }\) and \(\frac{\partial P_{\text {hole,2}}(t)}{ \partial a_{\text {hole}}(t) }\), are given by the expressions,

$$\begin{aligned} \frac{\partial P_{\text {hole,2}}(t)}{\partial a_{\text {hole}}(t)}= & {} \frac{ 2[ a_{\text {hole,2}}(t) + b_{\text {hole,2}}(t) ]^2 [a_{\text {hole,2}}(t) - b_{\text {hole,2}}(t)] }{ [ a_{\text {hole,2}}(t) + b_{\text {hole,2}}(t) ]^4 } \\ \nonumber&- \frac{ 2[ a_{\text {hole,2}}(t) - b_{\text {hole,2}}(t) ]^2 [a_{\text {hole,2}}(t) + b_{\text {hole,2}}(t)] }{ [ a_{\text {hole,2}}(t) + b_{\text {hole,2}}(t) ]^4 } , \\ \nonumber \frac{\partial P_{\text {hole,2}}(t)}{\partial b_{\text {hole}}(t)}= & {} \frac{ - 2[ a_{\text {hole,2}}(t) + b_{\text {hole,2}}(t) ]^2 [a_{\text {hole,2}}(t) - b_{\text {hole,2}}(t)] }{ [ a_{\text {hole,2}}(t) + b_{\text {hole,2}}(t) ]^4 } \\ \nonumber&- \frac{ 2[ a_{\text {hole,2}}(t) - b_{\text {hole,2}}(t) ]^2 [a_{\text {hole,2}}(t) + b_{\text {hole,2}}(t)] }{ [ a_{\text {hole,2}}(t) + b_{\text {hole,2}}(t) ]^4 }. \nonumber \end{aligned}$$
(24)
Fig. 16
figure 16

Perimeter of hole obtained from measured tracking data and model predictions with a Ramanujan I, b Ramanujan II (green dashed lines)

Full size image

Figure 16a and b shows the perimeter of the hole obtained from position measurement tracking data and predictions of the ellipse model (green dashed line) using (a) Ramanujan I and (b) Ramanujan II .

4.5 Hole circularity

The hole circularity, \(f_{\text {hole}}(t)\), can be written as functions of the hole area, \(A_{\text {hole}}(t)\), and hole perimeter, \(P_{\text {hole}}(t)\), as,

$$\begin{aligned} f_{\text {hole}} (t) = \frac{4 \pi A_{\text {hole}}(t) }{P_{\text {hole} }^2 (t)}. \end{aligned}$$
(25)

For a circle with width \(w_{\text {circle}}(t)\), the circularity takes on a value of unity,

$$\begin{aligned} f_{\text {circle}} (t)=\, \frac{4 \pi A_{\text {circle}}(t) }{P_{\text {circle} }^2 (t)}, \\ \nonumber= & {} \frac{4 \pi \pi w^2_{\text {circle}} (t) }{[2 \pi w_{\text {circle}}(t)]^2}, \\ \nonumber= & {} 1. \end{aligned}$$
(26)

The standard deviation in the hole circularity, \(\sigma _{f_{\text {hole}}}(t)\), can be calculated from the variances in the area, \(\sigma _{A_{\text {hole}}}^2(t)\), and perimeter, \(\sigma _{P_{\text {hole}}}^2(t)\), respectively,

$$\begin{aligned} \sigma _{f_{\text {hole}}}(t)= & {} \sqrt{ \sigma ^2_{f_{\text {hole}}}(t)}, \\ \nonumber= & {} \sqrt{ \sigma _{A_{\text {hole}}}^2(t) \left[ \frac{\partial f_{\text {hole}}(t)}{ \partial A_{\text {hole}}(t) } \right] ^2 + \sigma _{P_{\text {hole}}}^2(t) \left[ \frac{\partial f_{\text {hole}}(t)}{ \partial P_{\text {hole}}(t) } \right] ^2 },\\ \nonumber= & {} \frac{4 \pi }{ P^2_{\text {hole}} (t)} \sqrt{ \sigma _{A_{\text {hole}}}^2(t) + \sigma _{P_{\text {hole}}}^2(t) \left[ \frac{ A^2_{\text {hole}} (t)}{ P^2_{\text {hole}} (t)} \right] }, \end{aligned}$$
(27)

where \(\frac{\partial f_{\text {hole}}(t)}{ \partial A_{\text {hole}}(t) } = \frac{ 4 \pi }{ P^2_{\text {hole}} (t)}\), and \(\frac{\partial f_{\text {hole}}(t)}{ \partial P_{\text {hole}}(t) }= -\frac{ 4 \pi A_{\text {hole}} (t)}{ P^3_{\text {hole}} (t)}\).

Now, using Ramanujan I, Eqns. 25 and 27 can be written as

$$\begin{aligned} f_{\text {hole,1}} (t) = \frac{4 \pi A_{\text {hole} }(t) }{P_{\text {hole,1} }^2 (t)}, \end{aligned}$$
(28)

and

$$\begin{aligned} \sigma _{f_{\text {hole,1}}}(t) = \frac{4 \pi }{ P^2_{\text {hole,1}} (t)} \sqrt{ \sigma _{A_{\text {hole}}}^2(t) + \sigma _{P_{\text {hole,1}}}^2(t) \left[ \frac{ A^2_{\text {hole}} (t)}{ P^2_{\text {hole,1}} (t)} \right] }. \end{aligned}$$
(29)

With Ramanujan II, Eqns. 25 and 27 can be written as

$$\begin{aligned} f_{\text {hole,2}} (t) = \frac{4 \pi A_{\text {hole} }(t) }{P_{\text {hole,2} }^2 (t)}, \end{aligned}$$
(30)

and

$$\begin{aligned} \sigma _{f_{\text {hole,2}}}(t) = \frac{4 \pi }{ P^2_{\text {hole,2}} (t)} \sqrt{ \sigma _{A_{\text {hole}}}^2(t) + \sigma _{P_{\text {hole,2}}}^2(t) \left[ \frac{ A^2_{\text {hole}} (t)}{ P^2_{\text {hole,2}} (t)} \right] }. \end{aligned}$$
(31)
Fig. 17
figure 17

Circularity of hole obtained from measured tracking data and predictions of the ellipse model of hole expansion

Full size image

Figure 17a and b shows the hole circularity (solid blue circles) obtained with approximations of the perimeter provided by Ramanujan I and Ramanujan II, respectively, and position measurement tracking data. The values obtained using predictions of the ellipse model are shown in dashed green lines in each figure. The figures show that the values of the hole circularity obtained with the measurement data show very good agreement with the values obtained with the model predictions for both approximations to the perimeter. The results show that the values of the hole circularity also decrease in the very initial stage of the hole expansion, and this trend is also predicted by the ellipse model.

5 Conclusion

In summary, this paper presents the formation of a single liquid drop of molten steel followed by rapid freezing of the molten steel neck upon cooling to room temperature. The drop falls under gravity and oscillates as surface tension tends to make the drop round. The paper also proposes a kinematic model of hole expansion for the very early stages in the bursting of the hole. Research on the hole morphology with this model provides estimates of physical properties of the hole, including hole eccentricity, hole area, hole perimeter, and hole circularity. Future work aims to gain a greater fundamental understanding of the reason that molten liquid drains preferentially at the front face of the steel sheet. See the supplementary material for hole formation, drop formation, and the falling drop with tracking using MotionStudio software (My-Movie-25).