Stimulated Brillouin scattering in metamaterials: a new method for estimation based on homogenization approach

Abstract

We propose a theoretical method for calculating the stimulated Brillouin scattering (SBS) gain coefficient in metamaterials. The presented model is based on homogenization and effective medium theories. We examined all of the optical, acoustic, and opto-acoustic parameters required to calculate SBS gain coefficient in metamaterials and proposed an approximate method for calculating each one. We have shown that the electrostriction is not the only important mechanism, and for different metamaterials, other parameters can play a significant role in the enhancement and suppression of the SBS gain coefficient. This result is consistent with previous work.

1 Introduction

Although optics and acoustics have separate long histories, opto-acoustics is considered a recent science, which began in 1922 with Brillouin's prediction of scattering of light by acoustic waves in a medium [1]. The incident electromagnetic wave fields on a material induce density variations at different points of that material. Such density changes introduce refraction index variations at different points, which in turn results in the scattering of light through that medium (Fig. 1). In general, stimulated Brillouin scattering (SBS) refers to the scattering of light by acoustic waves (e.g., pressure or mechanical waves) [2]. SBS is normally observed in an isotropic material [3]. From the viewpoint of quantum mechanics, this phenomenon can be interpreted as the scattering of photons by acoustic phonons.

Fig. 1

Schematic view of the SBS process in a linear elastic medium [9]

Researchers have long been interested in controlling the scattering of the propagated light through a medium and employing metamaterials is a new way of controlling optical properties. The term “metamaterial” was first used in 2001 by Walser [4]. The prefix “meta” indicates that the material does not exist in nature, but it can be produced artificially in the laboratory. Therefore, metamaterial is meant to convey a notion of superiority to the materials normally available in nature. In some literature, metamaterial is used to describe left-handed materials (i.e., materials with simultaneously negative electric permittivity and magnetic permeability) [5], whereas, in others, metamaterial is synonymous with a heterostructure of two or more different materials [6]. Although no exact definition so far has been presented for metamaterials, the following seems to have been recognized as a common definition by researchers: A metamaterial is an engineered composite with a rational ordered structure composed of two or more constituent materials [4, 6, 7]. Here, the constituent materials are just considered from a macroscopic perspective without taking into account their microscopic structure (i.e., their atoms and molecules). This is a correct and reasonable assumption aimed at distinguishing a metamaterial from an ordinary crystal [8]. Disregarding the microscopic structure of a material makes it possible to use the continuum mechanics theory in studying that material. A continuous material retains its properties even if it is broken into very small segments. A continuum medium was assumed in the present article, where linear conditions are dominant. These are conditions we encounter and experience in our daily life. To express the laws of physics in a continuum medium, the tensor analysis should be utilized. Tensors are mathematical tools we use to describe the phenomena, events, and interactions that occur within a continuum medium.

In this paper, an analytical framework is proposed for calculating the SBS gain coefficient in a metamaterial consisting of spheres embedded in a matrix. The proposed framework enables scholars to obtain a reasonable and fast approximation of enhancement or suppression of the SBS gain coefficient in a new metamaterial. Such theoretical studies may shed light on the way of experimental efforts in this field. The paper is organized as follows. In Sect. 2, we present an overview of SBS and the parameters required for determining SBS gain coefficient in the constituent media [10]. The following section then considers techniques to determine these parameters for a metamaterial. The methods used for determining the properties of the metamaterial are discussed in Sects. 3.1–3.4. Numerical examples are presented in Sect. 4, and also the results of the proposed model are compared with those obtained by Smith et al. [10]. The difference between our model and the previous study is in the employed theories. While we utilize the homogenization model and effective theory, they use a combination of energy density methods and perturbation theory.

2 SBS in constituent media

SBS is an opto-acoustic phenomenon. When matter (fiber) is exposed to a coherent, high-power laser beam, most of the laser energy is reflected, creating what is known as the Stokes wave. According to quantum mechanics, a photon scatters when it comes into collision with a particle—often a molecule. In the analysis of SBS, from a quantum mechanics perspective, the incident beam and matter are assumed to be made up of photons and phonons, respectively. In contrast, in classical mechanics, the incident light is assumed as an electromagnetic wave and matter as a linear medium that follows tensor analysis relationships. According to the classical approach, illuminating a material medium with a strong enough light field of the amplitude ${E}_{1}$, frequency ${\omega }_{1}$, and wave vector ${k}_{1}$ results in periodic changes in the material density. In other words, a matter wave (sound) with the wavelength Ω is produced. The density variations cause periodic changes in the refractive index, too, creating a Bragg grating. The Bragg grating scatters the incident light in the opposite direction at $\omega_{2}$ with the wave vector $k_{2}$. In this process, the intensities of the incident $I_{1}$ and scattered waves $I_{2}$ are related as

$$\begin{gathered} \frac{{dI_{1} }}{{dx_{1} }} = - gI_{1} I_{2} \hfill \\ \frac{{dI_{2} }}{{dx_{1} }} = gI_{1} I_{2} \hfill \\ \end{gathered}$$

(1)

where $x_{1}$ is the direction of propagation as shown in Fig. 1 and $g$ is the SBS gain coefficient at the spectrum line-center which is defined as [11]

$$g = \frac{{4\pi^{2} \gamma^{2} }}{{nc\lambda_{1}^{2} \rho \nu_{l} \Gamma_{B} }}$$

(2)

Here, γ is the electrostriction, n is the refractive index, c is the speed of light in vacuum, $\lambda_{1}$ is the incident optical wavelength in vacuum, $\rho$ is the material density, $\nu_{l}$ is the longitudinal acoustic wave velocity, and $\Gamma_{B}$ is the Brillouin linewidth (a measure of the acoustic loss). Equation (2) is also known as the SBS maximum gain coefficient that, for the sake of simplicity, we call it the SBS gain in the rest of this article. The SBS gain consists of the optical parameter $n$, the acoustic parameter $\nu_{l}$, the opto-acoustic parameter $\Gamma_{B}$, the electrostriction $\gamma^{2}$, and the density $\rho$. The present work studies all the parameters in Eq. (2) then proposes analytical techniques to determine these parameters for a metamaterial composed of spheres embedded in a matrix. Here, it is assumed that the acoustic properties of the material system remain unchanged; and the nonlinear optical effects, including four-wave mixing and the magnetic reactions of the metamaterial, are ignored. Throughout the article, we assume that the medium is linear elastic.

3 SBS in metamaterial

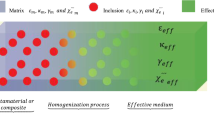
In this section, we calculate the SBS gain for a metamaterial using homogenization model. To this end, we examined all the parameters in Eq. (2) for metamaterials to finally construct a general equation for the SBS gain in metamaterials. Figure 2 illustrates the homogenization process (effective medium theory). Effective medium theory refers to an analytical or theoretical model that describes the macroscopic properties of the metamaterial. In this context, instead of two materials (matrix and inclusion), we use an equivalent material (effective material) with new macroscopic properties. Figure 2a schematically depicts the composition of a metamaterial (spheres embedded in a matrix). Figure 2(b) illustrates the equivalent or effective medium which represents the real composite medium. The combined stresses exerted on a small element in this system are second-order tensors shown in Fig. 2(c). We define the filling fraction:

$$f = \frac{{V^{i} }}{{V^{i} + V^{m} }}$$

(3)

where $V^{i}$ is the volume of inclusion and V^m is the volume of matrix. Here, superscripts i, m, and eff refer to the inclusion, matrix, and effective medium (metamaterial), respectively. The outline in this section is as follows: In Sect. 3.1, we examine the longitudinal acoustic velocity in metamaterials. In Sect. 3.2, we describe methods to determine the effective permittivity. In Sect. 3.3, we investigate the electrostriction in metamaterials. Finally, in Sect. 3.4, we examine the Brillouin linewidth in metamaterials.

Fig. 2

a Schematic representation of a metamaterial; spherical particles are embedded homogeneously within a matrix; $\eta^{i}$, $\kappa^{i}$, and $n^{i}$ are shear modulus, bulk modulus, and refractive index of the inclusions, while $\eta^{m}$, $\kappa^{m}$, and $n^{m}$ are shear modulus and bulk modulus, and refractive index of the matrix, respectively. b Outline of Homogenization process. c Stress vectors along three perpendicular directions, each shown by a face of the cube represents a small element of the volume

3.1 Longitudinal acoustic velocity in metamaterials

First of all, we investigate the acoustic parameter ${\nu }_{l}$ in metamaterials. According to Fig. 2 the stress–strain equation for a continuous medium is written as [12]

$$\left[ {\begin{array}{*{20}l} {\sigma_{11} } \hfill \\ {\sigma_{22} } \hfill \\ {\sigma_{33} } \hfill \\ {\sigma_{12} } \hfill \\ {\sigma_{23} } \hfill \\ {\sigma_{13} } \hfill \\ {\sigma_{21} } \hfill \\ {\sigma_{32} } \hfill \\ {\sigma_{31} } \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {C_{1111} } \hfill & {C_{1122} } \hfill & {C_{1133} } \hfill & {C_{1112} } \hfill & {C_{1123} } \hfill & {C_{1113} } \hfill & {C_{1121} } \hfill & {C_{1132} } \hfill & {C_{1131} } \hfill \\ {C_{2211} } \hfill & {C_{2222} } \hfill & {C_{2233} } \hfill & {C_{2212} } \hfill & {C_{2223} } \hfill & {C_{2213} } \hfill & {C_{2221} } \hfill & {C_{2232} } \hfill & {C_{2231} } \hfill \\ {C_{3311} } \hfill & {C_{3322} } \hfill & {C_{3333} } \hfill & {C_{3312} } \hfill & {C_{3323} } \hfill & {C_{3313} } \hfill & {C_{3321} } \hfill & {C_{3332} } \hfill & {C_{3331} } \hfill \\ {C_{1211} } \hfill & {C_{1222} } \hfill & {C_{1233} } \hfill & {C_{1212} } \hfill & {C_{1223} } \hfill & {C_{1213} } \hfill & {C_{1221} } \hfill & {C_{1232} } \hfill & {C_{1231} } \hfill \\ {C_{2311} } \hfill & {C_{2322} } \hfill & {C_{2333} } \hfill & {C_{2312} } \hfill & {C_{2323} } \hfill & {C_{2313} } \hfill & {C_{2321} } \hfill & {C_{2332} } \hfill & {C_{2331} } \hfill \\ {C_{1311} } \hfill & {C_{1322} } \hfill & {C_{1333} } \hfill & {C_{1312} } \hfill & {C_{1323} } \hfill & {C_{1313} } \hfill & {C_{1321} } \hfill & {C_{1332} } \hfill & {C_{1331} } \hfill \\ {C_{2111} } \hfill & {C_{2122} } \hfill & {C_{2133} } \hfill & {C_{2212} } \hfill & {C_{2123} } \hfill & {C_{2213} } \hfill & {C_{2121} } \hfill & {C_{2132} } \hfill & {C_{2131} } \hfill \\ {C_{3211} } \hfill & {C_{3222} } \hfill & {C_{3233} } \hfill & {C_{3212} } \hfill & {C_{3223} } \hfill & {C_{3213} } \hfill & {C_{3221} } \hfill & {C_{3232} } \hfill & {C_{3231} } \hfill \\ {C_{3111} } \hfill & {C_{3122} } \hfill & {C_{3133} } \hfill & {C_{3312} } \hfill & {C_{3123} } \hfill & {C_{3113} } \hfill & {C_{3121} } \hfill & {C_{3132} } \hfill & {C_{3131} } \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {e_{11} } \hfill \\ {e_{22} } \hfill \\ {e_{33} } \hfill \\ {e_{12} } \hfill \\ {e_{23} } \hfill \\ {e_{13} } \hfill \\ {e_{21} } \hfill \\ {e_{32} } \hfill \\ {e_{31} } \hfill \\ \end{array} } \right]$$

(4)

Equation (4) can be rewritten using the Voigt indexes as

$$\sigma_{ij} = C_{ijkl} e_{kl}$$

(5)

where $\sigma_{ij}$ represents the stress tensor, $C_{ijkl}$ the stiffness tensor, $e_{kl}$ the strain tensor, and i,j,k,l = 1,2,3. For a metamaterial with a cubic array, the number of components in the stiffness tensor $C_{ijkl}$ reduces from 81 to 3, and therefore the elastic behavior of the system can be evaluated using only the three components $C_{1111}$, $C_{1122}$, and $C_{2323}$. Illustrative representations of the bulk and shear moduli are shown in Fig. 3c and d, respectively. They are geometrically related to the stiffness tensor components:

$$\kappa = C_{1122} + \frac{2}{3}C_{2323}$$

(6a)

$$\eta = C_{2323}$$

(6b)

where $\kappa$ and $\eta$ are the bulk and shear moduli, respectively. The following well-known Hashin formulas are used to calculate the effective bulk and shear moduli [13,14,15]:

$$\kappa^{eff} = \kappa^{m} + f\frac{{\kappa^{i} - \kappa^{m} }}{{\kappa^{i} + \frac{4}{3}\eta^{m} }}\left( {\kappa^{m} + \frac{4}{3}\eta^{m} } \right)$$

(7)

Fig. 3

Illustrative representation of a) A longitudinal wave, b) A transverse wave, c) Bulk modulus, and d) Shear modulus [16]

and

$$\eta^{eff} = \eta^{m} + f\frac{{\eta^{i} - \eta^{m} }}{{\eta^{i} + \frac{3}{2}\left( {\frac{1}{{\eta^{m} }} + \frac{10}{{9\kappa^{m} + 8\eta^{m} }}} \right)^{ - 1} }}\left( {\eta^{m} + \frac{3}{2}\left( {\frac{1}{{\eta^{m} }} + \frac{10}{{9\kappa^{m} + 8\eta^{m} }}} \right)^{ - 1} } \right)$$

(8)

Equations (7) and (8) can be valid over the range 0 < f < 0.5.

Here, using the above-defined effective moduli, we are going to study the propagation of the sound wave in a metamaterial medium. In contrary to the gas state that is only able to transmit longitudinal sound waves, solids are capable of transmitting both longitudinal and transverse sound waves. Figure 3a and b illustrate the propagation of longitudinal and transverse sound waves, respectively. The velocities of longitudinal and transverse sound waves are expressed as [6]

$$v_{l} = \sqrt {\frac{{C_{1111} }}{\rho }} = \sqrt {\frac{{\kappa + \frac{4}{3}\eta }}{\rho }}$$

(9a)

$$v_{s} = \sqrt {\frac{{C_{2323} }}{\rho }} = \sqrt { \frac{ \eta }{{ \rho }}}$$

(9b)

where $v_{l}$ and $v_{s}$ are the velocities of longitudinal and transverse sound waves, respectively. In order to determine the SBS, just the velocity of the longitudinal sound wave is required. Substituting Eqs. (7) and Eq. (8) in Eq. (9a), the velocity of the longitudinal sound wave in the effective medium is obtained

$$v_{l}^{eff} = \sqrt {\frac{{\kappa^{eff} + \frac{4}{3}\eta^{eff} }}{{\rho^{eff} }}}$$

(10)

where the effective density is defined as $\rho^{eff} = f\rho^{i} + \left( {1 - f} \right)\rho^{m}$. Obviously, the sound velocity is higher in materials having a higher stiffness tensor than those with a lower one. For example, the sound velocity in silica is two times of that in Arsenic trisulfide.

3.2 Permittivity in metamaterials

In the following, we review different methods for calculating the effective permittivity of metamaterials. Although various methods have been proposed for this purpose, the validity of each method depends on the geometry of composite, the homogeneity of inclusions, isotropy, filling fraction, etc. An efficient numerical method is to use the optical wave with Bloch’s boundary conditions. This indirect method can only be used for dielectrics with cubic symmetry. The refractive index in this method is defined as $n = c\left| {\varvec{k}} \right|/\omega$, where ${\varvec{k}}$ represents Bloch’s wave vector. The cubic dielectric metamaterial is investigated at long wavelengths, then $\mu = 1$, and the effective refractive index can be written as $n = \sqrt \varepsilon$ [18]. Another model that researchers consider is the Maxwell–Garnett (MG) model. This model is valid for a cubic structure consists of spherical particles embedded in a matrix provided that the diameter of spherical particles is much less than the incident wave. Table 1 lists the available methods for calculating the refractive index of a composite material. To the best of our knowledge, there is not a comprehensive map to determine which model is suitable for which composite material. However, it is evident that the MG model is not valid for all f values but is suitable for simple cubic metamaterials [17]. The Bruggeman (BR) model may be accurate when the two materials occupy comparable filling fraction of the composite, and also it is valid for multilayer composites [19]. The series and parallel models are also used to estimate the effective refractive index. Moreover, these two models are used for estimating thermal and electrical conductivities of a composite material [17].

Table 1 Different effective methods for calculating the effective permittivity [17]

3.3 Electrostriction in metamaterials

As another key parameter, we are going to derive the electrostriction for metamaterials [20]. We begin by considering the potential electric energy per unit volume [11, 21]

$$u = \frac{{\varepsilon E^{2} }}{8\pi }$$

(11)

where $\varepsilon$ is permittivity. When an electromagnetic wave of an adequate intensity passes through a dielectric material, it causes displacement of the dielectric molecules and subsequently changes the density. The change in density, in turn, causes a change in permittivity:

$$\Delta \varepsilon = \frac{\partial \varepsilon }{{\partial \rho }}\Delta \rho$$

(12)

Therefore, the change in the energy density can be written as

$$\Delta u = \frac{{E^{2} }}{8\pi }\left( {\frac{\partial \varepsilon }{{\partial \rho }}} \right)\Delta \rho$$

(13)

According to the law of conservation of energy, the change in energy of a system is equal to the negative of the work done during the process of compression or expansion of that system. Hence,

$$\Delta u = - W = \frac{{E^{2} }}{8\pi }\left( {\frac{\partial \varepsilon }{{\partial \rho }}} \right)\Delta \rho = - p_{et} \frac{\Delta \rho }{\rho }$$

(14)

where $p_{et}$ represents the alternating pressure exerted on the system by the electric field called the electrostriction pressure. Using Eq. (14), electrostriction pressure is

$$p_{et} = - \frac{{E^{2} }}{8\pi }\rho \left( {\frac{\partial \varepsilon }{{\partial \rho }}} \right) = - \gamma \frac{{E^{2} }}{8\pi }$$

(15)

where $\gamma$ is the electrostriction constant and is defined as [11]

$$\gamma = \rho \frac{\partial \varepsilon }{{\partial \rho }}$$

(16)

Here, $\gamma$ denotes the electrostriction for constituent media. In the following, we try to derive electrostriction for metamaterials ( $\gamma^{eff}$). We present two methods for determining $\gamma^{eff}$. First, we calculate $\gamma^{eff}$ using Bruggeman (BR) model. This model has the form [22]

$$\left( {1 - f} \right)\left[ {\left( {\frac{{\varepsilon^{eff} }}{{\varepsilon^{m} }}} \right)^{\frac{1}{3}} \left( {1 - \frac{{\varepsilon^{i} }}{{\varepsilon^{m} }}} \right)} \right] = \left( {\frac{{\varepsilon^{eff} }}{{\varepsilon^{m} }} - \frac{{\varepsilon^{i} }}{{\varepsilon^{m} }}} \right)$$

(17)

where $\varepsilon^{i}$ and $\varepsilon^{m}$ are the permittivities of the matrix and inclusion, respectively. By substituting Eq. (17) in Eq. (16), we write the electrostriction of a composite as

$$\gamma^{eff} = \rho^{eff} \left( {\frac{{\partial \varepsilon^{eff} }}{{\partial \rho^{eff} }}} \right) = \rho \left( {\frac{{\partial \varepsilon^{eff} }}{{\partial \varepsilon^{m} }}.\frac{{\partial \varepsilon^{m} }}{{\partial \rho^{eff} }} + \frac{{\partial \varepsilon^{eff} }}{{\partial \varepsilon_{i} }}.\frac{{\partial \varepsilon_{i} }}{{\partial \rho^{eff} }} + \frac{{\partial \varepsilon^{eff} }}{\partial f}.\frac{\partial f}{{\partial \rho^{eff} }}} \right)$$

(18)

With hydrostatic and boundary conditions we evaluate six derivatives in Eq. (18):

$$\frac{{\partial \varepsilon_{eff} }}{{\partial \varepsilon_{m} }} = \frac{{\left( {1 - f} \right)\left( {\varepsilon^{m} - \varepsilon^{i} } \right)\varepsilon^{eff} - 3\left( {\varepsilon^{m} \left( {\varepsilon^{eff} } \right)^{2} } \right)^{\frac{1}{3}} \left( {\varepsilon^{eff} - \varepsilon^{i} } \right) - \left( {1 - f} \right)3\varepsilon^{i} \varepsilon^{eff} }}{{\left( {1 - f} \right)\left( {\varepsilon^{m} - \varepsilon^{i} } \right)\varepsilon^{m} - 3\varepsilon^{m} \left( {\varepsilon^{m} (\varepsilon^{eff} )^{2} } \right)^{1/3} }}$$

(19a)

$$\frac{{\partial \varepsilon_{m} }}{{\partial \rho^{eff} }} = \frac{{\gamma^{m} }}{{\rho^{eff} \left( {f\left( {\frac{{k^{m} }}{{k^{i} }} - 1} \right) + 1} \right)}}$$

(19b)

$$\frac{{\partial \varepsilon^{eff} }}{{\partial \varepsilon_{i} }} = \frac{{3\varepsilon^{m} \left( {\left( {1 - f} \right)\varepsilon^{eff} - \left( {\varepsilon^{m} (\varepsilon^{eff} )^{2} } \right)^{1/3} } \right)}}{{\left( {1 - f} \right)\left( {\varepsilon^{m} - \varepsilon^{i} } \right)\varepsilon^{m} - 3\varepsilon^{m} \left( {\varepsilon^{i} (\varepsilon^{eff} )^{2} } \right)^{1/3} }}$$

(19c)

$$\frac{{\partial \varepsilon_{i} }}{{\partial \rho^{eff} }} = \frac{{\gamma^{i} }}{{\rho^{eff} \left( {f + \frac{{k^{i} }}{{k^{m} }}\left( {1 - f} \right)} \right)}}$$

(19d)

$$\frac{{\partial \varepsilon^{eff} }}{\partial f} = \frac{{3\left( {\varepsilon^{m} - \varepsilon^{i} } \right)\varepsilon^{eff} \varepsilon^{m} }}{{\left( {1 - f} \right)\left( {\varepsilon^{m} - \varepsilon^{i} } \right)\varepsilon^{m} - 3\varepsilon^{m} \left( {\varepsilon^{m} (\varepsilon^{eff} )^{2} } \right)^{1/3} }}$$

(19e)

$$\frac{\partial f}{{\partial \rho^{eff} }} = \frac{{f\left( {1 - f} \right)\left( {k^{i} - k^{m} } \right)}}{{\rho^{eff} \left( {k^{m} f + k^{i} \left( {1 - f} \right)} \right)}}$$

(19f)

For a detailed discussion on hydrostatics condition of the calculated derivatives in Eqs. 19a–f see “Appendix”. Substituting Eqs. 19a–f in Eq. (18), the electrostriction for our metamaterial is given by

$$\begin{aligned} \gamma^{eff} = & \frac{{\left( {1 - f} \right)\left( {\varepsilon^{m} - \varepsilon^{i} } \right)\varepsilon^{eff} - 3\left( {\varepsilon^{m} \left( {\varepsilon^{eff} } \right)^{2} } \right)^{\frac{1}{3}} \left( {\varepsilon^{eff} - \varepsilon^{i} } \right) - \left( {1 - f} \right)3\varepsilon^{i} \varepsilon^{eff} }}{{\left( {1 - f} \right)\left( {\varepsilon^{m} - \varepsilon^{i} } \right)\varepsilon^{m} - 3\varepsilon^{m} \left( {\varepsilon^{m} (\varepsilon^{eff} )^{2} } \right)^{1/3} }}.\frac{{\gamma^{m} }}{{\rho^{eff} \left( {f\left( {\frac{{k^{m} }}{{k^{i} }} - 1} \right) + 1} \right)}} \\ & \quad + \frac{{3\varepsilon^{m} \left( {\left( {1 - f} \right)\varepsilon^{eff} - \left( {\varepsilon^{m} (\varepsilon^{eff} )^{2} } \right)^{1/3} } \right)}}{{\left( {1 - f} \right)\left( {\varepsilon^{m} - \varepsilon^{i} } \right)\varepsilon^{m} - 3\varepsilon^{m} \left( {\varepsilon^{i} (\varepsilon^{eff} )^{2} } \right)^{1/3} }}.\frac{{\gamma^{i} }}{{\rho^{eff} \left( {f + \frac{{k^{i} }}{{k^{m} }}\left( {1 - f} \right)} \right)}} \\ & \quad + \frac{{3\left( {\varepsilon^{m} - \varepsilon^{i} } \right)\varepsilon^{eff} \varepsilon^{m} }}{{\left( {1 - f} \right)\left( {\varepsilon^{m} - \varepsilon^{i} } \right)\varepsilon^{m} - 3\varepsilon^{m} \left( {\varepsilon^{m} (\varepsilon^{eff} )^{2} } \right)^{1/3} }}.\frac{{f\left( {1 - f} \right)\left( {k^{i} - k^{m} } \right)}}{{\rho^{eff} \left( {k^{m} f + k^{i} \left( {1 - f} \right)} \right)}} \\ \end{aligned}$$

(20)

To complete our discussion, we mention the method proposed in ref. [22]for calculating effective electrostriction of the metamaterial. They derived the effective electrostriction using the MG model:

$$\begin{aligned} \gamma^{eff} = & + \left( {\frac{{\left[ {\left( {\varepsilon^{i} + 2\varepsilon^{m} } \right)^{2} + 2f\left( {\varepsilon^{i} - \varepsilon^{m} } \right)^{2} } \right]\left( {1 - f} \right)}}{{\left[ {\left( {\varepsilon^{i} + 2\varepsilon^{m} } \right) - \left( {\varepsilon^{i} - \varepsilon^{m} } \right)f} \right]^{2} }}} \right)\left( {\frac{{\gamma^{m} }}{{\rho^{eff} \left( {f\left( {\frac{{k^{m} }}{{k^{i} }} - 1} \right) + 1} \right)}}} \right) \\ & + \left( {\frac{{\left[ {\left( {\varepsilon^{i} + 2\varepsilon^{m} } \right) - \left( {\varepsilon^{i} - \varepsilon^{m} } \right)} \right]^{2} f}}{{\left[ {\left( {\varepsilon^{i} + 2\varepsilon^{m} } \right) - \left( {\varepsilon^{i} - \varepsilon^{m} } \right)f} \right]^{2} }}} \right)\left( {\frac{{\gamma^{i} }}{{\rho^{eff} \left( {f + \frac{{k^{i} }}{{k^{m} }}\left( {1 - f} \right)} \right)}}} \right) \\ & + \left( {\frac{{3\varepsilon^{m} \left( {\varepsilon^{i} - \varepsilon^{m} } \right)\left( {\varepsilon^{i} + 2\varepsilon^{m} } \right)}}{{\left[ {\left( {\varepsilon^{i} + 2\varepsilon^{m} } \right) - \left( {\varepsilon^{i} - \varepsilon^{m} } \right)f} \right]^{2} }}} \right)\left( {\frac{{f\left( {1 - f} \right)\left( {k^{i} - k^{m} } \right)}}{{\rho^{eff} \left( {k^{m} f + k^{i} \left( {1 - f} \right)} \right)}}} \right) \\ \end{aligned}$$

(21)

The relation is valid for a diluted array. In Sect. 4, we investigate the effective electrostriction relations Eqs. (20) and (21), using a combination of different materials, and also compare the two models.

3.4 Brillouin linewidth

The last important parameter in metamaterials we are discussing is the Brillouin linewidth [23]. The wave equation in a very simple particle-spring system with no energy loss is expressed as $m\frac{{d^{2} x}}{{dt^{2} }} = - kx$. Mapping the mass and spring constant to the density and stiffness tensor, respectively, the mechanical wave (or the oustic wave) equation in an isotropic continuous medium with no loss becomes [24]

$$\frac{{\partial^{2} u_{l} }}{{\partial t^{2} }} - c_{ijkl} \frac{{\partial^{2} u_{l} }}{{\partial x_{j} \partial x_{i} }} = 0$$

(22)

Indeed, the loss is an integrated part of the elastic wave propagation. Loss may be originated from the thermal conductivity, viscosity, etc. It has been experimentally shown that loss is proportional to $\omega^{2}$. In the presence of loss, the stiffness tensor is written as [25]

$$c_{ijkl}^{\prime } = c_{ijkl} + i\xi_{ijkl}$$

(23)

where $c_{ijkl}$ and $c_{ijkl}^{\prime }$ are the stiffness tensors without and with loss, respectively, and ${\xi }_{ijkl}$ denotes the tensor of phonon viscosity. Using the concept of Eq. (23), Eq. (22) will be as follows [11]

$$\frac{{\partial^{2} u_{l} }}{{\partial t^{2} }} - \Gamma^{\prime } \frac{{\partial^{2} }}{{\partial x_{j} \partial x_{i} }}\left( {\frac{{\partial u_{l} }}{\partial t}} \right) - \upsilon^{2} \frac{{\partial^{2} u_{l} }}{{\partial x_{j} \partial x_{i} }} = 0$$

(24)

where $\Gamma^{\prime }$ is the damping parameter and is defined as [11, 26]

$$\Gamma^{\prime } = \frac{1}{\rho }\left( {\frac{4}{3}\eta_{ph} + \kappa_{ph} } \right)$$

(25)

where $\kappa_{ph}$ and $\eta_{ph}$ are the bulk and shear phonon viscosity coefficients, respectively, and are defined as

$$\eta_{ph} = \xi_{2323}$$

(26)

The Brillouin linewidth in Eq. (2), which is also known as the phonon half-life, is given by

$$\Gamma_{B} = q^{2} \Gamma^{\prime } = \frac{{4n^{2} \omega^{2} }}{{\rho c^{2} }}\left( {\frac{4}{3}\eta_{ph} + \kappa_{ph} } \right)$$

(27)

where q is the sound wave vector and is defined as $q = 2k = {\raise0.7ex\hbox{${2n\omega }$} \!\mathord{\left/ {\vphantom {{2n\omega } c}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$c$}}$. To the best of the authors’ knowledge, there are no established methods for calculating ${\Gamma }_{B}^{eff}$ of a metamaterial [27]. We suppose that $\xi_{ijkl} = \alpha C_{ijkl}$, where $\alpha$ is constant. Therefore, we can define effective bulk phonon viscosity and shear phonon viscosity as

$$\kappa_{ph}^{eff} = \kappa_{ph}^{m} + f\frac{{\kappa_{ph}^{i} - \kappa_{ph}^{m} }}{{\kappa_{ph}^{i} + \frac{4}{3}\eta_{ph}^{m} }}\left( {\kappa_{ph}^{m} + \frac{4}{3}\eta_{ph}^{m} } \right)$$

(28)

and

$$\eta_{ph}^{eff} = \eta_{ph}^{m} + f\frac{{\eta_{ph}^{i} - \eta_{ph}^{m} }}{{\eta_{ph}^{i} + \frac{3}{2}\left( {\frac{1}{{\eta_{ph}^{m} }} + \frac{10}{{9\eta_{ph}^{m} + 8\eta_{ph}^{m} }}} \right)^{ - 1} }}\left( {\eta_{ph}^{m} + \frac{3}{2}\left( {\frac{1}{{\eta_{ph}^{m} }} + \frac{10}{{9\eta_{ph}^{m} + 8\eta_{ph}^{m} }}} \right)^{ - 1} } \right)$$

(29)

by substituting Eqs. (28) and (29) in Eq. (27), the effective Brillouin linewidth for a metamaterial is given by

$${\Gamma }_{B}^{eff} = \frac{{4(n^{eff} )^{2} \omega^{2} }}{{\rho^{eff} c^{2} }}\left[ {\frac{4}{3}\eta_{ph}^{eff} + \kappa_{ph}^{eff} } \right]$$

(30)

4 Discussion

To describe the procedure outlined in the previous sections, we investigate the effective SBS gain for a metamaterial consists of spheres embedded in a dielectric matrix. According to the previous sections, we define the effective SBS gain as

$$g^{eff} = \frac{{4\pi^{2} \left( {\gamma^{eff} } \right)^{2} }}{{nc\lambda_{1}^{2} \rho^{eff} \nu_{l}^{eff} \Gamma_{B}^{eff} }}$$

(31)

By rewriting Eq. (31) as follows, we examine the contribution from each term in Eq. (31) to the enhancement or suppression of the SBS gain when the filling fraction is changing:

$$\begin{gathered} 10\log \left( {\frac{{{\text{max}}\left( {g^{eff} } \right)}}{{max\left( {g^{m} } \right)}}} \right) \hfill \\ = 10\log \left( {\frac{{n^{m} }}{{n^{eff} }}} \right) + 10\log \left( {\frac{{\rho^{m} }}{{\rho^{eff} }}} \right) + 10\log \left( {\frac{{{\Gamma }_{B}^{m} }}{{{\Gamma }_{B}^{eff} }}} \right) \hfill \\ + 10\log \left( {\frac{{v_{l}^{m} }}{{v_{l}^{eff} }}} \right) + 10\log \left( {\left( {\frac{{\gamma^{eff} }}{{\gamma^{m} }}} \right)^{2} } \right) \hfill \\ \end{gathered}$$

(32)

In this way, the contribution from each parameter to the enhancement or suppression of the SBS gain can be investigated by simply adding the value taken from each curve at a specified filling fraction. Some material parameters are shown in Tab. 2. In Fig. 4a and b, we have plotted the contribution from each term in Eq. (32) for SiO₂ spheres in As₂S₃ and As₂S₃ spheres in Si, respectively. In the case of SiO₂ spheres embedded in As₂S₃, we showed that the electrostriction and velocity try to reduce the SBS gain and other terms try to enhance the gain. In this example, we found that the velocity and electrostriction are important parameters in the suppression of the SBS gain. In the case of As₂S₃ spheres embedded in Si, the only term that always goes against the enhancement of the gain is the density and all other parameters try to enhance the SBS gain. We can conclude that the SBS gain increases in this metamaterial because there is no effective reducing factor. Unlike the case of SiO₂ spheres in As₂S₃, we see that the Brillouin linewidth and density affect the enhancement and suppression of the SBS gain as much as the velocity.

Table 2 Electrostriction ${\upgamma }$, bulk modulus ${\upkappa }$ (in GPa), shear modulus $\eta$ (in GPa), refractive index n, Brillouin linewidth ${\Gamma }_{{\text{B}}} /2{\uppi }$ (in MHz), phonon viscosity coefficient ${\upxi }_{2323}$ (in m.Pa.s), stiffness tensor coefficient ${\text{C}}_{1111}$ (in GPa), material density ${\uprho }$ (in ${\text{Kg}}/{\text{m}}^{3}$), and acost velocity $v_{{\text{l}}}$ (in m/s) for SiO₂ and As₂S₃ compounds [9, 10]

Fig. 4

Contribution from each term in Eq. (2) to improvement in SBS gain for a) SiO₂ spheres in As₂S₃ and b) As₂S₃ spheres in Si

In figure 5, we have plotted the SBS gain as a function of the filling fraction for SiO₂ spheres in As₂S₃ (red curve). From the graph, one can find out that the SBS gain for this metamaterial is suppressed by 13% and 38% at f = 0.05 and f = 0.2, respectively. This result is consistent with the results of Smith et al. (blue carve). For a more accurate comparison of the results shown in Fig. 5, we present the numerical results in Table 3. Comparing the analytical calculations of the previous section with these numerical results, we deduce that our formalism provides a logical approximation for the rapid calculation of the SBS gain in a metamaterial in different filling fractions. Moreover, within our formalism, we can easily calculate the contribution from each parameter in the enhancement or suppression of the SBS gain.

Fig. 5

SBS gain for ${\mathrm{SiO}}_{2}$ spheres in ${\mathrm{As}}_{2}{\mathrm{S}}_{3}$; our model (red) versus Smith’s simulation [10] (blue)s

Table 3 SBS gain g (in ${\text{nm W}}^{ - 1}$) for $SiO_{2}$ spheres in $As_{2} S_{3}$ for various fill fraction

In Fig. 6, we investigate the effective electrostriction expressions (20) and (21), using a combination of different materials, and also compared the two models. The solid green curves represent the electrostriction obtained from the MG model and the red stars show the electrostriction obtained from the BR model. In Fig. 6a, we showed the electrostrictions of GaAs spheres in Si over the full range of filling fractions (0 < f < 1) obtained from both models. Here, we observe that the behavior of $\gamma^{eff}$ over the full range of filling fractions is almost entirely independent of the choice of model. This suggests that the suppression or enhancement of electrostriction in this metamaterial is independent of the lattice structure. In Fig. 6(b), we showed the electrostriction of SiO₂ spheres in Si. In this example, the $\gamma^{eff}$ is completely suppressed (at $f \approx 0.08$) which can be attributed to a totally vanished SBS. We also observe that the difference between the two models is negligible over the ranges of f < 0.17 and 0.8 < f.

Fig. 6

Electrostriction of two composites: a) GaAs spheres in Si and b) SiO₂ heres in Si

Finally, it is important to keep in mind that the MG model is suitable for low solute concentrations such as a dilute array with a simple cubic structure. On the other hand, the BR model may be accurate for high filling fraction such as face-centered cubic structure.

5 Conclusion

We presented a formalism for calculating the SBS gain in metamaterials consist of spheres embedded in a matrix using homogenization and effective theory. The procedure involves the calculation of the mechanical, optical, and opto-acoustic properties involved in Eq. (2). The effect of each parameter on the SBS enhancement or suppression was studied. The results demonstrated the electrostriction is not always the only important mechanism, and other parameters can play a significant role in the enhancement or suppression of the SBS. Finally, the results of the proposed model were compared with those obtained by Smith et al. The numerical comparison showed that the model presented in this paper can be considered as an acceptable approximation for examining changes in the SBS gain of a new metamaterial.

Appendix

In this section, we present a discussion on the hydrostatics condition for evaluating the derivatives in Eq. (18). To evaluate these six derivatives, we use the mechanical condition of a material. During the electrostriction process, for each volume element, the product of density and volume is constant. Thus,

$$\begin{gathered} \rho^{i} V^{i} = m^{i} = constant \hfill \\ \rho^{m} v^{m} = m^{m} = constant \hfill \\ \end{gathered}$$

(33)

Another condition we use in our analysis is that the pressure that particles exert on matter is equal to the pressure that matter exerts on particles

$$\Delta P^{m} |_{\Omega } = \Delta P^{i} |_{\Omega }$$

(34)

Here Ω represent boundary and $P^{m,i}$ denotes pressure. With this condition, we write [22]

$$\frac{{\kappa^{i} \Delta V^{i} }}{{V^{i} }} |_{\Omega } = \frac{{\kappa^{m} \Delta V^{m} }}{{V^{m} }} |_{\Omega }$$

(35)

Integrating both sides, we have

$$V^{m} = C\left( {V^{i} } \right)^{{{\raise0.7ex\hbox{${\kappa^{i} }$} \!\mathord{\left/ {\vphantom {{\kappa^{i} } {\kappa^{m} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\kappa^{m} }$}}}}$$

(36)

where C is constant.