1 Introduction

Carbon structures such as graphene flakes and carbon nanotubes (CNTs) have attracted huge attention among researchers because of their exceptional characteristics, including electrical, chemical, and mechanical properties [1,2,3,4,5]. Monolayer graphene is a two-dimensional tightly packed honeycomb lattice with the thickness of one carbon atom. Up to now, the one-layer graphene is the thinnest and strongest known substance in nature. Graphene papers present almost all the peculiar features of carbon nanotubes, while the price of their production is lower than CNTs. A graphene sheet can carry on electrical-current densities six orders of magnitude higher than that of copper. It possesses record thermal conductivity and stiffness. It reconciles highly conflicting qualities of brittleness and ductility [6]. Because of its high ratio of the stiffness to inertia, it can expose extraordinary resonant frequencies in order of mega- or giga-hertz [7, 8]. This feature is the reason that high-frequency sensors are broadly composed of graphene papers in nano–microelectromechanical systems (NEMs–MEMs). Hence, many experimental and analytical investigations were accomplished on the study of mechanical behavior of mono- and multilayer graphene sheets by researchers [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. The occurrence of effective phenomena such as localized ripple [25], out of plane deformation [26], nonlocality [20, 23, 27,28,29], imperfection [30], and porosity [31] have been experimentally seen in graphene sheets. These can affect their mechanical behavior, and it seems crucial to have a model which accounts for all the effective parameters for the optimal design of graphene-based resonators.

The shear effect between layers is the most important phenomenon which highly affects their characteristics in mechanical designing, notably natural and resonant frequencies, maximum deflection, and buckling resistance [7, 8, 32,33,34,35,36,37,38,39]. Accordingly, some investigations have been experimentally carried out on the interlayer shear effect in graphene layers. In this regard, Tan et al. [40] disclosed the interlayer shear mode of multilayer graphene flakes, in the range of bi-layer graphene to bulk graphite, and suggested that the corresponding Raman peak measures the interlayer coupling. Boschetto et al. [39] reported real-time observation of the interlayer shearing mode, corresponding to the lateral oscillation of graphene planes, for bi- and few-layer grapheme sheets, utilizing femtosecond pump–probe technique. They suggested strong dependence of shearing-mode frequency on the number of layers. The frequency was reported to change from 1.32 THz for the bulk limit to 0.85 THz for the bi-layer graphene.

In addition to those experimental investigations, a few simple models have been developed to study the shear effect of the graphene layers analytically. In this regard, Liu et al. [8] studied the mechanical properties of various interlayer crosslinks and intralayer crosslinks, and then made continuum model analysis for the estimating overall mechanical properties of graphene-based paper materials. They proposed a deformable tension–shear (DTS) model by considering deformation of graphene sheets, and also deformation of the interlayer crosslinks and intralayer crosslinks. Liu et al. [7] presented a multi-beam shear model (MBSM) that accounted for the interlayer shear, and compared the natural frequency results of their model with molecular dynamics (MD) simulation in the case of the cantilever multilayer graphene-based resonator. Using the multi-beam shear model and taking into account the surface effect, Rokni and Lu [36] studied the pull-in instability of wedged/curved multilayer graphene nanoribbon (GNR) electrostatic nanoactuators subjected to the Casimir force. By comparison of the results obtained from the MBSM analysis [7] and experimental tests [39, 40], it can be readily concluded that the MBSM is very useful to investigate the vibration of graphene strips, but it is not well able to predict accurately the design parameters of graphene layers in which the width of layers is in the order of their length. Thus, it is required to develop a new model on the basis of the plate models to more accurately study such multilayer grapheme sheets. Although many studies have been done on the mono- and multilayer graphene flakes modeled as plates [9, 23, 27, 41,42,43,44,45], the interlayer shear between graphene layers has not been well addressed by them.

As mentioned above, no report has been presented which considers the interlayer shear effect of multilayer graphene sheets in plate models. The present work is an attempt to fill this gap in the literature by developing analytical plate model to study multilayer graphene-based nanoresonators incorporating interlayer shear effect.

First, the partial differential equation of motion is derived for multilayer graphene sheets modeled as multi-plates with interlayer shear effect utilizing the Hamilton’s principle. Moreover, the general form of boundary conditions, including geometrical (essential) boundary conditions and load-type (natural) boundary conditions, is obtained for any point on the periphery of rectangular sheets. Then, by pursuing an analytical approach, a closed-form expression for the natural frequencies of simply supported multilayer rectangular grapheme sheets is obtained. Meanwhile, molecular dynamics (MD) simulations of the simply supported multilayer graphene sheets are carried out to verify numerical results obtained from the analytical approach.

2 Formulation

2.1 Preliminaries

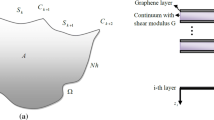
A 3D schematic view and a side view of a section of an N-layer graphene sheet under transverse load \(q(x,y)\) are depicted in Fig. 1a, b, respectively. Parameters \(\Omega\), \(h\), and \(A\) denote the occupied space by the N-layer graphene, the interlayer spacing between graphene layers, and the upper surface of the top layer, respectively. The structure of the multilayer graphene sheet is modeled as the combination of N thin graphene layers, with one-atom thickness each, and (N − 1) crosslinks considered as continuums between any two adjacent layers. The model is considered only under transverse loads, and in-plane loads are considered to be absent.

Fig. 1
figure 1

Simply supported rectangular N-layer graphene sheet with transverse load q(x,y): a 3D schematic and b side view of a section of the multilayer graphene sheet

Full size image

Every layer is considered as a homogeneous, isotropic, elastic thin plate. Since each layer is very thin, the classical (Kirchhoff) plate model is chosen for expressing its bending (flexural) deformation. According to this model, the plane sections initially normal to the mid-surface remain plane and normal to that surface after deformation; consequently, the components of the infinitesimal displacement field at any time t are written as follows [46]:

$$\begin{gathered} ~u_{{{\text{layer}}}}^{{(i)}}= - z\frac{{\partial {w^{(i)}}(x,y,t)}}{{\partial x}},\,\, \hfill \\ v_{{{\text{layer}}}}^{{(i)}}= - z\frac{{\partial {w^{(i)}}(x,y,t)}}{{\partial y}},\, \hfill \\ w_{{{\text{layer}}}}^{{(i)}}={w^{(i)}}(x,y,t), \hfill \\ \end{gathered}$$
(1)

in which, \(~u_{{{\text{layer}}}}^{{(i)}}\), \(v_{{{\text{layer}}}}^{{(i)}}\), and \(w_{{{\text{layer}}}}^{{(i)}}\) are the components of the displacement vector field of ith layer along the axes of the depicted coordinate system in Fig. 1. Parameter z stands for the distance of the point from the mid-plane of its layer. In this way, the deformation of each layer is assumed to be of only flexural type, i.e., without in-plane deformation.

From the reported results observed in MD simulations, the deflections of all the layers are almost the same [7]. Thus, in view of Eq. (1), it can be written as follows:

$$\begin{gathered} ~w_{{{\text{layer}}}}^{{(1)}}=w_{{{\text{layer}}}}^{{(2)}}= \cdots =w_{{{\text{layer}}}}^{{(N)}}=w(x,y,t), \hfill \\ u_{{{\text{layer}}}}^{{(1)}}=u_{{{\text{layer}}}}^{{(2)}}= \cdots =u_{{{\text{layer}}}}^{{(N)}}=u(x,y,t)= - z\frac{{\partial w(x,y,t)}}{{\partial x}},\,\, \hfill \\ v_{{{\text{layer}}}}^{{(1)}}=v_{{{\text{layer}}}}^{{(2)}}= \cdots =v_{{{\text{layer}}}}^{{(N)}}=v(x,y,t)= - z\frac{{\partial w(x,y,t)}}{{\partial x}}. \hfill \\ \end{gathered}$$
(2)

At least at one edge of the multilayer sheet, there should be a support to avoid the rigid-body translation of the layers in x–y plane; so that there is no slipping between layers. Considering this and the fact that the layers do not undergo in-plane deformation, one can conclude that there are no in-plane displacements for the particles of the layers. Consequently, the in-plane displacements for the points within interlayer continuum attached to the two adjacent layers vanish, and there is only the transverse displacement for those particles. Hence, one can write

$$\begin{gathered} ~{u_{{\text{continuum}}}}=0, \hfill \\ {v_{{\text{continuum}}}}=0,\, \hfill \\ {w_{{\text{continuum}}}}=w(x,y,t), \hfill \\ \end{gathered}$$
(3)

where, \({u_{{\text{continuum}}}}\), \({v_{{\text{continuum}}}}\), and \({w_{{\text{continuum}}}}\) are the components of the displacement vector field for the interlayer continuum along x, y, and z axes, respectively.

The variation of the strain energy for an elastic solid occupying region Ω is written as follows:

$$\delta U=\iiint\limits_{\Omega } {\left( {{\sigma _{ij}}\delta {\varepsilon _{ij}}} \right)\,\,{\text{d}}\Omega ,}$$
(4)

where \({\sigma _{ij}}\) and \({\varepsilon _{ij}}\) denote the components of the stress and strain tensors, i.e., \(\sigma\) and \(\varepsilon\), respectively. The components of the strain tensor, \(\varepsilon\), and the rotation vector \(\theta\) of the material elements are generally related to the displacement field \(u\) according to the following relations:

$$\begin{gathered} {\varepsilon _{ij}}=\frac{1}{2}{(\nabla u+\nabla {u^T})_{ij}}=\frac{1}{2}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}}+\frac{{\partial {u_j}}}{{\partial {x_i}}}} \right), \hfill \\ {\theta _i}=\frac{1}{2}{\left( {\nabla \times u} \right)_i}= - \frac{1}{2}\left( {{\int _{ijk}}\frac{{\partial {u_j}}}{{\partial {x_k}}}} \right), \hfill \\ \end{gathered}$$
(5)

where \({\varepsilon _{ijk}}\) is the permutation symbol and \(\nabla\) stands for the gradient operator.

The constitutive relation between the stresses and the strain components for an isotropic linearly elastic is as follows:

$${\sigma _{ij}}=\lambda tr\left( {\mathbf{\varepsilon }} \right){\delta _{ij}}+2\mu {\varepsilon _{ij}},$$
(6)

in which λ and µ are the Lame constants, and can be represented in terms of Young’s modulus E and Poisson’s ratio v as \(\lambda =\frac{{Ev}}{{\left( {1+v} \right)\left( {1 - 2v} \right)}}\) and \(\mu =G=\frac{E}{{2\left( {1+v} \right)}}\).

2.2 Derivation of the governing equation of motion

In this section, the governing equation of motion and boundary conditions of an N-layer graphene sheet are derived by considering interlayer shear effect. For this purpose, the strain and kinetic energies of an N-layer graphene sheet and work done by the external loads are written and substituted in the equation of Hamilton’s principle. It should be noted that the strain energy includes two parts, i.e., one part \({U_{{\text{bend}}}}\) corresponding to the bending of layers and the other part \({U_{{\text{shear}}}}\) corresponding to the shear deformation between the layers. Thus, the variation of the strain energy of an N-layer graphene sheet is decomposed as follows:

$$\delta U=\delta {U_{{\text{bend}}}}+\delta {U_{{\text{shear}}}},$$
(7)

By substitution of Eq. (1) into Eq. (5), the non-zero components of the strain tensor \(\varepsilon\) and rotation vector \(\theta\) for layers are obtained as follows:

$$\begin{gathered} \varepsilon _{{xx}}^{{{\text{layer}}}}= - z\frac{{{\partial ^2}w(x,y,t)}}{{\partial x_{{}}^{2}}},\,\,\,\,\,\,\,\varepsilon _{{yy}}^{{{\text{layer}}}}= - z\frac{{{\partial ^2}w(x,y,t)}}{{\partial y_{{}}^{2}}}, \hfill \\ \varepsilon _{{xy}}^{{{\text{layer}}}}=\varepsilon _{{yx}}^{{{\text{layer}}}}= - z\frac{{{\partial ^2}w(x,y,t)}}{{\partial x\,\partial y}}, \hfill \\ \theta _{x}^{{{\text{layer}}}}=\frac{{\partial w(x,y,t)}}{{\partial y}},\,\,\,\,\,\,\,\,\theta _{y}^{{{\text{layer}}}}= - \frac{{\partial w(x,y,t)}}{{\partial x}}. \hfill \\ \end{gathered}$$
(8)

Similarly, by inserting Eq. (3) into Eq. (5), the non-zero components of the strain tensor for the continuum between layers are determined as follows:

$$\varepsilon _{{zx}}^{{{\text{continuum}}}}=\frac{1}{2}\left( {\frac{{\partial w(x,y,t)}}{{\partial x}}} \right),{\kern 1pt} \quad \;\varepsilon _{{zy}}^{{{\text{continuum}}}}=\frac{1}{2}\left( {\frac{{\partial w(x,y,t)}}{{\partial y}}} \right).$$
(9)

For the plate analysis, the values of the normal tractions on the top and bottom of the plate as well as the plate thickness are relatively small. Hence, the value of the stress component \(\sigma _{{zz}}^{{}}\) in all points of the plate is negligible compared to the other stress components. Therefore, it is assumed that \(\sigma _{{zz}}^{{}}=0\) in Eq. (6). As a consequence of this assumption, the components \(\sigma _{{xx}}^{{}}\) and \(\sigma _{{yy}}^{{}}\) can be obtained as follows:

$$\begin{gathered} \sigma _{{xx}}^{{}}=\frac{E}{{1 - {\nu ^2}}}\left( {{\varepsilon _{xx}}+\nu {\varepsilon _{yy}}} \right), \hfill \\ \sigma _{{yy}}^{{}}=\frac{E}{{1 - {\nu ^2}}}\left( {{\varepsilon _{yy}}+\nu {\varepsilon _{xx}}} \right). \hfill \\ \end{gathered}$$
(10)

Inserting Eq. (8) into Eqs. (6) and (10) yields

$$\begin{aligned} \sigma _{{xx}}^{{\text{layer}}} & = - \frac{{Ez}}{{1 - {\nu ^2}}}\left( {\frac{{{\partial ^2}w(x,y,t)}}{{\partial x_{{}}^{2}}}+\,\nu \frac{{{\partial ^2}w(x,y,t)}}{{\partial y_{{}}^{2}}}} \right), \\ \sigma _{{yy}}^{{\text{layer}}} & = - \frac{{Ez}}{{1 - {\nu ^2}}}\left( {\frac{{{\partial ^2}w(x,y,t)}}{{\partial y_{{}}^{2}}}+\,\nu \frac{{{\partial ^2}w(x,y,t)}}{{\partial x_{{}}^{2}}}} \right), \\ \sigma _{{xy}}^{{\text{layer}}} & =\sigma _{{yx}}^{{\text{layer}}}= - \frac{{Ez}}{{1+\nu }}\left( {\frac{{{\partial ^2}w(x,y,t)}}{{\partial x\,\partial y}}} \right). \\ \end{aligned}$$
(11)

By combining Eqs. (6) and (9), the interlayer shear stresses, i.e., \(\tau _{{zx}}^{{{\text{continuum}}}}\) and \(\tau _{{zy}}^{{{\text{continuum}}}}\), are also obtained as follows:

$$\begin{gathered} \tau _{{zx}}^{{{\text{continuum}}}}(x,y,t)=G\left( {\frac{{\partial w(x,y,t)}}{{\partial x}}} \right), \hfill \\ \tau _{{zy}}^{{{\text{continuum}}}}(x,y,t)=G\left( {\frac{{\partial w(x,y,t)}}{{\partial y}}} \right), \hfill \\ \end{gathered}$$
(12)

in which G is the interlayer shear modulus.

Substituting Eq. (8) into Eq. (4), then integrating over the thickness of the layers, one can obtain

$$\delta {U_{{\text{bend}}}}= - N\iint\limits_{A} {\left[ {{M_{xx}}\delta \left( {\frac{{{\partial ^2}w(x,y,t)}}{{\partial {x^2}}}} \right)+{M_{yy}}\delta \left( {\frac{{{\partial ^2}w(x,y,t)}}{{\partial {y^2}}}} \right)+2{M_{xy}}\delta \left( {\frac{{{\partial ^2}w(x,y,t)}}{{\partial y\partial x}}} \right)} \right]}{\text{d}}A,$$
(13)

in which

$${M_{xx}}=\int\limits_{{ - h/2}}^{{h/2}} {\sigma _{{xx}}^{{{\text{layer}}}}\,} z\,{\text{d}}z,\,\,\,\,\,\,\,{M_{yy}}=\int\limits_{{ - h/2}}^{{h/2}} {\sigma _{{yy}}^{{{\text{layer}}}}\,} z\,{\text{d}}z,\,\,\,\,\,\,\,{M_{xy}}=\int\limits_{{ - h/2}}^{{h/2}} {\sigma _{{xy}}^{{{\text{layer}}}}\,} z\,{\text{d}}z.$$
(14)

Similarly, the variation of the strain energy due to the interlayer shear deformation is obtained as the following expression by inserting Eq. (9) into Eq. (4) and then integrating over each interlayer spacing:

$$\delta {U_{{\text{Shear}}}}=(N - 1)\iint\limits_{A} {\left[ {{Q_x}\delta \left( {\frac{{\partial w(x,y,t)}}{{\partial x}}} \right)+{Q_y}\delta \left( {\frac{{\partial w(x,y,t)}}{{\partial y}}} \right)} \right]{\text{d}}A},$$
(15)

where

$${Q_x}=\int\limits_{{ - h/2}}^{{h/2}} {\tau _{{zx}}^{{{\text{continuum}}}}\,\,{\text{d}}z} ,\,\,\,\,\,\,{Q_y}=\int\limits_{{ - h/2}}^{{h/2}} {\tau _{{zy}}^{{{\text{continuum}}}}\,\,{\text{d}}z} .$$
(16)

By employing the divergence theorem of Gauss on Eqs. (13) and (15) and then substituting the outcomes into Eq. (7), the variation of the total strain energy takes the following form:

$$\begin{gathered} \delta U=\iint\limits_{A} { - N\left( {\left( {\frac{{{\partial ^2}{M_{xx}}}}{{\partial {x^2}}}+2\frac{{{\partial ^2}{M_{xy}}}}{{\partial y\partial x}}+\frac{{{\partial ^2}{M_{yy}}}}{{\partial {y^2}}}} \right)+(N - 1)\left( {\frac{{\partial {Q_{zx}}}}{{\partial x}}+\frac{{\partial {Q_{zy}}}}{{\partial y}}} \right)} \right)\delta w(x,y,t)\,{\text{d}}A} \hfill \\ \,\quad \quad \quad +\int\limits_{0}^{a} {\left[ {\left( {N\left( {\frac{{\partial {M_{yy}}}}{{\partial y}} - 2\frac{{\partial {M_{xy}}}}{{\partial x}}} \right)+(N - 1){Q_{zy}}} \right)\delta w(x,y,t)\, - N\,{M_{yy}}\,\frac{{\partial (\delta w(x,y,t))}}{{\partial y}}\,} \right]_{{y=0}}^{{y=b}}{\text{d}}x} \hfill \\ \,\quad \quad \quad +\int\limits_{0}^{b} {\left[ {\left( {N\left( {\frac{{\partial {M_{xx}}}}{{\partial x}} - 2\frac{{\partial {M_{xy}}}}{{\partial y}}} \right)+(N - 1){Q_{zx}}} \right)\delta w(x,y,t)\, - N\,{M_{xx}}\,\frac{{\partial (\delta w(x,y,t))}}{{\partial x}}\,} \right]_{{x=0}}^{{x=a}}{\text{d}}y} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+{\left( {{M_{xy}}\delta w(x,y,t)} \right)_{(x=0\,\,or\,a)\,\,{\text{and}}\,\,(y=0\,\,or\,b)}}. \hfill \\ \end{gathered}$$
(17)

In addition, the kinetic energy of the N-layer graphene sheet is written as follows:

$$\begin{gathered} T=N\int\limits_{{ - h/2}}^{{h/2}} {\int\int\limits_{A} {\frac{\rho }{2}\left( {{{\dot {u}}^2}+{{\dot {v}}^2}+{{\dot {w}}^2}} \right){\text{d}}A{\text{d}}z} } , \hfill \\ \,\,\,\,\,=\frac{N}{2}\iint\limits_{A} {\left( {I\left( {{{(\frac{{\partial \dot {w}(x,y,t)}}{{\partial x}})}^2}+{{(\frac{{\partial \dot {w}(x,y,t)}}{{\partial y}})}^2}} \right)+M{{(\dot {w}(x,y,t))}^2}} \right){\text{d}}A,} \hfill \\ \end{gathered}$$
(18)

where \(\rho\) is the density of the layers and

$$M=\rho h,\,\,\,\,\,I=\int\limits_{{ - h/2}}^{{h/2}} {\rho \,{z^2}\,{\text{d}}z} =\frac{1}{{12}}\rho {h^3},\,\,\,\,\,\,\,\,\mathop {\left( {} \right)}\limits^{ \bullet } =\frac{\partial }{{\partial t}}\left( {} \right).$$
(19)

The variation of Eq. (18) is written as follows:

$$\begin{gathered} \delta T=N\iint\limits_{A} {\left[ {I\left( {\frac{{\partial \dot {w}(x,y,t)}}{{\partial x}}\, \times \,\frac{{\partial (\delta \dot {w}(x,y,t))}}{{\partial x}}+\frac{{\partial \dot {w}(x,y,t)}}{{\partial y}}\,\,} \right.} \right.} \hfill \\ \quad \quad \quad \quad \quad \left. {\quad \left. { \times \frac{{\partial (\delta \dot {w}(x,y,t))}}{{\partial y}}} \right)+M\,\dot {w}(x,y,t)\,\,\delta \dot {w}(x,y,t)} \right]{\text{d}}A. \hfill \\ \hfill \\ \end{gathered}$$
(20)

By applying the integration by parts to Eq. (18) on variable t, the variation of the kinetic energy is rewritten as follows:

$$\begin{gathered} \delta T=N\iint\limits_{A} {\left[ {I\left( { - \frac{{\partial \ddot {w}(x,y,t)}}{{\partial x}} \times \frac{{\partial (\delta w(x,y,t))}}{{\partial x}}+\frac{\partial }{{\partial t}}\left( {\frac{{\partial \dot {w}(x,y,t)}}{{\partial x}} \times \frac{{\partial (\delta w(x,y,t))}}{{\partial x}}} \right)} \right)} \right.} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\quad +\,I\left( { - \frac{{\partial \ddot {w}(x,y,t)}}{{\partial y}} \times \frac{{\partial (\delta w(x,y,t))}}{{\partial y}}+\frac{\partial }{{\partial t}}\left( {\frac{{\partial \dot {w}(x,y,t)}}{{\partial y}} \times \frac{{\partial (\delta w(x,y,t))}}{{\partial y}}} \right)} \right)\,\,\, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left. {\quad +\left. {M\left( { - \ddot {w}(x,y,t) \times \delta w(x,y,t)+\frac{\partial }{{\partial t}}\left( {\dot {w}(x,y,t) \times \delta w(x,y,t)} \right)} \right)} \right)} \right]\,\,{\text{d}}A. \hfill \\ \end{gathered}$$
(21)

On the basis of the divergence theorem of Gauss, the variation of the kinetic energy takes its final form as follows:

$$\begin{gathered} \delta T=N\iint\limits_{A} {\left\{ {\left( {I\left( {\frac{{{\partial ^2}\ddot {w}(x,y,t)}}{{\partial {x^2}}}+\frac{{{\partial ^2}\ddot {w}(x,y,t)}}{{\partial {y^2}}}} \right) - M\,\ddot {w}(x,y,t)} \right)\delta w(x,y,t)} \right.} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+\,\,\,\frac{\partial }{{\partial t}}\left[ { - I\left( {\frac{{{\partial ^2}\dot {w}(x,y,t)}}{{\partial {x^2}}}\delta w(x,y,t)+\frac{{{\partial ^2}\dot {w}(x,y,t)}}{{\partial {y^2}}}\delta w(x,y,t)} \right)} \right. \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\left. {\left. {+\,M\left( {\dot {w}(x,y,t)\,\,\delta w(x,y,t)} \right)} \right]\,} \right\}\,{\text{d}}A - \left[ {\int\limits_{0}^{b} {I\frac{{\partial \ddot {w}(x,y,t)}}{{\partial x}}\,} \delta w(x,y,t)\,{\text{d}}y} \right]_{{x=0}}^{{x=a}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \,\left[ {\int\limits_{0}^{a} {I\frac{{\partial \ddot {w}(x,y,t)}}{{\partial y}}\,} \delta w(x,y,t){\text{d}}x} \right]_{{y=0}}^{{y=b}}+\frac{\partial }{{\partial t}}\left[ {\int\limits_{0}^{b} {I\frac{{\partial \dot {w}(x,y,t)}}{{\partial x}}\,} \delta w(x,y,t)\,{\text{d}}y} \right]_{{x=0}}^{{x=a}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+\,\frac{\partial }{{\partial t}}\left[ {\int\limits_{0}^{a} {I\frac{{\partial \dot {w}(x,y,t)}}{{\partial y}}\,} \delta w(x,y,t){\text{d}}x} \right]_{{y=0}}^{{y=b}}. \hfill \\ \end{gathered}$$
(22)

The virtual work of the external load on the multilayer graphene sheet due to the transverse load q(x,y,t) can be acquired as follows:

$$\delta W=\iint\limits_{A} {q(x,y,t)}\,\delta w(x,y,t){\text{d}}A.$$
(23)

Eventually, the variations of the strain energy, virtual work, and kinetic energy obtained in Eqs. (17), (23) and (22), respectively, are inserted to the Hamilton’s principle equation on the time interval between \({t_1}\) and \({t_2}\):

$$\int\limits_{{{t_1}}}^{{{t_2}}} {\left( {\delta T+\delta W - \delta U} \right)\,} {\text{d}}t=0.$$
(24)

This leads to the governing equation of motion and also the boundary conditions with the aid of the fundamental lemma of calculus of variations. The governing equation of motion reads:

$$\begin{aligned} & N\left( {\frac{{{\partial ^2}{M_{xx}}}}{{\partial {x^2}}}+2\frac{{{\partial ^2}{M_{xy}}}}{{\partial y\partial x}}+\frac{{{\partial ^2}{M_{yy}}}}{{\partial {y^2}}}} \right)+(N - 1)\left( {\frac{{\partial {Q_{zx}}}}{{\partial x}}+\frac{{\partial {Q_{zy}}}}{{\partial y}}} \right) \\ & \quad \quad +\,N\,I\left( {\frac{{{\partial ^2}\ddot {w}(x,y,t)}}{{\partial {x^2}}}+\frac{{{\partial ^2}\ddot {w}(x,y,t)}}{{\partial {y^2}}}} \right)\,\, - N\,M\,\ddot {w}(x,y,t)+q(x,y,t)=0. \\ \end{aligned}$$
(25)

Similarly, the boundary conditions at the points on the two edges with x = 0 and x = a are expressed as follows:

$$\begin{gathered} N\left( {\frac{{\partial {M_{xx}}}}{{\partial x}} - 2\frac{{\partial {M_{xy}}}}{{\partial y}}} \right)\,+(N - 1){Q_{zx}}\,\,\,\,+N\,I \times \,\frac{{\partial \ddot {w}(x,y,t)}}{{\partial x}}=0,\,\quad {\text{OR}}\,\quad \delta w(x,y,t)\,=0, \hfill \\ {M_{xx}}=0,\,\quad {\text{OR}}\,\quad \delta \left( {\frac{{\partial w(x,y,t)}}{{\partial x}}} \right)\,=0.\,\,\, \hfill \\ \end{gathered}$$
(26)

In addition, for the two edges with y = 0 and y = b, we have the following boundary conditions:

$$\begin{gathered} N\left( {\frac{{\partial {M_{yy}}}}{{\partial y}} - 2\frac{{\partial {M_{xy}}}}{{\partial x}}} \right)+(N - 1){Q_{zy}}+NI\left( {\frac{{\partial \ddot {w}(x,y,t)}}{{\partial y}}} \right)=0,\,\quad {\text{OR}}\,\quad \delta w(x,y,t)\,=0, \hfill \\ {M_{yy}}=0,\,\quad {\text{OR}}\,\quad \delta \left( {\frac{{\partial w(x,y,t)}}{{\partial y}}} \right)\,=0.\,\, \hfill \\ \end{gathered}$$
(27)

In addition, at the four corners of the rectangular sheet, the boundary conditions read

$${M_{xy}}=0\quad {\text{OR}}\quad \delta w(x,y,t)\,=0\,.$$
(28)

Now, the governing equation of motion and the corresponding boundary conditions are rewritten in terms of the kinematic function \(w(x,y,t)\) explicitly. To do this, the stress components from Eqs. (11) and (12) are inserted in Eqs. (14) and (16), respectively. Then, the results are substituted into Eqs. (25–28). In this manner, the governing equation of motion takes the following form:

$$\begin{gathered} N\,{D_{{\text{bend}}}}{\nabla ^4}w(x,y,t) - (N - 1){D_{{\text{shear}}}}{\nabla ^2}w(x,y,t) \hfill \\ \quad \quad =q(x,y,t)\,+N\left[ {I\left( {\frac{{{\partial ^2}\ddot {w}(x,y,t)}}{{\partial {x^2}}}+\frac{{{\partial ^2}\ddot {w}(x,y,t)}}{{\partial {y^2}}}} \right) - M\,\ddot {w}(x,y,t)} \right], \hfill \\ \end{gathered}$$
(29)

where

$${D_{{\text{bend}}}}=\frac{{E\,{h^3}}}{{12(1 - {v^2})}},\,\quad {D_{{\text{shear}}}}=Gh.$$
(30)

In addition, for the boundary conditions at the points on the two edges with x = 0 and x = a:

$$\begin{gathered} N\,{D_{{\text{bend}}}}\left( {\frac{{{\partial ^3}w(x,y,t)}}{{\partial {x^3}}}+\left( {2 - \nu } \right)\frac{{{\partial ^3}w(x,y,t)}}{{\partial x\partial {y^2}}}} \right) \hfill \\ \quad \quad - \, (N - 1){D_{{\text{shear}}}}\,\,\frac{{\partial w(x,y,t)}}{{\partial x}}\,\, - N \times \,I \times \frac{{\partial \ddot {w}(x,y,t)}}{{\partial x}}=0,\,\,\,\,\,\,\,{\text{OR}}\,\,\,\,\,\,\delta w(x,y,t)\,=0, \hfill \\ \frac{{{\partial ^2}w(x,y,t)}}{{\partial {x^2}}}+\nu \frac{{{\partial ^2}w(x,y,t)}}{{\partial {y^2}}}=0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,OR\,\,\,\,\,\,\,\,\,\,\delta \left( {\frac{{\partial w(x,y,t)}}{{\partial x}}} \right)\,=0. \hfill \\ \end{gathered}$$
(31)

In addition, at the points on the two edges with y = 0 and y = b:

$$\begin{gathered} N\,{D_{{\text{bend}}}}\left( {\frac{{{\partial ^3}w(x,y,t)}}{{\partial {y^3}}}+\left( {2 - \nu } \right)\frac{{{\partial ^3}w(x,y,t)}}{{\partial {x^2}\partial y}}} \right) \hfill \\ \quad \quad - \, (N - 1){D_{{\text{shear}}}}\,\,\frac{{\partial w(x,y,t)}}{{\partial y}} - N \times \,I \times \frac{{\partial \ddot {w}(x,y,t)}}{{\partial y}}=0,\,\quad {\text{OR}}\quad \delta w(x,y,t)\,=0, \hfill \\ \frac{{{\partial ^2}w(x,y,t)}}{{\partial {y^2}}}+\nu \frac{{{\partial ^2}w(x,y,t)}}{{\partial {x^2}}}=0,\quad {\text{OR}}\quad \delta \left( {\frac{{\partial w(x,y,t)}}{{\partial y}}} \right)\,=0. \hfill \\ \end{gathered}$$
(32)

In addition, at the four corners:

$$\frac{{{\partial ^2}w}}{{\partial x\,\partial y}}=0\,\quad {\text{OR}}\quad \delta w(x,y,t)\,=0\,.$$
(33)

2.3 Analytical expression for the natural frequencies

In this section, the simply supported condition is considered. For this type of support, the boundary conditions are as follows:

$$w(x,y,t)=\delta w(x,y,t)\, \equiv 0;\quad {\text{at}}\,{\text{every}}\,{\text{point}}\,\,{\text{on}}\,\,{\text{the}}\,\,{\text{boundary}},$$
(34)
$$\frac{{{\partial ^2}w(x,y,t)}}{{\partial {x^2}}}+\nu \frac{{{\partial ^2}w(x,y,t)}}{{\partial {y^2}}}=0;\quad {\text{at}}\;{\text{the}}\;{\text{points on the two edges with}}\;x=0{\text{ and }}x=a,$$
(35)
$$\frac{{{\partial ^2}w(x,y,t)}}{{\partial {y^2}}}+\nu \frac{{{\partial ^2}w(x,y,t)}}{{\partial {x^2}}}=0;\quad {\text{at}}\;{\text{the}}\;{\text{points on the two edges with}}\;y=0{\text{ and }}y=b.$$
(36)

With the following series solution for deflection function \(w(x,y,t)\), all these mentioned boundary conditions are satisfied:

$$w(x,y,t)=\sum\limits_{{m=1}}^{\infty } {\sum\limits_{{n=1}}^{\infty } {{A_{mn}}\,\sin \left( {\frac{{m\pi }}{a}x} \right)} } \sin \left( {\frac{{n\pi }}{b}y} \right)\exp (i{\omega _{mn}}t),$$
(37)

where m and n are called half-wavenumbers in the x- and y-directions, respectively. Moreover, \({A_{mn}}\) and \({\omega _{mn}}\) are equivalent to the amplitude of vibration and resonant frequency corresponding to m and n, respectively. To get the natural frequencies, in the governing Eq. (29), we set \(q(x,y,t)=0\) and substitute Eq. (37) for \(w(x,y,t)\) into it. Then, the natural frequencies are obtained as follows:

$$\omega _{{mn}}^{{}}=\sqrt {\frac{{{K_{{\text{eq}}}}}}{{{M_{{\text{eq}}}}}}} ,$$
(38)

where

$$\begin{gathered} {K_{{\text{eq}}}}=N\,{D_{{\text{bend}}}}{\left( {{{\left( {\frac{{m\pi }}{a}} \right)}^2}+{{\left( {\frac{{n\pi }}{b}} \right)}^2}} \right)^2}+(N - 1){D_{{\text{shear}}}}\left( {{{\left( {\frac{{m\pi }}{a}} \right)}^2}+{{\left( {\frac{{n\pi }}{b}} \right)}^2}} \right) \hfill \\ {M_{{\text{eq}}}}=N\left[ {I\left( {{{\left( {\frac{{m\pi }}{a}} \right)}^2}+{{\left( {\frac{{n\pi }}{b}} \right)}^2}} \right)+M} \right]. \hfill \\ \end{gathered}$$
(39)

3 Molecular dynamics simulations

For carrying out the molecular dynamics simulations, the adaptive intermolecular reactive empirical bond order (AIREBO) potential [47] is applied to describe interactions between carbon atoms. AIREBO potential can be utilized to model both chemical reactions and intermolecular interactions in condensed-phase hydrocarbon systems such as liquids, graphite, and polymers [47]. The bond interactions, bond breaking, and bond re-forming between carbon atoms are precisely captured in this potential [34, 48,49,50,51,52,53,54]. The software programs LAMMPS [55] and VMD [56] are used for the MD simulations and visualization of the MD simulation results, respectively. In these MD simulations, the graphene layers are square plates with length 10 nm and thickness 0.34 nm. The between layer spacing is equal to the thickness of each layer. At the onset of the simulation and after structural relaxation, a displacement equal to 1 nm in the normal direction is applied to the center of the simply supported multilayer graphene to initialize a transverse vibration. The time step size is chosen as 1 fs and the simulations are performed in an NVE ensemble. The natural frequency can be calculated by tracking the transverse deflection of the center for each multilayer graphene, then applying the fast Fourier transformation (FFT) on it. Some MD outputs with VMD visualization are shown in Fig. 2 for one- to four-layer graphene nanosheets.

Fig. 2
figure 2

Modeling of the multilayer graphene sheets with dimensions of 10 nm × 10 nm: a one-layer graphene and b two- to four-layer graphene

Full size image

4 Numerical results

In this section, numerical results are given for the free-vibration analysis of simply supported rectangular multilayer graphene sheet incorporating interlayer shear effect. For all cases, the thickness of graphene, its bending rigidity, and mass density are assumed to be h = 0.34 nm, Dbend = 23.1073 eV, and ρ = 2250 kg/m3, respectively [9].

The interlayer shear modulus and bending rigidity of multilayer graphene have been reported within the wide range in the literature depending on the various parameters such as number of layers, stacking pattern, chirality angle, and depth of the Lennard-Jones potential function. The interlayer shear modulus for 2–6 layers graphene is within the range of 0.36–0.49 GPa [57]. For graphene with random stacking, the values between 0.19 and 0.34 GPa from ab initio [58] and 0.25–0.29 GPa from molecular dynamics simulations [7, 34] have been reported. The interlayer shear modulus for graphene/graphite with perfect AB stacking is in the order of 5 GPa [34, 40, 58, 59]. In addition, the bending rigidity of mono- and multilayer graphene flakes has been reported within the range from 0.76 [62] to 126 eV [60]. The comparison of the effective elastic constants of mono- and multilayer graphene reported in the literature has been provided in Table 1. In the following, the effects of these parameters on the natural frequency of multilayer graphene sheets have been investigated.

Table 1 Comparison of the effective elastic constants of mono- and multilayer graphene reported in the literature
Full size table

The comparison of the natural frequencies obtained from Ref. [9]; and this study for square simply supported multilayer graphene with a = 10 nm, different m and n, and the interlayer shear modulus 0.49 GPa is presented in Table 2. The results presented in the study [9] are based on the model which considers no interlayer shear effect. From this table, it can be concluded that if the interlayer shear effect is neglected, the natural frequency, which named classical natural frequency in Ref. [9], will be independent of the number of layers. This result means that for multilayer graphene sheets with increasing the number of layers, the stiffness and mass will increase with the same coefficient. By considering the interlayer shear effect, the increments of equivalent stiffness are larger than those of equivalent mass with increase in the number of layers. Therefore, the natural frequency is dependent on the number of layers. Since the equivalent stiffness increases by considering the shear effect, the values of the natural frequencies are predicted to be larger than those obtained from models neglecting it.

Table 2 Comparison of the natural frequencies (THz) obtained from Ref. [9] and this study for square simply supported multilayer graphene with a = 10 nm, different m and n, and interlayer shear modulus 0.49 GPa
Full size table

Table 3 shows the comparison of the natural frequencies obtained from Ref. [9], and this study with different aspect ratios and different values of interlayer shear modulus for simply supported 15-layered graphene with b = 10 nm and different m and n. In the table, the natural frequencies obtained from this study have been evaluated by different interlayer shear moduli, i.e., G = 0.25, 0.4, and 0.49 GPa. From this table, it can be concluded that with rising the aspect ratio, the relative error percentage increases for model without interlayer shear. Therefore, the importance of considering the interlayer shear becomes more vital.

Table 3 Comparison of the natural frequencies (THz) obtained from Ref. [9] and this study with different aspect ratios and interlayer shear moduli for simply supported 15-layered graphene with b = 10 nm and different m and n
Full size table

The comparison of the natural frequencies obtained from the analytical model and MD simulation versus number of layers in the case of square multilayer simply supported graphene sheet with 10 nm length is illustrated in Fig. 3. As we can see, MD simulation results are close to those obtained from the analytical model and confirm the variations trend of the natural frequency versus number of layers. From this figure, it is deduced that the natural frequency increases with the rise in the layers number. The analysis of the natural frequency sensitivity to the layers number by both the MD simulation and analytical approach reveals that the effect of layers number on the natural frequency decreases with the increase in the layers number.

Fig. 3
figure 3

Comparison of the natural frequencies of present study, MD simulation, and the model without interlayer shear effect versus number of layers for 10 nm × 10 nm multilayer simply supported graphene sheet with m = n = 1 and G = 0.49 GPa

Full size image

The effects of the interlayer shear modulus and bending rigidity on the natural frequency for various numbers of layers are depicted in Figs. 4 and 5, respectively. With respect to the values of the interlayer shear modulus reported in the literature, i.e., G = 0.19–5 GPa [7, 34, 41, 57,58,59], the natural frequency of the multilayer graphene sheet can be in the wide range, as shown in Fig. 4. This figure shows that the natural frequency sensitivity of the multilayer graphene sheets with respect to the interlayer shear modulus, i.e., the slope of each curve in Fig. 4, increases with the rise in the layers number; but the intensity of this increase, i.e., the change in the slope of the curve from N layers to (N + 1) layers, decreases for greater number of layers. In other words, with depiction of the natural frequency versus interlayer shear modulus, we get curves that approach to a specific curve when we raise the number of layers. It can be seen that for multilayer graphene sheets with more than seven layers, the number of layers has no significant effect on the variations trend of the natural frequency with respect to the interlayer shear modulus. This conclusion is applicable to the sensitivity of the natural frequency to bending rigidity with rising the layer number and the specific curve is obtained for multilayer graphene sheets with more than four layers (Fig. 5). From Fig. 6, it is deduced that the values of the natural frequency are independent of aspect ratio for multilayer graphene sheets with a/b > 5. In addition, the most difference between natural frequencies can be observed in the cases of plates with the range of 1 < a/b < 2.

Fig. 4
figure 4

Comparison of the natural frequencies versus interlayer shear modulus for 10 nm × 10 nm multilayer simply supported graphene sheet with m = n = 1 and various numbers of layers

Full size image
Fig. 5
figure 5

Comparison of the natural frequencies versus bending rigidity for 10 nm × 10 nm multilayer simply supported graphene sheet with m = n = 1 and various numbers of layers

Full size image
Fig. 6
figure 6

Comparison of the natural frequencies versus aspect ratio of simply supported multilayer graphene sheet with m = n = 1, b = 10 nm, G = 0.49 GPa for various numbers of layers

Full size image

5 Conclusion

In this paper, a comprehensive model was presented to study mechanical behavior of multilayer graphene sheets with rectangular shape incorporating interlayer shear effect. A model composed of the layers with flexural flexibility and the interlayer continuums with shear flexibility was considered for the grapheme sheets. The governing equation of motion and the general form of the boundary conditions were derived by utilization of the Hamilton principle. For the case of simply supported grapheme sheets, closed-form results were obtained to express the natural frequencies. Moreover, molecular dynamics (MD) simulations were accomplished to evaluate the accuracy of the results of the analytical approach. Comparison of the results obtained from the analytical approach and MD simulations demonstrates that the proposed analytical model can predict the natural frequencies of the multilayer graphene sheets with a good accuracy. The results show that as the layers number increases, the natural frequency also increases until a few numbers of layers, and afterward, the influence of the layers number on the natural frequency significantly decreases. In addition, with an increase in the graphene sheet’s aspect ratio, the natural frequency decreases until a characteristic aspect ratio and then, the changes in the plate aspect ratio have no significant effect on the natural frequency.