Simulation of the spherical aberration of focused laser radiation in transparent materials: comparison of different simulation approaches

Abstract

Creating microvoids, cracks or refractive index modifications within dielectrics focusing intense laser radiation into the transparent material offers many promising applications, such as holographic data storage, laser-written waveguides or optical gratings. For further improvements in the quality of the named applications, a deep understanding of the involved processes during interaction of laser radiation with material is necessary. In this work, the change in the laser intensity distribution of focused laser radiation into PMMA by spherical aberration, caused by the transition of the radiation from air to matter, is discussed. Theoretical and numerical investigations including nonlinear effects of laser radiation material interaction as well as multi-physical approaches, such as combined calculation of the beam propagation, the temperature distribution and induced tensions, require a lot of effort and long computation time. Therefore, simple linear simulations are performed including calculation of the beam propagation without nonlinear optical effects, like self-focusing. Comparing the calculated intensity distributions with experimental data, regarding the lateral and axial size as well as the position of the laser-generated voids within PMMA, the applicability of the simulation approaches is demonstrated. The different simulation approaches are characterized in regard to their calculation time and accuracy depending on the simulation task.

1 Introduction

Ultrafast laser radiation offers the opportunity to process materials with a high quality as well as a high precision. Due to the high intensity resulting from concentrating the pulse energy within a temporal range of a few hundred femtoseconds and a spatial range of a few micrometers, all known materials are decomposed. This allows especially the processing of transparent material by nonlinear processes. In recent years, an increased interest on creating microvoids or the modification of the refractive index within transparent materials took place [1–4]. The formation process of the laser-induced voids is very complex and not fully understood in all details. For the understanding of the involved processes and to identify the limiting processes, a simulation of the laser radiation material interaction is necessary. To cover most of processes, a multi-physical simulation approach including calculations such as the calculation of the beam propagation [5, 6], absorption of the laser radiation resulting in an induced temperature [7] and tension distribution [8] should be performed. On the other hand, this approach is computationally expensive and a clear identification of the driving mechanism can be realized by single observation of each physical process in comparison with the whole result. Therefore, this article focuses on the separate calculation of the beam propagation to identify the relevant driving mechanism. In contrast to other authors, such as [6, 9] where analytical formulas proposed by [10] have been used to calculate the intensity distribution within the focal region or as an input for considering nonlinear effects [11], in this article the experimental setup is reproduced and includes a gaussian intensity distribution as input for the calculations of the intensity distribution within the focal region, instead of a plane wave.

This article is subdivided into five sections. The first part describes the experimental setup followed by investigations on the different simulation approaches facing their advantages and disadvantages in order to identify the optimized simulation approach to reproduce the experimental setup. Subsequent, a comparison between the experimental and simulated results, regarding to the lateral and axial size as well as the position of the laser-generated voids, is described. Finally, the results are summarized and a short outlook to further work is given.

2 Experimental setup

Experiments were performed producing voids by ultrafast laser radiation (wavelength $\lambda = 1030$ nm, pulse duration (${\mathrm{sech}}^2$) $\tau _H = 180$ fs, gaussian beam diameter before objective $d_{\mathrm{Obj},1/{\mathrm{e}}^2} = 3.3$ mm, pulse energy $Q\,=\,$60–230$\,{\mathrm{nJ}}$) within PMMA (refractive index $n = 1.415,$ surface at $z = 0$) at the optical distances $d_{\mathrm{opt}} = n\cdot z_0$ by using an infinity-corrected microscope objective ($NA = 0.65,$ focal length $f' = 4$ mm). $z_0$ represent the experimentally defined geometrical positions with 50, 80, 110, 140 and $170\,\upmu \hbox {m}$ (Fig. 1). The threshold intensity was calculated to $I_{\mathrm{thr}} = 27\, {\mathrm{TW/cm}}^2$ by determination of the beam diameter to $d_{D^2} = 1.66\,\upmu \hbox {m}$ using the method of squared diameter D over log fluence H [12].

Fig. 1

Schematic representation of focusing of laser radiation into PMMA and the effect of spherical aberration (dashed line ideal focus in air and solid line real focus within material)

3 Conceptioning of optimized simulation approaches

In order to perform an optimized simulation of the beam propagation, with respect to the computation time and accuracy, the most appropriate simulation approach depending on the simulation task has to be identified. Therefore, the experimental setup is divided into two sub-zones, whereas the first zone (zone I) represents the beam propagation beginning from the microscope objective to the material surface and the second zone (zone II) represents the beam propagation within the material. As an assumption, no interaction of the laser radiation with the material occurs in zone I. Therefore, only the electric field strength on the interface air—PMMA is of interest and a boundary element method (BEM), like Kirchhoff’s diffraction formula (KDF) or the spectrum of plane waves (SPW) can be chosen [13, 14] (see “Appendix”). Zone II contains the focal region. The calculation of the focal region within material can be achieved by using full discretization method, like the finite-difference time-domain (FDTD) method [15–17] or a flexible choice of the target plane $A_1$ by using BEM (see “Appendix”). The polarization is considered as fully linear polarized.

3.1 Zone I

The first zone models the beam propagation beginning from the microscope objective up to the interface of air to PMMA, and the result is the input of the calculations in zone II. As no data of the corresponding lens system of the microscope objective are known, the objective is approximated by a phase term $\varphi$ of an ideal lens according to

$$\begin{aligned} \varphi =-{\mathrm{sign}}(f^{\prime })\cdot \sqrt{f^{\prime }+x^2+y^2}. \end{aligned}$$

(1)

In general, KDF and SPW are both suitable for calculating the beam propagation up to the surface of PMMA, but SPW has a large benefit in computation time compared to KDF using the same number of elements (Fig. 2). For SPW (SPW 2D), the complete electric field strength distribution on the plane $A_1$ results automatically, whereas for KDF (KDF 2D) the algorithm has to be repeated for every element of plane $A_1$. By taking advantage of symmetries (2Da and 1D versions of BEM) given by the spatial intensity profile and geometry, and performing parallelization particularly by using multiple graphic processor units (GPU), the computation time can be reduced significantly. The same reduction can be achieved for SPW resulting clearly to the least computation time by a factor of more than $10^3$ compared to KDF. It should be noted, using GPU is only an advantage, in regard to calculcation time, for a large number of elements (${>}2^{14}$ elements).

Fig. 2

Comparison of the calculation time depending on the number of elements N per direction for different simulation methods, open symbols computation using CPU (Intel Xeon E5-2690 0) is faster than GPU (4× NVIDIA Tesla C2075) or too much elements were used for GPU, closed symbols GPU is faster than CPU, line fits to guide the eye

In contrast to the fast computation of the 1D versions of the propagation methods compared to 2Da or 2D, 1D simulations are restricted to non-diffractive and non-aberrative propagations of a beam with a spatial axially symmetric intensity distribution. Otherwise, if diffraction effects or aberrations occur, changes in the intensity distribution correspond to wrong physical effects, like a ${\mathrm{sinc}}^2$ function in 1D calculations instead of an airy disk for limiting apertures in 2D or 2Da calculations. Based on the given numerical aperture NA and focal length $f^{\prime }$, the clear aperture $d_A$ can be calculated to $d_A= 6.84$ mm, which is approximately twice of the beam diameter. Therefore, diffraction effects can be neglected and 1D methods can be used to calculate beam propagation for the given setup of beam diameter and microscope objective. Especially SPW 1D is the first choice based on Fig. 2. By using SPW resolution problems, called undersampling (see Fig. 4 squares), resulting from the same sampling of $A_0$ and $A_1$ occur in the chosen setup. To avoid it, a larger number of elements, here $2^{17}$ elements, or a gradually refinement of the grid, as shown in Fig. 3, is necessary. By inserting some extra or auxiliary planes $A_{\mathrm{ap}_{ i}}$ between plane $A_0$ and $A_1$, calculating the beam diameter on each plane $A_{\mathrm{ap}_{ i}}$, cut off the planes at the beginning of nearly zero intensity, and interpolating the intensity distribution within the new boundaries, a higher resolution is achieved. This approach is recommended for SPW 2D, as $2^{17}$ elements in each direction cannot be processed due to large memory requirements. For SPW 1D, the approach of gradually refinement is not necessary, as the number of elements is only used in one direction, and the memory requirements, depending on the total number of elements of all arrays, are in most of the simulation tasks less than the limiting memory capacity.

The intensity distribution is compared in the focal plane instead of a geometrical position $z_0$, since changes caused by diffraction effects or aberrations can be clearly identified in the focal plane, because the intensity distribution in the focal plane can easy be calculated analytically. Finally, the calculated intensity distributions at the focal plane, for the described BEM, are found in Fig. 4.

Fig. 3

Schematic representation of the used multi-plane approach (refinement of the grid) for SPW

Based on the comparison with the analytical solution, diffraction effects cannot be fully neglected. Therefore, the calculated intensity distribution of all 1D methods slightly differs from the correct results given by 2Da or 2D versions. Furthermore, only five elements are calculated by SPW without gradually refinement within the displayed range of x-coordinates demonstrating the necessity of refining the grid. For this example, the benefit of the fast calculation time of SPW is compensated by the limited resolution and the necessary refinement, so KDF is finally faster due to the big change in the size of the planes. The higher resolution caused by the multi-plane approach leads to much longer computation times, here more than 600 times longer (Table 1). Furthermore, the experimentally obtained focal radius of $d_{D^2}/2 = 0.83\,\upmu \hbox {m}$, by the method of squared diameter over log fluence [12], can be reproduced by the simulations.

Table 1 Comparison of the calculation time of the different simulation methods normalized to the fastest method, gr gradually refinement

Fig. 4

Comparison of the calculated relative intensity distributions $I_{\mathrm{rel}}$ at the focal plane for KDF 1D, KDF 2Da, SPW 1D ($2^{17}$ elements), SPW 2D without ($2^{14}$ elements) and with gradually refinement (five auxiliary planes, beginning with $2^{14}$ elements, $2^{11}$ elements at the end) as well as the analytical solution and the experimentally obtained focal radius $d_{D^2}/2$

All in all, KDF 2Da is the best choice for zone I, since correct results are calculated and the calculation time is shorter than for SPW 2D. On the other hand, KDF 1D and SPW 1D produce very fast results which can be used as an estimation or a approximate solution.

3.2 Zone II

The second zone contains the beam propagation within PMMA and includes the interaction of the laser radiation with the material, like linear absorption, which is automatically calculated by FDTD, and defining the complex refractive index $\tilde{n}$. Here, no nonlinear effects are considered. Further, the simulation of pulsed (pw) and continuous (cw) radiation is investigated, instead of only cw radiation for BEM. The input of zone II is given by the results of zone I for the several positions $z_0$ calculated with KDF 2Da. For FDTD, the whole area must be discretized with at least 20 elements per wavelength in each direction leading to a larger number of elements, and for reasons of stability, the time step ${\Delta }t$ is less than a femtosecond, depending on the CFL number [15]

$$\begin{aligned} \hbox {CFL} = \frac{\max (c_{ i})\cdot{\Delta }t}{\min ({\Delta }x, {\Delta }z)}, \end{aligned}$$

(2)

where $c_{ i}$ represents the speed of light in the medium i, and ${\Delta }x$ and ${\Delta }z$ the element sizes in direction x and z. As a result, the computation time is very long compared to BEM and it has to be clarified, if the use of FDTD is necessary or similar results can be achieved by BEM, especially if no nonlinear effects are included in the simulations. Therefore, numerical calculations are performed to compare the calculated intensity distribution within the focal region by FDTD for pw and cw with the results of BEM (Fig. 5). The simulations are performed for pw, since pw is used in the experimental, and cw is performed for comparisons by BEM. In the case of 1D BEM, the intensity $I_{\mathrm{norm}}$ is calculated by the peak power

$$\begin{aligned} P_{\mathrm{pk}}&= \frac{Q}{1.135\cdot \tau _H},\nonumber \\ I_{\mathrm{norm}} (x,z)&= I(x,z)\cdot \frac{P_{\mathrm{pk}}}{2\cdot {\pi } \cdot \int r\cdot I(x,z) {\mathrm {d}} r}, \,{\mathrm{and}} \nonumber \\ r &= \left| x\right| . \end{aligned}$$

(3)

Only relative values can be calculated by 1D methods due to the missing information about the element size along the perpendicular dimension.

Fig. 5

a Snapshot of the calculated intensity distribution at different time points simulated with FDTD pw, b calculated intensity distributions for cw using different calculation methods, pulse energy 360 nJ, set geometrical position 110$\,\upmu \hbox {m}$

The coupling of FDTD and KDF is applicable leading to focusing of the radiation without detectable disorders of the intensity or numerical artifacts (Fig. 5). Before the focal point, at about $160\,\upmu \hbox {m}$, the intensity distribution corresponds nearly to an ideal gaussian intensity distribution. After the focal point, $z> 160\,\upmu \hbox {m}$, spherical aberration occurs resulting in a disturbed intensity distribution. Comparable results are obtained for cw laser radiation and all axially symmetric methods result in a similar intensity distribution, as well as all 1D (BEM) and 2D (FDTD) reproduce the same result. The intensity distributions of all axially symmetric methods contain larger spherical aberration, since all dimension are included in the simulations. Therefore, 1D calculations are again a good estimation, but differ significantly from the correct result of the axially symmetric (2Da) methods.

By comparing the results of pw radiation for the time $t= \hbox {1200 fs}$ with cw radiation, only small differences due to a spatial elongation of the pulse with $c\cdot \tau _H$, $c=c_0/n$ are obtained. Therefore, a description by cw radiation can be applied for the following calculations. The calculations by using KDF 2Da are much faster compared to FDTD or SPW 2D. Therefore, and as FDTD has no benefit regarding accuracy, KDF 2Da is also the best choice for zone II.

4 Results and discussion

After determining the best qualified simulation methods, all calculations are performed according to the experimental setup in Sect. 2. Zone I and zone II are calculated by KDF 2Da, supported by SPW 1D as an estimation for the necessary size of the planes. In order to save calculation time, the simulations are only performed for all geometrical positions $z_0$ and the intensity is calculated according to Eq. (3). The resulting positions $I \ge I_{\mathrm{thr}}$, of the calculated intensity distribution I, are plotted in Fig. 6 in comparison with the experimental obtained distribution of the voids. The simulated areas with higher intensity than $I_{\mathrm{thr}}$ demonstrate a qualitative agreement to the experimental results. The spherical aberration increases with increasing material depth leading to lower intensities in the focal region due to the distortion of the intensity profile. Therefore, no voids can be obtained deep within the material for low pulse energy irradiation. For the shortest and longest position $z_0$ combined with small pulse energies, the simulated areas deviate from the experimental data. Furthermore, the experimentally obtained voids arise closer to the surface compared to the simulations, which is explained by the missing description of the nonlinear interaction of the laser radiation with the material, here especially self-focusing and channeling as well as modifications and the phase transition of the material. PMMA has a large self-focusing coefficient [2], and self-focusing will arise assuredly by the applied intensities.

Fig. 6

Above simulated area with higher intensity than $I_{\mathrm{thr}} =27\hbox { TW/cm}^{2}$ (black). Below laser-induced voids by ultrashort laser radiation within PMMA for different pulse energies at distinct z-positions (optical microscopy)

Fig. 7

Comparison of simulated and measured lateral (above) and axial (below) size of the voids in geometrical depth $z_0 = 70\,\upmu \hbox {m}$

The qualitative agreement of the results is also confirmed by the direct comparison of the determined lateral and axial sizes of the voids measured by optical microscopy (Fig. 7). Both present an increased size by increasing the pulse energy. Large differences in the sizes between simulation and experiment are given for low pulse energies caused again from neglecting nonlinear effects.

Fig. 8

Calculated axial (middle) and lateral (below) size of the voids for different set geometrical position in comparison with the experimental detected axial sizes (above)

Despite the difference between experiment and simulation in regard to the positions of the voids and the deviation at low pulse energies, a qualitative agreement is confirmed for all set of geometrical positions and high pulse energies (Fig. 8). The experimental detected and simulated axial lengths increase with increasing pulse energy. Up to a pulse energy of about 150 nJ, the axial length of the voids is smaller for longer geometrical positions $z_0$ than for shorter positions, and vice versa for pulse energies above 150 nJ. This dependency occurs in the experiment and in the simulation equally. Therefore, the dependence of the axial length on the pulse energy for different positions is explainable by spherical aberration and can be estimated by simple calculations of the beam propagation without taking any nonlinear effects into account.

Furthermore, the calculated diameters of the voids increase with increasing pulse energy (Fig. 8). Smaller diameters are obtained for longer geometrical positions. The sizes of the diameter are getting equal for high pulse energy. No comparable measurements of the experimental diameter of the voids, except for $z_0=70\,\upmu \hbox {m}$, were performed.

5 Summary and outlook

Experimentally obtained axial and radial sizes of created microvoids within PMMA using ultrashort pulsed laser radiation were compared with the calculated intensity distribution by linear beam propagation. The calculations were performed without taking nonlinear optical effects or laser radiation material interaction into account.

The calculation methods Kirchhoff’s diffraction formula (KDF), the SPW and the finite-difference time-domain (FDTD) method were characterized in order to calculate the beam propagation given by the experimental setup. The calculation of the beam propagation was divided into two zones. Zone I models the beam propagation beginning from the microscope objective up to the surface of PMMA, and zone II includes the beam propagation within PMMA. For both zones, KDF, using axial symmetry, is the best calculation method in regard to accuracy and calculation time for the given simulation tasks.

Using KDF for calculating the intensity distribution within PMMA describes qualitatively the experiments. Due to an increasing spherical aberration with increasing depth within the material, the beam size gets larger and the threshold intensity for the modification of the material is not reached anymore. In contrast to simulation, the measured voids are generated before the simulated focal points, which can be explained by the missing nonlinear effects, like self-focusing [2]. Furthermore, differences between the experimentally obtained and simulated diameters for small pulse energies occur due to the non-included modeling of nonlinear laser radiation material interaction. Further work will consider this as well as simulations of the temperature distribution due the heating of matter and the simulation of the thermal stress induced by ultrashort pulsed laser radiation.

Appendix: Simulation methods

1.1 Kirchhoff’s diffraction formula (KDF)

Kirchhoff’s diffraction formula represents a calculation method in the field of scalar diffraction theory and is based on the mathematical formulation of Huygens principle. The electric field strength can be calculated by

$$\begin{aligned} E_1 (x_1,y_1,z_1 )&= \frac{n_0}{{\mathrm {i}}\cdot \lambda _0} \oint _{A_0}\frac{E_0 (x_0, y_0, z_0 )}{r}\cdot {\mathrm {e}}^{{\mathrm {i}}\cdot n_0\cdot k_0\cdot r} \\&\quad \cdot N (x_0,y_0,z_0 )~{\mathrm {d}}A_0. \end{aligned}$$

(4)

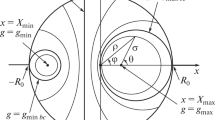
The used parameters are visualized in Fig. 9. $A_0$ represents the source plane for elementary waves with the incident complex electrical field $E_0$ and $A_1$ represents the target plane with the electric field strength $E_1$. The elementary waves are represented by the terms $\frac{E_0 (x_0,y_0,z_0)}{r}\cdot {\mathrm {e}}^{{\mathrm {i}}\cdot n_0\cdot k_0\cdot r}$, where

$$\begin{aligned} r=\sqrt{(x_0-x_1 )^2+(y_0-y_1 )^2+(z_0-z_1 )^2 } \end{aligned}$$

(5)

represents the distance between point $P_0 (x_0;y_0;z_0 )$ on the plane $A_0$ and point $P_1 (x_1;y_1;z_1 )$ on the plane $A_1$ [13, 14]. The form and position of the two planes can be chosen arbitrarily. $\mathbf {k}$ represents the wave vector of the incident wave at point $P_0$, with the wave number $k_0=\frac{2\cdot {\pi }}{\lambda _0}$, $\lambda _0$ the wavelength of the radiation in vacuum, $n_0$ the refractive index between plane $A_0$ and $A_1$, $\mathbf {n}$ the normal vector at point $P_0$. N represents the slope factor and can be calculated by $N(x_0, y_0, z_0) = \frac{1}{2}(\cos (\mathbf {n},\mathbf {r})-(\cos (\mathbf {n},\mathbf {k}))$.

Fig. 9

Schematic representation of the used planes and variables

In most of the cases, the distance of $A_1$ to $A_0$ is large enough to neglect any dependency on N, therefore $N\approx 1$. The summation of all elementary waves is mathematically realized by the integration over the plane $A_0$.

1.2 Angular spectrum of plane waves (SPW)

In the case that the planes $A_0$ and $A_1$ are both perpendicular to the propagation direction, and having the same sampling, the SPW can be applied [13, 14]. The electric field strength $E_1$ is calculated by the Fourier transform ${\mathcal {F}}$ according to

$$\begin{aligned} E_1={\mathcal {F}}^{-1}\left( {\mathcal {F}}(E_0)\cdot {\mathrm {e}}^{2\cdot{\pi }\cdot\mathrm{i} \cdot {\Delta }z\cdot \sqrt{ \frac{n_0^2}{\lambda _0^2} -(\nu _x^2 + \nu _y^2) }}\right) . \end{aligned}$$

(6)

$\nu _x$ and $\nu _y$ represent the spatial frequencies used for the fourier transform and can be calculated by ${\Delta }x\cdot {\Delta }\nu _x =\frac{1}{N_x}$ and $\nu _x=-\frac{N_x}{2}{\Delta }\nu _x\ldots \frac{N_x}{2}{\Delta }\nu _x$. KDF and SPW represents a BEM.

1.3 Finite-difference time-domain (FDTD)

The simplest form of FDTD includes only Faraday’s law

$$\begin{aligned} \nabla \times \mathbf {E}=-\sigma _{\rm m}\cdot \mathbf {H} -\mu \cdot \frac{\partial \mathbf {H}}{\partial t}, \end{aligned}$$

(7)

and Ampère’s law [15–17]

$$\begin{aligned} \nabla \times \mathbf {H}=\sigma \cdot \mathbf {E} -\varepsilon \cdot \frac{\partial \mathbf {E}}{\partial t}. \end{aligned}$$

(8)

$\sigma _\mathrm{m}$ represents the magnetic conductivity, $\sigma$ the electric conductivity, $\mu$ the permeability, $\varepsilon$ the permittivity and $\mathbf {H}$ the magnetic field strength. Equations (7) and (8) are discretized using finite differences. The derivations are solved by a convolution of the data matrices of each field and a convolution kernel as widely used in digital image processing [18].

1.4 Symmetry and locations of planes used by the simulation methods

The used simulations methods can be subdivided resulting from to the considered symmetry. On each plane, there are $N_x$ elements in $x-$direction and $N_y$ elements in $y-$direction, respectively. Plane $A_0$ has the subindex $i=0$ and plane $A_1$ has the subindex $i=1$. The total number of elements per matrix $N_{\mathrm{tot}}$ on each plane is $N_{\mathrm{tot }_i} = N_{x_i} \cdot N_{y_i}$ (Fig. 10).

Fig. 10

Schematic representation of the used elements on plane $A_0$ and $A_1$

If no symmetry can be used for BEM, all elements of plane $A_0$ and $A_1$ have to be considered. These methods are marked with 2D. In the case of considering axially symmetric intensity distributions, only the calculation of the intensity along a half coordinate axis, e. g. the $x-$axis beginning from element 1 up to $N_{x_1} / 2$, on plane $A_1$ is necessary. In this case, the calculation methods are marked with 2Da. Furthermore, for a spatial gaussian beam intensity distribution, the source plane $A_0$ can be a line too. Therefore, the methods are called 1D methods. The total number of elements, resulting from the considered symmetry, are summarized in Table 2.

For KDF, the location of the target plane $A_1$ is very flexible and the x–z plane or the y–z plane are often used as $A_1$. In contrast to KDF and SPW, for FDTD the whole area has to be discretized. The discretization includes $x-, y-,$ and $z-$coordinates of the area. If only the x–z plane or the y–z plane is considered, FDTD is marked with 2D, and neglects the third dimension. By taking advantage of axial symmetry, the differential operators in Eqs. (7) and (8) can be formulated in cylindrical coordinates and all dimensions are included. Therefore, the addition is 2Da.

Table 2 Summary of the used elements for BEM