1 Introduction

Lead–tin alloys have been used extensively as solders in electronics due to excellent mechanical, physical and chemical properties and their relatively low cost. The toxic nature of lead has been the main reason that major industrialized countries have legislated to limit the application of solders containing lead. Therefore, the development of alternative lead-free solders with the same or possibly better characteristics than those of traditional Pb–Sn alloys has become an important task in the electronic industry [1–11].

In the past years, many binary and multicomponent alloy systems have been investigated in order to design lead-free solders with required properties [1–3, 7, 8, 10, 12]. The systems investigated are Sn-based alloys, while other constituents are Al, In, Sb, Zn, Bi, Au, Tl, Al and Ag. In particular, studies have indicated that Sn is the major component in binary solders and that Sn-based multicomponent alloys, such as ternary (Al–Sn–Zn, Sn–Bi–Cu, Sn–Ag–Cu) and/or quaternary (Sn–Ag–Cu–Sb, Sn–Ag–Cu–Zn) systems are considered as primary high-temperature alternative lead-free solders in the electronic industries [1, 6]. Sn-rich alloys of the Al–Sn and Sn–Tl systems investigated were also proposed as binary lead-free solders [13, 14] respectively, or as subsystems of complex alloy systems, such as the Sn–Zn–Al [15] or the Sn–Zn–Al–Ag [16]. The thermodynamic and electrical properties of some of these Sn-based systems have been studied by many authors [4, 6, 8, 10, 11], but only few works are related to their surface properties [5, 7, 10, 12]. A good knowledge of surface and wetting properties such as surface tension and interfacial adhesion is a necessary prerequisite in the development of lead-free solder alloys [2, 5, 10, 12, 16]. These properties will not only encourage the formation of high-quality solder joints, but will also play a significant role in the understanding of surface related phenomena like heterogeneity, epitaxial growth, catalysis, corrosion and wettability behaviour in molten alloys [8]. Nonetheless, how the surface properties depend on the structure and the thermodynamics of the liquid, remain to be fully understood in the framework of different theoretical approaches [4, 17, 18].

Some other requirements for the substitute solder would be: wetting properties, joint strength, fatigue resistance, non-toxicity and relatively low cost. Apart from high academic interest, the bulk thermodynamic properties of the two Sn-Based alloys, namely: Al–Sn and Sn–Tl have been investigated in this study from a theoretical point of view with the main objective of correlating the properties of both liquid alloys in the bulk and at the surface as proposed promising alternative lead-free solder materials. Despite the great industrial and technological relevance of the Al–Sn [9, 13] and Sn–Tl [14, 19], the literature data on their thermophysical properties [13] are scarce. As concerns the surface tension data of liquid Al–Sn [20, 21] and Sn–Tl [22] alloys, difficulties in performing the surface tension measurements can be attributed to a high chemical affinity of the alloy components for oxygen, as reported in [9, 10]. In addition, only a few reference data are available for metals [23], while for high-melting binary alloys or in the case of complex alloys a nearly complete lack of data is evident [24]. To compliment experimental efforts and fill the needed data gaps, it is anticipated that most thermophysical data on binary and multi-components systems will come from theoretical calculations.

The surface properties have been studied using different theories [5, 8, 25], notable among them are the statistical mechanical theory [26], density functional theory [27] and computer simulations [17]. The calculations in the present paper used the approach proposed by Prasad et al. [5, 25]. The concept is used within the framework of the self-association model (SAM) which has been shown to be a good approach for studying segregating binary liquid alloys [4]. The various force fields, such as the nature of the atomic interaction, and the structural readjustment of the constituent atoms of the liquid Al–Sn and Sn–Tl alloys are deduced from the theoretical observable indicators in terms of metallurgical and chemical constructs, such as the electronegativity difference (=−0.35 and −0.34) [28], the size ratio \(\frac{V_{\mathrm{Sn}}}{V_{\mathrm{Al}}} \approx 1.50\) and \(\frac{V_{\mathrm{Sn}}}{V_{\mathrm{Tl}}} \approx 1.06\) respectively [29]. The microscopic functions: the concentration–concentration fluctuations in the long-wavelength limit, \(S_{\mathrm{cc}}(0)\) [30–32] and the Warren–Cowley chemical short-range order parameter (CSRO), \(\alpha _{1}\) [33] are capable of providing an immediate insight into the nature of ordering and the degree of segregation in the melt. Both liquid Al–Sn and Sn–Tl alloys are characterized by positive ordering energy, W as well as positive deviation from the ideality as observed in various thermodynamic quantities such as the activity, \(a_{i}\), the enthalpy of mixing, \(H_{\mathrm{M}}\), the entropy of mixing, \(S_{\mathrm{M}}\) and the diffusion coefficient, \(\frac{D_{\mathrm{M}}}{D_{\mathrm{id}}}\) calculated at respective temperatures. Positive values of W for Al–Sn and Sn–Tl liquid phases indicate repulsive interactions between constituent components in the alloy melts and thereby supporting a weak demixing (segregation) tendency in both systems [4]. For segregating alloys like Al–Sn and Sn–Tl, it is important to note that size effects have an appreciable influence on their surface properties [4, 34], and the magnitude of these effects increases with the tendency of a system to phase separation.

The theoretical formulations for the various thermodynamic, structural functions as well as diffusion coefficient in the frame of the self-association model are presented in Sect. 2. The surface properties calculations in Sect. 3. Followed by a presentation of results and discussion in Sect. 4 and concluding remarks in Sect. 5.

2 The self-association model (SAM)

2.1 Bulk properties: free energy of mixing and activity

Singh and Sommer [4] developed a simple model which is employed for studying demixing binary liquid alloys. The model assumes that a binary alloy consists of \(N_{A}=Nc_{A}\) atoms of element A and \(N_{B}=Nc_{B}\) atoms of element B, so that the total number of atoms \(N=N_{A}+N_{B}\). Here \(c_{A}\) is the mole fraction of A component in the alloy. In addition, the model (SAM) is based on the assumption that the elements of the constituent atoms A and B exist in the form of a polyatomic matrix, leading to the formation of like-atom cluster or self-associates of the type \(A_{\mu }\) and \(B_{\nu }\), i.e.

$$\mu A\rightleftharpoons A_{\mu };\quad \nu B\rightleftharpoons B_{\nu }$$
(1)

where \(\mu\) and \(\nu\) are the numbers of atoms in the cluster of type A and B matrices, respectively. The thermodynamic properties of the demixing liquid alloys is dependent on the number of self-associates, \(n=\frac{\mu }{\nu }\). Thus, the following two assumptions are made that (1) all the atoms are located on a set of equivalent lattice sites with each having Z nearest neighbour, (2) the interaction is short-ranged and effective only between nearest neighbours. Using the Flory approximation [4, 30] (i.e. \(Z\rightarrow \infty )\), a simple relation for the Gibbs free energy of mixing is expressed as

$$\begin{aligned} \frac{G_{\mathrm{M}}}{RT}&= {} \left\{ c_{A}\ln c_{A}+(1-c_{A})\ln (1-c_{A})+c_{A}\ln (1-\beta )+\ln \eta \right\} \nonumber \\&\quad + c_{A}(1-c_{A})\eta W \end{aligned}$$
(2)

with

$$W=\mu w, \quad n=\frac{\mu }{\nu } ,\quad \beta =1-\frac{1}{n} ,\quad \eta =\frac{1}{1-c_{A}\beta }$$
(3)

and W is the ordering energy or the interchanged energy whose value by definition gives information about the alloying behaviour in binary liquid alloys. Here, n and W are the model parameters to be fitted at a given temperature to calculate the bulk thermodynamic and structural properties of a binary liquid alloy. These parameters (n, W) are independent of concentration but may depend on pressure, P and temperature, T.

An expression for the activity, \(a_{i}\,(i = A, B),\) is obtained with the aid of Eq. (2) as:

$$RT\ln a_{i}=\left( \frac{\partial G_{M}}{\partial N_{i}} \right) _{T,P,N}$$
(4)

on solving Eq. (4) and recalling that \(N=N_{A}+N_{B}\) with \(c_{A}=N_{A}/N\), the component activities are expressed as:

$$\ln a_{A}=\ln \left[ c_{A}\eta (1-\beta )\right] +(1-c_{A})\eta \beta +(1-c_{A})^2\eta ^2\frac{W}{RT}$$
(5)

and

$$\ln a_{B}=\ln (c_{A}\eta )+c_{A}(1-\beta )\eta (1-n)+nc_{A}^2(1-\beta )\eta ^2\frac{W}{RT}$$
(6)

Once the expressions for the \(G_{M}\) and \(a_{i}\) (\(i = A, B\)) are known, other thermodynamic functions simply follows.

2.2 Entropy of mixing and enthalpy of mixing

The entropy of mixing, \(S_{\mathrm{M}}\), for binary alloys can be obtained using the thermodynamic relation

$$S_{\mathrm{M}}=-\left( \frac{\partial G_{\mathrm{M}}}{\partial T}\right)$$
(7)

by inserting Eq. (2) in Eq. (7), the entropy of mixing is expressed as:

$$\begin{aligned} S_{\mathrm{M}}&=-R\left[ c_{A}\ln c_{A}+(1-c_{A})\ln (1-c_{A})+c_{A}\ln (1-\beta )+\eta \right]\\ &\quad +c_{A}(1-c_{A})\eta \frac{\partial W}{\partial T}\end{aligned}$$
(8)

and the enthalpy of mixing, \(H_{\mathrm{M}}\), is given by:

$$H_{\mathrm{M}}=G_{\mathrm{M}}+TS_{\mathrm{M}}$$
(9)

2.3 Microscopic functions: S cc(0) and α 1

The concentration–concentration fluctuations at the long-wavelength limits, \(S_{\mathrm{cc}}(0)\) can be easily obtained from standard relationship in terms of the free energy of mixing or in terms of activity, \(a_{i}\) as [4–6, 8, 9]:

$$\begin{aligned} S_{\mathrm{cc}}(0)&= {} RT \left( \frac{\partial ^{2} G_{\mathrm{M}}}{\partial c_{A}^{2}} \right) _{T,P,N}^{-1} \nonumber \\&= {} \left( 1-c_{A}\right) a_{A}\left( \frac{\partial a_{A}}{\partial c_{A}} \right) _{T,P,N}^{-1}\\&= {} c_{A}a_{B} \left( \frac{\partial a_{B}}{\partial (1-c_{A})} \right) _{T,P,N}^{-1} \nonumber \end{aligned}$$
(10)

Using Eqs. (2) and (10), an expression to calculate \(S_{\mathrm{cc}}(0)\) is given by:

$$S_{\mathrm{cc}}(0)=\frac{c_{A}(1-c_{A})}{1-c_{A}(1-c_{A})g(n,W)}$$
(11)

where

$$g(n,W)={2n^2\left( \frac{W}{RT}\right) -(n-1)^2\left[ (c_{A}+n(1-c_{A})\right] \over \left[ (c_{A}+n(1-c_{A})\right] ^3}$$
(12)

and for ideal mixing the energy parameter, \(\omega ,\) given in Eq. (3) is equal to zero, and Eq. (11) reduces to

$$S_{\mathrm{cc}}^{\mathrm{id}}(0)= c_{A}(1-c_{A})$$
(13)

Once \(S_{\mathrm{cc}}(0)\) is fitted from Eq. (11), then all other parameters can be calculated.

The Warren–Cowley chemical short-range order parameter, \((\alpha _{1})\) [32] has been used in this study to quantify the degree of order and segregation in the liquid alloys. This parameter \(\alpha _{1}\) can be computed theoretically [4, 11, 35, 36] using the relation:

$$\alpha _{1}=\frac{P-1}{P(Z-1)+1}, \quad P=\frac{S_{\mathrm{cc}}(0)}{c(1-c)}$$
(14)

Z in Eq. (14) is the coordination number whose value is usually taken as ten [8, 31, 35].

2.4 Diffusivity

The mixing behaviour of two atomic species of a binary liquid alloy is required for a proper understanding of the dynamical properties such as diffusion at the microscopic level. Based on Darken’s thermodynamic equation [4, 24, 36], the relation between diffusion and \(S_{\mathrm{cc}}(0)\) can be written as:

$$\frac{D_{\mathrm{M}}}{D_{\mathrm{id}}}=\left[ 1-\frac{2W}{RT}S_{\mathrm{cc}}^{\mathrm{id}}(0)\right] =\frac{S_{\mathrm{cc}}^{\mathrm{id}}(0)}{S_{\mathrm{cc}}(0)}$$
(15)

where \(D_{\mathrm{M}}\) is the mutual diffusion coefficient and \(D_{\mathrm{id}}\) is the intrinsic diffusion coefficient for ideal mixture. It is given as follows:

$$D_{\mathrm{id}}= cD_{A}+ (1-c)D_{B}$$
(16)

where \(D_{A}\) and \(D_{B}\) are the self-diffusion coefficients of pure components A and B in the alloy. Equations (2), (8)–(11), (14) and (15) are the essential expressions for the bulk thermodynamic calculations.

3 Surface properties: surface concentration and surface tension

The concept of layered structure near the interface has been used to establish a link between the bulk and the surface properties within the framework of the statistical mechanical approach [5, 25]. This concept has yielded a lot of success in modelling the surface tension in binary liquid alloys [5, 8, 25]. The grand partition functions set up for the surface layer and that of the bulk [25] provide a relation between surface \(c_{i}^{\mathrm{s}}\) and bulk \(c_{i}\) concentrations. The pair of net expression relating the surface tension, \(\sigma\) and the surface concentration, \(c_{i}^{\mathrm{s}}\) are:

$$\begin{aligned} \sigma&=\sigma _{A}+\frac{k_{B}T}{S} \ln \frac{c_{A}^{s}}{c_{A}}+\frac{k_{B}T}{S} \ln \frac{\gamma _{A}^{s}}{\gamma _{A}} \nonumber \\&=\sigma _{B}+\frac{k_{B}T}{S} \ln \frac{c_{B}^{s}}{c_{B}}+\frac{k_{B}T}{S} \ln \frac{\gamma _{B}^{s}}{\gamma _{B}} \end{aligned}$$
(17)

where \(\sigma _{A}\) and \(\sigma _{B}\) are the surface tensions of the components A and B, respectively. S is the mean atomic surface area of the alloy, calculated using the relation [5]

$$S = \sum _{i} c_{i} S_{i} \quad (i= A,B)$$
(18)

with \(S_{i}\) given in terms of the atomic volumes \(\varOmega _{i}\) as

$$S_{i} = 1.102 \left( \frac{\varOmega _{i}}{N_{\mathrm{o}}}\right)$$
(19)

\(N_{\mathrm{o}}\) is Avogadro’s number. \(c_{i}^{\mathrm{s}}\) and \(\gamma _{i}^{\mathrm{s}}\) refer, respectively, to the concentration and activity coefficient of the ith component at the surface. \(\gamma _{i}\) and \(\gamma _{i}^{\mathrm{s}}\) are assumed to be related through:

$$\ln \gamma _{i}^{\mathrm{s}}= p\left[ \ln \gamma _{i} \left( c_{i}^{\mathrm{s}}\right) +q \ln \gamma _{i}\right]$$
(20)

where p and q are termed the surface coordination fractions and they are defined as the fractions of the total number of nearest neighbours made by an atom within its own layer and that in the adjoining layer such that \(p + 2q = 1.\) For a closed-packed structure values of these parameters are usually taken as \(p = \frac{1}{2}\) and \(q = \frac{1}{4}\) [37].

4 Results and discussion

The bulk thermodynamic properties of Al–Sn and Sn–Tl liquid alloys were calculated in this work from Eqs. (2) and (4) by using the model parameters n, \(\frac{W}{RT}\) and \(\frac{\partial W}{\partial T}\) given in Table 1 for each of the two liquid alloys investigated. These are the values of the parameters that reproduced fairly well the thermodynamic experimental data of \(\frac{G_{\mathrm{M}}}{RT}\) and \(S_{\mathrm{cc}}(0)\) taken from Hultgren et al. [38], while the experimental values of \(S_{\mathrm{cc}}(0)\) used in all aspect of our calculations for these liquid alloys at respective temperatures were obtained via the experimental free energy of mixing, \(\frac{G_{\mathrm{M}}}{RT}\), data also taken from Hultgren et al. [38] using Eq. (10). It is important to add that keeping these fitted parameters, which gives the best reproduction of the experimental Gibbs free energy of mixing \(G_{\mathrm{M}}\) data unchanged in all calculations, one then proceeds using these fixed values to compute such properties as the thermodynamic activity, \(a_{i}, (i=A,B)\), short-range order parameter, \(\alpha _{1}\), diffusion coefficient, \(\frac{D_{\mathrm{M}}}{D_{\mathrm{id}}}\), the enthalpy of mixing, \(H_{\mathrm{M}}\) and the entropy of mixing, \(S_{\mathrm{M}}\) and thus, forming the basis to elucidate the energetics in the liquid alloys.

4.1 Thermodynamic properties: a i , G M , H M and S M

In Figs. 1 and 2, the calculated activities for both liquid alloys investigated were compared with experimental values. It can be seen that there are fairly reasonable agreement between the calculated and experimental values especially below 0.5 atomic fraction of Sn in Al–Sn liquid alloys (Fig. 1). Above this concentration, the calculated values have some form of disagreement with experimental values. On the other hand, there is an excellent agreement with experimental values of activity of Sn and Tl in Sn–Tl liquid alloys at 723 K. This is given in Fig. 2.

Fig. 1
figure 1

Activity coefficients of (\(a_{\mathrm{Al}}\) and \(a_{\mathrm{Sn}}\)) in Al–Sn liquid alloys computed via Eqs. (5) and (6) at 973 K, respectively. The solid line denotes theoretical values, while the times symbol denotes experimental activity data for components of Al–Sn liquid alloys. \(c_{\mathrm{Sn}}\) is the bulk concentration of Sn in the liquid alloys. The experimental data were taken from [38]

Full size image
Fig. 2
figure 2

Activity coefficients of (\(a_{\mathrm{Sn}}\) and \(a_{\mathrm{Tl}}\)) in Sn–Tl liquid alloys computed via Eqs. (5) and (6) at 723 K, respectively. The solid line denotes theoretical values, while the times symbol denote experimental activity data for components of Sn–Tl liquid alloys. \(c_{\mathrm{Sn}}\) is the bulk concentration of Sn in the liquid alloys. The experimental data were taken from [38]

Full size image

Figure 3 shows the comparison of the calculated free energy of mixing along with the experimental values given as symbols for Al–Sn and Sn–Tl liquid alloys, respectively. A perusal of the figure shows that there is an excellent agreement between the calculated and experimental values across the whole concentration range with Al–Sn alloys exhibiting minimum \(G_{\mathrm{M}}\) value of −0.3479RT at \(c_{\mathrm{Sn}} = 0.62\) and Sn–Tl alloys with minimum value of −0.5145RT at \(c_{\mathrm{Sn}} = 0.50\), an indication that the interactions between constituent species in the alloy melts may be considered to be weak in nature. The excellent agreement between the two sets of data confirms that the choice of n and \(\frac{W}{RT}\) for the two alloys are quite reasonable. Also, in view of the following observations, Fig. 3 indicates that although the two alloys are segregating systems, the degree of segregation in Al–Sn with \((G_{\mathrm{M}}^{\mathrm{min}} = -0.3479 RT)\) is more than in Sn–Tl with \((G_{\mathrm{M}}^{\mathrm{min}}= -0.5145RT).\) On the contrary, the tendency for heterocoordination of unlike atoms in the liquid phase is weaker in Al–Sn alloys than in Sn–Tl liquid alloys, since for strongly interacting liquid alloys, \(\frac{G_{\mathrm{M}}}{RT} \le -3.0\) [31]. In addition, it is noticed that while the Gibbs free energy of mixing of Sn–Tl liquid alloy is symmetric around the equiatomic composition \((c_{\mathrm{Sn}}=0.5),\) Al–Sn liquid alloy exhibits an anomalous asymmetric behaviour with respect to equiatomic composition typical of systems with atomic volume ratio \(\left( \frac{\varOmega _{B}}{\varOmega _{A}}\right) \ge\) about 2.0 [31, 32] which in the present study is about 1.50 for Al–Sn and 1.06 for Sn–Tl liquid alloys, respectively.

Fig. 3
figure 3

Free energy of mixing: \(\frac{G_{\mathrm{M}}}{RT}\) versus concentration for Al–Sn and Sn–Tl liquid alloys at 973 and 723 K, respectively. The solid line denotes theoretical values, while stars and times symbol denote experimental data for Al–Sn and Sn–Tl liquid alloys at respective temperatures. \(c_{\mathrm{Sn}}\) is the bulk concentration of Sn in the liquid alloys. The experimental data were taken from [38]

Full size image

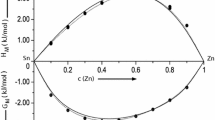
It is observed that if the energy parameters are supposed to be independent of temperature, i.e. if \(\frac{\partial W}{\partial T}= 0\), then \(\frac{S_{\mathrm{M}}}{R}\) and \(\frac{H_{\mathrm{M}}}{RT}\) so obtained are in very poor agreement with experimental data. This simply indicates the importance of the dependence of interaction energy, W, on temperature. The plots of \(\frac{S_{\mathrm{M}}}{R}\) and \(\frac{H_{\mathrm{M}}}{RT}\) computed via Eqs. (8) and (9) for the two liquid alloys are shown in Figs. 4 and 5, respectively. From the figures, it is noticed that the temperature dependence of interaction energy parameters, \(\frac{\partial W}{\partial T}\) (Table 1) obtained by successive approximation of the computed values of \(\frac{S_{\mathrm{M}}}{R}\) and \(\frac{H_{\mathrm{M}}}{RT}\) with the respective available experimental data taken from [38] for each liquid alloys give a remarkable agreement between the calculated and experimental values. Moreover, the curves describing both the calculated and experimental values of the entropy of mixing and enthalpy of mixing of the two liquid alloys investigated are symmetric and positive with respect to the equiatomic composition (typical of segregating systems), although their Gibbs free energy of mixing are indicative of weakly interacting systems. Table 1 also shows that the value of temperature dependence of the ordering energy \(\left( \hbox {i.e.}\,\frac{\partial W}{\partial T}\right)\) is positive for liquid Al–Sn alloys and negative for Sn–Tl alloys.

Fig. 4
figure 4

Entropy of mixing: \(\frac{S_{\mathrm{M}}}{R}\) versus concentration for Al–Sn and Sn–Tl liquid alloys at 973 and 723 K, respectively. The solid line denotes theoretical values, while stars and times symbol denote experimental data for Al–Sn and Sn–Tl liquid alloys at respective temperatures. \(c_{\mathrm{Sn}}\) is the concentration of Sn in the liquid alloys. The experimental data were taken from [38]

Full size image
Fig. 5
figure 5

Enthalpy of mixing: \(\frac{H_{\mathrm{M}}}{RT}\) versus concentration for Al–Sn and Sn–Tl liquid alloys at 973 and 723 K, respectively. The solid line denotes theoretical values, while stars and times symbol denote experimental data for Al–Sn and Sn–Tl liquid alloys at respective temperatures. \(c_{\mathrm{Sn}}\) is the concentration of Sn in the liquid alloys. The experimental data were taken from [38]

Full size image
Table 1 Energy parameters used for the bulk properties calculation
Full size table

4.2 Microscopic functions

An insight into the nature of ordering in the melts is provided by critically assessing the results of the structure related quantities. In this light, the first quantity investigated is the concentration–concentration fluctuations at the long-wavelength limits, \(S_{\mathrm{cc}}(0)\) which is one of the most sensitive properties of demixing liquid alloys [4], and usually exhibits a distinct variation around the critical concentration and temperature. The deviation of \(S_{\mathrm{cc}}(0)\) from ideal value \(S_{\mathrm{cc}}^{\mathrm{id}}(0)=c_{A}(1-c_{A})\) is an essential parameter in order to visualize the nature of atomic interactions in the liquid mixture such that if at a given concentration calculated \(S_{\mathrm{cc}}(0) \gg S^{\mathrm{id}}_{\mathrm{cc}}(0)\), then there is a tendency for segregation and demixing in liquid alloys; on the contrary, if \(S_{\mathrm{cc}}(0) \ll S^{\mathrm{id}}_{\mathrm{cc}}(0)\), is an indicator of heterocoordination (preference for unlike atoms to pair as nearest neighbours) in the liquid alloys.

\(S_{\mathrm{cc}}(0)\) can be obtained via Eq. (10) directly from the experimental Gibbs energy of mixing or from the activity data. This is usually referred to as an experimental \(S_{\mathrm{cc}}(0)\) in literature [4, 31, 32]. Equation (11) has been used to obtain the computed \(S_{\mathrm{cc}}(0)\) for these liquid alloys, whereas the measured \(S_{\mathrm{cc}}(0)\) were obtained from the experimental Gibbs free energy of mixing data taken from [38] upon solving the first term of Eq. (10) numerically. It is necessary to add that Eq. (13) was used to compute \(S^{\mathrm{id}}_{\mathrm{cc}}(0)\). The results of \(S_{\mathrm{cc}}(0)\) as a function of concentration for both systems are as presented in Fig. 6. From the figure, it is obvious that the computed \(S_{\mathrm{cc}}(0)>S^{\mathrm{id}}_{\mathrm{cc}}(0)\) for both Al–Sn and Sn–Tl liquid alloys at T = 973 and 723 K, respectively. This implies a tendency for homocoordination (preference for like atoms Al–Al, Sn–Sn or Tl–Tl to pair as nearest neighbours) which is consistent with the ordering energy, W. A more closer look at Fig. 6 reveals that in the concentration range of \(0.9 \le c_{\mathrm{Sn}} \le 1.0\), the calculated \(S_{\mathrm{cc}}(0)\) values for both liquid alloys almost attain ideal values. This observed behaviour of \(S_{\mathrm{cc}}(0)\) depends on the number of atoms in the cluster n and the interaction energy, W [4]. For \(n<1\) and \(W < 1\) as in the case of Sn–Tl alloys, the \(S_{\mathrm{cc}}(0)\) is symmetrical at \(c_{\mathrm{Tl}} = c_{\mathrm{Sn}} = \frac{1}{2},\) while on the other hand, Al–Sn liquid alloys with \(n<1\) and \(W > 1,\) exhibits asymmetry and positive deviation in \(S_{\mathrm{cc}}(0)\) as expected as a function of both n and W.

Fig. 6
figure 6

Concentration–concentration fluctuations at long-wavelength limits, \(S_{\mathrm{cc}}(0)\) as a function of concentration for Al–Sn and Sn–Tl liquid alloys at 973 and 723 K, respectively. The solid line denotes theoretical values while stars and times symbol denote experimental data for Al–Sn and Sn–Tl liquid alloys at respective temperatures. The dots, computed from Eq. (13), denote the ideal values of concentration–concentration fluctuations, \(S_{\mathrm{cc}}^{\mathrm{id}}(0)\). \(c_{\mathrm{Sn}}\) is the concentration of Sn in the liquid alloys. The experimental data were taken from [38]

Full size image

A second microscopic function given by Eq. (14), known as the Warren–Cowley short-range order parameter, \(\alpha _{1},\) is further used to quantify the nature of atomic interactions in the liquid alloys and gain insight into the local arrangement of atoms. For equiatomic composition, \(\alpha _{1}\) is found to be \(-1 \le \alpha _{1} \le +1.\) Positive values of \(\alpha _{1}\) as shown in Fig. 7, in the whole concentration range for both alloys, are sufficient indicators of the presence of segregation in the liquid alloys. In addition, it is noticed from Fig. 7 that while \(\alpha _{1} \ll 1.0\) and symmetric about \(c_{\mathrm{Tl}} = c_{\mathrm{Sn}} = \frac{1}{2}\) for Sn–Tl liquid alloys, \(\alpha _{1} \ll 1.0\) and shows an asymmetric behaviour in liquid Al–Sn alloy with respect to equiatomic composition. \(S_{\mathrm{cc}}(0)\) values that are greater than \(S^{\mathrm{id}}_{\mathrm{cc}}(0)\) and small positive values of \(\alpha _{1},\) classify both liquid alloys studied as weakly segregating alloys [4], but the degree of segregation of atoms is higher in liquid Al–Sn alloys than in Sn–Tl alloys. It could also be observed that varying the value of Z does not have any significant effect on \(\alpha _{1}-c\) curves, the only effect is to vary the position of the maxima while the overall features remain invariant.

Fig. 7
figure 7

Warren–Coyley short-range order parameter, (\(\alpha _{1}),\) computed using Eq. (14) versus concentration for Al–Sn and Sn–Tl liquid alloys at 973 and 723 K, respectively. \(c_{\mathrm{Sn}}\) is the bulk concentration of Sn in the liquid alloys

Full size image

4.3 Diffusivity

The calculated values of \(S_{\mathrm{cc}}(0)\) have been used in Eq. (15) to evaluate diffusion coefficient, \(\frac{D_{\mathrm{M}}}{D_{\mathrm{id}}}\), another sensitive property of demixing liquid alloys as a function of concentration. This shows that \(\frac{D_{\mathrm{M}}}{D_{\mathrm{id}}}<1\) across the whole concentration range as given in Fig. 8, indicating a phase separation tendency in both liquid alloys. \(\frac{D_{\mathrm{M}}}{D_{\mathrm{id}}}\) is sharply reduced to a very small value of \(\approx\)0.243 for Al–Sn at \(c_{\mathrm{Sn}} = 0.3\) and \(\approx\)0.640 for Sn–Tl at \(c_{\mathrm{Sn}}= 0.5.\) Such an effect is more pronounced with increase in the number of atoms in the self-associates, n. Thus the tendency for self-coordination of atoms and demixing in the liquid alloys is expected to be favoured (Fig. 8), as observed by the \(S_{\mathrm{cc}}(0)\) and \(\alpha _{1},\) respectively.

Fig. 8
figure 8

Diffusion coefficients, \(\frac{D_{\mathrm{M}}}{D_{\mathrm{id}}},\) computed using Eq. (15) versus concentration for Al–Sn and Sn–Tl liquid alloys at 973 and 723 K, respectively. \(c_{\mathrm{Sn}}\) is the concentration of Sn in the liquid alloys

Full size image

4.4 Surface properties

For the calculations of the surface properties at the working temperature of 973 K for Al–Sn and 723 K for Sn–Tl liquid alloys, the relationships between the temperature dependence of surface tension and atomic volume as given in Refs. [29, 39] were used to obtain the atomic volume and these are given as:

$$\sigma _{i}=\sigma _{\mathrm{im}}+\left( T-T_{\mathrm{m}}\right) \frac{\partial \sigma _{i}}{\partial T}$$
(21)

and

$$\varOmega _{i}=\varOmega _{\mathrm{im}}\left[ 1+\theta \left( T-T_{\mathrm{m}}\right) \right]$$
(22)

where \(\theta\) is the thermal coefficient of expansion, \(\varOmega _{\mathrm{im}}\), \(\sigma _{\mathrm{im}}\) are the atomic volume and surface tension of the alloy components at their melting temperature \(T_{\mathrm{m}}\) and T is the working temperature in Kelvin. The values of \(\frac{\partial \sigma _{i}}{\partial T}\) and \(\theta\) for the pure components of the alloy were obtained from Ref. [29]. S and \(S_{i}\) for each atomic species of the alloy systems were computed using Eqs. (19) and (20), respectively.

We then proceeded to calculate the surface properties in the framework of SAM using available thermodynamic data and the interaction energy parameters (given in Tables 1, 2) as the input to predict the values of the surface tension and surface segregation. Equation (18) was solved numerically with respect to the surface concentration, \((c_{i}^{\mathrm{s}})\) and the concentration dependence of surface tension, \(\sigma\) as a function of bulk concentration \(c_{i}\) (i = Sn) for the two alloys. Figures 9 and 10 shows the results obtained using the parameters in Tables 1 and 2 for the surface concentration, \((c_{i}^{\mathrm{s}})\) and surface tension, \(\sigma\), respectively. The lack of experimental data on surface tensions for the two liquid alloys at the working temperatures justifies the interest that can be given to the theoretical calculations, nonetheless, as seen from Fig. 9 the calculated values of surface concentration follow the usual trend of surface concentration increasing with increasing bulk concentration. This suggests that Sn atoms (with lower value of surface tension relative to Al atoms in Al–Sn) and Tl atoms (having lower value of surface tension relative to Sn atoms in Sn–Tl) segregate respectively at the surface of Al–Sn and Sn–Tl liquid alloys throughout the entire bulk concentrations, with both curves exhibiting a large deviations from ideal values. When compared, the curves describing the surface segregation indicate that the rates at which Sn atoms segregate at the surface of Al–Sn alloys is more than the rate at which Tl atoms segregate at the surface in Sn–Tl liquid alloys for the same bulk concentration. For instance, at the bulk concentration when both \(c_{\mathrm{Tl}}\) and \(c_{\mathrm{Sn}}\) are equal to 20 %, the surface is enriched with about 41 % of Tl atoms in Sn–Tl, whereas about 88 % of Sn atoms segregate at the surface of Al–Sn alloys. An important reason for the surface enrichment could be due to the fact that there exists a higher tendency for unlike atoms to pair as nearest neighbours in Sn–Tl alloys, than in Al–Sn alloys which exhibits a higher degree of segregation.

Table 2 Essential parameters used for the surface properties calculation for Al–Sn and Sn–Tl at respective temperatures
Full size table

Once the surface concentration is obtained, the surface tensions of the liquid alloys were computed by substituting the surface concentration \((c_{i}^{\mathrm{s}})\) values into Eq. (18). The surface tension isothermal plots of the two liquid alloys exhibit negative deviations from the ideal values as shown in Fig. 10. This implies that Sn atoms segregate to the surface of Al–Sn while Tl atoms segregate to the surface of Sn–Tl. It is noticeable that although there is not much deviation between the calculated surface tension and the ideal values of surface tension of Sn–Tl alloys, but there is a significant deviation between the ideal values of the surface tension and the calculated values of the surface tension of Al–Sn liquid alloys. An indication that addition of Tl atoms to Sn–Tl and Sn atoms to Al–Sn liquid alloys causes an observable decrease in the values of their respective surface tension. It is further noted that the rate of decrease of \(\sigma\) with respect to bulk concentration in Sn–Tl alloys is comparatively lower than that of Al–Sn alloys. This might be ascribed to earlier submission that Sn–Tl is a weakly segregating alloy compare to Al–Sn alloy, as observed from Figs. 6, 7 and 9, respectively. The negative deviation between calculated surface tension isotherms of both systems and ideal values of the surface tensions (Fig. 10), further confirms that the two liquid alloys are segregating systems. This assertion is consistent with the positive deviations of their bulk properties from the Raoult’s law [40, 41].

Fig. 9
figure 9

Computed values of the surface concentration, \(c_{\mathrm{Sn}}^{\mathrm{s}}\) for Al–Sn liquid alloy at 973 K and surface concentration, \(c_{\mathrm{Tl}}^{\mathrm{s}}\) for Sn–Tl liquid alloy at 723 K. These two curves were computed via Eq. (18). The dots denote the ideal values of the surface concentration, \(c_{\mathrm{id}}^{\mathrm{s}}\) computed from: \(c_{\mathrm{id}}^{\mathrm{s}} =c^{\mathrm{b}}.\) \(c_{\mathrm{Sn}}\) is the concentration of Sn in the liquid alloys

Full size image
Fig. 10
figure 10

Computed values of the surface tension, \(\sigma\) for Al–Sn and Sn–Tl liquid alloys at 973 and 723 K, respectively, computed via Eq. (18). The dots labelled \(c_{\mathrm{Al-Sn}}^{\mathrm{id}}\) and \(c_{\mathrm{Sn-Tl}}^{\mathrm{id}}\) denote the ideal values of the surface tension of the Al–Sn and Sn–Tl, respectively, obtained from the relation: \(\sigma _{i}^{\mathrm{id}}=\sigma _{A}c_{A}+\sigma _{B}c_{B}\). \(c_{\mathrm{Sn}}\) is the bulk concentration of Sn in the liquid alloys

Full size image

5 Concluding remarks

The energetics of mixing and its effects on the bulk and surface properties of Al–Sn and Sn–Tl liquid alloys at 973 and 723 K, respectively were studied using the SAM. The results reveal that both Sn and Ti atoms segregate to the surface at all bulk concentration of Sn in Al–Sn and Sn–Tl liquid alloys. The degree of segregation is however predicted to be more pronounced in Al–Sn liquid alloys than Sn–Tl. The calculated surface tension isothermal curves exhibit negative deviation from the ideal both in Al–Sn and Sn–Tl alloys. The surface tension decreases with an increase in the bulk concentration and this, suggests that Al–Sn and Sn–Tl liquid alloys are segregated systems both in the bulk and at the surface across the entire concentration range. This observation is in agreement with the behaviour of the microscopic functions, \(S_{\mathrm{cc}}(0)\), \(\alpha _{1}\) as well as diffusion coefficients, \(\frac{D_{\mathrm{M}}}{D_{\mathrm{id}}}\) of both systems.