Equilateral Chains and Cyclic Central Configurations of the Planar Five-Body Problem

Abstract

Central configurations and relative equilibria are an important facet of the study of the N-body problem, but become very difficult to rigorously analyze for $N>3$. In this paper, we focus on a particular but interesting class of configurations of the five-body problem: the equilateral pentagonal configurations, which have a cycle of five equal edges. We prove a variety of results concerning central configurations with this property, including a computer-assisted proof of the finiteness of such configurations for any positive five masses with a range of rational-exponent homogeneous potentials (including the Newtonian case and the point-vortex model), some constraints on their shapes, and we determine some exact solutions for particular N-body potentials.

1 Introduction

In this work, we consider some particular classes of relative equilibria (i.e., equilibria in a uniformly rotating coordinate system) of a planar N-body problem, in which N point particles with non-negative masses $m_i$ interact through a central potential U:

$$\begin{aligned}&m_i \ddot{q}_{i;j} = \frac{\partial U}{\partial q_{i;j}}, \ \ i \in \{0,\ldots N-1\},\\&U = \sum _{i<j} m_i m_j/ r_{i,j}^{A-2} \end{aligned}$$

where $q_i \in \mathbf {R}^2$ is the position of particle i, $q_{i;j}$ denotes the jth component of $q_i$, and $r_{i,j} = |q_i - q_j|$ are the mutual distances between the particles. The exponent A is a real parameter in $(2,\infty )$.

The most interesting and important case is the Newtonian gravitational model with $A=3$, but we believe it can be useful to generalize the problem since many features of the relative equilibria do not strongly depend on the exponent A. The potential can be extended to the case $A=2$ by using

$$\begin{aligned} U = \sum _{i<k} m_i m_k \log (r_{i,k}) \end{aligned}$$

which has been used in models of fluid vortex tubes (Helmholtz 1858; Kirchhoff 1883; Aref et al. 1992).

The relative equilibria (equilibria in a uniformly rotating reference frame) must satisfy the equations for a central configuration (Wintner 1941), defined as configurations for which

$$\begin{aligned} \lambda (q_i - c) = \sum _{j = 1, j \ne i}^n \frac{m_j (q_i - q_j)}{r_{i,j}^A} \end{aligned}$$

(1)

The vector c is the center of mass,

$$\begin{aligned} c = \frac{1}{M} \sum _{i=1}^n m_i q_i, \end{aligned}$$

with

$$\begin{aligned} M = \sum _{i=1}^{n} m_i \end{aligned}$$

the total mass, which we will always assume to be nonzero (for the special case in which $M=0$, see Celli (2005)). The parameter $\lambda$ is real. The masses $m_i$ are also assumed to be real, and we are primarily interested in positive masses.

In some earlier literature, central configurations are also referred to as permanent configurations (MacMillan and Bartky 1932; Rayl 1939; Brumberg 1957). The study of central configurations and relative equilibria provides an avenue for progress into the N-body problem, which otherwise presents formidable difficulty. There is a rich literature on these configurations, starting with Euler (1767) and Lagrange (1772) who completely characterized the relative equilibria for the Newtonian three-body problem. The collinear three-body configurations studied by Euler were further elucidated by Moulton (1910), who showed there is a unique (up to scaling) central configuration for any ordering of N positive masses on a line.

Besides their interest as simple orbits, central configurations also play an important role in the topology of the integral manifolds of the N-body problem (Cabral 1973; Albouy 1993), in multiple-body collision orbits (Moeckel 1981; Saari and Hulkower 1981; ElBialy 1990), and in the proof of chaotic dynamics in the three-body problem (Moeckel 1989).

For $N>3$, it is much harder to characterize the central configurations. One of the most basic questions is whether there are finitely many equivalence classes of central configurations for each choice of positive masses. This question has been highlighted in the planar case by several authors (Chazy 1918; Wintner 1941; Smale 1998). It has been resolved for the Newtonian four-body problem (Hampton and Moeckel 2005), the four-vortex problem (Hampton and Moeckel 2009), and partially for the Newtonian five-body problem (Hampton 2010; Albouy and Kaloshin 2012). The spatial version of the five-body finiteness problem has also been partially resolved (Hampton and Jensen 2011), although with similar limitations to the planar case.

Much is still unknown about the central configurations and relative equilibria in the five-body problem. An attempt to extend the approach of MacMillan and Bartky was undertaken by Williams (1938), but without as much success and there appear to be some errors in the restrictions of the shapes of configurations in that work. Another line of inquiry is to consider five-body configurations with some small or infinitesimal masses, to leverage the knowledge of three- and four-body configurations (Xia 1991; Moeckel 1997; Hampton 2005). In the equal mass case, the planar central configurations have been characterized with high-quality numerical methods (Lee and Santoprete 2009; Moczurad and Zgliczyński 2019).

In this manuscript, we consider a special case of the five-body problem in which the configurations are an equilateral cyclic chain (defined in the next section). This special case has some interesting properties and can be generalized to larger numbers of masses. This problem was suggested to us by Manuele Santoprete in 2020; more or less simultaneously, this approach seems to have been taken up by a separate group, who proved some properties of these configurations in the Newtonian case that are complementary to our results (Alvarez-Ramírez et al. 2022).

There is much work on other interesting questions on central configurations, such as their stability. Rather than attempt to summarize this work, we recommend the excellent surveys by Moeckel (2015, 1990).

2 Equations for Central Configurations and Equilateral Chains

Choosing two indices i and j, we can take the inner product of (1) with $q_i - q_j$ to get

$$\begin{aligned} \lambda (q_i - c) \cdot (q_i - q_j) = \sum _{k = 1, k \ne i}^n \frac{m_k (q_i - q_k) \cdot (q_i - q_j)}{r_{i,k}^A} \end{aligned}$$

and then the left-hand side becomes

$$\begin{aligned} \lambda (q_i - c) \cdot (q_i - q_j) = \frac{\lambda }{M} \sum _{k=1}^n m_k (q_i - q_j) \cdot (q_i - q_k) = {\tilde{\lambda }}\sum _{k=1}^n m_k (r_{i,j}^2 + r_{i,k}^2 - r_{j,k}^2)/2 \end{aligned}$$

in which we have introduced ${\tilde{\lambda }}= \frac{\lambda }{M}$. The inner-products on the right-hand side can be rewritten in terms of the mutual distances as well. After putting all the terms on one side of the equation and cancelling a factor of 1/2, we obtain for each choice of $i \ne j$ the equations

$$\begin{aligned} \sum _{k=1, k \ne i}^n m_k (r_{i,k}^{-A} - {\tilde{\lambda }}) (r_{i,j}^2 + r_{i,k}^2 - r_{j,k}^2) = 0 \end{aligned}$$

(2)

If we now introduce variables $S_{i,j} = r_{i,k}^{-A} - {\tilde{\lambda }}$ and $A_{i,j,k} = r_{j,k}^2 - r_{i,k}^2 - r_{i,j}^2$, we obtain the compact form

$$\begin{aligned} f_{i,j} = \sum _{k = 1, k \ne i}^n m_k S_{i,k} A_{i,j,k} = 0. \end{aligned}$$

Gareth Roberts has observed that these equations follow from the developments given in Albouy and Chenciner (1997); they are sometimes referred to as the ‘asymmetric Albouy–Chenciner equations.’

If we combine $f_{i,j}$ and $f_{j,i}$, we obtain $n(n-1)/2$ equations

$$\begin{aligned} g_{i,j} = f_{i,j} + f_{j,i} = \sum _{k = 1, k \ne i,j}^n m_k (S_{i,k} A_{i,j,k} + S_{j,k} A_{j,i,k}) = 0. \end{aligned}$$

These are the equations presented as the Albouy–Chenciner equations in Hampton and Moeckel (2005).

By taking the wedge product instead of the inner product, we obtain a different set of equations referred to as the Laura–Andoyer equations (Laura 1905; Andoyer 1906)

$$\begin{aligned} L_{i,j} := \sum _{k \ne i,j} m_k (R_{i,k} - R_{j,k}) \Delta _{i,j,k} = 0 \end{aligned}$$

(3)

where $\Delta _{i,j,k}$ is twice the oriented area of the triangle $(q_i, q_j, q_k)$, i.e., $(q_i - q_j) \wedge (q_i - q_k)$, $q_i \in \mathbb {R}^2$ and $R_{i,j} = r_{i,j}^{-A} = (|q_i - q_j|)^{-A}$. Sometimes the $\Delta _{i,j,k}$ will be replaced by the non-negative $D_{i,j,k} = |\Delta _{i,j,k}|$ in order to make the sign of the terms in our equations more apparent. When explicit coordinates are needed, $q_i = (x_i, y_i)$.

We define an N-body configuration to be an equilateral chain if at least $N-1$ consecutive distances involving all of the points are equal; we will choose the particular convention with

$$\begin{aligned} r_{1,2} = r_{2,3} = \ldots = r_{N-2,N-1} = r_{N-1,N} \end{aligned}$$

Similarly, an equilateral cyclic configuration has a N equal distances in a complete cycle, and we will choose our indexing so that

$$\begin{aligned} r_{1,2} = r_{2,3} = \cdots = r_{1,N} \end{aligned}$$

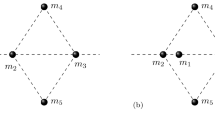
An example of such a configuration is shown in Fig. 1.

Fig. 1

A five-body equilateral cyclic configuration with the labeling convention used in this paper

The five-body cyclic configurations generalize the rhomboidal configurations of the four-body problem which have been well-studied in both the Newtonian and vortex cases (Long and Sun 2002; Perez-Chavela and Santoprete 2007; Hampton et al. 2014; Leandro 2019; Oliveira and Vidal 2020). The five-body configurations of a rhombus with a central mass are another interesting and well-studied extension, which contain continua of central configurations if a negative central mass is allowed (Roberts 1999; Gidea and Llibre 2010; Albouy and Kaloshin 2012; Cornelio et al. 2021).

The Laura–Andoyer equations for the equilateral pentagon case fall into two sets of five; in the first of these sets, each equation only involves two of the masses:

$$\begin{aligned}&m_4 \Delta _{1,3,4}(R_{1,4}-R_{1,2}) + m_5 \Delta _{1,3,5} (R_{1,2} - R_{3,5}) = 0 , \nonumber \\&m_1 \Delta _{1,2,4}(R_{1,4}-R_{1,2}) + m_5 \Delta _{2,4,5} ( R_{1,2}-R_{2,5} ) = 0 ,\nonumber \\&m_3 \Delta _{2,3,5}(R_{3,5}-R_{1,2}) + m_4 \Delta _{2,4,5} (R_{1,2} - R_{2,4}) = 0 , \nonumber \\&m_1 \Delta _{1,3,5} (R_{1,3} -R_{1,2}) + m_2 \Delta _{2,3,5} (R_{1,2} - R_{2,5}) = 0, \nonumber \\&m_2 \Delta _{1,2,4} ( R_{2,4}-R_{1,2}) + m_3 \Delta _{1,3,4} (R_{1,2}- R_{1,3} ) = 0, \end{aligned}$$

(4)

while in the second set, each equation involves three of the masses:

$$\begin{aligned}&m_3 \Delta _{1,2,3} (R_{1,3} -R_{1,2} ) + m_4 \Delta _{1,2,4} (R_{1,4}- R_{2,4})+ m_5 \Delta _{1,2,5} (R_{1,2} - R_{2,5} ) = 0, \\&m_2 \Delta _{1,2,5} (R_{2,5} -R_{1,2} ) + m_3 \Delta _{1,3,5} (R_{3,5}- R_{1,3})+ m_4 \Delta _{1,4,5} (R_{1,2} - R_{1,4} ) = 0, \\&m_1 \Delta _{1,2,3} (R_{1,2} - R_{1,3} ) + m_4 \Delta _{2,3,4} (R_{2,4}- R_{1,2})+ m_5 \Delta _{2,3,5} (R_{2,5} - R_{3,5} ) = 0, \\&m_1 \Delta _{1,3,4} (R_{1,3} -R_{1,4} ) + m_2 \Delta _{2,3,4} (R_{1,2}- R_{2,4})+ m_5 \Delta _{3,4,5} (R_{3,5} - R_{1,2} ) = 0, \\&m_1 \Delta _{1,4,5} (R_{1,4} -R_{1,2} ) + m_2 \Delta _{2,4,5} (R_{2,4}- R_{2,5})+ m_3 \Delta _{3,4,5} (R_{1,2} - R_{3,5} ) = 0, \end{aligned}$$

If we normalize the configurations by choosing $q_1 = (-1/2, 0)$ and $q_2 = (1/2,0)$ (so $r_{1,2} = 1$), then the $\Delta _{i,j,k}$ are

$$\begin{aligned}&\Delta _{1,2,3} = y_3, \ \ \ \ \Delta _{1,2,4} = y_4, \ \ \ \ \Delta _{1,2,5} = y_5,\\&\Delta _{1,3,4} = -x_{4} y_{3} + x_{3} y_{4} + \frac{1}{2} (y_{4} - y_{3} ),\\&\Delta _{1,3,5} = -x_{5} y_{3} + x_{3} y_{5} + \frac{1}{2} (y_{5} - y_{3} ),\\&\Delta _{1,4,5} = -x_{5} y_{4} + x_{4} y_{5} + \frac{1}{2} (y_{5} - y_{4} ),\\&\Delta _{2,3,4} = -x_{4} y_{3} + x_{3} y_{4} + \frac{1}{2} (y_{3} - y_{4} ),\\&\Delta _{2,3,5} = -x_{5} y_{3} + x_{3} y_{5} + \frac{1}{2} (y_{3} - y_{5} ),\\&\Delta _{2,4,5} = -x_{5} y_{4} + x_{4} y_{5} + \frac{1}{2} (y_{4} - y_{5} ),\\&\Delta _{3,4,5} = -x_{4} y_{3} + x_{5} y_{3} + x_{3} y_{4} - x_{5} y_{4} - x_{3} y_{5} + x_{4} y_{5}. \end{aligned}$$

3 Finiteness Results

To study the finiteness of the planar equilateral configurations, we use the asymmetric Albouy–Chenciner equations $f_{i,j}=0$ and the Cayley–Menger determinants for all four-point subconfigurations

$$\begin{aligned} C_{i,j,k,l} = det \left( \begin{array}{ccccc} 0 &{} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 0 &{} r_{i,j}^2 &{} r_{i,k}^2 &{} r_{i,l}^2 \\ 1 &{} r_{i,j}^2 &{} 0 &{} r_{j,k}^2 &{} r_{j,l}^2 \\ 1 &{} r_{i,k}^2 &{} r_{j,k}^2 &{} 0 &{} r_{k,l}^2 \\ 1 &{} r_{i,l}^2 &{} r_{j,l}^2 &{} r_{k,l}^2 &{} 0 \\ \end{array} \right) = 0 \end{aligned}$$

(5)

(with distinct i, j, k, and l).

Our strategy uses what is now mostly referred to as tropical geometric techniques, or sometimes as BKK (Bernshtein, Khovanskii, and Kushnirenko) theory in our context (Bernshtein 1975; Kushnirenko 1976; Khovanskii 1978). The first application of these techniques to celestial mechanics problems was pioneered by Richard Moeckel (Hampton and Moeckel 2005; Moeckel 2008). It has been shown to be a powerful technique for finiteness problems, and to a lesser extent for enumeration of central configurations. Subsequent work using these ideas include (Hampton and Moeckel 2009; Hampton 2010; Hampton and Jensen 2015; Kulevich et al. 2009). The work of Albouy and Kaloshin (2012) on the Newtonian four- and five-body planar central configurations uses related ideas although not presented within the framework of tropical geometry.

Here, we follow a very similar procedure to that described in (Hampton and Jensen 2011) to study the question of finiteness of the five-body equilateral central configurations. The general strategy is to convert the system of equations for central configurations into a polynomial system, and study the behavior of the resulting algebraic variety in $(\mathbb {C}^*)^m$ as some subset of the m variables approach 0 or $\infty$. Much of this analysis can be done using the Newton polytopes of the polynomials, which are much simpler than the algebraic varieties themselves. If we have a polynomial

$$\begin{aligned} p = \sum _{v \in \mathcal {S}} a_v x^v \end{aligned}$$

where the $a_v$ are nonzero coefficients, the $x^v = \prod x_i^{v_i}$, and $\mathcal {S}$ is a finite subset of $\mathbb {Z}_{\ge 0}^m$, then the Newton polytope N(p) of p is defined as the convex hull of the exponent vectors v. A vector w induces an initial form $in_w(p)$ of a polynomial, which is the sum of the terms $a_v x^v$ in p which attain the maximum value of $w \cdot v$. The tropical variety of p is defined to be the set of vectors $w \in \mathbb {R}^n$ such that $in_w(p)$ is not monomial. For a system of polynomials $\{p_i\}$ the tropical prevariety is defined to be the intersection of the tropical varieties $T(p_i)$. If we can show that the tropical prevariety is trivial (consisting of only the zero vector), then there are only finitely many solutions to the polynomial system.

With the assistance of the software Sage (2020), Singular Decker et al. (2021), and Gfan Jensen (2011) we find relatively easily that there are finitely many equilateral central configurations for $A=2$ and $A=3$, for any positive masses. The tropical prevariety of the system is much simpler in the vortex case $A=2$, having only 22 generating rays compared to 37 in the Newtonian case. In fact, the Newtonian case generalizes for potential exponents greater than 3 as well.

Because Gfan cannot currently compute a prevariety for variable exponents, we used a slight variation of the Albouy–Chenciner equations to compute and to analyze the initial form systems for rational exponents $A>2$. We found it was helpful to introduce the variables $Q_{i,j} = r_{i,j}^{-A+2} = r_{i,j}^{-B}$, where $B=A-2$, since the quantity $A-2$ appears so often. With this notation,

$$\begin{aligned} f_{i,j} = \sum _{k = 1}^n m_k S_{i,k} A_{i,j,k} = \sum _{k = 1}^n m_k (Q_{i,j}r_{i,j}^{-2} - {\tilde{\lambda }}) A_{i,j,k} \end{aligned}$$

We used Gfan to compute the tropical prevariety of these equations with the normalization ${\tilde{\lambda }}= 1$, and cleared denominators to obtain a polynomial system in $r_{i,j}$ and $Q_{i,j}$, combined with the four-point Cayley–Menger determinants. We denote the polynomial versions of the $f_{i,j}$ by $p_{i,j}$.

For rational $A > 2$, the rays of the tropical prevariety fall into nine equivalence classes under the action of the cyclic group $\mathcal {C}_5$ on the indices of the $r_{i,j}$. Since we have chosen the equilateral configurations to have $r_{i,j} = r_{i+1, j+1}$, this action fixes our first coordinate $r_{i,j}$ and cyclically permutes the remaining five distances. In the table below, the coordinate exponents are in the order $(r_{1,2}, r_{1,3}, r_{1,4}, r_{2,4}, r_{2,5}, r_{3,5})$. Six of these rays are independent of A (Table 1).

Table 1 Representative rays of the tropical prevariety of the asymmetric Albouy–Chenciner equations and Cayley–Menger determinants

Because of the balance condition for tropical varieties (Maclagan and Sturmfels 2015), we can restrict our analysis to cones that intersect the half-space containing exponent vectors with a non-negative sum. This excludes the first ray in our list. Again after reducing by the $\mathcal {C}_5$ symmetry, we have a set of 22 representative cones (Table 2).

Table 2 Representative cones of the tropical prevariety of the asymmetric Albouy–Chenciner equations and Cayley–Menger determinants in the non-negative sum half-space of weights

Remarkably, for each cone in the tropical prevariety, the initial form polynomials factor enough that we can compute the elimination ideal of the initial form system in the ring $\mathbb {Q} [m_1, m_2, m_3, m_4, m_5]$ (using Singular within Sage), without the need to specialize to a particular value of B (apart from the condition that $B > 0$, i.e., $A>2$). To rule out a nontrivial (i.e., nonmonomial) initial form ideal, we only need to assume that no subset of the masses has a vanishing sum, including the total mass.

As an example of this analysis, we will consider the initial forms induced by weight vectors in cone $C_{22}$. This is one of the simplest cases—since the higher-dimensional cones induce sparser initial forms, they are usually easier to analyze. For the cone $C_{22}$, we do not even need most of our equations; out of the five Cayley–Menger determinants $C_{i,j,k,l}$ and 20 asymmetric Albouy–Chenciner equations $f_{i,j}$ it is sufficient to use the six polynomials $C_{1,2,3,4}$, $C_{2,3,4,5}$, $C_{1,3,4,5}$, and $p_{2,4}$, $p_{2,5}$ and $p_{4,5}$. For any $w \in C_{22}$, the initial forms for those six polynomials are

$$\begin{aligned} in_w(C_{1,2,3,4})&= r_{1,2}^2 (r_{1,2}^2 - r_{1,4}^2)^2, \\ in_w(C_{2,3,4,5})&= r_{1,2}^2 (r_{1,2}^2 - r_{2,5}^2)^2, \\ in_w(C_{1,3,4,5})&= r_{1,2}^{6} - 3 r_{1,2}^{2} r_{1,4}^{2} r_{3,5}^{2} + r_{1,4}^{4} r_{3,5}^{2} + r_{1,4}^{2} r_{3,5}^{4},\\ in_w(p_{2,4})&= r_{1,2}^{2B+2} r_{1,3}^{A} r_{1,4}^{A} ( r_{1,2}^{2} m_{2} - m_4( r_{1,2}^{2}- r_{1,4}^{2}) +m_5(r_{2,5}^{2}- 2 r_{1,2}^{2})), \\ in_w(p_{2,5})&= r_{1,2}^{2A} r_{1,3}^B r_{1,3}^A (m_4 (r_{1,2}^{2} - r_{1,4}^{2}) + m_5(r_{3,5}^{2} - r_{1,2}^{2} )), \\ in_w(p_{4,5})&= r_{1,2}^{2B+2} r_{2,4}^A r_{2,5}^A (-2 r_{1,2}^{2} (m_{1} + m_{3}) +m_5(- r_{1,2}^{2}- r_{2,5}^{2} + r_{3,5}^{2} )). \end{aligned}$$

If we discard common monomial factors and eliminate the $r_{i,j}$ from the ideal generated by these six polynomials, we are left with the sum of the masses $m_1 + m_2 + m_3 + m_4 + m_5$. Fortunately, this example is typical of the systems from all of the cones, in that most or all of the dependence on the exponent B in the initial forms appears as a common factor.

It seems possible that this formulation of the equations with the $Q_{i,j}$ may be useful in studying central configurations in other contexts.

We can include the case of rational A in this result, since if $A = p/q$, then we can use the polynomial conditions $Q_{i,j}^q r_{i,j}^p - r_{i,j}^{2 q}=0$ to define the $Q_{i,j}$.

Altogether this gives a computer-assisted proof of the following result:

Theorem 1

For nonzero masses with nonzero subset sums (i.e., $m_i + m_j \ne 0$, $m_i + m_j + m_k \ne 0$, $m_i + m_j + m_k + m_l \ne 0$, $m_1 + m_2 + m_3 + m_4 + m_5 \ne 0$), there are finitely many planar equilateral five-body central configurations for any rational potential exponent $A \ge 2$.

This result strongly suggests the conjecture that there are finitely many planar equilateral five-body central configurations for any real $A \ge 2$, but the proof of that would require different methods.

4 The Symmetric Case

In this section, we impose the further restrictions of an axis of symmetry $r_{1,3} = r_{2,5}$, $r_{1,5} = r_{2,3}$, and $r_{1,4} = r_{2,4}$.

In addition to normalizing the size of the configuration with $r_{1,2} = 1$, we can choose Cartesian coordinates $q_1 = (-1/2, 0)$, $q_2 = (1/2,0)$, $q_3 = (x_3, y_3)$, $q_4 = (0, y_4)$, and $q_5 = (-x_3, y_3)$. The equilateral constraints in these coordinates become:

$$\begin{aligned}&4 x_3^2 - 4 x_3 + 4 y_3^2 - 3 = 0 \\&x_3^2 + y_3^2 - 2 y_3 y_4 + y_4^2 - 1 = 0 \end{aligned}$$

We can parameterize the configurations by $y_4$, in terms of which

$$\begin{aligned}&y_3 = \frac{8 \, y_{4}^{3} + 2 \, y_{4} \pm \sqrt{-16 \, y_{4}^{4} + 56 \, y_{4}^{2} + 15}}{4 \, {\left( 4 \, y_{4}^{2} + 1\right) }} \\&x_3 = \frac{4 \, y_{4}^{2} + 1 \pm 2 \, y_4 \sqrt{-16 \, y_{4}^{4} + 56 \, y_{4}^{2} + 15} }{4 \, {\left( 4 \, y_{4}^{2} + 1\right) }} \end{aligned}$$

Note that the choices of sign must be the same, giving us two curves of configurations. We will refer to the positive choice of sign as branch $\mathcal {A}$, and the other as branch $\mathcal {B}$.

The wedge products $\Delta _{i,j,k}$ in these coordinates are

$$\begin{aligned} \Delta _{1,2,3}&= y_3, \\ \Delta _{1,2,4}&= y_4, \\ \Delta _{1,3,4}&= x_3 y_4 + (y_4 - y_3)/2, \\ \Delta _{1,3,5}&= 2 y_3 x_3, \\ \Delta _{1,4,5}&= x_3 y_4 - (y_4 - y_3)/2, \\ \Delta _{3,4,5}&= 2 x_3 (y_4 - y_3). \end{aligned}$$

These configurations are shown in Fig. 2.

Fig. 2

Some examples of normalized symmetric equilateral pentagons. i Branch $\mathcal {A}$ is in blue, and ii branch $\mathcal {B}$ in red (Color figure online)

For the vortex case $A=2$, it is possible to compute a Groebner basis of the system used in the finiteness proof. This basis shows there are only two possible symmetric equilateral configurations: the regular pentagon with equal masses, and a configuration (using normalized masses $m_1 = m_2 = 1$) with $m_4$ satisfying

$$\begin{aligned} 64 m_4^9- & {} 752 m_4^8 + 2316 m_4^7 - 109 m_4^6 - 2830 m_4^5 + 45 m_4^4 + 1362 m_4^3 \\+ & {} 215 m_4^2 - 149 m_4 - 17 = 0 \end{aligned}$$

which has a single positive root at $m_4 \approx 0.34199$, and then there is a unique choice for $m_3=m_5 \approx 2.32$. This configuration is shown in Fig. 3.

We were also able to compute a Groebner basis for $A=4$, with the mass polynomial

$$\begin{aligned}&12288 m_4^{16} - 232064 m_4^{15} + 636883 m_4^{14} + 5616221 m_4^{13} + 2342977 m_4^{12} - 15626678 m_4^{11} \\&- 6546497 m_4^{10} + 17143788 m_4^9 - 1407668 m_4^8 - 5326884 m_4^7 + 456601 m_4^6 + 2374416 m_4^5 \\&- 239673 m_4^4 - 387130 m_4^3 - 33431 m_4^2 + 25519 m_4 + 957 = 0 \end{aligned}$$

The Laura–Andoyer equations for the symmetric case are

$$\begin{aligned}&L_{1,3} = m_3 (1 - R_{3,5}) \Delta _{1,3,5} + m_4 (R_{1,4} - 1) \Delta _{1,3,4} = 0 \\&L_{1,4} = m_1 (1 - R_{1,4}) \Delta _{1,2,4} + m_3 (R_{1,3} - 1) \Delta _{1,3,4}= 0 \\&L_{1,5} = m_1 (1 - R_{1,3}) \Delta _{1,2,3} + m_3 (R_{1,3} - R_{3,5}) \Delta _{1,3,5} + m_4 (R_{1,4} - 1)\Delta _{1,4,5} = 0 \\&L_{3,4} = m_1 \left[ (R_{1,3} - R_{1,4}) \Delta _{1,3,4} + (1 - R_{1,4}) \Delta _{2,3,4} \right] + m_3 (R_{3,5} - 1) \Delta _{3,4,5} = 0 \end{aligned}$$

We can highlight the linearity of these equations in the masses by forming the mass coefficient matrix:

$$\begin{aligned} \left( \begin{array}{ccc} 0 &{} ( 1- R_{3,5}) \Delta _{1,3,5} &{} (R_{1,4} - 1) \Delta _{1,3,4} \\ (1 - R_{1,4}) \Delta _{1,2,4} &{} (R_{1,3} - 1) \Delta _{1,3,4} &{} 0 \\ (1 - R_{1,3}) \Delta _{1,2,3} &{} (R_{1,3} - R_{3,5}) \Delta _{1,3,5} &{} (R_{1,4} - 1)\Delta _{1,4,5} \\ (R_{1,3} - R_{1,4}) \Delta _{1,3,4} + (1 - R_{1,4}) \Delta _{1,4,5} &{} (R_{3,5} - 1) \Delta _{3,4,5} &{} 0 \end{array}\right) \end{aligned}$$

We can row-reduce this a little to get

$$\begin{aligned} \left( \begin{array}{ccc} 0 &{} ( 1- R_{3,5} )\Delta _{1,3,5} &{} (R_{1,4} - 1) \Delta _{1,3,4} \\ (1 - R_{1,4}) \Delta _{1,2,4} &{} (R_{1,3} - 1) \Delta _{1,3,4} &{} 0 \\ (1 - R_{1,3}) \Delta _{1,2,3} &{} \left[ (R_{1,3} - R_{3,5}) - (1 - R_{3,5}) \frac{\Delta _{1,4,5}}{\Delta _{1,3,4}} \right] \Delta _{1,3,5}&{} 0 \\ (R_{1,3} - R_{1,4}) \Delta _{1,3,4} + (1 - R_{1,4}) \Delta _{1,4,5} &{} (R_{3,5} - 1) \Delta _{3,4,5} &{} 0 \end{array}\right) \nonumber \\ \end{aligned}$$

(6)

Fig. 3

Symmetric vortex ($A=2$) central configuration

This matrix must have a kernel vector of masses in the positive orthant. This imposes many constraints. To simplify the analysis of these constraints, we assume (without loss of generality) that $y_4 \ge 0$. This convention means that $\Delta _{1,2,4} \ge 0$. It is immediate from equation $L_{1,4}$ that $y_4$ cannot be zero, so we can assume that $\Delta _{1,2,4}$ is strictly positive.

In terms of the signs of the $\Delta _{i,j,k}$ and the magnitude of the mutual distances relative to $r_{1,2}$, there are five cases for the branch $\mathcal {A}$ configurations. Representatives of these are shown in Fig. 4.

Fig. 4

Sign type representatives of $\mathcal {A}$ branch configurations

All of the branch $\mathcal {A}$ configurations have $\Delta _{1,2,3} > 0$, $\Delta _{1,2,4} > 0$, $\Delta _{1,3,5} > 0$, $\Delta _{1,4,5} > 0$, and $r_{1,3}> \frac{\sqrt{6}}{2} > 1$. The distinguishing geometric properties of the branch $\mathcal {A}$ configurations are:

$\mathcal {A}1$):

Concave, $\Delta _{1,3,4} < 0$, $\Delta _{3,4,5} < 0$, $r_{1,4} < 1$, $r_{3,5} < 1$.

$\mathcal {A}2$):

Concave, $\Delta _{1,3,4} < 0$, $\Delta _{3,4,5} < 0$, $r_{1,4} < 1$, $r_{3,5} > 1$.

$\mathcal {A}3$):

Concave, $\Delta _{1,3,4} > 0$, $\Delta _{3,4,5} < 0$, $r_{1,4} < 1$, $r_{3,5} > 1$.

$\mathcal {A}4$):

Convex, $\Delta _{1,3,4} > 0$, $\Delta _{3,4,5} > 0$, $r_{1,4} > 1$, $r_{3,5} > 1$.

$\mathcal {A}5$):

Convex, $\Delta _{1,3,4} > 0$, $\Delta _{3,4,5} > 0$, $r_{1,4} > 1$, $r_{3,5} > 1$.

Theorem 2

The only possible branch $\mathcal {A}$ central configurations are of type $\mathcal {A}2$ or $\mathcal {A}4$. There is a unique type $\mathcal {A}2$ central configuration for all $A \ge 2$.

Proof

For type $\mathcal {A}1$ configurations, we can immediately verify that $L_{1,3} < 0$, so no such central configurations are possible. This is also true for configurations on the border between $\mathcal {A}1$ and $\mathcal {A}2$ with $r_{3,5} = 1$.

The type $\mathcal {A}2$ configurations contain an interesting central configuration.

For the mass coefficient matrix (6) to have nonzero mass solutions, the following minor must vanish:

$$\begin{aligned} F(y_4)&= \det \left( \begin{array}{cc} (1 - R_{1,4}) \Delta _{1,2,4} &{} (R_{1,3} - 1) \Delta _{1,3,4} \\ (R_{1,3} - R_{1,4}) \Delta _{1,3,4} + (1 - R_{1,4}) \Delta _{1,4,5} &{} (R_{3,5} - 1) \Delta _{3,4,5} \end{array}\right) \\&= (1 - R_{1,4})(R_{3,5} - 1) \Delta _{1,2,4} \Delta _{3,4,5} \\&\ \ + (1 - R_{1,3}) \Delta _{1,3,4} ((R_{1,3} - R_{1,4}) \Delta _{1,3,4} + (1 - R_{1,4}) \Delta _{1,4,5}) = 0 \end{aligned}$$

We can prove the existence of a type $\mathcal {A}2$ central configuration for any $A \ge 2$ by examining the sign of F at the regional endpoints. At the lower endpoint, where $y_4 = \frac{2 - \sqrt{3}}{2}$, the points 1,2,3, and 5 form a square, with $r_{3,5} = 1$, $r_{1,4} = \sqrt{ 2 - \sqrt{3}}$, $\Delta _{1,3,4} = \frac{1 - \sqrt{3}}{2} < 0$, and $\Delta _{1,4,5} = \frac{1}{2}$. Since $R_{3,5} = 1$, the first portion of F is zero, which makes it elementary to check the sign of the remaining terms and see that $F(\frac{2 - \sqrt{3}}{2}) > 0$.

At the other endpoint, $y_4 = \frac{\sqrt{5 - 2 \sqrt{5}}}{2}$, and the points 1,4, and 3 are collinear (as are points 2, 4, and 5) so $\Delta _{1,3,4} = 0$. Only the first portion of F is nonzero for this configuration, and it is straightforward to see that $F(\frac{\sqrt{5 - 2 \sqrt{5}}}{2}) < 0$.

We can prove the uniqueness of the type $\mathcal {A}2$ central configuration for each $A \ge 2$ using interval arithmetic, simply evaluating F and $\frac{d F}{d y_4}$ for intervals of $y_4$ and A. The lack of any common zeros shows that no bifurcations occur, and it suffices to check the uniqueness for $A=2$, for which we have a Groebner basis.

For type $\mathcal {A}3$ configurations, and the boundary case with $D_{1,3,4} = 0$, it is immediate that $L_{1,3} > 0$, so no such central configurations are possible.

Type $\mathcal {A}4$ configurations include the regular pentagon, which is a central configuration for equal masses for all potential exponents A. Remarkably, there is a bifurcation at $A_c \approx 3.12036856$. It appears that for $A \in [2, A_c]$, the regular pentagon is the only central configuration of type $\mathcal {A}4$, and for $A>A_c$, there are three type $\mathcal {A}4$ central configurations (including the regular pentagon). For large A, these two new central configurations converge to the $\mathcal {A}3$/$\mathcal {A}4$ boundary case for which $D_{3,4,5} = 0$, and the house-like configuration with $r_{3,5} = 1$ and $y_4 = 1 + \frac{\sqrt{3}}{2}$. With interval arithmetic, we can prove the uniqueness of the regular pentagon for $A \in [2,3]$, but we do not have an exact value for the bifurcation value $A_c$.

For type A5 configurations, once again $L_{1,3} < 0$, and no such central configurations are possible. $\square$

For the branch $\mathcal {B}$ configurations, there are three subcases of convex configurations and two concave, along with some exceptional cases on the borders between them. For all branch $\mathcal {B}$ configurations, $\Delta _{1,4,5} < 0$ and $r_{3,5} < 1$. The subcases are:

$\mathcal {B}1$):

Convex, $\Delta _{1,2,3} < 0$, $\Delta _{1,3,4} > 0$, $\Delta _{1,3,5} < 0$, $\Delta _{3,4,5} > 0$, $r_{1,3} > 1$, and $r_{1,4} < 1$.

$\mathcal {B}2$):

Convex, $\Delta _{1,2,3} < 0$, $\Delta _{1,3,4} > 0$, $\Delta _{1,3,5} > 0$, $\Delta _{3,4,5} < 0$, $r_{1,3} < 1$, and $r_{1,4} < 1$.

$\mathcal {B}3$):

Convex, $\Delta _{1,2,3} > 0$, $\Delta _{1,3,4} < 0$, $\Delta _{1,3,5} < 0$, $\Delta _{3,4,5} < 0$, $r_{1,3} < 1$, and $r_{1,4} > 1$.

$\mathcal {B}4$):

Concave, $\Delta _{1,2,3} > 0$, $\Delta _{1,3,4} \ge 0$, $\Delta _{1,3,5} < 0$, $\Delta _{3,4,5} < 0$, $r_{1,3} < 1$, and $r_{1,4} > 1$.

$\mathcal {B}5$):

Concave, $\Delta _{1,2,3} > 0$, $\Delta _{1,3,4} > 0$, $\Delta _{1,3,5} > 0$, $\Delta _{3,4,5} > 0$, $r_{1,3} > 1$, and $r_{1,4} > 1$ (Fig. 5).

Fig. 5

Sign-type representatives of $\mathcal {B}$ branch configurations

Theorem 3

The only possible branch $\mathcal {B}$ central configuration is the regular pentagon for all $A \ge 2$ (type $\mathcal {B}2$).

Proof

The case $\mathcal {B}1$ has no solutions with positive masses, as both terms in equation $L_{1,3}$ are positive.

The case $\mathcal {B}2$ contains the regular pentagon. Using interval arithmetic with the function $F(y_4)$ and its derivative, we can verify that there are no other type $\mathcal {B}2$ central configurations for all $A \ge 2$.

The case $\mathcal {B}3$ has no solutions with positive masses, as both terms in equation $L_{1,3}$ are positive.

The case $\mathcal {B}4$ has no solutions with positive masses, as both terms in equation $L_{1,4}$ are positive.

The case $\mathcal {B}5$ has no solutions with positive masses, as both terms in equation $L_{1,3}$ are negative. $\square$

5 General Planar Equilateral Pentagons

We know that two diagonals are always greater than the four exterior edges for planar convex four-body central configurations. For strictly convex planar five-body problem, Chen and Hsiao (2018) showed that at least two interior edges are less than the exterior edges if the five bodies form a central configuration. They also showed numerical examples of strictly convex central configurations with five bodies that have either one or two interior edges less than the exterior edges. However, for convex planar equilateral five-body central configurations, we have the following result:

Lemma 1

For planar convex equilateral five-body central configurations, all interior edges are greater than the exterior edges.

Proof

We consider the Laura–Andoyer equations involving only two of the masses (equations (4)). For the convex case, we know that $\Delta _{1,2,3}, \Delta _{1,2,4}, \Delta _{1,2,5}, \Delta _{1,3,4}, \Delta _{1,3,5}, \Delta _{1,4,5}, \Delta _{2,3,4}, \Delta _{2,3,5}$ and $\Delta _{3,4,5}$ are all positive.

There is at least one interior edge greater than the exterior edges for any planar equilateral five-body configuration. Without loss of generality, let $r_{1,4} > r_{1,2}$, and then $R_{1,4} < R_{1,2}$ and $R_{1,4} - R_{1,2} < 0$ . From the first equation of (4), we must have $R_{1,2} - R_{3,5} >0$. So $R_{1,2} > R_{3,5}$ and $r_{3,5} > r_{1,2}$. Similarly, from the third equation, we have $r_{2,4} > r_{1,2}$; from the second equation above, we get $r_{1,3} > r_{1,2}$; from the fifth equation, we obtain $r_{2,5} > r_{1,2}$. Thus, we have

$$\begin{aligned} r_{1,3}, r_{1,4}, r_{2,4}, r_{2,5}, r_{3,5} > r_{1,2}. \end{aligned}$$

$\square$

The five simpler Laura–Andoyer equations (4) can be used to further restrict the possible configurations of planar equilateral five-body central configurations.

The allowed regions fall into three classes:

• Region I: defined by $r_{1,2} < r_{i,j}$ and containing the regular pentagon (in 12345 order)

• Region II: defined by $r_{1,2} > r_{i,j}$ and containing the regular pentagon (in 13524 order)

• Region III: five disjoint regions, which are equivalent under permutations. These are concave configurations. For instance, the region with mass 5 in the interior is defined by $\theta _{1,2,3} + \theta _{2,3,4} \le 3 \pi$, $\theta _{1,2,3} \le 5 \pi /3$, $\theta _{2,3,4} \le 5 \pi /3$, $\Delta _{1,3,5} \ge 0$, and $\Delta _{2,4,5} \ge 0$. We label these with a subscript indicating which of the five points is inside the convex hull of the other four, i.e., $\text {III}_{1}, \ldots , \text {III}_{5}$.

These regions are shown in Fig. 6.

Fig. 6

Regions of allowable angles $\theta _{1,2}$ and $\theta _{2,3}$ for positive mass equilateral central configurations (white). The more heavily shaded central oval consists of angles that are not geometrically realizable. The regular pentagon configurations are indicated as icons in green (in Region II) and red (in Region I) (Color figure online)

From our analysis and the closely related theorems in Alvarez-Ramírez et al. (2022), the only positive mass symmetric planar equilateral cyclic five-body central configurations in the Newtonian case are the regular pentagon and star with equal masses and the symmetric configurations discussed above. The proof in Alvarez-Ramírez et al. (2022) does not seem to cover the case of the regular star (in our $\mathcal {B}2$-type configurations), whose uniqueness within the $\mathcal {B}2$-type configurations we validated using interval arithmetic.

If the symmetry condition is removed, it seems from numerical investigations that there are no other equilateral cyclic central configurations, leading us to conjecture:

Conjecture 1

The only positive mass planar equilateral cyclic five-body central configurations in the Newtonian case are the regular pentagon and star with equal masses and the concave symmetric configuration discussed above.