Nonintegrability of Nearly Integrable Dynamical Systems Near Resonant Periodic Orbits

Abstract

In a recent paper by the author (K. Yagasaki, Nonintegrability of the restricted three-body problem, submitted for publication), a technique was developed for determining whether nearly integrable systems are not meromorphically Bogoyavlenskij-integrable such that the first integrals and commutative vector fields also depend meromorphically on the small parameter. Here we continue to demonstrate the technique for some classes of dynamical systems. In particular, we consider time-periodic perturbations of single-degree-of-freedom Hamiltonian systems and discuss a relationship of the technique with the subharmonic Melnikov method, which enables us to detect the existence of periodic orbits and their stability. We illustrate the theory for the periodically forced Duffing oscillator and two more additional examples: second-order coupled oscillators and a two-dimensional system of pendulum-type subjected to a constant torque.

1 Introduction

In this paper, we consider systems of the form

$$\begin{aligned} {\dot{I}}=\varepsilon h(I,\theta ;\varepsilon ),\quad {\dot{\theta }}=\omega (I)+\varepsilon g(I,\theta ;\varepsilon ),\quad (I,\theta )\in {\mathbb {R}}^\ell \times {\mathbb {T}}^m, \end{aligned}$$

(1.1)

and study its nonintegrability near resonant periodic orbits, where $\ell ,m\in {\mathbb {N}}$, ${\mathbb {T}}^m=({\mathbb {R}}/2\pi {\mathbb {Z}})^m$, $\varepsilon$ is a small parameter such that $0<|\varepsilon |\ll 1$, and $\omega :{\mathbb {R}}^\ell \rightarrow {\mathbb {R}}^m$, $h:{\mathbb {R}}^\ell \times {\mathbb {T}}^m\times {\mathbb {R}}\rightarrow {\mathbb {R}}^\ell$ and $g:{\mathbb {R}}^\ell \times {\mathbb {T}}^m\times {\mathbb {R}}\rightarrow {\mathbb {R}}^m$ are meromorphic or analytic in the arguments. We extend the domain of the independent variable t to a domain including ${\mathbb {R}}$ in ${\mathbb {C}}$ and do so for the dependent variables. We mean a non-empty connected open set by “a domain” through this paper. The system (1.1) is Hamiltonian if $\ell =m$ as well as $\varepsilon =0$ or

$$\begin{aligned} \mathrm {D}_I h(I,\theta ;\varepsilon )\equiv -\mathrm {D}_\theta g(I,\theta ;\varepsilon ), \end{aligned}$$

and non-Hamiltonian if not. When $\varepsilon =0$, Eq. (1.1) becomes

$$\begin{aligned} {\dot{I}}=0,\quad {\dot{\theta }}=\omega (I), \end{aligned}$$

(1.2)

which we refer to as the unperturbed system for (1.1). Here we adopt the following definition of integrability due to Bogoyavlenskij (1998).

Definition 1.1

(Bogoyavlenskij) For $n\in {\mathbb {N}}$ an n-dimensional dynamical system

$$\begin{aligned} {\dot{x}}=f(x),\quad x\in {\mathbb {R}}^n\text { or }{\mathbb {C}}^n, \end{aligned}$$

is called $(q,n-q)$-integrable or simply integrable if there exist q vector fields $f_1(x)(:= f(x)),f_2(x),\dots ,f_q(x)$ and $n-q$ scalar-valued functions $F_1(x),\dots ,F_{n-q}(x)$ such that the following two conditions hold:

• (i) $f_1(x),\dots ,f_q(x)$ are linearly independent almost everywhere and commute with each other, i.e., $[f_j,f_k](x):=\mathrm {D}f_k(x)f_j(x)-\mathrm {D}f_j(x)f_k(x)\equiv 0$ for $j,k=1,\ldots ,q$, where $[\cdot ,\cdot ]$ denotes the Lie bracket; 

• (ii) The derivatives $\mathrm {D}F_1(x),\dots , \mathrm {D}F_{n-q}(x)$ are linearly independent almost everywhere and $F_1(x),\dots ,F_{n-q}(x)$ are first integrals of $f_1, \dots ,f_q$, i.e., $\mathrm {D}F_k(x)\cdot f_j(x)\equiv 0$ for $j=1,\ldots ,q$ and $k=1,\ldots ,n-q$, where “$\cdot$” represents the inner product.

We say that the system is meromorphically (resp. analytically) integrable if the first integrals and commutative vector fields are meromorphic (resp. analytic).

Definition 1.1 is considered as a generalization of Liouville-integrability for Hamiltonian systems (Arnold 1989; Morales-Ruiz 1999) since an n-degree-of-freedom Liouville-integrable Hamiltonian system with $n\ge 1$ has not only n functionally independent first integrals but also n linearly independent commutative (Hamiltonian) vector fields generated by the first integrals. The unperturbed system (1.2) is meromorphically or analytically $(m,\ell )$-integrable in the Bogoyavlenskij sense: $F_j(I,\theta )=I_j$, $j=1,\ldots ,\ell$, are first integrals, and $f_j(I,\theta )=(0,e_j)\in {\mathbb {R}}^\ell \times {\mathbb {R}}^m$, $j\ne j_0$, give m commutative vector fields along with its own vector field if $\omega _{j_0}(I)\ne 0$ almost everywhere, where for $j=1,\ldots ,m$, $\omega _j(I)$ is the jth element of $\omega (I)$ and $e_j$ is the m-dimensional vector of which the jth element is the unit and the other elements are zero. Conversely, a general $(m,\ell )$-integrable system is transformed to the form (1.2) if the level set for the first integrals $F_1(x),\ldots ,F_m(x)$ has a connected compact component. See Bogoyavlenskij (1998); Motonaga and Yagasaki (2021b); Zung (2018) for more details. Thus, the system (1.1) can be regarded as a normal form for perturbations of general $(m,\ell )$-integrable systems.

In a recent paper (Yagasaki 2021a), a technique was developed for determining whether the system (1.1) is not meromorphically Bogoyavlenskij-integrable such that the first integrals and commutative vector fields also depend meromorphically on the small parameter $\varepsilon$ near $\varepsilon =0$. Moreover, the technique was applied to prove that the restricted three-body problem is not meromorphically integrable in both the planar and spatial cases even if the first integrals are not required to depend meromorphically on the parameter, the mass ratio of the primaries. The basic idea used there was similar to that of Morales-Ruiz (2002), who studied time-periodic Hamiltonian perturbations of single-degree-of-freedom Hamiltonian systems and showed a relationship of their nonintegrability with a version due to Ziglin (1982) of the Melnikov method (Melnikov 1963). The version of the Melnikov method enables us to detect transversal self-intersection of complex separatrices of periodic orbits unlike the standard version (Guckenheimer and Holmes 1983; Melnikov 1963; Wiggins 1990). More concretely, under some restrictive conditions, he essentially proved that they are meromorphically nonintegrable when the small parameter is taken as one of the state variables if the Melnikov functions are not identically zero, based on a generalized version due to Ayoul and Zung (2010) of the Morales-Ramis theory (Morales-Ruiz 1999; Morales-Ruiz and Ramis 2001). Their generalized versions for the Morales-Ramis theory and its extension, the Morales-Ramis-Simó theory (Morales-Ruiz et al. 2007), were also used in Yagasaki (2021a). The developed technique was also applied to give a new proof of the result of Poincaré (1992) on the restricted three-body problem in Yagasaki (2021b).

In this paper, we continue to demonstrate the technique of Yagasaki (2021a) for some classes of dynamical systems. In particular, we consider time-periodic perturbations of single-degree-of-freedom Hamiltonian systems and discuss a relationship of the technique with the subharmonic Melnikov method (Guckenheimer and Holmes 1983; Wiggins 1990; Yagasaki 1996), which enables us to detect the existence of periodic orbits and their stability and bifurcations, like Morales-Ruiz (2002) for homoclinic orbits. So we show that they are nonintegrable in the meaning stated above if certain complex integrals similar to the subharmonic Melnikov functions are not zero. See Theorem 3.1 for the precise statement. The similarity of this result to that of Morales-Ruiz (2002) is very remarkable.

We also illustrate the theory for the periodically forced Duffing oscillator

$$\begin{aligned} \ddot{w}+\varepsilon \delta {\dot{w}}+aw+w^3=\varepsilon \beta \cos \nu t,\quad w\in {\mathbb {R}}, \end{aligned}$$

or as a first-order system

$$\begin{aligned} {\dot{x}}_1=x_2,\quad {\dot{x}}_2=-ax_1-x_1^3+\varepsilon (\beta \cos \nu t-\delta x_2),\quad x_1,x_2\in {\mathbb {R}}, \end{aligned}$$

(1.3)

where $a=\pm 1$ or 0, and $\beta ,\nu >0$ and $\delta \ge 0$ are constants. It is well known that Duffing (1918) studied this type of system early in the twentieth century, but it is interesting that Poincaré (1992) also discussed the existence of periodic solutions for $\delta =0$ about the end of the nineteenth century in his memoir. See also Sect. 5.6 of Barrow-Green (1996). Holmes (1979) used the homoclinic Melnikov method (Guckenheimer and Holmes 1983; Melnikov 1963; Wiggins 1990) to prove the occurrence of transverse intersection between the stable and unstable manifolds of a periodic orbit near $(x_1,x_2)=(0,0)$ for $a=-1$ with $\varepsilon >0$ sufficiently small. The occurrence of such transverse intersection implies, e.g., by Theorem 3.10 of Moser (1973), the nonexistence of real-analytic first integrals near the unperturbed homoclinic orbit. Motonaga and Yagasaki (2021b) recently showed the real-analytic nonintegrability of (1.3) with $a=-1$ near the unperturbed homoclinic orbits in the meaning stated above even when such transverse intersection does not occur (see Remark 4.6(ii) for more details). Ueda (1978) also found chaotic motions in both analog and numerical simulations when $a=0$, but $\varepsilon$ is not small. Moreover, the rational nonintegrability of the parametric excitation case, e.g.,

$$\begin{aligned} {\dot{x}}_1=x_2,\quad {\dot{x}}_2=ax_1-x_1^3-\delta x_2+\beta x_1\cos \nu t, \end{aligned}$$

was proved in Motonaga and Yagasaki (2018) when $\mathrm {e}^{i\nu t}=\cos \nu t+i\sin \nu t$ is taken as a state variable. So the Duffing oscillator (1.3) has been believed to be nonintegrable besides near the unperturbed homoclinic orbits for $a=-1$, but its proof has not been given. We show that the system (1.3) is meromorphically nonintegrable near the resonant periodic orbits in the meaning stated above when $a=\pm 1$ and 0.

Moreover, we give two more concrete examples. The first one is second-order coupled oscillators of which the special case is often referred to as the second-order Kuramoto model (Rodrigues et al. 2016). The second one is a two-dimensional system of pendulum-type subjected to a constant torque. We show that it is not integrable as a system on ${\mathbb {C}}\times ({\mathbb {C}}/2\pi {\mathbb {Z}})$ although it has a first integral as a system on ${\mathbb {R}}^2$ or ${\mathbb {C}}^2$.

This paper is organized as follows: In Sect. 2, we review the technique of Yagasaki (2021a) in a necessary context. In Sect. 3, we apply the technique to time-periodic perturbations of single-degree-of-freedom Hamiltonian systems and discuss a relationship of the result with the subharmonic Melnikov method. We illustrate the theory for the periodically forced Duffing oscillator (1.3) in Sect. 4. Finally, we provide the additional two examples in Sect. 5.

2 General Technique

In this section, we review the technique of Yagasaki (2021a) for the nonintegrability of (1.1). We make the following assumption on the unperturbed system (1.2):

(A1):

For some $I^*\in {\mathbb {R}}^\ell$, a resonance of multiplicity $m-1$,

$$\begin{aligned} \dim _{\mathbb {Q}}\langle \omega _1(I^*),\ldots ,\omega _m(I^*)\rangle =1, \end{aligned}$$

occurs with $\omega (I^*)\ne 0$, i.e., there exists a constant $\omega ^*>0$ such that

$$\begin{aligned} \frac{\omega (I^*)}{\omega ^*}\in {\mathbb {Z}}^m\setminus \{0\}. \end{aligned}$$

Note that we can replace $\omega ^*$ with $\omega ^*/k$ for any $k\in {\mathbb {N}}$ in (A1). We refer to the m-dimensional torus ${\mathscr {T}}^*=\{(I^*,\theta )\mid \theta \in {\mathbb {T}}^m\}$ as the resonant torus and to periodic orbits $(I,\theta )=(I^*,\omega (I^*)t+\theta _0)$, $\theta _0\in {\mathbb {T}}^m$, on ${\mathscr {T}}^*$ as the resonant periodic orbits. Let $T^*=2\pi /\omega ^*$. We also make the following assumption.

Fig. 1

Assumption (A2)

• (A2) For some $\theta \in {\mathbb {T}}^m$, there exists a closed loop $\gamma _\theta$ in a domain including $(0,T^*)\subset {\mathbb {R}}$ in ${\mathbb {C}}$ such that $\gamma _\theta \cap (i{\mathbb {R}}\cup (T^*+i{\mathbb {R}}))=\emptyset$ and

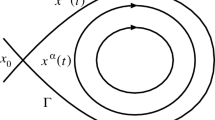
  $$\begin{aligned} {\mathscr {I}}(\theta ) :=\mathrm {D}\omega (I^*)\int _{\gamma _\theta }h(I^*,\omega (I^*)\tau +\theta ;0)\mathrm {d}\tau \end{aligned}$$

  (2.1)

  is not zero. See Fig. 1

Note that the condition $\gamma _\theta \cap (i{\mathbb {R}}\cup (T^*+i{\mathbb {R}}))=\emptyset$ is not essential in (A2), since it always holds by replacing $\omega ^*$ with $\omega ^*/k$ for sufficiently large $k\in {\mathbb {N}}$ and shifting the time variable by a positive constant if necessary. We can prove the following theorem which guarantees that conditions (A1) and (A2) are sufficient for nonintegrability of (1.1) in the meaning stated in Sect. 1.

Theorem 2.1

Let $\Gamma$ be any domain in ${\mathbb {C}}/T^*{\mathbb {Z}}$ containing ${\mathbb {R}}/T^*{\mathbb {Z}}$ and $\gamma _\theta$. Suppose that assumptions (A1) and (A2) hold for some $\theta _0\in {\mathbb {T}}^m$. Then the system (1.1) is not meromorphically integrable in the Bogoyavlenskij sense near the resonant periodic orbit $(I,\theta )=(I^*,\omega (I^*)\tau +\theta _0)$ with $\tau \in \Gamma$ such that the first integrals and commutative vector fields also depend meromorphically on $\varepsilon$ near $\varepsilon =0$. Moreover, if (A2) holds for $\theta \in \Delta$, where $\Delta$ is a dense set in ${\mathbb {T}}^m$, then the conclusion holds for any resonant periodic orbit on the resonant torus ${\mathscr {T}}^*$.

Note that the first integrals and commutative vector fields are assumed to depend meromorphically not only on $\varepsilon$ but also on the state variables $(I,\theta )$ in the conclusion of Theorem 2.1. See Sect. 2 of Yagasaki (2021a) for a proof of Theorem 2.1. A more general result was obtained there.

Systems of the form (1.1) have attracted much attention, especially when they are Hamiltonian. See (Arnold 1989; Arnold et al. 2006; Kozlov 1996) and references therein for more details. In particular, Kozlov (1996) extended the famous result of Poincaré (1890, 1992) for Hamiltonian systems to the general case of (1.1) and gave sufficient conditions for nonexistence of additional real-analytic first integrals depending analytically on $\varepsilon$ near $\varepsilon =0$. See also Arnold et al. (2006); Kozlov (1983) for his result in Hamiltonian systems. Moreover, Motonaga and Yagasaki (2021b) gave sufficient conditions for the system (1.1) to be real-analytically nonintegrable in the Bogoyavlenskij sense such that the first integrals and commutative vector fields also depend real-analytically on $\varepsilon$ near $\varepsilon =0$. Some details on these results are provided in our context and compared with Theorem 2.1 in Appendix A. We remark that the results of Kozlov (1996), Motonaga and Yagasaki (2021b), Poincaré (1890, 1992) say nothing about the integrability of (1.1) under the hypotheses of Theorem 2.1.

3 Time-Periodic Perturbations of Single-Degree-of-Freedom Hamiltonian Systems

We next apply the technique of Sect. 2 to time-periodic perturbations of single-degree-of-freedom Hamiltonian systems, and discuss a relationship of our result with the subharmonic Melnikov method (Guckenheimer and Holmes 1983; Wiggins 1990; Yagasaki 1996), as in the related work (Motonaga and Yagasaki 2021a, b).

Consider two-dimensional systems of the form

$$\begin{aligned} {\dot{x}}=J\mathrm {D}H(x)+\varepsilon u(x,\nu t),\quad x\in {\mathbb {R}}^2, \end{aligned}$$

(3.1)

where $\nu >0$ is a constant, $H:{\mathbb {R}}^2\rightarrow {\mathbb {R}}$ and $u:{\mathbb {R}}^2\times {\mathbb {S}}^1$ are analytic, and J is the $2\times 2$ symplectic matrix,

$$\begin{aligned} J=\begin{pmatrix} 0 &{} 1\\ -1 &{} 0 \end{pmatrix}. \end{aligned}$$

When $\varepsilon =0$, Eq. (3.1) becomes a planar Hamiltonian system

$$\begin{aligned} {\dot{x}}=J\mathrm {D}_x H(x) \end{aligned}$$

(3.2)

with a Hamiltonian function H(x). Letting $\psi =\nu t\mod 2\pi$, we rewrite (3.1) as an autonomous system

$$\begin{aligned} {\dot{x}}=J\mathrm {D}H(x)+\varepsilon u(x,\psi ),\quad {\dot{\psi }}=\nu , \end{aligned}$$

(3.3)

and discuss its meromorphic Bogoyavlenskij-nonintegrability under condition that the first integrals and commutative vector fields also depend meromorphically on $\varepsilon$ near $\varepsilon =0$, as in Theorem 2.1.

We make the following assumptions on the unperturbed system (3.2):

(M1):

There exists a one-parameter family of periodic orbits $x^\alpha (t)$, $\alpha \in (\alpha _1,\alpha _2)$, with period $T^\alpha >0$ for some $\alpha _1<\alpha _2$ (see Fig. 2);

(M2):

$x^\alpha (t)$ is analytic with respect to $\alpha \in (\alpha _1,\alpha _2)$.

Note that in assumption (M1) $x^\alpha (t)$ is automatically analytic with respect to t since the vector field of (3.2) is analytic. Following an approach of Yagasaki (1996), we can transform (3.1) into the form (1.1) as follows.

We first assume that $\mathrm {d}T^\alpha /\mathrm {d}\alpha \ne 0$ and define the scalar action variable I for each periodic orbit $x^\alpha (t)=(x_1^\alpha (t),x_2^\alpha (t))$ as

$$\begin{aligned} I=\frac{1}{2\pi }\int _{x^\alpha }x_2\mathrm {d}x_1 =\frac{1}{2\pi }\int _0^{T^\alpha }x_2^\alpha (t){\dot{x}}_1^\alpha (t)\mathrm {d}t \end{aligned}$$

(3.4)

in the standard manner (see, e.g., Chapter 10 of Arnold (1989)). The action variable I can thus be determined only by $\alpha$. We assume that $\mathrm {d}\alpha /\mathrm {d}I>0$ without loss of generality, and apply the implicit function theorem to (3.4) to represent $\alpha$ as a function of I: $\alpha =\alpha (I)$. We can show that the symplectic transformation from $(I,\theta _1)$ to x is given by

$$\begin{aligned} x=x^{\alpha (I)}\left( \frac{\theta _1}{\Omega (I)}\right) , \end{aligned}$$

(3.5)

where

Fig. 2

Assumption (M1)

$$\begin{aligned} \Omega (I)=\frac{2\pi }{T^{\alpha (I)}}. \end{aligned}$$

We see that $\mathrm {d}\Omega /\mathrm {d}I\ne 0$ at $I=I^\alpha$ since $\mathrm {d}T^\alpha /\mathrm {d}\alpha \ne 0$. Moreover, we have the relations

$$\begin{aligned} \mathrm {D}_xI=-J\frac{\partial x}{\partial \theta _1},\quad \mathrm {D}_x\theta _1=J\frac{\partial x}{\partial I}. \end{aligned}$$

(3.6)

Let $\theta _2=\nu t\mod 2\pi$ in (3.1). Using (3.5) and (3.6), we transform (3.1) into

$$\begin{aligned} {\dot{I}}=\varepsilon h(I,\theta _1,\theta _2),\quad {\dot{\theta }}_1=\Omega (I)+\varepsilon g_1(I,\theta _1,\theta _2),\quad {\dot{\theta }}_2=\nu , \end{aligned}$$

(3.7)

where

$$\begin{aligned}&h(I,\theta _1,\theta _2) =\frac{1}{\Omega (I)}\mathrm {D}H\left( x^{\alpha (I)}\left( \frac{\theta _1}{\Omega (I)}\right) \right) \cdot u\left( x^{\alpha (I)}\left( \frac{\theta _1}{\Omega (I)}\right) ,\theta _2\right) ,\\&g_1(I,\theta _1,\theta _2) =J\frac{\partial }{\partial I}x^{\alpha (I)}\left( \frac{\theta _1}{\Omega (I)}\right) \cdot u\left( x^{\alpha (I)}\left( \frac{\theta _1}{\Omega (I)}\right) ,\theta _2\right) . \end{aligned}$$

See Sect. 2 of Yagasaki (1996) for the details on these computations. The system (3.7) has the form (1.1) with $\ell =1$, $m=2$ and $\omega (I)=(\Omega (I),\nu )^\mathrm {T}$, where the superscript “$\mathrm {T}$” represents the transpose operator.

We assume that at $\alpha =\alpha ^{l/n}$

$$\begin{aligned} \frac{2\pi }{T^\alpha }=\frac{n}{l}\nu , \end{aligned}$$

where l and n are relatively prime integers, so that assumption (A1) holds with $\omega ^*=2\pi /nT^\alpha =\nu /l$. We define the subharmonic Melnikov function as

$$\begin{aligned} M^{l/n}(\phi )=\int _0^{2\pi l/\nu }\mathrm {D}H(x^{\alpha }(t))\cdot u(x^\alpha (t),\nu t+\phi )\mathrm {d}t, \end{aligned}$$

(3.8)

where $\alpha =\alpha ^{l/n}$. If $M^{l/n}(\phi )$ has a simple zero at $\phi =\phi _0$ and $\mathrm {d}T^\alpha /\mathrm {d}\alpha \ne 0$, i.e., $\mathrm {d}\Omega (I^\alpha )/\mathrm {d}I\ne 0$, then there exists a periodic orbit near $(x,\phi )=(x^\alpha (t),\nu t+\phi _0)$ in (3.1). See Theorem 3.1 of Yagasaki (1996). A similar result is also found in Guckenheimer and Holmes (1983); Wiggins (1990). The stability of the periodic orbit can also be determined easily (Yagasaki 1996). Moreover, several bifurcations of periodic orbits when $\mathrm {d}\Omega (I^\alpha )/\mathrm {d}I\ne 0$ or not were discussed in Yagasaki (1996, 2002, 2003).

Noting that $\Omega (I^\alpha )=n\nu /l$ at $\alpha =\alpha ^{l/n}$ and applying Theorem 2.1 to (3.7), we obtain the following.

Theorem 3.1

Suppose that at $\alpha =\alpha ^{l/n}$, $\mathrm {d}T^\alpha /\mathrm {d}\alpha \ne 0$ and there exists a closed loop $\gamma _\phi$ in a domain including $(0,2\pi l/\nu )$ in ${\mathbb {C}}$ such that $\gamma _\phi \cap (i{\mathbb {R}}\cup (2\pi l/\nu +i{\mathbb {R}}))=\emptyset$ and

$$\begin{aligned} {\hat{{\mathscr {I}}}}(\phi ) =\int _{\gamma _\phi }\mathrm {D}H(x^\alpha (\tau )) \cdot u\left( x^\alpha (\tau ),\nu \tau +\phi \right) \mathrm {d}\tau \end{aligned}$$

(3.9)

is not zero for some $\phi =\phi _0\in {\mathbb {S}}^1$. Then the system (3.7), equivalently (3.3), is not meromorphically integrable in the meaning of Theorem 2.1 near the resonant periodic orbit $(x,\phi )=(x^\alpha (t),\nu t+\phi _0)$ with $\alpha =\alpha ^{l/n}$ on any domain ${\hat{\Gamma }}$ in ${\mathbb {C}}/(2\pi l/\nu ){\mathbb {Z}}$ containing ${\mathbb {R}}/(2\pi l/\nu ){\mathbb {Z}}$ and $\gamma _\phi$. Moreover, if the integral ${\hat{{\mathscr {I}}}}(\phi )$ is not zero for any $\phi \in {\hat{\Delta }}$, where ${\hat{\Delta }}$ is a dense set of ${\mathbb {S}}^1$, then the conclusion holds for any periodic orbit on the resonant torus ${\mathscr {T}}^*=\{(x^\alpha (\tau ),\nu \tau +\phi )\mid \tau \in {\hat{\Gamma }},\phi \in {\mathbb {S}}^1,\alpha =\alpha ^{l/n}\}$.

Remark 3.2

• (i) We see that when the closed loop $\gamma _\phi$ can be taken independently of $\phi$, the integral ${\hat{{\mathscr {I}}}}(\phi )$ is an analytic function of $\phi$, so that by the identity theorem (e.g., Theorem 3.2.6 of Ablowitz and Fokas (2003)) it is not zero on a dense set of ${\mathbb {S}}^1$ if it is not identically zero.

• (ii) Let U be a neighborhood of $\alpha =\alpha _0\in (\alpha _1,\alpha _2)$. From Theorem A.2, we obtain the following for (3.1) (see Theorem 5.2 of Motonaga and Yagasaki (2021b)): If there exists a key set $D\subset D_\mathrm {R}:=\{\alpha ^{l/n}\in U\mid l,n\in {\mathbb {N}}\text { are relatively prime}\}$ for $C^\omega (U)$ such that $M^{l/n}(\phi )$ is not constant for $\alpha ^{l/n}\in D$, then for $|\varepsilon |\ne 0$ sufficiently small the system (3.1) is not real-analytically integrable in the meaning of Theorem A.2 near $\{x^\alpha (t)\mid t\in [0,T^\alpha )\}\times {\mathbb {S}}^1$ with $\alpha =\alpha _0$. See Appendix A for the definition of a key set. Note that $D_\mathrm {R}$ is a key set for $C^\omega (U)$.

Note that the integrand in (3.9) is the same as in the Melnikov function (3.8) although the path of integration is different. An integral similar to (3.9) for not periodic but homoclinic orbits was used in Morales-Ruiz (2002); Ziglin (1982).

4 Periodically Forced Duffing oscillator

We now consider the periodically forced Duffing oscillator (1.3) and apply Theorem 3.1. When $\varepsilon =0$, Eq. (1.3) becomes a single-degree-of-freedom Hamiltonian system with the Hamiltonian

$$\begin{aligned} H=\frac{1}{2}ax_1^2+\frac{1}{4}x_1^4+\frac{1}{2}x_2^2, \end{aligned}$$

and it is a special case of (3.2). Letting $\psi =\nu t\mod 2\pi$, we also rewrite (1.3) as an autonomous system

$$\begin{aligned} {\dot{x}}_1=x_2,\quad {\dot{x}}_2=-ax_1-x_1^3+\varepsilon (\beta \cos \nu t-\delta x_2),\quad {\dot{\psi }}=\nu , \end{aligned}$$

(4.1)

as in (3.3).

4.1 Case of $a=1$

We begin with the case of $a=1$. The phase portraits of (1.3) with $\varepsilon =0$ are shown in Fig. 3. In particular, there exists a one-parameter family of periodic orbits

$$\begin{aligned} x^k(t) =&\biggl (\frac{\sqrt{2}k}{\sqrt{1-2k^2}}{{\,\mathrm{cn}\,}}\left( \frac{t}{\sqrt{1-2k^2}}\right) ,\\&\quad -\frac{\sqrt{2}k}{1-2k^2}{{\,\mathrm{sn}\,}}\left( \frac{t}{\sqrt{1-2k^2}}\right) {{\,\mathrm{dn}\,}}\left( \frac{t}{\sqrt{1-2k^2}}\right) \biggr ),\quad k\in \bigl (0,1/\sqrt{2}\bigr ), \end{aligned}$$

Fig. 3

Phase portraits of (1.3) with $\varepsilon =0$ and $a=1$

and their period is given by $T^k=4K(k)\sqrt{1-2k^2}$ (see Yagasaki (1994, 1996)), where sn, cn and dn represent the Jacobi elliptic functions, k is the elliptic modulus and K(k) is the complete elliptic integral of the first kind. See, e.g., Byrd and Friedman (1954); Whittaker and Watson (1927) for general information on elliptic functions. We see that $\mathrm {d}T^k/\mathrm {d}k>0$ for $k\in (0,1/\sqrt{2})$. Assume that the resonance condition

$$\begin{aligned} nT^k=\frac{2\pi l}{\nu },\quad \text{ i.e., }\quad \nu =\frac{\pi l}{2nK(k)\sqrt{1-2k^2}}, \end{aligned}$$

(4.2)

holds at $k=k^{l/n}$ for $l,n>0$ relatively prime integers. We compute the subharmonic Melnikov function (3.8) for $x^k(t)$ as

$$\begin{aligned} M^{l/n}(\phi )=&\int _0^{2\pi l/\nu }x_2^k(t)(-\delta x_2^k(t)+\beta \cos (\nu t+\phi ))\mathrm {d}t\nonumber \\ =&-\delta J_1(k,n)+\beta J_2(k,l,n)\sin \phi , \end{aligned}$$

where

$$\begin{aligned}&J_1(k,n)=\frac{8n[(2k^2-1)E(k)+k'^2K(k)]}{3(1-2k^2)^{3/2}},\\&J_2(k,l,n)= {\left\{ \begin{array}{ll} \displaystyle 2\sqrt{2}\pi \nu {{\,\mathrm{sech}\,}}\left( \frac{\pi lK(k')}{2K(k)}\right) &{} \text{(for } n=1 \text{ and } l \text{ odd) };\\ 0\quad &{} \text{(for } n\ne 1 \text{ or } l \text{ even) }. \end{array}\right. } \end{aligned}$$

Here E(k) is the complete elliptic integral of the second kind and $k'=\sqrt{1-k^2}$ is the complementary elliptic modulus. See also Yagasaki (1994, 1996) for the computations of the Melnikov function.

On the other hand, we write the integral (3.9) as

$$\begin{aligned} {\hat{{\mathscr {I}}}}(\phi )=&-\frac{2k^2 \delta }{(1-2k^2)^2}\int _{\gamma _\phi } {{\,\mathrm{sn}\,}}^2\left( \frac{\tau }{\sqrt{1-2k^2}}\right) {{\,\mathrm{dn}\,}}^2\left( \frac{\tau }{\sqrt{1-2k^2}}\right) \mathrm {d}\tau \nonumber \\&-\frac{\sqrt{2}k\beta }{1-2k^2}\int _{\gamma _\phi } {{\,\mathrm{sn}\,}}\left( \frac{\tau }{\sqrt{1-2k^2}}\right) {{\,\mathrm{dn}\,}}\left( \frac{\tau }{\sqrt{1-2k^2}}\right) \cos (\nu \tau +\phi )\mathrm {d}\tau . \end{aligned}$$

(4.3)

Letting $\gamma _\phi$ be a circle centered at $\tau =i\sqrt{1-2k^2}K(k')$ with a sufficiently small radius, we compute

$$\begin{aligned} {\hat{{\mathscr {I}}}}(\phi ) =-2\sqrt{2}\pi \nu \beta \biggl (\cosh \biggl (\frac{\pi l K(k')}{2nK(k)}\biggr )\sin \phi&-i\sinh \biggl (\frac{\pi l K(k')}{2nK(k)}\biggr )\cos \phi \biggr ), \end{aligned}$$

(4.4)

which is not zero for any $\phi \in {\mathbb {S}}^1$. See Appendix B for the derivation of (4.4). Applying Theorem 3.1, we obtain the following.

Proposition 4.1

Let ${\hat{\Gamma }}$ be a domain in ${\mathbb {C}}/(2\pi l/\nu ){\mathbb {Z}}$ containing ${\mathbb {R}}/(2\pi l/\nu ){\mathbb {Z}}$ and $\tau =i\sqrt{1-2k^2}K(k')$. The periodically forced Duffing oscillator (4.1) with $a=1$ is meromorphically nonintegrable in the meaning of Theorem 2.1 near any periodic orbit on the resonant torus ${\mathscr {T}}^k=\{(x^k(\tau ),\nu \tau +\phi )\mid \tau \in {\hat{\Gamma }},\phi \in {\mathbb {S}}^1,k=k^{l/n}\}$ for $l,n>0$ relatively prime integers.

Remark 4.2

• (i) If $\beta =0$, then Proposition 4.1 says nothing about the nonintegrability of (4.1) since the integral (4.4) is identically zero.

• (ii) For any neighborhood U of $k\in (0,1/\sqrt{2})$ there is not a key set $D\subset U$ for $C^\omega (U)$ such that $M^{l/n}(\phi )$ is not constant for $k\in D$ satisfying (4.2). Hence, Theorem A.2 is not applicable. See also Remark 3.2(ii).

4.2 Case of $a=0$

Fig. 4

Phase portraits of (1.3) with $\varepsilon =0$ and $a=0$

We turn to the case of $a=0$ in (1.3) or (4.1). The phase portraits of (1.3) with $\varepsilon =0$ are shown in Fig. 4. In particular, there exists a one-parameter family of periodic orbits

$$\begin{aligned} x^\alpha (t) =&(\alpha {{\,\mathrm{cn}\,}}\alpha t, -\alpha ^2{{\,\mathrm{sn}\,}}\alpha t {{\,\mathrm{dn}\,}}\alpha t),\quad \alpha \in \bigl (0,\infty ), \end{aligned}$$

and their period is given by $T^\alpha =4K(1/\sqrt{2})/\alpha$, where the elliptic modulus in the Jacobi elliptic functions is $k=1/\sqrt{2}$ and $K(1/\sqrt{2})=1.854\ldots$. Assume that the resonance condition

$$\begin{aligned} nT^\alpha =\frac{2\pi l}{\nu },\quad \text{ i.e., }\quad \nu =\frac{\pi l\alpha }{2nK(1/\sqrt{2})}, \end{aligned}$$

(4.5)

holds at $\alpha =\alpha ^{l/n}$ for $l,n>0$ relatively prime integers. As in the case of $a=1$, we compute the subharmonic Melnikov function (3.8) for $x^k(t)$ as

$$\begin{aligned} M^{l/n}(\phi )=&\int _0^{2\pi l/\nu }x_2^\alpha (t)(-\delta x_2^\alpha (t)+\beta \cos (\nu t+\phi ))\mathrm {d}t\nonumber \\ =&-\delta J_1(\alpha ,n)+\beta J_2(\alpha ,l,n)\sin \phi , \end{aligned}$$

where

$$\begin{aligned}&J_1(\alpha ,n)=\frac{4n\alpha ^3 K(1/\sqrt{2})}{3},\\&J_2(\alpha ,l,n)= {\left\{ \begin{array}{ll} \displaystyle 2\sqrt{2}\pi \nu {{\,\mathrm{sech}\,}}\left( \frac{\pi l}{2}\right) &{} \text{(for } n=1 \text{ and } l \text{ odd) };\\ 0\quad &{} \text{(for } n\ne 1 \text{ or } l \text{ even) }. \end{array}\right. } \end{aligned}$$

On the other hand, we write the integral (3.9) as

$$\begin{aligned} {\hat{{\mathscr {I}}}}(\phi )=-\alpha ^4\delta \int _{\gamma _\phi } {{\,\mathrm{sn}\,}}^2\alpha t\,{{\,\mathrm{dn}\,}}^2\alpha \tau \mathrm {d}\tau -\alpha ^2\beta \int _{\gamma _\phi } {{\,\mathrm{sn}\,}}\alpha \tau \,{{\,\mathrm{dn}\,}}\alpha \tau \,\cos (\nu \tau +\phi )\mathrm {d}\tau . \end{aligned}$$

We take a circle centered at $\tau =i\alpha K(1/\sqrt{2})$ with a sufficiently small radius as $\gamma _\phi$, and compute

$$\begin{aligned} {\hat{{\mathscr {I}}}}(\phi ) =-2\sqrt{2}\pi \nu \beta \biggl (\cosh \biggl (\frac{\pi l }{2n}\biggr )\sin \phi -i\sinh \biggl (\frac{\pi l}{2n}\biggr )\cos \phi \biggr ), \end{aligned}$$

(4.6)

which is not zero for any $\phi \in {\mathbb {S}}^1$, as in (4.4).

Proposition 4.3

Let ${\hat{\Gamma }}$ be a domain in ${\mathbb {C}}/(2\pi l/\nu ){\mathbb {Z}}$ containing ${\mathbb {R}}/(2\pi l/\nu ){\mathbb {Z}}$ and $\tau =i\alpha K(1/\sqrt{2})$. The periodically forced Duffing oscillator (4.1) with $a=0$ is meromorphically nonintegrable in the meaning of Theorem 2.1 near any periodic orbit on the resonant torus ${\mathscr {T}}^\alpha =\{(x^\alpha (\tau ),\nu \tau +\phi )\mid \tau \in {\hat{\Gamma }},\phi \in {\mathbb {S}}^1,\alpha =\alpha ^{l/n}\}$ for $l,n>0$ relatively prime integers.

Remark 4.4

• (i) As in Remark 4.2(i), if $\beta =0$, then Proposition 4.3 says nothing about the nonintegrability of (4.1) since the integral (4.6) is identically zero.

• (ii) For any neighborhood U of $\alpha \in (0,\infty )$ there is not a key set $D\subset U$ for $C^\omega (U)$ such that $M^{l/n}(\phi )$ is not constant for $\alpha \in D$ satisfying (4.5). Hence, Theorem A.2 is not applicable, as in Remark 4.2(ii).

4.3 Case of $a=-1$

Fig. 5

Phase portraits of (1.3) with $\varepsilon =0$ and $a=-1$

We turn to the case of $a=-1$ in (1.3) or (4.1). The phase portraits of (1.3) with $\varepsilon =0$ are shown in Fig. 5. In particular, there exist a pair of homoclinic orbits

$$\begin{aligned} x^\mathrm {h}_\pm (t)=(\pm \sqrt{2}{{\,\mathrm{sech}\,}}t, \mp \sqrt{2}{{\,\mathrm{sech}\,}}t\,\tanh t), \end{aligned}$$

a pair of one-parameter families of periodic orbits

$$\begin{aligned} x^k_{\pm }(t) =&\biggl (\pm \frac{\sqrt{2}}{\sqrt{2-k^2}}{{\,\mathrm{dn}\,}}\left( \frac{t}{\sqrt{2-k^2}}\right) ,\\&\quad \mp \frac{\sqrt{2}k^2}{2-k^2}{{\,\mathrm{sn}\,}}\left( \frac{t}{\sqrt{2-k^2}}\right) {{\,\mathrm{cn}\,}}\left( \frac{t}{\sqrt{2-k^2}}\right) \biggr ),\quad k\in (0,1), \end{aligned}$$

inside each of them, and a one-parameter periodic orbits

$$\begin{aligned} {\tilde{x}}^k(t) =&\biggl (\frac{\sqrt{2}k}{\sqrt{2k^2-1}}{{\,\mathrm{cn}\,}}\left( \frac{t}{\sqrt{2k^2-1}}\right) ,\\&\quad -\frac{\sqrt{2}k}{2k^2-1}{{\,\mathrm{sn}\,}}\left( \frac{t}{\sqrt{2k^2-1}}\right) {{\,\mathrm{dn}\,}}\left( \frac{t}{\sqrt{2k^2-1}}\right) \biggr ),\quad k\in \bigl (1/\sqrt{2},1\bigr ), \end{aligned}$$

outside of them. The periods of $x^k_{\pm }(t)$ and ${\tilde{x}}^k(t)$ are given by $T^k=2K(k)\sqrt{2-k^2}$ and ${\tilde{T}}^k=4K(k)\sqrt{2k^2-1}$, respectively (see Greenspan and Holmes 1983; Guckenheimer and Holmes 1983; Wiggins 1990). We see that $\mathrm {d}T^k/\mathrm {d}k>0$ and $\mathrm {d}{\tilde{T}}^k/\mathrm {d}k>0$ for $k\in (0,1)$ and $(1/\sqrt{2},1)$, respectively. Note that $x^k_{\pm }(t)$ and ${\tilde{x}}^k(t)$ approach $x^\mathrm {h}_{\pm }(t)$ as $k\rightarrow 1$.

Assume that the resonance conditions

$$\begin{aligned} nT^k=\frac{\pi l}{\nu },\quad \text{ i.e., }\quad \nu =\frac{\pi l}{nK(k)\sqrt{2-k^2}}, \end{aligned}$$

(4.7)

and

$$\begin{aligned} n{\tilde{T}}^k=\frac{2\pi l}{\nu },\quad \text{ i.e., }\quad \nu =\frac{\pi l}{2nK(k)\sqrt{2k^2-1}}, \end{aligned}$$

(4.8)

hold at $k=k^{l/n}$ with $l,n>0$ relatively prime integers for $x_\pm ^k(t)$ and ${\tilde{x}}^k(t)$, respectively. We compute the subharmonic Melnikov function (3.8) as

$$\begin{aligned} M_\pm ^{l/n}(\tau )=-\delta J_1(k,n)\pm \beta J_2(k,l,n)\sin \tau \end{aligned}$$

and

$$\begin{aligned} {\tilde{M}}^{l/n}(\tau )=-\delta {\tilde{J}}_1(k,n)+\beta {\tilde{J}}_2(k,l,n)\sin \tau , \end{aligned}$$

for $x_\pm ^k(t)$ and ${\tilde{x}}^k(t)$, respectively, where

$$\begin{aligned}&J_1(k,n)=\frac{4n[(2-k^2)E(k)-2k'^2K(k)]}{3(2-k^2)^{3/2}},\\&J_2(k,l,n)= {\left\{ \begin{array}{ll} \sqrt{2}\pi \nu {{\,\mathrm{sech}\,}}\left( \displaystyle \frac{\pi lK(k')}{K(k)}\right) &{} \text{(for } n=1);\\ 0\quad &{} \text{(for } n\ne 1),\ \end{array}\right. }\\&{\tilde{J}}_1(k,n)=\frac{8n[(2k^2-1)E(k)+k'^2K(k)]}{3(2k^2-1)^{3/2}},\\&{\tilde{J}}_2(k,l,n)= {\left\{ \begin{array}{ll} 2\sqrt{2}\pi \nu {{\,\mathrm{sech}\,}}\left( \displaystyle \frac{\pi lK(k')}{2K(k)}\right) &{} \text{(for } n=1 \text{ and } l \text{ odd) }; \\ 0 &{} \text{(for } n\ne 1 \text{ or } l \text{ even). } \end{array}\right. } \end{aligned}$$

See also Greenspan and Holmes (1983); Guckenheimer and Holmes (1983); Wiggins (1990) for the computations of the Melnikov functions.

On the other hand, we write the integral (3.9) as

$$\begin{aligned} {\hat{{\mathscr {I}}}}(\phi )=&-\frac{2k^4\delta }{(2-k^2)^2}\int _{\gamma _\phi } {{\,\mathrm{sn}\,}}^2\left( \frac{\tau }{\sqrt{2-k^2}}\right) {{\,\mathrm{cn}\,}}^2\left( \frac{\tau }{\sqrt{2-k^2}}\right) \mathrm {d}\tau \nonumber \\&\mp \frac{\sqrt{2}k^2\beta }{2-k^2}\int _{\gamma _\phi } {{\,\mathrm{sn}\,}}\left( \frac{\tau }{\sqrt{2-k^2}}\right) {{\,\mathrm{cn}\,}}\left( \frac{\tau }{\sqrt{2-k^2}}\right) \cos (\nu \tau +\phi )\mathrm {d}\tau \end{aligned}$$

(4.9)

and

$$\begin{aligned} {\hat{{\mathscr {I}}}}(\phi )=&-\frac{2k^2\delta }{(2k^2-1)^2}\int _{\gamma _\phi } {{\,\mathrm{sn}\,}}^2\left( \frac{\tau }{\sqrt{2k^2-1}}\right) {{\,\mathrm{dn}\,}}^2\left( \frac{\tau }{\sqrt{2k^2-1}}\right) \mathrm {d}\tau \nonumber \\&-\frac{\sqrt{2}k\beta }{2k^2-1}\int _{\gamma _\phi } {{\,\mathrm{sn}\,}}\left( \frac{\tau }{\sqrt{2k^2-1}}\right) {{\,\mathrm{dn}\,}}\left( \frac{\tau }{\sqrt{2k^2-1}}\right) \cos (\nu \tau +\phi )\mathrm {d}\tau \end{aligned}$$

(4.10)

for $x_\pm ^k(t)$ and ${\tilde{x}}^k(t)$, respectively. We take circles centered at $\tau =i\sqrt{2-k^2}K(k')$ and $\tau =i\sqrt{2k^2-1}K(k')$ with sufficiently small radii as $\gamma _\phi$, and compute (4.9) and (4.10) as

$$\begin{aligned} {\hat{{\mathscr {I}}}}(\phi ) =\mp 2\sqrt{2}\pi \nu \beta \biggl (\cosh \biggl (\frac{\pi l K(k')}{nK(k)}\biggr )\sin \phi&-i\sinh \biggl (\frac{\pi l K(k')}{nK(k)}\biggr )\cos \phi \biggr ), \end{aligned}$$

(4.11)

and

$$\begin{aligned} {\hat{{\mathscr {I}}}}(\phi ) =-2\sqrt{2}\pi \nu \beta \biggl (\cosh \biggl (\frac{\pi l K(k')}{2nK(k)}\biggr )\sin \phi&-i\sinh \biggl (\frac{\pi l K(k')}{2nK(k)}\biggr )\cos \phi \biggr ), \end{aligned}$$

(4.12)

respectively. See Appendix C for the derivation of (4.11). The expression (4.12) is derived as in (4.4). Note that the integrals (4.11) and (4.12) are not zero for any $\phi \in {\mathbb {S}}^1$. Applying Theorem 3.1, we obtain the following.

Proposition 4.5

Let ${\hat{\Gamma }}$ be a domain in ${\mathbb {C}}/(2\pi l/\nu ){\mathbb {Z}}$ containing ${\mathbb {R}}/(2\pi l/\nu ){\mathbb {Z}}$ and $\tau =i\sqrt{2-k^2}K(k')$ (resp. $\tau =i\sqrt{2k^2-1}K(k'))$. The periodically forced Duffing oscillator (4.1) with $a=-1$ is meromorphically nonintegrable in the meaning of Theorem 2.1 near any periodic orbit on the resonant torus ${\mathscr {T}}^k=\{(x^k(\tau ),\nu \tau +\phi )\mid \tau \in {\hat{\Gamma }},\phi \in {\mathbb {S}}^1,k=k^{l/n}\}$ (resp. ${\mathscr {T}}^k=\{({\tilde{x}}^k(\tau ),\nu \tau +\phi )\mid \tau \in {\hat{\Gamma }},\phi \in {\mathbb {S}}^1,k=k^{l/n}\})$ for $l,n>0$ relatively prime integers.

Remark 4.6

• (i) As Remarks 4.2(i) and 4.4(i), if $\beta =0$, then Propositions 4.5 says nothing about the nonintegrability of (4.1) since the integral (4.4) is identically zero.

• (ii) Since for any neighborhood U of $k\in (0,1)$ (resp. $k\in (1/\sqrt{2},1))$ there is not a key set $D\subset U$ for $C^\omega (U)$ such that $M^{l/n}(\phi )$ (resp. ${\tilde{M}}^{l/n}(\phi ))$ is not constant for $k\in U$ satisfying (4.7) (resp. (4.8)), Theorem A.2 is not applicable, as in Remarks 4.2(ii) and 4.4(ii). On the other hand, for any neighborhood U of $k=1$ there is a key set $D\subset U$ for $C^\omega (U)$ such that $M^{l/n}(\phi )$ (resp. ${\tilde{M}}^{l/n}(\phi ))$ is not constant for $k\in D$ satisfying (4.7) (resp. (4.8)). Hence, Theorem A.2 is applicable to show that the periodically forced Duffing oscillator (4.1) with $a=-1$ is real-analytically nonintegrable near the surface $(\{x^\mathrm {h}(t)\mid t\in {\mathbb {R}}\}\cup \{0\})\times {\mathbb {S}}^1$.

5 Additional Examples

We give two more examples to illustrate Theorem 2.1.

5.1 Second-order Coupled Oscillators

Let $m=\ell$ and consider

$$\begin{aligned} {\dot{I}}_j&=\varepsilon \biggl (-\delta I_j+\Omega _j +\beta \sum _{k=1}^\ell \frac{\sin (\theta _k-\theta _j)}{1-\kappa \cos (\theta _k-\theta _j)}\biggr ),\quad {\dot{\theta }}_j=I_j,\nonumber \\ j&=1,\ldots ,\ell , \end{aligned}$$

(5.1)

where $\delta ,\beta ,\kappa ,\Omega _j>0$, $j=1,\ldots ,\ell$, are constants such that $\kappa <1$. Equation (5.1) is rewritten in a system of second-order differential equations as

$$\begin{aligned} \ddot{\theta }_j+\varepsilon \delta {\dot{\theta }} =\varepsilon \biggl (\Omega _j +\beta \sum _{l=1}^\ell \frac{\sin (\theta _l-\theta _j)}{1-\kappa \cos (\theta _l-\theta _j)}\biggr ),\quad j=1,\ldots ,\ell , \end{aligned}$$

which is often referred to as second-order Kuramoto model (Rodrigues et al. 2016) when $\kappa =0$. When $\delta ,\Omega _j=0$, $j=1,\ldots ,\ell$, the system (5.1) is an $\ell$-degree-of-freedom Hamiltonian system with the Hamiltonian

$$\begin{aligned} H(I,\theta )=\tfrac{1}{2}|I|^2+\frac{\varepsilon \beta }{\kappa } \sum _{j=2}^\ell \sum _{l=1}^{j-1}\log (1-\kappa \cos (\theta _l-\theta _j)). \end{aligned}$$

Henceforth we only treat a special case of condition (A1) in which

$$\begin{aligned} 2I_1=I_2=\cdots =I_\ell \ne 0 \end{aligned}$$

although infinitely many resonances of multiplicity $\ell -1$ can occur in (5.1).

Let $\omega ^*=I_1$, so that $T^*=2\pi /I_1$. Assume that

$$\begin{aligned} |\theta _j-\theta _k|\ne |\theta _1-\theta _2|\quad \text{ for } (j,k)\ne (1,2), \end{aligned}$$

and let $\gamma _\theta$ be a closed loop with a center at

$$\begin{aligned} \tau =\frac{\theta _1-\theta _2}{\omega ^*} +\frac{i}{\omega ^*}{{\,\mathrm{arccosh}\,}}\biggl (\frac{1}{\kappa }\biggr )=:\tau ^*, \end{aligned}$$

and a sufficiently small radius. Using the method of residues, we compute the first and second components of (2.1) as

$$\begin{aligned} {\mathscr {I}}_1(\theta )=\beta \int _{\gamma _\theta }\frac{\sin (\omega ^*\tau +\theta _2-\theta _1)}{1-\kappa \cos (\omega ^*\tau +\theta _2-\theta _1)}\mathrm {d}\tau =2\pi i\kappa \omega ^*\beta \end{aligned}$$

and

$$\begin{aligned} {\mathscr {I}}_2(\theta )=-\beta \int _{\gamma _\theta }\frac{\sin (\omega ^*\tau +\theta _2-\theta _1)}{1-\kappa \cos (\omega ^*\tau +\theta _2-\theta _1)}\mathrm {d}\tau =-2\pi i\kappa \omega ^*\beta , \end{aligned}$$

respectively, while its other components are zero since the integrands are analytic inside of the loop $\gamma _\theta$. Applying Theorem 2.1, we obtain the following.

Proposition 5.1

Let $\Gamma$ be a domain in ${\mathbb {C}}/T^*{\mathbb {Z}}$ containing ${\mathbb {R}}/T^*{\mathbb {Z}}$ and $\tau =\tau ^*$. The system (5.1) is nonintegrable near any periodic orbit on

$$\begin{aligned} \{(I,\omega ^*\tau +\theta )\mid \tau \in \Gamma ,I\in {\mathbb {R}}^\ell ,\theta \in {\mathbb {T}}^\ell ,2I_1=I_2=\cdots =I_\ell \ne 0\} \end{aligned}$$

in the meaning of Theorem 2.1.

5.2 Pendulum-Type Oscillator with a Constant Torque

We finally set $\ell =m=1$ and consider the two-dimensional system

$$\begin{aligned} {\dot{I}}=\varepsilon \biggl (\frac{\sin \theta }{1-\kappa \cos \theta }+1\biggr ),\quad {\dot{\theta }}=I, \end{aligned}$$

(5.2)

where $\kappa \in (0,1)$ is a constant. When $\kappa =0$, Eq. (5.2) represents an equation of motion for the pendulum subjected to a constant torque. A similar example was treated in Motonaga and Yagasaki (2021b). Assumption (A1) holds for any $I^*=I\ne 0$ as $\omega ^*=I$ and $T^*=2\pi /I$. Let $\gamma _\theta$ be a closed loop with a center at

$$\begin{aligned} \tau =-\frac{\theta }{I}+\frac{i}{I}{{\,\mathrm{arccosh}\,}}\biggl (\frac{1}{\kappa }\biggr )=:\tau ^*, \end{aligned}$$

and a sufficiently small radius, as in Sect. 5.2. Noting that $\mathrm {D}\omega (I)=1$ and using the method of residues, we compute (2.1) as

$$\begin{aligned} {\mathscr {I}}(\theta )=\int _{\gamma _\theta }\frac{\sin (I\tau +\theta )}{1-\kappa \cos (I\tau +\theta )}\mathrm {d}\tau =2\pi i\kappa \omega ^*. \end{aligned}$$

Applying Theorem 2.1, we obtain the following.

Proposition 5.2

Let $\Gamma$ be a domain in ${\mathbb {C}}/T^*{\mathbb {Z}}$ containing ${\mathbb {R}}/T^*{\mathbb {Z}}$ and $\tau =\tau ^*$. The system (5.2) is nonintegrable near any periodic orbit $\{(I,\omega ^*\tau +\theta \mid \tau \in \Gamma \}$ for any $I\in {\mathbb {R}}$ and $\theta \in {\mathbb {S}}^1$ in the meaning of Theorem 2.1.

We easily see that the system (5.2) has the first integral

$$\begin{aligned} F_1(I,\theta )=\tfrac{1}{2}I^2-\varepsilon (\log (1-\kappa \cos \theta )+\theta ) \end{aligned}$$

and it is integrable as a system on ${\mathbb {R}}\times {\mathbb {R}}$, although $F_1(I,\theta )$ is not even a function on ${\mathbb {R}}\times {\mathbb {S}}^1$.

Appendices

Appendix A. Previous related results for (1.1)

In this appendix, we review some previous related results for the integrability of (1.1). We begin with the work of Kozlov (1996).

We first expand $h(I,\theta ;0)$ in Fourier series as

$$\begin{aligned} h(I,\theta ;0)=\sum _{r\in {\mathbb {Z}}^m}{\hat{h}}_r(I)\exp (i r\cdot \theta ), \end{aligned}$$

where ${\hat{h}}_r(I)$, $r\in {\mathbb {Z}}^m$, are the Fourier coefficients, and assume the following for (1.1):

(K1):

The system (1.1) has s first integrals $F_j(I,\theta ;\varepsilon )$, $j=1,\ldots ,s$, which are real-analytic in $(I,\theta ,\varepsilon )$;

(K2):

If $r\in {\mathbb {Z}}^m$ and $r\cdot \omega (I)=0$ for any $I\in {\mathbb {R}}^\ell$, then $r=0$.

Under assumptions (K1) and (K2), we can show that $F_j(I,\theta ;0)$, $j=1,\ldots ,s$, are independent of $\theta$ (see Lemma 1 in Sect. 1 of Chapter IV of Kozlov (1996)), and write $F_{j0}(I;0)=F_j(I,\theta ;0)$ and $F_0(I)=(F_{10}(I),\ldots ,F_{s0}(I))$. We refer to ${\mathscr {P}}_s\subset {\mathbb {R}}^\ell$ as a Poincaré set if for each $I\in {\mathscr {P}}_s$ there exists linearly independent vectors $r_j\in {\mathbb {Z}}^m$, $j=1,\ldots ,\ell -s$, such that

• (i) $r_j\cdot \omega (I)=0$, $j=1,\ldots ,\ell -s$;

• (ii) ${\hat{h}}_{r_j}(I)$, $j=1,\ldots ,\ell -s$, are linearly independent.

Let U be a domain in ${\mathbb {R}}^\ell$. A set $\Delta \subset U$ is called a key set (or uniqueness set) for $C^\omega (U)$ if any analytic function vanishing on $\Delta$ vanishes on U. For example, any dense set in U is a key set for $C^\omega (U)$. In this situation, we can prove the following theorem (see Sect. 1 of Chapter IV of Kozlov (1996) for its proof).

Theorem A.1

(Kozlov) Suppose that assumptions (K1) and (K2) hold, the Jacobian matrix $\mathrm {D}F_0(I)$ has a maximum rank at a point $I^*\in {\mathbb {R}}^\ell$ and a Poincaré set ${\mathscr {P}}_s\subset U$ is a key set for $C^\omega (U)$, where U is a neighborhood of $I^*$ in ${\mathbb {R}}^\ell$. Then the system (1.1) has no first integral which is real-analytic in $(I,\theta ,\varepsilon )$ and functionally independent of $F_j(I,\theta ;\varepsilon )$, $j=1,\ldots ,s$, in $U\times {\mathbb {T}}^m$ near $\varepsilon =0$.

A version of Theorem A.1 for the Hamiltonian case $\ell =m$ was given in Kozlov (1983) earlier (see also Theorem 7.1 of Arnold et al. (2006)). When $s=0$ in (K1), Theorem A.1 means that under the hypotheses there exists no first integral which is real-analytic in $(I,\theta ,\varepsilon )$. When $s=1$ in (K1), which always occurs if the system (1.1) is Hamiltonian, it means that under the hypotheses, which hold for $\ell ,m=2$ if besides (K1) and (K2) there exists a key set ${\mathscr {P}}_1$ for $C^\omega (U)$ with $\mathrm {D}F_{10}(I)\ne 0$ at a point of U such that $r\cdot \omega (I)=0$ and ${\hat{h}}_r(I)\ne 0$ for some $r\in {\mathbb {Z}}^2$ on ${\mathscr {P}}_1$, there exists no first integral which is real-analytic in $(I,\theta ,\varepsilon )$ and functionally independent of $F_1(I,\theta ,\varepsilon )$. In the Hamiltonian case, the conclusion implies that the system (1.1) is not Liouville-integrable in such a meaning of Theorem 2.1. However, in the non-Hamiltonian case, this is not generally true: it may be Bogoyavlenskij-integrable since it may have $m+\ell -1$ commutative vector fields satisfying Definition 1.1. Thus, it is difficult from Theorem A.1 to say anything about Bogoyavlenskij-integrability of non-Hamiltonian systems directly.

On the other hand, Motonaga and Yagasaki (2021b) recently discussed nonintegrability of perturbations of general analytically integrable systems such that the first integrals and commutative vector fields depend analytically on the small parameter, based on the result of Motonaga and Yagasaki (2021a). Let U be a domain in ${\mathbb {R}}^\ell$, as above. We assume the following:

(MY1):

A resonance of multiplicity $m-1$,

$$\begin{aligned} \dim _{\mathbb {Q}}\langle \omega _1(I),\ldots ,\omega _m(I)\rangle =1, \end{aligned}$$

occurs with $\omega (I)\ne 0$ for $I\in D_\mathrm {R}$, where $D_\mathrm {R}$ is a key set for $C^\omega (U)$.

(MY2):

For some $I^*\in U$ ${{\,\mathrm{rank}\,}}\mathrm {D}\omega (I^*)=\ell$.

Assumption (MY1) is similar to assumption (A1) in Sect. 1 but more restrictive. We easily see that if ${{\,\mathrm{rank}\,}}\mathrm {D}\omega ({\bar{I}})=m$ for some ${\bar{I}}\in {\mathbb {R}}^\ell$, then assumption (MY1) as well as (K2) hold for a neighborhood U of ${\bar{I}}$ in ${\mathbb {R}}^\ell$. In (MY1) we take a constant $T_I>0$ for $I\in D_\mathrm {R}$ such that

$$\begin{aligned} \omega _j(I)T_I\in 2\pi {\mathbb {Z}},\quad j=1,\ldots ,m. \end{aligned}$$

Let

$$\begin{aligned} {\bar{{\mathscr {I}}}}_I(\theta )=\int _0^{T_I}h(I,\omega (I)\tau +\theta ;0)\mathrm {d}\tau . \end{aligned}$$

(A.1)

Their result is stated for (1.1) as follows.

Theorem A.2

(Motonaga and Yagasaki) Suppose that assumptions (K2), (MY1) and (MY2) hold. If there exists a key set $D\subset D_\mathrm {R}$ for $C^\omega (U)$ such that ${\bar{{\mathscr {I}}}}_I(\theta )$ is not constant for $I\in D$, then for $|\varepsilon |\ne 0$ sufficiently small the system (1.1) is not real-analytically integrable in the Bogoyavlenskij sense in $U\times {\mathbb {T}}^m$ such that the first integrals and commutative vector fields also depend real-analytically on $\varepsilon$ near $\varepsilon =0$.

Remark A.3

• (i) If assumption (A1) with ${{\,\mathrm{rank}\,}}\mathrm {D}\omega (I^*)=m$ holds, then we can take a neighborhood of the resonant torus ${\mathscr {T}}^*$ as $U\times {\mathbb {T}}^m$ in Theorem A.2, like Theorem 2.1. See Sect. 2 of Motonaga and Yagasaki (2021b) for the details.

• (ii) The integral can also be expressed by the Fourier coefficient ${\hat{h}}_r(I)$, $r\in {\mathbb {Z}}^m$. See Sect. 4 of Motonaga and Yagasaki (2021b) for the details.

Using Theorem A.2, we can discuss Bogoyavlenskij-integrability of (1.1) even in the non-Hamiltonian case. However, to determine whether a specific system of the form (1.1) is nonintegrable in the meaning of Theorem A.2 or not, we need to show that ${\bar{{\mathscr {I}}}}_I(\theta )$ is not constant for infinitely many values of I since the key set D is an infinite set. See Sect. 4 of Motonaga and Yagasaki (2021b) for more details.

Appendix B. Derivation of (4.4)

We use the method of residues and compute the integral (4.3). We begin with the first term in (4.3). Letting $s=1/{{\,\mathrm{sn}\,}}\zeta$, we have

$$\begin{aligned} \int {{\,\mathrm{sn}\,}}^2\zeta \,{{\,\mathrm{dn}\,}}^2\zeta \,\mathrm {d}\zeta =-\int \frac{1}{s^4}\sqrt{\frac{k^2-s^2}{1-s^2}}\mathrm {d}s \end{aligned}$$

(B.1)

from the basic properties of the Jacobi elliptic functions,

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}\zeta }{{\,\mathrm{sn}\,}}\zeta ={{\,\mathrm{cn}\,}}\zeta {{\,\mathrm{dn}\,}}\zeta ,\quad {{\,\mathrm{cn}\,}}^2\zeta =1-{{\,\mathrm{sn}\,}}^2\zeta ,\quad {{\,\mathrm{dn}\,}}^2\zeta =1-k^2{{\,\mathrm{sn}\,}}^2\zeta . \end{aligned}$$

(B.2)

Obviously, the integrand in the right-hand side of (B.1) has a pole of order 4 at $s=0$. Since $s=1/{{\,\mathrm{sn}\,}}\zeta =0$ when $\zeta =iK(k')$ and

$$\begin{aligned} \frac{\mathrm {d}^3}{\mathrm {d}s^3}\sqrt{\frac{k^2-s^2}{1-s^2}}=0 \end{aligned}$$

at $s=0$, we obtain

$$\begin{aligned} \int _{{\hat{\gamma }}_\phi }{{\,\mathrm{sn}\,}}^2\zeta \,{{\,\mathrm{dn}\,}}^2\zeta \,\mathrm {d}\zeta =-\int _{|s|=\rho }\frac{1}{s^4}\sqrt{\frac{k^2-s^2}{1-s^2}}\mathrm {d}s=0 \end{aligned}$$

by the method of residues, where ${\hat{\gamma }}_\phi =\{\zeta \in {\mathbb {C}}\mid \zeta /\sqrt{1-2k^2}=\gamma _\phi \}$ and $\rho >0$ is sufficiently small.

We turn to the second term in (4.3). We have

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}\zeta }{{\,\mathrm{cn}\,}}\zeta =-{{\,\mathrm{sn}\,}}\zeta \,{{\,\mathrm{dn}\,}}\zeta =\frac{i}{k(\zeta -iK(k'))^2}+O(1) \end{aligned}$$

near $\zeta =iK(k')$ since

$$\begin{aligned} {{\,\mathrm{cn}\,}}\zeta =-\frac{i}{k(\zeta -iK(k'))}+O(1). \end{aligned}$$

Hence,

$$\begin{aligned}&{{\,\mathrm{sn}\,}}\zeta \,{{\,\mathrm{dn}\,}}\zeta \,\cos \bigl (\sqrt{1-2k^2}\,\nu \zeta \bigr )\\&=-\frac{i\cosh \bigl (\sqrt{1-2k^2}\,\nu K(k')\bigr )}{k(\zeta -iK(k'))^2} -\frac{\nu \sqrt{1-2k^2}\sinh \bigl (\sqrt{1-2k^2}\,\nu K(k')\bigr )}{k(\zeta -iK(k'))}+O(1) \end{aligned}$$

near $\zeta =iK(k')$, so that

$$\begin{aligned} \int _{{\hat{\gamma }}_\phi }{{\,\mathrm{sn}\,}}\zeta \,{{\,\mathrm{dn}\,}}\zeta \,\cos \bigl (\sqrt{1-2k^2}\,\nu \zeta \bigr )\mathrm {d}\zeta =&-\frac{2\pi i\nu \sqrt{1-2k^2}}{k} \sinh \biggl (\frac{\pi l K(k')}{2nK(k)}\biggr ), \end{aligned}$$

where we have used the relation (4.2). Similarly,

$$\begin{aligned} \int _{{\hat{\gamma }}_\phi }{{\,\mathrm{sn}\,}}\zeta \,{{\,\mathrm{dn}\,}}\zeta \,\sin \bigl (\sqrt{1-2k^2}\,\nu \zeta \bigr )\mathrm {d}\zeta = \frac{2\pi i\nu \sqrt{1-2k^2}}{k}\cosh \biggl (\frac{\pi l K(k')}{2nK(k)}\biggr ). \end{aligned}$$

Thus, we obtain (4.4).

Appendix C. Derivation of (4.11)

We use the method of residues and compute the integral (4.9), as in Appendix B. We begin with the first term in (4.9). Letting $s=1/{{\,\mathrm{sn}\,}}\zeta$, we have

$$\begin{aligned} \int {{\,\mathrm{sn}\,}}^2\zeta \,{{\,\mathrm{cn}\,}}^2\zeta \,\mathrm {d}\zeta =-\int \frac{1}{s^4}\sqrt{\frac{1-s^2}{k^2-s^2}}\mathrm {d}s \end{aligned}$$

(C.1)

by (B.2). Obviously, the integrand in the right-hand side of (C.1) has a pole of order 4 at $s=0$. Since $s=1/{{\,\mathrm{sn}\,}}\zeta =0$ when $\zeta =iK(k')$ and

$$\begin{aligned} \frac{\mathrm {d}^3}{\mathrm {d}s^3}\sqrt{\frac{1-s^2}{k^2-s^2}}=0 \end{aligned}$$

at $s=0$, we obtain

$$\begin{aligned} \int _{{\hat{\gamma }}_\phi }{{\,\mathrm{sn}\,}}^2\zeta \,{{\,\mathrm{cn}\,}}^2\zeta \,\mathrm {d}\zeta =-\int _{|s|=\rho }\frac{1}{s^4}\sqrt{\frac{1-s^2}{k^2-s^2}}\mathrm {d}s=0 \end{aligned}$$

by the method of residues, where ${\hat{\gamma }}_\phi =\{\zeta \in {\mathbb {C}}\mid \zeta /\sqrt{2-k^2}=\gamma _\phi \}$ and $\rho >0$ is sufficiently small.

We turn to the second term in (4.9). We have

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}\zeta }{{\,\mathrm{dn}\,}}\zeta =-k^2{{\,\mathrm{sn}\,}}\zeta \,{{\,\mathrm{cn}\,}}\zeta =\frac{i}{(\zeta -iK(k'))^2}+O(1) \end{aligned}$$

near $\zeta =iK(k')$ since

$$\begin{aligned} {{\,\mathrm{dn}\,}}\zeta =-\frac{i}{\zeta -iK(k')}+O(1). \end{aligned}$$

Hence,

$$\begin{aligned}&{{\,\mathrm{sn}\,}}\zeta \,{{\,\mathrm{cn}\,}}\zeta \,\cos \bigl (\sqrt{2-k^2}\,\nu \zeta \bigr )\\&=-\frac{i\cosh \bigl (\sqrt{2-k^2}\,\nu K(k')\bigr )}{k^2(\zeta -iK(k'))^2} -\frac{\nu \sqrt{2-k^2}\sinh \bigl (\sqrt{2-k^2}\,\nu K(k')\bigr )}{k^2(\zeta -iK(k'))}+O(1) \end{aligned}$$

near $\zeta =iK(k')$, so that

$$\begin{aligned} \int _{{\hat{\gamma }}_\phi }{{\,\mathrm{sn}\,}}\zeta \,{{\,\mathrm{cn}\,}}\zeta \,\cos \bigl (\sqrt{2-k^2}\,\nu \zeta \bigr )\mathrm {d}\zeta =&-\frac{2\pi i\nu \sqrt{2-k^2}}{k^2} \sinh \biggl (\frac{\pi l K(k')}{nK(k)}\biggr ), \end{aligned}$$

where we have used the relation (4.7). Similarly,

$$\begin{aligned} \int _{{\hat{\gamma }}_\phi }{{\,\mathrm{sn}\,}}\zeta \,{{\,\mathrm{cn}\,}}\zeta \,\sin \bigl (\sqrt{2-k^2}\,\nu \zeta \bigr )\mathrm {d}\zeta = \frac{2\pi i\nu \sqrt{2-k^2}}{k^2}\cosh \biggl (\frac{\pi l K(k')}{nK(k)}\biggr ). \end{aligned}$$

Thus, we obtain (4.11).