Hamel’s Formalism for Infinite-Dimensional Mechanical Systems

Abstract

In this paper, we introduce Hamel’s formalism for infinite-dimensional mechanical systems and in particular consider its applications to the dynamics of nonholonomically constrained systems. This development is a nontrivial extension of its finite-dimensional counterpart. The analysis is applied to several continuum mechanical systems of interest, including coupled systems and systems with infinitely many constraints.

1 Introduction

Hamel’s formalism is a natural extension of Euler’s ideas of using nonmaterial velocity in mechanics. Nonmaterial velocity carries information about system’s velocity, but is not the rate of change of system’s configuration with respect to time. For a system with finite number of degrees of freedom, nonmaterial velocity is a collection of velocity components relative to a set of vector fields that span the fibers of the tangent bundle of the configuration space. In the finite-dimensional setting, this development was carried out by Hamel himself in Hamel (1904). Here we introduce Hamel’s formalism for infinite-dimensional mechanical systems.

One of the reasons for using nonmaterial velocity is that the Euler–Lagrange equations are not always effective for analyzing the dynamics of a mechanical system of interest. For example, it is difficult to study the motion of the Euler top if the Euler–Lagrange equations are used to represent the dynamics. On the other hand, the use of the angular velocity components relative to a body frame as pioneered by Euler (1752) results in a much simpler representation of dynamics. In a similar fashion, Euler (1757a, (1757b, (1761) uses convective velocity to represent the dynamics of ideal incompressible fluid. Euler’s approach was further developed by Lagrange (1788) for reasonably general Lagrangians on the rotation group and by Poincaré (1901) for arbitrary Lie groups (see Marsden and Ratiu 1999 for details and history).

The nonmaterial velocity used in Lagrange (1788) and Poincaré (1901) is associated with a group action. Hamel (1904) obtained the equations of motion in terms of nonmaterial velocity that is unrelated to a group action on the configuration space. Hamel’s equations include both the Euler–Lagrange and Euler–Poincaré equations (for the rigid body for example) as special cases.

As clearly seen from his paper, Hamel was particularly motivated by nonholonomic mechanics. His formalism features the simplicity of an analytic representation of constraints and the intrinsic absence of Lagrange multipliers in equations of motion. It is exceptionally effective for studying (finite-dimensional) constrained systems and understanding their dynamics, both analytically and numerically; see e.g., Bloch et al. (2009), Ball and Zenkov (2015), Zenkov et al. (2012) and references therein.

As mentioned above, in finite dimensions nonmaterial velocity refers to velocity components relative to a set of vector fields that span the fibers of the tangent bundle of the configuration space. Alternatively, one interprets nonmaterial velocity as a result of configuration-dependent velocity substitution. In the infinite-dimensional setting, the former interpretation fails to work as generically bases fail to exist.

General properties of infinite-dimensional constrained systems are studied from the field-theoretic viewpoint in e.g., Binz et al. (2002) and Vankerschaver (2005, (2007a, (2007b). Infinite-dimensional nonholonomic mechanics, in relation to electromechanical systems, diffeomorphism groups, and optimal transport, has been utilized in Neimark and Fufaev (1972) and Khesin and Lee (2009), respectively. At the moment, the general theory of infinite-dimensional nonholonomic systems in the form of ordinary differential equations on an infinite-dimensional configuration space does not exist. As demonstrated by Ebin and Marsden (1970) (see also Ebin 2015), the use of the infinite-dimensional formalism in combination with nonmaterial (spatial) velocity is crucial for proving existence of solutions in fluid mechanics. Motivated by this and as a part of the development of Hamel’s formalism, we introduce the general theory of infinite-dimensional nonholonomic systems.

Our paper develops the general formalism of Hamel’s equations in infinite-dimensions with careful attention to the analytic setting in which the equations are well defined. We also discuss mechanical examples, including a string, a constrained string, and strings attached to rigid bodies. The differential equations describing these systems are derived and analyzed.

Having in mind possible future applications to the dynamics of systems with nonBanach configuration manifolds (such as infinite-dimensional Lie groups), we develop the formalism on convenient manifolds. These are (infinite-dimensional) manifolds modeled on convenient spaces. A convenient space is a locally convex space with ‘tweaked’ topology. By definition, the $c^\infty$-topology on a locally convex space E is the final topology with respect to all smooth curves $\gamma :{\mathbb {R}} \rightarrow E$, i.e., it is the finest topology on E with respect to which the aforementioned curves are continuous. Recall that smoothness is a bornological concept and is independent of the choice of topology of a locally convex space. In general, the $c^\infty$-topology is finer than any locally convex topology with the same collection of bounded sets. A locally convex vector space is said to be $c^\infty$-complete or convenient if it is $c^\infty$-closed in any locally convex space. For a Fréchet space, the $c^\infty$-topology coincides with the given locally convex topology. In general, a convenient space is not a topological vector space.

A mapping between two convenient spaces is called smooth if it maps smooth curves to smooth curves. The important property of the smooth mappings,

$$\begin{aligned} C^\infty (E \times F, G) \cong C^\infty (E, C^\infty (F,G)), \end{aligned}$$

is known as the Cartesian closedness. We refer the reader to Kriegl and Michor (1997) for details and proofs.

The use of such general spaces is natural in variational calculus and helps to clarify various technical assumptions one needs to impose in the infinite-dimensional setting with velocity constraints. Meanwhile, the complexity of proofs is unaffected by the use of convenient analysis. Moreover, the results remain correct after a rollback to ‘simpler’ (e.g., Fréchet or Banach) manifolds.

Based on the earlier observations of the authors in the finite-dimensional setting and recent publications on geometric continuum mechanics, we expect that the proposed formalism will be useful in:

• Systematic derivation of simple representations of equations of motion in continuum mechanics, which includes elimination of unnecessary Lagrange multipliers from the equations of motion and singling out control directions when they are inconsistent with configuration coordinates and/or do not commute.

• Multibody dynamics of systems with continuum components.

• Dynamics of contacting elastic rods (Gay-Balmaz and Putkaradze 2012, 2015), molecular strands (Ellis et al. 2010), and certain non-Newtonian fluids (Gay-Balmaz and Yoshimura 2015).

• Stability and qualitative analysis, including existence of conservation laws in constrained systems and Lyapunov function construction strategies for partial stability analysis, with applications to stability of rigid bodies with fins moving in a fluid, fluid-filled bodies, and rolling elastic bodies.

• Development of structure-preserving integrators for constrained infinite-dimensional systems.

The paper is organized as follows: In Sect. 2 we review the finite-dimensional Euler–Lagrange, Euler–Poincaré, and Hamel equations. In Sect. 3, the infinite-dimensional Hamel formalism is introduced. In Sects. 4 and 5, systems with constraints and symmetry are treated. In particular, systems with infinitely many constraints are studied, which, in the presence of symmetry, requires a somewhat different approach than the standard formalism for systems with symmetry. Numerous illustrative examples are given.

2 Preliminaries

Lagrangian mechanics provides a systematic approach to deriving the equations of motion as well as establishes the equivalence of force balance and variational principles.

2.1 The Euler–Lagrange Equations

A Lagrangian mechanical system is specified by a smooth manifold Q called the configuration space and a function $L:TQ\rightarrow {\mathbb {R}}$ called the Lagrangian. In many cases, the Lagrangian is the kinetic minus potential energy of the system, with the kinetic energy defined by a Riemannian metric and the potential energy being a smooth function on the configuration space Q. If necessary, nonconservative forces can be introduced (e.g., gyroscopic forces that are represented by terms in L that are linear in the velocity), but this is not discussed in detail in this paper.

In local coordinates $q=(q^1,\ldots ,q^n)$ on the configuration space Q, we write $L=L(q,\dot{q})$. The dynamics is given by the Euler–Lagrange equations

$$\begin{aligned} \frac{d}{\mathrm{d}t} \frac{\partial L}{\partial \dot{q}^i } = \frac{\partial L}{\partial q^i},\quad i = 1,\ldots ,n. \end{aligned}$$

These equations were originally derived by Lagrange (1788) by requiring that simple force balance be covariant, i.e., expressible in arbitrary generalized coordinates. A variational derivation of the Euler–Lagrange equations, namely Hamilton’s principle (see Theorem 2.1 below), came later in the work of Hamilton (1834, 1835).

Let q(t), $a \le t \le b$, be a smooth curve in Q. A variation of the curve q(t) is a smooth map $\beta : [a,b] \times [- \varepsilon , \varepsilon ] \rightarrow Q$ that satisfies the condition $\beta (t, 0) = q(t)$. This variation defines the vector field

$$\begin{aligned} \delta q(t) = \frac{\partial \beta (t,\tau )}{\partial \tau } \bigg |_{\tau =0} \end{aligned}$$

along the curve q(t).

Theorem 2.1

The following statements are equivalent:

• (i) The curve q(t), where $a \le t \le b$, is a critical point of the action functional

  $$\begin{aligned} \int _a^b L (q,{\dot{q}})\,\mathrm{d}t \end{aligned}$$

  on the space of curves in Q connecting $q_a$ to $q_b$ on the interval [a, b], where we choose variations of the curve q(t) that satisfy $\delta q(a) = \delta q(b) = 0$.

• (ii) The curve q(t) satisfies the Euler–Lagrange equations.

We point out here that this principle assumes that a variation of the curve q(t) induces the variation $\delta \dot{q}(t)$ of its velocity vector according to the formula

$$\begin{aligned} \delta \dot{q}(t):=\frac{d}{\mathrm{d}t} \delta q(t). \end{aligned}$$

For more details and a proof, see e.g., Bloch (2015) and Marsden and Ratiu (1999).

2.2 The Euler–Poincaré Equations

The classical Euler equations for freely rotating rigid body read

$$\begin{aligned} J \dot{\Omega }= J \Omega \times \Omega , \end{aligned}$$

where $\Omega$ is the body angular velocity and J is the inertia tensor. First derived by Euler (1752), these equations, as well as the Euler equation for an incompressible fluid flow,

$$\begin{aligned} \frac{\partial v}{\partial t} + \nabla _v v = - \nabla p, \quad {\text {div}} v = 0, \end{aligned}$$

were generalized by Poincaré (1901, 1910) to any Lie algebra. These Euler–Poincaré equations for a Lagrangian $l(\xi )$ defined on a Lie algebra $\mathfrak g$ are

$$\begin{aligned} \frac{d}{\mathrm{d}t} \frac{\partial l}{\partial \xi } = \pm {\text {ad}}^{*}_\xi \frac{\partial l}{\partial \xi }. \end{aligned}$$

(2.1)

These equations are variational, with variations satisfying certain constraints, as the following theorem clarifies.

Theorem 2.2

Let $\mathfrak g$ be a Lie algebra and $l:\mathfrak g \rightarrow \mathbb R$ be a Lagrangian. The following statements are equivalent:

• (i) The variational principle

  $$\begin{aligned} \delta \int _a^b l (\xi (t))\,\mathrm{d}t = 0 \end{aligned}$$

  holds on $\mathfrak {g}$, using variations of the form

  $$\begin{aligned} \delta \xi = \dot{\eta }\pm {\text {ad}}_\xi \eta , \end{aligned}$$

  where $\eta$ vanishes at the endpoints.

• (ii) The Euler–Poincaré Eq. (2.1) hold.

See Bloch et al. (1996b), Cendra et al. (1988), Marsden (1992), Holm et al. (1998), and Marsden and Ratiu (1999) for details, history, and proofs.

2.3 Lagrangian Mechanics in Non-Coordinate Frames

In many cases, the Lagrangian and the equations of motion have a simpler structure when the velocity components are measured against a frame that is unrelated to the system’s local configuration coordinates. An example of such a system is the rigid body.

Let $q=(q^1,\ldots , q^n)$ be local coordinates on the configuration space Q and $u_i \in TQ$, $i = 1,\ldots ,n$, be smooth independent local vector fields on Q defined in the same coordinate neighborhood. In certain cases, some or all of the fields $u_i$ can be chosen to be global vector fields on Q.

Let $\xi = (\xi ^1,\ldots ,\xi ^n) \in {\mathbb {R}}^n$ be the components of the velocity vector $\dot{q} \in TQ$ relative to the frame $u(q) = (u_1(q),\ldots , u_n(q))$, i.e.,

$$\begin{aligned} \dot{q} = \xi ^i u_i(q). \end{aligned}$$

The Lagrangian of the system written in the local coordinates $(q, \xi )$ on the velocity phase space TQ reads

$$\begin{aligned} l(q, \xi ):= L(q, \xi ^i u_i(q)). \end{aligned}$$

The coordinates $(q, \xi )$ are Lagrangian analogue of noncanonical variables in Hamiltonian dynamics.

Define the structure functions $c_{ij}^k (q)$ by the equations

$$\begin{aligned}{}[u_i (q),u_j (q)] = c^k_{ij} (q) u_k (q), \end{aligned}$$

$i, j, k = 1,\ldots , n$. These quantities vanish if and only if the vector fields $u_i (q)$, $i = 1,\ldots , n$, commute.

Viewing $u _i$ as vector fields on TQ whose fiber components equal 0 (that is, taking the vertical lift of the frame vector fields), one defines the directional derivatives $u_i [l]$ for a function $l:TQ\rightarrow {\mathbb {R}}$ in a usual way.

The evolution of the variables $(q,\xi )$ is governed by the Hamel equations

$$\begin{aligned} \frac{d}{\mathrm{d}t} \frac{\partial l}{\partial \xi ^j} = c^k_{ij}\frac{\partial l}{\partial \xi ^k} \xi ^i + u_j[l], \end{aligned}$$

(2.2)

$i, j, k = 1,\ldots ,n$, coupled with equation $\dot{q} = \xi ^i u_i(q)$. These equations were introduced in Hamel (1904) (see also Neimark and Fufaev 1972 and Bloch et al. 2009 for details, history, and contemporary geometric exposition). If $u_i = \partial / \partial q^i$, the Hamel equations become the Euler–Lagrange equations.

2.4 Ideal Constraints

Assume now that there are velocity constraints imposed on the system. We confine our attention to constraints that are linear and homogeneous in the velocity. Accordingly, we consider a configuration space Q and a distribution ${\mathcal {D}}$ on Q that describes these constraints. Recall that a distribution ${\mathcal {D}}$ is a collection of linear subspaces of the tangent spaces of Q; we denote these subspaces by ${\mathcal {D}}_q\subset T_q Q$, one for each $q \in Q$.

A curve $q(t) \in Q$ is said to satisfy the constraints if $\dot{q}(t)\in {\mathcal {D}}_{q(t)}$ for all t. This distribution will, in general, be nonintegrable, i.e., the constraints will be, in general, nonholonomic.¹

As discussed in e.g., Suslov (1946) and Chetaev (1989), it is assumed in classical mechanics that the constraints imposed on the system can be replaced with the reaction force. This means that after the force is imposed on the unconstrained system, the constraint distribution ${\mathcal {D}} \subset TQ$ becomes a conditional invariant manifold of the forced unconstrained Lagrangian system whose dynamics on this invariant manifold is identical to that of the constrained system.

Definition 2.3

Constraints (either holonomic or nonholonomic) are called ideal if their reaction force at each $q\in Q$ belong to the null space ${\mathcal {D}}^\circ _q \subset T_q^{*}Q$ of ${\mathcal {D}}_q\subset T_q Q$.

As shown in Suslov (1946) and Chetaev (1989), the reaction force of ideal constraints is defined uniquely at each state $(q, \dot{q}) \in TQ$.

In summary, for a system subject to ideal constraints, the forced dynamics is equivalent to the Lagrange–d’Alembert principle. We refer the reader to books Suslov (1946) and Chetaev (1989) for a more detailed exposition and history of the concept of ideal constraints.

Utilizing Hamel’s formalism and assuming the ideal velocity constraints read $\xi ^{m+1}=\cdots =\xi ^n=0$, the dynamics of the constrained system is given by (2.2) for $j=1,\ldots ,m$. The remaining $n-m$ equations serve for computing the reaction force and do not affect the dynamics of the system.

For the early development of these equations see Poincaré (1901) and Hamel (1904). We refer the readers to Marsden and Ratiu (1999) and Bloch et al. (2009) for the history and development of variational principles for the Euler–Lagrange, Euler–Poincaré, and Hamel equations, and to Ball et al. (2012) for the Hamilton–Pontryagin principle for the Hamel equations.

2.5 The Chaplygin Sleigh

Here we describe the Chaplygin sleigh which is one of the simplest but nonetheless instructive example of a nonholonomic mechanical system. The sleigh is essentially a vertical blade moving on a horizontal plane, with no motion perpendicular to the blade allowed. There is a single contact point of the blade and the plane, and the center of mass of the blade coincides with this contact point. The sleigh is often thought of as a balanced platform on the top of the blade. See Fig. 1 where the platform, the blade, and the contact point are depicted as an oval, a bold segment, and a bold dot, respectively.

Fig. 1

The Chaplygin sleigh

Let $\theta$ be the angular orientation of the sleigh and (x, y) be the coordinates of the contact point as shown in Fig. 1. The configuration space for the sleigh is the Euclidean group ${\text {SE}}(2) = {\text {SO}}(2) {\circledS } {\mathbb {R}}^2$. We parametrize the elements of SE(2) as $(\theta , x, y)$. The body frame is

$$\begin{aligned} \frac{\partial }{\partial \theta }, \quad \cos \theta \frac{\partial }{\partial x} + \sin \theta \frac{\partial }{\partial y}, \quad - \sin \theta \frac{\partial }{\partial x} + \cos \theta \frac{\partial }{\partial y}. \end{aligned}$$

Using this frame,

$$\begin{aligned} \dot{\theta }= \omega , \quad \dot{x} = v^1 \cos \theta - v^2 \sin \theta , \quad \dot{y} = v^1 \sin \theta + v^2 \cos \theta , \end{aligned}$$

(2.3)

where $\omega$ is the angular velocity of the sleigh relative to the vertical line through the contact point and where $(v^1, v^2)$ are the components of the linear velocity of the contact point in the directions along and orthogonal to the blade, respectively. Thus, the constraint reads $v^2 = 0$.

Having in mind infinite-dimensional generalizations of the Chaplygin sleigh, we start using the complex configuration variable $z = x + iy$ on the plane. Similarly, the linear velocity relative to the body frame is written as $v = v^1 + iv^2$. Formulae (2.3) become

$$\begin{aligned} \dot{\theta }= \omega , \quad \dot{z} = \hbox {e}^{i \theta } v, \end{aligned}$$

(2.4)

whereas the constraint in this complex representation reads

$$\begin{aligned} v = \bar{v}. \end{aligned}$$

Denote the mass and the moment of inertia of the sleigh by m and J. The Lagrangian is just the kinetic energy of the sleigh, which is the sum of the kinetic energies of the linear and rotational modes of the sleigh. Therefore, the reduced Lagrangian of the Chaplygin sleigh is

$$\begin{aligned} l=\tfrac{1}{2}\big (J \omega ^2 + mv \bar{v}\,\big ). \end{aligned}$$

The elements of the algebra $\mathfrak {se}(2) = \mathfrak {so}(2) {\circledS } {\mathbb {C}}$ in the complex representation used here are written as $(i \omega , v)$, where $i \omega \in \mathfrak {so}(2)$, $\omega \in {\mathbb {R}}$, and $v \in {\mathbb {C}}$. The bracket operation on the algebra $\mathfrak {se}(2)$ reads

$$\begin{aligned}{}[(i \omega _1, v_1), (i \omega _2, v_2)] = (0, i \omega _1 v_2 - i \omega _2 v_1). \end{aligned}$$

(2.5)

Using (2.5), the constrained Hamel equations for the Chaplygin sleigh are computed to be

$$\begin{aligned} \dot{\omega }= 0,\quad \dot{v} = 0. \end{aligned}$$

(2.6)

Recall that in (2.6) the quantity v is real-valued. The reduced dynamics of the Chaplygin sleigh is given by the constrained Hamel Eq. (2.6) along with the kinematic Eq. (2.4).

Solving these equations gives

$$\begin{aligned} \omega= & {} {\mathrm {const}},\quad v = {\mathrm {const}},\quad \theta = \theta _0 + \omega t,\\ z= & {} \left\{ \begin{aligned}&z_0 + \hbox {e}^{i\theta _0} v t&\text {if}&\omega&= 0\\&z_0 - \frac{i v}{\omega } \big (\hbox {e}^{i(\theta _0 + \omega t)} - \hbox {e}^{i \theta _0}\big )&\text {if}&\omega&\ne 0 \end{aligned}\right. \end{aligned}$$

and so generically the sleigh moves along a circle at a uniform rate.

3 Infinite-Dimensional Systems

Starting from this section, we no longer assume that systems have a finite number of degrees of freedom. As the use of frames and bases in the infinite-dimensional setting is unnatural, cumbersome, and not even always possible, we introduce a coordinate-free approach to Hamel’s formalism. Thus, instead of frames, we use linear velocity substitutions. These substitutions, however, are not induced by a (local) configuration coordinate change.

3.1 Lagrangian Mechanics

Let M be an infinite-dimensional smooth manifold modeled on a convenient vector space W and let TM be its kinematic tangent bundle with the projection $\pi _M:TM\rightarrow M$. Consider the initial inclusion map $i: Q\rightarrow M$ and the pullback vector bundle $P=i^{*}TM$.² The importance of the manifold Q will be demonstrated shortly.

A Lagrangian is a smooth function $L:P\rightarrow \mathbb R$. The dynamics for this Lagrangian is defined in a usual way by Hamilton’s principle: The curve $\gamma :[a,b] \rightarrow Q$ is a trajectory if

$$\begin{aligned} \delta \int _a^b L \,\mathrm{d}t = 0 \end{aligned}$$

along $\gamma$.

To demonstrate the necessity of the initial inclusion map in infinite-dimensional mechanics, consider the wave equation

$$\begin{aligned} \phi _{tt} = \nabla ^2 \phi \end{aligned}$$

on ${\mathbb {R}}^n$. This is the Euler–Lagrange equation for the Lagrangian

$$\begin{aligned} L(\phi , \dot{\phi }) = \tfrac{1}{2} \big \langle \dot{\phi }, \dot{\phi }\big \rangle - \tfrac{1}{2} \big \langle \nabla \phi , \nabla \phi \big \rangle , \end{aligned}$$

where $\langle \cdot , \cdot \rangle$ is the standard Riemann metric on $L^2 ({\mathbb {R}}^n)$. This Lagrangian is defined on the space $P=H^1 \times L^2 \subset L^2 \times L^2 = TL^2$ and not on the entire $TL^2$. Using our notations, $Q = H^1 \subset L^2 = M$. See Marsden and Hughes (1983) for details.

3.2 Hamel’s Formalism and Hamilton’s Principle

Turning to Hamel’s formalism, let U be an open subset of M containing $q\in Q$ and let

$$\begin{aligned} U\times W \ni (q, \xi ) \mapsto (q, {\Psi }_q \xi ) \in \pi _M^{-1}(U) \subset TM \end{aligned}$$

(3.1)

be a fiber-preserving diffeomorphism that is linear in the second input. Hence, for each $q \in U$, both $\Psi _q:W\rightarrow T_q M$ and $\Psi _q^{-1}:T_q M\rightarrow W$ are invertible bounded linear operators smoothly dependent on q in an open subset $i^{-1}(U)\subset Q$. The latter is verified by selecting the map (3.1) as a bundle chart on TM and using the Cartesian closedness $C^\infty (U\times W, W)\cong C^\infty (U,C^\infty (W,W))$ along with the fact that the space of all bounded linear operators from a convenient vector space E to a convenient vector space F is a closed linear subspace of $C^\infty (E,F)$.³

Remark

As pointed out in Marsden and Ratiu (1999), the space W and its dual are chosen to be suitable, in the functional-analytic sense, to the problem in question. As the Lagrangian fails to be defined, in general, on TM, it is necessary to consider various forms of equations of motion, such as weak and strong forms. In particular, the weak form is important in understanding the existence of solutions as well as in numerical methods. Further, the objects involved may not even be defined on the entire TM but only on a dense subset already in the Banach case. See Marsden and Ratiu (1999) for details and references.

For each $q \in U$ and $\xi \in W$, the operator $\Psi _q: W \rightarrow T_q M$ introduced in (3.1) outputs the vector ${\Psi }_q \xi \in T_q M$.⁴ Thus, each $\xi \in W$ defines the vector field

$$\begin{aligned} {\Psi } \xi := \cup _{q \in U} (q, {\Psi }_q \xi ) \end{aligned}$$

on U, which usually will be written as

$$\begin{aligned} {\Psi } \xi (q):= {\Psi }_q \xi . \end{aligned}$$

Given two vectors $\xi ,\eta \in W$, define an antisymmetric bilinear operation $[\cdot , \cdot ]_q:W \times W \rightarrow W$ by

$$\begin{aligned} {\Psi }_q [\xi , \eta ]_q = [{\Psi } \xi , {\Psi } \eta ](q), \end{aligned}$$

(3.2)

where $[\cdot , \cdot ]$ is the Jacobi–Lie bracket of two vector fields on the manifold M. Next, for arbitrary $\xi$, $\eta$, $\zeta \in W$, we have

$$\begin{aligned}&{\Psi }_q\big ([[\xi ,\eta ]_q, \zeta ]_q + [[\eta , \zeta ]_q, \xi ]_q + [[\zeta , \xi ]_q, \eta ]_q\big )\\&\quad =[[{\Psi } \xi , {\Psi } \eta ], {\Psi } \zeta ](q) +[[{\Psi } \eta , {\Psi } \zeta ], {\Psi } \xi ](q) +[[{\Psi } \zeta , {\Psi } \xi ], {\Psi } \eta ](q)=0, \end{aligned}$$

implying, in view of invertibility of $\Psi _q$, the Jacobi identity for the bracket $[\cdot , \cdot ]_q$. Therefore, for each $q \in U$, the space W with the operation $[\cdot , \cdot ]_q$ is a Lie algebra, denoted hereafter $W_q$.

The dual of $[\cdot ,\cdot ]_q$ is, by definition, the operation $[\cdot ,\cdot ]_q^{*}: W_q \times W_q^{*} \rightarrow W_q^{*}$ given by

$$\begin{aligned} \big \langle [\xi , \alpha ]_q^{*}, \eta \big \rangle _W := \big \langle \alpha , [\xi , \eta ]_q \big \rangle _W, \quad \xi , \eta \in W,\quad \alpha \in W^{*}. \end{aligned}$$

As in the finite-dimensional setting, let $\dot{q}$ and $\delta q$ denote the velocity and the virtual displacement at $q \in Q$. From now on, the inverse images of $\dot{q}$ and $\delta q$ are written as $\xi , \eta \in W$, that is, $\dot{q} = {\Psi }_q \xi$ and $\delta q = {\Psi }_q \eta$.

Interpreting $\xi$ as an independent variable that replaces $\dot{q}$ (locally) defines the Lagrangian as a smooth function of $(q, \xi )$ on $V \times W$:

$$\begin{aligned} l(q, \xi ):= L(q, {\Psi }_q \xi ), \end{aligned}$$

where we used the smoothness of the mapping $V\times W \ni (q, \xi ) \mapsto {\Psi }_q \xi \in \pi _M^{-1}(U)$. The equations of motion written when $(q, \xi )$ are selected as (local) coordinates on the velocity phase space are called the Hamel equations.

Recall that, given a smooth curve $q(t) \in Q$, $t \in [a, b]$, its variation is a smooth one-parameter family of curves

$$\begin{aligned}{}[a, b] \times [-\varepsilon , \varepsilon ] \ni (t, \tau ) \mapsto \beta (t,\tau ) \in Q, \quad \text {such that} \quad \beta (t, 0) = q(t). \end{aligned}$$

An infinitesimal variation, also known as variation field $\delta q$, is defined by

$$\begin{aligned} \delta q(t, \tau ):= \frac{\partial }{\partial \tau } \beta (t,\tau ). \end{aligned}$$

When this field is evaluated along the curve q(t), we write $\delta q(t)$, i.e.,

$$\begin{aligned} \delta q(t):= \delta q(t,0) = \frac{\partial }{\partial \tau }\bigg |_{\tau =0}\,\beta (t,\tau ). \end{aligned}$$

(3.3)

Thus, a variation of a smooth curve $q(t) \in Q$ defines a curve $\eta (t) \in W$

$$\begin{aligned} \delta q(t) = {\Psi }_{q(t)} \eta (t). \end{aligned}$$

Theorem 3.1

(Hamilton’s Principe for Hamel’s Equations). Let $L:P\rightarrow {\mathbb {R}}$ be a Lagrangian and l be its representation in local coordinates $(q,\xi )$. Then, the following statements are equivalent:

• (i) The curve q(t), where $a \le t \le b$, is a critical point of the action functional

  $$\begin{aligned} \int _a ^b L (q, \dot{q})\,\mathrm{d}t \end{aligned}$$

  on the space of curves in Q connecting $q_a$ to $q_b$ on the interval [a, b], where we choose variations of the curve q(t) that satisfy $\delta q(a) = \delta q(b) = 0$.

• (ii) The curve q (t) satisfies the weak form of the Euler–Lagrange equations

  $$\begin{aligned} \int _a^b \bigg \langle \frac{\delta L}{\delta q} - \frac{d}{\mathrm{d}t} \frac{\delta L}{\delta \dot{q}}, \delta q\bigg \rangle \,\mathrm{d}t = 0. \end{aligned}$$

  (3.4)

  Furthermore, if $\delta L / \delta q \in T_q^{*} M$ and $i_{*} T_q Q$ is dense in $T_q M$ for every $q\in Q$, the curve q (t) satisfies the strong form of the Euler–Lagrange equations

  $$\begin{aligned} \frac{d}{\mathrm{d}t} \frac{\delta L}{\delta \dot{q}} - \frac{\delta L}{\delta q}=0. \end{aligned}$$

  (3.5)

• (iii) The curve $(q(t), \xi (t))$ is a critical point of the functional

  $$\begin{aligned} \int _a^b l(q, \xi )\,\mathrm{d}t \end{aligned}$$

  (3.6)

  with respect to variations $\delta \xi$, induced by the variations

  $$\begin{aligned} \delta q = {\Psi }_q \eta , \end{aligned}$$

  and given by

  $$\begin{aligned} \delta \xi = \dot{\eta }+ [\xi , \eta ]_q. \end{aligned}$$

  (3.7)

• (iv) The curve $(q(t), \xi (t))$ satisfies the weak form of the Hamel equations

  $$\begin{aligned} \int _a^b \bigg \langle {\Psi }^{*}_q \frac{\delta l}{\delta q} + \bigg [\xi , \frac{\delta l}{\delta \xi } \bigg ]_q^{*} - \frac{d}{\mathrm{d}t} \frac{\delta l}{\delta \xi }, \eta \bigg \rangle \,\mathrm{d}t = 0, \quad \eta \in {\Psi }^{-1}_q (T_q Q) \end{aligned}$$

  (3.8)

  coupled with the equations $\dot{q} = {\Psi }_q \xi .$ If $\delta l /\delta q \in T_q^{*} M$ and $i_{*}T_q Q$ is dense in $T_q M$ for every $q\in Q$, the curve $(q(t), \xi (t))$ satisfies the strong form of the Hamel equations

  $$\begin{aligned} \frac{d}{\mathrm{d}t} \frac{\delta l}{\delta \xi } = \bigg [\xi , \frac{\delta l}{\delta \xi }\bigg ]_q^{*} + {\Psi }^{*}_q \frac{\delta l}{\delta q} \end{aligned}$$

  (3.9)

  coupled with the equation $\dot{q} = {\Psi }_q \xi$.

For the early development of these equations in the finite-dimensional setting see Poincaré (1901) and Hamel (1904).

Proof

The equivalence of (i) and the weak form of the Euler–Lagrange Eq. (3.4) is proved by integration by parts:

$$\begin{aligned} \delta \int _a^b L(q, \dot{q})\,\mathrm{d}t = \int _a^b \bigg ( \bigg \langle \frac{\delta L}{\delta q}, \delta q \bigg \rangle + \bigg \langle \frac{\delta L}{\delta \dot{q}}, \delta \dot{q} \bigg \rangle \bigg ) \,\mathrm{d}t = \int _a ^b \bigg \langle \frac{\delta L}{\delta q} - \frac{d}{\mathrm{d}t}\frac{\delta L}{\delta \dot{q}},\delta q \bigg \rangle \,\mathrm{d}t, \end{aligned}$$

where $\langle \cdot ,\cdot \rangle$ is the paring of $T_q^{*}Q$ with $T_q Q$. The strong form of the Euler–Lagrange Eq. (3.5) follows easily from a standard contradiction argument,⁵ which finishes the proof of the equivalence of (i) and (ii).

To prove the equivalence of (i) and (iii), we first compute the quantities $\delta \dot{q}$ and $d(\delta q)/\mathrm{d}t$. Recall that

$$\begin{aligned} \delta q(t) = \frac{\partial }{\partial \tau }\bigg |_{\tau =0}\,\beta (t,\tau ) = {\Psi }_{q(t)} \eta (t),\quad \text {where}\quad \eta (t)\in W. \end{aligned}$$

Using the definition (3.3) of the field $\delta q$, one concludes that

$$\begin{aligned} \delta \Psi _{q(t)} = \frac{\partial }{\partial \tau }\bigg |_{\tau =0}\,\Psi _{\beta (t,\tau )} = \delta q(t) \big [{{\Psi }}_{q(t)}\big ] =\big ({\Psi }_{q(t)} \eta (t)\big ) \big [{\Psi }_{q(t)}\big ]. \end{aligned}$$

(3.10)

Hereafter, v[f] denotes the derivative of the function f along the vector filed v; in particular, in (3.10) an operator-valued function is differentiated.

Similarly,

$$\begin{aligned} \tfrac{d}{\mathrm{d}t} \Psi _{q(t)} = \dot{q} (t) \big [\Psi _{q(t)}\big ] = \big ({\Psi }_{q(t)} \xi (t)\big ) \big [{{\Psi }}_{q(t)}\big ], \end{aligned}$$

and therefore

$$\begin{aligned} \delta \dot{q} = \big ({\Psi }_q \eta \big ) [{\Psi }_q]\xi + {\Psi }_q \delta \xi , \quad \tfrac{d}{\mathrm{d}t} \delta q = \big ({\Psi }_q \xi \big ) [{\Psi }_q]\eta + {\Psi }_q \dot{\eta }. \end{aligned}$$

From $\delta \dot{q} = \frac{d}{\mathrm{d}t} \delta q$, we obtain

$$\begin{aligned} {\Psi }_q \big (\delta \xi - \dot{\eta }\big ) = \big ({\Psi } \xi \big ) [{\Psi } \eta ] (q) - \big ({\Psi } \eta \big ) [{\Psi }\xi ] (q) = [{\Psi } \xi , {\Psi } \eta ](q) = {\Psi }_q [\xi , \eta ] _{q}, \end{aligned}$$

which implies formula (3.7).

To prove the equivalence of (iii) and the weak form of Hamel’s Eq. (3.8), we use the above formula and compute the variation of the action (3.6):

$$\begin{aligned} \delta \int _a^b l(q, \xi )\,\mathrm{d}t&= \int _a^b \bigg (\bigg \langle \frac{\delta l}{\delta q}, \delta q \bigg \rangle +\bigg \langle \frac{\delta l}{\delta \xi },\delta \xi \bigg \rangle \bigg )\,\mathrm{d}t\\&= \int _a^b \bigg ( \bigg \langle \frac{\delta l}{\delta q},{\Psi }_q \eta \bigg \rangle + \bigg \langle \frac{\delta l}{\delta \xi }, \dot{\eta }+ [\xi , \eta ]_q \bigg \rangle \bigg )\,\mathrm{d}t\\&= \int _a^b \bigg \langle {\Psi }^{*}_q \frac{\delta l}{\delta q} + \bigg [\xi , \frac{\delta l}{\delta \xi } \bigg ]_q^{*} - \frac{d}{\mathrm{d}t} \frac{\delta l}{\delta \xi }, \eta \bigg \rangle \,\mathrm{d}t. \end{aligned}$$

If $\delta l/\delta q \in T_q^{*} M$ and $i_{*}T_q Q$ is dense in $T_q M$ for every $q\in Q$, then for each t the subspace ${\Psi }^{-1}_{q(t)}(i_{*}T_{q(t)}Q)$ is dense in W, and the variational derivative vanishes if and only if the strong form of the Hamel Eq. (3.9) is satisfied. $\square$

Example 3.2

For an incompressible fluid flow in a compact domain $D \subset {\mathbb {R}}^3$ with a smooth boundary the configuration space is the group ${\text {Diff}} (D)$ of (volume-preserving) diffeomorphism of D, which is a regular Lie group in convenient setting. Let q(t) be a curve in this group, one may think of q(t) as a particular fluid flow. Following Euler (1757a, (1757b, (1761), one typically uses the spatial velocity $\xi := \dot{q} \circ q^{-1} \in T_e {\text {Diff}} (D)$. Selecting $W = T_e {\text {Diff}} (D) = {\mathcal {X}} (D)$, the space of smooth vector fields on D tangent to the boundary, and $\Psi _q = TR_q$ gives $\dot{q} = {\Psi }_q \xi$. Therefore, the use of spatial velocity in fluid dynamics is an instance of infinite-dimensional Hamel’s formalism. The variation formula (3.7) becomes

$$\begin{aligned} \delta \xi = \dot{\eta }- {\text {ad}}_\xi \eta \equiv \dot{\eta }+ [\xi , \eta ], \end{aligned}$$

where $[\cdot , \cdot ]$ is the Jacobi–Lie bracket on D. The dynamics, in the form of Hamel’s equations, reads

$$\begin{aligned} \frac{d}{\mathrm{d}t} \frac{\delta l}{\delta \xi } +{\text {ad}}^{*}_\xi \frac{\delta l}{\delta \xi } = 0. \end{aligned}$$

The latter are the Euler–Poincaré equations, as established by Poincaré (1901) and Arnold (1966).

Remark

The convective representation of fluid dynamics is straightforward to obtain by setting $\Psi _q = TL_q$. See Gay-Balmaz et al. (2012) for details on the convective representation in continuum mechanics.

Example 3.3

For an inextensible string moving in the plane, the configuration manifold is the space of smooth embeddings ${\text {Emb}}([0,1],{\mathbb {R}}^2)$. We will view ${\mathbb {R}}^2$ as a complex plane.

Given $z \in {\text {Emb}}([0,1], {\mathbb {C}})$, the inextensibility constraint reads $\Vert z_s\Vert = 1$, $0\le s\le 1$. For simplicity, we assume no resistance to bending. Therefore, the Lagrangian reads

$$\begin{aligned} L(z) = \int _0^1 \tfrac{1}{2} \big (\Vert \dot{z}\Vert ^2 - \lambda (\Vert z_s\Vert ^2 - 1)\big )\,\mathrm{d}s, \end{aligned}$$

where $\lambda :[0,1]\rightarrow {\mathbb {R}}$ is the Lagrange multiplier (tension). The boundary conditions for the Lagrange multiplier are a part of the requirement $\delta L = 0$. For a free motion of a string, these conditions read

$$\begin{aligned} \lambda |_{s=0} = \lambda |_{s=1} = 0. \end{aligned}$$

(3.11)

Let

$$\begin{aligned} \dot{z} = {\Psi }_z \xi = z_s \xi , \end{aligned}$$

(3.12)

so the velocity components to be used to construct Hamel’s equations are represented by a complex-valued function $\xi = \xi (s)$. The real and imaginary parts of $\xi$ are the tangent and normal velocity components of the points of the string, as is illustrated in Fig. 2.

Fig. 2

An inextensible planar string

The Lagrangian becomes

$$\begin{aligned} l = \int _0^1 \tfrac{1}{2} \big ( \bar{z}_s z_s \bar{\xi }\xi - \lambda (\bar{z}_s z_s - 1) \big ) \,\mathrm{d}s, \end{aligned}$$

in which the density should be understood as a function of $(z_s, \bar{z}_s, \xi , \bar{\xi })$ and the Lagrange multiplier $\lambda$.

Next, the bracket formula (3.2) for the string becomes

$$\begin{aligned}{}[{\Psi } \xi , {\Psi } \eta ] (z)= & {} \frac{d}{\mathrm{d}\tau } \bigg |_{\tau = 0} \big ( (z + \tau z_s \xi )_s \eta - (z + \tau z_s \eta )_s \xi \big )\\= & {} z_s (\xi _s \eta - \eta _s \xi ) = {\Psi }_z [\xi , \eta ]_z. \end{aligned}$$

That is,

$$\begin{aligned}{}[\xi , \eta ]_z = \xi _s \eta - \xi \eta _s. \end{aligned}$$

(3.13)

Instead of establishing the formulae for the dual bracket and dual operator $\Psi ^{*}$, it is more efficient in this example to directly work with the variational principle. We have:

$$\begin{aligned} \frac{\delta l}{\delta z} \delta z + \frac{\delta l}{\delta \xi } \delta \xi + \frac{\delta l}{\delta \bar{z}} \delta \bar{z} + \frac{\delta l}{\delta \bar{\xi }} \delta \bar{\xi }, \end{aligned}$$

(3.14)

and since l is real-valued, the two last terms are obtained from the first two by conjugation. Thus, it is sufficient to evaluate the last two terms in (3.14):

$$\begin{aligned} \frac{\delta l}{\delta \bar{z}} \delta \bar{z} + \frac{\delta l}{\delta \bar{\xi }} \delta \bar{\xi }&= \frac{\delta l}{\delta \bar{z}} \delta \bar{z} + \frac{\delta l}{\delta \bar{\xi }} \big (\bar{\xi }_s \bar{\eta }- \bar{\xi }\bar{\eta }_s\big ) - \frac{d}{\mathrm{d}t} \frac{\delta l}{\delta \bar{\xi }} \bar{\eta }\\&= \int _0^1 \tfrac{1}{2} \Big ( \big (\lambda z_s - z_s \bar{\xi }\xi \big )_s \delta \bar{z} + \bar{z}_s z_s \xi \big (\bar{\xi }_s \bar{\eta }- \bar{\xi }\bar{\eta }_s\big ) - \tfrac{d}{\mathrm{d}t} \big (\bar{z}_s z_s \xi \big ) \bar{\eta }\Big )\,\mathrm{d}s\\&\quad -\tfrac{1}{2} \bar{z}_s z_s \big (\lambda - \bar{\xi }\xi \big )\bar{\eta }\big |_{s=0}^{s=1}\\&= \int _0^1 \tfrac{1}{2} \Big ( z_s \bar{z}_{ss} \xi \bar{\xi }+ z_s \bar{z}_s \xi \bar{\xi }_s + \lambda _s \bar{z}_s z_s + \lambda z_{ss} \bar{z}_s - \tfrac{d}{\mathrm{d}t} \big (\bar{z}_s z_s \xi \big ) \Big ) \bar{\eta }\,\mathrm{d}s\\&\quad -\tfrac{1}{2} \bar{z}_s z_s \lambda \bar{\eta }\big |_{s=0}^{s=1}, \end{aligned}$$

which, after imposing the constraint

$$\begin{aligned} \bar{z}_s z_s = 1, \end{aligned}$$

(3.15)

implies Hamel’s string equation

$$\begin{aligned} \dot{\xi }= \xi \bar{\xi }_s + \lambda _s + i \varkappa \big (\lambda - \bar{\xi }\xi \big ) \end{aligned}$$

(3.16)

as well as the tension conditions (3.11). Here $\varkappa = i z_s \bar{z}_{ss}$ is the signed curvature of the curve $[0,1] \ni s \mapsto z(s) \in {\mathbb {C}}$. One of the implications of (3.16) is

$$\begin{aligned} \lambda _s = {\text {Re}}\big (\xi _t - \xi \bar{\xi }_s\big ), \end{aligned}$$

(3.17)

it will be used to identify the Lagrange multiplier $\lambda$ in terms of the state of the string.

Using the identity

$$\begin{aligned} \xi _s + \bar{\xi }_s + \bar{z}_s z_{ss} \big (\xi - \bar{\xi }\,\big ) = 0 \end{aligned}$$

(3.18)

that follows from (3.12) and (3.15), one obtains an alternative representation of Eq. (3.16),

$$\begin{aligned} \dot{\xi }= -\xi \xi _s + \lambda _s + i \varkappa \big (\lambda - \xi \xi \big ). \end{aligned}$$

(3.19)

Either of the Eqs. (3.16) and (3.19) is equivalent to the Euler–Lagrange equations for the string.

The Lagrange multiplier as a function of string’s state is obtained by solving the differential equation

$$\begin{aligned} \lambda _{ss} - \varkappa ^2 \lambda + | \xi _s + i \varkappa \xi |^2 = 0 \end{aligned}$$

(3.20)

subject to the boundary conditions (3.11). To derive Eq. (3.20), one differentiates (3.17) with respect to s to obtain

$$\begin{aligned} \lambda _{ss} = - |\xi _s |^2 + {\text {Re}}\big (\xi _{st} - \xi \bar{\xi }_{ss}\big ). \end{aligned}$$

(3.21)

Formula (3.21) becomes (3.20) after a transformation using the identity

$$\begin{aligned} {\text {Re}} \big (\xi _{st} - \xi \bar{\xi }_{ss} + i \varkappa \big (\xi _t - \bar{\xi }\xi _s\big )\big ) = 0 \end{aligned}$$

that follows from (3.12) and (3.15).

Remark

Alternatively, one defines the operator $\Psi$ by

$$\begin{aligned} {\Psi }_z \xi := \frac{z_s}{|z_s|} \xi . \end{aligned}$$

Because of the constraint $|z_s| = 1$, the resulting Hamel equation is (3.16). However, the bracket $[\xi , \eta ]_z$ is now given not by (3.13) but by a slightly different formula. This latter bracket is in fact induced by the (standard) bracket of the Lie algebra of the infinite-dimensional group

$$\begin{aligned} G = \big \{[0,1] \ni s \mapsto g(s) \in {\text {SE}}(2)\big \}. \end{aligned}$$

To see that, the string dynamics should be interpreted as a motion on G specified by the degenerate Lagrangian

$$\begin{aligned} l = \int _0^1 \tfrac{1}{2} \big ( \bar{\xi }\xi - \lambda (\bar{z}_s z_s - 1) \big )\,\mathrm{d}s \end{aligned}$$

subject to the constraint

$$\begin{aligned} \frac{z_s}{|z_s|} = \hbox {e}^{i \theta }, \end{aligned}$$

(3.22)

where $(\theta , z)$ are the (standard) coordinates on ${\text {SE}}(2) = {\text {SO}}(2) \mathop {\circledS } {\mathbb {C}}$ and $\xi$ is the ${\mathbb {C}}$-component of the body velocity $g^{-1} \dot{g}$. One then composes the ${\mathbb {C}}$-component of the Euler–Poincaré equations on G and imposes constraint (3.22). This results in the string Eq. (3.16). It is worth noticing that the derivation of these equations using formula (3.12) is simper and more efficient.

3.3 The Hamilton–Pontryagin Principle

Here we utilize the Hamilton–Pontryagin principle of Yoshimura and Marsden (2006a, (2006b, (2007) for the derivation of Hamel’s equations. This approach provides an alternative interpretation of Hamel’s formalism in general and of the bracket term in particular. The Hamilton–Pontryagin principle for finite-dimensional systems of Hamel type was introduced in Ball et al. (2012).

Recall that the Hamilton–Pontryagin principle identifies the trajectories for the Lagrangian $L:TQ\rightarrow \mathbb R$ with the critical points of the functional

$$\begin{aligned} \int _a^b \big (L(q,v) + \langle p, \dot{q} - v \rangle \big ) \,\mathrm{d}t, \end{aligned}$$

and so the curves the functional is calculated along belong to the Whitney sum $TQ \oplus T^{*}Q$. See Yoshimura and Marsden (2006a, (2006b, (2007) for details, motivation, and history.

Theorem 3.4

(The Hamilton–Pontryagin Principe for Hamel’s Equations). Let $L:P\rightarrow \mathbb R$ be a Lagrangian and l be its representation in local coordinates $(q,\xi )$ on P. Then, the following statements are equivalent:

• (i) The curve $(q(t),\xi (t),\mu (t)) \in V\times (W\oplus W^{*})$ is a critical point of the action functional

  $$\begin{aligned}\int _a^b \big ( l(q, \xi ) + \big \langle \mu , \Psi ^{-1}_q \dot{q} - \xi \big \rangle \big ) \,\mathrm{d}t \end{aligned}$$

  with respect to independent variations $\delta q = {\Psi }_q \eta$, $\delta \xi$, and $\delta \mu$, with $\eta (a)=\eta (b)=0$.

• (ii) The curve $(q(t), \xi (t),\mu (t))$ satisfies the weak form of the implicit Hamel equations

  $$\begin{aligned} \int _a^b \bigg \langle \Psi _q^{*} \frac{\delta l}{\delta q} - \dot{\mu }+[\xi ,\mu ]_q^{*}, \eta \bigg \rangle = 0, \quad \frac{\delta l}{\delta \xi } = \mu , \quad \mathrm{where}\quad \eta \in {\Psi }^{-1}_q (T_q Q), \end{aligned}$$

  together with the constraint $\xi =\Psi ^{-1}_q \dot{q}.$ If $\delta l / \delta q \in T_q^{*} M$ and $i_{*}T_q Q$ is dense in $T_q M$ for every $q\in Q$, the curve $(q(t), \xi (t),\mu (t))$ satisfies the strong form of the implicit Hamel equations

  $$\begin{aligned} \Psi _{q}^{*}\frac{\delta l}{\delta q} - \dot{\mu }+ [\xi ,\mu ]^{*}_q = 0,\quad \frac{\delta l}{\delta \xi } = \mu , \end{aligned}$$

  together with the constraint $\xi =\Psi ^{-1}_{q}\dot{q}.$

Proof

From $\Psi _q^{-1}\Psi _q = {\text {id}}$ we have

$$\begin{aligned} \delta \left( \Psi _q^{-1}\Psi _q\right) = \delta \Psi _q^{-1}\Psi _q + \Psi _q^{-1}\delta \Psi _q = 0, \end{aligned}$$

which implies

$$\begin{aligned} \delta \Psi _q^{-1} = - \Psi _q^{-1} \delta \Psi _q \Psi _q^{-1}. \end{aligned}$$

Therefore, using earlier calculation,

$$\begin{aligned} \delta ({\Psi }^{-1}_q\dot{q})&=\left( \delta \Psi ^{-1}_q\right) \,\dot{q} + \Psi ^{-1}_q \delta \dot{q}\\&= - \Psi _q^{-1} \delta \Psi _q \Psi _q^{-1} \dot{q} - \big (\tfrac{d}{\mathrm{d}t} \Psi ^{-1}_q\big ) \,\delta q + \tfrac{d}{\mathrm{d}t} \big (\Psi _q^{-1} \delta q\big )\\&= - \Psi _q^{-1} \delta \Psi _q \Psi _q^{-1} \dot{q} + \Psi _q^{-1} \tfrac{d}{\mathrm{d}t} \Psi _q \Psi _q^{-1} \delta q + \dot{\eta }\\&= \big [\Psi _q^{-1} \dot{q}, \eta \big ]_q + \dot{\eta }, \end{aligned}$$

where $\eta = \Psi _q^{-1} \delta q \in {\Psi }^{-1}_q (T_q Q)$.

Finally, taking the variation and using the above formula along with integration by parts gives

$$\begin{aligned}&\delta \int _a^b \big ( l(q, \xi ) + \big \langle \mu ,\Psi ^{-1}_q \dot{q} - \xi \big \rangle \big ) \,\mathrm{d}t\\&\quad = \int _a^b \bigg ( \bigg \langle \frac{\delta l}{\delta q},\delta q \bigg \rangle + \bigg \langle \frac{\delta l}{\delta \xi } - \mu ,\delta \xi \bigg \rangle - \big \langle \delta \mu ,\xi - \Psi ^{-1}_q \dot{q} \big \rangle + \big \langle \mu ,\delta (\Psi ^{-1}_q \dot{q}) \big \rangle \bigg ) \,\mathrm{d}t\\&\quad = \int _a^b \bigg ( \bigg \langle \frac{\delta l}{\delta q},\Psi _q \eta \bigg \rangle - \big \langle \dot{\mu }, \eta \big \rangle + \big \langle \mu , \big [ \Psi ^{-1}_q \dot{q}, \eta \big ]_q \big \rangle + \bigg \langle \frac{\delta l}{\delta \xi } - \mu , \delta \xi \bigg \rangle - \big \langle \delta \mu ,\xi \\ {}&\quad \ -\, \Psi ^{-1}_q \dot{q} \big \rangle \bigg ) \,\mathrm{d}t\\&\quad =\int _a^b \bigg ( \bigg \langle \Psi _q^{*} \frac{\delta l}{\delta q} - \dot{\mu }+ \big [\Psi ^{-1}_q \dot{q}, \mu \big ]^{*}_q, \eta \bigg \rangle + \bigg \langle \frac{\delta l}{\delta \xi } - \mu , \delta \xi \bigg \rangle - \big \langle \delta \mu , \xi - \Psi ^{-1}_q \dot{q} \big \rangle \bigg ) \,\mathrm{d}t. \end{aligned}$$

Setting the latter equal to zero and noting that $\delta \xi$ is an arbitrary element of W yields the desired results. $\square$

4 Systems with Constraints

In this section, we consider systems with ideal velocity constraints, both holonomic and nonholonomic. The dynamics of such systems is equivalent to the Lagrange–d’Alembert principle. To simplify the exposition, in the rest of the paper, we assume that $\delta L / \delta q \in T_q^{*} M$ and $i_{*} T_q Q$ is dense in $T_q M$ for every $q\in Q$, and thus all results will be stated for strong equations of motion. Similar statements for weak equations are straightforward to obtain.

4.1 The Lagrange–d’Alembert Principle

Recall that in this paper the constraints imposed on on the system are assumed linear and homogeneous in the velocity. Such constraints are specified by a vector subbundle ${\mathcal {D}}$ of the bundle $P=i^{*}TM$. The base of this subbundle is the manifold Q. This subbundle will, in general, be nonintegrable.

One of the ways to construct a subbundle of P is to take a pullback (induced by the initial inclusion map $i:Q\rightarrow M$) of a distribution on the manifold M. Verification of integrability of a distribution in the infinite-dimensional setting may be nontrivial as the Frobenius theorem has not been established in the general infinite-dimensional setting. See Kriegl and Michor (1997), Hiltunen (2000), Teichmann (2001), Filipović and Teichmann (2003) for some of the infinite-dimensional versions of Frobenius theorem.

The condition for a curve to satisfy the constraints is of course insufficient for the development of constrained mechanics. One needs a mechanism for constructing the vector field that captures the dynamics of the constrained system. For the ideal constraints in the finite-dimensional setting, this is accomplished by a projection. Such constraints define a submanifold of the velocity phase space and a projection onto this submanifold.

For a projection to be meaningful in the infinite-dimensional case, a submanifold has to be splitting. Thus, in the infinite-dimensional setting, we require that ${\mathcal {D}}$ is a locally splitting subbundle of P. That is, for each $q \in Q$ there exists a chart (U, h) of M with $i(q) \in U$ such that

$$\begin{aligned} Th(\pi _M^{-1} (U) \cap {\mathcal {D}}) = h(U) \times W^{{\mathcal {D}}}, \end{aligned}$$

where the closed subspace $W^{{\mathcal {D}}}$ of the model space W is splitting, or complemented, i.e., there is a closed subspace $W^{{\mathcal {U}}}$ of W such that $W^{{\mathcal {D}}} \oplus W^{\mathcal {U}} = W$ and the projection $\pi ^{{\mathcal {D}}}$ uniquely determined by setting $({\text {Ker}} \pi ^{{\mathcal {D}}}, {\text {Im}} \pi ^{{\mathcal {D}}}) = (W^{\mathcal {U}}, W^{{\mathcal {D}}})$ is continuous. Note that the continuous projection $\pi ^{{\mathcal {D}}}$ in the convenient space W is automatically smooth as a bounded linear mapping.⁶

The following Lagrange–d’Alembert principle is known to be equivalent to the dynamics of systems with ideal holonomic and nonholonomic constraints:

Definition 4.1

The Lagrange–d’Alembert equations of motion for the system are those determined by

$$\begin{aligned} \delta \int ^b_a L(q, \dot{q})\,\mathrm{d}t = 0, \end{aligned}$$

where we choose variations $\delta q(t)$ of the curve q(t) that satisfy $\delta q(a) = \delta q(b) = 0$ and $\delta q(t) \in {\mathcal {D}}_{q(t)}$ for each t where $a\le t\le b$.

This principle is supplemented by the condition that the curve q(t) itself satisfies the constraints. Note that we take the variation before imposing the constraints; that is, we do not impose the constraints on the family of curves defining the variation. This is well known to be important to obtain the correct mechanical equations (see Arnold et al. 2006 and Bloch 2015 for a discussion of other types of constraints and references).

The Lagrange–d’Alembert principle is equivalent to the equations

$$\begin{aligned} \frac{d}{\mathrm{d}t} \frac{\delta L}{\delta \dot{q}} -\frac{\delta L}{\delta q} \in {\mathcal {D}}^\circ _q,\quad \dot{q} \in {\mathcal {D}}_q. \end{aligned}$$

(4.1)

Here,

$$\begin{aligned} {\mathcal {D}}^\circ _q = \big \{a \in T_q^{*}M \mid \langle a, v \rangle = 0, v \in {\mathcal {D}}_q\big \}. \end{aligned}$$

One way to give a more explicit representation of dynamics (4.1), under certain technical conditions, is to make use of the Euler–Lagrange equations with multipliers. Let the fibers of the subbundle ${\mathcal {D}}$ be locally written as

$$\begin{aligned} {\mathcal {D}}_q = \{v \in T_q M \mid \mathop {A(q)} v = 0\}, \end{aligned}$$

where A(q) for each $q \in Q$ is a continuous linear operator on $T_q M$ with values in the vector space $W^{\mathcal {U}}$. For instance, if there is a single constraint imposed on the system, A(q) is a linear functional. We assume smooth dependence of A(q) on q.

The constrained variations $\delta q(t) \in T_{q(t)}Q$ satisfy the condition

$$\begin{aligned} \mathop {A(q)} \delta q = 0. \end{aligned}$$

(4.2)

Using Definition 4.1 and formula (4.2), one writes the equations of motion as

$$\begin{aligned} \frac{d}{\mathrm{d}t} \frac{\delta L}{\delta \dot{q}} - \frac{\delta L}{\delta q} \in \overline{{\text {Im}} A^{*}(q)}, \quad \mathop {A(q)} \dot{q} = 0, \end{aligned}$$

where $A^{*}(q):{W^{\mathcal {U}}}^{*} \rightarrow T_q^{*}M$ is the adjoint of A(q) and where the closure should be understood as weak* closure. Thus, if $A^{*}(q)$ has a weak* closed range,⁷ there exist Lagrange multipliers $\lambda \in {W^{\mathcal {U}}}^{*}$ such that

$$\begin{aligned} \frac{d}{\mathrm{d}t} \frac{\delta L}{\delta \dot{q}} - \frac{\delta L}{\delta q} = \mathop {A^{*}(q)}\lambda ,\quad \mathop {A(q)}\dot{q} = 0. \end{aligned}$$

4.2 The Constrained Hamel Equations

Given a nonholonomic system, that is, a Lagrangian $L:P\rightarrow \mathbb R$ and constraint distribution ${\mathcal {D}}$, select the operators $\Psi _q:W \rightarrow T_q M$, $q\in U \subset Q$, such that there exist closed subspaces $W^{{\mathcal {D}}}$, $W^{\mathcal {U}} \subset W$ with the properties $W = W^{{\mathcal {D}}} \oplus \, W^{\mathcal {U}}$ and $\Psi _q = \Psi _q^{{\mathcal {D}}} \oplus \, \Psi _q^{\mathcal {U}}$, where $\Psi _q^{{\mathcal {D}}}: W^{{\mathcal {D}}} \rightarrow {\mathcal {D}}_q$ and $\Psi _q^{\mathcal {U}}: W^{\mathcal {U}} \rightarrow \mathcal U_q$ and their inverses are bounded linear operators smoothly dependent on $q \in U$. One way to choose the operators $\Psi _q$ is to use the above subbundle chart. In general, $U \ne Q$, as numerous finite-dimensional examples demonstrate.

Each $\dot{q}\in TM$ is then uniquely written as

$$\begin{aligned} \dot{q} = {\Psi }_q \xi ^{{\mathcal {D}}} + {\Psi }_q \xi ^{\mathcal {U}}, \quad \text{ where } \quad {\Psi }_q \xi ^{{\mathcal {D}}} \in {\mathcal {D}}_q, \end{aligned}$$

(4.3)

i.e., ${\Psi }_q \xi ^{{\mathcal {D}}}$ is the component of $\dot{q}$ along ${\mathcal {D}}_q$. Similarly, each $\alpha \in W^{*}$ can be uniquely decomposed as

$$\begin{aligned} \alpha = \alpha _{{\mathcal {D}}} +\alpha _{\mathcal {U}}, \end{aligned}$$

where $\alpha _{{\mathcal {D}}}$ and $\alpha _{\mathcal {U}}$ denote the component of $\alpha$ along the duals of $W^{{\mathcal {D}}}$ and $W^{\mathcal {U}}$, respectively. Actually, we have

$$\begin{aligned} \alpha _{{\mathcal {D}}} = \big (\pi ^{{\mathcal {D}}}\big )^{*} \circ \alpha |_{W^{{\mathcal {D}}}} \quad \text {and}\quad \alpha _{\mathcal {U}} = \Big ( {\text {id}} - \big (\pi ^{{\mathcal {D}}}\big )^{*} \Big ) \circ \alpha |_{W^{\mathcal {U}}}, \end{aligned}$$

where $\big (\pi ^{{\mathcal {D}}}\big )^{*}$ is the adjoint of $\pi ^{{\mathcal {D}}}$. Using (4.3), the constraints read

$$\begin{aligned} \xi = \xi ^{{\mathcal {D}}} \quad \text{ or } \quad \xi ^{\mathcal {U}} = 0. \end{aligned}$$

This implies

$$\begin{aligned} \delta \xi = \delta \xi ^\mathcal {D} \quad \text{ or } \quad \delta \xi ^\mathcal {U} = 0. \end{aligned}$$

The Lagrange–d’Alembert principle then implies the following theorem:

Theorem 4.2

The dynamics of a nonholonomic system is represented by the strong form of constrained Hamel equations

$$\begin{aligned} \bigg ( \frac{d}{\mathrm{d}t} \frac{\delta l}{\delta \xi } - \bigg [ \xi ^\mathcal {D},\frac{\delta l}{\delta \xi } \bigg ]^*_q - \Psi _q^{*} \frac{\delta l}{\delta q} \bigg )_\mathcal {D} = 0, \quad \xi ^\mathcal {U} = 0, \quad \dot{q} = {\Psi }_q \xi ^{{\mathcal {D}}}. \end{aligned}$$

(4.4)

Example 4.3

Consider an inextensible string moving in the plane subject to the vanishing normal velocity constraint. See Fig. 2. One may think of a motion of a ‘sharp’ string on the horizontal ice. Using the notations introduced in Example 3.3, the constraint reads

$$\begin{aligned} \xi = \bar{\xi }, \end{aligned}$$

(4.5)

i.e., $\xi \in \mathbb R$. Equations (4.4) for the constrained string thus become

$$\begin{aligned} \dot{\xi }&= \xi \xi _s + \lambda _s, \end{aligned}$$

(4.6)

$$\begin{aligned} \dot{z}&= z_s \xi , \end{aligned}$$

(4.7)

supplemented by the inextensibility condition.

Identity (3.18) in the presence of constraint (4.5) implies

$$\begin{aligned} \xi _s = 0. \end{aligned}$$

That is, all points of the string have the same speed, and (4.6) becomes

$$\begin{aligned} \dot{\xi }= \lambda _s. \end{aligned}$$

(4.8)

Using the boundary conditions (3.11), we conclude that

$$\begin{aligned} \dot{\xi }= 0. \end{aligned}$$

Summarizing, $\xi ={\mathrm {const}}$ throughout the motion. This is in agreement with the motion of the Chaplygin sleigh for which the velocity of the contact point relative to the body frame is constant. Unlike the sleigh, the constrained string motion is not completely determined by the initial state: Any solution of (4.7) is of the form

$$\begin{aligned} z = \phi (s + \xi t), \end{aligned}$$

where $\phi$ is an arbitrary twice-differentiable complex-valued function. The initial conditions define $\phi$ on the segment [0, 1]. Outside this segment, the function $\phi$ is unknown, unless, for example, the motion of the front end of the string is prescribed. The motion of the constrained string is therefore purely kinematic: The string follows its front end at a constant speed.

This behavior is similar to that of the degenerate Chaplygin sleigh specified by the Lagrangian $l = \tfrac{1}{2} \xi \bar{\xi }$ and the constraint $\xi = \bar{\xi }$, where $\xi = e ^{-i \theta } \dot{z}$. The Lagrangian is degenerate as the term quadratic in $\dot{\theta }$ is absent, i.e., the moment of inertia of the sleigh equals zero.

For the degenerate sleigh, the dynamics reads

$$\begin{aligned} \dot{\xi }= 0, \quad \dot{z} = e ^{i \theta } \xi , \end{aligned}$$

where $\theta (t)$ is an arbitrary function. Thus, the motions are not identified by the initial conditions.⁸

Another remark about the string on ice is that, similar to ${\text {SE}}(2)$-snakes of Krishnaprasad and Tsakiris (1994), it is almost holonomic: Adding a single (holonomic) constraint $z(0,t) = z(1,t)$ renders the system holonomic. The string becomes closed and will slide, at a constant speed, along its initial shape.

5 Systems with Symmetry

Here we present infinite-dimensional analogues of some of the results of Bloch et al. (1996a, (2009) on systems with symmetry. The mechanical and nonholonomic connections, the momentum equation, and mechanics of systems with infinitely many velocity constraints are discussed. Recall that $\delta L / \delta q \in T_q^{*} M$ and $i_{*} T_q Q$ is dense in $T_q M$ for every $q\in Q$, and thus all results are stated for strong equations of motion.

5.1 The Lagrange–Poincaré Equations

Recall that in finite-dimensional mechanics with symmetry one starts with an action of a Lie group G on the configuration space Q and Lagrangian and constraints (if any) that are invariant with respect to the lifted action on the velocity phase space. The quotient space Q / G, whose points are the group orbits, is called the shape space. It is known that if the group action is free and proper, the shape space is a smooth manifold and the projection $\pi :Q\rightarrow Q/G$ is a smooth surjective map with a surjective derivative at each point. The configuration space thus has the structure of a principal fiber bundle, with the group acting on the fibers by (left) multiplication.

We thus assume that in the general infinite-dimensional setting in the presence of symmetry the manifold M is a principal fiber bundle (see Kriegl and Michor 1997 for details in the infinite-dimensional case). The base of this bundle is a smooth manifold, and the group G involved in the construction of this bundle may be finite- or infinite-dimensional. In the latter case, the group is assumed regular (see Kriegl and Michor 1997 and Omori 1997).⁹

We denote the bundle coordinates (r, g) where r is a local coordinate in the base, or shape space M / G, and g is a group coordinate. Such a local trivialization is characterized by the fact that in such coordinates the group does not act on the factor r but acts on the group coordinate by group multiplication. Thus, locally in the base, the space M is isomorphic to the product $M/G \times G$, and in this local trivialization the map $\pi$ becomes the projection onto the first factor. The model space of the manifold M / G is denoted $W_B$.

Recall that in general in the infinite-dimensional setting Lagrangians are defined on the bundle $P = i^{*} TM$, where $i:Q\rightarrow M$ is the initial inclusion map and Q is a manifold. We will assume in the rest of the paper that Q is a principal fiber bundle with the same group G and that in the aforementioned local trivialization the group component of the initial inclusion map is the identity map.

Definition 5.1

We say that the Lagrangian is G-invariant if L is invariant under the induced action of G on P.

Both left and right actions may be of interest. Below we develop the formalism assuming that the action is left; the case of the right action is similar.

We start with the construction of the operator $\Psi$. Let $\mathfrak g$ be the Lie algebra, and thus the model space, of the group G. When the configuration space is a principal fiber bundle, the group component of the operator $\Psi$ can be defined globally, as shown below. For the fibers of T(M / G) we write the corresponding operator as $\psi _r: W_B \rightarrow T_r (M/G)$, i.e., $\dot{r}=\mathop {\psi _r} \xi$, whereas for the fibers of TG we set $\dot{g}:=\mathop {L_{g^{*}} \circ \varphi _r} \zeta$, where $q = (r, g)$ in a local trivialization and $\varphi _r:\mathfrak g_r \rightarrow \mathfrak g$ is a linear operator. The operators $\psi _r$ and $\varphi _r$ and their inverses are, for each $r \in Q/G$, bounded, continuous, and depend smoothly on r. This implies that the algebras $\mathfrak g$ and $\mathfrak g_r$ are isomorphic. The bracket on the space $W_B$ is

$$\begin{aligned}{}[\xi _1, \xi _2]_r:=\psi _r^{-1} [{\psi }_r \xi _1, {\psi }_r \xi _2], \end{aligned}$$

whereas the bracket on $\mathfrak g_r$ is defined by

$$\begin{aligned}{}[\zeta _1, \zeta _2]_{\mathfrak g_r}:= \varphi _r^{-1} [{\varphi }_r \zeta _1, {\varphi }_r \zeta _2]_\mathfrak {g}. \end{aligned}$$

The use of the nonmaterial shape velocity is of importance already in the finite-dimensional setting in some of the problem involving the rolling rigid body, such as the rattleback. In a number of interesting finite-dimensional instances, it suffices to use the shape velocity $\dot{r}$. The version of the infinite-dimensional formalism developed here is motivated by the utility of nonmaterial velocity in accounting for fluid- and elastic-type shapes.

The operator $\varphi _r$ is important for accounting for various subbundle structures associated with subspaces of the Lie algebra $\mathfrak g$. Such structures originate in the presence of control inputs and/or velocity constraints, particularly in the motion generation problems (see Ostrowski et al. 1994 and Bloch et al. 1996a for the details in the finite-dimensional setting). In general, the position of these subspaces in the Lie algebra $\mathfrak g$ is shape-dependent. While this operator may not appear to be important in the current part of the paper, it is more straightforward to introduce it here in order to make the exposition of the rest of the paper more straightforward.

Let ${\mathcal {A}}_\text {s}$ be a principal connection on the bundle $Q \rightarrow Q/G$ (see Kriegl and Michor 1997 for details on principal connections in the infinite-dimensional setting). Below we will discuss how the structure of the Lagrangian facilitates the selection of a connection. Tangent vectors in a local trivialization $Q = Q/G \times G$ at the point (r, g) are denoted (x, y). We write the action of ${\mathcal {A}}_\text {s}$ on this vector as ${\mathcal {A}}_\text {s} (x, y)$.¹⁰ Using this notation, we write the connection form in the local trivialization as

$$\begin{aligned} {\mathcal {A}}_\text {s} (x, y) = {\text {Ad}}_g (y_\text {c} + {\mathcal {A}}_\text {c} x), \end{aligned}$$

where $y_\text {c}$ is the left translation of y to the identity and, since we are working locally in shape space, we regard ${\mathcal {A}}_\text {c}$ as a $\mathfrak g$-valued one-form on Q / G.

The curvature of the principal connection ${\mathcal {A}}_\text {s}$ is the $\mathfrak g$-valued two-form

$$\begin{aligned} {\mathcal {B}}_\text {s} (X_1, X_2):=\mathrm{d}{\mathcal {A}}_{\text {s}} ({\text {hor}} X_1, {\text {hor}} X_2), \end{aligned}$$

where $X_1$ and $X_2$ are two vector fields and ${\text {hor}} X_1$ and ${\text {hor}} X_2$ are their horizontal components. In a local trivialization one writes

$$\begin{aligned} {\mathcal {B}}_\text {s} ((x_1, y_1), (x_2, y_2)) = {\text {Ad}}_g {\mathcal {B}}_\text {c} (x_1, x_2). \end{aligned}$$

(5.1)

where $x_1, x_2 \in T(Q/G)$, $y_1, y_2 \in \mathfrak g$, and where

$$\begin{aligned} {\mathcal {B}}_\text {c} (x_1, x_2)=\mathrm{d}{\mathcal {A}}_\text {c} (x_1, x_2) - [{\mathcal {A}}_\text {c} x_1, {\mathcal {A}}_\text {c} x_2]_{\mathfrak g}. \end{aligned}$$

The quantity $y_\text {c} + {\mathcal {A}}_\text {c} x$ regarded as an element of ${\mathfrak {g}}_r$ will be denoted $\zeta + {\mathcal {A}} x$, i.e.,

$$\begin{aligned} y_{\text {c}} + {\mathcal {A}}_{\text {c}} x = \varphi _r (\zeta + {\mathcal {A}} x), \quad x \in T_r(Q/G), \quad \zeta \in {\mathfrak {g}}_r. \end{aligned}$$

Thus, the velocity vector $\dot{q}$ in such a representation is characterized by the components

$$\begin{aligned} \dot{r} \quad \text {and}\quad \Omega = \zeta + {\mathcal {A}} \dot{r}, \end{aligned}$$

where $\mathop {\varphi _r} \zeta = g^{-1} \dot{g} \in \mathfrak g$. The curvature of the connection ${\mathcal {A}}$ on Q / G in this representation is hereafter denoted ${\mathcal {B}}$.

With nonmaterial shape velocity being used, the velocity components become

$$\begin{aligned} \xi \quad \text {and}\quad \Omega = \zeta + {\mathcal {A}} \psi _r \, \xi . \end{aligned}$$

(5.2)

Summarizing,

$$\begin{aligned} \dot{q} = \Psi _q (\xi , \Omega ) = \big (\psi _r \,\xi , L_{g^{*}} \varphi _r (\Omega - {\mathcal {A}} \psi _r \, \xi ) \big ). \end{aligned}$$

(5.3)

Theorem 5.2

The strong Lagrange–Poincaré equations ¹¹ for a system with a G-invariant Lagrangian $L:P \rightarrow {\mathbb {R}}$ are

$$\begin{aligned} \frac{d}{\mathrm{d}t} \frac{\delta l}{\delta \xi } - \psi _r^{*} \frac{\delta l}{\delta r}&= \bigg [ \xi , \frac{\delta l}{\delta \xi } \bigg ]_r^{*} - \bigg <\frac{\delta l}{\delta \Omega }, \mathbf {i}_\xi \psi _r^{*} {\mathcal {B}}+ \langle \mathbf {i}_\xi \psi _r^{*}\gamma , \psi _r^{*}{\mathcal {A}} \rangle \nonumber \\&\quad - \langle \psi _r^{*}\gamma , \mathbf {i}_\xi \psi _r^{*}{\mathcal {A}} \rangle + \langle \psi _r^{*}\mathcal E, \Omega \rangle \bigg >, \end{aligned}$$

(5.4)

$$\begin{aligned} \frac{d}{\mathrm{d}t} \frac{\delta l}{\delta \Omega }&= \bigg [ \Omega , \frac{\delta l}{\delta \Omega } \bigg ]_{\mathfrak g_r}^{*} + \bigg < \frac{\delta l}{\delta \Omega }, \mathbf {i}_\xi \psi _r^{*}\mathcal {E} \bigg >, \end{aligned}$$

(5.5)

where ${\mathcal {B}}$ is the curvature of ${\mathcal {A}}$, $\gamma := \varphi _r^{-1} \circ \mathrm{d}\varphi _r$, and ${\mathcal {E}}:= \gamma -{\text {ad}}_{{\mathcal {A}}}$, so that $\gamma$ and ${\mathcal {E}}$ are ${\mathfrak {g}}_r\otimes {\mathfrak {g}}_{r}^{*}$-valued one-forms on Q / G. The shape equation (5.4) and the momentum equation (5.5) govern the reduced dynamics for the Lagrangian L. The full dynamics is given by equations (5.4) and (5.5) along with the kinematic shape equation

$$\begin{aligned} \dot{r} = {\psi }_r \xi \end{aligned}$$

and reconstruction equation

$$\begin{aligned} \dot{g} = g \varphi _r (\Omega - \mathbf {i}_\xi \psi _r^{*}{\mathcal {A}}). \end{aligned}$$

(5.6)

Proof

The principal step is to uncover the structure of the bracket terms in the Hamel equations. Recall that these terms are induced by the map $\Psi$ defined in (5.3). Evaluating the Jacobi–Lie brackets of two vector fields $X_1$ and $X_2$ whose components in local trivialization are $(\xi _i, \zeta _i)$, that is,

$$\begin{aligned} X_i = \big ( \psi _r \, \xi _i, L_{g^{*}} \varphi _r (\zeta _i - {\mathcal {A}}\psi _r \,\xi _i) \big ), \quad \xi _i = {\text {const}},\quad \zeta _i = {\text {const}}, \quad i = 1, 2, \end{aligned}$$

gives:

$$\begin{aligned} \big [X_1, X_2\big ]&= \big [ \big (\psi _r \,\xi _1, 0\big ), \big (\psi _r \,\xi _2, 0\big ) \big ] + \big [ \big (\psi _r \,\xi _1, 0\big ), \big (0, L_{g^{*}} \varphi _r (\zeta _2 - {\mathcal {A}} \psi _r \,\xi _2)\big ) \big ]\\&\quad +\big [ \big (0, L_{g^{*}} \varphi _r (\zeta _1 - {\mathcal {A}} \psi _r \,\xi _1)\big ), \big (\psi _r \,\xi _2, 0\big ) \big ]\\&\quad +\big [\big (0, L_{g^{*}} \varphi _r (\zeta _1 - {\mathcal {A}} \psi _r \,\xi _1)\big ), \big (0, L_{g^{*}} \varphi _r (\zeta _2 - {\mathcal {A}} \psi _r \,\xi _2)\big ) \big ]. \end{aligned}$$

Next,

$$\begin{aligned}&\big [ \big (\psi _r \, \xi _1, 0\big ), \big (\psi _r \, \xi _2, 0\big ) \big ] = \big ( \psi _r [\xi _1, \xi _2]_r, 0 \big ),\\&\big [ \big (\psi _r \,\xi _1, 0\big ), \big (0, L_{g^{*}} \varphi _r (\zeta _2 - {\mathcal {A}} \psi _r \,\xi _2)\big ) \big ] = \big ( 0, L_{g^{*}} d_{\psi _r \xi _1} (\varphi _r (\zeta _2 - {\mathcal {A}} \psi _r \, \xi _2) \big ),\\&\big [ \big (0, L_{g^{*}} \varphi _r (\zeta _1 - {\mathcal {A}} \psi _r \,\xi _1)\big ), \big (0, L_{g^{*}} \varphi _r (\zeta _2 - {\mathcal {A}} \psi _r \,\xi _2)\big ) \big ]\\&\quad = \big (0, L_{g^{*}}\varphi _r [\zeta _1 - {\mathcal {A}} \psi _r \,\xi _1, \zeta _2 - {\mathcal {A}} \psi _r \,\xi _2]_{\mathfrak g_r} \big ). \end{aligned}$$

Summarizing the components of $[X_1, X_2]$ are

$$\begin{aligned} \psi _r [\xi _1, \xi _2]_r \end{aligned}$$

and

$$\begin{aligned}&L_{g^{*}} \varphi _r \big ( \langle \mathbf {i}_{\psi _r \xi _1} \mathcal E, \zeta _2\rangle - \langle \mathbf {i}_{\psi _r \xi _2} \mathcal E, \zeta _1\rangle + \langle \mathbf {i}_{\psi _r \xi _2} \gamma , {\mathcal {A}} \psi _r \,\xi _1\rangle - \langle \mathbf {i}_{\psi _r \xi _1} \gamma , {\mathcal {A}} \psi _r \,\xi _2\rangle \\&\quad -\,(\psi _r\,\xi _1) [{\mathcal {A}} \psi _r\,\xi _2] + (\psi _r\,\xi _2) [{\mathcal {A}} \psi _r\,\xi _1] + [{\mathcal {A}} \psi _r \,\xi _1, {\mathcal {A}} \psi _r \,\xi _2]_{\mathfrak g_r} + [\zeta _1,\zeta _2]_{\mathfrak g_r} \big ). \end{aligned}$$

Applying the inverse of $\Psi _q$ outputs the components

$$\begin{aligned}{}[\xi _1, \xi _2]_r \in W_B \end{aligned}$$

and

$$\begin{aligned}&\langle \mathbf {i}_{\psi _r \xi _1} \mathcal E, \zeta _2\rangle - \langle \mathbf {i}_{\psi _r \xi _2} \mathcal E, \zeta _1\rangle + \langle \mathbf {i}_{\psi _r \xi _2} \gamma , {\mathcal {A}} \psi _r \,\xi _1\rangle - \langle \mathbf {i}_{\psi _r \xi _1} \gamma , {\mathcal {A}} \psi _r \,\xi _2\rangle - (\psi _r \,\xi _1) [{\mathcal {A}} \psi _r \,\xi _2]\\&\quad +\,(\psi _r \,\xi _2) [{\mathcal {A}} \psi _r \,\xi _1] + {\mathcal {A}} ([\psi _r\, \xi _1, \psi _r\, \xi _2]) + [{\mathcal {A}} \psi _r \,\xi _1, {\mathcal {A}} \psi _r \,\xi _2]_{\mathfrak g_r} \\&\quad +\,[\zeta _1,\zeta _2]_{\mathfrak g_r} \in \mathfrak g_r. \end{aligned}$$

Utilizing the formula

$$\begin{aligned} \mathrm{d}\omega (X_1,X_2) = X_1 [\omega (X_2)] - X_2[\omega (X_1)] - \omega ([X_1,X_2]) \end{aligned}$$

for the exterior derivative of one-forms, the definition of the curvature, and the Cartan structure equation, the bracket $\big [(\xi _1, \zeta _1), (\xi _2, \zeta _2)\big ]_r$ on $W_B \oplus \mathfrak g_r$ reads

$$\begin{aligned}&\Big ( [\xi _1, \xi _2]_r, \left\langle \mathbf {i}_{\xi _1} \psi _r^{*} \mathcal E, \zeta _2\right\rangle - \left\langle \mathbf {i}_{\xi _2} \psi _r^{*} \mathcal E, \zeta _1\right\rangle + \left\langle \mathbf {i}_{\xi _2} \psi _r^{*} \gamma , \mathbf {i}_{\xi _1} \psi _r^{*} {\mathcal {A}}\right\rangle \nonumber \\&\quad -\,\langle \mathbf {i}_{\xi _1} \psi _r^{*} \gamma , \mathbf {i}_{\xi _2}\psi _r^{*} {\mathcal {A}}\rangle - \psi _r^{*} {\mathcal {B}} (\xi _1, \xi _2) + [\zeta _1,\zeta _2]_{\mathfrak g_r} \Big ). \end{aligned}$$

(5.7)

From (5.7), the components of the dual bracket $[(\xi , \zeta ), (\alpha , \beta )]^{*}_q$ are given by the formulae

$$\begin{aligned}&[\xi , \alpha ]_r^{*} - \big \langle \beta , \mathbf {i}_\xi \psi _r^{*} {\mathcal {B}} + \left\langle \mathbf {i}_\xi \psi _r^{*}\gamma , \psi _r^{*}{\mathcal {A}} \right\rangle - \left\langle \psi _r^{*}\gamma , \mathbf {i}_\xi \psi _r^{*}{\mathcal {A}} \right\rangle + \left\langle \psi _r^{*}\mathcal E, \zeta \right\rangle \big \rangle \nonumber \\&\quad \text {and}\quad [\zeta , \beta ]_{\mathfrak g_r}^{*} + \big \langle \beta , \mathbf {i}_\xi \psi _r^{*}\mathcal {E} \big \rangle . \end{aligned}$$

(5.8)

Equations (5.4) and (5.5) then follow from Theorem 3.1 and formula (5.8). $\square$

In certain situations, it may be useful to know the formulae for variations. For systems considered in this part of the paper, the general formula (3.7) transforms into

$$\begin{aligned} \delta \xi&= \dot{\eta }+ [\xi , \eta ]_r,\\ \delta \Omega&= \dot{\Sigma }+ [\Omega ,\Sigma ]_{\mathfrak g_r} + \left\langle \mathbf {i}_\xi \psi _r^{*}{\mathcal E}, \Sigma \right\rangle -\left\langle \mathbf {i}_\eta \psi _r^{*}{\mathcal E}, \Omega \right\rangle + \left\langle \mathbf {i}_\eta \psi _r^{*}\gamma , \mathbf {i}_\xi \psi _r^{*}{\mathcal {A}} \right\rangle \\&\quad -\,\left\langle \mathbf {i}_\xi \psi _r^{*}\gamma , \mathbf {i}_\eta \psi _r^{*}{\mathcal {A}} \right\rangle - \psi _r^{*} {\mathcal {B}} (\xi , \eta ), \end{aligned}$$

where the curves $\eta (t) \in W_B$ and $\mathop {\varphi _{r(t)}} \Sigma (t) \in \mathfrak g$ satisfy the boundary conditions $\eta (a) = \eta (b)= 0$ and $\Sigma (a) = \Sigma (b) = 0$, respectively. The reconstruction Eq. (5.6) is just the group component of the equation $\dot{q} = {\Psi }_q \xi$.

In the case that the material shape velocity is utilized, Eqs. (5.4) and (5.5) read

$$\begin{aligned} \frac{d}{\mathrm{d}t} \frac{\delta l}{\delta \dot{r}} - \frac{\delta l}{\delta r}&= -\; \bigg< \frac{\delta l}{\delta \Omega }, \mathbf {i}_{\dot{r}} {\mathcal {B}} + \langle \mathbf {i}_{\dot{r}} \gamma , {\mathcal {A}} \rangle - \langle \gamma , \mathbf {i}_{\dot{r}} {\mathcal {A}} \rangle + \langle \mathcal E, \Omega \rangle \bigg>,\\ \frac{d}{\mathrm{d}t} \frac{\delta l}{\delta \Omega }&= {\text {ad}}^{*}_\Omega {\frac{\delta l}{\delta \Omega }} + \bigg < \frac{\delta l}{\delta \Omega }, \mathbf {i}_{\dot{r}} \mathcal {E} \bigg >. \end{aligned}$$

whereas the reconstruction equation becomes

$$\begin{aligned} \dot{g} = g \varphi _r (\Omega - \mathbf {i}_{\dot{r}} {\mathcal {A}}). \end{aligned}$$

Now assume that the G-invariant Lagrangian equals the kinetic minus potential energy of the system and that the kinetic energy is given by a (weak) Riemannian metric $\left\langle \left\langle \,\cdot \,, \, \cdot \, \right\rangle \right\rangle$ on the configuration space Q. In such a setting, the isomorphism $\varphi _r$ is usually selected to be the identity map.

Definition 5.3

The mechanical connection ${\mathcal {A}}^{\mathrm {mech}}$ is, by definition, the connection on Q regarded as a bundle over shape space Q / G that is defined by declaring its horizontal space at a point $q\in Q$ to be the subspace that is the orthogonal complement to the tangent space to the group orbit through $q\in Q$ using the kinetic energy metric. The locked inertia tensor ${\mathcal {I}} (q): {\mathfrak {g}} \rightarrow {\mathfrak {g}}^{*}$ is defined by $\langle {\mathcal {I}} (q)\,\xi ,\eta \rangle =\langle \!\langle \xi _Q (q), \eta _Q (q) \rangle \!\rangle$, where $\xi _Q$ is the infinitesimal generator of $\xi \in {\mathfrak {g}}$ and where $\langle \!\langle \cdot \,, \cdot \rangle \!\rangle$ is the kinetic energy inner product.

Of course, in the infinite-dimensional setting the mechanical connection may fail to exist when the group metric is not strong.¹² It is certain to exist in the important case of a finite-dimensional symmetry group.

Given a system with symmetry, one may use the mechanical connection to set up Eq. (5.4) and (5.5). This choice of a connection changes the Lie algebra variables from $\zeta$ to the local version of the locked group velocity $\Omega$. With this connection choice the kinetic energy metric becomes block-diagonal, that is,

$$\begin{aligned} \langle \!\langle \dot{q}, \dot{q} \rangle \!\rangle = \langle \!\langle \xi , \xi \rangle \!\rangle + \langle \!\langle \Omega , \Omega \rangle \!\rangle . \end{aligned}$$

For a rotating rigid body, the locked group velocity has the physical interpretation of the body angular velocity.

Example 5.4

Here we revisit the planar string motion, but now derive the dynamics with an emphasis on the ${\text {SE(2)}}$ symmetry. We also assume that one of the ends of the string is attached to a platform (a flat rigid body). Both the platform and string move in the same horizontal plane.

The elements of the Euclidean group ${\text {SE(2)}}$ are written using complex notation, $g = (\hbox {e}^{i \theta }, w)$, i.e., the points of the $\mathbb R^2$ are identified with complex numbers, as before. The group ${\text {SE(2)}}$ is the configuration space of the platform and simultaneously the symmetry group of the entire system.

The angular and linear velocities of the platform (measured relative to the platform) are denoted $\omega \in \mathbb R$ and $v \in {\mathbb {C}}$, so that

$$\begin{aligned} (i \omega ,v):=(i{\dot{\theta }}, \hbox {e}^{-i\theta }\dot{w}) = g^{-1} \dot{g} \end{aligned}$$

and the operator $\varphi$ in (5.3) is the identity operator. The position of the string relative to the platform is given by the embedding map $z \in {\text {Emb}}([0,1], {\mathbb {C}})$ subject to the conditions $z(0) = 0$ and $z_s (0) = 1$.

The absolute position of the points of the string is

$$\begin{aligned} w + \hbox {e}^{i \theta } z(s), \end{aligned}$$

(5.9)

and thus the velocity of the points of the string is given by

$$\begin{aligned} \dot{w} + \hbox {e}^{i \theta } (iz \dot{\theta }+ \dot{z}). \end{aligned}$$

(5.10)

Written relative to the platform’s frame, the absolute velocity of the point z of the string reads

$$\begin{aligned} v + i \omega z + \dot{z} \equiv v + i \omega z + z_s \xi . \end{aligned}$$

That is, the operator $\psi$ is defined by $\dot{z} = \psi _z \xi = z_s \xi$.

The Lagrangian reads

$$\begin{aligned} \int _0^1 \tfrac{1}{2} \Big ( J \omega ^2 + m \bar{v} v + \big (\bar{v} - i \omega \bar{z} + \bar{z}_s \bar{\xi }\,\big ) \big (v + i \omega z + z_s \xi \big ) - \lambda \big (\bar{z}_s z_s - 1\big ) \Big ) \,\mathrm{d}s, \end{aligned}$$

where m and J are the mass and inertia of the platform. Recall that the quantities $\omega$ and v are s-independent. The components of the mechanical connection denoted here ${\mathcal {A}}_\theta$, ${\mathcal {A}}_w$, and ${\mathcal {A}}_{\bar{w}}$, so that

$$\begin{aligned} \omega = \Omega - {\mathcal {A}}_\theta \dot{z} - \bar{{\mathcal {A}}}_\theta \dot{\bar{z}}, \quad v = \mathrm {V} - {\mathcal {A}}_w \dot{z} - \bar{{\mathcal {A}}}_{\bar{w}} \dot{\bar{z}}, \end{aligned}$$

are computed to be

$$\begin{aligned} {\mathcal {A}}_\theta = - \frac{im \bar{z}}{2 \big (J(m + 1) + m \bar{z} z\big )}, \quad {\mathcal {A}}_w = \frac{1 - iz {\mathcal {A}}_\theta }{m +1} , \quad {\mathcal {A}}_{\bar{w}} = \frac{i \bar{z} {\mathcal {A}}_\theta }{m + 1}. \end{aligned}$$

The reduced dynamics is given by Eq. (5.4) and (5.5), where $[\cdot , \cdot ]_r^{*}$ is the dual of the bracket (3.13) and $[\cdot , \cdot ]_{\mathfrak g_r}^{*}$ is the operator ${\text {ad}}^{*}$ on the algebra $\mathfrak {se}(2)$.

5.2 Nonholonomic Systems with Symmetry

Recall that the manifolds M and Q are principal fiber bundles. The Lagrangian L and constraint distribution ${\mathcal {D}}$ are now invariant with respect to the induced action of G on P. Recall also that ${\mathcal {D}}$ is a (locally) splitting subbundle of P.

Assumption 5.5

The constraints and the orbit directions span the entire tangent space to the configuration space:

$$\begin{aligned} {\mathcal {D}}_q + T_q {\text {Orb}}(q) = T_q Q, \end{aligned}$$

for each $q \in Q$.¹³ If this condition is satisfied, we say that the principal case holds.

Let $\mathcal {S}$ be the subbundle of ${\mathcal {D}}$ whose fiber at q is $\mathcal S_q = {\mathcal {D}}_q \cap T_q {\text {Orb}}(q)$. We assume here that $\mathcal S_q \ne \{0\}$.¹⁴ The subbundle $\mathcal S$ is invariant with respect to the action of G on P induced by the left action of G on M. We assume that ${\mathcal {S}}$ is a (locally) splitting subbundle.¹⁵ Therefore, for each $q\in Q$ there exist a subspace $\mathcal U_q \subset {\text {Orb}}(q)$ such that ${\text {Orb}}(q) = \mathcal S_q \oplus \, \mathcal U_q$ and the subbundle $\mathcal U$ is (locally) splitting and G-invariant. Since the distributions $\mathcal S$ and $\mathcal U$ are left-invariant, for each $r \in Q/G$ there exist subspaces $\mathfrak b^{\mathcal S}_r$ and $\mathfrak b^{\mathcal {U}}_r$ of the Lie algebra $\mathfrak g_r = \mathfrak b^{\mathcal S}_r\! \oplus \mathfrak b^{\mathcal {U}}_r$ and an operator $\varphi _r:\mathfrak g_r \rightarrow \mathfrak g$ such that in a local trivialization

$$\begin{aligned} \mathcal S_q = L_{g^*} \varphi _r \mathfrak b^{\mathcal S}_r \quad \text {and}\quad \mathcal U_q = L_{g^{*}}\varphi _r \mathfrak b^{\mathcal {U}}_r. \end{aligned}$$

The operators $\varphi _r$ are constructed in such a way that $\mathfrak b_r^{\mathcal S}$ and $\mathfrak b_r^{\mathcal {U}}$ are fixed subspaces of $\mathfrak g_r$. Such an arrangement is necessary for accounting for constraint subspaces that change their location in the Lie algebra $\mathfrak g$ of the symmetry group depending on system’s shape configuration.

Let $\mathfrak b^{\mathcal S}$ and $\mathfrak b^{\mathcal {U}}$ be the bundles over Q / G whose fibers are the subspaces $\mathfrak b^{\mathcal S}_r$ and $\mathfrak b^{\mathcal {U}}_r$ of $\mathfrak g_r$. Given $\zeta \in \mathfrak g_r$, we write its components along these subspaces as $\zeta ^{\mathcal S}$ and $\zeta ^{\mathcal {U}}$ so that for each $r\in Q/G$ we have

$$\begin{aligned} g^{-1} \dot{g} = {\varphi }_r \zeta \equiv {\varphi }_r \zeta ^{\mathcal S} + {\varphi }_r \zeta ^{\mathcal {U}}, \quad \text {where} \quad \zeta ^{\mathcal S} \in \mathfrak b^{\mathcal S}_r \quad \text {and} \quad \zeta ^{\mathcal {U}} \in \mathfrak b^{\mathcal {U}}_r. \end{aligned}$$

Let ${\mathcal {A}}_\text {s}$ be a connection defined in a local trivialization by the formula

$$\begin{aligned} {\mathcal {A}}_\text {s} (\dot{r}, \dot{g}) = {\text {Ad}}_g (\varphi _r (\zeta + {\mathcal {A}} \dot{r})), \end{aligned}$$

where $\zeta \in \mathfrak g_r$ and where ${\mathcal {A}}$ is a $\mathfrak g_r$-valued one-form on Q / G. This form is such that the constraints in a local trivialization read

$$\begin{aligned} \Omega ^{\mathcal {U}} \equiv \zeta ^{\mathcal {U}} + {\mathcal {A}}^{\mathcal {U}} \dot{r} = 0. \end{aligned}$$

(5.11)

That is, the $\mathcal {U}$-component of the connection $\mathcal {A}$ is defined by the constraints. The $\mathcal {S}$-component of $\mathcal {A}$ is arbitrary at the moment; later on we will see how the structure of the Lagrangian affects the choice of this component.

As in Sect. 5.1, introduce the operator $\psi _r:W_B \rightarrow T_r (M/G)$ (locally), so that $\dot{r} = \mathop {\psi _r} \xi$ and $\xi$ is now the shape velocity component used instead of $\dot{r}$. Utilizing the constrained Hamel Eq. (4.4) and the G-invariance of the constraint distribution $\mathcal {D}$, one obtains the reduced nonholonomic equations of motion from (5.4) and (5.5) by projecting equation (5.5) onto the fibers of the bundle ${\mathfrak {b}}^*_{\mathcal {S}}$ and imposing constraints, i.e., setting $\Omega = \Omega ^{\mathcal {S}}$. Summarizing, we have:

Theorem 5.6

The strong form of the reduced nonholonomic dynamics is given by the equations

$$\begin{aligned} \frac{d}{\mathrm{d}t} \frac{\delta l}{\delta \xi } - \psi _r^{*} \frac{\delta l}{\delta r}&= \bigg [ \xi , \frac{\delta l}{\delta \xi } \bigg ]_r^{*} - \bigg < \frac{\delta l}{\delta \Omega }, \mathbf {i}_\xi \psi _r^{*} {\mathcal {B}} + \big \langle \mathbf {i}_\xi \psi _r^{*}\gamma , \psi _r^{*}{\mathcal {A}} \big \rangle \nonumber \\&\quad -\big \langle \psi _r^{*}\gamma , \mathbf {i}_\xi \psi _r^{*}{\mathcal {A}} \big \rangle + \big \langle \psi _r^{*}\mathcal E, \Omega ^{\mathcal S}\big \rangle \bigg >, \end{aligned}$$

(5.12)

$$\begin{aligned} \bigg [ \frac{d}{\mathrm{d}t} \frac{\delta l}{\delta \Omega } \bigg ]_{\mathcal S}&= \left[ \bigg [ \Omega ^{\mathcal S}, \frac{\delta l}{\delta \Omega } \bigg ]_{\mathfrak g_r}^{*} + \bigg < \frac{\delta l}{\delta \Omega }, \mathbf {i}_\xi \psi _r^{*}\mathcal {E} \bigg > \right] _{\mathcal S}, \end{aligned}$$

(5.13)

coupled with the kinematic shape equation

$$\begin{aligned} \dot{r}&= {\psi }_r \xi . \end{aligned}$$

(5.14)

In the above, the Lagrangian l is written as a function of $(r, \xi , \Omega )$, $\mathcal {B}$ is the curvature of $\mathcal {A}$ on Q / G (see (5.1)), and the quantities $\gamma$ and $\mathcal {E}$ are defined as in Theorem 5.2. Note that the partial derivatives of l in (5.12) and (5.13) are evaluated before setting $\Omega = \Omega ^{\mathcal S}$, i.e., before imposing the constraints.

The shape and momentum Eqs. (5.12) and (5.13) can be rewritten as

$$\begin{aligned} \frac{d}{\mathrm{d}t} \frac{\delta l_\text {c}}{\delta \xi } - \psi _r^{*}\frac{\delta l_\text {c}}{\delta r}&= \bigg [ \xi , \frac{\delta l}{\delta \xi } \bigg ]_r^{*}-\bigg<\frac{\delta l}{\delta \Omega }, \mathbf {i}_\xi \psi _r^{*} {\mathcal {B}} + \big \langle \mathbf {i}_\xi \psi _r^{*}\gamma , \psi _r^{*}{\mathcal {A}} \big \rangle \\&\quad - \big \langle \psi _r^{*}\gamma , \mathbf {i}_\xi \psi _r^{*}{\mathcal {A}} \big \rangle + \big \langle \psi _r^{*}\mathcal E, \Omega ^{\mathcal S}\big \rangle \bigg>,\\ \frac{d}{\mathrm{d}t} \frac{\delta l_\text {c}}{\delta \Omega ^{\mathcal S}}&= \left[ \bigg [ \Omega ^{\mathcal S}, \frac{\delta l}{\delta \Omega } \bigg ]_{\mathfrak g_r}^{*} + \bigg < \frac{\delta l}{\delta \Omega }, \mathbf {i}_\xi \psi _r^{*}\mathcal {E} \bigg > \right] _{\mathcal S}, \end{aligned}$$

where $l_\text {c} (r, \xi , \Omega ^{\mathcal S}):= l(r,\xi , \Omega ^{\mathcal S})$ is the constrained reduced Lagrangian. These equations follow directly from (5.12) and (5.13) as

$$\begin{aligned} \frac{\delta l_\text {c}}{\delta \xi } = \frac{\delta l}{\delta \xi } \Big |_{\Omega = \Omega ^{\mathcal S}}, \quad \frac{d}{\mathrm{d}t} \frac{\delta l_\text {c}}{\delta \xi } = \frac{d}{\mathrm{d}t} \frac{\delta l}{\delta \xi } \Big |_{\Omega = \Omega ^{\mathcal S}}, \quad \frac{\delta l_\text {c}}{\delta r} = \frac{\delta l}{\delta r} \Big |_{\Omega = \Omega ^{\mathcal S}}, \quad \frac{\delta l_\text {c}}{\delta \Omega ^{\mathcal S}} = \frac{\delta l}{\delta \Omega ^{\mathcal S}} \Big |_{\Omega = \Omega ^{\mathcal S}}. \end{aligned}$$

Note that in general

$$\begin{aligned} \frac{\delta l_\text {c}}{\delta \Omega ^{\mathcal S}} \ne \frac{\delta l}{\delta \Omega } \Big |_{\Omega = \Omega ^{\mathcal S}}. \end{aligned}$$

5.3 The Nonholonomic Connection

In the rest of the section, we assume that the Lagrangian equals the kinetic minus potential energy, that the kinetic energy is given by a (weak) Riemannian metric on the manifold M, and that the principal case holds (see Assumption 5.5).

Definition 5.7

The nonholonomic connection ${\mathcal {A}}^{\mathrm {nhc}}$ is, by definition, the connection on the principal bundle $Q \rightarrow Q/G$ whose horizontal space at $q \in Q$ is given by the orthogonal complement to the space $\mathcal S_q = {\mathcal {D}}_q \cap T_q {\text {Orb}}(q)$ within the space ${\mathcal {D}}_q$.

Similar to the remark on the existence of the mechanical connection, in the infinite-dimensional setting, the nonholonomic connection may fail to exist when the group metric is not strong, but is certain to exist when the symmetry group is finite-dimensional.

Under the assumption that the distribution $\mathcal {D}$ is invariant and from the fact that the group action preserves orthogonality (since it is assumed to preserve the Lagrangian and hence the kinetic energy metric), it follows that the distribution and the horizontal spaces transform to themselves under the group action. Therefore, the nonholonomic connection in a local trivialization is defined by the formula

$$\begin{aligned} {\mathcal {A}}^\mathrm {nhc} (\dot{r}, \dot{g}) = {\text {Ad}}_g (y_\text {c} + {\mathcal {A}}_\text {c} \dot{r}), \end{aligned}$$

(5.15)

where $y_\text {c}\in \mathfrak g$ and where ${\mathcal {A}}_\text {c}$ is a $\mathfrak g$-valued one-form on Q / G. Given $\dot{q} = (\dot{r}, \dot{g}) \in T_q Q$, the horizontal and vertical components of $\dot{q}$ in a local trivialization are

$$\begin{aligned} (\dot{r}, - {\mathcal {A}}_\text {c} \dot{r}) \quad \text {and}\quad (0, y_\text {c} + {\mathcal {A}}_\text {c} \dot{r}). \end{aligned}$$

In order to reflect the bundle structure associated with velocity constraints, we use Definition 5.7 and the map $\varphi _r$ and rewrite $y_\text {c} + {\mathcal {A}}_\text {c}\dot{r}$ in (5.15) as $\varphi _r (\zeta + {\mathcal {A}} \dot{r})$, where

$$\begin{aligned} \zeta = \zeta ^{\mathcal S} + \zeta ^{\mathcal {U}}, \quad {\mathcal {A}} = {\mathcal {A}}^{\mathcal S} + {\mathcal {A}}^{\mathcal {U}}, \quad \zeta ^{\mathcal S} + {\mathcal {A}}^{\mathcal S} \dot{r} \in \mathfrak b^{\mathcal S}, \quad \zeta ^{\mathcal {U}} + {\mathcal {A}}^{\mathcal {U}} \dot{r} \in \mathfrak b^{\mathcal {U}}. \end{aligned}$$

Using the nonholonomic connection, define the group velocity $\Omega \in \mathfrak g$ by the formula

$$\begin{aligned} \Omega = \zeta + {\mathcal {A}} \dot{r}. \end{aligned}$$

The constraints then are represented by formula (5.11).

Let the kinetic energy metric in a local trivialization be written as

$$\begin{aligned} \langle \!\langle \dot{q}, \dot{q} \rangle \!\rangle = \langle \mathop {G(r)} \dot{r}, \dot{r} \rangle + 2 \langle \mathop {\mathcal K (r)} \dot{r}, \zeta \rangle + \langle \mathop {\mathcal I (r)}\zeta , \zeta \rangle . \end{aligned}$$

(5.16)

The constrained locked inertia tensor $\mathcal I_{\mathcal S}: \mathfrak b^{\mathcal S} \rightarrow \big (\mathfrak b^{\mathcal S}\big )^{*}$ is given in a local trivialization by

$$\begin{aligned} \langle \mathop {\mathcal I_{\mathcal S} (r)}\zeta _1, \zeta _2 \rangle = \langle \!\langle L_{g^{*}} \varphi _r \,\zeta _1, L_{g^{*}} \varphi _r \,\zeta _2 \rangle \!\rangle , \quad \zeta _1, \zeta _2 \in \mathfrak b^{\mathcal S}. \end{aligned}$$

Similarly, define $\mathcal I_{\mathcal {U}} (r): \mathfrak b^{\mathcal {U}} \rightarrow \big (\mathfrak b^{\mathcal {U}}\big )^{*}$, $\mathcal I_{\mathcal S \mathcal U} (r): \mathfrak b^{\mathcal {U}} \rightarrow \big (\mathfrak b^{\mathcal S}\big )^{*}$, and $\mathcal I_{\mathcal U \mathcal S} (r):\mathfrak b^{\mathcal S} \rightarrow \big (\mathfrak b^{\mathcal {U}}\big )^{*}$ by

$$\begin{aligned} \langle \mathop {\mathcal I_{\mathcal {U}} (r)} \zeta _1, \zeta _2\rangle&= \langle \!\langle L_{g^{*}} \varphi _r \,\zeta _1, L_{g^{*}} \varphi _r \,\zeta _2 \rangle \!\rangle , \quad \zeta _1, \zeta _2 \in \mathfrak b^{\mathcal {U}}, \\ \langle \mathop {\mathcal I_{\mathcal S \mathcal U} (r)} \zeta _1, \zeta _2 \rangle&= \langle \!\langle L_{g^{*}} \varphi _r \,\zeta _1, L_{g^{*}} \varphi _r \,\zeta _2 \rangle \!\rangle , \quad \zeta _1 \in \mathfrak b^{\mathcal {U}}, \quad \zeta _2 \in \mathfrak b^{\mathcal S}, \\ \langle \mathop {\mathcal I_{\mathcal U \mathcal S} (r)} \zeta _1, \zeta _2 \rangle&= \langle \!\langle L_{g^{*}} \varphi _r \,\zeta _1, L_{g^{*}} \varphi _r \,\zeta _2\rangle \!\rangle , \quad \zeta _1 \in \mathfrak b^{\mathcal S}, \quad \zeta _2 \in \mathfrak b^{\mathcal {U}}, \end{aligned}$$

respectively.

Definition 5.7 implies that the constrained kinetic energy metric written as a function of $(\dot{r}, \Omega ^{\mathcal S})$ is block-diagonal, that is, it reads

$$\begin{aligned} \big \langle G(r)\, \dot{r}, \dot{r} \big \rangle + \Big \langle \mathcal I_{\mathcal S} (r)\,\Omega ^{\mathcal S}, \Omega ^{\mathcal S} \Big \rangle . \end{aligned}$$

Substituting $\zeta = \Omega ^{\mathcal S} - {\mathcal {A}} \dot{r}$ in (5.16), one concludes that the $\mathcal S$-component of the nonholonomic connection satisfies the equation

$$\begin{aligned} \Big \langle \big ( \mathcal I_{\mathcal S} (r)\,{\mathcal {A}}^{\mathcal S} - \mathcal K_{\mathcal S} (r) + \mathcal I_{\mathcal S \mathcal U} (r)\, {\mathcal {A}}^{\mathcal {U}} \big ) \dot{r}, \Omega ^{\mathcal S} \Big \rangle =0. \end{aligned}$$

This equation may or may not have a solution in the infinite dimensional setting. If the restriction of the metric on the subspace $\mathfrak b^{\mathcal S}$ is strong, the $\mathcal S$-component of the nonholonomic connection is well defined and reads

$$\begin{aligned} {\mathcal {A}}^{\mathcal S} = \mathcal I_{\mathcal S}^{-1} (r) \mathcal K_{\mathcal S} (r) - \mathcal I_{\mathcal S}^{-1} (r) \mathcal I_{\mathcal S \mathcal U} (r)\, {\mathcal {A}}^{\mathcal {U}}. \end{aligned}$$

The $\mathcal U$-component of the nonholonomic connection is defined by the constraints. As in Sect. 5.2, the reduced dynamics is given by Eqs. (5.12)–(5.14).

Example 5.8

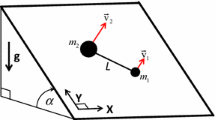
Consider the planar motion of an inextensible string coupled with the two identical Chaplygin sleighs. Assume that the ends of the string are attached at the contact points of the sleighs and the plane. See Fig. 3 for the illustration of the basic configuration.

Fig. 3

The string with Chaplygin sleighs attached at the ends

The manifold $M (= Q)$ for this system is ${\text {SE}}(2)\times {\text {SE}}(2)\times {\text {Emb}}([0,1], {\mathbb {C}})$, and the system is invariant with respect to the diagonal action of the group ${\text {SE}}(2)$ on M. We identify the symmetry group with configurations of the sleigh at $s = 0$. In such a representation, the position of the sleigh at the front end of the string (i.e., at $s = 0$) is characterized by the element $(\hbox {e}^{i\theta _0}, w_0) \in {\text {SE(2)}}$, while the relative position of the sleigh at the opposite end of the string is $(\hbox {e}^{i\phi _1}, z_1) \in {\text {SE(2)}}$, so that the absolute position of that sleigh is

$$\begin{aligned} (\hbox {e}^{i\theta _1}, w_1) = (\hbox {e}^{i\theta _0}, w_0) \cdot (\hbox {e}^{i\phi _1}, z_1) = (\hbox {e}^{i(\theta _0 + \phi _1)}, w_0 + \hbox {e}^{i\theta _0} z_1). \end{aligned}$$

The angular and linear velocity (relative to the body frame) of the sleigh at the front end of the string are

$$\begin{aligned} \omega _0 = \dot{\theta }_0 \quad \text {and}\quad v_0 = \hbox {e}^{-i\theta _0} \dot{w}_0, \end{aligned}$$

while the angular and linear velocity of the other sleigh are

$$\begin{aligned} \omega _0 + \dot{\phi }_1 \quad \text {and}\quad \hbox {e}^{- i \phi _1} (v_0 + i z_1 \omega _0 + \dot{z}_1). \end{aligned}$$

Thus, the constraints are

$$\begin{aligned} \bar{v}_0 = v_0 \quad \text {and}\quad \hbox {e}^{- i \phi _1} (v_0 + i z_1 \omega _0 + \dot{z}_1) = \hbox {e}^{i \phi _1} (\bar{v}_0 - i \bar{z}_1 \omega _0 + \dot{\bar{z}}_1). \end{aligned}$$

(5.17)

Formulae (5.17) define the operator $\varphi$ and the constraint component of the nonholonomic connection. Both are nontrivial for this coupled system.

Recall that the nonholonomic connection modifies the elements of the Lie algebra of the symmetry group. The equations of motion that use such ‘shifted’ Lie algebra elements are useful in numerous situations, including stability analysis of relative equilibria. However, one may verify that this form of equations is rather complicated for the system considered here. Below we give a simpler representation of system’s dynamics using the operators introduced earlier for the sleigh and string.

Using the notations introduced in Sect. 2.5 and Example 3.3, parametrize the configuration spaces of the sleighs as $(\theta _j, w_j)$, $j =0,1$, where $w_j=x_j+i y_j$, and denote the absolute position of the string by $w\in {\text {Emb}}([0,1], {\mathbb {C}})$. The Lagrangian reads

$$\begin{aligned} l= & {} \tfrac{1}{2} \big ( J \omega _0^2 + m\bar{v}_0 v_0 \big ) + \tfrac{1}{2} \big ( J \omega _1^2 + m\bar{v}_1 v_1 \big )\nonumber \\&+\int _0^1 \tfrac{1}{2} \big (\bar{w}_s w_s \bar{\xi }\xi - \lambda (\bar{w}_s w_s - 1) \big ) \,\mathrm{d}s. \end{aligned}$$

(5.18)

Coupling is accomplished by matching the position of the sleighs and the string’s ends:

$$\begin{aligned} w_0 = w|_{s=0} \quad \text {and}\quad w_1 = w|_{s=1}. \end{aligned}$$

(5.19)

That is, the string is attached at and can rotate freely around the contact point of each sleigh.

The constrained Hamel equations for this system read

$$\begin{aligned} J \dot{\omega }_0&= 0, \end{aligned}$$

(5.20)

$$\begin{aligned} m \dot{v}_0&= \tfrac{1}{2} \lambda _0 \big (\bar{w}_s^0 \hbox {e}^{i \theta _0} + w_s^0 \hbox {e}^{-i \theta _0}\big ), \end{aligned}$$

(5.21)

$$\begin{aligned} J \dot{\omega }_1&= 0, \end{aligned}$$

(5.22)

$$\begin{aligned} m \dot{v}_1&= - \tfrac{1}{2} \lambda _1 \big (\bar{w}_s^1 \hbox {e}^{i \theta _1} + w_s^1 \hbox {e}^{-i \theta _1}\big ), \end{aligned}$$

(5.23)

$$\begin{aligned} \dot{\xi }&= \xi \bar{\xi }_s + \lambda _s + i \varkappa \big (\lambda - \bar{\xi }\xi \big ), \end{aligned}$$

(5.24)

where, by definition, $\lambda _0:=\lambda |_{s=0}$, $\lambda _1:= \lambda |_{s=1}$, $w_s^0:= w_s |_{s=0}$, and $w_s^1:= w_s |_{s=1}$. Equations (5.20), (5.22), (5.24) and the left-hand sides of (5.21), (5.23) have been obtained earlier. The right-hand sides of (5.21) and (5.23) account for the coupling constraints (5.19) and are obtained as projections of the external terms (i.e., those due to integration by parts) associated with the Lagrange multiplier $\lambda$ in (5.18) along the sleigh directions.

5.4 Systems with Shape Constraints

Here we study systems with a ‘slim’ constraint distribution. That is, at each $q \in Q$, the complimentary subspace of ${\mathcal {D}}_q \subset T_q M$ is ‘larger’ than the tangent space to the group orbit at q. While this may happen when the symmetry group is infinite-dimensional as well as when the system is finite-dimensional, our main objects of interest here are systems with finite-dimensional symmetry group and constraint distributions of infinite codimension. Assumption 5.5 does not hold for such systems, and the formalism of Bloch et al. (1996a) and its infinite-dimensional analogue presented in Sect. 5.2 should be modified.

Fig. 4

The Chaplygin sleigh coupled to a constrained string

Example 5.9

Consider the Chaplygin sleigh with an inextensible string attached at and allowed to rotate around the contact point of the sleigh and the plane, as shown in Fig. 4. Assume that the string is constrained as in Example 4.3. This system is ${\text {SE}}(2)$-invariant. Using formulae (5.9) and (5.10) there, the condition of vanishing normal velocity component is equivalent to

$$\begin{aligned} \bar{z}_s (v + i \omega z + \dot{z}) = z_s (\bar{v} - i \omega \bar{z} + \dot{\bar{z}}). \end{aligned}$$

(5.25)

Here the string position z is measured relative to the sleigh, and $\omega$ and v are the sleigh’s angular and linear velocity measured relative to its frame. Formula (5.25) imposes infinitely many constraints on the system, one for each $s \in [0,1]$.

For a generic string placement, constraints (5.25) exhaust the Lie algebra $\mathfrak {se}(2)$. Indeed, the vectors that span the constraint subspaces for $s_0 = 0$ and $0< s_1< s_2 <1$ are verified to be $\mathbb R$-independent if and only if

$$\begin{aligned} (\bar{z}_s z + z_s \dot{\bar{z}})|_{s = s_1} (z_s - \bar{z}_s)|_{s = s_2} - (\bar{z}_s z + z_s \dot{\bar{z}})|_{s = s_2} (z_s - \bar{z}_s)|_{s = s_1} \ne 0, \end{aligned}$$

which generically holds. The rest of the constraints are effectively imposed on the shape degrees of freedom of the system, and thus Assumption 5.5 does not hold in this example and is void in the rest of the paper.

We begin by developing a special version of the formalism for unconstrained G-invariant systems. Using notations introduced in Sect. 5.1, this system is characterized by the Lagrangian $l(r, \xi , \zeta )$. Recall that $\dot{r} = \psi _r \xi$. In order to simplify the exposition, we assume here that $\varphi _r$ is the identity operator so that $\dot{g} = L_{g^{*}} \zeta$. Instead of the velocity components (5.2), we will use

$$\begin{aligned} \eta = \xi + {\mathcal {C}} \zeta \in W_B \quad \text {and}\quad \zeta \in \mathfrak g, \end{aligned}$$

where ${\mathcal {C}}:\mathfrak g \rightarrow W_B$ is a linear map. It depends parametrically and smoothly on $r \in U$, where U is an open subset of Q / G. This is motivated by the structure of the constraints (5.25). Thus, for the operator $\Psi _q$ we have

$$\begin{aligned} \dot{q} = (\dot{r}, \dot{g}) = \Psi _q (\eta , \zeta ) = \big ( \psi _r (\eta - {\mathcal {C}} \zeta ), L_{g^{*}} \zeta \big ). \end{aligned}$$

The inverse of $\Psi _q$ is

$$\begin{aligned} (\eta , \zeta ) = \Psi _q^{-1} (\dot{r}, \dot{g}) = \big ( \psi ^{-1}_r \dot{r} + {\mathcal {C}} L_{g^{*}}^{-1} \dot{g}, L_{g^{*}}^{-1} \dot{g} \big ). \end{aligned}$$

One can think of ${\mathcal {C}}$ as a connection on the local fiber bundle whose base and fiber are open subsets of G and Q / G, respectively.

Theorem 5.10

The strong Lagrange–Poincaré equations are

$$\begin{aligned} \frac{d}{\mathrm{d}t} \frac{\delta l}{\delta \eta } - \psi _r^{*} \frac{\delta l}{\delta r}&= \bigg [ \eta - {\mathcal {C}} \zeta , \frac{\delta l}{\delta \eta } \bigg ]_r^{*} + \bigg \langle \frac{\delta l}{\delta \eta }, \psi ^{*}_r \mathrm{d}{\mathcal {C}}\, \zeta \bigg \rangle ,\\ \frac{d}{\mathrm{d}t} \frac{\delta l}{\delta \zeta }&= {\text {ad}}^{*}_\zeta \bigg ( \frac{\delta l}{\delta \zeta } + {\mathcal {C}}^{*} \frac{\delta l}{\delta \eta } \bigg ) - \bigg \langle \bigg [\eta - {\mathcal {C}} \zeta , \frac{\delta l}{\delta \eta } \bigg ]_r^{*}, {\mathcal {C}} \bigg \rangle \\&\quad - \bigg \langle \frac{\delta l}{\delta \eta }, \mathbf {i}_{(\eta - {\mathcal {C}} \zeta )}\psi ^{*}_r \mathrm{d} {\mathcal {C}} + \mathbf {i}_{{\mathcal {C}}} \psi ^{*}_r \mathrm{d} {\mathcal {C}}\, \zeta \bigg \rangle . \end{aligned}$$

Proof

The key step is to establish the bracket operation associated with the operator $\Psi _q$. One begins with the computation of the Jacobi–Lie bracket

$$\begin{aligned}{}[\Psi (\eta _1, \zeta _1), \Psi (\eta _2, \zeta _2)] = [ (\psi (\eta _1 - {\mathcal {C}} \zeta _1), L_{*} \zeta _1), (\psi (\eta _2 - {\mathcal {C}} \zeta _2), L_{*} \zeta _2) ], \end{aligned}$$

where $\eta _i$ and $\zeta _i$ are constant vectors. For the M / G-component of the Jacobi–Lie bracket, we have, using the chain rule:

$$\begin{aligned}&[ \psi (\eta _1 - {\mathcal {C}} \zeta _1), \psi (\eta _2 - {\mathcal {C}} \zeta _2) ]_{M/G} = \psi [ \eta _1 - {\mathcal {C}} \zeta _1, \eta _2 - {\mathcal {C}} \zeta _2 ]_r\\&\quad - \psi (\psi \eta _1 - \psi {\mathcal {C}} \zeta _1) [{\mathcal {C}} \zeta _2] + \psi (\psi \eta _2 - \psi {\mathcal {C}} \zeta _2) [{\mathcal {C}} \zeta _1]. \end{aligned}$$

For the G-component, we obtain

$$\begin{aligned}{}[L_{*} \zeta _1,L_{*} \zeta _2]_G = L_{*} [\zeta _1, \zeta _2]_{\mathfrak g} = L_{*} {\text {ad}}_{\zeta _1} \zeta _2. \end{aligned}$$

Applying the inverse operator $\Psi _q$ outputs the bracket operation on $W_B \oplus \mathfrak g$:

$$\begin{aligned}{}[(\eta _1, \zeta _1),(\eta _2, \zeta _2)]= & {} \big ( [ \eta _1 - {\mathcal {C}} \zeta _1, \eta _2 - {\mathcal {C}} \zeta _2 ]_r - (\psi \eta _1 - \psi {\mathcal {C}} \zeta _1) [{\mathcal {C}} \zeta _2] \\&\quad +(\psi \eta _2 - \psi {\mathcal {C}} \zeta _2) [{\mathcal {C}} \zeta _1] + {\mathcal {C}} {\text {ad}}_{\zeta _1} \zeta _2, {\text {ad}}_{\zeta _1} \zeta _2 \big ). \end{aligned}$$

Pairing with an element $(\alpha , \beta ) \in W_B^{*} \oplus \mathfrak g^{*}$, we obtain:

$$\begin{aligned}&\big \langle \alpha , [\eta _1 - {\mathcal {C}} \zeta _1, \eta _2 - {\mathcal {C}} \zeta _2 ]_r - (\psi \eta _1 - \psi {\mathcal {C}} \zeta _1) [{\mathcal {C}} \zeta _2] + (\psi \eta _2 - \psi {\mathcal {C}} \zeta _2) [{\mathcal {C}} \zeta _1]\\&\quad +{\mathcal {C}}{\text {ad}}_{\zeta _1}\zeta _2 \big \rangle _{W_B}+\big \langle \beta , {\text {ad}}_{\zeta _1} \zeta _2 \big \rangle _{\mathfrak g}=\big \langle [\eta _1 - {\mathcal {C}} \zeta _1, \alpha ]_r^{*} + \langle \alpha , \psi ^{*} \mathrm{d}{\mathcal {C}} \zeta _1 \rangle _{W_B}, \eta _2 \big \rangle _{W_B}\\&\quad + \big \langle {\text {ad}}^{*}_{\zeta _1} (\beta + {\mathcal {C}}^{*} \alpha ) - \langle [\eta _1 - {\mathcal {C}} \zeta _1, \alpha ]_r^{*}, {\mathcal {C}} \rangle _{W_B} -\langle \alpha , \mathbf {i}_{(\eta _1 - {\mathcal {C}} \zeta _1)} \psi ^{*} \mathrm{d}{\mathcal {C}} \rangle _{W_B}\\&\quad -\langle \alpha , \mathbf {i}_{{\mathcal {C}}}\psi ^{*} \mathrm{d}{\mathcal {C}} \zeta _1 \rangle _{W_B},\zeta _2 \big \rangle _{\mathfrak g}, \end{aligned}$$

which yields the components of the dual bracket,

$$\begin{aligned}&\big \langle [\eta _1 - {\mathcal {C}} \zeta _1, \alpha ]_r^{*}+\langle \alpha , \psi ^{*}_r \mathrm{d}{\mathcal {C}} \zeta _1 \rangle _{W_B}, \end{aligned}$$

(5.26)

$$\begin{aligned}&\big \langle {\text {ad}}^{*}_{\zeta _1} (\beta + {\mathcal {C}}^{*} \alpha ) - \langle [\eta _1 - {\mathcal {C}} \zeta _1, \alpha ]_r^{*}, {\mathcal {C}} \rangle _{W_B} - \langle \alpha , \mathbf {i}_{(\eta _1 - {\mathcal {C}} \zeta _1)} \psi ^{*}_r \mathrm{d}{\mathcal {C}} \rangle _{W_B}\nonumber \\&\quad -\langle \alpha ,\mathbf {i}_{{\mathcal {C}}}\psi ^{*}_r \mathrm{d}{\mathcal {C}} \zeta _1 \rangle _{W_B}. \end{aligned}$$

(5.27)

Utilizing the dual bracket (5.26) and (5.27) and composing Eq. (3.9) completes the proof. $\square$

Next, assume that there exists a splitting distribution ${\mathcal {D}}$ along with its complimentary distribution $\mathcal U$ such that the constraint $\eta \in {\mathcal {D}}_q$ reads

$$\begin{aligned} \xi ^{\mathcal {U}} + {\mathcal {C}}^{\mathcal {U}} \zeta = 0. \end{aligned}$$

(5.28)

Thus, the constraint is defined by the operator ${\mathcal {C}}^{\mathcal {U}}:\mathfrak g \rightarrow \mathcal U _q$. This representation is, in general, local, i.e., (5.28) represents the constraint on an open subset U of the shape space Q / G. The operator ${\mathcal {C}}^{\mathcal {U}}$ is then extended to ${\mathcal {C}}: \mathfrak g \rightarrow W_B$ at each $r \in U$.

There are, of course, infinitely many such extensions, and one needs to utilize additional requirements to single out the desired one. Utilizing the general Hamel’s equations established in Sect. 4.2, the reduced dynamics becomes

$$\begin{aligned}&\left( \frac{d}{\mathrm{d}t} \frac{\delta l}{\delta \eta } - \psi _r^{*} \frac{\delta l}{\delta r} - \bigg [ \eta - {\mathcal {C}} \zeta , \frac{\delta l}{\delta \eta } \bigg ]_r^{*} - \bigg \langle \frac{\delta l}{\delta \eta }, \psi ^{*}_r \mathrm{d}{\mathcal {C}}\, \zeta \bigg \rangle \right) _{{\mathcal {D}}} = 0, \end{aligned}$$

(5.29)

$$\begin{aligned}&\left( \frac{d}{\mathrm{d}t} \frac{\delta l}{\delta \zeta } - {\text {ad}}^{*}_\zeta \bigg ( \frac{\delta l}{\delta \zeta } - {\mathcal {C}}^{*} \frac{\delta l}{\delta \eta } \bigg ) + \bigg \langle \bigg [\eta - {\mathcal {C}} \zeta , \frac{\delta l}{\delta \eta } \bigg ]_r^{*}, {\mathcal {C}} \bigg \rangle \right. \nonumber \\&\quad \left. + \bigg \langle \frac{\delta l}{\delta \eta }, \mathbf {i}_{(\eta - {\mathcal {C}} \zeta )}\psi ^{*}_r \mathrm{d} {\mathcal {C}} + \mathbf {i}_{{\mathcal {C}}} \psi ^{*}_r \mathrm{d} {\mathcal {C}}\, \zeta \bigg \rangle \right) _{{\mathcal {D}}} = 0. \end{aligned}$$

(5.30)

If desired, one can give the representation of these equations using the constrained Lagrangian and constrained versions of the velocity components $\eta$ and $\zeta$, as in the approach in Sect. 5.2.

Example 5.9 (continued). Consider again the motion of the Chaplygin sleigh with the flexible string attached. The normal velocity component of the string at each point is constrained to be zero, as in (5.25). The system is ${\text {SE(2)}}$-invariant and the symmetry group is also the configuration space of the sleigh. The Lagrangian of the system is the sum of the kinetic energy of the sleigh and the string Lagrangian and reads

$$\begin{aligned} \tfrac{1}{2} \big ( J \omega ^2 + m \bar{v} v \big ) + \int _0^1 \tfrac{1}{2} \Big ( \big (\bar{v} - i \omega \bar{z} + \bar{z}_s \bar{\xi }\,\big ) \big (v + i \omega z + z_s \xi \big ) - \lambda \big (\bar{z}_s z_s - 1\big ) \Big ) \,\mathrm{d}s, \end{aligned}$$

where $\xi = \bar{z}_s \dot{z}$ is string’s shape velocity. The coupling is accomplished by setting

$$\begin{aligned} z |_{s=0} = 0,\quad z_s |_{s = 0} = 1,\quad \xi |_{s=0} = 0, \end{aligned}$$

and the constraint is given by formula (5.25). We assume from now on that $v>0$, i.e., the string trails the sleigh.

Define the quantity $\eta$ and the operator ${\mathcal {C}}$ by the formula

$$\begin{aligned} \eta = \xi + \bar{z}_s (v + i \omega z), \end{aligned}$$

so that $\eta$ is string’s absolute velocity. Doing so results in the Lagrangian

$$\begin{aligned} l = \tfrac{1}{2} \big ( J \omega ^2 + m\bar{v} v \big ) + \int _0^1 \tfrac{1}{2} \big ( \bar{\eta }\eta - \lambda (\bar{z}_s z_s - 1) \big ) \,\mathrm{d}s. \end{aligned}$$

The constraint in this representation reads $\eta = \bar{\eta }$, which is formula (5.28) written for the string. Equations (5.29) and (5.30) for the sleigh-string system become

$$\begin{aligned} J \dot{\omega }&= 0, \end{aligned}$$

(5.31)

$$\begin{aligned} m \dot{v}&= \lambda |_{s=0}, \end{aligned}$$

(5.32)

$$\begin{aligned} \dot{\eta }&= \eta \eta _s + \lambda _s, \end{aligned}$$

(5.33)

where v and $\eta$ are real-valued. These equations should be amended with the coupling conditions

$$\begin{aligned} \eta |_{s = 0} = v. \end{aligned}$$

(5.34)

Note also that the position of the front end of the string coincides with the position of the contact point of the sleigh and the plane.

Arguing as in Example 4.3, one concludes that $\eta$ is independent of s. Thus, equation (5.33) becomes

$$\begin{aligned} \dot{\eta }= \lambda _s. \end{aligned}$$

(5.35)

Equation (5.31) implies $\omega = \mathrm {const}$.

The tension $\lambda$ is obtained by integrating (5.35) with respect to s and, since $\lambda |_{s=1} = 0$, we conclude that

$$\begin{aligned} \lambda = (s - 1) \dot{\eta }. \end{aligned}$$

(5.36)

Therefore, $\lambda |_{s=0} = -\dot{\eta }$, which in combination with (5.32) and (5.34) yields $v = \mathrm {const}$. The velocity coupling condition then implies that the blade moves at the constant speed $\eta = v$. Using (5.36), we conclude that $\lambda = 0$.

Summarizing, the Chaplygin sleigh with the constrained string attached generically undergoes uniform circular motion. Nongeneric trajectories are straight lines. The string (possibly after some period of time) follows the trajectory of the contact point of the sleigh.

It is interesting to point out that in this example the shape dynamics (string’s motion) is modulated by the group dynamics (skate’s motion). This is the opposite of typical reconstruction in finite-dimensional constrained systems discussed in Bloch et al. (1996a).

We note also that the qualitative dynamics of this system—uniform circular or straight line motion—is consistent with the behavior of integrable Hamiltonian systems. One may raise the question of whether it is integrable in a more precise sense—with infinitely many conserved quantities. We intend to return to this issue in a forthcoming publication.

6 Conclusions

This paper introduced Hamel’s formalism for infinite-dimensional mechanical systems, proved some general results, and illustrated them with examples. A number of topics remain outside the scope of the paper. For instance, the nature of nonholonomic constraints in the infinite-dimensional setting should be studied in more detail and will be addressed in a forthcoming publication. We also intend to develop Hamel’s formalism for field theories and apply it for constructing structure-preserving integrators for constrained continuum mechanical systems.

Examples in this paper were intentionally kept relatively simple for pedagogical reasons, and solutions there are classical, i.e., not generalized. More realistic examples, including systems with generalized solutions, will be treated in the forthcoming paper on the field-theoretic Hamel formalism.