Experimental investigation on the yield behavior of PMMA

Abstract

Quasi-static compression, tension and combined shear–compression tests were conducted to characterize the mechanical behavior of PMMA. The cylinder samples and dog-bone samples were used for uniaxial testing. The shear–compression samples of four different angles (15°, 30°, 45°, and 50°) were used to obtain the multiaxial stress state instead of complex loading equipment. The yield behaviors of PMMA cannot be described by the Tresca or Mises criterion due to the effects of both the first invariant of the stress and the third invariant of deviatoric stress. A criterion is proposed that includes the first invariant of the stress and the third invariant of deviatoric stress in this paper. In other word, the effects of hydrostatic pressure and Lode angle are considered. The proposed yield criterion has the capability to precisely capture the experimental yield loci of PMMA.

Introduction

PMMA (polymethyl-methacrylate) is a kind of low-cost and light-weight material with excellent physical and optical properties. It is widely used in aviation, architecture, biomedicine and other fields [1,2,3,4]. Many previous literatures have made contributions to the understanding of the uniaxial mechanical properties of PMMA. Holmquist et al. [5] had presented the response of polymethyl methacrylate (PMMA) subjected to large strains, high strain rates, high pressures, a range in temperatures, and variations in the intermediate principal stress. Richeton et al. [6] investigated that uniaxial compression stress–strain tests were carried out on three commercial amorphous polymers. Chen et al. [7] researched the mechanical behavior of PMMA under uniaxial tension and compression loading conditions. The results show that the compressive strength is higher than tensile strength. Jerabek et al. [8] investigated and compared the pre- and post-yield regime by two uniaxial compression test methods. Wu.et al. [9] investigated the PMMA tensile capability at a medium strain rate and found that the strain rate greatly influenced these properties. Additionally, the yield behavior of PMMA exhibit obvious strain rate and temperature sensitivity, which have been substantiated by many experimental investigations. Methiesen et al. [10] described the glass transition through temperature-dependent material properties. Richeton et al. [11] found that the initial Young’s modulus is forcefully affected by strain rates. Nasrouri et al. [12] investigated the effect of strain rate, temperature, and adiabatic heating on the mechanical behavior of PMMA and the negative correlation between temperature and the PMMA yield stress was found. It should be noted that PMMA may be subjected to complex multiaxial stress states under actual circumstances. Therefore, it is essential to analyze the multiaxial yield behavior of PMMA and establish a yield criterion based on multiaxial experimental results. Forquin et al. [13] investigated the confined behavior of PMMA by quasi-oedometric compression. They adopted the cylindrical PMMA specimens enclosed in a brass or high-strength aluminium alloy confinement vessel. Jin et al. [14] investigated compression–shear failure behavior of PMMA using a cylindrical specimen with beveled ends of different angles and experimental results show that the failure force of PMMA decreased as the tilt angle of the specimen increased. Zhou et al. [15] used complex loading equipment to achieve the combined shear–compression stress state and different kind of combined shear–compression experiments were achieved through changing pressure head angle. On the other hand, many researches indicated that the Tresca and Mises criterion cannot give an appropriate description of the yield behavior of PMMA. Because the yield behaviors of PMMA affected by first invariant of stress tensor ($I_{1}$) and third invariant of deviatoric stress ($J_{3}$) [16, 17]. Therefore, Farrokh et al. [18] proposed a strain rate sensitivity yield criterion $f(I_{1} ,J_{2} )$ by experimental investigation. The relationship between $I_{1}$ and $\sqrt {J_{2} }$ is liner. It does not have a high capability of charactering the main deformation mechanism of relating shear banding. Ghorbel [19] proposed a viscoplastic constitutive model for polymeric materials based on the parabolic Drucker and Prager criterion. The criterion that was proposed by Ghorbel includes the effects of the first invariant of the stress, the second invariant of deviatoric stress ($J_{2}$) and the third invariant of deviatoric stress, respectively.

From the above discussions, it can be concluded that the multiaxial experimental data of the PMMA are limited. Especially, the configuration of yield criterion has not yet been clearly understood. Therefore, present research employs a new test method (i.e., shear–compression samples [20]) to explore the multiaxial yield behavior of PMMA. Furthermore, a yield criterion is extended to include a quadratic $I_{1}$ term for accurately predicting the yield locus of PMMA.

Experimental procedure

The test samples were machined by ordinary commercial PMMA bar (Φ 10 mm × 1000 mm). In this paper, the shear–compression specimen (SCS) was used to generate the additional shear, then the stress state can be controlled by changing the angle of the sample (SCS) which is named loading angle. That is, a slot with a certain angle is introduced on the surface of the cylinder sample. There are four kinds of loading angle α in this paper: 15°, 30°, 45°, 50°. In addition, this investigation applied the cylindrical specimen and dog-bone specimen to obtain the mechanical behavior of compression and tensile. The specific sizes of tested samples are shown in Figs. 1 and 2.

Fig. 1

Schematic of compression and tension specimens

Fig. 2

Schematic of SCS and the yield loci in shear–compression stress space

Combined shear–compression and uniaxial tensile/compressive tests were conducted by the universal materials testing machine (CMT5105A, SANS, Shenzhen, PRC) with the load cell of 100 kN. The loading rate is 6 mm/min with the corresponding nominal strain rate of $\dot{\varepsilon } = 0.01{\text{ s}}^{ - 1}$. The specimen was located between two metal heads. The lower end surface of the specimen is limited in the direction of compression (tension), and the upper end surface of the specimen is subjected to the displacement boundary condition. The loading and displacement signals of the specimen during testing were recorded by a computer for subsequent data processing.

Results

The compression and tensile nominal stress–strain curves exhibit nonlinear elastic behavior before the yielding. The softening behavior is observed after the yield point. Stress and strain of tension and compression can be calculated from the following equations and as plotted in Fig. 1.

$$ \sigma_{\text{n}} = \frac{{F_{\text{UTM}} }}{{A_{0} }},\quad \varepsilon_{\text{n}} = \frac{S}{L} $$

(1)

Where F_UTM and S are the load and displacements obtained by the universal testing machine, respectively, A₀ and L are original cross-sectional area and the height of specimen. VURAL et al. [21] provided the state of stress at a point within the gage section for the SCS geometry, as shown in Fig. 2. The normal stress $\sigma_{\text{n}}$ and shear stress $\tau$ can be written as:

$$ \sigma_{\text{n}} = \frac{{F_{\text{UTM}} }}{Dt}\cos^{ 2} \alpha ,\quad \tau = \frac{{F_{\text{UTM}} }}{Dt}\cos \alpha \sin \alpha . $$

(2)

Rather detailed explanations of the stress state and derivations of the expressions can be found in the previous literature. Similarly, the corresponding normal strains $\varepsilon_{\text{n}}$ and shear strains $\gamma_{\text{s}}$ can be given by the following equations:

$$ \varepsilon_{\text{n}} = \frac{S}{h}\cos^{2} \alpha ,\quad \gamma_{\text{s}} = \frac{S}{h}\cos \alpha \sin \alpha $$

(3)

Where D and t are the diameter and the thickness of the gage section of SCS, S and h are the displacement of SCS recorded by the universal materials testing machine and the height of the gage section, respectively. The additional $h = \frac{w}{\cos \alpha }$ and $w = 2$ is the width of the gage section of all the SCS. Based on above analyzing components of compression and shear stresses are listed in Table 1. Then the maximum principal stress $\sigma_{ \hbox{max} }$ and the minimum principal stress $\sigma_{\hbox{min} }$ under the shear–compression conditions can be expressed as flowing:

$$ \left. \begin{aligned} \sigma_{ \hbox{max} } \hfill \\ \sigma_{ \hbox{min} } \hfill \\ \end{aligned} \right\} = \frac{\sigma }{2} \pm \left[ {\left( {\frac{\sigma }{2}} \right)^{2} \, + \, \tau^{2} } \right]^{{\frac{1}{2}}} . $$

(4)

Table 1 Values of yield stresses and invariants under different loading conditions

The principal stresses under different loading condition are given in Table 1. The tensile stress is generally assumed as a positive value and the compressive stress is opposite. The principal stress value $\sigma_{1} > \sigma_{2} > \sigma_{3}$ is also assumed and in other word $\sigma_{1} = \sigma_{\hbox{max} }$ and $\sigma_{3} = \sigma_{\hbox{min} }$. The first invariant of stress, the second invariant of the deviatoric stress and the third invariant of the deviatoric stress are denoted by $I_{1}$, $J_{2}$ and $J_{3}$, respectively, which written as:

$$ I_{1} = {\text{tr(}}\sigma_{ij} ) ,\; \, {\kern 1pt} J_{2} = \frac{1}{2} \cdot {\text{tr}}(s_{ij}^{2} ),{\kern 1pt} \;J_{3} = \frac{1}{3} \cdot {\text{tr}}(s_{ij}^{3} ) $$

(5)

Where the $s_{ij} = \sigma_{ij} - \frac{{I_{1} }}{3} \cdot {\mathbf{I}}$ is deviatoric stress tensor and ${\mathbf{I}}$ is the second order unit tensor. As discussed above, the values of experimental yield stresses, which are obtained in the $I_{1}$ − $\sqrt {J_{2} }$ − $\sqrt[3]{{J_{3} }}$ stress space, are tabulated in Table 1.

Discussion

The yield behavior

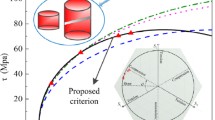
The comparisons between the experimental yield loci of PMMA and the Tresca, von-Mises criteria in the shear–compression stress space are shown in Fig. 2. Obviously, the two yield criteria may not have the capability to predict the yield behavior of PMMA precisely. Therefore, it is necessary to introduce the correlative parameters into the yield criterion to describe the mechanical behavior of the PMMA materials under multiaxial loading. As mentioned in introduction, different yield criterions have been proposed, i.e., $f(J_{2} )$, $f(J_{2} ,J_{3} )$, $f(I_{1} ,J_{2} )$. As well known, $I_{1}$, $J_{2}$ and $J_{3}$ mean different physical meanings, hydrostatic pressure, shear deformation and directional deformation, respectively [19]. Then different yield criteria are plotted in the principal stress space, as represented in Fig. 3. It indicated that $I_{1}$, $J_{2}$ and $J_{3}$ have significant influence on the shape of yield surface. $J_{2}$ is the foundation of yield criteria. It shows a cylinder surface in full stress space for the yield function $f(J_{2} )$. The influence of hydrostatic pressure is considered for the yield function of $f(I_{1} ,J_{2} )$ with the yield surface shows conical (linear relation) or ellipsoid surface in full stress space. The yield surface $f(J_{2} ,J_{3} )$ which takes the effects of Lode angle into consideration is a prismatic surface in full stress space.

Fig. 3

Yield surfaces of different forms in principal stress space

The influence of hydrostatic pressure about PMMA yield behavior is explored by plotting the yield loci of PMMA in $I_{1}$ − $\sqrt {J_{2} }$ space. Figure 4 shows the comparison of the D–P criterion and Von-Mises criterion. Obviously, the values of $\sqrt {J_{2} }$ have significant changes, with the increase of $I_{1}$. This phenomenon reveals that the yield behavior of PMMA is hydrostatic sensitive. Therefore, the D–P criterion that considers hydrostatic pressure term has a high capability of describing the yield behavior of PMMA than the Von-Mises criterion.

Fig. 4

Yield loci of PMMA in I₁− $\sqrt {J_{2} }$ space

Furthermore, to analyze the ability of the $J_{3}$ to effect the yield behavior, the yield loci was drawn in the $I_{1}$ − $\sqrt {J_{2} }$ − $\sqrt[3]{{J_{3} }}$ space. $\sqrt {J_{2} }$ varies with $\sqrt[3]{{J_{3} }}$ as well shown in Fig. 5. The yield loci under the different loading conditions are highlighted in the full stress space as well. Obviously, the effect of $J_{3}$ for the yield behavior of PMMA cannot be neglected. It must be emphasized that based on the experimental results in Figs. 4 and 5, the complex stress state can be easily obtained through SCS with different loading angles.

Fig. 5

Yield loci of PMMA in I₁− $\sqrt {J_{2} }$− $\sqrt[3]{{J_{3} }}$ space (unit: MPa)

Ghorbel yield criterion

As discussed above, the influences of $I_{1} ,J_{2} ,J_{3}$ must be considered simultaneously, when establishing the yield criterion of PMMA. Consequently, Ghorbel [19] proposed a yield criterion, as follows:

$$ f = \frac{{3J_{2} }}{{\sigma_{\text{t}} }}\left( {1 - \frac{27}{32}\frac{{J_{3}^{2} }}{{J_{2}^{3} }}} \right) + \frac{7(m - 1)}{8}I_{1} - \frac{7}{8}m\sigma_{\text{t}} ,\quad m = \frac{{\sigma_{\text{c}} }}{{\sigma_{\text{t}} }} $$

(6)

Where $\sigma_{\text{c}}$ and $\sigma_{\text{t}}$ are compression strength and tension strength, respectively. And m is the ratio of the compression and tension which can be used to describe the asymmetry of the yield surface. Figure 6 compares the yield loci and the yield surface proposed by Ghorbel in the $I_{1}$ − $\sqrt {J_{2} }$ − $\sqrt[3]{{J_{3} }}$ pace. Meanwhile, the yield surface shape of the positive view and the side view are given in Fig. 6a, b, respectively. The prediction data slightly deviates from the experimental results. If we choose three principal stress of PMMA instead of the three invariant of the stress and deviatoric stress in Eq. 6, we can rewrite the yield criterion as:

$$ \begin{aligned} f &= \frac{{\left[ {(\sigma_{1}^{{}} - \sigma_{2}^{{}} )^{2} + (\sigma_{2}^{{}} - \sigma_{3}^{{}} )^{2} + (\sigma_{3}^{{}} - \sigma_{1}^{{}} )^{2} } \right]}}{{2\sigma_{\text{t}} }} \hfill \\ &\quad \cdot \left( {1 - \frac{1}{32} \cdot \frac{{((2\sigma_{1} - \sigma_{2} - \sigma_{3} ) \cdot (2\sigma_{2} - \sigma_{1} - \sigma_{3} ) \cdot (2\sigma_{3} - \sigma_{1} - \sigma_{2} ))^{2} }}{{\left[ {\frac{{(\sigma_{1}^{{}} - \sigma_{2}^{{}} )^{2} + (\sigma_{2}^{{}} - \sigma_{3}^{{}} )^{2} + (\sigma_{3}^{{}} - \sigma_{1}^{{}} )^{2} }}{2}} \right]^{3} }}} \right) \hfill \\ &\quad+ \frac{{7\left( {m - 1} \right)}}{8} \cdot (\sigma_{1} + \sigma_{2} + \sigma_{3} ) - \frac{7}{8} \cdot m \cdot \sigma_{\text{t}} . \hfill \\ \end{aligned} $$

(7)

Fig. 6

Yield surface proposed by Ghorbel in I₁− $\sqrt {J_{2} }$− $\sqrt[3]{{J_{3} }}$ space, front view (a) and side view (b) (unit: MPa)

Then, the three-dimensional yield surface can be plotted in principal stress space as shown in Fig. 7. It is clear that the shape of yield surface has distinct difference between Ghorbel and Mises yield criteria. The end of yield surface is closed, which indicates that hydrostatic tensile could lead to the yielding of PMMA. In addition, the yield surface on π plane is no longer a circle due to the effect of $J_{3}$ and the area of the yield surface on the deviatoric plane changes with hydrostatic pressure axis ($\sigma_{1} = \sigma_{2} = \sigma_{3}$) due to the effect of $I_{1}$. Furthermore, the experimental yield loci and theoretical yield surface are plotted in the $\sigma_{1} - \sigma_{3}$ stress space as shown in Fig. 8. It can be found that the Ghorbel yield criterion has higher agreement than the Mises yield criterion, especially for the tension and compression asymmetry. However, Ghorbel yield criterion underestimates the yield strength of materials under shear-compressive stress to some extent.

Fig. 7

Mises and Ghorbel yield surfaces in principal stress space (unit: MPa)

Fig. 8

Comparison between the experimental loci and theoretical yield surfaces (Ghorbel and Mises)

Proposed yield criterion

Ghorbel yield criterion underestimates the yield strength of materials under shear-compressive stress to some extent. This is mainly because Ghorbel yield criterion assumes linear variation between $I_{1}$ and $J_{2}$. Actually, the relationship is nonlinear as shown in Fig. 9.

Fig. 9

Yield surface proposed in this paper in I₁− $\sqrt {J_{2} }$− $\sqrt[3]{{J_{3} }}$ space, front view (a) and side view (b) (unit: MPa)

Therefore, in this paper, the Ghorbel yield criterion are extended for the PMMA by introducing a quadratic dependence on the $I_{1}$. Then, a new yield criterion can be proposed as:

$$ f = \frac{a}{{\sigma_{t} }} \cdot J_{2} \cdot \left( {1 - \frac{27}{32} \cdot \frac{{J_{3}^{2} }}{{J_{2}^{3} }}} \right) + b \cdot I_{1} + \frac{c}{{\sigma_{t} }} \cdot I_{1}^{2} - \frac{7}{8} \cdot m \cdot \sigma_{\text{t}} . $$

(8)

Here a, b, c are material parameters and can be calibrated by utilizing the experimental results. To solve the three parameters substitute three experimental results (compression, tension, SCS of 45°) substituted into Eq. (8). Then the solution is a = 1.97, b = 0.77 and c = 0.30. Figure 10 compares the difference between the modified yield criterion (see Eq. 8) and the original yield criterion (see Eq. 6).

Fig. 10

Comparison between the yield criterion by Ghorbel [16] and present paper in I₁− $\sqrt {J_{2} }$ space

Obviously, the proposed yield criterion gives better description for the experimental results. Similarly, the proposed yield criterion can be plotted in principal stress pace using the method presented above. One must note here that the new yield surface becomes totally closed, which means that not only biaxial tension can lead to yielding but also biaxial compression can cause yield of PMMA. The quadratic relationship between $\sqrt {J_{2} }$ and $I_{1}$ can be indicated by the yield surface whose both ends are also closed. Meanwhile, the influence of lode angle can be indicated by the noncircular yield surface in the $\pi$ plane (see Fig. 11).

Fig. 11

The Ghorbel and the proposed yield surfaces in principal stress space (unit: MPa)

The experimental yield data, corresponding yield surfaces obtained from Eqs. 6 and 8 are summarized in $\sigma_{1} - \sigma_{3}$ stress space, as shown in Fig. 12. It is clear that the proposed yield surface accords better with the experimental loci of PMMA than other yield surface.

Fig. 12

Experimental yield surface of PMMA in principle stress space

Furthermore, a series of yield surfaces are summarized in Fig. 13 to investigate the influence of material parameters on the shape of yield surfaces. As the parameter a increases, the yield surface area decreases, namely that parameter a reflects how difficulty the materials yield is. However, it has less influence on the biaxial tensile strength. The yield surface offset to third quadrants with increasing parameter b. In other words, the parameter b characterizes the effects on the tension and compression asymmetry. With the increase of parameter c, the yield surface is shrinkage especially in the third quadrant. This result shows that parameter c has a strong influence on biaxial compression.

Fig. 13

Effects of materials parameters, i.e., a (I), b (II) and c (III) on the yield surface

Summary

In this paper, the mechanical responses of PMMA under tension, compression and combine shear–compression stress states are investigated by employing the dog-bone sample, cylinder sample and SCS with four different loading angles, respectively. Comparisons between experimental results and Tresca, Mises, D–P, Ghorbel yield criterion predictions are conducted and discussed. The experimental results indicate that the first invariant of the stress and the third invariant of deviatoric stress behave strong influences on the yield behaviors of PMMA. Meanwhile, a modified yield criterion f(I₁, J₂, J₃) that incorporates the quadratic relationship between I₁ and $\sqrt {J_{2} }$ is proposed in this paper. The accuracy and effectiveness of the proposed yield criterion are verified utilizing the yield data under the complex stress states. Based on the proposed yield criterion, the influences of the material parameters on the shape of yield surfaces have been analyzed. Furthermore, it is indicated that the modified yield criterion provides satisfactory prediction results and expands original scope of applications.