Dynamical analysis of a glucose-insulin regulatory system with insulin-degrading enzyme and multiple delays

Abstract

This paper investigates the dynamics of a glucose-insulin regulatory system model that incorporates: (1) insulin-degrading enzyme in the insulin equation; and (2) discrete time delays respectively in the insulin production term, hepatic glucose production term, and the insulin-degrading enzyme. We provide rigorous results of our model including the asymptotic stability of the equilibrium solution and the existence of Hopf bifurcation. We show that analytically and numerically at a certain value the time delays driven stability or instability occurs when the corresponding model has an interior equilibrium. Moreover, we illustrate the oscillatory regulation and insulin secretion via numerical simulations, which show that the model dynamics exhibit physiological observations and more information by allowing parameters to vary. Our results may provide useful biological insights into diabetes for the glucose-insulin regulatory system model.

1 Introduction

Diabetes mellitus is a chronic disease of the glucose-insulin regulatory system, which is characterized by hyperglycemia resulting from none or little insulin release for type 1 diabetes mellitus (TDM1), or for type 2 diabetes mellitus (T2DM) due to primarily insulin resistance, a concept that the cells, e.g., muscle cells and adipose cells, are unable to utilize insulin efficiently (Chen and Tsai 2010). Diabetes mellitus can cause a variety of serious health complications including possible blindness, heart disease, kidney failure, stroke, nerve damage, and lower extremity amputations. The diabetic population in the world is rapidly rising in recent decades. International Diabetes Federation estimates that the number of subjects around the world living with diabetes is expected to hit 700 million people in 2045 (IDF 2020). It is critical to prevent the onset of diabetes or slow down its progression and thus the characteristic complications by efficient and effective interventions, for example, developing algorithms for insulin administration protocols through great understanding of the homeostasis of the glucose-insulin regulatory system.

It is well known that natural sciences and mathematical modeling have impelled each other in their progress in the long time history, well documented usefulness of mathematical models in physics and technologies, from the days of Glileo, Kepler, and Newton to present, and also in biology, for example, the Hodgkin-Huxley model of the action potentials in neurons. Particularly and naturally physiological systems are refractory to precise quantitative description by mathematical models as numerous details exit in each different level of subtle interactions (Torres and Santos 2015), which requires model refinements with the progress of deeper understandings and new findings in the related area. A footmark for the mathematical modeling approach in the study of diabetic disease can be found in 1961 by Bolie (1961). Gradually and increasingly more models are proposed to be more accurate and clinically feasible, making them a valuable resource for clinical research and applications. One example is the Minimal Model by Bergman et al. (1979) and many consequent works for the intravenous glucose tolerance test (IVGTT) used to assess insulin sensitivity and glucose effectiveness. Another example is a series of models proposed and refined or extended by Chen and Tsai (2010), Sturis et al. (1991), Tolic et al. (2000), Engelborghs et al. (2001), Li et al. (2006), Li and Kuang (2007) for understanding the regulating mechanisms of the glucose-insulin system including the sustained ultradian oscillations of insulin secretion. Among which, as commented by Batzel and Kappel (2011), the delay differential equation model refined by Li et al. (2006), Li and Kuang (2007) is extended by Wang et al. (2007), Sarika et al. (2008), Wu et al. (2011), Nguyen et al. (2012), Wu et al. (2013), Huang et al. (2012), Song et al. (2014), Kissler et al. (2014) to develop control algorithms for exogenous insulin injections in artificial pancreas devices, applied by Strilka et al. (2014); Stull et al. (2016); Strilka et al. (2016) in studies of laboratory experiments for subcutaneous injection of insulin analogues, and also inspired theoretical analyses (Huard et al. 2015; Pei et al. 2011).

Clearly, insulin is a critical and necessary hormone for energy metabolism in humans. The insulin-degrading enzyme (IDE), also known as insulynsin or insulin protease, is an enzyme, probably the most critical enzyme, to degrade and inactivate insulin action and many functions in the termination of the insulin response. Such activity is biologically important because of the limited half-life of the crucial hormone in humans (Broh-Kahn and Mirsky 1949). IDE deficiency leads to abundant insulin in circulation and further causes $\beta$-cell degeneration (Merino et al. 2020). Since the rate of insulin degradation at the cell level is basically determined by IDE activity, it is necessary to understand the relationship between improvements in IDE activity and the occurrence and development of insulin resistance (IR). IDE is known as an inhibitor of type 2 diabetes therapeutics (Maianti et al. 2014; Pivovarova-Ramich et al. 2016). Some research has shown that IDE plays an important role in the degradation and clearance of insulin in cells, promotes insulin receptor recycling and new insulin secretion, and maintains a relatively stable insulin level in the body (Kuo et al. 1994; Gu et al. 2004; Tundo et al. 2017). The inhibitors of this activity may improve the action of insulin in rabbits was discovered in Mirsky et al. (1955). IDE mice have high insulin levels, but they show reduced glucose tolerance rather than increased, which may result from compensatory deficiency signaling of insulin (Farris et al. 2003; Abdul-Hay et al. 2011). Insulin is a biologically essential IDE substrate; abnormal insulin levels and inadequate insulin and other hormone responses that control glucose levels are the main causes of T2DM. According to the findings by Maianti et al. (2014), Farris et al. (2003), Malito et al. (2008), Shen et al. (2006), IDE as a disease susceptibility gene in both AD and T2DM. In the review (González-Casimiro et al. 2021), González-Casimiro et al. deliberated current knowledge about IDE’s function as a regulator of insulin secretion and hepatic insulin sensitivity and showed that IDE has an additional role in regulating hepatic insulin action and sensitivity through studying on mice with tissuse-specific genetic deletion of IDE in the liver and pancreas $\beta$-cells. So it is worthwhile to investigate the impact of IDE in the regulation system. We refine the model in Li et al. (2006), Li and Kuang (2007) by involving the subtle processes regarding insulin degradation enzyme and study the inhibitory role of IDE in the degradation of insulin and glucagon in humans with the aim to elucidate certain intrinsic factors for IDE playing a critical role in the metabolic system.

We organize our paper as follows. In the next section, we carefully extend the two time delays model in Li et al. (2006), Li and Kuang (2007) by incorporating IDE according to physiology. In Sect. 3, we first show that the proposed model is well-posed and then investigate biological dynamical behaviors. When the analytical study is tedious and of limitation, we continue in Sect. 4 to numerically investigate the model behaviors within biological meaningful scopes. In Sect. 5, we will discuss our findings. The proofs of the main results are carried out in “Appendices”.

2 Model derivations

The two time delays model for the glucose-insulin regulatory system formulated by Li et al. (2006) with G(t) and I(t) stand for the glucose and insulin concentration at time t, respectively, is given as follows

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\text {d}G(t)}{\text {d} t}=G_{in}-f_2(G(t))-f_3(G(t))f_4(I(t))+f_5(I(t-\tau _2)), \\&\frac{\text {d}I(t)}{\text {d} t}=f_1(G(t-\tau _1))-d_i I(t), \end{aligned}\right. \end{aligned}$$

(1)

where the initial conditions are given by $G(t)\equiv G_0>0$ for $t\in [-\tau _1, 0]$ and $I(t)\equiv I_0>0$ for $t\in [-\tau _2, 0],\, \tau _1,\tau _2>0$. The functions $f_1$ through $f_5$ are a set of highly non-linear and $d_iI$ is the insulin degradation with $d_i>0$ as the constant degradation rate. (The physiological meanings of each term will be explained below.) This has been studied by its original form or extended forms widely as stated as aforementioned in the last section.

In the case of the metabolism of hepatic IDE in mice (González-Casimiro et al. 2021), hepatic IDE overexpression will not alter insulin clearance, displaying that the pancreas decreased insulin production and secretion as a result of increased insulin sensitivity. This research evidences that in a preclinical mouse model of obesity and diabetes, reinforcing hepatic IDE function in the liver can regulate insulin resistance and glucose intolerance to some extent. Galagovsky et al. (2014) found that the highest Drosophila IDE (DIDE) /tubulin expression occurs in the fat body. They raised that DIDE is an insulin signaling modulator, and its loss of function promotes insulin resistance, a symptom of T2DM. Tsuda et al. (2010) shown that the overexpression of DIDE causes phenotypes that are presumably related to insulin deficiency. Now, we incorporate the functionalities of IDE on regulating insulin levels in this model and apply a function $\varvec{\alpha }(I)$ to capture the dynamic of IDE. Since the lack of a study on delay in activation of IDE due to insulin change, we try to take the time delay $\tau _3$ in the insulin secretion to be equal to the amount of time that elapses before insulin secretion would respond to the changes in IDE.

In the second equation of model (1), Li et al. (2006) only considered the glucose concentration G(t) as the sole stimuli ($f_1(G(t-\tau _1))$) to stimulate the production of insulin without the impact by IDE, where $\tau _1 > 0$ represents the time delay of the insulin response to the glucose stimulation and the time needed for the newly synthesized insulin crossing the endothelial barrier to become remote insulin. It is known that after insulin enters the liver through the portal vein, part of it is inactivated in the liver or re-enters the systemic circulation. Specifically, insulin enters the cell for degradation by IDE in the cytoplasm (Fawcett and Duckworth 2009). Excessive degradation of insulin in the cytoplasm can lead to a decrease in the amount of insulin that acts per unit of time and weaken the effect of insulin, thereby stimulating islet cells to secrete excessive insulin for compensation, which causes IR and hyperinsulinemia (Tandl and Kolb 1984; Abdul-Hay et al. 2011). IDE deficiency increases insulin secretion, which will eventually have deleterious effects on $\beta$-cell function leading to type 2 diabetes (Costes and Butler 2014; Fernández-Díaz et al. 2019). On the other hand, IDE overexpression improves glucose tolerance and insulin sensitivity, but, IDE overexpression in the liver does not affect insulin clearance (Merino et al. 2020). The work in Kukday et al. (2012) reveals that insulin is a dynamic factor impacting IDE effects. Dose-response studies reported in Fig. 4C by Kukday et al. (2012) reveal that IDE activity including insulin secretion over a range of human insulin (0–17.2 $\upmu$M) follows a reverse Hill function kinetics with a tiny half-saturation value at 0.92 $\upmu$M through data fitting. Thus, taking the impact of IDE on insulin secretion into account, we assume reasonably that the factor function $\varvec{\alpha }(I)$ satisfies the following assumptions:

(A1)::

$\varvec{\alpha }(0)>0$;

(A2)::

$\varvec{\alpha }(I)|_{I>0}> 0,\, \frac{\text {d} \varvec{\alpha }(I)}{\text {d} I}<0$, and $\lim \limits _{I\rightarrow +\infty }\varvec{\alpha }(I)=0$,

The shapes, rather than the form, of the response functions matter (Keener and Sneyd 2009). Thus, for the sake of convenience, we choose the multiplier $\varvec{\alpha }(I):=\tfrac{k_0 I(t)}{\text {e}^{cI}-1}$, $k_0, c>0$, where $k_0 I(t-\tau _3)$ represents the delayed effect of insulin degradation product under the action of IDE on insulin secretion at time t, and the term $\tfrac{1}{\text {e}^{c I(t-\tau _3)}-1}$ represents the probability of affecting the insulin secretion with time delay $\tau _3$, which correlates to the total amount of the biomass of insulin consumption with a constant $c>0$. In which, $\varvec{\alpha }(0)=\tfrac{k_0}{c}$, and $\varvec{\alpha }(I)>1$ indicates IDE deficiency, $\varvec{\alpha }(I)<1$ stands for IDE overexpression, and $\varvec{\alpha }(I)=1$ is for normal IDE level. Let ${\hat{I}}>0$ be the unique value such that $\varvec{\alpha }({\hat{I}})=1$. The above assumption can be described as: when the peripheral insulin is below ${\hat{I}}$, IDE is deficit; when the peripheral insulin is above ${\hat{I}}$, IDE is overexpressed. ${\hat{I}}$ monotonically decreases when c increases.

Fig. 1

Modeling framework showing the regulatory mechanisms. The functions represent $f_1$—effect of glucose on insulin secretion, $f_2$—insulin independent glucose utilization, $f_3f_4$—insulin dependent glucose utilization, and $f_5$—effect of insulin on glucose production

According to the above physiological findings in rodents (Mirsky et al. 1955; Farris et al. 2003; Shen et al. 2006) and physiological observations discussed above, we extend Model (1) as below with the aim to investigate the links of defect in IDE with T2DM and/or AD in human. The novel model is given by

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\text {d}G(t)}{\text {d} t}=G_0-f_2(G(t))-f_3(G(t))f_4(I(t))+f_5(I(t-\tau _2)),\\&\frac{\text {d}I(t)}{\text {d} t}=f_1(G(t-\tau _1))\frac{k_0 I(t-\tau _3)}{\text {e}^{c I(t-\tau _3)}-1}-{d_i} I(t), \\ \end{aligned} \right. \end{aligned}$$

(2)

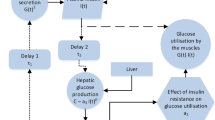
where the constant glucose infusion term $G_0$ models the continuous intestinal glucose absorption after a meal or oral glucose. The diagram of this glucose-insulin model is shown in Fig. 1.

The function $f_1(G(t))$ is bounded and sigmoidal shape with $f_1(0)>0,\, f_1(x)>0,\, \frac{\text {d}f_1(x)}{\text {d} x}>0$ for $x>0$. The functions $f_2(G(t))$ and $f_3(G(t))f_4(I(t))$ respectively denote the insulin-independent and insulin-dependent glucose utilization [see Li et al. (2006) for more details], where $f_2(x)>0$ is in sigmoidal shape with $f_2(0)=0$ and $\frac{\text {d}f_2(x)}{\text {d} x}>0$ is bounded for $x>0$; $f_3(0)=0,\, \frac{\text {d}f_3(x)}{\text {d} x}>0$ for $x>0$; and $f_4(0)>0,\, f_4(x)>0,\, \frac{\text {d}f_4(x)}{\text {d} x}>0$ are bounded above for $x>0$, $f_4(x)$ is in sigmoidal shape. Glucose production is denoted as $f_5(I(t))$ controlled by insulin concentration I(t). $f_5(x)$ is in inverse sigmoidal shape, $f_5(0)>0,\, f_5(x)>0,\, \frac{\text {d}f_5(x)}{\text {d} x}<0$ for $x>0$, and $f_5(x),\, \big |\frac{\text {d}f_5(x)}{\text {d} x}\big |$ are bounded above for $x>0$. The function $f_5(I(t-\tau _2))$ represents the delayed HGP, indicating that the production is controlled by insulin with time delay $\tau _2>0$.

3 Stability analysis

In this section, we will focus on the existence of positive steady state solutions and local stability of the time-delay model (2). For simplicity, let $\tau _3=\tau _2$.

Throughout this paper, we assume $f_i(x)\,(i=1,2,3,4,5)$ satisfies the following conditions:

(H1):

$\lim \limits _{x\rightarrow \infty }f_1(x)=M_1,\> f_1(0):=m_1>0$, $\frac{\text {d}f_1(x)}{\text {d} x}$ is bounded by a constant $M'_1>0$ for $x>0$;

(H2):

$\lim \limits _{x\rightarrow \infty }f_2(x)=M_2$ and there exists a constant $M'_2$ such that $\frac{\text {d}f_2(x)}{\text {d} x}<M'_2$ for $x>0$;

(H3):

$f_4(0):=m_4>0$, there exist constants $M_3>0,\,M_4>0$ and $M'_4>0$ such that $0<f_3(x)\le M_3x,\,\lim \limits _{x\rightarrow \infty } f_4(x)=M_4$ and $\frac{\text {d}f_4(x)}{\text {d} x}<M'_4$ for $x>0$;

(H4):

$\lim \limits _{x\rightarrow \infty } f_5(x)=0$ and there exist constant $M_5,\,M'_5>0$ such that $f_5(x)\le M_5$ and $\big |\frac{\text {d}f_5(x)}{\text {d} x}\big |\le M'_5$ for $x>0$.

The boundedness of the solutions for the model (2) is presented in the following Proposition (the proof will be carried out in “Appendices”).

Proposition 3.1

For Model (2), the following hold:

• (i) If $\lim \limits _{x\rightarrow \infty }f_{3}(x) >\frac{G_0-M_2+f_5(\frac{1}{c}\ln ({k_0}M_1+{d_i}))}{m_4}$, then Model (2) has a unique positive steady state $(G^*, I^*)$, where $I^*=\frac{1}{c}\ln ({k_0}f_1(G^*)+{d_i})$. Furthermore, all solutions are positive and bounded.

• (ii) If $\lim \limits _{x\rightarrow \infty }f_3(x)<\frac{G_0-M_2}{m_4}$, then $\limsup \limits _{t\rightarrow \infty } G(t)=\infty$.

3.1 The case $\mathbf {\tau _1\tau _2=0}$

Although an explicit expression cannot be obtained, Model (2) possesses a unique steady state $(G^*, I^*)$, defined by the equations $\frac{\text {d}G(t)}{\text {d} t}=\frac{\text {d}I(t)}{\text {d} t}=0$. In this subsection, we analyze the local stability of Model (2) at $(G^*, I^*)$ in the case of $\tau _1\tau _2=0$.

Letting ${\widehat{G}}(t)=G(t)-G^*$ and ${\widehat{I}}(t)=I(t)-I^*$, for simplicity we will not write the hat ( $\widehat{}$ ) in the rest of this paper, then Model (2) is linearized around $(G^*, I^*)$ as follows:

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\text {d}G(t)}{\text {d} t}=-W_1G(t)-W_2I(t)-W_3I(t-\tau _2), \\&\frac{\text {d}I(t)}{\text {d} t}=W_4G(t-\tau _1)-W_5I(t-\tau _2)-{d_i}I(t). \end{aligned} \right. \end{aligned}$$

(3)

Because $f_1$ through $f_4$ are monotonically increasing functions and $f_5$ is monotonically decreasing, it is easy to check that all the following parameters are positive,

$$\begin{aligned} \left\{ \begin{array}{l} W_1=\frac{\text {d}}{\text {d} G}f_2(G^*)+\frac{\text {d}}{\text {d} G}f_3(G^*)f_4(I^*)>0,\\ W_2=f_3(G^*)\frac{\text {d}}{\text {d} I}f_4(I^*)>0,\\ W_3=-\frac{\text {d}}{\text {d} I}f_5(I^*)>0,\\ W_4=\frac{\text {d}}{\text {d} G}f_1(G^*)\frac{k_0I^*}{\text {e}^{c I^*}-1}>0,\\ W_5=\frac{f_1(G^*)k_0[(1-c I^*)\text {e}^{c I^*}-1]}{(\text {e}^{c I^*}-1)^2}>0. \end{array} \right. \end{aligned}$$

(4)

The characteristic equation of (3) is

$$\begin{aligned} \begin{array}{llll} {\mathcal {F}}(\lambda )&{}=\lambda ^2+(W_1+W_5\text {e}^{-\lambda \tau _2}+{d_i})\lambda +W_1{d_i}+W_2W_4\text {e}^{-\lambda \tau _1} \\ &{}\quad +W_1W_5\text {e}^{-\lambda \tau _2}+W_3W_4\text {e}^{-\lambda (\tau _1+\tau _2)}=0. \end{array} \end{aligned}$$

(5)

For Model (2), the equilibrium point $(G^*, I^*)$ will be asymptotically stable if all the roots of the characteristic equation (5) have negative real parts. In the case of a non-delayed model, we will assume that the equilibrium point $(G^*, I^*)$ is asymptotically stable and then find conditions for which $(G^*, I^*)$ is still asymptotically stable with all delays.

It is clear that ${\mathcal {F}}(0)=W_1({d_i}+W_5)+(W_2+W_3)W_4>0$, then $\lambda =0$ is not a root of equation (5). Thus, if there is some stability switch of the trivial solution of the linearized model (3), there must be a pair of pure conjugate imaginary roots of Eq. (5). Equation (5) with $\tau _1=\tau _2=0$ is equivalent to $\lambda ^2+(W_1+W_5+{d_i})\lambda +W_1({d_i}+W_5)+(W_2+W_3)W_4=0$, we then have

Proposition 3.2

Under the conditions $W_1+W_5+{d_i}>0$ and $W_1({d_i}+W_5)+(W_2+W_3)W_4>0$, the steady state solution $(G^*, I^*)$ of Model (2) with $\tau _1=\tau _2=0$ is asymptotically stable.

When $\tau _1>0$ and $\tau _2=0$, Eq. (5) is equivalent to

$$\begin{aligned} \begin{array}{l} {\mathcal {F}}(\lambda )=\lambda ^2+(W_1+W_5+{d_i})\lambda +W_1({d_i}+W_5)+(W_2+W_3)W_4\text {e}^{-\lambda \tau _1}=0. \end{array} \end{aligned}$$

(6)

Referring to Lemma 4.1 in Li and Kuang (2007), we get $2W_1({d_i}+W_5)-(W_1+W_5+{d_i})^2=-(W^2_1+(W_5+{d_i})^2)<0$ and state the following results without proofs.

Proposition 3.3

For Model (2) with $\tau _1>0$ and $\tau _2=0$,

• (i) If $W_1({d_i}+W_5)>(W_2+W_3)W_4$, then the positive stationary solution $(G^*, I^*)$ of model (2) is always stable for $\tau _1>0$;

• (ii) If $W_1({d_i}+W_5)<(W_2+W_3)W_4$, there exists a constant $\tau _1^0>0$ such that $(G^*, I^*)$ of model (2) is stable for $\tau _1\in (0,\tau _1^0)$ and unstable for $\tau _1> \tau _1^0$. A Hopf bifurcation occurs as $\tau _1$ passes through the critical value $\tau _1^0$.

When $\tau _1=0$ and $\tau _2>0$, Eq. (5) is equivalent to

$$\begin{aligned} \begin{array}{l} {\mathcal {F}}(\lambda )=\lambda ^2+(W_1+{d_i}+W_5\text {e}^{-\lambda \tau _2})\lambda +W_1{d_i}+W_2W_4\\ \hspace{1.5cm} +(W_1W_5+W_3W_4)\text {e}^{-\lambda \tau _2}=0. \end{array} \end{aligned}$$

(7)

Let

$$\begin{aligned} \left\{ \begin{array}{l} A =W_1+{d_i}>0,\\ B=W_5>0,\\ C=W_1W_5+W_3W_4>0,\\ D=W_1{d_i}+W_2W_4>0, \end{array} \right. \end{aligned}$$

(8)

then Eq. (7) becomes

$$\begin{aligned} \begin{array}{l} {\mathcal {F}}(\lambda )=\lambda ^2+A\lambda +B\lambda \text {e}^{-\lambda \tau _2}+D +C\text {e}^{-\lambda \tau _2}=0. \end{array} \end{aligned}$$

(9)

Applying the Lemma in Cooke and Grossman (1982), Wei and Ruan (1999), we deduce the following results and the proof can be found in “Appendices”.

Lemma 3.1

For Eq. (9), we have

• (i) If $D<C$ holds and $\tau _2=\tau _2^{n,1}$, then Eq. (9) has a pair of purely imaginary roots $\pm \textrm{i}\omega _+$;

• (ii) If $(A^2-B^2-2D)^2> 4(D+C)(D-C)> 0>A^2-B^2-2D$ holds and $\tau _2=\tau _2^{n,1}$ (res. $\tau _2=\tau _2^{n,2}$), then Eq. (9) has a pair of purely imaginary roots $\pm \textrm{i}\omega _+$ (res. $\pm \textrm{i}\omega _-$);

• (iii) If neither $D<C$ nor $(A^2-B^2-2D)^2> 4(D+C)(D-C)> 0>A^2-B^2-2D$ and $\tau _2>0$, then Eq. (9) has no purely imaginary root, where

  $$\begin{aligned} \begin{array}{lll} \omega _{\pm }^2=\dfrac{-(A^2-B^2-2D)\pm \sqrt{(A^2-B^2-2D)^2-4(D+C)(D-C)}}{2},\\ \tau _2^{n,1}=\dfrac{1}{\omega _+}\left[ \arccos \left( \dfrac{C(\omega _{+}^2-D)-AB\omega _{+}^2}{C^2+B^2\omega _{+}^2}\right) +2n\pi \right] ,\\ \tau _2^{n,2}=\dfrac{1}{\omega _-}\left[ \arccos \left( \dfrac{C(\omega _{-}^2-D)-AB\omega _{-}^2}{C^2+B^2\omega _{-}^2}\right) +2n\pi \right] ,\quad n=0,1,\ldots \end{array} \end{aligned}$$

  (10)

Consider the characteristic roots of Eq. (9) as

$$\begin{aligned} \lambda _{k,n}(\tau _2)=\alpha _{k,n}(\tau _2)+\text {i}\omega _{k,n}(\tau _2),\quad k=1, 2; \quad n=0,1,\ldots \end{aligned}$$

(11)

where

$$\begin{aligned} \alpha _{1,n}\left( \tau _2^{n,1}\right) =0, \quad \omega _{1,n}\left( \tau _2^{n,1}\right) =\omega _+ \end{aligned}$$

(12)

and

$$\begin{aligned} \alpha _{1,n}\left( \tau _2^{n,2}\right) =0, \quad \omega _{2,n}\left( \tau _2^{n,2}\right) =\omega _-. \end{aligned}$$

(13)

It can be verified that the following lemma is true.

Lemma 3.2

Let $\tau _2^{n,k}\>(k=1,2)$ associated with $\omega _{k,n}$. For $\tau _2=\tau _2^{n,k}$, the characteristic Eq. (9) has a pair purely imaginary roots $\pm \text {i}\omega _{k,n}$, satisfying

$$\begin{aligned} \text {sign}\left\{ \dfrac{\text {d}\text {Re}(\lambda )}{\text {d}\tau _2}\bigg |_{\tau _2=\tau _2^{n,k}} \right\} =\text {sign}\big \{A^2-B^2-2D+2\omega _{k,n}^2\big \}, \end{aligned}$$

where $\tau _2^{n,k}$ and $\omega _{k,n}$ are defined in Eqs. (10), (12) and (13).

The proof of Lemma 3.2 is attached in “Appendices”.

Thus, applying the Lemma in Wei and Ruan (1999), we obtain the distribution of the characteristic roots of Eq. (9).

Lemma 3.3

For Eq. (9), we have the following

• (i) If $D<C$ holds, then when $\tau _2\in \left[ 0, \tau _2^{0,1}\right)$ all roots of Eq. (9) have negative real parts, and when $\tau _2>\tau _2^{0,1}$ Eq. (9) has at least one root with positive real part.

• (ii) If $(A^2-B^2-2D)^2>4(D+C)(D-C)>0>A^2-B^2-2D$ holds, then there are j switches from stability to instability, that is, when $\tau _2\in \left( \tau _2^{n,2},\,\tau _2^{n+1,1}\right) \>(n=-1,0,1,\cdots , j-1)$, all roots of Eq. (9) have negative real parts, where $\tau _2^{-1,2}=0$, and when $\tau _2\in \left[ \tau _2^{n,1},\, \tau _2^{n,2}\right)$ and $\tau _2>\tau _2^{j,1}\,(n=0,1,\cdots , j-1)$, Eq. (9) has at least one root with positive real part.

Based on the above analysis, we thus obtain the following results on the stability of the steady state solution $(G^*, I^*)$ of Model (2).

Theorem 3.1

For Model (2), the number of different imaginary roots with positive (negative) imaginary parts of Eq. (9) can be zero, one, or two only.

• (i) If $D>C$ and $A^2-B^2-2D>0$ hold, then the stability of the steady state solution $(G^*, I^*)$ does not change for all $\tau _2> 0$.

• (ii) If $D<C$ holds, there is one imaginary root with a positive imaginary part, an unstable steady state solution $(G^*, I^*)$ never becomes stable for any $\tau _2> 0$. If the steady state solution $(G^*, I^*)$ is asymptotically stable for $\tau _2=0$, then it is uniformly asymptotically stable for $0<\tau _2<\tau _2^{0,1}$, and it becomes unstable for $\tau _2>\tau _2^{0,1}$. A Hopf bifurcation occurs as $\tau _2$ passes through the critical value $\tau _2^{0,1}$, where $\tau _2^{0,1}$ is given in (10).

• (iii) If $(A^2-B^2-2D)^2>4(D+C)(D-C)>0>A^2-B^2-2D$ holds, there are two imaginary roots with positive imaginary part, $\text {i}\omega _+$ and $\text {i}\omega _-$, such that $\omega _+>\omega _->0$, then the stability of the steady state solution $(G^*, I^*)$ can change a finite number of times at most as $\tau _2$ is increased, and eventually it becomes unstable.

Remark 1

See the “Appendices” for the detailed proof of Theorem 3.1. From Theorem 3.1, it is easy to find that Model (2) undergoes a Hopf bifurcation related not only to the value of $\tau _2$ but also to the value of the rate of insulin release $k_0$. We shall demonstrate numerical investigation in Sect. 4.

3.2 The case $\mathbf {\tau _1\tau _2\ne 0}$

In this subsection, we assume both $\tau _1>0$ and $\tau _2>0$. We first let $\tau _1=\tau _2=\tau$, Eq. (5) equals to

$$\begin{aligned} \lambda ^2+(W_1+{d_i})\lambda +W_1{d_i}+(W_5\lambda +W_2W_4+W_1W_5+W_3W_4\text {e}^{-\lambda \tau })\text {e}^{-\lambda \tau }=0,\qquad \end{aligned}$$

(14)

and $\lambda =0$ is not a characteristic root of Eq. (14). Set

$$\begin{aligned} \begin{array}{l} \Phi (\lambda ,\tau ):=\lambda ^2+(W_1+{d_i})\lambda +W_1{d_i},\\ \Psi (\lambda ,\tau ):=W_5\lambda +W_2W_4+W_1W_5+W_3W_4\text {e}^{-\lambda \tau }, \end{array} \end{aligned}$$

(15)

we consider $\lambda =\text {i}\omega$ is a root of the characteristic Eq. (14), where $\omega$ is assumed to be strictly greater than 0. From (15), we denote by $\Phi _R,\,\Psi _R$ the real parts of $\Phi ,\,\Psi$, and by $\Phi _I,\,\Psi _I$ the imaginary parts of $\Phi ,\,\Psi$, respectively. Thus, $\Phi _R(\text {i}\omega ,\tau )=W_1{d_i}-\omega ^2,\,\Phi _I(\text {i}\omega ,\tau )=(W_1+{d_i})\omega$, $\Psi _R(\text {i}\omega ,\tau )=W_1W_5+W_2W_4+W_3W_4\cos \omega \tau$, $\Psi _I(\text {i}\omega ,\tau )=W_5\omega -W_3W_4\sin \omega \tau$. Therefore, $\omega$ satisfies the following equations,

$$\begin{aligned} \left\{ \begin{array}{l} \Psi _I(\text {i}\omega ,\tau )\sin \omega \tau +\Psi _R(\text {i}\omega ,\tau )\cos \omega \tau =-\Phi _R(\text {i}\omega ,\tau ),\\ \Psi _I(\text {i}\omega ,\tau )\cos \omega \tau -\Psi _R(\text {i}\omega ,\tau )\sin \omega \tau =-\Phi _I(\text {i}\omega ,\tau ), \end{array} \right. \end{aligned}$$

(16)

which gives

$$\begin{aligned} \begin{array}{lll} \sin \omega \tau =\dfrac{-\Phi _R(\text {i}\omega ,\tau )\Psi _I(\text {i}\omega ,\tau )+\Phi _I(\text {i}\omega ,\tau )\Psi _R(\text {i}\omega ,\tau )}{\Psi ^2_R(\text {i}\omega ,\tau )+\Psi ^2_I(\text {i}\omega ,\tau )}=\text {Im}\left( \dfrac{\Phi (\text {i}\omega ,\tau )}{\Psi (\text {i}\omega ,\tau )}\right) ,\\ \cos \omega \tau =-\dfrac{\Phi _R(\text {i}\omega ,\tau )\Psi _R(\text {i}\omega ,\tau )+\Phi _I(\text {i}\omega ,\tau )\Psi _I(\text {i}\omega ,\tau )}{\Psi ^2_R(\text {i}\omega ,\tau )+\Psi ^2_I(\text {i}\omega ,\tau )}=-\text {Re}\left( \dfrac{\Phi (\text {i}\omega ,\tau )}{\Psi (\text {i}\omega ,\tau )}\right) . \end{array} \end{aligned}$$

(17)

Then, we derive

$$\begin{aligned} \begin{array}{lll} {\mathfrak {F}}(\omega ,\tau )=|\Phi (\text {i}\omega ,\tau )|^2-|\Psi (\text {i}\omega ,\tau )|^2\\ \quad =\omega ^4+(W_1^2+{d_i^2}-W_5^2)\omega ^2+2\omega W_3W_4W_5\sin \omega \tau +W_1^2{d_i^2}-W_3^2W_4^2\\ \qquad -(W_2W_4+W_1W_5)^2-2(W_2W_4+W_1W_5)W_3W_4\cos \omega \tau , \end{array} \end{aligned}$$

(18)

and $\omega$ satisfies the transcendental equation ${\mathfrak {F}}(\omega ,\tau )=0$ which implies

$$\begin{aligned} \begin{array}{l} \omega ^4+\big (W_1^2+{d_i^2}-W_5^2\big )\omega ^2+W_1^2{d_i^2}-W_3^2W_4^2-(W_2W_4+W_1W_5)^2\\ \quad =2(W_2W_4+W_1W_5)W_3W_4\cos \omega \tau -2\omega W_3W_4W_5\sin \omega \tau . \end{array} \end{aligned}$$

(19)

If $\omega =0$, we check that

$$\begin{aligned} \begin{array}{l} {\mathfrak {F}}(0)=W_1^2{d_i^2}-W_3^2W_4^2-(W_2W_4+W_1W_5)^2-2(W_2W_4+W_1W_5)W_3W_4, \end{array} \end{aligned}$$

(20)

when $W_1^2{d_i^2}<W_3^2W_4^2+(W_2W_4+W_1W_5)(W_2W_4+W_1W_5+2W_3W_4)$, then ${\mathfrak {F}}(0)<0$. Also, it is easy to check that ${\mathfrak {F}}(+\infty )>0$, so we can obtain that Eq. (19) has finite positive roots.

Let us define $\phi (\tau )\in [0,2\pi ]$ such that

$$\begin{aligned} \begin{array}{llll} \sin \phi (\tau )=\frac{-(W_1{d_i}-\omega ^2)(W_5\omega -W_3W_4\sin \omega \tau )+\omega (W_1+{d_i})(W_2W_4+W_1W_5+W_3W_4\cos \omega \tau )}{(W_2W_4+W_1W_5+W_3W_4\cos \omega \tau )^2+(W_5\omega -W_3W_4\sin \omega \tau )^2},\\ \cos \phi (\tau ) =-\frac{(W_1{d_i}-\omega ^2)(W_2W_4+W_1W_5+W_3W_4\cos \omega \tau )+\omega (W_1+{d_i})(W_5\omega -W_3W_4\sin \omega \tau )}{(W_2W_4+W_1W_5+W_3W_4\cos \omega \tau )^2+(W_5\omega -W_3W_4\sin \omega \tau )^2}, \end{array} \end{aligned}$$

(21)

where $\phi (\tau )=\omega \tau -2n\pi ,\,n\in {\mathbb {N}}_0$. Define the maps $\varvec{\tau }_n$ given by

$$\begin{aligned} \varvec{\tau }_n(\tau ):=\frac{\phi (\tau )+2n\pi }{\omega },\quad n\in {\mathbb {N}}_0, \end{aligned}$$

(22)

where $\omega$ is a positive root of Eq. (19). Then, Eq. (21) jointly with (19) defines the functions

$$\begin{aligned} \Gamma _n(\tau ):=\tau -\varvec{\tau }_n(\tau ),\quad n\in {\mathbb {N}}_0, \end{aligned}$$

(23)

which are continuous and differentiable. From (18) we have

$$\begin{aligned} \begin{array}{l} \dfrac{\text {d}{\mathfrak {F}}(\omega ,\tau )}{\text {d}\omega }=4\omega ^3+2(W_1^2+{d_i^2}-W_5^2)\omega +2W_3W_4W_5\sin \omega \tau \\ \hspace{2cm} +2\tau W_3W_4(\omega W_5\cos \omega \tau +(W_2W_4+W_1W_5)\sin \omega \tau ). \end{array} \end{aligned}$$

(24)

By virtue of Beretta and Kuang (2002) and Kuang (2012), we set the following results.

Theorem 3.2

Assume that $\omega$ is a positive real root of Eq. (19) and there exist some positive constants $\tau ^*$ such that $\Gamma _n(\tau ^*)=0$ for some $n\in {\mathbb {N}}_0$. Then a pair of simple conjugate pure imaginary roots $\lambda _{\pm }(\tau ^*)=\pm \text {i}\omega (\tau ^*)$ of Eq. (14) exists at $\tau =\tau ^*$ which crosses the imaginary axis from left to right if ${\Theta }(\tau ^*)>0$ and crosses the imaginary axis from right to left if ${\Theta }(\tau ^*)<0$, where

$$\begin{aligned} {\Theta }(\tau ^*)= & {} \text {sign}\left\{ \dfrac{\text {d}\text {Re}(\lambda )}{\text {d}\tau }\bigg |_{\lambda =\text {i}\omega (\tau ^*)}\right\} \nonumber \\= & {} \text {sign}\left\{ \dfrac{\text {d}}{\text {d}\omega }{\mathfrak {F}}(\omega (\tau ^*),\tau ^*)\right\} \text {sign}\left\{ \dfrac{\text {d}\Gamma _n(\tau )}{\text {d}\tau }\bigg |_{\tau =\tau ^*}\right\} . \end{aligned}$$

(25)

In the following, we consider the case where $\tau _1\ne \tau _2\>(\tau _1>0,\,\tau _2>0)$. For the characteristic equation of (3)

$$\begin{aligned} {\mathcal {F}}(\lambda )= & {} \lambda ^2+(W_1+d_i)\lambda +W_1d_i+(\lambda +W_1)W_5\text {e}^{-\lambda \tau _2}+W_2W_4\text {e}^{-\lambda \tau _1}\nonumber \\{} & {} +W_3W_4\text {e}^{-\lambda (\tau _1+\tau _2)}=0, \end{aligned}$$

(26)

we set

$$\begin{aligned} \begin{array}{l} {\textbf{f}}(\lambda ):=\lambda ^2+(W_1+{d_i})\lambda +W_1d_i,\\ {\textbf{g}}(\lambda ):=(\lambda +W_1)W_5\text {e}^{-\lambda \tau _2}+W_2W_4\text {e}^{-\lambda \tau _1} +W_3W_4\text {e}^{-\lambda (\tau _1+\tau _2)}. \end{array} \end{aligned}$$

(27)

Applying Rouch$\grave{e}$’s theorem, we get the following result.

Theorem 3.3

For Model (2), the characteristic Eq. (26) with $W_i>0\>(i=1,2,3,4,5)$ and assume that

• (i) $\tau _2-\tau _1\le \dfrac{1}{W_1}\ln \dfrac{W_2W_4+W_3W_4}{\omega _0W_5}$;

• (ii) $W_1W_5+W_2W_4>W_3W_4$,

then there exists a constant $r_0>0$ such that $r_0^2+(W_1+{d_i})r_0+W_1{d_i}<\min \big \{\frac{W_1W_5+W_2W_4}{2},$ $W_1W_5+W_2W_4-W_3W_4\big \}$, Eq. (26) has at least one root with negative real part for all $0<r<r_0$.

Remark 2

The details about the proof of Theorem 3.3 are given in “Appendix”. In the case when $\tau _1\tau _2>0$, it can be obtained that for any given $\tau _1>0$, there exists $\tau _2(\tau _1)>0$ such that a Hopf bifurcation occurs at $(\tau _1, \tau _2)$. Mathematically, Model (2) allows the interaction of unstable modes, but this tends to occur only with large delay values.

When considering Eq. (26) with $\tau _2$ in its stable intervals, we take $\tau _1$ into consideration as a parameter in accordance with Ruan and Wei’s method (Wei and Ruan 1999; Ruan and Wei 2003) and arrive at the following lemma regarding the sign of the real parts of characteristic roots of (26). The proof of the lemma is shown in “Appendices”.

Lemma 3.4

Assume that all roots of Eq. (9) have negative real parts for $\tau _2>0$, then there exists a $\tau _1^*(\tau _2)>0$ such that all roots of Eq. (26) have negative real parts if $0<\tau _1<\tau _1^*(\tau _2)$.

From Theorem 3.1, notice that all roots of Eq. (9) have negative real parts when $0<\tau _2<\tau _2^{0,1}$ ($\tau _2^{0,1}$ is given in Eq. (10)), then we obtain the following asymptotic stability of the steady state $(G^*, I^*)$ of Model (2).

Theorem 3.4

Assume that $D<C$ or $(A^2-B^2-2D)^2>4(D+C)(D-C)>0>A^2-B^2-2D$ holds, for any $0<\tau _2<\tau _2^{0,1}$, there is a $\tau _1^*(\tau _2)>0$ such that the steady state $(G^*, I^*)$ of Model (2) is locally asymptotically stable when $0<\tau _2<\tau _1^*(\tau _2)$, where $\tau _2^{0,1}$ is taken as Eq. (10).

4 Numerical simulations

In this section, we present numerical analysis to investigate the model (2) behaviors. The functions and parameters we use are listed in Table 1.

Table 1 Functions and parameters values used for simulation of Model (2)

4.1 Effects of the two time delays $\tau _1$ and $\tau _2$

By opting the time delays $\tau _1,\,\tau _2$ as bifurcation parameters and fixing other parameters as given in Table 1, we investigate the influence of $\tau _1$ and $\tau _2$ on the glucose-insulin regulatory system and analyze the relationship between the two delays while $G_0=1.35\, (mg/dl/min),\, d_i=0.1$ and the insulin degradation rate $k_0=0.1\>(/min)$ are fixed.

Fig. 2

Amplitudes of glucose (top) and insulin (bottom) concentrations when $\tau _1$ and $\tau _2$ vary, where $G_0=1.35$ (mg/dl/min), $d_i=0.1,\,k_0=0.1\>(/\hbox {min})$ are fixed. Rest of the parameters values are given in Table 1

The top and bottom meshes in Fig. 2 demonstrate the amplitudes of glucose and insulin concentrations, respectively. Figure 2 shows that a complex curve divides $[0, 100]\times [0,100]$ in the $(\tau _1, \tau _2)$-plane into two regions. The steady state is stable in one region and unstable in the other. From the figure, glucose and insulin concentrations have larger amplitudes when the insulin response delay $\tau _1$ is small and the HGP delay $\tau _2$ is big.

Fig. 3

Period of the glucose concentration (a) and insulin concentration (b), where $G_0=1.35,\,d_i=0.1,\,k_0=0.1$ are fixed. All other parameters are given in Table 1

Glucose and insulin concentrations have amplitudes of (50, 120) and (10, 35), respectively when $\tau _2\in (30,100)$ with increasing the value of $\tau _1$.

Figure 3a, b show the period variations of glucose concentration and insulin concentration with respect to the time delays $\tau _1$ and $\tau _2$ for $G_0$ fixed at 1.35 and $k_0=0.1,\,d_i=0.1$, respectively. There are sudden jumps in glucose and insulin concentration amplitudes when $\tau _1>60$ and $\tau _2>40$ approximately. In such cases, the periods of periodic solutions will decrease with increasing the values of $\tau _1$ and $\tau _2$. Longer $\tau _1$ and $\tau _2$ would increase the oscillation period of the dynamic system and result in higher glucose concentration.

Fig. 4

Codimension-two bifurcation diagram, where $G_0=1.35,\,k_0=0.1,\,d_i=0.1$ are fixed. Rest of the parameters are the same as in Table 1

We let both $\tau _1$ and $\tau _2$ vary simultaneously and investigate the codimension-two bifurcation. Figure 4 displays that a bifurcation curve in the window $[0, 50]\times [0, 100]$ divides the $(\tau _1, \tau _2)$-plane into two regions, in one of the regions the equilibrium point is stable and in the other one a limit cycle exists. Moreover, we calculate that the Hopf bifurcation occurs at $(G^*, I^*)$ when $\tau _1=0$ for $\tau _2$ about 30 min. The oscillating solutions are observed for $\tau _2$ values higher than the critical value.

Fig. 5

Time series and phase diagram of glucose and insulin in Model (2). The time delays are a $(\tau _1,\,\tau _2)=(10, 60)$ and b $(\tau _1,\,\tau _2)=(10, 100)$, where $G_0=1.35,\,k_0=0.1,\,d_i=0.1$ are fixed. All other parameters are given in Table 1

Figure 5 exhibits the profiles obtained from the time delay model (2) with different parameter values. Figure 5a, b show the corresponding time evolution and phase diagram of glucose and insulin concentrations at $(\tau _1,\,\tau _2)=(10, 60)$ and $(\tau _1,\,\tau _2)=(10, 100)$, respectively. For both the glucose (the blue line) and the insulin (the red line), oscillating solutions are visible with periods of approximately 162 min (see Fig. 5a). This periodic solution can be regarded as the sustained oscillation of glucose and insulin concentrations. The steady state $(G^*, I^*)$ of Model (2) is unstable in this case. We get oscillations with longer periods-about $240\>\>min$-when $\tau _2$ continues to rise above the critical value (see Fig. 5b). For instance, we can see that every $240\>\>min$, the glucose concentration drops to very low levels and the varying range of glucose concentration is scope [58, 119]. It should be noted that as $\tau _2$ increases, the amplitudes of the oscillations of the glucose G(t) and insulin I(t) grow.

Fig. 6

Time series and phase diagram of glucose and insulin in Model (2). The time delays are a $(\tau _1,\,\tau _2)=(20, 60)$ and b $(\tau _1,\,\tau _2)=(100, 100)$, where $G_0=1.35,\,k_0=0.1,\,d_i=0.1$ are fixed. All other parameters are given in Table 1

When $\tau _1$ is destabilized and elevated, longer periods for both glucose and insulin can be seen. Figure 6a illustrates the solutions of the model (2) for the time delays $\tau _1=20$ and $\tau _2=60$ with periods of about 174 min. It also depicts a phase space project of two coexisting stable periodic solutions on (G, I) for $(\tau _1,\, \tau _2)=(20, 60)$. Chaotic behavior is shown in Fig. 6b which could explain the observed irregular oscillations of glucose and insulin concentrations. It confirms that the glucose level in an early time becomes higher and the oscillations become damped when the delays $\tau _1$ and $\tau _2$ become longer. Figure 6 displays that the occurrence and properties of oscillations are dependent on the magnitude of time delays. In addition, the duration time at the first high peak as $G>100\> mg/dl$ in Fig. 6a is 190 min. It is shorter than all two peaks in Fig. 6b which spend 318 min and 672 min, respectively, to return the glucose level $G=100\> mg/dl$.

4.2 Effects of the time delay $\tau _1$ or $\tau _2$, the insulin degradation rate $k_0$ and glucose infusion rate $G_0$

In order to illustrate the model dynamics and the evolution of solutions, we change four parameters to reveal the Hopf bifurcation dynamics. The parameters that will be chosen are the time delays ($\tau _1$ and $\tau _2$), the exogenous glucose infusion rate $G_0$, and the insulin degradation rate $k_0$.

Fig. 7

a Hopf bifurcation diagram for values of $\tau _2$, b the phase portrait of glucose and insulin level with values of $\tau _2$, c, d the glucose and insulin level distributions for values of $\tau _2$, respectively, where $\tau _1=20,\, G_0=1.35,\,k_0=0.1,\,d_i=0.1$ are fixed. All other parameters are given in Table 1

Figure 7a, b show the bifurcation diagram and phase portrait for varying $\tau _2\in [0, 100]$ and fixing $\tau _1=20,\,G_0=1.35,\,k_0=0.1,\,d_i=0.1$. A critical value of $\tau _2$ to sustain the oscillation is found to be about 45 min (see Fig. 7a). For $\tau _2$ shorter than 45 min, the oscillations are damped quickly. This shows that for values of $\tau _2$ less than the critical value for which a Hopf bifurcation occurs (i.e., $\tau _2^{0,1}$, as stated in Theorem 3.1), then $(G^*, I^*)$ is asymptotically stable for small values of $\tau _1$ (see Theorem 3.4). It can be seen from Fig. 7b that our model is also capable of reproducing sustainable oscillations for different values of $\tau _2$. A range of $\tau _2$ is estimated at $45-100$ to sustain the oscillation of Model (2) when $\tau _1=20$ is fixed (see Fig. 7b). The oscillation orbits gradually grow into large-sized with increasing the value of $\tau _2$. Figure 7c, d are respectively the phase planes of glucose and insulin concentrations among various values of $\tau _2\in [0, 100]$. The observation indicates that both glucose and insulin fluctuations become more significant with a longer delay.

Fig. 8

a Hopf bifurcation diagram for values of $\tau _1$ and b the phase portrait of glucose and insulin level with values of $\tau _1$, where $\tau _2=50,\, G_0=1.35,\,k_0=0.1,\,d_i=0.1$ are fixed. All other parameters are given in Table 1

A similar procedure is applied to analyzing the time delay $\tau _1$. Figure 8a, b show the bifurcation diagram and phase portrait for $\tau _2=50,\,G_0=1.35,\,k_0=0.1,\,d_i=0.1$ and varying $\tau _1\in [0, 100]$. For $\tau _1$ out of the ranges of $0-40$ and $50-100$, the oscillations of glucose and insulin are damped when $\tau _2=50$ is fixed (see Fig. 8b). For $\tau _1$ greater than 40 and less than 50, the glucose-insulin system reached a steady state quickly. For $\tau _1$ in the 0–40 and 50–100 range, glucose concentration is changing within the optimal range.

Fig. 9

a Hopf bifurcation diagram for the rate of insulin degradation values of $k_0$, b the phase portrait of glucose and insulin level with values of $k_0$, c, d the glucose and insulin level distributions for values of $k_0$, respectively, where $\tau _1=20,\,\tau _2=60,\, G_0=1.35,\,d_i=0.1$ are fixed. All other parameters are given in Table 1

We define the rate of insulin degradation $k_0$ to illustrate the effect of IDE, the degradative process may also be involved in mediating some aspects of insulin action. Fixing $\tau _1=20,\,\tau _2=60$ and $G_0=1.35,\,d_i=0.1$, Fig. 9a shows the bifurcation diagram for the parameter range $k_0\in [0, 0.15]$. For $k_0$ greater than 0.09, the glucose and insulin concentrations hardly change. The phase plane diagram for $k_0$ at Fig. 9b exhibits the oscillation variation behavior. An optimal range of $k_0$ is estimated at $0.01-0.15$ for the periodic solution of the dynamics system (see Fig. 9b). When $k_0$ increased from 0 to 0.15, glucose and insulin concentrations change stably within the normal ranges. The magnitude of glucose level is between 82 and 107 responds to $k_0\in [0, 0.15]$ at Fig. 9c with $\tau _1=20$ and $\tau _2=60$. The range of insulin concentrations is between 17.5 and 21.5 as the parameter $k_0$ located in [0, 0.15] according to Fig. 9d. This indicates a good degree of stability in the inter-regulation of the glucose-insulin system.

Fig. 10

Glucose infusion rate $G_0$ vs. insulin degradation rate $k_0$ while $\tau _1=25,\,\tau _2=50,\,d_i=0.1$. The steady state of Model (2) is stable in one region and unstable in the other. All other parameters are given in Table 1

Taking both the glucose infusion rate $G_0$ and the insulin degradation rate $k_0$ as bifurcation parameters while $\tau _1=25,\,\tau _2=50$ and $d_i=0.1$ are fixed, we identify the stability regions in $(k_0, G_0)\in [0, 0.15]\times [0, 2]$. Figure 10 displays that a simple curve divides the rectangular $(k_0, G_0)\in [0, 0.15]\times [0, 2]$ into two regions. The steady state of Model (2) is stable in one region and unstable in the other region. It is clear that a larger insulin degradation rate $k_0$ facilitates the oscillatory regulation.

4.3 Glucose infusion rate $G_0$ vs. $\tau _1$, and $G_0$ vs. $\tau _2$

Taking the insulin response delay $\tau _1$ and the glucose infusion rate $G_0$ as bifurcation parameters, we try to recognize the stability regions when $(\tau _1, G_0)\in [0, 100] \times [0, 2]$.

Fig. 11

Amplitudes of glucose (top) and insulin (bottom) concentrations when $G_0$ and $\tau _1$ vary while a $\tau _2=40$ and b $\tau _2=80$, where $k_0=0.1,\,d_i=0.1$

Fig. 12

Periods of glucose (a) and insulin (b) concentrations when $G_0$ and $\tau _1$ vary while a $\tau _2=40$ and b $\tau _2=80$, where $k_0=0.1,\,d_i=0.1$ are fixed

Let $k_0=0.1,\,d_i=0.1$ be fixed and vary the value of $\tau _2$, the computation results are shown in Fig. 11a ($\tau _2=40$) and Fig. 11b ($\tau _2=80$). The meshes are the amplitudes of glucose (top) and insulin (bottom) concentrations for $(\tau _1, G_0)\in [0, 100] \times [0, 2]$. When $\tau _1=40$ (see Fig. 11a), it can be seen that two curves divide the rectangular $[0, 100] \times [0, 2]$ in the $(\tau _1, G_0)$-plane into three regions. Increasing the value of $\tau _2$, the rectangular $(\tau _1, G_0)\in [0, 100] \times [0, 2]$ is divided into two regions by one curve (see Fig. 11b). The relationship between $G_0$ and $\tau _1$ is nonlinear, and the sustained oscillations of Model (2) occur in the unstable regions.

Fig. 13

Periods of glucose (left) and insulin (right) concentrations when $G_0$ and $\tau _2$ vary, where $\tau _1=20,\>k_0=0.1,\,d_i=0.1$ are fixed

Figure 12 shows the periods of periodic solutions with different values of $\tau _2$, where $\tau _2=40$ in Fig. 12a and $\tau _2=80$ in Fig. 12b. Figure 13 shows the periods of periodic solutions with $\tau _1=20$. When $\tau _2<40$, the steady state is stable and no sustained oscillation will occur regardless of what value $G_0$ assumes where $\tau _1=20$ is fixed.

5 Discussion

The proposed model (2) takes a key biological factor IDE into account, which depicts the glucose-insulin regulatory slightly more comprehensive. Through the model, we qualitatively and quantitatively investigated the interaction between glucose and insulin under the impact of IDE. The existence of the Hopf bifurcations shows the systematic and intrinsic sustained oscillatory behavior of the regulatory system with various varying parameters, including the time delay $\tau _1,\,\tau _2$, the meal ingestion rate $G_0$, and the natural insulin degradation rate $k_0$.

By choosing time delays as the bifurcation parameters, the characteristic equation of Model (2) with two delays is investigated, and some conditions for the appearance of Hopf bifurcation that leads to the appearance of periodic solutions are obtained. We also obtain stability results for the model with two independent delays. It is worth noting that the stability of the steady state solution depends on both $\tau _1$ and $\tau _2$ (see Figs. 2, 4). These are the time delays that reflect the naturally occurring glucose-insulin oscillations: they reflect the finite time needed for the pancreas and the liver to secrete insulin and glucose. Glucose and insulin oscillations occur only for relatively long periods of time delay due to the instability of the stationary solution of Model (2), we observe a periodic behavior when a small time delay and chaotic behavior under long time delay in the glucose-insulin regulatory system (see Figs. 5, 6). We analytically show the existence of Hopf bifurcation when the delay parameter $\tau _2$ increases from small, $\tau _1$ varies in certain ranges, and $k_0$ increases from small, respectively (see Figs. 7, 8, 9, 10). The parameter $G_0$ and the delays $\tau _1,\,\tau _2$ are analyzed for their influence on the glucose-insulin regulatory system. The ranges of these parameters are estimated for sustaining the oscillation of glucose and insulin, and ranges for different subjects are discussed based on simulation results (see Figs. 11, 12, 13).

In addition, simple numerical simulations (not shown) reveal that IDE deficiency (smaller c and larger ${\hat{I}}$) demonstrated the potential for abundant insulin, glucose tolerance, and possibly insulin sensitivity, while IDE overexpression (larger value of c and smaller ${\hat{I}}$) could potentially cause type 2 diabetes.

Certain limitations still exist in our proposed model (2). The time scale is relatively short to capture the slow and gradual loss of $\beta$-cell function in longitudinal dynamics observed in Costes and Butler (2014). The time delay $\tau _3$ in the IDE impact might not be the same as the time delay $\tau _2$ in the HGP. Also, the liver takes an important role in this metabolic system. Both HGP and IDE conduct stochastically due to the complexity of metabolism, particularly, when the pathological changes. We shall deploy these in future work.

Appendices

Appendices

1.1 Proof of Proposition 3.1

Proof

For the positive steady state solution of Model (2), we let

$$\begin{aligned} F(x)=G_0-f_2(x)-f_3(x)f_4\left( \frac{\ln ({k_0}f_1(x)+{d_i})}{c}\right) +f_5\left( \frac{\ln ({k_0}f_1(x)+{d_i})}{c}\right) =0,\> x\ge 0,\nonumber \\ \end{aligned}$$

(28)

and derive

$$\begin{aligned} \begin{array}{l} \frac{\text {d}F(x)}{\text {d}x}=-\frac{\text {d}f_2(x)}{\text {d}x}-\frac{\text {d}f_3(x)}{\text {d}x}f_4\left( \frac{\ln ({k_0}f_1(x)+{d_i})}{c}\right) -f_3(x)\frac{\text {d}}{\text {d}x}f_4\left( \frac{\ln ({k_0}f_1(x)+{d_i})}{c}\right) \\ \hspace{1.5cm} \cdot \frac{\text {d}f_1(x)}{\text {d}x}\frac{{k_0}}{c({k_0}f_1(x)+{d_i})} +\frac{\text {d}}{\text {d}x}f_5\left( \frac{\ln ({k_0}f_1(x)+{d_i})}{c}\right) \frac{\text {d}f_1(x)}{\text {d}x}\frac{{k_0}}{c({k_0}f_1(x)+{d_i})}. \end{array} \end{aligned}$$

Observing that $\frac{\text {d}f_i(x)}{\text {d}x} > 0 \,(i=1,2,3,4)$ and $\frac{\text {d}f_5(x)}{\text {d}x} < 0$, we obtain $\frac{\text {d}F(x)}{\text {d}x} < 0$. Notice that $F(0)=G_0-f_2(0)-f_3(0)f_4\big (\frac{\ln ({k_0}f_1(0)+{d_i})}{c}\big )+f_5\big (\frac{\ln ({k_0}f_1(0)+{d_i})}{c}\big )=G_0+f_5\big (\frac{\ln ({k_0}f_1(0)+{d_i})}{c}\big )>0$, and based on the conditions $(H1)-(H5)$, then

$$\begin{aligned} \lim \limits _{x\rightarrow \infty } F(x)= & {} G_0-\lim \limits _{x\rightarrow \infty }f_2(x)-\lim \limits _{x\rightarrow \infty }f_3(x)f_4\left( \frac{1}{c}\ln (\lim \limits _{x\rightarrow \infty }{k_0}f_1(x)+{d_i})\right) \\{} & {} + f_5\left( \frac{1}{c}\ln (\lim \limits _{x\rightarrow \infty }{k_0}f_1(x)+{d_i})\right) \\= & {} G_0-M_2-\lim \limits _{x\rightarrow \infty }f_3(x)f_4\left( \frac{1}{c}\ln ({k_0}M_1+{d_i})\right) +f_5\left( \frac{1}{c}\ln ({k_0}M_1+{d_i})\right) \\< & {} G_0- M_2-\lim \limits _{x\rightarrow \infty }f_3(x)m_4+f_5\left( \frac{1}{c}\ln ({k_0}M_1+{d_i})\right) <0. \end{aligned}$$

Due to $f_1(x)$ strictly monotone increasing, thus the proof is complete. It can be seen that $G^*$ is the root of (28) and $I^*=\frac{1}{c}\ln ({k_0}f_1(G^*)+{d_i})$.

For the second part of (i), we observe that

• (a) $\big |\frac{\text {d}f_i(x)}{\text {d}x}\big |,\,i=1,2,3,4,5$ are bounded;

• (b) $f_i(x),\,i=2,3,4$ and $f_j(x_t),\,j=1,5$ are Lipschitzian and completely continuous in $x\ge 0$ and $x_t\in {\mathbb {C}}([-\max \{\tau _1,\tau _2\},0])$, respectively;

• (c) $\frac{x}{\text {e}^{cx}-1}>0$, $\frac{\text {d}}{\text {d}x}\big (\frac{x}{\text {e}^{cx}-1}\big )=\frac{(1-cx)\text {e}^{cx}-1}{(\text {e}^{cx}-1)^2}<0$ and $\frac{\text {d}^2}{\text {d}x^2}\big (\frac{x}{\text {e}^{cx}-1}\big )=\frac{c\text {e}^{cx}(\text {e}^{cx}(cx-2)+cx+2)}{(\text {e}^{cx}-1)^3}$ $>0$ for $x>0$, $\lim \limits _{x\rightarrow 0^+}\frac{x}{\text {e}^{cx}-1}=\frac{1}{c}>0$, then $\frac{x}{\text {e}^{cx}-1}$ is monotonically decreasing and bounded for $x>0$;

• (d) let $\frac{x}{\text {e}^{cx}-1}|_{x=0}=\frac{1}{c}$, then $\frac{x}{\text {e}^{cx}-1}$ and $\frac{x_t}{\text {e}^{cx_t}-1}$ are respectively Lipschitzian and continuous in $x\ge 0$ and $x_t\in {\mathbb {C}}([-\tau _2,0])$.

Therefore, referring to Theorems 2.1, 2.2, and 2.4 in Kuang (2012), the solution of Model (2) with the given initial condition exists and is unique for all $t\ge 0$. If there exists a $t_0>0$ such that $G(t_0)=0$ and $G(t)>0$ for $0<t<t_0$, then $\frac{\text {d}}{\text {d} t}G(t_0)\le 0$. But

$$\begin{aligned} \begin{array}{l} \dfrac{\text {d}}{\text {d} t}G(t_0)=G_0-f_2(G(t_0))-f_3(G(t_0))f_4(I(t_0))+f_5(I(t_0-\tau _2))\\ \hspace{1.4cm} =G_0+f_5(I(t_0-\tau _2))>0, \end{array} \end{aligned}$$

this contradiction implies that $G(t)>0$ for all $t>0$. If there exists a $t'_0>0$ such that $I(t'_0)=0$ and $I(t)>0$ for all $0<t<t'_0$, then $I(t'_0)<0$. Notice that

$$\begin{aligned} \begin{array}{ll} \dfrac{\text {d}}{\text {d} t}I(t'_0) &{}=f_1(G(t'_0-\tau _1))\frac{k_0I(t'_0-\tau _2)}{\text {e}^{c I(t'_0-\tau _2)}-1}-k_0I(t'_0) \\ &{}=f_1(G(t'_0-\tau _1))\frac{k_0I(t'_0-\tau _2)}{\text {e}^{c I(t'_0-\tau _2)}-1}>0, \\ \end{array} \end{aligned}$$

this implies that $I(t)>0$ for all $t>0$.

Here, we prove that any given solution (G(t), I(t)) of Model (2) is bounded for $t>0$. If $\limsup \nolimits _{t\rightarrow \infty }G(t)=\infty$, there exists a sequence $\{t_n\}_{n=1}^\infty \uparrow \infty$ such that $\lim \limits _{n\rightarrow \infty }G(t_n)=\infty$ and $\frac{\text {d}}{\text {d}t}G(t_n)\ge 0$. Thus $0<\frac{\text {d}}{\text {d}t}G(t_n)=G_0-f_2(G(t_n))-f_3(G(t_n))f_4(I(t_n))+f_5(I(t_n-\tau _2))\le G_0-f_2(G(t_n))-f_3(G(t_n))m_4+M_5$, and therefore

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\frac{\text {d}}{\text {d}t} G(t_n){} & {} =G_0-\lim \limits _{n\rightarrow \infty }f_2(G(t_n))-\lim \limits _{n\rightarrow \infty }f_3(G(t_n))f_4(I(t_n)) \\{} & {} \quad +\lim \limits _{n\rightarrow \infty }f_5(I(t_n-\tau _2)) \\ \hspace{2.4cm}{} & {} \le G_0-M_2-\lim \limits _{n\rightarrow \infty }f_3(G(t_n))m_4+M_5<0. \end{aligned}$$

This contradiction shows that there is a $M_G>0$ such that $G(t)<M_G$ for all $t>0$. For the second equation in (2), since $|f_1(x)|\le M_1$, for $\epsilon >0$, $\frac{\text {d}I(t)}{\text {d}t}\le f_1(M_G+\epsilon )\frac{k_0I(t-\tau _2)}{\text {e}^{cI(t-\tau _2)}-1}-k_0I(t)$ for sufficiently large $t>0$. If $\limsup \limits _{t\rightarrow \infty }I(t)=\infty$, there exists a sequence $\{t'_n\}_{n=1}^\infty \uparrow \infty$ such that $\lim \limits _{n\rightarrow \infty }I(t'_n)=\infty$ and $\frac{\text {d}}{\text {d}t}I(t_n)\ge 0$. Then, $0<\frac{\text {d}}{\text {d}t}I(t'_n)\le f_1(M_G+\epsilon )\frac{k_0I(t'_n-\tau _2)}{\text {e}^{cI(t'_n-\tau _2)}-1}-{d_i}I(t'_n)$ and

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\frac{\text {d}}{\text {d}t}I(t'_n){} & {} \le f_1(M_G+\epsilon )\lim \limits _{n\rightarrow \infty }\frac{k_0I(t'_n-\tau _2)}{\text {e}^{cI(t'_n-\tau _2)}-1}-\lim \limits _{n\rightarrow \infty }{d_i}I(t'_n) \\{} & {} =0-\lim \limits _{n\rightarrow \infty }{d_i}I(t'_n) <0, \end{aligned}$$

this shows that there exists a $M_I>0$ such that $I(t)<M_I$ for all $t>0$.

If (ii) is not true, assume $\limsup \nolimits _{t\rightarrow \infty }G(t)=M_G<\infty$. There exists $\{t_n\}_{n=1}^\infty \uparrow \infty$ such that $\frac{\text {d}}{\text {d}t}G(t_n)=0,\,n=1,2,3,\cdots$, and $\lim \limits _{n\rightarrow \infty }G(t_n)=M_G$ according to Lemma 3.1 (fluctuation lemma) in Li and Kuang (2007). Then $\frac{\text {d}}{\text {d}t}G(t_n)=G_0-f_2(G(t_n))-f_3(G(t_n))f_4(I(t_n))+f_5(I(t_n-\tau _2))\ge G_0-f_2(G(t_n))-f_3(G(t_n))m_4$. Let $n\rightarrow \infty$, thus $0\ge G_0-f_2(M_G)-f_3(M_G)m_4$, that is, $f_3(M_G)\ge \frac{G_0-f_2(M_G)}{m_4}$. In addition, $f_3(M_G)\le \lim \limits _{x\rightarrow \infty }f_3(x)<\frac{G_0-M_2}{m_4}\le \frac{G_0-f_2(M_G)}{m_4}$. $\square$

1.2 Proof of Lemma 3.1

Proof

If $\lambda =\pm \text {i}\omega \,(\omega >0)$ is a pair of purely imaginary roots of Eq. (9) and $\omega$ then satisfies the following equation

$$\begin{aligned} -\omega ^2+(A+B\text {e}^{-\text {i}\omega \tau _2})\text {i}\omega +D+C\text {e}^{-\text {i}\omega \tau _2}=0. \end{aligned}$$

(29)

Separating the real and imaginary parts of Eq. (29) leads to

$$\begin{aligned} \left\{ \begin{array}{l} -\omega ^2+B\omega \sin \omega \tau _2+C\cos \omega \tau _2+D=0,\\ \omega (A+B\cos \omega \tau _2)=C\sin \omega \tau _2, \end{array} \right. \end{aligned}$$

(30)

which implies that

$$\begin{aligned} \sin \omega \tau _2=\frac{AC\omega +B\omega (\omega ^2-D)}{C^2+B^2\omega ^2}, \quad \cos \omega \tau _2=\frac{C(\omega ^2-D)-AB\omega ^2}{C^2+B^2\omega ^2}, \end{aligned}$$

(31)

and $\omega =0$ is not a solution of (31) since $C+D>0$. From Eq. (31), we obtain

$$\begin{aligned} \omega ^4+(A^2-B^2-2D)\omega ^2+(D+C)(D-C)=0, \end{aligned}$$

(32)

then

$$\begin{aligned} \omega ^2:=\omega _{\pm }^2=\frac{-(A^2-B^2-2D)\pm \sqrt{(A^2-B^2-2D)^2-4(D+C)(D-C)}}{2}.\nonumber \\ \end{aligned}$$

(33)

Clearly, if $D>C$ and $A^2-B^2-2D>0$, there are no $\omega$ such that Eq. (9) has purely imaginary roots $\pm \text {i}\omega$. If $D<C$, the number of pairs of purely imaginary roots of (9) is one. If $(A^2-B^2-2D)^2> 4(D+C)(D-C)> 0>A^2-B^2-2D$, the number of pairs of purely imaginary roots of Eq. (9) is two.

From Eq. (30), we get the following two sets of values of $\tau _2$ for which there are imaginary roots:

$$\begin{aligned} \tau _2^{n,1}=\frac{\theta _1+2n\pi }{\omega _+}=\frac{1}{\omega _+}\left[ \arccos \left( \frac{C(\omega _{+}^2-D)-AB\omega _{+}^2}{C^2+B^2\omega _{+}^2}\right) +2n\pi \right] ,\quad n=0,1,\cdots \nonumber \\ \end{aligned}$$

(34)

where

$$\begin{aligned} \sin \theta _1=\frac{AC\omega _{+}+B\omega _{+}(\omega _{+}^2-D)}{C^2+B^2\omega _{+}^2},\quad \cos \theta _1=\frac{C(\omega _{+}^2-D)-AB\omega _{+}^2}{C^2+B^2\omega _{+}^2}, \quad 0\le \theta _1\le 2\pi ,\nonumber \\ \end{aligned}$$

(35)

and

$$\begin{aligned} \tau _2^{n,2}=\frac{\theta _2+2n\pi }{\omega _-}=\frac{1}{\omega _-}\left[ \arccos \left( \frac{C(\omega _{-}^2-D)-AB\omega _{-}^2}{C^2+B^2\omega _{-}^2}\right) +2n\pi \right] ,\quad n=0,1,\cdots \nonumber \\ \end{aligned}$$

(36)

where

$$\begin{aligned} \sin \theta _2=\frac{AC\omega _{-}+B\omega _{-}(\omega _{-}^2-D)}{C^2+B^2\omega _{-}^2},\quad \cos \theta _2=\frac{C(\omega _{-}^2-D)-AB\omega _{-}^2}{C^2+B^2\omega _{-}^2},\quad 0\le \theta _2\le 2\pi .\nonumber \\ \end{aligned}$$

(37)

$\square$

1.3 Proof of Lemma 3.2

Proof

By differentiating Eq. (9) with respect to $\tau _2$, we derive

$$\begin{aligned} \left( 2\lambda +A+(B-B\lambda \tau _2-C\tau _2)\text {e}^{-\lambda \tau _2}\right) \frac{\text {d}\lambda }{\text {d}\tau _2}=(B\lambda +C)\lambda \text {e}^{-\lambda \tau _2}, \end{aligned}$$

(38)

and

$$\begin{aligned} \Big (\frac{\text {d}\lambda }{\text {d}\tau _2}\Big )^{-1}=\frac{(2\lambda +A)\text {e}^{\lambda \tau _2}+B}{(B\lambda +C)\lambda }-\frac{\tau _2}{\lambda }, \end{aligned}$$

(39)

where

$$\begin{aligned} \text {e}^{\lambda \tau _2}=-\frac{B\lambda +C}{\lambda ^2+A\lambda +D}. \end{aligned}$$

(40)

Then,

$$\begin{aligned} \Big (\frac{\text {d}\lambda }{\text {d}\tau _2}\Big )^{-1}=-\frac{2\lambda +A}{\lambda (\lambda ^2+A\lambda +D)}+\frac{B}{(B\lambda +C)\lambda }-\frac{\tau _2}{\lambda }, \end{aligned}$$

(41)

Let $\tau _2=\tau _2^{n,k}\>(k=1,2)$, therefore,

$$\begin{aligned}{} & {} \text {sign}\left\{ \dfrac{\text {d}\text {Re}(\lambda )}{\text {d}\tau _2}\bigg |_{\tau _2=\tau _2^{n,k}} \right\} \nonumber \\{} & {} \quad =\text {sign}\left\{ \text {Re}\left( \dfrac{\text {d}\lambda }{\text {d}\tau _2}\right) ^{-1}\right\} \bigg |_{\tau _2=\tau _2^{n,k}} \nonumber \\{} & {} \quad =\text {sign}\left\{ \text {Re}\left( -\dfrac{2\lambda +A}{\lambda (\lambda ^2+A\lambda +D)}\right) \bigg |_{\tau _2=\tau _2^{n,k}}+\text {Re}\left( \dfrac{B}{(B\lambda +C)\lambda }\right) \bigg |_{\tau _2=\tau _2^{n,k}}\right\} \nonumber \\{} & {} \quad =\text {sign}\left\{ \dfrac{A^2-2(D-\omega _{k,n}^2)}{(D-\omega _{k,n}^2)^2+A^2\omega _{k,n}^2}-\dfrac{B^2}{C^2+B^2\omega _{k,n}^2}\right\} \nonumber \\{} & {} \quad =\text {sign}\big \{A^2-B^2-2D+2\omega _{k,n}^2\big \}. \end{aligned}$$

(42)

By inserting the expression for $\omega _{k,n}^2\>(k=1,2)$, it is seen that $\text {sign}\{A^2-B^2-2D+2\omega _{k,n}^2\}>0$ for $\tau _2^{n,1}$ and $\omega _{+}^2$; and $\text {sign}\{A^2-B^2-2D+2\omega _{k,n}^2\}<0$ for $\tau _2^{n,2}$ and $\omega _{-}^2$. $\square$

1.4 Proof of Theorem 3.1

Proof

Based on the above Lemmas 3.1 and 3.2, we note that if $D<C$, a pair of purely imaginary roots exists $\lambda (\tau _2)|_{\tau _2=\tau _2^{n,1}}=\pm \text {i}\omega _+\>(n=0,1,\cdots )$, then the only crossing of the imaginary axis is from left to right as $\tau _2^{n,1}$ increases, and the stability of the steady state solution can only be lost and not regained. If $A^2-B^2-2D<0$ and $(A^2-B^2-2D)^2>4(D+C)(D-C)>0$, crossing from left to right with increasing $\tau _2^{n,1}$ occurs whenever $\tau _2^{n,1}$ assumes a value corresponding to $\omega _+$, and crossing from right to left occurs for values of $\tau _2^{n,2}$ corresponding to $\omega _{-}$.

In the case that $D<C$, only $\tau _2^{0,1}$ need be considered, since if Model (2) is asymptotically stable for $\tau _2=0$, then it remains asymptotically stable until $\tau _2^{0,1}$, and it is unstable thereafter. At $\tau _2=\tau _2^{0,1}$, Eq. (9) has pure imaginary roots $\pm \text {i}\omega _+$.

In the case of $(A^2-B^2-2D)^2>4(D+C)(D-C)>0>A^2-B^2-2D$, if Model (2) is stable for $\tau _2=0$, then it must follow that $\tau _2^{0,1}<\tau _2^{0,2}$ since the multiplicity of roots with positive real parts cannot become negative. We observe that

$$\begin{aligned} \tau _2^{n+1,1}-\tau _2^{n,1}=\frac{2\pi }{\omega _+}<\frac{2\pi }{\omega _{-}}=\tau _2^{n+1,2}-\tau _2^{n,2}, \end{aligned}$$

(43)

with $\omega _+>\omega _->0$. Thus, there can be only a finite number of switches between stability and instability. Moreover, there exist values of the parameters that realize any number of such stability switches. However, there exists a ${\hat{\tau }}_2$ such that at $\tau _2={\hat{\tau }}_2$ a stability switch occurs from stable to unstable, and for $\tau _2>{\hat{\tau }}_2$ the solution remains unstable. If Model (2) is unstable for $\tau _2=0$, then a similar argument as before can be made. Model (2) can either be unstable for $\tau _2>0$ or exhibit any number of stability switches as in the preceding case.

As $\tau _2$ is increased, the multiplicity of roots for which $\text {Re}(\lambda )>0$ is increased by two whenever $\tau _2$ passes through a value of $\tau _2^{n,1}$ and it is decreased by two whenever $\tau _2$ passes through a value of $\tau _2^{n,2}$.

When the steady state solution is stable for $\tau _2=0$, j switches from stability to instability to stability occur when the parameters are such that

$$\begin{aligned} \tau _2^{0,1}<\tau _2^{0,2}<\tau _2^{1,1}<\cdots<\tau _2^{j-1,1}<\tau _2^{j-1,2}<\tau _2^{j,1}<\tau _2^{j+1,1}<\tau _2^{j,2}\cdots , \end{aligned}$$

or j switches from instability to stability to instability may occur when

$$\begin{aligned} \tau _2^{0,2}<\tau _2^{0,1}<\tau _2^{1,2}<\cdots<\tau _2^{j-1,2}<\tau _2^{j-1,1}<\tau _2^{j,1}<\tau _2^{j,2}\cdots , \end{aligned}$$

when the steady state solution is stable for $\tau _2=0$. The conditions on the parameters in order that the preceding orderings be valid can be formulated directly from Eqs. (34)-(37).

From the above analysis, we obtain the theorem results. $\square$

1.5 Proof of Theorem 3.3

Proof

Let $\lambda =\alpha +\text {i}\omega _0\>(\alpha \in {\mathbb {R}},\,\omega _0=2q\pi >0)$ be a root of Eq. (5), then for ${\textbf{g}}(\lambda )=W_5\text {e}^{-\lambda \tau _2}\lambda +W_2W_4\text {e}^{-\lambda \tau _1}+W_1W_5\text {e}^{-\lambda \tau _2}+W_3W_4\text {e}^{-\lambda (\tau _1+\tau _2)}=0$ we have

$$\begin{aligned} \left\{ \begin{array}{lll} \text {Re}({\textbf{g}}(\lambda ))=W_5\text {e}^{-\alpha \tau _2}(\alpha \cos \omega _0\tau _2+\omega _0\sin \omega _0\tau _2)+W_2W_4\text {e}^{-\alpha \tau _1}\cos \omega _0\tau _1\\ \hspace{2cm} +W_1W_5\text {e}^{-\alpha \tau _2}\cos \omega _0\tau _2+W_3W_4\text {e}^{-\alpha (\tau _1+\tau _2)}\cos \omega _0(\tau _1+\tau _2)=0,\\ \text {Im}({\textbf{g}}(\lambda ))=W_5\text {e}^{-\alpha \tau _2}(\omega _0\cos \omega _0\tau _2-\alpha \sin \omega _0\tau _2)-W_2W_4\text {e}^{-\alpha \tau _1}\sin \omega _0\tau _1\\ \hspace{2cm} -W_1W_5\text {e}^{-\alpha \tau _2}\sin \omega _0\tau _2-W_3W_4\text {e}^{-\alpha (\tau _1+\tau _2)}\sin \omega _0(\tau _1+\tau _2)=0. \end{array} \right. \end{aligned}$$

(44)

In order to simplify, let us consider $q\tau _2\in {\mathbb {Z}}^+$, Eq. (44) has the following form

$$\begin{aligned} \left\{ \begin{array}{l} \text {Re}({\textbf{g}}(\lambda ))=(\alpha W_5+W_1W_5)\text {e}^{-\alpha \tau _2}+\big (W_2W_4\text {e}^{-\alpha \tau _1} +W_3W_4\text {e}^{-\alpha (\tau _1+\tau _2)}\big )\cos \omega _0\tau _1=0,\\ \text {Im}({\textbf{g}}(\lambda ))=\omega _0W_5\text {e}^{-\alpha \tau _2}-\big (W_2W_4\text {e}^{-\alpha \tau _1} +W_3W_4\text {e}^{-\alpha (\tau _1+\tau _2)}\big )\sin \omega _0\tau _1=0, \end{array} \right. \nonumber \\ \end{aligned}$$

(45)

we can obtain

$$\begin{aligned} \left\{ \begin{array}{l} \tan (\omega _0\tau _1)=-\dfrac{\omega _0}{\alpha +W_1},\\ \quad \big (W_2W_4\text {e}^{-\alpha \tau _1}+W_3W_4\text {e}^{-\alpha (\tau _1+\tau _2)}\big )^2=\big (\omega _0^2+(\alpha +W_1)^2\big )W^2_5\text {e}^{-2\alpha \tau _2}. \end{array} \right. \end{aligned}$$

(46)

If there exists a constant $\alpha _0<0$ satisfies (46), then ${\textbf{g}}(\lambda )$ has at least one zero $\lambda _0=\alpha _0+\text {i}\omega _0$ with $\alpha _0<0$.

Let

$$\begin{aligned} X(\alpha )=\big (W_2W_4\text {e}^{-\alpha \tau _1}+W_3W_4\text {e}^{-\alpha (\tau _1+\tau _2)}\big )^2-\big (\omega _0^2+(\alpha +W_1)^2\big )W^2_5\text {e}^{-2\alpha \tau _2}.\qquad \end{aligned}$$

(47)

Notice that $X(0)=(W_2W_4+W_3W_4)^2-\omega ^2_0W_5^2-W_1^2W_5^2<0$ if $W_2W_4+W_3W_4\le W_1W_5$ and $\lim \limits _{\alpha \rightarrow -\infty }X(\alpha )=+\infty$. Furthermore, taking $\alpha =-W_1$, then

$$\begin{aligned} \begin{array}{l} X(-W_1)=\big (W_2W_4\text {e}^{W_1\tau _1}+W_3W_4\text {e}^{W_1(\tau _1+\tau _2)}\big )^2-\omega _0^2W^2_5\text {e}^{2W_1\tau _2}\\ \hspace{1.7cm} >\big (W_2W_4\text {e}^{W_1\tau _1}+W_3W_4\text {e}^{W_1\tau _1}\big )^2-\omega _0^2W^2_5\text {e}^{2W_1\tau _2}. \end{array} \end{aligned}$$

(48)

If $\tau _2-\tau _1\le T_0=\frac{1}{W_1}\ln \frac{W_2W_4+W_3W_4}{\omega _0W_5}$ such that $X(-W_1)\ge 0$, then there is a constant $\alpha _0\in (-W_1, 0)$ satisfies $X(\alpha _0)=0$. Thus, $\lambda _0=\alpha _0+\text {i}\omega _0$ is the zero point of ${\textbf{g}}(\lambda )$.

In the following, we construct a simple loop L homotopic to a point and then show $|{\textbf{g}}(\lambda )|>|{\textbf{f}}(\lambda )|$ on L. We divide the simple loop L into two parts as: one is defined by taking $(-W_1, 0)$ and $\sqrt{W_1^2+\omega _0^2}$ as a center point and the radius, respectively; the other is defined as $\lambda =\text {i}\omega ,\>\omega \in [-\omega _0, \omega _0]$.

Let $\lambda =x+\text {i}\omega$ with $x\in \big [-W_1-\sqrt{W_1^2+\omega _0^2}, 0\big ]$ and $\omega \in [-\omega _0,\omega _0]$, we set $x=b\alpha _0\,(b>0)$ and then deduce

$$\begin{aligned} |{\textbf{g}}(\lambda )|= & {} |xW_5\text {e}^{-x\tau _2}\text {e}^{-\text {i}\omega \tau _2}+\text {i}\omega W_5\text {e}^{-x\tau _2}\text {e}^{-\text {i}\omega \tau _2}+W_2W_4\text {e}^{-x\tau _1}\text {e}^{-\text {i}\omega \tau _1}\nonumber \\{} & {} +W_1W_5\text {e}^{-x\tau _2}\text {e}^{-\text {i}\omega \tau _2}+W_3W_4\text {e}^{-x(\tau _1+\tau _2)}\text {e}^{-\text {i}\omega (\tau _1+\tau _2)}|\nonumber \\= & {} \big |xW_5\text {e}^{-x\tau _2}\cos \omega \tau _2+\omega W_5\text {e}^{-x\tau _2}\sin \omega \tau _2+W_2W_4\text {e}^{-x\tau _1}\cos \omega \tau _1\nonumber \\{} & {} +W_1W_5\text {e}^{-x\tau _2}\cos \omega \tau _2+W_3W_4\text {e}^{-x(\tau _1+\tau _2)}\cos \omega (\tau _1+\tau _2)\nonumber \\{} & {} +\text {i}\big (\omega W_5\text {e}^{-x\tau _2}\cos \omega \tau _2-xW_5\text {e}^{-x\tau _2}\sin \omega \tau _2-W_2W_4\text {e}^{-x\tau _1}\sin \omega \tau _1\nonumber \\{} & {} -W_1W_5\text {e}^{-x\tau _2}\cos \omega \tau _2-W_3W_4\text {e}^{-x(\tau _1+\tau _2)}\sin \omega (\tau _1+\tau _2)\big )\big |\nonumber \\{} & {} >W_1W_5\text {e}^{-b\alpha _0\tau _2}+W_2W_4\text {e}^{-b\alpha _0\tau _1}-W_3W_4\text {e}^{-b\alpha _0(\tau _1+\tau _2)}>\frac{W_1W_5+W_2W_4}{2}.\nonumber \\ \end{aligned}$$

(49)

Let $\lambda =\text {i}\omega ,\,\omega \in [-\omega _0,\omega _0]$, then

$$\begin{aligned} |{\textbf{g}}(\lambda )|{} & {} =|W_5\text {e}^{-\text {i}\omega \tau _2}\text {i}\omega +W_2W_4\text {e}^{-\text {i}\omega \tau _1}+W_1W_5\text {e}^{-\text {i}\omega \tau _2}+W_3W_4\text {e}^{-\text {i}\omega (\tau _1+\tau _2)}|\nonumber \\{} & {} \ge W_1W_5+W_2W_4-W_3W_4:=\eta _1>0.\nonumber \\ \end{aligned}$$

(50)

Let $\eta =\min \left\{ \frac{W_1W_5+W_2W_4}{2}, \eta _1\right\}$. Denote

$$\begin{aligned}{} & {} L:=\Big \{\lambda =x+\text {i}\omega \in {\mathbb {C}}: \nonumber \\{} & {} \qquad (x+W_1)^2+\omega ^2=W_1^2+\omega _0^2,\, x\in \big [-W_1-\sqrt{W_1^2+\omega _0^2}, 0\big ], \nonumber \\{} & {} \qquad \>\text {or}\> \lambda =\text {i}\omega ,\,\omega \in [-\omega _0, \omega _0]\Big \}. \end{aligned}$$

(51)

where ${\mathbb {C}}$ is a connected region. It is known that L is a simple loop homotopic to the original, $\lambda _0=\alpha _0+\text {i}\omega _0\in L$ and $|{\textbf{g}}(\lambda )|>\eta$ on L. Taking $r_0>0$ such that $L\subset \Omega :=\{\lambda \in {\mathbb {C}}: |\lambda |<r_0\}$. Denote $\partial \Omega :=\{\lambda \in {\mathbb {C}}: |\lambda |=r_0\}$, then for all $\lambda \in \partial \Omega$, $\lambda =r_0\text {e}^{\text {i}\phi },\,\phi \in [\frac{\pi }{2}, \frac{3\pi }{2}]$, we obtain

$$\begin{aligned} \begin{array}{l} |{\textbf{f}}(\lambda )|=|\lambda ^2+(W_1+{d_i})\lambda +W_1{d_i}|\le r_0^2+(W_1+{d_i})r_0+W_1{d_i}. \end{array} \end{aligned}$$

(52)

If $r_0^2+(W_1+{d_i})r_0+W_1{d_i}<\eta$, then for all $\lambda \in \Omega$, $\lambda =r\text {e}^{\text {i}\phi }$ and $r<r_0$, we have $|{\textbf{f}}(\lambda )|<r_0^2+(W_1+{d_i})r_0+W_1{d_i}<\eta$ for $\lambda \in L$. Therefore $|{\textbf{g}}(\lambda )|>|{\textbf{f}}(\lambda )|$ on L. By Rouch$\grave{e}$’s theorem, ${\textbf{g}}(\lambda )$ and ${\textbf{g}}(\lambda )+{\textbf{f}}(\lambda )$ have the same number of zero in L. That is, ${\textbf{g}}(\lambda )+{\textbf{f}}(\lambda )=0$ has at least one root $\lambda ^* \in L$. $\square$

1.6 Proof of Lemma 3.4

Proof

Suppose that Eq. (9) has no root with nonnegative real parts for $\tau _2>0$, which means the characteristic Eq. (26) with $\tau _1=0$ and $\tau _2>0$ has no root with a nonnegative real part.

Using $\tau _1$ as a variable, then the left-hand side of Eq. (26) is analytic in $\lambda$ and $\tau _1$, and the sum of the multiplicities of zeros of the left-hand side of Eq. (26) in the open right half-plane can only change if a zero appears on or crosses the imaginary axis.

Due to Eq. (26) with $\tau _1=0$ has no root with nonnegative real part, there is $\tau _1^*(\tau _2)>0$ such that all roots of Eq. (26) have negative real parts when $0<\tau _1<\tau _1^*(\tau _2)$. $\square$