Abstract
Autocatalysis underlies the ability of chemical and biochemical systems to replicate. Recently, Blokhuis et al. (PNAS 117(41):25230–25236, 2020) gave a stoechiometric definition of autocatalysis for reaction networks, stating the existence of a combination of reactions such that the balance for all autocatalytic species is strictly positive, and investigated minimal autocatalytic networks, called autocatalytic cores. By contrast, spontaneous autocatalysis—namely, exponential amplification of all species internal to a reaction network, starting from a diluted regime, i.e. low concentrations—is a dynamical property. We introduce here a topological condition (Top) for autocatalysis, namely: restricting the reaction network description to highly diluted species, we assume existence of a strongly connected component possessing at least one reaction with multiple products (including multiple copies of a single species). We find this condition to be necessary and sufficient for stoechiometric autocatalysis. When degradation reactions have small enough rates, the topological condition further ensures dynamical autocatalysis, characterized by a strictly positive Lyapunov exponent giving the instantaneous exponential growth rate of the system. The proof is generally based on the study of auxiliary Markov chains. We provide as examples general autocatalytic cores of Type I and Type III in the typology of Blokhuis et al. (PNAS 117(41):25230–25236, 2020) . In a companion article (Unterberger in Dynamical autocatalysis for autocatalytic cores, 2021), Lyapunov exponents and the behavior in the growth regime are studied quantitatively beyond the present diluted regime .
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Context and applications
The chemical mechanism that epitomizes the ability of living systems to reproduce themselves is autocatalysis, namely, catalysis brought about by one of the products of the reactions. Autocatalysis must have been present from the early stages of the origin of life, from primitive forms of metabolism (Preiner et al. 2019), to autocatalytic sets based on the first catalytic biopolymers (Kauffman 1986) and the emergence of sustained template-based replication of nucleic acids (Eigen 1971). Diverse artificial autocatalytic systems have been implemented in the laboratory (Hanopolskyi et al. 2021), and remnants of ancestral autocatalytic networks may be found in extant metabolic networks (Kun et al. 2008). These examples reveal the diversity of autocatalytic mechanisms and chemistries. However, the stoichiometry of autocatalytic has been characterized only recently (Blokhuis et al. 2020) and we still lack a systematic understanding of dynamical conditions for autocatalysis (Andersen et al. 2020) which limits our ability to conceive plausible prebiotic scenarios (Jeancolas et al. 2020).
To fill this gap, it is necessary to investigate how autocatalysis may emerge in complex mixtures. This would help us understand the appearance of self-sustaining reactions in messy prebiotic mixtures (Danger et al. 2020), and interpret experiments that search for such reactions (Vincent et al. 2019). Identifying autocatalytic systems is also critical to explain the appearance of Darwinian evolution, from complex mixtures (Danger et al. 2020), to autocatalytic sets (Hordijk et al. 2012) and ultimately template-based replication (Nghe 2015), a path which comprises multiple transitions and can be studied experimentally in RNA reaction networks (Arsène et al. 2018; Ameta et al. 2021).
In Blokhuis et al. (2020), the authors give a classification of all autocatalytic cores, that is of all minimal autonomous sub-networks satisfying the above criteria, into 5 types I–V. (Types I and III are presented in Suppl. Info.). Among foremost questions raised by this new classification, let us single out the two following:
-
(A)
Are stoechiometrically autocatalytic networks able to replicate ? Conversely, are chemical networks capable of replication stoechiometrically autocatalytic ?
-
(B)
(If the answer to (A) is: yes, and assuming some natural form for the rates, in particular, for mass-action rates.) Under which conditions over the concentrations and the rates does an autocatalytic network indeed replicate ? If it does, can one estimate its replication rate ?
Partial answers to questions (A) and (B) are already available in Blokhuis et al. (2020); they are based on self-consistent equations for survival probability, and are therefore rather given in the framework of stochastic networks, assuming only a few molecules are initially present. Generally speaking, survival criteria are given in a form akin to that given by King King (1982).
The present work presents an essentially complete answer to question (A) in a specific regime which we call diluted regime, where all concentrations of dynamical species are low, and assuming that there are no degradation reactions, or that these have sufficiently small rates. Mass-action rates are assumed throughout. The companion article (Unterberger 2021), on the other hand, presents a detailed case study for question (B) for a broad class of autocatalytic cores in a large part of the growth regime, well beyond the diluted regime, and in presence of degradation reactions; it rests on the notations and concepts introduced here, which are therefore presented in great generality.
1.2 Our main result in a nutshell
The focus in the present work is on spontaneous autocatalysis in chemical reaction networks, namely, exponential amplification of a set of species with low initial concentrations. This requires that certain other species, from which the network feeds, are provided in sufficiently large quantities in the environment. These resource species, sometimes called the ’food-set’, may be constantly supplied from a large reservoir or external fluxes, or may be the products of reactions that already self-sustain in the milieu (Fontana and Buss 1994).
Our main results, Theorems 2.1 and 2.2, give a general condition, denoted (Top), for spontaneous autocatalysis to be possible in a stoechiometric, respectively dynamical sense, understood as the existence of, respectively: combinations of reactions that lead to an increase of every autocatalytic species, and instantaneous growth of the dynamical system associated with the reaction network. Our result holds provided that the reaction set satisfies the formal conditions stated in Blokhuis et al. (2020): (i) autonomy: reactions should possess at least one reactant and one product; (ii) non-ambiguity: a species cannot be both a reactant and a product of the same reaction. Point (i) ensures that concentrations do not increase merely due to reactions that only consume species from the environment. Said differently, it ensures that any concentration increase depends on the presence of another autocatalytic species, as required by the definition of autocatalysis (Blokhuis et al. 2020). Point (ii) imposes a formal choice of coarse-graining in the description of the reaction network. This choice ensures that catalytic steps can be distinguished at the level of the stoechiometric matrix as the catalysts then appear in the stoichiometry (as shown in Blokhuis et al. (2020)). Note that such a choice implies no restriction of generality, as it is always possible to introduce additional reaction intermediates in the description so that (ii) is respected (Blokhuis et al. 2020).
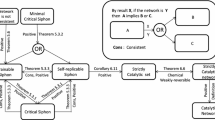
Given the above conventions, verifying autocatalysis consists in isolating subsets of reactions that obey the topological criteria below (Fig. 1):
-
1.
Retain only species that are initially absent or rare and discard from the description those that are abundant (the environment).
-
2.
Dismiss reactions that have more than one reactant among the absent or rare species.
-
3.
In the resulting network, identify strongly connected components which possess at least one reaction with multiple products within the component, including the case of multiple copies of a single species.
Strongly connected components are defined as subgraphs in which any pair of vertices (species) are connected by a chain of reactions. Successful verification of the steps above implies stoechiometric autocatalysis, independently of the reaction rates. It further implies dynamical autocatalysis for sufficiently small degradation rates, as characterized by an exponential increase of every species in the component assuming initially low concentrations, at least in the early phase of the dynamics.
Species c and j (gray squares) are initially abundant in the environment, thus can be safely ignored. The reaction \(g+d \rightarrow h+f\) (dashed) has multiple reactants that are initially rare or absent, thus has a negligible rate compared to others and is discarded from the description. In the remaining graph, the set \(\{a,b,d,e,g,i\}\) forms a strongly connected component (SCC), as there exists a directed path between any two of its members. Species h and f (dashed gray circles) are not part of the SCC. The SCC comprises a reaction (\(e \rightarrow a+d\)) with multiple products. Thus, the SCC is stoechiometrically autocatalytic (note that it is actually a Type III autocatalytic core according to Blokhuis et al. (2020), see Supplementary Information Sect. 7.2). Furthermore, it is dynamically autocatalytic provided degradation rates of the species of the SCC are sufficiently small
1.3 Outline of the article
Section 2 introduces the framework and definitions we use for chemical reaction networks: open chemical networks with mass-action rates, autonomy, non-ambiguity, diluted networks, degradation-less networks, Lyapunov exponents, linearized dynamics, graph theoretical concepts. We also state a key topological condition denoted (Top) and our main results, namely Theorems 2.1 and 2.2. Section 3 presents an elementary motivating example. Section 4 reports the proof of Theorem 2.1 characterizing stoechiometric autocatalysis. Section 5 reports the proof of Theorem 2.2) giving a sufficient condition for dynamical autocatalysis. We present perspectives for future work in Sect. 6. Finally, Sect. 7 provides supplementary information for the main text: a presentation of type I and type III cycles, and mathematical concepts and results used in the article, based on general Markov theory.
2 General setup
We now introduce the framework of the present article, which is a mathematical and physical elaboration on the recent theoretical work (Blokhuis et al. 2020) on autocatalysis in chemical reaction networks.
2.1 Open autonomous unambiguous reaction networks
The general setting is that of open reaction networks with mass-action rates, see e.g. Esposito (2016) and references within. Chemical species fall into two categories: dynamical (or non-chemostatted) species, whose concentrations vary over time according to kinetic (or stochastic, if present in small number) equations, as opposed to chemostatted species, whose concentrations are fixed (or large w.r. to dynamical species, so that their concentrations may be considered as almost constant). Chemostatted species influence rates, but are not included into the stoechiometric matrix (see below), therefore they need not even be specified when dealing with stoechiometry alone.
Following (Blokhuis et al. 2020), we consider only autonomous and unambiguous (or non-ambiguous) networks. An autonomous network is a network such that every reaction has at least one (dynamical) reactant (or educt) and at least one (dynamical) product. Note however that degradation reactions \(A\rightarrow \emptyset \) are natural in a biological or chemical setting and do not respect the autonomy criterion. As will be more precise below, we do not include degradation reactions in the description of our networks, but we will include degradation as perturbations of effective reaction rates.
An unambiguous network is written in such a way that no chemical species can be both a reactant and a product of a reaction. For instance, this avoids reactions to be written as \(A+E\leftrightarrows B+E\) where the catalyst E appears on both sides, thus cancels from the total stoechiometric balance. Instead, the reaction should be written in two steps \(A+E \leftrightarrows EA \leftrightarrows E+B\) which formally ensures that E appears in the stoechiometric balance and ultimately makes it possible to recognize the catalytic cycle associated with the enzyme E in the structure of the stoechiometric matrix (see Blokhuis et al. (2020) for details).
In the sequel, we speak simply of reaction networks (or: networks), intending: open, autonomous, unambiguous reaction networks with mass-action rates.
2.2 Linearized dynamics of reaction networks
Despite the fact that kinetic equations are not linear in general, our work is largely based on the study of the time-evolution of linear evolution models of the type
with negative diagonal coefficients \(M_{ii} \le 0\) and positive off-diagonal coefficients \(M_{ij} \ge 0, i\not =j\), which are found in different contexts in the literature. Note that these equations are formally similar to linear mutation-selection models, where off-diagonal coefficients are interpreted as mutation rates, and selection rates related to diagonal coefficients; see e.g. (Eigen 1971; Kussell and Leibler 2005). Since we are mainly inspired by Markov techniques, we speak here of M as generalized adjoint Markov generator, see Supp. Info. Indeed, when the sum of coefficients on any column is zero, the total concentration \(\sum _{i=1}^{|{{\mathcal {S}}}|} [A_i]\) is a constant. Normalizing it to one, (1) yields a master equation, namely, the time-evolution of a probability measure. On the other hand, he case \(|M_{j,j}|>\sum _{i\not =j} M_{ij}\) yields the time-evolution of a sub-Markov process, i.e. a Markov process with killing rates \(a_j=|M_{j,j}|-\sum _{i\not =j} M_{ij}\). The case when some \(a_j\) are negative—indicating ’source’ terms—is not standard in probability theory, but remains mathematically valid. Indeed, whatever the sign of \(a_j\), the Feynman-Kac formula yields the solution to (1) in terms of a sum over paths with transition rates \(w_{i\rightarrow j}\) proportional to \(M_{ji}\) (mind the index transposition due to the fact that M is a backward generator). Thinking in terms of kinetic networks (and in spite of the fact that these are assumed to be written as autonomous systems), a positive killing rate \(a_j\) is associated to a degradation reaction \(A_j \rightarrow \emptyset \), whereas a negative killing rate is associated to an inverse creation reaction \(\emptyset \rightarrow A_j\). (Since chemostatted species are left out of the equations, the latter, seemingly creation-ex-nihilo, reaction should be thought of really as \(A'\rightarrow A_j+A''\), where \(A',A''\) are chemostatted species).
Markov generators come out by linearizing the kinetic equations. Formally, the time-evolution of concentrations may be expressed in terms of the stoechiometric matrix and the current vector \(J=(J_i)_{i=1,\ldots ,n}\),
Linearizing around given concentrations \(([A_i])_{i=1,\ldots ,|{{\mathcal {S}}}|}\), one gets for infinitesimal variations \([A]\longrightarrow [A]+A\) (mind the notation without square brackets for variations)
where \(J_{lin,i}([A],A)=\sum _{\ell } J_{lin,i}^{\ell }([A]) A_{\ell }\) is linear in the variations. Letting
we get the linear system
The matrix M([A]) is sometimes (but not always) a generalized Markov generator. A case for which M([A]) is indeed a generalized Markov generator is when each reaction has exactly one reactant, so that its rate is linear in its concentration, and \(M([A])=M([A]=0)\) does not depend on concentrations: the reaction \(A_1\overset{k_+}{\longrightarrow } s_1 B_1+\ldots + s_n B_n\), \(n\ge 1\) makes the following additive contribution to M([A]),

An important particular case is that of a 1–1 reaction \(A_1 \overset{k_+}{\rightarrow } B_1\); the contribution to M([A]) is then simply

for which the sum of coefficients on the \(A_1\)-column is zero, in coherence with probability preservation.
Interestingly, autocatalytic cores, as proved in Blokhuis et al. (2020), satisfy condition of having only one reactant—except that the stoechiometry is more general, allowing for reactions of type \(s A {\longrightarrow } s_1 B_1+\ldots + s_n B_n\), \(s\ge 1\). This only turns the top coefficient \(M_{A,A}\) into \(-sk_+\). The associated killing rate for species A is \((1-(s_1+\ldots +s_n))k_+\), it is \(\le 0\) for reactions of the type \(A\overset{k_+}{\longrightarrow } s_1 B_1+\ldots + s_n B_n\), \(n\ge 1\) (but not necessarily when \(s\not =1\)).
Going one step further, we note that reactions with \(\ge 2\) reactants have a vanishing rate in the limit when concentrations go to zero. In that limit, furthermore, all killing rates are \(\le 0\). We call this the zero concentration limit of networks. In this limit, where the linearized time evolution generator involves only mutations and creation reactions, it is easily conceived that autocatalysis should hold in any reasonable sense. Diluted networks, which are the subject of the present article, and are introduced in the Sect. 2.4, are perturbations of the zero concentration limit.
2.3 Graph of the reaction network
Definition 2.1
(adjacency graph \(G({{\mathbb {S}}})\)) The (directed) adjacency graph associated to the stoechiometry matrix \({\mathbb {S}}\) is the directed graph \(G({{\mathbb {S}}})=({{\mathcal {S}}},E)\) with vertex set \({{\mathcal {S}}}=\{\)set of species\(\}=\{A_1,\ldots ,A_{|{{\mathcal {S}}}|}\}\), and edge set
i.e. (i, j) is an oriented edge (from i to j) if and only if there exists a reaction \({{\mathcal {R}}}: s_1 A_i + s_2 A_{i_2} + \ldots + s_n A_{i_n} \rightarrow s'_1 A_j + s'_2 A_{i'_2}+\ldots +s'_{n'} A_{i'_{n'}}\), with \(s_1,s'_1\not =0,n\ge 1\), \(s'_1\not =0,n'\ge 1\) having \(A_i\) as reactant and \(A_j\) as product.
Equivalently, if each reaction has a single reactant, \(G({{\mathbb {S}}})\) may be defined as the directed adjacency graph associated to the generalized Markov generator \(M([A]=0)\). By its very definition, it depends only on the stoechiometric matrix \({\mathbb {S}}\), not on kinetic rates. Later on, for reasons developed in Sect. 4, the adjacency graph will be referred to as the split graph. The correspondence between the generalized Markov generator \(M([A]=0)\) and the adjacency graph \(G({{\mathbb {S}}})\) may be stated as follows:
Lemma 2.2
Let \(\Gamma \) be a reaction network such that all reactions have a single reactant, M be the associated (concentration independent) generalized Markov generator, and \(G({{\mathbb {S}}})\) the associated adjacency graph. Then \(M_{ji}>0\) if and only if \(G(\mathbb {S})\) contains the edge \(i\rightarrow j\).
This is clear from the elementary matrix entry specifications given below (5).
Class decomposition of a directed graph. Let \(\Gamma \) be a directed graph. It is strongly connected if and only if it contains a directed path from x to y (and from y to x) for every pair of vertices (x, y). In general, strongly connected components of \(\Gamma \) are its maximal strongly connected subgraphs. Two distinct strongly connected components \({{\mathcal {C}}},{{\mathcal {C}}}'\) may be connected by a directed path, but by construction, one cannot have both a directed path from \({\mathcal {C}}\) to \({{\mathcal {C}}}'\) and a directed path from \({{\mathcal {C}}}'\) to \({\mathcal {C}}\). A minimal class \({\mathcal {C}}\) of \(\Gamma \) is a source, i.e. there exists no directed path from a class \({{\mathcal {C}}}'\not ={{\mathcal {C}}}\) to \({\mathcal {C}}\).
Case of \(G({{\mathbb {S}}})\). The above notions (strong connectivity, strongly connected components, minimal classes) apply to \(G({{\mathbb {S}}})\). Alternatively, one may think of the latter as the graph of a conventional Markov matrix. By reference to standard Markov terminology, we say that the reaction network is irreducible if \(G({{\mathbb {S}}})\) is strongly connected, otherwise it is reducible. A strongly connected component is a (communication) class (see Suppl. Info. Sect. 7.5), with probability flow flowing downstream from minimal to maximal classes. Letting \({{\mathcal {C}}}\) be one of the classes, we now define its set of internal reactions. If \({{\mathcal {R}}} \, :\, A\rightarrow s_1 A'_1+\cdots + s_n A'_n\) is an irreversible reaction such that \(A\in {{\mathcal {C}}}\), and \(\{i=1,\ldots ,n \ |\ A'_i\in {{\mathcal {C}}}\}=\{1,\ldots ,n'\}\) for some \(n'\ge 1\), then we introduce the truncated reaction \({{\mathcal {R}}}_{{{\mathcal {C}}}}\, :\, A\rightarrow s_1 A'_1+\cdots + s_{n'} A'_{n'}\). Note that we do not discuss the case of reactions with more than one reactant, since diluted networks (to be defined in Sect. 2.4 below) do not contain any such reactions, or only at the level of perturbation (with a negligible rate). Thus:
Definition 2.3
(internal/purely external reactions of a class) Let \({\mathcal {C}}\) be a class of a reaction network \(\Gamma \). We assume that all reactions of \(\Gamma \) have a unique reactant. Then:
-
1.
Internal reactions of \({\mathcal {C}}\) are :
-
(i)
reversible reactions \(A\leftrightarrows A'\) with \(A,A'\in {{\mathcal {C}}}\);
-
(ii)
truncated reactions \({{\mathcal {R}}}_{{{\mathcal {C}}}}\, :\, A\rightarrow s_1 A'_1+\cdots + s_{n'} A'_{n'}\) as above, with \(A,A'_1,\ldots ,A'_{n'}\in {{\mathcal {C}}}\).
-
(i)
-
2.
All other irreversible reactions, i.e. reactions of the form \({{\mathcal {R}}}\, :\, A\rightarrow s_1 A'_1+\cdots + s_n A'_n\) with \(A\in {{\mathcal {C}}}\) and \(A'_1,\ldots ,A'_n\not \in {{\mathcal {C}}}\) are purely external reactions.
Note that in case 1. (ii), if \(n'=1\), we obtain a reaction of a new type: an irreversible 1–1 reaction. Note also that purely external reactions can appear only in reducible networks.
2.4 Definition of diluted networks and statement of condition (Top)
The present study is devoted to diluted networks. These are (open, autonomous, unambiguous, mass-action rate) reaction networks (as formalized in Sect. 2.1) with low, but nonzero, concentrations, for which reactions with \(\ge 2\) reactants exist but have a negligible rate compared to the others. The physical picture is that of a system of reactions of three types:
-
(i)
reversible reactions, with linear rates, involving one reactant and one product,
$$\begin{aligned} A_i \leftrightarrows A_j; \end{aligned}$$(7) -
(ii)
irreversible forward reactions involving one reactant and several products, with linear rates,
$$\begin{aligned} A_i\rightarrow s'_1 A_{i'_1}+ s'_2 A_{i'_2}+\ldots , \qquad \sum _{\ell } s'_{\ell }\ge 2; \end{aligned}$$(8)such reactions are totally irreversible in the zero concentration limit;
-
(iii)
and, possibly, the reverse reactions associated to the reactions in (ii),
$$\begin{aligned} s'_1 A_{i'_1}+ s'_2 A_{i'_2}+\ldots \rightarrow A_i,\qquad \sum _{\ell } s'_{\ell }\ge 2 \end{aligned}$$(9)with nonlinear, but low (compared to (i) and (ii)) or zero reaction rates. Since such reactions are only treated in perturbation, we choose not to include them into the stoechiometric matrix \({\mathbb {S}}\).
Degradation reactions
(which are non-autonomous) may also be included (they are not part of \({\mathbb {S}}\)); they modify additively the diagonal coefficients of the matrix M([A]), namely, turning on degradation turns \(M([A])_{ii}\) into \(M([A])_{ii}-\alpha _i\). Degradationless diluted networks are diluted networks in which degradation reactions are either absent or have small enough rates. When discussing only stoechiometric properties (such as stoechiometric autocatalysis) and not dynamics, diluted networks are characterized as open reaction networks (as formalized in Sect. 2.1) whose reactions can only be of type (i) (reversible reactions) or (ii) (irreversible one-to-several reactions). We may summarize the above by the following stoechiometric (matrix) characterization:
Lemma 2.4
(stoechiometric characterization of diluted networks) A matrix M is the stoechiometric matrix \(G({{\mathbb {S}}})\) of a diluted network if and only if each column of M has non-negative coefficients, except for exactly one entry \(-1\).
The entry \(-1\) corresponds to the reactant of the reaction encoded by the column. Note also that Lemma 2.2 still holds in this context, provided \(M=M([A]=0)\) is the generalized Markov generator computed in the zero-concentration limit.
Generally speaking, reactions such as (7), (8) or (9) may be represented in the form of a hypergraph called hypergraph associated to \({{\mathbb {S}}}\) (Andersen et al. 2019, Sect. 2), with ’pitchforks’ connecting \(A_i\) to \(A_{i'_{\ell }}\) by \(s'_{\ell }\) arrows in the case of a one-to-several irreversible reaction. In the limit of extreme dilution (or zero-concentration limit), \(M([A])\rightarrow M([A]=0)\), the time-evolution is linear, and Markovian in the generalized sense defined above. Considering more generally diluted networks, it is natural to approximate reactions (iii) by their linearizations, which have in any case a small rate compared to reactions of type (i) or (ii). We do not get in general a generalized adjoint Markov generator, because off-diagonal coefficients of M([A]) are not necessarily positive. (They are positive when reverse reactions are strictly of the form \(mA_{i'}\rightarrow A_i\) with \(m\ge 2\); see Suppl. Info. for examples and general statements). Even in that case, however, the Feynman-Kac formula holds (see Suppl. Info.), which we use in the proofs of the theorems.
Definition 2.5
((Top) condition) We say that the diluted network satisfies condition (Top) if all minimal classes of \(G({{\mathbb {S}}})\) contain at least one internal one-to-several irreversible reaction, i.e. each minimal class \({\mathcal {C}}\) contains a truncated reaction \({{\mathcal {R}}}_{{{\mathcal {C}}}}\, :\, A\rightarrow s_1 A'_1+\cdots + s_{n'} A'_{n'}\) with \(s:=\sum _{i=1}^{n'} s_i\ge 2\).
Note that this is a topological condition on the network, i.e. it does not depend on kinetic rates. However, in general it depends on the structure of the hypergraph associated to \({{\mathbb {S}}}\) (or, to put it differently, on the non-zero coefficients of the columns of the matrix \({\mathbb {S}}\)), and not solely on \(G({{\mathbb {S}}})\). For example, a network with 3 species A, B, C and reaction set \(\{{{\mathcal {R}}}_1,\overline{{\mathcal {R}}}_1,{{\mathcal {R}}}_2,\overline{{\mathcal {R}}}_2, {{\mathcal {R}}}_3,\overline{{\mathcal {R}}}_3\}\) with \({{\mathcal {R}}}_1: A\rightarrow B\), \({{\mathcal {R}}}_2:A\rightarrow C\), \({{\mathcal {R}}}_3:B\rightarrow C\), has same graph \(G({{\mathbb {S}}})\) (= total graph) as a network with reaction set \(\{\overline{{\mathcal {R}}}_1,\overline{{\mathcal {R}}}_2,{{\mathcal {R}}}_3,\overline{{\mathcal {R}}}_3,{{\mathcal {R}}}_4\}\) featuring the irreducible reaction \({{\mathcal {R}}}_4 : A\rightarrow B+C\). However, only the second one is autocatalytic.
2.5 Stoechiometric and dynamical autocatalysis
Following Blokhuis et al. (2020), we use a stoechiometric criterion for autocatalysis that depends only on the stoechiometric matrix \({{\mathbb {S}}}\), an integer-coefficient matrix with columns indexed by reactions (and not on the rates).
Definition 2.6
(stoechiometric autocatalysis) A diluted network (see Sect. 2.4) is stoechiometrically autocatalytic if there exists a positive reaction vector c such that \({{\mathbb {S}}}c>0\), where the orientation of reversible, type (i) reactions is arbitrary, but forward reactions (ii) are given positive orientation.
Turning now to dynamical autocatalysis, we consider a priori a general reaction network, in the definition of Sect. 2.1. Listing reactions (other than degradation reactions) \(({{\mathcal {R}}}_1,\ldots , {{\mathcal {R}}}_N)\), and rows indexed by the set \({{\mathcal {S}}}=\{A_1,\ldots ,A_{|{{\mathcal {S}}}|}\}\) of dynamical chemical species, by definition, each column of \({\mathbb {S}}\) corresponds to the stoechiometry of a given reaction
that is, \({{\mathbb {S}}}_{j,{{\mathcal {R}}}}=-\sum _{\ell =1}^n s_{\ell } \delta _{i_{\ell },j} + \sum _{\ell '=1}^{n'} s'_{\ell '} \delta _{i'_{\ell '},j}\) (note that the coefficients of \({\mathbb {S}}\) depend on the choice of an orientation for every reaction). Stoechiometric autocatalysis requires that there should exist
-
(i)
a choice of orientations for reactions, and
-
(ii)
a positive reaction vector \(c\in (\mathbb {R}_+)^{N}\) such that \({\mathbb {S}}c>0\).
This means that the reaction obtained by taking the linear combination \(\sum _{{\mathcal {R}}} c_{{{\mathcal {R}}}} {{\mathcal {R}}}\) strictly increases the number of molecules of all species in \({\mathcal {S}}\); in other terms, the chemical balance \(({{\mathbb {S}}}c)_i\) for species i is \(>0\). By Gordan’s theorem (Borwein and Adrian 2006), (ii) holds if and only if there is no mass-like conservation law, i.e. there exists no linear combination \(\sum n_i [A_i]\) with positive coefficients \(\mathbf{n}=(n_i)_{i\in {{\mathcal {S}}}}>0\) such that \(\mathbf{n}\, \cdot \, {{\mathbb {S}}}=0\), i.e. preserved under all reactions.
To characterize dynamics, under the conditions of dilution and linearization, a natural quantity characterizing the replication rate is the Lyapunov exponent \(\lambda _{max}\equiv \lambda _{max}(M([A]))\), by definition
Note that \(\lambda _{max}=\lambda _{max}([A])\) depends on concentrations; however, by standard spectral perturbation arguments, \(\lambda _{max}([A])\rightarrow _{[A]\rightarrow 0} \lambda _{max}^0\) in the dilute regime, where
is the Lyapunov exponent in the zero concentration limit. Roughly speaking, the network is dynamically autocatalytic if \(\lambda _{max}^0>0\). We need however a more precise definition. Since it is given in the zero-concentration limit, it may be stated equivalently for diluted networks (see Sect. 2.4).
Definition 2.7
(dynamical autocatalysis)
-
(i)
A network is (strongly) autocatalytic in the dynamical sense—or (strongly) dynamically autocatalytic—if \(\lambda ^0_{max}>0\) is an eigenvalue of \(M([A]=0)\) with multiplicity 1, and if an eigenvector v associated to \(\lambda ^0_{max}\) can be chosen in such a way that all its coordinates are \(>0\).
-
(ii)
Generalizing, we say that it is weakly autocatalytic in the dynamical sense (or weakly dynamically autocatalytic) if \(\lambda ^0_{max}>0\) is an eigenvalue of \(M([A]=0)\) (multiplicity can be arbitrary, and Jordan blocks associated to \(\lambda ^0_{max}\) may be non-trivial), and an eigenvector \(v\not =0\) associated to \(\lambda ^0_{max}\) may be chosen in such a way that all its coordinates are \(\ge 0\).
It follows from the Perron-Frobenius theorem that, for irreducible networks, \(\lambda _{max}^0=\lambda _{max}([A]=0)\) is an eigenvalue of \(M([A]=0)\) with multiplicity 1, and that an eigenvector associated to \(\lambda _{max}^0\) can be chosen in such a way that all its coordinates are \(>0\). When \(\lambda _{max}^0\) is positive, it characterizes the onset of the exponential growth regime of the system, namely, for small initial concentrations,
for all species \(A_j\in {{\mathcal {S}}}\), for not-too-large time values t. This property (discussed in Sect. 5 and after Lemma 7.2) we call spontaneous autocatalysis.
For reducible networks (see Sect. 5), only weak dynamical autocatalysis can be expected in general. Then (14) remains valid for all species \(A_j\) such that \(v_j > 0\).
For non-zero concentrations [A], more generally, one may define (weak or strong) dynamical autocatalysis as in Definition 2.7, with \(M([A]=0)\) replaced by M([A]), and \(\lambda ^0_{max}= \lambda _{max}([A]=0)\) by \(\lambda _{max}=\lambda _{max}[A]\). As mentioned above, by standard perturbation theory, weak/strong autocatalysis holds for small enough [A] if it holds for \([A]=0\). The dynamical autocatalysis properties for \([A]\not =0\) are however not quite as meaningful as for \([A]=0\) because the Perron-Frobenius does not hold any more in general (off-diagonal coefficients of M([A]) can be negative), so that spontaneous autocatalysis does not necessarily follow. This is the reason which Definition 2.7 is stated in the zero concentration limit.
2.6 Statement of the theorems
Let us first discuss stoechiometric autocatalysis. As discussed in Sect. 2.4, diluted networks are stoechiometrically characterized as open (autonomous, unambiguous) reaction networks (as defined in Sect. 2.1 whose reactions can only be of type (i) (reversible 1–1 reactions) or (ii) (irreversible one-to-several reactions). This excludes reactions with several non-chemostatted (non-buffered) reactants.
Theorem 2.1
(necessary and sufficient condition for stoechiometric autocatalysis) A diluted network (see Sect. 2.4) is stoechiometrically autocatalytic if and only if the topological condition (Top) holds.
The proof of this theorem is the purpose of Sect. 4. It uses the generalized Markov generators, used to prove the next theorem as well. Note however that a more elementary proof using \(G({{\mathbb {S}}})\) only is provided in Sect. 7.3 in the case of irreducible networks.
Before moving to the statement of the second theorem, let us comment on this first theorem. When \(G({{\mathbb {S}}})\) is irreducible, Theorem 2.1 states that at least one irreversible forward reaction (8) must be present in the system for stoechiometric autocatalysis to hold. That this condition is necessary can be deduced from Gordan’s theorem since \(\mathbf{n} \, \cdot \, {{\mathbb {S}}}=0\) if \(\mathbf{n}=\left( \begin{array}{c} 1 \\ \vdots \\ 1 \end{array}\right) \) and only \(1-1\) reversible reactions (7) are present in the system. The proof in Sect. 4 shows that this is a sufficient condition.
When \(G({{\mathbb {S}}})\) is reducible, a similar argument holds for (Top) to be a necessary condition. Namely, let \({\mathcal {C}}\) be one of the minimal classes, and \({{\mathbb {S}}}_{{\mathcal {C}}}\) the stoechiometric matrix associated with species in \({\mathcal {C}}\) and internal reactions of \({\mathcal {C}}\). If all internal reactions are 1–1, then the same argument based on Gordan’s theorem implies that, for every positive reaction vector \(c_{{{\mathcal {C}}}}\), the balance \(({{\mathbb {S}}}_{{{\mathcal {C}}}} \, c_{{\mathcal {C}}})_i\) is \(\le 0\) for at least one of the species \(i\in {{\mathcal {C}}}\). Now, including external (for \({\mathcal {C}}\)) reactions \({{\mathcal {R}}}\, :\, A_i\rightarrow s_1 A'_1+\ldots + s_n A'_n\) with \(A_i\in {{\mathcal {C}}}\) and \(A'_1,\ldots ,A'_n\not \in {{\mathcal {C}}}\) can only worsen the balance for species \(A_i\), while other reactions \(A'\rightarrow s_1 A'_1+\ldots +s_n A'_n\) with \(A'\not \in {{\mathcal {C}}}\)—and therefore, \(A'_1,\ldots ,A'_n\not \in {{\mathcal {C}}}\) also since \({\mathcal {C}}\) is minimal—do not change it. Thus, for example, the network with the hypergraph below

featuring two reversible reactions \(A_0\leftrightarrows A_1, A_1\leftrightarrows A_2\) (in blue) and an irreversible reaction \({{\mathcal {R}}}\, :\, A_0\rightarrow A_2+A'_0\) (in red) coupling the minimal class \({{\mathcal {C}}}=\{A_0,A_1,A_2\}\) to another class \({{\mathcal {C}}}'=\{A'_0\}\), does not satisfy (Top), because the truncated irreversible reaction \({{\mathcal {R}}}_{{\mathcal {C}}} \, : \, A_0 \rightarrow A_2\) is 1–1.
Anticipating on the theorem below, note that the presence of irreversible forward reactions is also necessary for dynamical autocatalysis to hold—otherwise only mutation-like coefficients are present, kinetic equations are those of a conventional Markov system, and then it is known that all generator eigenvalues have \(\le 0\) real part. Theorem 2.2 (ii) states again that this is a sufficient condition, provided degradation is negligible.
Theorem 2.2
(sufficient condition for dynamical autocatalysis in the diluted regime) Consider a diluted (see Sect. 2.4) network (\({{\mathcal {S}}}, \{{{\mathcal {R}}}_1,\ldots , {{\mathcal {R}}}_N\}\)), with kinetic rates \(k_{{{\mathcal {R}}}_i}, i=1,\ldots ,N\), and a concentration vector [A]. The following two results hold,
-
(i)
(weak dynamical autocatalysis) The topological condition (Top) implies weak dynamical autocatalysis in the diluted regime, i.e. for small enough concentrations, if there are no degradation reactions nor purely external reactions, or, more generally, if the rates of those are small enough. In other words, there exist \(C_{max}=C_{max}({{\mathbb {S}}}, (k_{{{\mathcal {R}}}_i})_{i=1,\ldots ,N})>0\) and \(K_{max}=K_{max}({{\mathbb {S}}}, (k_{{{\mathcal {R}}}_i})_{i=1,\ldots ,N})>0\) such that, if \(\max ([A_1],\ldots ,[A_{|{{\mathcal {S}}}|}])<C_{max}\) and
$$\begin{aligned} \max (\max ((\alpha _i)_{1\le i\le |{{\mathcal {S}}}|}),\max (k_{{{\mathcal {R}}}_i})_{1\le i\le N})< K_{max}, \end{aligned}$$(15)where \(\alpha _i,i=1,\ldots ,|{{\mathcal {S}}}|\) are the rates of the degradation reactions \(A_i\rightarrow \emptyset \), and \({\mathcal {R}}\) ranges in the set of purely external reactions, then condition (ii) in Definition 2.7 holds.
-
(ii)
(strong dynamical autocatalysis) Furthermore, strong dynamical autocatalysis holds in the specific case of an irreducible network in absence of degradation reactions, or if the rates of those are small enough. In other words, if the network is irreducible, then there exist \(C_{max}=C_{max}({{\mathbb {S}}}, (k_{{{\mathcal {R}}}_i})_{i=1,\ldots ,N})>0\) and \(\alpha _{max}=\alpha _{max}({{\mathbb {S}}}, (k_{{{\mathcal {R}}}_i})_{i=1,\ldots ,N})>0\) such that, if \(\max ([A_1],\ldots ,[A_{|{{\mathcal {S}}}|}])<C_{max}\) and
$$\begin{aligned} \max ((\alpha _i)_{1\le i\le |{{\mathcal {S}}}|})< \alpha _{max}, \end{aligned}$$(16)where \(\alpha _i,i=1,\ldots ,|{{\mathcal {S}}}|\) are the rates of the degradation reactions \(A_i\rightarrow \emptyset \), then condition (i) in Definition 2.7 holds.
The proof of this theorem is the purpose of Sect. 5. We here make a few remarks concerning this theorem. Looking closely at the (generalized) eigenspace associated to \(\lambda _{max}\) in the reducible case, one realizes that a complete discussion of the nature of dynamical autocatalysis (e.g. multiplicity of \(\lambda _{max}\), and support of an associated eigenvector v, i.e. the set of species \(A_j\) such that \(v_j > 0\)) cannot rely only on topological considerations (see a detailed example p. 32). In addition, the presence of reverse reactions (9), even at negligible rates from a biological or chemical point of view, introduces some subtleties on the interpretation of the theorem. We illustrate these on two minimal examples. Assume there are two classes \({{\mathcal {C}}},{{\mathcal {C}}}'\) with probability flowing out of \({{\mathcal {C}}}\) into \({{\mathcal {C}}}'\),

and that, as a first case, (i) only the maximal (downstream) class \({{\mathcal {C}}}'\) contains an internal irreversible reaction (so that (Top) is not satisfied); then (excluding reverse reactions going upstream from \({{\mathcal {C}}}'\) to \({{\mathcal {C}}}\)) the network restricted to \({{\mathcal {C}}}'\) is irreducible and (strongly) dynamically autocatalytic; thus the whole network is weakly dynamically autocatalytic. In this case however, whatever \({{\mathcal {C}}}\) reactants present in the solution disappear exponentially in time in favor of species in \({{\mathcal {C}}}'\). Now imagine choosing one of the reactions (8) connecting \({{\mathcal {C}}}\) to \({{\mathcal {C}}}'\) and adding the reverse reaction with a negligible rate \(O(\varepsilon )\), \(0 <\varepsilon \ll 1\). This makes the network irreducible, implying strong dynamical autocatalysis, while perturbing only slightly \(\lambda _{max}\). The associated positive eigenvector \(v = v(\varepsilon )\)—unique up to normalization—will have nonzero but very small coefficients along \({\mathcal {C}}\), making it probably difficult in practice to observe exponential increase of the corresponding species. Next, consider as a second case the possibility that (ii) (Top) is satisfied, so that the network restricted to \({\mathcal {C}}\) (i.e. suppressing all \({{\mathcal {C}}}'\)-products of reactions with reactant in \({\mathcal {C}}\)) is autocatalytic, but \({{\mathcal {C}}}'\) contains no irreversible reaction, hence is not autocatalytic. Then the network (as proved in Sect. 5) is already strongly autocatalytic in itself.
For irreducible networks, Eq. (56) yields an explicit but technical expression for \(\alpha _{max}\) in the zero concentration limit, see (16) in the above Theorem; namely, if all \(\alpha _i< \alpha _{max}\), then \(\lambda ^0_{max}>0\). On the other hand, we do not obtain an explicit expression for \(\alpha _{max}\) for \([A]\not =0\) small (shifting interest from \(\lambda ^0_{max}\) to \(\lambda _{max}([A])\)), nor for \(K_{max}\) in the reducible case, since these are treated by spectral perturbation, which makes explicit bounds difficult.
3 A motivating example: the simplest autocatalytic core
We treat in this section the simplest type I autocatalytic core in the classification of Blokhuis et al. (2020). It involves two chemostatted species \((A,A')\), which may be thought of as a redox or energy carrier (ATP/ADP) couple, or as fuel and waste (Esposito 2019); two dynamical species \((B,B_1)\); and two reactions
Autocatalysis is made possible by the duplication reaction \(B_1 \overset{\nu _+}{\rightarrow } 2B+A'\). We also include degradation reactions
The degradationless diluted regime which is the main topic of the article is defined by
-
(i)
(low concentrations) \([B],[B_1]\ll 1\). Kinetic equations lack any reference concentration or volume to produce adimensional quantities, and chemostatted quantities \([A],[A']\) are not limited, so (by rescaling of the concentrations) this criterion is equivalent to
$$\begin{aligned} \nu _-[B]\ll 1. \end{aligned}$$(19)In other words, the reverse of the duplication reaction is rate-limited.
-
(ii)
(no degradation) \(a_0,a_1=0\). Our analysis actually extends (by perturbation) to low enough degradation rates,
$$\begin{aligned} a_0,a_1\ll 1. \end{aligned}$$(20)
Kinetic equations are:
When \(\nu _-=0\), these equations are linear, otherwise we linearize around \(([B],[B_1])\), and find the system
where \((B,B_1)\) is an infinitesimal variation around \(([B],[B_1])\) , and
Note that off-diagonal elements of M are \(> 0\), so that, by the Perron-Frobenius theorem, the spectrum of M consists of two complex numbers \(\lambda _{max}(M),\lambda _{min}(M)\) with \(\lambda _{max}(M)\) real, and \(\lambda _{max}(M)>\mathrm{Re\ }\lambda _{min}(M)\). Furthermore, M has an eigenvector for the eigenvalue \(\lambda _{max}(M)\) with positive coefficients. Write \(M=\left[ \begin{array}{cc} -a &{} b \\ c &{} -d \end{array} \right] \). Explicit computations actually produce two real numbers,
and \(\lambda _{min}(M)= {1\over 2}\Big (-(a+d)- \sqrt{(a-d)^2+ 4bc}\Big )\).
Lemma 3.1
(see Sarkar and England (2019)) Let \(M=\left[ \begin{array}{cc} -a &{} b \\ c &{} -d \end{array} \right] \) \((a,b,c,d>0)\) and \(\lambda _{max}=\lambda _{max}(M)\) the eigenvalue of M with largest real part. Then the following alternative holds,
-
(i)
If \(\det (M)= ad-bc<0\), then \(\lambda _{max}>0\);
-
(ii)
if \(\det (M)=0\), then \(\lambda _{max}=0\);
-
(iii)
if \(\det (M)>0\), then \(\lambda _{max}<0\).
Autocatalysis is then equivalent to the condition \(\det (M)<0\). We now check that, in the degradationless diluted regime defined by (19), (20),
Going beyond this particular regime, autocatalysis is not the rule. Let us consider two specific cases:
-
(i)
(no reverse reaction) We neglect reverse reactions by setting \(k_{off}=0\) and \(\nu _-=0\). Then
$$\begin{aligned} \det (M)=-2k_{on}[A] \nu _+ + (k_{on}[A]+ a_0)( \nu _+ + a_1) <0 \end{aligned}$$(27)if and only if (see King’s criterion (King 1982)) the product of the specificities of positively oriented reactions along the replication cycle \(B\rightarrow B_1\rightarrow 2B\) is larger than \({1\over 2}\),
$$\begin{aligned} \frac{k_{on}[A]}{k_{on}[A]+a_0} \frac{\nu _+}{\nu _++a_1}>{1\over 2}. \end{aligned}$$(28) -
(ii)
(no degradation) We assume here that \(a_0=a_1=0\). Then
$$\begin{aligned} \det (M)=-k_{on} [A] \nu _+ + 2k_{off} \nu _- [A'][B] <0 \end{aligned}$$(29)if and only if
$$\begin{aligned}{}[B]< [B]_{max}:= \frac{k_{on}[A]}{k_{off}} \, \times \, \frac{\nu _+}{2\nu _-[A']},\end{aligned}$$(30)or equivalently,
$$\begin{aligned} \frac{k_{on}[A]}{k_{off}} \, \times \, \frac{\nu _+}{2\nu _-[A'][B]}>1, \end{aligned}$$(31)a criterion somewhat analogous to King’s criterion, but featuring the ratio (product of forward reaction rates)/(product of reverse reaction rates).
4 (Top) characterizes stoechiometric autocatalysis in diluted networks
We prove in this section Theorem 2.1 for diluted networks (see Sects. 2.1 and 2.4 for a definition). We recall that reverse reactions, i.e. reactions involving \(>1\) reactants are not included in \({\mathbb {S}}\). Degradation reactions are also not taken into account. We must prove that (Top) implies the existence of a reaction vector \(c\in \mathbb {R}^N\) such that \({{\mathbb {S}}}c>0\). Equivalently, asumming (Top), one may choose an orientation for all \(1-1\) reactions and a positive reaction vector \(c\in (\mathbb {R}_+)^{N}\) such that \({\mathbb {S}}c>0\).
The main concept is this section is the following.
Definition 4.1
(Split reactions) Split reactions of a reaction network with stoechiometric matrix \({\mathbb {S}}\) are \(1-1\) reactions \(A\rightarrow B\) which either are reversible \(1-1\) reactions belonging to the reaction network, or come from an irreversible one-to-several reaction of the form
Split reactions form the edges of a graph which is (by construction) the adjacency graph \(G({{\mathbb {S}}})\), see Definition 2.1. Thus we preferably speak about split graph in this section instead of adjacency graph, but the two actually coincide. The split graph corresponds mathematically and graphically to the linearization of the kinetic network in the zero concentration limit. It may be defined topologically as follows: (direct) reactions of the type \(A\rightarrow s_1 B_1 + \ldots + s_n B_n\) \((n\ge 1, s_1,\ldots ,s_n\in \mathbb {N}^*)\) such that \(s_1+\ldots +s_n\ge 2\), i.e. with \(>1\) products, are totally irreversible in the limit of vanishing concentrations, therefore they contribute to \(G({{\mathbb {S}}})\) irreversible arrows
upon splitting the reaction into reactions with unique products. On the other hand, forward reactions of the type \(A\rightarrow B\) with only one product are reversible; therefore, they contribute to \(G({{\mathbb {S}}})\) reversible arrows \(A\leftrightarrows B\). In case of multiple arrows \(A\rightarrow B\), we only keep one, in order not to have multiple edges from A to B. This happens if there are several competing irreversible reactions \(A\rightarrow s B+ s_2 B_2+\ldots + s_n B_n\), \(A\rightarrow s'B+ s'_2 B'_2+\ldots +s'_{n'} B'_{n'}\), or if irreversible reactions \(A\rightarrow sB+\cdots \) and a reversible reaction \(A\leftrightarrows B\) coexist. We always assume that \(G({{\mathbb {S}}})\) is connected (otherwise one can reduce the analysis to each of the subsystems defined by the connected components).
Having a graph instead of a hypergraph with pitchforks connecting several reactants and several products (see below, and examples in Sects. 5.1 and 5.2) is a major simplification. To be precise, we note that \(G({{\mathbb {S}}})\) is sometimes not quite enough to caracterize stoechiometric autocatalysis: in case an irreversible reaction \(A\rightarrow sB+\cdots \) and the reversible reaction \(A\leftrightarrows B\) coexist (so that A and B are in the same class \({{\mathcal {C}}}\), see below), the graph \(G({{\mathbb {S}}})\) by itself does not keep track of the existence of the irreversible reaction. Then we keep the memory of the irreversible transition \(A\rightarrow B\) by saying that \({{\mathcal {C}}}\) contains an internal irreversible reaction. In case \(A\rightarrow B+\cdots \) is not in competition with a reversible reaction, but A and B are in the same class thanks to the presence of an irreversible reaction \(B\rightarrow A+\cdots \), both split reactions \(A\rightarrow B\) and \(B\rightarrow A\) are considered as internal irreversible reactions. A simple way to summarize these rules is to decide that reversible arrows are painted blue, irreversible arrows are painted red, and red prevails. Thus we get a graph with two-colored edges. This is sometimes useful, but still not enough to define our topological condition (Top) when the graph is not irreducible (see Sect. 2.4). Classes are defined below without taking the color of the arrows into account.
Classes. Upon linearizing the time-evolution equations, while neglecting reverse reactions, one obtains a generalized Markov matrix (see Suppl. Info.) M with graph \(G({{\mathbb {S}}})\). This justifies resorting to the usual description of G in terms of communicating classes, connected by irreversible arrows. Arrows define a partial order of classes, with \({{\mathcal {C}}'}>{{\mathcal {C}}}\) if there is a path from \({{\mathcal {C}}}\) to \({{\mathcal {C}}}'\), i.e. if \({{\mathcal {C}}}'\) is downstream of \({{\mathcal {C}}}\). In Suppl. Info. (Sect. 7.5), the reader will find several examples worked out in details: cores of type I and III,

and the "\(A_1 A_2 A_3 \longrightarrow B_1 B_2 B_3\)" autocatalytic kinetic reaction network, and its graph \(G_{(123)\rightarrow (1'2'3')}\), where \((A_1,A_2,A_3)\), resp. \((B_1,B_2,B_3)\) are encoded by indices (1, 2, 3), resp. \((1',2',3')\):

Note that the stoechiometry is not indicated, nor is it important in the analysis that follows, once understood that irreversible arrows come from splitting reactions with \(>1\) products. As a matter of fact, Type (I) cores (\(B_0,\ldots ,B_n)\) have originally a "pitchfork" reaction \(B_n\rightarrow 2B_0\)

Type (III) cores, involving species \(A_i\), \(i=0,\ldots ,n\), \(B'_{i'}\), \(i'=0',\ldots ,n'\), \(B''_{i''}\), \(i''=0'',\ldots ,n''\), have originally a pitchfork

Only one-sided arrows indicate the location of the original hypergraph pitchforks. The one-sided arrow \(n\rightarrow 0\) in (I) indicates any reaction \(B_n\rightarrow m B_0\) with \(m=2,3,\ldots \). The one-sided arrows \(A_n\rightarrow B''_{0''}, A_n\rightarrow B'_{0'}\) come either from \(A_n\rightarrow s'' B''_{0''}+s'B'_{0'}\), \(s',s''=1,2,\ldots \) or from \((A_n\rightarrow m'' B''_{0''}, A_n\rightarrow m' B'_{0'})\), \(m',m''=2,3,\ldots \), or from a combination of these.
All cores are irreducible. The "\(A_1 A_2 A_3 \longrightarrow B_1 B_2 B_3\)" network, on the other hand, has two classes, \({{\mathcal {C}}}=(1,2,3)\) and \({{\mathcal {C}}}'=(1',2',3')\), with \({{\mathcal {C}}}'\) downstream of \({{\mathcal {C}}}\). The partial ordering defines in particular minimal (upstream) and maximal (downstream) classes; here, \({{\mathcal {C}}}\) is minimal, and \({{\mathcal {C}}}'\) is maximal.
Proof of Theorem 2.1
We prove in the rest of the section that (Top) implies stoechiometric autocatalysis.
Stoechiometric autocatalysis, at least in the case of an irreducible network, can be proven quite simply by playing directly with the columns of the stoechiometric matrix \({{\mathbb {S}}}\); see Suppl. Info. Sect. 7.3. Instead, we provide here a general demonstration using properties of \(G({{\mathbb {S}}})\). Though a little more involved, it has the advantage of exploiting the properties of an underlying auxiliary Markov chain, which will also play a major role in Sect. 5. Also, the proof yields easily explicit choices of positive reaction vectors c for which \({{\mathbb {S}}}c>0\); this is done in a simple example below, see (40). In the case of a reducible network, arguments rely on the class decomposition of the graph \(G({{\mathbb {S}}})\).
We have already proved in the Introduction that (Top) is necessary for a diluted network to be autocatalytic. So the interesting part is to show that (Top) is a sufficient condition for autocatalysis. We split the proof into several points. The general idea is to construct an explicit reaction vector c which depends on the choice of a kinetic rate for each reaction, and is a perturbation of the stationary flow vector for an auxiliary Markov chain.
The chemical balance for species \(A_k\) associated to a reaction \({{\mathcal {R}}}\ :\, s_1 A_{i_1}+ \ldots + s_n A_{i_n}\rightarrow s'_1 A_{i'_1}+\ldots +s'_{n'} A_{i'_{n'}}\) will be denoted \(\delta _{{\mathcal {R}}}[A_k]= -\sum _j s_j\delta _{k,i_j} + \sum _{j'} s'_{j'} \delta _{k,i'_{j'}}\). Then the total chemical balance for species \(A_k\) associated to the combination of reactions represented by the reaction vector c is \(\delta [A_k]=\sum _{{\mathcal {R}}} c_{{\mathcal {R}}}\, \delta _{{\mathcal {R}}}[A_k]\).
A. (stationary flows for split graph). Theorem 2.1 is obtained by perturbation from the following remark. One can define an auxiliary Markov chain \((\tilde{X}(t))_{t\ge 0}\) (a conventional, continuous-time Markov chain, i.e. with vanishing killing rates) with transition rates \(\tilde{k}_{i\rightarrow j}\) obtained by superposing the following transitions:
-
(i)
Reversible transitions with rates \(k_{i\rightarrow j}, k_{j\rightarrow i}\) are associated to 1–1 reactions of the type \({{\mathcal {R}}}_{i\rightarrow j}:\ \ A_i \overset{k_{i\rightarrow j}}{\rightarrow } A_j, \ {{\mathcal {R}}}_{j\rightarrow i}:\ \ A_j \overset{k_{j\rightarrow i}}{\rightarrow } A_i\);
-
(ii)
Irreversible transitions with rates \(s_j k_i^+\)are associated to split irreversible 1–1 reactions \(\tilde{{\mathcal {R}}}: \ \ A_i \overset{s_j k^+_{i}}{\rightarrow } A_j\), \(j=i_1,\ldots ,i_n\) coming from the one-to-several irreversible reaction \(A_i\overset{k_i^+}{\rightarrow } s_{i_1} A_{i_1}+\ldots +s_{i_n} A_{i_n}\).
The associated adjoint Markov generator is obtained by summing matrices with only two non-vanishing coefficients as on p.9; then the sum of coefficients on any column is zero, which ensures probability preservation. In other words, \(\tilde{k}_{i\rightarrow j}=\sum _{{{\mathcal {R}}}\, :\, A_i\rightarrow A_j} \tilde{k}_{i\rightarrow j}(\tilde{{\mathcal {R}}})\), where, depending on the split reaction \(\tilde{{\mathcal {R}}}\, :\, A_i\rightarrow A_j\), one has defined: \(\tilde{k}_{i\rightarrow j}(\tilde{{\mathcal {R}}})=k_{i\rightarrow j}\) (one-to-one reaction) or \(s_j k^+_i\) (split forward reaction \(A_i\rightarrow A_j\) coming from a one-to-several reaction \(A_i\rightarrow s_j A_j+\cdots \)) or 0 (excluded reverse reaction).
Assume the graph \(G({{\mathbb {S}}})\) is irreducible. Then the auxiliary Markov chain \((\tilde{X}(t))_{t\ge 0}\) is irreducible; it reproduces correctly the transition rates of the kinetic network from \(A_i\) to \(A_{i_{\ell }}\) for irreversible transitions (ii), but increases the exit rate from \(A_i\), since \(\frac{d[A_i]}{dt}= -sk_i^+ [A_i]\) (by probability conservation) with \(s=\sum _{\ell } s_{i_{\ell }}\ge 2\) for the Markov chain, as compared to \(\frac{d[A_i]}{dt}=-k_i^+[A_i]\) for the kinetic network. The auxiliary Markov chain admits exactly one stationary probability measure \(\mu =(\mu _i)_{i=1,\ldots ,|{{\mathcal {S}}}|}\). Define \(\tilde{c}_{i\rightarrow j}(\tilde{{\mathcal {R}}}):= {\left\{ \begin{array}{ll} \mu _i \tilde{k}_{i\rightarrow j}(\tilde{{\mathcal {R}}}) \qquad {\mathrm {if}}\ \tilde{{\mathcal {R}}}\, :\, i\rightarrow j \\ 0 \qquad {\mathrm {else}} \end{array}\right. }\), and let \(\tilde{c}_{i\rightarrow j}=\sum _{\tilde{{\mathcal {R}}}\, :\, i\rightarrow j} \tilde{c}_{i\rightarrow j}(\tilde{{\mathcal {R}}})= \mu _i \tilde{k}_{i\rightarrow j} \) be the stationary flow along the edges. Then the antisymmetrized quantity \(\tilde{J}_{i\rightarrow j}:= \sum _{\tilde{{\mathcal {R}}}} \tilde{J}_{i\rightarrow j}(\tilde{{\mathcal {R}}})\equiv \sum _{\tilde{{\mathcal {R}}}} \Big \{\tilde{c}_{i\rightarrow j}(\tilde{{\mathcal {R}}})- \tilde{c}_{j\rightarrow i}(\tilde{{\mathcal {R}}})\Big \}=\tilde{c}_{i\rightarrow j} - \tilde{c}_{j\rightarrow i}\) is the associated current, and the total current for species i vanishes by stationarity, i.e. hence
Choice of the reaction vector c. Going back to the initial network, we now define \(c({{\mathcal {R}}}):=\tilde{c}_{i\rightarrow j}({{\mathcal {R}}})=\mu _i k_{i\rightarrow j}\) for the reversible one-to-one reaction \({{\mathcal {R}}}\, :\, A_i\overset{k_{i\rightarrow j}}{\rightarrow } A_j\), and \(c({{\mathcal {R}}}):=\mu _i k_i^+\) for the irreversible one-to-several reaction \({{\mathcal {R}}}\, :\, A_i \overset{k_i^+}{\rightarrow } s_{i_1}A_{i_1}+\ldots +s_{i_n}A_{i_n}\). Note that (for convenience) we have chosen to accept both orientations for reversible 1–1 reactions; this is equivalent to choosing an orientation for each of them and letting \(c({{\mathcal {R}}}_{(i,j)}):=c({{\mathcal {R}}}_{i\rightarrow j})-c({{\mathcal {R}}}_{j\rightarrow i})\) (the orientation may be chosen in such a way that \(c({{\mathcal {R}}}_{(i,j)})\ge 0\)). The chemical balance \(\delta [A_i]:=({{\mathbb {S}}}c)_i\) for species i is obtained by summing
for a reversible one-to-one reaction \({{\mathcal {R}}}\) connecting i and j,
for the reactant of a one-to-several reaction \({{\mathcal {R}}}\, :\, A_i\rightarrow \cdots \), and
for products of a one-to-several reaction \({{\mathcal {R}}}\,:\, A_j\rightarrow s_i A_i+\cdots \), split into several 1–1 reactions including \(\tilde{{\mathcal {R}}}\, :\, A_j\rightarrow s_i A_i\). By construction, we obtain
if species i is not the reactant of a one-to-several reaction; thus, in that case, \(\delta [A_i]=0\). If, on the other hand, i is the reactant of a one-to-several reaction \(A_i \overset{k_i^+}{\rightarrow } s_{i_1}A_{i_1}+\ldots +s_{i_n}A_{i_n}\) with associated split reactions \(\tilde{{\mathcal {R}}}_{i,i_{\ell }}\, :\, A_i \rightarrow A_{i_{\ell }}\), then the associated balance for \([A_i]\) is
with \(s=\sum _{\ell } s_{i_{\ell }}>1. \) Comparing with the above stationarity Eq. (34), we may conclude: our choice for the vector c yields a strictly positive balance for reactants of a one-to-several reaction, and zero balance for all other species.
Remark
If the graph is over-connected, i.e. if reversible 1–1, or one-to-several irreversible, reactions can be removed without breaking irreducibility, then the auxiliary Markov chain may be defined while leaving them out, yielding another simpler set of coefficients \(c_{{\mathcal {R}}}\) that vanish for left-out reactions.
B. (irreducible networks). The reaction vector c constructed in A. is not quite satisfactory yet. We now turn to a perturbation argument for irreducible networks, ensuring that there exist vectors \(\delta c^q=\left( \begin{array}{c} (\delta c^q)_{{{\mathcal {R}}}_1} \\ \vdots \\ (\delta c^q)_{{{\mathcal {R}}}_N} \end{array}\right) \), \(q=1,2,\ldots \) vanishing for q large enough such that \({{\mathbb {S}}} (c+\sum _{q\ge 1}\varepsilon ^q \delta c^q)>0\) for all small enough \(\varepsilon >0\). By hypothesis, there exists at least one irreversible reaction. Choose one, \({{\mathcal {R}}}_0:A_0 \overset{k_0^+}{\rightarrow } s_{i_1}A_{i_1}+\ldots +s_{i_n}A_{i_n}\), and define \(c\equiv c(\mu )\) as in the previous paragraph, \(\mu \) being the stationary probability measure for \(\tilde{X}\). Since the balance for \([A_0]\) is \(>0\), we can tilt \(\mu \) by a small amount in direction 0, i.e. replace \(\mu _0\) by \(\mu _0+\varepsilon \), while keeping \(\delta [A_0]>0\). This is equivalent to saying that \(c \rightsquigarrow c+\varepsilon \delta c^1\), with \(\delta c^1({{\mathcal {R}}}_0)=k_0^+\), yielding \((c+\varepsilon \delta c^1)({{\mathcal {R}}}_0)=(\mu _0+\varepsilon )k_0^+\); similarly, \(\delta c^1({{\mathcal {R}}})=k_{0\rightarrow j}\), resp. \((k'_0)^+\) for all other possible reactions \(A_0\overset{k_{0\rightarrow j}}{\rightarrow } A_j\) or \(A_0 \overset{(k'_0)^+}{\rightarrow } s'_{i'_1}A_{i'_1}+\ldots + s'_{i'_{n'}} A'_{i'_{n'}}\) with reactant \(A_0\); and \(\delta c^1({{\mathcal {R}}}')=0\) for all other reactions. But then \(\delta [A_{i_{\ell }}]\) is shifted by \(+ \varepsilon s_{i_{\ell }} k_0^+\), and possibly other positive coefficients \((+\varepsilon k_{0\rightarrow i_{\ell }}\) or \(+\varepsilon s'_{i_{\ell }} (k'_0)^+)\), so the balance for species 0 and for all products of \({{\mathcal {R}}}_0\) is now \(>0\); more precisely, \(\delta [A_0]\) is of order \(\varepsilon ^0\), while \(\delta [A_{i_{\ell }}]\), \(\ell =1,\ldots ,n\)—and similarly, the balance for all products of reactions with reactant \(A_0\)—are of order \(\varepsilon ^1\).
We now let \({{\mathcal {S}}}_0:=\{0\}\), define \({{\mathcal {S}}}_1\subset {{\mathcal {S}}}\) to be made up of 0, together with all products of reactions having 0 as reactant, and consider products of reactions having as reactant one of the elements of the set \({{\mathcal {S}}}_1\setminus {{\mathcal {S}}}_0\). Since the graph is irreducible, the corresponding set of reactions can be empty only if \({{\mathcal {S}}}_1={{\mathcal {S}}}\). If this is not the case, tilt \(\mu \) by a small uniform amount in all directions indexed by the set \({{\mathcal {S}}}_1\setminus {{\mathcal {S}}}_0\), i.e. replace \(\mu _i\) by \(\mu _i+\varepsilon ^2\) for all \(i\in {{\mathcal {S}}}_1\setminus {{\mathcal {S}}}_0\). For convenience, we reindex the set of species so that \({{\mathcal {S}}}_1\setminus {{\mathcal {S}}}_0=\{1,\ldots \}\). Choosing one of the above reactions, either one-to-several \({{\mathcal {R}}}_1: A_1 \overset{k_1^+}{\rightarrow } s_{i_1} A_{i_1}+\ldots +s_{i_n}A_{i_n}\) or one-to-one, \({{\mathcal {R}}}_{1\rightarrow j}:A_i \overset{k_{i\rightarrow j}}{\rightarrow } A_j\), this is equivalent to saying that \(c\rightsquigarrow c+\varepsilon \delta c^1+\varepsilon ^2 \delta c^2\), with \(\delta c^2({{\mathcal {R}}}_1)=k_1^+\), resp. \(\delta c^2({{\mathcal {R}}}_{1\rightarrow j})=k_{1\rightarrow j}\). We thus shift \(\delta [A_i]\), \(i\in {{\mathcal {S}}}_1\setminus {{\mathcal {S}}}_0\), by \(-O(\varepsilon ^2)\), and simultaneously \(\delta [A_{i'}]\) (\(i'\) ranging in the set of products of reactions having as reactant one of the elements of \({{\mathcal {S}}}_1\setminus {{\mathcal {S}}}_0\), including possibly species in \({{\mathcal {S}}}_1\)) by \(+O(\varepsilon ^2)\). The \(\delta [A_i]\) were of order \(\varepsilon ^0\), resp. \(\varepsilon ^1\) at previous step for \(i\in {{\mathcal {S}}}^0\), resp. \({{\mathcal {S}}}^1\setminus {{\mathcal {S}}}^0\); the \(\varepsilon ^2\)-corrections do not change these orders, but ensure that now \(\delta [A_i]\), \(i\in {{\mathcal {S}}}_2\setminus {{\mathcal {S}}}_1\) are of order \(\varepsilon ^2\), where \({{\mathcal {S}}}_2\setminus {{\mathcal {S}}}_1\) is the set of new products. We stop the induction in q as soon as we have exhausted all species, i.e. the maximum index q is the minimum index such that \({{\mathcal {S}}}_q={{\mathcal {S}}}\).
A simple example. Consider the network with species \(A_0,A_1,A_2\), reversible 1–1 reactions \(A_0\leftrightarrows A_2\) and \(A_1\leftrightarrows A_2\), and a single irreversible one-to-several reaction \({{\mathcal {R}}}_0\, :\, A_0\rightarrow A_1+A_2\) with \(s=2\). The graph is

following the convention that "red prevails". The network is irreducible. Choose all rates to be equal to 1. Then the adjoint Markov generator of the auxiliary chain is
Stationary measures are multiples of \(\mu :=\left( \begin{array}{c} 1 \\ 4 \\ 3 \end{array}\right) \). Stationary flows are \(\tilde{c}_{0\rightarrow 1}=1,\tilde{c}_{0\rightarrow 2}=2; \ \tilde{c}_{1\rightarrow 0}=0,\tilde{c}_{1\rightarrow 2}=4; \ \tilde{c}_{2\rightarrow 0}=3,\tilde{c}_{2\rightarrow 1}=3\), and then stationary currents are \(\tilde{J}_{0\rightarrow 1}=1, \tilde{J}_{0\rightarrow 2}=-1, \tilde{J}_{1\rightarrow 2}=1\). Following our construction, we choose for reaction vector c with \(c({{\mathcal {R}}}_0)=1\) and \(c({{\mathcal {R}}}_{0\rightarrow 2})=1,c({{\mathcal {R}}}_{2\rightarrow 0})=3, c({{\mathcal {R}}}_{1\rightarrow 2})=4,c({{\mathcal {R}}}_{2\rightarrow 1})=3\). Then
similarly, \(\delta [A_2]=0\); and \(\delta [A_0]=-c({{\mathcal {R}}}_0)-c({{\mathcal {R}}}_{0\rightarrow 2}) + c({{\mathcal {R}}}_{2\rightarrow 0})=1\), which can be identified with \((s-1)\mu _0 k_0^+\) using the notations of the proof. We perturb it by a one-step construction since \({{\mathcal {S}}}_1=\{0,1,2\}\): we replace c by \(c+\varepsilon \delta c^1\) with \(\delta c^1({{\mathcal {R}}}_0)=\delta c^1({{\mathcal {R}}}_{0\rightarrow 1})=\delta c^1({{\mathcal {R}}}_{0\rightarrow 2})\). Thus the perturbed balance \(\delta [A_0]=1-\varepsilon , \delta [A_1]=+\varepsilon , \delta [A_2]=+2\varepsilon \) is \(>0\) for all species as soon as \(0<\varepsilon <1\).
C. (reducible networks). We must finally adapt the above argument to the case of a reducible network. To have a picture in mind, the reader may think of the "contracted graph"

of the “\(A_1 A_2 A_3 \longrightarrow B_1 B_2 B_3\)” network (see Sect. 7.5), or, for a more general example,

In both examples here, there is a unique minimal class, \({{\mathcal {C}}}\), and a unique maximal class, \({{\mathcal {C}}}'\). Note that arrows go downwards, defining a probability flow from minimal classes to maximal classes. We define the height \(h({{\mathcal {C}}}'')\) of a class \({{\mathcal {C}}}''\) to be the minimal distance on the contracted graph from a minimal class to it. Here e.g. \(h({{\mathcal {C}}})=0,h({{\mathcal {C}}}')=1\) on our first example, and \(h({{\mathcal {C}}})=0, h({{\mathcal {C}}}_1)=h({{\mathcal {C}}}_2)=1,h({{\mathcal {C}}}')=2\) on our second example. Our proof is by induction on the maximal height \(h_{max}\). The case \(h_{max}=0\) has been solved in B., so we assume \(h_{max}\ge 1\).
The argument goes as follows. Consider a minimal class \({{\mathcal {C}}}\) connected downwards to \({{\mathcal {C}}}_1, \ldots ,{{\mathcal {C}}}_m\). A reaction \({{\mathcal {R}}}\) is internal to \({{\mathcal {C}}}\) if its reactant and all its products belong to \({{\mathcal {C}}}\); one then writes \({{\mathcal {R}}}: {{\mathcal {C}}}\rightarrow {{\mathcal {C}}}\). On the other hand, irreversible arrows from \({{\mathcal {C}}}\) to \({{\mathcal {C}}}_i\) represent split irreversible reactions \(\tilde{{\mathcal {R}}}\,:\, A\rightarrow A_i\) with \(A\in {{\mathcal {C}}}\) and \(A_i\in {{\mathcal {C}}}_i\), coming from the linearization of a one-to-several reaction \({{\mathcal {R}}}\, :\, A\rightarrow s_1 A'_1+\ldots + s_n A'_n\). There are two cases:
-
(i)
(purely external reaction) either \(A'_i,i=1,\ldots ,n\) all belong to \(\uplus _{j=1}^m {{\mathcal {C}}}_j\), so that all split reactions \(\tilde{{\mathcal {R}}}\, :\, A \rightarrow A'_i\) are external;
-
(ii)
(mixed reaction) or one of the \(A'_i\) belongs to \({{\mathcal {C}}}\), so that \(\tilde{{\mathcal {R}}}\, :\, A\rightarrow A'_i\) is an internal irreversible reaction of \({{\mathcal {C}}}\).
The second case is called a mixed case because some of the \(A'_i\) belong to \({{\mathcal {C}}}\), and some do not, hence the one-to-several reaction \({{\mathcal {R}}}\) is neither internal nor external. Now, if there is no mixed reaction with reactant in \({{\mathcal {C}}}\), we can extract from the set of reactions those which are internal to \({{\mathcal {C}}}\), and build the \({{\mathcal {C}}}\)-valued auxiliary Markov chain \((\tilde{X}_{{{\mathcal {C}}}}(t))_{t\ge 0}\) as in A. with set of transitions associated to those internal reactions. The construction in A. and B. yields a positive vector \(c_{{{\mathcal {C}}}}=(c_{{\mathcal {R}}})_{{{\mathcal {R}}}\, :\, {{\mathcal {C}}} \rightarrow {{\mathcal {C}}}}\) such that the associated chemical balance for all species in \({{\mathcal {C}}}\) is \(>0\).
Considering now the case of a mixed reaction \({{\mathcal {R}}} \, :\, A\rightarrow s_1 A'_1+\ldots +s_n A'_n\) with \(A'_1,\ldots ,A'_{n'}\in {{\mathcal {C}}}, (A'_{\ell })_{\ell >n'}\in \uplus _{j=1}^m {{\mathcal {C}}}_j\), we split it for our purposes into a truncated internal reaction \({{\mathcal {R}}}_{{{\mathcal {C}}}} \, :\, A\rightarrow s_1 A'_1+\ldots +s_{n'} A'_{n'}\), and \(n-n'\) external split reactions \(\tilde{{\mathcal {R}}}\, :\, A\rightarrow A'_i\), \(i=n'+1,\ldots ,n\). Joining truncated internal reactions \({{\mathcal {R}}}_{{{\mathcal {C}}}}\) to the set of internal reactions, one proceeds as in the previous paragraph, and obtains a positive vector \(c_{{{\mathcal {C}}}}=(c({{\mathcal {R}}}))_{{{\mathcal {R}}}\, :\, {{\mathcal {C}}}\rightarrow {{\mathcal {C}}}}\), where now \( {{\mathcal {R}}}\, :\, {{\mathcal {C}}}\rightarrow {{\mathcal {C}}}\) represents the set of all (truncated or not) reactions internal to \({\mathcal {C}}\), such that the associated chemical balance for all species in \({{\mathcal {C}}}\) is \(>0\).
We proceed similarly for all minimal classes.
Consider now a height 1 class \({{\mathcal {C}}}_1\). Start as in the previous paragraph by constructing a \({{\mathcal {C}}}_1\)-valued auxiliary Markov chain with set of transitions associated to the (truncated or not) reactions internal to \({{\mathcal {C}}}_1\). Proceed similarly for all classes of height 1. Using the construction in A. and coupling with the height 0 class reaction vectors obtained in the previous step, one obtains a reaction vector \(c=(c_0,c_1)\) such that \(c_0({{\mathcal {R}}})>0\), resp. \(c_1({{\mathcal {R}}}) >0\) iff \({{\mathcal {R}}}\) is (truncated or not) internal to a height 0, resp. 1 class, and the associated balance is \(>0\), resp. \(\ge 0\), for species belonging to height 0, resp. height 1 classes.
We now adapt the perturbation argument of B. First, if \({{\mathcal {R}}}\, :\, A\rightarrow \cdots \), A belonging to a minimal class \({\mathcal {C}}\), is of mixed type, we redefine \(c( {{\mathcal {R}}})=c_{{{\mathcal {C}}}}({{\mathcal {R}}}_{{{\mathcal {C}}}})\). Choosing a class \({{\mathcal {C}}}'\) of height 1, we now explain how to obtain a strictly positive balance for species in \({{\mathcal {C}}}'\). There are two cases:
-
(i)
(purely external case) Assume that all reactions \({{\mathcal {R}}}\, :\, A\rightarrow s' A'+\cdots \), such that \(A'\in {{\mathcal {C}}}'\) and A in a class of height 0, are purely external, so none of these have been taken into account previously in the auxiliary Markov chains. The balance associated to such reactions is strictly negative for the reactant A, and strictly positive for products, including \(A'\). Choosing a small enough coefficient \(c({{\mathcal {R}}})\) for them, the net balance for height 0 species remains \(>0\), and we get a strictly positive balance for \(A'\).
-
(ii)
(mixed case) Assume there exists a mixed reaction \({{\mathcal {R}}}\, :\, A\rightarrow (s_1 A'_1+\ldots +s_{n'} A'_{n'}) + A'+ \cdots \), with \(A,A'_1,\ldots ,A'_{n'}\) in a height 0 class \({{\mathcal {C}}}\), and \(A'\in {{\mathcal {C}}}'\). This reaction has already been taken into account, by construction \(c_{{{\mathcal {C}}}}({{\mathcal {R}}}_{{{\mathcal {C}}}})>0\). Replacing the truncated internal reaction \({{\mathcal {R}}}_{{{\mathcal {C}}}}\) by \({{\mathcal {R}}}\) only increases the balance for external species, including \(A'\).
In both cases, one has obtained a positive balance for at least one species in each height 1 class, which can be considered as a local influx. One may now modify the construction in B. by simply using the local influx (instead of the positive balance due to an internal irreversible reaction) to perturb \(c_1\), and obtains a positive vector \(c'\) such that \(c'({{\mathcal {R}}})=c({{\mathcal {R}}})\) if the reactant of \({{\mathcal {R}}}\) belongs to a height 0 class, and the balance associated to \(c'\) is \(>0\) for species belonging to classes of height \(\le 1\).
Proceeding by induction on \(h\le h_{max}\) and using reactions connecting classes of height \(h-1\) to classes of height h, we get the result. \(\square \)
5 (Top) implies dynamical autocatalysis for dilute networks
We show here Theorem 2.2 (see Sects. 5.1, 5.2) from which we deduce by a simple argument spontaneous autocatalysis (i.e. exponential amplification of all species starting from an arbitrary initial condition with low concentrations) for irreducible networks and also some classes of reducible networks (see Sect. 5.3). We work in the zero concentration limit.
The following notations are used. Reversible 1–1 reactions (for which some arbitrary orientation is chosen) are denoted
Forward, irreversible split reactions coming from a reaction
are denoted
Combining all these reactions defines (see Sect. 4A.) an auxiliary Markov chain \((\tilde{X}(t))_{t\ge 0}\), whose adjoint generator we denote \(\tilde{M}\). On the other hand, the linearized time-evolution generator of the reaction network containing all reversible 1–1 reactions and forward, irreversible reactions (excluding possible degradation reactions) is called M. It is a generalized adjoint Markov generator; we shall use the path representation of resolvents of \(\tilde{M}\) and M introduced in Suppl. Info. (Sect. 7.5). M is actually shorthand for the zero concentration limit generator \(M([A]=0)\).
Choose a set of degradation rates \((\alpha _i)_{i\in {{\mathcal {S}}}}>0\)—we remind the reader that M itself involves by assumption no degradation reaction. Discrete-time transition rates are
for \(M_{\alpha }:=M-\alpha \), and similarly
for \(\tilde{M}_{\alpha }:=\tilde{M}-\alpha \).
The general purpose of this section is to prove that a diluted network satisfying the topological hypothesis (Top) is weakly dynamically autocatalytic, provided it is degradationless, or degradation reactions have small enough rates. Furthermore, we shall be able to prove strong dynamical autocatalysis in some cases, including the irreducible case.
5.1 Irreducible case
We first prove Theorem 2.2 (ii). We assume here that the split graph \(G({{\mathbb {S}}})\) is irreducible, and prove strong dynamical autocatalysis. Define M as above (or replace M by \(M-\beta \), where \((\beta _i)_{i\in {{\mathcal {S}}}}\) is a set of small enough degradation rates). For any \(\alpha \ge 0\), let \( R(\alpha )\) be its resolvent, with coefficients in \([0,+\infty ]\) given by the path representation (79); in Suppl. Info., it is proved that positivity of the Lyapunov exponent \(\lambda _{max}\) of M is equivalent to having
for some (or all) \(i,j\in {{\mathcal {S}}}\) and some \(\alpha >0\). Then this condition implies dynamical autocatalysis for degradation rates \(<\alpha \). In turn, Lemma 7.2 and the discussion below give quantitative criteria for spontaneous autocatalysis. So let us prove (47).
By hypothesis, there exists at least one forward irreversible reaction as in (43); reindexing, we assume that \(i=0\) and \(j_{\ell }=\ell ,\ell =1,\ldots ,n\). Choose a set of degradation rates \((\alpha _i)_{i\in {{\mathcal {S}}}}>0\), and call \(k_0^+\) the kinetic rate of a forward irreversible reaction with reactant \(A_0\). The generalized adjoint Markov generator \(M-\alpha \) and the adjoint sub-Markov generator \(\tilde{M}-\alpha \) have same off-diagonal coefficients, but diagonal coefficients of M are larger than those of \(\tilde{M}\). Namely (decomposing M into a sum of contributions by individual split reactions, see Sect. 7.4), \(M({{\mathcal {R}}})=\tilde{M}({{\mathcal {R}}})\) if \({{\mathcal {R}}}\) is reversible, while
for a forward irreversible reaction. Now
The inequality is strict for \(i=0\); more precisely, \(M_{0,0}-\tilde{M}_{0,0}\ge (\sum _{i=1}^n s_i-1) k_0^+ \ge k_0^+\). It follows: \(\tilde{w}(\alpha )_{i\rightarrow j}\le w(\alpha )_{i\rightarrow j}\), and in particular, \(\tilde{w}(\alpha )_{0\rightarrow j}<w(\alpha )_{0\rightarrow j}\) if \(j=1,\ldots ,n\). Actually, \(w(\alpha )_{0\rightarrow j} > \tilde{w}(0)_{0\rightarrow j} \ge \tilde{w}(\alpha )_{0\rightarrow j}\) provided \(k_0^+>\alpha _0\) (see (54) below for more details).
Then
where \(f(\alpha )_{0\rightarrow 0}\) is the total weight of excursions from 0 to 0, computed using transition rates \(w(\alpha )\), namely, \(f(\alpha )_{0\rightarrow 0}=\sum _{\ell \ge 1} \sum _{0=x_0\rightarrow x_1\rightarrow \cdots \rightarrow x_{\ell }\rightarrow 0=x_{\ell +1}} \prod _{k=0}^{\ell } w(\alpha )_{x_k\rightarrow x_{k+1}}\), where the sum is restricted to paths \((x_k)_{1\le k\le \ell }\) of length \(\ge 1\) in \({{\mathcal {S}}}\setminus \{0\}\). Summing over all possible first steps, we get
where \(f(\alpha )_{i\rightarrow 0}\) is the total weight of paths in \({{\mathcal {S}}}\setminus \{0\}\) issued from i, with a final additional step leading back to 0. In turn, using again the path representation, we see that \(f(\alpha )_{i\rightarrow 0}\) may be written as an infinite series whose coefficients are products of transition rates \(w(\alpha )\).
Similarly, one may define \(\tilde{f}(\alpha )_{0\rightarrow 0}= \sum _{i\not =0} \tilde{w}(\alpha )_{0\rightarrow i} \tilde{f}(\alpha )_{i\rightarrow 0}\), where \(\tilde{f}(\alpha )_{i\rightarrow 0}\) is the same sum as \(f(\alpha )_{i\rightarrow 0}\), but with transition rates \(w(\alpha )\) replaced by \(\tilde{w}(\alpha )\).
When \(\alpha =0\), \(\tilde{f}(0)_{0\rightarrow 0}\) is simply the probability for the true (i.e. probability-preserving) Markov chain \(\tilde{X}\) to get back to 0. Irreducible Markov chains with finite state space are recurrent, so \( \tilde{f}(0)_{0\rightarrow 0}=1\). Now \(w(\alpha )\ge \tilde{w}(\alpha )\) (implying \(f(\alpha )_{i\rightarrow 0}\ge \tilde{f}(\alpha )_{i\rightarrow 0})\) and \(w(\alpha )_{0\rightarrow i}> \tilde{w}(\alpha )_{0\rightarrow i}\), hence (by continuity w. r. to \(\alpha \)) \(f(\alpha )_{0\rightarrow 0}>1\) for \(\alpha >0\) small enough, implying
A quantitative criterion for autocatalysis. As proved above Eq. (50), the condition \(k_0^+>\alpha _0\) implies \(w(\alpha )_{0\rightarrow j}> \tilde{w}(0)_{0\rightarrow j}\). However, \(f(\alpha )_{i\rightarrow 0}\ge \tilde{f}(\alpha )_{i\rightarrow 0}\) but, depending on \(\alpha \), one may have \(f(\alpha )_{i\rightarrow 0}<\tilde{f}(0)_{i\rightarrow 0}\), so (see (51)) \(k_0^+>\alpha _0\) does not necessarily imply that \(f(\alpha )_{0\rightarrow 0}>\tilde{f}(0)_{0\rightarrow 0}=1\). To ensure autocatalysis, one needs to quantify the dependence of \(f(\alpha )\) or \(\tilde{f}(\alpha )\) on \(\alpha \), which is not as straightforward. As follows from Lemma 7.1 (i), \(\lambda _{max}(\alpha )>0\) if \(\lambda _{max}(\alpha ')>0\), where \(\alpha '=(\alpha '_i)_i\), and \( \alpha '_i=\alpha _{max}:=\max _j \alpha _j\) is for each i the maximum of the \(\alpha \)-coefficients. Thus we may assume that \(\alpha \) is a constant vector, \(\alpha =(\alpha _0,\cdots ,\alpha _0)\). Define the susceptibility \(\omega =(\omega _{ij})_{i\not =j}\) to be the derivative \(\omega _{ij}:= - \frac{\partial \tilde{f}(\alpha )_{i\rightarrow j}}{\partial \alpha }\Big |_{\alpha =0}\) where \(\alpha \) is a constant vector (equivalently, \(\omega _{ij} = -\sum _k \frac{\partial \tilde{f}(\alpha )_{i\rightarrow j}}{\partial \alpha _k}\Big |_{\alpha =0}\)); note that \(\omega _{ij}>0\). Taylor expanding to order 1 w.r. to \(\alpha \) around 0, we get
Then (see paragraph above Eq. (50))
(51), (53) and (54) together yield (using the identity \(\tilde{f}(0)_{0\rightarrow 0}=1\))
which is \(>1\), implying dynamical autocatalysis, as soon as
5.2 Reducible case
We prove here Theorem 2.2 (i).
5.2.1 Examples
We start with a one-parameter family of examples to show the variety of autocatalytic behaviors (see p. 13) . Let \({{\mathcal {C}}} = \{A_1,A_2\}\) and \({{\mathcal {C}}}'=\{B\}\) be two classes with probabilistic flow flowing from \({{\mathcal {C}}}\) into \({{\mathcal {C}}}'\), and (in the \((A_1,A_2,B)\)-basis) \(M := \left[ \begin{array}{ccc} -1 \quad &{} \quad 2 &{} \quad 0 \\ 1 \quad &{} -1-k \quad &{} 0 \\ 0 \quad &{} 1+k \quad &{} m-1 \end{array}\right] \) corresponding to the reaction network
with \(m > 0\); all kinetic rates, except for the last one, are equal to 1. This network satisfies (Top), hence is stoechiometrically autocatalytic, but its dynamical status turns out to depend on the kinetic rate k of the purely external reaction \(A_2\rightarrow B\) coupling \({{\mathcal {C}}}\) to \({{\mathcal {C}}}'\). Namely, the determinant of \( M\Big |_{{{\mathcal {C}}}}=\left[ \begin{array}{cc} -1 &{} 2 \\ 1 &{} -1 -k \end{array}\right] \) is \(k-1\), and its trace is \(<0\), implying that both its eigenvalues are \(<0\) if the coupling constant k is \(>1\). If, furthermore, \(m=1\) (i.e. \(M\Big |_{{{\mathcal {C}}}'}\) is not autocatalytic), then the Lyapunov exponent is 0. This is easily understandable: the purely external reaction \(A_2\rightarrow B\) acts as a degradation reaction for the system restricted to the minimal class \({\mathcal {C}}\), and k as a degradation rate.
Assuming a weaker degradation rate (\(k<1\)), the Lyapunov exponent becomes \(>0\). To keep computations simple, we let \(k=0\) (no degradation rate). Then the Lyapunov exponent of \(M\Big |_{{{\mathcal {C}}}}\) is \(\lambda _{max} :=\sqrt{2}-1\), and \(v_{{\mathcal {C}}} := \left[ \begin{array}{c} \sqrt{2} \\ 1\end{array}\right] \) is an associated positive eigenvector; that of \(M\Big |_{{{\mathcal {C}}}'}= \, [ m-1 \, ]\) is \(m-1\). The maximum (Lyapunov) eigenvalue of M is \(\max (\lambda _{max},m-1)\). There are three cases, depending on the spectral parameter m:
-
1.
if \(\lambda _{max} > m - 1\), then \(v_{{\mathcal {C}}}\) can be extended into a positive Lyapunov eigenvector for M, implying strong dynamical autocatalysis;
-
2.
if \(\lambda _{max} = m - 1\) (resonant case), then this is not possible (the associated Jordan block is not trivial). Instead, one gets the downstream Lyapunov eigenvector \(\left[ \begin{array}{c} 0 \\ 0 \\ 1 \end{array}\right] \). Thus dynamical autocatalysis holds only in the weak sense;
-
3.
if \(\lambda _{max} < m - 1\), then \(\left[ \begin{array}{c} 0 \\ 0 \\ 1 \end{array}\right] \) is again a downstream Lyapunov eigenvector, and dynamical autocatalysis holds only in the weak sense.
5.2.2 Proof of Theorem 2.2 (i)
Our proof of weak autocatalysis encompasses all cases without addressing such spectral considerations. It follows from our argument in Sect. 5.1 through an elementary perturbation argument. Namely, replace the above matrix M by \( M(\eta ,\varepsilon ) := M(\eta ) + \varepsilon J\), where \(\varepsilon > 0\) is a small parameter, J is an off-diagonal matrix with non-negative coefficients, and \(M(\eta ):= M_+ + \eta M_{ext}\), where \(\eta M_{ext}\) is the sum of the generators associated to purely external reactions; the parameter \(\eta >0\) determines the order of magnitude of the coupling between classes induced by purely external reactions. If J has enough nonzero coefficients, then \(M(\eta ,\varepsilon )\) will be irreducible. (Assuming all concentrations of all species are \(> 0\), this may e.g. be achieved by including also some split reverse reactions coming from reverse reactions \(s_1 A_{j_1}+s_2 A_{j_2}+\ldots +s_n A_{j_n} \overset{k_i^-}{\rightarrow } A_i\) connecting classes upwards,
with \(k^-_{j_{\ell }\rightarrow i}= k_i^- s_{j_{\ell }} [A_{j_{\ell }}]^{s_{\ell }-1} \ \prod _{\ell '\not =\ell } [A_{j_{\ell '}}]^{s_{\ell '}}\), see Sect. 7.4).
Now \(M(\eta ,\varepsilon )\) is an irreducible generalized Markov matrix. The Perron-Frobenius theorem implies that \(\lambda _{max}(\eta ,\varepsilon ) := \lambda _{max}(M(\eta ,\varepsilon ))\) has multiplicity 1, and that there exists a unique associated eigenvector \(v(\eta ,\varepsilon ) = (v_i(\eta ,\varepsilon ))_{i\in {{\mathcal {S}}}}\) such that \(v_i(\eta ,\varepsilon ) > 0\) for all i, and \(\sum _{i\in {{\mathcal {S}}}} v_i(\eta ,\varepsilon ) = 1\). Following the arguments in A. for \(M_+\), one sees that the addition of \(\eta M_{ext}\) and \(\varepsilon J\) modifies transition rates \(w(\alpha )\) only by \(O(\eta )+ O(\varepsilon )\), thus \(\lambda _{max}(\eta ,\varepsilon ) \ge \lambda > 0\) for some constant \(\lambda \) uniformly in \(\eta ,\varepsilon \) if \(\eta ,\varepsilon \) are small enough. Following the compacity argument in (Stewart and Sun 1990, Th. 6.10.), and assuming \(\eta \) to be small enough, one proves the existence of a limiting eigenvector \(v(\eta )\) such that
where \(v(\eta )\) is the limit of some subsequence \((v(\eta ,\varepsilon _k))_{k=1,2,\ldots }\) with \(\varepsilon _k\rightarrow 0\), and
By continuity, \(\sum _{i\in {{\mathcal {S}}}} v_i(\eta )= 1\) so that \(v(\eta )\) is normalized, but coefficients \(v_i(\eta ), i \in {{\mathcal {S}}}\) are only non-negative in general. Thus we have shown the following: the network with generator \(M(\eta )\) is weakly dynamically autocatalytic with Lyapunov eigenvalue \(\lambda _{max}(\eta )\), provided the coupling coefficient \(\eta \) is small enough.
5.2.3 Strong dynamical autocatalysis
Let us briefy discuss specific hypotheses (generalizing case 1. above) under which strong dynamical autocatalysis holds (for \(\eta \) small enough). First, the Perron block decomposition (see (Stewart and Sun 1990)) of M implies that its spectrum \(\Sigma (M)\) is the union of the spectra \( (\Sigma (M\Big |_{{\mathcal {C}}}))_{{\mathcal {C}}}\) of its restrictions to all classes \({\mathcal {C}}\). We assume (i) that there exists a minimal class \({\mathcal {C}}\) from which all classes can be attained from it following the probabilistic flow (i.e. following arrows downward); (ii) that \(\lambda _{max}(M\Big |_{{\mathcal {C}}})= \lambda _{max} := \max (\Sigma (M))>0\) is the maximum of all Lyapunov exponents of all classes, more precisely, \(\lambda _{max}(M\Big |_{{{\mathcal {C}}}'}) < \lambda _{max} \) for all \({{\mathcal {C}}}'\not ={{\mathcal {C}}}\). By the above compacity argument, there exists a nonzero eigenvector \(v\ge 0\) such that \(Mv = \lambda _{max}v\). Restricting to \({\mathcal {C}}\), we get a positive Lyapunov eigenvector \(v_{{\mathcal {C}}} = (v_i)_{i\in {{\mathcal {C}}}} > 0\) for \(M\Big |_{{\mathcal {C}}}\). Hypothesis (i) then implies that \(e^{tM}v > 0\) for all \(t > 0\). Now \(e^{tM}v = e^{t\lambda _{max}}v\), so that \(v > 0\) is positive, and strong autocatalysis is proven.
5.3 Spontaneous autocatalysis
For an irreducible network, M satisfies the Perron-Frobenius theorem, hence exponential growth (86) will hold for all components i for time values \( t > \tau \) , where \(\tau > 0\) is a homogeneization time as in Lemma 7.2 (ii) (see discussion below the Lemma). The same conclusion holds for reducible networks under the hypotheses considered in Sect. 5.2.3.
6 Perspectives
We have introduced in our main results, Theorems 2.1 and 2.2, a condition (Top) that provides a topological characterization of autocatalysis in the dilute regime (i.e. for low concentrations). This characterization is complete in the limit of negligible degradation rates for irreducible networks: indeed, in this case, (Top) is necessary and sufficient for autocatalysis both in the stoechiometric and in the dynamical sense. For reducible networks, (Top) is also necessarily and sufficient for stoechiometric autocatalysis, and implies dynamical autocatalysis when degradation rates are small, and concentrations small enough so that purely external reactions (connecting classes) have small rates.
We have furthermore shown that, in this limit, an infinitesimal amount of any species participating in the autocatalytic network ensures the onset of dynamical autocatalysis (see Lemma 7.2). In practice, this means that autocatalytic amplification can start spontaneously upon the rare appearance of a single autocatalyst. Interestingly, these conclusions directly apply to the universal minimal autocatalytic networks (autocatalytic cores) found in any autocatalytic system (Blokhuis et al. 2020), as they all respect (Top).
A first excursion out of this well-understood regime consists in including significant degradation reactions. Then condition (Top) remains necessary and sufficient for stoechiometric autocatalysis, but is only necessary for dynamical autocatalysis. Determining viability thresholds, i.e. maximum combinations of degradation rates which allow dynamical autocatalysis, is critical for the design of autocatalytic reaction networks and in origin of life studies (Jeancolas et al. 2020). Using branching processes, viability thresholds were determined for autocatalytic cores in the stochastic regime where only a few molecules are present (Blokhuis et al. 2020). Specifically, it was shown there that a single molecule survives with positive probability if and only if a certain inequality involving kinetic and degradation rates is satisfied. A next step of the treatment presented here will be to characterize viability thresholds allowing positivity of the Lyapunov exponent, and understand the relationship between the continuous and stochastic treatments of the viability thresholds. Notably, a conclusion of the stochastic treatment is that a multiplicity of internal catalytic cycles within the autocatalytic network favors survival (equivalently, allows larger degradation rates). It is tempting to speculate that this conclusion should apply as well to viability thresholds in the kinetic limit, as derived from the study of Lyapunov exponents.
Another direction for generalization is to go beyond the diluted regime. Away from it, Lyapunov exponents characterize stability in the neighborhood of stationary points other than the zero concentration limit, including equilibrium for networks satisfying detailed balance and growth modes for systems with dilution rate ensuring constant total concentration (as in Eigen and Schuster (1979)). However, in all generality, there is not necessarily a direct relationship between positivity of the Lyapunov exponent (growth rate) of the linearized system and the growth of the original nonlinear dynamical system.
In a companion paper (Unterberger 2021), we discuss all these points using an approach based on the analysis of Sects. 7.4 and 7.5. We obtain the following tentative conclusions, valid in the non-diluted regime: (i) Topology and thermodynamics together inform about autocatalysis; (ii) Estimating the Lyapunov exponent is (despite objections raised in the previous paragraph) a useful ‘proxy’ allowing quantitative estimates of the growth rate. General quantitative statements include: the computation of certain autocatalytic thresholds in the diluted regime; and estimates for Lyapunov exponents depending essentially on the topology of the network and on thermodynamics for arbitrary concentrations. We also show on examples that the curves of ‘proxy’ dynamical systems based on the above estimates compare well to the curves obtained by numerical integration, over a surprisingly large range of growth regimes.
The approach developed here and in our companion paper is a promising one for the investigation of more complex networks. Indeed, it shows that partial knowledge based on topology and thermodynamics informs on dynamics, independently of the knowledge of reaction rate constants, which is generally missing. A particularly important question is to understand the conditions for the existence of multiple growth modes that could support rudimentary forms of Darwinian evolution (Vasas et al. 2011). Together with threshold estimates, this may allow us to build scenarios for the emergence of evolution during the origin of life (Jeancolas et al. 2020).
7 Supplementary information
For simplicity, the reaction networks we consider in this appendix contain only forward reactions with one reactant,
and the corresponding reverse reactions,
All reaction networks discussed in the article are of this type.
This section is organized as follows. We start by presenting Type I and Type III cycles; contrary to Blokhuis et al. (2020), we assume stoechiometry 1 for reactants, in conformity with (61). Extended results for these cycles are presented in the companion paper (Unterberger 2021). A short argument for Theorem 2.1 (characterization of stoechiometric autocatalysis) is presented in Sect. 7.3 in the case of an irreducible network. Then (Sect. 7.4), we write down explicit formulas for the linearized time-evolution generator M of a reaction network. Finally, we present in Sect. 7.5 a “theory in a nutshell” for generalized adjoint Markov generators, extending results known from Markov chain theory; see in particular Lemmas 7.1 and 7.2.
7.1 Presentation of type I cycles
We consider in this subsection type I cycles of arbitrary length in the Blokhuis-Lacoste-Nghe classification,

The simple model studied in Sect. 2 corresponds to the special case \(n=1\). Chemostatted species—to be thought of e.g. as redox/energy carrier couple as in Sect. 2—are \((A,A')\) (in red). Dynamical species are \((B,B_1,\ldots ,B_n)\). Leaving out chemostatted species, we have a cycle \(B\leftrightarrows B_1 \leftrightarrows B_2\leftrightarrows \cdots \leftrightarrows B_n\leftrightarrows 2B\).
We have assumed trivial \(1\leftrightarrow 1 \) stoechiometry for all reactions along the cycle, except for the duplication reaction \(({{\mathcal {R}}}_n): B_n\longrightarrow 2B\) closing the cycle. There is nothing special about stoechiometry 2. The extension to the case when \(({{\mathcal {R}}}_n) : B_n\longrightarrow mB\) with arbitrary \(m=2,3,\ldots \) is straightforward.
Type I cycles are autocatalytic in the stoechiometric sense, as seen by choosing any reaction vector \(c=(c_0,\ldots ,c_n)\) such that \(c_0>c_1>\ldots>c_n>c_0/2>0\). On the other hand, choosing \(c=(1,\ldots ,1)\) yields the coarse-grained duplication reaction for species B
7.2 Presentation of type III cycles

Chemostatted species (in red) are \((A,A',A'')\). Dynamical species are \((A_i)_{0\le i\le n},(B'_i)_{0\le i\le n'}\),
\((B''_i)_{0\le i\le n''} \).
We have trivial \(1\leftrightarrow 1 \) stoechiometry for all reactions along the two cycles, and \(1\rightarrow 1+1\) for the pitchfork reaction \(A_n\rightarrow B'_0+B''_0\). Choosing a positive reaction vector such that \(c_0>\ldots >c_n\), \(c'_0>\ldots >c'_{n'}\), \(c''_0>\ldots >c''_{n''}\), and \(c_n>\max (c'_0,c''_0)\), \(c'_{n'}+c''_{n''}>c_0\), one obtains a positive balance for all species. Choosing instead \(c=(1,\ldots ,1)\) yields the coarse-grained duplication reaction for species \(A_0\)
7.3 Autocatalysis from the stoechiometric matrix
We give here a short argument for Theorem 2.1 in the irreducible case.
We consider an irreducible component of the reaction network with n species verifying (Top): every reaction has exactly one reactant and at least one reaction has \(\ge 2\) products or a product with a stoechiometry strictly \(\ge 2\). Correspondingly, each column j of the stoechiometric matrix \({{\mathbb {S}}}\) possesses a coefficient \(s_{ij}=-1\) and otherwise positive coefficients such that
Additionally, there is a column index k such that \(\sum _{i=1}^n s_{ik} > 0\).
We want to show that there exists a reaction vector \(c>0\) such that \({{\mathbb {S}}}c>0\), i.e. \(({{\mathbb {S}}}c)_i>0\) for all i. For this, it is sufficient to show that \(Mc'>0\) for a certain reaction vector \(c'>0\), where M is a matrix whose columns are positive linear combinations of those of \({{\mathbb {S}}}\), as constructed below.
Let \(J(i)=\{j\ |\ s_{ij} = -1\}\) be the set of reactions having species i as reactant, and \(N_i\) the cardinal of J(i). As the network is irreducible, \(N_i \ge 1\) for all i. Let \(n:=|{{\mathcal {S}}}|\). Denoting \(C_M^j\), resp. \(C_S^j\) the j-th column of M, resp. \({{\mathbb {S}}}\), we let, for \(j=1,\ldots ,n\):
By construction, \(M \equiv A-I\), where A is square and non-negative, i.e. \(A_{ij}\ge 0\) for all i, j. Given that the network is strongly connected, A is irreducible. Stoechiometric hypotheses (67) impose \(\sum _{i=1}^n A_{ij} \ge 1\) for every j and \(\sum _{i=1}^n A_{ik} > 1\) for a certain k. By the Perron-Frobenius theorem, the largest eigenvalue \(\lambda \) of A is positive and associated with an eigenvector \(c'>0\). We have:
This implies \(\lambda >1\). Hence \(c'\) is a positive eigenvector of \(M=A-I\) with eigenvalue \(\lambda -1>0\).
7.4 Linearized time-evolution generator for reaction networks
The linearized time-evolution generator \(M=M([A])\) of a reaction network has been defined in Eqs. (2)–(5). The current \(J_{{{\mathcal {R}}}}=k_+[A_i]\) associated to a forward reaction \({{\mathcal {R}}}\) as in (61) is straightforwardly linearized to \(J_{lin,{{\mathcal {R}}}}(A)=k_+ A_i\). Considering now a reverse reaction (62), the reverse current is \(k_- \prod _{\ell =1}^n [A_{i'_{\ell }}]^{s_{\ell }}\), yielding a linearized current
The coefficients of the matrix M are obtained by summing individual matrices \(M({{\mathcal {R}}})\) associated to linearized forward reactions \({{\mathcal {R}}}: A_i \overset{k_+}{\rightarrow } s_1 A_{i'_1}+\ldots +s_{n} A_{i'_{n}}\),
and matrices \(\sum _{\ell } M(\bar{{\mathcal {R}}},\ell )\) associated to linearized reverse reactions \(\bar{{\mathcal {R}}}\) (see (68))
If \({\mathcal {R}}\) is a forward reaction, the corresponding contribution \(M({{\mathcal {R}}})\) to M is (see below (5)) a generalized adjoint Markov generator with negative killing rate \(a_i({{\mathcal {R}}})=k_+(1-\sum _{\ell } s_{\ell })\), which vanishes precisely in the case of a reversible reaction \(A_i\leftrightarrows A_j\).
Consider now a reverse reaction \(\bar{{\mathcal {R}}}\). The matrix \(M(\bar{{\mathcal {R}}},\ell )\) is not a generalized adjoint Markov generator if \(n\ge 2\), because of the probability leak currents \(-s_{\ell '}J^{\ell }_{lin}A_{i'_{\ell }}=(M(\bar{{\mathcal {R}}},\ell ))_{i'_{\ell '},i'_{\ell }}\) from state \(i'_{\ell }\not =i'_{\ell '}\); also, it features \(\ge 0\) killing rates \(a_{i'_{\ell }}(\bar{{\mathcal {R}}},\ell )= J^{\ell }_{lin} \Big [s_{\ell }-1\Big ] \), computed without considering probability leak currents, considered as external non-diagonal terms without probabilistic interpretation. The reverse reaction \(\bar{{\mathcal {R}}}\ :\ B''_0+B'_0\overset{\nu _-}{\longrightarrow } A_n\) in type III cores has \(n=2\), and does exhibit leak currents. Matrices \(M(\bar{{\mathcal {R}}},0')\), resp. \(M(\bar{{\mathcal {R}}},0'')\), are identified with the two columns of the matrix

Reverse reactions putting into contact \(n\ge 2\) different species produce negative off-diagonal coefficients, here emphasized in red. If the resulting matrix \(M=\sum _{{{\mathcal {R}}}} M({{\mathcal {R}}}) +\sum _{\bar{{\mathcal {R}}},\ell } M(\bar{{\mathcal {R}}},\ell )\) has negative off-diagonal coefficients, it cannot be interpreted as a generalized Markov generator, therefore Lemma 7.1 below (allowing easy upper bounds for the Lyapunov exponent) does not hold.
7.5 Generalized Markov generators
A central notion in this article is that of generalized Markov processes, i.e. discrete- or continuous-time Markov processes which are not necessarily probability-preserving; a general introductory reference is (Norris 1997, Chap. 2). Let \({{\mathcal {S}}}=\{1,\ldots ,n\}\) be a finite state space. Then an \(n\times n\) matrix M is a generalized adjoint Markov generator if
-
(i)
diagonal coefficients \(M_{i,i}\), \(1\le i\le n\) are \(<0\);
-
(ii)
and off-diagonal coefficients \(M_{i,j}\), \(i\not =j\) are \(\ge 0\).
If \(\sum _{i=1}^n M_{i,j}=0\) for all j, then coefficients of the transposed matrix \(M^t\) sum up to zero on each line, so that \(M^t\) is a conventional probability-preserving Markov generator: \(\mathbf{1}^t=\left( \begin{array}{ccc} 1&\cdots 1 \end{array}\right) \) is a left-eigenvector of M with eigenvalue 0. The probability measure \( \mu (t)\) of the process at time t is \( e^{tM}\mu (0)\), solution of the master equation \(\frac{d}{dt}\mu =M\mu \); probability preservation means that \(\sum _i \mu _i(t)=1\) for all time. Assume, more generally, that \(a_{j}:=|M_{j,j}|- \sum _{i\not =j} M_{i,j}\ge 0\), then the total probability \(\sum _i \mu _i(t)\) is a decreasing function of time, and \(a_j\) can be interpreted as a killing rate (biologically, a degradation rate) in state j. For a finite set of states, there is no obstacle in considering the case when killing rates \(a_j\) can have either sign. We discuss the associated random process \((X(t))_{t\ge 0}\) later on; by definition \(X(t)\in {{\mathcal {S}}}\) has transition rate \(M_{i,j}\) from j to i. By construction, \(\mu _i(t)\equiv {\mathbb {P}}[X(t)=i]=(e^{tM}\mu (0))_i\), generalizing the above master equation, where \(\mathbb {P}\) is a (non-normalized) measure on trajectories. Probabilistic tools give an intuitive access to the resolvent in terms of trajectories of the Markov process, from which we derive a characterization and properties of the Lyapunov exponent.
Communicating classes, irreducibility. Example of the "\(A_1 A_2 A_3 \longrightarrow B_1 B_2 B_3\)" autocatalytic reaction network. Let M be a generalized adjoint Markov generator on \({{\mathcal {S}}}=\{1,\ldots ,n\}\). The matrix M defines a graph G(M) with vertex state \({\mathcal {S}}\) and oriented edge set \({{\mathcal {E}}}(M)\): a pair \(e=(x\rightarrow y)\), \(x\not =y\) is an edge if \(M_{y,x}>0\); the probability flow follows edges. Following standard terminology in Markov chains, we say that \(x\not =y\) communicate (which we denote \(x\sim y\)) if there exists a path from x to y and a path from y to x, namely, a chain of edges \((x\rightarrow x_1),(x_1\rightarrow x_2),\ldots , (x_{n}\rightarrow y)\) and a chain of edges \((y\rightarrow \tilde{x}_1), (\tilde{x}_1 \rightarrow \tilde{x}_2),\ldots ,(\tilde{x}_{n'} \rightarrow x)\) with \(n,n'\ge 0\). Letting also \(x\sim x\) for all x, this defines equivalence classes called communicating classes. M is said to be irreducible if there is only one class.
M is clearly reducible if the graph is not connected, but this means that we are dealing with several independent systems, an uninteresting situation. We may assume instead that the graph G(M) is always connected. On the other hand, there exist connected graphs which are not irreducible, for instance the graph of the "\(A_1 A_2 A_3 \longrightarrow B_1 B_2 B_3\)" autocatalytic reaction network (also discussed in Sect. 4), a graph on the set \({{\mathcal {S}}}=\{1,2,3,1',2',3'\}\),

The associated reaction network is
(with arbitrary transition rates) whose graph coincides in the zero-concentration limit with \(G_{(123)\rightarrow (1'2'3')}\) through the state identification \((A_1,A_2,A_3,B_1,B_2,B_3)\leftrightarrow (1,2,3,1',2',3')\). Adding all the forward reactions \((\rightarrow )\) with coefficients \(c_{{{\mathcal {R}}}_1}=5, c_{{{\mathcal {R}}}_2}=4, c_{{{\mathcal {R}}}_3}=3\); \(c_{{{\mathcal {R}}}_{1,1'}}={1\over 2}\); \(c_{{{\mathcal {R}}}_{1'}}=\frac{5}{6}\), \(c_{{{\mathcal {R}}}_{2'}}=\frac{4}{6}, c_{{{\mathcal {R}}}_{3'}}=\frac{3}{6}\) yields the result
Thus this network is autocatalytic in the stoechiometric sense.
Partial order, minimal classes, maximal classes. Generalizing the above example, one sees that, by shrinking communicating classes to single points, one reduces the oriented graph G(M) to an oriented "contracted" graph \({{\mathcal {T}}}(M)\) which has no loops. (Mind that the associated unoriented graph may have loops, so that \({{\mathcal {T}}}(M)\) is not necessarily a topological tree.) It is possible to represent this graph with edge arrows going downwards, e.g. in the above example,

with \({{\mathcal {C}}}=\{1,2,3\},\, {{\mathcal {C}}}'=\{1',2',3'\}\). Note that the graph would become irreducible if (as discussed above) one added the reverse arrow \(1'\rightarrow 1\) corresponding to the reverse reaction \(2B_1\rightarrow A_1\). We get a partial order on the set of classes by letting \({{\mathcal {C}}}'\succ {{\mathcal {C}}}\) if there is a \({{\mathcal {T}}}\)-path downstream (i.e. following the probability flow) from \({{\mathcal {C}}}\) to \({{\mathcal {C}}}'\). Maximal (downstream) elements (here \({{\mathcal {C}}}'\)) are called closed classes, because they have no outgoing arrows: one cannot escape from them. Minimal (upstream) classes (here \({{\mathcal {C}}}\)), on the other hand, have no ingoing arrows.
Autocatalysis in the stoechiometric sense. Let us now discuss the connection between reaction networks and graphs. Consider a reaction network with species set \({{\mathcal {S}}}=\{A_1,\ldots ,A_{|{{\mathcal {S}}}|}\}\), forward reaction set \(\{1,\ldots ,N\}\) and positive (mass-action) reaction rates for both forward and reverse reactions. We are particularly interested in the limit of small concentrations, so we distinguish:
-
(i)
reversible reactions \(A_i\leftrightarrows A_j\) (\(i\not =j\));
-
(ii)
and irreversible reactions \(A_i\overset{k_+}{\underset{k_-}{\rightleftarrows }} s_1 A_{i'_1}+\cdots + s_n A_{i'_n}\), with \(n\ge 1\), \(s_i\in \mathbb {N}^*\), \(\sum _{i=1}^n s_i>1\).
Let us construct the graph associated to the linearized time-evolution generator M in the zero-concentration limit; note that the graph actually depends only on the stoechiometry matrix \({\mathbb {S}}\), not on the rates, so we can call it \(G({{\mathbb {S}}})\). As discussed in Sect. 4, in case of multiple arrow \(i\rightarrow j\), we keep only one.
-
(i)
Reversible reactions \(A_i\leftrightarrows A_j\) contribute to \(G({{\mathbb {S}}})\) two arrows \(i\rightarrow j\) and \(j\rightarrow i\).
-
(ii)
Forward reactions \( {{\mathcal {R}}}: \qquad A_i\overset{k_+}{\rightarrow } s_1 A_{i'_1}+\cdots + s_n A_{i'_n}\) (\(\sum _i s_i>1\)) contribute to \(G({{\mathbb {S}}})\) an arrow \(i\rightarrow i'_{\ell }\) for each \(\ell =1,\ldots ,n\). Reversible reactions \(A_i\leftrightarrows A_j\) decompose into two forward reactions \(A_i\rightarrow A_j\) and \( A_j\rightarrow A_i\).
On the other hand, reverse reactions \(\bar{{\mathcal {R}}}: s_1 A_{i'_1}+\cdots + s_n A_{i'_n} \overset{k_-}{\rightarrow } A_i\), with \(\sum _i s_i>1\) contribute no arrow.
Case of the "\(A_1 A_2 A_3 \longrightarrow B_1 B_2 B_3\)" autocatalytic kinetic reaction network.
The linearized evolution generator is a sum of 7 matrices, one per reaction (provided paired generators associated to forward/reverse reversible reactions \(i\leftrightarrows j\), \(i'\leftrightarrows j'\) are summed together), \(M=\sum _{i} M({{\mathcal {R}}}_{i}) + M({{\mathcal {R}}}_{11'})+ \sum _{i'} M({{\mathcal {R}}}_{i'})\), with

and similarly for the four other reversible generators \(A_2\leftrightarrows A_3\), \(B_i\leftrightarrows B_j\); these are probability preserving adjoint Markov generators since the sum of coefficients on any column is zero;

which is an adjoint Markov generator with negative killing rate; and

for the irreversible reaction \({{\mathcal {R}}}_{11'}\) coupling \({{\mathcal {C}}}_1\) to \({{\mathcal {C}}}_{1'}\), to which one has added the (red) reverse reaction, with rate proportional to the low concentration \([B_1]\), absent in the zero-concentration limit.
Path measure for generalized Markov generators (see Norris (1997), Chap. 2). When killing rates vanish, one has a probability law \(\mathbb {P}\) on trajectories \((X(t))_{0\le t\le T}\): letting \(t_1=0\), \((T_k)_{k\ge 2} \le T\) be the jumping times,
Integrating over the jumping times, one obtains the law of the trajectories \(\underline{X}=(\underline{X}_k)_{k\ge 0}\) of the underlying "skeleton" discrete-time Markov chain,
with transition rates
featuring the Markov generator \(M^t\). We generalize to arbitrary killing rates and use (75), (76) as a definition for an unnormalized measure \(\mathbb {P}\) over trajectories.
A path representation of the resolvent. When killing rates vanish, \(\sum _{j\not =i} w_{i\rightarrow j}=1\), and \(w_{i\rightarrow j}\) are simply the transition rates of the underlying skeleton discrete-time Markov chain; by extension, the coefficients \(w_{i\rightarrow j}\) will be called transition rates in the general case. In chemical terms, \(w_{i\rightarrow j}\) measures the specificity of the reaction \(i\rightarrow j\). Let \(\alpha :=\)diag((\(\alpha _i)_{1\le i\le |{{\mathcal {S}}}|})\) a positive diagonal matrix, and \(M_{\alpha }:=M-\alpha \). Then
defines a matrix with positive coefficients, which can be computed as a sum over backward paths \(i= x_1\rightarrow x_2\rightarrow \cdots \rightarrow x_{\ell -1}\rightarrow x_{\ell }=j\) of arbitrary length \(\ell \ge 0\),
where
When finite, \((R(\alpha ))_{i,j}<\infty \) are the coefficients of the resolvent \((\alpha -M)^{-1}=(-M_{\alpha })^{-1}\); see e.g. (Revuz and Yor 1999, Chap. III), or (Norris 1997, Sect. 4.2) for an introduction in connection to potential theory.
Proof
The \(\ell =0\) contribution is non-zero only if \(i=j\), in which case it corresponds to the integral \(\int _0^{+\infty } dt \, e^{t(M_{\alpha })_{j,j}} = \frac{1}{|M_{jj}|+\alpha _j}\). Splitting \(M_{\alpha }\) into \((M_{\alpha })_{diag}+ (M_{\alpha })_{off}\), where \((M_{\alpha })_{diag}\), resp. \((M_{\alpha })_{off}=M_{off}\), is its diagonal part, resp. its off-diagonal (jump) part, and expanding the exponential \((e^{tM_{\alpha }})_{i,j}\) using the Feynman-Kac (or Trotter product) formula, one obtains a sum over trajectories \((x(t'))_{0\le t'\le t}\) such that \(x|_{[t_k,t_{k+1})}=x_k\), \(k=1,\ldots ,\ell -1\), and \(x|_{[t_{\ell },t]}=j\), with \(0=t_1<t_2<\ldots<t_{\ell }<t\). Integrating over t, one obtains multiple integrals
yielding (79).
Lemma 7.1
(Properties of the resolvent for M irreducible) We assume that M is irreducible. Then:
-
(i)
Coefficient functions \(\alpha \mapsto (R(\alpha ))_{i,j}\) are decreasing, namely, if \(\alpha \le \alpha '\), i.e. \(\alpha _i\le \alpha '_i\) for all i, then \(R(\alpha ')\le R(\alpha )\);
-
(ii)
let \(t\mapsto \alpha (t)\) \((t\ge 0)\) be an increasing function of time, i.e. \((t'\le t)\Rightarrow (\alpha (t')\le \alpha (t))\); then there exists a transition time \(t=t_0\) (possibly, \(t_0=0\)) such that all coefficients of \(R(\alpha (t))\) are \(<\infty \) if \(t> t_0\), and all coefficients of \(R(\alpha (t))\) are \(\infty \) if \(0\le t< t_0\). If \(t>t_0\), then \(R(\alpha (t))=(-M_{\alpha (t)})^{-1}\).
-
(iii)
(Lyapunov exponent) Let \(\lambda _{max}:= \max \{\mathrm{Re\ }(\lambda ) \ |\ \lambda \) eigenvalue of \(M\}\) be the Lyapunov exponent of M. If one lets \(\alpha (t):=t{\mathrm {Id}}\), and the transition time \(t_0\) is \(>0\), then \(\lambda _{\max }=t_0\). Conversely, if \(t_0=0\), then \(\lambda _{max}\le 0\).
-
(iv)
(positivity criterion for Lyapunov exponent) assume \(R(\alpha )=+\infty \) for some \(\alpha \ge 0\) which is not identically zero, then \(\lambda _{max}>0\).
Proof
For (ii) we need only remark that \(\Big (\exists i,j,\, (R(\alpha ))_{i,j}=+\infty \Big )\!\Rightarrow \!\Big (\forall i,j,\, (R(\alpha ))_{i,j}=+\infty \Big )\). Namely, let \(i',j'\) be indices; M being irreducible, there exists a backward path from \(i'\) to i, and a backward path from j to \(j'\); sandwiching \((R(\alpha ))_{i,j}\)—which is the sum of the weights of all backward paths from i to j—between them, one gets \((R(\alpha ))_{i',j'}=+\infty \).
Let now \(\alpha (t)=t{\mathrm {Id}}\). If \(t>\max (0,\lambda _{max})\), then (as can be proved by standard arguments using e.g. Jordan’s form for M) there exists some constant \(c>0\) s.t. for all \(\tau >0\), \( ||| e^{\tau M_{\alpha (t)}} |||=O(e^{-c\tau })\) \((|||\ \cdot \ |||\) being any norm), hence \(R(\alpha (t))_{ij}<\infty \) for all i, j. Conversely, if \(R(\alpha (t))_{ij}<\infty \) for all i, j, then \(\lambda -M\) is invertible if \(\mathrm{Re\ }\lambda \ge \alpha (t)\), as follows from the path representation (79). This implies (iii).
Discussing finally (iv), assume that \(R(\alpha )=+\infty \) with \(\alpha _i>0\). Let \({{\mathcal {W}}}_i(\alpha )\) be the weight of excursions from i, i.e. the total weight of all backward paths \(i=x_1\rightarrow x_2\rightarrow \cdots \rightarrow x_{\ell -1}\rightarrow x_{\ell }=i\) such that \(x_2,\ldots ,x_{\ell -1}\not =i\). Then
hence
The function \(\alpha \mapsto {{\mathcal {W}}}_i(\alpha )\) is a strictly decreasing function, so \({{\mathcal {W}}}_i(\alpha /2)>1\). This strict inequality remains true (by continuity) in a neighborhood \(\Omega \) of \(\alpha /2\) in \(\mathbb {R}_+^{{{\mathcal {S}}}}\), and (by monotony) for all \(\alpha '\) such that \(\alpha '\le \alpha ''\) for some \(\alpha ''\in \Omega \). In particular, for t small enough, \(R(t{\mathrm {Id}})=+\infty \), so that \(\lambda _{max}>0\). \(\square \)
To finish with, we study in some details the onset of the exponential growth using the Perron-Frobenius theorem.
Lemma 7.2
-
(i)
If \(\lambda \) is an eigenvalue of M and \(\mathrm{Re\ }\lambda =\lambda _{max}\), then \(\lambda =\lambda _{max}\). In particular, \(\lambda _{max}\) is an eigenvalue of M. Furthermore, the multiplicity of \(\lambda _{max}\) is 1, and there exists an associated eigenvector with \(>0\) coefficients.
-
(ii)
Let \(\tau >0\). There exist two constants \(c=c(\tau ),C=C(\tau )>0\) such that, for every nonzero initial concentration vector v with \(\ge 0\) coefficients, and for every \(t>\tau \),
$$\begin{aligned} c\Big (\max _i v_i\Big )\, e^{\lambda _{max}t} \le \Big (e^{tM} v\Big )_i \le C\Big (\max _i v_i\Big ) \, e^{\lambda _{max}t}. \end{aligned}$$(84)
The upper bound (84) holds uniformly in \(\tau \), but the lower bound degenerates as \(\tau \rightarrow 0\) (because \((e^{tM} v)_i\rightarrow _{t\rightarrow 0} v_i\) can vanish). The homogenization time \(\tau \) is discussed below.
Proof
-
(i)
This is a consequence of the Perron-Frobenius theorem, since (for \(C>0\) large enough constant) \(M+C{\mathrm {Id}}\) has positive coefficients and is irreducible.
-
(ii)
Fix the eigenvector \(v_{max}\) associated to the maximal eigenvalue \(\lambda _{max}\) by requiring that \(v_{max,i}>0\) for all i and \(||v_{max}||_{\infty }:=\max _i v_{max,i} =1\). The upper bound follows by standard computations from splitting v into \(v_{//}+w\), where \(v_{//}\) is the linear projection of v onto the one-dimensional eigenspace \(\mathbb {R}v_{max}\) parallel to the sum of all other generalized eigenspaces. For the lower bound, we note that \((e^{\tau M})_{ij}>0\) for all indices i, j and \(\tau >0\). Fix some (small) instant \(\tau >0\); there exists then \(c>0\) such that that
$$\begin{aligned} (e^{\tau M} v)_i \ge c||v||_{\infty } v_{max,i}. \end{aligned}$$(85)Let \(t\ge \tau \). Since the matrix \(e^{(t-\tau )M}\) has positive coefficient, we get \((e^{tM}v)_i \ge c ||v||_{\infty } \, \Big ( e^{(t-\tau )M}v_{max}\Big )_i = c||v||_{\infty }\, e^{(t-\tau ) \lambda _{max}} v_{max,i}.\)
\(\square \)
For applications, we are mostly interested in the onset of the exponential growth regime, and may assume that \(\lambda _{max}>0\). Let \(M:=M([A]=0)\) be the generalized Markov generator obtained by linearizing the kinetic equations at zero concentrations. By definition, \(\frac{d[A]}{dt}=M[A]+O([A]^2)\). Hence it follows from the above Corollary that, for all \(i\in {{\mathcal {S}}}\) and \(t>\tau \),
for time values t such that \(\max _i \, [A_i](t=0) \, \times \, e^{\lambda _{max}t} \) is small enough (depending on kinetic rates), where \(a\approx b\) \((a,b>0)\) means: \(ca<b<Ca\) for constants \(c,C>0\) independent of t, i and \([A](t=0)\), but depending on the homoegeneization time \(\tau \). Equation (86) may be regarded as a mathematical expression for spontaneous autocatalysis. The homoegeneization time \(\tau \) should be chosen as small as possible in order for (85) to hold for a not too small constant c, with \(M=M([A]=0)\).
Data availability statement
There are no associated data.
References
Ameta S, Arsène S, Foulon S, Saudemont B, Clifton BE, Griffiths AD, Nghe P (2021) Darwinian properties and their trade-offs in autocatalytic RNA networks. Nat Commun 12:842
Andersen JL, Flamm C, Merkle D, Stadler PF (2019) Chemical transformation motifs—modelling pathways as integer hyperflows. EEE/ACM Trans Comput Biol Bioinform 16(2):510–523
Andersen JL, Flamm C, Merkle D, Stadler PF (2020) Defining autocatalysis in chemical reaction networks. J Syst Chem 8:121–133
Arsène S, Ameta S, Lehman N, Griffiths AD, Nghe P (2018) Coupled catabolism and anabolism in autocatalytic RNA sets. Nucleic Acids Res 46(18):9660–9666
Blokhuis A, Lacoste D, Nghe P (2020) Universal motifs and the diversity of autocatalytic systems. PNAS 117(41):25230–25236
Borwein J, Adrian S (2006) Convex analysis and nonlinear optimization. Springer, Berlin
Danger G, d’Hendecourt V, Pascal R (2020) On the conditions for mimicking natural selection in chemical systems. Nature Rev Chem 4(2):102–109
Eigen M (1971) Selforganization of matter and the evolution of biological macromolecules. Naturwissenschaften 58:465
Eigen M, Schuster P (1979) The hypercycle. A principle of natural self-organization. Springer, Berlin
Eigen M, McCaskill J, Schuster P (1989) The molecular quasi-species. Adv Chem Phys 75:149
Esposito M (2016) Nonequilibrium thermodynamics of chemical reaction networks: wisdom from stochastic thermodynamics. Phys Rev X 6:041064
Fontana W, Buss LW (1994) “The arrival of the fittest’’: toward a theory of biological organization. Bull Math Biol 56(1):1–64
Hanopolskyi AI, Smaliak VA, Novichko AIV, Semenov SN (2021) Autocatalysis: kinetics, mechanisms and design. ChemSystemsChem 3(1):e2000026
Hordijk W, Steel M, Kauffman S (2012) The structure of autocatalytic sets: evolvability, enablement, and emergence. Acta biotheoretica 60(4):379–392
Jeancolas C, Malaterre C, Nghe P (2020) Thresholds in origin of life scenarios. Iscience 23(11):101756
Kauffman SA (1986) Autocatalytic sets of proteins. J Theor Biol 119(1):1–24
King GAM (1982) Recycling, reproduction, and life’s origins. BioSystems 15:89–97
Kun A, Papp B, Szathmáry E (2008) Computational identification of obligatorily autocatalytic replicators embedded in metabolic networks. Genome Biol 9(3):1–11
Kussell E, Leibler S (2005) Phenotypic diversity, population growth, and information in fluctuating environments. Science 309:2075–2078
Nghe P (2015) Prebiotic network evolution: six key parameters. Mol BioSyst 11–12:3206–3217
Norris JR (1997) Markov chains. Cambridge University Press, Cambridge
Peng Z, Plum AM, Gagrani P, Baum DA (2020) An ecological framework for the analysis of prebiotic chemical reaction networks. J Theor Biol 507:110451
Penocchio E, Rao R, Esposito M (2019) Thermodynamic efficiency in dissipative chemistry. Nat Commun 0:3865
Preiner M, Xavier JC, Vieira ADN, Kleinermanns K, Allen JF, Martin WF (2019) Catalysts, autocatalysis and the origin of metabolism. Interface Focus 9(6):20190072
Revuz D, Yor M (1999) Continuous martingales and Brownian motion. Springer, Berlin
Sarkar S, England JL (2019) Design of conditions for self-replication. Phys Rev E 100:022414
Stewart GW, Sun J-G (1990) Matrix perturbation theory. Academic Press, Cambridge
Unterberger J (2021) Dynamical autocatalysis for autocatalytic cores, in preparation
Vasas V, Fernando C, Santos M, Kauffman S, Szathmáry E (2011) Evolution before genes. Biol Direct 7(1):1–14
Vincent L, Berg M, Krismer M, Saghafi ST, Cosby J, Sankari T, Vetsigian HK, Cleaves HJ, Baum DA (2019) Chemical ecosystem selection on mineral surfaces reveals long-term dynamics consistent with the spontaneous emergence of mutual catalysis. Life 9(4):80
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
P. Nghe acknowledges support from Institut Pierre-Gilles de Gennes (laboratoire d’excellence, “Investissements d’avenir” program ANR-10-IDEX-0001-02 PSL and ANR-10-LABX-31) and the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant Agreement No. [101002075]).
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Unterberger, J., Nghe, P. Stoechiometric and dynamical autocatalysis for diluted chemical reaction networks. J. Math. Biol. 85, 26 (2022). https://doi.org/10.1007/s00285-022-01798-0
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00285-022-01798-0
Keywords
- Autocatalysis
- Chemical reaction networks
- Origin of life
- Lyapunov exponent
- Growth rate
- Continuous-time Markov chains