Classification of infinitesimal homeostasis in four-node input–output networks

Abstract

An input–output network has an input node $\iota$, an output node o, and regulatory nodes $\rho _j$. Such a network is a core network if each $\rho _j$ is downstream from $\iota$ and upstream from o. Wang et al. (J Math Biol 82:62, 2021. https://doi.org/10.1007/s00285-021-01614-1) show that infinitesimal homeostasis can be classified in biochemical networks through infinitesimal homeostasis in core subnetworks. Golubitsky and Wang (J Math Biol 10:1–23, 2020) show that there are three types of 3-node core networks and three types of infinitesimal homeostasis in 3-node core networks. This paper uses the theory developed in Wang et al. (2021) to show that there are twenty types of 4-node core networks (Theorem 1.3) and seventeen types of infinitesimal homeostasis in 4-node core networks (Theorem 1.7). Biological contexts illustrate the classification theorems and show that the theory can be an aid when calculating homeostasis in specific biochemical networks.

1 Introduction

In this introduction we recall from Golubitsky and Stewart (2017), Wang et al. (2021) the notions: input–output networks, input–output functions, infinitesimal homeostasis, homeostasis matrices, core networks, core equivalence, and infinitesimal homeostasis types. We also present our two principal results: Theorems 1.3 and 1.7. These theorems classify the twenty 4-node input–output core networks up to core equivalence and the seventeen different types of infinitesimal homeostasis that occur in these networks.

1.1 Input–output functions and infinitesimal homeostasis

Homeostasis is an important biological concept where the output of a system is held approximately constant as an ambient variable changes. For example, Best et al. (2009) ask how extracellular dopamine changes as dopamine transporter (DAT) varies. The literature contains many examples of mathematical models of homeostasis in biochemical networks. In these models the network nodes represent biochemical substrates, the network arrows indicate when one substrate affects another, and the associated differential equations model the biochemical reactions.

For example, feed-forward excitation [taken from Reed et al. (2017)] that occurs when substrate X activates substrate Y which catabolizes substrate Z is an example of a 3-node biochemical network, see Fig. 1a. The kinetic functions $g_j$ indicate the flux into or away from a substrate. The arrow f indicates that substrate X modulates flux $g_3$.

Fig. 1

a Feed-forward excitation motif from Reed et al. (2017). b Input–output network associated with the feed-forward excitation motif

The differential equations that model the substrate concentrations are given in (1.1) (left). Here x is the concentration of X, y is the concentration of Y, and z is the concentration of Z. The form of the $g_j$ and of f gives further details of the biochemical modeling and that form is often a sigmoid function with additional parameters. Note that ${{\mathcal {I}}}$ represents the concentration of the ambient variable.

$$\begin{aligned} \begin{array}{rcl} &{} &{} \text{ biochemical } \\ {\dot{x}} &{} = &{} {{\mathcal {I}}}-g_1(x) - g_4(x) \\ {\dot{y}} &{} = &{} g_1(x) - g_2(y) - g_5(y)\\ {\dot{z}} &{} = &{} g_2(y) - f(x)g_3(z) \end{array} \qquad \begin{array}{rcl} &{}&{} \text{ math } \\ {\dot{x}}_\iota &{} = &{} f_\iota (x_\iota ,{{\mathcal {I}}}) \\ {\dot{x}}_\rho &{} = &{} f_\rho (x_\iota ,x_\rho ) \\ {\dot{x}}_o &{} = &{} f_o(x_\iota , x_\rho , x_o) \end{array} \end{aligned}$$

(1.1)

This information is abstracted in Fig. 1b. The abstract form of the differential equations indicating how the different substrates evolve in time is given in (1.1) (right). These systems of differential equations are called admissible systems associated with the input–output math network in Fig. 1b (Golubitsky and Stewart 2006).

In general an input–output network ${{\mathcal {G}}}$ consists of $n+2$ nodes $(\iota ,\rho _1,\ldots ,\rho _n, o)$ where $\iota$ is the input node, $\rho _1,\ldots ,\rho _n$ are the n regulatory nodes, and o is the output node. An admissible system associated with an input–output network has the form

$$\begin{aligned} {\dot{X}} = F(X, {{\mathcal {I}}}) \end{aligned}$$

(1.2)

where $X = (x_\iota , x_{\rho _1}, \ldots , x_{\rho _n},x_o) \in {\mathbb {R}}^{n+2}$ are the state variables associated with the nodes, ${{\mathcal {I}}}$ is the external input parameter, and $F = (f_\iota ,f_{\rho _1},\ldots ,f_{\rho _n},f_o)$ is the associated vector field. We assume the following:

• (a) There exists at least one path from the input node $\iota$ to the output node o.

• (b) $f_j$ depends on $x_\ell$ only if there is an arrow in the network ${{\mathcal {G}}}$ from $\ell \rightarrow j$.

• (c) $f_\iota$ is the only vector field coordinate that depends explicitly on ${{\mathcal {I}}}$.

An input–output function $x_o({{\mathcal {I}}})$ is obtained from a stable equilibrium $(X_0,{{\mathcal {I}}}_0)$ of F as follows. The implicit function theorem implies that for every ${{\mathcal {I}}}$ near ${{\mathcal {I}}}_0$ there is a stable equilibrium at $X({{\mathcal {I}}})$. The last coordinate of $X({{\mathcal {I}}})$ is the input–output function $x_o({{\mathcal {I}}})$. Homeostasis occurs when $x_o({{\mathcal {I}}})$ is approximately constant on a neighborhood of ${{\mathcal {I}}}_0$. Infinitesimal homeostasis occurs when $x_o'({{\mathcal {I}}}) = 0$, where $'$ indicates differentiation with respect to ${{\mathcal {I}}}$. The concept of infinitesimal homeostasis has been studied in a series of papers Golubitsky and Stewart (2017), Reed et al. (2017), Golubitsky and Stewart (2018), Antoneli et al. (2018), Golubitsky and Wang (2020), Wang et al. (2021).

Note that if assumption (a) fails then there is no path from $\iota$ to o and the input–output function $x_o({{\mathcal {I}}})$ is the trivial constant function. Such an input–output function is not useful.

1.2 Homeostasis matrix

Let J be the $(n+2)\times (n+2)$ Jacobian matrix of (1.2) at the equilibrium $X_0$.

Definition 1.1

The $(n+1)\times (n+1)$ homeostasis matrix H is obtained from the Jacobian matrix J by eliminating the first row and the last column. Specifically:

$$\begin{aligned} H= \left[ \begin{array}{cccccccccccc} f_{\rho , x_\iota } &{} f_{\rho , x_\rho }\\ f_{o, x_\iota } &{} f_{o, x_\rho } \end{array}\right] . \end{aligned}$$

(1.3)

It has been shown that infinitesimal homeostasis occurs at a stable equilibrium of (1.2) if and only if $\det (H) = 0$ (Ma et al. 2009; Wang et al. 2021). It follows that infinitesimal homeostasis can occur in 3-node feed-forward excitation if and only if

$$\begin{aligned} \det (H) = f_{\rho ,x_{\iota }} f_{o,x_\rho } - f_{o,x_{\iota }}f_{\rho ,x_{\rho }} = 0. \end{aligned}$$

(1.4)

Reed et al. (2017) show that infinitesimal homeostasis can occur in the biochemical model (1.1) (left) if and only if the model system satisfies

$$\begin{aligned} f'(x_0) = \frac{ g_1'(x_0)g_2'(y_0)}{(g_2'(y_0)+g_5'(y_0))g_3(z_0)} \end{aligned}$$

(1.5)

where $X_0 = (x_0,y_0,z_0)$ is a stable equilibrium of the admissible system (1.1) (left). This result is reproduced in Golubitsky and Wang (2020) by computing

$$\begin{aligned} f_{\rho ,x_\iota } = g_1'(x) \quad f_{o,x_\rho } = g_2'(y) \quad f_{o,x_\iota }=-f'(x)g_3(z) \quad f_{\rho ,x_\rho } = -g_2'(y)-g_5'(y) \end{aligned}$$

The formula in (1.5) can then be derived from (1.4).

1.3 Core networks and core equivalence classes

Wang et al. (2021) observe that homeostasis in a given network can often be determined by analyzing a simpler network by eliminating certain nodes and arrows. We review the concepts of core network and core equivalence.

Definition 1.2

• (a) A node $\tau$ in ${{\mathcal {G}}}$ is downstream from a node $\rho$ in ${{\mathcal {G}}}$ if there exists a path from $\rho$ to $\tau$. Node $\tau$ is upstream from node $\rho$ if $\rho$ is downstream from $\tau$.

• (b) An input–output network is core if every node is downstream from the input–node $\iota$ and upstream from the output-node o.

• (c) Two $(n+2)$-node core networks are core equivalent if they have the same polynomials $\det (H)$. Two $(n+2)$-node core networks are core inequivalent if they are not core equivalent.

Every input–output network ${{\mathcal {G}}}$ has a core subnetwork ${{\mathcal {G}}}_c$ whose nodes are the nodes in ${{\mathcal {G}}}$ that are both upstream from the output node and downstream from the input node and whose arrows are the arrows in ${{\mathcal {G}}}$ whose head and tail nodes are both nodes in ${{\mathcal {G}}}_c$. It has been proved that to classify infinitesimal homeostasis for a given network ${{\mathcal {G}}}$, it suffices to classify infinitesimal homeostasis for its core subnetwork ${{\mathcal {G}}}_c$ (Wang et al. 2021).

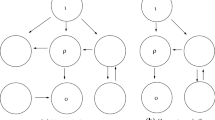
As observed in Golubitsky and Wang (2020), up to relabeling, there are 13 connected 3-node networks. They then show that there are 78 3-node input–output networks and prove that up to core equivalence there are three 3-node core networks. The networks are shown in Fig. 2.

Fig. 2

Representatives of the 3-node core equivalence classes. See Golubitsky and Wang (2020). a Core equivalence class with two possible Haldane homeostasis types ($\iota \rightarrow \rho$ and $\rho \rightarrow o$). b Core equivalence class with both Haldane type ($\iota \rightarrow o$) and null-degradation type ($\tau$) homeostasis. c Core equivalence class with feed-forward loop homeostasis type

In this paper we generalize the results of 3-node networks to networks with four nodes and unidirectional arrows. Up to relabeling, there are 199 connected 4-node networks (Harary and Palmer 1973). We observe that there are $199 \times 12 = 2388$ 4-node input–output networks. Theorem 1.3 classifies twenty 4-node core networks up to core equivalence. The original version appeared in Huang (2021).

Theorem 1.3

Up to node relabeling, there are twenty 4-node core equivalence classes. A representative of each core equivalence class is shown in Fig. 3.

Fig. 3

Representatives of the 4-node core equivalence classes. Networks (16–18) have one appendage node, networks (19, 20) have two appendage nodes, and the remaining networks have no appendage nodes

Table 1 lists the 20 networks, their corresponding homeostasis matrices $H$, and the determinants of $H$. Given any biochemical network whose core subnetwork has four nodes one can use the formulae of $\det (H)$ provided in Table 1 to compute infinitesimal homeostasis.

Proposition 1.4

Up to node relabeling, networks in Fig. 3 are pairwise core inequivalent.

Proof

It follows from Table 1 that the 20 determinants of homeostasis matrices associated with the networks in Fig. 3 are distinct; hence, these networks are pairwise core inequivalent. $\square$

Table 1 Enumeration of $H$ matrix and $\det (H)$ for networks in Fig. 3

1.4 Infinitesimal homeostasis types

Note that $\det (H)$ is a polynomial of degree $n+1$ of the partial derivatives of the coordinate functions of F. Using combinatorial graph theory, Wang et al. (2021) show that $H$ can be decomposed into square blocks $B_\eta$ such that

$$\begin{aligned} \det (H) = \det (B_1)\cdots \det (B_m) \end{aligned}$$

(1.6)

is a unique factorization of $\det (H)$ and each $\det (B_\eta )$ is an irreducible polynomial in the partial derivatives $f_{j,x_\ell }$. It follows that for each $\eta = 1, \ldots , m$ the vanishing of $\det (B_\eta )$ is a defining condition for a type of infinitesimal homeostasis.

Each irreducible block in (1.6) is called an irreducible component. If $\det (B_\eta ) = 0$ and $\det (B_\zeta ) \ne 0$ for all $\zeta \ne \eta$, then homeostasis in ${{\mathcal {G}}}$ is categorized as type $B_\eta$. We say a type of infinitesimal homeostasis is of degree k if it corresponds to an irreducible polynomial of degree k. Each block $B_\eta$ can be associated to a homeostasis subnetwork ${{\mathcal {K}}}_\eta$ of ${{\mathcal {G}}}$ (see Wang et al. 2021, Definition 1.14).

Definition 1.5

We call the irreducible polynomial $\det (B_\eta )$ associated with a $k \times k$ irreducible component $B_\eta$ in (1.6) a homeostasis factor type of degree k.

• (a) Two homeostasis factor types of the same degree are equivalent if up to node relabeling of their associated homeostasis subnetworks, they have the same polynomials $\det (B_\eta )$.

• (b) Two homeostasis factor types of the same degree are inequivalent if they are not equivalent.

There are three inequivalent homeostasis factor types in 3-node core networks. They are: $f_{\ell ,x_j}$ ($\ell \ne j$; Haldane homeostasis), $f_{\tau ,x_\tau }$ (null-degradation homeostasis), and (1.4) (feed-forward homeostasis) (Golubitsky and Wang 2020). See Fig. 4 subgraphs (1-3).

Remark 1.6

• (a) Haldane homeostasis occurs when an arrow changes from excitation to inhibition as ${{\mathcal {I}}}$ varies. Null-degradation homeostasis occurs when an individual node changes from degradation to production as ${{\mathcal {I}}}$ varies. Feed-forward homeostasis occurs when the difference of fluxes along two paths go through 0 as in (1.4).

• (b) In Wang et al. (2021) we observe that the homeostasis factor types divide into two distinct classes: structural and appendage (see Wang et al. 2021, Definition 4.3, Theorem 4.7). Structural corresponds to subnetworks with feed-forward motifs and appendage to subnetworks with cycles, hence, feedback motifs.

Theorem 1.7 classifies the homeostasis factor types in 4-node input–output networks. The proof of this theorem relies on results from Wang et al. (2021) and is given in Sect. 4.

Theorem 1.7

In 4-node input–output core networks, there are fifteen inequivalent structural homeostasis factor types and two inequivalent appendage homeostasis factor types. Representatives of their associated subnetworks are shown in Fig. 4.

Fig. 4

Representatives of subnetworks associated with homeostasis factor types in 4-node input–output networks. Note that subgraphs (1–3) occur in 3-node networks (see Fig. 2)

1.5 Structure of the paper

In Sect. 2 we provide three 4-node biochemical examples that exhibit homeostasis: E. coli chemotaxis, allosteric regulation of PFKL/M, and intracellular copper regulation. We also show that classification theorems can simplify the calculations of infinitesimal homeostasis. In Sect. 3 we review concepts introduced in Wang et al. (2021) and prove Theorem 1.3. In Sect. 4 we classify the types of homeostasis factors in 4-node networks as shown in Fig. 4. The paper ends with a discussion Sect. 5.

2 Biochemical examples

In this section we illustrate our classification results with biochemical examples. We analyze three specific network systems that are taken from the literature and exhibit homeostasis. The core subnetworks of the corresponding systems are shown in Fig. 5. In each network, we identify the input node, the output node, and the regulatory nodes. Then, we associate the core network with one of the twenty 4-node core equivalence classes as shown in Fig. 3.

Fig. 5

Core subnetworks of three biochemical examples: a E. coli chemotaxis network from Ma et al. (2009); b Allosteric regulation of PFKL/M from Mulukutla et al. (2014); c Intracellular copper regulation network from Andrade et al. (in preparation)

Figure 5a shows the 4-node input–output core network corresponding to the E. coli chemotaxis network, where the input node $\iota$ is receptor complex, the output node o is enzyme CheY, and regulatory nodes $\rho , \tau$ are methylation level and enzyme CheB respectively. This input–output core network is core equivalent to Fig. 3 (19). Table 2 lists the homeostasis subnetworks, their corresponding homeostasis factor type, and names of the factors.

Table 2 Homeostasis factor types in Fig. 5a

Figure 5b shows the 4-node input–output core network corresponding to the allosteric regulation of PFKL/M, where the input node $\iota$ is fructose 6-phosphate (F6P), the output node o is 6-phosphofructokinase liver/muscle type (PFKL/M), and the regulatory nodes $\rho ,\tau$ are fructose 1,6-bisphosphate (F16BP) and fructose 2,6-bisphosphate (F26BP) respectively. This network is core equivalent to Fig. 3 (6) whose homeostasis condition is listed in Table 3.

Table 3 Homeostasis factor types in Fig. 5b

Remark 2.1

Mulukutla et al. (2014) show that the steady state of PFKL/M concentration increases slowly as the concentration of F6P node varies. The allosteric regulation network consists of feedback activation of PFK via F16BP and feed-forward activation of PFK via F26BP. Mathematically it shows the differences of fluxes along two simple paths (see Definition 3.1 (b)) must balance.

Figure 5c shows a 4-node input–output core network of intracellular copper regulation. In this example extracellular copper ($\text {Cu}_{\text {ext}}$) is the input node, cytosis copper ($\text {Cu}_{\text {cyt}}$) is the output node, and antioxidant protein 1 ($\text {ATOX1}$) and trans-Golgi copper ($\text {Cu}_{\text {TG}}$) are regulatory nodes $\rho ,\tau$ respectively. The 4-node input–output network is core equivalent to Fig. 3 (20). Table 4 lists the homeostasis conditions for this network.

Table 4 Homeostasis factor types in Fig. 5c

The following modeling systems of differential equations associated with the intracellular copper regulation was derived in (Andrade et al. in preparation):

$$\begin{aligned} \begin{array}{rclcl} {\dot{x}}_\iota &{} = &{} {{\mathcal {I}}}- k_0 x_\iota &{} = &{} f_{\iota }(x_\iota ,{{\mathcal {I}}})\\ {\dot{x}}_\rho &{} = &{} g k_3 x_\tau + \omega _2 \frac{x_\tau (x_\rho - x_\tau )}{1+ x_\tau } - k_4 x_\rho &{} = &{} f_\rho (x_\rho ,x_\tau ) \\ {\dot{x}}_\tau &{} = &{} f k_1x_o - k_3 x_\tau - \omega _2 \frac{x_\tau (x_\rho - x_\tau )}{1+x_\tau } &{} = &{} f_\tau (x_\rho ,x_\tau ,x_o)\\ {\dot{x}}_o &{} = &{} \frac{k_0}{N}x_\iota -k_1x_o(1+\omega _1x_o)+k_2G(x_\rho ) &{} = &{} f_o(x_\iota ,x_\rho ,x_o) \end{array} \end{aligned}$$

(2.1)

where $N, f, g, \omega _1, \omega _2, k_0, k_1, k_2, k_3, k_4$ are positive constants, and $G(x_\rho )$ is a quadratic Hill function given by:

$$\begin{aligned} G(x) = \frac{1}{1+x^2} - 1 \end{aligned}$$

It follows from Table 4 that infinitesimal homeostasis can occur if

$$\begin{aligned} 0 = - f_{\rho ,x_\tau }f_{\tau ,x_\rho }&+ f_{\rho ,x_\rho }f_{\tau ,x_\tau } = k_4 \left( k_3 +\omega _2 \frac{x_\rho - 2 x_\tau - {x_\tau }^2}{(1+x_\tau )^2}\right) \nonumber \\&+(g-1) k_3\omega _2\frac{x_\tau }{1+x_\tau } \end{aligned}$$

(2.2)

or

$$\begin{aligned} 0 = f_{o,x_\iota } = \frac{k_0}{N} \end{aligned}$$

(2.3)

Note $\frac{k_0}{N} > 0$; so, infinitesimal homeostasis occurs if and only if (2.2) is satisfied.

3 Enumeration of four-node core equivalent classes

In this section we identify all 4-node core networks up to core equivalence. The mathematics needed to prove these results depend on results in Wang et al. (2021).

Definition 3.1

(Wang et al. 2021, Definition 1.15)

• (a) A directed path connecting two nodes is a simple path if it visits each node on the path exactly once.

• (b) An $\iota o$-simple path is a simple path connecting the input node $\iota$ to the output node o.

• (c) A node in ${{\mathcal {G}}}$ is simple if the node lies on an $\iota o$-simple path and appendage if the node is not simple.

• (d) The appendage subnetwork $A_{{\mathcal {G}}}$ of ${{\mathcal {G}}}$ is the subnetwork consisting of all appendage nodes and all arrows in ${{\mathcal {G}}}$ connecting appendage nodes.

• (e) The complementary subnetworks of an $\iota o$-simple path S is the subnetwork $C_S$ consisting of all nodes not on S and all arrows in ${{\mathcal {G}}}$ connecting those nodes.

• (f) A backward arrow is an arrow whose head is the input node $\iota$ or whose tail is the output node o.

Note that the input node $\iota$ and the output node o are simple nodes (see Definition 1.2(b)). Thus, a 4-node input–output core network can have a minimum of two simple nodes and a maximum of four simple nodes.

Theorem 3.2

(Wang et al. 2021, Theorem 3.2) Two core networks are core equivalent if and only if they have the same set of $\iota o$-simple paths and the Jacobian matrices of the complementary subnetworks to any simple path have the same determinant up to sign.

Proposition 3.3

If two $(n+2)$-node core networks differ from each other by the presence or absence of backward arrows, then they are core equivalent.

Proof

The proof follows directly from Theorem 3.2. $\square$

Proposition 3.3 implies that when classifying homeostasis we can ignore backward arrows. A natural question arises: Can we ignore backward arrows when enumerating all 4-node core equivalence classes? The answer is no: There are core networks containing backward arrows that are non-core if the backward arrows are removed. For example, Fig. 6 is a non-core network obtained by eliminating the backward arrow of the core network shown in Fig. 3 (19). This network is non-core since nodes $\tau$ and $\rho$ are not downstream from the input node $\iota$.

Fig. 6

Example of a non-core network obtained from Fig. 3 (19) by deleting the backward arrow

Proposition 3.4

Let ${{\mathcal {G}}}$ be an input–output core network without appendage nodes. Let ${\tilde{{{\mathcal {G}}}}}$ be the network obtained from ${{\mathcal {G}}}$ by deleting all backward arrows. Then ${\tilde{G}}$ is a core network and is core equivalent to ${{\mathcal {G}}}$.

Proof

Since ${{\mathcal {G}}}$ has no appendage nodes, every node of ${{\mathcal {G}}}$ lies on an $\iota o$-simple path. Because simple paths do not contain backward arrows, ${\tilde{{{\mathcal {G}}}}}$ has the same set of simple paths as ${{\mathcal {G}}}$. Hence, ${\tilde{{{\mathcal {G}}}}}$ is a core network. It follows from Proposition 3.3 that ${{\mathcal {G}}}$ and ${{\tilde{{{\mathcal {G}}}}}}$ are core equivalent. $\square$

Theorem 3.2 implies that the classification of 4-node core equivalence classes can be done by enumerating all possible sets of simple paths and their corresponding complementary subnetworks. Note ${{\mathcal {G}}}$ can have up to five of the following $\iota o$-simple paths:

$$\begin{aligned} \iota \rightarrow o \qquad \iota \rightarrow \rho \rightarrow o \qquad \iota \rightarrow \tau \rightarrow o \qquad \iota \rightarrow \rho \rightarrow \tau \rightarrow o \qquad \iota \rightarrow \tau \rightarrow \rho \rightarrow o. \end{aligned}$$

We classify the 4-node core equivalence classes as follows. First, we enumerate all fifteen 4-node core networks without appendage nodes and backward arrows up to core equivalence (Theorem 3.5). Next, we enumerate five 4-node core equivalence classes with one appendage node (Theorem 3.6) and two appendage nodes (Theorem 3.7).

Theorem 3.5

In 4-node networks without appendage nodes there are fifteen core equivalence classes up to node relabeling. The representative networks are those without backward arrows and they are shown in Fig. 3 (1–15).

Proof

Let ${{\mathcal {G}}}$ be a 4-node core network without appendage nodes. Proposition 3.4 implies we can delete the backward arrows of ${{\mathcal {G}}}$. In addition, it follows from Theorem 3.2 that to classify all 4-node core equivalence classes it suffices to enumerate the networks ${{\mathcal {G}}}$ with all possible sets of simple paths and the determinant of the Jacobian matrix of the corresponding complementary subnetworks. It follows from Proposition 1.4 that the networks in Fig. 3 (1–15) are pairwise core inequivalent. We will show every core network ${{\mathcal {G}}}$ is core equivalent to one of the networks in Fig. 3 (1–15) up to node relabeling.

We observe that every node of ${{\mathcal {G}}}$ lies on at least one $\iota o$-simple path. Note that ${{\mathcal {G}}}$ can have up to five of the following $\iota o$-simple paths:

$$\begin{aligned} \iota \rightarrow o \qquad \iota \rightarrow \rho \rightarrow o \qquad \iota \rightarrow \tau \rightarrow o \qquad \iota \rightarrow \rho \rightarrow \tau \rightarrow o\qquad \iota \rightarrow \tau \rightarrow \rho \rightarrow o. \end{aligned}$$

In particular, the pair of simple paths:

$$\begin{aligned} \iota \rightarrow \rho \rightarrow \tau \rightarrow o \qquad \text{ and } \qquad \iota \rightarrow \tau \rightarrow \rho \rightarrow o \end{aligned}$$

will give rise to two additional simple paths:

$$\begin{aligned} \iota \rightarrow \rho \rightarrow o \qquad \text{ and } \qquad \iota \rightarrow \tau \rightarrow o. \end{aligned}$$

Also note the complementary subnetworks of ${{\mathcal {G}}}$ associated with the simple path $\iota \rightarrow o$ have two nodes $\rho , \tau$; thus, the complementary subnetwork associated with $\iota \rightarrow o$ can have the following different forms:

$$\begin{aligned} \{\tau ,\rho \} \qquad \tau \rightarrow \rho \qquad \rho \rightarrow \tau \qquad \tau \leftrightarrow \rho . \end{aligned}$$

where the determinants of Jacobian matrices associated with the first three forms are the same and they are given by $f_{\tau ,x_\tau } f_{\rho ,x_\rho }$. The determinant of the last form is given by:

$$\begin{aligned} f_{\tau ,x_\tau } f_{\rho ,x_\rho } - f_{\tau ,x_\rho } f_{\rho ,x_\tau } \end{aligned}$$

We classify the core equivalence classes based on the number of simple paths. We proceed as follows. First, suppose ${{\mathcal {G}}}$ has $k = 1,2,3,4,5$ simple paths. Then, we list all possible sets of simple paths $S_1,\ldots , S_k$ and their associated complementary subnetworks $C_{S_1}, \ldots , C_{S_k}$ of the networks ${{\mathcal {G}}}$. Next, we eliminate networks that are the same up to node relabeling. Lastly, we identify the network in Fig. 3 that ${{\mathcal {G}}}$ is core equivalent to (up to node relabeling).

Suppose ${{\mathcal {G}}}$ has only one $\iota o$-simple path. Then both the node $\rho$ and the node $\tau$ are contained in S; in Table 5 we list all possible sets of simple path (S), their corresponding complementary subnetwork $(C_S)$, and representative of their associated core equivalence classes (indicated by net). Up to node relabeling, we obtain one network and it is core equivalent to Fig. 3 (1).

Table 5 Network with one simple path. Net refers to the subgraph in Fig. 3

Next, suppose ${{\mathcal {G}}}$ has two $\iota o$-simple paths. In Table 6 we display the combinations of simple paths $S_1,S_2$, their corresponding complementary subnetworks $C_{S_1},C_{S_2}$, and representative of their associated core equivalence classes. Up to node relabeling, it yields five different networks. The core equivalence classes associated to these networks are shown in Fig. 3 (2)–(6).

Table 6 Networks with two simple paths

Suppose ${{\mathcal {G}}}$ has three simple paths. As shown in Table 7 up to node relabeling, we obtain six core equivalence classes given by Fig. 3 (7–12).

Table 7 Networks with three simple paths

Assume ${{\mathcal {G}}}$ has four simple paths. As shown in Table 8 up to node relabeling, we obtain two core equivalence classes given by Fig. 3 (13, 14).

Table 8 Networks with four simple paths

If ${{\mathcal {G}}}$ has five simple paths, then there is only one enumeration of core network as shown in Fig. 3 (15). $\square$

Theorem 3.6

In networks with one appendage node, there are three 4-node core equivalence classes up to node relabeling. They are illustrated in Fig. 3 (16–18).

Proof

WLOG, let ${{\mathcal {G}}}$ be a 4-node core network with input node $\iota$, output node o, simple node $\rho$, and appendage node $\tau$. ${{\mathcal {G}}}$ can have two possible $\iota o$- simple paths: $\iota \rightarrow o$ and $\iota \rightarrow \rho \rightarrow o$. We classify all three networks by the number of simple paths in ${{\mathcal {G}}}$.

One simple path Suppose ${{\mathcal {G}}}$ has only one simple path. Since $\rho$ is a simple node, we have $\iota \rightarrow \rho \rightarrow o$ as the only simple path of ${{\mathcal {G}}}$. Note that the Jacobian matrix of the complementary subnetwork to this simple path is the trivial term $f_{\tau ,x_\tau }$. It follows from Theorem 3.2 that up to core equivalence, there is only one network associated with this simple path, and it is given by Fig. 3 (16).

Two simple paths Suppose ${{\mathcal {G}}}$ has both simple paths: $\iota \rightarrow o$ and $\iota \rightarrow \rho \rightarrow o$. The Jacobian matrix of the complementary subnetwork to the simple path $\iota \rightarrow \rho \rightarrow o$ contains the internal dynamic $f_{\tau ,x_\tau }$. However, the Jacobian matrix of the complementary subnetwork to the simple path $\iota \rightarrow o$ is a $2 \times 2$ matrix, whose determinant can have two different forms: $f_{\tau ,x_\tau } f_{\rho ,x_\rho }$ and $f_{\rho ,x_\rho }f_{\tau ,x_\tau } -f_{\rho ,x_\tau }f_{\tau ,x_\rho }$; thus, we obtain two different networks up to core equivalence as shown in Fig. 3 (17, 18).

$\square$

Theorem 3.7

Up to core equivalence, there are two 4-node core networks with two appendage nodes and they are given by Fig. 3 (19, 20).

Proof

Let ${{\mathcal {G}}}$ be a 4-node core network with input node $\iota$, output node o, and appendage nodes $\tau ,\rho$. The only $\iota o$-simple path is the arrow $\iota \rightarrow o$. The Jacobian matrix of the complementary subnetwork to the simple path $\iota \rightarrow o$ is a $2 \times 2$ matrix, whose determinant can have two different forms: $f_{\tau ,x_\tau } f_{\rho ,x_\rho }$ and $f_{\rho ,x_\rho }f_{\tau ,x_\tau } -f_{\rho ,x_\tau }f_{\tau ,x_\rho }$; hence, it yields two different networks up to core equivalence given by Fig. 3 (19, 20).

$\square$

4 Classification of infinitesimal homeostasis in four-node input–output networks

In this section we determine the infinitesimal homeostasis types that can occur in 4-node input–output networks through classifying homeostasis blocks in the 4-node core equivalence classes. We first introduce the following definition of reducibility:

Definition 4.1

Let $H$ be a homeostasis matrix of the input–output network ${{\mathcal {G}}}$. Then ${{\mathcal {G}}}$ is irreducible if the polynomial $\det (H)$ cannot be factored and is reducible if $\det (H)$ can be factored.

Wang et al. (2021) prove that when a degree k irreducible component $B_\eta$ of (1.6) is appendage, its associated homeostasis subnetwork $K_\eta$ has k nodes; on the other hand, if $B_\eta$ is structural, it has $k+1$ nodes.

Proposition 4.2

Homeostasis factor types found in the irreducible networks of Fig. 3 are pairwise inequivalent and they are associated with structural homeostasis factor types of degree 3.

Proof

First we note that each irreducible network contains only one homeostasis factor $\det (H)$. It follows from Theorem 1.3 that irreducible networks in Fig. 3 are pairwise core inequivalent up to node relabeling. Table 1 then implies that these factor types are pairwise inequivalent. It follows that these factors belong to structural homeostasis factor types of degree 3. $\square$

We recall the following inequivalent homeostasis factor types of degree 1 and 2 as identified in Wang et al. (2021).

4.1 Degree 1 no cycle appendage homeostasis (null-degradation)

This corresponds to the vanishing of a degree 1 irreducible factor of the form $f_{\tau , x_\tau }$. It arises when the degradation constant of the appendage node $\tau$ is zero.

4.1.1 Degree 1 structural homeostasis (Haldane)

This corresponds to the vanishing of a degree 1 irreducible factor of the form $f_{j,x_\ell }$ ($j\ne \ell$). It arises when the arrow $\ell \rightarrow j$ changes from excitation to inhibition as ${{\mathcal {I}}}$ varies.

4.1.2 Degree 2 structural homeostasis (feed-forward loop)

This corresponds to the vanishing of a degree 2 irreducible factor of the form:

$$\begin{aligned} f_{\rho ,x_{\ell }} f_{j,x_{\rho }} - f_{j,x_{\ell }}f_{\rho ,x_{\rho }} \end{aligned}$$

It occurs when the difference of fluxes along two paths ($\ell \rightarrow \rho \rightarrow j$ and $\ell \rightarrow j$) go through 0.

4.1.3 Degree 2 no cycle appendage homeostasis

This is associated with the vanishing of a degree 2 irreducible factor of the form:

$$\begin{aligned} f_{\tau _1, x_{\tau _1}} f_{\tau _2, x_{\tau _2}} - f_{\tau _1, x_{\tau _2}} f_{\tau _2, x_{\tau _1}} \end{aligned}$$

It occurs when the difference of fluxes along the appendage path component ($\tau _1 \Leftrightarrow \tau _2$) goes to 0.

Table 9 Networks with low degree $k=1$ and $k=2$ structural homeostasis factor types

Table 10 Networks with low degree $k=1$ and $k=2$ appendage homeostasis factor types

4.1.4 Proof of Theorem 1.7

Proof

It follows from Table 1 that we can partition the twenty 4-node core equivalence classes into the following three categories:

• (a) Irreducible networks: 2, 3, 6-15, 17.

• (b) Networks with three degree 1 irreducible factors: 1, 16, 19.

• (c) Networks with one degree 1 and one degree 2 irreducible factors: 4, 5, 18, 20.

First we show there are fifteen inequivalent structural homeostasis factor types in 4-node networks. It follows from (a) and Proposition 4.2 that there are thirteen inequivalent structural homeostasis factor types in 4-node irreducible networks. In addition, it follows from Table 9 that all two structural homeostasis factor types of degree 1 and 2 can be found in networks of category (b) and (c).

It remains to show there are two inequivalent appendage homeostasis factor types. It follows from Table 10 that all two appendage homeostasis factor types of degree 1 and 2 can be found in networks of category (b) and (c). $\square$

Remark 4.3

In general, structural homeostasis types do not result from neutral coupling and require a balance of coupling strengths between two or more simple paths.

5 Discussion

In this paper we categorize twenty core equivalence classes and seventeen inequivalent infinitesimal homeostasis factor types in 4-node networks. We note that certain issues are not addressed yet in this paper. The literature contains many biochemical examples of 3-node networks to support how low degree homeostasis types can arise (Ma et al. 2009; Reed et al. 2017; Golubitsky and Wang 2020). Future work includes finding biochemical examples of 4-node networks that lead to different types of infinitesimal homeostasis. A natural question is whether the different types of infinitesimal homeostasis lead to different types of biochemical behavior. Answering this question requires investigation into how homeostasis can arise in different biochemical networks. The finding of more 4-node biochemical examples could potentially help us to better understand structural homeostasis types of degree 3 or higher. Moreover, we wish to explore how we can use the classification theorem to find infinitesimal homeostasis in specific biochemical networks.