1 Introduction

Bone tissue is constantly being renewed. Its remodeling is a dynamic, spatially heterogeneous process, for which several mathematical models have been proposed in the literature. Such models may concern only healthy bone tissue (Komarova et al. 2003; Lemaire et al. 2004; Komarova 2005; Pivonka et al. 2008; Ryser et al. 2009, 2010; Pivonka et al. 2010; Buenzli et al. 2011; Zumsande et al. 2011; Graham et al. 2013; Pivonka et al. 2013), or may include also the effects of tumors (Wang et al. 2011; Ryser et al. 2012); in the latter case, the effects of cancer treatments can be included too (Ayati et al. 2010; Araujo et al. 2014; Coelho et al. 2016a; Christ et al. 2016). This paper reviews those models and concentrates on those that employ fractional derivatives, i.e. models with derivatives of orders that are not necessarily integer (Christ et al. 2016). Such orders can, in fact, be fractional or irrational; they can also be time-varying. These variable order derivatives allow simpler formulations of the models (Neto et al. 2017a, b; Valério et al. 2019; Neto et al. 2019; Coelho et al. 2016b). This paper collects and reviews mostly published models, but the explicit consideration of variable order models for tumorous bone tissue, including the effects of available treatments for bone metastasis, including both anti-cancer and anti-resorptive therapies, as well as its spatial diffusion, and its pharmacokinetics (PK) and pharmacodynamics (PD) effects, is a novelty.

The remainder of this paper is organized as follows. Section 2 surveys the mechanisms of bone remodeling, explaining how it takes place. In Sect. 3, existing mathematical models, with integer order derivatives, for bone remodeling, metastasis and therapy are passed in review. Pharmacokinetics (PK) and pharmacodynamics (PD) control mechanisms of applied drugs are also included in this section. In Sect. 4, important mathematical formulations for fractional and variable order derivatives are introduced, focusing on Grünwald-Letnikoff constructions. In Sect. 5, variable order models are presented. The models which are novel in this paper are found here, in Sect. 5.2. Obtained simulation results are also discussed. Finally, conclusions and future work are summed up in Sect. 6.

2 Processes of bone remodeling

Bone remodeling takes place in cycles, which are regular, yet asynchronous. Such cycles affect at each instant 5 to 25 % of the total bone surface available (Crockett et al. 2011). Bone remodeling takes place in temporary anatomical structures within the bone, called Basic Multicellular Units (BMUs). In a BMU, bone is resorbed and then sequentially formed (Parfitt 1994). An active BMU can travel across the tissue at a constant speed of 20 to 40 \(\mu \)m/day, for up to 6 months. Autocrine and paracrine factors controlled the interaction between the different clusters of bone cells tightly (Raggatt and Partridge 2010).

Bone degrading occurs due to multinucleated cells called osteoclasts. There are 10 to 20 osteoclasts in a BMU (Ryser 2011). These cells are the result of the fusion of mononucleated hematopoietic stem with progenitors cells, that express Receptor Activator of Nuclear Factor kB (RANK) and Macrophage Colony-stimulating Factor Receptor (c-fms). They differentiate into active osteoclasts, able to resorb bone, by biding to RANK-ligand (RANKL) and Colony-stimulating Factor 1 (CSF-1), respectively. Osteoclast performance is also due to osteoprotegerin (OPG), which is a soluble decoy receptor for RANKL, and a physiological negative regulator of osteoclastogenesis (Boyce 2012; Raggatt and Partridge 2010). BMU extension is due to the generation rate of osteoclasts. BMU life span determines the depth of the resorption (Bellido et al. 2014).

Bone formation occurs due to mononucleated cells called osteoblasts. There are 1000 to 2000 ostoblats in a BMU, secreting and depositing unmineralized bone matrix, directing its formation and mineralization into mature lamellar bone (Ryser 2011). Osteoblasts differentiate from mesenchymal stem cells (MSC). These are controlled, among other factors, by bone morphogenetic protein (BMP), Wnt-signaling, and vitamin D. Osteoblasts express parathyroid hormone (PTH) receptors. The expression of RANKL is upregulated by osteoblasts and cells of the osteoblastic lineage in response to PTH. RANKL binds to RANK, expressed in osteoclasts precursors, and promotes their activation (i.e. promotes bone resorption). Osteoclasts precursors also produce OPG, which binds to RANKL thus inhibiting osteoclastogenesis. OPG secretion is reduced in response to PTH, thereby furthering osteoclastogenesis. Osteoblasts can undergo apoptosis, differentiate into osteocytes, or differentiate into bone lining cells (Crockett et al. 2011; Roodman 2004).

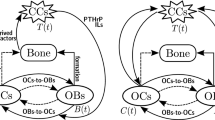
PTH and the RANK/RANKL/OPG pathway are the principal regulators of bone resorption and formation. Bone remodeling can be activated by a mechanical stimulus on the bone, or due to systemic changes in homeostasis producing estrogen or PTH (Raggatt and Partridge 2010). The latter is triggered in response to a reduced calcium concentration. This leads to calcium release from the bone matrix. An elevated calcium concentration, on the other hand, inhibits the process (Silva and Bilezikian 2015). Bone remodeling begins when PTH triggers two mechanisms in the osteoblasts. First, existing PTH reduces osteoblasts secretion of OPG. OPG is a soluble decoy receptor for RANKL and thus allows it to bind to RANK. It promotes osteoclastogenesis in this way. Second, PTH receptors also upregulate the expression of RANKL. Again, RANKL binds to RANK, and this promotes osteoclast activation and bone resorption (Raggatt and Partridge 2010). How the formation phase is coupled to the resorption phase is not yet fully understood, since factors released from the bone matrix during resorption (Insulin Growth Factors I and II (IGF-I, IGF-II), and Transforming Growth Factor-\(\beta \) (TGF-\(\beta \))) may be involved. Figure 1 shows a diagram of the healthy bone remodeling process. Bone formation takes place even in the presence of malfunctioning osteoclasts. This has led to the hypothesis that the coupling factors responsible for attracting and regulating osteoblasts to the sites of bone resorption are produced by osteoclasts (Boyce 2012). Osteoblasts begin forming bone at the resorpted site. Resorpted bone is replaced by the same amount of bone. This ends the bone remodeling cycle.

Fig. 1
figure 1

Biochemical processes of healthy bone remodeling. For a healthy bone environment, PTH stimulates RANKL production by osteoblasts as the RANK/RANKL/OPG pathway plays an important role in bone resorption and formation. See also Fig. 2 for abnormal bone remodeling

Full size image

From this description it is seen that the BMU can be seen as a mediator mechanism. It bridges individual cellular activity to whole bone morphology (Raggatt and Partridge 2010).

Bone pathologies disrupt the biochemical regulation of bone remodeling. They can affect and deregulate it significantly. Consequently, bone integrity may be lost. Tumors have the capacity of spreading into organs other than its primary site. They often form metastasis in bone, according to the seed and soil hypothesis of Paget. Tumor cells interfere with the bone marrow to grow and proliferate. Sites of cancer metastasis are usually those where bone remodeling rates are high. The pelvis, the axial skeleton, or bones with abundant bone marrow are examples thereof (Boyce 2012; Schneider et al. 2005).

Bone metastases can be of two kinds. In osteolytic metastases, bone resorption is increased; in osteoblastic ones, bone formation is stimulated, but in an unstructured way. In both, bone resorption and formation take place but out of balance. Thus bone resistance and integrity decrease. Metastases in bone tissue originated from breast or prostate cancer often develop osteolytic or osteoblastic respectively (Suva et al. 2011).

In the bone remodeling deregulation resulting from osteolytic metastases, tumor cells stimulate bone resorption (Chen et al. 2010; Huang et al. 2020). Considering the vicious cycle theory proposed in Mundy and Calcium (1998), cancer cells resident in bone can cause its destruction by stimulating osteoclast activity and receiving, in return, positive feedback from humoral factors released by the bone micro-environment during bone destruction (Casimiro et al. 2016). TGF-\(\beta \) is released from the bone matrix during resorption stimulating both tumor growth and parathyroid hormone-related protein (PTHrP) production in the cells of the metastasis. RANKL levels increase by binding to PTH receptors on cells of osteoblastic lineage. Osteoclasts are then activated, and this has two consequences: bone resorption increases (Casimiro et al. 2016), and TGF-\(\beta \) is released from the degraded bone. TGF-\(\beta \) further stimulates tumor growth and PTHrP secretion. Thus the vicious cycle is closed. This disruption of bone homeostasis is represented in Fig. 2.

Fig. 2
figure 2

Biochemical processes of abnormal bone remodeling. For the progression of osteolytic bone metastases, the vicious cycle is due to bone-derived tumor growth factors (IGFs,TGF-\(\beta \), BMP, among others), tumor-derived factors that stimulate bone resorption (PTHrP, TGF-\(\beta \), among others), and to tumor derived factors that affect bone formation (BMP, IGFs, among others) while PTHrP stimulates RANKL production by osteoblasts. See also Fig. 1 for healthy bone remodeling, and its caption for the symbols not explained in this figure

Full size image

In the bone remodeling deregulation resulting from osteoblastic metastases, tumorous cells grow because bone expresses endothelin-1 (ET-1), which stimulates osteoblasts by means of the endothelin A receptor (ETR), activating Wnt-signaling. Tumor-derived proteases increase the release of osteoblastic factors, including TGF-\(\beta \) and IGF-I, from the extracellular matrix. Osteoblast activity induced by the tumor increases RANKL. This leads to PTH release and promotes osteoclast activity (Casimiro et al. 2016). Thus, the micro-environment of the tumor leads to the accumulation of new bone tissue.

There are different possible treatments of bone tumors, be they primary or methastatic. Treatments affect healthy cells as well. Thus a possible treatment strategy is to target not the tumor alone, but also the bone and its micro-environment (Li et al. 2019). In the case of an osteolytic metastatic bone disease, osteoclasts are targeted by anti-resorptive therapy, using bisphosphonates (such as alendronate or zoledronic acid) (Zometa 2017; Chen et al. 2002) and monoclonal antibodies (like denosumab) (Sohn et al. 2014; Gibiansky et al. 2012). Bisphosphonates lodge in bone and poison osteoclasts that degrade it. Monoclonal antibodies bind exclusively to RANKL, increase the OPG/RANKL ratio, and inhibit osteoclast formation. Therapies for other diseases such as multiple myeloma (MM) include daily doses of PTH, endothelin and proteasome inhibitors. These target osteoblasts to recover bone mass (Oyajobi et al. 2007). Anti-cancer agents (hormone therapy and chemotherapy such as paclitaxel Perez et al. 2001) that directly target metastatic and primary tumor cells are employed together with the aforementioned therapies (Casimiro et al. 2009).

The biochemical process of bone remodeling can be replicated through mathematical and computational models. The comparison of a healthy bone behavior with pathological states (Komarova et al. 2003; Ayati et al. 2010) was made possible, serving these models as clinical decision support systems for the implementation of therapeutic regimes (Ayati et al. 2010; Coelho et al. 2016a, 2015; Christ et al. 2016; Araujo et al. 2014). They consist of a system of ordinary differential equations that relate the interactions between osteoclasts and osteoblasts, by reproducing the effects of autocrine and paracrine control mechanisms. The resulting calculation of the dynamic response of these cells populations determines the changes in bone mass in the bone remodeling cycles. A local model, for healthy bone tissue, was initially proposed in Komarova et al. (2003) and further extended in Ayati et al. (2010) to include the influence of multiple myeloma (MM) disease and the counteraction of a treatment in the bone dynamics, based in proteasome inhibitors. It also proposed a non-local approach with diffusion.

Biological processes often present anomalous diffusion (Magin 2006), allowing for fractional derivatives to be introduced in the existing models (Sierociuk et al. 2013; Rahimy 2010). Many physical processes, however, also appear to exhibit a fractional order behavior that varies with time or space (Valério and Sá da Costa 2013; Lorenzo and Hartley 2002). Consequently, variable order derivatives can be introduced in the biochemical models of bone remodeling. This strategy, as a simplification technique, was already implemented in Neto et al. (2017a) and Neto et al. (2017b). Although models with more physiological details were proposed (reviewed below in Sects. 3.1 and 3.2 ), variable order derivatives were applied only to the simpler models of Komarova et al. (2003) and Ayati et al. (2010). However, the scope of applications of variable order derivatives is only expected to grow (Magin 2006).

All models presented here use dimensionless variables and parameters, including the cell populations, except when explicitly said otherwise in Table 2. \(D^1\) refers to the first order derivative in time, \(\frac{\mathrm {d}}{\mathrm {d}t}\) and \(D^{\alpha (t)}\) or \(D^{\alpha (t,x)}\) refers to the Grünwald-Letnikoff type-\(\mathcal {D}\) variable order derivative, \({^{\mathcal {D}}_{-\infty }\mathrm {D}^{\alpha (t)}_t}\) or \({^{\mathcal {D}}_{-\infty }\mathrm {D}^{\alpha (t,x)}_t}\).

3 Models for bone remodeling using integer order derivatives

Mathematical and computational models can replicate the dynamics of bone remodeling, and its interaction with tumor cells. As a tool for an augmented experimental analysis, these models are important to simulate the biochemical processes occurring in the bone micro-environment that promote the progression of such disease (Pivonka and Komarova 2010).

Differential equations model the biochemical and biomechanical interactions in bone. Such models can be local or non-local; the latter are usually formulated in one-dimension, the extension to three-dimensions being trivial. Three cases can be consideder: healthy bone, tumorous bone, and tumorous bone undergoing treatment. Table 1 provides a useful road-map into the published models.

Table 1 Classification of the published models for biochemical bone remodeling, considering: H for a healthy bone environment; T for a tumor disrupted bone; and T&T for a bone tumor counteracted with therapy
Full size table

In Sect. 3.1, several local models for bone remodeling dynamics found in the literature are reviewed. Section 3.2 does the same for non-local models. In Sect. 3.3, PK/PD relations are explained, as progress in understanding the genetic basis of cancer coupled to molecular pharmacology of potential new anticancer drugs calls for new approaches that are able to address key issues in the drug development process.

3.1 Local models

The very simple model of Komarova et al. (2003)

$$\begin{aligned} D^1 C(t) =&\alpha _{_C} C(t)^{g_{_{CC}}} B(t)^{g_{_{BC}}} - \beta _{_C} C(t) \end{aligned}$$
(1a)
$$\begin{aligned} D^1 B(t) =&\alpha _{_B} C(t)^{g_{_{CB}}} B(t)^{g_{_{BB}}} - \beta _{_B} B(t) \end{aligned}$$
(1b)
$$\begin{aligned} D^1 z(t) =&- \kappa _{_C}\max \left[ 0,C(t)-C_{_{ss}}\right] + +\kappa _{_B}\max \left[ 0, B(t)-B_{_{ss}}\right] \end{aligned}$$
(1c)

takes the form of an S-system (Savageau 1988). Exponents implicitly express biochemical autocrine (\(g_{_{CC}}\), \(g_{_{BB}}\)) and paracrine (\(g_{_{BC}}\), \(g_{_{CB}}\)) factors that couple the behavior of osteoclasts, C(t), and osteoblasts, B(t). The excess of C(t) and B(t) over their respective nontrivial steady states \(C_{_{SS}}\) and \(B_{_{SS}}\) determines the evolution of the bone mass density z(t) through bone resorption and formation coefficients \(\kappa _{_C}\) and \(\kappa _{_B}\). \(\alpha _{_C,B}\) and \(\beta _{_C,B}\) are the rates of production and death of the bone cells.

Depending on the values of autocrine and paracrine parameters, and in particular of the osteoblast-derived osteoclast paracrine regulator \(g_{_{BC}}\) that implicitly represents the RANK/RANKL/OPG pathway, this model may represent a single remodeling cycle or periodic remodeling cycles, with amplitude and frequency determined by initial conditions. A deviation from the steady-state triggers the cycles. Simulation results for this model can be found in Fig. 3. Used parameters are the same as in Ayati et al. (2010) and presented in Table 3, as the osteoclast population triggered the periodical remodeling response by an increase 10 units above its steady-state.

Fig. 3
figure 3

Osteoclasts, Osteoblasts and Bone Mass evolutions, respectively. Dotted line: simulation of (1) for the existing model replicating a healthy bone micro-environment. Full line: simulation of (2), for a bone micro-environment disrupted by a developing tumor. Dashed line: simulation of the simplified tumorous model (16), considering the treatment parameters to be null, as in Neto et al. (2017b). Parameters were set according to Ayati et al. (2010), and can be found in Table 3. The variable order model was simulated with the same values as the healthy case, except the actualized resorption rate of \(\kappa _{_C}=0.1548\), \(\kappa _{_B}=6.4924\times 10^{-4}\) for \(R = 238.43\), and \(\theta =4\times 10^{-8}\). Corresponding tumor evolution, equal for both model with metastases, can be found in the first graphic of Fig. 11

Full size image

In Komarova (2005), the anabolic and catabolic effects of the external administration of PTH are included, for a single remodeling cycle behavior of the model explained in Komarova et al. (2003). A bifurcation analysis to the generalized bone remodeling model is performed in Zumsande et al. (2011), and then applied to the models of Komarova et al. (2003), and extended incorporating osteoblasts precursors as a variable in the system. In Ryser et al. (2009), the influence of the OPG and RANKL concentrations were explicitly added into the system of Komarova et al. (2003). A parameter estimation and sensitivity analysis of this model is presented in Ryser et al. (2010). The original model of Komarova et al. (2003) was further extended in Graham et al. (2013). Osteocytes and pre-osteoblasts were included in the model, predicting an osteocyte induced bone remodeling, after the global apoptosis of a specific BMU. A new approach is presented in Lemaire et al. (2004), where the RANK/RANKL/OPG pathway, TGF-\(\beta \) and PTH were explicitly incorporated in the proposed model. Bone cells were mathematically encompassed as osteoblasts percursors, active osteoblasts and active osteoclasts, and their interaction is represented through the kinetic reaction of these molecules. Pivonka et al. (2008) extends the previous model to include bone mass dynamics and the production of both OPG and RANKL by the two types of osteoblastic lineage cells. Pivonka et al. (2010) provides a theoretical study on the role of the RANK/RANKL/OPG pathway in the system. It simulated several bone diseases by changing the values of the parameters, proposing treatment strategies for disturbances in this pathway.

More recently, Coelho et al. (2016a) proposed the integration of PTH into the model of Komarova et al. (2003), by adding a differential equation for its concentration. An increase in PTH increases the production of RANKL by osteoblasts, thus affecting \(g_{_{BC}}\) and initiating a single remodeling cycle.

The models can be adapted to include effects of pathologies. The model proposed in Ayati et al. (2010) extends the one in Komarova et al. (2003), incorporating in the bone dynamics the effect of MM:

$$\begin{aligned} D^1 C(t)=&\alpha _{_C}{C(t)}^{{g_{_{CC}}}\left( 1+r_{_{CC}}\frac{T(t)}{L_T}\right) }{B(t)}^{{g_{_{BC}}}\left( 1+r_{_{BC}}\frac{T(t)}{L_T}\right) } -\beta _{_C}C(t) \end{aligned}$$
(2a)
$$\begin{aligned} D^1 B(t)=&\alpha _{_B}{C(t)}^{\left( \frac{{g_{_{CB}}}}{1+r_{_{CB}}\frac{T(t)}{L_T}}\right) }{B(t)}^{\left( {g_{_{BB}}}-r_{_{BB}}\frac{T(t)}{L_T}\right) } -\beta _{_B}B(t) \end{aligned}$$
(2b)
$$\begin{aligned} D^1 T(t)=&\gamma _{_T}T(t)\log {\left( \frac{L_T}{T(t)}\right) } \end{aligned}$$
(2c)

T(t) is the density of tumor cells at time t, with a Gompertz form of constant growth \(\gamma _{_T} > 0\). The tumor affects the autocrine and paracrine regulation pathways through \(r_{_{ij}}\) parameters. The effect of the tumor is assumed to be independent of the bone mass; periodic remodeling cycles are deregulated; bone mass density decreases. The maximum tumor size is \(L_T\). The bone mass equation is the same of (1c) In Fig. 3, a simulation of the bone micro-environment for (2) can be found, for parameters set according to Ayati et al. (2010) and given in Table 3.

In Wang et al. (2011), the model of Pivonka et al. (2008) is also extended to include the influence of MM in the bone micro-environment. It was done by considering the disease vicious cycle results from the interaction between the bone micro-environment and MM cells, by explicitly including interleukin-6 (IL-6) and MM marrow stromal cell adhesion in the model. Coelho et al. (2016a) also allowed for the disruptive action of an osteolytic tumor to be included. Growth of bone metastasis, and its influence in the bone micro-environment, is achieved by encoding the production of PTHrP by the metastatic cells, when TGF-\(\beta \) is released from the bone in the resorption phase. Tumor treatment was also proposed. Proteasome inhibitors are known to have direct anti-myeloma effects and to have direct effect on osteoblasts, to stimulate osteoclast differentiation and bone formation. They were added into model proposed in Ayati et al. (2010), as two time dependent step functions.

In Coelho et al. (2015), a treatment of osteolytic bone metastases through anti-cancer and anti-resorptive therapy is proposed, adapting the model of Ayati et al. (2010) as presented in (3). It corresponds to the administration of two different chemotherapy (\(d_{c_{34}}\)) drugs combined with either bisphosphonates (\(d_{_2}\)) or monoclonal antibodies (\(d_{_1}\)). Bisphosphonates (e.g. zoledronic acid or alendronate) promote osteoclast apoptosis, and monoclonal antibodies (e.g. denosumab) indirectly inhibit osteoclast formation (Camacho and Jerez 2019) by acting as a decoy receptor for RANKL. Together with chemotherapy, the drug effect of this treatment was included in the model through their PK/PD action. The bone mass equation, z(t), remains equal to (1c).

$$\begin{aligned} D^1 C(t) =&\alpha _{_C}{C(t)}^{{g_{_{CC}}}\left( 1+{r_{_{CC}}}\frac{T(t)}{L_T}\right) } {B(t)}^{{g_{_{BC}}}\left( 1+{r_{_{BC}}}\frac{T(t)}{L_T}\right) \left( 1+K_{s_{1}}d_{_1}(t)\right) }\nonumber \\&-\left( 1+K_{s_{2}}d_{_2}(t)\right) \beta _{_C}C(t) \end{aligned}$$
(3a)
$$\begin{aligned} D^1B(t)=&\alpha _{_B}{C(t)}^{\left( \frac{{g_{_{CB}}}}{1+{r_{_{CB}}}\frac{T(t)}{L_T}}\right) }{B(t)}^{\left( {g_{_{BB}}}-{r_{_{BB}}}\frac{T(t)}{L_T}\right) } -\beta _{_B}B(t) \end{aligned}$$
(3b)
$$\begin{aligned} D^1 T(t)=&\left( 1-K_{i_{34}}d_{c_{34}}(t)\right) \gamma _{_T}T(t)\log {\left( \frac{L_T}{T(t)}\right) } \end{aligned}$$
(3c)

This treatment structure is also adpated in Coelho et al. (2016a), based on pharmacological PK/PD effect of anti-cancer and anti-resorptive therapy.

3.2 Non-local models

The previous models can be extended to include diffusion processes in the bone through partial differential equations.

Ayati et al. (2010) also extended its model to

$$\begin{aligned} D^1C(t,x)=&\sigma _{_C} \frac{\partial ^2}{\partial x^2}C(t,x)+\alpha _{_C} {C(t,x)}^{g_{_{CC}}}{B(t,x)}^{g_{_{BC}}}-\nonumber \\&-\beta _{_C} C(t,x) \end{aligned}$$
(4a)
$$\begin{aligned} D^1B(t,x)=&\sigma _{_B} \frac{\partial ^2}{\partial x^2}B(t,x)+\alpha _{_B} {C(t,x)}^{g_{_{CB}}}{B(t,x)}^{g_{_{BB}}}-\nonumber \\&-\beta _{_B} B(t,x) \end{aligned}$$
(4b)
$$\begin{aligned} D^1z(t,x)=&\sigma _{_z}\frac{\partial ^2}{\partial x^2}z(t,x)-\kappa _{_{C}} \max [0,C(t,x)-{\overline{C}}_{_{SS}}(x)]+\nonumber \\&+\kappa _{_{B}}\max [0,B(t,x)-{\overline{B}}_{_{SS}}(x)] \end{aligned}$$
(4c)

allowing diffusion over one-dimension, \(\sigma _{_i}\frac{\partial ^2}{\partial x^2}\), of osteoclasts, osteoblasts, and bone mass. These variables now depend on both t and \(x\in [0,1]\). The diffusion of z accounts for the stochastic nature of bone dynamics and not necessarily migration of cells.

MM influence was also added:

$$\begin{aligned} D^1 C(t,x)=&\sigma _{_C} \frac{\partial ^2}{\partial x^2}C(t,x)-\beta _{_C}C(t,x)+\nonumber \\&+\alpha _{_C}{C(t,x)}^{{g_{_{CC}}}\left( 1+{r_{_{CC}}}\frac{T(t)}{L_T}\right) }{B(t,x)}^{{g_{_{BC}}}\left( 1+{r_{_{BC}}}\frac{T(t)}{L_T}\right) } \end{aligned}$$
(5a)
$$\begin{aligned} D^1 B(t,x)=&\sigma _{_B} \frac{\partial ^2}{\partial x^2}B(t,x)-\beta _{_B}B(t,x)+\nonumber \\&+\alpha _{_B}{C(t,x)}^{\left( \frac{{g_{_{CB}}}}{1+{r_{_{CB}}}\frac{T(t)}{L_T}}\right) }{B(t,x)}^6{\left( {g_{_{BB}}}-{r_{_{BB}}}\frac{T(t)}{L_T}\right) } \end{aligned}$$
(5b)
$$\begin{aligned} D^1 T(t,x)=&\sigma _{_T} \frac{\partial ^2}{\partial x^2}T(t,x)+\gamma _{_T}T(t,x)\log {\left( \frac{L_T}{T(t,x)}\right) } \end{aligned}$$
(5c)

Tumor cells undergo diffusion in \(x\in [0,1]\). The diffusion coefficient for the tumor is given by \(\gamma _{_T}\), which allows for its spatial growth. Regarding the bone mass equation, z(t, x), the expression is the same as in (4c) and all variables are subjected to null Newmann boundary conditions. Initial conditions, now depending on x, can be found in Ayati et al. (2010). Simulations for a healthy and tumor bone micro-environment, for these non-local models, are presented in the first two rows of Fig. 4, respectively. The tumor evolution, with an initial development on the right side on the normalized bone, can be found in the second graphic of Fig. 11.

Fig. 4
figure 4

Non-local simulation of Osteoclasts, Osteoblasts and Bone Mass. Fisrt row, for healthy remodeling cycles (4). Second row, for a tumor disrupted bone micro environment (5). Third row, for the simplified model for bone remodeling with tumor (15). Parameters, initial and boundary conditions follow exactly what was presented in Ayati et al. (2010), and can be found in Table 3. Variable order model parameters follow the integer healthy model values, except the actualized resorption rates of \(\kappa _{_C}=0.1548\), \(\kappa _{_B}=6.4924\times 10^{-4}\) for \(R = 238.43\) (equal for the analogous variable order local model), and \(\theta =2.5\times 10^{-7}\). Untreated tumor evolution, for all metastases disrupted models, is presented in the second graphic of Fig. 11

Full size image

Christ et al. (2016) further extends the model of Ayati et al. (2010), adapted in Coelho et al. (2015), to include the PK/PD action of anti-cancer and anti-resorptive therapy, in a one-dimensional model:

$$\begin{aligned} D^1 C(t,x)=&\sigma _{_C} \frac{\partial ^2}{\partial x^2}C(t,x)-\left( 1+K_{s_{2}}d_{_2}(t)\right) \beta _{_C}C(t,x)+\nonumber \\&+\alpha _{_C}{C(t,x)}^{{g_{_{CC}}}\left( 1+{r_{_{CC}}}\frac{T(t)}{L_T}\right) }\times \nonumber \\&\times {B(t,x)}^{{g_{_{BC}}}\left( 1+{r_{_{BC}}}\frac{T(t)}{L_T}\right) \left( 1+K_{s_{1}}d_1(t)\right) } \end{aligned}$$
(6a)
$$\begin{aligned} D^1 B(t,x)=&\sigma _{_B} \frac{\partial ^2}{\partial x^2}B(t,x)-\beta _{_B}B(t,x)+\nonumber \\&+\alpha _{_B}{C(t,x)}^{\left( \frac{{g_{_{CB}}}}{1+{r_{_{CB}}}\frac{T(t)}{L_T}}\right) }\times \nonumber \\&\times {B(t,x)}^{\left( {g_{_{BB}}}-{r_{_{BB}}}\frac{T(t)}{L_T}\right) } \end{aligned}$$
(6b)
$$\begin{aligned} D^1 T(t,x)=&\sigma _{_T} \frac{\partial ^2}{\partial x^2}T(t,x)+\nonumber \\&+\left( 1-K_{i_{34}}d_{c_{34}}(t)\right) \gamma _{_T}T(t,x)\log {\left( \frac{L_T}{T(t,x)}\right) } \end{aligned}$$
(6c)

In Ryser et al. (2009), a spatial evolution of a single BMU was also included, and further extended in Ryser et al. (2012) to include the effect of bone metastasis in the remodeling process, as to study the ambiguous role of OPG in the system. From Pivonka et al. (2008), Buenzli et al. (2011) also added spatial evolution to different components of the model, introducing the appropriated fluxes in cells and regulatory agents. This model is able to capture the known organized structure of the BMU, presenting a resorption zone at the front, then a reversal zone, and how PTH and the RANK/RANKL/OPG pathway affects the bone cells in the different stages of maturation and during bone remodeling. Pivonka et al. (2013) proposed a model that takes into account biochemical, biomechanical and geometrical regulations, as it numerically investigates the influence of bone surface availability in bone remodeling. More recently, Capacete (2016) proposed a combined approach. The interactions between bone cells are again described by ordinary differential equations, based on the work of Komarova et al. (2003) and Ayati et al. (2010), but also by a finite element model of a proximal femur to account for the mechanical stimulus in a bi-dimensional construction, based in Rubin et al. (2006). It was also extended to include the disruptive action of MM. On a different approach, Araujo et al. (2014) uses a Hybrid Cellular Automata to describe spatial and temporal interactions of bone cells and micro-environment, the viscious cycles imposed by prostate cancer metastases, and the effect of anti-resorptive treatment on the bone dynamics, though bisphosphonates and anti-RANKL therapy; Scheiner et al. (2013) includes the biomechanical regulation of bone remodeling and the treatment of osteoporosis by means ofthe PK/PD of monoclonal antibodies (denosumab).

3.3 Pharmacokinectics and pharmacodynamics (PK/PD)

Pharmacokinetic (PK) models are based on mass balance differential equations that characterize drug absorption and disposition within the body (Dhillon and Gill 2006). For a one-compartment model for oral administration, the remaining drug concentration to be absorbed (\(C_{_g}\), in mg/L) and the effective drug concentration in the plasma (\(C_{_p}\), in mg/L) are described by

$$\begin{aligned}&D^1C_{_g}=-\kappa _{_g}C_{_g} \end{aligned}$$
(7a)
$$\begin{aligned}&D^1C_{_p}=\kappa _{_g}C_{_g}-\kappa _{_p}C_{_p} \end{aligned}$$
(7b)

where \(\kappa _{_g}\) and \(\kappa _{_p}\) are the absorption and elimination rates, respectively (Mager et al. 2003).

For a single dosage drug of initial concentration \(C_{_0}\), the plasma concentration can be determined by (8a). For multiple doses, the plasma concentration of the n\(^{th}\) dose is given by

$$\begin{aligned} C_{_p}=&C_{_0}\frac{\kappa _{_g}}{\kappa _{_g}-\kappa _{_p}}(e^{-\kappa _{_p} t}-e^{\kappa _{_g} t}) \end{aligned}$$
(8a)
$$\begin{aligned} C_{_p}(n,t')=&C_{_0}\frac{\kappa _{_g}}{\kappa _{_g}-\kappa _{_p}} \left( \frac{1-e^{-n\kappa _{_p}\tau }}{1-e^{-\kappa _{_p}\tau }}e^{-\kappa _{_p} t'}-\frac{1-e^{-n\kappa _{_g}\tau }}{1-e^{-\kappa _{_g}\tau }}e^{-\kappa _{_g} t'}\right) \end{aligned}$$
(8b)

Initial conditions are \(C_{_0}=\frac{D_{_0}F}{V_{_d}}\), administrated at equally spaced intervals \(t'=t-(n-1)\tau \), where \(D_{_0}\) is the dosage, F the bioavailability, and \(V_{_d}\) the volume distribution. Multiple dosage is governed by the steady-state \(C_{_{pss}}=\frac{C_{_0}}{\tau \kappa _{_p}}\). For a subcutaneous drug administration, the initial concentration is applied in the remaining drug to be absorbed (\(C_{_g}(0)=C_{_0}\)); for the intravenous case, the initial concentration goes directly to the concentration in the plasma (\(C_{_p}(0)=C_{_0}\)).

The Pharmacodynamic (PD) consists in a drug effect, \(d(t)=\frac{C_{_p}}{C_{_p}^{50}(t)+C_{_p}}\), that can be described by a Hill function depending on the drug’s concentration (Pinheiro et al. 2011). It varies between 0 and 1, where \(C_{_p50}(t)=f(t)C_{_p}^{50/base}\) represents the concentration at 50% of its maximum effect, \(C_{_p}^{50/base}\) is the initial value of \(C_{_p}^{50}(t)\), and resistance to a drug can be described by \(f(t)=1+K_{_r}\int _{0}^{t}\max \left[ 0,L_{_r}-C_{_p}(\lambda )\right] d\lambda \) (Pinheiro et al. 2011).

Through the combination of pharmacokinetic and pharmacodynamic models, a PK/PD model for a drug is achieved. Since a drug pathway can have either an inhibitory (i: −) or a stimulatory (s: \(+\)) effect on a given metabolism, a control action (CA) to the tumorous presence in the mathematical models for bone remodeling is given by \(CA(t)=1 \pm K_{i,s} d(t)\). Constants \(K_i,K_s>0\) represent the maximum effect of a drug in a specific mechanism, with d(t) being the PD response of a single drug or a combination of drugs.

4 Variable order derivatives

Fractional calculus generalizes differentiation and integration notions of order \(n \in \mathbb {N}\) to that of orders \(\alpha \in \mathbb {R}\). An appealing generalization is based on the exponential function, \(D^n(e^{ax})=a^{n}e^{ax}\), which suggests defining the derivative of order \(\alpha \), not necessarily integer, as \(D^\alpha (e^{ax})=a^{\alpha }e^{\alpha x}\) (Valério and Sá da Costa 2013).

There are several alternative definitions for fractional derivatives (Ortigueira and Machado 2019). The definition considered here is the Grünwald-Letnikoff construction, based upon the usual definition of derivative \(D^1 f(t) = \frac{\mathrm {d}f(t)}{\mathrm {d}t} = \lim _{h \rightarrow 0} \frac{f(t) - f(t-h)}{h}\), from which it can be easily shown, using mathematical induction, that

$$\begin{aligned} D^n f(t) = \frac{\mathrm {d}^n f(t)}{\mathrm {d}t^n} = \lim _{h \rightarrow 0} \frac{\displaystyle \sum \nolimits _{k=0}^n (-1)^k \left( \begin{array}{c} n\\ k \end{array} \right) f(t-kh)}{h^n}, \ n\in \mathbb {N} \end{aligned}$$
(9)

Since combinations \(\left( \begin{array}{c} a\\ b \end{array} \right) = \frac{a!}{b!(a-b)!}\) can be redefined for arbitrary real numbers a and b as \(\left( \begin{array}{c} a\\ b \end{array} \right) = \frac{\varGamma (a+1)}{\varGamma (b+1)\varGamma (a-b+1)}\) or \(\left( \begin{array}{c} a\\ b \end{array} \right) = \frac{(-1)^b \varGamma (b-a)}{\varGamma (b+1)\varGamma (-a)}\), it is reasonable to define

$$\begin{aligned} _c^{}D_t^\alpha f(t) = \lim _{h \rightarrow 0^+} \frac{\displaystyle \sum \nolimits _{k=0}^{\lfloor \frac{t-c}{h}\rfloor } (-1)^k \left( \begin{array}{c} \alpha \\ k \end{array} \right) f(t-kh)}{h^\alpha }, \ \alpha \in \mathbb {R} \end{aligned}$$
(10)

where the upper limit of the summation ensures that the case \(\alpha \in \mathbb {Z}^-\) is compatible with Riemann integrals, while the case \(\alpha \in \mathbb {N}\) still gives the same result as (9).

This Grünwald-Letnikoff can be approximated as (11a), or, recursively, as (11b):

$$\begin{aligned} _0D^{\alpha }_t f(t) \approx&\frac{1}{h^{\alpha }} \sum ^{n}_{r=0} {(-1)}^r \left( {\begin{array}{c}\alpha \\ r\end{array}}\right) f(t-rh) \end{aligned}$$
(11a)
$$\begin{aligned} ^{\mathrm {rec}}_0\mathrm {D}_t^\alpha f(t) \approx&\left( \frac{f(t)}{h^{\alpha }} - \displaystyle \sum _{r=1}^{n}(-1)^{r} \left( {\begin{array}{c}-\alpha \\ r\end{array}}\right) {^r_0\mathrm {D}_{t-rh}^{\alpha }}f(t-rh)\right) \end{aligned}$$
(11b)

In both cases, the step time is \(h\in \mathbb {R}^+\), and \(n=\lfloor t/h \rfloor \). If implemented for the entire length of the simulation, without any truncation of the series, both formulations are equivalent (Sierociuk et al. 2015c).

From all existing definitions, a common characteristic arises: operator D always depends on the integration limits c (here taken to be \(c=0\)) and t. D is then a non-local operator and, consequently, it has memory of past values of f(t) (Valério and Sá da Costa 2013).

Fractional calculus provides explicit expressions for new non-integer order dynamics. This characteristic makes it particularly well suited to describe the behavior of biological systems (e.g. subthreshold nerve conduction, viscoelasticity, bioelectrodes), since fractional derivatives occur most frequently, and naturally, in physical problems where the essential mechanisms, reactions, or interactions are governed by diffusion processes. Consequently, besides non-local spatial and prior temporal information, it also allows for anomalous diffusion to be mathematically described (Magin 2006).

The fractional order of integrals and derivatives can be a function of time or some other variable (Ortigueira et al. 2019; Lorenzo and Hartley 2002). Here, for time t, Grünwald-Letnikoff type-\(\mathcal {D}\) formulation was used (Sierociuk et al. 2015a, b):

$$\begin{aligned} ^\mathcal {D}_0D^{\alpha (t)}_t f(t)&\approx \left( \frac{f(t)}{h^{\alpha (t)}} - \sum _{r=1}^{n}(-1)^{r} \left( {\begin{array}{c}-\alpha (t)\\ r\end{array}}\right) {_0^{\mathcal {D}}D_{t-rh}^{\alpha (t)}f(t)}\right) \end{aligned}$$
(12a)
$$\begin{aligned} {^{\mathcal {D}}_{_{-\infty }}D^{\alpha (t)}_t} f(t)&\approx \left[ \frac{f(t)}{h^{\alpha (t)}}-\right. \nonumber \\&\left. -\displaystyle \sum _{j=1}^{n}{(-1)}^{j} \left( {\begin{array}{c}-\alpha (t)\\ j\end{array}}\right) \left( {^\mathcal {D}_{-\infty }D^{\alpha (t-jh)}_{t-jh}} f(t)-c\right) +c \right] \end{aligned}$$
(12b)

It can be approximated according to (12a). This derivative, successfully used for modeling the heat transfer process in a media with a time varying structure (Sierociuk et al. 2013), corresponds to an input-reductive strategy that assumes the rejection of input differentiators. That translates an immediate effect of order switching, schematically represented in Fig. 5. Additionally, this construction also allows for the effect of initial conditions having no memory of accumulated values, as formulated in (12b), where \(^{\mathcal {D}}_{-\infty }D_l^\alpha f(t)=c=\mathrm {const}\) for \(l=(-\infty ,0)\). These characteristics are essential for the application of the type-\(\mathcal {D}\) variable order definition to the bone remodeling models presented below.

Fig. 5
figure 5

Schematic representation of the input-reductive switching order scheme, in serial form, from orders \(\alpha _1\) to \(\alpha _2\). From Sierociuk et al. (2015b)

Full size image

5 Simplified models for bone remodelling using variable order derivatives

Fractional and variable order derivatives have been already successfully used in modeling the dynamics of bone remodeling. Many dynamic relations in reality are fractional, even if that fractionality is very low (Petrás 2009). Consequently Christ et al. (2016) studied the effect of fractional derivatives in the model of Ayati et al. (2010). As to variable order derivatives, in Neto et al. (2017a, 2017b) they have been introduced as a simplification technique in the same models of Ayati et al. (2010) and Coelho et al. (2015), in an effort to replicate the same bone micro-environment response but recurring to less parameters to imposed the known bone behavior. In fact, these tumor-disrupted bone remodeling models, as well as their extensions of Coelho et al. (2016a), Coelho et al. (2015) and Christ et al. (2016), can be simplified using variable order derivative methods.

In what follows, variable order models of bone remodelling are revisited in Sect. 5.1. The extension of these models to include the PK/PD action of combined anti-resorptive therapy is described in Sect. 5.2 (this extension is being published for the first time). Results and their discussion follow, in Sect. 5.3.

5.1 Revisiting simplified bone remodeling models

Fractional calculus allows considering orders not required to be integer numbers, which is specially adapted to describe biological processes with diffusion (Magin 2006). The same can be said for bone remodeling. However, introducing variable order derivatives also allows changing the dynamic response of a system, using less parameters to do so.

For the simplest biochemical model including the nefarious action of a tumor, type-\(\mathcal {D}\) variable order derivatives were introduced in the cell populations of the bone micro-environment of Ayati et al. (2010). MATLAB/Simulink toolbox Fractional Variable Order Derivative Simulink Toolkit was used, where the buffer size is given by \(n=\frac{t}{h}\), t being the simulation time, and h the sample time taken to be 1 day in all further addressed cases (Sierociuk et al. 2015b).

Considering that the tumor derived bone remodeling equations presented, either in their local version (2) or non-local version (5), are said to be independent of the bone micro-environment (Ayati et al. 2010), and that bone mass variations are but a reflection of osteoclasts and osteoblasts activity (Komarova et al. 2003), a new model is formulated by changing the derivative’s order of the osteoclasts and osteoblasts equations only, and by removing all \(r_{_{ij}}\) coefficients. The variable order, \(\alpha (t)\) or \(\alpha (t,x)\), influenced by the tumor dynamics, is now responsible for inducing in the original healthy model, (1) and (4), the same response as the tumorous one, (2) and (5). This allows for a simpler model to represent the tumorous action in the bone dynamics, even when therapy is applied, (3) and (6).

The new equation associated with the required order format, for local and non-local scenarios, is

$$\begin{aligned}&\alpha (t)=1-\theta \times t\times T(t) \end{aligned}$$
(13a)
$$\begin{aligned}&\alpha (t,x)=1-\theta \times t\times T(t,x) \end{aligned}$$
(13b)

where \(\theta \) is a constant term experimentally determined. Time t is related to the beginning of the tumor growth.

Since the resulting models’ steady-state, from a mathematical standpoint, is the same as the integer local healthy one’s, for all contemplated cases here, and most parameters remain with the same values used in Ayati et al. (2010), the associated activity of osteoclasts and osteoblasts in bone mass must differ from the original case. As such, the bone resorption-formation ratio, given by \(R=\frac{\int _{0}^{{\overline{t}}}\max \left[ 0,C(t)-C_{_{SS}}\right] }{\int _{0}^{{\overline{t}}}\max \left[ 0,B(t)-B_{_{SS}}\right] }\), is determined; it assumes values between 0 and \({\overline{t}}\), and corresponds to the completion time of a single cycle of C(t) in the new model (Ayati et al. 2010). Bone resorption and formation activities are then given by \(\kappa _{_C}=rR\) and \(\kappa _{_B}=r\), respectively. For the local case

$$\begin{aligned}&D^{\alpha (t)}C(t)=\alpha _{_C}C(t)^{g_{_{CC}}}B(t)^{g_{_{BC}}}-\beta _{_C}C(t) \end{aligned}$$
(14a)
$$\begin{aligned}&D^{\alpha (t)}B(t)=\alpha _{_B}C(t)^{g_{_{CB}}}B(t)^{g_{_{BB}}}-\beta _{_B}B(t) \end{aligned}$$
(14b)
$$\begin{aligned}&D^1z(t) = -\kappa _{_{C}}\max \left[ 0, C(t)-C_{_{SS}}\right] + \kappa _{_{B}}\max \left[ 0, B(t)-B_{_{SS}}\right] \end{aligned}$$
(14c)
$$\begin{aligned}&D^1T(t)=\gamma _{_T}T(t)\log {\left( \frac{L_{_T}}{T(t)}\right) } \end{aligned}$$
(14d)
$$\begin{aligned}&\alpha (t)=1-\theta \times t \times T(t) \end{aligned}$$
(14e)

simulation of the bone micro-environment (osteoclasts, osteoblasts and bone mass) can be found in Fig. 3. For comparison purposes, the results for the healthy and integer tumor disrupted bone remodeling versions of Ayati et al. (2010) are also presented. The tumor evolution remains the same, since it is considered independent of the bone micro-environment, even though such is not physiologically correct. The evolution can be found in the first graphic of Fig. 11.

Figure 6 allows a better analysis of the influence of \(\theta \) in the order’s expression. It is worth noticing that the numerical method used is extremely sensitive, as the order of the system is globally very close to 1. It is limited to values bigger than the magnitude of \(\theta =10^{-11}\), as is it not possible to run simulations with this value or smaller. For \(\theta \ge 10^{-6}\) values the dynamic response is also not favorable, as it enhances the remodeling cycle period to values bigger than simulation time and with out-bounded amplitude. For \(\theta = 10^{-7}\) the periodic dynamic response was recuperated. The magnitude of \(\theta = 10^{-8}\) was chosen but \(\theta = 10^{-9}\) also reproduces qualitatively good results.

Fig. 6
figure 6

Study of the influence of \(\theta \) on the dynamic response of the simplified models (14)

Full size image

For the non-local case

$$\begin{aligned} D^{\alpha (t,x)}C(t,x)=&\sigma _{_C} \frac{\partial ^2}{\partial x^2}C(t,x)-\beta _{_C}C(t,x) + \nonumber \\&+\alpha _{_C}C(t,x)^{g_{_{CC}}}B(t,x)^{g_{_{BC}}} \end{aligned}$$
(15a)
$$\begin{aligned} D^{\alpha (t,x)}B(t,x)=&\sigma _{_B}\frac{\partial ^2}{\partial x^2}B(t,x)-\beta _{_B}B(t,x)+\nonumber \\&+\alpha _{_B}C(t,x)^{g_{_{CB}}}B(t,x)^{g_{_{BB}}} \end{aligned}$$
(15b)
$$\begin{aligned} D^1z(t,x)=&\sigma _{_z} \frac{\partial ^2}{\partial x^2}z(t,x)-\kappa _{_C} \max [0,C(t,x)-C_{_{SS}}]+\nonumber \\&+\kappa _{_B}\max [0,B(t,x)-B_{_{SS}}] \end{aligned}$$
(15c)
$$\begin{aligned} D^1T(t,x)=&\sigma _{_T}\frac{\partial ^2}{\partial x^2}T(t,x)+\gamma _{_T}T(t,x)\log {\left( \frac{L_T}{T(t,x)}\right) } \end{aligned}$$
(15d)
$$\begin{aligned} \alpha (t,x)=&1- \theta \times t \times T(t,x) \end{aligned}$$
(15e)

simulation of the simplified model (15) can be found in the third row of Fig. 4, for the osteoclasts, osteoblasts and bone mass. Again for comparison purposes, in the first row healthy bone remodeling dynamics is presented, and in the second row integer tumor bone micro-environment with \(r_{_{ij}}\) parameters. The tumor one-dimensional evolution can be found, again, in the first graphic of Fig. 11.

For either case, used parameters can be found in Table 3 (the same ones used in Ayati et al. (2010)), save for the values in the captions. Initial conditions with spatial distributions (C(0, x) and T(0, x)) are the same used in Ayati et al. (2010), as are the boundary conditions.

In MM, osteoblast activity is known to be severely suppressed (Silbermann and Roodman 2012), which results in aggravated bone loss as osteoclasts are continuously promoted. However, in the results for the biochemical mathematical model presented not only in Ayati et al. (2010) as in the simplified models of this section, the bone forming cells still have some degree of action. Such behavior was considered in Neto et al. (2017a, 2017b) to better fit a metastatic bone disease of osteolytic nature, such as a typical metastization to the bone of breast cancer (Holen (2012)), as achieved results for the bone micro-environment simulation were physiologically better described by such a new approach. It was also concluded in Neto et al. (2017a, 2017b) that the variable order models provide qualitatively good results regarding both what is known of the bone micro-environment.

5.2 Therapy and variable order derivatives—a simplified extension

Both local and non-local version of the simplified model of Neto et al. (2017b) (14) and (15) can be extended to include therapy counteraction.

PK/PD of anti-cancer and anti-resorptive therapy was locally introduced in Coelho et al. (2015), to the models of Ayati et al. (2010), and further extended in Christ et al. (2016) to one dimensional geometries. Such models can be found in (3) and (6), that can be simplified by again removing all \(r_{_{ij}}\) parameters and by adding a variable order to C(t) and B(t) (or to C(t, x) and B(t, x)).

Given that the tumor base model of Ayati et al. (2010) is said to better describe an osteolytic metastatic bone disease, anti-cancer is combined with anti-resorptive therapy, instead of the initially proposed osteoblastic promotion based treatment for MM (Neto et al. 2017b; Coelho et al. 2015; Christ et al. 2016). Here, the effects of chemotherapy are given by \(K_{i_{3}}d_{_3}(t)\), considering the intravenous application of paclitaxel (Perez et al. 2001). It directly acts by targeting tumor cells, promoting their apoptosis in (3c) and (6c), and now in (16e) and (17d). Anti-resorptive therapy can be included using one of two possible treatments. Monoclonal antibodies, as denosumab, act as a decoy receptor for RANKL, lowering the RANKL concentration and hence the activation of osteoclasts. The term \(K_{s_{1}}d_{_1}(t)\) is consequently added to exponent \(g_{_{BC}}\), to represent the inhibition of RANKL produced by osteoblasts though the subcutaneous application of denosumab (Gibiansky et al. 2012; Sohn et al. 2014). Bisphosphonates, as zoledronic acid, lay on the bone matrix being released and absorbed by osteoclasts as they degrade bone. Bone resorption is then inhibited and osteoclast apoptosis promoted. Bisphosphonates are only considered to promote apoptosis of osteoclasts, influencing the \(\beta _{_C}\) term.

The resulting simplified models are given by

$$\begin{aligned} D^{\alpha (t)}C(t)=&\alpha _{_C}C(t)^{g_{_{CC}}}B(t)^{g_{_{BC}}\left( 1+K_{s_1}d_{_1}(t)\right) }-\nonumber \\&-\left( 1+K_{s_2}d_{_2}(t)\right) \beta _{_C}C(t) \end{aligned}$$
(16a)
$$\begin{aligned} D^{\alpha (t)}B(t)=&\alpha _{_B}C(t)^{g_{_{CB}}}B(t)^{g_{_{BB}}}-\beta _{_B}B(t) \end{aligned}$$
(16b)
$$\begin{aligned} D^{\alpha (t)}z(t) =&- \kappa _{_C} \max \left[ 0, C(t)-C_{_{SS}}\right] +\nonumber \\&+ \kappa _{_B} \max \left[ 0, B(t)-B_{_{SS}}\right] \end{aligned}$$
(16c)
$$\begin{aligned} D^{\alpha (t)}T(t)=&\left( 1+K_{i_{3}}d_{_{3}}(t)\right) \gamma _{_T}T(t)\log {\left( \frac{L_T}{T(t)}\right) } \end{aligned}$$
(16d)
$$\begin{aligned} \alpha (t) =&1-\theta \times t \times T(t) \end{aligned}$$
(16e)

and

$$\begin{aligned} D^{\alpha (t,x)}C(t,x)=&\sigma _{_C}\frac{\partial ^2}{\partial x^2}C(t,x)-\left( 1+K_{s_2}d_{_2}(t)\right) \beta _{_C}C(t,x)+\nonumber \\&+\alpha _{_C}C(t,x)^{g_{_{CC}}}B(t,x)^{g_{_{BC}}\left( 1+K_{s_1}d_{_1}(t)\right) } \end{aligned}$$
(17a)
$$\begin{aligned} D^{\alpha (t,x)}B(t,x)=&\sigma _{_B}\frac{\partial ^2}{\partial x^2}B(t,x)-\beta _{_B}B(t,x)+\nonumber \\&+\alpha _{_B}C(t,x)^{g_{_{CB}}}B(t,x)^{g_{_{BB}}} \end{aligned}$$
(17b)
$$\begin{aligned} D^{\alpha (t,x)}z(t,x) =&\sigma _{_z}\frac{\partial ^2}{\partial x^2}z(t,x)- \kappa _{_C} \max \left[ 0, C(t,x)-C_{_{SS}}(x)\right] +\nonumber \\&+ \kappa _{_B} \max \left[ 0, B(t,x)-B_{_{SS}}(x)\right] \end{aligned}$$
(17c)
$$\begin{aligned} D^{\alpha (t,x)}T(t,x)=&\sigma _{_T}\frac{\partial ^2}{\partial x^2}T(t,x)+\nonumber \\&+\left( 1+K_{i_{3}}d_{_{3}}(t)\right) \gamma _{_T}T(t,x)\log {\left( \frac{L_T}{T(t,x)}\right) } \end{aligned}$$
(17d)
$$\begin{aligned} \alpha (t,x) =&1-\theta \times t \times T(t,x) \end{aligned}$$
(17e)

When treatments are applied, however, the duration of an individual remodeling cycle is changed. Consequently, three resorption rates must be determined: when the tumor begins, \(R_{ \text{ tumor }}\); when treatment is applied, \(R_{ \text{ treat }}\); and when the tumor is extinguished and the treatment is consequently stopped, \(R_{ \text{ healthy }}\). Each ratio is determined for the first complete cycle after the induced change. All involved variables and parameters are explained in Table 2. Non-local initial conditions, C(0, x) and T(0, x), are the same as presented in Ayati et al. (2010), as are the null Newmann boundary conditions applied to all variables in \(x=0\) and \(x=1\).

Table 2 Summary and description of the variables and parameters for the proposed model (16) and (17)
Full size table
Table 3 Variables and parameters, from Ayati et al. (2010), used for the simulations and equations of local and non local models presented in this paper, except when explicitly said otherwise
Full size table
Table 4 Simulation parameters used for the local and non local models with PK/PD action of treatment, for (3) and (6): monoclonal antibodies, \(d_{_1}\) (denosumab), bisphosphonates, \(d_{_2}\) (zoledronic acid) and anti-cancer therapy, \(d_{_3}\) (paclitaxel)
Full size table
Fig. 7
figure 7

Osteoclasts, Osteoblasts and Bone Mass evolutions, respectively, where treatment was applied combining chemotherapy (paclitaxel—\(d_{_3}\)) with monoclonal antibodies (denosumab—\(d_{_1}\)). The integer model, as presented in (3) (Coelho et al. 2015) and here adapted for the anti-resorptive therapy of Coelho et al. (2016a), is simulated in a darker dashed line (parameters in Table 3, for the metastatic case). For the new model proposed, the simulation of (16) is presented in a light full line (parameters in Table 3, for the healthy case; the order parameter was \(\theta _{_{deno}}=8.25\times 10^{-8}\), and the resorption rates were \(R_{ \text{ tumor }}=239.1189\), \(R_{ \text{ treat }}=101.44\), and \(R_{ \text{ healthy }}=123.26\), for \(\kappa _{_C}=0.1548\)). The corresponding tumor evolution, equal for both models with metastases, can be found in the dashed line in the first graphic of Fig. 11 (applied PK/PD chemotherapy is independent of the anti-resorptive therapy chosen), and used PK/PD parameters are presented in Table 4

Full size image
Fig. 8
figure 8

Osteoclasts, Osteoblasts and Bone Mass evolutions, respectively, where treatment was applied combining chemotherapy (paclitaxel—\(d_{_3}\)) with bisphosphonates (zoledronic acid—\(d_{_2}\)). The integer model, as presented in (3) (Coelho et al. 2015) and here adapted for the anti-resorptive therapy of Coelho et al. (2016a), is simulated in a darker dashed line (parameters in Table 3, for the metastatic case). For the new model here proposed, the simulation of (16) is presented in a light full line (parameters in Table 3, for the healthy case; the order parameter was \(\theta _{_{BP}}=6.034\times 10^{-8}\), and the resorption rates were \(R_{ \text{ tumor }}=239.1189\), \(R_{ \text{ treat }}=97.98\), and \(R_{ \text{ healthy }}=123.26\), for \(\kappa _{_C}=0.1548\)). The corresponding tumor evolution, equal for both models with metastases, can be found in the dashed line in the first graphic of Fig. 11 (applied PK/PD chemotherapy is independent of the anti-resorptive therapy chosen), and used PK/PD parameters are presented in Table 4

Full size image
Fig. 9
figure 9

Non-local simulation of Osteoclasts, Osteoblasts and Bone Mass, for an applied PK/PD treatment of anti-cancer (chemotherapy—paclitaxel \(d_{_3}\)) and anti-resorptive therapy (monoclonal antibodies—denosumab \(d_{_1}\)) with parameters given in Table 4. First row, integer model simulation of (6), as presented in Christ et al. (2016) with \(d_{c_{34}}=d_{_3}\). Second row, proposed simplified variable order model of (17). Parameters, initial and boundary conditions follow exactly what was presented in Ayati et al. (2010), and can be found in Table 3. Variable order model parameters follow the integer healthy non-local model values, except the actualized resorption rates of \(R_{ \text{ tumor }}=239.1189\), \(R_{ \text{ treat }}=93.21\), and \(R_{ \text{ healthy }}=98.56\), for \(\kappa _{_C}=0.1548\), and \(\theta _{_{deno}}=4\times 10^{-7}\). The corresponding tumor evolution, for either the integer or the variable order models, is presented in the third graphic of Fig. 11

Full size image
Fig. 10
figure 10

Non-local simulation of Osteoclasts, Osteoblasts and Bone Mass, for an applied PK/PD treatment of anti-cancer (chemotherapy—paclitaxel \(d_{_3}\)) and anti-resorptive therapy (bisphophonates—zoledronic acid \(d_{_2}\)) with parameters given in Table 4. First row, integer model simulation of (6), as presented in Christ et al. (2016) with \(d_{c_{34}}=d_{_3}\). Second row, proposed simplified variable order model of (17). Parameters, initial and boundary conditions follow exactly what was presented in Ayati et al. (2010), and can be found in Table 3. Variable order model parameters follow the integer healthy non-local model values, except the actualized resorption rates of \(R_{ \text{ tumor }}=239.1189\), \(R_{ \text{ treat }}=93.21\), and \(R_{ \text{ healthy }}=98.56\), for \(\kappa _{_C}=0.1548\), and \(\theta _{_{BP}}=6\times 10^{-7}\). The corresponding tumor evolution, for either the integer or the variable order models, is presented in the third graphic of Fig. 11

Full size image

5.3 Results and discussion

For the local models of (16), simulation results can be found in Figs. 7 and 8, for chemotherapy combined with either denosumab (\(d_{_1}\)) or zoledronic acid (\(d_{_2}\)), respectively. Osteoclasts, osteoblasts, and bone mass are, for both cases, compared to the analogous integer order models. The tumor grows from \(t=0\) days, both treatments are applied at \(t=600\) days, and the tumor is considered extinct and the treatments are halted at \(t=2340\) days. Since the chemotherapy applied is always the same, the treated tumor evolution is presented in the first graphic of Fig. 11.

Non-local results from (17) are presented in the second row of both Figs. 9 and 10. Again, in the first row, analogous integer model results with \(r_{_{ij}}\) parameters can be found for the osteoclasts, osteoblasts and bone mass. Figure 9 referrers to chemotherapy (paclitaxel, \(d_{_3}\)) combined with monoclonal antibodies (denosumab, \(d_{_1}\)), and Fig. 10 to chemotherapy with bisphosphonates (zoledronic acid, \(d_{_2}\)).

Fig. 11
figure 11

Local and non-local tumor evolution. First graphic, local tumor evolutions are presented for chemotherapy treatments, (2c) and (14d), and for the untreated case, (16d). Second graphic, untreated spatial tumor evolution for an initial location on the right side of the normalized bone, (5c) and (15d) . Third graphic, tumor counteracted with the PK/PD chemotherapy action of paclitaxel (17d). Anti-tumor therapy parameters, either local or non-local, follow Table 4

Full size image

Regardless of the simulation, the resorption ratios R reflect what is known for each stage. As the tumor develops, the tightly coupled mechanism between resorption and formation is disrupted, as bone destruction is promoted by osteolytic metastases. Hence, \(R_{ \text{ tumor }}\) has a bigger value than in the remaining stages. When treatment is applied, it acts by generally inhibiting the osteoclastic action, which results in a lower value of R as formation is, consequently, promoted. When the tumor is extinct and treatment stopped, the resulting ratio is higher than the latter, as now healthy coupling is resumed regardless of the new stabilized value of z.

The value of \(\theta \) slightly differs with the specified treatment, as \(d_{_1}\) (denosumab) acts through the S-system exponent \(g_{_{BC}}\), and \(d_{_2}\) (zoledronic acid) acts through the coefficent \(\beta _{_C}\). Translating from local to non-local, the order coefficient needs not to be adapted since the used \(\theta \) is local simulations provides good results, not disturbed by acting diffusion processes. However, for all local and non-local cases, the order’s magnitude is higher then the untreated tumor bone model counterpart.

For the local models, and overall consequence of introducing variable order derivatives results in wider remodeling cycles, and that the tumor acts more severely in beginning of the simulation but with a slower development. With both denosumab and zoledronic acid, osteoclasts see their number slightly diminish with an opposed reaction from the osteoblasts. As a consequence, bone mass stabilizes with very small recuperation, which reflects the nefarious action of an ostelytic tumor in the bone micro-environment. For the non-local cases, the same behavior is replicated.

As a conclusion, these simplified models mimicking bone behavior, tumorous action, and therapy counteraction, extending Neto et al. (2017a, 2017b) to include therapy counter-action for an osteolytic metastization to the bone, can be said—even though they do not replicate the analogous integer case results precisely—to be qualitatively accurate. They are in accord with the known characteristics of the bone micro-environment response, namely the oscillations around homeostatic equilibrium and their amplitude and period (Komarova et al. 2003; Ayati et al. 2010). They are also in accord with the known characteristics of the bone micro-environment dynamics disrupted by an osteolytic tumor, namely the way how homeostatic equilibrium is affected by the tumor, and slowly recuperated by treatments (Casimiro et al. 2016; Ryser et al. 2012). The selected therapy employed is based on a combination of anti-cancer (chemotherapy—paclitaxel) with anti-resoprtive treatment (bisphosphonates—zoledronic acid; monoclonal antibodies—denosumab). The main goal of these models is to replicate analogous integer model results, with less parameters: an overall counting gives 1 equation added, for the system’s order \(\alpha (t)\)/\(\alpha (t,x)\), and 3 parameters suppressed, as all four \(r_{_{ij}}\) were removed and \(\theta \) was added to the order’s equation. Hence, it can be concluded that variable order derivatives are a powerful tool that can be used to adequately replicate bone behavior.

6 Conclusions and future work

While detailed experimental data sufficient to quantitatively validate all the models passed in review in this paper does not yet exist, we have shown that the behavior obtained reproduces the characteristics of the physiological and clinical evolution of both disease and treatment. For this reason, biochemical models for bone remodeling, which are based upon existing knowledge of biochemical processes involved, are also expected to provide further valuable insights about the bone complex system. These models are also necessary to support the development of clinical decision systems for bone pathologies with efficient targeted therapies; in fact, control system techniques can be used to tailor treatments for patients, if models accurate and reliable enough are available (Camacho and Jerez 2019).

This is why the computational analysis of bone physiological models is expected to have an impact on the development of clinical decision support systems in the future. Here are highlighted the road-map steps in an effort to bring that desired reality closer.

  • Add diffusion terms, and consequent boundary conditions, for the PK/PD treatments prescribed, considering that, when a treatment is applied, it is done in a specific site and not uniformly in a region, regardless of intravenous or subcutaneous application methods;

  • Add a more detailed tumor evolution, as it is here considered that tumor growth is independent of the bone micro-environment, which is physiologically incorrect;

  • Applying the techniques here developed to models that include a more detailed and accurate description of the biochemical processes involved (Coelho et al. 2016a);

  • Extending the models originally proposed in Komarova et al. (2003) and Ayati et al. (2010) to incorporate the biomechanical effects in the bone, which translates in adding mechanical solicitations in the original equations (Belinha et al. 2015; Capacete 2016), inasmuch such work would be simplified by using variable order derivatives in the resulting equations;

  • Adapting these models to stochastic formulations such as those in Jerez and Cantó (2019);

  • Finally, coefficients should be measured from experimental data, possibly data extrapolated from experiments with animals or in vitro experiments. The used parameters are not more than educated guesses by clinicians and oncobiologists at the magnitude of the values, leading to reasonable results from the qualitative point of view. Finding actual experimental values is probably the biggest challenge in the future.