1 Introduction

The process of running involves a control phenomenon in the human body. Indeed, the optimal pace to run a fixed distance requires to use the maximal available propulsive force and energy in order to produce the optimal running strategy. This optimal strategy is a combination of cost and benefit: a runner usually wants to finish first or beat the record but minimizing his effort. The issue of finding the optimal pacing is a crucial one in sports sciences (Aragón et al. 2016; Foster et al. 2019; Hettinga et al. 2019; Hanley and Hettinga 2018; Hanley et al. 2019; Thiel et al. 2012; Tucker et al. 2006; Tucker and Noakes 2009) and is still not solved. In tactical races, depending on the level of the athlete, and the round on the competition (heating, semi-final or final), the strategy is not always the same: the pacing can either be U-shaped (the start and the finish are quicker), J-shaped (greater finishing pace) or reverse J-shaped (greater starting pace) (Casado et al. 2020; Hettinga et al. 2019).

In this paper, we want to model this effort minimization as a control problem, solve it and find estimates of the velocity using the turnpike theory of Trélat (2020) and Trélat and Zuazua (2015). We will build on a model introduced by Keller (1974), improved by Aftalion (2017), Aftalion and Bonnans (2014), Aftalion and Martinon (2019), Aftalion and Trélat (2020), Behncke (1993, 1994), Mathis (1989), and Mercier et al. (2021). The extension by Aftalion (2017), Aftalion and Bonnans (2014) and Aftalion and Martinon (2019) is sufficiently accurate to model real races. We add a motivation equation inspired from the analysis of motor control in the human body (Le Bouc et al. 2016). This is related to the minimal intervention principle (Todorov and Jordan 2002) so that human effort is minimized through penalty terms. We have developed this model for the 200 m in Aftalion and Trélat (2020) and extend it here for middle distance races.

Let us go back to the various approaches based on Newton’s second law and energy conservation. Let \(d>0\) be the prescribed distance to run. Let x(t) be the position, v(t) the velocity, e(t) the anaerobic energy, f(t) the propulsive force per unit mass. Newton’s second law allows to relate force and acceleration through:

$$\begin{aligned} \begin{array}{ll} \dot{x}(t) = v(t) &{}\quad x(0)=0, \quad x(t_f)=d, \\ \dot{v}(t) = -\frac{v(t)}{\tau }+f(t) &{}\quad v(0)=v^0, \end{array} \end{aligned}$$

where \(\tau \) is the friction coefficient related to the runner’s economy, \(t_f\) the final time and \(v_0\) the initial velocity. An initial approach by Keller (1974) consists in writing an energy balance: the variation of aerobic energy and anaerobic energy is equal to the power developed by the propulsive force, f(t)v(t). He assumes that the volume of oxygen per unit of time which is transformed into energy is constant along the race and we call it \({\bar{\sigma }}\). If \(e^0\) is the initial anaerobic energy, then \(\dot{e} (t)\) is the variation of anaerobic energy and this yields

$$\begin{aligned} -\dot{e}(t) +{\bar{\sigma }} =f(t)v(t)\qquad e(0)=e^0,\quad e(t)\geqslant 0,\quad e(t_f)=0. \end{aligned}$$

The control problem is to minimize the time \(t_f\) to run the prescribed distance \(d=\int _0^{t_f} v(t)\ dt\) using a control on the propulsive force \(0\leqslant f(t)\leqslant f_M\). This model is able to predict times of races but fails to predict the precise velocity profile.

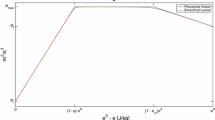
Experiments have been performed on runners to understand how the aerobic contribution varies with time or distance (Hanon and Thomas 2011). Because the available flow of oxygen which transforms into energy needs some time to increase from its rest value to its maximal value, for short races up to 400 m, the function \(\sigma \) (which is the energetic equivalent of the oxygen flow) is increasing with time but does not reach its maximal value \({\bar{\sigma }}\) or \(\dot{V}O2_{\mathrm {max}}\). For longer distances, the maximal value \(\bar{\sigma }\) is reached and \(\sigma \) decreases at the end of the race. The longer the race, the longer is the plateau at \(\sigma =\bar{\sigma }\). The time when the aerobic energy starts to decrease is assumed to be related to the residual anaerobic supplies (Billat et al. 2009). Therefore, in Aftalion and Bonnans (2014), to better encompass the link between aerobic and anaerobic effects, the function \(\sigma \) is modelled to depend on the anaerobic energy e(t), instead on directly time or distance. This leads to the following function \(\sigma (e)\) illustrated in Fig. 1:

Fig. 1
figure 1

The function \(\sigma (e)\) from (1) for \(e^0=4651\), \({\bar{\sigma }}=22\), \(\sigma _f=20\), \(\sigma _r=6\), \(\gamma _2=566\), \(\gamma _1=0.15\)

Full size image
$$\begin{aligned} \sigma (e)=\left\{ \begin{array}{ll} \displaystyle {\bar{\sigma }} \frac{e}{e^0\gamma _1}+\sigma _f \left( 1-\frac{e}{e^0 \gamma _1}\right) &{} \displaystyle \quad \hbox {if}\quad \frac{e}{e^0}<\gamma _1 \\ \displaystyle {\bar{\sigma }} &{} \displaystyle \quad \hbox {if}\quad \frac{e}{e^0}\geqslant \gamma _1 \quad \hbox {and}\quad e^0 -e\geqslant \gamma _2\\ \displaystyle ({\bar{\sigma }} -\sigma _r) \frac{e^0 -e}{\gamma _2}+\sigma _r &{} \displaystyle \quad \hbox {if}\quad e^0-e<\gamma _2 \end{array}\right. \end{aligned}$$
(1)

where \({\bar{\sigma }}\) is the maximal value of \(\sigma \), \(\sigma _f\) is the final value at the end of the race, \(\sigma _r\) is the rest value, \(e^0\) is the initial value of energy, \(\gamma _1 e^0\) is the critical energy at which the rate of aerobic energy starts to depend on the residual anaerobic energy and \(\gamma _2\) is the energy at which the maximal oxygen uptake \({\bar{\sigma }}\) is achieved. Because the anaerobic energy starts at the value \(e^0\) and finishes at zero, it depletes in time. We observe in our numerical simulations that e(t) decreases, so that \(\sigma (e(t))\) and \(\sigma (e)\) have opposite monotonicities. The function \(\sigma (e(t))\) obtained in our simulations and illustrated in Fig. 2 is consistent with the measurements of Hanon et al. (2008) or of Hanon and Thomas (2011). The parameters \(e^0\), \(\gamma _1\), \(\gamma _2\), \({\bar{\sigma }}\), \(\sigma _f\), \(\sigma _r\) depend on the runner and on the length of the race.

A runner, who speeds up and slows down, chooses to modify his effort. There is a neuro-muscular process controlling human effort. The issue is how to model mathematically this control, coming from motor control or neural drive. In Keller’s paper (1974), the mathematical control is on the propulsive force. But this yields derivatives of the force which are too big with respect to human ones. Indeed, a human needs some time between the decision to make an effort and the effective change of propulsive force in the muscle. Therefore, in Aftalion (2017) and Aftalion and Bonnans (2014), the control is the derivative of the propulsive force. Nevertheless, putting the control on the derivative of the force seems artificial and it is more satisfactory to actually model the process going from the decision to the muscle. For this purpose, we use the model of mechanisms underlying motivation of mental versus physical effort of Le Bouc et al. (2016). They define the motor cost of changing a force as the integral of the square of the neural drive u(t). Motor control theory has shown that optimizing this cost minimizes the signal-dependent motor variability and reproduces the cardinal features of movement production. In Le Bouc et al. (2016), the authors derive the equation for the derivative of the force which limits the variation of the force through the neural drive u(t):

  • the force increases with the neural drive so that \(\dot{f}\) is proportional to u;

  • the force is bounded by a maximal force even when the neural drive increases so that \(\dot{f}\) is proportional to \(u(F_{\text {max}}-f)\);

  • without excitation, it decreases exponentially so that \(\dot{f}\) is proportional to \(u(F_{\text {max}}-f)-f\);

  • the dynamics of contraction and excitation depends on the muscular efficiency \(\gamma \) so that \(\dot{f}\) is proportional to \(\gamma \).

Therefore, following Le Bouc et al. (2016), and as in Aftalion and Trélat (2020), we add an equation for the variation of the force. This leads to the following system:

$$\begin{aligned}&\dot{x}(t) = v(t)&\quad x(0)=0, \quad x(t_f)=d, \end{aligned}$$
(2)
$$\begin{aligned}&\dot{v}(t) = -\frac{v(t)}{\tau }+f(t)&\quad v(0)=v^0, \end{aligned}$$
(3)
$$\begin{aligned}&\dot{f}(t) = \gamma \Big ( u(t) (F_{\text {max}}-f(t)) - f(t) \Big )&\quad f(t)\geqslant 0, \end{aligned}$$
(4)
$$\begin{aligned}&\dot{e}(t) = \sigma (e(t)) -f(t)v(t)&\quad e(0)=e^0,\quad e(t)\geqslant 0,\quad e(t_f)=0, \end{aligned}$$
(5)

where \(e^0\) is the initial energy, \(\tau \) the friction coefficient related to the runner’s economy, \(F_{\mathrm {max}}\) is a threshold upper bound for the force, \(\gamma \) the time constant of motor activation and u(t) the neural drive which will be our control. We observe in our simulations that, in order to minimize the time, the force f(t) remains positive along the race without the need to put it as a constraint. Let us point out that it follows from Equation (4) that f(t) cannot cross \(F_{\mathrm {max}}\) increasing. Therefore, with our choice of parameters (the value of \(e^0\) is not large enough), we observe that f(t) always remains below \(F_{\mathrm {max}}\) without putting any bound on the maximal force. In this paper, we do not take into account the effect of bends because for long races, they have minor effects on the velocity.

The optimization problem consists in minimizing the difference between the cost and the benefit. In Le Bouc et al. (2016), the expected cost is proportional to the motor control which is the \(L^2\) norm of the neural drive u(t). On the other hand, the benefit is proportional to the reward, and can be estimated for instance to be proportional to \(-t_f\). Indeed, one could imagine the reward is a fixed amount to which is subtracted a number proportional to the difference between the world record and the final time. Similarly, one could add other benefits or costs linked to multiple attempts or the presence of a supporting audience. One could think of adding other costs, for instance in walking modeling, the cost is proportional to the jerk, which is the \(L^2\) norm of the derivative of the centrifugal acceleration (Arechavaleta et al. 2008; Bravo et al. 2015). In this paper, we choose to model the simplest case where the benefit is the final time and the cost is the motor control. This leads to the following minimization:

$$\begin{aligned} \min \left( t_f+\frac{\alpha }{2} \int _0^{t_f} u(t)^2\, dt \right) \end{aligned}$$
(6)

where \(\alpha >0\) is a weight to be determined so that the second term is a small perturbation of the first one, and therefore both terms are minimized.

As soon as the race is sufficiently long (above 1500 m), one notices [see Hanon and Thomas (2011) and our numerical simulations] the existence of a limiting problem where v and f are constant and e is linearly decreasing. Therefore, it is natural to expect that the turnpike theory of Trélat and Zuazua (2015) [see also Trélat 2020] provides very accurate estimates for the mean velocity, force and the energy decrease. The turnpike theory in optimal control stipulates that, under general assumptions, the optimal solution of an optimal control problem in sufficiently large fixed final time remains essentially constant, except at the beginning and at the end of the time-frame. We refer the reader to Trélat and Zuazua (2015) for a complete state-of-the-art and bibliography on the turnpike theory. Actually, according to Trélat and Zuazua (2015), due to the particular symplectic structure of the first-order optimality system derived from the Pontryagin maximum principle, the optimal state, co-state (or adjoint vector) and optimal control are, except around the terminal points, exponentially close to steady-states, which are themselves the optimal solutions of an associated static optimal control problem. In this result, the turnpike set is a singleton, consisting of this optimal steady-state which is of course an equilibrium of the control system. This is the so-called turnpike phenomenon. A more general version has recently been derived in Trélat (2020), allowing for more general turnpike sets and establishing a turnpike result for optimal control problems in which some of the coordinates evolve in a monotone way while some others are partial steady-states.

This result applies to our problem and we want to use it to simplify the runner’s model for potential software applications.

The paper is organized as follows. Firstly, we present numerical simulations of (2)–(3)–(4)–(5)–(6), then we describe our simplified problem and how to derive it. In Sect. 4, we study a more realistic \(\dot{V}O2\) and in Sect. 5, the effects of slopes.

2 Numerical simulations

Optimization and numerical implementation of the optimal control problem (2)–(3)–(4)–(5)–(6) are done by combining automatic differentiation softwares with the modeling language AMPL (Fourer et al. 1987) and expert optimization routines with the open-source package IpOpt Wächter and Biegler (2006). This allows to solve for the velocity v, force f, energy e in terms of the distance providing the optimal strategy and the final time. As advised in Trélat (2020) and Trélat and Zuazua (2015), we initialize the optimization algorithm at the turnpike solution that we describe below.

We have chosen numerical parameters to match the real race of 1500 m described in Hanon et al. (2008) so that \(d=1500\). The final experimental time for real runners is 245 s. The runners are middle distance runners successful in French regional races. Their \(\dot{V}O2_{\mathrm {max}}\) is around 66 ml/mn/kg. Because it is estimated that one liter of oxygen produces an energy of about 21.1 kJ via aerobic cellular mechanisms (Peronnet and Massicote 1991), the energetic equivalent of 66 ml/mn/kg is \(66\times 21.1\) kJ/mn/kg. Since we need to express \(\sigma \), the energetic equivalent of \(\dot{V}O2\) in SI units, we have to turn the minutes into seconds and this provides an estimate of the available energy per kg per second which is \( 66/60\times 21.1 \simeq 22\). This leads to a maximum value \({\bar{\sigma }}=22\) of \(\sigma \). From Hanon et al. (2008), the decrease in \(\dot{V}O2\) at the end of the race is of about \(10\%\) when the anaerobic energy left is \(15\%\). Therefore, we choose the final value of \(\sigma \) to be \(10\%\) less than the maximal value, that is \(\sigma _f=20\), and \(\gamma _1=0.15\). To match the usual rest value of \(\dot{V}O2\), we set \(\sigma _r = 6\). The other parameters are identified so that the solution of (2)–(3)–(4)–(5)–(6) matches the velocity data of Hanon et al. (2008): \(\gamma _2 = 566\), \(\alpha =10^{-5}\), \(F_{\mathrm {max}} = 8\), \(\tau = 0.932\), \( e^0 = 4651\), \(\gamma =0.0025\), \( v^0 = 3\). Let us point out that our model of effort is not appropriate to describe the very first seconds of the race. Therefore, we choose artificially \(v_0=3\) which allows, with our equations, to have a more realistic curve for the very few points, than starting from \(v_0=0\). Otherwise, one would need to refine the model for the start.

In Le Bouc et al. (2016), the equivalent of \(\alpha \) is determined by experimental data. In our case, we have noticed that, depending on \(\alpha \), either u is negative with a minimum or changes sign with a minimum and a maximum. Also, when \(\alpha \) gets too small, \(\dot{f}\) is almost constant. The choice of \(\alpha \) is made such that the second term of the objective is a small perturbation of the first one, and can act at most on the tenth of second for the final time.

With these parameters, we simulate the optimal control problem (2)–(3)–(4)–(5)–(6) and plot the velocity v, the propulsive force f, the motor control u, the energetic equivalent of the oxygen uptake \(\sigma (e)\), and the anaerobic energy e vs distance in Fig. 2. Though they are computed as a function of time, we find it easier to visualize them as a function of distance.

Fig. 2
figure 2

Velocity v, force f, energetic equivalent of the oxygen uptake \(\sigma (e)\), motor control u and energy e vs distance on a 1500 m. All functions (except e) display a plateau in the middle of the race corresponding to the turnpike phenomenon, except the energy which is affine. In this numerical simulation, the duration of the race is 244 s

Full size image

The velocity increases until reaching a peak value, then decreases to a mean value, before the final sprint at the end of the race. This is consistent with usual tactics which consist in an even pace until the last 300 m where the final sprint starts. This final sprint takes place when the function \(\sigma (e(t))\) starts decreasing. The function \(\sigma \) is the energetic equivalent of \(\dot{V}O2\). It increases to its plateau value, then decreases at the end of the race when the anaerobic supply gets too low. The control u also has a plateau at the middle of the race leading to a plateau for the force as well. The velocity and force follow the same profile. The energy is decreasing and almost linear when the velocity and force are almost constant.

In Fig. 2, we point out that we obtain an almost steady-state in the central part of the race for the motor control, the force and the velocity. We find from Fig. 2 the central value for the motor control \( u_{\text {turn}}=4.26\), the force \(f_{\text {turn}}=6.48\) and the velocity \(v_{\text {turn}} = 6.04\). We want to analyze this limit analytically. We will also try to construct local models for the beginning and end of the race.

3 Main results using turnpike estimates

The optimal control problem (2)–(3)–(4)–(5)–(6) involves a state variable, namely, the energy e(t), which goes from \(e^0\) to 0, and thus has no equilibrium. The turnpike theory has been extended in Trélat (2020) to this situation when the steady-state is replaced by a partial steady-state (namely, v and f are steady), and e(t) is approximated by an affine function satisfying the imposed constraints \(e^0\) at initial time and 0 at final time. In what follows, we denote the approximating turnpike trajectory with an upper bar, corresponding to a constant function \(\sigma (e)={\bar{\sigma }}\). More precisely, we denote by \(t\mapsto ({\bar{v}}_c, {\bar{e}}_c(t), {\bar{f}}_c)\) the turnpike trajectory defined on the interval \([0,{\bar{t}}_c]\) so that \({\bar{v}}_c\) and \(\bar{f}_c\) are steady-states (equilibrium of the control dynamics (2)–(3)–(4)) with \({\bar{v}}_c ={\bar{f}}_c \tau \), and \({\bar{e}}_c(t)\) is affine:

$$\begin{aligned} \dot{{\bar{e}}}_c (t)={\bar{\sigma }} -{\bar{f}}_c{\bar{v}}_c \end{aligned}$$

and satisfies the terminal constraints \(\bar{e}_c(0)=e^0\) and \({\bar{e}}_c({\bar{t}}_c)=0\), while \(d={\bar{v}}_c {\bar{t}}_c\). Integrating yields

$$\begin{aligned} \frac{{\bar{v}}_c^2}{\tau }-{\bar{\sigma }} =e^0 \frac{{\bar{v}}_c}{d}. \end{aligned}$$
(7)

The mean velocity \({\bar{v}}_c\) can be solved from (7) to get

$$\begin{aligned} {\bar{v}}_c =\frac{e^0 \tau }{2d} +\sqrt{{\bar{\sigma }}\tau +\left( \frac{e^0\tau }{2d}\right) ^2}. \end{aligned}$$
(8)

We observe that the value of \({\bar{v}}_c\) increases with \(e^0\), \(\tau \) (which is the inverse of friction) and \({\bar{\sigma }}\), but is not related to the maximal force. Indeed, the maximal propulsive force controls the acceleration at the beginning and end of the race, but not the mean velocity in the middle of the race. In the case of our simulations, \({\bar{v}}_c= 6.2\) which is slightly overestimated with respect to the simulation value \(v_{\text {turn}}=6.04\).

We next elaborate to show how the turnpike theory can be applied to the central part of the race where \(\sigma \) is constant and allows to derive very accurate approximate solutions.

If one takes into account the full shape of \(\sigma (e)\), made up of three parts, then the velocity curve is made up of three parts. In the rest of the paper, we will derive the following approximation for the velocity:

figure a

The parameters appearing in the formula are defined as follows: \(v_0\) is the initial velocity in (3), \({\bar{v}}\) is obtained as the positive root that is bigger than \(\sqrt{{\bar{\sigma }} \tau }\) of

$$\begin{aligned} d=\frac{{\bar{v}}\gamma _2}{\frac{{\bar{v}}^2}{\tau }-\sigma _r}+{\bar{v}}\frac{e^0(1-\gamma _1)-\gamma _2}{\frac{{\bar{v}}^2}{\tau }-{\bar{\sigma }}}+\frac{{\bar{v}}e^0\gamma _1}{\frac{{\bar{v}}^2}{\tau }-\sigma _f}, \end{aligned}$$
(10)

\(t_1\) is given by

$$\begin{aligned} t_1=\frac{\gamma _2}{\frac{{\bar{v}}^2}{\tau }-\sigma _r}, \end{aligned}$$
(11)

\(v_{\max }=f^0\tau \), where \(f^0\) is the positive root of the trinomial

$$\begin{aligned}&\int _0^{t_1} \left( f^0+t\frac{{\bar{v}}/ \tau -f^0}{t_1}\right) \left( v_0 e^{-t/\tau }+\left( \tau f^0+t\frac{{\bar{v}}-\tau f^0}{t_1}\right) (1-e^{-t/\tau })\right) e^{\frac{{\bar{\sigma }} -\sigma _r}{\gamma _2}(t-t_1)} \, dt \nonumber \\&\quad = \gamma _2+\frac{\sigma _r\gamma _2}{{\bar{\sigma }} -\sigma _r}\left( 1-e^{-\frac{{\bar{\sigma }} -\sigma _r}{\gamma _2}t_1}\right) ; \end{aligned}$$
(12)

from this, we compute \(d_1=\int _0^{t_1} v(t) \, dt\). We define \({\bar{d}}=\frac{e^0(1-\gamma _1)-\gamma _2}{\frac{{\bar{v}}^2}{\tau }-{\bar{\sigma }}}\), the length of the turnpike, and

$$\begin{aligned} \Delta t_{\text {end}}= \frac{d-d_1-{\bar{d}}}{{\bar{v}}}; \end{aligned}$$
(13)

\(\lambda \) is chosen such that, if \(A=\frac{{\bar{\sigma }} -\sigma _r}{\gamma _1 e^0}\), then there is an \(L^2\) estimate for the velocity at the end of the race:

$$\begin{aligned} \int _{0}^{\Delta t_{\text {end}}} \left( \frac{ \tau F_{\text {max}}}{ (1+ ( {F_{\text {max}}}/ {{\bar{f}}}-1) e^{-\gamma \lambda F_{\text {max}}t})} \right) ^2 e^{-At}\ dt=\tau \frac{\sigma _f}{A} (1-e^{-A \Delta t_{\text {end}}})+ \tau \gamma _1 e^0; \end{aligned}$$
(14)

moreover, the time \(t_2\) is defined so that

$$\begin{aligned} t_2-t_1=\frac{1}{{\bar{v}}} \left( d-\int _0^{t_1}v(t)\ dt -\int _0^{\Delta t_{\text {end}}}\frac{\tau F_{\text {max}}}{ 1+ ( {F_{\text {max}}}/ {{\bar{f}}}-1) e^{-\gamma \lambda F_{\text {max}}t}}\ dt\right) . \end{aligned}$$
(15)

and \(t_f=t_2+\Delta t_{\text {end}}\).

Let us explain the general meaning of these computations. Equation (10) is based on the hypothesis that v and f are constant values and uses the shape of \(\sigma \) and the energy equation to compute the duration and length of each phase. From the first phase, we derive the value of \(t_1\) in (11). Then we compute the initial force that corresponds to the correct energy expenditure in the first phase through (12). This provides, through the integral of the velocity the distance \(d_1\) of the first phase. We next approximate the distance and time of the last phase using the distance and time of turnpike through (13). Once we have the duration of the last phase, we again match the energy expenditure in (14). This provides the velocity profile of the last phase and therefore the distance of the last phase. In order to match the total distance, we have to slightly modify the length of the central turnpike part in (15). From the computational viewpoint, these steps correspond to the first successive approximations in the Newton-like solving of a system of nonlinear equations.

The velocity curve (9) goes from the initial velocity \(v_0\) to a maximum velocity, then down to \({\bar{v}}\), which is the turnpike value. At the end of the race, the velocity increases to the final velocity. This type of curve is quite consistent with velocity curves in the sports literature, see for instance Foster et al. (2019) and Hanley et al. (2019), and with our simulations illustrated in Fig. 2.

We see that \(t_1\) increases with \(\gamma _2\), while \(t_f-t_2\) increases with \(\gamma _1\).

For the values of parameters of Section 2, we find from (10) that \({\bar{v}}=6.06\), which is to be compared to the value in Fig. 2, \(v_{\text {turn}}=6.04\). Then from (11) \(t_1=16.95\), from (12) that \(f^0=8.2\), \(d_1=111.84\). We deduce from (13) \(\Delta t_{\text {end}}=34.42\), from (14), \(\lambda =0.39\), from (15) \(t_2=210.76\), \(t_f=245.19\) (very close to the 244 s obtained in the numerical simulation in Fig. 2 and to the experimental value of 245 s) and we find \(v_f=6.33\) at the final time. We point out that in the turnpike region, this yields \({\bar{f}}={\bar{v}}/\tau =6.5\) and \({\bar{u}}={\bar{f}}/(F_{\text {max}}-f)= 4.34\), very close to the values in Fig. 2, \(f_{\text {turn}}=6.48\) and \( u_{\text {turn}}=4.26\).

We have illustrated in Fig. 3 the approximate solution (9) together with the numerical solution of the full optimal control problem (2)–(3)–(4)–(5)–(6). We see that the duration of the initial phase is slightly underestimated, while the duration of the final phase is very good. The estimate of the sprint velocity at the end is also very good. Note that the simulation of the full optimal control problem produces a decrease of velocity at the very end of the race which is not captured by our approximation, but this changes very slightly the estimate on \(t_f-t_2\) or on the sprint velocity at the end and is not meaningful for a runner, so we can safely ignore it for our approximations.

Fig. 3
figure 3

Velocity v as a solution of the simulation (blue) of (2)–(3)–(4)–(5)–(6) and approximate solution given by (9) (red) (color figure online)

Full size image

The advantage of formulation (9) is that if we have velocity data of a runner on a race, and have access to his \(\dot{V}O2_{\mathrm {max}}\), that is \({\bar{\sigma }}\), then we can infer the values of all the physiological parameters: from the velocity curve at the beginning, we can determine \(\tau \) and \(v_{\max }\). The value of \({\bar{v}}\) and (8) yield \(e^0\). From the values of \(t_1\) and \(t_2\), we deduce \(\gamma _1\) and \(\gamma _2\). In order to have more precise values, we can always perform an identification of the parameters using the full numerical code, but from these approximate values, we have enough information to determine the runner’s optimal strategy on other distances.

The rest of the section is devoted to deriving (9).

3.1 Central turnpike estimate

In the central part of the race, \(\sigma (e)={\bar{\sigma }}\) is constant. Therefore in this part, when e(t) is between \(e^0-\gamma _2\) and \(\gamma _1 e^0\), we can apply the turnpike theory of Trélat (2020). Then we have \(v(t)\simeq {\bar{v}}\), \(f(t)\simeq {\bar{f}}\), \(u(t)\simeq {\bar{u}}\) with

$$\begin{aligned} {\bar{f}}=\frac{{\bar{v}}}{\tau },\quad {\bar{u}} = \frac{{\bar{f}}}{F_{\mathrm {max}}-{\bar{f}}}. \end{aligned}$$

We have to integrate

$$\begin{aligned} \dot{{\bar{e}}}(t)=\sigma ({\bar{e}}(t))-\frac{{\bar{v}}^2}{\tau },\qquad {\bar{e}}(t_1)=e^0-\gamma _2\quad {\bar{e}}(t_2)=\gamma _1 e^0. \end{aligned}$$

We find

$$\begin{aligned} e^0(1-\gamma _1)-\gamma _2=(t_2- t_1) \left( {\frac{{\bar{v}}^2}{\tau }-{\bar{\sigma }}}\right) . \end{aligned}$$

This is consistent with (7) which is the same computation but on the whole interval, that is with \(\gamma _1=\gamma _2=0\). The value for \(t_2-t_1\) is 194.64.

As a first approximation, we can assume that on the two extreme parts of the race, v and f can be taken to be constants. We will see below why this assumption is reasonable. Therefore we can solve

$$\begin{aligned} \dot{{\bar{e}}}(t)=\sigma ({\bar{e}}(t))-\frac{{\bar{v}}^2}{\tau }\qquad {\bar{e}}(0)=e^0,\quad {\bar{e}}(t_1)=e^0-\gamma _2, \quad {\bar{e}}(t_2)=\gamma _1 e^0,\quad e({\bar{t}})=0. \end{aligned}$$

Therefore, \({\bar{t}}\) is the final time of the turnpike trajectory defined by \({\bar{e}}({\bar{t}})=0\). The initial and final parts of the race produce exponential terms, namely

$$\begin{aligned} \frac{{\bar{\sigma }} -\sigma _r}{\frac{{\bar{v}}^2}{\tau }-\sigma _r}=1-e^{-\frac{({\bar{\sigma }}-\sigma _r)t_1}{\gamma _2}} \qquad \hbox {and}\qquad \frac{{\bar{\sigma }} -\sigma _f}{\frac{{\bar{v}}^2}{\tau }-\sigma _f}=1-e^{-\frac{({\bar{\sigma }}-\sigma _f)({\bar{t}} -t_2)}{e^0\gamma _1}} . \end{aligned}$$
(16)

Therefore, for the total distance d, we find, summing our estimates,

$$\begin{aligned} {\bar{t}}=\frac{d}{{\bar{v}}}=\frac{e^0(1-\gamma _1)-\gamma _2}{\frac{{\bar{v}}^2}{\tau }-{\bar{\sigma }}}-\frac{\gamma _2}{{\bar{\sigma }} -\sigma _r} \ln \left( 1-\frac{{\bar{\sigma }} -\sigma _r}{\frac{{\bar{v}}^2}{\tau }-\sigma _r}\right) -\frac{e^0\gamma _1}{{\bar{\sigma }} -\sigma _f} \ln \left( 1-\frac{{\bar{\sigma }} -\sigma _f}{\frac{{\bar{v}}^2}{\tau }-\sigma _f}\right) .\nonumber \\ \end{aligned}$$
(17)

If the initial and final parts are not too long, then (16) can be approximated by

$$\begin{aligned} t_1\simeq \frac{\gamma _2}{\frac{{\bar{v}}^2}{\tau }-\sigma _r} \quad \hbox {and}\quad {\bar{t}} -t_2\simeq \frac{e^0\gamma _1}{\frac{{\bar{v}}^2}{\tau }-\sigma _f} \end{aligned}$$
(18)

and therefore, from (17), \({\bar{v}}\) can be approximated by (10). For the values of parameters of Section 2, (10) yields \({\bar{v}}=6.06\). The intermediate times can be computed from (18): \(t_2=35.96\) s and \(t_1=16.95\) s. This also yields the distances of each part by multiplying by \({\bar{v}}\). In the following, we will keep this value of \(t_1\) but improve the estimate for \(t_2\).

Note that this turnpike calculation can be used the other way round: if one knows the mean velocity, d, \(\tau \) and \({\bar{\sigma }}\), it yields an estimate of the energy \(e^0\) used while running, as well as the aerobic part which is \({\bar{\sigma }} d/{\bar{v}}\).

The next step is to identify reduced problems for the beginning (interval \((0,t_1)\)) and end of the race (interval \((t_2,{\bar{t}} )\)). The two are not totally equivalent since at the beginning we have an initial condition for the velocity v whereas on the final part the final velocity is free.

3.2 Estimates for the beginning of the race

The problem is to approximate the equations for v, f, e with boundary conditions

$$\begin{aligned} v(0)=v^0,\quad v(t_1)={\bar{v}},\quad f(t_1)={\bar{f}},\quad e(0)=e^0,\quad e(t_1)= e^0-\gamma _2. \end{aligned}$$

Here, f(0) is free.

We integrate the energy equation and find

$$\begin{aligned} \int _0^{t_1} f(t) v(t) \ dt=\int _0^{t_1} \left( \dot{e}(t) -\sigma (e(t))\right) dt. \end{aligned}$$

In this regime, \(\sigma (e)\) is linear, and this equation can be integrated explicitly. Indeed, let \(A=\frac{{\bar{\sigma }} -\sigma _r}{\gamma _2}\), then

$$\begin{aligned} -\gamma _2=\frac{\sigma _r\gamma _2}{{\bar{\sigma }} -\sigma _r}(1-e^{-At_1})-e^{-At_1}\int _0^{t_1}f(t)v(t)e^{At}\ dt.\end{aligned}$$
(19)

Because we are in a regime of parameters where At is small, we can expand the exponential terms. The approximation which consists in assuming that the integral of fv can be approximated by the mean value of fv is good, and therefore this justifies the turnpike estimate of the previous section and this yields the estimate (11) of \(t_1\).

Now let us assume \(t_1\) is prescribed. If we fix the interval \((0,t_1)\), we have the equations for v and f with

$$\begin{aligned} v(0)=v^0,\quad v(t_1)={\bar{v}},\quad f(0)=f^0,\quad f(t_1)={\bar{f}}. \end{aligned}$$
(20)

Here \(f^0\) is unknown and we want to minimize the motor control only. For this part, we can assume that the minimization of the motor control leads to a linear function f as explained in the Appendix. Therefore, \(f(t)=f^0+t({\bar{f}}-f^0)/t_1\) and \(v(t)=v_0 e^{-t/\tau }+\tau f(t)(1-e^{-t/\tau })\) to approximate (3). We plug this into (19) and then we find that \(f^0\) is a solution of (12). This can be integrated analytically or numerically to determine \(f^0\). In our case, \(f^0=8.2\). This yields the first line of (9) with \(v_{\mathrm {max}}=\tau f^0\).

3.3 End of the race

Once the beginning and central part of the race are determined, the duration of the end of the race is determined so that the prescribed distance d is run through (13).

The problem describing the end of the race consists in solving the equations for v, f, e on the interval \((t_2,t_f)\) with initial and final values

$$\begin{aligned} v(t_2)={\bar{v}},\quad f(t_2)={\bar{f}},\quad e(t_2)=\gamma _1 e^0,\quad e(t_f)=0. \end{aligned}$$
(21)

This yields the simulation in Fig. 4. We observe that f(t) and \(v(t)/\tau \) are very close, as expected.

Fig. 4
figure 4

Velocity and force solving the equations for v, f, e on the interval \((t_2,t_f)\) with initial and final values (21). The force f(t) is compared to the value \(v(t)/\tau \)

Full size image

In the following, we will assume that \(\dot{v}\) is negligible in front of \(v/\tau \), so that \(v\simeq f\tau \), which removes an equation. Then using the specific shape of \(\sigma \), the energy equation becomes, denoting \(A=\frac{{\bar{\sigma }}-\sigma _f}{e^0\gamma _1}\simeq 0.0028\),

$$\begin{aligned} e^{A(t-t_2)}\frac{d}{dt}{{\left( e(t)e^{-A(t-t_2)}\right) }}=\sigma _f-\tau f(t)^2. \end{aligned}$$

Then we need to integrate this energy equation and find

$$\begin{aligned} \tau \int _{t_2}^{t_f} f(t)^2 e^{-A(t-t_2)}\, dt=\frac{\sigma _f}{A} (1-e^{-A(t_f-t_2)})+ \gamma _1 e^0. \end{aligned}$$
(22)

The reduced optimal control problem for the end of the race is therefore

$$\begin{aligned}&\min \int _{t_2}^{t_f} u(t)^2\, dt \nonumber \\&\dot{f}(t)=\gamma (u(t)(F_{\text {max}}-f(t)) -f(t)) \nonumber \\&f(t_2)={\bar{f}}, \qquad \tau \int _{t_2}^{t_f} f(t)^2 e^{-A(t-t_2)}\ dt=\frac{\sigma _f}{A} (1-e^{-A(t_f-t_2)})+ \gamma _1 e^0. \end{aligned}$$
(23)

This problem can be kept as the full problem for the end of race. It provides a solution which is very close to that of Fig. 4. Otherwise, one can try to reduce further the problem to have a simple expression for the velocity. In Le Bouc et al. (2016), an approximation for such a problem by a sigmoid function is used. In our case, as computed in the Appendix, this yields the following sigmoid

$$\begin{aligned} f(t) =\frac{ F_{\text {max}}}{ 1+ ( {F_{\text {max}}}/ {{\bar{f}}}-1) e^{-\gamma \lambda F_{\text {max}}(t-t_2)}} \end{aligned}$$
(24)

where \(\lambda \) is chosen such that the \(L^2\) norm of f satisfies condition (22). Then, since \(v=\tau f\), this provides the final estimate for the velocity. This estimate yields an increasing velocity at the end of the race. It does not capture the short decrease at the very end of the race. But this changes very slightly the estimate on \(t_f-t_2\) or on the sprint velocity at the end and is not meaningful for a runner, so we can safely ignore it for our approximations.

Once we have this final approximation for the velocity, we have to match the length of the turnpike central phase so that the integral of v is exactly d, which yields (15). This reduces very slightly the turnpike phase from 194.64 seconds to 193.81 seconds for our simulations.

Our distance is made up of 3 parts: the turnpike distance which is totally determined by \(\gamma _1\) and \(\gamma _2\) and the distance run in the initial and final parts. Of course, since the sum is prescribed, only one of the two is free. So for instance, in the final phase if we determine the duration of this final phase by some estimate like above, the initial phase has to match the total distance, but nevertheless is safely estimated from the turnpike.

4 Comparison with a real 1500 m

The runners’ oxygen uptake was recorded in Hanon et al. (2008) by means of a telemetric gas exchange system. This allowed to observe that the \(\dot{V}O2\) reached a peak in around 450 m from start, with a significant decrease between 450 and 550 meters. Then the \(\dot{V}O2\) remained constant for 800 meters, before a decrease of \(10\%\) at the end of the race. To match more precisely the \(\dot{V}O2\) curve of Hanon et al. (2008), we add an extra piece to the curve of \(\sigma \), before the long mean value \({\bar{\sigma }}\): after the initial increase, there is a local maximum before decreasing to the constant turnpike value:

$$\begin{aligned} \sigma (e)=\left\{ \begin{array}{ll} \displaystyle {\bar{\sigma }} \frac{e}{e^0\gamma _1}+\sigma _f \left( 1-\frac{e}{e^0 \gamma _1}\right) &{} \displaystyle \quad \hbox {if}\quad \frac{e}{e^0}<\gamma _1\\ \displaystyle {\bar{\sigma }} &{} \displaystyle \quad \hbox {if}\quad \gamma _1\leqslant \frac{e}{e^0}\leqslant \gamma _+ \\ \displaystyle {\bar{\sigma }}+0.8 \frac{e-\gamma _+e^0}{e^0-\gamma _2-\gamma _+e^0} &{} \displaystyle \quad \hbox {if}\quad \frac{e}{e^0}\geqslant \gamma _+ \quad \hbox {and}\quad e^0-e>\gamma _2 \\ \displaystyle ({\bar{\sigma }}+0.8 -\sigma _r) \frac{e^0 -e}{\gamma _2}+\sigma _r &{} \displaystyle \quad \hbox {if}\quad e^0 -e<\gamma _2 \end{array}\right. \end{aligned}$$

We take roughly the same parameters as before except for \(\gamma _2=2000\) and \(\gamma _+=1-\gamma _2/e^0-400/e^0\). The others are \(\sigma _r=6\), \(\sigma _f=20\), \({\bar{\sigma }}=22\), \(\gamma _1=0.15\), \(F_{\mathrm {max}}=8\), \(\tau =1.032\), \(e^0=4651\), \(\gamma =0.0025\), \(v_0=1\).

Fig. 5
figure 5

Modified \(\sigma \) in four pieces and optimal velocity versus distance for a 1500 m

Full size image

Then we see in Fig. 5 that the velocity has a local minimum in the region where \(\sigma \) has a local maximum,which matches exactly the velocity profile in Hanon et al. (2008). Small variations in \(\sigma \) always provide variations in the velocity profile with the opposite sense.

It is well known that successful athletes in a race are not so much those who speed up a lot at the end but those who avoid slowing down too much . We have noticed that if the maximal force at the beginning of the race is too high, then the velocity tends to fall down at the end of the race, leading to a bad performance. For a final in a world competition, it is observed in Hanley et al. (2019) that the best strategy is J-shaped, which means reaching maximal speed at the end of the race. But this is not available to all athletes. The runners profile of these simulations are not world champions but only successful in French regional races. Therefore, their pacing strategy is either U-shaped (the start and the finish are quicker) or reverse J-shaped (greater starting pace). This is very dependent on the relative values of running economy \(\tau \), anaerobic energy \(e^0\) and profile of \(\dot{V}O2\). Moreover, top runners use pace variation according to laps as their winning tactics (Aragón et al. 2016), but this is not active on the level of runners we have analyzed in this paper.

5 Running uphill or downhill

Our model also allows to deal with slope or ramps. Indeed, one has to change the Newton law of motion to take into account a dependence on the slope \(\beta (x)\) at distance x from the start, which is the cosine of the angle. If we denote by g the gravity, the velocity equation changes into

$$\begin{aligned} \dot{v}(t) = -\frac{v(t)}{\tau }+f(t)-g\beta (x(t)) . \end{aligned}$$

If the track goes uphill or downhill with a constant rate \(\delta \), then in the turnpike estimate, this becomes

$$\begin{aligned} {\bar{v}}=\tau {\bar{f}} -g\tau \delta \end{aligned}$$

where \(\delta \) is positive when the track goes up and negative when it goes down. If the slope is constant for the whole race, the turnpike estimate can be computed.

If we assume a slope \(\beta (x)\) which is constant equal to \(\delta \), the new turnpike estimate is

$$\begin{aligned} {\bar{v}}=\frac{(e^0-dg\delta ) \tau }{2d} +\sqrt{{\bar{\sigma }}\tau +\left( \frac{(e^0-dg\delta )\tau }{2d}\right) ^2}. \end{aligned}$$

If the slope is small, one can make an asymptotic expansion in terms of \(\delta \) to find the difference in velocity

$$\begin{aligned} \triangle v=-g\delta \tau \left( \frac{1}{2}+\frac{1}{\sqrt{\frac{{\bar{\tau }}}{4}+{\bar{\sigma }}\left( \frac{d}{e^0}\right) ^2}}\right) . \end{aligned}$$

But if the slope is constant for a small part of the race, then the variation of velocity cannot be computed locally because the whole mean velocity of the race is influenced by a local change of slope as we will see in the last part of the paper.

Nevertheless, because the energy is involved, a change of slope, even locally implies a change of the turnpike velocity on the whole race. We have chosen to put slopes and ramps of \(3\%\) for 300 m. We see in Fig. 6 that without slope we have an intermediate turnpike value, but with a slope or ramp even only for 300 m, the whole turnpike velocity is modified.

Fig. 6
figure 6

Velocity versus distance for a 1500 m, on a flat track (red), on a track with a \(3\%\) slope between 700 m and 1000 m (orange) and on a track with a \(3\%\) ramp between 700 m and 1000 m (blue) (color figure online)

Full size image
Fig. 7
figure 7

Slope, velocity, zoom on the velocity and force for a 1500 m with slopes and ramps. There is a slope of \(2\%\) between 400 m and 600 m and then between 800 m and 1000 m. There is a ramp of \(2\%\) between 600 m and 800 m and then between 1000 m and 1200 m

Full size image

To illustrate further the slope effect, we have put a periodic slope and ramp of 200 m between 300 m and 1200 m. We use the same parameters as in the previous section. We see in Fig. 7 that the turnpike velocity is affected. When going down, a runner speeds at the end of the ramp, but his velocity has a local maximum at the middle of the ramp. Similarly, it has a local minimum at the middle of the slope. The variations in velocity are very small since they are of order of a few percents. But this allows to understand that slopes and ramps are not local perturbations on the pacing profile.

6 Conclusion

We have provided a model for pace optimization. This involves a control problem in order to use the maximal available propulsive force and energy to produce the optimal running strategy and minimize the time to run and the motor control. For sufficiently long races (above 1500 m), the optimal strategy is well approximated by a turnpike problem that we describe. Simplified estimates for the peak velocity and velocity profiles related to aerobic, anaerobic energy and effect of the motor control are obtained and fit the simulations. The effect of the parameters and slope and ramps are analyzed. The potential applications of this turnpike theory would be to derive a simpler model for pacing strategy that could be encompassed in a running app. Indeed, the advantage of our simplified formulation for the velocity is that if we have velocity data of a runner on a race, and have access to his \(\dot{V}O2_{\mathrm {max}}\), then we can infer the values of all the physiological parameters and therefore predict his optimal strategy on a fixed distance.