A game-theoretical dynamic imitation model on networks

Abstract

A game-theoretical model is constructed to capture the effect of imitation on the evolution of cooperation. This imitation describes the case where successful individuals are more likely to be imitated by newcomers who will employ their strategies and social networks. Two classical repeated strategies ‘always defect (ALLD)’ and ‘tit-for-tat (TFT)’ are adopted. Mathematical analyses are mainly conducted by the method of coalescence theory. Under the assumption of a large population size and weak selection, the results show that the evolution of cooperation is promoted in this dynamic network. As we observed that the critical benefit-to-cost ratio is smaller compared to that in well-mixed populations. The critical benefit-to-cost ratio approaches a specific value which depends on three parameters, the repeated rounds of the game, the effective strategy mutation rate, and the effective link mutation rate. Specifically, for a very high value of the effective link mutation rate, the critical benefit-to-cost ratio approaches 1. Remarkably, for a low value of the effective link mutation rate, by letting the effective strategy mutation is nearly equal to zero, the critical benefit-to-cost ratio approaches $1+\frac{1}{m-1}$ for the resulting highly connected networks, which allows TFT to be evolutionary stable. It illustrates that dominance of TFTs is associated with more connected networks. This research can enrich the theory of the coevolution of game strategy and network structure with dynamic imitation.

1 Introduction

To explain the universal phenomena of cooperation in nature has fascinated scientists in many fields, including biology, economy, sociology and so on. Cooperative behavior violates Darwinia selection, because cooperators incur costs to benefit others while defectors reap the benefits without bearing the costs. This naturally arises the question how cooperative entities can overcome the obvious fitness disadvantages and survive when confronting cheating. Evolutionary game theory has been used as a standard mathematical tool to investigate the problem of cooperation in social dilemma (Nowak and Sigmund 2004; Doebeli and Hauert 2005).

Since the pioneering work by Nowak and May (1992), spatial structure was verified to promote the evolution of cooperation in the Prisoner’s dilemma game(PD). Spatial game models assume individuals are more likely to interact with their neighbors than with distant ones. The spatial game dynamics has attracted increasing interest from different aspects and a considerable amount of research has been devoted (Nowak and May 1992; Lindgren and Nordahl 1994; Killingback and Doebeli 1996; Nakamaru et al. 1997, 1998; Szabó and Tőke 1998; van Baalen and Rand 1998; Brauchli et al. 1999; Mitteldorf and Wilson 2000; Nowak and Sigmund 2000; Hauert 2002; Le Galliard et al. 2003; Doebeli and Hauert 2005; Roca et al. 2009; Tarnita et al. 2009a; Nowak et al. 2010a, b). The main result is that spatial structure enables cooperators to form clusters and thereby reduces exploitation by defectors.

Specifically, for games on graphs, individuals with different strategies are arranged on the vertices of a graph, and edges denote who interacts with whom. Each individual obtains its payoff by playing a game with all its connected individuals. A number of different updating mechanisms can be used to determine the evolving state of the graph, specifying how the composition of the populations changes under natural selection (Abramson and Kuperman 2001; Ebel and Bornholdt 2002; Kim et al. 2002; Lieberman et al. 2005; Santos and Pacheco 2005; Antal et al. 2006; Ohtsuki and Nowak 2006a, b, 2007; Ohtsuki et al. 2006, 2007; Pacheco et al. 2006a, b; Santos et al. 2006a, c; Szabó and Fáth 2007; Lehmann et al. 2007; Taylor et al. 2007; Fu and Wang 2008; Fu et al. 2011; Wu et al. 2010).

Recent studies on the structure of a social, technological and biological networks have shown that they share salient features which situate them far from being completely regular or random. Most of the models proposed to construct these networks are grounded in a graph-theoretical approach, i.e., algorithm methods to build graphs formed by elements (the nodes) and links that evolve according to pre-specified rules. Despite the progress made so far, there are still several open questions. An important issue is that networks are dynamical entities that evolve and adopt driven by the actions of the elements involved (Pacheco et al. 2006a, b; Santos et al. 2006b). For example, some social, biological and economic networks grow and decline with occasional fragmentation and reformation (Davies et al. 1998; Rainey and Rainey 2003; Jackson 2008; Schweitzer et al. 2009). These phenomena could be a direct consequence of simple imitation and internal conflicts between ‘cooperators’ and ‘defectors’ (Cavaliere et al. 2012).

Direct reciprocity (Trivers 1971) has been indicated as one mechanism for the evolution of cooperation (Nowak 2006). The Repeated Prisoner’s Dilemma (Repeated PD) is a reflection of the concept of direct reciprocity under the framework of game theory, which has been the subject of various and large numbers of investigations (Rapoport and Chammah 1965; Axelrod and Hamilton 1981; Axelrod 1984; Imhof et al. 2005). In the computer tournaments by Axelrod and Hamilton (1981) and Axelrod (1984), the famous strategy tit-for-tat (TFT) was proven as the only successful strategy against a range of other strategies. Such as the extreme unconditional strategy “always defect(ALLD)”. TFT strategy cooperates on the first round of the game then does whatever the opponent did on the previous round of the game. But TFT does not always perform well when erroneous behaviors are incorporated (Doebeli and Hauert 2005). Actually, there are other prominent strategies in the Repeated PD, such as generous-tit-for-tat (GTFT) (Nowak and Sigmund 1992), win-stay and lose-shift (Nowak and Sigmund 1993), and so on. TFT strategy is mainly used as a cooperative strategy in this paper, because it greatly grasps the essential of the Repeated PD.

The interaction between TFT and always defect (ALLD) strategies was studied on lattice-structured populations by Nakamaru et al. (1997, 1998). Lattice structure was found to be beneficial for the evolution of cooperation, where TFT can invade an ALLD population. Two different updating rules were respectively used in their studies, the score-dependent fertility model (Nakamaru et al. 1997) and the score-dependent viability model (Nakamaru et al. 1998) . The former is verified to be more favorable for cooperation than the latter. Nowak et al. (2004) developed a stochastic model of two player games and specified the conditions required for natural selection to favour the emergence of cooperation in finite populations. They demonstrated for sufficiently large population and for sufficiently weak selection that the fixation probability of TFT is larger than 1/N if the fitness of the invading TFT at a frequency of 1/3 is greater than the fitness of the resident ALLD (i.e. the ‘one-third’ law). Kurokawa and Ihara (2009) considered a stochastic model of n-player repeated Prisoner’s Dilemma game by extending the model of Nowak et al. (2004). They revealed that a single TFT replacing a population of ALLD can be favoured by natural selection in their n-player repeated Prisoner’s Dilemma game given that the number of rounds is sufficiently large. A generalized version of the one-third law was also derived in their work. In addition, the fundamental conditions for the evolution of cooperation was derived in a model where direct reciprocity and static network reciprocity are combined together by Ohtsuki and Nowak (2007). It was founded that TFT can dominate ALLD on a graph for four different updating mechanisms, which is never possible in well-mixed populations. Especially, a smaller value of the average number of neighbors and a larger value of the probability of playing in next round of game favors cooperation more. These results qualitatively agree with that of Nakamaru et al. (1997, 1998). Moreover, Pacheco et al. (2008) examinized the evolution of cooperation under direct reciprocity in dynamically structured populations, where individuals meet non-randomly and control over the frequency or duration of interactions. Specifically, individual differ in the rate at which they seek new interactions. The main conclusion is that the feasibility of cooperation relies on the propensity to form links. The more long-lived the links are between reciprocators, the better for cooperation; The longer the lifetime of links between reciprocator and defectors, the better for cooperation. Here, we give a dynamical model to mainly understand the role of imitation in the interplay between direct reciprocity and network reciprocity.

In this paper, direct reciprocity and network reciprocity are brought together to study the evolution of cooperation in social networks with dynamical linking, where the competition of two strategies TFT and ALLD are considered. The aim of this paper is to theoretically analyze a simple setting of such adaptive and evolving network, in which co-evolution of the state of the elements in the nodes of the network and the interaction links defines the network.

2 Models and analyses

2.1 Direct reciprocity in well-mixed populations

For the two strategies TFT and ALLD, the payoff matrix is defined as

$$\begin{aligned} \begin{array}{cl} &{}\qquad \text {ALLD}~~~~~~\text {TFT}\\ \begin{array}{c} \text{ ALLD }\\ \text{ TFT }\\ \end{array}&{} \left( \begin{array}{cc} 0 &{}\quad ~ b\\ -c &{}\qquad \qquad ~ m(b-c)\\ \end{array} \right) \\ \end{array}, \end{aligned}$$

(1)

where the parameter b represents the benefit received by a recipient from a cooperator who pays cost c, assuming a defector pays no cost and distributes no benefits, and m represents the number of the interaction rounds. This payoff matrix is equivalent to that in Pacheco et al. (2008) by letting $m=\frac{1}{1-w}$, where w denotes the probability of playing another round of the game.

We firstly study an infinitely complete mixing model in which each player interacts with another player randomly chosen from the whole population. Replicator equations are introduced as a corresponding mathematical tool to describe evolutionary dynamics in the deterministic limit of an infinitely large and well-mixed populations (Taylor and Jonker 1978; Weibull 1995).

• (1) In an infinitely well-mixed population of ALLD players, it cannot be invaded by TFT under deterministic selection dynamics because of $0>-c$. That is , ALLD is both a strict Nash equilibrium and an evolutionarily stable strategy (ESS).

• (2) In an infinitely well-mixed population of TFT players, it cannot be invaded by ALLD players under deterministic selection dynamics if $m(b-c)>b$. That is, TFT is both a strict Nash equilibrium and an evolutionarily stable strategy (ESS). The inequality now reads

  $$\begin{aligned} \frac{b}{c}>1+\frac{1}{m-1}. \end{aligned}$$

  (2)

• (3) Both ALLD and TFT strategies are ESS whenever $0>-c, m(b-c)>b$. The replicator dynamics admits an unstable mixed equilibrium, located at $x^{*}_{T}=\frac{c}{(m-1)(b-c)}$, where $x^{*}_{T}$ is the equilibrium frequency of TFT players in the population. This means that the TFT players can spread in the population when its frequency $x_{T}$ is larger than $x^{*}_{T}$ in well-mixed populations. From it, we can derive

  $$\begin{aligned} \frac{b}{c}>1+\frac{1}{x_T(m-1)}. \end{aligned}$$

  (3)

• (4) TFT strategy is risk-dominant (RD) (Harsanyi and Selten 1988) if it has a larger basin of attraction than ALLD, that is, $-c+m(b-c)>b$ which equivalents to

  $$\begin{aligned} \frac{b}{c}>1+\frac{2}{m-1}. \end{aligned}$$

  (4)

  Note also if TFT is RD when compared to ALLD, then the fixation probability of TFT is greater than the fixation probability of ALLD for weak selection and large population size (Nowak et al. 2004; Imhof and Nowak 2006).

In finite population, the crucial quantity is the fixation probability of a strategy, defined as the probability that a lineage of offspring generated by a single mutant of that strategy introduced in a population of $N-1$ the other strategy players will take over the entire population (Nowak et al. 2004). Selection for TFT replacing ALLD if the fixation probality of TFT is larger than 1/N. For the limit of large N and sufficiently weak selection, the fixation probality of TFT is larger than 1/N equivalents to the condition $-c+2m(b-c)>0+2b$ (Nowak et al. 2004). This is also called the 1/3 rule: $x^*<1/3$. Therefore, there can be positive selection for TFT to replace AllD in a finite population, if the invasion barrier of TFT is less than 1/3. This condition ensures that the basin of attraction of cooperators is greater than 2/3. The inequality can be rewritten as

$$\begin{aligned} \frac{b}{c}>1+\frac{\frac{3}{2}}{m-1}. \end{aligned}$$

(5)

2.2 Direct reciprocity in a dynamic imitation model

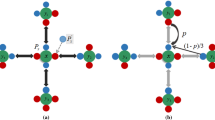
We secondly study a dynamic imitation model. A population of N individuals are distributed on a randomly connected network. Each node in the network represents an individual who adopts one of the two strategies, TFT and ALLD. The edgs on the network denote who interacts with whom. A modified ‘Birth-death (BD)’ updating rule is used for renewing the network. In each time step, a newcomer is added to the network and chooses one of the existing individuals as a role model for the newcomer. It means an individual is probabilistically selected as a key node who will directly connect to the newcomer. The newcomer tries to construct connections with the neighbors of the selected key node, and a randomly chosen existing node is removed from the system. Therefore, the number of all nodes on the entire network is assumed to be constant during the evolutionary process. Our model is a Moran process which describes the evolution of finite resource-limited populations.

The probability of a node i to be selected as the key node is proportional to its effective fitness. The effective fitness is assumed to be $1+W\cdot \text {payoff}$, where $W \ge 0$ specifies a tunable intensity of selection. We are interested in the limit of weak selection ($W\ll 1$) and large population size. At each time step for each node i, its payoff is calculated as the sum of pair-wise interactions with its neighbors. The payoff of the individual i can be represented as $\sum _{j}v_{ij}[-cs_{i}+bs_{j}+(m-1)(b-c)s_{i}s_{j}$]. It is reasonable according to the payoff matrix in Eq. (1). For example, if a cooperator node i ($s_i=1$) connects to a neighboring cooperator node j ($s_j=1$), the payoff of the node i interacts with the node j will be $m(b-c)$. Therefore, the effective fitness of the individual i is $1+W\sum _{j}v_{ij}[-cs_{i}+bs_{j}+(m-1)(b-c)s_{i}s_{j}]$. Furthermore, owing to the fact that each individual i survives with probability $1-1/N$ and gives birth with a probability proportional to his effective fitness $f_i$, the expected number of offspring of individual i is described as

$$\begin{aligned} w_i=1-\frac{1}{N}+\frac{f_{i}}{\sum _{j}f_{j}}. \end{aligned}$$

(6)

In the following time, the newcomer who connects to the key node will choose to imitate both the strategy and social relationships of its parent as a given probability. We should note here the difference from Cavaliere et al. (2012) is that the key node will directly link to the role model but not there as a given probability link to the role model. In one side, the newcomer imitates the strategy of the role model with probability $1-u$ or mutates to the alternative strategy with probability u. For $u=0$, there is no mutation, only selection. For $u=1$, there is no selection, only mutation. In the other side, the newcomer is embedded into the network and it has the possibility to imitate the social networks of the key node. That means, the newcomer establishes a connection with every neighbors of the key node with probability q which represents the embedding ratio, the offspring connects to all r neighbors of the key node with probability $q^r$.

2.3 Analyses of the dynamic imitation model

A detailed analysis of the mode will be given in this part, by using the similar method in Cavaliere et al. (2012). The number of the nodes on the network is denoted as N, which is a constant in the evolutionary process according to the model assumption. The model is a Markov process over a state space. A state S is denoted by a binary strategy vector $S=(s_1,...,s_N)$ and a binary connection matrix $V=(v_{i,j})_{N\times N}$, where $s_i$ denotes the strategy of individual i, $s_i$ equals 1 for a TFT player, and 0 for an ALLD player; $v_{i,j}$ equals 1 when i and j connects, or else, it will be 0. Denote x as the frequency of TFT players. On average, cooperation can be favored if the frequency of TFT players satisfies the condition,

$$\begin{aligned} \left\langle x \right\rangle >\frac{1}{2}, \end{aligned}$$

(7)

where $\langle .\rangle$ denotes the average taken over the stationary distribution of the Markov process. Denote the change of the frequency of cooperators from a state to another due to selection as $\Delta x^{sel}$. The condition in Eq. (7) means that the average change due to selection in the frequency of TFT is positive (Tarnita et al. 2009a, b). That is

$$\begin{aligned} \left\langle \Delta x^{sel}\right\rangle >0, \end{aligned}$$

(8)

where

$$\begin{aligned} \left\langle \Delta x^{sel}\right\rangle =\sum _{S}\Delta x^{sel}\beta _{S}. \end{aligned}$$

(9)

In Eq. (9), $\Delta x^{sel}$ is the change of the frequency of TFT due to selection in state S, $\beta _S$ is the probability that the system is in state S.

Based on the assumption that the transition probabilities are analytic at $W=0$. It can be concluded that the probabilities $\beta _S$ and the change due to selection in each state $\Delta x_{S}$ are also analytic at $W=0$ (Tarnita et al. 2009b). Hence, $\langle \Delta x^{sel}\rangle$ can be written as the Taylor expansion of the average change due to selection at $W=0$:

$$\begin{aligned} \left\langle \Delta x^{sel}\right\rangle = \left( \sum _{S}\Delta x^{sel}\beta _{S}\right) |_{W=0}+W\left( \frac{d}{dW}\sum _{S}\Delta x^{sel}\beta _{S}\right) |_{W=0}+o\left( (W)^2\right) .\nonumber \\ \end{aligned}$$

(10)

Under the assumption of weak selection limit, $W\rightarrow 0$, the higher order terms of W in Eq. (10) will be omitted in order to make the analytical analysis convenient, only the constant and the first-order terms left. In addition, the constant term stands for the average change in the frequency of TFT at neutrality, which is zero. Then the last equation becomes

$$\begin{aligned} \left\langle \Delta x^{sel}\right\rangle \approx W\left( \sum _{S}\frac{\partial \Delta x^{sel}_{S}}{\partial W}|_{W=0}\beta _{S}(W=0)+\sum _{S}\Delta x^{sel}_{S}(W=0)\frac{\partial \beta _{S}}{\partial W}|_{W=0}\right) .\nonumber \\ \end{aligned}$$

(11)

In particular, we should note that the change in frequency at neutrality in each state is zero because we calculate global updating with constant death (individuals are replaced at random with probability 1/N). Thus, the second term in Eq. (11) is zero and hence, in the limit of weak selection, Eq. (11) becomes

$$\begin{aligned} \left\langle \Delta x^{sel}\right\rangle \approx \sum _{S}\frac{\partial \Delta x^{sel}_{S}}{\partial W}|_{W=0}\beta _{S}(W=0):=\left\langle \frac{\partial \Delta x^{sel}}{\partial W}|_{W=0}\right\rangle _{0}>0. \end{aligned}$$

(12)

In Eq. (12), $\langle .\rangle _{0}$ specifies the average over the stationary distribution at neutrality, $W=0$. Next, a detailed expansion of Eq. (12) and followed analysis will be given in Appendix A. We thus get that in the limit of a large population size, the critical benefit-to-cost ratio for TFT to be favored can be calculated as

$$\begin{aligned} \left( \frac{b}{c}\right) ^{*}= & {} \frac{c_1}{c_2}.\nonumber \\ c_1= & {} (m+1)\mu ^3+(6m+4mv+2v+4)\mu ^2\nonumber \\&\quad +&(5mv^2+15mv+11m+v^2+3v+3)\mu +2mv^3\nonumber \\&\quad +&8mv^2+12mv+6m;\nonumber \\ c_2= & {} (m-1)\mu ^3+(6m+4mv-2v-6)\mu ^2\nonumber \\&\quad +&(5mv^2+15mv+11m-v^2-9v-11)\mu +2mv^3\nonumber \\&\quad +&8mv^2+12mv+6m-2v^2-8v-6. \end{aligned}$$

(13)

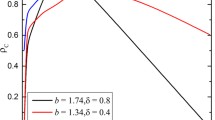
where $\mu =2Nu$ and $v=N(1-q)$, which can be taken as the effective strategy mutation rate and the effective link mutation rate. Compared to the results of Eq. (4) that the fixation probability of TFT is larger than ALLD in well-mixed populations, from $\frac{b}{c}^{*}<1+\frac{2}{m-1}$ we can derive $m>\frac{3+4v+4\mu +3\mu v+\mu ^2+v^2}{3+8v+4\mu +9\mu v+\mu ^2+7v^2+2\mu ^2v+4\mu v^2+v^3}$. The inequality hlods for any $m>1$. Therfore, it is obvious that this dynamic network facilitates the evolution of cooperation because the critical benefit-to-cost ratio becomes smaller. It is obvious that the value of $(\frac{b}{c})^{*}$ is larger than one, through comparing the coefficients of the same order of $\mu$ in numerator and denominator. For a specific value of $\mu$, the critical benefit-to-cost ratio approaches 1 for a very large v (small values of q)(see Fig. 1a, c as examples). The reason is that $c_1$ and $c_2$ can also be represented to be polynomials of the variable v. Obviously, the coefficient of the highest order of parameter v is the same for $c_1$ and $c_2$, so the conclusion is easy to access. This can be explained as that isolated nodes and very small components offer a benefical structure for cooperation (Cavaliere et al. 2012). With increase of v (decrease of q), the critical benefit-to-cost ratio decreases. It illustrates that the higher connected network, the worser it is for the evolution of cooperation. Certainly this model confirms the result already obtained before that sparse static graphs favor cooperation (Ohtsuki and Nowak 2007).

However, for a specific value of v(q), with the increase of $\mu$, the critical benefit-to-cost ratio increases and reaches an equilibrium (see Fig. 1b, d as examples). It means that the increase of the rate of mutation of strategy will have a negative effect on the evolution of cooperation. We can also observe that the smaller v (high values of q), the higher the critical benefit-to-cost ratio is, no matter what the $\mu$ value is. This is due to that the resulting highly connected network is inversely adverse for the evolution of cooperation (Cavaliere et al. 2012; Lieberman et al. 2005; Ohtsuki and Nowak 2006a, b; Szabó and Fáth 2007).

Actually, with the increase of m, the critical benefit-to-cost ratio will approach 1, no matter what the value of $\mu$ and v are (see Fig. 2 as an example). The reason is that $c_1$ and $c_2$ can also be represented to be polynomials of the variable m. Obviously, the coefficient of the highest order of parameter m is the same for $c_1$ and $c_2$, so the conclusion is easy to access. For a small value of m, it requires a relatively larger value of $\mu$ and v, in order to make the benefit-to-cost ratio reach one. This is in consistent well with the conclusion that repeated interaction facilitates the evolution of cooperation.

In all, Figs. 1 and 2 both illustrate that a small value of $\mu$ or v has a large effect on the large variation of the critical benefit-to-cost ratio. This means that the low strategy mutation rate or the high imitation the link relationships rate will cause a large variation of the critical benefit-to-cost ratio.

In addition, we will give illustrations for two special cases. For one side, when $\mu$ approaches infinity, the critical benefit-to-cost ratio becomes $1+\frac{2}{m-1}$, which correspondes to the results of Eq. (4) that TFT is RD when compared to ALLD in well-mixed populations. It means that TFT can be favored in our stochastic model for a sufficiently large effective strategy mutation rate $\mu$ is equivalent to the basin of attraction for TFT is larger than the basin of attraction of ALLD in the determinisitc model. We can give explanations here. For a very large population, $\mu$ approaches infinity requires $N\rightarrow \infty$ for an arbitrarily positive u ($0<u<1$) because of $\mu =2Nu$. Refer to the work of Tarnita et al. (2009b), for a positive strategy mutation rate u ($0<u<1$), the condition for strategy A to be favored over strategy B in structured populations is $\langle x_A \rangle >\frac{1}{2}$, where $x_A$ is the frequency of A individuals in the population. They have deduced that in structrued populations and the limit of weak selection, the condtion $\langle x_A \rangle >\frac{1}{2}$ is equivalent to the single parameter condition $\sigma a_{AA}+a_{AB}>a_{BA}+\sigma a_{BB}$, by assuming the interaction payoff matrix of the two strategies is $\left( \begin{array}{cc} a_{AA} &{} a_{AB}\\ a_{BA} &{} a_{BB}\\ \end{array} \right)$. Where $\sigma$ depends on the population structure, the update rule and the mutation rate. We can see $\sigma =1$ corresponds to the standard condition for RD. Therefore, for the weak selection, this frequency dependent Moran process in the limit of $N\rightarrow \infty$ brings about $\sigma =1$, which yields the standard condition of RD of TFT. The dynamic network thus behaves as an infinitely well-mixed population (Tarnita et al. 2009b).

For another side, when v is nearly equal to 0 (q is nearly equal to 1), by letting $\mu$ approaches 0, the critical benefit-to-cost ratio becomes $1+\frac{1}{m-1}$. Compared to Eq. (2), It illustrates that TFT can be favored in our stochastic model for a very small effective strategy mutation rate $\mu$ and a very small effective link mutation rate v, which is equivalent to that TFT is evolutionary stable in the deterministic well-mixed model. The case in our dynamic network corresponds to that there is almost no mutation of strategy in the imitation process, and the newcomer almost completely imitates the link of the role model. Then the network functions as a highly connected component. It illustrates that the dominance of TFTs is associated with a more connected network. In other words, the network tends to contain a large and well-connected component on condition that TFTs prevalent. This can also be explained as follows. Refer to the work of Tarnita et al. (2009a, 2009b), in the limit of low strategy mutation rate u, the condtion $\langle x_A \rangle >\frac{1}{2}$ is equivalent to $\rho _{A}>\rho _{B}$ (Tarnita et al. 2009b), where $\rho _{A},\rho _{B}$ represent the fixation probabilities of strategies A and B, respectively. We should note that $\rho _{A}>\rho _{B}$ equivalents A is RD when compared to B, for weak selection and large population size (Nowak et al. 2004; Imhof and Nowak 2006). Back to our stochastic model, $\mu$ approaches 0 happens at $u\rightarrow 0$, the condition $\langle x \rangle >\frac{1}{2}$ in Eq. (7) deduces to that TFT is RD over ALLD for weak selection and large population size. If the condition that TFT is RD in Eq. (4) holds, then the condition in Eq. (2) also holds.

Fig. 1

The critical benefit-to-cost ratio as a function of the effective connection mutation rate $v=N(1-q)$ and the effective connection mutation rate $\mu =2Nu$. The populatio size is fixed at $N=10000$. In a, b, the number of the interaction rounds is fixed at $m=100$; In c, d, $m=10$

Fig. 2

The critical benefit-to-cost ratio as a function of the effective connection mutation rate $v=N(1-q)$ and the effective connection mutation rate $\mu =2Nu$. The populatio size is fixed at $N=10000$. In a, c, $\mu =0.1$ and $\mu =1$, respectively; In b, d, $v=0.1$ and $v=1$, respectively

3 Conclusions and discussion

More and more attention has been paid to the subject of coevolution of game strategy and network structure in recent years, which is more realistic for lots of social networks changing continuously in real world (Skyrms and Pemantle 2000; Zimmermann and Eguluz 2005; Fu et al. 2008; Santos et al. 2006a, b, c; Pacheco et al. 2006a, b, 2008; Segbroeck et al. 2009). Different from the static network configuration, the structure of the dynamic network is assumed to change with dynamic process. The goal of this study is to investigate the effect of dynamic imitation on the evolution of cooperation in networks. In game-theoretical networks, the formation and fragmentation of complex structures are correlated (Barabási and Albert 1999; Albert et al. 2000; Paperin et al. 2011). Especially, the imitation and internal conflicts between cooperators and defectors play an important role in dynamic process. The networks growing and declining with occasional fragmentation and reformation can be a direct consequence of the simple imitation and internal conflicts between ‘ALLD’ and ‘TFT’ players. We found that the critical benefit-to-cost ratio depends on the effective strategy mutation rate, the effective link mutation rate, and the repeated rounds of the game.

In this model, one offspring born in a site will not only imitate the strategy but also copy the social relationship of its parent with a certain probability, which is different from the classical BD updating (Ohtsuki et al. 2006). What makes it different is that in the latter case, a child of a randomly selected individual will take up the place of one of a neighbors of the parent. It means one offspring will absolutely imitate the strategy of its parent, and the structure of the network is always kept to be static in that classical one. Whilst in our model, after a newcomer is introduced into the network, an individual will be randomly selected to die from the whole network but not in the local configuration. With the link imitation process, the structure of the network always keep changing.

Moreover, in the active linking model of Pacheco et al. (2008), active rewiring and time scales are explicitly taken into consideration, where individuals seek new partners and break existing ties at different rate. The competition between the lifetime of reciprocator–reciprocator links and reciprocator–defector links and the rates of link formation are important to decide the evolutionary dynamics. As a result, in the limit in which link dynamics is faster than evolutionary dynamics of strategies, they obtained a game-theoretical problem equivalent to a conventional evolutionary game in a well-mixed population, with a rescaled payoff matrix. Their model allows one to assess the role of dynamic linking in the evolution of cooperation under direct reciprocity. Compared to that, our model gives a perspective to understand the role of imitation in the evolution of cooperation. Individuals will not only imitation the strategy of the role model, but also the linking relationships of it.

Coevolution of individual strategy and network structure opens a new door to the evolution of cooperation. The investigation of dynamical social network is an important step towards more realistic models of social interactions in structured populations. Our model gives an analogous description to human society, in which one people quits a company or an institution, then a new one enters. The new individual may keep in touch with others who link to the predecessor, and it may either adopt the strategy adopted by the predecessor or take another strategy. Actually, human resource replacement is very complex in reality, due to diverse factors involved in social, physiological, emotional and so on. However, the problem can still be simplified in one sentence indicated by vanVeelen et al. (2012). That is, the essence of conditional strategies under social networks is “a strong dose of repetition and a pinch of population structure”. To some extent, our work makes a small contribution towards understanding cooperation among humans.

In the present work, the dynamic linking network was investigated by using a modified BD updating rule. Actually, other complex learning rules could also be taken into account and were expected to have interesting results. In addition, we should note that stochasticity plays an important role when individuals make decisions (Traulsen et al. 2006). Therefore, works along these directions will be expanded in future.

Appendices

Appendices

1.1 Appendix A: Derivation of the condition for TFT to be favored over AllD

At first, $\Delta x^{sel}$ can be represented as

$$\begin{aligned} \Delta x^{sel}=\sum _{i}s_{i}(w_i-1), \end{aligned}$$

(A.1)

Actually, it represents a conditional expected change in the number of TFT individuals. $w_i$ is the expected number of offspring of individual i which has been given in main text in Eq. (6).

Next, to give a more general conclusion we consider a general two-strategy case, where we have two strategies D and C. The following payoff matrix will be used

$$\begin{aligned} \begin{array}{cc} &{}\text {D}~~~~\text {C}\\ \begin{array}{c} \text{ D }\\ \text{ C }\\ \end{array}&{} \left( \begin{array}{cc} a_{11} &{}\quad ~ a_{12}\\ a_{21} &{}\quad ~ a_{22}\\ \end{array} \right) \\ \end{array}, \end{aligned}$$

(A.2)

where the parameter $a_{11}$ represents the payoff of a defective individual interacts with a cooperative one. Similar definitions can be applied to other cases.

According to model description in the main text, the effective fitness of individual i can be described as

$$\begin{aligned} f_i= & {} 1+W\sum _{j}v_{ij}[a_{11}+(a_{21}-a_{11})s_{i}+(a_{12}-a_{11})s_{j}\nonumber \\&+ (a_{11}+a_{22}-a_{21}-a_{12})s_{i}s_{j}]. \end{aligned}$$

(A.3)

The equation is reasonable according to the payoff matrix in Eq. (A.2). For example, if a cooperator node i ($s_i=1$) connects to a neighboring cooperator node j ($s_j=1$), the payoff of the node i interacts with the node j will be $a_{22}$. Then, by inserting Eq. (A.3) into Eq. (6), we can get

$$\begin{aligned}&w_i=1-\frac{1}{N}\nonumber \\&\qquad +\frac{1+W\sum _{j}v_{ij}[a_{11}+(a_{21}-a_{11})s_{i}+(a_{12}-a_{11})s_{j}+(a_{11}+a_{22}-a_{21}-a_{12})s_{i}s_{j}]}{N+W\sum _{j,k}v_{jk}[a_{11}+(a_{21}-a_{11})s_{j}+(a_{12}-a_{11})s_{k}+(a_{11}+a_{22}-a_{21}-a_{12})s_{j}s_{k}]}\nonumber \\&\quad =1-\frac{1}{N}+\frac{1}{N}\left( 1+W\sum _{j}v_{ij}[a_{11}+(a_{21}-a_{11})s_{i}+(a_{12}-a_{11})s_{j}\right. \nonumber \\&\qquad \left. +(a_{11}+a_{22}-a_{21}-a_{12})s_{i}s_{j}]\right) \nonumber \\&\qquad \times \left( 1-\frac{1}{N}W\sum _{j,k}v_{jk}[a_{11}+(a_{21}-a_{11})s_{j}+(a_{12}-a_{11})s_{k}\right. \nonumber \\&\qquad \left. +(a_{11}+a_{22}-a_{21}-a_{12})s_{j}s_{k}]\right) +o(W^{2})\nonumber \\&\quad =1+\frac{W}{N}\left( \sum _{j}v_{ij}[a_{11}+(a_{21}-a_{11})s_{i}+(a_{12}-a_{11})s_{j}\right. \nonumber \\&\qquad \left. +(a_{11}+a_{22}-a_{21}-a_{12})s_{i}s_{j}]\right. \nonumber \\&\qquad -\frac{1}{N}\sum _{j,k}v_{jk}[a_{11}+(a_{21}-a_{11})s_{j}+(a_{12}-a_{11})s_{k}\nonumber \\&\qquad \left. +(a_{11}+a_{22}-a_{21}-a_{12})s_{j}s_{k}]\right) +o(W^{2}).\nonumber \\ \end{aligned}$$

(A.4)

Substituting Eq. (A.4) into Eq. (A.1) and taking the limit of weak selection, we can get

$$\begin{aligned}&\Delta x^{sel}=\frac{W}{N}\left( \sum _{i,j}(a_{21}-a_{11})s_{i}^2v_{ij}+\sum _{i,j}a_{11}s_{i}v_{ij}+\sum _{i,j}(a_{12}-a_{11})s_{i}s_{j}v_{ij}\right. \nonumber \\&\qquad +\sum _{i,j}(a_{11}+a_{22}-a_{21}-a_{12})s_{i}^2s_{j}v_{ij}\nonumber \\&\qquad -\frac{1}{N}\sum _{i,j,k}(a_{21}-a_{11})s_{i}s_{j}v_{jk}-\frac{1}{N}\sum _{i,j,k}a_{11}s_{i}v_{jk}-\frac{1}{N}\sum _{i,j,k}(a_{12}-a_{11})s_{i}s_{k}v_{jk}\nonumber \\&\qquad \left. -\frac{1}{N}\sum _{i,j,k}(a_{11}+a_{22}-a_{21}-a_{12})s_{i}s_{j}s_{k}v_{jk}\right) +o(W^{2})\nonumber \\&\quad =\frac{W}{N}\left( \sum _{i,j}a_{21}s_{i}v_{ij}+\sum _{i,j}(a_{22}-a_{21})s_{i}s_{j}v_{ij}-\frac{1}{N}\sum _{i,j,k}(a_{21}+a_{12}-2a_{11})s_{i}s_{k}v_{ij}\right. \nonumber \\&\qquad \left. -\frac{1}{N}\sum _{i,j,k}a_{11}s_{k}v_{ij}-\frac{1}{N}\sum _{i,j,k}(a_{11}+a_{22}-a_{21}-a_{12})s_{i}s_{j}s_{k}v_{ij}\right) +o(W^{2}).\nonumber \\ \end{aligned}$$

(A.5)

We should note $s_{i}^{2}=s_{i}$ in the above derivation process. In addition, the rotating symmetry will be used because the role of individuals i, j and k are equal. Next, we then calculate the first order patical derivative of function $\Delta x^{sel}$ with respect to independent variable W. After that, by lettting $W=0$, we can get

$$\begin{aligned}&\frac{\partial \Delta x^{sel}}{\partial W}|_{W=0}\nonumber \\&\quad =\left( \sum _{i,j}a_{21}s_{i}v_{ij}+\sum _{i,j}(a_{22}-a_{21})s_{i}s_{j}v_{ij}-\frac{1}{N}\sum _{i,j,k}(a_{21}+a_{12}-2a_{11})s_{i}s_{k}v_{ij}\right. \nonumber \\&\qquad \left. -\frac{1}{N}\sum _{i,j,k}a_{11}s_{k}v_{ij}-\frac{1}{N}\sum _{i,j,k}(a_{11}+a_{22}-a_{21}-a_{12})s_{i}s_{j}s_{k}v_{ij}\right) |_{W=0}. \end{aligned}$$

(A.6)

Applying Eq. (A.6) into Eq. (12), the condition for cooperators to be favored over defector will be

$$\begin{aligned} \begin{aligned}&\left\langle \sum _{i,j}a_{21}s_{i}v_{ij}\right\rangle _{0}+\left\langle \sum _{i,j}(a_{22}-a_{21})s_{i}s_{j}v_{ij}\right\rangle _{0}-\left\langle \frac{1}{N}\sum _{i,j,k}(a_{21}+a_{12}-2a_{11})s_{i}s_{k}v_{ij}\right\rangle _{0}\\&~~~~-\left\langle \frac{1}{N}\sum _{i,j,k}a_{11}s_{k}v_{ij}\right\rangle _{0}-\left\langle \frac{1}{N}\sum _{i,j,k}(a_{11}+a_{22}-a_{21}-a_{12})s_{i}s_{j}s_{k}v_{ij}\right\rangle _{0} >0. \end{aligned} \end{aligned}$$

(A.7)

Moreover, we can get

$$\begin{aligned}&\left\langle \sum _{i,j}s_{i}v_{i,j}\right\rangle _{0}=N^2 Pr_{0}(s_{i}=1, v_{ij}=1)=\frac{N^2}{2}Pr_{0}(v_{ij}=1); \end{aligned}$$

(A.8.1)

$$\begin{aligned}&\left\langle \sum _{i,j}s_{i}s_{j}v_{i,j}\right\rangle _{0}=N^2 Pr_{0}(s_{i}=s_{j}=1, v_{ij}=1)=\frac{N^2}{2}Pr_{0}(s_{i}=s_{j}, v_{ij}=1);\nonumber \\ \end{aligned}$$

(A.8.2)

$$\begin{aligned}&\left\langle \sum _{i,j,k}s_{k}v_{ij}\right\rangle _{0}=N^3 Pr_{0}(s_{k}=1, v_{ij}=1)=\frac{N^3}{2}Pr_{0}(v_{ij}=1); \end{aligned}$$

(A.8.3)

$$\begin{aligned}&\left\langle \sum _{i,j,k}s_{i}s_{k}v_{ij}\right\rangle _{0}=N^3 Pr_{0}(s_{i}=s_{k}=1, v_{ij}=1)=\frac{N^3}{2}Pr_{0}(s_{i}=s_{k}, v_{ij}=1);\nonumber \\ \end{aligned}$$

(A.8.4)

$$\begin{aligned}&\left\langle \sum _{i,j,k}s_{i}s_{j}s_{k}v_{ij}\right\rangle _{0}\nonumber \\&\quad =N^3 Pr_{0}(s_{i}=s_{j}=s_{k}=1, v_{ij}=1)=\frac{N^3}{2}Pr_{0}(s_{i}=s_{j}=s_{k}, v_{ij}=1)\nonumber \\&\quad =\frac{N^3}{2}Pr_{0}(s_{i}=s_{j}|v_{ij}=1)Pr_{0}(s_{i}=s_{k}|v_{ij}=1)Pr_{0}(v_{ij}=1). \end{aligned}$$

(A.8.5)

In Eq. (A.8.1), to get the sum $\sum _{i,j}s_{i}v_{i,j}$, we add the term $v_{ij}$ only if $s_{i}=1$ and $v_{ij}=1$. our sum has $N^2$ terms. This leads to the first equality. The second equality comes from that the two strategies are equivalent in the neutral stationary state. Thus, $Pr_{0}(s_{i}=s_{j}=1)=\frac{1}{2}Pr_{0}(s_{i}=s_{j})$. The notation $Pr_{0}$ represents the probabilities calculated at neutrality. The same idea will be used for the other terms in Eqs. (A.8.1)-(A.8.5).

Denote that

$$\begin{aligned}&G=Pr_{0}(s_{i}=s_{j}|v_{ij}=1), \end{aligned}$$

(A.9)

$$\begin{aligned}&{{\bar{G}}}=Pr_{0}(s_{i}=s_{k}|v_{ij}=1). \end{aligned}$$

(A.10)

G is the probability that two individuals connected each other also have the same strategy, whereas ${{\bar{G}}}$ is the probability that two random individuals have the same strategy. More explicitly, three individuals i, j, and k were picked randomly with replacement such that i and j are connected. Given it, G is the probability that i and j have the same strategy and ${{\bar{G}}}$ is the probability that i and k have the same strategy. Therefore, Eq. (A.7) becomes

$$\begin{aligned}&a_{21}-a_{11}+(a_{22}-a_{21})G-(a_{21}+a_{12}-2a_{11}){{\bar{G}}}\nonumber \\&\quad -(a_{11}+a_{22}-a_{21}-a_{12})G{{\bar{G}}}>0. \end{aligned}$$

(A.11)

We should note that the probabilities of Eqs. (A.9)-(A.10) two individuals were picked with replacement, can be expressed as the probabilities without replacement. We need to introduce several notations first as follows.

$$\begin{aligned}&z=Pr_{0}(v_{ij}=1, i \ne j), \end{aligned}$$

(A.12)

$$ \begin{aligned}&g=Pr_{0}(v_{ij}=1~ \& ~s_{i}=s_{j}, i \ne j), \end{aligned}$$

(A.13)

$$ \begin{aligned}&h=Pr_{0}(v_{ij}=1~ \& ~s_{i}=s_{k}, i \ne j \ne k ). \end{aligned}$$

(A.14)

Here, the definition z means the probability that two distinct randomly selected individuals are connected. The definition g means the probability that they are not only connected but also have the same strategy. The definition h means the probability that for three distinct individuals randomly selected, the first two are connected and the latter two have the same strategy. Now, it needs to find z, g and h in the neutral case. After calculations, these probabilities are

$$\begin{aligned}&Pr_{0}(v_{ij}=1)=\frac{1}{N}[(N-1)z+1], \end{aligned}$$

(A.15)

$$ \begin{aligned}&Pr_{0}(v_{ij}=1~ \& ~s_{i}=s_{j})=\frac{1}{N}[(N-1)g+1], \end{aligned}$$

(A.16)

$$ \begin{aligned}&Pr_{0}(v_{ij}=1~ \& ~s_{i}=s_{k})=\frac{1}{N^2}[(N-1)(N-2)h+(N-1)(z+g+1)+1].\nonumber \\ \end{aligned}$$

(A.17)

Therefore,

$$\begin{aligned}&G=\frac{\frac{1}{N}[(N-1)g+1]}{\frac{1}{N}[(N-1)z+1]},\nonumber \\&{{\bar{G}}}=\frac{\frac{1}{N^2}[(N-1)(N-2)h+(N-1)(z+g+1)+1]}{\frac{1}{N}[(N-1)z+1]}. \end{aligned}$$

(A.18)

By using the payoff matrix in Eq.(1), we get the condition for TFT to be favored over AllD,

$$\begin{aligned} \frac{b}{c}>\frac{1+(m-1)G-{{\bar{G}}}-(m-1)G{{\bar{G}}}}{mG-{{\bar{G}}}-(m-1)G{{\bar{G}}}}. \end{aligned}$$

(A.19)

Moreover, in the large N limit, $\lim _{N\rightarrow \infty } G=\frac{g}{z}$, $\lim _{N\rightarrow \infty }{{\bar{G}}}=\frac{h}{z}$, $\lim _{N\rightarrow \infty }{{{\bar{G}}} G}=\frac{gh}{z^2}$. Therefore, Eq. (A.11) can be represented as

$$\begin{aligned}&a_{21}-a_{11}+(a_{22}-a_{21})\frac{g}{z}-(a_{21}+a_{12}-2a_{11})\frac{h}{z}\nonumber \\&\quad -(a_{11}+a_{22}-a_{21}-a_{12})\frac{gh}{z^2}>0. \end{aligned}$$

(A.20)

Here, for simplicity, the same notations are used, z, g and h mean their large N limits. Specifically, for the large N limit, the critical condition for TFT to be favored over AllD (A.19) becomes,

$$\begin{aligned} \frac{b}{c}>1+\frac{z(z-g)}{mgz-(m-1)gh-hz}. \end{aligned}$$

(A.21)

In following, the method proposed in Wakeley (2008) and Cavaliere et al. (2012) will be used to calculate the quantities z, g, and h. In the limit of large population size, the probability that two individuals are connected and have the same strategy at time $\tau$ after the most recent common ancestor (MRCA) is a product of the respective independent probabilities (Wakeley 2008; Antal et al. 2009; Tarnita et al. 2009a; Cavaliere et al. 2012). The quantities can be got in the continuous time limit as follows (Cavaliere et al. 2012)

$$\begin{aligned} z= & {} \sum _{t=1}^{\infty }Pr(v_{ij}=1, i \ne j|T=t)Pr(T=t)=\int _0^{\infty }p_2(\tau )p(\tau )d\tau =\frac{1}{1+v}, \nonumber \\ \end{aligned}$$

(A.22)

$$\begin{aligned} g= & {} \sum _{t=1}^{\infty }Pr(v_{ij}=1, s_{i}=s_{j}, i \ne j|T=t)Pr(T=t)\nonumber \\= & {} \sum _{t=1}^{\infty }Pr(v_{ij}=1, i \ne j|T=t)Pr(s_{i}=s_{j}, i \ne j|T=t)Pr(T=t)\nonumber \\= & {} \int _0^{\infty }p_2(\tau )p_1(\tau )p(\tau )d\tau =\frac{2+2v+\mu }{2(1+v)(1+v+\mu )}, \end{aligned}$$

(A.23)

$$\begin{aligned} h= & {} \sum _{t=1}^{\infty }Pr(v_{ij}=1, s_{i}=s_{k}, i \ne j \ne k |T=t)Pr(T=t)\nonumber \\= & {} \sum _{t=1}^{\infty }Pr(v_{ij}=1, i \ne j \ne k |T=t)Pr(s_{i}=s_{k}, i \ne j \ne k |T=t)Pr(T=t)\nonumber \\= & {} \frac{1}{3}\int _0^{\infty } d\tau _2\int _0^{\infty }d\tau _1[p_1(\tau _2)p_2(\tau _2+\tau _1)\nonumber \\&+p_1(\tau _2+\tau _1)p_2(\tau _2)+p_1(\tau _2+\tau _1)p_2(\tau _2+\tau _1)]p(\tau _2,\tau _1)\nonumber \\= & {} \frac{\mu ^3+2\mu ^2(3+v)+2(1+v)(3+v)+\mu (11+v(9+v))}{2(1+\mu )(1+v)(1+\mu +v)(3+\mu +v)}. \end{aligned}$$

(A.24)

Here we have used the property, for any given time t, factorizing the conditional probabilities in Eq. (A.23) and Eq. (A.24) is possible. The reason is that the connection of nodes occurs independently in the strategy space. Where $p(t)=e^{-t}$ is the probability density that two individuals coalesced in time $T=t$ from the MRCA as given in Eq. (B.1.3); $p(t_2,t_1)=3e^{-3t_2-t_1}$ is the probability density that three individuals coalesced in time $T=t$ from the MRCA as given in Eq. (B.1.4); $p_1(t)=\frac{1+e^{-\mu t}}{2}$ is the probability density that two individuals have the same strategy at time $T=t$ from the MRCA as given in Eq. (B.2.3); $p_2(t)=e^{-vt}$ is the probability density that two individuals are connected at time $T=t$ from the MRCA as given in Eq. (B.3.3). The details for the derivation of the four probability densities above can be obtained from the Appendix B.

The integral expressions in z and g are easy to understand, whereas more detail analysis of the expression in h should be given here. The scaled time when individuals i, j coalescence is denoted as $\tau _{i,j}$, and when j, k coalescence $\tau _{j,k}$. Individuals i, j coalesce first at $\tau _{i,j}=\tau _{3}$ and they coalesce with k at $\tau _{j,k}=\tau _{3}+\tau _{2}$ with probability 1/3. Similarly, individuals j, k coalesce first at $\tau _{j,k}=\tau _{3}$ and they coalesce with i at $\tau _{i,j}=\tau _{3}+\tau _{2}$ with probability 1/3. Otherwise, k, i coalesce first with probability 1/3, it makes $\tau _{i,j}=\tau _{j,k}=\tau _{3}+\tau _{2}$. Owing to the fact that we know the probability density $p_1(\tau )$ that two individuals with a MRCA at time $\tau$ back have the same strategy, as well as the probability density $p_2(\tau )$ that two individuals are connected at time $T=\tau$ from the MRCA. Then we can simply obtain the three point correlation as shown in Eq. (A.24).

After that, by mainly using $\int _0^{\infty } e^{-dx}=1/d$ (d is a constant) to calculate, final results of these integrals can be derived. Next, by using Eq. (A.20), the critical benefit-to-cost ratio is derived as shown in Eq. (13).

1.2 Appendix B: Derivation of the probability densities

1.2.1 Appendix B.1: Probability of given coalescence time

To obtain the quantities z, g, and h, we have to know the probability $Pr\{T=t\}=pr(t)$, which represents that the time to the MRCA of two randomly selected individuals is $T=t$. Two individuals always have a common ancestor if we go back in time far enough. However, we don’t know how far we should go back. Thus, the possibility that $T=t$ takes values anywhere between 1 and $\infty$ should be calculated. Note that $T=0$ is excluded because we assume that the two individuals are distinct. This time is affected neither by the strategies, nor by the link connections of the two individuals. It is solely a consequence of the Birth-Death dynamics.

We can first get the probability that the two individuals coalesced in time $t=1$. For BD updating, it must have that one of them is the parent and the other is offspring; Besides, the parent needed not to be died in the last update step. Hence the probability that they coalesced in time $t=1$ is $C_2^1\frac{1}{N}\frac{1}{N}$ which gives the probability

$$\begin{aligned} pr(t)=\left( 1-\frac{2}{N^2}\right) ^{t-1}\frac{2}{N^2}. \end{aligned}$$

(B.1.1)

Similarly, the probability that three individuals coalesce can be derived. If we follow the trajectories of these individuals back in time, the probabilities that two individuals coalesce with probability $\frac{C_3^2C_2^1}{N^2}$, there was no coalescence event in one time step is $(1-\frac{C_3^2C_2^1}{N^2})$. When two individuals have coalesced, the remaining two merge with probability $\frac{C_2^1}{N^2}$ during an update step. For the probability that the first merging happens at time $t_2\ge 1$ and the second takes $t_1\ge 1$ more time steps, we obtain

$$\begin{aligned} pr(t_2,t_1)= & {} \left( 1-\frac{6}{N^2}\right) ^{t_2-1}\frac{6}{N^2}\left( 1-\frac{2}{N^2}\right) ^{t_1-1}\frac{2}{N^2}\nonumber \\= & {} \left. \left( 1-\frac{6}{N^2}\right) \right) ^{t_2-1}\left( 1-\frac{2}{N^2}\right) ^{t_1-1}\frac{6}{N^2}\frac{2}{N^2}. \end{aligned}$$

(B.1.2)

Next, we deal with the $N \rightarrow \infty$ limit, and introduce the notations $\tau =t/N, \tau _1=t_1/N, \tau _2=t_2/N$. A continuous time description was used, with $\tau , \tau _1, \tau _2$ ranging between 1 and $\infty$. In the continuous time limit, the probability density functions in the above two probability representations are given by

$$\begin{aligned}&p(\tau )=e^{-\tau } . \end{aligned}$$

(B.1.3)

$$\begin{aligned}&p(\tau _2,\tau _1)=3e^{-3\tau _2-\tau _1}. \end{aligned}$$

(B.1.4)

1.2.2 Appendix B.2: Probability that two individuals have the same strategy at time $T=t$ from the MRCA

Denote $pr_1(t)$ as the probability that two individuals have the same strategy at time $T=t$ from the MRCA. $pr_1(1)=1-u$ at time $T=1$. Let $p_{B}$ be the probability that a birth event happened in the ancestry lines of two individuals in the previous update step, $p_{B}=2(N-2)/[N(N-1)-2]=2/(N+1)$ for BD updating. Then $pr_1(t)$ can be represented by $pr_1(t-1)$, by considering the mutation and reproduction process in the ancestry line. That is,

$$\begin{aligned} pr_1(t)=pr_1(t-1)(1-p_{B}+p_{B}(1-u))+(1-pr_1(t-1))up_{B}. \end{aligned}$$

(B.2.1)

Through mathematical induction calculations, the probability is

$$\begin{aligned} pr_1(t)=\frac{1}{2}+\frac{1-2u}{2}(1-2up_{B})^{t-1}. \end{aligned}$$

(B.2.2)

Letting $\tau =t/(N^2/2)$ and $\mu =2Nu$, by taking the limits of large N and small u at the same time, we obtain the probability density function for the continuous time process,

$$\begin{aligned} p_1(\tau )=\frac{1+e^{-\mu \tau }}{2}. \end{aligned}$$

(B.2.3)

1.2.3 Appendix B.3: Probability that two individuals are connected at time $T=t$ from the MRCA

Let $pr_2(t)$ be the probability that two individuals are connected at time $T=t$ from the MRCA. $pr_2(1)=p$ at time $T=1$. The probability $pr_2(t)$ equals that the probability of their ancestor of the two individuals were connected at time $T=t-1$ multiplied by the probability that in the subsequent update step they stayed connected. The last probability includes two cases: neither of them was picked for reproduction; if either was picked then the offspring established a connection. Thus, we can get

$$\begin{aligned} pr_2(t)=pr_2(t-1)((1-p_{B})+qp_{B}). \end{aligned}$$

(B.3.1)

Through mathematical induction calculation, we obtain

$$\begin{aligned} pr_2(t)=(1-(1-q)p_{B})^{t-1}. \end{aligned}$$

(B.3.2)

Letting $\tau =t/(N^2/2)$ and $v=N(1-q)$, by taking the limit of large N and large q, we obtain the probability density function for the continuous time process,

$$\begin{aligned} p_2(\tau )=e^{-v\tau }. \end{aligned}$$

(B.3.3)

Note that after the MRCA two individuals are not connected if at time $T=1$, then their offspring will never be connected. However, after $T=1$ the important thing is that offspring add links to their parents’ neighbours with the probability q.