Quantitative approximation of the discrete Moran process by a Wright–Fisher diffusion

Abstract

The Moran discrete process and the Wright–Fisher model are the most popular models in population genetics. The Wright–Fisher diffusion is commonly used as an approximation in order to understand the dynamics of population genetics models. Here, we give a quantitative large-population limit of the error occurring by using the approximating diffusion in the presence of weak selection and weak immigration in one dimension. The approach is robust enough to consider the case where selection and immigration are Markovian processes, whose large-population limit is either a finite state jump process, or a diffusion process.

1 Introduction

Diffusion approximation is a technique in which a complicated and intractable (as the dimension increases) discrete Markovian process is replaced by an appropriate diffusion which is generally easier to study. This technique is used in many domains and genetics and population dynamics are no exceptions to the rule. Two of the main models used in population dynamics are the Wright–Fisher (see for example Fisher 1922, 1930; Wright 1931, 1945) and the Moran model (Moran 1958) which describe the evolution of a population having a constant size and subject to immigration end environmental variations. In the case of a large population limit, it is well known that the Moran process is quite difficult to handle mathematically and numerically. For example, the convergence to equilibrium (independent of the population size) or the estimation of various biodiversity indices such as the Simpson index are not known. It is thus tempting to approach the dynamics of these Markovian processes by a diffusion, called the Wright–Fisher diffusion, (see for example Ethier 1976, Ethier et al. 1986 or Kimura 1983), and work on this simpler (low dimensional) process to get good quantitative properties.

A traditional way to prove this result is to consider a martingale problem, as was developed by Stroock and Varadhan (1997). See also Dawson (2009), Ethier et al. (1986) and Ethier and Nagylaki (1989) to illustrate the Wright–Fisher process with selection but they do not provide any estimate of the error. This technique ensures us that the discrete process converges to a diffusion when the size of the population grows to infinity. If the setting is very general and truly efficient, it is usually not quantitative as it does not give any order of the error done in replacing the discrete process by the diffusion for a fixed population size. To obtain an estimation of this error we will consider another approach by Ethier and Norman (1977), which makes for a quantitative statement of the convergence of the generator using heavily the properties of the diffusion limit. For the Wright–Fisher model with immigration but without selection they showed that the error is of the order of the inverse of the population size, and uniform in time. Our main goal here, and the improvements compared to existing results, will be to consider the more general model where

• (1) weak selection is involved

• (2) immigration and selection may be also Markov processes.

To include selection, constant or random is of course fundamental for modelisation, (see for example Ewens and Warren 2004; Depperschmidt et al. 2012; Kalyuzhny et al. 2015; Danino et al. 2016; Fung et al. 2017; Danino and Shnerb 2018a, b) for recent references. Also, to study biodiversity, a common index is the Simpson index called also heterozigosity, which is intractable in non neutral model (see Etienne and Olff (2004) or Etienne (2005) in the neutral case), and is not even easy to approximate via Monte Carlo simulation when the population is large. Based on the Wright–Fisher diffusion, an efficient approximation procedure has been introduced by Jabot et al. (2018). Other properties, such as estimating the invariant distribution of the Moran process or fixation probabilities when the population is large are intractable. It is thus a crucial issue to get quantitative diffusion approximation results in the case of random selection to get a full approximation procedure for this biodiversity index.

We will focus in this paper on the two species (or dialellic) case. We may then denote the proportion of one species by $X^J$ when the total population size is J, and $Y^J$ the rescaled Wright Fisher process (see Sect. 2). Let us now state the main result of this paper: for f regular enough, when immigration and selection are weak (namely scaled in 1/J) we have

$$\begin{aligned} \left\| \mathbb {E}_x \Big [f(X_{[tJ^2]}^{J} )-f(Y_{[tJ^2]}^{J} ) \Big ] \right\| _J \le \frac{K(t)}{J}. \end{aligned}$$

where K(t) may be exponential or linear in time (t) depending on the coefficients of immigration (or mutation) and selection. One point is that we may consider here random immigration and selection (under proper scaling).

It gives the first order of the error made in approximating the discrete Moran model by the Wright–Fisher diffusion in weak selection and immigration when the population size tends to infinity. Here the error is inversely proportional to the population size.

Let us give the structure of this paper. First in Sect. 2, we present the discrete Moran model. As an introduction to the method, we first deal with the case of constant selection and we find an error of the order of the inverse of the population size but growing exponentially or linearly in time. It will be done in Sect. 3. Sects. 4 and 5 deal with the case of random environment. Section 4 considers the case when the limit of the selection is a pure jump process and Sect. 5 when it is a diffusion process. We will indicate the main modifications of the previous proof to adapt to this setting. An “Appendix” indicates how to adapt the preceding proofs to the case of the Wright–Fisher discrete process.

2 The discrete Moran model and its approximating diffusion

Consider to simplify a population of J individuals with only two haploid species (in genetics diallelic). At each time step, one individual dies and is replaced by one member of the community or a member of a distinct (infinite) pool, which is called immigration (but can also be interpreted as mutation in genetics). We may refer for example to Etheridge (2011) or Moran (1958) for the genetics point of view for the description of this simple birth and death process, or to Hubbell (2001), Kalyuzhny et al. (2015) for the population dynamics point of view. To clarify the evolution mechanism, let us introduce the following parameters:

• m is the immigration probability, i.e. the probability that the next member of the population comes from the exterior pool;

• p is proportion of the first species in the pool;

• s is the selection parameter, which favors one of the two species when the parent is chosen in the initial population.

Let us first consider that m, p and s are functions depending on time (but not random to simplify) and taking values in [0, 1] for the first two and in $]-1;+\infty [$ for the selection parameter.

Note that our process may also be described considering mutations, rather than immigration but there is a one to one corres. Our time horizon will be denoted by T, it corresponds to the upper limit of the time interval during which the process evolves.

Rather than considering the process describing the number of elements in each species, we will study the proportion in the population of the first species. To do so, let $I_{J}=\lbrace \frac{i}{J}: i=0,1,2,\ldots ,J\rbrace$, and we denote for all f in $B(I_J)$, the bounded functions on $I_{J}$,

$$\begin{aligned} \Vert f\Vert _{J}=\max \limits _{x\in I_{J}}|f(x)|. \end{aligned}$$

And for bounded a function $g: \mathbb {R}\rightarrow \mathbb {R}$, we denote by $\Vert g\Vert =\sup |g|$ the supremum norm of g.

Then, let $C^i$ the set of i times continuously differentiable functions, and for $f \in C^i$, let $f^{(i)}$ be the $i{\mathrm{th}}$ derivative of f.

Let $X_{n}^{J}$, with values in $I_{J}$, be the proportion of individuals of the first species in the community.

In this section, $X_{n}^{J}$ stands for the Moran process, namely a Markov chain with the following transition probabilities: denote $\Delta =\frac{1}{J}$

$$\begin{aligned} \left\{ \begin{aligned} \mathbb {P}(X^J_{n+1}=x+\Delta |X^J_{n}=x)&=(1-x)\left( m_{n}p_{n}+(1-m_{n})\frac{x(1+s_{n})}{1+xs_{n}}\right) \\&:=P_{x+}\\ \mathbb {P}(X^{J}_{n+1}=x-\Delta |X^J_{n}=x)&=x\left( m_{n}(1-p_{n})+(1-m_{n})\Big (1-\frac{x(1+s_{n})}{1+xs_{n}}\Big )\right) \\&:=P_{x-}\\ \mathbb {P}(X^{J}_{n+1}=x|X^J_{n}=x)&=1-P_{x+}-P_{x-}. \end{aligned} \right. \end{aligned}$$

To study the dynamical properties of this process a convenient method developped first by Fisher (1922, (1930) and then by Wright (1931, (1945), aims at approximating this discrete model by a diffusion when the size of the population tends to infinity.

In the special case of the discrete Moran model with weak selection and weak immigration, meaning that the parameters s and m are inversely proportional to the population size J, we usually use the diffusion process $\lbrace Y_{t}^{J}\rbrace _{t \ge 0}$ taking values in $I=[0,1]$ with the generator:

$$\begin{aligned} L=\frac{1}{J^{2}}x(1-x)\frac{{\partial }^2}{\partial {x}^2}+ \frac{1}{J}[ sx(1-x)+m(p-x)]\frac{\partial }{\partial {x}}. \end{aligned}$$

Note that, in weak selection and immigration, $s=s'/J$ and $m=m'/J$, so the process defined by $\lbrace Z_{t}\rbrace _{t \ge 0}=\lbrace Y_{J^{2}t}^{J}\rbrace _{t \ge 0}$ does not depend on J. Its generator is

$$\begin{aligned} \mathscr {L}=x(1-x)\frac{{\partial }^2}{\partial {x}^2}+ [ s'x(1-x)+m'(p-x)]\frac{\partial }{\partial {x}}. \end{aligned}$$

Equivalently, we can consider $(Z_t)_{t>0}$ as the solution of the stochastic differential equation

$$\begin{aligned} dZ_t=\sqrt{2Z_t(1-Z_t)}dB_t+\left[ s'Z_t(1-Z_t)+m'(p-Z_t)\right] dt. \end{aligned}$$

Our aim is to find for a sufficiently regular test function, say $f \in C^{4}$, an estimate of:

$$\begin{aligned} \left\| \mathbb {E}_x\Big [f(Z_{[t]})\Big ]-\mathbb {E}_x\Big [f(X_{[J^{2}t]}^{J})\Big ] \right\| _J \end{aligned}$$

for $0\le t \le T$ and for all x in $I_J$. By replacing $Z_{t}$ by $Y_{J^{2}t}^{J}$ we thus get:

$$\begin{aligned} \left\| \mathbb {E}_x\Big [f(X_{[J^{2}t]}^{J}) \Big ]-\mathbb {E}_x\Big [f(Y_{[J^{2}t]}^{J}) \Big ] \right\| _J \end{aligned}$$

for $0 \le t \le T$, and $x \in I_J$.

So equivalently it is convenient to study, if we note $n=[J^{2}t]$:

$$\begin{aligned} \Vert \mathbb {E}_x\Big [f(X_{n}^{J} )\Big ]-\mathbb {E}_x\Big [f(Y_{n}^{J}) \Big ] \Vert _J \end{aligned}$$

on $0 \le n \le J^2T$, and $x \in I_J$.

Note, once again, that such a limit has been derived (non quantitatively) in many papers, by the martingale methods (or convergence of the generators in this simple setting), see for example Etheridge (2011) where it is even hinted that the order of error should be 1/J but no quantitative statements are given. The only quantitative statement that we know is given by Ethier and Norman (1977), both without selection and in the case of a constant non random selection coefficient.

3 Estimate of the error in the approximation diffusion for constant weak immigration and selection

3.1 Main result

We now state our main result in the case where immigration and selection are constant. It furnishes an estimation of the error when the discrete Moran process $X_{n}$ converges toward the Wright–Fisher diffusion process $Y_{n}$. The method used here is that developed by Ethier and Norman (1977). In the present section, we extend their results to the case of a constant selection, and we still find a error inversely proportional to a given population size.

Theorem 1

Let us consider the weak immigration and selection case, so that $s=\frac{s'}{J}$ and $m=\frac{m'}{J}$ for some $s'\in \mathbb {R}$, $m'\in \mathbb {R}_+$. Let $f \in C^{4}(I)$, then there exist positive functions a, b and K (depending on $m'$ and $s'$ but not on f) such that:

$$\begin{aligned} \left\| \mathbb {E}_x \Big [f(X_{[tJ^2]}^{J} )-f(Y_{[tJ^2]}^{J} ) \Big ] \right\| _J \le a(e^{bt}-1)\left( \frac{\left( \Vert f^{(1)} \Vert _{J} +\Vert f^{(2)} \Vert _{J}\right) }{J}+K\frac{\sum \nolimits _{i=1}^4\Vert f^{(i)} \Vert _{J}}{J^2}\right) . \end{aligned}$$

If we suppose moreover that $m'>|s'|$ then there exists a positive constant a such that

$$\begin{aligned} \left\| \mathbb {E}_x \Big [f(X_{[tJ^2]}^{J} )-f(Y_{[tJ^2]}^{J} ) \Big ] \right\| _J \le a(t+1)\left( \frac{\left( \Vert f^{(1)} \Vert _{J} +\Vert f^{(2)} \Vert _{J}\right) }{J}+\frac{\sum \nolimits _{i=1}^4\Vert f^{(i)} \Vert _{J}}{J^2}\right) . \end{aligned}$$

Remark 1

In the case $s=0$, the previous theorem still hold with $b=0$, and we find back the uniform in time approximation diffusion with speed 1/J. Our method of proof, requiring the control of some Feynman–Kac formula based on the limiting process, seems limited to give a non uniform in time result. Our hope is that we may get weaker conditions than $m>|s|$ to get linear in time estimates. Another possibility is to mix these dependance in time approximation with known ergodicity of the Wright–Fisher process, as Norman (1977) do. It is left for future work.

Remark 2

We have considered to simplify $s=\frac{s'}{J}$ and $m=\frac{m'}{J}$ but one may generalize a little bit the condition to locally bounded s and m such that $\lim Js<\infty$ and $\lim Jm<\infty$. In the same way, one can also follow closely our proofs to get estimates based directly on s, m, p without requiring any scaling (in the population size).

Remark 3

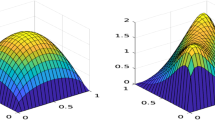
The following figures show that the obtained rate $\frac{1}{J}$ is of the good order. Indeed, on the left figure, the trajectory is (roughly) proportional to $\frac{1}{J}$, whereas it has a quasi-constant (random fluctuations) trajectory if we multiply the error by J.

Fig. 1

Conditions: $s=1$, $m=0.2$, $p=0.5$, $X_0=0.7$, for each point 1000 trajectories has been simulated. Left hand side : Monte Carlo estimation of the error in the approximation, using $f(x)=x$. Right hand side: same Monte Carlo estimation of the error times J

Remark 4

By using an approximation procedure, one may show that for $f \in C^{2}(I)$, then there exist positive functions a, b and K (depending on $m'$ and $s'$) such that:

$$\begin{aligned} \lim _{J\rightarrow \infty }\left\| \mathbb {E}_x \Big [f(X_{[tJ^2]}^{J} )-f(Y_{[tJ^2]}^{J} ) \Big ] \right\| _J \le a(e^{bt}-1)\left( \left( \Vert f^{(1)} \Vert _{\infty } +\Vert f^{(2)} \Vert _{\infty }\right) \right) , \end{aligned}$$

so that we may relax assumptions on the derivatives of f but only gets asymptotic result. One can also get non asymptotic results with an approximation procedure of $C^2$ functions by $C^4$ functions, but then losing the decay in 1/J (by playing with the approximation bounds and the already obtained decay rate 1/J).

3.2 Application: Simpson index

This index commonly used in ecology to measure abundance was proposed by Simpson in the late 1950s, and repeated in many articles dealing with neutral models (e.g., Etienne and Olff (2004); Simpson (1949)). The Simpson index measures the probability that two individuals randomly selected (and uniformly) belong to the same species. It thus varies from 1 to 0 and makes it possible to express the dominance of a species when it tends to 1, or the codominance of several species when it tends to 0. Thus it is a good indicator of the community’s heterogeneity, which is called heterozigosity in genetics.

Let ${\mathcal {S}}^J_n$ denote the Simpson index for the discrete Moran process, and ${\mathcal {S}}_t$ the Simpson index for the Wright–Fisher diffusion. It is a polynomial function of $X_n$ or $Y_t$ verifying: ${\mathcal {S}}_t= Y_t(1-Y_t)$. There exists an efficient algorithm able to approximate $E[{\mathcal {S}}_t]$ see Jabot et al. (2018). Let us denote by $\tilde{{\mathcal {S}}_t}$ this approximation and $\epsilon _t$ the error made in this approximation.

Then, thanks theorem 1 it is possible to estimate the full error made in the approximation of $E[{\mathcal {S}}^J_t]$ by $\tilde{{\mathcal {S}}_t}$:

$$\begin{aligned} \mathbb {E}_{x} \Big [\vert {\mathcal {S}}^J_{[t^2J]} - \tilde{{\mathcal {S}}}_{t}\vert \Big ]&\le \mathbb {E}_{x} \Big [ \vert {\mathcal {S}}^J_{[t^2J]}-{\mathcal {S}}_{[t^2J]} \vert \Big ]+\mathbb {E}_{x} \Big [ \vert \tilde{{\mathcal {S}}}_{t}-{\mathcal {S}}_{[t^2J]} \vert \Big ]\\&\le \epsilon _t + \frac{4a(e^{bt}-1)}{J}+o\left( \frac{1}{J}\right) \end{aligned}$$

The following figure compare ${\mathcal {S}}^J_{[t^2J]}$ calculated by Monte-Carlo with 1000 trajectories, with $\tilde{{\mathcal {S}}}_{t}$. Parameters are $J=1000$, $m=0$, $s=1$.

Fig. 2

Simpson index expectancy

Remark 5

There are also other applications that can be considered, such as estimating the stationary distributions, fixation probabilities, average time to fixation to a mutant. It has been explored for example by Bürger and Ewens (1995), McCandlish et al. (2015), Chumley et al. (2018) for the fixation probabilities. Note however two important characteristics of our results. The first one is that our bounds depend on time, so that for the estimation of the invariant measure it may needs a careful tuning of the speed of convergence to equilibrium of the Wright–Fisher process and a quite large J to get good approximations. Of course, when the error between the Moran process and the Wright–Fisher one is linear, it may give interesting results with a limited size of population. The second point is that we need to consider regular functional, and fixation probabilities are by essence discontinuous (namely an indicator function). It will thus need further approximations to consider such a case that we will consider in future work.

3.3 Proof

The proof relies on three arguments:

• (1) a “telescopic” decomposition of the error;

• (2) a quantitative estimate of the error at time 1 of the approximation of the Moran process by the diffusion;

• (3) a quantitative control of the regularity of the Wright–Fisher process.

Note also that in the sequel we will not make distinction between function on C(I) to $I_J$.

Let $S_n$ be defined on $B(I_J)$ (the space of bounded functions on $I_J$) by:

$$\begin{aligned} (S_nf)(x)=\mathbb {E}_x[f(X_{n}^J)] \quad \forall n \in \mathbb {N}. \end{aligned}$$

As is usual $S_{n}$ verifies for all k in $\mathbb {N}$ the semigroup property, namely that $S_{n+k}=S_nS_k$.

Let $T_{t}$ be the operator defined on the space of bounded continuous function by:

$$\begin{aligned} (T_tf)(x)=\mathbb {E}_x[f(Y_{t}^{J})] \quad \forall t \ge 0. \end{aligned}$$

It also defines a semigroup $T_{s+t}=T_sT_t$, $\forall s \ge 0.$

Thanks to these properties, we have

$$\begin{aligned} S_nT_0f-S_0T_nf&=\sum _{k=0}^{n-1}S_{n-k}T_kf-S_{n-k-1}T_{k+1}f\\&=\sum _{k=0}^{n-1}S_{n-k-1}S_1T_kf-S_{n-k-1}T_1T_kf\\&=\sum _{k=0}^{n-1}S_{n-k-1}(S_1-T_1)T_kf \end{aligned}$$

and as $\Vert S_nf \Vert _J \le \Vert f \Vert _J$ by triangular inequality, we get that $\forall n \in \mathbb {N}$, $\forall f \in C(I_J)$.

$$\begin{aligned} \Vert S_nf -T_nf \Vert _J \le \sum _{k=0}^{n-1} \Vert S_{n-k-1}(S_1-T_1)T_kf \Vert _J \le \sum _{k=0}^{n-1} \Vert (S_1-T_1)T_kf \Vert _J . \end{aligned}$$

(1)

We have two mains operations to analyze : $S_1-T_1$ for a “one-step” difference between the Moran process and the Wright–Fisher diffusion process, and $T_kf$ for which we need regularity estimates.

3.3.1 Control of $(S_1-T_1)$

Let us first study, for f in $C^4$ , $(S_1-T_1)f$. The main goal is to obtain the Taylor expansion of this function when J is big enough.

Lemma 1

Assume $s>-1+\varepsilon$ and write $s'=Js$, then there exists $K_1(\varepsilon ) >0$ independant on J such that

$$\begin{aligned} \Vert (S_1-T_1)f\Vert _{J}&\le \frac{|s'|m'+s'^2}{4\varepsilon J^3} \Vert f^{(1)} \Vert _{J} +\frac{m'p+\frac{|s'|}{4}+m'(1+|s'|)}{2\varepsilon J^3} \Vert f^{(2)} \Vert _{J}\\&\quad +\frac{K_{1}(\varepsilon )\Big (\sum \limits _{i=1}^4\Vert f^{(i)}\Vert _J\Big )}{J^4} \end{aligned}$$

Proof

Let us begin by some known facts on the Wright–Fisher diffusion process. Note, as usual for this diffusion process

$$\begin{aligned} \lim _{t \rightarrow 0} \left\| \frac{T_tf-f}{t}- Lf \right\| _J=0 ,\forall f \in C^2(I). \end{aligned}$$

The Chapman–Kolmogorov backward equation reads

$$\begin{aligned} \frac{\partial }{\partial t}(T_tf)(x)=L(T_tf)(x)=T_t(Lf)(x) \end{aligned}$$

and more generally if f is regular enough, for j in $\mathbb {N}$ it is possible to define $L^j$ the $j-\mathrm{th}$ iterate of L, which satisfies:

$$\begin{aligned} \frac{\partial ^{j}}{\partial t^j}(T_tf)(x)=(T_tL^jf)(x),\forall x \in I, t \ge 0. \end{aligned}$$

For this proof, we only need to go to the fourth order in j. So let $f\in C^4(I)$ (possibly depending on J), using the Taylor expansion of $(T_1f)(x)$ there exists $w_{2}$, independent of J, such that:

$$\begin{aligned} (T_1f)(x)= & {} (T_0f)(x)+(T_0 f)^{(1)}(x)(1-0)+w_{2}\frac{1}{2!}(T_0f)^{(2)}(x)\nonumber \\= & {} f(x)+(L^{1}f)(x)+\frac{w_{2}}{2}(L^{2} f)(x) \end{aligned}$$

(2)

Recall

$$\begin{aligned} L^{1}f(x)=\frac{x(1-x)}{J^2}f^{(2)}(x)+\frac{sx(1-x)+m(p-x)}{J}f^{(1)}(x). \end{aligned}$$

By direct calculations, we have

$$\begin{aligned} L^{2}f(x)&=\frac{(x(1-x))^2}{J^4}f^{(4)}(x)\\&\quad + \Big [ \frac{2(1-2x)x(1-x)}{J^4}+\frac{2x(1-x)(sx(1-x)+m(p-x))}{J^3}\Big ]f^{(3)}(x)\\&\quad + \Big [ \frac{-2x(1-x)}{J^4} \\&\quad +\frac{2x(1-x)(s(1-2x)-m)+(1-2x)(sx(1-x)+m(p-x))}{J^3}\\&\quad +\frac{(sx(1-x)+m(p-x))^2}{J^2}\Big ]f^{(2)}(x) + \Big [\frac{-2sx(1-x)}{J^3}\\&\quad +\frac{(s(1-2x)-m)(sx(1-x)+m(p-x))}{J^2}\Big ]f^{(1)}(x). \end{aligned}$$

Remark now that by our assumption on the boundedness of the successive derivatives of f that there exists $K_0$ (depending also on $m',p,s'$)

$$\begin{aligned} \Vert L^2f\Vert _J\le \frac{K_{0}}{J^4}. \end{aligned}$$

Thus, in the following this term could be neglected.

Let us now look at the Moran process and so get estimates on $S_1$. The quantity $X^J_1-x$ is at least of the order of $\frac{1}{J}$ and when J goes to infinity, goes to 0. So using Taylor’s theorem, there exists $\zeta$ such that:

$$\begin{aligned} f(X^J_1)&=f(x) +f^{(1)}(x)(X^J_1-x)+\frac{f^{(2)}(x)}{2}\big (X^J_1-x\big )^{2}+\frac{1}{3!}(X^J_1-x)^3 f^{(3)} \\&\quad + \frac{1}{4!}(X^J_1-x)^4 f^{(4)}(\zeta ) \end{aligned}$$

and thus

$$\begin{aligned} (S_1f)(x)= & {} \mathbb {E}_x[f(X^J_1)]\nonumber \\= & {} f(x) +f^{(1)}(x)\mathbb {E}_x[X^J_1-x]+ \frac{1}{2!}\mathbb {E}_x[(X^J_1-x)^2] f^{(2)}(x)\nonumber \\&+\frac{1}{3!}\mathbb {E}_x[(X^J_1-x)^3] f^{(3)}(x) + \frac{1}{4!}\mathbb {E}_x[(X^J_1-x)^4 f^{(4)}(\zeta )] \end{aligned}$$

(3)

Direct estimates on the centred moments of the Moran process give:

$$\begin{aligned}&\mathbb {E}_x[X^J_1-x]=\frac{sx(1-x)(1-m)}{J(1+sx)}+\frac{m(p-x)}{J} \end{aligned}$$

(4)

$$\begin{aligned}&\mathbb {E}_x[(X^J_1-x)^2]=\frac{1}{J^2} \Big (mp(1-2x)+\frac{(1-m)(1+s)x(1-2x)}{1+sx}+x\Big ) \end{aligned}$$

(5)

$$\begin{aligned}&\mathbb {E}_x[(X^J_1-x)^3]<K_{3}\frac{1}{J^4} \end{aligned}$$

(6)

$$\begin{aligned}&\mathbb {E}_x[(X^J_1-x)^4]<K_{4}\frac{1}{J^4} \end{aligned}$$

(7)

where $K_{3}, L_4$ are constant (independent of J).

We may then consider $(S_1-T_1)f$ through (3) and (2) so that there exists a constant $K_{1}$ such as:

$$\begin{aligned} (S_1f)(x)-(T_1f)(x)=&f^{(1)}(x)\mathbb {E}_x[(X^J_1-x)]+\frac{1}{2}\mathbb {E}_x[(X^J_1-x)^2] f^{(2)} (x) \nonumber \\&+\frac{1}{3!}\mathbb {E}_x[(X^J_1-x)^3] f^{(3)}(x) + \frac{1}{4!}\mathbb {E}_x[(X_1^J-x)^4] f^{(4)}(\zeta )\nonumber \\&-\Big ( (L^1f)(x)+\frac{w_{2}}{2}(L^2f)(x) \Big ) \end{aligned}$$

(8)

and

$$\begin{aligned} \Big |(S_1f)(x)-(T_1f)(x)\Big |\le&|\gamma ^J_1|\Vert f^{(1)}\Vert _J +|\gamma ^J_2 |\Vert f^{(2)} \Vert _J+\frac{K_{1}\Big (\sum \limits _{i=1}^4\Vert f^{(i)}\Vert _J\Big )}{J^4} \end{aligned}$$

(9)

with

$$\begin{aligned} \gamma ^J_{1}&=\frac{-sx(1-x)(m+sx)}{J(1+sx)}\\ \gamma ^J_2&=\frac{1}{2J^2}\left[ mp(1-2x) +\frac{(1-m)(1+s)x(1-2x)}{1+sx} -x(1-2x) \right] \\&=\frac{1}{2J^2}\left[ mp(1-2x) +x(1-2x)\frac{s(1-x)-m(1+s)}{1+sx} \right] . \end{aligned}$$

As selection and immigration are weak, $\gamma ^J_{1}$ and $\gamma ^J_{2}$ are at most of the order of $\frac{1}{J^3}$. Then the fact that $s>-1+\epsilon$ and $x<1$ implies $\frac{1}{1+sx}<\frac{1}{\epsilon }$ and we obtain:

$$\begin{aligned} \Vert (S_1-T_1)f\Vert _{J}&\le \frac{|s'|m'+s'^2}{4\varepsilon J^3} \Vert f^{(1)} \Vert _{J} +\frac{m'p+\frac{|s'|}{4}+m'(1+|s'|)}{2\varepsilon J^3} \Vert f^{(2)} \Vert _{J}\\&\quad +\frac{K_{1}(\varepsilon )\Big (\Vert f^{(3)} \Vert _{J}+\Vert f^{(4)} \Vert _{J}\Big )}{J^4} \end{aligned}$$

which concludes the proof. $\square$

In the following we write:

$$\begin{aligned} \gamma ^{J,\epsilon }_{1}&=\frac{|s'|m'+s'^2}{4\varepsilon J^3}\\ \gamma ^{J,\epsilon }_{2}&=\frac{m'p+\frac{|s'|}{4}+m'(1+|s'|)}{2\varepsilon J^3} \end{aligned}$$

3.3.2 Regularity estimates on $T_t$

We now need to prove regularity estimates on $T_t$. By (Ethier 1976, Th.1), we have that $T_t:C^{j}(I)\rightarrow C^j(I)$ for all j. Assume for now that $f \in C^4(I)$ and $\forall j\in \{1,2\}$, $\forall k\leqslant j$, there are $c_j$ and $a_{k,j}$$\in \mathbb {R}^{+}$ independent of J such that:

$$\begin{aligned} \Vert (T_tf)^{(j)} \Vert _J \le e^{c_j\frac{t}{J^2}}\,\sum \limits _{i=1}^{j} a_{i,j}\Vert f^{(i)} \Vert _J \end{aligned}$$

(10)

with $c_{j}=\sup \limits _{x\in [0,1]}|j(j-1)-Js(1-2x)-Jm |$.

Let us first see how to conclude under the assumption (10). For $1\le j\le 4$, there exists a continuous function $R_j$ of the time variable t, which is independent of J and a function of $\epsilon$, $K(\epsilon )$ such that:

$$\begin{aligned} \Vert S_nf-T_nf \Vert _{J}&\le \sum _{k=0}^{n-1}\Vert (S_1-T_1)T_kf \Vert _{J} \\&\le \sum _{k=0}^{n-1}\left( \sum \limits _{i=1}^2\vert \gamma ^{J,\epsilon }_{i}\vert \Vert (T_kf)^{(i)} \Vert _{J} +K_1(\epsilon )\frac{\sum \limits _{i=1}^4\Vert (T_kf)^{(i)}\Vert _{J}}{J^4} \right) \\&\le \sum _{j=1}^{2}\vert \gamma ^{J,\epsilon }_j \vert \sum \limits _{i=1}^{j} a_{i,j}\Vert f^{(i)} \Vert _{J}\sum \limits _{k=0}^{n-1}\exp (c_j\frac{k}{J^2})\\&\quad + K_1 (\epsilon )\frac{\sum \nolimits _{j=1}^4\sum \nolimits _{i=1}^{j} a_{i,j}\Vert f^{(i)} \Vert _{J}\sum \limits _{k=0}^{n-1}\exp (c_j\frac{k}{J^2})}{J^4} \\&\le \sum _{j=1}^{2}\vert \gamma ^{J,\epsilon }_j\vert \times R_{j}(t)J^2 \times \Vert f^{(j)} \Vert _{J}\\&\quad +K (\epsilon )\frac{\sum \nolimits _{j=1}^4\Vert f^{(j)}\Vert _{J}R_{j}(t)}{J^2} \underset{J\rightarrow +\infty }{\longrightarrow }0 \end{aligned}$$

since for J large enough,

$$\begin{aligned} \sum \limits _{i=1}^{j} a_{i,j}\sum _{k=0}^{n-1}\exp \left( c_j\frac{k}{J^2}\right) =&\sum \limits _{i=1}^{j} a_{i,j}\frac{1-\exp (c_{j}\frac{n}{J^2})}{1-\exp \left( \frac{c_j}{J^2}\right) }\\ \le&J^2 \frac{\exp (c_j\frac{n}{J^2})-1}{c_j}+O\left( \frac{1}{J^2}\right) \end{aligned}$$

and $R_{j}(t)=\sup \nolimits _{J\in \mathbb {N}}\frac{\exp (c_j\frac{n}{J^2})-1}{c_j}$ is finite because $n\le tJ^2$. So there exists a, $b \in \mathbb {R}^+$ such as $a(e^{bt}-1)\ge \sup \nolimits _{J\in \mathbb {N}}\max \nolimits _{j\in \{1,2\}}\Big (\vert \gamma ^{J,\epsilon }_j\vert R_{j}(t)J^3 \Big )$ and $a(e^{bt}-1)\ge \max \nolimits _{j\in \{1,\ldots ,4\}}R_{j}(t)$. The conclusion follows:

$$\begin{aligned}&\left\| \mathbb {E}_x \Big [f(X_{[tJ^2]}^{J} )-f(Y_{[tJ^2]}^{J} ) \Big ] \right\| _J \\&\quad \le a(e^{bt}-1)\left( \frac{\left( \Vert f^{(1)} \Vert _{J} +\Vert f^{(2)} \Vert _{J}\right) }{J}+K\frac{\sum \limits _{i=1}^4\Vert f^{(i)} \Vert _{J}}{J^2}\right) . \end{aligned}$$

This concludes the proof in the first case. Indeed, we see that the function $R_j(t)$ is exponential in time in the general case.

But we will see later how, when some additional conditions are added on $m'$ and $s'$, one may obtain a linear in time function.

We will now prove the crucial (10). It will be done through the following proposition.

Proposition 1

Let $\phi (t,x)=(T_tf)(x)$, $x \in I_J$ and $t \ge 0$. Assume $f\in C^{j+2}(I)$ then for fixed t, $\phi (t,x) \in C^{j+2}(I)$ and for $j\in \mathbb {N}$, $\forall k\leqslant j$, there are ${c}_j$and $a_{k,j}$$\in \mathbb {R}$ independent of J such as $\Vert \phi (t,x)^{(j)} \Vert \le \exp ({c}_j\frac{t}{J^2} )\sum \nolimits _{k=1}^{j} a_{k,j}\Vert f^{(k)} \Vert$

Proof

First remark that the Chapman–Kolmogorov backward equation may be written:

$$\begin{aligned} \frac{\partial }{\partial t}\phi =L\phi , \qquad \qquad \phi (0,.)=f. \end{aligned}$$

The following lemma gives the equations verified by $\frac{\partial }{\partial t}\phi ^{(j)}$:

Lemma 2

Let $\phi ^{(j)}$ be the $j{\mathrm{th}}$ derivative of $\phi$ with respect to x then we get:

$$\begin{aligned} \frac{\partial }{\partial t}\phi ^{(j)}=L_j\phi ^{(j)}-\nu _j\phi ^{(j)}+\psi _{j}\phi ^{(j-1)},\qquad \qquad \phi ^{(j)}(0,.)=f^{(j)} \end{aligned}$$

where

$$\begin{aligned}&L_j\phi ^{(j)}=L\phi ^{(j)}+j\frac{1-2x}{J^2}\phi ^{(j+1)}\\&\nu _j(x)=\left( \frac{j(j-1)}{J^2}-j\frac{s(1-2x)-m}{J}\right) \\&\psi _{j}=\frac{-sj(j-1)}{J}. \end{aligned}$$

Let us remark that there are two new terms when there is selection in Moran processes, i.e. $\psi _j$ which will lead to the dependence in time of our estimates handled via the Feynman–Kac formula, and one in $\nu _j$ which will be the key to the condition to get only linear dependence in time.

Proof

A recurrence is sufficient to prove this result; for for the sake of simplicity, let us only consider the case $j=1$,

$$\begin{aligned} \frac{\partial }{\partial t}\phi ^{(1)}&=\frac{\partial }{\partial x}\left( \frac{\partial }{\partial t}\phi \right) =\frac{\partial }{\partial x}L\phi \\&=\frac{\partial }{\partial x} \Big (\frac{x(1-x)}{J^2}\phi ^{(2)}+\frac{sx(1-x)+m(p-x)}{J}\phi ^{(1)} \Big ) \\&=\frac{x(1-x)}{J^2}\phi ^{(3)}+\frac{1}{J}(sx(1-x)+m(p-x))\phi ^{(2)}+\frac{1-2x}{J^2}\phi ^{(2)}\\&\qquad +(s(1-2x)-m)\frac{1}{J}\phi ^{(1)}\\&= (L+\frac{1-2x}{J^2}\frac{\partial }{\partial x })\phi ^{(1)}+\frac{s(1-2x)-m}{J} \phi ^{(1)}\\&=L_1\phi ^{(1)}+\frac{s(1-2x)-m}{J}\phi ^{(1)}. \end{aligned}$$

With $L_1\phi ^{(1)}=L\phi ^{(1)}+\frac{1-2x}{J^2}\frac{\partial \phi ^{(1)}}{\partial x }$, we find the good initial coefficients. $\square$

Let us now use the Feymann-Kac formula to get,

$$\begin{aligned} \begin{aligned} \phi ^{(j)}(t,x)&=\mathbb {E}_x\left[ f^{(j)}({\tilde{Y}}^{j}_t)\exp \left( -\int _{0}^{t}\frac{j(j-1)}{J^2}+\frac{m-s(1-2{\tilde{Y}}^{j}_{u})}{J}du\right) \right. \\&\qquad -\left. \int \limits _{0}^{t}\frac{sj(j-1)}{J}\phi ^{(j-1)}({\tilde{Y}}^{j}_{h})e^{-\int _{0}^{h}\frac{j(j-1)}{J^2}+\frac{m-s(1-2{\tilde{Y}}^{j}_{u})}{J}du}dh\right] \end{aligned} \end{aligned}$$

with ${\tilde{Y}}^{j}_t$ the Markov process with generator $L_{j}$. Then look first in $j=1$. As we are in regime of weak selection and weak immigration,

$$\begin{aligned} \Vert \phi ^{(1)} (x,t)\Vert&\le \mathbb {E}_x\left[ \Vert f^{(1)} ({\tilde{Y}}^J_t)\Vert \exp \left( \frac{t}{J^2} \sup \limits _{x\in [0,1]}J(m-s(1-2x)\right) \right] \\&\le \Vert f^{(1)} \Vert _J \exp \left( \frac{t}{J^2} \lambda _{1}\right) \end{aligned}$$

where $\lambda _{1}=\sup \nolimits _{x\in [0,1]}J(m-s(1-2x))= m'+|s'|$ is independent of J. The result in case $j=1$ is proved.

We will then prove the result by recurrence: suppose true this hypothesis until $j-1$.

For $j>1$, denote $c_{j}=\sup \nolimits _{x\in [0,1]}|J^2\nu _{j}(x)|$, and remark that $c_{j}$ is no equal to zero and is independent of J because the selection and immigration are weak. Thus

$$\begin{aligned} \Vert \phi ^{(j)}(t,x)\Vert _J&\le \mathbb {E}_x\Big [| f^{(j)}({\tilde{Y}}^{j}_t)| e^{c_{j}\frac{t}{J^2}}+\int \limits _{0}^{t}\frac{sj(j-1)}{J}\Vert \phi ^{(j-1)}({\tilde{Y}}^{j}_{h})\Vert _J e^{\frac{hc_{j}}{J^2}}dh\Big ]\\&\leqslant \Vert f^{(j)}\Vert _J e^{c_{j}\frac{t}{J^2}}+\frac{sj(j-1)}{J}\Vert \phi ^{(j-1)}\Vert _J \int \limits _{0}^{t}e^{\frac{hc_{j}}{J^2}}dh\\&\leqslant \Vert f^{(j)}\Vert _J e^{c_{j}\frac{t}{J^2}}+\frac{sj(j-1)}{J}\Vert \phi ^{(j-1)}\Vert _J \frac{J^2}{c_{j}}\big (e^{\frac{tc_{j}}{J^2}}-1\big )\\&\leqslant \Vert f^{(j)}\Vert _J e^{c_{j}\frac{t}{J^2}}\\&\qquad + \exp ({c}_{j-1}\frac{t}{J^2} )\sum \limits _{k=1}^{j-1} a_{k,j-1}\Vert f^{(k)} \Vert _J \frac{Jsj(j-1)}{c_{j}}\Big (e^{\frac{tc_{j}}{J^2}}-1\Big )\\&\leqslant e^{\frac{tc_{j}}{J^2}}\left( \Vert f^{(j)}(x)\Vert _J+ e^{{c}_{j-1}\frac{t}{J^2} }\sum \limits _{k=1}^{j-1} a_{k,j-1}\Vert f^{(k)} \Vert _J \frac{Jsj(j-1)}{c_{j}}\right) \\&\leqslant e^{\frac{t{c}_{j}}{J^2}}\left( \sum \limits _{k=1}^{j} a_{k,j}\Vert f^{(k)} \Vert _J\right) . \end{aligned}$$

The $a_{k,j}$ do not depend on J, because $\frac{Jsj(j-1)}{c_{j}}$ , the $a_{k,j-1}$ and $\exp (\lambda _j\frac{t}{J^2} )$ can be bounded independently of J.

To conclude we have to justify that $c_j$ is finite for all j. For it we just need to note that the processes ${\tilde{Y}}_{t}^{j}$ are bounded by 0 and 1 for all j.

This is partly due to the fact that their generator $L_j\phi ^{(j)}(x)=L\phi ^{(j)}+j\frac{1-2x}{J^2}\phi ^{(j+1)}$ has a negative drift at the neighbourhood of 1 and a positive drift in the neighbourhood of 0 and the diffusion vanishes at these points, see Feller (1954). This argument completes the proof. $\square$

Let us now consider the case where $m>|s|$, we will show that in this case we obtain a linear in time dependence rather than an exponential one. Then, in the equation (11) we can use the following:

$$\begin{aligned} \Vert \phi ^{(1)} (.,t)\Vert _J&\le \Vert f^{(1)} \Vert _J \exp (-\frac{t}{J^2} \lambda _{1}) \\ \Vert \phi ^{(2)} (.,t)\Vert _J&\le c_{1}\left( \Vert f^{(1)} \Vert _J+\Vert f^{(2)} \Vert _J \right) \end{aligned}$$

where $c_{1}$ is a constant independent of time. And then,

$$\begin{aligned} \Vert S_nf-T_nf \Vert _J&\le \sum _{k=0}^{n-1}\Vert (S_1-T_1)T_kf \Vert _J \\&\le \sum _{k=0}^{n-1}\left( |\gamma _1^{J,\epsilon }| \Vert (T_kf)^{(1)} \Vert _J +|\gamma _2^{J,\epsilon } |\Vert (T_kf)^{(2)} \Vert _J+O\left( \frac{1}{J^4}\right) \right) \\&\le | \gamma _1^{J,\epsilon }|\, \Vert f^{(1)} \Vert _J \sum _{k=0}^{n-1}\exp (-\frac{k}{J^2}\times \lambda _{1})+|\gamma _2^{J,\epsilon } |\,c_{1}\left( \Vert f^{(1)} \Vert _J+\Vert f^{(2)} \Vert _J\right) n \\&\quad +O\left( \frac{1}{J^2}\right) \\&\le \max (|\gamma _1^{J,\epsilon }|,|\gamma _2^{J,\epsilon }|)\times J^2c(t+1)\left( \Vert f^{(1)} \Vert _J+\Vert f^{(2)} \Vert _J\right) +O\left( \frac{1}{J^2}\right) \end{aligned}$$

because if J is big enough,

$$\begin{aligned} \sum _{k=0}^{n-1}\exp (-\frac{k}{J^2}\times \lambda _{1})=\frac{1-\exp (-\frac{n}{J^2}\times \lambda _{1})}{1-\exp (-\frac{\lambda _{1}}{J^2})}\le c_{2}J^2 \end{aligned}$$

and $c=max(c_{1},c_{2})$ is independent of J and independent of time.

4 Random selection as a limiting jump process

To simplify, we will consider a constant immigration, in order to see where the main difficulty arises. The results would readily apply also to a random immigration case.

Let us now assume that s is no longer a constant but a Markovian jump process $(s_{n})_{n\in \mathbb {N}}$ with homogeneous transition probability $(P^J_{s,s'})$. We are in the weak selection case so $s_{n}$ is still of the order of $\frac{1}{J}$ and takes values in a finite space $E_s$, having the cardinality K.

Assume furthermore that there exists $Q\in M_{K}(\mathbb {R})$ and $\alpha \in (\mathbb {R}^+)^K$

$$\begin{aligned}&P^{J}_{s,s'}\times J^2 \underset{J\rightarrow +\infty }{\longrightarrow }\alpha _{s}Q_{s,s'}\qquad \qquad \forall s \ne s' . \end{aligned}$$

(11)

As in the previous section, $(X^J_{n})_{n\in \mathbb {N}}$ is the Moran process, but with a Markovian selection and $(X^J_{n})_{n\in \mathbb {N}}$ takes values in $I_{J}$. Finally denote $W^J_{n}=(X^J_n,s_n)$. Consider now the Markov process ${\tilde{W}}^J_{t}$ tacking values in $\mathscr {I}=[0,1]\times E_s$ with the following generator:

$$\begin{aligned} \forall f \in C^2(\mathscr {I}) \quad L_{x,s}f(x,s)&=L_xf(x,s)+L_sf(x,s)\\ \end{aligned}$$

with $L_xf(x,s)=\frac{1}{J^{2}}x(1-x)\frac{{\partial }^2}{\partial {x}^2}f(x,s)+ \frac{1}{J}[ sx(1-x)+m(p-x)]\frac{\partial }{\partial {x}}f(x,s)$ and $L_sf(x,s)=\sum \limits _{s'\in E_s}\frac{\alpha (s)Q_{s,s'}}{J^2}\big (f(x,s')-f(x,s)\big )$

Its first coordinate is the process $Y^J_{t}$ having the same s-dependent generator as in the first part and the second is ${\tilde{s}}_{t}$ the Markovian jump process having $(Q_{s',s})_{s,s'\in E_s}$ for generator and $\frac{\alpha }{J^2}$ for transition rates.

As in the previous part we want to quantify the convergence of $({\tilde{W}}^J_{n})_{N\in \mathbb {N}}$ towards $(W^J_{n})_{n\in \mathbb {N}}$ in law, when J goes to infinity. We now write $f^{(j)}$ for the the jth derivative in x of f. And let denote in this section, for $f:I_J\times E_s\rightarrow \mathbb {R}$, $\Vert f \Vert _J=\sup \limits _{I_J\times E_s}|f(x,s)|$. Moreover $T_tf(x,s)=\mathbb {E}_{x,s}[f({\tilde{W}}^J_t)]$ and $S_nf(x,s)=\mathbb {E}_{x,s}[f(W^J_n)]$.

Theorem 2

Assume $\forall s$ and $\forall f \in C^2(\mathscr {I})$, $T_{t}f(.,s)$ is in $C^2(\mathscr {I})$ . Let f such as $\forall s$$f(.,s) \in C^{4}(\mathscr {I})$ then it exists a, $b\in \mathbb {R}$ and a function $k_0$ linear in time (t) which verifies when J goes to infinity:

$$\begin{aligned} \left\| \mathbb {E}_{x,s} \Big [f(W_{[tJ^2]}^{J} )-f({\tilde{W}}_{[tJ^2]}^{J} ) \Big ] \right\| _J\le & {} \frac{a(e^{bt}-1)}{J}\Big (\Vert f^{(1)} \Vert _{J}+\Vert f^{(2)} \Vert _{J}\Big )\\&+k_0\max \limits _{s,s' \in E_s}\Big |J^2P_{s,s'}-\alpha _{s}Q_{s,s'}\Big |\Vert f\Vert _{J}\\&+\frac{a(e^{bt}-1)}{J^2}\sum _{i=1}^4\Vert f^{(i)}\Vert _J. \end{aligned}$$

The theorem shows the balance between the approximation of the Moran process and the random selection process.

Proof

The structure of proof is the same as for constant selection. Let us focus on the first lemma, where some changes have to be highlighted.

Lemma 3

There exists bounded functions of (x, s), $\Gamma _{j}^{J}$ ($j=1,2$) of the order of $\frac{1}{J^3}$, and a constant $K'$ such that :

$$\begin{aligned} \Vert (S_1-T_1)f\Vert _{J}&\le \vert \Gamma _1^{J}\vert \, \Vert f^{(1)} \Vert _{J} +\vert \Gamma _2^{J}\vert \, \Vert f^{(2)} \Vert _{J}\\ {}&+\Vert \sum \nolimits _{s'\in E_s} \left( P^{J}_{s,s'}-\frac{\alpha _{s}}{J^2}Q_{s,s'}\right) \ \big (f(x,s')-f(x,s)\big ) \Vert _{J}+\frac{K'\sum \nolimits _{i=1}^4\Vert f^{(i)}\Vert _J}{J^4} \end{aligned}$$

Proof

We provide first the equivalent of (1) in our context, i.e. there exists $|w'_2|<1$ such that

$$\begin{aligned} (S_1-T_1)f(x,s)&= \mathbb {E}_{x,s} \Big [f(X^J_1,s_1)\Big ]-f(x,s)- L_{x,s}f(x,s)+w'_{2}L_{x,s}^2f(x,s)\\&= \mathbb {E}_{x,s} \Big [f(X^J_1,s_1)-f(X^J_{1},s)\Big ]+\mathbb {E}_{x} \Big [f(X^J_1,s)-f(x,s)\Big ]\\&\quad -L_{x}f(x,s)-\sum \limits _{s'\in E_s} \frac{\alpha _{s}}{J^2}Q_{s,s'}\left( f(x,s')-f(x,s) \right) \\&+w'_{2}L^2_{x,s}f(x,s) \end{aligned}$$

Note that $L_{x,s}^2f$ is still of the order of $\frac{1}{J^4}$, then

$$\begin{aligned}&\Big |(S_1-T_1)f(x,s)\Big | \leqslant \Big |\mathbb {E}_{x} \Big [\mathbb {E}_{s}\big [f(x_1,s_1)-f(x_{1},s)|X^J_{1}=x_1\big ]\Big ]-L_{x}f(x,s)\nonumber \\ \nonumber&\qquad +\mathbb {E}_{x} \Big [f(X^J_1,s)-f(x,s)\Big ] -\sum \limits _{s'\in E_s} \frac{\alpha _{s}}{J^2}Q_{s,s'}\left( f(x,s')-f(x,s) \right) \Big |\nonumber \\&\qquad +\frac{K\sum \nolimits _{i=1}^4\Vert f^{(i)}\Vert _J}{J^4}\nonumber \nonumber \\&\leqslant \Big |\mathbb {E}_{x} \left[ \sum \nolimits _{s'\in E_s} P_{s,s'}\big (f(X^J_{1},s')-f(X^J_{1},s)\big )-\frac{\alpha _{s}}{J^2}Q_{s,s'} \big (f(x,s')-f(x,s)\big ) \right] \nonumber \\&\qquad +\mathbb {E}_{x} \Big [f(X^J_1,s)-f(x,s)\Big ] -L_{x}f(x,s)\Big |+\frac{K\sum \nolimits _{i=1}^4\Vert f^{(i)}\Vert _J}{J^4}\nonumber \\&\leqslant \Big |\mathbb {E}_{x} \left[ \sum \limits _{s'\in E_s} P_{s,s'}\big (f(X^J_{1},s')-f(x,s')\big )+f(x,s')\Big (P_{s,s'}-\frac{\alpha _{s}}{J^2}Q_{s,s'} \Big ) \right] \Big |\nonumber \\&\qquad +\sum \limits _{s'\in E_s}\Big |-P_{s,s'}f(X^J_{1},s)+\frac{\alpha _{s}}{J^2}Q_{s,s'}f(x,s)\Big |\nonumber \\&\qquad +\Big |\mathbb {E}_{x} \Big [f(X^J_1,s)-f(x,s)\Big ] -L_{x}f(x,s)\Big |+\frac{K\sum \nolimits _{i=1}^4\Vert f^{(i)}\Vert _J}{J^4}\nonumber \\&\leqslant \Big |\mathbb {E}_{x} \Big [f(X^J_1,s)-f(x,s)\Big ] -L_{x}f(x,s)\Big | \end{aligned}$$

(12)

$$\begin{aligned}&\qquad + \Big |\sum \nolimits _{s'\in E_s} P_{s,s'}\left( \mathbb {E}_{x}\big [f(X^J_{1},s')-f(x,s')\big ]+\mathbb {E}_{x}\big [f(x,s)-f(X^J_{1},s)\big ]\right) \Big | \end{aligned}$$

(13)

$$\begin{aligned}&\qquad +\Vert \sum \limits _{s'\in E_s} \left( P_{s,s'}-\frac{\alpha _{s}}{J^2}Q_{s,s'}\right) \big (f(x,s')-f(x,s)\big )\Vert _{J}\nonumber \\&\qquad +\frac{K\sum \nolimits _{i=1}^4\Vert f^{(i)}\Vert _J}{J^4} . \end{aligned}$$

(14)

Let now look at the order in J of each term of the previous inequality. First with the arguments used in (9), there exists $K_1$ constant , $\Gamma ^J_1$ and $\Gamma ^J_2$ of the order of $\frac{1}{J^3}$ such as:

$$\begin{aligned} |\mathbb {E}_{x} \Big [f(X_1,s)-f(x,s)\Big ]-L_{x}f(x,s)|\leqslant |\Gamma _1^{J}|\Vert f ^{(1)}\Vert _J +|\Gamma _2^{J}| \Vert f^{(2)}\Vert _J+\frac{K_{1}}{J^4}. \end{aligned}$$

Then recall that $P_{s,s'}$ is of the order of $\frac{1}{J^2}$ and by the same calculations than in (4567), | $\mathbb {E}_{x}\big [f(X^J_{1},s')-f(x,s')\big ]$| is also of the order of $\frac{1}{J^2}$ so (13) is at most of the order of $\frac{1}{J^4}$.

Finally (14) can be written

$$\begin{aligned} \Vert \sum \limits _{s'\in E_s} \frac{1}{J^2}\Big (J^2P_{s,s'}-\alpha _{s}Q_{s,s'}\Big )\big ( f(x,s')-f(x,s)\big )\Vert _J \end{aligned}$$

and by (11) is at least $o(\frac{1}{J^2})$.

Note, if f is Lipschitz in the second variable, since s is of the order of $\frac{1}{J}$, it is possible to obtain a better order, $o(\frac{1}{J^3})$. Anyway,

$$\begin{aligned} |(S_1-T_1)f(x,s)|\leqslant&\vert \Gamma _1^{J}\vert \Vert f^{(1)} \Vert +\vert \Gamma _2^{J} \vert \Vert f^{(2)}\Vert \\&+\Vert \sum \limits _{s'\in E_s} \frac{1}{J^2}\Big (J^2P_{s,s'}-\alpha _{s}Q_{s,s'}\Big ) \big (f(x,s')-f(x,s)\big )\Vert _{J}\\&+\frac{K'}{J^4}. \end{aligned}$$

$\square$

Note that the Lemma 2 holds even if s is no longer constant. Indeed $L_s$ is not affected by the derivative in x. So we get $\forall j\in \{1,2\}$and $\forall k\leqslant j$, that there exist $c'_j$and $a'_{k,j}\in \mathbb {R}^{+}$ independent of J such that:

$$\begin{aligned} \Vert (T_tf)^{(j)} \Vert _J \le \exp \left( c'_j\frac{t}{J^2} \right) \sum \limits _{k=1}^{j} a'_{k,j}\Vert f^{(j)} \Vert _J \end{aligned}$$

with $c'_j=\sup \nolimits _{x\in [0,1]}|j(j-1)-Js(1-2x)-Jm|$.

We still have $T_t(.,s):C^{2}(I)\rightarrow C^2(I)$,$\forall s$. And then, there exists a continuous function $R_{j}$ at most exponential in time and a linear function of time $k_0$ independent of J verifying:

$$\begin{aligned} \Vert S_nf-T_nf \Vert _{J}&\le \sum _{k=0}^{n-1}(\Vert (S_1-T_1)T_kf \Vert _{J} \\&\le \sum _{k=0}^{n-1}\Big (\vert \Gamma _1^{J}\vert \Vert (T_kf)^{(1)} \Vert _{J} +\vert \Gamma _2^{J} \vert \Vert (T_kf)^{(2)} \Vert _{J}\\&\quad +\Vert \sum \limits _{s'\in E_s} \frac{1}{J^2}\Big (J^2P_{s,s'}-\alpha _{s}Q_{s,s'}\Big )\big ( T_kf(x,s')-T_kf(x,s)\big )\Vert _{J}\\&\quad +O\left( \frac{1}{J^4}\right) \Big ) \\&\le \sum _{j=1}^{2}\vert \Gamma ^{J}_j \vert \sum \limits _{k=1}^{j} a'_{k,j}\Vert f^{(j)} \Vert _{J}\sum _{k=0}^{n-1}\exp \left( c'_j\frac{k}{J^2}\right) +O\left( \frac{1}{J^2}\right) \\&\quad +k_0\max \limits _{s,s' \in E_s}\Big |J^2P_{s,s'}-\alpha _{s}Q_{s,s'}\Big |\Vert f\Vert _J\\&\le \sum _{j=1}^{2}\vert \Gamma ^{J}_j\vert R_{j}(t)J^2 \Vert f^{(j)} \Vert _{J}+k_0\max \limits _{s,s' \in E_s}\Big |J^2P_{s,s'}-\alpha _{s}Q_{s,s'}\Big |\Vert f\Vert _J\\&\quad +O\left( \frac{1}{J^2}\right) \underset{J\rightarrow +\infty }{\longrightarrow }0 \end{aligned}$$

because if J is big enough,

$$\begin{aligned} \sum \limits _{k=1}^{j} a'_{k,j}\sum _{k=0}^{n-1}\exp \left( c'_j\frac{k}{J^2}\right) =\sum \limits _{k=1}^{j} a'_{k,j}\frac{1-\exp (c'_{j}\frac{n}{J^2})}{1-\exp \left( \frac{c'_j}{J^2}\right) }\le J^2R_{j}(t) \end{aligned}$$

and $R_{j}(t)$ is finite and independent of J, because $n=[J^2t]$ is of the order of $J^2$. Finally, it exists a, $b\in \mathbb {R}$ such as $a\big (\exp (bt)-1\big )= \sup \limits _{J\in \mathbb {N}}\max \nolimits _{j\in \{1,2\}}\vert \Gamma ^{J}_j\vert R_{j}(t)J^3$. Then

$$\begin{aligned} \Vert S_nf-T_nf \Vert _{J}&\le \frac{a\big (\exp (bt)-1\big )}{J}\Big (\Vert f^{(1)} \Vert _{J}+\Vert f^{(2)} \Vert _{J}\Big )\\&\quad +k_0\max \limits _{s,s' \in E_s}\Big |J^2P_{s,s'}-\alpha _{s}Q_{s,s'}\Big |\Vert f\Vert _{J} +O\left( \frac{1}{J^2}\right) . \end{aligned}$$

And this concludes the proof. $\square$

5 Random limiting selection as a diffusion process

In this section, we assume that the limiting selection is an homogeneous diffusion process. Once again for simplicity we will suppose that the immigration coefficient is constant. First consider the following stochastic differential equation:

$$\begin{aligned} d\mathscr {S}^J_t&=\frac{1}{J^2}b(\mathscr {S}^J_t)dt+\frac{\sqrt{2}}{J}\sigma (\mathscr {S}^J_t)dB_t\\ \mathscr {S}^J_0&=s \end{aligned}$$

with b and $\sigma$ are both bounded and Lipschitz functions, i.e.: $\forall t\ge 0$,$s,s' \in \mathbb {R}$, it exists $k \ge 0$ such that:

$$\begin{aligned} \vert b(s)-b(s') \vert + \vert \sigma (s)-\sigma (s') \vert \le L \vert s-s' \vert \end{aligned}$$

for some constant L. These assumptions guarantee the existence of strong solutions of $(\mathscr {S}_t)_{t\ge 0}$ and $(\mathscr {S}_t)_{t\ge 0}$ has for generator

$$\begin{aligned} L^J_s=\frac{\sigma ^2(s)}{J^2}\frac{\partial ^2}{\partial s^2}+ \frac{b(s)}{J^2} \frac{\partial }{\partial s}. \end{aligned}$$

Let $\tilde{\mathscr {S}}_t=\mathscr {S}^J_{tJ^2}$, then the process $(\tilde{\mathscr {S}}_t)_{t \ge 0 })$ is independent of J.

$$\begin{aligned} d\tilde{\mathscr {S}}_t=\sqrt{2}\sigma (\tilde{\mathscr {S}}_t)dB_t+b(\tilde{\mathscr {S}}_t)dt,\qquad \tilde{\mathscr {S}}_0=s. \end{aligned}$$

Suppose now that $T\in \mathbb {N}$, We use the standard Euler discretization and consider $(U^J_n)_{n<J^2T}$ defined by the relation:

$$\begin{aligned} U^J_{k+1}=U^J_{k}+\frac{1}{J^2}b(U^J_{k})+\sqrt{2}\sigma (U^J_{k})(B^J_{k+1}-B^J_{k}) \end{aligned}$$

where the quantity $(B^J_{k+1}-B^J_{k})_{k\le J^2T}$ are i.i.d and follow a $\mathscr {N} (0,\frac{1}{J^2})$.

It is of course possible to use another discretization to approach $\mathscr {S}^J_{[t]}$ and the following method will still hold. There is however a small issue: in the model described in first part, for rescaling argument, the selection parameters must be in $]-1,\infty [$. Our Markov process $(\mathscr {S}^J_t)_{t\ge 0}$ lives in $\mathbb {R}$.

It is thus necessary to introduce the function $h: \mathbb {R} \longrightarrow E_s$ where $E_s$ is a closed bounded interval included in $]-1+\varepsilon , \infty [$ for some $\varepsilon >0$.

We assume h is in $C^2$ and is of the order of $\frac{1}{J}$. We consider now $h( (\mathscr {S}_t))_{t\ge 0}$ for the selection parameter.

Let denote in this section, for $f:I_J\times \mathbb {R}\rightarrow \mathbb {R}$, $\Vert f \Vert _J=\sup \limits _{I_J\times \mathbb {R}}|f(x,s)|$.

Note that to have a non trivial stochastic part in our final equation, we need as in the first section that h is of the order of $\frac{1}{J}$. Many choices are possible for h and will depend on modelisation issue.

Let us give back the definition of our Moran process in this context.

$$\begin{aligned}&P_{x+}=(1-x)\left( mp+(1-m)\frac{x(1+h(s))}{1+h(s)x} \right) \\&P_{x-}=x\left( m(1-p)+(1-m) \left( 1-\frac{x(1+h(s))}{1+h(s)x}\right) \right) \\ \end{aligned}$$

Its first moments are given by, still denoting $\Delta =J^{-1}$,

$$\begin{aligned} \mathbb {E}_{x} \left[ X^J_{n+1}-x |X^J_n=x,U^J_n=s\right] =\Delta \Big [m(p-x)+\frac{(1-m)h(s)x(1-x)}{1+h(s)x}\Big ]\\ Var\left( X^J_{n+1}-x|X^J_n=x,U^J_n=s\right) = \Delta ^2\Big [\frac{(1-m)h(s)x(1-x)(1-2x)}{1+h(s)x}\\ +mp(1-2x)+x -\left( m(p-x)+\frac{(1-m)h(s)x(1-x)}{1+h(s)x}\right) ^2 \Big ]. \end{aligned}$$

As in the previous case we use the process $\left( Y^J_{t}\right) _{t \ge 0 }$ having the following generator to approach the Moran process when J tends to infinity:

$$\begin{aligned} L^J_xf(x,s)=\frac{x(1-x)}{J^2}\frac{\partial ^2f}{\partial x^2}(x,s)+\frac{1}{J}[m(p-x)+h(s)x(1-x)]\frac{\partial f}{\partial x}(x,s) \end{aligned}$$

So our aim is to give an upper bound for the error done when

$$\begin{aligned} \left( X^J_n,U^J_n\right) \underset{J \rightarrow \infty }{\longrightarrow }\left( Y^J_n,\mathscr {S}^J_n \right) . \end{aligned}$$

Let denote by H the generator of the two dimensional process $\left( Y^J_t,\mathscr {S}^J_t \right)$.

$$\begin{aligned} H= & {} L^J_x+L^J_s=\frac{x(1-x)}{J^2}\frac{\partial ^2}{\partial x^2}+\frac{1}{J^2}\Big [h(s)x(1-x)+m(p-x)\Big ]\frac{\partial }{\partial x}\\&+\frac{\sigma ^2(s)}{J^2}\frac{\partial ^2}{\partial s^2}+\frac{b(s)}{J^2}\frac{\partial }{\partial s} \end{aligned}$$

Let now state the main result of this section:

Theorem 3

Let f be in $C^4$ then there exists a, $b \in \mathbb {R^+}$ such that

$$\begin{aligned} \Vert \mathbb {E}_{x,s}\left( f( X^J_{[tJ^2]},Z^J_{[tJ^2]}) - f( Y^J_{[tJ^2]},S^J_{[tJ^2]}) \right) \Vert _J \le&\frac{a(e^{bt}-1) }{J}(\Vert \nabla f\Vert _J+\Vert \mathrm{Hess} f\Vert _J)\\&+ \frac{a(e^{bt}-1)}{J^2}\big (\Vert f^{(3)}\Vert _J+\Vert f^{(4)}\Vert _J\big ). \end{aligned}$$

Proof

Let $P_n$ be the operator defined on the space of bounded functions on E by:

$$\begin{aligned} \left( P_nf \right) (x,s)=\mathbb {E}_{x,s}\Big [f\left( X^J_n,U^J_n \right) \Big ] \end{aligned}$$

It is of course a semigroup so that $P_{n+m}=P_nP_m ,\forall m,n \in \mathbb {N}$. In parallel, let $(T_t)_{t \ge 0 }$ be defined on the space of bounded continuous functions by :

$$\begin{aligned} \left( T_tf \right) (x,s)=\mathbb {E}_{x,s} \Big [ f \left( Y^J_t,\mathscr {S}^J_t \right) \Big ] \end{aligned}$$

also verifying,$T_{t+s}=T_sT_t, \forall s\ge 0,t \ge 0.$ The starting point is as in the first part of (1),

$$\begin{aligned} \vert P_nf(x,s)-T_nf(x,s) \vert \le \sum _{k=0}^{n-1} \Vert \left( P_1-T_1 \right) T_kf \Vert _J. \end{aligned}$$

We now focus on the quantity $\Vert \left( P_1-T_1 \right) T_kf \Vert _J$, the following lemma gives a upper bound of the quantity $\Vert \left( P_1-T_1 \right) f \Vert _J$ for f in $C^4$.

Lemma 4

Let f be in $C^4$ it exists $\gamma ^J_{1}$ ,and $\gamma _{2}^J$ such as :

$$\begin{aligned} \Vert (P_1f)(x,s)-(T_1f)(x,s) \Vert _J =&\gamma ^J_{1} \Vert \frac{\partial }{\partial x} f(x,s) \Vert _J + \gamma ^J_{2} \Vert \frac{\partial ^2}{\partial x^2} f(x,s) \Vert _J +O\left( \frac{1}{J^4}\right) \end{aligned}$$

where $\gamma ^J_1$ and $\gamma ^J_2$ are of order $\frac{1}{J^3}$.

Proof

We will use the same methodology than before. First the Taylor expansion (in space) of $P_1$ gives:

$$\begin{aligned} (P_1f)(x,s)=&f(x,s)+\mathbb {E}_{x,s}\Big [X^J_1-x \Big ]\frac{\partial }{\partial x}f(x,s)+\mathbb {E}_{x,s}\Big [U^J_1-s \Big ]\frac{\partial }{\partial s}f(x,s)\\&+\frac{1}{2}\mathbb {E}_{x,s}\Big [(X^J_1-x )^2 \Big ]\frac{\partial ^2}{\partial x^2}f(x,s)+\frac{1}{2}\mathbb {E}_{x,s}\Big [(U^J_1-s)^2 \Big ]\frac{\partial ^2}{\partial s^2}f(x,s)\\&+2\mathbb {E}_{x,s}\Big [(X^J_1-x)(U^J_1-s) \Big ]\frac{\partial ^2}{\partial x \partial s}f(x,s)+O\left( \frac{1}{J^4}\right) . \end{aligned}$$

Indeed we have the quantities:

$$\begin{aligned}&\mathbb {E}_{x,s}\Big [X^J_1-x \Big ]=\frac{1}{J}\Big [m(p-x)+\frac{(1-m)h(s)x(1-x)}{1+h(s)x}\Big ]\\&\mathbb {E}_{x,s}\Big [(X^J_1-x)^2 \Big ]=\frac{1}{J^2}\Big [mp(1-2x)+x+\frac{(1-m)x(1+h(s))(1-2x)}{1+h(s)x}\Big ]\\&\mathbb {E}_{x,s}\Big [U^J_1-s \Big ]=\frac{b(s)}{J^2}\\&\mathbb {E}_{x,s}\Big [(U^J_1-s)^2 \Big ]=\frac{b^2(s)}{J^4}+\frac{2\sigma ^2(s)}{J^2}=\frac{2\sigma ^2(s)}{J^2}+O\Big (\frac{1}{J^4}\Big )\\&\mathbb {E}_{x,s}\Big [(X^J_1-x)(U^J_1-s) \Big ]=\mathbb {E}_{x,s}\Big [X^J_1-x \Big ]\mathbb {E}_{x,s}\Big [U^J_1-s \Big ]\\&\qquad = \frac{b(s)}{J^3}\Big [m(p-x)+\frac{(1-m)h(s)x(1-x)}{1+h(s)x}\Big ]=O\Big (\frac{1}{J^4}\Big )\\&\mathbb {E}_{x,s}\Big [(X^J_1-x)^3 \Big ]=O\Big (\frac{1}{J^4}\Big ),\qquad \qquad \mathbb {E}_{x,s}\Big [(U^J_1-s)^3 \Big ]=O\Big (\frac{1}{J^4}\Big ). \end{aligned}$$

And the Taylor expansion of $T_1$ in times gives:

$$\begin{aligned} \left( T_1f \right) (x,s)=f(x,s)+ L^J_xf(x,s)+L^J_sf(x,s)+O\left( \frac{1}{J^4}\right) . \end{aligned}$$

Indeed it is easy to see that $H^2$ is $O(\frac{1}{J^4})$. We now evaluate the difference

$$\begin{aligned} (P_1-T_1)f(x,s)=&\mathbb {E}_{x,s}\Big [X^J_1-x \Big ]\frac{\partial }{\partial x}f(x,s)+\mathbb {E}_{x,s}\Big [U^J_1-s \Big ]\frac{\partial }{\partial s}f(x,s)\\&+\frac{1}{2}\mathbb {E}_{x,s}\Big [(X^J_1-x )^2 \Big ]\frac{\partial ^2}{\partial x^2}f(x,s)\\&+\frac{1}{2}\mathbb {E}_{x,s}\Big [(U^J_1-s)^2 \Big ]\frac{\partial ^2}{\partial s^2}f(x,s)\\&- L^J_xf(x,s)-L^J_sf(x,s) +O\Big (\frac{1}{J^4}\Big ). \end{aligned}$$

Finally,

$$\begin{aligned}&(P_1-T_1)f(x,s)\\&\quad =-\frac{1}{J}\Big [\frac{h(s)x(1-x)}{1+h(s)x}(m+h(s)x)\Big ]\frac{\partial }{\partial x}f(x,s)\\&\quad +\frac{h(s)x^2+x(1-2x)(h(s)-m-mh(s))-2x(1-x)h(s)}{1+h(s)x}\frac{\partial ^2}{\partial x^2}f(x,s)\\&\qquad +\frac{b^2(s)}{J^4}\frac{\partial ^2}{\partial s^2}f(x,s)+O\Big (\frac{1}{J^4}\Big ). \end{aligned}$$

Let us conclude by taking the norm to get

$$\begin{aligned}&\gamma ^J_{1}=\sup \limits _{(x,s)\in E_s\times [0,1]}\frac{1}{J}\Big |\frac{h(s)x(1-x)}{1+h(s)x}(m+h(s)x)\Big |\\&\gamma ^J_{2}=\sup \limits _{(x,s)\in E_s\times [0,1]}\frac{1}{2J^2}\Big |mp(1-2x)+ \frac{(1-m)(1+h(s))x(1-2x)}{1+h(s)x}-x(1-2x) \Big | \end{aligned}$$

so that we obtain the result. $\square$

Then (11) still holds for this case as the Proof of 1 is exactly the same, so the end follows as in the first part. $\square$

Appendis: Discrete Wright–Fisher model and its approximating diffusion

Let consider the Wright–Fisher discrete model with selection and immigration. The population still consists of two species, immigration and selection are still the same. But the Markovian process $X^n_J$ evolves according to the following probability:

$$\begin{aligned} \mathbb {P}\left( X^J_{n+1}=\frac{k}{J}|X^J_{n}=x\right) = \left( \begin{array}{c} J\\ k\end{array}\right) P_x^k(1-P_x)^{J-k} \end{aligned}$$

with $P_x=mp+(1-m)\frac{(1+s)x}{1+sx}$.

At each step, all the population is renewed, so this process runs J times faster than the Moran process. And we usually, in the case of weak selection and immigration, it is usual to use the diffusion $\{Y_t\}_{t>0}$ defined by the following generator to approach this discrete model, when the population goes to infinity.

$$\begin{aligned} L=\frac{1}{2J}x(1-x)\frac{{\partial }^2}{\partial {x}^2}+ \left( sx(1-x)+m(p-x)\right) \frac{\partial }{\partial {x}} \end{aligned}$$

Theorem 4

Let f be in $C^5(I)$ then there exist a, $b\in \mathbb {R}^+$, depending on $m'$ and $s'$ (but not on f), and a constant K which satisfy when J goes to infinity:

$$\begin{aligned} \Vert \mathbb {E}_x \Big [f(X_{n}^{J} )\Big ]-\mathbb {E}_x \Big [f(Y_{n}^{J} ) \Big ] \Vert _J \le&a(e^{bt}-1)\left( \sum \limits _{i=1}^3\frac{\Vert f^{(i)\Vert _J} }{J}+K\frac{\sum \limits _{i=1}^5\Vert f^{(i)} \Vert _{J}}{J^2}\right) . \end{aligned}$$

Proof

Even if the structure of the proof is the same as for the discrete Moran model, however the difference of scale (in $\frac{1}{J}$ now) causes some small differences. Mainly, the calculation of the $\{\gamma _j\}_{j \in \{1,2,3,4\}}$ is a bit different. Note that we need to have $f \in C^5$ in the present theorem, which is stronger than for the Moran process. The main explanation comes from the calculation of $E[(X_{n+1}^J-x)^k|X_{n}^J=x]$, for which for the Wright–Fisher discrete process it is no longer of the order of $\frac{1}{J^k}$. Let us give some details.

First consider the moments $\{ E[\big (X_{n+1}^J-x\big )^k|X^J_n=x]\}_{k\leqslant 5}$:

$$\begin{aligned} E[X_{n+1}^J-x|X^J_n=x]=&m(p-x)+\frac{sx(1-x)}{1+sx}\\ E[\big (X_{n+1}^J-x\big )^2|X^J_n=x]=&\frac{1}{J}x(1-x)+\frac{1}{J}\left( m(p-x)+\frac{sx(1-x)}{1+sx}\right) \\&+\left( m(p-x)+\frac{sx(1-x)}{1+sx}\right) ^2+O\Big (\frac{1}{J^3}\Big )\\ E[\big (X_{n+1}^J-x\big )^3|X^J_n=x]=&x(x-1)(2x-1)\frac{1}{J^2}\\&-\frac{1}{J}3x(x-1)\big (m(p-x)+sx(1-x)\big )+O\Big (\frac{1}{J^3}\Big )\\ E[\big (X_{n+1}^J-x\big )^4|X^J_n=x]=&\frac{1}{J^2}3x^2(1-x)^2+O\Big (\frac{1}{J^3}\Big )\\ E[\big (X_{n+1}^J-x\big )^5|X^J_n=x]=&O\Big (\frac{1}{J^3}\Big ). \end{aligned}$$

To get a quantity of the order of $\frac{1}{J^3}$ we need to go to the fifth moment of $X_{n+1}^J-x$, so in the Taylor development we need to have f in $C^5$. Then,

$$\begin{aligned} L^{1}f(x)=&\;\frac{x(1-x)}{2J}f^{(2)}(x)+sx(1-x)+m(p-x)f^{(1)}(x)\\ L^{2}f(x)=&\;\frac{(x(1-x))^2}{4J^2}f^{(4)}(x)\\&+ \Big [ \frac{2(1-2x)x(1-x)}{4J^2}+\frac{2x(1-x)(sx(1-x)+m(p-x)}{2J}\Big ]f^{(3)}(x)\\&+ \Big [ \frac{-2x(1-x)}{4J^2} \\&+\frac{2x(1-x)(s(1-2x)-m)+(1-2x)(sx(1-x)+m(p-x))}{2J}\\&+\frac{(sx(1-x)+m(p-x))^2}{4J^2}\Big ]f^{(2)}(x) \\&+ \Big [\frac{-2sx(1-x)}{2J}\\&+(s(1-2x)-m)(sx(1-x)+m(p-x))\Big ]f^{(1)}(x)\\ L^{3}f(x)=&\;O\Big (\frac{1}{J^3}\Big ). \end{aligned}$$

We are now able to give the expression of the $\{\gamma _j\}_{j \in \{1,2,3,4\}}$, as in the Lemma 1.

Lemma 5

It exists bounded functions of x, $\{\gamma _j\}_{j \in \{1,2,3\}}$ such as when J is big enough,

$$\begin{aligned} \Vert (S_1-T_1)f\Vert _{J}\le \vert \gamma _1^{J}\vert \Vert f^{(1)} \Vert _{J} +\vert \gamma _2^{J}\vert \Vert f^{(2)} \Vert _{J}+\vert \gamma _3^{J}\vert \Vert f^{(3)} \Vert _{J}+\frac{K_{1}}{J^3} \end{aligned}$$

where for $i=1,\ldots ,3$, $\vert \gamma _i^{J}\vert$ is of the order of $\frac{1}{J^2}$.

Proof

The proof of this lemma is exactly the same as in lemma 1. Just the calculations are a little bit more tedious:

$$\begin{aligned}&\gamma _1^J=\frac{-sx(1-x)}{J} +(s(1-2x)-m)(sx(1-x)+m(p-x))\\&\gamma _2^J= \frac{-x(1-x)}{4J^2} +\frac{xs(6x^2-7x+1)+m(4x^2-2xp-x-p)}{4J}+O\Big (\frac{1}{J^3}\Big )\\&\gamma _3^J=\frac{x(x-1)(2x-1)}{12J^2}+O\Big (\frac{1}{J^3}\Big )\\&\gamma _4^J=O\Big (\frac{1}{J^3}\Big ) \end{aligned}$$

$\square$

The end of the proof follow exactly the same pattern. $\square$

So The Wright–Fisher dynamics requires more tricky calculations than the discrete Moran model but the spirit of the proof is the same. All the methods studied in this paper can be adapted in order to treat the Wright–Fisher model.