Stochastic neural field model: multiple firing events and correlations

Abstract

This paper studies a nonlinear dynamical phenomenon called the multiple firing event (MFE) in a spatially heterogeneous stochastic neural field model, which is extended from that in our previous paper (Li et al. in J Math Biol 78:83–115, 2018). MFEs are a partially synchronized spiking barrages that are believed to be responsible for the Gamma oscillation. Rigorous results about the stochastic stability and the law of large numbers are proved, which further imply the well-definedness and computability of many quantities related to MFEs. Then we devote to study spatial and temporal properties of MFEs. Our key finding is that MFEs are spatially correlated but the spatial correlation decays quickly. Detailed mathematical justifications are made based on our qualitative models that aim to demonstrate the mechanism of MFEs.

1 Introduction

The dynamics of a single neuron is relatively simple and has been well studied for decades. Many models such as the Hodgkin-Huxley model can well describe the biophysical process of a neuronal spike. However, a mathematical study of interactions of inhibitory and excitatory neuron populations is much harder, as they can produce very rich spiking patterns ranging from independent spiking activities to full synchronizations like the PING mechanism (Börgers et al. 2005; Börgers and Kopell 2003, 2005). Among numerous spiking patterns generated by different mechanisms, one nonlinear emergent phenomenon called the multiple firing event (MFE) is particularly interesting. In an MFE, a large amount of local neurons, but not the entire local population, fire a spike during a relatively small time window and form a rapid spiking barrage. This spiking activity lies between two extremes (homogeneity and synchrony), and have been reported in many experimental studies about different neuronal networks in the real brain (Beggs and Plenz 2003; Churchland et al. 2010; Mazzoni et al. 2007; Petermann et al. 2009; Plenz et al. 2011; Samonds et al. 2006; Shew et al. 2011; Yu and Ferster 2010; Yu et al. 2011). It is also believed that such semi-synchronized burst is responsible for the Gamma oscillation in the brain (Börgers et al. 2005; Henrie and Shapley 2005; Rangan and Young 2013a, b). Early mathematical studies of MFEs can be found in Chariker and Young (2015), Newhall et al. (2010), Rangan and Young (2013a), Rangan and Young (2013b), Zhang et al. (2014a) for various different integrate-and-fire models.

The purpose of this paper is to investigate several spatial and temporal properties of MFEs in spatially heterogeneous neuron populations. This has not been properly addressed by pioneer studies (Chariker and Young 2015; Li et al. 2018; Newhall et al. 2010; Rangan and Young 2013b; Zhang et al. 2014a). To do so, we need a suitable neural field model that can both produce desired MFEs and make analytical studies feasible. Neuronal models with plenty of anatomical and physiological details (ionic channels, dendritic tree, spatial structure of axon, synapse .etc) involved are usually too complex to study, especially when applying to a large-scale network. On the other end of the spectrum, mean field models such as Wilson–Cowan model (1972; 1973) and various population density models (Cai et al. 2006, 2004; Haskell et al. 2001) are often to simple to reflect many emergent spiking dynamics including MFEs.

The first part of this paper introduces a neural field model that aims to strike a balance between biological accuracy and mathematical/computational tractability. We include some spatial structures to the stochastic model studied in our earlier paper (Li et al. 2018). More precisely, we consider the coupling of finitely many local neuron populations, each of which is described by a stochastic model studied in Li et al. (2018). This is a biologically plausible extension because the real cerebral cortex consists of numerous relatively homogeneous local structures, while the neuronal activities in different local structures can be very different. Take the visual cortex as an example again. The pinwheel formation makes responses to stimulus orientation very different in orientation columns with different orientation preferences, even if they are spatially close to each other (Hubel 1995; Kaschube et al. 2010). Different from many detailed spiking neuron models, some mathematical properties of this neural field model can be rigorously proved. We first follow the approach as in Li et al. (2018) to prove the existence and uniqueness of an invariant probability measure, and the exponential speed of convergence to this invariant measure. Then we prove the law of large numbers of a class of sample-path dependent observables by constructing a martingale difference sequence. The well-definedness and computability of many quantities related to the spike count correlation follows from the law of large numbers.

Then our study focuses on multiple firing events (MFEs) produced by our stochastic neural field model. As introduced before, an MFE is a partially synchronous spike barrage that involves a proportion of a local neuron population. The MFE is an important network feature and plays a significant role in the network’s dynamics. For example, in Li et al. (2018), we have observed that strong MFEs can significantly divert a network model from its mean field approximation. The neural field model introduced in this paper is spatially heterogeneous. It can produce rich spike patterns, including MFEs with different degrees of synchrony within a local population, and MFEs with various spatial correlations between different local populations. In addition, our network model is fairly mathematically tractable, which makes a deeper study of MFEs possible.

The first study on MFEs attempts to reveal its mechanism. Heuristically, an MFE is caused by recurrent excitations that are terminated by the later onset of network inhibitions. Due to the significant complexity of working on a network model directly, we propose two qualitative models that help us to understand the properties of MFEs. The first qualitative model is an SIR disease model that describes the average trend of neuronal activities during an MFE. The pending postsynaptic kicks are like infected patients that can “infect” other neurons and make them fire a spike. Once a neuron spikes, it jumps to the refractory state and is “immuned” from further “infections”. With this SIR model, we can prove that the slower onset of inhibitory spikes is always responsible for a stronger synchronization. Then, to depict a caricature of stochastic properties of MFEs, we construct a Galton–Waston branching process that terminates at a random time. The branching process corresponds to the recurrent excitation, while the random termination time approximates the onset of the network inhibition. This model well captures the diversity of sizes of MFEs.

We then carry out a numerical study on temporal and spatial properties of MFEs. The numerical study is done by simulating a number of networks with different magnitudes of local and long distance synchronizations. The correlation of spike count among different local populations are estimated by Monte Carlo simulations. Our numerical simulation results show that MFEs in nearest-neighbor local populations are highly correlated. However, this correlation decays quickly with increasing distance between two local populations. No significant correlation between MFEs is observed if two local populations are 5–10 “blocks” away. This is consistent with the experimental observations that the Gamma rhythm is very local in many scenarios (Goddard et al. 2012; Lee et al. 2003; Menon et al. 1996). Of course this study does not exclude the possibility that a neuronal network with a more heterogeneous architecture or multiple types of inhibitory neurons could steadily generate smaller MFEs with less volatility and stronger spatial correlation. But we believe our study can shed some light to the population spiking dynamics of neuronal networks that include large and relatively homogeneous local populations, such as the visual cortex.

These numerical observations can be analytically justified by the qualitative models of MFEs mentioned above. The SIR model is used to explain the mechanism of spatial correlations of MFEs. We find that an MFE is very likely to induce another MFE in a neighboring local population, although the initial profile may be fairly different. The Galton–Waston branching process helps us to explain the possible mechanism of the spatial correlation decay. One salient feature of MFEs is its diversity. When starting from the same profile, the spike count of an MFE can have very high volatility, measured by the coefficient of variation. This high coefficient of variation is justified analytically by studying a Galton–Waston branching process. The volatility significantly decreases when the MFE is so large that it is close to a synchronous spike volley, which means the branching process has used up all neurons and has to stop. We believe that this diversity at least partially contributes to the quick decay of spatial correlations in our model. This is consistent with our numerical simulation result, in which the most synchronous network has the slowest decay of the spatial correlation.

We remark that this paper is not a trivial extension of Li et al. (2018). The model studied in this paper is a spatially heterogeneous version of that proposed in Li et al. (2018). And we need to include the stochastic stability result, which follows a similar approach as in Li et al. (2018), for the sake of completeness of the paper. However, the main focus of these two papers are very different. Paper Li et al. (2018) mainly compares the network model and its several mean-field approximations. MFEs (or correlated spiking activities in general) are observed in Li et al. (2018) but have not been fully addressed. In this paper, we focus on properties, statistics, and mechanism related to MFEs. This has not been done in either (Li et al. 2018) or other pioneer work (Chariker and Young 2015; Rangan and Young 2013a, b). In addition, the law of large numbers of sample-path dependent observables proved in Sect. 3 is also new.

Finally, we would like to refer Newhall et al. (2010), Zhang et al. (2014a), Zhang et al. (2014b)) for some earlier attempts of studying the mechanism of MFEs. They investigated a class of simple and spatially homogeneous integrate-and-fire model that can produce MFEs, and proposed a coarse-grained model reduction. In their model, spikes take effects instantaneously without any delay. Hence MFE can be approximated by a map from the pre-event voltage distribution to the post-event voltage distribution. Later, it has been discovered in Chariker and Young (2015), Li et al. (2018) that the synapse delay actually plays a significant role in the excitatory-inhibitory competition and should not be neglected. Also, none of those earlier work considers spatial factors. Our study is further developed from these important earlier investigations conducted by Young, Rangan and their collaborators. Both the synapse delay and the spatial factor are incorporated into our stochastic neural field model. Hence our study can cover more detail and allow more rigorous analysis than these pioneer works.

The organization of this paper is as follows. Section 1 is the introduction. We provide the mathematical description of the neural field model in Sect. 2. Section 3 is devoted to the proof of the stochastic stability and the law of large numbers, which gives the well-definedness of observables studied in the later part of the paper. The reader who is not interested in technical details can skip this section. Then we provide five network examples with distinct features in Sect. 4 for later investigations. Two qualitative models, the SIR model and the branching process model of MFE, are proposed and studied in Sect. 5. Section 6 is devoted to the spatial correlation. We demonstrate both phenomena and mechanisms of spatial correlations of MFEs in different local populations. Section 7 is the conclusion.

2 Stochastic model of many interacting neural populations

We consider a stochastic model that describes the interaction of many local populations in the cerebral cortex. Each local population consists of hundreds of interacting excitatory and inhibitory neurons. The setting of this model is quite generic, but it aims to describe some of the spiking activities of realistic brain parts. In particular, one can treat a local population as an orientation column in the primary visual cortex. We will only prescribe the rules of external inputs and interactions between neurons. All spatial and temporal correlated spiking activities in this model are emergent from interactions of neurons.

2.1 Model description

We consider an ${\mathbf {M}} \times {\mathbf {N}}$ array of local populations of neurons, each of which are homogeneous and densely connected by local circuitries. In addition, neurons in nearest neighbor of local populations are connected. Each local population consists of $N_{E}$ excitatory neurons and $N_{I}$ inhibitory neurons. We have the following assumptions in order to describe activities of this population by a Markov process. The dynamics in each local population follows the rule as given in Li et al. (2018). The interaction between local populations only occurs between nearest neighbors.

• The membrane potential of each neuron can only take finitely many discrete values.

• The external inputs to neurons are in the form of independent Poisson processes. The rate of Poisson kicks to all neurons of the same type in each local population is a constant.

• A neuron spikes when its membrane potential reaches a given threshold. After a spike, a neuron stays at a refractory state for an exponentially distributed amount of time.

• When an excitatory (resp. inhibitory) spike occurs at a local population, a set of postsynaptic neurons from this local population and its nearest neighbor local populations are randomly chosen. After an exponenitally distributed random time, the membrane potential of each chosen postsynaptic neuron goes up (resp. down).

More precisely, we consider ${\mathbf {M}} \times {\mathbf {N}}$ local populations $\{ L_{m,n}\}$ with $m = 1 , \ldots , {\mathbf {M}}$ and $n = 1, \ldots , {\mathbf {N}}$. $L_{m,n }$ and $L_{m', n'}$ are considered to be nearest neighbors if and only if $| n - n'| = 1$, $m = m'$ or $|m - m'| = 1$, $n = n'$. For each (m, n), denote the set of indices of its nearest neighbor local populations by ${\mathcal {N}}(m,n)$. Each population $L_{m,n}$ consists of $N_{E}$ excitatory neurons, labeled as

$$\begin{aligned} (m, n, 1), (m, n, 2), \ldots , (m, n, N_{E}) \end{aligned}$$

and $N_{I}$ inhibitory neurons, labeled as

$$\begin{aligned} (m, n, N_{E}+1), (m, n, N_{E} + 2), \ldots , (m, n, N_{E} + N_{I}). \end{aligned}$$

In other words, each neuron has a unique label (m, n, k). The membrane potential of neuron (m, n, k), denoted $V_{(m, n, k)}$, takes value in a finite set

$$\begin{aligned} \Gamma := \{ - \Sigma _{r}, - \Sigma _{r} + 1, \ldots , -1, 0, 1, 2, \ldots , \Sigma \} \cup \{{\mathcal {R}} \} , \end{aligned}$$

where $\Sigma$ and $\Sigma _{r}$ are two integers for the threshold potential and the inhibitory reversal potential, respectively. When $V_{(m, n, k)}$ reaches $\Sigma$, the neuron fires a spike and resets its membrane potential to ${\mathcal {R}}$. After an exponentially distributed amount of time with mean $\tau _{R}$, $V_{(m, n, k)}$ leaves ${\mathcal {R}}$ and jumps to 0.

We first describe the external current that models the input from other parts of the brain or the sensory input. As in Li et al. (2018), the external current received by a neuron is modeled by a homogeneous Poisson process. The rate of this Poisson process is identical for the same type of neurons in the same local population. Neurons in different local populations receive different external inputs, which makes this model spatially heterogeneous. More precisely, we assume the rate of such Poisson kick to an excitatory (resp. inhibitory) neuron in local population $L_{m,n}$ to be $\lambda _{m,n}^{E}$ (resp. $\lambda _{m,n}^{I}$). When a kick is received by a neuron (m, n, k) that is not at state ${\mathcal {R}}$, $V_{(m,n,k)}$ jumps up by 1 immediately. If it reaches $\Sigma$, a spike is fired. Neurons at state ${\mathcal {R}}$ do not respond to external kicks.

The rule of interactions among neurons is the following. We assume that a postsynaptic kick from an E (resp. I) neuron takes effect after an exponentially distributed amount of time with mean $\tau _{E}$ (resp. $\tau _{I}$). To model this delay effect, we describe the state of neuron (m, n, k) by a triplet $(V_{(m,n,k)}, H^{E}_{(m,n,k)}, H^{I}_{(m,n,k)})$, where $H^{E}_{(m, n, k)}$ (resp. $H^{I}_{(m,n,k)}$) denotes the number of received E (resp. I) postsynaptic kicks that has not yet taken effect. Further, we assume that the delay of postsynaptic kicks are independent. Therefore, two exponential clocks corresponding to excitatory and inhibitory kicks are associated to each neuron, with rates $H^{E}_{(m, n, k)} \tau _{E}^{-1}$ and $H^{I}_{(m, n, k)} \tau _{I}^{-1}$ respectively. When the clock corresponding to excitatory (resp. inhibitory) kicks rings, an excitatory (resp. inhibitory) kick takes effect according to the rules described in the following paragraph.

Let $Q, Q'\in \{E, I\}$. When a postsynaptic kick from a neuron of type Q takes effect at a neuron of type $Q'$ after the delay time as described above, the membrane potential of the postsynaptic neuron, say neuron (m, n, k), jumps instantaneously by a constant $S_{Q', Q}$ if $V_{(m,n,k)} \ne {\mathcal {R}}$. No change happens if $V_{(m,n,k)} = {\mathcal {R}}$. If after the jump we have $V_{(m,n,k)} \ge \Sigma$, neuron (m, n, k) fires a spike and jumps to state ${\mathcal {R}}$. Same as in Li et al. (2018), if constant $S_{Q', Q}$ is not an integer, we let u be a Bernoulli random variable with ${\mathbb {P}}[u = 1] = S_{Q', Q} - \left\lfloor S_{Q', Q} \right\rfloor$ that is independent of all other random variables in the model. Then the magnitude of the postsynaptic jump is set to be the random number $\left\lfloor S_{Q', Q} \right\rfloor + u$.

It remains to describe the connectivity within and between local populations. We assume that each local population is densely connected and homogeneous, while different local populations are heterogeneous in a way that the external currents are different. For example, each local population can be thought as an orientation column in the primary visual cortex. Hence nearest-neighbor populations receive very different external drives due to their different orientational preferences. Same as in Li et al. (2018), the connectivity in our model is random and time-dependent. For $Q, Q' \in \{E, I\}$, we choose two parameters $P_{Q, Q'}, \rho _{Q, Q'} \in [0, 1]$ representing the local and external connectivity, respectively. When a neuron of type $Q'$ in a local population $L_{m,n}$ fires a spike, every neuron of type Q in the local population $L_{m,n}$ is postsynaptic with probability $P_{Q, Q'}$, while every neuron of type Q in the nearest-neighbor populations $L_{m', n'}$ receives this postsynaptic kick with probability $\rho _{Q, Q'}$. In other words, neurons of the same type in the same local population are assumed to be exchangeable.

Comparing with the stochastic integrate-and-fire model introduced in Li et al. (2018), one simplification we made is the independence of the strength of postsynaptic kicks on membrane potential. In the real brain, it is known that the reverse potential of inhibitory neurons are much closer to the reset potential than its excitatory counterpart. Hence the inhibition is stronger to neurons with higher membrane potential. Theoretically this should enhance MFEs, because inhibitory kicks tend to pack non-firing neurons closer, which makes the next MFE larger. But our simulation found that this is not the primary factor comparing with the very sensitive dependence of MFE characteristics on synapse delay times $\tau _{E}$ and $\tau _{I}$. We drop the voltage-dependency on postsynaptic kicks because this can significantly simplify two qualitative models proposed in Sect. 5 that aim to investigate the mechanism of MFEs.

2.2 Common model parameters for simulations

Although our theoretical results are valid for all parameters, in numerical simulations we will stick to the following set of parameters in order to be consistent with Li et al. (2018). Throughout this paper, we assume that $N_{E} = 300$, $N_{I} = 100$ for the size of local populations, $\Sigma = 100$, $\Sigma _{r} = 66$ for thresholds, $P_{EE} = 0.15$, $P_{IE} = P_{EI} = 0.5$ and $P_{II} = 0.4$ for local connectivity. The connectivity to nearest neighbors are assumed to be proportional to the corresponding local connectivity. We set two parameters $\text{ ratio }_{E}$ and $\text{ ratio }_{I}$ and let $\rho _{QE} = \text{ ratio }_{E} P_{QE}$, $\rho _{QI} = \text{ ratio }_{I} P_{QI}$ for $Q = I, E$. Further, we assume that $\text{ ratio }_{I} = 0.6 \text{ ratio }_{E}$ as inhibitory neurons are known to be more “local”. Strengths of postsynaptic kicks are assumed to be $S_{EE} = 5$, $S_{IE} = 2$, $S_{EI} = 3$, and $S_{II} = 3.5$. The length of the refractory period is $\tau _{{\mathcal {R}}} = 4 \text{ ms }$. Since AMPA synapses act faster than GABA synapses, in general $\tau _{E}$ is assumed to be faster than $\tau _{I}$. Values of $\tau _{E}$ and $\tau _{I}$ are two changing parameters that are used to control the degree of synchrony of MFEs produced by the network. External drive rates $\lambda _{m,n}^{E}$ and $\lambda _{m,n}^{I}$ are determined when describing examples with different spatial structures.

3 Stochastic stability and law of large numbers

The aim of this section is to prove several probabilistic results of the model presented in Sect. 2. Readers who are not interested in theoretical results can skip this section and jump to Sect. 4. The stochastic stability theorem (Theorem 3.1) roughly follows the same approach in our previous paper (Li et al. 2018). We include this result for the sake of completeness of this paper. The law of large numbers for sample-path dependent observables (Theorem 3.3) is new. As a corollary of law of large numbers, we have well-defined and computable local and global firing rates, and the spike count correlation between local populations.

3.1 Stochastic stability

The neural field model described above generates a Markov jump process $\Phi _{t}$ on a countable state space

$$\begin{aligned} {\mathbf {X}} = ( \Gamma \times {\mathbb {Z}}_{+} \times {\mathbb {Z}}_{+})^{{\mathbf {M}}\times {\mathbf {N}} \times (N_{E} + N_{I})}. \end{aligned}$$

By the stochastic stability, we mean the existence, uniqueness, and ergodicity of the invariant measure for $\Phi _{t}$. Note that ${\mathbf {X}}$ has infinite many states. Hence the existence of an invariant probability measure of $\Phi _{t}$ is not guaranteed.

The state of a neuron (m, n, k) is given by the triplet $(V_{(m,n,k)}, H^{E}_{(m,n,k)}, H^{I}_{(m,n,k)})$, where $V_{(m,n,k)} \in \Gamma$ and $H^{E}_{i}, H^{I}_{i} \in {\mathbb {Z}}_{+} := \{ 0, 1, 2, \ldots \}$. The transition probabilities of $\Phi _{t}$ are denoted by $P^{t}( {\mathbf {x}}, {\mathbf {y}})$, i.e.,

$$\begin{aligned} P^{t}( {\mathbf {x}}, {\mathbf {y}}) = {\mathbb {P}}[ \Phi _{t} = {\mathbf {y}} \,|\, \Phi _{0} = {\mathbf {x}}]. \end{aligned}$$

If $\mu$ is a probability distribution on ${\mathbf {X}}$, the left operator of $P^{t}$ acting on $\mu$ is

$$\begin{aligned} \mu P^{t}( {\mathbf {x}}) = \sum _{{\mathbf {y}} \in {\mathbf {X}}} \mu ( {\mathbf {y}}) P^{t}( {\mathbf {y}}, {\mathbf {x}}). \end{aligned}$$

Similarly, the right operator of $P^{t}$ acting on a real-valued function $\eta : {\mathbf {X}} \rightarrow {\mathbb {R}}$ is

$$\begin{aligned} P^{t} \eta ( {\mathbf {x}}) = \sum _{ {\mathbf {y}} \in {\mathbf {X}}} P^{t}( {\mathbf {x}}, {\mathbf {y}}) \eta ( {\mathbf {y}}). \end{aligned}$$

For any probability distribution $\mu$ and any real-valued function $\eta$ on ${\mathbf {X}}$, we take the convention that

$$\begin{aligned} \mu (\eta ) = \sum _{{\mathbf {x}} \in {\mathbf {X}}} \eta ({\mathbf {x}})\mu ({\mathbf {x}}). \end{aligned}$$

Finally, if Z is an observable related to $\Phi _{t}$, throughout this section we denote the conditional expectation with respect to initial value (resp. initial distribution) ${\mathbb {E}}[Z \,|\, \Phi _{0} = {\mathbf {x}}]$ (resp. ${\mathbb {E}}[Z \,|\, \Phi _{0} \sim \mu ]$) by ${\mathbb {E}}_{{\mathbf {x}}}[Z]$ (resp. ${\mathbb {E}}_{\mu }[Z]$).

Define the total number of pending excitatory (resp. inhibitory) kicks at a state ${\mathbf {x}} \in {\mathbf {X}}$ as

$$\begin{aligned} H^{E}( {\mathbf {x}}) = \sum _{m = 1}^{M} \sum _{n = 1}^{N} \sum _{k = 1}^{N_{E} + N_{I}} H^{E}_{(m, n, k)} \end{aligned}$$

and

$$\begin{aligned} H^{I}( {\mathbf {x}}) = \sum _{m = 1}^{M} \sum _{n = 1}^{N} \sum _{k = 1}^{N_{E} + N_{I}} H^{I}_{(m, n, k)} . \end{aligned}$$

Let $U( {\mathbf {x}}) = H^{E}( {\mathbf {x}}) + H^{I}({\mathbf {x}}) + 1$. For any signed distribution $\mu$ on the Borel $\sigma$-algebra of ${\mathbf {X}}$, denoted by ${\mathcal {B}}(X)$, we define the U-weighted total variation norm to be

$$\begin{aligned} \Vert \mu \Vert _{U} = \sum _{ {\mathbf {x}} \in {\mathbf {X}}} U( {\mathbf {x}}) |\mu ( {\mathbf {x}}) | , \end{aligned}$$

and let

$$\begin{aligned} L_{U}( {\mathbf {X}}) = \{ \mu \text{ on } {\mathbf {X}} \, | \, \Vert \mu \Vert _{U} < \infty \} . \end{aligned}$$

In addition, for any function $\eta ( {\mathbf {x}})$ on ${\mathbf {X}}$, we let

$$\begin{aligned} \sup _{ {\mathbf {x}} \in {\mathbf {X}}} \frac{|\eta ( {\mathbf {x}})|}{U({\mathbf {x}})} \end{aligned}$$

be the U-weighted supreme norm.

Theorem 3.1

$\Phi _{t}$ admits a unique invariant probability distribution $\pi \in L_{U}( {\mathbf {X}})$. In addition, there exist constants $C_{1}$, $C_{2} > 0$ and $r \in (0, 1)$ such that

• (a) for any initial distribution $\mu , \nu \in L_{U}( {\mathbf {X}})$,

  $$\begin{aligned} \Vert \mu P^{t} - \nu P^{t}\Vert _{U} \le C_{1} r^{t} \Vert \mu - \nu \Vert _{U}; \end{aligned}$$

• (b) for any function $\eta$ with $\Vert \eta \Vert _{U} < \infty$,

  $$\begin{aligned} \Vert P^{t} \eta - \pi (\eta ) \Vert _{U} \le C_{2} r^{t} \Vert \eta - \pi (\eta ) \Vert _{U} . \end{aligned}$$

Theorem 3.1 also implies the exponential decay of correlation. Let $\xi$ and $\eta$ be two observables on ${\mathbf {X}}$ and $\mu$ be a probability distribution on ${\mathbf {X}}$. The time correlation function of $\xi$ and $\eta$ with respect to $\mu$ is defined as

$$\begin{aligned} C^{\mu }_{\xi , \eta } = \sum _{{\mathbf {x}} \in {\mathbf {X}}} (P^{t}\eta )({\mathbf {x}}) \xi ( {\mathbf {x}}) \mu ({\mathbf {x}}) - \left( \sum _{{\mathbf {x}} \in {\mathbf {X}}} (P^{t}\eta )( {\mathbf {x}}) \mu ( {\mathbf {x}}) \right) \left( \sum _{ {\mathbf {x}} \in {\mathbf {X}}} \xi ( {\mathbf {x}}) \mu ( {\mathbf {x}}) \right) . \end{aligned}$$

The following corollary holds.

Corollary 3.2

Let $\mu \in L_{U}({\mathbf {X}})$ and $\xi$, $\eta$ be two functions on ${\mathbf {X}}$ such that $\Vert \xi \Vert _{\infty } < \infty$ and $\Vert \eta \Vert _{U} < \infty$. Then

$$\begin{aligned} | C^{\mu }_{\xi , \eta } (t) | \le 2C_{1}\Vert \xi \Vert _{\infty } \Vert \eta \Vert _{U} \Vert \mu \Vert _{U} r^{t} , \end{aligned}$$

where constants $C_{1} < \infty$ and $r \in (0, 1)$ are from Theorem 3.1.

3.2 Law of large numbers

Let $t_{2} > t_{1} \ge 0$ be two arbitrary times. A function Y is said to be a sample-path dependent observable on $[t_{1}, t_{2})$ if it maps a sample path of $\Phi _{t}$ between $t_{1}$ and $t_{2}$ to a real number. In other words, Y is a function from $C_{{\mathbf {X}}}([t_{1}, t_{2}))$ to ${\mathbb {R}}$, where $C_{{\mathbf {X}}}([t_{1}, t_{2}))$ is the collection of càdlàg paths from $t_{1}$ to $t_{2}$ on ${\mathbf {X}}$. A sample-path dependent observable is said to be Markov if its law only depends on the initial value $\Phi _{t_{1}}$. Obvious examples of sample-path dependent observables is the number of visits of $\Phi _{t}$ to a given set A during a time span $[t_{1}, t_{2})$.

Let $T > 0$ be a given time window size. Let $Y_{1}, Y_{2}, \ldots , Y_{n}, \ldots$ be a sequence of sample-path dependent observables on $[0, T), [T, 2T), \ldots , [ (n-1)T, nT)$ respectively. Define

$$\begin{aligned} {\mathbb {E}}_{\pi }[Y_{1}] = {\mathbb {E}}[ Y( \{ \Phi _{t} \,| 0 \le t < T\}) \,|\, \Phi _{0} \sim \pi ] \end{aligned}$$

as the expectation of $Y_{1}$ with respect to the invariant probability measure.

The following law of large numbers holds for any sequence of Markov sample-path dependent observables with finite moments.

Theorem 3.3

Let $Y_{1}, Y_{2}, \ldots , Y_{n}, \ldots$ be a sequence of Markov sample-path dependent observables of $\Phi _{t}$ on $[0, T), [T, 2T), \ldots , [ (n-1)T, nT), \ldots$. Assume there exists $M < \infty$ such that ${\mathbb {E}}[Y_{k}^{2} \,|\, \Phi _{(k-1)T} = {\mathbf {x}}] < M$ for any ${\mathbf {x}} \in {\mathbf {X}}$. Then

$$\begin{aligned} \lim _{N \rightarrow \infty }\frac{1}{N}\sum _{n = 1}^{N}Y_{n} = {\mathbb {E}}_{\pi }[Y_{1}] \end{aligned}$$

almost surely.

Theorem 3.3 guarantees that the local/global firing rate and the spike count correlation between local populations are well defined and computable. Let $L_{m,n}$ be a given local population. For $Q \in \{ E, I \}$, let $N^{Q}_{(m,n)}([a, b])$ be the number of neuron spikes fired by type Q neurons in $L_{m,n}$ on the time interval [a, b]. As discussed in Li et al. (2018), the mean firing rate of the local population (m, n) is defined to be

$$\begin{aligned} F^{Q}_{m,n} = \frac{1}{t}{\mathbb {E}}_{\pi }[ N^{Q}_{(m,n)}([0, t))] , \end{aligned}$$

where ${\mathbb {E}}_{\pi }$ is the expectation with respect to the invariant probability measure $\pi$. This definition is independent of t by the invariance of $\pi$.

Let T be a fixed time window size, for $Q_{1}, Q_{2} \in \{E, I\}$, we can further define the covariance of spike count between $Q_{1}$-population in $L_{m,n}$ and $Q_{2}$-population in $L_{m', n'}$ as

$$\begin{aligned} \text{ cov }_{T}^{Q_{1}, Q_{2}}(m,n; m', n') = {\mathbb {E}}_{\pi }[N^{Q_{1}}_{(m,n)}([0, T)) N^{Q_{2}}_{(m',n')}([0, T)) ] - T^{2}N_{Q_{1}}N_{Q_{2}} F^{Q_{1}}_{m,n} F^{Q_{2}}_{m',n'}. \end{aligned}$$

The Pearson correlation coefficient of spike count can be defined similarly. For $Q_{1}$-population in $L_{m,n}$ and $Q_{2}$-population in $L_{m', n'}$, we have

$$\begin{aligned} \rho ^{Q_{1}, Q_{2}}_{T}(m,n; m',n') = \frac{\text{ cov }_{T}^{Q_{1}, Q_{2}}(m,n; m',n')}{\sigma ^{Q_{1}}_{T}(m,n) \sigma ^{Q_{2}}_{T}(m',n')}, \end{aligned}$$

where

$$\begin{aligned} \sigma ^{Q}_{T}(m,n) = \sqrt{\text{ var }_{\pi }(N^{Q}_{(m,n)}([0, T)))} \end{aligned}$$

for $Q \in \{E, I\}$.

One can also consider the correlation of the total spike count between two local populations. Let $N_{(m,n)}([0, T))$ be the total number of excitatory and inhibitory spikes produced by $L_{m,n}$ on [0, T) when starting from the steady state. Then the correlation $\text{ cov }_{T}(m,n; m',n')$ and the Pearson correlation coefficient $\rho _{T}(m,n; m',n')$ can be defined analogously.

The following corollaries imply that the mean firing rate and the spike count correlation are computable.

Corollary 3.4

For $Q \in \{E, I\}$, $1 \le m \le {\mathbf {M}}$, and $1 \le n \le {\mathbf {N}}$, the local firing rate $F^{Q}_{m,n} < \infty$. In addition, for any initial value ${\mathbf {x}} \in X$,

$$\begin{aligned} \lim _{t \rightarrow \infty } \frac{N^{Q}_{(m,n)}([0, t))}{N_{Q}t} = F^{Q}_{(m,n)} \end{aligned}$$

almost surely.

Corollary 3.5

For $Q_{1}, Q_{2} \in \{E, I\}$, $1 \le m, m' \le {\mathbf {M}}$, and $1 \le n, n' \le {\mathbf {N}}$, the covariance $\text{ cov }_{T}^{Q_{1}, Q_{2}}(m,n; m', n') < \infty$. In addition, for any initial value ${\mathbf {x}} \in X$,

$$\begin{aligned} \lim _{K \rightarrow \infty } \frac{1}{K} \sum _{ k = 0}^{K-1} N^{Q_{1}}_{(m,n)}([kT, (k+1)T)) N^{Q_{2}}_{(m',n')}([kT, (k+1)T)) = {\mathbb {E}}_{\pi }\big [N^{Q_{1}}_{(m,n)}([0, T)) N^{Q_{2}}_{(m',n')}([0, T))\big ] \end{aligned}$$

almost surely. In other words $\text{ cov }_{T}^{Q_{1}, Q_{2}}(m,n; m', n')$ is computable.

Corollary 3.6

For $1 \le m, m' \le {\mathbf {M}}$, and $1 \le n, n' \le {\mathbf {N}}$, the covariance $\text{ cov }_{T}(m,n; m', n') < \infty$. In addition, for any initial value ${\mathbf {x}} \in X$,

$$\begin{aligned} \lim _{K \rightarrow \infty } \frac{1}{K}\sum _{ k = 0}^{K-1} N_{(m,n)}([kT, (k+1)T]) N_{(m',n')}([kT, (k+1)T)) = {\mathbb {E}}_{\pi }\big [N_{(m,n)}([0, T]) N_{(m',n')}([0, T])\big ] \end{aligned}$$

almost surely. In other words $\text{ cov }_{T}(m,n; m', n')$ is computable.

It follows from Corollaries 3.4–3.6 that the Pearson correlation coefficient $\rho ^{Q_{1}, Q_{2}}_{T}(m,n; m',n')$ (resp. $\rho _{T}(m,n; m',n')$) is also computable, as the standard deviation $\sigma ^{Q}_{T}(m,n)$ (resp. $\sigma _{T}(m,n)$) is a special case of the square root of the covariance $\text{ cov }_{T}^{Q_{1}, Q_{2}}(m,n; m', n')$ (resp. $\text{ cov }_{T}(m,n; m', n')$).

3.3 Probabilistic preliminaries

Let $\Psi _{n}$ be a Markov chain on a countable state space $(X, {\mathcal {B}})$ with a transition kernel ${\mathcal {P}}(x, \cdot )$. Let $W: X \rightarrow [1, \infty )$ be a real-valued function. Assume $\Psi _{n}$ satisfies the following conditions.

• (a) There exist constants $K \ge 0$ and $\gamma \in (0, 1)$ such that

  $$\begin{aligned} ({\mathcal {P}}W)(x) \le \gamma W(x) + K \end{aligned}$$

  for all $x \in X$.

• (b) There exists a constant $\alpha \in (0, 1)$ and a probability distribution $\nu$ on ${\mathbf {X}}$ so that

  $$\begin{aligned} \inf _{x\in C} {\mathcal {P}}(x, \cdot ) \ge \alpha \nu (\cdot ) , \end{aligned}$$

  with $C = \{x \in X \, | \, W(x) \le R \}$ for some $R > 2K/ (1 - \gamma )$, where K and $\gamma$ are from (a).

Then the following result follows from Hairer and Mattingly (2011).

Theorem 3.7

Assume (a) and (b). Then $\Psi _{n}$ admits a unique invariant probability measure $\pi \in L_{W}(X)$. In addition, there exist constants $C, C' > 0$ and $\rho \in (0, 1)$ such that (i) for all $\mu , \nu \in L_{W}(X)$,

$$\begin{aligned} \Vert \mu {\mathcal {P}}^{n} - \nu {\mathcal {P}}^{n} \Vert _{W} \le C \rho ^{n} \Vert \mu - \nu \Vert _{W} , \end{aligned}$$

and (ii) for all $\xi$ with $\Vert \xi \Vert _{W} < \infty$,

$$\begin{aligned} \Vert {\mathcal {P}}^{n} \xi - \pi ( \xi ) \Vert _{W} \le C' \rho ^{n} \Vert \xi - \pi (\xi ) \Vert _{W} . \end{aligned}$$

The following result was proved in Meyn and Tweedie (2009) and Hairer and Mattingly (2011) using different methods. Note that the original result in Hairer and Mattingly (2011), Meyn and Tweedie (2009) is for a generic measurable state space. The result applies to countable state space with the Borel $\sigma$-algebra (which is essentially the discrete $\sigma$-algebra). There is no additional assumption about W besides measurability. But assumption (a) basically means W is a Lyapunov function when its value is large enough. A heuristic interpretation of Theorem 3.7 is that the Markov chain is drifted to the “bottom” of a Lyapunov function W. Then assumption (b) guarantees independent trajectories of $\Psi _{n}$ can couple with a strictly positive probability. This is usually called the coupling approach. See Hairer (2010) for the full detail. Comparing with spectrum methods, the advantage of this coupling approach is that the stochastic stability can be proved under much weaker assumptions. However, the coupling approach usually only guarantees exponential speed of convergence at some rate. It is difficult to relate this exponential rate, e.g., r in Theorem 3.1, to model parameters.

We also need the following law of large numbers for martingale difference sequence to prove Theorem 3.3. Let ${\mathcal {F}}_{n}$ be a filtration on a probability space $\Omega$. A sequence of random variables $X_{n}$ is said to be a martingale difference sequence if ${\mathbb {E}}[|X_{n}|] < \infty$ and ${\mathbb {E}}[ X_{n} \,|\, {\mathcal {F}}_{n-1}] = 0$.

Theorem 3.8

(Theorem 3.3.1 of Stout 1974) Let $X_{n}$ be a martingale difference sequence with respect to ${\mathcal {F}}_{n}$. If

$$\begin{aligned} \sum _{n = 1}^{\infty } \frac{{\mathbb {E}}[|X_{n}|^{2}]}{n^{2}} < \infty , \end{aligned}$$

then

$$\begin{aligned} \frac{1}{N}\sum _{n = 1}^{N} X_{n} \rightarrow 0 \quad a.s. \end{aligned}$$

3.4 Proof of results

For a step size $h > 0$ that will be described later, we define the time-h sample chain as $\Phi ^{h}_{n} = \Phi _{nh}$. The superscript h is dropped when it leads to no confusion. Recall that $U({\mathbf {x}}) = H^E({\mathbf {x}}) + H^I({\mathbf {x}})+1$. The following two lemmas verify conditions (a) and (b) for Theorem 3.7.

Lemma 3.9

For $h > 0$ sufficiently small, there exist constants $K > 0$ and $\gamma \in (0, 1)$, such that

$$\begin{aligned} P^{h}U \le \gamma U + K . \end{aligned}$$

Proof

During (0, h], let $N_{out}$ be the number of pending kicks from $H^E({\mathbf {x}})$ and $H^I({\mathbf {x}})$ that takes effect and $N_{in}$ be the number of new spikes produced. We have

$$\begin{aligned} P^{h}U( {\mathbf {x}}) = {\mathbb {E}}_{{\mathbf {x}}}[ U( \Phi _{h})] = U( {\mathbf {x}}) - {\mathbb {E}}_{{\mathbf {x}}}[ N_{out}] + {\mathbb {E}}_{{\mathbf {x}}}[N_{in}] . \end{aligned}$$

The probability that an excitatory (resp. inhibitory) pending kick takes effect on (0, h] is $(1-e^{- h/ \tau ^E})$ (resp. $(1-e^{- h/ \tau ^I})$). Hence for h sufficiently small, we have

$$\begin{aligned} {\mathbb {E}}_{{\mathbf {x}}}[ N_{out}] \ge (H^E({\mathbf {x}}) + H^I({\mathbf {x}})) ( 1 - e^{-h/\max \{\tau ^E, \tau ^I\}} ) \ge \frac{1}{2 \max \{\tau ^E, \tau ^I\}} \ h \ (U({\mathbf {x}})-1) . \end{aligned}$$

For a neuron (m, n, k), after each spike it spends an exponentially distributed random time with mean $\tau _{{\mathcal {R}}}$ at state ${\mathcal {R}}$. Hence the number of spikes produced by neuron (m, n, k) is at most

$$\begin{aligned} 1 + {\mathbb {E}}[ \text{ Pois }(h/\tau _{{\mathcal {R}}})] = 1 + h/\tau _{{\mathcal {R}}} , \end{aligned}$$

where $\text{ Pois }(\lambda )$ is a Poisson random variable with rate $\lambda$. Hence

$$\begin{aligned} {\mathbb {E}}_{{\mathbf {x}}}[N_{in}] \le {\mathbf {M}}{\mathbf {N}}(N_{E} + N_{I})\cdot (1 + h/\tau _{{\mathcal {R}}}) . \end{aligned}$$

The proof is completed by letting

$$\begin{aligned} \gamma = 1 - h/(2 \max \{\tau ^E, \tau ^I\}) \qquad \text{ and } \qquad K = {\mathbf {M}}{\mathbf {N}}(N_{E} + N_{I})\cdot (1 + h/\tau _{{\mathcal {R}}})\ +\frac{h}{2 \max \{\tau ^E,\tau ^I\}}. \end{aligned}$$

$\square$

For $b \in {\mathbb {Z}}_{+}$, let

$$\begin{aligned} C_{b} = \{ {\mathbf {x}} \in {\mathbf {X}} | H^E( {\mathbf {x}}) + H^I( {\mathbf {x}}) \le b \} . \end{aligned}$$

Lemma 3.10

Let ${\mathbf {x}}_{0}$ be the state that $H^E = H^I = 0$ and $V_{(m,n,k)} = {\mathcal {R}}$ for all $1 \le m \le {\mathbf {M}}$, $1 \le n \le {\mathbf {N}}$, and $1 \le k \le N_{E} + N_{I}$. Then for any $h > 0$, there exists a constant $\delta = \delta (b, h)$ depending on b such that there exists a constant $c > 0$ depending on b and h such that,

$$\begin{aligned} P^{h}({\mathbf {x}}, {\mathbf {x}}_{0}) > c \quad \text{ for } \text{ all } {\mathbf {x}} \in C_{b} \end{aligned}$$

Proof

For each ${\mathbf {x}} \in C_{b}$, it is sufficient to construct an event that moves from ${\mathbf {x}}$ to ${\mathbf {x}}_{0}$ with a uniform positive probability. Below is one of many possible constructions.

• (i) On (0, h / 2], a sequence of external Poisson kicks drives each $V_{(m,n,k)}$ to the threshold value $\Sigma$, hence puts $V_{(m,n,k)}={\mathcal {R}}$. Once at ${\mathcal {R}}$, $V_{(m,n,k)}$ remains there before $t = h$. In addition, no pending kicks take effect on (0, h / 2].

• (ii) All pending kicks at state ${\mathbf {x}}$ take effect on (h / 2, h]. Obviously this has no effect on membrane potentials.

Since b is bounded, the number of pending kicks is less than $b + {\mathbf {M}}{\mathbf {N}}(N_{E} + N_{I}) < \infty$. It is easy to see that this event happens with positive probability. $\square$

Lemmas 3.9 and 3.10 together imply Theorem 3.1.

Proof of Theorem 3.1

The proof of Theorem 3.1 is identical to that of Theorem 2.1 in Li et al. (2018). We need to carry out the following three steps.

• (i) Choose the step size h as in Lemma 3.9. Apply Lemmas 3.9, 3.10, and Theorem 3.7 to show that $\Phi ^{h}$ admits a unique invariant probability distribution $\pi _{h}$ in $L_{U}({\mathbf {X}})$. Note that ${\mathbf {X}}$ is countable so there is no need to check the measurability condition in Theorem 3.7 (b).

• (ii) Show that $\Phi _{t}$ satisfies the “continuity at zero” condition. For any probability distribution $\mu$ on ${\mathbf {X}}$, $\lim _{t \rightarrow 0} \Vert \mu P^{t} - \mu \Vert _{TV} = 0$, where $\Vert \cdot \Vert _{TV}$ is the total variation norm.

• (iii) Use the “continuity at zero” condition and the fact that ${\mathbb {Q}}$ is dense in ${\mathbb {R}}$ to show that $\pi _{h}$ must be invariant for $P^{t}$. Then show that the convergence result still holds for $\Phi _{t}$.

We refer the proof of Theorem 2.1 in Li et al. (2018) for full details. $\square$

Proof of Corollary 3.2

It is easy to see that

$$\begin{aligned} |C^{\mu }_{\xi , \eta } (t) |= & {} \sum _{ {\mathbf {x}} \in {\mathbf {X}}} \xi ({\mathbf {x}}) \left( (P^{t} \eta ) ({\mathbf {x}}) - \sum _{{\mathbf {x}}\in {\mathbf {X}}} (P^{t}\eta )( {\mathbf {x}}) \mu ({\mathbf {x}})\right) \mu ({\mathbf {x}}) \\\le & {} \Vert \xi \Vert _{\infty } \sum _{{\mathbf {x}} \in {\mathbf {X}}}\left( \sum _{{\mathbf {x}} \in {\mathbf {X}}} |\eta |({\mathbf {x}}) | \delta _{ {\mathbf {x}}}P^{t} - \mu P^{t}|( {\mathbf {x}}) \right) \mu ({\mathbf {x}})\\\le & {} \Vert \xi \Vert _{\infty }\Vert \eta \Vert _{U} \sum _{{\mathbf {x}} \in {\mathbf {X}}}\left( \sum _{{\mathbf {x}} \in {\mathbf {X}}} U({\mathbf {x}})| \delta _{ {\mathbf {x}}}P^{t} - \mu P^{t}|( {\mathbf {x}}) \right) \mu ( {\mathbf {x}})\\= & {} \Vert \xi \Vert _{\infty } \Vert \eta \Vert _{U} \sum _{{\mathbf {x}} \in {\mathbf {X}}} \Vert \delta _{{\mathbf {x}}} P^{t} - \mu P^{t} \Vert _{U} \mu ( {\mathbf {x}}) . \end{aligned}$$

Then by Theorem 3.1, we have

$$\begin{aligned} |C^{\mu }_{\xi , \eta } (t) |\le & {} \Vert \xi \Vert _{\infty } \Vert \eta \Vert _{U} C_{1} r^{t} \cdot \sum _{{\mathbf {x}} \in {\mathbf {X}}} \Vert \delta _{{\mathbf {x}}} - \mu \Vert _{U} \mu ({\mathbf {x}}) \\\le & {} \Vert \xi \Vert _{\infty } \Vert \eta \Vert _{U} C_{1} r^{t} \cdot \sum _{{\mathbf {x}} \in {\mathbf {X}}} (U( {\mathbf {x}}) + \Vert \mu \Vert _{U}) \mu ( {\mathbf {x}})\\= & {} 2C_{1} \Vert \xi \Vert _{\infty } \Vert \eta \Vert _{U}\Vert \mu \Vert _{U} r^{t} . \end{aligned}$$

This completes the proof. $\square$

Proof of Theorem 3.3

Since $Y_{1}, Y_{2}, \ldots , Y_{n} , \ldots$ are Markov sample-path dependent observables, ${\mathbb {E}}_{{\mathbf {x}}}[Y_{n}]$ only depends on $\Phi _{(n-1)T}$. Denote $Z_{n} = {\mathbb {E}}[Y_{n} \,|\, \Phi _{(n-1)T}]$ for $n \ge 1$. It is easy to see that $Z_{n}$ is a deterministic function about $\Phi _{(n-1)T}$.

Let ${\mathcal {F}}_{n}$ be the $\sigma$-field generated by $\{\Phi _{0}, \Phi _{T}, \ldots , \Phi _{nT} \}$. Let $W_{n} = Y_{n} - Z_{n}$. Then $W_{n}$ is a martingale difference sequence because ${\mathbb {E}}[ W_{n} \,|\, {\mathcal {F}}_{n-1}] = 0$. Since ${\mathbb {E}}[W_{n}^{2} \,|\, \Phi _{(n-1)T} ]< {\mathbb {E}}[Y_{n}^{2} \,|\, \Phi _{(n-1)T} ] < M$ uniformly, we have the uniform bound

$$\begin{aligned} \sum _{n = 1}^{\infty } \frac{{\mathbb {E}}[ W_{n}^{2}]}{n^{2}} \le \frac{M \pi ^{2}}{6} < \infty . \end{aligned}$$

By Theorem 3.8, we have

$$\begin{aligned} \lim _{N \rightarrow \infty } \frac{1}{N} \sum _{n = 1}^{N} W_{n} = 0 \end{aligned}$$

almost surely.

Recall that $Z_{n}$ is a deterministic function of $\Phi _{(n-1)T}$. By theorem 3.1, $\Phi _{t}$ admits a unique invariant probability measure $\pi$. In addition, $\pi$ is the ergodic invariant probability measure of the time-T sample chain $\Phi ^{T}_{n}$. Apply the law of large numbers for Markov process to $\Phi ^{T}_{n}$ and $Z_{n}$, we have

$$\begin{aligned} \lim _{N \rightarrow \infty }\frac{1}{N}\sum _{n = 1}^{N}Z_{n} = {\mathbb {E}}_{\pi }[Z_{1}] \end{aligned}$$

almost surely. By the law of total expectation, ${\mathbb {E}}_{\pi }[Z_{1}] = {\mathbb {E}}_{\pi }[Y_{1}]$.

Combine two limits, we have

$$\begin{aligned} \lim _{N \rightarrow \infty } \frac{1}{N} \sum _{n = 1}^{N} Y_{n} = {\mathbb {E}}_{\pi }[Y_{1}] . \end{aligned}$$

This completes the proof. $\square$

Proof of Corollary 3.4

By the invariance of $\pi$, for any local population $L_{m,n}$ and any $Q \in \{E, I\}$, we have

$$\begin{aligned} F^{Q}_{m,n} = {\mathbb {E}}_{\pi }[N^{Q}_{(m,n)}([0, 1))] . \end{aligned}$$

For every ${\mathbf {x}} \in {\mathbf {X}}$ we have

$$\begin{aligned} {\mathbb {E}}_{{\mathbf {x}}}[N^{Q}_{m,n}([0, 1))] \le N_{Q}(1 + {\mathbb {E}}[ \text{ Pois }(1/\tau _{{\mathcal {R}}})] )= N_{Q}(1 + 1/\tau _{{\mathcal {R}}}) . \end{aligned}$$

Thus $F^{Q}_{m,n} = {\mathbb {E}}_{\pi }[N^{Q}_{(m,n)}([0, 1))] < \infty$.

It remains to prove the law of large number. Since ${\mathbb {E}}_{{\mathbf {x}}}[N^{Q}_{m,n}([0, 1))]$ is bounded independent of ${\mathbf {x}}$, it is sufficient to prove

$$\begin{aligned} \lim _{K \rightarrow \infty } \frac{N^{Q}_{(m,n)}([0, K))}{N_{Q}K} = F^{Q}_{(m,n)} \end{aligned}$$

almost surely for integers K. Define the mean spike count in a unit time interval by

$$\begin{aligned} Y_{n} = \frac{1}{N_{Q}}N^{Q}_{(m,n)}([n-1, n)) . \end{aligned}$$

It is easy to see that $Y_{n}$ is a Markov sample-path dependent observable because the distribution of $Y_{n}$ only depends on the initial state $\Phi _{(n-1)T}$. In addition, for any $\Phi _{(n-1)T}$,

$$\begin{aligned} {\mathbb {E}}[Y_{n}^{2} \,|\, \Phi _{(n-1)T}] \le {\mathbb {E}}[ (1 + \text{ Pois }(1/\tau _{{\mathcal {R}}}))^{2}] < \infty \end{aligned}$$

uniformly. Corollary 3.4 then follows from Theorem 3.3. $\square$

Proof of Corollary 3.5

The boundedness is similar as that in the proof of Corollary 3.4. For every ${\mathbf {x}} \in {\mathbf {X}}$ we have the uniform bound

$$\begin{aligned} {\mathbb {E}}_{{\mathbf {x}}}[N^{Q_{1}}_{m,n}([0, T))N^{Q_{2}}_{m',n'}([0, T))] \le N_{Q_{1}}N_{Q_{2}}(1 + {\mathbb {E}}[ \text{ Pois }(T/\tau _{{\mathcal {R}}})] )^{2} < \infty . \end{aligned}$$

Combine with Corollary 3.4 that the mean firing rate is bounded, it is easy to see that $\text{ cov }^{Q_{1}Q_{2}}_{T}(m, n; m', n')$ must be finite.

For the law of large numbers, define a sequence $Y_{k}, k \ge 1$ such that

$$\begin{aligned} Y_{k} = N^{Q_{1}}_{(m,n)}( [(k-1)T, k T )) N^{Q_{2}}_{(m', n')}([(k-1)T, kT)) . \end{aligned}$$

By Hölder’s inequality, we have

$$\begin{aligned} {\mathbb {E}}[|Y_{k}|^{2} \,|\, \Phi _{(n-1)T}] \le {\mathbb {E}}\big [ (N^{Q_{1}}_{(m,n)}( [(k-1)T, kT )))^{4} \,| \, \Phi _{(n-1)T}\big ]^{1/2}{\mathbb {E}}\big [ (N^{Q_{2}}_{(m',n')}( [(k-1)T, kT )))^{4} \,| \, \Phi _{(n-1)T}\big ]^{1/2} . \end{aligned}$$

Same as before, we have uniform bounds

$$\begin{aligned} {\mathbb {E}}\left[ (N^{Q_{1}}_{(m,n)}( [kT, (k+1)T )))^{4} \,|\, \Phi _{(n-1)T}\right] \le {\mathbb {E}}\left[ \left( 1 + \text{ Pois }\left( \frac{T}{\tau _{{\mathcal {R}}}}\right) \right) ^{4} \right] < \infty \end{aligned}$$

and

$$\begin{aligned} {\mathbb {E}}\left[ (N^{Q_{2}}_{(m',n;)}( [kT, (k+1)T )))^{4} \,|\, \Phi _{(n-1)T}\right] \le {\mathbb {E}}\left[ \left( 1 + \text{ Pois }\left( \frac{T}{\tau _{{\mathcal {R}}}}\right) \right) ^{4}\right] < \infty . \end{aligned}$$

The proof is then completed by applying Theorem 3.3. $\square$

The proof of Corollary 3.6 is identical to that of Corollary 3.5. We leave the detail to the reader.

4 Numerical examples with different spiking patterns

As introduced before, the neural field model $\Phi _{t}$ can produce semi-synchronous spike volleys, called the multiple-firing events (MFEs). Because of the spatial heterogeneity of $\Phi _{t}$, patterns of MFEs produced by $\Phi _{t}$ consist of two factors: the degree of local synchrony and the spatial correlation. By adjusting parameters, we can change not only the degree of synchrony of MFEs within a local population, but also the spike count correlation between MFEs produced by two local populations. As mentioned in the introduction, these local and global MFE patterns are emergent from network activities. One goal of this paper is to interpret how these emergent patterns arise from the interaction of neurons. It is not practical to test all possible parameters. In this section, we demonstrate five representative network examples corresponding to five different local and global MFE patterns.

4.1 Parameters of example networks

We will use common parameters prescribed in Sect. 2.2. In addition, we use ${\mathbf {N}} = {\mathbf {M}} = 3$ in all five examples. For the sake of simplicity, 9 populations are label as $1, 2, \ldots , 9$ from upper left corner to lower right corner. In order to have heterogeneous external drive rates, we assume that $\lambda ^{E}_{m,n} = \lambda ^{I}_{m,n} = \lambda _{Even}$ if $(n-1){\mathbf {M}} + m$ is even, and $\lambda ^{E}_{m,n} = \lambda ^{I}_{m,n} = \zeta \lambda _{Even}$ if $(n-1){\mathbf {M}} + m$ is odd. This alternating external drive rates mimic the sensory input to the visual cortex if a local population models an orientation column. The main varying parameters in our numerical examples are the strength of nearest-neighbor connectivity ${ ratio }_{E}$, the ratio of external drive rates in nearest neighbors $\zeta$, and the synapse delay time $\tau _{E}, \tau _{I}$ after the occurrence of a spike. We first follow the idea of Li et al. (2018) to produce three examples with “homogeneous”, “regular”, and “synchronized” patterns respectively by varying the synapse delay time. Then we change $\text{ ratio }_{E}$ and external drive rates for the “regular” network to produce two more examples with different global synchrony. As in Li et al. (2018), we replace a single $\tau ^{E}$ by two synapse times $\tau ^{EE}$ and $\tau ^{IE}$ to denote the expected delay times after an excitatory spike takes effect in excitatory and inhibitory neurons, respectively. The network characterization, the notation, and parameters of each example is presented in the following table.

Notation	Network characterization	$\tau _{EE}$ (ms)	$\tau _{IE}$ (ms)	$\tau _{I}$ (ms)	${ ratio }_{E}$	$\zeta$
HOM	“Homogeneous” neural field	4	1.2	4.5	0.1	11/12
SYN	Synchronized neural field	0.9	0.9	4.5	0.15	11/12
REG1	“Regular” neural field. Weak nearest neighbor connectivity. Low fluctuation in external drive.	1.6	1.2 ms	4.5	0.05	11/12
REG2	“Regular” neural field. Strong nearest neighbor connectivity. Low fluctuation in external drive.	1.6	1.2	4.5	0.15	11/12
REG3	“Regular” neural field. Strong nearest neighbor connectivity. High fluctuation in external drive.	1.6	1.2	4.5	0.15	1/2

Fig. 1

Mean firing rate at the central local population verses $\lambda _{Even}$ for all five networks. The drive rate at even-indexed local populations increases from $\lambda _{Even} = 1000$ to 8000 spikes/s

4.2 Statistics and raster plots of example networks

We first present mean firing rates of the five example networks. Mean firing rates of the central local population $L_{(2,2)}$ under different external drive rates are plotted in Fig. 1. The firing rate plot is consistent with that studied in Li et al. (2018).

The detailed spiking pattern is a more interesting subject. We can see that the raster plots generated by networks HOM and SYN are not very different from what we have presented in Li et al. (2018). In the HOM network, the spike train is quite homogeneous and MFEs are not very prominent. The SYN network produces almost synchronized MFEs in all local populations. Since in these two networks the spiking pattern has no significant difference across local populations, we only show the raster plot of the central local population $L_{2,2}$ in Fig. 2.

The three REG networks exhibit clear spatial heterogeneities. Different spike count correlations among different local populations are observed when parameters change. With higher ${ ratio }_{E}$ (${ ratio }_{E} = 0.15$), MFEs in all 9 blocks are quite correlated (Fig. 3 middle panel). When ${ ratio }_{E} = 0.05$, much less correlation among MFEs is seen. And the raster plot also looks less synchronized (Fig.  3 left panel). If the long range connectivity remains ${ ratio }_{E} = 0.15$ but we drive odd-indexed local populations only half strong as even-indexed local populations, the correlation among MFEs appears to be between the previous two cases (Fig. 3 right panel). From the three raster plots presented in Fig. 3, we can conclude that both stronger long range connectivity and more homogeneous drive rate contribute to stronger correlations of MFEs among different local populations. A natural question is how such correlated spiking activity changes when two local populations that are further apart. We will extensively study this issue in Sect. 6.

Fig. 2

Raster plot of the central local population of SYN and HOM networks. The drive rate at even-indexed local populations is $\lambda _{Even} = 6000$ spikes/s. The index of neuron (m, n, k) is $[(n-1)M + m](N_{E} + N_{I}) + k$

5 Mechanism of multiple firing events

The raster plots in Figs. 2 and  3 clearly demonstrate multiple firing events (MFEs) within local populations. As described before, in an MFE a proportion of the population, but not all of them, fire a spike in a relatively short time window. The spiking pattern of MFEs observed in our paper is consistent with earlier numerical results in Chariker and Young (2015), Rangan and Young (2013a, b). The heuristic reason of the occurrence of MFEs is quite straightforward. An MFE is a milder version of the PING mechanism (Börgers and Kopell 2003). Inhibitory (GABAergic) synapses in a population usually act a few milliseconds more slowly than excitatory (AMPA) synapses. As a result, an excitatory spike excites many postsynaptic neurons quickly and forms a cascade, which will be terminated when the pending inhibitory kicks take effect. However, very limited mathematical justification is available so far. Early works that attempt to investigate the mechanism of MFEs usually assume that a synapse takes effect instantaneously without a delay (Newhall et al. 2010; Zhang et al. 2014a, b). It makes the analysis easier but ignore the significant dependence of MFEs on synapse delay times. It was numerically shown later that strength of MFEs is extremely sensitive with respect to small changes of the synapse delay times $\tau _{E}$ and $\tau _{I}$ (Chariker and Young 2015; Li et al. 2018). Hence it is necessary to incorporate more details into the modeling and treat the excitatory-inhibitory interplay during an MFE as a dynamical process.

This section is devoted to the study of possible mechanism of MFEs in one local population. Two qualitative models are proposed to depict a caricature of the excitatory-inhibitory interactions during an MFE. We will apply results in this section to study the mechanism of spatial correlation of MFEs in our neural field model.

Fig. 3

Raster plot of the full population of three REG networks. The drive rate at even-indexed local populations is $\lambda _{Even} = 6000$ spikes/s. The index of neuron (m, n, k) is $[(n-1)M + m](N_{E} + N_{I}) + k$

5.1 The SIR model

The mechanism of an MFE in a local population is a dynamical process that lasts only a few milliseconds. The excitatory neurons stimulate each other and form an avalanche of spikes. Many inhibitory spikes are also induced by these excitatory spikes, which eventually act on the excitatory population and terminate the avalanche.

In this subsection, we propose an SIR disease model for a qualitative description of the excitatory-inhibitory interaction during an MFE. The heuristic description is as follows. When an excitatory spike is fired but has not yet affected its postsynaptic neurons, it is like an “infected patient” (I) of a disease. If a neuron has high membrane potential such that it can reach the threshold after receiving an excitatory kick, it is labeled as “susceptible” (S). Further, after a spike is fired, the neuron reaches the refractory state, becomes “recovered” (R) and is immuned from further “infections”. Therefore, the interplay of excitatory and inhibitory populations largely mimics an SIR disease model.

The main changing parameters in our SIR model are $\tau _{E}$ and $\tau _{I}$. Other parameters like $N_{E}$, $N_{I}$, $S_{EE}$, .etc are same as in the network model. This system contains six variables $G_{E}, G_{I}, H_{E}, H_{I}, R_{E}$, and $R_{I}$. Variables $G_{E}$ and $G_{I}$ are the numbers of excitatory and inhibitory neurons that are located in the “gate area”, which means their membrane potentials lie within one excitatory spike from the threshold. We denote the set of neurons in this “gate area” by $G_{E}$ and $G_{I}$ when it does not lead to confusions. $G_{E}$ and $G_{I}$ correspond to “susceptible population” in the SIR model. Variables $H_{E}$ and $H_{I}$ are the “effective number” of excitatory and inhibitory neurons who just spiked but the spikes have not taken effects yet. If, for example, $50\%$ of postsynaptic kicks from a neuron spike have already taken effects, the “effective number” of this pending kick is 0.5. $H_{E}$ and $H_{I}$ play the role of “infected people” in the SIR model. Finally, $R_{E}$ and $R_{I}$ are the number of excitatory and inhibitory neurons that are at refractory, or the “recovered” population in the SIR model. Since we only study the dynamics of one MFE, we assume that a neuron stays at ${\mathcal {R}}$ after a spike. Let $c_{E}, c_{I}$ be two parameters that will be described later. The following dynamical system describes time evolution of $H_{E}, H_{I}, G_{E}, G_{I}, R_{E}$, and $R_{I}$ during an MFE.

$$\begin{aligned} \begin{aligned} \frac{{\mathrm {d}} H_{E}}{{\mathrm {d}} t}&= - \tau _{E}^{-1} H_{E} + \tau _{E}^{-1}P_{EE}H_{E}G_{E} + \frac{\lambda _{E}}{S_{EE}} G_{E}\\ \frac{{\mathrm {d}} G_{E}}{{\mathrm {d}}t}&= c_{E} \max \left\{ \tau _{E}^{-1}P_{EE}S_{EE}H_{E} + \lambda _{E} - \tau _{I}^{-1}P_{EI}S_{EI}H_{I}, 0\right\} \cdot ( N_{E} - G_{E} - R_{E}) \\&\quad -\tau _{I}^{-1}P_{EI}\max \left\{ \frac{S_{EI}}{S_{EE}}, 1\right\} H_{I}G_{E} - \left( \tau _{E}^{-1}P_{EE}H_{E} + \frac{\lambda _{E}}{S_{EE}}\right) G_{E} \\ \frac{{\mathrm {d}} R_{E}}{{\mathrm {d}}t}&= \tau _{E}^{-1}P_{EE}H_{E}G_{E} + \frac{\lambda _{E}}{S_{EE}} G_{E}\\ \frac{{\mathrm {d}} H_{I}}{{\mathrm {d}} t}&= - \tau _{I}^{-1} H_{I} + \tau _{E}^{-1}P_{IE}H_{E}G_{I} + \frac{ \lambda _{I}}{S_{IE}}G_{I}\\ \frac{{\mathrm {d}} G_{I}}{{\mathrm {d}}t}&= c_{I} \max \left\{ \tau _{E}^{-1}P_{IE}S_{IE}H_{E} + \lambda _{I} - \tau _{I}^{-1}P_{II}S_{II}H_{I}, 0\right\} \cdot ( N_{I} - G_{I} - R_{I}) \\&\quad -\tau _{I}^{-1}P_{II}\max \left\{ \frac{S_{II}}{S_{IE}}, 1\right\} H_{I}G_{I} - \left( \tau _{E}^{-1}P_{IE}H_{E} + \frac{\lambda _{I}}{S_{IE}}\right) G_{I}\\ \frac{{\mathrm {d}} R_{I}}{{\mathrm {d}}t}&= \tau _{E}^{-1}P_{IE}H_{E}G_{I} + \frac{ \lambda _{I}}{S_{IE}}G_{I} \end{aligned} \end{aligned}$$

(5.1)

We emphasis that the aim of this SIR model is to qualitatively describe the excitatory-inhibitory interplay, instead of making any precise predictions. Some parameters in this model are difficult to calculate. The first equation in (5.1) describes the rate of change of $H_{E}$, which decreases with rate $\tau _{E}^{-1}$. The source of input to $H_{E}$ is neurons in the “gate area” $G_{E}$. We assume that neurons in $G_{E}$ have uniformly distributed membrane potentials. The second equation describes the rate of change of $G_{E}$. The source of $G_{E}$ is neurons that are not at $G_{E}$ or $R_{E}$. We assume that the upward drift of $G_{E}$ is proportional to both the number of relevant neurons and the net current, if the net current is positive. We denote the coefficient of this proportion by parameter $c_E$. The downward drift of $G_{E}$ comes from both spiking neurons that receive excitatory kicks and neurons dropping below the “gate area” when receiving inhibitory input. This is represented by the last two terms in the second equation in (5.1). The third equation in (5.1) is about $R_{E}$, whose increase rate equals the rate of producing new spikes. The case of inhibitory neurons is analogous, represented by the last three equations in (5.1) about $H_{I}, G_{I}, R_{I}$, where the parameter $c_I$ stands for the coefficient of net current for inhibitory neurons.

The most salient feature of this SIR system is its very sensitive dependence of MFE sizes on $\tau _{E}$ and $\tau _{I}$. When $\tau _{I}$ is much larger than $\tau _{E}$, one can expect larger MFE sizes for both populations. This is demonstrated in Fig.  4. We assume that $\tau _{E} = 2$ ms and plot the mean MFE size with varying $\tau _{I}$. The initial condition is $H_{E} = 0, G_{E} = 20, R_{E} = 0, H_{I} = 0, G_{I} = 5$, and $R_{I} = 0$. We showed three cases with varying drive rates, where $\lambda _{E} = \lambda _{I} = 0, 2000$, and 4000. The sizes of MFE produced by excitatory and inhibitory populations are $R_{E}(T)$ and $R_{I}(T)$ respectively, where T is the minimum of 20 ms and the first local minimum of $H_{E}(t)$. The reason of looking for the local minimum is because when the network is driven, this ODE model might generate a “second wave” after the first MFE. Figure 4 confirms two observations in our simulation results of the full network model. First, MFE sizes of both excitatory and inhibitory populations increase quickly with larger $\tau _{I}$. Secondly, the network tends to produce bigger MFEs when it is strongly driven by external signals. These observations are consistent with numerical results of the network model.

Fig. 4

Event size versus $\tau _{I}$ in one local population

In the limiting senario when $\tau _{I}^{-1}$ is very small, we have the following theorem.

Theorem 5.1

Assume $\tau _{E} = 1$, $\lambda _{E} = \lambda _{I} = 0$. Let $\delta _{E} = c_{E}S_{EE}$, $\delta _{I} = c_{E}S_{IE}$, $m = \min \{\delta _{E}, P_{EE}\}$,

$$\begin{aligned} \alpha = P_{EE}N_{E}^{2}e^{-N_{E}m} , \end{aligned}$$

and

$$\begin{aligned} \beta = N_{I}\left( e^{-\delta _{I}N_{E}} + e^{-P_{IE}N_{E}}\right) . \end{aligned}$$

Assume $N_{E} > m$. Let the initial condition be $(H_{0}, 0, 0, 0, 0, 0)$ for $H_{0} > \alpha$. Then there exist constants C and T, such that when $\tau _{I} > C$ and $t > T$, we have $R_{E}(t) > N_{E} - \alpha$ and $R_{I}(t) > N_{I} - \beta$.

Proof

Let $\delta _{E} = c_{E}S_{EE}P_{EE}$, $\delta _{I} = c_{E}S_{IE}P_{IE}$, $\tau _{E} = 0$, $\tau _E = 1$, $\tau _{I} =\infty$, and $\lambda _{E} = \lambda _{I } = 0$. Let $(H_{0}, 0, 0, 0, 0, 0)$ be the initial condition. Then the ODE system becomes

$$\begin{aligned} \frac{{\mathrm {d}}H_{E}}{{\mathrm {d}}t}= & {} - H_{E} + P_{EE}H_{E}G_{E} \\ \frac{{\mathrm {d}}G_{E}}{{\mathrm {d}}t}= & {} \delta _{E} H_{E}(N_{E} - G_{E} - R_{E}) - P_{EE}H_{E}G_{E}\\ \frac{{\mathrm {d}}R_{E}}{{\mathrm {d}}t}= & {} P_{EE}H_{E}G_{E}\\ \frac{{\mathrm {d}}H_{I}}{{\mathrm {d}}t}= & {} - H_{I} + P_{IE}H_{E}G_{I} \\ \frac{{\mathrm {d}}G_{I}}{{\mathrm {d}}t}= & {} \delta _{I} H_{E}(N_{I} - G_{I} - R_{I}) - P_{IE}H_{E}G_{I}\\ \frac{{\mathrm {d}}R_{I}}{{\mathrm {d}}t}= & {} P_{IE}H_{E}G_{I} . \end{aligned}$$

Let $u_{E} = G_{E} + R_{E}$ and $v_{E} = H_{E} - R_{E}$, we have

$$\begin{aligned} \frac{{\mathrm {d}}H_{E}}{{\mathrm {d}}t}= & {} -H_{E} + P_{EE}H_{E}(u_{E} + v_{E} - H_{E}) \\ \frac{{\mathrm {d}} u_{E}}{ {\mathrm {d}} t}= & {} \delta _{E} H_{E}(N_{E} - u_{E})\\ \frac{ {\mathrm {d}} v_{E}}{ {\mathrm {d}}t}= & {} -H_{E} , \end{aligned}$$

with $H_{E}(0) = v_{E}(0) = H_{0}$ and $u_{E}(0) = 0$. Divide ${\mathrm {d}}u_{E}/ {\mathrm {d}}t$ by ${\mathrm {d}}v_{E}/ {\mathrm {d}}t$, we have

$$\begin{aligned} \frac{{\mathrm {d}}u_{E}}{ {\mathrm {d}} v_{E}} = \delta _{E} (u_{E} - N_{E}), \quad u_{E}(H_{0}) = 0. \end{aligned}$$

Solving this initial value problem, one obtains

$$\begin{aligned} u_{E} (v_{E})= N_{E}( 1 - e^{\delta _{E} (v_{E} - H_{0})}) . \end{aligned}$$

Similarly, divide ${\mathrm {d}}H_{E}/ {\mathrm {d}}t$ by ${\mathrm {d}}v_{E} /{\mathrm {d}}t$, we have

$$\begin{aligned} \frac{{\mathrm {d}}H_{E}}{{\mathrm {d}}v_{E}} = 1 - P_{EE}(u_{E} + v_{E} - H_{E}) , \quad H_{E}(H_{0}) = H_{0} . \end{aligned}$$

This is a first order linear equation. The solution is

$$\begin{aligned} H_{E}(v_{E}) = N_{E} + v_{E} + \frac{N_{E}}{\delta _{E} - P_{EE}}\left( P_{EE}e^{\delta _{E} (v_{E} - H_{0})} - \delta _{E} e^{P_{EE}(v_{E} - H_{0})}\right) . \end{aligned}$$

Therefore, equation

$$\begin{aligned} \frac{{\mathrm {d}}v_{E}}{{\mathrm {d}}t} = - H_{E}(v_{E}), \quad v_E(0) = H_0 \end{aligned}$$

becomes an autonomous equation. Let $- R^{*}$ be the greatest root of $H_{E}(v_{E})$ that is less than $H_{0}$. It is easy to check that $R_{E}^{*} < N_{E}$. Hence as $t \rightarrow \infty$ we have $v_{E}(t) \rightarrow R^{*}$. This implies $H_{E}(t) \rightarrow 0$ and $R_{E}(t) \rightarrow R^{*}$ as $t \rightarrow \infty$.

It remains to estimate $R^{*}$. We have

$$\begin{aligned} H_{E}(-N_{E}) \le \frac{N_{E}}{\delta _{E} - P_{EE}}\left( P_{EE} e^{\delta _{E}(-N_{E} - H_{0})} - \delta _{E} e^{ (-N_{E} - H_{0})}\right) < 0. \end{aligned}$$

On the other hand, let $A = N_{E} + H_{0} - \alpha$, we have

$$\begin{aligned} H_{E}( - N_{E} +\alpha ) = \alpha + N_{E}e^{-P_{EE}A} + \frac{P_{EE}N_{E}}{\delta _{E} - P_{EE}}(e^{-\delta _{E}A} - e^{-P_{EE}A}) . \end{aligned}$$

By the mean value theorem, we have

$$\begin{aligned} H_{E}( - N_{E} +\alpha ) \ge \alpha + N_{E}e^{-P_{EE}A} - P_{EE}N_{E}Ae^{-A m} , \end{aligned}$$

where $m = \min \{\delta _{E}, P_{EE}\}$. Since $A > N_{E}$ by the assumption of the theorem, we have

$$\begin{aligned} H_{E}( - N_{E} +\alpha ) \ge \alpha - P_{EE}N_{E}^{2}e^{-m N_{E}} >0 \end{aligned}$$

provided $N_{E} m > 1$. By the intermediate value theorem, $R_{*}$ must be between $N_{E}$ and $N_{E} - \alpha$. This implies $R_{E}(\infty ) = R_{*} > N_{E} - \alpha$.

It remains to check $R_{I}(\infty )$. Let $B = R^{*} + H_{0}$. Recall that we have

$$\begin{aligned} u_{E}(\infty ) = N_{E}(1 - e^{-\delta _{E}B}) . \end{aligned}$$

On the other hand, if we treat $H_{E}(t)$ as a time-dependent variable, we have

$$\begin{aligned} u_{E}(\infty ) = N_{E}\left( 1 - e^{-\delta _{E} \int _{0}^{\infty } H_{E}(s) {\mathrm {d}}s}\right) . \end{aligned}$$

This implies

$$\begin{aligned} \int _{0}^{\infty }H_{E}(s) {\mathrm {d}}s = B . \end{aligned}$$

Now let $u_{I} = R_{I} + G_{I}$, we have

$$\begin{aligned} \frac{{\mathrm {d}}u_{I}}{{\mathrm {d}}t} = \lambda _{I}H_{E}(t)(N_{I} - u_{I}) , \end{aligned}$$

which is again a separable equation. This implies

$$\begin{aligned} u_{I}(\infty ) = N_{I}(1 - e^{-\delta _{I}B}) . \end{aligned}$$

Finally, we have

$$\begin{aligned} \frac{{\mathrm {d}}G_{I}}{{\mathrm {d}}t} = \frac{{\mathrm {d}}u_{I}}{{\mathrm {d}}t} - P_{IE}H_{E}G_{I} , \end{aligned}$$

which is a first order linear equation. Consider the initial condition $G_{I}(0) = u_{I}(0) = 0$, we have

$$\begin{aligned} e^{P_{IE}\int _{0}^{\infty } H_{E}(s) {\mathrm {d}}s}G_{I}(\infty ) = u_{I}(\infty ) . \end{aligned}$$

Therefore, we have

$$\begin{aligned} R_{I}(\infty ) = N_{I} - N_{I}e^{-\delta _{I}B} - e^{-P_{IE}B}N_{I}(1 - e^{-\delta _{I}B}) > N_{I} - N_{I}(e^{-\delta _{I}B} + e^{-P_{IE}B}) . \end{aligned}$$

Since $B = R^{*} + H_{0}> N_{E} - \alpha + H_{0} > N_{E}$, we have

$$\begin{aligned} R_{I}(\infty ) \ge N_{I} - N_{I}(e^{-\delta _{I}N_{E}} + e^{-P_{IE}N_{E}}) = N_{I} - \beta . \end{aligned}$$

The theorem then follows by the definition of limit and the continuous dependency of the solution on parameters. $\square$

Theorem 5.1 implies that as long as $\tau _{I}$ is sufficiently large, even if without external drive, most neurons will eventually spike provided that there are enough pending excitatory spikes in the beginning. Note that m is typically not a very small number ($\approx 0.1$ in our case). Hence $\alpha$ and $\beta$ are both very small numbers.

Needless to say, this theoretical result only describes the limit senario in which $\tau _{I}$ is extremely slow. Usually much stronger assumptions are needed to prove theorems rigorously. In the real brain, GABA is only a few milliseconds slower than AMPA. Hence a more realistic $\tau _{I}$ is only 2–3 times larger than $\tau _{E}$. Theorem 5.1 should be interpreted together with the continuous dependency on parameters of ordinary differential equations. When $\tau _{I}$ is very large, almost all neurons participate in an MFE. And obviously only a few neurons have chance to spike if $\tau _{I}$ is much smaller than $\tau _{E}$. Then because of the continuous dependency on parameters, there must exists a pair of $(\tau _{E}, \tau _{I})$ that can produce desired MFE size in the SIR model above. Our simulation shows that in practice, when $\tau _{I}$ is about 5 times larger than $\tau _{E}$, an MFE is close to a fully synchronized spike volley (network SYNC). And moderate sized MFE are produced when $\tau _{I}$ is 2–3 times larger than $\tau _{E}$ (network $\mathbf{REG1}\sim \mathbf{3}$).

5.2 The branching process model

The SIR model describes the trend of pending number of spikes during an MFE, but not its stochastic properties. However, later we will see that the fluctuation of MFE sizes plays a significant role in the mechanism of spatial correlation decay. In this subsection, we introduce another qualitative process that aims to depict a caricature of an MFE from a probabilistic point of view.

Consider two integer-valued processes with a “switch” $(Y^{E}_{t}, Y^{I}_{t}, S_{t})$ that describes the pending excitatory spikes, pending inhibitory spikes, and the value of the “switch”, respectively. $S_{t} = 1$ means the switch is on, and an MFE is running. A random clock is associated with the switch when it is on, whose ringing time is a random variable $\Theta$ that is independent of $Y^{E}_{t}$ and $Y^{I}_{t}$. The switch is turned off when either (1) this clock rings or (2) $Y^{E}_{t}$ or $Y^{I}_{t}$ is greater than or equal to $N_{E}$ or $N_{I}$, respectively. In other words, $\Theta$ represents the arrival time of inhibitory flux generated by the network. In this subsection we further assume that T is an exponential random variable with mean $a\tau _{I}$, where a is a constant.

When the switch is on, $Y^{E}_{t}$ (resp. $Y^{I}_{t}$) evolves according to the following rules. For $0 < h \ll 1$,

$$\begin{aligned} Y^{E}_{t+h} = \left\{ \begin{array}{lll} Y^{E}_{t} + i - 1&{} \text{ with } \text{ probability } &{} Y^{E}_{t} \tau _{E}^{-1} p^{E}_{i} \cdot h + o(h) \\ Y^{E}_{t} &{} \text{ with } \text{ probability } &{} 1 - Y^{E}_{t} \tau _{E}^{-1} \cdot h + o(h) \end{array} \right. \end{aligned}$$

(resp.

$$\begin{aligned} Y^{I}_{t+h} = \left\{ \begin{array}{lll} Y^{I}_{t} + i &{} \text{ with } \text{ probability } &{} Y^{E}_{t} \tau _{E}^{-1} p^{I}_{i} \cdot h + o(h) \\ Y^{I}_{t} - 1 &{} \text{ with } \text{ probability } &{}Y^{I}_{t} \tau _{I}^{-1} \cdot h + o(h)\\ Y^{I}_{t} &{} \text{ with } \text{ probability } &{} 1 - (Y^{E}_{t} \tau _{E}^{-1} + Y^{I}_{t} \tau ^{-1}_{I})\cdot h + o(h) \end{array} \right. \end{aligned}$$

)

for $i = 0, 1, \ldots , N_{E}$ (resp. $i = 0, 1, \ldots , N_{I}$), where $p^{E}_{i}$ (resp. $p^{I}_{i}$) is the probability that a binomial distribution $B(N_{E}, \delta _{E})$ (resp. $B(N_{I}, \delta _{I})$) equals i, and $\delta _{E}$, $\delta _{I}$ are two model parameters. In other words $Y^{E}_{t}$ is a continuous-time Galton–Watson branching process, while $Y^{I}_{t}$ is driven by $Y^{E}_{t}$.

If the switch is off, the reproduction is stopped and the time evolution of $Y^{E}_{t}$ (resp. $Y^{I}_{t}$) becomes

$$\begin{aligned} Y^{E}_{t+h} = \left\{ \begin{array}{lll} Y^{E}_{t} - 1&{} \text{ with } \text{ probability } &{} Y^{E}_{t} \tau _{E}^{-1} \cdot h + o(h) \\ Y^{E}_{t} &{} \text{ with } \text{ probability } &{} 1 - Y^{E}_{t} \tau _{E}^{-1} \cdot h + o(h) \end{array} \right. . \end{aligned}$$

(resp.

$$\begin{aligned} Y^{I}_{t+h} = \left\{ \begin{array}{lll} Y^{I}_{t} - 1 &{} \text{ with } \text{ probability } &{}Y^{I}_{t} \tau _{I}^{-1} \cdot h + o(h)\\ Y^{I}_{t} &{} \text{ with } \text{ probability } &{} 1 - Y^{I}_{t} \tau ^{-1}_{I}\cdot h + o(h) \end{array} \right. . \end{aligned}$$

) In other words the cumulated pending spikes will take effect at random times and eventually disappear.

Finally, when the switch is off, it waits for a random time period ${\mathcal {T}}$ before being turned on again. When the switch is on, another MFE starts to evolve as described above.

It remains to describe the “neuron spikes” generated by $Y^{E}_{t}$ and $Y^{I}_{t}$. Let $X^{E}_{t}$ (resp. $X^{I}_{t}$) be a point process that takes value on ${\mathbb {R}}^{+} \times \{1, \ldots , N_{E}\}$ (resp. ${\mathbb {R}}^{+} \times \{1, \ldots , N_{I}\}$). If $Y^{E}_{t}$ (resp. $Y^{I}_{t}$) changes its value (resp. jumps down by one) at time t, $X^{E}_{t}$ (resp. $X^{I}_{t}$) produces a point at $(t, u_{E})$ (resp. $(t, u_{I})$), where $u_{E}$ (resp. $u_{I}$) is a uniformly distributed random variable on $\{1, \ldots , N_{E}\}$ (resp. $\{1, \ldots , N_{I}\}$).

Similar to the SIR model, it is not easy to determine many parameters in this branching process model. Therefore, it only attempts to capture main qualitative features of an MFE. When an MFE starts, excitatory neurons excite themselves so that more and more excitatory neurons spike. This cascade of excitatory spikes behaves like a branching process. This recurrent excitation is eventually curbed by inhibitory kicks (which are assumed to be slower). It’s not easy to model the second phase in a mathematical tractable way. In our branching process model, we mimic this phase by terminating the branching process at a random time $\Theta$.

The branching process model can also qualitatively demonstrate the dependency of MFE sizes on $\tau _{E}$ and $\tau _{I}$. When $\tau _{I}$ is sufficiently long, the branching process keeps evolving. A branching process approaches to infinity if it does not extinct. The extinction probability of $Y^{E}_{t}$ (assuming $\tau _{I} = \infty$) is $s_{*}^{Y^{E}_{0}}$, where $H_{0}$ is the number of pending kicks at $t = 0$, and $s_{*}$ is the smallest root of $(1 - \delta _{E} + \delta _{E}s)^{N_{E}} = s$ on [0, 1]. (See Athreya et al. 2004 for standard results of Galton–Waston branching processes.) It is easy to see that $s_{*}$ is very small if $N_{E}\delta _{E} \gg 1$. For example, if $N_{E} = 300$, we have $s_{*} = 0.0586$ when $\delta _{E} = 0.01$ and $s_{*} = 0.00237$ when $\delta _{E} = 0.02$. Therefore, if $\tau _{I}$ is large, $Y^{E}_{t}$ (resp. $Y^{I}_{t}$) has high probabilities to reach $N_{E}$ (resp. $N_{I}$), which produces a full synchronization. This is consistent with observations of our network model and the result of Theorem 5.1.

In practice, $(X^{E}_{t}, X^{I}_{t})$ are able to produce raster plots that look very similar to those produced by the real network model. In Fig. 5, we demonstrate a fake “raster plot” produced by the $X^{E}_{t}$ and $X^{I}_{t}$. Many MFEs can be observed in this figure.

Fig. 5

The fake “raster plot” generated by point processes $X^{E}_{t}$ and $X^{I}_{t}$. Parameters are chosen as $\tau _{E} = 2$ ms, $\tau _{I} = 4$ ms, $\delta _{E} = 0.01$, $\delta _{I} = 0.02$. The termination time $\Theta$ is the minimum of an exponential random variable with mean 4 ms, $Y^{E}_{t}$ reaches $N_{E}/2$, and $Y^{I}_{t}$ reaches $N_{I}/2$. ${\mathcal {T}}$ equals 10 ms plus an exponential random variable with mean 5 ms

6 Spatial correlation of multiple firing events

As mentioned in Sect. 4, MFEs generated by different local populations are very correlated. (See Fig. 3.) We call such correlated MFEs among different local populations the spatial correlation. One interesting observation is that under “reasonable” parameter settings, this correlated spiking activity can only spread to several blocks away. The aim of this section is to investigate two questions: (i) What is the mechanism of this spatial correlation? and (ii) How far away could this spatial correlation spread? We describe our quantification and numerical results of spatial correlations in Sects. 6.1 and 6.2. Studies of mechanisms of spatial correlations and the spatial correlation decay are based on the qualitative MFE models studied in Sect. 5, which are carried out in Sects. 6.3 and 6.4, respectively.

6.1 Quantifying spatial correlations

The quantification of spatial correlations relies on the ergodicity of the Markov process. It follows from Corollary 3.5 that for any two local populations (m, n) and $(m', n')$ and any $Q_{1}, Q_{2} \in \{E, I\}$, we have well-defined and computable covariance $\text{ cov }_{T}^{Q_{1}, Q_{2}}(m,n; m', n')$ and Pearson’ correlation coefficient $\rho ^{Q_{1}, Q_{2}}_{T}(m,n; m',n')$. By Corollary 3.6, the covariance $\text{ cov }_{T}(m,n; m',n')$ and correlation coefficient $\rho _{T}(m,n; m',n')$ for the total spike count between two local population (regardless the synapse type) are also well defined and computable. We can use a long trajectory of $\Phi _{t}$ to generate large sample of spike counts in time bins to compute these quantities.

It remains to comment on the size of a time window T. An ideal time window should be large enough to contain an MFE, but not as large as the time between two consecutive MFEs. There is no silver lining of time-window size that fits all parameter sets. A (very) rough estimate is that T should be greater than the maximum of $N_{Q}$ i.i.d exponential random variables with mean $\tau _{Q}$, but less than $\Sigma /\lambda ^{Q}_{m,n} + \tau _{{\mathcal {R}}}$. It is well known that the maximum of $N_{Q}$ i.i.d exponential random variables with mean $\tau _{Q}$, denoted by Z, can be represented as the sum of independent exponential random variables $Z = \xi _{1} + \cdots + \xi _{N_{Q}}$, where exponential random variable $\xi _k$ has mean $\frac{\tau _Q}{k}$. Hence the expectation of Z is $\tau _Q H_{N_Q}$, where $\{H_{n}\}$ is the Harmonic number $H_{n} = \sum _{k = 1}^{n} \frac{1}{k}$.

It is clear that $H_{N_{Q}} \tau _{Q}$ overestimates because an MFE may not involve all neurons. At the same time, it also underestimates because it takes some time for the cascade of excitatory spikes to excite all neurons participating in an MFE. But our simulations shows that the qualitative properties of the spatial correlation is not very sensitive with respect to the choice of time-window size. For the parameters of a “regular” network, we have $H_{300}\tau _{EE} \approx 10$ ms. Also we have $\Sigma /\lambda _{E} + \tau _{{\mathcal {R}}}\approx 19$ ms if $\lambda _{E} = 6000$ (strong drive). Hence we choose $T = 15$ ms in our simulation works.

6.2 Spatial correlation decay

Our key observation is that in many settings, the spatial correlation decays quickly when two local populations are further apart. As discussed in the last subsection, we choose $T = 15$ ms as the size of a time window. Since the qualitative result for the spatial correlation among E–E, E–I .etc are the same, we select $\rho _{T}(m,n; m',n')$ as the metrics of the spatial correlation. All cases of $\rho ^{Q_{1},Q_{2}}_{T}(m,n; m',n'), Q_{1}, Q_{2} \in \{E, I\}$ have little qualitative difference.

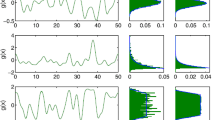
In order to effectively simulate large scale neural fields in which two local populations can be far apart, we choose to study an 1-D network with ${\mathbf {M}} = 1$. The length of array is chosen to be ${\mathbf {N}} = 22$ in all of our simulations. We will compare the Pearson’s correlation coefficient between local populations $L_{1,2}$ and $L_{1,k}$ for $k = 2, \ldots , 21$. The reason of doing this is to exclude the boundary effect at $L_{1,1}$ and $L_{1, 22}$. In our simulation, we run 240 independent long-trajectories of $\Phi _{t}$. In each trajectory, spike counts in 2000 time windows are collected after the process is stabilized. The result of this simulation is presented in Fig. 6. We find that in all five example networks, the spike count correlation decays quickly with increasing distance between local populations. In the homogeneous network HOM, correlation is only observed for nearest neighbor local populations. In three regular networks REG1, REG2, and REG3, no significant correlations are observed when two local populations are 4–8 blocks away. The speed of correlation decay is higher when external drive rates have higher difference (REG1) and when the external connection is weaker (REG3). The synchronized network SYN has the slowest decay rate and obvious fluctuations induced by alternating external drive rate at local populations. If one local population models a hypercolumn in the visual cortex, our simulation suggests that the Gamma wave does not have significant correlation at two locations that are 2–4 mm away. This is consistent with experimental observations.

Fig. 6

Change of spike count correlation coefficient with increasing distance between to local populations. Correlation coefficients are measured between $L_{1,2}$ and $L_{1, k}$ for $k = 2, \ldots , 21$ in five example networks

6.3 Mechanism of spatial correlation

The mechanism of the spatial correlation between neighboring local populations can be explained by our SIR model introduced in Sect.  5. When many local populations form a ${\mathbf {M}}\times {\mathbf {N}}$ array, an SIR system with $6{\mathbf {M}}{\mathbf {N}}$ variables can be derived using the same approach as in Sect. 5. Let $m = 1, \ldots , {\mathbf {M}}$ and $n = 1, \ldots , {\mathbf {N}}$ be indice of local populations. The SIR system contains variables $H^{m,n}_{E}, G^{m,n}_{E}, R^{m,n}_{E}, H^{m,n}_{I}, G^{m,n}_{I}, R^{m,n}_{I}$, whose roles are the same as in Eq. (5.1). For the sake of simplicity denote

$$\begin{aligned} J^{m,n}_{Q_{1}Q_{2}} = P_{Q_{1}Q_{2}}H^{m,n}_{Q_{2}} + \rho _{Q_{1}Q_{2}}\sum _{(m',n') \in {\mathcal {N}}(m,n)}H^{m',n'}_{Q_{2}} . \end{aligned}$$

For each (m, n), the time evolution of variables $H^{m,n}_{E}, G^{m,n}_{E}, R^{m,n}_{E}, H^{m,n}_{I}, G^{m,n}_{I}, R^{m,n}_{I}$ are given by equations

$$\begin{aligned} \begin{aligned} \frac{{\mathrm {d}} H^{m,n}_{E}}{{\mathrm {d}} t}&= - \tau _{E}^{-1} H^{m,n}_{E} + \tau _{E}^{-1}J^{m,n}_{EE}G^{m,n}_{E} + \frac{\lambda _{E}}{S_{EE}} G^{m,n}_{E}\\ \frac{{\mathrm {d}} G^{m,n}_{E}}{{\mathrm {d}}t}&= c_{E} \max \left\{ \tau _{E}^{-1}S_{EE}J^{m,n}_{EE} + \lambda _{E} - \tau _{I}^{-1}S_{EI}J^{m,n}_{EI}, 0\right\} \cdot \left( N_{E} - G^{m,n}_{E} - R^{m,n}_{E}\right) \\&\quad -\tau _{I}^{-1}\max \left\{ \frac{S_{EI}}{S_{EE}}, 1\right\} J^{m,n}_{EI}G^{m,n}_{E} - \left( \tau _{E}^{-1}J^{m,n}_{EE} + \frac{\lambda _{E}}{S_{EE}}\right) G^{m,n}_{E} \\ \frac{{\mathrm {d}} R^{m,n}_{E}}{{\mathrm {d}}t}&= \tau _{E}^{-1}P_{EE}J^{m,n}_{EE} + \frac{\lambda _{E}}{S_{EE}} G^{m,n}_{E}\\ \frac{{\mathrm {d}} H^{m,n}_{I}}{{\mathrm {d}} t}&= - \tau _{I}^{-1} H^{m,n}_{I} + \tau _{E}^{-1}J^{m,n}_{IE}G^{m,n}_{I} + \frac{ \lambda _{I}}{S_{IE}}G^{m,n}_{I}\\ \frac{{\mathrm {d}} G^{m,n}_{I}}{{\mathrm {d}}t}&= c_{I} \max \left\{ \tau _{E}^{-1}S_{IE}J^{m,n}_{IE} + \lambda _{I} - \tau _{I}^{-1}S_{II}J^{m,n}_{II}, 0\right\} \cdot \left( N_{I} - G^{m,n}_{I} - R^{m,n}_{I}\right) \\&\quad -\tau _{I}^{-1}\max \left\{ \frac{S_{II}}{S_{IE}}, 1\right\} J^{m,n}_{II}G^{m,n}_{I} - \left( \tau _{E}^{-1}J^{m,n}_{IE} + \frac{\lambda _{I}}{S_{IE}}\right) G^{m,n}_{I}\\ \frac{{\mathrm {d}} R^{m,n}_{I}}{{\mathrm {d}}t}&= \tau _{E}^{-1}J^{m,n}_{IE}G^{m,n}_{I} + \frac{ \lambda _{I}}{S_{IE}}G^{m,n}_{I} . \end{aligned} \end{aligned}$$

(6.1)

A direct analysis of Eq. 6.1 is too complicated to be interesting. But the numerical result reveals the mechanism of spatial correlation. For the sake of simplicity we consider two local populations, say populations $L_{1,1}$ and $L_{1,2}$. Assume that the local population $L_{1,1}$ is ready for an MFE with initial condition $H_{E} = 1, G_{E} = 30, R_{E} = 0, H_{I} = 0, G_{I} = 10, R_{I} = 0$, while $L_{1,2}$ has a very different profile with $H_{E} = 0, G_{E} = 10, R_{E} = 0, H_{I} = 0, G_{I} = 2, R_{I} = 0$. We further assume that $\tau _{E} = 2$ ms and $\lambda _{E} = \lambda _{I} = 0$. It is easy to see that without $L_{1,1}$, $L_{1,2}$ will not have any spikes because it is not driven. We compare the “event size” of excitatory and inhibitory populations at $L_{1,1}$ and $L_{1,2}$, which is measured at time $T = 20$ ms. This is demonstrated in Fig. 7. With strong connectivity $\text{ ratio }_{E} = 0.15$, the MFE in local population $L_{1,1}$ will induce an MFE at local population $L_{1,2}$, even if local population $L_{1,2}$ has much fewer neurons at the “gate area”.

Fig. 7

Event size versus $\tau _{I}$ for two local populations

We believe that this is the mechanism of spatial correlations in our model. When an MFE occurs in one local population, it sends excitatory and inhibitory input to its neighboring local populations. If the membrane potential of a neighboring local population is properly distributed, an MFE at its neighbor will be induced by this spiking activity. Similar to the case of one local population, the size of an MFE sensitively depends on the excitatory and inhibitory synapse delay times. Slower inhibitory synapses always correspond to bigger MFEs in both local populations.

6.4 Mechanism of spatial correlation decay

Our final task is to investigate the mechanism of spatial correlation decay, as described in Fig. 6, where the spatial correlation of MFEs can only spread to several local populations away.

Why the spatial correlation can not spread to very far away? We believe that (at least in this model) such correlation decay is due to the volatility of spike count in MFEs. The excitatory-inhibitory interplay during an MFE occurs at a very fast time scale with lots of randomness involved. As a result, the spike count in a local population usually has large variance. The variance will be even larger if the external drive rate is heterogeneous. Therefore, even if the initial distributions of the membrane potential and the external drive rates are identical throughout all local populations, the voltage distribution will be very different after the first MFE in each local population. Hence the next wave of MFEs in different local populations will be less coordinated, which destroys the synchronization. We believe this high volatility of MFE sizes significantly contributes to the spatial correlation decay. As shown in Fig. 6, in examples REG1 and REG2, $\lambda ^{E}_{m,n}$ and $\lambda ^{I}_{m,n}$ have very small difference in different local populations. But the spatial correlation decay is still strong. This also explains why the SYN network has the weakest spatial correlation decay. When the sizes of MFEs are close to the size of the entire local population, there will be much less variation in the after-event voltage distribution because most neurons have just spiked. Hence the voltage distributions in different local populations are relatively similar in an SYN network, which contributes to the observed slower decay of the spatial correlation.

This explanation is supported by both analytical calculation and numerical simulation result. We did the following numerical simulation to investigate the volatility of MFE sizes. Assume ${\mathbf {M}} = {\mathbf {N}} = 1$, $\lambda _{E} = \lambda _{I} = 3000$, and the initial voltage distribution is generated in the following way: With probability 0.2, the neuron membrane potential is uniformly distributed on $\{0, 1, \ldots , 80 \}$. With probability 0.8, the neuron membrane potential takes the integer part of a normal random variable with mean 0 and standard deviation 20. This initial voltage distribution roughly mimics the voltage distribution after a large MFE. The synapse delay times are $\tau _{E} = 2$ ms and $\tau _{I} = 1 {-} 9$ ms. For each $\tau _{I} = 1.0, 1.1, \ldots , 9.0$, we simulate this model repeatedly for 10,000 times and count the number of excitatory spikes of the first MFE. Then we plot the mean MFE size and the coefficient of variation (standard deviation divided by mean) of the spike count samples for each $\tau _{I}$. Note that the coefficient of variation is a better metrics than the standard deviation as it is a dimensionless number that measures the relative volatility of an MFE.

Of course this study does not exclude the situation that in a more heterogeneous network or a network with multiple types of inhibitory neurons, MFEs can be reliably generated with much smaller variance. And the spatially correlation of MFEs can be bigger than demonstrated in this paper. But we believe our study at least shed some light to the study of neuronal networks with relatively large, dense, and homogeneous local populations, such as the visual cortex. And the diversity of MFE sizes should partially contributes to the mechanism of spatial correlation decay of Gamma rhythm that is experimentally observed.

Fig. 8

Left: mean event size versus $\tau _{I}$. Right: coefficient of variation versus $\tau _{I}$

This numerical result is shown in Fig. 8. We can see that when $\tau _{I}$ become larger, the MFE size increases and the coefficient of variation decreases. This decrease is a finite size effect. In the extreme case an MFE becomes a fully synchronized spike volley. But even the size of such a spike volley can not be much larger than the number of neurons. Only a very small number of neurons have the chance to spike twice in a spike volley, even if in the most synchronized network. This gives a smaller variance of MFE sizes. The change of coefficient of variation partially explains the observation in Fig. 6, in which the decay of spatial correlation is weaker when the $\tau _{I}$-to-$\tau _{E}$ ratio is larger (means the network is more synchronized).

It is difficult to directly study the MFE size distribution by working on the network model. But our qualitative model in Sect. 5 can help us to explain the mechanism of the high variance of MFE sizes. Recall that in Sect. 5.2, we model an MFE by stopping a Galton–Watson branching process at a random time. Some calculation for a Galton–Watson process will qualitatively explain the reason of high coefficient of variation of sizes of MFEs.

To simplify the calculation, we only consider $Y^{E}_{t}$ and discretize it into a discrete-time Galton–Watson process. Let $X_{i} \sim B(N_{E}, \delta _{E})$ be i.i.d Binomial random variables that represent the numbers of new excitatory spike stimulated by an excitatory spike. Let $Y^{E}_{n}$ be a branching process such that $Y_{0} = 1$ and

$$\begin{aligned} Y^{E}_{n+1} = X_{1} + \cdots + X_{Y^{E}_{n}} . \end{aligned}$$

Let $\Theta$ be a random time that is independent of all $X_{i}$ and $Y^{E}_{i}$, which is the approximate onset time of network inhibition. Here we do not put any assumption on $\Theta$. It is easy to see that $Y^{E}_{n}$ mimics the Galton–Watson branching process $Y^{E}_{t}$ introduced in Sect. 5.2. The “unit time” of $Y^{E}_{n}$ is $\tau _{E}$.

Let the total number of spikes before step n be $S^{E}_{n} = Y^{E}_{1} + \cdots + Y^{E}_{n}$. Then the MFE size equals

$$\begin{aligned} S_{T} = Y^{E}_{1} + \cdots + Y^{E}_{\Theta } . \end{aligned}$$

Let

$$\begin{aligned} \text{ CV }(X) = \frac{\sqrt{{\mathbb {E}}[(X - {\mathbb {E}}[X])^{2}]}}{{\mathbb {E}}[X]} \end{aligned}$$

be the coefficient of variation of a positive-valued random variable X. The following proposition is straightforward. Note that the bound of $\text{ CV(X) }$ does not depend on $\Theta$.

Proposition 6.1

Let $\sigma ^{2} = N_{E}\delta _{E}(1-\delta _{E})$ and $\mu = N_{E}\delta _{E}$. Assume $\Theta$ has finite moment generating function $M_{\Theta }(t)$ such that $M_{\Theta }(2 \log \mu ) < \infty$. We have

$$\begin{aligned} \text{ CV }(S_{\Theta }) \ge \frac{\sigma \sqrt{\mu - 1}}{\mu \sqrt{\mu + 1}} . \end{aligned}$$

Proof

The proof follows from straightforward elementary calculations. By the property of the Galton–Watson process, we have

$$\begin{aligned} {\mathbb {E}}[Y^{E}_{n}] = \mu ^{n} \end{aligned}$$

and

$$\begin{aligned} \text{ Var }[Y^{E}_{n}] = \mu ^{n-1}\sigma ^{2}(1 + \mu + \cdots + \mu ^{n-1}) \ge \mu ^{2n-2}\sigma ^{2} . \end{aligned}$$

In addition, for $n \ge m$ we have

$$\begin{aligned} \text{ cov }(Y^{E}_{m}, Y^{E}_{n})= & {} = {\mathbb {E}}[ Y^{E}_{m}Y^{E}_{n}] - {\mathbb {E}}[Y^{E}_{m}] {\mathbb {E}}[Y^{E}_{n}]\\= & {} \mu ^{n - m} {\mathbb {E}}[(Y^{E}_{m})^{2}] - \mu ^{m+n}\\\ge & {} \mu ^{n-m} {\mathbb {E}}[Y^{E}_{m}]^{2} - \mu ^{m+n} = 0 \, \end{aligned}$$

Therefore, we have

$$\begin{aligned} {\mathbb {E}}[S_{n}] = \sum _{k = 1}^{n} \mu ^{k} = \frac{\mu ^{n+1} - 1}{\mu - 1} \end{aligned}$$

and

$$\begin{aligned} \text{ Var }[S_{n}]\ge & {} \sum _{k = 1}^{n} \text{ Var }[Y^{E}_{k}] \\= & {} \sigma ^{2}(1 + \cdots + \mu ^{2n - 2}) = \sigma ^{2}\frac{\mu ^{2n} - 1}{\mu ^{2} - 1} . \end{aligned}$$

By the law of total expectation,

$$\begin{aligned} {\mathbb {E}}[S_{\Theta }] = {\mathbb {E}}\left[ \frac{\mu ^{\Theta +1} - 1}{\mu - 1} \right] = \frac{\mu M_{\Theta }(\log \mu ) - 1}{\mu - 1}. \end{aligned}$$

By the law of total variance we have

$$\begin{aligned} \text{ Var }[S_{\Theta }] \ge {\mathbb {E}}[\text{ Var }[S_{\Theta }|\Theta ]] \ge \frac{\sigma ^{2}}{\mu ^{2} - 1} {\mathbb {E}}[ \mu ^{2\Theta } - 1] = \frac{\sigma ^{2}}{\mu ^{2} - 1} (M_{\Theta }(2 \log \mu ) - 1) . \end{aligned}$$

By Jensen’s inequality

$$\begin{aligned} M_{\Theta }(2 \log \mu ) = {\mathbb {E}}[ (\mu ^{\Theta })^{2}] \ge ({\mathbb {E}}[\mu ^{\Theta }])^{2} = M_{\Theta }(\log \mu )^{2} . \end{aligned}$$

Let $C = M_{\Theta }(\log \mu ) > 1$. We have

$$\begin{aligned} \text{ CV }(S_{\Theta })\ge & {} \sigma \frac{\mu - 1}{\mu \sqrt{\mu ^{2} - 1}} \cdot \frac{ \sqrt{C^{2} - 1}}{C - \mu ^{-1}}\\\ge & {} \sigma \frac{\mu - 1}{\mu \sqrt{\mu ^{2} - 1}} \cdot \sqrt{\frac{C+1}{C - 1}} \ge \frac{\sigma \sqrt{\mu - 1}}{\mu \sqrt{\mu + 1}} . \end{aligned}$$

$\square$

Note that the effective $\delta _{E}$ is usually a small number such that $N_{E}\delta _{E} = O(1)$. For example, if membrane potential is uniformly distributed on $\{0, 1, \ldots , \Sigma -1\}$ then the effective $\mu = N_{E}\delta _{E}$ is $N_{E}P_{EE}S_{EE}/\Sigma = 2.25$ for the parameter set used in this paper. This corresponds to $\frac{\sigma \sqrt{\mu - 1}}{\mu \sqrt{\mu + 1}} \approx 0.4$. According to the assumption in Sect. 5.2, this branching process is terminated when $Y^{E}_{n}$ reaches $N_{E}$. If this happens before $\Theta$ with high probability, the coefficient of variation will be significantly smaller, as the MFE has to stop at that time.

7 Conclusion

In this paper we study a stochastic model that models a large and heterogeneous brain area consisting of many relatively homogeneous local populations. Each local population has many densely connected excitatory and inhibitory neurons. In addition, nearest-neighbor local populations are coupled. One can think of a local population as an orientation hypercolumn of the primary visual cortex. Similar to our previous paper (Li et al. 2018), one salient feature of this model is the occurrence of multiple firing event (MFE), in which a proportion of neurons in the population (but not all of them) spike in a small time window. An MFE is an emergent neuronal activity that lies between full synchronization and independent spiking, which is widely believed to be responsible for the Gamma rhythm in the cortex.

We first work on the stochastic stability of the Markov process produced by this model. This further allows us to rigorously prove the well-definedness and computability of many observables related to the network dynamics, including MFEs. Then we propose two qualitative models to further investigate the mechanism of a MFE. The first model mimics an SIR disease model, which treats a pending spike as an infected patient that can make other neurons spike. The “infected” neuron jumps to the refractory state immediately and is “immuned” from further postsynaptic kicks. The second model uses a Galton–Waston branching process to address the recurrent excitatory during an MFE. This Galton–Waston branching process is eventually terminated at a random time $\Theta$, corresponding to the onset of inhibition from the network.

Then we investigate the decay of spatial correlation of MFEs in the model. Our simulation shows that correlated MFEs can usually only spread to several local populations away. This is consistent with the physiological fact that the Gamma rhythm is often very local. We use the SIR model to explain why an MFE in a local population could induce a spike barrage in its neighboring local populations. Further, we find that unless all MFEs are so strong that it becomes fully synchronized spike volleys, the spike count in MFEs should have a very high diversity. As a result, voltage profiles after an MFE are very different among local populations, even if the external drive rate is fairly homogeneous. This diversity of MFEs at least partially explains the mechanism of the spatial correlation decay. This mechanism is analytically justified by working on our branching process MFE model.