Abstract
We survey recent work on extending neural field theory to take into account synaptic noise. We begin by showing how mean field theory can be used to represent the macroscopic dynamics of a local population of N spiking neurons, which are driven by Poisson inputs, as a rate equation in the thermodynamic limit N → ∞. Finite-size effects are then used to motivate the construction of stochastic rate-based models that in the continuum limit reduce to stochastic neural fields. The remainder of the chapter illustrates how methods from the analysis of stochastic partial differential equations can be adapted in order to analyze the dynamics of stochastic neural fields. First, we consider the effects of extrinsic noise on front propagation in an excitatory neural field. Using a separation of time scales, it is shown how the fluctuating front can be described in terms of a diffusive–like displacement (wandering) of the front from its uniformly translating position at long time scales, and fluctuations in the front profile around its instantaneous position at short time scales. Second, we investigate rare noise-driven transitions in a neural field with an absorbing state, which signals the extinction of all activity. In this case, the most probable path to extinction can be obtained by solving the classical equations of motion that dominate a path integral representation of the stochastic neural field in the weak noise limit. These equations take the form of nonlocal Hamilton equations in an infinite–dimensional phase space.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
The spike trains of individual cortical neurons in vivo tend to be very noisy, having interspike interval (ISI) distributions that are close to Poisson [58]. The main source of intrinsic fluctuations at the single cell level is channel noise , which arises from the variability in the opening and closing of a finite number of ion channels [57]. On the other hand, extrinsic fluctuations in membrane voltage are predominantly due to synaptic noise. That is, cortical neurons are bombarded by thousands of synaptic inputs, many of which are not correlated with a meaningful input and can thus be treated as background synaptic noise [31]. It is not straightforward to determine how noise at the single cell level translates into noise at the population or network level. One approach is to formulate the dynamics of a population of spiking neurons in terms of the evolution of the probability density of membrane potentials – the so–called population density method [1, 16, 17, 21, 36, 39, 46, 48, 52, 53]. Usually, a simple model of a spiking neuron is used, such as the integrate–and–fire model [35], and the network topology is assumed to be either fully connected or sparsely connected. It can then be shown that under certain conditions, even though individual neurons exhibit Poisson–like statistics, the neurons fire asynchronously so that the total population activity evolves according to a mean–field rate equation with a characteristic activation or gain function. This gain firing rate function can then be used to construct rate–based models. Formally speaking, the asynchronous state only exists in the thermodynamic limit N → ∞, where N determines the size of the population. This then suggests a possible source of intrinsic noise at the network level arises from fluctuations about the asynchronous state due to finite size effects [7, 37, 41, 44, 59].
In this chapter we review recent work on incorporating synaptic noise into continuum neural fields, and methods for analyzing the resulting stochastic dynamics. Neural field equations can be derived under two basic assumptions: (i) the spike trains of individual neurons are decorrelated (asynchronuous) so that the total synaptic input to a neuron is slowly varying and deterministic, and (ii) there exists a well–defined continuum limit of the resulting network rate equations. So far there has been no rigorous proof that either of these assumptions hold in large–scale spiking network models of cortex . In particular, there has been no systematic scaling up of population density methods to derive continuum neural field models that take proper account of noise–induced fluctuations and statistical correlations between neurons at multiple spatial and temporal scales. Consequently, current formulations of stochastic neural field theory tend to be phenomenologically based. One approach is to consider a Langevin version of the deterministic neural field equations involving some form of extrinsic spatiotemporal white noise [15, 32, 38], whereas another is to treat the neural field equations as the thermodynamic limit of an underlying master equation [9, 10, 19, 20]. In the latter case, a diffusion approximation leads to an effective Langevin equation with multiplicative noise.
In order to motivate the construction of stochastic neural field equations, we begin by reviewing the population density method for analyzing the stochastic dynamics of a local population of leaky integrate-and-fire neurons (Sect. 9.2), following along similar lines to Gerstner and Kistler [35]. We then describe how finite–size effects at the level of local populations can be incorporated into stochastic versions of rate–based models (Sect. 9.3). In Sect. 9.4 we show how stochastic PDE methods can be used to analyze traveling waves in stochastic neural fields. Finally, we derive a path integral formulation of a stochastic neural field and show how this can be used to analyze rare events (Sect. 9.5). Note that a related survey of stochastic neural fields can be found in Ref. [12].
2 Population Density Method and Mean Field Theory
Integrate-and-fire (IF) neuron models neglect details regarding the spike generation process by reducing the latter to an all–or–nothing threshold event. That is, whenever the membrane potential crosses a firing threshold, the neuron fires a spike, typically modeled as a Dirac delta function, and the membrane potential is reset to some subthreshold value. Although they are less realistic than conductance–based models, they have provided a very useful platform for exploring probabilistic models of spiking neurons [35]. Consider a homogeneous population of N identical uncoupled leaky IF neurons. The membrane potential (internal state) of the ith neuron evolves according to the equation
where C, R are the capacitance and resistance of the cell membrane and I i (t) represents the sum of synaptic and external currents. The form of the action potential is not described explicitly. Spikes are formal events characterized by the ordered sequence of firing times \(\{T_{i}^{m},m \in \mathbb{Z}\}\) determined by the threshold crossing conditions
where κ is the firing threshold. Immediately after firing, the potential is reset to a value V r < κ,
For simplicity we set V r = 0, CR = τ and absorb C into I i (t).
Suppose that all neurons in the population receives the same driving current I ext. Each neuron also receives a stochastic background input consisting of a set of spike trains stimulating different synapses labeled k = 1, …, K. An input spike of the kth synapse causes a jump of the membrane potential by an amount w k , and the spikes are generated by a time-dependent Poisson process at a rate ν k (t). This means that in each small time interval [t, t +Δ t] the probability that a spike arrives on the kth synapse is ν k (t)Δ t, and each spike is uncorrelated with any other. Although the spike rates ν k (t) are the same for all neurons, the actual spike trains innervating different synapses of different neurons are statistically independent. Let p(v, t) denote the membrane potential density, that is, p(v, t)dv is the fraction of neurons i that have a membrane potential v ≤ V i (t) ≤ v + dv in the limit N → ∞. Whenever a neuron fires it’s membrane is reset. This has two important implications. First, conservation of probability implies that
Second, the fraction of neurons (probability flux J(κ, t)) that flow across the threshold κ per unit time determines the population activity A(t):
The reset condition means that neurons that “disappear” across threshold “re-enter” the population at the reset potential v = 0. This implies that there is an absorbing boundary condition at threshold
and a discontinuity in the probability fluxes at reset:
The probability density p(v, t) evolves according to the Chapman-Kolmogorov equation [35]Footnote 1
In the limit of small jump amplitudes w k , Eq. (9.8) can be approximated by a diffusion equation. That is, Taylor expanding to second order in w k gives
where μ(t) is the mean background synaptic input
and σ(t) determines the size of the membrane fluctuations,
The Fokker-Planck equation determines the time evolution of the probability density of a membrane potential evolving according to the equivalent stochastic differential equation (Langevin equation )
where W(t) is a Wiener process,
In the case of constant rates ν k , the resulting Langevin equation describes the well known Ornstein–Uhlenbeck process .
The Fokker–Planck equation (9.9) can be rewritten as a continuity equation reflecting conservation of probability:
where
Equations (9.5) and (9.15) together with the absorbing boundary condition (9.6) implies that
Continuity of p at reset, \(p(0^{+},t) = p(0^{-},t)\), together with Eqs. (9.7) and (9.15) show that there is a discontinuity in the first derivative of p(v, t) at v = 0:
Hence, one has to solve the Fokker–Planck equation (9.9) together with the boundary conditions (9.6), (9.16), and (9.17).
Now suppose that the background rates ν k and external input I ext are time–independent so that the total mean input
is a constant. The steady–state Fokker–Planck equation implies that the flux
with \(\sigma _{0} =\sum _{k}\nu _{k}w_{k}^{2}\) for time-independent rates, is constant except at v = 0 where it jumps by an amount A 0, which is the steady–state population activity. Taking J(v) = 0 for v < 0, one can solve Eq. (9.19) to obtain the Gaussian distribution
for some constant c 1. However, such a solution cannot be valid for v > 0, since it does not satisfy the absorbing boundary condition p 0(κ) = 0. It turns out that in this domain the solution is of the form [17, 35]
for some constant c 2. Equation (9.19) shows that c 2 = 2J(v) for 0 < v ≤ κ with J(v) = A 0. Continuity of the solution at u = 0 implies that
Finally, the constant c 2 is determined by the normalization condition for p. On setting A 0 = c 2∕2κ, one finds a firing rate
where F is the so–called gain function for the population [17, 35, 46].
The above analysis assumed that the neurons were independent of each other so that the only synaptic inputs were from some stochastic background. Now suppose that we have a fully connected network such that there is an additional contribution to the synaptic input into each neuron of the form
where Γ 0∕N is the strength of connection between any pair of neurons within the population , and we have used the definition (9.5) of the population activity A(t). Suppose that the neuronal population is in a macroscopic state with constant activity A(t) = A 0, which is referred to as a state of asynchronous firing. (Formally speaking, such an asynchronuous state only makes sense in the thermodynamic limit N → ∞.) The steady–state activity can then be determined self–consistently from Eq. (9.23) by setting
and solving the implicit equation for A 0 in terms of \(I_{\mathrm{ext}} +\sum _{k}\nu _{k}w_{k}\), which leads to an effective gain function \(A_{0} = F_{\mathrm{eff}}(I_{\mathrm{ext}} +\sum _{k}\nu _{k}w_{k})\). One can also determine the stability of the asynchronous state by considering small perturbations of the steady–state probability distribution. One finds that in the limit of low noise, the asynchronous state is unstable and the neurons tend to split up into several synchronized groups that fire alternately. The overall activity then oscillates several times faster than the individual neurons [17, 36, 63]. One of the interesting properties of the asynchronous state from a computational perspective is that the population activity can respond rapidly to a step input [35]. The basic intuition behind this is that in the asynchronous state there will always be a significant fraction of neurons that are sitting close to the firing threshold so that as soon as a step increase in input current occurs they can respond immediately. However, the size of the step has to be at least as large as the noise amplitude σ, since the threshold acts as an absorbing boundary, that is, the density of neurons vanishes as v → κ.
So far noise has been added explicitly in the form of stochastic background activity as described in the paragraph below equation (3). It is also possible for a network of deterministic neurons with fixed random connections to generate its own noise [3, 16, 17, 64]. In particular, suppose that each neuron in the population of N neurons receives input from C randomly selected neurons in the population with C ≪ N. The assumption of sparse connectivity means that two neurons share only a small number of common inputs. Hence, if the presynaptic neurons fire stochastically then the input spike trains that arrive at distinct postsynaptic neurons can be treated as statistically independent. Since the presynaptic neurons belong to the same population, it follows that each neuron’s output should itself be stochastic in the sense that it should have a sufficiently broad distribution of interspike intervals. This will tend to occur if the neurons operate in a subthreshold regime, that is, the mean total input is below threshold so that threshold crossings are fluctuation driven.
3 Stochastic Rate–Based Models
Now suppose that a network of synaptically coupled spiking neurons is partitioned into a set of P homogeneous populations with \(N_{\alpha } =\delta _{\alpha }N\) neurons in each population, \(\alpha = 1,\ldots,P\). Let p denote the population function that maps the single neuron index \(i = 1,\ldots,N\) to the population index α to which neuron i belongs: p(i) = α. Furthermore, suppose the synaptic interactions between populations are the same for all neuron pairs. (Relaxing this assumption can lead to additional sources of stochasticity as explored in Refs. [32, 61].) Denote the sequence of firing times of the jth neuron by \(\{T_{j}^{m},\,m \in \mathbb{Z}\}\). The net synaptic current into postsynaptic neuron i due to stimulation by the spike train from presynaptic neuron j, with p(i) = α, p(j) = β, is taken to have the general form \(N_{\beta }^{-1}\sum _{m}\varPhi _{\alpha \beta }(t - T_{j}^{m})\), where \(N_{\beta }^{-1}\varPhi _{\alpha \beta }(t)\) represents the temporal filtering effects of synaptic and dendritic processing of inputs from any neuron of population β to any neuron of population α. (A specific form for Φ α β (t) will be given in Sect. 9.3.1; a more general discussion of different choices of Φ α β (t) can be found in the review of Ref. [12].) Assuming that all synaptic inputs sum linearly, the total synaptic input to the soma of the ith neuron, which we denote by u i (t), is
for all p(i) = α, where \(a_{j}(t) =\sum _{m\in \mathbb{Z}}\delta (t - T_{j}^{m})\). That is, a j (t) represents the output spike train of the jth neuron in terms of a sum of Dirac delta functions. In order to obtain a closed set of equations, we have to determine the firing times T i m given by Eq. (9.2), where V i (t) evolves according to the LIF model (9.1) with \(I_{i}(t) \rightarrow u_{i}(t)\), or the more general conductance-based model
supplemented by additional equations for various ionic gating variables [30]. It follows that, after transients have decayed away, \(u_{i}(t) = u_{\alpha }(t)\) for all p(i) = α with
and a α (t) is the output activity of the αth population:
In general, Eqs. (9.26) and (9.27) are very difficult to analyze. However, considerable simplification can be obtained if the total synaptic current u i (t) is slowly varying compared to the membrane potential dynamics given by Eq. (9.27). This would occur, for example, if each of the homogeneous subnetworks fired asynchronously as described in Sect. 9.2. One is then essentially reinterpreting the population activity variables u α (t) and a α (t) as mean fields of local populations. (Alternatively, a slowly varying synaptic current would occur if the synapses are themselves sufficiently slow [13, 28].) Under these simplifying assumptions, one can carry out a short–term temporal averaging of Eq. (9.28) in which the output population activity is approximated by the instantaneous firing rate \(a_{\alpha }(t) = F_{\alpha }(u_{\alpha }(t))\) with F α identified with the population gain function calculated in Sect. 9.2. (In practice, the firing rate function is usually approximated by a sigmoid.) Equation (9.28) then forms the closed system of integral equations
The observation that finite–size effects provide a source of noise within a local population then suggests one way to incorporate noise into rate–based models, namely, to take the relationship between population output activity a α (t) and effective synaptic current u α (t) to be governed by a stochastic process.
3.1 Neural Langevin Equation
The simplest approach is to assume that population activity is a stochastic variable A α (t) evolving according to a Langevin equation (stochastic differential equation) of the form
with the stochastic current U α (t) satisfying the integral equation (9.28). Here W α (t), \(\alpha = 1,\ldots,P\) denotes a set of P independent Wiener processes with
and σ α is the strength of noise in the αth population. In general, the resulting stochastic model is non-Markovian. However, if we take \(\varPhi _{\alpha \beta }(t) = w_{\alpha \beta }\varPhi (t)\) with \(\varPhi (t) =\tau ^{-1}\mathrm{e}^{-t/\tau }H(t)\) and H(t) the Heaviside function , then we can convert the latter equation to the form
It is important to note that the time constant τ α cannot be identified directly with membrane or synaptic time constants. Instead, it determines the relaxation rate of a local population to the mean–field firing rate. In the limit τ α → 0, Eqs. (9.31) and (9.33) reduce to a “voltage–based” rate model perturbed by additive noise:
Here \(\tilde{W}_{\alpha }(t) =\sum _{ \beta =1}^{P}w_{\alpha \beta }\sigma _{\beta }W_{\beta }(t)\) so that
Thus eliminating the dynamics of the firing rate leads to spatially correlated noise for the dynamics of U α . On the other hand, in the limit τ → 0, we obtain a stochastic “activity–based” model
Here the dynamical variable A α represents the firing rate of a local population. For a detailed discussion of the differences between activity-based and voltage-based neural rate equations, see Refs. [12, 30].
3.2 Neural Master Equation
An alternative approach to incorporating noise into the population firing rate has been developed in terms of a jump Markov process [9, 10, 19, 20, 47]. Such a description is motivated by the idea that each local population consists of a discrete number of spiking neurons, and that finite–size effects are a source of intrinsic rather than extrinsic noise [7, 59]. The stochastic output activity of a local population of N neurons is now expressed as \(A_{\alpha }(t) = N_{\alpha }(t)/(N\varDelta t)\) where N α (t) is the number of neurons in the αth population that fired in the time interval [t −Δ t, t], and Δ t is the width of a sliding window that counts spikes. Suppose that the discrete stochastic variables N α (t) evolve according to a one–step jump Markov process:
in which \(\varOmega _{\alpha }^{\pm }(t)\) are functions of N α (t) and U α (t) with U α (t) evolving according to the integral equation (9.28) or its differential version (9.33). Thus, synaptic coupling between populations occurs via the transition rates. The transition rates are chosen in order to yield a deterministic rate–based model in the thermodynamic limit N → ∞. One such choice is
The resulting stochastic process defined by Eqs. (9.37), (9.38) and (9.33) is an example of a stochastic hybrid system based on a piecewise deterministic process [14]. That is, the transition rates \(\varOmega _{\alpha }^{\pm }(t)\) depend on U α (t), with the latter itself coupled to the associated jump Markov according to Eq. (9.33), which is only defined between jumps, during which U α (t) evolves deterministically. (Stochastic hybrid systems also arise in applications to genetic networks [65] and to excitable neuronal membranes [18, 50].) A further simplification is obtained in the limit τ → 0, since the continuous variables U α (t) can be eliminated to give a pure birth–death process for the discrete variables N α (t). Let \(P(\mathbf{n},t) = \text{Prob}[\mathbf{N}(t) = \mathbf{n}]\) denote the probability that the network of interacting populations has configuration \(\mathbf{n} = (n_{1},n_{2},\ldots,n_{P})\) at time t, t > 0, given some initial distribution P(n, 0). The probability distribution then evolves according to the birth–death master equation [9, 19, 20]
where \(\varOmega _{\alpha }^{\pm }(\mathrm{n}) =\varOmega _{ \alpha }^{\pm }(t)\) with N α (t) = n α and \(U_{\alpha }(t) =\sum _{\beta }w_{\alpha \beta }n_{\beta }/(N\varDelta t)\), and \(\mathbb{E}_{\alpha }\) is a translation operator: \(\mathbb{E}_{\alpha }^{\pm 1}F(\mathrm{n}) = F(\mathrm{n}_{\alpha \pm })\) for any function F with n α± denoting the configuration with n α replaced by n α ± 1. Equation (9.39) is supplemented by the boundary conditions P(n, t) ≡ 0 if \(n_{\alpha } = N_{\alpha } + 1\) or n α = −1 for some α. The birth–death master equation (9.39) has been the starting point for a number of recent studies of the effects of intrinsic noise on neural fields, which adapt various methods from the analysis of chemical master equations including system size expansions and path integral representations [9, 19, 20]. However, there are a number of potential problems with the master equation formulation. First, there is no unique prescription for choosing transition rates that yield a given rate–based model in the mean–field limit. Moreover, depending on the choice of how the transition rates scale with the system size N, the statistical nature of the dynamics can be Gaussian–like [9] or Poisson–like [19, 20]. Second, the interpretation of N α (t) as the number of spikes in a sliding window of width Δ t implies that τ ≫ Δ t so the physical justification for taking the limit τ → 0 is not clear. Finally, for large N the master equation can be approximated by a Langevin equation with multiplicative noise (in the sense of Ito), and thus reduces to the previous class of stochastic neural field model [10].
3.3 Continuum Limit
So far we have indicated how to incorporate noise into a discrete network of neuronal populations. In order to obtain a corresponding stochastic neural field equation it is now necessary to take an appropriate continuum limit. For simplicity, we will focus on the simplest stochastic rate model given by Eqs. (9.31) and (9.33). The continuum limit of Eq. (9.33) proceeds heuristically as follows. First, set \(U_{\alpha }(t) = U(\alpha \varDelta d,t),A_{\alpha }(t) = A(\alpha \varDelta d,t)\) and \(w_{\alpha \beta } =\rho \varDelta dw(\alpha \varDelta d,\beta \varDelta d)\) where ρ is a synaptic density and Δ d is an infinitesimal length scale. Taking the limit Δ d → 0 and absorbing ρ into w gives
We also assume that the noise strength \(\sigma _{\alpha } =\sigma /\sqrt{\varDelta d}\) and define \(W_{\alpha }(t)/\sqrt{\varDelta d} = W(\alpha \varDelta d,t)\). Taking the limit Δ d → 0 in Eq. (9.31) with \(\tau _{\alpha } =\hat{\tau }\) for all α gives
with
In the limit \(\hat{\tau }\rightarrow 0\) we obtain a stochastic version of a voltage-based neural field equation, namely,
with
Similarly, in the limit τ → 0 we have a stochastic version of an activity–based neural field equation
From a numerical perspective, any computer simulation would involve rediscretizing space and then solving a time–discretized version of the resulting stochastic differential equation. On the other hand, in order to investigate analytically the effects of noise on spatiotemporal dynamics, it is more useful to work directly with stochastic neural fields. One can then adapt various PDE methods for studying noise in spatially extended systems [55], as illustrated in the next section.
4 Traveling Waves in Stochastic Neural Fields
In this section we review some recent work on analyzing traveling waves in stochastic neural fields [15].
4.1 Traveling Fronts in a Deterministic Neural Field
Let us begin by briefly reviewing front propagation in a scalar neural field equation of the voltage-based form
For concreteness F is taken to be a sigmoid function
with gain γ and threshold κ. In the high–gain limit γ → ∞, this reduces to the Heaviside function
The weight distribution is taken to be a positive (excitatory), even function of x, w(x) ≥ 0 and w(−x) = w(x), with w(x) a monotonically decreasing function of x for x ≥ 0. The weight distribution is typically taken to be an exponential weight distribution
where σ determines the range of synaptic connections. The latter tends to range from 100 μm to 1 mm. We fix the units of time and space by setting τ = 1, σ = 2.
A homogeneous fixed point solution U ∗ of Eq. (9.46) satisfies
In the case of a sigmoid function with appropriately chosen gain and threshold, it is straightforward to show that there exists a pair of stable fixed points U ∗ ± separated by an unstable fixed point U 0 ∗, see also Fig. 9.3a. In the high gain limit F(U) → H(U −κ) with 0 < κ < W 0, the unstable fixed point disappears and \(U_{+}^{{\ast}} = W_{0}\), U − ∗ = 0. As originally shown by Amari [2], an explicit traveling front solution of Eq. (9.46) that links U + ∗ and U − ∗ can be constructed in the case of a Heaviside nonlinearity. In order to construct such a solution, we introduce the traveling wave coordinate ξ = x − ct, where c denotes the wavespeed, and set \(u(x,t) = \mathcal{U}(\xi )\) with \(\lim _{\xi \rightarrow -\infty }\mathcal{U}(\xi ) = U_{+}^{{\ast}}> 0\) and \(\lim _{\xi \rightarrow \infty }\mathcal{U}(\xi ) = 0\) such that \(\mathcal{U}(\xi )\) only crosses the threshold κ once. Since Eq. (9.46) is equivariant with respect to uniform translations, we are free to take the threshold crossing point to be at the origin, \(\mathcal{U}(0) =\kappa\), so that \(\mathcal{U}(\xi ) <\kappa\) for ξ > 0 and \(\mathcal{U}(\xi )>\kappa\) for ξ < 0. Substituting this traveling front solution into Eq. (9.46) with F(u) = H(u −κ) then gives
where \(\mathcal{U}^{{\prime}}(\xi ) = d\mathcal{U}/d\xi\). Multiplying both sides of the above equation by e−ξ∕c and integrating with respect to ξ leads to the solution
Finally, requiring the solution to remain bounded as ξ → ∞ (ξ → −∞) for c > 0 implies that κ must satisfy the condition
and thus
In the case of the exponential weight distribution (9.49), the relationship between wavespeed c and threshold κ for right-moving fronts is
A similar expression holds for left-moving fronts (c < 0) for which 1 > κ > 0. 5. Using Evans function techniques, it can also be shown that the traveling front is stable [24, 66]. Finally, given the existence of a traveling front solution for a Heaviside rate function, it is possible to prove the existence of a unique front in the case of a smooth sigmoid nonlinearity using a continuation method [29].
4.2 Stochastic Neural Field with Extrinsic Noise
Let us now consider a stochastic version of the scalar neural field (9.46) given by the neural Langevin equation
We assume that dW (x, t) represents an independent Wiener process such that
where 〈 ⋅ 〉 denotes averaging with respect to the Wiener process. Here λ is the spatial correlation length of the noise such that C(x∕λ) → δ(x) in the limit λ → 0, and ε determines the strength of the noise, which is assumed to be weak. For the sake of generality, we take the extrinsic noise to be multiplicative rather than additive. Following standard formulations of Langevin equations [34], the extrinsic noise term is assumed to be of Stratonovich form. Note, however, that a Kramers-Moyal expansion of the neural master equation (9.39) yields a Langevin neural field equation with multiplicative noise of the Ito form [9, 10]. The main results highlighted below do not depend on the precise form of the noise.
The effects of multiplicative noise on front propagation can be analyzed using methods previously developed for reaction–diffusion equations [4, 25, 55, 56], as recently shown in Ref. [15]. The starting point of such methods is the observation that multiplicative noise in the Stratonovich sense leads to a systematic shift in the speed of the front (assuming a front of speed c exists when \(\varepsilon = 0\) ). This is a consequence of the fact that 〈g(U)dW 〉 ≠ 0 even though 〈dW 〉 = 0. The former average can be calculated using Novikov’s theorem [45]:
The above result also follows from Fourier transforming Eq. (9.56) and evaluating averages using the Fokker–Planck equation in Fourier space [15, 55]. Note that in the limit λ → 0, C(0) → 1∕Δ x where Δ x is a lattice cut–off, which is typically identified with the step size of the spatial discretization scheme used in numerical simulations. The method developed in Ref. [4] for stochastic PDEs is to construct an approximation scheme that separates out the diffusive effects of noise from the mean drift. Applying a similar method to the neural field equation (9.56) [15], we first rewrite the equation as
where
and
The stochastic process R has zero mean (so does not contribute to the effective drift) and correlation
The next step in the analysis is to assume that the fluctuating term in Eq. (9.59) generates two distinct phenomena that occur on different time–scales: a diffusive–like displacement of the front from its uniformly translating position at long time scales, and fluctuations in the front profile around its instantaneous position at short time scales [4, 55]. In particular, following Ref. [15], we express the solution U of Eq. (9.59) as a combination of a fixed wave profile U 0 that is displaced by an amount Δ(t) from its uniformly translating mean position \(\xi = x - c_{\varepsilon }t\), and a time–dependent fluctuation Φ in the front shape about the instantaneous position of the front:
Here \(c_{\varepsilon }\) denotes the mean speed of the front. The wave profile U 0 and associated wave speed \(c_{\varepsilon }\) are obtained by solving the modified deterministic equation
Both \(c_{\varepsilon }\) and U 0 depend non–trivially on the noise strength \(\varepsilon\) due to the \(\varepsilon\) –dependence of the function h. Thus, \(c_{\varepsilon }\neq c\) for \(\varepsilon> 0\) and c 0 = c, where c is the speed of the front in the absence of multiplicative noise. It also follows that the expansion (9.63) is not equivalent to a standard small–noise expansion in \(\varepsilon\). Equation (9.64) is chosen so that to leading order, the stochastic variable Δ(t) undergoes unbiased Brownian motion with a diffusion coefficient \(D(\varepsilon ) = \mathcal{O}(\varepsilon )\) (see below). Thus Δ(t) represents the effects of slow fluctuations, whereas Φ represents the effects of fast fluctuations.
The next step is to substitute the decomposition (9.63) into Eq. (9.59) and expand to first order in \(\mathcal{O}(\varepsilon ^{1/2})\). Imposing Eq. (9.64), after shifting \(\xi \rightarrow \xi -\varDelta (t)\), and dividing through by \(\varepsilon ^{1/2}\) then gives
where \(\hat{L}\) is the non–self–adjoint linear operator
for any function \(A(\xi ) \in L_{2}(\mathbb{R})\). The non-self-adjoint linear operator \(\hat{L}\) has a 1D null space spanned by \(U_{0}^{{\prime}}(\xi )\), which follows from differentiating equation (9.64) with respect to ξ. We then have the solvability condition for the existence of a nontrivial solution of Eq. (9.66), namely, that the inhomogeneous part is orthogonal to the null space of the adjoint operator. The latter is defined with respect to the inner product
where A(ξ) and B(ξ) are arbitrary integrable functions. Hence,
Taking the null space of \(\hat{L}\) to be spanned by the function \(\mathcal{V}(\xi )\), we have
Thus Δ(t) satisfies the stochastic ODE
Using the lowest order approximation \(\mathit{dR}(U_{0},\xi,t) = g(U_{0}(\xi ))\mathit{dW }(\xi,t)\), we deduce that (for Δ(0) = 0)
where \(D(\varepsilon )\) is the effective diffusivity
4.3 Explicit Results for a Heaviside Rate Function
We now illustrate the above analysis by considering a particular example where the effective speed \(c_{\varepsilon }\) and diffusion coefficient \(D(\varepsilon )\) can be calculated explicitly [15]. That is, take g(U) = g 0 U for the multiplicative noise term and set F(U) = H(U −κ). (The constant g 0 has units of \(\sqrt{\mathrm{length/time}}\).) The deterministic equation (9.64) for the fixed profile U 0 then reduces to
with
The analysis of the wave speeds proceeds along identical lines to the deterministic model. Thus, multiplying both sides of Eq. (9.73) by \(\mathrm{e}^{-\xi \gamma (\varepsilon )/c_{\varepsilon }}\) and integrating with respect to ξ gives
Finally, requiring the solution to remain bounded as ξ → ∞ (ξ → −∞) for \(c_{\varepsilon }> 0\) implies that κ must satisfy the condition
Hence, in the case of the exponential weight distribution (9.49), we have
for \(c_{\varepsilon }> 0\) with c +(κ) defined in Eq. (9.55). Assuming that \(0 \leq \gamma (\varepsilon ) \leq 1\), we see that multiplicative noise shifts the effective velocity of front propagation in the positive ξ direction.
In order to calculate the diffusion coefficient, it is first necessary to determine the null vector \(\mathcal{V}(\xi )\) of the adjoint linear operator \(\hat{L}^{{\ast}}\) defined by Eq. (9.68). Setting F(U) = H(U −κ) and g(U) = g 0 U, the null vector \(\mathcal{V}\) satisfies the equation
This can be solved explicitly to give [8]
We have used the fact that the solution to Eq. (9.73) is of the form
with \(\hat{w}(\xi )\) defined in Eq. (9.51) and, hence,
Using Eq. (9.79), Eq. (9.72) reduces to the form
which can be evaluated explicitly for an exponential weight distribution to give
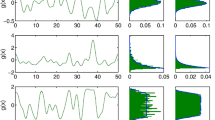
Numerical simulation showing the propagation of a front solution of the stochastic neural field equation (9.56) for Heaviside weight function F(U) = H(U −κ) with κ = 0. 35, exponential weight function (9.49) with σ = 2, and multiplicative noise g(U) = U. Noise strength ε = 0. 005 and C(0) = 10. The wave profile is shown at successive times (a) t = 12 (b) t = 18 and (c) t = 24, with the initial profile at t = 0 (smooth curve in (a)) given by Eq. (9.80). In numerical simulations we take the discrete space and time steps Δ x = 0. 1, Δ t = 0. 01. The deterministic part U 0 of the stochastic wave is shown by the more advanced curves and the corresponding solution in the absence of noise \((\varepsilon = 0\) ) is shown by the less advanced curves
(a) Variance σ X 2(t) of front position as a function of time, averaged over N = 4, 096 trials. Same parameter values as Fig. 9.1. (b) Plot of wave speed \(c_{\varepsilon }\) (black curve) and diffusion coefficient \(D(\varepsilon )\) (gray curve) as a function of threshold κ. Numerical results (solid dots) are obtained by averaging over N = 4, 096 trials starting from the initial condition given by Eq. (9.80). Corresponding theoretical predictions (solid curves) for \(c_{\varepsilon }\) and \(D(\varepsilon )\) are based on Eqs. (9.77) and (9.82), respectively. Other parameters are as in Fig. 9.1
In Fig. 9.1 we show the temporal evolution of a single stochastic wave front, which is obtained by numerically solving the Langevin equation (9.56) for F(U) = H(U −κ), g(U) = U and an exponential weight distribution w. In order to numerically calculate the mean location of the front as a function of time, we carry out a large number of level set position measurements. That is, the positions X a (t) are determined such that U(X a (t), t) = a, for various level set values a ∈ (0. 5κ, 1. 3κ) and the mean location is defined to be \(\overline{X}(t) = \mathbb{E}[X_{a}(t)]\), where the expectation is first taken with respect to the sampled values a and then averaged over N trials. The corresponding variance is given by \(\sigma _{X}^{2}(t) = \mathbb{E}[(X_{a}(t) -\bar{ X}(t))^{2}]\). In Fig. 9.2a, \(\sigma _{X}^{2}(t)\) is plotted as a function of t. It can be seen that it varies linearly with t, consistent with the assumption that there is a diffusive–like displacement of the front from its uniformly translating position at long time scales. The slope of the curve then determines the effective diffusion coefficient according to \(\sigma _{X}^{2}(t) \sim 2D(\varepsilon )t\). In Fig. 9.2b, the numerically estimated speed and diffusion coefficient are plotted for various values of the threshold κ and are compared to the corresponding theoretical curves obtained using the above analysis. It can be seen that there is excellent agreement with the theoretical predictions provided that κ is not too large. Note that as κ → 0. 5, the wave speed decreases towards zero so that the assumption of relatively slow diffusion breaks down. Note that the analysis of freely propagating fronts can be extended to the case of fronts locked to an externally moving stimulus [15]. One finds that the latter are much more robust to noise , since the stochastic wandering of the mean front profile is now described by an Ornstein–Uhlenbeck process rather than a Wiener process, so that the variance in front position saturates in the long time limit rather than increasing linearly with time.
5 Path Integral Representation of a Stochastic Neural Field
Recently, Buice and Cowan [19] have used path integral methods and renormalization group theory to establish that a stochastic neural field with an absorbing state, which evolves according to a birth–death master equation of the form (9.39), belongs to the universality class of directed percolation, and consequently exhibits power law behavior suggestive of many measurements of spontaneous cortical activity in vitro and in vivo [6, 51]. (If a network enters an absorbing state all activity is extinguished.) Although the existence of power law behavior is still controversial [5], the application of path integral methods provides another example of how analytical techniques familiar in the study of PDEs and chemical master equations are being adapted to studies of continuum neural fields. (For reviews on path integral methods for stochastic differential equations see Refs. [22, 60, 67].) In this section, we show how a stochastic neural field with extrinsic noise and an absorbing state can be reformulated as a path integral , and use this to estimate the time to extinction of network activity. A more detailed discussion can be found in Ref. [11]
5.1 Pulled Fronts, Absorbing States and Extinction Events
In order to construct a neural field with an absorbing state, it is convenient to consider an activity–based rather than a voltage-based neural field of the form
For the moment, we consider an unbounded domain with \(x \in \mathbb{R}\). We also have the additional constraint that a(x, t) ≥ 0 for all (x, t), since the field a(x, t) represents the instantaneous firing rate of a local population of neurons at position x and time t. Suppose that F(a) in Eq. (9.84) is a positive, bounded, monotonically increasing function of a with F(0) = 0, \(\lim _{a\rightarrow 0^{+}}F^{{\prime}}(a) = 1\) and lim a → ∞ F(a) = κ for some positive constant κ. For concreteness, we take
A homogeneous fixed point solution a ∗ of Eq. (9.84) satisfies \(a^{{\ast}} = F(W_{0}a^{{\ast}})\) with \(W_{0} =\int _{ -\infty }^{\infty }w(y)\mathit{dy}\). In the case of the given piecewise linear firing rate function , we find that if W 0 > 1, then there exists an unstable fixed point at a ∗ = 0 (absorbing state) and a stable fixed point at a ∗ = κ, see Fig. 9.3a. The construction of a front solution linking the stable and unstable fixed points differs considerably from that considered in neural fields with sigmoidal or Heaviside nonlinearities as considered in Sect. 9.4, where the front propagates into a metastable state. Following the PDE theory of fronts propagating into unstable states [62], we expect there to be a continuum of front velocities and associated traveling wave solutions; the particular velocity selected depends on the initial conditions. Fronts propagating into unstable states can be further partitioned into two broad categories: the so–called pulled and pushed fronts [62] emerging from sufficiently localized initial conditions. Pulled fronts propagate into an unstable state such that the asymptotic velocity is given by the linear spreading speed v ∗, which is determined by linearizing about the unstable state within the leading edge of the front. That is, perturbations around the unstable state within the leading edge grow and spread with speed v ∗, thus “pulling along” the rest of the front . On the other hand, pushed fronts propagate into an unstable state with a speed greater than v ∗, and it is the nonlinear growth within the region behind the leading edge that pushes the front speeds to higher values. One of the characteristic features of pulled fronts is their sensitivity to perturbations in the leading edge of the wave. This means that standard perturbation methods for studying the effects of spatial heterogeneities [43] or external noise fluctuations [54] break down. The effects of spatial heterogeneities on neural fields that support pulled fronts is explored elsewhere [11, 23].
(a) Plots of piecewise linear and sigmoidal firing rate functions. Intercepts of y = F(W 0 a) with straight line y = a determine homogeneous fixed points. Stable (unstable) fixed pints indicated by filled (unfilled) circles. (b) Stable steady state solution a(x, t) = A s (x) of neural field equation (9.84) on a finite spatial domain of length L with boundary conditions a(0, t) = a(L, t) = 0. Here W 0 = 1. 2, σ = 1, κ = 0. 4 and L = 5 in the presence of multiplicative noise, fluctuations can drive the network to the zero absorbing state resulting in the extinction of activity
Consider a traveling wave solution \(\mathcal{A}(x - ct)\) of Eq. (9.84) with \(\mathcal{A}(\xi ) \rightarrow \kappa\) as ξ → −∞ and \(\mathcal{A}(\xi ) \rightarrow 0\) as ξ → ∞. One can determine the range of velocities c for which such a solution exists by assuming that \(\mathcal{A}(\xi ) \approx \mathrm{ e}^{-\lambda \xi }\) for sufficiently large ξ. The exponential decay of the front suggests that we linearize equation (9.84), which in traveling wave coordinates (with τ = 1) takes the form
However, in order to make the substitution \(\mathcal{A}(\xi ) \approx \mathrm{ e}^{-\lambda \xi }\) we need to restrict the integration domain of ξ ′ to the leading edge of the front . Suppose, for example that w(x) is given by the Gaussian distribution
Given the fact that the front solution \(\mathcal{A}(\xi )\) is bounded, we introduce a cut-off X with σ ≪ X ≪ ξ, and approximate Eq. (9.86) by
Substituting the exponential solution in (9.86) then yields the dispersion relation c = c(λ) with
Finally, we now take the limit X → ∞ under the assumption that w(y) is an even function to yield
where \(\mathcal{W}(\lambda ) =\hat{ w}(\lambda ) +\hat{ w}(-\lambda )\) and \(\hat{w}(\lambda ) =\int _{ 0}^{\infty }w(y)\mathrm{e}^{-\lambda y}\mathit{dy}\) is the Laplace transform of w(x). We are assuming that w(y) decays sufficiently fast as | y | → ∞ so that the Laplace transform \(\hat{w}(\lambda )\) exists for bounded, negative values of λ. This holds in the case of the Gaussian distribution (9.87) for which \(\mathcal{W}(\lambda ) = W_{0}\mathrm{e}^{\lambda ^{2}\sigma ^{2}/2 }\). Hence,
If W 0 > 1 (necessary for the zero activity state to be unstable) then c(λ) is a positive unimodal function with c(λ) → ∞ as λ → 0 or λ → ∞ and a unique minimum at λ = λ 0 with λ 0. Assuming that the full nonlinear system supports a pulled front then a sufficiently localized initial perturbation (one that decays faster than \(\mathrm{e}^{-\lambda _{0}x}\)) will asymptotically approach the traveling front solution with the minimum wave speed \(c_{0} = c(\lambda _{0})\). Note that \(c_{0} \sim \sigma\) and \(\lambda _{0} \sim \sigma ^{-1}\).
In the above analysis, the effects of boundary conditions on front propagation were ignored, which is a reasonable approximation if the size L of the spatial domain satisfies L ≫ σ, where σ is the range of synaptic weights. In the case of a finite domain, following passage of an invasive activity front, the network settles into a non–zero stable steady state, whose spatial structure will depend on the boundary conditions . The steady–state equation takes the form
In the case of Dirichlet boundary conditions , a(0, t) = a(L, t) = 0 with L ≫ σ, the steady–state will be uniform in the bulk of the domain with a(x) ≈ a 0 except for boundary layers at both ends. Here a 0 is the nonzero solution to the equation \(a_{0} = F(W_{0}a_{0})\). An example of a steady–state solution is plotted in Fig. 9.3b. (Note that the sudden drop to zero right on the boundaries reflects the non-local nature of the neural field equation.)
Now suppose some source of extrinsic noise is added to the neural field equation (9.84):
for 0 ≤ t ≤ T and initial condition A(x, 0) = Φ(x). Here \(\varepsilon\) determines the noise strength and Σ = [0, L] denotes the spatial domain of the neural field. We will assume that g(0) = 0 so that the uniform zero activity state \(A \equiv 0\) is an absorbing state of the system; any noise–induced transition to this state would then result in extinction of all activity. An example of multiplicative noise that vanishes at A = 0 is obtained by carrying out a diffusion approximation of the neural master equation previously introduced by Buice et al. [19, 20], see Bressloff [9, 10]. Based on the analysis of stochastic traveling waves in Sect. 9.4, we would expect the noise to induce a stochastic wandering of a pulled front solution of the corresponding deterministic equation. However, in the case of stochastic PDEs, it has previously been shown that the stochastic wandering of a pulled front about its mean position is subdiffusive with \(\text{var}\varDelta (t) \sim t^{1/2}\), in contrast to the diffusive wandering of a front propagating into a metastable state for which varΔ(t) ∼ t [54]. Such scaling is a consequence of the asymptotic relaxation of the leading edge of the deterministic pulled front. Since pulled front solutions of the neural field equation (9.84) exhibit similar dynamics, it suggests that there will also be subdiffusive wandering of these fronts in the presence of multiplicative noise. This is indeed found to be the case [15]. Another consequence of the noise is that it can induce a transition from the quasi-uniform steady state to the zero absorbing state. In the case of weak noise , the time to extinction is exponentially large and can be estimated using path integral methods as outlined below, see also Ref. [11].
5.2 Derivation of Path Integral Representation
In order to develop a framework to study rare extinction events in the weak noise limit, we construct a path integral representation of the stochastic Langevin equation (9.93) along the lines of Ref. [11]. We will assume that the multiplicative noise is of Ito form [34]. For reviews on path integral methods for stochastic differential equations, see Refs. [22, 60, 67]. Discretizing both space and time with \(A_{i,m} = A(m\varDelta d,i\varDelta t)\), \(W_{i,m}\sqrt{\varDelta t/\varDelta d} = \mathit{dW }(m\varDelta d,i\varDelta t)\), \(w_{\mathit{mn}}\varDelta d = w(m\varDelta d,n\varDelta d)\) gives
where \(i = 0,1,\ldots,N\) for T = NΔ t, \(n = 0,\ldots,\hat{N}\) for \(L =\hat{ N}\varDelta d\), and
Let A and W denote the vectors with components A i, m and W i, m respectively. Formally, the conditional probability density function for A given a particular realization of the stochastic process W (and initial condition Φ) is
Inserting the Fourier representation of the Dirac delta function,
gives
Each W i, m is independently drawn from a Gaussian probability density function \(P(W_{i,m}) = (2\pi )^{-1/2}\mathrm{e}^{-W_{i,m}^{2}/2 }\). Hence, setting
and performing the integration with respect to W j, n by completing the square, gives
Finally, taking the continuum limits Δ d → 0, and Δ t → 0, \(N,\hat{N} \rightarrow \infty\) for fixed T, L with A i, m → A(x, t) and \(i\tilde{U}_{i,m}/\varDelta d \rightarrow \tilde{ U}(x,t)\) results in the following path integral representation of a stochastic neural field:
with
Here \(\mathcal{D}\tilde{U}\) denotes the path-integral measure
Given the probability functional P[A], a path integral representation of various moments of the stochastic field A can be constructed [22]. For example, the mean field is
whereas the two–point correlation is
Another important characterization of the stochastic neural field is how the mean activity (and other moments) respond to small external inputs (linear response theory). First, suppose that a small external source term h(x, t) is added to the right–hand side of the deterministic version (g ≡ 0) of the field equation (9.93). Linearizing about the time–dependent solution A(x, t) of the unperturbed equation (h ≡ 0) leads to an inhomogeneous linear equation for the perturbed solution \(\varphi (x,t) = A^{h}(x,t) - A(x,t)\):
Introducing the deterministic Green’s function or propagator \(\mathcal{G}_{0}(x,t;x^{{\prime}},t^{{\prime}})\) according to the adjoint equation
with \(\mathcal{G}_{0}(x,t;x^{{\prime}},t^{{\prime}}) = 0\) for t ≤ t ′ (causality), the linear response is given by
In other words, in terms of functional derivatives
Now suppose that a corresponding source term \(\int \mathit{dx}\int \mathit{dt}\,h(x,t)\tilde{U}(x,t)\) is added to the action (9.100). The associated Green’s function for the full stochastic model is defined according to
with
and \(\mathcal{G}(x,t;x^{{\prime}},t^{{\prime}}) = 0\) for t ≤ t ′. The above analysis motivates the introduction of the generating functional
Various moments of physical interest can then be obtained by taking functional derivatives with respect to the “current sources” \(\boldsymbol{J},\tilde{\boldsymbol{J}}\). For example,
5.3 Hamiltonian–Jacobi Dynamics and Population Extinction in the Weak-Noise Limit
In Ref. [11], the path-integral representation of the generating functional (9.108) is used to estimate the time to extinction of a metastable non–trivial state. That is, following along analogous lines to previous studies of reaction–diffusion equations [27, 42], the effective Hamiltonian dynamical system obtained by extremizing the associated path integral action is used to determine the most probable or optimal path to the zero absorbing state. (Alternatively, one could consider a WKB approximation of solutions to the corresponding functional Fokker–Planck equation or master equation [26, 33, 40].) In the case of the neural field equation, this results in extinction of all neural activity. For a corresponding analysis of a neural master equation with x–independent steady states, see Refs. [9, 10].
The first step is to perform the rescalings \(\tilde{A} \rightarrow \tilde{ A}/\sigma ^{2}\) and \(\tilde{J} \rightarrow \tilde{ J}/\sigma ^{2}\), so that the generating functional (9.108) becomes
In the limit σ → 0, the path integral is dominated by the “classical” solutions q(x, t), p(x, t), which extremize the exponent or action of the generating functional:
In the case of zero currents \(J =\tilde{ J} = 0\), these equations reduce to
where
such that
Equations (9.114) take the form of a Hamiltonian dynamical system in which q is a “coordinate” variable, p is its “conjugate momentum” and \(\mathcal{H}\) is the Hamiltonian functional. Substituting for \(\mathcal{H}\) leads to the explicit Hamilton equations
It can be shown that q(x, t), p(x, t) satisfy the same boundary conditions as the physical neural field A(x, t) [49]. Thus, in the case of periodic boundary conditions, q(x + L, t) = q(x, t) and p(x + L, t) = p(x, t). It also follows from the Hamiltonian structure of Eqs. (9.116) and (9.117) that there is an integral of motion given by the conserved “energy” \(E = \mathcal{H}[q,p]\).
The particular form of \(\mathcal{H}\) implies that one type of solution is the zero energy solution p(x, t) ≡ 0, which implies that q(x, t) satisfies the deterministic scalar neural field equation (9.84). In the t → ∞ limit, the resulting trajectory in the infinite dimensional phase space converges to the steady state solution \(\mathcal{O}_{+} = [q_{s}(x),0]\), where q s (x) satisfies Eq. (9.92). The Hamiltonian formulation of extinction events then implies that the most probable path from [q s (x), 0] to the absorbing state is the unique zero energy trajectory that starts at \(\mathcal{O}_{+}\) at time t = −∞ and approaches another fixed point \(\mathcal{P} = [0,p_{e}(x)]\) at t = +∞ [27, 49]. In other words, this so–called activation trajectory is a heteroclinic connection \(\mathcal{O}_{+}\mathcal{P}\) (or instanton solution) in the functional phase space [q(x), p(x)]. It can be seen from Eq. (9.117) that the activation trajectory is given by the curve
so that
assuming F(q) ∼ q for 0 < q ≪ 1. Note that the condition that p e (x) exists and is finite is equivalent to the condition that there exists a stationary solution to the underlying functional Fokker–Planck equation – this puts restrictions on the allowed form for g. For the zero energy trajectory emanating from \(\mathcal{O}_{+}\) at t = −∞, the corresponding action is given by
and up to pre-exponential factors, the estimated time τ e to extinction from the steady–state solution q s (x) is given by [27, 49]
For x–dependent steady–state solutions q s (x), which occur for Dirichlet boundary conditions and finite L, one has to solve Eqs. (9.116) and (9.117) numerically. Here we will consider the simpler case of x–independent solutions, which occur for periodic boundary conditions or Dirichlet boundary conditions in the large L limit (where boundary layers can be neglected). Restricting to x-independent state transitions, the optimal path is determined by the Hamilton equations (9.116) and (9.117):
Phase portrait of constant energy trajectories for the Hamiltonian system given by Eqs. (9.122) and (9.123) with F(q) = tanh(q) and g(q) = q s for q > 0. Zero–energy trajectories are indicated by thick curves. The stable and unstable fixed points of the mean–field dynamics are denoted by \(\mathcal{O}_{+}\) and \(\mathcal{O}_{-}\). (a) s = 1∕2: There exists a non-zero fluctuational fixed point \(\mathcal{P}\) that is connected to \(\mathcal{O}_{+}\) via a zero–energy heteroclinic connection. The curve \(\mathcal{O}_{+}P\) is the optimal path from the metastable state to the absorbing state. (b) s = 1∕4: There is no longer a fluctuational fixed point \(\mathcal{P}\) so the optimal path is a direct heteroclinic connection between \(\mathcal{O}_{+}\) and \(\mathcal{O}_{-}\)
In Fig. 9.4 we plot the various constant energy solutions of the Hamilton equations (9.122) and (9.123) for the differentiable rate function F(q) = tanh(q) and multiplicative noise factor g(q) = q s. In the first case p e = 0. 2 and in the second p e = 0. The zero–energy trajectories are highlighted as thicker curves. Let us first consider the case s = 1∕2 for which p e = 0. 2, see Fig. 9.4a. As expected, one zero–energy curve is the line p = 0 along which Eq. (9.122) reduces to the x–independent version of Eq. (9.84). If the dynamics were restricted to the one–dimensional manifold p = 0 then the non–zero fixed point \(\mathcal{O}_{+} = (q_{0},0)\) with \(q_{0} = F(W_{0}q_{0})\) would be stable. However, it becomes a saddle point of the full dynamics in the (q, p) plane, reflecting the fact that it is metastable when fluctuations are taken into account. A second zero–energy curve is the absorbing line q = 0 which includes two additional hyperbolic fixed points denoted by \(\mathcal{O}_{-} = (0,0)\) and \(\mathcal{P} = (0,p_{e})\) in Fig. 9.4. \(\mathcal{O}_{-}\) occurs at the intersection with the line p = 0 and corresponds to the unstable zero activity state of the deterministic dynamics, whereas \(\mathcal{P}\) is associated with the effects of fluctuations. Moreover, there exists a third zero–energy curve, which includes a heteroclinic trajectory joining \(\mathcal{O}_{-}\) at t = −∞ to the fluctuational fixed point \(\mathcal{P}\) at t = +∞. This heteroclinic trajectory represents the optimal (most probable) path linking the metastable fixed point to the absorbing boundary. For s < 1∕2, p e = 0 and the optimal path is a heteroclinic connection from \(\mathcal{O}_{+}\) to \(\mathcal{O}_{-}\). In both cases, the extinction time τ e is given by Eq. (9.121) with
where the integral evaluated along the heteroclinic trajectory from \(\mathcal{O}_{+}\) to \(\mathcal{P}\), which is equal to the area in the shaded regions of Fig. 9.4.
Note that since the extinction time is exponentially large in the weak noise limit, it is very sensitive to the precise form of the action S 0 and thus the Hamiltonian \(\mathcal{H}\). This implies that when approximating the neural master equation of Buice et al. [19, 20] by a Langevin equation of the form (9.93) with \(\sigma \sim 1/\sqrt{N}\), where N is the system size, the resulting Hamiltonian differs from that obtained directly from the master equation and can thus generate a poor estimate of the extinction time. This can be shown either by comparing the path integral representations of the generating functional for both stochastic processes or by comparing the WKB approximation of the master equation and corresponding Fokker–Planck equation . This particular issue is discussed elsewhere for neural field equations [9, 10].
Notes
- 1.
Equation (9.8) and various generalizations have been used to develop numerical schemes for tracking the probability density of a population of synaptically coupled spiking neurons [46, 48], which in the case of simple neuron models, can be considerably more efficient than classical Monte Carlo simulations that follow the states of each neuron in the network. On the other hand, as the complexity of the individual neuron model increases, the gain in efficiency of the population density method decreases, and this has motivated the development of a moment closure scheme that leads to a Boltzmann–like kinetic theory of IF networks [21, 52]. However, as shown in Ref. [39], considerable care must be taken when carrying out the dimension reduction, since it can lead to an ill–posed problem over a wide range of physiological parameters. That is, the truncated moment equations may not support a steady-state solution even though a steady–state probability density exists for the full system. An alternative approach is to develop a mean field approximation as highlighted here.
References
Abbott, L.F., van Vresswijk, C.: Asynchronous states in networks of pulse–coupled oscillators. Phys. Rev. E 48(2), 1483–1490 (1993)
Amari, S.: Dynamics of pattern formation in lateral inhibition type neural fields. Biol. Cybern. 27, 77–87 (1977)
Amit, D.J., Brunel, N.: Model of global spontaneous activity and local structured activity during delay periods in the cerebral cortex. Cereb Cortex 7, 237–252 (1997)
Armero, J., Casademunt, J., Ramirez-Piscina, L., Sancho, J.M.: Ballistic and diffusive corrections to front propagation in the presence of multiplicative noise. Phys. Rev. E 58, 5494–5500 (1998)
Bedard, C., Destexhe, A.: Macroscopic models of local field potentials the apparent 1/f noise in brain activity. Biophys. J. 96, 2589–2603 (2009)
Beggs, J.M., Plenz, D.: Neuronal avalanches are diverse and precise activity patterns that are stable for many hours in cortical slice cultures. J. Neurosci. 24, 5216–5229 (2004)
Boustani, S.E., Destexhe, A.: A master equation formalism for macroscopic modeling of asynchronous irregular activity states. Neural Comput. 21, 46–100 (2009)
Bressloff, P.C.: Traveling fronts and wave propagation failure in an inhomogeneous neural network. Physica D 155, 83–100 (2001)
Bressloff, P.C.: Stochastic neural field theory and the system-size expansion. SIAM J. Appl. Math. 70, 1488–1521 (2009)
Bressloff, P.C.: Metastable states and quasicycles in a stochastic Wilson-Cowan model of neuronal population dynamics. Phys. Rev. E 85, 051,903 (2010)
Bressloff, P.C.: From invasion to extinction in heterogeneous neural fields. J. Math. Neurosci. 2, 6 (2012)
Bressloff, P.C.: Spatiotemporal dynamics of continuum neural fields. J. Phys. A 45, 033,001 (109pp.) (2012)
Bressloff, P.C., Coombes, S.: Dynamics of strongly coupled spiking neurons. Neural Comput. 12, 91–129 (2000)
Bressloff, P.C., Newby, J.M.: Metastability in a stochastic neural network modeled as a velocity jump markov process. SIAM J. Appl. Dyn. Syst. 12, 1394–1435 (2013)
Bressloff, P.C., Webber, M.A.: Front propagation in stochastic neural fields. SIAM J. Appl. Dyn. Syst. 11, 708–740 (2012)
Brunel, N.: Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons. J. Comput. Neurosci 8, 183–208 (2000)
Brunel, N., Hakim, V.: Fast global oscillations in networks of integrate–and–fire neurons with low firing rates. Neural Comput. 11, 1621–1671 (1999)
Buckwar, E., Riedler, M.G.: An exact stochastic hybrid model of excitable membranes including spatio-temporal evolution. J. Math. Biol. 63, 1051–1093 (2011)
Buice, M., Cowan, J.D.: Field-theoretic approach to fluctuation effects in neural networks. Phys. Rev. E 75, 051,919 (2007)
Buice, M., Cowan, J.D., Chow, C.C.: Systematic fluctuation expansion for neural network activity equations. Neural Comput. 22, 377–426 (2010)
Cai, D., Tao, L., Shelley, M., McLaughlin, D.W.: An effective kinetic representation of fluctuation–driven neuronal networks with application to simple and complex cells in visual cortex. Proc. Natl. Acad. Sci. USA 101, 7757–7562 (2004)
Chow, C.C., Buice, M.: Path integral methods for stochastic differential equations (2011). arXiv nlin/105966v1
Coombes, S., Laing, C.R.: Pulsating fronts in periodically modulated neural field models. Phys. Rev. E 83, 011,912 (2011)
Coombes, S., Owen, M.R.: Evans functions for integral neural field equations with Heaviside firing rate function. SIAM J. Appl. Dyn. Syst. 4, 574–600 (2004)
de Pasquale, F., Gorecki, J., Poielawski., J.: On the stochastic correlations in a randomly perturbed chemical front. J. Phys. A 25, 433 (1992)
Dykman, M.I., Mori, E., Ross, J., Hunt, P.M.: Large fluctuations and optimal paths in chemical kinetics. J. Chem. Phys. A 100, 5735–5750 (1994)
Elgart, V., Kamenev, A.: Rare event statistics in reaction–diffusion systems. Phys. Rev. E 70, 041,106 (2004)
Ermentrout, G.B.: Reduction of conductance-based models with slow synapses to neural nets. Neural Comput. 6, 679–695 (1994)
Ermentrout, G.B., McLeod, J.B.: Existence and uniqueness of travelling waves for a neural network. Proc. R. Soc. Edinb. A 123, 461–478 (1993)
Ermentrout, G.B., Terman, D.: Mathematical Foundations of Neuroscience. Springer, Berlin (2010)
Faisal, A.A., Selen, L.P.J., Wolpert, D.M.: Noise in the nervous system. Nat. Rev. Neurosci. 9, 292 (2008)
Faugeras, O., Touboul, J., Cessac, B.: A constructive mean–field analysis of multi–population neural networks with random synaptic weights and stochastic inputs. Front. Comput. Neurosci. 3, 1–28 (2009)
Freidlin, M.I., Wentzell, A.D.: Random perturbations of dynamical systems. Springer, New York (1984)
Gardiner, C.W.: Handbook of Stochastic Methods, 4th edn. Springer, Berlin (2009)
Gerstner, W., Kistler, W.: Spiking Neuron Models. Cambridge University Press, Cambridge (2002)
Gerstner, W., Van Hemmen, J.L.: Coherence and incoherence in a globally coupled ensemble of pulse–emitting units. Phys. Rev. Lett. 71(3), 312–315 (1993)
Ginzburg, I., Sompolinsky, H.: Theory of correlations in stochastic neural networks. Phys. Rev. E 50, 3171–3191 (1994)
Hutt, A., Longtin, A., Schimansky-Geier, L.: Additive noise-induces turing transitions in spatial systems with application to neural fields and the Swift-Hohenberg equation. Physica D 237, 755–773 (2008)
Ly, C., Tranchina, D.: Critical analysis of a dimension reduction by a moment closure method in a population density approach to neural network modeling. Neural Comput. 19, 2032–2092 (2007)
Maier, R.S., Stein, D.L.: Limiting exit location distribution in the stochastic exit problem. SIAM J. Appl. Math. 57, 752–790 (1997)
Mattia, M., Guidice, P.D.: Population dynamics of interacting spiking neurons. Phys. Rev. E 66, 051,917 (2002)
Meerson, B., Sasorov, P.V.: Extinction rates of established spatial populations. Phys. Rev. E 83, 011,129 (2011)
Mendez, V., Fort, J., Rotstein, H.G., Fedotov, S.: Speed of reaction-diffusion fronts in spatially heterogeneous media. Phys. Rev. E 68, 041,105 (2003)
Meyer, C., van Vreeswijk, C.: Temporal correlations in stochastic networks of spiking neurons. Neural Comput. 14, 369–404 (2002)
Novikov, E.A.: Functionals and the random-force method in turbulence theory. Sov. Phys. JETP 20, 1290 (1965)
Nykamp, D., Tranchina, D.: A population density method that facilitates large–scale modeling of neural networks: analysis and application to orientation tuning. J. Comput. Neurosci. 8, 19–50 (2000)
Ohira, T., Cowan, J.D.: Stochastic neurodynamics and the system size expansion. In: Ellacott, S., Anderson, I.J. (eds.) Proceedings of the First International Conference on Mathematics of Neural Networks, pp. 290–294. Academic (1997)
Omurtag, A., Knight, B.W., Sirovich, L.: On the simulation of large populations of neurons. J. Comput. Neurosci. 8, 51–63 (2000)
Ovaskainen, O., Meerson, B.: Stochsatic models of population extinction. Trends Ecol. Evol. 25, 643–652 (2010)
Pakdaman, K., Thieullen, M., Wainrib, G.: Fluid limit theorems for stochastic hybrid systems with application to neuron models. J. Appl. Probab. 24, 1 (2010)
Plenz, D., Thiagarajan, T.C.: The organizing principles of neuronal avalanches: cell assemblies in the cortex? Trends Neurosci. 30, 101–110 (2007)
Rangan, A.V., Kovacic, G., Cai, D.: Kinetic theory for neuronal networks with fast and slow excitatory conductances driven by the same spike train. Phys. Rev. E 77, 041,915 (2008)
Renart, A., Brunel, N., Wang, X.J.: Mean–field theory of irregularly spiking neuronal populations and working memory in recurrent cortical networks. In: Feng, J. (ed.) Computational Neuroscience: A Comprehensive Approach, pp. 431–490. CRC, Boca Raton (2004)
Rocco, A., Ebert, U., van Saarloos, W.: Subdiffusive fluctuations of “pulled” fronts with multiplicative noise. Phys. Rev. E. 65, R13–R16 (2000)
Sagues, F., Sancho, J.M., Garcia-Ojalvo, J.: Spatiotemporal order out of noise. Rev. Mod. Phys. 79, 829–882 (2007)
Schimansky-Geier, L., Mikhailov, A.S., Ebeling., W.: Effects of fluctuations on plane front propagation in bistable nonequilibrium systems. Ann. Phys. 40, 277 (1983)
Smith, G.D.: Modeling the stochastic gating of ion channels. In: Fall, C., Marland, E.S., Wagner, J.M., Tyson, J.J. (eds.) Computational Cell Biology, chap. 11. Springer, New York (2002)
Softky, W.R., Koch, C.: The highly irregular firing of cortical cells is inconsistent with temporal integration of random EPSPS. J. Neurosci. 13, 334–350 (1993)
Soula, H., Chow, C.C.: Stochastic dynamics of a finite-size spiking neural network. Neural Comput. 19, 3262–3292 (2007)
Tauber, U.C.: Field-theory approaches to nonequilibrium dynamics. Lect. Notes Phys. 716, 295–348 (2007)
Touboul, J., Hermann, G., Faugeras, O.: Noise–induced behaviors in neural mean field dynamics. SIAM J. Appl. Dyn. Syst. 11(1), 49–81 (2012)
van Saarloos, W.: Front propagation into unstable states. Phys. Rep. 386, 29–222 (2003)
van Vreeswijk, C., Abbott, L.F.: Self–sustained firing in populations of integrate–and–fire neurons. SIAM J. Appl. Math. 53(1), 253–264 (1993)
van Vreeswijk, C., Sompolinsky, H.: Chaotic balanced state in a model of cortical circuits. Neural Comput. 10, 1321–1371 (1998)
Zeisler, S., Franz, U., Wittich, O., Liebscher, V.: Simulation of genetic networks modelled by piecewise deterministic markov processes. IET Syst. Biol. 2, 113–135 (2008)
Zhang, L.: On the stability of traveling wave solutions in synaptically coupled neuronal networks. Differ. Integral Equ. 16, 513–536 (2003)
Zinn-Justin, J.: Quantum Field Theory and Critical Phenomena, 4th edn. Oxford University Press, Oxford (2002)
Acknowledgements
This work was supported by the National Science Foundation (DMS-1120327).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2014 Springer-Verlag Berlin Heidelberg
About this chapter
Cite this chapter
Bressloff, P.C. (2014). Stochastic Neural Field Theory. In: Coombes, S., beim Graben, P., Potthast, R., Wright, J. (eds) Neural Fields. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-54593-1_9
Download citation
DOI: https://doi.org/10.1007/978-3-642-54593-1_9
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-54592-4
Online ISBN: 978-3-642-54593-1
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)