How well do reduced models capture the dynamics in models of interacting neurons?

Abstract

This paper introduces a class of stochastic models of interacting neurons with emergent dynamics similar to those seen in local cortical populations. Rigorous results on existence and uniqueness of nonequilibrium steady states are proved. These network models are then compared to very simple reduced models driven by the same mean excitatory and inhibitory currents. Discrepancies in firing rates between network and reduced models are investigated and explained by correlations in spiking, or partial synchronization, working in concert with “nonlinearities” in the time evolution of membrane potentials. The use of simple random walks and their first passage times to simulate fluctuations in neuronal membrane potentials and interspike times is also considered.

1 Introduction

The two goals of this paper are: (1) to introduce a relatively tractable class of stochastic models of interacting neurons that encode some degree of biological realism, and (2) to carry out a study in which the stochastic network models introduced are compared to a few highly reduced models and to explain the discrepancies observed. Item (2) is in fact the primary goal of this paper, so we begin with that.

1.1 Comparison of network and reduced models in neuroscience

Models in neuroscience come in an extraordinarily wide range, from very simple, seeking to describe complex neural behavior using a few coarse-grained variables, to extremely complex, as in Connectome type projects that seek to provide a complete map of all neuronal connections—with a myriad of possibilities in between. The modeling of individual neurons alone can vary from a single number that describes its firing rate, to the Hodgkin–Huxley model, or one that treats individual ionic channels and the biochemical reactions that are triggered with each synapse.

A question that we believe has not received adequate attention is: how do models of different levels of complexity compare? One does not expect a reduced mean-field model to provide the same kind of detailed information as a large-scale network of spiking neurons, but does it provide basic information more or less reliably? If not, what causes the discrepancies? What are the mechanisms mean-field-type models lack that cause them to produce inaccurate results? The primary goal of this paper is to tackle questions of this type.

Needless to say, the questions above are too broad, nor can they be studied in the abstract. In this paper, we will limit our study to the comparison of firing rates between models of specific kinds. We would like our “detailed” models to possess some degree of biological realism, such as the dynamical interaction of Excitatory and Inhibitory neurons, and will use a class of stochastic models of interacting neurons with integrate-and-fire type dynamics; they can be thought of as modeling the dynamical interactions that take place in local circuitries in the mammalian cortex. Inspired by mean-field ideas, our reduced models will be simple ODEs of Wilson–Cowan type and random walks to simulate fluctuations in membrane potentials.

There is no such thing as “typical” network behavior, however. To select representative network models in a meaningful way, we made the following a priori observation: the emergence of correlations in spiking activity is likely the single most important difference between network models of interacting neurons and mean-field models, which do not have the capacity to capture such correlations. This prompted us to conjecture that the performance of reduced models to correctly predict the firing rates of network models vary depending on the network’s degree of synchrony, and to study not a single network model but a few of them with different amounts of correlations.

The reduction of complicated network systems to simpler mathematical objects, such as systems defined by mean field or Fokker–Planck type equations, is by now standard in mathematical neuroscience (Brunel 2000; Brunel and Hakim 1999; Brunel and Wang 2003; Cai et al. 2004, 2006; Bressloff 1999, 2009); many authors also show numerical simulations to demonstrate the similarity between the original and reduced models. What is different here is that we investigate systematically the discrepancy between our network and reduced models. That is not usually done; the only other paper we know of that has done that is (Grabska-Barwińska and Latham 2014), which compared network and mean field models. Our findings have some overlap with (Grabska-Barwińska and Latham 2014). But we take it another step further: we identify and dissect the underlying mechanisms that lead to the discrepancies between network and mean-field models.

The analysis of dynamical mechanisms is an important feature of the present paper. As we will show, the discrepancy in firing rates between networks of interacting neurons and linear ODE-type reduced models is caused largely by nonlinearities in the system accentuated by spike correlations or partial synchronization. Our analysis sheds light on the circumstances under which reduced models accurately predict firing rates of networks, and when corrections might be warranted. To our knowledge analyses of this kind have never been carried out before.

1.2 A class of stochastic models of interacting neurons

Turning now to the motivation for the new class of models introduced in this paper, one of the biggest challenges in mathematical biology is to find models that encode some degree of biological realism and that are mathematically tractable at the same time. Analytical approximations such as Fokker–Planck, mean field, rate models etc. have been used a great deal; all serve useful purposes but none captures directly the interaction among neurons. Large scale network models, some quite realistic, have also been used mostly in computational modeling; such models are usually not analytically tractable.

Many of the models that are analytically tractable or can be approximated by such are sparsely connected or near the weak coupling limit (Brunel and Hakim 1999; Brunel 2000; Cai et al. 2006), a mathematical idealization that is fruitful from the analytical point of view but one that does not accurately reflect the state of affairs in real cortex, where connectivity is not all that sparse and synaptic coupling strengths are not infinitesimally small. Indeed much of cortical activity is shaped by the dynamical interaction between Excitatory (E) and Inhibitory (I) populations. The models presented in this paper are focused on elucidating the dynamics of this interaction. In these models, connectivity and the strengths of E–E, E–I, I–E and I–I couplings are easily compared to those in real neuronal populations. Neurons interact freely; emergent behaviors abound, many beyond the reach of rate models. These models are a step away from well established mathematical idealizations, and a tiny bit closer to biological realism.

We have elected to use stochastic models, as Markov models are usually easier to work with than purely deterministic ones. The models presented in Sect. 1 have facilitated our numerical investigations. We have reason to believe that they are analytically tractable beyond the basic results we have proved, and would like to present them to the mathematical neuroscience community for further study.

The organization of this paper is as follows: In Sect. 1, we introduce a class of stochastic models of interacting neurons. These will be our “detailed” models. A mathematical treatment of these models is given in Sect. 2; this section can be skipped if the reader so chooses. In Sect. 3, we produce some network models with different degrees of synchrony, to be used for comparison with reduced models later on. In Sect. 4, we consider reduced models defined by simple ODEs, and in Sect. 5, we model fluctuations in membrane potential as random-walks.

2 A stochastic model of interacting neurons

In this section, we introduce a stochastic model of interacting neurons representing a local population in the cerebral cortex. Though not intended to depict any specific part of the brain, this model has some of the features of realistic cortical models. Importantly, the dynamics are driven by neuronal interactions, with all the attendant correlated spiking behaviors that emerge as a result of these interactions. We have elected to use a stochastic model because with the aid of ergodicity, firing rates are represented simply and convergence is fast. The model presented here will be used in the rest of this paper to evaluate the performance of reduced models that are much simpler.

2.1 Model description

We consider a population of neurons connected by local circuitry, such as neurons in an orientation domain of one layer of the primary visual cortex. We assume that this population contains $N_{E}$ excitatory (E) neurons and $N_{I}$ inhibitory (I) neurons, which are sparsely and homogeneously connected. The following assumptions are made in order to formulate a simple Markov process that describes the spiking activity of this population.

• 1. We assume for simplicity that the membrane potential of a neuron takes only finitely many discrete values.

• 2. Each neuron receives synaptic input from an external source in the form of Poisson kicks; these kicks are independent from neuron to neuron.

• 3. When the membrane potential of a neuron reaches a certain threshold, the neuron spikes, after which it goes to a refractory state and remains there for an exponentially distributed random time.

• 4. Every time an E (respectively I) neuron in the population spikes:

  • (a) a random set of postsynaptic neurons is chosen;

  • (b) the membrane potential of each chosen postsynaptic neuron goes up (respectively down) after an exponentially distributed random time.

More precisely, we assume that in our population there are $N_E$ excitatory neurons, labeled $1,2,\ldots , N_E$, and $N_I$ inhibitory neurons, labeled $N_E+1, N_E+2, \ldots , N_E + N_I$. The membrane potential of neuron i, denoted $V_i$, takes values in

$$\begin{aligned} \Gamma := \{-M_r, -M_r+1, \ldots , -1, 0,1,2, \ldots , M\} \cup \{{\mathcal {R}}\}. \end{aligned}$$

Here $M, M_r \in {\mathbb {Z}}^+$; M represents the threshold for spiking, $-M_r$ the inhibitory reversal potential, and ${\mathcal {R}}$ the refractory state. When $V_i$ reaches M, the neuron is said to spike, and $V_i$ is instantaneously set to ${\mathcal {R}}$, where it remains for a duration given by an exponential random variable with mean $\tau _{{\mathcal {R}}}>0$. When $V_i$ leaves ${\mathcal {R}}$, it goes to 0.

We describe first the effects of the “external drive”, external in the sense that this input comes from outside of the population in question; for example it can be thought of as coming from a region of cortex closer to sensory input. This input is delivered in the form of impulsive kicks, arriving at random (Poissonian) times, the Poisson processes being independent from neuron to neuron. For simplicity, we assume there are two parameters, $\lambda ^E, \lambda ^I>0$, representing the rates of the Poisson kicks to the E and I neurons in the population. These rates are low in background; they increase with the strength of the stimulation. When a kick arrives and $V_i \ne {\mathcal {R}}$, $V_i$ jumps up by 1, until it reaches M, at which time the neuron spikes. Kicks received by neuron i when $V_i={\mathcal {R}}$ have no effect.

Each neuron also receives synaptic input from within the population. We assume that an excitatory kick received by a neuron “takes effect” (the meaning of which will be made precise momentarily) at a random time after its arrival. This delay is given by an exponential random variable with mean $\tau ^E$; it is independent from spike to spike and from neuron to neuron. Similarly, an inhibitory kick received takes effect after a random time with mean $\tau ^I$. We let $H^E_i$ denote the number of E-kicks received by neuron i that has not yet taken effect, and let $H^I_i$ denote the corresponding number of I-kicks. That is to say, every time an E-kick is received by neuron i, $H^E_i$ goes up by 1; every time an E-kick received by neurons i takes effect, $H^E_i$ goes down by 1, and so on. The state of neuron i at any one moment in time is then described by the triplet $(V_i, H^E_i, H^I_i)$. We will refer to $H^E_i$ and $H^I_i$ as the numbers of kicks “in play”; these two numbers may be viewed as stand-ins for the E and I-conductances of neuron i.

We now explain what it means for an E or I-kick to take effect. Each E or I-kick received by neuron i carries with it an (independent) exponential clock as discussed above. When this clock rings, what happens depends on whether or not $V_i = {\mathcal {R}}$. If $V_i = {\mathcal {R}}$, then $V_i$ is unchanged. If $V_i \ne {\mathcal {R}}$, then $V_i$ is modified instantaneously according to the numbers $S_{Q,Q'}, \ Q, Q' \in \{ E, I\}$, where $S_{Q,Q'}$ denotes the synaptic coupling when a neuron of type $Q'$ synapses on a neuron of type Q. In the case of an I-kick, this modification also depends on $V_i$.

Here is how $V_i$ is modified in the case of an E-kick, i.e., when $Q'=E$: Assume first that the numbers $S_{Q,Q'}$ are nonnegative integers. When an E-neuron spikes and it synapses on neuron i, $V_i$ jumps up by $S_{\textit{EE}}$ if i is an E-neuron, by $S_{\textit{IE}}$ if i is an I-neuron; and if the jump takes $V_i$ to an integer $\ge M$, it simply goes to ${\mathcal {R}}$. For non-integer values of $S_{Q,Q'}$, let $p = \left\lfloor S_{Q,Q'} \right\rfloor$ be the greatest integer less than or equal to $S_{Q,Q'}$. Then $S_{Q,Q'} = p + u$ where u be a Bernoulli random variable taking values in $\{0,1\}$ with ${\mathbb {P}}[ u = 1] = S_{Q,Q'} - p$ independent of all other random variables in the model.

When I-spikes take effect, the rule is analogous to that for E-spikes, with the following exception: $V_i$ jumps down instead of up by an amount proportional to $V_i+M_r$, where $-M_r$ is the reversal potential for I-currents. The numbers $S_{Q,Q'}$ are assumed to be positive, and for definiteness, let us declare $S_{Q,I}$ to be the size of the jump at $V_i=M$, so that in general, the size of the jump is

$$\begin{aligned} S_{Q, I}(V_{i}) := (V_i+M_r)/(M+M_r)*S_{Q,I}. \end{aligned}$$

We remark that we have incorporated into the numbers $S_{Q,Q'}$ the changes in current in the postsynaptic neuron. We have assumed that E-currents are independent of the membrane potential of the postsynaptic neuron, which is not unreasonable since the reversal potential for excitatory current is quite large ($>4M$ in our setup). Changes in I-current are more sensitive to membrane potential, and that is reflected in the formula above.

It remains to stipulate the “connectivity” of the network, i.e., the set of neurons postsynaptic to each neuron. We assume for simplicity that connectivity in our model is random and time-dependent, so that every time a neuron spikes, a random set of postsynaptic neurons is chosen anew (independently of history). More precisely, for $Q,Q' \in \{E,I\}$, we let $P_{Q,Q'} \in [0,1]$ be the probability that a neuron of type Q is postsynaptic when a neuron of type $Q'$ spikes, and the set of postsynaptic neurons is determined by a coin flip with these probabilities following each spike. We do not pretend this assumption is realistic; in the real brain connectivities between neurons are fixed and far from random. But unlike longer range projections, which tend to target specific regions or even neurons, exact connectivities within local populations are not known to be important. This is a rationale behind our assumption of random postsynaptic neurons. Another is that this assumption simplifies the analysis considerably. In particular, it makes the behaviors of all neurons in the E-population, respectively the I-population, statistically indistinguishable.

This completes our description of the model.

2.2 Parameters used in numerical results

There is an analytical and a numerical part to our results. Our rigorous results apply to all parameter choices that satisfy the hypotheses in the theorems or propositions. We give a sense here of the parameters we use in simulations. More details are given in Sect. 3 when we construct networks with specific properties. We generally take $N_E$ to range from 300 to 1000, and $N_I= \frac{1}{3} N_E$, as is typically the case in local populations in the real cortex. We set $M = 100$, $M_r=66$, the ratio of $M_r$ to M reflecting biologically realistic ranges of membrane potentials. We fix $P_{\textit{EE}} = 0.15$, $P_{\textit{IE}} = P_{\textit{EI}} = 0.5$ and $P_{\textit{II}}=0.4$, these numbers chosen to resemble the usual connectivities in networks such as those in the visual cortex; see e.g. Chariker et al. (2016). There is less experimental guidance for the synaptic couplings $S_{Q,Q'}$; we take them to be 2–6, out of the 100 units between reset and threshold (cf $S_{\textit{EE}} =5$ means it takes 20 consecutive E-kicks to drive a neuron from $V_i=0$ to $V_i=M$). We set $\tau _{{\mathcal {R}}}=2$–3 ms, consistent with usual estimates for refractory periods, and set $\tau ^E$ and $\tau ^I$ to be a few ms, with $\tau ^E < \tau ^I$, as AMPA is known to act faster than GABA and both act within milliseconds. We will, on occasion, deliberately choose parameters that are a little unbiological to make a point. Finally, the Poisson rates of the external drive, $\lambda ^E, \lambda ^I$ will be varied as we study the model’s responses to drives of various strengths.

Readers who wish to bypass the technical mathematics pertaining to the class of models described above can proceed without difficulty to Sect. 3.

3 Theoretical results and proofs

Some basic results for the model presented in Sect. 1.1 are stated in Sect. 2.1, and their proofs are given in Sect. 2.3, after a brief review of probabilistic preliminaries.

3.1 Statement of results

The model described above is that of a Markov jump process $\Phi _{t}$ on a countable state space

$$\begin{aligned} {\mathbf {X}} = ( \Gamma \times {\mathbb {Z}}_{+} \times {\mathbb {Z}}_{+} )^{N_{E} + N_{I}}, \end{aligned}$$

as the state of neuron i is given by the triplet $(V_i, H^E_i, H^I_i)$ where $V_i \in \Gamma$ and $H^E_i, H^I_i \in {\mathbb {Z}}_{+}:= \{0,1,2,\dots \}$. We assume the paths of $\Phi _{t}$ are càdlàg. The transition probabilities of $\Phi _{t}$ are denoted by $P^{t}({\mathbf {x}}, {\mathbf {y}})$, i.e.,

$$\begin{aligned} P^{t}({\mathbf {x}},{\mathbf {y}}) = {\mathbb {P}}[ \Phi _{t} = {\mathbf {y}} \,|\, \Phi _{0} = {\mathbf {x}}]. \end{aligned}$$

The left operator of $P^{t}$ acting on a probability distribution $\mu$ is

$$\begin{aligned} \mu P^{t} ({\mathbf {x}}) = \sum _{{\mathbf {y}} \in {\mathbf {X}}} \mu ( {\mathbf {y}})P^{t}( {\mathbf {y}}, {\mathbf {x}}). \end{aligned}$$

The right operator of $P^{t}$ acting on an observable $\xi : {\mathbf {X}} \rightarrow {\mathbb {R}}$ is

$$\begin{aligned} P^{t} \xi ( {\mathbf {x}}) = \sum _{{\mathbf {y}} \in {\mathbf {X}}} P^{t}( {\mathbf {x}}, {\mathbf {y}})\xi ( {\mathbf {y}}). \end{aligned}$$

Our first result pertains to the existence and uniqueness, hence ergodicity, of invariant measure for the Markov chain $\Phi _{t}$. Notice that as $H^E_i$ and $H^I_i$ can take arbitrarily large values, the state space for $\Phi _{t}$ is noncompact, and such Markov chains need not possess invariant probabilities in general.

For $U: {\mathbf {X}} \mapsto (0, \infty )$, we define the U-weighted total variation norm of a signed measure $\mu$ on ${\mathcal {B}}({\mathbf {X}})$, the Borel $\sigma$-algebra of ${\mathbf {X}}$, to be

$$\begin{aligned} \Vert \mu \Vert _{U} = \sum _{{\mathbf {x}} \in {\mathbf {X}}} U({\mathbf {x}})|\mu ( {\mathbf {x}})|, \end{aligned}$$

and let

$$\begin{aligned} L_{U}({\mathbf {X}}) = \{ \mu \text{ on } {\mathcal {B}}({\mathbf {X}}) \,|\, \Vert \mu \Vert _{U} < \infty \}. \end{aligned}$$

To state the main result, we need the following definitions. For each state ${\mathbf {x}} \in {\mathbf {X}}$, we let

$$\begin{aligned} H^E({\mathbf {x}}) = \sum _{i = 1}^{N_{E}+N_I} H^{E}_{i} \qquad \text{ and } \qquad H^I({\mathbf {x}}) = \sum _{i = 1}^{N_{E}+N_I} H^{I}_{i} \end{aligned}$$

be the total number of E-kicks and I-kicks in play.

Theorem 2.1

The Markov chain $\Phi _{t}$ admits a unique invariant probability measure $\pi \in L_{U}( {\mathbf {X}})$ where

$$\begin{aligned} U({\mathbf {x}}) = H^E( {\mathbf {x}}) + H^I( {\mathbf {x}}) + 1. \end{aligned}$$

This stationary measure is ergodic with exponential convergence to equilibrium, equivalently exponential decay of time correlations. More precisely, there exist constants $C_{1}, C_{2}>0$ and $r \in (0, 1)$, such that

• (a) for any initial distribution $\mu \in L_{U}({\mathbf {X}})$,

  $$\begin{aligned} \Vert \mu P^{t} - \pi \Vert _{U} \le C_{1} r^{t} \Vert \mu - \pi \Vert _{U}\,; \end{aligned}$$

• (b) for any observable $\xi$ with $\Vert \xi \Vert _{U} < \infty$,

  $$\begin{aligned} \Vert P^{t} \xi - \pi ( \xi ) \Vert _{U} \le C_{2} r^{t} \Vert \xi - \pi ( \xi ) \Vert _{U}, \end{aligned}$$

  where

  $$\begin{aligned} \pi ( \xi ) = \sum _{ {\mathbf {x}} \in {\mathbf {X}}} \pi ({\mathbf {x}}) \xi ( {\mathbf {x}}). \end{aligned}$$

For $T >0$, we let $N_E(T)$ denote the total number of spikes fired by the E-population on the time interval [0, T], and let $\mathbb E_\mu [N_E(T)]$ denote the expected value of $N_E(T)$ starting from initial condition $\mathbf{x}$ with distribution $\mu$. We may then define the steady state firing rate of the E-population to be

$$\begin{aligned} \lim _{T\rightarrow \infty } \frac{1}{T} {\mathbb {E}}_\pi [N_E(T)] = \mathbb E_\pi [N_E(1)] \end{aligned}$$

where $\pi$ is the invariant probability measure given by Theorem  2.1. That the limit on the left exists and is equal to the quantity on the right follows from the invariance of $\pi$. It is not guaranteed a priori, however, that ${\mathbb {E}}_\pi [N_E(1)] < \infty$. The steady state firing rate of the I-population is defined similarly.

For $Q \in \{E,I\}$, since all neurons of type Q are indistinguishable, we have, by exchangeability, that the steady state firing rate of individual neurons of type Q is given by

$$\begin{aligned} {\bar{F}}_Q = {\mathbb {E}}_\pi [N_Q(1)] / N_Q\ . \end{aligned}$$

The next corollary asserts that these firing rates are both finite and computable.

Corollary 2.2

• (a) ${\bar{F}}_E, {\bar{F}}_I < \infty$;

• (b) for every $\mathbf{x} \in X$ and a.e. sample path,

  $$\begin{aligned} \frac{1}{N_Q} \cdot \frac{N_Q(T)}{T} \ \rightarrow \ {\bar{F}}_Q \qquad \text{ as } \quad T \rightarrow \infty \ \qquad \text{ for } Q = E, I. \end{aligned}$$

3.2 Probabilistic preliminaries

We review the following general results on geometric ergodicity. Let $\Psi _{n}$ be a Markov chain on a countable state space $(X, {\mathcal {B}})$ with transition kernels ${\mathcal {P}}(x, \cdot )$, and let $W: X \rightarrow [1, \infty )$. Consider the following conditions:

• (a) There exist constants $K \ge 0$ and $\gamma \in (0, 1)$ such that

  $$\begin{aligned} ({\mathcal {P}}W)(x) \le \gamma W(x) + K \end{aligned}$$

  for all $x \in X$.

• (b) There exists a constant $\alpha \in (0, 1)$ and a probability measure $\nu$ so that

  $$\begin{aligned} \inf _{x\in C} {\mathcal {P}}(x, \cdot ) \ge \alpha \nu (\cdot ), \end{aligned}$$

  with $C = \{x \in X \, | \, W(x) \le R \}$ for some $R > 2K(1 - \gamma )$, where K and $\gamma$ are from (a).

The following was first proved in Meyn and Tweedie (2009). The version we use is proved in Hairer and Mattingly (2011).

Theorem 2.3

Assume (a) and (b). Then $\Psi _{n}$ admits a unique invariant measure $\pi \in L_{W}(X)$. In addition, there exist constants $C, C' > 0$ and $r \in (0, 1)$ such that (ii) for all $\mu , \nu \in L_{W}(X)$,

$$\begin{aligned} \Vert \mu {\mathcal {P}}^{n} - \nu {\mathcal {P}}^{n} \Vert _{W} \le C r^{n} \Vert \mu - \nu \Vert _{W}, \end{aligned}$$

and (i) for all $\xi$ with $\Vert \xi \Vert _{W} < \infty$,

$$\begin{aligned} \Vert {\mathcal {P}}^{n} \xi - \pi ( \xi ) \Vert _{W} \le C' r^{n} \Vert \xi - \pi (\xi ) \Vert _{W}. \end{aligned}$$

3.3 Proof of Theorem 2.1 and Corollary 2.2

For a step size $h > 0$, we define the time-h sample chain as $\Phi ^{h}_{n} = \Phi _{nh}$, and drop the superscript h when it leads to no confusion. We first show for this discrete-time chain that $U({\mathbf {x}}) = H^E({\mathbf {x}}) + H^I({\mathbf {x}})+1$ is a natural Lyapunov function that satisfies conditions (a) and (b) in the previous subsection.

Lemma 2.4

For $h > 0$ sufficiently small, there exist constants $K > 0$ and $\gamma \in (0, 1)$, such that

$$\begin{aligned} P^{h}U \le \gamma U + K. \end{aligned}$$

Intuitively, this is true because on a short time interval (0, h), U decreases at a rate proportional to $H^E+H^I$ as kicks received prior to time 0 take effect, while it can increase at most by a fixed constant related to $N_E +N_I$ due to the presence of the refractory period.

Proof

We have

$$\begin{aligned} P^{h}U( {\mathbf {x}}) = {\mathbb {E}}_{{\mathbf {x}}}[ U( \Phi _{h})] \le U( {\mathbf {x}}) - {\mathbb {E}}_{{\mathbf {x}}}[ N_{out}] + {\mathbb {E}}_{{\mathbf {x}}}[N_{in}], \end{aligned}$$

where $N_{out}$ is the number of kicks from $H^E+H^I$ that takes effect on (0, h], and $N_{in}$ is the number of new spikes produced during the time period (0, h].

To estimate $N_{out}$, recall that the clocks associated with each of the $H^E+H^I$ kicks are independent, with each E-kick taking effect on (0, h] with probability $(1-e^{- h/ \tau ^E})$ and each I-kick taking effect on (0, h] with probability $(1-e^{-h/\tau ^I})$. This gives

$$\begin{aligned} {\mathbb {E}}_{{\mathbf {x}}}[ N_{out}] \ge (H^E + H^I) ( 1 - e^{-h/\max \{\tau ^E, \tau ^I\}} ) \ge \frac{1}{2 \max \{\tau ^E, \tau ^I\}} \ h \ U( {\mathbf {x}}) \end{aligned}$$

for h sufficiently small.

To estimate $N_{in}$, consider neuron i, and let $f_i$ be the number of spikes generated by neuron i during the time period (0, h]. Since after each spike neuron i spends an exponential time with mean $\tau _{{\mathcal {R}}}$ in state ${\mathcal {R}}$, we have

$$\begin{aligned} {\mathbb {E}}_{{\mathbf {x}}}[f_{i}] \le 1 + {\mathbb {E}}[ \text{ Poisson } \text{ distribution } \text{ with } \text{ parameter } h/\tau _{{\mathcal {R}}}] = 1 + h/\tau _{{\mathcal {R}}}. \end{aligned}$$

Hence

$$\begin{aligned} {\mathbb {E}}_{{\mathbf {x}}}[N_{in}] \le (N_{E} + N_{I})(1 + h/\tau _{{\mathcal {R}}}). \end{aligned}$$

The proof is completed by letting

$$\begin{aligned} \gamma = 1 - h/(2 \max \{\tau ^E, \tau ^I\}) \qquad \text{ and } \qquad K = (N_{E} + N_{I})(1 + h/\tau _{{\mathcal {R}}})\ . \end{aligned}$$

$\square$

For $b \in {\mathbb {R}}$, let

$$\begin{aligned} C_{b} = \{ {\mathbf {x}} \in {\mathbf {X}} | H^E( {\mathbf {x}}) + H^I( {\mathbf {x}}) \le b \}. \end{aligned}$$

Lemma 2.5

Let ${\mathbf {x}}_{0}$ be the state that $H^E = H^I = 0$ and $V_i = {\mathcal {R}}$ for all i. Then for any $h > 0$, there exists a constant c depending on b and h such that for all ${\mathbf {x}} \in C_{b}$,

$$\begin{aligned} P^{h}({\mathbf {x}}, {\mathbf {x}}_{0}) > c. \end{aligned}$$

Proof

It is sufficient to construct, for each ${\mathbf {x}} \in C_{b}$, a sample path that goes from ${\mathbf {x}}$ to ${\mathbf {x}}_{0}$ with a uniform lower bound on its probability. Consider the following sequence of events.

• (i) A sequence of Poisson kicks increases each $V_i$ to the threshold value M, hence puts $V_i={\mathcal {R}}$, by time $t=h/2$; once in ${\mathcal {R}}$, $V_i$ remains there through time $t = h$. No kick in play takes effect on [0, h / 2].

• (ii) All kicks in play at time h / 2 take effect on (h / 2, h], but that has no effect as all $V_i$ are in ${\mathcal {R}}$.

To prove that the events above occur with a positive probability bounded from below, observe that in the scenario described, the number of kicks in play never exceeds $b+N_E +N_I$, hence only a finite number of conditions are imposed. $\square$

Lemmas 2.4 and 2.5 together imply Theorem 2.1.

Proof of Theorem 2.1

Choose step size h as in Lemma 2.4. It follows from Lemmas 2.4 and 2.5 that the assumptions in Theorem 2.3 are satisfied. Therefore, the discrete-time chain $\Phi ^{h}$ admits a unique invariant probability measure $\pi _{h}$ in $L_{U}( {\mathbf {X}})$.

We will show that $\pi _{h}$ is invariant under $\Phi _t$ for any $t > 0$. This is because $\Phi _{t}$ satisfies the “continuity at zero” condition, meaning for any probability measure $\mu$ on ${\mathbf {X}}$,

$$\begin{aligned} \lim _{t \rightarrow 0}\Vert \mu P^{t} - \mu \Vert _{TV} = 0. \end{aligned}$$

To see this, let $\epsilon > 0$ be an arbitrary small number. Since $\mu$ is finite, there exists a finite set $A\subset {\mathbf {X}}$ such that $\mu (A) > 1 - \epsilon /4$. By the definition of A, clock rates for initial values in A are uniformly bounded. Therefore, one can find a sufficiently small $\delta > 0$, such that ${\mathbb {P}}[ \text{ no } \text{ clock } \text{ rings } \text{ on } [0, \delta ) ] \ge 1 - \epsilon /4$. For any set $U \subset {\mathbf {X}}$, we have

$$\begin{aligned} (\mu P^{\delta }) (U)= & {} \sum _{{\mathbf {x}} \in {\mathbf {X}}} P^{\delta }( {\mathbf {x}} , U) \mu ( {\mathbf {x}} )\\= & {} \sum _{{\mathbf {x}}\in A \cap U} P^{\delta }({\mathbf {x}}, U) \mu ( {\mathbf {x}} ) + \sum _{{\mathbf {x}} \in A - U} P^{\delta }({\mathbf {x}}, U) \mu ( {\mathbf {x}} ) + \sum _{{\mathbf {x}} \in A_{c}} P^{\delta }({\mathbf {x}}, U) \mu ( {\mathbf {x}}) \\= & {} \mu (A \cap U) - a_{1} + a_{2} + a_{3}, \end{aligned}$$

where

$$\begin{aligned} a_{1}= & {} \sum _{{\mathbf {x}} \in A \cap U} (1 - P^{\delta }({\mathbf {x}}, U) )\mu ({\mathbf {x}}) \le \frac{\epsilon }{4} \mu ( A \cap U) \le \frac{\epsilon }{4}\\ a_{2}= & {} \sum _{{\mathbf {x}} \in A \setminus U} P^{\delta }({\mathbf {x}}, U) \mu ( {\mathbf {x}}) \le \frac{\epsilon }{4} \mu ( A \setminus U) \le \frac{\epsilon }{4}\\ a_{3}= & {} \sum _{{\mathbf {x}} \in A^{c}} \frac{\epsilon }{4} \mu ( A \cap U) \le \frac{\epsilon }{4} \le \mu ( A^{c}) \le \frac{\epsilon }{4}. \end{aligned}$$

In addition we have $\mu (U) - \mu (A \cap U) \le \mu (A^{c}) < \frac{\epsilon }{4}$. Hence

$$\begin{aligned} | (\mu P^{\delta })(U) - \mu (U) | < \epsilon \end{aligned}$$

for any $U \subset {\mathbb {R}}^{N}_{+}$. By the definition of the total variation norm, we have

$$\begin{aligned} \Vert \mu P^{\delta } - \mu \Vert _{TV} \le \epsilon . \end{aligned}$$

This implies the “continuity at zero” condition.

Notice that $\pi _{h}$ is invariant for any $\Psi ^{hj/k}_{n}$, where $j, k \in {\mathbb {Z}}^{+}$ (Theorem 10.4.5 of Meyn and Tweedie 2009). Then without loss of generality, assume $t/h \notin {\mathbb {Q}}$. By the density of orbits in irrational rotations, there exists sequences $a_{n}$, $b_{n} \in {\mathbb {Z}}^{+}$ such that

$$\begin{aligned} d_{n} := t - \frac{a_{n}}{b_{n}}h \rightarrow 0 \end{aligned}$$

from right. Then

$$\begin{aligned} \pi _{h} P^{t} = \pi _{h}P^{\frac{a_{n}}{b_{n}} h} P^{d_{n}}. \end{aligned}$$

Therefore,

$$\begin{aligned} \Vert \pi _{h}P^{t} - \pi _{h} \Vert _{TV} \le \lim _{n \rightarrow \infty } \Vert \pi _{h}P^{d_{n}} - \pi _{h} \Vert _{TV} = 0 \end{aligned}$$

by the “continuity at zero” condition. Hence $\pi _{h}$ is invariant with respect to $P^{t}$.

It remains to prove the exponential convergence for any $t > 0$. By Lemma 2.4, there exists B such that $P^{t}V \le B V$ for all $t < h$. Let n be the largest integer that is smaller than t / h and let $d = t - hn$. Then we have

$$\begin{aligned} \Vert \mu P^{t} - \nu P^{t}\Vert _{V}= & {} \Vert (\mu P^{d}) P^{nh} - (\nu P^{d}) P^{hn}\Vert _{V}\\= & {} C r^{n} \cdot \Vert \mu P^{d} - \nu P^{d} \Vert _{V}\ \le \ BC r^{n} \Vert \mu - \nu \Vert _{V}. \end{aligned}$$

Similarly,

$$\begin{aligned} \Vert P^{t} \xi - \pi (\xi )\Vert _{V}= & {} \Vert P^{nh} (P^{d \xi })- P^{hn} (P^{d} \pi (\xi ))\Vert _{V}\\= & {} C r^{n} \cdot \Vert P^{d} \xi - P^{d} \pi (\xi ) \Vert _{V} \ \le \ BC r^{n} \Vert \xi - \pi (\xi ) \Vert _{V}. \end{aligned}$$

This completes the proof. $\square$

Proof of Corollary 2.2

• (a) Let $N_i(T)$ denote the number of spikes fired by neuron i on the time interval [0, T]. Then as in the proof of Lemma 2.4, we have that for every ${\mathbf {x}}$ and every i,

  $$\begin{aligned} {\mathbb {E}}_{{\mathbf {x}}}[N_i(1)] \le 1 + {\mathbb {E}}[ \text{ Poisson } \text{ distribution } \text{ with } \text{ parameter } 1/\tau _{{\mathcal {R}}}] = 1 + 1/\tau _{{\mathcal {R}}}. \end{aligned}$$

  Thus if neuron i is of type Q, then ${\bar{F}}_Q = {\mathbb {E}}_{\pi }[N_i(1)] < \infty$.

• (b) Without loss of generality let $Q = E$. Let

  $$\begin{aligned} \xi ( {\mathbf {x}}) = \sum _{ i = 1}^{N_{E}} {\mathbf {1}}_{\{V_{i} = {\mathcal {R}} \}}. \end{aligned}$$

  Then by the Ergodic Theorem, for every $\mathbf{x}$ and a.e. sample path $\Phi _t$ with $\Phi _0=\mathbf{x}$,

  $$\begin{aligned} \lim _{T \rightarrow \infty }\frac{1}{T}\int _{0}^{T} \xi ( \Phi _{t}) \mathrm {d}t = \pi ( \xi ). \end{aligned}$$

  Clearly,

  $$\begin{aligned} \pi (\xi ) = N_E \tau _{{\mathcal {R}}} \bar{F}_{E}\ . \end{aligned}$$

  Since the time durations that neurons stay at ${\mathcal {R}}$ are independent, we have, by the law of large numbers,

  $$\begin{aligned} \lim _{T \rightarrow \infty } \frac{\int _{0}^{T} \xi ( \Phi _{t}) \mathrm {d}t }{N_E(T)} = \tau _{R}. \end{aligned}$$

  The desired result follows. $\square$

4 Three populations with different degrees of synchrony

As explained in the Introduction, the primary purpose of this paper is a comparative study of more detailed and relatively realistic network models of interacting neurons and highly reduced ones, to explain what causes the discrepancies in their firing rates. The models introduced in Sect. 1.1 will be taken to be our “detailed and realistic” models; candidate reduced models are discussed in Sects. 4.1 and 5.1. The purpose of this section is to prepare for this study.

As also noted in the Introduction, different choices of parameters can lead to a wide range of dynamical behaviors that may potentially play a role in the proposed study. Intuitively, at least, it seemed to us that the single most salient difference between our network and reduced models lies in the ability of the first to produce correlated behavior but not the second. Indeed in networks in which connectivities are far from zero (unlike the setting in e.g., Brunel and Hakim 1999; Brunel 2000), different neurons share large subsets of inputs, and self-organized correlated spiking or partial synchronizations are well known to occur. We conjecture that the performance of reduced models to correctly predict the firing rates of network models vary depending on the network’s degree of synchrony.¹

To test this hypothesis, we design in this section three networks with different amounts of correlated spiking to be used in the comparative study to follow. We will give their precise parameters, record their firing rates and correlation statistics, and explain how models with these distinct synchrony properties were obtained.

4.1 Three example networks

We introduce here three models of the type described in Sect. 1.1, with identical parameters except for $\tau ^E$ and $\tau ^I$, the expected time between the occurrence of a spike and when it takes effect. As we will see, different choices of these values will lead to different degrees of synchrony.

We first give the parameters common to all three models: $N_E$ and $N_I$, the numbers of E and I neurons in the population, are 300 and 100 respectively. The connectivities $P_{QQ'}$ are as in Sect. 2.1, namely $P_{\textit{EE}} = 0.15$, $P_{\textit{IE}} = P_{\textit{EI}} = 0.5$ and $P_{\textit{II}}=0.4$. The synaptic weights $S_{QQ'}$ are as follows: $S_{\textit{EE}}=5$, $S_{\textit{IE}}=2$, and $S_{\textit{EI}}= S_{\textit{II}}=4.91$ (recall that this corresponds to coupling weights when $V_i$, the membrane potential of the postsynaptic neuron, is at threshold, i.e. at $V_i=100$). The expected time to stay in the refractory state, ${\mathcal {R}}$, is 2.5 ms, and the external drive rates to E and I neurons will be taken to be equal, i.e., $\lambda ^E=\lambda ^I$, and a range of values of the drive will be considered.

The parameters above, for the most part, are similar to those used in the realistic models of visual cortex (Chariker et al. 2016), realistic in the sense that its architecture and functional properties were benchmarked by dozens of sets of experimental data. From (Chariker et al. 2018), we learned also that varying the rise and decay times of E and I conductances, especially the relation between the two, is a very effective way to change the degree of synchrony of a local population. We now use this technique to produce the following three examples:

• 1. The “homogeneous” network, abbreviated as “Hom” in the figures:

  $$\begin{aligned} \tau ^{EE} = 4 , \quad \tau ^{IE} = 1.2 , \quad \tau ^I = 4.5 \qquad \text{(in } \text{ ms) } \end{aligned}$$

• 2. The “regular” network, abbreviated as “Reg” in the figures:

  $$\begin{aligned} \tau ^{EE} = 2.0 , \quad \tau ^{IE} = 1.2 , \quad \tau ^I = 4.5 \qquad \text{(in } \text{ ms) } \end{aligned}$$

• 3. The “synchronized” network, abbreviated as “Sync” in the figures:

  $$\begin{aligned} \tau ^{EE} = 1.3 , \quad \tau ^{IE} = 0.95 , \quad \tau ^I = 4.5 \qquad \text{(in } \text{ ms) } \end{aligned}$$

Instead of $\tau ^E$, we have used here $\tau ^{\textit{EE}}$ and $\tau ^{\textit{IE}}$ to denote the expected times between the occurrence of an E-spike and when it takes effect in E, respectively I, neurons. These numbers are roughly consistent with biological values: $\tau ^I>\tau ^{\textit{EE}}, \tau ^{\textit{IE}}$ is consistent with the fact that GABA acts more slowly than AMPA, and $\tau ^{\textit{EE}} > \tau ^{\textit{IE}}$ is consistent with the fact that E-spikes can synapse on dendrites of E-neurons, taking a bit longer for its effect to reach the soma, while they synapse directly on the soma of I-cells. That aside, there is nothing special about these choices, other than that they produce the distinct degrees of synchrony that we would like to have.

Figure 1 shows the E- and I-firing rates of the three networks above in response to a range of drives of magnitude $\lambda = \lambda ^E=\lambda ^I$ spikes/sec. Both firing rates increase monotonically as a function of drive. We think of $\lambda \sim 1000$ spikes/sec as low drive, or spontaneous activity, and $\lambda \ge 6000$ spikes/sec as strong drive.

Fig. 1

Firing rates of three example networks in response to increasing drive. In the x-axis, $\lambda =\lambda ^E=\lambda ^I$ is external drive. The graphs labeled “Hom” (bottom), “Reg” (middle) and “Sync” (top) give the firing rates of the corresponding networks

Fig. 2

Statistics of the Hom, Reg and Sync networks: All statistics are collected in response to a strong drive of $\lambda ^E=\lambda ^I=7000$ spikes/s. For each network we show in the top panel rasters (E-neurons in red, I-neurons in blue) over a 1/2 s time interval; mean firing rates are shown above the rasters. In the middle panel are corresponding summed spike plots for E-neurons, showing the percentage of the E-population spiking in each 5 ms window. Below the summed spike plots are correlation diagrams: a histogram labeled “X conditioned on Y at $t=0$”, $X,Y = E, I$, shows the percentage of the X-population spiking on 1 ms windows on the time interval $t \in [-15, 15]$ ms conditioned on a Y-spike occurring at time $t=0$. Labels for the Reg and Sync networks, which are omitted, are to be read as identical to those for the Hom network (color figure online)

4.2 Statistics of the “Hom”, “Reg” and “Sync” networks

Here we present more detailed information on the three networks defined in the last subsection, focusing on their responses to relatively strong drive, at $\lambda =7000$ spikes/s. Figure 2 shows, for each network, spike rasters, summed spike plots, and correlation diagrams.

The raster-plots are self-explanatory. Clearly visible in the rasters of the Reg and Synch networks are coordinated spiking that emulate gamma band oscillations (at 30–90 Hz) in the real cortex (Andrew Henrie and Shapley 2005). These spiking events are entirely emergent, or self-organized, in the sense that there is nothing built into the network architecture or dynamics that lead directly to these spiking events. Comparing the frequency of these events with mean E-firing rate (given above the rasters), one sees that most E-neurons do not participate in all spiking events.

The summed spike plots give the fractions of the E-population spiking in 5-ms time bins. Though they show the same behaviors as the rasters, we have included these plots because rasters can be deceiving when used to depict the spiking activity of hundreds of neurons: what appear to be population spikes may in fact involve fewer neurons than the rasters suggest. For the Sync network, one sees from the summed spike plots that most spiking events do not involve the entire population, even though the rasters may give an impression to the contrary. As for the Reg network, Fig. 2 shows that the larger spiking events usually involve no more than 30–40% of the population. Nor do identical fractions of neurons spike in each 5 ms bin in the Hom network: there is some amount of synchronization that is entirely emergent, natural and hard to avoid.

The correlation diagrams describe not correlations between pairs of neurons but how the spiking of individual neurons is correlated to that of the rest of the population. We describe precisely what is plotted in, for example, the second histogram from the left, labeled “Conditioned on E at $t=0$” with an “I” in the box. Here we run the network for 10–20 s. Each time an E-neuron spikes, we record all the I-spikes fired within 15 ms of its occurrence, both before and after, computing the fraction of the I-population spiking in each 1-ms time bin on this time interval. This is then averaged over all E-spikes that occur during the simulation. The other three plots are interpreted analogously. A comparison of these plots for the three networks confirms the increasing amounts of correlated spiking, or partial synchrony, that are clearly visible in the rasters as we go from the Hom to the Sync network.

Analysis We have presented three example networks defined by essentially the same parameters yet exhibiting remarkably dissimilar spiking patterns, from very homogeneous to strongly synchronized. The only differences in network parameters are $\tau ^E$ and $\tau ^I$, which describe how long after one neuron synapses on another before the effect of the spike is fully felt. Even here, the differences are subtle: the homogeneous and regular networks differ only in $\tau ^{\textit{EE}}$ and by only 2 ms, while all three $\tau$-parameters differ by $<1$ ms between the regular and synchronized networks.

Two points here are of note. First, when under drive, the most salient kind of correlations among neurons in the model are semi-regular bursts of elevated spiking occurring with frequencies in the gamma band (not to suggest that these are the only correlations). Second, our simulations confirm that small changes in $\tau ^E$ and $\tau ^I$, intended to represent how AMPA and GABA affect conductance properties in the postsynaptic neuron in the real brain, have a strong impact on the amount of correlated spiking or degree of synchronization in the local population.

The mechanism behind gamma band oscillations has been much studied. An extreme form of it involving full population spikes, called PING, was first described in Börgers and Kopell (2003). Milder and more realistic forms producing spectral power densities much closer to data were studied in Rangan and Young (2013), Chariker and Young (2015) and Chariker et al. (2018). We refer the reader to these papers for a more detailed discussion. Very briefly, these rhythms occur as a result of recurrent excitation and the fact that the time course for GABA is generally a few ms slower than that of AMPA, allowing some fraction of the E- and I-population to spike before a sufficient amount of GABA is released to curb the spiking activity.

Finally, to be clear, we do not claim that the examples above are representative of all network models. If anything, they illustrate that neuronal interactions can produce a wide range of dynamical characteristics, and that these characteristics can depend on model parameters in subtle ways. But with partial synchronization being one of the most salient features of driven neuronal dynamics, these three examples allow us close-up looks into how reduced models perform when used to predict the dynamics of networks with different degrees of synchronization.

5 Firing rates: comparison of reduced and network models

Up until now, we have focused on models defined by populations of interacting neurons. We now turn to the use of mean-field-type models to estimate their firing rates. Three very simple ODEs describing the evolution of membrane potential are proposed in Sect.  4.1. No novelty is claimed here with regard to these reduced models; many similar ideas for deducing firing rates by balancing one quantity or another have been proposed in the literature (see e.g. Wilson and Cowan 1972, 1973; Knight et al. 1996; Amit and Brunel 1997a, b; Vreeswijk and Sompolinsky 1998; Omurtag et al. 2000; Gerstner 2000; Brunel 2000; Haskell et al. 2001; Cai et al. 2004, 2006; Rangan and Cai 2006). The reduced models we have selected for consideration were chosen for their simplicity, and the fact that they allow a direct comparison with the network models studied in Sects. 1–3. Such a comparison is carried out in Sect. 4.2, followed by an analysis of the discrepancies.

5.1 Three reduced models and their firing rates

The models below will be referred to by their names in italics in later discussion.

(1) Linear model In this first reduced model we regard the membrane potential v of each neuron as drifting upward at constant speed, i.e.,

$$\begin{aligned} \frac{dv}{dt} = F^+ - F^- \ , \qquad \text{ for } \ v \in [0,1]\ . \end{aligned}$$

(4.1)

Upon reaching 1, v is instantaneously reset to 0, and the climb starts immediately (with no refractory period). Here $F^+$ and $F^-$ are the forces that drive v upward, respectively downward. They are connected to the quantities that describe the network models in Sect. 1.1 as follows: Let

$$\begin{aligned}&C_{\textit{EE}} = N_{E}P_{\textit{EE}}S_{\textit{EE}}\ , \qquad C_{\textit{IE}} = N_{E}P_{\textit{IE}}S_{\textit{IE}}\ , \nonumber \\&C_{\textit{EI}} = N_{I}P_{\textit{EI}}{\hat{S}}_{\textit{EI}} \ , \qquad C_{\textit{II}} = N_{I}P_{\textit{II}}{\hat{S}}_{\textit{II}}, \end{aligned}$$

(4.2)

where ${\hat{S}}_{\textit{EI}}$ and ${\hat{S}}_{\textit{II}}$ are to be taken to be the value of $S_{\textit{EI}}(v)$ and $S_{\textit{II}}(v)$ at $v=M/2=50$ in the model in Sect. 1.1. Then for E-neurons,

$$\begin{aligned} F^+ = \frac{1}{M} \left( f_E * C_{EE} + \lambda ^E\right) \qquad \text{ and } \qquad F^- = \frac{1}{M} \ f_I * C_{EI}\ , \end{aligned}$$

and for I-neurons,

$$\begin{aligned} F^+ = \frac{1}{M} \left( f_E * C_{IE} + \lambda ^I\right) \qquad \text{ and } \qquad F^- = \frac{1}{M} \ f_I * C_{II}\ . \end{aligned}$$

Here $f_E$ and $f_I$ are to be thought of as mean E- and I-firing rates of the population.

The mean excitatory and inhibitory firing rates $f^{(1)}_E$ and $f^{(1)}_I$ of this reduced model are defined to be the values of $f_E$ and $f_I$ that satisfy the self-consistency condition that when these values are plugged into the equations above, they produce the same firing rates (the number of times per sec v in (4.1) reaches 1). They can be computed explicitly as follows:

Lemma 4.1

The values $(f^{(1)}_E, f^{(1)}_I)$ are uniquely defined and are given by the formulas below, provided the quantities on the right side are $\ge 0$:

$$\begin{aligned} f^{(1)}_{E}= & {} \frac{\lambda ^{E}(M + C_{II}) - \lambda ^{I}C_{EI} }{(M - C_{EE})(M + C_{II}) + (C_{EI}C_{IE})} \nonumber \\ f^{(1)}_{I}= & {} \frac{\lambda ^{I}(M - C_{EE}) + \lambda ^{E}C_{IE} }{(M - C_{EE})(M + C_{II})+ (C_{EI}C_{IE})}, \end{aligned}$$

(4.3)

With $\lambda ^E=\lambda ^I$ as we have done in Sect. 3, it is easy to see that $f^{(1)}_E$ and $f^{(1)}_I$ increase linearly as functions of drive.

(2) Linear model with refractory This model is similar to the previous one, except for the presence of a (fixed) refractory period. That is to say, here

$$\begin{aligned} \frac{dv}{dt} = F^+ - F^- , \qquad \text{ for } \ v \in [0,1]\ , \end{aligned}$$

except that every time v reaches 1 and is reset to 0, it remains there for a time interval of length $\tau _{{\mathcal {R}}}$ before resuming its linear climb. See Fig. 3a (second from left).

The mean E- and I-firing rates of this model, $(f^{(2)}_E, f^{(2)}_I)$, are then given by the pair $(f_E, f_I)$ satisfying the quadratic equations

$$\begin{aligned} M * f_E= & {} (1-\tau _{{\mathcal {R}}}f_{E})\left( f_E * C_{EE} + \lambda ^E - f_I * C_{EI}\right) \end{aligned}$$

(4.4)

$$\begin{aligned} M * f_I= & {} (1-\tau _{{\mathcal {R}}}f_{E})\left( f_E * C_{IE} + \lambda ^E - f_I * C_{II}\right) \ . \end{aligned}$$

(4.5)

Theoretically, these equations can be solved analytically. From the first equation of (4.4), it is easy to see that

$$\begin{aligned} f_{I} = \frac{(1 - \tau _{{\mathcal {R}}} f_{E})\left( C_{EE} f_{E} + \lambda ^{E}\right) - M f_{E} }{C_{EI}(1 - \tau _{{\mathcal {R}}} f_{E})}. \end{aligned}$$

Putting $f_{I}$ into the second equation of (4.4) and multiplying both sides by $(1 - \tau _{{\mathcal {R}}} f_{E})^{2}$, we obtain a quartic equation for $f_{E}$ of the form

$$\begin{aligned} A_{0}(\tau _{{\mathcal {R}}}) + A_{1}(\tau _{{\mathcal {R}}})f_{E} + A_{2}(\tau _{{\mathcal {R}}})f_{E}^{2} + A_{3}(\tau _{{\mathcal {R}}})f_{E}^{3} + A_{4}(\tau _{{\mathcal {R}}})f_{E}^{4} = 0, \end{aligned}$$

where $A_0, \dots , A_4$ are polynomials of $\tau _{{\mathcal {R}}}$. In particular, when $\tau _{{\mathcal {R}}} = 0$, this quartic equation reduces to the linear equation

$$\begin{aligned}{}[(M - C_{EE})(M + C_{II}) + (C_{EI}C_{IE})] f_{E} = \lambda ^{E}(M + C_{II}) - \lambda ^{I}C_{EI}, \end{aligned}$$

(4.6)

which produces $f_{E}^{(1)}$ in (4.3). It is well known that quartic equations have a root formula, which is unfortunately too complicated to be practical, but it gives the existence of solution to the quadratic system. In addition, for sufficiently small $\tau _{{\mathcal {R}}}$, the quartic equation is a small perturbation of Eq. (4.6). By the intermediate value theorem, it is easy to show that the quartic equation must admit a root that is close to $f_{E}^{(1)}$. We leave this elementary proof to the reader.

(3) Thev-dependentmodel Here v satisfies the same equation as before, except that $S_{\textit{EI}}$ and $S_{\textit{II}}$ depend on the distance of v to the reversal potential. To separate the effects of refractory and v-dependence of synaptic weights, let us assume for definiteness that there is no refractory period, that is to say, all is as in the linear model except for the following:

$$\begin{aligned} S_{\textit{EI}}(v) = \frac{Mv+ M_{r}}{M+ M_{r}}*S_{\textit{EI}} \qquad \text{ and } \qquad S_{\textit{II}}(v) = \frac{Mv+ M_{r}}{M+ M_{r}}*S_{\textit{II}}\ . \end{aligned}$$

For a given pair $(f_{E}, f_{I})$, this gives us two first order linear ODEs

$$\begin{aligned} \frac{\mathrm {d}v_{E}}{\mathrm {d}t} = A_{E} - B_{E} v_{E} \qquad \text{ and } \qquad \frac{\mathrm {d}v_{I}}{\mathrm {d}t} = A_{I} - B_{I} v_{I}, \end{aligned}$$

where $A_E, A_I, B_E$ and $B_I$ are easily computed from network parameters. We let $t_{E}$ and $t_{I}$ be the times $v_E$ and $v_I$ first reaches 1. Then the desired spike rates $f_E$ and $f_I$ should satisfy $f_E = t_E^{-1}$ and $f_I=t_I^{-1}$. That is, the firing rates $f^{(3)}_E$ and $f^{(3)}_I$ of this ODE model is the pair $(f_E, f_I)$ that solves the two nonlinear equations

$$\begin{aligned} 1 = \frac{A_{E}}{B_{E}}\left( 1 - e^{- B_{E}f_{E}^{-1}}\right) \quad , \quad 1 = \frac{A_{I}}{B_{I}}\left( 1 - e^{- B_{I}f_{I}^{-1}}\right) . \end{aligned}$$

(4.7)

These equations can be solved numerically.

Needless to say, one can also consider the combined effects of (2) and (3), to obtain a v-dependent model with refractory. In this case, Eq. (4.7) becomes

$$\begin{aligned} 1 = \frac{A_{E}}{B_{E}}\left( 1 - e^{- B_{E}(f_{E}^{-1} - \tau _{{\mathcal {R}}})} \right) , \quad 1 = \frac{A_{I}}{B_{I}}\left( 1 - e^{- B_{I}(f_{I}^{-1} - \tau _{{\mathcal {R}}})}\right) . \end{aligned}$$

Firing rates for the first two reduced models are shown in Fig. 3b (left) using the parameters of the network models studied in Sect. 3. An immediate observation is that the model with refractory has higher firing rates, which may be somewhat counter-intuitive as the delay during refractory should, on the face of it, lead to lower firing rates. We have omitted the firing rates for the v-dependent model because they are ridiculously low (close to 0) and numerically unstable, and that requires an explanation as well. (Please ignore the plot with open circles for now.)

Analysis The following is a heuristic explanation for $f^{(2)}_E > f^{(1)}_E$: As is usually the case, I-firing rate is significantly higher than E-firing rate in the models considered. With refractory, every time a neuron spikes, it “misses” some amount of the incoming drive, the net value of which is positive. Since the fraction of drive “missed” is proportional to the firing rate of a neuron in these models, the I-neuron “misses” a larger fraction of its drive than the E-neuron. This may cause the system to become more excited than in the case of no refractory. (In the argument above we have taken into account first order effects only, ignoring the secondary effect that higher E-firing will boost I-firing.)

With regard to the v-dependent model, our analysis shows that the root $(f^{(3)}_E, f^{(3)}_I)$ is very sensitive with respect to small change of constants $B_E$ and $B_I$. Small errors in $B_E$ or $B_I$ caused by the inhomogeneous arrival of spikes are dramatically amplified by the v-dependent model. As a result, the computed values are usually too low and not sufficiently reliable to be useful.

That begs the question then: why are firing rates in the network models so much higher than in the v-dependent model, and so robust? We believe stochastic fluctuations is the answer, and will study that in the next section.

Fig. 3

Comparison of firing rates. a Trajectories of the membrane potential v as functions of time, for 4 reduced models. From left to right: the linear model, the linear model with refractory, the v-dependent model, and the random-walk model considered in Sect. 5. b The left panel shows graphs of E-firing rates as functions of drive of the two linear reduced models, with and without refractory, and of the random walk model discussed in Sect. 5 (black with open circles). Firing rates of the v-dependent model are omitted as they cannot be computed reliably. The right panel shows firing rates of the network models (from Fig. 1) superimposed on the graphs from the left panel. c Percentage error if one uses the linear model with refractory to predict firing rates of network models. For example, $-\,20\%$ means the reduced model predicts a firing rate $20\%$ lower than that of the network model (color figure online)

5.2 Comparison of firing rates with network models

We now compare the firing rates of the network models in Sect. 3 and the reduced models in Sect. 4.1. The right panel of Fig. 3b shows the firing rates of the two linear reduced models (with and without refractory) copied from the panel on the left and superimposed on the firing rates of the Hom, Reg and Sync models copied from Fig. 1. We see immediately that the linear reduced model underestimates the firing rates of all three networks for moderate and strong drives; and the linear model with refractory, which has higher firing rates as explained earlier, underestimates the firing rates of the Sync model and overestimates that of the Hom model. Figure 3c gives the percentage errors if the linear model with refractory was used to predict the firing rates of the network models. It confirms what is shown in Fig. 3b (right).

For definiteness, we now focus on a single reduced model, namely the linear model with refractory, and refer to it simply as “the reduced model” in the rest of this section. There are likely many reasons why network firing rates are not in total agreement those of this reduced model. We will focus on two of them: correlated spiking in the form of partial synchronization as depicted in Fig. 2, and the V-dependence of I-currents. The reason correlated spiking, or synchronization, may be relevant is that in this reduced model, the arrival of synaptic input to a neuron is assumed to be homogeneous in time. Indeed such an assumption is implicit (or explicit) in most reduced models, even though it is in direct contradiction to correlations in spiking or partial synchronization, phenomena that are well known to occur in the real brain.

One of the effects of correlated spiking is that a disproportionately large fraction of synaptic input may be missed during refractory. Some statistics pertinent to our investigation are shown in Fig. 4. The bar graphs in Fig. 4a show the percentages of E and I-spikes missed during refractory. Here we have distinguished between spikes from interactions among neurons within the population and from external drive. As external drive is assumed to be constant in time, one may equate the percentage of spikes from external drive missed with the percentage of time a neuron spends in refractory. As expected, the percentages of E- and I-spikes missed in the Hom network are reasonably close to those predicted by the reduced model. In the Sync network, the percentages of synaptic input missed are considerably higher than the percentage of time spent in refractory, consistent with the fact that spike times in this network are strongly correlated; see the correlation diagrams in Fig. 2. That a smaller percentage of I-spikes are missed than E-spikes is likely due to $\tau ^I$ being large relative to $\tau _{{\mathcal {R}}}$, so more I-spikes arrive after the neuron leaves refractory. Figure 4b shows the empirical mean values of V in the three network models, which are well above the mean values of V when I-spikes take effect.

Fig. 4

Challenging the homogeneity of drive assumption in reduced models. a Percentages of external drive, E and I-spikes missed during refractory, for E and I neurons, for the Hom, Reg and Sync networks, for postsynaptic E-cells (left) and postsynaptic I-cells (right). The percentage of external drive missed can be taken to be $\%$ time spent in refractory; E and I input here refer to synaptic input from within the population. b Mean V-values when I-spikes take effect, as functions of drive, for the three networks. Corresponding graphs for I-neurons are qualitatively similar (color figure online)

Analysis We now attempt to explain the deviations of network firing rates from those predicted by the linear model with refractory.

(a) Discrepancy caused by lack of V-dependence of I-currents Our reduced model used $S_{EI}$ and $S_{II}$ values that correspond to network values at $V=M/2 =50$. This choice is based on the assumptions that V marches at constant speed from reset to threshold, that I-spikes arrive in a time-homogeneous way, and act with constant strength. None of these assumptions is true in the network, and the situation is complicated: That I-spikes have stronger effect for postsynaptic neurons at larger V should slow down the upward drift of V at larger values, causing V to linger longer in the region $\{V>50\}$; but strong synchronization is likely to cause more I-spikes to arrive when V is lower. Indeed according to Fig. 4b, at drive = 7000 sp/s, the mean V-value when I-spikes take effect are $\sim 54.5, 52$ and 48 respectively for the Hom, Reg and Sync networks.

This means using $S_{EI}$ and $S_{II}$ values at $V=M/2$ underestimates the mean values of these parameters for the Hom and Reg networks, and overestimates it for the Sync network. Underestimating $S_{EI}$ means that the network is in fact more suppressed than this reduced model suggests. To summarize: based on this one property alone, we would expect the reduced model to have a higher firing rate than the Hom and Reg networks (with a smaller error for the Reg network) and to have a lower firing rate than the Sync network.

(b) The effects of partial synchronization working in concert with refractory Because the arrival of synaptic input is not necessarily homogeneous in time, the fraction of E and I-spikes “missed” during refractory can be nontrivially altered by partial synchronization. There is no easy way to predict the net effect of this phenomenon, however, because it involves both E- and I-inputs missed by both E and I neurons, leading to a not-so-simple cancellation problem.

Consider first E-neurons. Suppose an additional fraction $\varepsilon _{EE}$ of E-input, and an additional fraction $\varepsilon _{EI}$ of I-input, to E-neurons are lost during refractory—“additional” in the sense that it is above and beyond what is assumed to be lost during refractory under the homogeneity of input assumption. Then compared to the reduced model, there is a net gain in (positive) current in the amount of

$$\begin{aligned} \Delta F_E \ = \ \varepsilon _{EI} f_I C_{EI} - \varepsilon _{EE} f_E C_{EE} = 172 \ \varepsilon _{EI} f_I - 225 \ \varepsilon _{EE} f_E \ . \end{aligned}$$

(This number can be positive or negative.) For an I-neuron, net gain relative to the reduced model is

$$\begin{aligned} \Delta F_I \ = \ \varepsilon _{II} f_I C_{II} - \varepsilon _{IE} f_E C_{IE} = 137 \ \varepsilon _{II} f_I - 300 \ \varepsilon _{IE} f_E \ . \end{aligned}$$

For the Sync model, we see from Fig. 4a that

$$\begin{aligned} \varepsilon _{EI} \approx 8 , \quad \varepsilon _{EE} \approx 14.5 , \quad \varepsilon _{II} \approx 11 , \quad \varepsilon _{IE} \approx 22\ . \end{aligned}$$

With $\frac{3}{2} f_E< f_I < 3 f_E$ (Fig. 1), it is easy to see that $\Delta F_I$ is significantly more negative than $\Delta F_E$. That is to say, synchronization causes I-neurons to lose more (positive) input current than E-neurons, so the system should be more excited and E-firing rate should be higher than predicted by the reduced model.

An analogous computation gives the same conclusion for the Reg network, but the difference between $\Delta F_E$ and $\Delta F_I$ is smaller. The $\varepsilon _{QQ'}$ values for the Hom network are too small to be significant.

Combining (a) and (b), we expect that the linear model with refractory will give E-firing rates that are higher than the Hom network (counting only the error from (a)), and lower than the Sync network (errors from both (a) and (b)). As for the Reg network, the two errors from (a) and (b) have opposite signs; one cannot say what it will be on balance except that it is likely to be smaller than the other two. This is consistent with the results in Fig. 3b (right).

A general remark. We have found that $\Delta F_I$ is generally larger in magnitude than $\Delta F_E$ when input currents are changed, due simply to the fact that I-neurons have higher firing rates, we believe. These changes depend on the composition of the current that is altered, however, and in the situation above that depends on the relative speeds at which E and I spikes take effect, i.e., on $\tau ^E$ and $\tau ^I$. A complete analysis of that is beyond the scope of this paper. Thus while we have often seen that synchronization leads to higher firing rates, we do not know if this is always the case, or the conditions under which this is true.

6 Modeling membrane potentials as random walks

In this section, we consider a different kind of reduced model, namely one in which membrane potentials of E and I neurons are modeled as (biased) random walks with reset at threshold. This model is in part motivated by the fact that reduced models defined by ODEs cannot reproduce the statistics of events observed in populations of interacting neurons, and that stochastic fluctuations—or population activity that give rise to behaviors that resemble stochastic fluctuations—seem to play a role in neuronal dynamics.

The reduced model considered in this section has the same flavor as that in Brunel and Hakim (1999), Brunel (2000), which considered sparse networks in the limit where system size tends to infinity. The authors of Brunel and Hakim (1999), Brunel (2000) argued that in their setting, because connectivity is sparse, the membrane potentials of neurons can be approximated by SDEs. The reduced model we consider here is effectively a discrete version of theirs, but the full network model in this study is far from sparsely connected, which in the sense of Brunel and Hakim (1999); Brunel (2000) means the number of connections per neuron divided by system size tends to zero. Our connectivity is 15% for E to E, and 40–50% for connections involving I-neurons (in accordance with experimental data from cortex). Thus in relation to Brunel’s earlier work, this section can be seen as a study of how well random-walk type models perform when used to approximate properties of networks the connectivity of which is far from sparse in the sense of Brunel and Hakim (1999), Brunel (2000), Vreeswijk and Sompolinsky (1998).

6.1 A random walk model and its firing rate

Here we model the membrane potentials of an E and an I-neuron by a continuous time Markov jump process $(X^E_t, X^I_t)$ where $X^E_t$ and $X^I_t$ are independent and each takes values in the state space $\{-M_{r}, \ldots , M-1, {\mathcal {R}}\}$. For definiteness we will consider a model that incorporates both refractory periods and the V-dependence of I-currents.

Given a pair $(f_E, f_I)$ which represents the firing rates of excitatory and inhibitory neurons from the local population, we assume that $X^E_t$ is driven by three independent Poisson processes that correspond to (i) external drive, (ii) excitatory and (iii) inhibitory synaptic inputs from the population. The Poisson process corresponding to (i) delivers kicks at rate $\lambda ^E$. The ones corresponding to (ii) and (iii) have rate $N_E P_{EE} f_E$ and $N_I P_{EI} f_I$ respectively. Upon receiving a kick from the external drive, $X^t_E$ moves up by 1. Upon receiving a kick from (ii), $X^E_t$ jumps up by $S_{EE}$ slots, and upon receiving a kick from (iii), it jumps down by $S_{EI}(X^E_t)$ slots. The interpretation of non-integer numbers of slots and the $X^E_t$-dependence of $S_{EI}$ are as in Sect. 1.1. Also as before, when $X^E_t$ reaches M, it goes to ${\mathcal {R}}$, where it remains for an exponential time of mean $\tau _{{\mathcal {R}}}$. The process $X^I_t$ is defined analogously.

It is well known that an irreducible Markov jump process on a finite state space admits a unique stationary distribution. Given $(f_E, f_I)$, let $\nu _Q$ denote the stationary distribution of $X^Q_t$ for $Q=E,I$. Clearly, $\nu _{Q}$ is a computable distribution satisfying

$$\begin{aligned} \left\{ \begin{array}{l} {\mathbf {A}}_{Q} \nu _{Q} = {\mathbf {0}}\\ {\mathbf {1}}^{T} \nu _{Q} = 1 \end{array} \right. \end{aligned}$$

(5.1)

where ${\mathbf {A}}_{Q}$ is the generator matrix of process $X^{Q}_{t}$, and ${\mathbf {1}}$ is a vector in ${\mathbb {R}}^{M + M_{r} + 1}$ all of whose entries are equal to 1. The firing rate of $X^{Q}_{t}$, $Q\in \{E, I\}$, can be defined as

$$\begin{aligned} {\tilde{f}}_{Q} = \lim _{T \rightarrow \infty }\frac{1}{T}\#\{ t \in (0, T) \,|\, X^{Q}_{t-} \ne {\mathcal {R}}, X^{Q}_{t} = {\mathcal {R}} \}. \end{aligned}$$

It is easy to see that

$$\begin{aligned} {\tilde{f}}_{Q} = N_{E}P_{QE}f_{E}\sum _{i = M - S_{QE}}^{M-1}\nu _{Q}(i) + \lambda ^{Q}\nu _{Q}(M-1). \end{aligned}$$

Of interest to us is $(f_E,f_I)$ satisfying the consistency condition $(f_E,f_I)=({{\tilde{f}}}_E,{{\tilde{f}}}_I)$. We prove the existence of a solution to this consistency equation.

Theorem 5.1

There exist $f_{E}, f_{I}>0$ such that when $(X^{E}_{t},X^{I}_{t})$ is driven by these firing rates, they produce mean firing rates ${{\tilde{f}}}_{E}$ and ${{\tilde{f}}}_{I}$ such that

$$\begin{aligned} {\tilde{f}}_{E} = f_{E}, \quad {\tilde{f}}_{I} = f_{I}. \end{aligned}$$

Proof

Let

$$\begin{aligned} \phi _{1}(f_{E}, f_{I}) = {\tilde{f}}_{E} - f_{E} \quad \text{ and } \quad \phi _{2}(f_{E}, f_{I}) = {\tilde{f}}_{I} - f_{I}. \end{aligned}$$

Observe that for any $f_I \ge 0$,

$$\begin{aligned} \phi _{1}(0, f_{I})> 0 \qquad \text{ and } \qquad \phi _{1}(f_{E}, f_{I}) < 0 \quad \text{ when } \quad f_{E} > \tau _{{\mathcal {R}}}^{-1}\ . \end{aligned}$$

The first inequality is true because independently of how high a rate the inhibitory clock rings, there exists $T_0>0$ and $\varepsilon >0$ (depending on $f_I$) such that starting from anywhere in $\Gamma$, external drive alone will, with probability $\ge \varepsilon$, cause $X^E_t$ to spike within $T_0$ units of time, rendering ${{\tilde{f}}}_E>0$. The second inequality is true because each time $X^E_t$ spikes, it has to spend time in refractory, so ${{\tilde{f}}}_E \le \tau _{{\mathcal {R}}}^{-1}$. Similarly, observe that for any $f_E \ge 0$,

$$\begin{aligned} \phi _{2}(f_{E}, 0)> 0 \qquad \text{ and } \qquad \phi _{2}(f_{E}, f_{I}) < 0 \quad \text{ when } \quad f_{I} > \tau _{{\mathcal {R}}}^{-1}\ . \end{aligned}$$

By the Poincare–Miranda Theorem (a version of intermediate value theorem in dimensions greater than one), we have the existence of a solution

$$\begin{aligned} \phi _{1}(f_{E}, f_{I}) = 0, \quad \phi _{2}(f_{E}, f_{I}) = 0. \end{aligned}$$

Moreover, from the boundary conditions above, we have that $f_E, f_I >0$. $\square$

Fig. 5

Traces of membrane potentials from sample E-neurons in the three networks. Top: Hom. Middle: Reg. Bottom: Sync. The networks are strongly driven with $\lambda ^E=\lambda ^I=7000$. Traces from the Hom model are not discernible by eye from corresponding traces from the biased random-walk model (not shown). Note the absence of characteristic time scales in its fluctuations. Traces from the Sync model have up- and down-swings that reflect the characteristic times in the population’s self-organized spiking events; see Fig. 2. Examples of these swings in the trace shown are clearly visible at $t \sim 50, 175, 350, 370$. Traces from the Reg model share some of the features of the Hom and the Sync models

Let $f_{E}^{rw}$ and $f_{I}^{rw}$ denote the mean firing rates obtained from Theorem 5.1. They were found to be unique in our numerical simulations, and very close to the empirical firing rates of the Hom network. See Fig. 3b, the graph in black with open circles. That this graph is close to the one for the Hom network and somewhat below those of the Reg and Sync network models is consistent with our analysis in Sect. 4.2: Here we have corrected the error due to V-dependence but not the one due to the combined action of synchronization and refractory. As explained in Sect. 4.2, such action causes E-firing rates of the Sync and Reg networks to be higher than that predicted under the assumption that the arrival of synaptic input is homogeneous in time.

Figure 5 shows traces of membrane potentials v(t) as functions of time for three model E-neurons under strong drive. Traces of neurons from the Hom model, the fluctuations of which are not significantly biased toward any particular time scale, are not discernible by eye from those produced by the random walk model. In contrast, traces from the Sync model show clearly identifiable upswings and downswings that reflect the characteristic times between large spiking events (see Fig. 2). These fluctuations are caused by currents from the population during coordinated spiking events even as the neuron itself does not participate in the event. Behavior of the Reg model is somewhere between that of the Hom and the Sync models; it has some of the features in the Sync model but they are not as prominent.

We conclude that for networks of the type considered, membrane potentials may or may not be well described by reduced random-walk models depending on the amount of correlations in the spiking patterns of the system.

6.2 Interspike intervals

As noted earlier, the random walk (rw) model above has, in principle, the capability of producing statistics that may emulate those in network models, something the reduced ODE models studied earlier cannot do. In this subsection, we focus on the distribution of interspike times, i.e., the times between consecutive spikes fired by a neuron.

Below we propose an explicit distribution that will be shown numerically to approximate well the distribution of interspike times for the rw model. We will then apply these ideas to the network models, and see how they fare.

Approximation of first passage times of the rw model by inverse Gaussians For convenience, we consider a rescaling of $(X^E_t, X^I_t)$ in which the interval [0, M] is scaled linearly to [0, 1], with jump sizes scaled accordingly. (We may assume for purposes of this discussion that jump sizes are given by $S_{QQ'}/M$ whether or not $S_{QQ'}$ is an integer.) Let us call this rescaled rw model $(Y^E_t, Y^I_t)$, and assume throughout that the population firing rates $(f_E, f_I)$ are those obtained from Theorem 5.1. Let us also agree to ignore the time spent in refractory, which is entirely irrelevant in this discussion.

The random variables of interest, then, are $T^{rw}_E$ and $T^{rw}_I$, the first passage times of $Y^E_t$ and $Y^I_t$ to 1 starting from $Y^E_0, Y^I_0=0$. For definiteness, we will work with $Y^E_t$; the analysis of $Y^I_t$ is entirely analogous. Below we make a sequence of approximations that will result in an explicit distribution to be compared to that of $T^{rw}_E$.

(i) For a small time interval $\mathrm {d} t$, we have

$$\begin{aligned} Y^{E}_{t + \mathrm {d} t} \approx Y^{E}_{t} + G^{E}(Y^{E}_{t}, \mathrm {d}t), \end{aligned}$$

where

$$\begin{aligned} G^{E}(Y_{t}, \mathrm {d}t)= & {} \frac{S_{EE}}{M} \mathrm {Pois}(N_{E}f_{E}P_{EE} \mathrm {d}t)\\&-\frac{S_{EI}}{M}(MY^{E}_{t}) \mathrm {Pois}(N_{I}f_{I}P_{EI} \mathrm {d}t) + \frac{1}{M} \mathrm {Pois}( \lambda ^{E} \mathrm {d}t), \end{aligned}$$

where $\mathrm {Pois}(\lambda )$ is a Poisson random variable with parameter $\lambda$. All Poisson random variables are assumed to be independent. It is easy to see that

$$\begin{aligned} {\mathbb {E}}[ G^{E}( Y^{E}_{t}, \mathrm {d}t)] = \frac{1}{M} \left( S_{EE}N_{E} f_{E} P_{EE} - S_{EI}(M Y^{E}_{t})N_{I}f_{I}P_{EI} + \lambda ^{E} \right) \mathrm {d}t := b_{E}(Y^{E}_{t})\mathrm {d}t \end{aligned}$$

and

$$\begin{aligned} \mathrm {Var}[ G^{E}( Y^{E}_{t}, \mathrm {d}t)]= & {} \frac{1}{M^2}\left( S_{EE}^{2} N_{E} f_{E} P_{EE} + S_{EI}(M Y^{E}_{t})^{2} N_{I}f_{I}P_{EI} + \lambda ^{E}\right) \mathrm {d}t \\:= & {} \sigma ^2_{E}(Y^{E}_{t}) \mathrm {d}t. \end{aligned}$$

(ii) Next we approximate $G^{E}(Y^{E}_{t}, \mathrm {d}t)$ by a random variable ${\hat{G}}^{E}(\mathrm {d}t)$ that is independent of $Y^E_t$. Specifically we seek ${\hat{G}}^{E}(\mathrm {d}t)$ with the property that

$$\begin{aligned} {\mathbb {E}}[ {\hat{G}}^{E}(\mathrm {d}t)] = f_E \mathrm {d}t \qquad \text{ and } \qquad \mathrm {Var}[{\hat{G}}^{E}(\mathrm {d}t)] \approx \mathrm {Var}[ G^{E}( 1/2, \mathrm {d}t)] := {\hat{\sigma }}_{E}^{2} \mathrm {d}t\ , \end{aligned}$$

i.e.,

$$\begin{aligned} {\hat{\sigma }}_{E} = \frac{1}{M}\sqrt{S^{2}_{EE}N_{E}f_{E}P_{EE} + S_{EI}(M/2)^{2}N_{I}f_{I}P_{EI} + \lambda ^{E} }. \end{aligned}$$

We leave it to the reader to check that the following might be a candidate:

$$\begin{aligned} {\hat{G}}^{E}( \mathrm {d}t)= & {} \left( \frac{S_{EE}}{M} + \epsilon \right) \mathrm {Pois}(N_{E}f_{E}P_{EE} \mathrm {d}t) - \left( \frac{S_{EI}(M/2)}{M} - \epsilon \right) \mathrm {Pois}(N_{I}f_{I}P_{EI} \mathrm {d}t) \\&+\left( \frac{1}{M }+ \epsilon \right) \mathrm {Pois}( \lambda ^{E} \mathrm {d}t) \, \end{aligned}$$

where

$$\begin{aligned} \epsilon = \frac{f_{E} - b_{E}(1/2)}{M(N_{E}f_{E}P_{EE} + N_{I}f_{I}P_{EI} + \lambda ^{E})}. \end{aligned}$$

(iii) It is well known that a Poisson distribution $\mathrm {Pois}(\lambda )$ is approximated by $N(\lambda , \lambda )$ where $N(\cdot , \cdot )$ is the normal distribution when $\lambda$ is large (usually larger than 10). In our model, the three constants $N_{E}f_{E}P_{EE}$, $N_{I}f_{I}P_{EI}$, and $\lambda ^{E}$ are $>10^{3}$ for strong drive. Under these conditions, for $\mathrm {d}t>0.01$, the three Poisson distributions can be approximated by normal distributions. Since a linear combination of independent normal random variables gives a normal random variable, we have the approximation

$$\begin{aligned} Y^{E}_{t + \mathrm {d}t} \approx Y^{E}_{t} + f_E \mathrm {d}t + {\hat{\sigma }}_{E} \mathrm {d} W_{ \mathrm {d}t}, \end{aligned}$$

where $\mathrm {d}W_{\mathrm {d}t} \sim N(0, \mathrm {d}t)$.

(iv) The formula above is the Euler–Maruyama scheme for the stochastic differential equation

$$\begin{aligned} \mathrm {d}Z_{t} = f_{E} \mathrm {d}t + {\hat{\sigma }}_{E} \mathrm {d}W_{t}, \quad Z_{0} = 0. \end{aligned}$$

(5.2)

This scheme is known to be strongly convergent, i.e., trajectories produced by the numerical scheme converges to trajectories of (5.2) when the step size approaches to 0 (Kloeden and Platen 2013).

(v) Finally, for a (true) Brownian motion with a drift, given by

$$\begin{aligned} f_E t + {{\hat{\sigma }}}_E W_t\ , \end{aligned}$$

the first passage time to 1 starting from 0 is given by the inverse Gaussian $IG(f_E^{-1}, {{{\hat{\sigma }}}}_{E}^{-2})$ (Chhikara 1988), where the inverse Gaussian $IG(\mu , \nu )$ is the probability distribution with density

$$\begin{aligned} \rho (x; \mu , \nu ) = \left[ \frac{\nu }{2\pi x^3}\right] ^\frac{1}{2} \text{ exp } \left\{ \frac{-\nu (x-\mu )^2}{2\mu ^2 x}\right\} \ . \end{aligned}$$

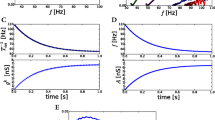
We remark that we do not claim to have control over the cumulative errors in steps (ii), (iii) and (iv), and that the argument above is intended only to be heuristic. Numerically, it appears to be a good approximation, as can be seen in Fig. 6a, where we have plotted the first passage times for $Y^E_t$ and $Y^I_t$ and their inverse Gaussian approximations.

Interspike times in network models and inverse Gaussians. The use of inverse Gaussian (IG) distributions to model interspike times is not new (George 1964; Iyengar and Liao 1997). The idea here is to start from a network model, pass to its accompanying random walk model, find the appropriate IG distribution as discussed above, and to study how well it approximates the interspike times of the network model. The match between inverse Gaussians and the pdf of interspike times for the Hom model is excellent as can be seen in Fig. 6b, c. As can be seen from the same figure, this match deteriorates with increased synchronization: First, the firing rate in the mean-field approximation becomes less accurate; this is reflected in errors in the drift term. Second, the semi-regularity of synchronized firing events produces multiple bumps in interspike times. In the case of the Sync network, the interspike time distribution is quite far from inverse Gaussian.

Fig. 6

Inverse Gaussians as approximations for distributions of interspike times. a Pdf of the inverse Gaussian distributions (solid lines, red for E, black for I) and empirical first passage time for the rescaled random walk model $Y^{E}_{t}$ and $Y^{I}_{t}$ (open circles, green for E, blue for I). For parameters of the IG-distributions, see the main text. b Comparison of inverse Gaussian distribution (red) and and empirical interspike times of Excitatory populations in the Hom, Reg, and Sync networks (blue). The resolution of Hom plot is 1000 bins. Resolutions of the plots for the Reg and Sync networks are both 50 bins. Deterioration of the match between empirical and predicted distributions with increased synchronization is very much in evidence. c Same as b, but for the I-population (color figure online)

7 Summary and conclusion

We introduced in Sect. 1 a family of stochastic networks of interacting neurons that we believe will be of independent interest because of its potential for tractability and biological realism. These models can support any amount dynamical interaction among neurons from the Excitatory and Inhibitory populations and are simpler than networks of integrate-and-fire neurons. For purposes of the rest of this paper, what is relevant is that these models have easily characterizable firing rates and correlation properties, which emerge as a result of the dynamical interaction among neurons.

We compared the firing rates of these network models to some very simple reduced models of mean-field type defined by a pair of ODEs representing the membrane potentials of an E and an I-neuron, taking care to give these neurons the same mean excitatory and inhibitory currents received per unit time by E and I-neurons in the stochastic network models.

A property common to many reduced models including ours is the underlying assumption that all inputs received by a neuron arrive in a time-homogeneous way. This assumption contradicts directly the presence of correlations in neuronal spiking, which are observed in network models as in the real brain. It is arguably the single biggest difference between reduced mean-field models and network models of interacting neurons.

How exactly does the uneven arrival of input affect firing rate? Does the Ergodic Theorem not tell us that in the long run, it is the integral of the net input current that determines firing rate? The answer would have been yes had it not been for the “nonlinearities” present in the time evolution of membrane potentials. We have focused on two of these nonlinearities: refractory, referring to a neuron’s momentary insensitivity after each spike, and the voltage-dependence of currents. With regard to their effects on firing rates, we demonstrated that the effects of these two nonlinearities can add or cancel, and the net effect can be considered modulatory except when the network is highly synchronized.

We considered also mean-field models consisting of biased random walks. We studied fluctuations in membrane potential and distributions of interspike times, and found that for both, the performance of random-walk models to approximate real network statistics deteriorated significantly with increased synchrony.

A main message, then, is that synchrony, by which we refer to the correlations in spike times of neurons, can impact nontrivially the performance of reduced models to predict real network behavior. Finally, unlike previous papers that have compared models, we have tried to offer analyses of dynamical mechanisms, which we view as a challenging yet integral part of understanding the brain.