Analysis of a model for banded vegetation patterns in semi-arid environments with nonlocal dispersal

Abstract

Vegetation patterns are a characteristic feature of semi-arid regions. On hillsides these patterns occur as stripes running parallel to the contours. The Klausmeier model, a coupled reaction–advection–diffusion system, is a deliberately simple model describing the phenomenon. In this paper, we replace the diffusion term describing plant dispersal by a more realistic nonlocal convolution integral to account for the possibility of long-range dispersal of seeds. Our analysis focuses on the rainfall level at which there is a transition between uniform vegetation and pattern formation. We obtain results, valid to leading order in the large parameter comparing the rate of water flow downhill to the rate of plant dispersal, for a negative exponential dispersal kernel. Our results indicate that both a wider dispersal of seeds and an increase in dispersal rate inhibit the formation of patterns. Assuming an evolutionary trade-off between these two quantities, mathematically motivated by the limiting behaviour of the convolution term, allows us to make comparisons to existing results for the original reaction–advection–diffusion system. These comparisons show that the nonlocal model always predicts a larger parameter region supporting pattern formation. We then numerically extend the results to other dispersal kernels, showing that the tendency to form patterns depends on the type of decay of the kernel.

1 Introduction

1.1 Ecological background

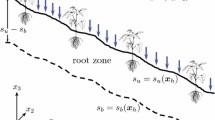
Semi-arid environments are regions in which the level of rainfall is below a certain threshold, dependent on the mean temperature and spread of rainfall across the year (Köppen 1936; Peel et al. 2007), creating a hostile environment for vegetation as plants compete for water. A characteristic feature of many of these semi-arid environments is self-organised patterns of vegetation. These occur due to a scale-dependent feedback, which is caused by the modification of the soil by the existing plants, creating a more favourable environment on a short range and the competition for water on a longer spatial distance (Rietkerk and van de Koppel 2008). On gentle slopes of a few percent gradient [0.2–2% (Valentin et al. 1999)] striped patterns occur along the contours of the hill. Being wide and with large distances between them, these stripes are extremely difficult to detect from the ground. They were therefore first discovered using aerial photography in the 1950s in British Somaliland (today Somalia) (Macfadyen 1950; Hemming 1965). Since then, striped patterns have been observed on slopes in the Chihuahuan Desert in Mexico and the US (Cornet et al. 1988; Montaña et al. 1990; Montaña 1992), New South Wales in Australia (Tongway and Ludwig 1990; Dunkerley and Brown 2002), Niger and other countries in the African Sahel (Thiery et al. 1995; Worrall 1959; White 1971) and many other regions as reviewed by Valentin et al. (1999, Table 1 and Figure 3). Many ecologists studying these patterns reported that the vegetation bands slowly move uphill (Valentin et al. 1999; Worrall 1959; Montaña 1992) with a migration speed varying between 0.2 and 1.5 m per year (Valentin et al. 1999). They argue that the reason for this is that the rainwater, which often falls in form of torrential rain at irregular intervals (Bromley et al. 1997), runs off the bare ground to the uphill edge of the vegetation band below, where it can infiltrate the ground more easily, providing a more favourable environment for plant growth on the uphill edge than on the downhill edge (Montaña et al. 2001; White 1971). Other authors observed stationary patterns (Dunkerley and Brown 2002), which they attribute to changes in the soil on bare ground that inhibits plant growth (Dunkerley and Brown 2002) and a skewed distribution of plant dispersal caused by seeds travelling downhill in the flow of the water (Saco et al. 2007; Thompson and Katul 2009). A more recent survey confirms the occurrence of both upward migration and static vegetation bands, by comparing satellite data from spy satellites used during the Cold War to more recent data (Deblauwe 2010). Studying these patterns is of crucial importance as changes in the width of and distance between vegetation stripes may be an indicator for an imminent and irreversible switch to desertification (Kéfi et al. 2007; Rietkerk et al. 2004).

The long timescale in the evolution of patterned vegetation and the inability to generate it in laboratory settings limit the availability of observed data. Instead various different theoretical models have been developed (Borgogno et al. 2009). These can be classified into two main groups; models based on plant to plant interactions, among other things including individual plant’s morphology such as its root network and shading (Gilad et al. 2004, 2007; Hardenberg et al. 2010; Lefever et al. 2009) and models focusing on water redistribution. The latter class of models are based on the Klausmeier model (Klausmeier 1999), on which we will focus here.

1.2 The models

The nondimensionalised form of the Klausmeier model (see Klausmeier (1999), Sherratt (2005) for details on the nondimensionalisation) is the reaction–advection–diffusion system

$$\begin{aligned} \frac{\partial u }{\partial t}&= \overbrace{u^2w}^{\text {plant growth}} - \overbrace{Bu}^{\text {plant loss}} + \overbrace{\frac{\partial ^2 u}{\partial x^2}}^{\text {plant dispersal}}, \end{aligned}$$

(1a)

$$\begin{aligned} \frac{\partial w }{\partial t}&= \underbrace{A}_{\text {rainfall}} - \underbrace{w}_{\text {evaporation}} - \underbrace{u^2w}_{\begin{array}{c} \text {water uptake} \\ \text {by plants} \end{array}} + \underbrace{\nu \frac{\partial w}{\partial x}}_{\begin{array}{c} \text {water flow}\\ \text {downhill} \end{array}} + \underbrace{d\frac{\partial ^2w}{\partial x^2}}_{\begin{array}{c} \text {diffusion} \\ \text {of water} \end{array}}. \end{aligned}$$

(1b)

Originally, this model did not include diffusion of water, but this term was added later and is now well established (Kealy and Wollkind 2012; Siteur et al. 2014; vander Stelt et al. 2013; Zelnik et al. 2013). This extended Klausmeier model will be referred to as the “local Klausmeier model” throughout the text. In the model, u(x, t) represents the plant density, w(x, t) the water density, $t>0$ the time and $x \in \mathbb {R}$ the space, where the positive direction is in the uphill direction of a one-dimensional domain of constant gradient. The system assumes constant rainfall, proportionality of water density to evaporation (Rodriguez-Iturbe et al. 1999; Salvucci 2001) and correlation of plant growth to water uptake. The latter is assumed to be proportional to the water density and the plant density squared, because the water infiltration capacity of the soil depends on the presence of plants (Rietkerk et al. 2000; Valentin et al. 1999). The ground where vegetation stripes are situated is estimated to receive around 1.5–2.5 times as much water as the annual precipitation due to water running off the bare ground towards the vegetation stripes (Cornet et al. 1988). The parameters $A>0$, $B>0$, $\nu >0$ and $d>0$ represent rainfall, plant loss, the rate of the water flow in the downhill direction and the rate of water diffusion, respectively. Due to the nondimensionalisation they are however a combination of different ecological quantities. Parameter estimates are $A\in [0.1, 3]$, $B \in [0.05, 2]$ (Klausmeier 1999; Rietkerk et al. 2002) and $\nu = 182.5$ (Klausmeier 1999). The large size of $\nu$ compared to the other parameters reflects the slow speed of plant dispersal compared to water flow, and it allows an analysis of patterned solutions of (1) by obtaining results for the model to leading order in $\nu$, such as by Sherratt (2005, 2010, 2011, 2013a, b, c). The model is deliberately kept simple. There are however a wide range of systems all based on the Klausmeier model (1) that take into account variable precipitation (Kletter et al. 2009) and grazing (HilleRisLambers et al. 2001; vande Koppel et al. 2002) and models that distinguish between the surface water density and the water density in the soil (Gilad et al. 2007; HilleRisLambers et al. 2001; Rietkerk et al. 2002).

In (1), plant dispersal is modelled by a diffusion term. In reality, nonlocal processes are often involved, such as seed dispersal by wind or separated stages for plant growth and seed dispersal (Pueyo et al. 2008). This can be modelled by integrodifferential equations (Allen et al. 1996; Powell and Zimmermann 2004). To do this, the change of the plant density u(x, t) at a point x that was caused by diffusion is replaced by the convolution integral

$$\begin{aligned} \int _{-\infty }^{\infty } \phi (x-y)\left( u(y,t)-u(x,t)\right) {{\text {d}}}y. \end{aligned}$$

The kernel function $\phi (x,y)$ is a probability density function, describing the probability per unit length of seeds originating at the point y being dispersed to point x (Pueyo et al. 2008). This approach is not only used in modelling plant dispersal but can, among others, be considered to model dispersal in general competition models (Hutson et al. 2003; Cosner et al. 2012) showing an evolutionary advantage of nonlocal dispersal under certain boundary conditions (Kao et al. 2010), or models describing a single species subject to a unidirectional flow (Lutscher et al. 2005). It is to assumed that seed dispersal only depends on the distance $x-y$ [i.e. assuming homogeneous and isotropic dispersion of seeds (Mistro et al. 2005)]. This kind of nonlocal seed dispersal is considered for example by Baudena and Rietkerk (2013), Pueyo et al. (2008), and Pueyo et al. (2010) for modified versions of the Klausmeier model that consider soil water separately from surface water (HilleRisLambers et al. 2001; Rietkerk et al. 2002). Motivated by this, we will consider the “nonlocal Klausmeier model”

$$\begin{aligned} \frac{\partial u}{\partial t}&= u^2w - Bu + C\left( \int _{-\infty }^\infty \phi (x-y)u(y,t) {{\text {d}}}y - u(x,t)\right) , \end{aligned}$$

(2a)

$$\begin{aligned} \frac{\partial w}{\partial t}&= A-w-u^2w + \nu \frac{\partial w}{\partial x}+ d\frac{\partial ^2w}{\partial x^2}. \end{aligned}$$

(2b)

The dispersal coefficient $C>0$, which scales the convolution term, describes the plant’s dispersal rate by taking into account the plant’s fecundity, seed mortality and germination rate and seed establishment ability (Pueyo et al. 2008).

If the kernel function $\phi (x)$ is decaying exponentially as $x \rightarrow \infty$, the local model can be obtained from the nonlocal model by setting $C = 2/\sigma (a)^2$, where $\sigma (a)$ denotes the standard deviation of the dispersal kernel with scaling parameter a, and taking the limit as $a\rightarrow \infty$. To show this, write $\phi (x) = a\varphi (ax)$. Then, the integral in the dispersal term can be transformed to

$$\begin{aligned} \int _{-\infty }^\infty \phi (x-y) u(y,t) {{\text {d}}}y = \int _{-\infty }^\infty \varphi (z) u\left( x-\frac{z}{a},t\right) {{\text {d}}}z, \end{aligned}$$

by using the change of variables $y = x-z/a$. Considering the Taylor expansion of $u(x-z/a,t)$ in z / a, an application of Watson’s lemma (i.e. integrating term-wise) gives

$$\begin{aligned}&\int _{-\infty }^\infty \phi (x-y) u(y,t) {{\text {d}}}y \nonumber \\&\quad = u(x,t) - \frac{1}{a} \frac{\partial u}{\partial x}(x,t) \int _{-\infty }^\infty \varphi (z) z {{\text {d}}}z + \frac{1}{2a^2}\frac{\partial ^2 u}{\partial x^2}(x,t) \int _{-\infty }^\infty \varphi (z) z^2 {{\text {d}}}z +O\left( \frac{1}{a^3}\right) .\nonumber \\ \end{aligned}$$

(3)

In this paper we will assume that the kernel $\phi$ is even with its mean located at $x=0$. Therefore the coefficient of the first order derivative in (3) is zero and thus

$$\begin{aligned} \int _{-\infty }^\infty \phi (x-y) u(y,t) {{\text {d}}}y = u(x,t) + \frac{\sigma (a)^2}{2}\frac{\partial ^2 u}{\partial x^2}(x,t) +O\left( \frac{1}{a^3}\right) , \end{aligned}$$

using $\varphi (x) = \phi (x/a)/a$ and the definition of the second moment of a probability distribution. Therefore, setting $C= 2/\sigma (a)^2$ gives

$$\begin{aligned} C\left( \int _{-\infty }^\infty \phi (x-y) u(y,t) {{\text {d}}}y - u(x,t)\right) = \frac{\partial ^2 u}{\partial x^2}(x,t)+O\left( \frac{1}{a}\right) \rightarrow \frac{\partial ^2 u}{\partial x^2}(x,t), \end{aligned}$$

as $a \rightarrow \infty$. This limiting behaviour will allow us to make comparisons between the local and the nonlocal model. Two kernel functions for which the derivation above holds true are the Laplacian

$$\begin{aligned} \phi (x) = \frac{a}{2}e^{-a|x|}, \end{aligned}$$

(4)

and the Gaussian distribution

$$\begin{aligned} \phi (x) = \frac{a_g}{\sqrt{\pi }}e^{-a_g^2x^2}, \end{aligned}$$

(5)

where $x\in \mathbb {R}$, and $a, a_g >0$ are the scale parameters of the distributions, respectively. The Laplacian kernel corresponds to plants (seeds) dispersing as a random walk with individual plants (seeds) settling at different random times (Bullock et al. 2017; Neubert et al. 1995). One main goal of this paper is to investigate how a change in the width of the kernel affects the tendency to form patterns. Closely related to this, a second main aspect we will address in this paper is a comparison between different dispersal kernels. In particular we will show that the type of decay (i.e. exponential or algebraic) has an influence on the tendency to form patterns. The Laplacian kernel is not only biologically relevant (Bullock et al. 2017; Johnson 1988; Neubert et al. 1995) but also allows us to obtain analytic results due to the form of its Fourier transform and will therefore be the main focus of this paper. Note that this kernel further allows a transformation from a nonlocal to a local model by introducing an additional variable (Britton 1990; Gourley et al. 2001; Merchant and Nagata 2015), but in the interest of considering other dispersal kernels we will not use this approach. To investigate the effects of the kind of decay of the kernel, we will finally consider the power law distribution

$$\begin{aligned} \phi (x) = \frac{(b-1)a_p}{2\left( 1+a_p|x|\right) ^b}, \quad b >3, \end{aligned}$$

(6)

where $x\in \mathbb {R}$, and $a_p >0$, $b>0$ are the scale and shape parameters of the distribution, respectively. Note that for this kernel function the derivation of the local model above does not hold. For a review of other biologically relevant plant dispersal kernels see (Bullock et al. 2017, Table 1).

The purpose of this paper is to gain an understanding of how the shape of the dispersal kernel in the nonlocal model (2) affects the tendency to form patterns. In particular, we will mainly focus on the maximum rainfall parameter $A_{\max }$ that supports the formation of patterns, or in other words, the lowest amount of precipitation that allows plants to form a homogeneous vegetation cover. This critical rainfall level will be determined using different approaches for the Laplacian kernel (4). While all those approaches provide the same information on $A_{\max }$, they all give different further insights into other properties of the model. In Sect. 2 we will investigate the model using linear stability analysis, obtaining information on the pattern wavelength alongside the upper bound on the rainfall. The constant uphill migration of the plants suggests studying the system in its travelling wave form. This will be done in Sect. 3, where the critical rainfall level can be deduced from the loci of a Hopf bifurcation. Finally, the asymptotic form of the model is studied in Sect. 4. All these approaches make use of the size of the parameter $\nu$ by obtaining conditions to leading order in $\nu$ as $\nu \rightarrow \infty$. A comparison to other dispersal kernels is shown in Sect. 5 using numerical simulations of the model. From these we will be able to deduce parametric trends on how the tendency to form patterns is affected by the width and the type of decay of the dispersal. Finally, we discuss our results from an ecological viewpoint in Sect. 6. Motivated by the discussion above, the analysis will be done in three different cases; the situation in which $C= 2/\sigma (a)^2$, which allows us to compare our results for the Laplacian kernel to the corresponding results for the local model obtained by Sherratt (2005, 2010, 2011, 2013a, b, c), and the cases in which one of C or a is kept constant, while the other parameter is varied.

2 Linear stability analysis

In this section we will use linear stability analysis to investigate to occurrence of spatial patterns in the nonlocal Klausmeier model (2) with the Laplacian kernel (4). We will show that the maximum rainfall parameter $A_{\max }$ supporting pattern formation is $O_s(\nu ^{1/2})$ ($f=O_s(\nu ) \Longleftrightarrow f = O(\nu )$ and $f \ne o(\nu )$), and will obtain an explicit expression for it. This will show that both an increase in a for C being kept constant and an increase in C for a being kept constant yields an increase of $A_{\max }$, while under the assumption that $C=a^2$ an increase in a (and thus C) results in a decrease of the critical value $A_{\max }$. Further this analysis will allow us to investigate the wavelength of the patterned solutions of the model.

The steady states of (2) are

$$\begin{aligned} (\overline{u}_1,\overline{w}_1)&= (0,A), \quad (\overline{u}_2,\overline{w}_2) = \left( \frac{2B}{A-\sqrt{A^2-4B^2}},\frac{A-\sqrt{A^2-4B^2}}{2}\right) , \\ (\overline{u}_3,\overline{w}_3)&= \left( \frac{2B}{A+\sqrt{A^2-4B^2}},\frac{A+\sqrt{A^2-4B^2}}{2}\right) , \end{aligned}$$

where $(\overline{u}_2,\overline{w}_2)$ and $(\overline{u}_3, \overline{w}_3)$ only exist if $A\ge 2B$. The steady state $(\overline{u}_1,\overline{w}_1)$ describing extinction of plants u is always stable, while $(\overline{u}_3,\overline{w}_3)$ is unstable for all choices of parameters, provided it exists. The steady state $(\overline{u},\overline{w}):=(\overline{u}_2,\overline{w}_2)$ is stable to spatially homogeneous perturbations if $B<2$. For $B>2$, it is only stable for sufficiently large values of A. Estimates of the parameters, however, suggest that $B<2$.

To investigate the possibility of spatial patterns, consider spatially heterogeneous perturbations $u=\overline{u}+\tilde{u}(x,t)$, $w= \overline{w}+\tilde{w}(x,t)$ proportional to $e^{\lambda t+ikx}$ for growth rate $\lambda \in \mathbb {C}$ and wavenumber $k>0$. Linearising the resulting system gives that $\lambda$ satisfies the dispersion relation

$$\begin{aligned} \lambda = \frac{1}{2} \left( C\left( \widehat{\phi }(k)-1\right) -dk^2+\alpha +\delta +i\nu k \pm \sqrt{R+iI} \right) , \end{aligned}$$

where $\widehat{\phi }(k)$ is the Fourier transform of $\phi$,

$$\begin{aligned} \begin{aligned} R&= \left( C\left( \widehat{\phi }(k)-1 \right) +dk^2 \right) ^2 +2C\left( \widehat{\phi }(k)-1 \right) (\alpha -\delta ) \\&\quad +\left( 2\alpha d-2\delta d -\nu ^2 \right) k^2+4\gamma \beta +\,(\alpha -\delta )^2, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} I&= -2\nu k\left( C\left( \widehat{\phi }(k)-1 \right) +dk^2+\alpha -\delta \right) . \end{aligned}$$

For a Turing–Hopf bifurcation to occur, at least one eigenvalue needs to have positive real part. Therefore, the condition for patterns to form is

$$\begin{aligned} {\mathfrak {R}}(\lambda ) = \frac{1}{2}\left( \alpha + \delta - dk^2 +C\left( \widehat{\phi }(k)-1 \right) + \frac{1}{\sqrt{2}}\left( \sqrt{R^2+I^2}+R \right) ^{\frac{1}{2}} \right) > 0. \end{aligned}$$

(7)

To investigate this further for $\phi$ being the Laplacian kernel (4), we will make use of $\nu \gg 1$, by expanding (7) in $\nu$. With all other parameters $O_s(1)$ as $\nu \rightarrow \infty$, this gives

$$\begin{aligned} {\mathfrak {R}}(\lambda ) = \alpha - \frac{Ck^2}{a^2+k^2}+ O\left( \frac{1}{\nu ^2}\right) , \end{aligned}$$

(8)

provided that $(a^2+k^2)(\delta -\alpha -dk^2)+Ck^2<0$. If this condition is not satisfied, the expansion is ${\mathfrak {R}}(\lambda ) = -dk^2+\delta <0$ for any $k>0$. Substituting $k=0$ into (8), yields ${\mathfrak {R}}(\lambda ) = \alpha >0$, which contradicts the stability of $(\overline{u},\overline{w})$ to spatially homogeneous perturbations. The occurrence of patterns is captured by assuming that A is $O_s(\nu ^{1/2})$. Expanding in $\nu \gg 1$ then gives

$$\begin{aligned} {\mathfrak {R}}(\lambda ) =&-{\frac{ \left( -{B}^{5}{\nu }^{2}+{B}^{4}C{\nu }^{2} \right) {k}^{4}+ \left( -{B}^{5}{a}^{2}{\nu }^{2}+{A}^{4}B+{A}^{4}C \right) {k}^{2}+{A} ^{4}B{a}^{2}}{ \left( {B}^{4}{\nu }^{2}{k}^{2}+{A}^{4} \right) \left( {a}^{2}+{k}^{2} \right) }} \nonumber \\&+\,O\left( \frac{1}{\nu }\right) . \end{aligned}$$

(9)

Therefore, ${\mathfrak {R}}(\lambda )>0$ if

$$\begin{aligned} q\left( k^2\right) :=\left( -{B}^{5}{\nu }^{2}+{B}^{4}C{\nu }^{2} \right) {k}^{4}+ \left( -{B}^{5}{a}^{2}{\nu }^{2}+{A}^{4}B+{A}^{4}C \right) {k}^{2}+{A} ^{4}B{a}^{2} <0. \end{aligned}$$

This polynomial in $k^2$ attains its minimum

$$\begin{aligned} q\left( k_{\min }^2\right) = {\frac{- \left( B+C \right) ^{2}{A}^{8}-2\,{B}^{5}{a}^{2}{\nu }^{ 2} \left( B-3C \right) {A}^{4}-{B}^{10}{a}^{4}{\nu }^{4}}{4{B}^{4}{\nu }^{2} \left( B-C \right) }}, \end{aligned}$$

(10)

at

$$\begin{aligned} k_{\min }^2 ={\frac{-{B}^{5}{a}^{2}{\nu }^{2}+{A}^{4}B+{A}^{4}C}{2{B}^{4}{\nu }^ {2} \left( B-C \right) }}. \end{aligned}$$

Solving $q(k_{\min }^2)<0$ for $A^4$ gives $A_1^4<A^4<A_2^4$, where $A_1^4<A_2^4$ are the roots of (10). Substituting $A_1^4$ into $k_{\min }^2$ gives $k_{\min }^2<0$, which contradicts $k_{\min } \in \mathbb {R}$. Therefore, the sufficient condition for patterns to occur is

$$\begin{aligned} A < A_{\max } = \left( \frac{3C-B-2\sqrt{2C}\sqrt{C-B}}{\left( B+C\right) ^2} \right) ^{\frac{1}{4}} a^{\frac{1}{2}} B^{\frac{5}{4}} \nu ^{\frac{1}{2}}, \end{aligned}$$

(11)

valid to leading order in $\nu$ as $\nu \rightarrow \infty$. As expected, setting $C=a^2$ and taking the limit $a \rightarrow \infty$ yields the corresponding condition for the local model obtained by Sherratt (2013b), which is

$$\begin{aligned} A< A_{\max } = \left( \sqrt{2}-1 \right) ^{\frac{1}{2}} B^{\frac{5}{4}} \nu ^{\frac{1}{2}}. \end{aligned}$$

(12)

2.1 Wavelength

It is of interest to investigate the wavelength of the patterns. While a rigorous analysis of this requires tools from nonlinear analysis, one can obtain some information about the wavelength from the results obtained in this section. For this we will assume that the patterns are dominated by the wavenumber giving the largest growth, that is the wavenumber $k_{\max }$ giving the maximum of ${\mathfrak {R}}(\lambda )$ given in (9). Differentiating ${\mathfrak {R}}(\lambda )$ with respect to $k^2$ shows that it obtains its maximum at

$$\begin{aligned} k_{\max }^2 = -{\frac{{A}^{2}a \left( 2{A}^{2}{B}^{2}a\nu \left( B-\frac{C}{2} \right) +\sqrt{2BC} \left( -{B}^{4}a^2\nu ^2+{A}^{4} \right) \right) }{-{B}^{6}C{a}^{2}{\nu }^{3}+2{A}^{4}{B}^{3}\nu }}. \end{aligned}$$

Therefore the wavelength L is given by

$$\begin{aligned} L= & {} \frac{2\pi }{k_{\max }} \nonumber \\= & {} 2\pi \left( \frac{-{B}^{6}C{a}^{2}{\nu }^{3}+2{A}^{4}{B}^{3}\nu }{{A}^{2}a \left( {A}^{2}{B}^{2}a\nu \left( 2B-C \right) +\sqrt{2}\sqrt{BC \left( -{B}^{2}a\nu +{A}^{2} \right) ^{2} \left( {B}^{2}a\nu +{A}^{2} \right) ^{2}} \right) }\right) ^{\frac{1}{2}}.\nonumber \\ \end{aligned}$$

(13)

The wavelength L is decreasing in the rainfall parameter A, decreasing in the dispersal parameter a if the dispersal coefficient C is fixed, increasing in C when a is kept constant, and increasing in a if one sets $C=a^2$. Figure 1a shows the wavelength as it varies with the rainfall parameter A for some fixed B, C, a and $\nu$. Also note that when $C=a^2$, the wavelength (13) for the nonlocal model approaches the wavelength predicted by the local model as $a\rightarrow \infty$, as expected by the limiting behaviour of the nonlocal model. Combining these two results shows that the nonlocal model predicts a shorter distance between vegetation stripes than the local model with this setting of C. This is visualised in Fig. 1b.

Fig. 1

Variation in pattern wavelength with rainfall A and standard deviation $\sigma (a)$. Part a shows the wavelength (13) of the patterns as it decreases with the rainfall A for nonlocal model. The parameter values are $B=0.45$, $\nu =182.5$, $C=1$ and $a=1$. Part b compares the wavelength predicted from the nonlocal model with the setting $C=a^2$ as it varies with the dispersal parameter a and compares it to the wavelength obtained from the local model. It shows that the nonlocal model predicts a shorter distance between the vegetation stripes, especially if the shape of the dispersal kernel is wide. However, the difference is very small (see the y-axis of the plot). The parameter values used for this are $A=1$, $B=0.45$, $\nu =182.5$

3 Travelling wave solutions

The constant uphill migration of the vegetation patterns suggests considering travelling waves. In this section we will investigate the travelling wave form of the nonlocal Klausmeier model (2). Pattern solutions of the original PDE model then correspond to periodic solutions of the travelling wave ODEs. From the equations in their travelling wave form we will not only be able to confirm the results on the maximum rainfall supporting pattern formation obtained by performing linear stability analysis in Sect. 2, but also deduce more information about the migration speed of the patterns. The nature of the patterned solutions fundamentally depends on the scaling of the migration speed c. The highest rainfall level supporting pattern formation occurs for $c=O_s(1)$. For this situation we determine conditions for Hopf bifurcations to occur; for the local Klausmeier model (1) the parameter range in the A–c plane that supports pattern formation is bounded above by the locus of a Hopf bifurcation (Sherratt and Lord 2007), and we anticipate the same for the nonlocal model.

Applying the travelling wave ansatz $u(x,t) = U(z)$, $w(x,t)=W(z)$, $z=x-ct$ to the nonlocal model (2), gives

$$\begin{aligned} \frac{{{\text {d}}}U}{{{\text {d}}}z}&= -\frac{1}{c} \left( U^2W-BU + C\left( \int _{-\infty }^\infty \phi (z-z')U(z') {{\text {d}}}z' - U(z)\right) \right) , \\ \frac{{{\text {d}}}W}{{{\text {d}}}z}&= -\frac{1}{c+\nu } \left( A-W-U^2W+d\frac{{{\text {d}}}^2 W}{{{\text {d}}}z^2} \right) . \end{aligned}$$

To investigate the occurrence of a Hopf bifurcation, consider perturbations $\tilde{U}(z)$, $\tilde{W}(z)$ proportional to $e^{\lambda z}$ of the steady state $(\overline{U},\overline{W}) = (\overline{u},\overline{w})$. Setting $\phi$ to be the Laplacian kernel (4) and linearising the resulting system gives that $\lambda$ satisfies

$$\begin{aligned} \lambda ^5+\alpha \lambda ^4+\beta \lambda ^3+\gamma \lambda ^2+\delta \lambda +\varepsilon = 0, \end{aligned}$$

(14)

where

$$\begin{aligned} \alpha&= \frac{d(B-C)+c(c+\nu )}{cd}, \\ \beta&= \frac{-2B^2\left( a^2cd-(B-C)(c+\nu ) \right) -Ac\left( A+\sqrt{A^2-4B^2}\right) }{2B^2cd}, \\ \gamma&= \frac{-2B^2a^2 \left( d+c(c+\nu ) \right) +A(B+C)\left( A+\sqrt{A^2-4B^2}\right) -4B^3}{2B^2cd}, \\ \delta&= \frac{a^2\left( -2B^3(c+\nu ) +Ac\left( A+\sqrt{A^2-4B^2}\right) \right) }{2B^2cd}, \\ \varepsilon&= \frac{a^2\left( -A\left( A+\sqrt{A^2-4B^2}\right) + 4B^2 \right) }{2B^2cd}. \end{aligned}$$

To find conditions for a Hopf bifurcation to occur, set $\lambda =i\omega$, $\omega \in \mathbb {R}$. This splits (14) into its real and imaginary parts, which after solving for and eliminating $\omega ^2$ gives the condition

$$\begin{aligned} \frac{\gamma \pm \sqrt{\gamma ^2-4\alpha \varepsilon }}{2\alpha } = \frac{\beta \pm \sqrt{\beta ^2-4\delta }}{2}. \end{aligned}$$

(15)

The assumption $\omega \in \mathbb {R}$ requires that the left and right hand sides of this equation are both positive. This leads to an additional condition (18) that will be considered later. To further investigate (15), we expand it in $1/\nu$. This gives

$$\begin{aligned} \frac{((B-C){\text {sign}}(c)+B+C)a^2}{B-C} + O\left( \frac{1}{\nu }\right) = 0. \end{aligned}$$

For the first term of the expansion to be zero, one would require $B>C$ with one of the parameters being equal to zero, depending on the sign of c. This is, however, not possible due to the positivity assumptions on the parameters. Investigating the next term of the expansion suggests using the scaling $A=O_s(\nu ^{1/2})$. Applying this scaling to (15), expanding in $\nu \gg 1$ and then solving for c shows that a Hopf bifurcation exists at

$$\begin{aligned} c_\pm= & {} \left( \frac{B}{2A^2} +\frac{A^2(2B-C)}{2\left( -B^4a^2\nu ^2+A^4 \right) }\right. \nonumber \\&\pm \, \left. \left( \frac{B^2}{4A^4} + \frac{3BC}{2\left( -B^4a^2\nu ^2+A^4 \right) } +\frac{4B^6a^2\nu ^2 - 4A^4BC +A^4C^2}{4\left( -B^4a^2\nu ^2+A^4 \right) ^2} \right) ^{\frac{1}{2}} \right) \nu B^2,\nonumber \\ \end{aligned}$$

(16)

to leading order in $\nu$ as $\nu \rightarrow \infty$. Since the migration speed $c \in \mathbb {R}$, this requires

$$\begin{aligned} A < A_{\max } = \left( \frac{3C-B-2\sqrt{2C}\sqrt{C-B}}{\left( B+C\right) ^2} \right) ^{\frac{1}{4}} a^{\frac{1}{2}} B^{\frac{5}{4}} \nu ^{\frac{1}{2}}, \end{aligned}$$

(17)

and $C>B$. This is the same condition as (11) obtained in Sect. 2.

In deriving this condition we assumed that the terms in (15) were positive. By applying the scaling $A=O_s(\nu ^{1/2})$ and expanding in $\nu \gg 1$, this yields the bounds

$$\begin{aligned} \max \left\{ 0, \frac{B^2(B-C)\nu }{A^2} \right\}< c < \frac{B^3 \nu }{A^2}, \end{aligned}$$

(18)

to leading order in $\nu$. This condition is satisfied if $C>B$. In the case of $C=a^2$ it holds if $a>\sqrt{B}$.

Setting $C=a^2$ and taking the limit $a\rightarrow \infty$ in both (16) and (17) gives, as expected by the considerations on the limiting behaviour of the model, the corresponding conditions obtained by Sherratt (2013b) for the local model. Further the right hand side of (17) is decreasing for all $a>\sqrt{B}$ in the setting $C=a^2$. Combined with the observation that it approaches the corresponding condition for the local model as $a \rightarrow \infty$, this shows that pattern formation is more likely in the nonlocal model with the tendency to form patterns increasing as the dispersal parameter a decreases, i.e. as the width of the kernel $\phi$ increases. Figure 2a shows this for some fixed parameter values. Finally, Fig. 2b combines these considerations by showing the loci (16) of the Hopf bifurcations of the nonlocal model for different values of the dispersal parameter a in the A–c plane and compares it to the corresponding locus of the local model. As shown previously, this implies that in the nonlocal model a larger parameter region supports pattern formation, especially as the dispersal parameter a is decreased, i.e. as the width of the kernel is increased. This means that the nonlocal model predicts that plants which disperse their seeds over a larger distance will undergo a change from homogeneous vegetation to patterns at a higher level of rainfall than those plants with a narrower and diffusion-like dispersal, as the amount of rainfall is gradually decreased.

Fig. 2

Variation in the loci of the Hopf bifurcation and maximum rainfall parameter $A_{\max }$ with kernel width in the case $C=a^2$. The plot in a compares the upper bound (11) on the rainfall parameter A of the nonlocal model using the Laplacian kernel with $C=a^2$ with condition (12) obtained for the local model. Note that one requires $a>\sqrt{B}$ for $A_{\max } \in \mathbb {R}$ in the case of the nonlocal model. Part b compares the loci (16) of the Hopf bifurcations of the nonlocal model for different values of the dispersal parameter a to the locus of the local model obtained by Sherratt (2013b). The parameter values used in both figures are $B=0.45$, $\nu =182.5$

If $C\ne a^2$, it is not appropriate to compare the nonlocal model to the local model. However, one can still investigate how a change in the dispersal parameter a affects the tendency to form patterns in this situation. We will first consider the case in which C is constant. In this situation (17) yields that the highest rainfall parameter supporting pattern formation $A_{\max }$ is proportional to $a^{1/2}$. This means that if the dispersal kernel gets narrower, a larger range of the rainfall parameter A supports pattern formation. This is visualised in Fig. 3a, which shows the maximum rainfall parameter $A_{\max }$ plotted against the dispersal parameter a and in Fig. 3b, which visualises the location of the Hopf bifurcation (16), where C is constant. This is contrary to the behaviour observed in the case of $C=a^2$, where a narrower kernel gave less tendency to form patterns.

Fig. 3

Variation in the loci of the Hopf bifurcation and maximum rainfall parameter $A_{\max }$ with kernel width in the case of constant C. The plot in a shows how upper bound $A_{\max }$ given in (17) of the rainfall parameter A that supports pattern formation in the nonlocal model using the Laplacian kernel varies as the dispersal parameter a is changed. Here $C=1$ is fixed. Part b shows the loci (16) of the Hopf bifurcations of the nonlocal model with the Laplacian kernel for different values of the dispersal parameter a, where the dispersal coefficient C is constant. The parameter values used here are $B=0.45$, $C=1$, $\nu =182.5$

Investigating the final case, i.e. the one of fixed a and varying C, shows that the critical rainfall parameter $A_{\max }$ is decreasing with increasing C for all $C>B$. This shows that the more the plants invest in their dispersal, the less likely is the formation of patterns. Similar to the previous two cases, the change in $A_{\max }$ is visualised in Fig. 4a and the loci of the Hopf bifurcations in the A–c plane is shown in Fig. 4b.

Fig. 4

Variation in the loci of the Hopf bifurcation and maximum rainfall parameter $A_{\max }$ with kernel width in the case of constant a. The plot in a shows how upper bound $A_{\max }$ given in (17) of the rainfall parameter A that supports pattern formation in the nonlocal model with Laplacian kernel varies as the dispersal coefficient C is changed. Here $a=1$ is fixed. Note that $C>B$ is required for $A_{\max } \in \mathbb {R}$. Part b shows the loci (16) of the Hopf bifurcations in the same situation. The parameter values used here are $B=0.45$, $C=1$, $\nu =182.5$

4 Asymptotic analysis of the integro-PDE model

In the previous sections we have applied different techniques to the model (2) to find conditions for pattern formation in their leading order form. In this section we will confirm these by first obtaining the leading order form of the Integro-PDE model and then deducing conditions for Hopf bifurcations from it.

Applying the rescalings $u=AB^{-1}u^*$, $w=A^{-1}B^2w^*$, $t=B^{-1}t^*$, $c=Bc^*$, $\nu = A^2B^{-2}\Gamma ^{-1}$, $B^{-1}C = D$ to (2) gives

$$\begin{aligned} \frac{\partial u}{\partial t}&= u^2w - u + D\left( \int _{-\infty }^\infty \phi (x-y)u(y,t) {{\text {d}}}y - u(x,t)\right) , \\ B\nu ^{-1}\frac{\partial w}{\partial t}&=\Gamma \left( 1-u^2w\right) - \nu ^{-1}w + \frac{\partial w}{\partial x}+ d\nu ^{-1} \frac{\partial ^2w}{\partial x^2}, \end{aligned}$$

where the $^*$’s were dropped for brevity. Again assuming that $A=O_s(\nu ^{1/2})$, the leading order form in $\nu$ of this is

$$\begin{aligned} \frac{\partial u}{\partial t}&= u^2w - u + D\left( \int _{-\infty }^\infty \phi (x-y)u(y,t) {{\text {d}}}y - u(x,t)\right) , \\ 0&=\Gamma \left( 1-u^2w\right) + \frac{\partial w}{\partial x}. \end{aligned}$$

Applying the travelling wave ansatz $u(x,t) = U(z)$, $w(x,t)=W(z)$, $z=x-ct$, gives

$$\begin{aligned} -c\frac{{{\text {d}}}U}{{{\text {d}}}z}&= U^2W-U + D\left( \int _{-\infty }^\infty \phi (z-z')U(z') {{\text {d}}}z' - U(z)\right) , \\ 0&= \Gamma \left( 1-U^2W\right) + \frac{{{\text {d}}}W}{{{\text {d}}}z}. \end{aligned}$$

This system has a unique steady state given by $(\overline{U},\overline{W}) = (1,1)$. Consider small perturbations $\tilde{U}$, $\tilde{W}$ of the steady state that are proportional to $e^{\lambda z}$. Letting $\phi$ to be the Laplacian kernel (4) and linearising the resulting system yields that $\lambda$ satisfies

$$\begin{aligned} \lambda ^4 +\overline{\alpha }\lambda ^3 + \overline{\beta }\lambda ^2 + \overline{\gamma }\lambda + \overline{\delta } = 0, \end{aligned}$$

(19)

where

$$\begin{aligned} \overline{\alpha } = \frac{1-D-\Gamma c}{c}, \quad \overline{\beta }=\frac{\Gamma (1-D) - a^2c}{c}, \quad \overline{\gamma } = \frac{a^2(\Gamma c -1)}{c}, \quad \overline{\delta } = -\frac{\Gamma a^2}{c}. \end{aligned}$$

To find conditions for a Hopf bifurcation to occur, again set $\lambda =i\omega$, $\omega \in \mathbb {R}$. Analogous to the preceding sections, this allows splitting (19) into its real and imaginary parts, which after solving for $\omega ^2$, assuming that $\omega \ne 0$, gives

$$\begin{aligned} \frac{\overline{\beta } \pm \sqrt{\overline{\beta }^2 - 4 \overline{\delta }}}{2} = \frac{\overline{\gamma }}{\overline{\alpha }}, \end{aligned}$$

(20)

as the leading order condition for a Hopf bifurcation to occur. The restriction $\omega \in \mathbb {R}$, implies the additional requirement

$$\begin{aligned} \max \left\{ 0, \frac{1-D}{\Gamma } \right\}< c < \frac{1}{\Gamma }. \end{aligned}$$

(21)

If $c>0$, then $\overline{\delta } <0$ and thus one needs to choose the plus sign on the left hand side in (20). Solving for c gives

$$\begin{aligned} c_\pm = {\frac{ \left( D-3 \right) {\Gamma }^{2}+{a}^{2} \pm \sqrt{ \left( D+1 \right) ^{2}{\Gamma }^{4}-2{a}^{2} \left( 3D-1 \right) {\Gamma }^{2}+{a}^{4}}}{2{\Gamma }\left( {a}^{2}-\Gamma ^2\right) }}. \end{aligned}$$

(22)

To satisfy (21), one requires $C>B$ and

$$\begin{aligned} \Gamma < \left( \frac{3D-1+2\sqrt{2D(D-1)}}{(D+1)^2} \right) ^{\frac{1}{2}}a. \end{aligned}$$

(23)

Therefore, the steady state $(\overline{U}, \overline{W}) = (1,1)$ undergoes a Hopf bifurcation if (21), (22) and (23) are satisfied. Substituting the rescalings used at the beginning of this section into these three conditions gives the same conditions (18), (16) and (17) that were obtained form the travelling wave equations in Sect. 3.

5 Numerical simulations

So far, we have only considered one particular form of dispersal kernel in the nonlocal Klausmeier model (2). In this section we will solve the model numerically for different kernel functions and use the solutions to estimate the maximum rainfall parameter giving patterns for each kernel. The simulations will show that the parametric trends that were obtained for the Laplacian kernel carry over to other kernel functions, i.e. a wider dispersal kernel and a higher dispersal rate decrease the tendency to form patterns, while under the assumption that $C=2/\sigma (a)^2$, an increase in kernel width causes an increase in the size of the parameter region giving patterns. Our numerical simulations will further show that the tendency to form patterns depends on the type of decay of the dispersal kernel.

In the analysis performed in previous sections, we considered the model on an infinite domain. To mimic this in the simulations, we will consider a subdomain centred in a larger domain with the following initial conditions; outside the smaller subdomain the system’s initial state will be set to the steady state, while on the subdomain a random perturbation will be added. The idea of this is to choose the outer domain large enough so that any conditions imposed on the boundary of this domain (which are set to be periodic in our simulations) do no affect the solution on the inner subdomain in the finite time that is considered in the simulation. The solution is then only considered on the subdomain on which a perturbation was introduced. To solve the Integro-PDE system (2), it is first transformed into an ODE system by discretising its space domain and then solved by the built-in MATLAB ODE solver ode15s. A significant simplification is made by computing the convolution term using the fast Fourier transform, as it reduces the number of operations required to find the convolution from $O(M^2)$ to $O(M\log (M))$ in each step [e.g. (Cooley et al. 1969)], where M is the number of points of the space domain. Figure 5 shows typical solutions obtained by this method; in Fig. 5a the rainfall was chosen large enough for the solution to converge to the steady state, while for Fig. 5b parameters that produce a patterned solution of the nonlocal Klausmeier model using the Laplacian kernel were used.

Fig. 5

Numerical solution of the nonlocal Klausmeier model (2) using the Laplacian kernel (4) for different rainfall levels. In a $A=2$ yields convergence to the coexisting steady state from which the system is perturbed initially. Part b displays a patterned solution obtained by setting $A=1$. The other parameter values used in both simulations are $B=0.45$, $\nu =50$, $d=100$, $a=2$, $C=4$ and the number of space points is $M=2^{9}$

Using these simulations, we set up a scheme, based on the amplitude of the oscillation of the solution of the nonlocal Klausmeier model (2) relative to the steady state that approximates the critical rainfall parameter $A_{\max }$, that is the maximum rainfall parameter supporting pattern formation, for different kernel functions $\phi (x)$. Unlike in the simulation results shown in Fig. 5, we run the simulations over a shorter amount of time (up to $t=30$), as we are only interested in the onset of spatial patterns rather than in any of their properties. The kernel functions used in our simulations are those introduced in Sect. 1, i.e. the Laplacian (4), the Gaussian (5) and the power law kernel (6). Note that the standard deviations $\sigma (a)$ are given by $\sigma (a) = \sqrt{2}/a$ for the Laplacian kernel, $\sigma (a_g) = 1/(\sqrt{2}\,a_g)$ for the Gaussian kernel and $\sigma (a_p) = \sqrt{2}/(\sqrt{b^2-5b+6}\,a_p)$ for the power law kernel, provided $b>3$. If the shape parameter of the power law kernel is $b\le 3$, its standard deviation is infinite and a meaningful comparison to other kernel functions cannot be performed based on their standard deviations. In our simulations we consider both $b=3.1$ and $b=4$. As in previous sections, we will consider the case in which $C=2/\sigma (a)^2$, motivated by the limiting behaviour of the nonlocal model, and the cases in which either C or a is assumed to be constant and the other parameter is varied.

Figure 6a shows the results of our simulations in the case of C being constant. The trend that a narrower dispersal kernel requires a higher level of rainfall to form homogeneous vegetation, which was predicted by the leading order form (17) of $A_{\max }$ for the Laplacian kernel, carries over to the other kernels used in the simulations. Further one can observe that the power law distributions which have algebraic decay give a larger value of $A_{\max }$ than those with exponential decay if the standard deviation is sufficiently large ($\sigma (a) \gtrapprox 0.3$), while for narrower kernels the opposite is true. While the results of our simulations for the Laplacian kernel and the corresponding leading order form of $A_{\max }$ fit well for sufficiently large values of the standard deviation $\sigma (a)$, the fit is poorer for narrower kernel functions (see Fig. 6b for a comparison). The reason for this is the relatively small choice of $\nu =50$, which was taken to improve the speed of the simulations. Solutions for larger $\nu$ indicate that the relative difference between $A_{\max }$ in our simulations and in the analytical approximation decreases (slowly) with increasing $\nu$.

Fig. 6

Illustration of the results of our numerical scheme to approximate the maximum rainfall parameter $A_{\max }$ in the case of constant C. Part a shows the results of our simulations in the case of C being constant. We have determined the maximum rainfall parameter giving patterns for the Laplacian kernel (4), the Gaussian kernel (5) and the power law kernel (6) for both $b=3.1$ and $b=4$, at $\sigma (a) = \{0.1,0.2, \dots 2.1\}$. The parameter values used in these simulations are $B=0.45$, $C=1$, $\nu = 50$, $d=1$. Part b compares the simulation results obtained for the Laplacian kernel to the corresponding condition (17) valid to leading order in $\nu$

We repeat the same scheme in the setting of $C=2/\sigma (a)^2$ for the same kernel functions. The results of this are shown in Fig. 7. Considering the type of decay of the kernel functions, the results of it are similar to the simulations of the case of C being constant. One can observe that the distributions with algebraic decay yield a larger value of $A_{\max }$ than the distributions with exponential decay if the kernel is sufficiently wide, while for narrow kernels the opposite is true. Further, considering one specific kernel on its own, a narrower dispersal kernel now gives a lower value of the maximum rainfall parameter supporting pattern formation. This is in contrast to the case in which C was kept constant but in accord with the leading order form (17) of $A_{\max }$. As before, it can also be observed from the simulations of the model using the Laplacian kernel that for the choice of $\nu =50$, the numerical simulations are a good approximation of the leading order result only for sufficiently wide kernels.

Fig. 7

Illustration of the results of our numerical scheme to approximate the maximum rainfall parameter $A_{\max }$ in the case of $C = 2/\sigma (a)^2$. We have considered the Laplacian kernel (4), the Gaussian kernel (5) and the power law kernel (6) for both $b=3.1$ and $b=4$ and determined the value of the maximum rainfall parameter giving patterns $A_{\max }$ at $\sigma (a) = \{0.1,0.2, \dots 2.1\}$ for each kernel function in the case of $C = 2/\sigma (a)^2$. The parameters used in this simulation are $B=0.45$, $\nu = 50$, $d=1$

Finally, we apply the same scheme to the case of fixed dispersal parameter a and varying dispersal coefficient C (Fig. 8). As in the previous cases, the trends of the simulations of other kernel functions are again in alignment with the leading order result (17) for the Laplacian kernel. An increase in dispersal rate C causes a decrease in $A_{\max }$ for each of the dispersal kernels considered in our simulations. Further, the comparison of kernels with algebraic and exponential decay depends on the choice of standard deviation $\sigma (a)$, as indicated by the previous simulations in which the standard deviation was varied. Figure 8b shows that for a small standard deviation ($\sigma (a)=0.2$ in this case), the kernels with exponential decay predict that a higher level of rainfall is required to form a uniform vegetation cover than those with algebraic decay. If the standard deviation is sufficiently large, the opposite trend is observed. This is visualised in Fig. 8a, where the standard deviation was set to $\sigma (a)=1$.

Fig. 8

Illustration of the results of our numerical scheme to approximate the maximum rainfall parameter $A_{\max }$ in the case of constant a. We have considered the Laplacian kernel (4), the Gaussian kernel (5) and the power law kernel (6) for both $b=3.1$ and $b=4$ and determined the value of the maximum rainfall parameter giving patterns $A_{\max }$ at $C = \{0.5,0.6, \dots 2\}$ for each kernel function, with a being fixed. In (a), the standard deviation was chosen as $\sigma (a)=1$, in (b) as $\sigma (a) = 0.2$. The other parameters used in this simulation are $B=0.45$, $\nu = 50$, $d=1$

6 Discussion

The main results of this paper are given by (16) and (18), which give an upper bound for the parameter region in the A–c plane supporting pattern formation, valid to leading order in $\nu$, for the nonlocal Klausmeier model (2) with the Laplacian kernel (4). In particular this gives the upper bound $A_{\max }$, defined in (17), on the rainfall parameter, again valid to leading order in $\nu$. In other words, $A_{\max }$ represents the lowest level of rainfall that allows plants to form a homogeneous vegetation cover, while lower amounts of water only support banded vegetation. These results hold under the assumptions that the migration speed c is $O_s(1)$ and that the parameter region supporting pattern formation is bounded above by the loci of Hopf bifurcations, which was shown by Sherratt and Lord (2007) for the local Klausmeier model (1). While the simple nature of the Klausmeier model makes it impossible to deduce any quantitative conclusions from these results, they do give a good insight into the parametric trends of the model. These trends fundamentally depend on the assumption made on the factor C scaling the convolution term in the nonlocal model.

In this paper we considered three different cases of the coefficient C in the nonlocal Klausmeier model; that of choosing it to be constant, the one of varying C for fixed dispersal parameter a and that of setting $C=2/\sigma (a)^2$. In the case of C being fixed, a change in the dispersal parameter a only affects the width of the dispersal kernel, but leaves the term scaling the nonlocal plant dispersal term unchanged. It can be immediately concluded from (17) that the threshold $A_{\max }$ increases as the kernel width decreases. This increase in the size of the parameter region supporting pattern formation is also visualised in Fig. 3b. This means that the wider plants disperse their seeds, the less water they require to form a homogeneous vegetation cover. In particular, our results show that if plant dispersal is wide enough, the location of the Hopf bifurcation bounding the pattern forming parameter region completely lies in the region that only supports the trivial steady state describing complete desertification. In this case, the assumptions taken in this paper predict that no striped vegetation can occur. Plants either form a homogeneous vegetation cover or disappear completely.

The expression given by (17) is only valid for the Laplacian kernel (4) and to leading order in $\nu$. The numerical simulations in Sect. 5 allow us to compare this condition to those for other kernel functions that have been suggested by studies on plant dispersal (see Bullock et al. 2017 for an overview). Our results suggest that the maximum rainfall level giving patterned vegetation depends on the width and therefore also on the type of decay of the dispersal kernel. It can be seen from Figs. 6a and 7 that those probability distributions that decay algebraically predict a larger pattern-giving parameter region for some fixed standard deviation than those decaying exponentially under all the different assumptions taken on C in this paper, if the dispersal kernel is sufficiently wide. If the kernel is narrow, the opposite behaviour is observed. Further, the simulations show that $A_{\max }$ for each individual kernel is decreasing as the width of the kernel is increased if one assumes that C is constant. This is in accord with the behaviour of the leading order form (17) of the Laplacian kernel. Combining these observations, we can conclude that the narrower a plant’s seed dispersal is, the more water is required to avoid the formation of patterns. Nevertheless, field data shows that plants in semi-arid ecosystems tend to establish narrow dispersal kernels (Ellner and Shmida 1981; van Rheede van Oudtshoorn and van Rooyen 2013). This is, however, only a side effect of other adaptations such as seed containers protecting seeds from flooding and predation (Ellner and Shmida 1981). Simulations show that short range dispersal yields a higher mean biomass in those ecosystems than a long distance spread of seeds (Pueyo et al. 2008). Combining this with the results of this paper shows that the shortening of dispersal ranges of plants in semi-arid environments increases their tendency to self-organise into patterns.

If one assumes that the width of the dispersal kernel is fixed and plant’s dispersal rate is changed, (17) shows that, under the assumption that the dispersal of seeds fits the Laplacian kernel, the more the species invests in its dispersal rate, the less water it requires to form a homogeneous vegetation cover. For the other dispersal kernels we have considered, the same behaviour is shown in our simulations. Those simulations also show the same trend regarding the type of decay of the dispersal kernels as the simulations in the case of fixed C and varying range of dispersal. For wider dispersal kernels, those plants whose kernel functions decay algebraically have a higher tendency to form patterns than those plants dispersing their seeds according to an exponentially decaying kernel. For sufficiently narrow kernels, the opposite observation can be made.

The final choice of C assumes that it is correlated with the standard deviation of the dispersal kernel as $C=2/\sigma (a)^2$. This choice is of particular significance because it leads to the local Klausmeier model being a limiting case of the nonlocal model using either the Laplacian or the Gaussian kernel. This allows us to compare our results to the corresponding results obtained for the local model by Sherratt (2013b). This choice is motivated purely mathematically and we are not aware of any evidence that the dispersal coefficient C is correlated with the seed distribution range in such a way. However, experiments have shown that plants’ rate of dispersal increases in semi-arid environments (Aronson et al. 1993), e.g. by the production of more but smaller seeds (Volis 2007) as well as that plants develop short range dispersal of seeds (Ellner and Shmida 1981; van Rheede van Oudtshoorn and van Rooyen 2013). The analysis of the previous two cases has shown that an increase in the dispersal coefficient reduces the critical level of rainfall required to form a homogeneous vegetation cover, while the establishment of a narrow dispersal kernel increases this threshold. Therefore, this could be seen as an evolutionary trade-off.

The leading order results on quantities such as $A_{\max }$ or the wavelength, obtained in Sects. 2 and 3, resemble the limiting behaviour of this case. Apart from the limiting case, the results for the nonlocal model using the Laplacian kernel behave monotonically as the width of the dispersal kernel is changed. In particular, the results on the loci of the Hopf bifurcation and the maximum rainfall parameter giving patterns allow us to make the crucial observation that the nonlocal model predicts a larger range of parameters supporting pattern formation. Our results further show that the size of the parameter region giving patterns is larger for a wider dispersal kernel, which makes the dispersal term less influential, i.e. it decreases the plant’s dispersal rate, due to the assumption $C=a^2$. This is most strikingly illustrated by Fig. 2b, which shows the increase of this region as the scale parameter a of the kernel decreases. Under this assumption on the dispersal rate and the kernel width, our simulation results show that establishing short range dispersal increases plants’ ability to form a homogeneous vegetation cover. This is further illustrated by Fig. 9, which shows shows the contours of $A_{\max }$ and the suggested evolutionary trade-off $C=2/\sigma (a)^2$. The latter crosses the contours as the standard deviation is varied and thereby shows that an increase in kernel width yields an increase in the maximum rainfall parameter supporting pattern formation.

Fig. 9

Contour plot of $A_{\max }$. This plot shows the contours of (17) as solid lines with the colours indicating the level of $A_{\max }$. The red dotted line is the suggested trade-off $C=2/\sigma (a)^2$, which was mathematically motivated by the limiting behaviour of the convolution integral (colour figure online)

In this paper we have also investigated the distance between the striped vegetation patches to leading order in $\nu$. It is of immense importance to have an understanding of the wavelength of the patterns as it might give an indication of whether the ecosystem is close to complete desertification. The results of this study show that the wavelength monotonically increases as the amount of rainfall decreases, before reaching a critical threshold, where patterns disappear and complete desertification takes over. While it is important to emphasise again that the simplifications assumed in deducing the Klausmeier model do not allow us to gain any quantitative information, we have shown how the wavelength is affected by changes in the width of the dispersal kernel or in the plant’s dispersal rate. Interestingly, in the case of $C=2/\sigma (a)^2$, the wavelength predicted by the nonlocal model using the Laplacian kernel does not differ much from the wavelength predicted by the local model, even for wide dispersal kernels (see the y-axis in Fig. 1b). This suggests that one could make predictions on the possibility of desertification without having any information on the range of plant dispersal under the assumption that the dispersal coefficient C is correlated with the standard deviation of the dispersal kernel in such a way.

The pattern solutions of the Klausmeier model fundamentally depend on how the migration speed c scales with the parameter $\nu$, describing the rate of the water flow downhill. In this paper we have only considered the case $c=O_s(1)$ and the patterns forming in the vicinity of the Turing–Hopf bifurcation. For the local Klausmeier model results have been obtained for a wide range of migration speeds (Sherratt 2010, 2011, 2013a, b, c). One natural extension of this work would be to do a similar comprehensive study of the whole parameter range for the nonlocal model. This would give insights into the existence and form of patterns away from the bifurcation point.

Another natural area for future work would be to consider other more realistic models for vegetation patterns. A number of such models and their underlying mechanisms and scale dependent feedbacks are reviewed by Meron (2012). Some of these models already include nonlocal dispersal via convolution integrals (Baudena and Rietkerk 2013; Pueyo et al. 2008, 2010), and in others (HilleRisLambers et al. 2001; Rietkerk et al. 2002) such a term could be added in place of plant diffusion. While these as well as the model considered in this paper assume an isotropic dispersal of plants, this simplification can be removed by including either advection of plants (Saco et al. 2007; Thompson and Katul 2009) or an asymmetric dispersal kernel (Thompson and Katul 2009). Similar to the relation between diffusion and the convolution with a symmetric kernel, both the advection and the diffusion terms arise from the convolution term with an asymmetric kernel. In this case the coefficient of the first order derivative in (3) is non-zero. Finally, some models use a nonlocal term for the water uptake and thus also for plant growth, reflecting the extensive root networks of plants in semi-arid regions (Gilad et al. 2004, 2007). Investigation of these models using an approach similar to that in the current paper would be of interest but would be particularly challenging because of the added complexity.