A discrete-time model for population persistence in habitats with time-varying sizes

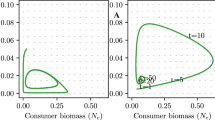
Abstract

In this paper, we use periodic and stochastic integrodifference models to study the persistence of a single-species population in a habitat with temporally varying sizes. We extend a persistence metric for integral operators on bounded domains to that of integral operators on unbounded domains. Using this metric in the periodic model, we present new perspectives of the critical habitat size problem in the case of dynamically changing habitat sizes. Specifically, we extend the concept of critical habitat size to that of lower minimal limit size in a period-2 scenario, and prove the existence of the lower minimal limit size. For the stochastic model, we point out the importance of considering multiple time scales in the temporal variability of the habitat size. The models are relevant to biological scenarios such as seasonal variability of wetland habitat sizes under precipitation variability.

1 Introduction

Habitat patches are dynamic entities that can change in size, shape, location, and quality. For instance, in the Florida Everglades, water levels rise during May to October because of precipitation, creating larger and more integrated aquatic habitats (Lodge 2004). Small fish species use these transient windows for connectivity (Zeigler and Fagan 2014) to redistribute themselves. Then, as water levels recede during the dry season, fish become restricted to permanent water bodies (Trexler et al. 2005; DeAngelis et al. 2010). The seasonal changes in habitat size observed in the Everglades are in fact a widespread phenomenon. Temporal variations in the size of aquatic systems have been documented in both ephemeral rivers such as the Mulligan River in Australia (Kerezsy et al. 2013), and perennial rivers such as the Gambia River of the West African tropical zone (Louca et al. 2009).

Changes in habitat size occur to terrestrial species as well. For example, seasonal variations in river flow patterns affect the recruitment of riparian tree species, because the establishment of trees requires both suitable flows to transport seeds and open substrates for deposition (Dixon 2003). Likewise, along barrier islands, the location and size of favorable microsites change due to shifting sands, setting limits on successful colonization (Shiflett and Young 2010).

For species living in such spatially dynamic environments, individual survival and species persistence often depend on the interplay between a species’ dispersal ability and fluctuations in habitat size (Unmack 2001). On one hand, dispersal during habitat expansion may benefit the population in various ways. For example, the ephemeral wetlands created by the rise of water levels in the Florida Everglades provide both forage resources and refuge from predation for small fish species (Cucherousset et al. 2007; Hohausová et al. 2010; Winemiller and Jepsen 1998; Yurek et al. 2013). On the other hand, exploiting ephemeral habitats carries risks. For example, as small fish species in the Everglades retreat to permanent water bodies when water levels fall, a large number of them are trapped in pools that eventually dry out (Gunderson and Loftus 1993; Kobza et al. 2004; Sheaves 2005). Such periodic bouts of mortality are also a regular occurrence for Death Valley Pupfish (Cyprinodon salinus salinus) that suffer extensive seasonal mortality when individuals disperse too far downstream as they search for resources, isolating themselves from the perennial upstream springs (Miller 1943; Moyle 2002).

Mathematical biologists have attended to the connections between dispersal, habitat size, and species persistence through the critical patch size (also named critical habitat size, critical domain size) framework (Kierstead and Slobodkin 1953; Skellam 1951). This approach suggests that patch size requirements (i.e., the minimum spatial extent of habitat that can support a species, or set of species) hinge on the balance between reproductive rate and dispersal-induced population loss. It asks the question: how small can a habitat patch be and still permit species persistence? In recent years, mathematical biologists have extended critical patch size models to consider the role of a number of other landscape- and species-level characteristics. Models have included spatially varying growth rates (Cantrell and Cosner 2001; Gurney and Nisbet 1975; Latore et al. 1998), multiple patches (Fagan et al. 2009), non-random dispersal behaviors (Cantrell and Cosner 2007), advective stream environments (Lutscher et al. 2006, 2007; Speirs and Gurney 2001), systems with Allee effects (Shi and Shivaji 2006), and interacting species (Cantrell et al. 2002). All of these extended approaches treat the habitat patch (or patches) as temporally static entities.

Recently, the critical patch size problem was considered for stream environments with temporal fluctuations in stream speed (Jacobsen et al. 2015; Jin and Lewis 2011). However, the scenario where the habitat size itself is time-dependent remains unexplored. In this paper, we consider the critical habitat size problem in a habitat whose size fluctuates periodically or randomly. What does a critical habitat size mean, when the size itself is changing? How does temporal fluctuations in the habitat size affect population persistence? We investigate these questions with an integrodifference equation model. The model framework is described below.

1.1 The model

Let us consider the time-dependent integrodifference equation model

$$\begin{aligned} n_{t+1}(x) = \int _{-\infty }^{\infty } k(x,y) Q_t(y) f[n_t(y)] dy. \end{aligned}$$

(1)

Model (1) describes the spatiotemporal dynamics of a single-species population. This population lives in a one-dimensional habitat. The population density at the tth time step at location x is described by the variable $n_t(x)$. The right hand side of Eq. (1) maps $n_t(x)$ to $n_{t+1}(x)$ through two stages: a sedentary stage and a dispersal stage.

The sedentary stage accounts for the gain or loss of population between time steps. The local population density $n_t(y)$ is mapped to the density $Q_t(y)$ $f[n_t(y)]$, according to a growth function f, and a habitat suitability function $Q_t$. Function f describes the density-dependent growth of the population, and is independent of spatial locations. We assume that function f is monotonic and concave. An example of the function f is the right hand side of the Beverton-Holt (1957) stock-recruitment curve,

$$\begin{aligned} n_{t+1} = f(n_t) = \dfrac{R_0 n_t}{1+ [(R_0-1)/K] n_t}, \end{aligned}$$

(2)

where $R_0$ is the net reproductive rate and K is the carrying capacity. The habitat suitability function $Q_t(y)$ quantifies the spatial dependence of population growth. It captures the effect of habitat quality at any location y on population growth (also see Latore et al. 1999). The range of $Q_t(y)$ is [0, 1], so that locations y where $Q_t(y) = 0$ are completely unsuitable for the species during the tth time step, and those where $Q_t(y) = 1$ are optimal for population growth during the tth time step. One choice for the habitat suitability function is the hat function

$$\begin{aligned} Q_t(y) = {\left\{ \begin{array}{ll} 1, \,\, y \in [-L_t/2, L_t/2],\\ 0, \,\, \text {otherwise}. \end{array}\right. } \end{aligned}$$

(3)

This habitat suitability function corresponds to a scenario where a species can live only within the suitable habitat $[-L_t/2, L_t/2]$ of size $L_t$. We assume that there is a bound L for the habitat sizes, so that $\forall \, t, L_t \le L$. In this case, Eq. (1) reduces to an integral equation defined on finite intervals $[-L_t/2, L_t/2]$,

$$\begin{aligned} n_{t+1}(x) = \int _{-L_t/2}^{L_t/2} k(x,y) f[n_t(y)] dy. \end{aligned}$$

(4)

Another reasonable choice for $Q_t(y)$ is the function

$$\begin{aligned} Q_t(y) = \exp \left( -\dfrac{y^2}{\sigma _t^2} \right) . \end{aligned}$$

(5)

In this case, the habitat quality smoothly declines as the location moves away from the center of the habitat, and the parameter $\sigma _t^2$ can be thought of as the size of the suitable habitat (Latore et al. 1999).

We consider two types of time-dependence for the habitat suitability function. We begin with deterministic, periodic $Q_t$ in Sect. 2, where the suitable habitat size is p-periodic. For example, for function (3), $L_{t+p} = L_t$. For function (5), $\sigma _{t+p}^2 = \sigma _t^2$. Then, in Sect. 3, we let the habitat size be randomly chosen at each time step t.

The sedentary stage is followed by the dispersal stage. The dispersal stage accounts for the spatial redistribution of the population due to dispersal. For a fixed origin y, the dispersal kernel k(x, y) is the probability density function for the destination x of individuals from y. In this paper, we assume that habitat quality does not affect dispersal, and dispersal only depends on the distance between the origin y and the destination x. That is, we assume that the dispersal kernel is a function of dispersal distance $|x-y|$, and can be written as

$$\begin{aligned} k(x,y) = k(|x-y|) = k(x-y). \end{aligned}$$

(6)

For example, the normal distribution

$$\begin{aligned} k(|x-y|) = \dfrac{1}{\sigma \sqrt{2\pi }} \exp \left[ -\dfrac{|x-y|^2}{2\sigma ^2} \right] , \end{aligned}$$

(7)

where $\sigma ^2$ is the variance, is a common choice of the probability density function. Because of its connection with the diffusion equation, we rewrite the kernel in terms of the diffusion coefficient $D = \sigma ^2/2$, and obtain the Gaussian kernel

$$\begin{aligned} k(x-y) = \dfrac{1}{2\sqrt{\pi D}} \exp \left[ -\dfrac{(x-y)^2}{4D} \right] . \end{aligned}$$

(8)

If the probability density function k(x) has finite moments, we can define the mean dispersal distance of the population as

$$\begin{aligned} \text {Mean dispersal distance} = \int _0^{\infty } xk(x)\,dx. \end{aligned}$$

(9)

For example, the mean dispersal distance for the Gaussian kernel (8) is $2\sqrt{D/\pi }$.

Finally, the integral on the right hand side of Eq. (1) tallies all the individuals dispersing to location x to form the population at the next time step.

Let X be the Banach space $BC(\varOmega )$ of bounded continuous functions on $\varOmega = \bigcup _{t} \varOmega _t$, where $\varOmega _t$ is the support of function $Q_t$. For example, for habitat suitability function (3), $\varOmega = [-L/2, L/2]$. For habitat suitability function (5), $\varOmega = \mathbb {R}$. Let X be equipped with the supremum norm, so

$$\begin{aligned} ||u|| = ||u || _{\infty } = \sup _{x\in \varOmega } |u(x)|, \,\, \forall u \in X. \end{aligned}$$

(10)

Throughout the paper, we will use ||K|| to denote the norm of any linear operator K, where

$$\begin{aligned} ||K|| = \sup _{u \ne 0, u\in X} \dfrac{||K [u]||_{\infty }}{||u||_{\infty }}. \end{aligned}$$

(11)

The set of nonnegative bounded continuous functions $BC^{+}(\varOmega )$ forms a cone of X. We may then rewrite model (1) in the form of

$$\begin{aligned} n_{t+1}(x) = F_t[n_t(x)], \end{aligned}$$

(12)

where $F_t: BC^{+}(\varOmega ) \rightarrow BC^{+}(\varOmega )$ is the integral operator

$$\begin{aligned} F_t[n_t(x)] = \int _{-\infty }^{\infty } k(x-y) Q_t(y) f[n_t(y)] dy. \end{aligned}$$

(13)

Let us now make some biologically reasonable assumptions. These assumptions make sure we are working with operators that are monotonic, completely continuous, and strongly subhomogeneous (Zhao 2003, Definition 2.3.1). We assume the following:

• (K1) k(x) is continuous on $(-\infty , \infty )$;

• (K2) $\forall \, x \in \mathbb {R}$, $k(x)>0$;

• (K3) k(x) is uniformly bounded;

• (K4) $\int _{-\infty }^{\infty } k(x)\, dx = 1$;

• (K5) k(x) is unimodal, and $k(x)=k(-x), \forall \, x \in \mathbb {R}$;

• (Q1) For each time step t, $Q_t: (-\infty , \infty ) \rightarrow [0,1]$ is continuous for $x \in \varOmega _t^{\circ }$;

• (Q2) For each time step t, $\varOmega _t$ is a connected subset of $\mathbb {R}$. In addition, $\cap _t \varOmega _t \ne \varnothing$;

• (Q3) $\int _{-\infty }^{\infty } Q(y) \,dy < \infty$;

• (F1) f(n) is differentiable for $n\ge 0$, and $\sup _{n \ge 0} f^{\prime }(n) < \infty$;

• (F2) $f(0) = 0$;

• (F3) $\forall \, n >0$, $0<f(n) < f^{\prime }(0)\,n$ ;

• (F4) $\exists \, M > 0$, so that $\forall \, n > 0$, $f(n) \le M$;

• (F5) if $n_1 > n_2$, then $f(n_1) > f(n_2)$;

• (F6) $\forall \, 0< \alpha < 1$, $n>0$, $f(\alpha n)> \alpha f(n)$;

Clearly, with the assumptions above, operator $F_t$ maps nonzero elements of cone $BC^{+}(\varOmega )$ to nonzero elements. When $\varOmega$ is compact, previous results by Hardin et al. (1988a, 1990) can be invoked to show there is a dichotomy of the asymptotic dynamics of the corresponding integrodifference equation (Jacobsen et al. 2015; Kot and Schaffer 1986; Van Kirk and Lewis 1997). More specifically, in the deterministic case, the population density $n_t(x)$ with a nonzero initial condition either converges to the trivial fixed point $n^*(x) = 0$ or a nonnegative nontrivial solution (Hardin et al. 1990). We will show in Sect. 2 that we can extend part of this dichotomy result to the case when $\varOmega = \mathbb {R}$ and $F_t$ is still compact.

1.2 Outline of the paper

The paper is organized as follows. In Sect. 2, we consider a periodic environment with seasonal changes in the habitat size. In Sect. 2.1, we present the extended dichotomy result and its proof, associating population persistence with the spectral radius of an integral operator. Examples for which this persistence metric is calculated are presented in Sect. 2.2. In Sect. 2.3, we consider a two-season environment, extending the critical patch size problem in static habitats to the lower minimal limit size problem in time-dependent habitats. We prove the existence of a lower minimal limit size in Sect. 2.3.2. We then consider a stochastic environment in Sect. 3, where we consider both seasonal and annual fluctuations in habitat size. Finally, Sect. 4 contains discussion of the results and future directions.

2 Environment with deterministic, periodic seasonal variations

In this section, we consider model (1) where the habitat suitability function $Q_t(x)$ is p-periodic. That is, $Q_t(x)$ satisfies

$$\begin{aligned} Q_{t+p}(x) = Q_t(x), \qquad \forall \, t \ge 0 , \end{aligned}$$

(14)

for an integer p, where p is the smallest period of $Q_t$.

2.1 A metric for population persistence

We will prove here that the persistence of the population is determined by the spectral radius, $\lambda$, of an operator. When $\lambda > 1$, the population will persist. When $\lambda < 1$, the population will go extinct. The number $\lambda$ is therefore a metric for population persistence.

We will begin our proof by showing, in the next three lemmas, that each $F_t$ is completely continuous and has a completely continuous Fréchet derivative at 0.

Lemma 1

Assume the dispersal kernel $k(x-y)$ satisfies assumptions (K1)−(K4), and the habitat suitability function $Q_t(y) = Q(y)$ satisfies assumptions (Q1)−(Q3). Then

$$\begin{aligned} \tilde{k}(x,y) = k(x-y) Q(y) \end{aligned}$$

(15)

satisfies conditions (KQ1) − (KQ3) listed below:

• (KQ1) $\sup \limits _{x}\int _{-\infty }^{\infty } |\tilde{k}(x,y)| \,dy < \infty$,

• (KQ2) $\int _{-\infty }^{\infty } | \tilde{k}(x,y) | dy \rightarrow 0 \,\, \text {as} \,\, x \rightarrow \infty$,

• (KQ3) $\sup \limits _{|x^{\prime }-x| \le h} \int _{-\infty }^{\infty } | \tilde{k}(x,y) - \tilde{k}(x^{\prime },y)| \,dy \rightarrow 0, \,\, \text {as} \,\, h \rightarrow 0$.

Proof

See “Appendix 1”. $\square$

Lemma 2

Let the integral operator A be defined as

$$\begin{aligned} A[u(x)] = \int _{-\infty }^{\infty } \tilde{k}(x,y) f[u(y)]\,dy. \end{aligned}$$

(16)

Suppose the integral kernel $\tilde{k}(x,y)$ satisfies the conditions (KQ1) − (KQ3) in Lemma 1. Suppose also that the nonlinear function f satisfies assumptions (F1)−(F3). Then the operator A on the cone $BC^{+}(\varOmega )$ is completely continuous.

Proof

See “Appendix 1”. $\square$

Combining Lemmas 1 and 2, we obtain the following corollary.

Corollary 1

Assume the dispersal kernel $k(x-y)$ satisfies assumptions (K1)−(K4), the habitat suitability function $Q_t(y)$ satisfies assumptions (Q1)−(Q3) for each t, and the growth function f satisfies assumptions (F1)−(F3). Then the integral operator $F_t$, as defined in (13), is completely continuous for each t.

Lemma 3

Assume the dispersal kernel $k(x-y)$ and habitat suitability functions $Q_t(y)$ satisfy assumptions (K1)−(K4) and (Q1)−(Q3), and the growth function f satisfies assumptions (F1)−(F3). Then operator $F_t$, as defined in (13), has a Fréchet derivative $F_t^{\prime }(0)$ at 0, and

$$\begin{aligned} F_t^{\prime }(0)[u](x) = f^{\prime }(0) \int _{-\infty }^{\infty } k(x-y) Q_t(y)u(y)\,dy. \end{aligned}$$

(17)

The linear integral operator

$$\begin{aligned} K_t = F_t^{\prime }(0) \end{aligned}$$

(18)

is completely continuous on $BC^{+}(\varOmega )$. Furthermore, for each i, the composition

$$\begin{aligned} F^{(i)} = F_{i+p-1} \circ \cdots \circ F_{i+1} \circ F_i \end{aligned}$$

(19)

is completely continuous. The Fréchet derivative of $F^{(i)}$ at 0 is

$$\begin{aligned} \begin{array}{lll} K^{(i)} &{}=&{} F_{i+p-1}^{\prime }(0) \circ \cdots \circ F_{i+1}^{\prime }(0) \circ F_i^{\prime }(0)\\ &{}=&{} K_{i+p-1}\circ \cdots \circ K_{i+1} \circ K_i\,, \end{array} \end{aligned}$$

(20)

and it has a positive eigenvalue $\lambda _i = r_{\sigma }(K^{(i)}) > 0$, where $r_{\sigma }(K^{(i)})$ is the spectral radius of $K^{(i)}$. In addition, $\lambda _i$ corresponds to a nonnegative eigenvector.

Proof

See “Appendix 1”. $\square$

The next lemma shows that all the $\lambda _i$’s are equal because of the periodicity.

Lemma 4

Assume the dispersal kernel $k(x-y)$ and habitat suitability functions $Q_t(y)$ satisfy assumptions (K1)−(K4) and (Q1)−(Q3), and let $\lambda _i$ be the eigenvalue of operator $K^{(i)}$ that is equal to the spectral radius, $r_{\sigma }(K^{(i)})$, of $K^{(i)}$. Then $\lambda _i$ is independent of i. That is, $\forall i,\lambda _i = \lambda$.

Proof

See “Appendix 1”. $\square$

We will now show that in the case where $\varOmega$ is bounded, there is a dichotomy of the asymptotic dynamics of the periodic system (12).

Theorem 1

Let $K_t$ be the linear operator defined in (18). Assume the dispersal kernel $k(x-y)$, the habitat suitability functions $Q_t$, and the growth function f satisfy assumptions (K1)−(K4), (Q1)−(Q3), and (F1)−(F6). In addition, assume that $\varOmega$ is compact.

Let $\lambda$ be the spectral radius of the linear operator

$$\begin{aligned} K= K_{p}\circ \cdots \circ K_{2} \circ K_1\,, \end{aligned}$$

(21)

then $\lambda$ is the largest positive eigenvalue of K, and the following are true.

• (1) If $\lambda > 1$, The solution $n_t(x)$ of the p-periodic nonlinear dynamical system (12) with a nonzero initial condition $n_0(x) \in BC^{+}(\cap _{t = 1}^{p} \varOmega _t)$ will converge to a unique positive periodic orbit $n_t^*(x)$ of system (12). That is, the population is able to persist. The periodic orbit $n_t^*(x)$ is of period at most p.

• (2) If $\lambda \le 1$, the solution $n_t(x)$ of the nonlinear dynamical system (12) with any initial condition $n_0(x) \in BC^{+}(\varOmega )$ will converge to the trivial fixed point $n_t^*(x) \equiv 0$ of system (12). That is, the population cannot persist and will become extinct.

Proof

See “Appendix 1”. $\square$

When $\varOmega = \mathbb {R}$, the operators $K^{(i)}$ may not be strongly positive, and therefore the proof of Theorem 1 fails. However, we can still prove that population persistence is determined by $\lambda$. We will prove this by approximating each operator $K_t$ with a sequence $\{K_{t_n}, n \in \mathbb {N} \}$ of integral operators with bounded integral domains. We then apply the results of Theorem 1 to the approximate operators $K_{t_n}$, and let $K_{t_n}$ approximate $K_t$ as closely as possible. The next lemma shows us how the approximate operators converge as their integral limits converge. For simplicity, Lemma 5 considers the approximation without the temporal variability, so that the habitat suitability function does not have the subscript t. To apply Lemma 5 to the operators $F_t$ for each t, the habitat suitability function Q(y) will need to be replaced with $Q_t(y)$, the operator $F^{\prime }(0)$ will need to be replaced with $F_{t}^{\prime }(0) = K_{t}$, and the operator $F_n^{\prime }(0)$ will need to be replaced with $F_{t_n}^{\prime }(0) = K_{t_n}$.

Lemma 5

Let $\{a_n\}_{n \in \mathbb {N}}$ be a decreasing sequence in $\mathbb {R}$, and $\{b_n\}_{n \in \mathbb {N}}$ an increasing sequence in $\mathbb {R}$, so that $a_0 < b_0$, and

$$\begin{aligned} \lim _{n\rightarrow +\infty } a_n = -\infty , \,\,\, \,\,\, \lim _{n\rightarrow +\infty } b_n = +\infty . \end{aligned}$$

(22)

Let the operators $F_{n}$ be defined as

$$\begin{aligned} F_{n}[u](x) = \int _{a_n}^{b_n} k(x-y) Q(y)f[u(y)]\,dy, \end{aligned}$$

(23)

where the dispersal kernel k, the habitat suitability function Q, and the growth function f satisfy assumptions (K1)−(K4), (Q1)−(Q3), and (F1)−(F6). Their corresponding Fréchet derivatives at 0 are

$$\begin{aligned} F_{n}^{\prime }(0)[u](x) = f^{\prime }(0) \int _{a_n}^{b_n} k(x-y) Q(y)u(y)\,dy. \end{aligned}$$

(24)

Let the operator F be defined as

$$\begin{aligned} F[u](x) = \int _{-\infty }^{\infty } k(x-y) Q(y)f[u(y)]\,dy. \end{aligned}$$

(25)

The Fréchet derivative of F is therefore

$$\begin{aligned} F^{\prime }(0)[u](x) = f^{\prime }(0) \int _{-\infty }^{\infty } k(x-y) Q(y)u(y)\,dy, \end{aligned}$$

(26)

and $F_{n}^{\prime }(0)$ are approximations of the operator $F^{\prime }(0)$.

Under these assumptions, we have the following results:

• (i) $||F_n^{\prime }(0) - F^{\prime }(0)|| \rightarrow 0$ as $n\rightarrow \infty$;

• (ii) $\lim _{n \rightarrow +\infty } \lambda _n = \lambda$, where $\lambda _n$ is the spectral radius of $F_n^{\prime }(0)$ and $\lambda$ is the spectral radius of $F^{\prime }(0)$.

Proof

See “Appendix 1”. $\square$

Theorem 2

Assume the dispersal kernel $k(x-y)$, the habitat suitability functions $Q_t$, and the growth function f satisfy assumptions (K1)−(K4), (Q1)−(Q3), and (F1)−(F6). In addition, assume that $\varOmega = \mathbb {R}$. Let $\lambda$ be the spectral radius of the linear operator

$$\begin{aligned} K= K_{p}\circ \cdots \circ K_{2} \circ K_1\,, \end{aligned}$$

(27)

where $K_t$ is defined by (18). Then $\lambda$ is the largest positive eigenvalue of K, and the following are true.

• (1) If $\lambda > 1$, the population will persist in the sense that for any nonzero initial population density $n_0(x) \in BC^{+}(\mathbb {R})$, $\exists \, T$ large enough and a constant $C > 0$, so that $\forall \, t > T$, the solution $n_t(x)$ of the nonlinear dynamical system (12) satisfies $||n_{t}(x)|| > C$.

• (2) If $\lambda <1$, for any initial population density $n_0(x) \in BC^{+}(\mathbb {R})$, the solution $n_t(x)$ of the nonlinear dynamical system (12) will converge to the trivial fixed point $n_t^*(x) \equiv 0$ of system (12). That is, the population cannot persist and will become extinct.

Proof

See “Appendix 1”. $\square$

2.2 Examples

In the previous section, we showed in Theorem 2 that the asymptotic dynamics of system (12) can be determined by solving the eigenvalue problem

$$\begin{aligned} \lambda u(x)= & {} [f^{\prime }(0)]^p \int _{\mathbb {R}} k(x-y_{p}) Q_{p}(y_{p}) \ldots \int _{\mathbb {R}} k(y_{p}-y_{p-1}) Q_{p-1}(y_{p-1}) \ldots \nonumber \\&\int _{\mathbb {R}} k(y_{2}-y_{1}) Q_{1}(y_{1}) u(y_1) dy_1 \ldots dy_{p-1}dy_{p}. \end{aligned}$$

(28)

Depending on the habitat suitability function and the dispersal kernel, Eq. (28) may be solved analytically or numerically. In this section, we will present four examples of the habitat suitability function $Q_t$, and present either analytic formulas for $\lambda$ or a numerical method for solving the eigenvalue problem (28).

In the first two examples, the “Flooding Pond” scenario and the “Flooding Pond-Surface” scenario, eigenvalue problem (28) can be solved analytically for certain dispersal kernels. In the other two examples, the “Connected Ponds” scenario and the “Flooding Pond-Margin” scenario, we employ a numerical method to solve eigenvalue problem (28) for $p = 2$.

2.2.1 Analytic Examples

Example 1

(The “Flooding Pond” scenario) In this example, we envision a pond whose volume changes over time because of seasonal variations in its water level. Assuming that habitat suitability scales with water depth, the center of the pond retains the highest suitability for the species at all times, but additional habitat becomes available at the margins when water levels are high. We thus use function (5) to model habitat suitability. The origin is the center of the pond, and variation in pond size is implemented by letting the parameter $\sigma _t^2$ depend periodically on time t. If we consider the Gaussian dispersal kernel (8), we can solve eigenvalue problem (28) analytically (see “Appendix 4”), and find that the spectral radius is

$$\begin{aligned} \lambda = [f^{\prime }(0)]^p \prod _{j=1}^{p} \left[ \dfrac{\sqrt{v_{j}-4D}}{\sqrt{v_{j}}} \right] , \end{aligned}$$

(29)

where $v_j$ is the solution of equation

$$\begin{aligned} v_j = g_{j+p} \circ \cdots \circ g_{j+2} \circ g_{j+1} (v_j), \end{aligned}$$

(30)

and each $g_j$ is defined to be the function

$$\begin{aligned} g_j(v) = 4D + \dfrac{\sigma _j^2 \cdot v}{\sigma _j^2+v}. \end{aligned}$$

(31)

Example 2

(The “Flooding Pond-Surface” scenario) In this example, we envision the same kind of pond and flooding dynamics as in Example 1, but now consider changes in habitat size for surface-dwelling species, such as water striders and other aquatic insects that seek out food on top of the pond. Therefore, the species activity does not depend on water depth but only on the existence of a water surface. We thus use the hat function (3) as the habitat suitability function, and let the habitat size $L_t$ depend periodically on time t. Eigenvalue problem (28) can be solved analytically for the Flooding Pond-Surface scenario for a specific dispersal kernel. Let the dispersal kernel be

$$\begin{aligned} k(x-y) = \left\{ \begin{array}{lr} \dfrac{\omega }{2} \cos {(\omega |x-y|)},&{} |x-y| \le \dfrac{\pi }{2\omega }\\ 0,&{} |x-y| > \dfrac{\pi }{2\omega } \end{array} \right. , \end{aligned}$$

(32)

where $\omega > 0$. Assume the dispersal radius $\pi /(2\omega )$ satisfies

$$\begin{aligned} \dfrac{\pi }{2\omega } > \max \{L_p, L_1/2+L_2/2, L_2/2+L_3/2, \ldots ,L_{p-1}/2+L_p/2 \}. \end{aligned}$$

(33)

Condition (33) ensures that $\forall \, t$ and $|x-y| \in [-L_t/2, L_t/2]$, $|x-y| < \pi /(2\omega )$ and $k(x-y) >0$. With these assumptions, we find in “Appendix 4” that the spectral radius is

$$\begin{aligned} \lambda = \max \{\lambda _1,\lambda _2\}, \end{aligned}$$

(34)

where

$$\begin{aligned} \lambda _1&= [f^{\prime }(0)]^p \int _{-L_p/2}^{L_p/2} \dfrac{\omega }{2} \cos (\omega y_p) \int _{-L_{p-1}/2}^{L_{p-1}/2} \dfrac{\omega }{2}\cos [\omega (y_p-y_{p-1})] \ldots \nonumber \\&\int _{-L_1/2}^{L_1/2} \dfrac{\omega }{2}\cos [\omega (y_2-y_1)] \cos (\omega y_1)\, dy_1 dy_2 \ldots dy_p, \end{aligned}$$

(35)

and

$$\begin{aligned} \lambda _2&= [f^{\prime }(0)]^p \int _{-L_p/2}^{L_p/2} \dfrac{\omega }{2} \sin (\omega y_p) \int _{-L_{p-1}/2}^{L_{p-1}/2} \dfrac{\omega }{2}\cos [\omega (y_p-y_{p-1})] \ldots \nonumber \\&\int _{-L_1/2}^{L_1/2} \dfrac{\omega }{2}\cos [\omega (y_2-y_1)] \sin (\omega y_1)\, dy_1 dy_2 \ldots dy_p. \end{aligned}$$

(36)

2.2.2 Examples with numerical computation

In general, eigenvalue problem (28) is not analytically solvable, and requires numerical schemes. We therefore use the Nyström method on multivariable integrals to calculate the largest positive eigenvalue in eigenvalue problem (28) when period $p=2$. The method essentially approximates the integral on the right hand side of Eq. (28) with a numerical quadrature on a two-dimensional grid. The two-dimensional grid is chosen by a triangulation of the computational domain, so that the triangles are pair-wise symmetric with respect to the origin. Atkinson (1997, chapter 5) detailed the derivation of composite quadrature rules and their accuracy for multivariable integrals, and demonstrated how to use these quadrature rules in the Nyström method. Here, we use the three-point quadrature rule provided by Atkinson (1997, eqn. 5.1.44) on a triangulation of the computational domain $[-G/2, G/2] \times [-G/2,G/2]$. Although the computational domain is compact, the numerically computed eigenvalue converges, according to Lemma 5, to the actual eigenvalue $\lambda$ when G is large enough.

The numerical method is tested on the analytic formula (41) for the “Flooding Pond Scenario”, and the numerical result agrees well with the analytic result (Fig. 9). Details of the numerical method setup can be found in “Appendix 5”.

With the help of the Nyström method, we investigated two examples.

Example 3

(The “Connected Ponds” scenario) In this scenario, we consider two ponds that are well-connected into a single large pond during high water periods but have less connection during periods of low water. This configuration may arise in a situation where two pieces of habitat, centered at $\mu$ and $-\mu$, are expanding and contracting their sizes concurrently. This is a simplified example of the kind of seasonal flooding dynamics that DeAngelis et al. (2010) modeled for fish inhabiting so-called “alligator holes” in the Florida Everglades.

For this scenario, we use the average of two Gaussian modes,

$$\begin{aligned} Q_t(y) = \dfrac{1}{2} \left\{ \exp \left[ -\dfrac{(y-\mu )^2}{\sigma _t^2}\right] + \exp \left[ -\dfrac{(y+\mu )^2}{\sigma _t^2}\right] \right\} , \end{aligned}$$

(37)

to be the habitat suitability function. Each Gaussian mode represents a pond. The centers of the two ponds are at $y = -\mu$ and $y = \mu$. The two ponds have the same sizes, which scale with the parameter $\sigma _t^2$. For this habitat suitability function, we use $2\sigma _t^2$ as a measure for the habitat size.

The parameter $\sigma _t^2$,

$$\begin{aligned} \sigma _t^2 = \left\{ \begin{array}{l} \sigma ^2-\epsilon \qquad \text {for t odd}, \\ \sigma ^2+\epsilon \qquad \text {for t even}, \end{array} \right. \end{aligned}$$

(38)

is periodic because of seasonal flooding. Here, $\epsilon$ is the seasonal variation.

Example 4

(The “Flooding Pond-Margin” scenario) In this scenario, we again consider a pond which floods and dries over time. However, in this case we envision the case of a nearshore, shallow water species that prefers to live at pond margins. Examples include aquatic plants such as some water lilies that root in pond bottoms but cannot live in deep water because of a lack of sunlight. Temperature-sensitive freshwater snails that forage in the warmer waters of pond margins would also match this scenario.

For this scenario, we use the habitat suitability function

$$\begin{aligned} Q_t(y) = \dfrac{1}{2} \left\{ \exp \left[ -\dfrac{(y-\mu _t)^2}{\sigma ^2}\right] + \exp \left[ -\dfrac{(y+\mu _t)^2}{\sigma ^2}\right] \right\} . \end{aligned}$$

(39)

The two peaks of the curve, representing the margin of the pond, are located at either side of the center of the pond, with equal distance $\mu _t$ from the center. We therefore use $2\mu _t$ as a measure for the habitat size. As the pond floods, the distance $\mu _t$ from the center to the margin increases, and as the pond dries, $\mu _t$ decreases.

We thus assume

$$\begin{aligned} \mu _t = \left\{ \begin{array}{l} \mu _0-\epsilon \qquad \text {for t odd}, \\ \mu _0+\epsilon \qquad \text {for t even}. \end{array} \right. \end{aligned}$$

(40)

Results of the numerical computations in Examples 3 and 4 are presented in the figures of the following section.

2.3 Population persistence in a two-season scenario

Many rivers and wetland systems experience two distinct seasons annually. For example, the Everglades receives most of its precipitation during the rainy season from May to October, and the other months constitute the dry season (Lodge 2004). Water levels between the rainy seasons and dry seasons may be drastically different (EDEN 2015). Likewise, the Gambia River experiences a rainy season from June to October, followed by a dry season for the rest of the year (Louca et al. 2009). While the amount of precipitation and the water levels may also vary on the annual and inter-annual time scale (EDEN 2015), we focus on the seasonal variation in this section. That is, we consider here an environment where the habitat size alternates between two sizes, a rainy season size and a dry season size, each year. Variations on the annual time scale will be discussed later in Sect. 3.

2.3.1 Effect of seasonal variations on population persistence

In this section, we are interested in knowing: how does seasonal variation in the habitat size affect population persistence? To answer this question, we examine the case where the average habitat size between two seasons is constant, and look at the effect of seasonal variation on the spectral radius $\lambda$ in all four examples in Sect. 2.2.

In the “Flooding Pond” scenario (Example 1), the measure for habitat size, $\sigma _t^2$, alternates between a large size, $\sigma _1^2$, for the rainy season, and a small size, $\sigma _2^2$, for the dry season. According to formula (29), the spectral radius $\lambda$ can be expressed in terms of $\sigma _1^2$ and $\sigma _2^2$ as

$$\begin{aligned} \lambda (\sigma _1^2, \sigma _2^2) = [f^{\prime }(0)]^2 \sqrt{1 - \dfrac{2}{1+\sqrt{\dfrac{(\sigma _1^2+2D)(\sigma _2^2+2D)}{2D(\sigma _1^2 + \sigma _2^2 + 2D)}}}}. \end{aligned}$$

(41)

How will $\lambda$ behave when $\sigma _1^2$ increases, $\sigma _2^2$ decreases, but the “average” between these two sizes holds constant? To answer this question, we first notice that there are different ways to take averages. For example, we may consider

$$\begin{aligned} m_1 = \dfrac{\sigma _1^2 + \sigma _2^2}{2} \end{aligned}$$

(42)

as the average habitat size. If $m_1$ is a constant, then $\sigma _1^2$ and $\sigma _2^2$ follow a trade-off relation

$$\begin{aligned} \sigma _2^2 = \varGamma _1(\sigma _1^2) = 2m_1- \sigma _1^2, \end{aligned}$$

(43)

which says the sum $\sigma _1^2 + \sigma _2^2$ is a constant. Therefore the curve $\varGamma _1(\sigma _1^2)$ is a straight line (see dashed line in Fig. 1). In this case, let the seasonal variation be

$$\begin{aligned} \epsilon = (\sigma _1^2-\sigma _2^2)/2, \end{aligned}$$

(44)

then $\lambda$ can be expressed in terms of $m_1$ and $\epsilon$ as

$$\begin{aligned} \lambda (m_1,\epsilon ) = [f^{\prime }(0)]^2 \sqrt{1 - \dfrac{2}{\sqrt{\dfrac{(m_1 + 2D)^2-\epsilon ^2}{4D(m_1 + D)}}+1}}. \end{aligned}$$

(45)

It is clear that $\lambda$ is monotonically decreasing with respect to $\epsilon$ (also see solid curve in Fig. 2a). That is, as the seasonal variation of habitat sizes increases, the asymptotic rate of growth for the population slows down. Once $\epsilon$ exceeds a critical level

$$\begin{aligned} \epsilon ^* = \sqrt{m_1^2 + 4D\left[ 1-\left( \dfrac{f^{\prime }(0)^4+1}{f^{\prime }(0)^4-1}\right) ^2 \right] m_1 + 4D^2\left[ 1-\left( \dfrac{f^{\prime }(0)^4+1}{f^{\prime }(0)^4-1}\right) ^2 \right] }, \end{aligned}$$

(46)

the spectral radius $\lambda$ will drop below 1, and the population will fail to persist (Fig. 2a).

Fig. 1

Three compensation relations $\sigma _2^2 = \varGamma (\sigma _1^2)$ are plotted in this figure. The dashed straight line is the compensation relation $\varGamma _1$ in (43), the dot dashed curve is the compensation relation $\varGamma _2$ in (48), and the solid curve is the compensation relation $\varGamma ^*$ in (49). All three curves of compensation relations intersect the diagonal line of the first quadrant at the point $(\sigma _0^{*2}, \sigma _0^{*2})$, where $\sigma _0^{*2}$ is the critical habitat size when there is no seasonal variation (see Eq. (59)). In this figure, $f^{\prime }(0) = 2.5$ and $D = 2$

Fig. 2

The spectral radius $\lambda$ decreases with respect to the seasonal variation $\epsilon$ for all four scenarios (Examples 1−4). In all four figures, $f^{\prime }(0)^2 = 6.25$, and dispersal parameters are chosen so that the mean dispersal distance is 2. a Results in Example 1, the “Flooding Pond” scenario, where $\lambda$ is calculated with formula (41) and $\epsilon$ is defined in Eq. (44). On the solid curve, $\sigma _1^2$ and $\sigma _2^2$ follows compensation relation (43) with $m_1 = 4$, while on the dot dashed curve, $\sigma _1^2$ and $\sigma _2^2$ follows compensation relation (48) with $m_1 = 2$. b Results in Example 2, the “Flooding Pond-Surface” scenario, where $\lambda$ is calculated with formula (50), and $\epsilon$ is defined in Eq. (51). In the solid curve in (b), $L_1$ and $L_2$ follow compensation relation (50) with $m_1 = 4$. c Results in Example 3, the “Connected Ponds” scenario, where $\lambda$ is calculated with the Nystöm method, and $\epsilon$ is defined in Eq. (38). Along the solid curve in (c), the habitat sizes $\sigma _1^2$ and $\sigma _2^2$ for each pond always sum up to 8. d Results in Example 4, the “Flooding Pond-Margin” scenario, where $\lambda$ is calculated with the Nystöm method, and $\epsilon$ is defined in Eq. (40). For the solid curve in (d), $\mu _0 = 3$ and $\sigma ^2 = 4$

We may also consider the average habitat size to be

$$\begin{aligned} m_2 = \dfrac{\sigma _1 + \sigma _2}{2}, \end{aligned}$$

(47)

in which case $\sigma _1^2$ and $\sigma _2^2$ follow a trade-off relation

$$\begin{aligned} \sigma _2^2 = \varGamma _2(\sigma _1^2) = \left( 2m_2-\sqrt{\sigma _1^2}\right) ^2. \end{aligned}$$

(48)

The curve of $\varGamma _2$ is the dot-dashed line in Fig. 1. The dot-dashed curve in Fig. 2a shows that $\lambda$ also decreases monotonically as the seasonal variation $\epsilon$ increases when $m_2$ holds constant.

In general, if the trade-off relation $\varGamma$ satisfies certain conditions, the dominant eigenvalue $\lambda$ will monotonically decrease as $\sigma _2^2$ and $\sigma _1^2$ deviate from the diagonal line along the curve of $\sigma _2^2 = \varGamma (\sigma _1^2)$.

Proposition 1

Assume that $\sigma _2^2 = \varGamma (\sigma _1^2)$, where $\varGamma$ is a monotonically decreasing function. Assume $\sigma _0^2 = \varGamma (\sigma _0^2)$ is a fixed-point for $\varGamma$. If $\varGamma$ satisfies the following conditions:

• 1. $\exists$ $\sigma _g^2 < \infty$, so that $\varGamma (\sigma _g^2) = 0$;

• 2. $\varGamma \in C^2(\sigma _0^2, \sigma _g^2)$;

• 3. $\varGamma ^{\prime \prime }(\sigma _1^2)$ does not change its sign for $\sigma _1^2 \in (\sigma _0^2, \sigma _{g}^2)$;

• 4. $\varGamma (\sigma _1^2) < \varGamma ^{*}(\sigma _1^2)$ for $\sigma _1^2 \in (\sigma _0^2, \sigma _{g}^2)$, where

  $$\begin{aligned} \varGamma ^{*}(\sigma _1^2) = \sigma _0^4 \left[ \dfrac{\sigma _1^2 + 2D}{ 2(\sigma _0^2+D) \sigma _1^2 - \sigma _0^4} \right] ; \end{aligned}$$

  (49)

• 5. $\varGamma ^{\prime }(\sigma _1^2) < (\varGamma ^{*})^\prime (\sigma _1^2)$ for $\sigma _1^2 \in (\sigma _0^2, \sigma _{g}^2)$;

then $\lambda (\sigma _1^2,\sigma _2^2)$ monotonically decreases as the point $(\sigma _1^2,\sigma _2^2)$ $\in \mathbb {R}^2$ deviates away from the point $(\sigma _0^2,\sigma _0^2)$ $\in \mathbb {R}^2$ along the curve of $\sigma _2^2 = \varGamma (\sigma _1^2)$ with the increase of $\sigma _1^2$.

Proof

See “Appendix 2”. $\square$

The monotonic decrease of $\lambda$ with respect to seasonal variation is observed in examples 2, 3, and 4 as well. In Example 2 (The “Flooding Pond-Surface” scenario), when $p=2$, the spectral radius $\lambda$ is

$$\begin{aligned} \begin{array}{lll} \lambda (L_1,L_2) &{}=&{} \max \left\{ \dfrac{f^{\prime }(0)^2}{16} [\omega L_1 + \sin (\omega L_1)] [\omega L_2 + \sin (\omega L_2)], \right. \\ &{}&{} \left. \dfrac{f^{\prime }(0)^2}{16} [\omega L_1 - \sin (\omega L_1)] [\omega L_2 - \sin (\omega L_2)] \right\} \end{array} \end{aligned}$$

(50)

according to formulae (34), (35) and (36). Let the seasonal variation be

$$\begin{aligned} \epsilon = \dfrac{|L_1-L_2|}{2}, \end{aligned}$$

(51)

then the spectral radius $\lambda$ also monotonically decreases with respect to $\epsilon$, if the average of $L_1$ and $L_2$, $(L_1+L_2)/2$, is a constant (see Fig. 2b). For Examples 3 and 4, the numerically computed curves of $\lambda$ with respect to seasonal variation are plotted in Fig. 2c, d, and we again observe a monotonic decrease.

2.3.2 “Lower minimal limit size”, a generalization of the “critical habitat size”

The “critical habitat size” is a classic concept in spatial ecology (Kierstead and Slobodkin 1953; Skellam 1951) about how large a suitable habitat must be for a population to persist. This concept is often used to guide conservation efforts, such as the design of marine reserves (Lockwood et al. 2002). Previous studies on the critical habitat size have focused on the case where there is no temporal variation in habitat sizes. In this case, $Q_t(x) = Q(x)$ for all t, and model (1) reduces to an autonomous system

$$\begin{aligned} n_{t+1}(x) = F_t[n_t](x) = \int _{-\infty }^{\infty } k(x,y)Q(y) f[n_t(y)]\,dy. \end{aligned}$$

(52)

For this autonomous system, population persistence is determined by the spectral radius $\lambda$ of operator $F_t$. In order to make sure that the critical habitat size problem is well-defined, we restrict our discussions in this section to habitat suitability functions satisfying the following additional assumptions:

• (Q4) Q(x) can be written as $Q(x;\alpha )$, where $\alpha > 0$ is a measure of habitat size, and

  • (a) $\forall \, \alpha _1 > \alpha _2$, $||Q(x; \alpha _1) - Q(x; \alpha _2)|| \ne 0$, but $\forall \, x$, $Q(x; \alpha _1) \ge Q(x; \alpha _2)$;

  • (b) $Q(x; \alpha ) \rightarrow Q(x; \beta )$ pointwise as $\alpha \rightarrow \beta$ for $\beta < \infty$. In addition, $Q(x; \alpha ) \rightarrow Q(x; \infty )$ pointwise as $\alpha \rightarrow \infty$.

When Q(x) satisfies assumption (Q4), the critical habitat size for the autonomous model (52) is the unique habitat size that corresponds to $\lambda = 1$.

In a two-season environment, the population cannot persist if the habitat size in both seasons is below the critical habitat size. The population can, however, persist if the habitat size is larger than the critical habitat size in one season, but smaller than that in the other season. In this section, we will discuss the habitat size requirements for a population to persist in a two-season environment. Let us first look at an example.

The “Flooding Pond” scenario In the “Flooding Pond” scenario (Example 1), the habitat sizes for the rainy and dry seasons, $\sigma _1^2$ and $\sigma _2^2$, jointly determine the spectral radius $\lambda$. According to Theorem 2, $\lambda =1$ is a threshold separating persistence and extinction. Letting $\lambda = 1$ in Eq. (41) and solving for $\sigma _2^2$, we obtain a critical value

$$\begin{aligned} \sigma _2^{2*} = \sigma _{\infty }^2 \left[ \dfrac{\sigma _1^2+2D}{\sigma _1^2-\sigma _{\infty }^2} \right] , \end{aligned}$$

(53)

where

$$\begin{aligned} \sigma _{\infty }^2 = 2D\left[ \dfrac{f^{\prime }(0)^4+1}{f^{\prime }(0)^4-1} \right] ^2 -2D, \end{aligned}$$

(54)

so that $\lambda (\sigma _2^{2*}) = 1$. Since $\lambda$ is monotonically increasing with respect to either $\sigma _1^2$ or $\sigma _2^2$ (see Fig. 4a), when $\sigma _1^2$ is fixed, $\lambda <1$ for any $\sigma _2^2<\sigma _2^{2*}$. Therefore $\sigma _2^{2*}$ is the smallest value of $\sigma _2^{2}$ required for the population to persist.

This critical value $\sigma _2^{2*}$ depends on $\sigma _1^2$. In Fig. 3, $\sigma _2^{2*}$ is plotted with respect to $\sigma _1^2$. We can see that the curve is a hyperbola, as described in expression (53). The grey area above the hyperbola is the region where the population can persist, and the white area below the hyperbola is where the population cannot.

We can see in Fig. 3 that $\sigma _2^{2*}$ decreases monotonically with respect to $\sigma _1^2$. Therefore, when the habitat size in one season is increased, the habitat size for the other season is allowed to take smaller values while still keeping the population persist. However, because

$$\begin{aligned} \lim _{\sigma _1^2 \rightarrow \infty } \sigma _2^{2*} = \sigma _{\infty }^2 >0, \end{aligned}$$

(55)

the critical value $\sigma _2^{2*}$ approaches a nonzero limit as $\sigma _1^2$ approaches infinity. That is, no matter how large the habitat size is for one season, the population cannot persist if the habitat size for the other season is smaller than a critical value $\sigma _{\infty }^2$. We will refer to $\sigma _{\infty }^2$ as the lower minimal limit size.

Fig. 3

The critical value $\sigma _2^{*2}$ is plotted with respect to $\sigma _1^2$ in a solid curve, which is a hyperbola, for the two-season environment in the “Flooding Pond” scenario with Gaussian dispersal kernel. The hyperbola intersects the diagonal line at $(\sigma _0^{*2}, \sigma _0^{*2})$, where $\sigma _0^{*2}$ is the critical habitat size when there is no seasonal variation (see Eq. (59)). This intersection is indicated by an asterisk. The population persists if $(\sigma _1^2, \sigma _2^2)$ is in the grey area above the hyperbola, and fails to persist if $(\sigma _1^2, \sigma _2^2)$ is in the white area below the hyperbola. As $\sigma _1^2 \rightarrow \infty$, the critical value $\sigma _2^{*2}$ approaches a limit. This limit, as indicated by the horizontal dashed line, is the lower minimal limit size $\sigma _{\infty }^2$ in (54). In this figure, $f^{\prime }(0) = 2.5$ and $D = 2$

Fig. 4

The spectral radius $\lambda$ in Examples 1−3 (a–c, respectively) are plotted with respect to the habitat size in even time steps, $\sigma _2^2$ (in a, c) or $L_2$ (in b), for different values of $\sigma _1^2$ (in a, c) or $L_1$ (in b). The dashed horizontal line corresponds to $\lambda = 1$, and its intersections with the $\lambda$-$\sigma _2^2$ or $\lambda$-$L_2$ curves mark the smallest $\sigma _2^2$ or $L_2$ for the population to persist when $\sigma _1^2$ or $L_1$ is given. In all three panels, $f^{\prime }(0) = 2.5$, and the dispersal parameters are chosen so that the mean dispersal distance is 2. For all three scenarios, the curves approach a limit curve as $\sigma _1^2$ or $L_1$ increase. As a result, the intersections of these curves with the horizontal dashed line approach the “lower minimal limit size”. In the solid curves in (a) and (c), $\sigma _1^2$ takes the values $\sigma _1^2 = 1, 20, 40, 60$, as labeled. The dashed curves in (a) and (c) correspond to $\sigma _1^2 = 80$. In (a), $\lambda$ is calculated with formula (41). In (c), $\lambda$ is calculated with the Nystöm method, the habitat suitability function is (37) with $\mu = 3$, and the dispersal kernel is the Gaussian kernel (8). In (b), $L_1$ takes the values $L_1 = 1, 5, 10$ in the solid curves, as labeled, and $L_1= 20$ in the dashed curve. The habitat suitability function is the hat function (3), the dispersal kernel is the Gaussian kernel (8), and $\lambda$ is calculated with the Nystöm method

We can compare this lower minimal limit size $\sigma _{\infty }^2$ with the critical habitat size. When there is no temporal variation in the habitat size, $\sigma _1^2 = \sigma _2^2$, the critical habitat size is the smallest habitat size $(\sigma _0^{*})^2$ so that

$$\begin{aligned} \lambda (\sigma _1^2,\sigma _2^2) = \lambda ((\sigma _0^{*})^2,(\sigma _0^{*})^2) = 1, \end{aligned}$$

(56)

where $\lambda (\sigma _1^2,\sigma _2^2)$ is defined by Eq. (41). Solving Eq. (56) for $(\sigma _0^{*})^2$, we find that

$$\begin{aligned}&\dfrac{(\sigma _0^*)^2+2D}{2 \sqrt{D((\sigma _0^*)^2+2D)}} = \dfrac{f^{\prime }(0)^4+1}{f^{\prime }(0)^4-1}, \end{aligned}$$

(57)

$$\begin{aligned}&\quad (\sigma _0^*)^4 + 4D \left[ 1 - \left( \dfrac{f^{\prime }(0)^4+1}{f^{\prime }(0)^4-1}\right) ^2 \right] (\sigma _0^*)^2 + 4D^2 \left[ 1 - \left( \dfrac{f^{\prime }(0)^4+1}{f^{\prime }(0)^4-1}\right) ^2 \right] = 0,\nonumber \\ \end{aligned}$$

(58)

and

$$\begin{aligned} (\sigma _0^{*})^2 = 2D\left( \dfrac{f^{\prime }(0)^4+1}{f^{\prime }(0)^4-1} \right) ^2-2D + 2D\left( \dfrac{f^{\prime }(0)^4+1}{f^{\prime }(0)^4-1} \right) \sqrt{\left( \dfrac{f^{\prime }(0)^4+1}{f^{\prime }(0)^4-1} \right) ^2-1}. \end{aligned}$$

(59)

This critical habitat size can be visualized in Fig. 3 by intersecting the hyperbola (53) with the diagonal line of the first quadrant, and obtaining the intersection point ($\sigma _0^{*2}$,$\sigma _0^{*2}$), marked with an asterisk in Fig. 3. In this example, the ratio between the critical habitat size and the lower minimal limit size,

$$\begin{aligned} \dfrac{\sigma _0^{*2}}{\sigma _{\infty }^2} = 1 + \sqrt{\dfrac{\left( \dfrac{f^{\prime }(0)^4+1}{f^{\prime }(0)^4-1} \right) ^2}{\left( \dfrac{f^{\prime }(0)^4+1}{f^{\prime }(0)^4-1} \right) ^2-1}}, \end{aligned}$$

(60)

depends only on the net reproductive rate $f^{\prime }(0)$, and does not depend on the dispersal parameter D. Also, we know that the ratio $\sigma _0^{*2}/\sigma _{\infty }^2 >2$ for any given $f^{\prime }(0)$, so the lower minimal limit size $\sigma _{\infty }^2$ is always smaller than 1 / 2 of the critical habitat size $\sigma _0^{*2}$ for this specific example. The lower minimal limit size generalizes the critical habitat size concept for a two-season environment. It is the smallest dry-season habitat size required for the population to persist, when the wet-season habitat size is $\infty$. We now show that this lower minimal limit size exists for other two-season examples where the habitat suitability function and dispersal kernel satisfy the model assumptions (K1)−(K5) and (Q1)−(Q4).

We will prove the existence of the lower minimal limit size by considering the limit case of the eigenvalue problem

$$\begin{aligned} \lambda u(x) = [f^{\prime }(0)]^2 \int _{-\infty }^{\infty } k(x-y) Q(y;\alpha _1) \left[ \int _{-\infty }^{\infty } k(y-z) Q(z;\alpha _2) u(z)\,dz \right] \,dy \end{aligned}$$

(61)

when $\alpha _1 \rightarrow \infty$. Here, $Q(x;\alpha _i)$ is the habitat suitability function for the ith season, and $\alpha _i$ is the parameter representing the habitat size.

We begin by noticing that we can change the order of integration in Eq. (61), and rewrite Eq. (61) as

$$\begin{aligned} \lambda u(x) = K_{\alpha _1} [u](x) = [f^{\prime }(0)]^2 \int _{-\infty }^{\infty } Q(z;\alpha _2) \tilde{k}(x,z;\alpha _1) u(z)\,dz, \end{aligned}$$

(62)

where

$$\begin{aligned} \tilde{k}(x,z;\alpha _1) = \int _{-\infty }^{\infty } k(x-y) Q(y;\alpha _1)k(y-z) \,dy. \end{aligned}$$

(63)

As $\alpha _1 \rightarrow \infty$, the following series of lemmas will show that the spectral radius $\lambda$ of $K_{\alpha _1}$ converges to that of $K_{\infty }$, where

$$\begin{aligned} K_{\infty }[u](x) = [f^{\prime }(0)]^2 \int _{-\infty }^{\infty } Q(z;\alpha _2) \tilde{k}(x,z;\infty ) u(z)\,dz. \end{aligned}$$

(64)

Lemma 6

Assume the dispersal kernel k(x) satisfies assumptions (K1)−(K5). Then the improper integral

$$\begin{aligned} \int _{-\infty }^{\infty } k(x-y) k(y-z)\,dy \end{aligned}$$

(65)

is uniformly convergent for $(x,z) \in I_1 \times I_2$, where $I_1 = [-L_1/2, L_1/2]$ and $I_2 = [-L_2/2, L_2/2]$ are bounded intervals in $\mathbb {R}$ for some arbitrary $L_1, L_2 > 0$.

Proof

See “Appendix 2”. $\square$

Lemma 7

Assume that the habitat suitability function $Q(x;\alpha )$ satisfies assumptions (Q1)−(Q4), and the dispersal kernel $k(x-y)$ satisfies assumptions (K1)−(K5). Let

$$\begin{aligned} p(x,z) = \int _{-\infty }^{\infty } k(x-y) k(y-z)\,dy, \end{aligned}$$

(66)

then for any $\alpha < \infty$, the integral $\int _{-L}^{L} Q(z;\alpha ) p(x,z)\,dz$ converges to the improper integral $\int _{-\infty }^{\infty } Q(z;\alpha ) p(x,z)\,dz$ uniformly as $L \rightarrow \infty$.

Proof

See “Appendix 2”. $\square$

Lemma 8

Assume that the habitat suitability function Q(x) satisfies (Q1)−(Q4), and the dispersal kernel $k(x-y)$ satisfies assumptions (K1)−(K5). Let $\bar{\lambda }_{\alpha _1}$ be the spectral radius of $K_{\alpha _1}$, and $\bar{\lambda }_{\infty }$ be the spectral radius of $K_{\infty }$, then $\bar{\lambda }_{\alpha _1} \rightarrow \bar{\lambda }_{\infty }$ as $\alpha _1$ $\rightarrow \infty$.

Proof

See “Appendix 2”. $\square$

Meanwhile, it is also obvious that eigenvalue $\lambda$ is monotonically increasing with respect to both $\alpha _1$ and $\alpha _2$, as stated in the following lemma.

Lemma 9

Assume that the habitat suitability function Q(x) satisfies (Q1)−(Q4), and the dispersal kernel $k(x-y)$ satisfies assumptions (K1)−(K5).

Let $\lambda (\alpha _1,\alpha _2)$ be the largest positive eigenvalue in eigenvalue problem (28) when $p = 2$. Then $\lambda (\alpha _1,\alpha _2)$ is continuous and monotonically increasing with respect to both $\alpha _1$ and $\alpha _2$.

Proof

For a given $\alpha _2$, we can prove that $\bar{\lambda }_{\alpha _1} \rightarrow \bar{\lambda }_{\beta }$ as $\alpha _1 \rightarrow \beta$ by replacing $\infty$ with $\beta$ in the proof of Lemma 8. Therefore $\lambda (\alpha _1,\alpha _2)$ is continuous with respect to $\alpha _1$. We can use the same method to show that $\lambda (\alpha _1,\alpha _2)$ is continuous with respect to $\alpha _2$, too. The monotonicity follows from assumption (Q4(a)). $\square$

From Lemma 9, it follows that any $\alpha _2^*$ satisfying $\lambda (\alpha _1,\alpha _2^*)=1$ for a given $\alpha _1$ is unique, and is the smallest habitat size in the even time steps required for the population to persist.

Theorem 3

Assume that the habitat suitability function Q(x) satisfies (Q1)−(Q4), the dispersal kernel k(x) satisfies assumptions (K1)−(K5), and for some given $\alpha _1^{\prime }$, there exists $\alpha _2^*>0$ that satisfies $\bar{\lambda }_{\alpha _1^{\prime }}(\alpha _2^*)=1$. Thus, for each given $\alpha _1>\alpha _1^{\prime }$, there exists a unique $\alpha _2^*$ satisfying $\bar{\lambda }_{\alpha _1}(\alpha _2^*)=1$. Then as $\alpha _1 \rightarrow \infty$, there exists $\alpha _{\infty }>0$, so that $\alpha _2^* \rightarrow \alpha _{\infty }$.

Proof

See “Appendix 2”. $\square$

It is not clear whether the “Flooding Pond-Margin” scenario meets the assumptions of Theorem 3, because we are not able to find an $\alpha$ that meets assumption (Q4(a)) or prove that such an $\alpha$ does not exist. In the mean time, the “Flooding Pond” scenario, the “Flooding Pond-Surface” scenario, and the “Connected Ponds” scenario meet the assumptions for Theorem 3. We therefore illustrate the convergence of $\bar{\lambda }_{\alpha _1}$ to $\bar{\lambda }_{\infty }$ and the existence of the lower minimal limit size for these three examples in Fig. 4. In Fig. 4b, each curve represents a function $\bar{\lambda }(L_2)$ of $L_2$ for the “Flooding Pond-Surface” scenario, for a given value of $L_1$. The values of $L_1$ are between $L_1 = 1$ and $L_1=20$. As $L_1$ approaches its largest value, the curves of $\bar{\lambda }(L_2)$ approach a limit. Intersecting these curves with $\lambda =1$, we can see that the critical values of $L_2$ for a given $L_1$ decrease to a limit. This limit is the lower minimal limit size. In Fig. 4c, we plotted the spectral radius for the “Connected Ponds” scenario with respect to $\sigma _2^2$ for different values of $\sigma _1^2$. Each curve in Fig. 4c represents a function $\bar{\lambda }(\sigma _2^2)$ of $\sigma _2^2$ for a given value of $\sigma _1^2$. The values of $\sigma _1^2$ are between $\sigma _1^2 = 1$ and $\sigma _1^2=80$. When $\sigma _1^2$ approaches its largest value, the curves of $\bar{\lambda }(\sigma _2^2)$ approach a limit. Intersecting these curves with $\lambda =1$, we can see that the critical values of $\sigma _2^2$ for a given $\sigma _1^2$ decrease to a limit, which is the lower minimal limit size.

2.3.3 Effect of dispersal on population persistence

The effect of dispersal on population persistence has been well-studied for environments with no temporal variation. For example, Hardin et al. (1988b) considered an integrodifference equation model and found that the persistence metric is optimized when there is no dispersal.

In the case when there is temporal variation in the habitat size, the effect of dispersal is more complex. When the habitat expands, dispersal may allow the population to take advantage of the extra habitat gained during expansion. However, it may also cause population loss when the habitat contracts. In this section, we will investigate the effect of dispersal in four examples: the “Flooding Pond” scenario, the “Flooding Pond-Surface” scenario, the “Connected Ponds” scenario, and the “Flooding Pond-Margin” scenario (see Sect. 2.2).

We find that in the first three examples, dispersal has a negative effect on population persistence. In Fig. 5, the spectral radius $\lambda$ is plotted against the mean dispersal distance for each example. We can see that the spectral radius $\lambda$ monotonically decreases with respect to mean dispersal distance.

We can look at this negative effect in more detail in the “Flooding Pond” scenario with dispersal kernel (8). For example, the critical variation $\epsilon ^*$ decreases as the dispersal parameter D increases, because

$$\begin{aligned} 1-\left( \dfrac{f^{\prime }(0)^4+1}{f^{\prime }(0)^4-1}\right) ^2<0 \end{aligned}$$

(67)

in Eq. (46). Thus the population has a smaller allowance of seasonal habitat size variations when its mean dispersal distance is larger. We can also take a look at the dependence of the critical habitat size and the lower minimal limit size on dispersal. Both the critical habitat size $\sigma _0^{*2}$ (see Eq. 59) and the lower minimal limit size $\sigma _{\infty }^2$ (see Eq. 54) increase linearly with respect to the dispersal parameter D. If the species has a larger mean distance of dispersal, it requires larger habitats to persist. In this example, dispersing farther in each time step provides no advantage for population persistence in this model, because the location of optimal habitat suitability does not move during seasonal changes, the habitat suitability for the area gained during range expansion is lower than the suitability of the habitat already occupied. Instead, dispersing imposes a great disadvantage during range contraction.

Fig. 5

The spectral radius $\lambda$ is plotted with respect to mean dispersal distance for Examples 1−3 (a–c respectively). For all three scenarios, $\lambda$ decreases as mean dispersal distance increases. The horizontal dashed line corresponds to $\lambda = 1$, and its intersection with the curves mark the maximal mean dispersal distance for the population to persist. In all three panels, $f^{\prime }(0)^2 = 6.25$, and seasonal variation $\epsilon = 2$. In (a), $\lambda$ is calculated with formula (41), the habitat suitability function is (5) with $\sigma _1^2 = 6$ and $\sigma _2^2 = 2$, and the dispersal kernel is the Gaussian kernel (8). In (b), $\lambda$ is calculated with formula (50), the habitat suitability function is the hat function (3) with $L_1 = 6$ and $L_2 = 2$, and the dispersal kernel is the cosine kernel (32). In (c), $\lambda$ is calculated with the Nystöm method, the habitat suitability function is (37) with $\mu = 3$, $\sigma _1^2 = 6$, and $\sigma _2^2 = 2$. The dispersal kernel is the Gaussian kernel (8)

Fig. 6

The spectral radius $\lambda$ is plotted with respect to the mean dispersal distance for Example 4. In (a), seasonal variation $\epsilon$ is small ($\epsilon = 0.5$), and $\lambda$ decreases as mean dispersal distance increases. In (b), seasonal variation $\epsilon$ is increased to $\epsilon = 2$, and $\lambda$ is no longer monotonic with respect to the mean dispersal distance. In both panels, $\lambda$ is calculated with the Nystöm method. The habitat suitability function is (39) with $f^{\prime }(0)^2 = 12$, $\sigma ^2 = 4$, and $\mu _0 = 4$. The dispersal kernel is the Gaussian kernel (8)

The “Flooding Pond-Margin” scenario is different from the other three examples in that the location of optimal habitat suitability moves during seasonal changes. As a result, the effect of dispersal on the spectral radius $\lambda$ depends on the parameter region we consider. Specifically, when the seasonal variation $\epsilon$ is small, $\lambda$ decreases with respect to the mean dispersal distance (Fig. 6a). But when the seasonal variation $\epsilon$ is large, the dependence of $\lambda$ on the mean dispersal distance is no longer monotonic (Fig. 6b). This can be explained when we look at the double-sided effect of dispersal in population persistence. When the suitable range expands, a higher dispersal ability helps the population take advantage of the more suitable parts of habitat that becomes available. But when the suitable range contracts, additional dispersal is disadvantage. This disadvantage is especially obvious when the seasonal variation is large, and the disadvantage of dispersal during range contraction overcompensates its advantage during range expansion.

3 Environment with random seasonal and annual fluctuations

In this section, we consider a stochastic setting of the model

$$\begin{aligned} n_{t+1}(x) = F_t[n_t](y) = \int _{\varOmega } k(x,y) Q_t(y) f[n_t(y)] dy, \end{aligned}$$

(68)

where the habitat suitability function $Q_t(y)$ is randomly chosen at each time step t, and $\varOmega$ is a compact subset of $\mathbb {R}$. We use this model to describe the population dynamics of a species residing in a habitat whose size fluctuates randomly. We first apply Hardin et al.’s results (1990) about a persistence metric, and then consider a two-season environment with both seasonal and annual fluctuations.

3.1 Persistence metric

Let us first rewrite Eq. (68) as

$$\begin{aligned} n_{t+1}(x) = F_{\alpha _t}[n_t](y)= & {} \int _{\varOmega } k(x,y) Q(y; \alpha _t) f[n_t(y)] dy\nonumber \\= & {} \int _{\varOmega } k(x,y) Q_{\alpha _t}(y) f[n_t(y)] dy, \end{aligned}$$

(69)

where $\{\alpha _t\}, t = 0,1,\ldots ,$ is a sequence of independent identically distributed random numbers prescribing the environmental condition. Specifically, $\alpha _t$ is a parameter in the habitat suitability function $Q_{\alpha _t}(y)$ that is a measure of the habitat size. Since $\varOmega$ is compact, Hardin et al.’s results (1990) for integral operators apply. We sum up the relevant results in the following theorem.

Theorem 4

(Theorems 4.1, 4.2, Hardin et al. 1990) Assume that for each t, the habitat suitability function $Q_{\alpha _t}$, the dispersal kernel k, and the growth function f satisfy conditions (Q1)−(Q4), (K1)−(K4), and (F1)−(F6). Then the limit

$$\begin{aligned} r = \lim _{t \rightarrow \infty } || K_{\alpha _t} \circ \cdots \circ K_{\alpha _1} ||^{1/t} \end{aligned}$$

(70)

exists, where $K_{\alpha _t}$ is the Fréchet derivative $F_{\alpha _t}^{\prime }(0)$ of $F_{\alpha _t}$ at 0. In addition, assume $Q_{\alpha _t}$ satisfies

• (Q5) $\exists \, a, b > 0$, so that $\forall \, y \in \varOmega$, $a \le Q_{\alpha _t}(y) \le b$ almost surely.

Let $n_0(x)$ be a nonzero function with probability one, and let the population density $n_t(x)$ describe the tth iteration of the dynamical system

$$\begin{aligned} n_{t+1}(x) = F_{\alpha _t}[n_t](x). \end{aligned}$$

(71)

Then $n_t(x)$ converges in distribution to a unique stationary distribution $\mu ^*$. Furthermore, the following are true.

• (1) If $r >1$, then $\mu ^*(\{0\}) = 0$, and $\lim _{\epsilon \rightarrow 0} \sup _t \mathrm {P} \{\max _{x \in \varOmega } n_t(x) < \epsilon \} = 0$. That is, the population persists almost surely.

• (2) If $r<1$, then $\mu ^*(\{0\}) = 1$ and $\lim _{t \rightarrow \infty } (\max _{x \in \varOmega } n_t(x)) = 0$ almost surely. That is, the population goes extinct almost surely.

Proof

See “Appendix 3”. $\square$

Jacobsen et al. (2015) have found an alternative metric,

$$\begin{aligned} \lambda = \lim _{t\rightarrow \infty } \left( \int _{\varOmega } n_t(x)\,dx \right) ^{1/t}, \end{aligned}$$

(72)

that is equal to r. This alternative metric is easier to compute than r in numerical computations. We therefore use the alternative metric (72) to approximate r in the numerical computation.

Fig. 7

The persistence metric $\lambda$ is plotted vs. the mean seasonal fluctuation $\epsilon$ for a two-season environment with seasonal fluctuations. The habitat sizes are prescribed by Eq. (73), where the seasonal fluctuation is chosen from a uniform distribution with mean $\epsilon$ and variance $\xi$. In this figure, the variances of the seasonal fluctuation are $\xi =$ 0, 0.75, and 3. The habitat suitability function is (5) and the dispersal kernel is the Gaussian kernel (8). The other parameters are $f^{\prime }(0) = 2.5$, mean dispersal distance = 2, annual total habitat size $\beta = 8$. When computing $\lambda$, the integral domain $\varOmega = [- 40,40]$ is discretized with $2^{16}$ grid points

3.2 Two-season environment with seasonal fluctuations

We now reconsider the two-season environment in Sect. 2. We assume that the annual total habitat size is the same, and the rainy season has a larger habitat size than the dry season. Thus the habitat sizes for the tth year are

$$\begin{aligned} \alpha _{t,rainy} = \beta /2 + \epsilon _t \,\,\, \text {and} \,\,\, \alpha _{t,dry} = \beta /2 - \epsilon _t, \end{aligned}$$

(73)

where $\beta$ is the annual total habitat size, and $\epsilon _t$ is the seasonal fluctuation. In contrast to a fixed seasonal variation in Sect. 2, $\epsilon _t$ is now a random variable following a uniform distribution. We assume the mean of $\epsilon _t$ is $E[\epsilon _t] = \epsilon$, and the variance is $Var[\epsilon _t] = \xi$. We assume that $\varOmega$ is a bounded interval $[-R, R]$. Then assumption (Q5) is met if the habitat suitability function is (5). In Fig. 7, we illustrate the relation between the persistence metric $\lambda$ and the mean fluctuation $\epsilon$ for different values of the variance $\xi$, when the habitat suitability function is (5), and the dispersal kernel is the Gaussian kernel (8). When $\xi = 0$, the model coincides with the deterministic case, and we see that $\lambda$ decreases as the mean seasonal fluctuation increases. When $\xi >0$, we see that $\lambda$ also tends to decrease as the mean seasonal fluctuation increases. Furthermore, when the variance $\xi$ is larger, $\lambda$ tends to be smaller. Thus the seasonal fluctuations in habitat size seem to have a negative impact on population persistence. This is consistent with what we found in the deterministic case (Sect. 2).

3.3 Two-season environment with seasonal and annual fluctuations

Besides seasonal fluctuations, habitat sizes may also fluctuate on an annual time scale. In this section, we consider random fluctuations in the annual total habitat size in addition to the seasonal fluctuations in the previous section. Thus the habitat sizes for the tth year are now

$$\begin{aligned} \alpha _{t,rainy} = \beta _t/2 + \epsilon _t \,\,\, \text {and} \,\,\, \alpha _{t,dry} = \beta _t/2 - \epsilon _t, \end{aligned}$$

(74)

where $\epsilon _t$ is the random seasonal fluctuation considered in the previous section, and the annual total habitat size $\beta _t$ is also a random variable following a uniform distribution with mean $E[\beta _t] = \beta$. The annual fluctuation is $\eta _t = \beta _t-\beta$. We assume the maximum annual fluctuation is $\eta$, so $\eta _t$ is a random variable uniformly distributed in $[-\eta ,\eta ]$. In addition, we assume $\varOmega$ is a bounded interval $[-R, R]$.

Fig. 8

The persistence metric $\lambda$ is plotted vs. the maximum annual fluctuations $\eta$ for a two-season environment with seasonal and annual fluctuations. The habitat sizes are prescribed by Eq. (74), where the seasonal fluctuation is chosen from a uniform distribution with mean $\epsilon$ and variance $\xi$, and the annual fluctuation is chosen from a uniform distribution with mean $\beta$ and variance $\eta$. In this figure, the mean seasonal fluctuations are $\epsilon =$ 3.75, 4, and 4.25. The habitat suitability function is (5) and the dispersal kernel is the Gaussian kernel (8). The other parameters are $f^{\prime }(0) = 2.5$, mean dispersal distance = 2, annual total habitat size $\beta = 8$. When computing $\lambda$, the integral domain $\varOmega = [-40,40]$ is discretized with $2^{16}$ grid points

In Fig. 8, we illustrate the relation between the persistence metric $\lambda$ and the maximal annual fluctuation $\eta$ for different values of the mean seasonal fluctuation $\epsilon$, when the habitat suitability function is (5) and the dispersal kernel is the Gaussian kernel (8). We see that $\lambda$ tends to decrease as the maximal annual fluctuation $\eta$ increases. That is, when the mean seasonal fluctuation is fixed, annual fluctuation in habitat size seems to have a negative impact on population persistence. Furthermore, when the mean seasonal fluctuation $\epsilon$ is larger, but the maximal annual fluctuation is the same, $\lambda$ tends to be smaller. Therefore, when fluctuations in either or both time scales increase, population persistence is negatively affected.

We also notice in Fig. 8 that when the maximum annual fluctuation increases, but the mean seasonal fluctuation decreases, the persistence metric can become either smaller or larger. For example, when the maximum annual fluctuation $\eta = 3.25$ and the mean seasonal fluctuation $\epsilon = 4.25$, the persistence metric $\lambda < 1$; but when the maximum annual fluctuation $\eta = 3.75$ and the mean seasonal fluctuation $\epsilon = 3.75$, the persistence metric $\lambda > 1$ (Fig. 8). Therefore, in a case where the fluctuations of habitat size are projected to increase in one time scale but decrease in another, conclusions about their effects on population persistence need to be drawn carefully.

4 Discussion

Fluctuations in habitat size are a regular occurrence in environments such as wetland systems. Changes in water availability often drive oscillations between wet-season and dry-season conditions. For example, impermanent water bodies, including ephemeral ponds and ’Delaware Bays,’ routinely vary in depth and surface area as a result of seasonal flooding and drought (Ripley and Simovich 2009; Deil 2005). On multi-year timescales, river flow reworks the size, composition, and spatial position of riverine sandbars, gravel beds, and deltaic features (Parker et al. 2011; Nelson et al. 2013). On still longer timescales, even more persistent geographic features such as offshore barrier islands are highly dynamic in location and size (Nebel et al. 2011).

Such spatial dynamics of the environment may be a driving force for the population dynamics of individual species, as they disperse to take advantage of the expanded habitat, taking serious risks associated with dispersal (Clobert et al. 2012). On multi-species level, these spatial dynamics may also be a support of biodiversity. For example, in the Florida Everglades, the expansion and contraction of water bodies cause small fish to become trapped in drying pools as the water level recedes during the dry season. As deadly as the trapping is for these fish species, such trapping provide a crucial mechanism to support the population of wading birds in the Everglades, who feast on the otherwise hard-to-detect small fishes (Bakun 2006). Understanding how the persistence of a single population, such as a fish population, depend on the interplay between its dispersal and habitat size fluctuations, therefore, is an important step towards understanding more complex dynamics across trophic levels.

Here we have explored the persistence criteria for a species inhabiting a habitat whose size changes periodically in time. As a result, we extended the critical habitat size concept to a new threshold size concept, lower minimal limit size, for the scenario of varying habitat sizes. The critical habitat size is a threshold size for a habitat with constant size to support a persistent population. When the habitat size is temporally varying, the critical habitat size concept does not directly apply. For example, requiring an average of the temporally varying habitat sizes to meet a threshold size may not work, because the same average size may result in different population dynamics (Fig. 2a). What we found instead is that, while there still exists a threshold habitat size to support a persistent population, this threshold size in the periodic system can be smaller than the critical habitat size (Fig. 3). This lower threshold is possible because dispersal allows the resident population to exploit the increased habitat that occurs when the habitat is large, compensating for losses accrued when the habitat shrinks. However, there are limits to this beneficial effect, and the threshold size approaches a constant in the two-season scenario (rather than declining to zero; Fig. 3) as the habitat size during the enlarged phase of its cycle becomes huge. We refer to this constant as the lower minimal limit size. In the context of wetland systems, the existence of a lower minimal limit size suggests that there are threshold drought levels. If water levels repeatedly drop below a certain threshold, floods following the droughts cannot provide enough relief to sustain the population.

We have also demonstrated that time scale matters when we consider fluctuations in habitat size. With the stochastic system in Sect. 3, we considered habitats with both seasonal and annual size fluctuations. While larger seasonal fluctuations or larger annual fluctuations alone affect population persistence negatively, the combined effects of larger fluctuations in one time scale and smaller fluctuations in another may be either positive or negative on the population (Fig. 8).

An emerging theme from this work is that increased dispersal can be quite disadvantageous when it traps individuals beyond the boundary of the habitat when the habitat is small. This kind of shrinkage-induced mortality is a recurring feature of desert streams (Moyle 2002; Kerezsy et al. 2013) but contrasts starkly with the fate of pond-dwelling fish and amphibians in more temperate habitats. In those cases, even though ponds may shrink and grow depending on the season, the patch edge is an impermeable boundary whose contraction serves to concentrate individuals within the patch. In those cases, mortality may occur because of increased crowding within the patch, but losses of residents across the patch edge do not occur unless there is a special circumstance (e.g., metamorphosis of amphibian larvae) that allows for emigration.

There are open questions in this project. First of all, we only examined the effects of habitat size fluctuations on population persistence. Whether the effects are similar on total population size is an open question and requires development of more mathematical tools. Also, our model is for an single-species, unstructured population, and extending the model to multi-species populations or a stage-structured population will allow us to studying interesting questions. The combination of structured populations, multiple species, and the total population size perspective may reveal fascinating effects of habitat size fluctuations (Henson and Cushing 1997; Costantino et al. 1998). In the mean time, preliminary research extending the model to a two-dimensional habitat suggests that fluctuations in habitat size may provide center-dwelling species with an advantage over edge-dwelling species. Therefore, increased fluctuations in habitat size may cause changes in community composition in a wetland system.

Appendices

Appendix 1: Proof of complete continuity and the dichotomy result

1.1 Proof of Lemma 1

Proof

From the assumptions (K2), (K3), and (Q3), we have

$$\begin{aligned} \sup \limits _{x}\int _{-\infty }^{\infty }|k(x-y) Q(y)| \,dy \le \sup \limits _{x,y} \, k(x-y) \cdot \int _{-\infty }^{\infty }Q(y) \, dy < \infty . \end{aligned}$$

(75)

Therefore property (KQ1) is satisfied by $\tilde{k}(x,y)$.

Next we will show that the convolution

$$\begin{aligned} h(x) = \int _{-\infty }^{\infty }|k(x-y) Q(y)| \,dy \end{aligned}$$

(76)

is integrable over $(-\infty , \infty )$. To see this, notice that

$$\begin{aligned} \int _{-\infty }^{\infty }h(x) \, dx= & {} \int _{-\infty }^{\infty }dx \int _{-\infty }^{\infty }|k(x-y) Q(y)|\,dy\nonumber \\= & {} \int _{-\infty }^{\infty }dx \int _{-\infty }^{\infty }k(x-y) Q(y) \,dy\nonumber \\= & {} \int _{-\infty }^{\infty }dy \, \int _{-\infty }^{\infty }k(x-y) Q(y) \, dx\nonumber \\= & {} \int _{-\infty }^{\infty }Q(y) dy \, \int _{-\infty }^{\infty }k(x-y) \, dx\nonumber \\= & {} \int _{-\infty }^{\infty }Q(y) \, dy \cdot 1\nonumber \\< & {} \infty . \end{aligned}$$

(77)

Therefore

$$\begin{aligned} h(x) \rightarrow 0 \,\,\,\text {as} \,\,x \rightarrow \infty , \end{aligned}$$

(78)

and property (KQ2) is satisfied by $\tilde{k}(x,y)$.

Next, notice that $\sup \limits _{x} Q(x) \le 1$ by the definition of the habitat suitability function. Thus

$$\begin{aligned}&\sup \limits _{|x^{\prime }-x|\le h} \int _{-\infty }^{\infty }\left| k(x^{\prime }-y)Q(y) - k(x-y)Q(y) \right| \, dy\nonumber \\&\quad \le \sup \limits _{y}Q(y) \cdot \sup \limits _{|x^{\prime }-x|\le h} \int _{-\infty }^{\infty }\left| k(x^{\prime }-y) - k(x-y) \right| \, dy\nonumber \\&\quad \le \, \sup \limits _{|\delta | \le h} \int _{-\infty }^{\infty } \left| k(s+\delta ) - k(s)\right| ds\nonumber \\&\quad \rightarrow 0, \qquad \text {as} \,\, h \rightarrow 0, \end{aligned}$$

(79)

where the last step was proved by Bochner and Chandrasekharan (1949, page 22, Theorem 10). Therefore, the integral kernel $\tilde{k}(x,y)$ also satisfies assumption (KQ3). $\square$

1.2 Proof of Lemma 2

Proof

We will first deduce compactness of A by extending the arguments for linear operators by Atkinson (1969) (also see Sloan 1981; Anselone and Sloan 1985) to include certain nonlinear operators. Atkinson (1969) provided a set of conditions to ensure that a linear integral operator K which maps $M_{+}$, the space of bounded measurable functions on $[0, \infty )$, to $C_{+}^{0}$, the space of continuous functions on $[0, \infty )$ which vanish at $\infty$, is compact. These conditions make sure the image of the unit ball $||u||\le 1$ under K is uniformly bounded, equicontinuous, and equiconvergent at $\infty$. This image of the unit ball is therefore compact because of an isometric isomorphism between a subset of C[0, 1] and $C^{+}[0, \infty )$, and the Arzelà–Ascoli theorem. Although this argument was originally derived for integral operators of the form

$$\begin{aligned} K[u](x) = \int _0^{\infty } k(x,y) u(y) \, dy \end{aligned}$$

(80)

on $M_{+}$, an analogous argument applies to operators on $BC[0, \infty )$ (Anselone and Sloan 1985) and $BC(-\infty ,\infty )$ as well (Chandler-Wilde et al. 2000; Sloan 1981). We now show that the same set of conditions also imply compactness of certain nonlinear operators.

Suppose a nonlinear operator A is defined by (16). Because of assumptions (F3) and (KQ1), for any u in the unit ball $||u|| \le 1$,

$$\begin{aligned} \sup \limits _{x}|A[u]| \le f^{\prime }(0) \sup \limits _{x} \int _{-\infty }^{\infty }|\tilde{k}(x,y)|\,dy < \infty . \end{aligned}$$

(81)

Thus the image of the unit ball $||u|| \le 1$ is uniformly bounded. Next, for any $x, x^{\prime } \in \mathbb {R}$,

$$\begin{aligned} \begin{array}{lll} \left| A[u](x^{'}) - A[u](x) \right| &{} = &{} \left| \displaystyle \int _{-\infty }^{\infty } [\tilde{k}(x^{'},y) - \tilde{k}(x,y)] \, f[u(y)] \, dy \right| \\ &{} \le &{} f^{\prime }(0) \left| \displaystyle \int _{-\infty }^{\infty } [\tilde{k}(x^{'},y) - \tilde{k}(x,y)] \, u(y)\, dy \right| \\ &{} \le &{} f^{\prime }(0) ||u|| \cdot \sup \limits _{x^{\prime },x} \displaystyle \int _{-\infty }^{\infty } |\tilde{k}(x^{'},y) - \tilde{k}(x,y) |\,dy. \end{array} \end{aligned}$$

(82)

Therefore, assumption (KQ3) implies that the image of $||u|| \le 1$ is equicontinuous at every point. Finally, because

$$\begin{aligned} \left| A[u](x) \right| \le f^{\prime }(0) ||u|| \int _{-\infty }^{\infty } \left| \tilde{k}(x,y) \right| dy , \end{aligned}$$

(83)

assumption (KQ2) implies that the image of $||u|| \le 1$ is equiconvergent. Therefore, as discussed in the previous paragraph, A is compact.

We then show that A is continuous. For all $n_1(x), n_2(x) \in BC^{+}(\varOmega )$,

$$\begin{aligned} ||A[n_1] - A[n_2]||\le & {} \sup \limits _{x} \int _{-\infty }^{\infty } |\tilde{k}(x,y)| \cdot \left| f[n_1(y)] - f[n_2(y)] \right| \,dy \end{aligned}$$

(84)

$$\begin{aligned}\le & {} \sup \limits _{n} |f^{\prime }(n)| \cdot \sup \limits _{x} \int _{-\infty }^{\infty } | \tilde{k}(x,y)| \cdot \left| n_1(y) - n_2(y) \right| \,dy \end{aligned}$$

(85)

$$\begin{aligned}\le & {} \sup \limits _{n} |f^{\prime }(n)| \cdot ||n_1 - n_2|| \cdot \sup \limits _{x} \int _{-\infty }^{\infty } |\tilde{k}(x,y)| \,dy. \end{aligned}$$

(86)

Therefore, assumptions (F1) and (KQ1) imply that A is continuous. Because A is also compact, it is completely continuous. $\square$

1.3 Proof of Lemma 3

Proof

Because each $F_t$ and $K_t$ are bounded, and

$$\begin{aligned} \sup \limits _{x} \int _{-\infty }^{\infty }k(x-y) Q_t(y) dy < \infty \end{aligned}$$

(87)

for each t, which was argued in the proof of Lemma 1, it is straightforward to deduce that $F_t^{\prime }(0)$ defined in (17) is the Fréchet derivative of $F_t$ at 0, and that $K^{(i)}$ is the Fréchet derivative of $F^{(i)}$ at 0. We therefore omit the details here. Because $F_t$ is completely continuous, its Fréchet derivative is also completely continuous, and so is the composition $K^{(i)}$. Meanwhile, because each $Q_t(y)$ is defined to be nonnegative, by assumptions (K2) and (Q2), each $F_t^{\prime }(0)$ is a positive operator. Therefore $K^{(i)}$ is also a positive operator.

We will now show that the spectral radius of $K^{(i)}$ is a positive eigenvalue of $K^{(i)}$. If $\varOmega$ is bounded, it is straightforward to show that each $F_t^{\prime }(0)$ is strongly positive, and therefore $K^{(i)}$ is strongly positive. The compactness and strong positivity of $K^{(i)}$ ensure that $K^{(i)}$ has a simple positive dominant eigenvalue (Krein and Rutman 1948, Theorem 6.3). This dominant eigenvalue of $K^{(i)}$ is equal to the spectral radius of $K^{(i)}$, because the spectrum of a compact linear operator contains only eigenvalues and the number 0 (Hutson and Pym 1980). Now suppose $\varOmega$ is unbounded. Let [a, b] be a bounded subset of $\varOmega$, and let $I_t$ be the operator defined as

$$\begin{aligned} I_t[u](x) = f^{\prime }(0) \int _a^b k(x-y) Q_t(y) u(y)\, dy. \end{aligned}$$

(88)

Then $I_t$ is an integral operator on $BC^{+}[a,b]$ with a nonnegative kernel, and therefore $r_{\sigma }(I_t) >0$ is a simple eigenvalue of $I_t$. Moreover, if we consider $I_t$ as an integral operator on $BC^{+}(\varOmega )$, it is still true that $r_{\sigma }(I_t) >0$ is a simple eigenvalue of $I_t$. Notice that for each t, $K_t \ge I_t$. Let $I^{(i)} = I_{i+p-1} \circ \cdots \circ I_{i+1} \circ I_i$, then $K^{(i)} \ge I^{(i)}$. Therefore, by the comparison theorem of positive operators (Marek 1970, Theorem 4.2), $r_{\sigma }(K^{(i)}) \ge r_{\sigma }(I^{(i)}) > 0$. Since $K^{(i)}$ is completely continuous, $\lambda _i = r_{\sigma }(K^{(i)})$ is a positive eigenvalue of $K^{(i)}$ with a nonnegative eigenvector (Krein and Rutman 1948, Theorem 6.1). $\square$

1.4 Proof of Lemma 4

Proof

By Lemma 3, the spectral radius $r_{\sigma }(K^{(i)}) = \lambda _i$ of each $K^{(i)}$ is a positive eigenvalue of $K^{(i)}$, and has a nonnegative eigenvector $u_i(x) \in BC^{+}(\varOmega )$ so that

$$\begin{aligned} K^{(i)} [u_i](x) = \lambda _i u_i(x), \end{aligned}$$

(89)

and $\lambda _i$ is not smaller than the modulus of any other eigenvalues of $K^{(i)}$.

We now show that $\lambda _i$ is also an eigenvalue of $K^{(i+1)}$. Since each $K_t$ maps the cone $BC^{+}(\varOmega )$ to itself, $K_i[u_i](x) \in BC^{+}(\varOmega )$. Applying operator $K_i$ on both sides of Eq. (89), we have

$$\begin{aligned} K^{(i+1)} \left\{ K_i [u_i](x) \right\} = \lambda _i K_i [u_i](x) . \end{aligned}$$

(90)

Therefore $\lambda _i$ is also an eigenvalue of $K^{(i+1)}$. By Lemma 3, the spectral radius $r_{\sigma }(K^{(i+1)})$ is a positive eigenvalue of $K^{(i+1)}$, and is no less than the modulus of any other eigenvalue of $K^{(i+1)}$. Therefore

$$\begin{aligned} r_{\sigma }(K^{(i)}) = \lambda _i \le r_{\sigma }(K^{(i+1)}). \end{aligned}$$

(91)

Applying the same argument to $K^{(i+1)}$ and $K^{(i+2)}$, we have

$$\begin{aligned} r_{\sigma }(K^{(i+1)}) \le r_{\sigma }(K^{(i+2)}). \end{aligned}$$

(92)

By induction,

$$\begin{aligned} r_{\sigma }(K^{(i+p-1)}) \le r_{\sigma }(K^{(i+p)}). \end{aligned}$$

(93)

Since $K^{(i+p)} = K^{(i)}$,

$$\begin{aligned} r_{\sigma }(K^{(i)}) \le r_{\sigma }(K^{(i+1)}) \le \cdots \le r_{\sigma }(K^{(i+p)}) = r_{\sigma }(K^{(i)}). \end{aligned}$$

(94)

Therefore $\lambda _i = \lambda , \forall i$. $\square$

1.5 Proof of Theorem 1

Proof

For each integer i, $i = 1, 2, \ldots , p$, the composition $F^{(i)}$ in Eq. (19) defines a time-independent dynamical system,

$$\begin{aligned} n_{i+p}(x) = F^{(i)} [n_{i}](x), \end{aligned}$$

(95)

that maps $n_{i}(x) \in BC^{+}(\varOmega _i)$ to $n_{i+p}(x) \in BC^{+}(\varOmega _i)$. The results of Theorem 1 can be verified by applying Theorem 2.3.4 of Zhao (2003) to each operator $F^{(i)}$ and their Fréchet derivatives at 0, $K^{(i)}$. In order to do this, we need to show that each operator $F^{(i)}$, which maps the positive cone $BC^{+}(\varOmega _i)$ to itself, satisfies the following assumptions of Theorem 2.3.4 (Zhao 2003):

• (1) $F^{(i)}$ is monotone (Zhao 2003, Definition 2.1.1);

• (2) $F^{(i)}$ is strongly subhomogeneous (Zhao 2003, Definition 2.3.1);

• (3) $F^{(i)}$ is asymptotically smooth (Zhao 2003, Definition 1.1.2);

• (4) every positive orbit of $F^{(i)}$ is bounded;

• (5) let $z_0(x) \equiv 0$ be the zero function in $BC^{+}(\varOmega _i)$, then $F^{(i)}[z_0](x) = z_0(x)$;

• (6) the Fréchet derivative of $F^{(i)}$ at 0, $K^{(i)}$, is completely continuous;

• (7) the Fréchet derivative of $F^{(i)}$ at 0, $K^{(i)}$, is strongly positive. That is, for any nonzero element $n(x) \in BC^{+}(\varOmega _i) \backslash \{0\}$, $K^{(i)} [n] \in \text {int}(BC^{+}(\varOmega _i))$.

We now verify assumptions (1)−(7).

• (1) For each t, the operator $F_t: BC^{+}(\varOmega ) \rightarrow BC^{+}(\varOmega )$ is monotone. To see this, let $n_1(x)$, $n_2(x)$ $\in BC^{+}(\varOmega )$ be any two elements of the cone $BC^{+}(\varOmega )$, and let $n_1(x) \ge n_2(x)$. We can see that

  $$\begin{aligned} \begin{array}{lll} F_t[n_1](x) &{}=&{} \displaystyle \int _{-\infty }^{\infty } k(x-y) Q_t(y) \, f[n_1(y)]\, dy \\ &{}\ge &{} \displaystyle \int _{-\infty }^{\infty } k(x-y) Q_t(y) \, f[n_2(y)]\, dy\\ &{}=&{} F_t[n_2](x) \end{array} \end{aligned}$$

  (96)

  because $k(x-y) Q_t(y) \ge 0$ and f satisfies (F5). Therefore, by induction, the composition $F^{(i)}$ is a monotone operator on the cone $BC^{+}(\varOmega )$. Since $\varOmega _i \subset \varOmega$, $F^{(i)}$ is a monotone operator on the cone $BC^{+}(\varOmega _i)$.

• (2) For each t, the operator $F_t$ is also strongly subhomogeneous. To see this, let n(x) be any element in the interior of the cone $BC^{+}(\varOmega )$. That is, $\forall \, x \in \varOmega , n(x) > 0$. Because of assumption (K2) and the definition of the suitability function $Q_t$, $k(x-y) Q_t(y) > 0$ for $y \in \varOmega _t$. Therefore, $\forall \, 0< \alpha < 1$, $\forall \, x \in \varOmega$,

  $$\begin{aligned} \begin{array}{lll} F_t[\alpha n] - \alpha F_t[n] &{}=&{}\displaystyle \int _{-\infty }^{\infty } k(x-y) Q_t(y) \{f[\alpha n(y)] - \alpha f[n(y)]\}\, dy\\[1em] &{}=&{}\displaystyle \int _{\varOmega _t} k(x-y) Q_t(y) \{f[\alpha n(y)] - \alpha f[n(y)]\}\, dy > 0 \end{array} \end{aligned}$$

  (97)

  by assumptions (F6), (Q1), and (Q2). Thus $F_t[\alpha n] - \alpha F_t[n]$ is an element in the interior of $BC^{+}(\varOmega )$. Therefore $F_t$ is strongly subhomogeneous. By induction, it is clear that the composition $F^{(i)}$ is a strongly subhomogeneous operator on the cone $BC^{+}(\varOmega )$. Therefore $F^{(i)}$ is a strongly subhomogeneous operator on the cone $BC^{+}(\varOmega _i)$.

• (3) By Corollary 1, $F^{(i)}$ is completely continuous. Therefore $F^{(i)}$ is asymptotically smooth (Zhao 2003, page 3).

• (4) For each t, the operator $F_t$ is uniformly bounded. In fact, since $f(n) \le M$ for any n by assumption (F4),

  $$\begin{aligned} \begin{array}{lll} || F_t[u] || &{}=&{} \sup \limits _{x \in \mathbb {R}} \left| \displaystyle \int _{-\infty }^{\infty } k(x-y) Q_t(y) f[u(y)]\,dy \right| \\ &{}\le &{} M \cdot \sup \limits _{x \in \mathbb {R}} \displaystyle \int _{-\infty }^{\infty } k(x-y) Q_t(y)\,dy. \end{array} \end{aligned}$$

  (98)

  Let

  $$\begin{aligned} M^{\prime } = \sup _{x \in \mathbb {R}} \int _{-\infty }^{\infty } k(x-y) Q_t(y)\,dy, \end{aligned}$$

  (99)

  then $M^{\prime } < \infty$ because of Lemma 1 and (KQ1). Therefore $F_t$ is uniformly bounded. Clearly, the composition $F^{(i)}$ is also uniformly bounded. Therefore, any positive orbit of $F^{(i)}$ is bounded.

• (5) Because of assumption (F2), $F_t[z_0(x)] \equiv 0$ for all t. Therefore the composition $F^{(i)}$ maps the zero function to the zero function.

• (6) By Corollary 1, $K^{(i)}$ is completely continuous.

• (7) We will first show that for each i, $K_i$ maps nonzero elements of $BC^{+}(\varOmega _i)$ to positive elements of $BC^{+}(\mathbb {R})$. To see this, let n(x) be any nonzero element of $BC^{+}(\varOmega _i)$. As argued in the verification of assumption (2), $k(x-y) Q_i(y) > 0$ for $y \in \varOmega _i$. Therefore, by assumptions (Q1) and (Q2), $\forall x \in \mathbb {R}$,

  $$\begin{aligned} \begin{array}{lll} K_i [n](x) &{}=&{}\displaystyle \int _{-\infty }^{\infty } k(x-y) Q_i(y) f^{\prime }(0) \, n(y)\, dy \\ &{}=&{} \displaystyle \int _{\varOmega _i} k(x-y) Q_i(y) f^{\prime }(0) \, n(y)\, dy > 0. \end{array} \end{aligned}$$

  (100)

  Therefore $K_i[n] \in BC^{+}(\mathbb {R})$, and $\forall x$,

  $$\begin{aligned} K_{i+1} \circ K_i [n] (x) >0. \end{aligned}$$

  (101)

  By induction, $K^{(i)}[n](x) > 0$ for any x. Since $\varOmega$ is compact, $\varOmega _i$ is bounded, and the interior of the cone $BC^{+}(\varOmega _i)$ contains positive elements of the cone. Therefore the composition $K^{(i)}$ is strongly positive.

By Theorem 2.3.4 of Zhao (2003), dynamical system (95) has the following threshold dynamics:

• (a) If $\lambda _i = r_{\sigma }(K^{(i)}) > 1$, then there exists a unique fixed point $n^{*}(x)$ of (95) in the interior of the cone $BC^{+}(\varOmega _i)$, such that every positive orbit

  $$\begin{aligned} \gamma ^{+}(n) = \{ [F^{(i)}]^t (n) : t \ge 0\} \end{aligned}$$

  (102)

  in $BC^{+}(\varOmega _i) \backslash \{0\}$ converges to $n^{*}(x)$.

• (b) If $\lambda _i = r_{\sigma }(K^{(i)}) \le 1$, then every positive orbit in $BC^{+}(\varOmega _i)$ converges to 0.

This threshold dynamics exists for every $F^{(i)}$ and $K^{(i)}$. In the mean time, from Lemma 4, $\lambda _i = \lambda$ for each i, and it is clear from Lemma 3 that $\lambda$ is the largest positive eigenvalue of K. Combining the threshold dynamics for all i, $i = 1, 2, \ldots , p$ allows us to deduce that

• (a) when $\lambda > 1$, the p-periodic dynamical system (12) has a unique positive periodic trajectory $n_t^*(x)$ $\in BC^{+}(\varOmega )$ of maximum period p. For any initial population density $n_0(x) \in BC^{+}(\cap _{i=1}^{p} \varOmega _i)$, the solution $n_t(x)$ of the p-periodic dynamical system (12) converges to this periodic trajectory;

• (b) when $\lambda \le 1$, for any initial population density $n_0(x) \in BC^{+}(\varOmega )$, the solution $n_t(x)$ of the p-periodic dynamical system (12) converges to the trivial fixed point.

$\square$

1.6 Proof of Lemma 5

Proof

Let

$$\begin{aligned} M_1 = \sup _{x, y \in \mathbb {R}} k(x-y), \end{aligned}$$

(103)

then $M_1 < \infty$ because of assumption (K3).

Because Q(y) is integrable, $\forall \, \epsilon > 0$, $\exists \, N > 0$, so that $\forall \, n > N$,

$$\begin{aligned} \int _{\mathbb {R}\backslash [a_n,b_n]} Q(y) \, dy < \dfrac{\epsilon }{f^{\prime }(0) M_1}. \end{aligned}$$

(104)

Therefore, $\forall \, n > N$, $\forall \, u(x) \in BC^{+}(\mathbb {R})$,

$$\begin{aligned} \begin{array}{lll} || F^{\prime }(0)[u] - F_n^{\prime }(0)[u] || &{}=&{} \sup _{x} \left| F^{\prime }(0)[u](x) - F_n^{\prime }(0)[u](x) \right| \\ &{} = &{} f^{\prime }(0) \displaystyle \int _{\mathbb {R}\backslash [a_n,b_n]} k(x-y) Q(y) u(y) \, dy \\ &{}\le &{} f^{\prime }(0) M_1\cdot ||u|| \cdot \displaystyle \int _{\mathbb {R}\backslash [a_n,b_n]} Q(y) \, dy \\ &{}<&{} \epsilon ||u||. \end{array} \end{aligned}$$

(105)

Thus $||F_n^{\prime }(0) - F^{\prime }(0)|| < \epsilon$ for $\forall \, n > N$, and $F_n^{\prime }(0) \rightarrow F^{\prime }(0)$ in norm. Therefore $\lambda _n \rightarrow \lambda$ as $n\rightarrow \infty$ (Chatelin and Lemordant 1978, page 259). $\square$

1.7 Proof of Theorem 2

Proof

From Lemma 3, it is clear that $\lambda$ is the largest positive eigenvalue of K. We now prove statements (1) and (2).

(1) Each linear operator $K_t$ in expression (27) can be approximated by a sequence of operators $K_{t_n}$,

$$\begin{aligned} K_{t_n}[u](x) = f^{\prime }(0)\int _{a_n}^{b_n} k(x-y) Q_t(y) u(y)\,dy, \end{aligned}$$

(106)

with the sequences $\{a_n\}$ and $\{b_n\}$ described in Lemma 5. In the mean time, the corresponding nonlinear operators $F_{t_n}$,

$$\begin{aligned} F_{t_n}[u](x) = \int _{a_n}^{b_n} k(x-y) Q_t(y) f[u(y)]\,dy, \end{aligned}$$

(107)

are approximations of $F_t$, $t = 1\ldots p$.

By Lemma 5, for each t, $||K_{t_n} - K_t|| \rightarrow 0$ as $n\rightarrow +\infty$. Let $F_n = F_{p_n}\circ \cdots \circ F_{2_n} \circ F_{1_n}$, and $K_{n} = K_{p_n}\circ \cdots \circ K_{2_n} \circ K_{1_n}$. Then it is straightforward to show that for each n, $K_n$ is the Fréchet derivative of $F_n$ at 0. Since $K_{n}$ is the composition of a finite number of operators $K_{t_n}$, and each $K_{t_n}$ converges uniformly to $K_t$ as $n \rightarrow \infty$, it can also be easily shown that $||K_n - K|| \rightarrow 0$ as $n \rightarrow +\infty$. Let the spectral radius of $K_n$ be $\lambda _n$, then by Lemma 5, $\lambda _n \rightarrow \lambda$ as $n \rightarrow +\infty$.

Since $\lambda > 1$, $\exists$ $N_1$ large enough and $\delta$ small enough, such that $\forall \, n \ge N_1$, $\lambda _{n}> \lambda -\delta > 1$. Let $n_0(x)$ be any nonzero element of $BC^{+}(\mathbb {R})$, then we can choose $N_2$ large enough, so that $n_0(x) \cdot \mathbbm {1}_{[a_{N_2}, b_{N_2}]}$ is a nonzero element of $BC^+([a_{N_2}, b_{N_2}])$. Let $N = \max \{N_1, N_2\}$, then $\tilde{n}_0(x) = n_0(x) \cdot \mathbbm {1}_{[a_{N}, b_{N}]}$ is a nonzero element of $BC^+([a_{N}, b_{N}])$, and $\lambda _N > 1$.

By Theorem 1, there is a unique nonzero solution $\tilde{n}^*(x)$ $\in BC^{+}(\varOmega )$ to the equation

$$\begin{aligned} \begin{array}{lll} \tilde{n}^*(x) &{}=&{} F_N[\tilde{n}^*](x)\\ &{}=&{} F_{p_N} \circ \cdots \circ F_{2_N} \circ F_{1_N}[\tilde{n}^*](x), \end{array} \end{aligned}$$

(108)

where $\varOmega = [a_N, b_N]$. Since $\varOmega \subset \mathbb {R}$, $\tilde{n}^*(x)$ is also a nonzero element of $BC^{+}(\mathbb {R})$. In addition, because $\tilde{n}_0(x)$ $\in BC^+(\varOmega )$ is nonzero, the series $\{\tilde{n}_{pt}(x), t = 0,1, \ldots \}$ defined by

$$\begin{aligned} \tilde{n}_{pt}(x) = F_N[\tilde{n}_{p(t-1)}](x) \end{aligned}$$

(109)

converges to $\tilde{n}^*(x)$ in $BC^{+}(\varOmega )$. Since $\varOmega$ is compact, this convergence is uniform.

Define the series $\{n_{pt}(x), t = 0,1, \ldots \}$ by

$$\begin{aligned} n_{pt}(x) = F[n_{p(t-1)}](x), \end{aligned}$$

(110)

where operator F is the composition $F = F_p \circ \cdots \circ F_2 \circ F_1$. Operators $F_N$ and F are both monotone operators because of the monotonicity of f assumed in (F5). Therefore

$$\begin{aligned} \tilde{n}_p(x) = F_N[\tilde{n}_0](x) \le F_N[n_0](x)< F[n_0](x) = n_p(x), \end{aligned}$$

(111)

where the first inequality comes from the monotonicity of $F_N$, and the second inequality comes from the fact that $F_N < F$. We can continue to deduce that

$$\begin{aligned} \tilde{n}_{pt}(x) = F_N[\tilde{n}_{p(t-1)}](x)< F[\tilde{n}_{p(t-1)}](x) < F[n_{p(t-1)}](x) = n_{pt}(x), \end{aligned}$$

(112)

where the last inequality comes from the monotonicity of F. Therefore for each t,

$$\begin{aligned} n_{pt}(x) > \tilde{n}_{pt}(x). \end{aligned}$$

(113)

That is, the series $\{n_{pt}(x)\}$ is bounded below by the series $\{\tilde{n}_{pt}(x)\}$. Because $\tilde{n}_{pt}(x)$ converges uniformly to the nonzero function $\tilde{n}^*(x)$ in $BC^{+}(\varOmega )$, $\exists \, T_1$ so that $\forall \, t > T_1$,

$$\begin{aligned} \sup _{x \in \varOmega } |\tilde{n}_{pt}(x)| = \sup _{x \in \varOmega } \tilde{n}_{pt}(x) > ||\tilde{n}^*(x)||/2. \end{aligned}$$

(114)

The inequality (113) therefore implies that $\forall \, t > T_1$,

$$\begin{aligned} ||n_{pt}(x)|| = \sup _{x \in \mathbb {R}} |n_{pt}(x)| \ge \sup _{x \in \varOmega } |\tilde{n}_{pt}(x)| > C_1, \end{aligned}$$

(115)

where $C_1 = ||\tilde{n}^*(x)||/2$.

Notice that each $F_t$ maps nonzero elements of $BC^+(\mathbb {R})$ to nonzero elements of $BC^+(\mathbb {R})$. Therefore

$$\begin{aligned} n_{i}(x) = F_{i-1} \circ \cdots \circ F_{1} [n_0](x), \;\,\, i = 2, 3, \ldots , p \end{aligned}$$

(116)

are all nonzero elements of $BC^+(\mathbb {R})$. Applying the arguments in the above paragraphs to each $K^{(i)}$ and $F^{(i)}$, $i = 2, 3,\ldots , p$, with the initial population density $n_i(x)$, we know that for each i, $\exists \, T_i$ and $C_i >0$, so that $\forall \, t > T_i$, $||n_{pt+i-1}(x)|| > C_i$, where $n_{pt+i-1}(x)$ is the $pt + i$th generation’s population density defined by the dynamical system (12). Let

$$\begin{aligned} T = \max _{i = 1, 2, \ldots , p} (pT_i + i), \end{aligned}$$

(117)

and

$$\begin{aligned} C = \min _{i = 1, 2, \ldots , p} C_i, \end{aligned}$$

(118)

then $C>0$, and $\forall \,t > T$, the solution $n_t(x)$ of the nonlinear dynamical system (12) with nonzero initial condition $n_0(x)$ satisfies

$$\begin{aligned} ||n_t|| > C. \end{aligned}$$

(119)

Therefore, when $\lambda > 1$, the population will persist in the sense that it will not go extinct.

(2) When $\lambda < 1$,

$$\begin{aligned} \lim _{n\rightarrow \infty } ||K^n||^{1/n} < 1. \end{aligned}$$

(120)

Thus $\exists \, N_3$, so that for all $n > N_3$, $||K^n|| < 1$. Therefore, for all nonzero u(x), for all $n > N_3$,

$$\begin{aligned} ||F^n [u] ||< ||K^n[u]|| \le ||K^n || \cdot ||u|| < ||u||. \end{aligned}$$

(121)

Therefore F cannot have a nonzero fixed point $n^*(x)$. Otherwise, $\forall n \in \mathbb {N}$,

$$\begin{aligned} || F^n [n^*] || = ||n^*||, \end{aligned}$$

(122)

contradicting inequality (121). Thus the operator F has only one fixed point, which is the trivial fixed point $n^*(x) \equiv 0$.

We can now apply Theorem 2.2.1 of Zhao (2003) to show that $n_t(x)$ converges to the trivial fixed point. As shown in the proof of Theorem 1, $F_t$ is uniformly bounded for each t. Therefore the composition F is uniformly bounded. Therefore there exists $R > 0$, so that $|| F^n[u] ||\le R$ for any u(x) and $n \in \mathbb {N}$. Therefore the ball $|| u || \le R$ of radius R attracts each point in $BC^+(\mathbb {R})$. Since $|| u || \le R$ is a bounded set in $BC^+(\mathbb {R})$, the operator F is point dissipative (Zhao 2003, Definition 1.1.2). The operator F is also $\alpha$-condensing (Zhao 2003, Definition 1.1.2) because it is compact (Zhao 2003, page 3). Since F is $\alpha$-condensing, point dissipative, uniformly bounded, monotone, and has exactly one fixed point in the cone $BC^+(\mathbb {R})$, Theorem 2.2.1 by Zhao (2003) applies, and we know the trivial fixed point $n^*(x) \equiv 0$ of the dynamical system

$$\begin{aligned} n_{pt}(x) = F[n_{p(t-1)}](x) \end{aligned}$$

(123)

is globally attractive in the sense that $\forall \, n_0(x)$, $n_{pt}(x) \rightarrow n^*(x)$. Applying the above argument for each $F^{(i)}$ and $K^{(i)}$, we know that the solution $n_t(x)$ of the dynamical system (12) converges to the trivial fixed point as $t \rightarrow \infty$. $\square$

Appendix 2: Proof of results for two-season environment

1.1 Proof of Proposition 1

Proof

First, notice that given any $\sigma _0^2$, there is a unique contour curve $\delta _{\sigma _0}$ in the $\sigma _1^2$–$\sigma _2^2$ plane, starting at $(\sigma _0^2, \sigma _0^2) \in \mathbb {R}^2$, along which $\lambda$ is constant. To see this, let $\lambda _0 = \lambda (\sigma _0^2, \sigma _0^2)$, where

$$\begin{aligned} \lambda _0 = \lambda (\sigma _0^2, \sigma _0^2) = [f^{\prime }(0)]^2 \sqrt{1 - \dfrac{2}{1+\dfrac{\sigma _0^2+2D}{2\sqrt{D( \sigma _0^2 + D)}}}} \end{aligned}$$

(124)

according to Eq. (41). Then the equation

$$\begin{aligned} \lambda (\sigma _1^2, \sigma _2^2) = \lambda _0 \end{aligned}$$

(125)

implicitly defines such a contour curve. Solving Eq. (125) for $\sigma _2^2$ in terms of $\sigma _1^2$, we find

$$\begin{aligned} \sigma _2^2 = \delta _{\sigma _0}(\sigma _1^2)= v^* \left( \dfrac{\sigma _1^2+2D}{\sigma _1^2-v^*} \right) , \end{aligned}$$

(126)

where

$$\begin{aligned} v^* = 2D \left[ \dfrac{f^{\prime }(0)^4 + \lambda _0^2}{f^{\prime }(0)^4 - \lambda _0^2} \right] ^2 - 2D. \end{aligned}$$

(127)

It can be easily shown that $\delta _{\sigma _0}(\sigma _1^2)$ is exactly the same curve as $\varGamma ^*(\sigma _1^2)$.

Substituting the variables $v_1 = \sigma _1^2$ and $v_2 = \sigma _2^2$ to simplify the notations, it can also be shown that $v^*_2 = \varGamma ^*(v_1)$ satisfies the ordinary differential equation

$$\begin{aligned} \dfrac{dv^*_2}{dv_1} = - \dfrac{v^*_2(v^*_2+2D)}{v_1(v_1+2D)}. \end{aligned}$$

(128)

To see this, notice first that letting $\sigma _2^2 = v_2^*$, $\sigma _1^2 = v_1$ in Eq. (126) yields

$$\begin{aligned} v_2^* = v^* \left( \dfrac{v_1+2D}{v_1-v^*} \right) . \end{aligned}$$

(129)

We then take the derivative of $v_2^*$ with respect to $v_1$ in Eq. (129), and obtain

$$\begin{aligned} \dfrac{dv_2^*}{dv_1} = - \left( \dfrac{v^*}{v_1-v^*}\right) \left( \dfrac{v^*+ 2D}{v_1-v^*} \right) . \end{aligned}$$

(130)

Solving for $v^*$ from Eq. (129), we find

$$\begin{aligned} v^* = \dfrac{v_1 v_2^*}{v_1 + v_2^* + 2D}. \end{aligned}$$

(131)

Therefore

$$\begin{aligned} \dfrac{v^*}{v_1 - v^*} = \dfrac{v_2^*}{v_1+2D} \end{aligned}$$

(132)

and

$$\begin{aligned} \dfrac{v^* + 2D}{v_1 - v^*} = \dfrac{v_2^* + 2D}{v_1}. \end{aligned}$$

(133)

Substituting fractions (132) and (133) into derivative (130) yields differential Eq. (128).

Suppose $v_{2} = \varGamma (v_1)$, where

$$\begin{aligned} \varGamma (v_1) < \varGamma ^*(v_1) \end{aligned}$$

(134)

and

$$\begin{aligned} \varGamma ^{\prime }(v_1) < (\varGamma ^{*})^\prime (v_1) \end{aligned}$$

(135)

for every $v_1$. Let

$$\begin{aligned} y(v_1,v_2) = \dfrac{(v_1+2D)(v_2+2D)}{v_1+v_2+2D}, \end{aligned}$$

(136)

then

$$\begin{aligned} \begin{array}{lll} (v_1+ v_2 + 2D)^2 \dfrac{dy}{dv_1} &{}=&{} \left[ (v_2+2D) + (v_1+2D) \dfrac{\partial v_2}{\partial v_1}\right] (v_1+v_2+2D) \\ &{}&{}- (v_1+2D)(v_2+2D)\left( 1+\dfrac{\partial v_2}{\partial v_1}\right) \\ &{}=&{} v_1(v_1+2D) \dfrac{\partial v_2}{\partial v_1} + v_2(v_2+2D)\\ &{}<&{} v_1(v_1+2D) \cdot \dfrac{\partial v^*_2}{\partial v_1} + v^*_2(v^*_2+2D) \end{array} \end{aligned}$$

(137)

because

$$\begin{aligned} v_2 < v^*_2 \end{aligned}$$

(138)

by condition (134), and

$$\begin{aligned} \dfrac{\partial v_2}{\partial v_1} < \dfrac{\partial v^*_2}{\partial v_1} \end{aligned}$$

(139)

by condition (135). Since

$$\begin{aligned}&v_1(v_1+2D) \cdot \dfrac{\partial v^*_2}{\partial v_1} + v^*_2(v^*_2+2D)\nonumber \\&\quad = v_1(v_1+2D) \left[ - \dfrac{v^*_2(v^*_2+2D)}{v_1(v_1+2D)}\right] + v^*_2(v^*_2+2D)\nonumber \\&\quad = 0, \end{aligned}$$

(140)

we have

$$\begin{aligned} \dfrac{dy}{dv_1} < 0. \end{aligned}$$

(141)

Therefore,

$$\begin{aligned} y(\sigma _1^2, \sigma _2^2) = \dfrac{(\sigma _1^2+2D)(\sigma _2^2+2D)}{\sigma _1^2 + \sigma _2^2 + 2D} \end{aligned}$$

(142)

is monotonically decreasing as $\sigma _1^2$ increases, and so is $\lambda (\sigma _1^2, \sigma _2^2)$. $\square$

1.2 Proof of Lemma 6

Proof

First of all, since the dispersal kernel k(x) is uniformly bounded, and $\int _{-\infty }^{\infty } k(x)\,dx = 1< \infty$, for any finite constant c,

$$\begin{aligned} \begin{aligned} \int _{-\infty }^{\infty } k^2(x-c)\,dx&= \int _{-\infty }^{\infty } k^2(x)\,dx\\&\le \sup _{x} |k(x)| \cdot \int _{-\infty }^{\infty } k(x)\,dx\\&< \infty \end{aligned} \end{aligned}$$

(143)

Therefore, $\forall \, \epsilon$, $\exists \, A_0>L_2/2$, such that for any $A, A^{\prime } > A_0$,

$$\begin{aligned} \int _A^{A^{\prime }} k^2(y-L_2/2) \,dy < \epsilon . \end{aligned}$$

(144)

We now define a function

$$\begin{aligned} g(y) = \sup _{x \in I_1, z \in I_2} |k(x-y)k(y-z)|. \end{aligned}$$

(145)

Since k(x) is a positive even function,

$$\begin{aligned} g(y) = \sup _{x \in I_1, z \in I_2} k(y-x)k(y-z). \end{aligned}$$

(146)

Without loss of generality, assume that $L_1 \le L_2$. Then $\forall \, x \in I_1$, $\forall \, z \in I_2$, $\forall \, y \in [A,A^{\prime }]$,

$$\begin{aligned} k(y-x) \le k(y-L_1/2) \le k(y-L_2/2) \end{aligned}$$

(147)

and

$$\begin{aligned} k(y-z) \le k(y-L_2/2) \end{aligned}$$

(148)

because of the monotonicity of k(x) on the half line $[0,\infty )$. Thus function g(y) is bounded by another function,

$$\begin{aligned} g(y) \le k^2(y-L_2/2), \end{aligned}$$

(149)

for $y \in [A,A^{\prime }]$. Therefore

$$\begin{aligned} \int _A^{A^{\prime }} g(y) \,dy \le \int _A^{A^{\prime }} k^2(y-L_2/2) \,dy < \epsilon . \end{aligned}$$

(150)

By Cauchy’s Theorem,

$$\begin{aligned} \int _0^{\infty } g(y) \, dy < \infty . \end{aligned}$$

(151)

We can show $\int _{-\infty }^{0} g(y) \, dy < \infty$ in the same way. Therefore

$$\begin{aligned} \int _{-\infty }^{\infty } g(y) \, dy < \infty . \end{aligned}$$

(152)

Since

$$\begin{aligned} |k(x-y) k(y-z)| \le g(y), \end{aligned}$$

(153)

for $(x,z) \in I_1 \times I_2$, the improper integral

$$\begin{aligned} \int _{-\infty }^{\infty } k(x-y) k(y-z)\,dy \end{aligned}$$

(154)

is uniformly convergent for $(x,z) \in I_1 \times I_2$ by the Weierstrass comparison rule. $\square$

1.3 Proof of Lemma 7

While proving Lemma 1, we showed that when k and $Q(z;\alpha )$ satisfy assumptions (K2)− (K4) and (Q3), the convolution

$$\begin{aligned} h(y) = \int _{-\infty }^{\infty }k(y-z)Q(z;\alpha )\, dz \end{aligned}$$

(155)

is integrable over $(-\infty , \infty )$. Therefore we can apply Lemma 1 again to see that

$$\begin{aligned} \begin{aligned} w(x)&= \int _{-\infty }^{\infty } Q(z;\alpha ) p(x,z)\,dz \\&= \int _{-\infty }^{\infty }Q(z;\alpha ) \int _{-\infty }^{\infty }k(x-y) k(y-z)\, dy \,dz\\&= \int _{-\infty }^{\infty }k(x-y) \int _{-\infty }^{\infty }Q(z;\alpha ) k(y-z) \, dz \, dy\\&= \int _{-\infty }^{\infty }k(x-y) h(y) \, dy \end{aligned} \end{aligned}$$

(156)

is integrable over $(-\infty , \infty )$. Therefore the function w(x) is well-defined, and $w(x) \rightarrow 0$ as $x \rightarrow \infty$. Since

$$\begin{aligned} \int _{-L}^{L} Q(z;\alpha ) p(x,z)\,dz \rightarrow 0 \end{aligned}$$

(157)

as $x \rightarrow \infty$ as well, the convergence of

$$\begin{aligned} \int _{-L}^{L} Q(z;\alpha ) p(x,z)\,dz \end{aligned}$$

(158)

to

$$\begin{aligned} \int _{-\infty }^{\infty } Q(z;\alpha ) p(x,z)\,dz \end{aligned}$$

(159)

as $L \rightarrow \infty$ is uniform.

1.4 Proof of Lemma 8

Proof

There are two approaches to prove $\bar{\lambda }_{\alpha _1} \rightarrow \bar{\lambda }_{\infty }$. One approach is to show that $\bar{\lambda }_{\infty }$ exists and is finite. This can be done by showing that the operator $K_\infty$ is completely continuous. The second approach is to show that $K_{\alpha _1} \rightarrow K_\infty$ uniformly. Here, we use the second approach.

Let $\alpha _2$ be fixed. For any $u(z) \in BC^{+}(\mathbb {R})$ with $||u(z)|| = 1$, $\forall x$, $\forall \alpha _1$,

$$\begin{aligned} \begin{aligned} (K_{\alpha _1} - K_{\infty })[u](x)&= [f^{\prime }(0)]^2 \int _{-\infty }^{\infty } Q(z;\alpha _2) \left[ \tilde{k}(x,z;\alpha _1) - \tilde{k}(x,z;\infty )\right] u(z) \,dz \\&\le [f^{\prime }(0)]^2 \int _{-\infty }^{\infty } Q(z;\alpha _2) \left[ \tilde{k}(x,z;\alpha _1) - \tilde{k}(x,z;\infty )\right] \,dz \\&= [f^{\prime }(0)]^2 \int _{-\infty }^{\infty } Q(z;\alpha _2) \int _{-\infty }^{\infty } k(x-y)k(y-z) \left[ Q(y;\alpha _1) \right. \\&\quad \, \left. - Q(y;\infty )\right] \,dy\,dz \\&\le \sup \limits _{y} \left[ Q(y;\alpha _1) - Q(y;\infty )\right] [f^{\prime }(0)]^2\int _{-\infty }^{\infty } Q(z;\alpha _2) \\&\int _{-\infty }^{\infty } k(x-y)k(y-z)\, dy\,dz \\&\le 2 [f^{\prime }(0)]^2 \int _{-\infty }^{\infty } Q(z;\alpha _2) p(x,z) \,dz. \end{aligned} \end{aligned}$$

(160)

According to Lemma 7, the above integral is uniformly convergent as an improper integral. Therefore $\forall \, \epsilon$, $\exists \, G$ independent of $\alpha _1$, s.t.

$$\begin{aligned} {[}f^{\prime }(0)]^2 \int _{\mathbb {R}\backslash [-G,G]} Q(z;\alpha _2) \left[ \tilde{k}(x,z;\alpha _1) - \tilde{k}(x,z;\infty )\right] \,dz < \epsilon /2. \end{aligned}$$

(161)

In the proof of Lemma 7, we have shown that

$$\begin{aligned} \int _{-\infty }^{\infty } Q(z;\alpha _2) p(x,z) \,dz \rightarrow 0 \end{aligned}$$

(162)

as $x \rightarrow \infty$. By inequality (160), we see that

$$\begin{aligned}{}[f^{\prime }(0)]^2 \int _{-\infty }^{\infty } Q(z;\alpha _2) \left[ \tilde{k}(x,z;\alpha _1) - \tilde{k}(x,z;\infty )\right] \,dz \rightarrow 0 \end{aligned}$$

(163)

as $x \rightarrow \infty$, and the convergence is uniform with respect to $\alpha _1$. Therefore $\exists \,L$ independent of $\alpha _1$, s.t.

$$\begin{aligned} \begin{aligned}&\sup \limits _{x} \left\{ [f^{\prime }(0)]^2 \int _{-\infty }^{\infty } Q(z;\alpha _2) \left[ \tilde{k}(x,z;\alpha _1) - \tilde{k}(x,z;\infty )\right] \,dz \right\} \\&\quad = \sup \limits _{x \in [-L,L]} \left\{ [f^{\prime }(0)]^2 \int _{-\infty }^{\infty } Q(z;\alpha _2) \left[ \tilde{k}(x,z;\alpha _1) - \tilde{k}(x,z;\infty )\right] \,dz \right\} \\&\quad = \sup \limits _{x \in [-L,L]} \left\{ [f^{\prime }(0)]^2 \int _{-G}^{G} Q(z;\alpha _2) \left[ \tilde{k}(x,z;\alpha _1) - \tilde{k}(x,z;\infty )\right] \,dz \right. \\&\qquad \left. + [f^{\prime }(0)]^2 \int _{\mathbb {R}\backslash [-G,G]} Q(z;\alpha _2) \left[ \tilde{k}(x,z;\alpha _1) - \tilde{k}(x,z;\infty )\right] \,dz \right\} \\&\quad \le \sup \limits _{x \in [-L,L]} \left\{ [f^{\prime }(0)]^2 \cdot 2G \cdot \sup \limits _{z \in [-G,G]} \left[ \tilde{k}(x,z;\alpha _1) - \tilde{k}(x,z;\infty )\right] + \epsilon /2 \right\} . \end{aligned} \end{aligned}$$

(164)

Meanwhile, because the integral $\int _{-\infty }^{\infty } k(x-y) k(y-z)\,dy$ is uniformly convergent when x and z are bounded, $\exists \, M$, s.t.

$$\begin{aligned} \sup \limits _{\begin{array}{c} x \in [-L,L] \\ z \in [-G,G] \end{array}}\int _{\mathbb {R}\backslash [-M,M]} k(x-y) k(y-z)\,dy < \dfrac{\epsilon }{16G [f^{\prime }(0)]^2}. \end{aligned}$$

(165)

Finally, by assumption (Q4(b)),

$$\begin{aligned} Q(y;\alpha ) \rightarrow Q(y; \infty ) \end{aligned}$$

(166)

as $\alpha \rightarrow \infty$. Therefore $\exists \, \bar{\alpha }_1$, s.t. $\forall \, \alpha _1 > \bar{\alpha }_1$,

$$\begin{aligned} \sup _{y\in [-M,M]} \left| Q(y;\alpha _1) - Q(y;\infty ) \right| < \dfrac{\epsilon }{8G [f^{\prime }(0)]^2 \int _{-M}^{M} g(y)\,dy}, \end{aligned}$$

(167)

where g(y) is the function (146) that bounds $k(x-y)k(y-z)$. Therefore

$$\begin{aligned} \begin{aligned}&\sup \limits _{\begin{array}{c} x \in [-L,L]\\ z \in [-G,G] \end{array}} \tilde{k}(x,z;\alpha _1) - \tilde{k}(x,z;\infty ) \\&\quad = \sup \limits _{\begin{array}{c} x \in [-L,L]\\ z \in [-G,G] \end{array}} \int _{-\infty }^{\infty } k(x-y)k(y-z) \left[ Q(y;\alpha _1) - Q(y;\infty )\right] \,dy \\&\quad = \sup \limits _{\begin{array}{c} x \in [-L,L]\\ z \in [-G,G] \end{array}} \left\{ \int _{-M}^{M} k(x-y)k(y-z) \left[ Q(y;\alpha _1) - Q(y;\infty )\right] \,dy \right. \\&\qquad \left. + \int _{\mathbb {R}\backslash [-M,M]} k(x-y)k(y-z) \left[ Q(y;\alpha _1) - Q(y;\infty )\right] \,dy \right\} \\&\quad \le \sup \limits _{\begin{array}{c} x \in [-L,L]\\ z \in [-G,G] \end{array}} \left\{ \dfrac{\epsilon }{8G [f^{\prime }(0)]^2\int _{-M}^{M} g(y)\,dy} \int _{-M}^{M} k(x-y)k(y-z) \,dy \right. \\&\qquad + \left. 2 \int _{\mathbb {R}\backslash [-M,M]} k(x-y) k(y-z)\,dy \right\} \\&\quad \le \dfrac{\epsilon }{8G [f^{\prime }(0)]^2\int _{-M}^{M} g(y)\,dy} \int _{-M}^{M} g(y)\,dy + 2 \cdot \dfrac{\epsilon }{16G [f^{\prime }(0)]^2} \\&\quad = \dfrac{\epsilon }{4G [f^{\prime }(0)]^2}, \end{aligned} \end{aligned}$$

(168)

and (164) continues as

$$\begin{aligned} \begin{aligned}&\sup \limits _{x} \left\{ [f^{\prime }(0)]^2 \int _{-\infty }^{\infty } Q(z;\alpha _2) \left[ \tilde{k}(x,z;\alpha _1) - \tilde{k}(x,z;\infty )\right] \,dz \right\} \\&\quad \le [f^{\prime }(0)]^2 \cdot 2G \cdot \dfrac{\epsilon }{4G [f^{\prime }(0)]^2} + \dfrac{\epsilon }{2} \\&\quad = \epsilon \end{aligned} \end{aligned}$$

(169)

By the first inequality in (160), $||(K_{\alpha _1} - K_{\infty })[u]|| < \epsilon$, $\forall \alpha _1 > \bar{\alpha }_1$. Therefore $K_{\alpha _1} \rightarrow K_{\infty }$ uniformly as $\alpha _1 \rightarrow \infty$, and $\bar{\lambda }_{\alpha _1} \rightarrow \bar{\lambda }_{\infty }$. $\square$

1.5 Proof of Theorem 3

Proof

Suppose $\alpha _{\infty }$ satisfies $\bar{\lambda }_{\infty }(\alpha _{\infty }) = 1$. Then $\alpha _{\infty } > 0$ because $\lambda (\alpha _1, \alpha _2)$ is monotonic with respect to $\alpha _1$ and $\alpha _2$, and $\lambda (0,0) = 0 < 1$. Because $\bar{\lambda }_{\alpha _1^{\prime }}(\alpha _2^*)=1$, and $\lambda (\alpha _1, \alpha _2)$ is monotonic with respect to $\alpha _1$ and $\alpha _2$, we can choose $\alpha > \alpha _1^{\prime }$ so that for all given $\alpha _1>\alpha _1^{\prime }$, the $\alpha _2^*$ satisfying $\bar{\lambda }_{\alpha _1}(\alpha _2^*) = 1$ is in the interval $[0,\alpha ]$. For each $\alpha _1$, $\bar{\lambda }_{\alpha _1}(\alpha _2)$ is continuous and monotonic with respect to $\alpha _2$. Therefore there exists a continuous inverse function $\alpha _2 = \bar{\lambda }_{\alpha _1}^{-1}(c)$ for $c \in [1/2, 3/2]$ and $\alpha _2 \in [0, \alpha ]$. On the bounded interval [1 / 2, 3 / 2], each inverse function $\bar{\lambda }_{\alpha _1}^{-1}(c)$ is uniformly continuous for any given $\alpha _1$. Therefore, $\forall \, \epsilon$, $\exists \, \delta$, so that when $|\bar{\lambda }_1 - 1|<\delta$, where $\bar{\lambda }_1 = \bar{\lambda }_{\alpha _1}(\alpha _{\infty })$,

$$\begin{aligned} |\bar{\lambda }_{\alpha _1}^{-1}(\bar{\lambda }_1)-\bar{\lambda }_{\alpha _1}^{-1}(1)| < \epsilon . \end{aligned}$$

(170)

Therefore

$$\begin{aligned} |\alpha _{\infty }-\alpha _2^*|<\epsilon , \end{aligned}$$

(171)

where $\alpha _2^*$ satisfies $\bar{\lambda }_{\alpha _1}(\alpha _2^*) = 1$.

Because $\bar{\lambda }_{\alpha _1}(\alpha _2)$ converges to $\bar{\lambda }_{\infty }(\alpha _2)$ for any $\alpha _2$ when $\alpha _1 \rightarrow +\infty$, the convergence at the point $\alpha _2 = \alpha _{\infty }$ tells us $\exists \,N = N(\delta )$, so that for $\forall \, \alpha _1 > N$,

$$\begin{aligned} |\bar{\lambda }_{\alpha _1}(\alpha _{\infty }) - \bar{\lambda }_{\infty }(\alpha _{\infty })| < \delta , \end{aligned}$$

(172)

which means

$$\begin{aligned} |\bar{\lambda }_1 - 1| < \delta . \end{aligned}$$

(173)

Therefore $\alpha _2^* \rightarrow \alpha _{\infty }$ as $\alpha _1 \rightarrow \infty$. $\square$

Appendix 3: Proof of Theorem 4

Proof

The results follow directly from Theorem 4.1 and Theorem 4.2 of Hardin et al. (1990). We will verify that the assumptions of these two theorems are met in our framework. Hardin et al. (1990) considered, in section 4, the random dynamical system

$$\begin{aligned} N_{t+1}(x) = \tilde{\varPhi }_t[N_t](x), \end{aligned}$$

(174)

where

$$\begin{aligned} \begin{aligned} \tilde{\varPhi }_t[N](x)&= \int _{\varOmega } k(x,y) f_t[y,G N(y)]\, dy + v(1-G) \int _{\varOmega } l(x,y)\, dy\\&= \int _{\varOmega } k(x,y) \lambda _t(y) GN(y) g[GN(y)]\, dy + v(1-G) \int _{\varOmega } l(x,y)\, dy. \end{aligned} \end{aligned}$$

(175)

In Eq. (175), $v \in [0, 1)$ and $G \in [0, 1]$ are constants, and $\varOmega$ is compact. Hardin et al. assumed that (Hardin et al. 1990) for all $t > 0$:

• (C1) $\lambda _t$ is an independent and identically distributed sequence of random functions which are continuous and nonnegative. Furthermore, there are constants $\lambda _l, \lambda _u > 0$ such that $\lambda _l \le \lambda _t(x) \le \lambda _u$ for $x \in \varOmega$ and $t = 0, 1, 2, \ldots$ almost surely;

• (C2) $f_t(x,N) = \lambda _t(x) N g(N)$ satisfy the following assumptions with probability one:

  • (G1) $f_t(x,N)$ and $\lambda _t(x) g(N)$ are continuous and nonnegative on $\varOmega \times [0, \infty )$;

  • (G2) $f_t(x,N)$ is bounded on $\varOmega \times [0, \infty )$;

  • (G3) If $x\in \varOmega$ and $N>0$ then

    $$\begin{aligned} \lambda _t(x) g(N) < \lambda _t(x) g(0); \end{aligned}$$

    (176)

  • (G4) For $x \in \varOmega , N> N^{\prime } \ge 0$,

    • (a) $\lambda _t(x) g(N) < \lambda _t(x) g(N^{\prime })$,

    • (b) $f_t(x,N) \ge f_t(x,N^{\prime })$.

• (C3) k is a continuous, strictly positive function on $\varOmega \times \varOmega$;

• (C4) l is a continuous, nonnegative function on $\varOmega \times \varOmega$ such that $\forall \, x \in \varOmega$,

  $$\begin{aligned} \int _{\varOmega } l(x,y)\, dy \le 1. \end{aligned}$$

  (177)

Condition (C1) is met because $\alpha _t$ is assumed to be an independent identically distributed sequence of random numbers, and (Q5) is assumed. To show that condition (C2) is met, we now show that conditions (G1) − (G4) are met.

• (G1) In our model, $f_t(x,N) = Q_t(x)f(N)$. We can therefore write $f_t(x,N)$ as $f_t(x,N) = \lambda _t(x) N g(N)$, where $\lambda _t(x) = Q_t(x)$, and

  $$\begin{aligned} g(N) = {\left\{ \begin{array}{ll} f(N)/N, \,\, N \ne 0,\\ f^{\prime }(0)N, \,\, N = 0. \end{array}\right. } \end{aligned}$$

  (178)

  By assumption (Q1), $Q_t(x)$ is continuous on its support $\varOmega _t^{\circ }$. By assumption (Q5), $\varOmega _t^{\circ } \supset \varOmega$. By assumption (F1), f(N) is continuous. Therefore $f_t(x,N)$ is continuous. Since $f^{\prime }(0)$ exists by assumption (F1),

  $$\begin{aligned} \lim _{N\rightarrow 0+} \lambda _t(x) g(N) = Q_t(x)f^{\prime }(0)N, \end{aligned}$$

  (179)

  and $\lambda _t(x) g(N)$ is also continuous. By assumptions (F2) and (F3), f(N) is nonnegative on $[0, \infty )$. Since $Q_t(x)$ is also nonnegative by assumptions (Q1) and (Q2), $f_t(x,N)$ and $\lambda _t(x)g(N)$ are nonnegative on $\varOmega \times [0, \infty )$.

• (G2) Because $Q_t(x)$ is bounded on $\varOmega$ by assumption (Q1), and f(N) is bounded on $[0, \infty )$ by assumption (F4), $f_t(x,N)$ is bounded on $\varOmega \times [0, \infty )$.

• (G3) By assumption (F3), for all $N> 0$,

  $$\begin{aligned} \dfrac{f(N)}{N} < f^{\prime }(0). \end{aligned}$$

  (180)

  Therefore $Q_t(x) f(N)/N < Q_t(x)f^{\prime }(0)$ for all $x \in \varOmega$ and $N>0$, and $\lambda _t(x)g(N) < \lambda _t(x)g(0)$ for all $x \in \varOmega$ and $N>0$.

• (G4) (a) For any $N> N^{\prime } > 0$, let $\alpha = N^{\prime }/N$. Then $0< \alpha < 1$. By assumption (F6),

  $$\begin{aligned} \dfrac{f(N)}{N} < \dfrac{f(\alpha N)}{\alpha N} = \dfrac{f(N^{\prime })}{N^{\prime }}. \end{aligned}$$

  (181)

  Therefore

  $$\begin{aligned} \lambda _t(x)g(N) = Q_t(x) \cdot \dfrac{f(N)}{N} < Q_t(x) \cdot \dfrac{f(N^{\prime })}{N^{\prime }} = \lambda _t(x)g(N^{\prime }). \end{aligned}$$

  (182)

  When $N^{\prime } = 0$, for any $N > N^{\prime }$, we have $g_t(x,N) < g_t(x,N^{\prime })$ by (G3). (b) We know that $f(N) > f(N^{\prime })$ from assumption (F5). Therefore

  $$\begin{aligned} f_t(x,N) = Q_t(x) f(N) > Q_t(x) f(N^{\prime }) = f_t(x,N^{\prime }). \end{aligned}$$

  (183)

Condition (C3) is met because of assumptions (K1) and (K2). Finally, let $l(x,y) \equiv 0$, then model (174) coincides with model (71). Therefore condition (C4) is met. Therefore Theorem 4.1 and Theorem 4.2 of Hardin et al. (1990) apply, and statements (1) and (2) follow directly from these theorems. $\square$

Appendix 4: Analytic calculations of the largest positive eigenvalue

1.1 Example 1 (The “Flooding Pond” scenario)

In this section, we will calculate the largest positive eigenvalue $\lambda$ of the operator K, where the habitat suitability function is (5) and the dispersal kernel is the Gaussian dispersal kernel (8). The linear eigenvalue problem we are trying to solve is

(184)

One can easily verify that the positive function (also see Latore et al. 1998 for a dynamical system perspective)

$$\begin{aligned} u(x) = \exp \left( -x^2/v \right) \end{aligned}$$

(185)

is an eigenfunction of the linear operator K, if v is the solution of

$$\begin{aligned} v = g_{p} \circ \cdots \circ g_{2} \circ g_1 (v), \end{aligned}$$

(186)

where each $g_j$ is defined by

$$\begin{aligned} g_j(v) = 4D + \dfrac{\sigma _j^2 \cdot v}{\sigma _j^2+v}, \qquad j = 1, \ldots , p. \end{aligned}$$

(187)

To see this, let us substitute $u(y_1)$, defined by (185), into the integral in the eigenvalue problem (184). We find that

(188)

where

$$\begin{aligned} C_1 = \sqrt{\dfrac{\sigma _1^2 \cdot v}{4D(\sigma _1^2+v) + \sigma _1^2 \cdot v}}, \end{aligned}$$

(189)

and $g_1(v)$ is defined by Eq. (187). Therefore, by deduction,

(190)

where

$$\begin{aligned} C_2 = \sqrt{\dfrac{\sigma _2^2 \cdot g_1(v)}{4D[\sigma _2^2+ g_1(v)] + \sigma _2^2 \cdot g_1(v)}}, \end{aligned}$$

(191)

and

$$\begin{aligned} \begin{array}{lll} K [u](x)= & {} [f^{\prime }(0)]^p \cdot C_1 \cdot C_2 \cdot \cdots \cdot C_p \cdot \exp {\left[ -\dfrac{x^2}{g_p \circ \cdots \circ g_2\circ g_1(v)}\right] }, \end{array} \end{aligned}$$

(192)

where

$$\begin{aligned} C_j = \sqrt{\dfrac{\sigma _j^2 \cdot g_{j-1} \circ \cdots \circ g_1(v)}{4D[\sigma _j^2+ g_{j-1} \circ \cdots \circ g_1(v)] + \sigma _j^2 \cdot g_{j-1} \circ \cdots \circ g_1(v)}}, \,\, j = 3, \ldots , p. \end{aligned}$$

(193)

Therefore, if v is the solution of Eq. (186), u(x) defined by (185) is an eigenfunction.

From Eq. (192), we can see that

$$\begin{aligned} \lambda = [f^{\prime }(0)]^p \cdot C_1 \cdot C_2 \ldots C_p \end{aligned}$$

(194)

is an eigenvalue. Compared with numerical computations, this eigenvalue is the largest positive eigenvalue for the eigenvalue problem (184). Let $v_0 = v$, $v_1 = g_1(v)$, and define $v_{i}$ to be

$$\begin{aligned} v_{i} = g_{i} \circ \cdots \circ g_1 (v), \qquad i = 2, \ldots , p. \end{aligned}$$

(195)

Then the expression for $\lambda$ simplifies to

$$\begin{aligned} \begin{array}{lll} \lambda &{}=&{} [f^{\prime }(0)]^p \prod _{j=0}^{p-1} \sqrt{\dfrac{\sigma _{j+1}^2 v_{j}}{4D (\sigma _{j+1}^2 + v_j) + \sigma _{j+1}^2 v_{j}}}\\ &{}=&{}[f^{\prime }(0)]^p \prod _{j=0}^{p-1} \left[ \dfrac{\sqrt{\dfrac{\sigma _{j+1}^2 v_{j}}{\sigma _{j+1}^2 + v_{j}}}}{\sqrt{4D + \dfrac{\sigma _{j+1}^2 v_j}{\sigma _{j+1}^2 + v_j}}} \right] . \end{array} \end{aligned}$$

(196)

We can further simplify expression (196) once we notice that definition (195) indicates

$$\begin{aligned} \begin{array}{lll} v_{j+1} &{}=&{} g_{j+1}(v_j)\\ &{}=&{} 4D + \dfrac{\sigma _{j+1}^2 \cdot v_j}{\sigma _{j+1}^2 + v_j}. \end{array} \end{aligned}$$

(197)

Equation (197) implies that

$$\begin{aligned} \begin{array}{lll} \dfrac{\sigma _{j+1}^2 v_{j}}{\sigma _{j+1}^2 + v_{j}} &{}=&{} g_{j+1}(v_{j})-4D\\ &{}=&{} v_{j+1}-4D. \end{array} \end{aligned}$$

(198)

Therefore, expression (196) further simplifies to

$$\begin{aligned} \lambda = [f^{\prime }(0)]^p \prod _{j=0}^{p-1} \left[ \dfrac{\sqrt{v_{j+1}-4D}}{\sqrt{v_{j+1}}} \right] = [f^{\prime }(0)]^p \prod _{j=1}^{p} \left[ \dfrac{\sqrt{v_{j}-4D}}{\sqrt{v_{j}}} \right] . \end{aligned}$$

(199)

It is also straightforward to show that, instead of using definition (195), each $v_j$ can be found alternatively by solving the equation

$$\begin{aligned} v_j = g_{j+p} \circ \cdots \circ g_{j+1}(v_j). \end{aligned}$$

(200)

1.2 Example 2 (The “Flooding Pond-Surface” scenario)

With habitat suitability function (3), dispersal kernel (32), and condition (33), eigenvalue problem (28) can be written as

$$\begin{aligned} \begin{aligned} \lambda u(x)&= [f^{\prime }(0)]^p \int _{-L_p/2}^{L_p/2} \dfrac{\omega }{2} \cos [\omega (x-y_p)] \int _{-L_{p-1}/2}^{L_{p-1}/2} \dfrac{\omega }{2}\cos [\omega (y_p-y_{p-1})] \cdots \\&\int _{-L_1/2}^{L_1/2} \dfrac{\omega }{2}\cos [\omega (y_2-y_1)] u(y_1) dy_1 dy_2 \cdots dy_p. \end{aligned} \end{aligned}$$

(201)

This is an eigenvalue problem with separable kernels. A kernel k(x, y) is separable when it can be written as a linear combination of functions about x alone, where the coefficients may depend on y (Pipkin 1991, Section 1.4). For example, the kernel

$$\begin{aligned} \begin{aligned} k(x,y)&= \dfrac{\omega }{2} \cos [\omega (x-y_p)] \\&= \dfrac{\omega }{2} \cos (\omega y_p) \cos (\omega x) + \dfrac{\omega }{2} \sin (\omega y_p)\sin (\omega x) \end{aligned} \end{aligned}$$

(202)

is separable. With separable kernels, we can write down the eigenfunctions as linear combinations of known functions. For example, from

$$\begin{aligned} \begin{aligned}&\int _{-L_1/2}^{L_1/2} \dfrac{\omega }{2} \cos [\omega (y_2-y_1)] u(y_1) \,dy_1 \\&\quad = \left[ \dfrac{\omega }{2} \int _{-L_1/2}^{L_1/2} \cos (\omega y_1)u(y_1)\,dy_1\right] \cos (\omega y_2) + \left[ \dfrac{\omega }{2} \int _{-L_1/2}^{L_1/2} \sin (\omega y_1)u(y_1)\,dy_1\right] \sin (\omega y_2), \end{aligned} \end{aligned}$$

(203)

we can deduce with induction that the right hand side expression of Eq. (201) is a linear combination of $\cos (\omega x)$ and $\sin (\omega x)$. Since the left hand side is $\lambda u(x)$, it is clear that we can write the eigenfunction u(x) as

$$\begin{aligned} u(x) = c_1\cos (\omega x) + c_2\sin (\omega x), \end{aligned}$$

(204)

where $c_1$ and $c_2$ are undetermined constants. Substituting eigenfunction (204) into eigenvalue problem (201) in the case of $p = 2$ and equating the coefficients of $\cos (\omega x)$ and $\sin (\omega x)$ on both sides, we obtain a $2\times 2$ linear system about the coefficients $c_1$ and $c_2$,

$$\begin{aligned} \begin{array}{lll} \lambda c_1 &{}=&{} a_{11} c_1 + a_{12}c_2,\\ \lambda c_2 &{}=&{} a_{21} c_1 + a_{22}c_2, \end{array} \end{aligned}$$

(205)

where

$$\begin{aligned}&\begin{aligned} a_{11}&= [f^{\prime }(0)]^p \int _{-L_p/2}^{L_p/2} \dfrac{\omega }{2} \cos (\omega y_p) \int _{-L_{p-1}/2}^{L_{p-1}/2} \dfrac{\omega }{2}\cos [\omega (y_p-y_{p-1})] \ldots \\&\quad \int _{-L_1/2}^{L_1/2} \dfrac{\omega }{2}\cos [\omega (y_2-y_1)] \cos (\omega y_1)\, dy_1 dy_2 \ldots dy_p, \end{aligned} \end{aligned}$$

(206)

$$\begin{aligned}&\begin{aligned} a_{12}&= [f^{\prime }(0)]^p \int _{-L_p/2}^{L_p/2} \dfrac{\omega }{2} \cos (\omega y_p) \int _{-L_{p-1}/2}^{L_{p-1}/2} \dfrac{\omega }{2}\cos [\omega (y_p-y_{p-1})] \ldots \\&\quad \int _{-L_1/2}^{L_1/2} \dfrac{\omega }{2}\cos [\omega (y_2-y_1)] \sin (\omega y_1)\, dy_1 dy_2 \ldots dy_p\\&=0, \end{aligned} \end{aligned}$$

(207)

$$\begin{aligned}&\begin{aligned} a_{21}&= [f^{\prime }(0)]^p \int _{-L_p/2}^{L_p/2} \dfrac{\omega }{2} \sin (\omega y_p) \int _{-L_{p-1}/2}^{L_{p-1}/2} \dfrac{\omega }{2}\cos [\omega (y_p-y_{p-1})] \ldots \\&\quad \int _{-L_1/2}^{L_1/2} \dfrac{\omega }{2}\cos [\omega (y_2-y_1)] \cos (\omega y_1)\, dy_1 dy_2 \ldots dy_p\\&=0, \end{aligned} \end{aligned}$$

(208)

and

$$\begin{aligned} \begin{aligned} a_{22}&= [f^{\prime }(0)]^p \int _{-L_p/2}^{L_p/2} \dfrac{\omega }{2} \sin (\omega y_p) \int _{-L_{p-1}/2}^{L_{p-1}/2} \dfrac{\omega }{2}\cos [\omega (y_p-y_{p-1})] \ldots \\&\quad \int _{-L_1/2}^{L_1/2} \dfrac{\omega }{2}\cos [\omega (y_2-y_1)] \sin (\omega y_1)\, dy_1 dy_2 \ldots dy_p. \end{aligned} \end{aligned}$$

(209)

For the eigenfunction (204) to be nontrivial, the coefficients $c_1$ and $c_2$ cannot be both zero. Therefore $\lambda$ may take two possible values,

$$\begin{aligned} \begin{aligned} \lambda _1&= [f^{\prime }(0)]^p \int _{-L_p/2}^{L_p/2} \dfrac{\omega }{2} \cos (\omega y_p) \int _{-L_{p-1}/2}^{L_{p-1}/2} \dfrac{\omega }{2}\cos [\omega (y_p-y_{p-1})] \ldots \\&\quad \int _{-L_1/2}^{L_1/2} \dfrac{\omega }{2}\cos [\omega (y_2-y_1)] \cos (\omega y_1)\, dy_1 dy_2 \ldots dy_p, \end{aligned} \end{aligned}$$

(210)

and

$$\begin{aligned} \begin{aligned} \lambda _2&= [f^{\prime }(0)]^p \int _{-L_p/2}^{L_p/2} \dfrac{\omega }{2} \sin (\omega y_p) \int _{-L_{p-1}/2}^{L_{p-1}/2} \dfrac{\omega }{2}\cos [\omega (y_p-y_{p-1})] \ldots \\&\quad \int _{-L_1/2}^{L_1/2} \dfrac{\omega }{2}\cos [\omega (y_2-y_1)] \sin (\omega y_1)\, dy_1 dy_2 \ldots dy_p. \end{aligned} \end{aligned}$$

(211)

The largest positive eigenvalue is therefore the larger one of these two possibilities,

$$\begin{aligned} \lambda = \max {\{\lambda _1,\lambda _2\}}. \end{aligned}$$

(212)

Appendix 5: Details of Nyström’s method

The Nyström’s method computes the eigenvalues of an integral operator by approximating the integral with a numerical quadrature and transforming the eigenvalue problem to the eigenvalue problem of a matrix. In this paper, we begin by discretizing a computational domain $[-G, G] \times [-G, G]$ with a triangularization to construct a two-dimensional grid, so that the triangles are pair-wise symmetric with respect to the origin. These triangles are right triangles. Let $\Delta \eta = \Delta \zeta$ be the length of their catheti, and

$$\begin{aligned} N = \dfrac{2G}{\Delta \eta } + 1. \end{aligned}$$

(213)

Then there are $N_p$ mid points of these triangles, where

$$\begin{aligned} N_p = N^2-\left( \dfrac{N+1}{2}\right) ^2. \end{aligned}$$

(214)

Denoting the mid points of the triangles with $N_p$ grid points $(\zeta _j,\eta _j), j = 1, \ldots ,N_p$, and applying Nyström’s method, we obtain the linear system

$$\begin{aligned} \lambda \rho (\zeta _i)= & {} 2 \text {Area}(\Delta ) \cdot \sum _{j=1}^{N_p} \omega _j k(\zeta _i-\eta _j) Q_1(\eta _j) k(\eta _j-\zeta _j) Q_2(\zeta _j) \rho (\zeta _j), \nonumber \\ i= & {} 1, \ldots ,N, \end{aligned}$$

(215)

where $\text {Area} (\Delta )$ is the area of the triangles,

$$\begin{aligned} \text {Area} (\Delta ) = \dfrac{1}{2}\Delta \eta \cdot \Delta \zeta = \dfrac{1}{2} \cdot 2\left( \dfrac{G}{N-1}\right) \cdot 2\left( \dfrac{G}{N-1}\right) = 2\left( \dfrac{G}{N-1} \right) ^2, \end{aligned}$$

(216)

and $\omega _j$ are determined by the quadrature rule. For the specific quadrature rule we use, Eq. (215) can be rewritten as

$$\begin{aligned} \begin{array}{lcl} \lambda \rho (\zeta _i) &{}=&{} \dfrac{1}{3} \text {Area}(\Delta ) \cdot \sum \limits _{\begin{array}{c} k=3\\ \text {k odd} \end{array}}^{N-2} \left[ \sum \limits _{p=1}^{\frac{N-1}{2}} 2k(\zeta _i-\eta _{2p}) Q_1(\eta _{2p}) k(\eta _{2p}-\zeta _k) Q_2(\zeta _k)\right] \rho (\zeta _k)\\ &{} &{} + \dfrac{1}{3} \text {Area}(\Delta ) \sum \limits _{k=1,N} \left[ \sum \limits _{p=1}^{\frac{N-1}{2}} k(\zeta _i-\eta _{2p}) Q_1(\eta _{2p}) k(\eta _{2p}-\zeta _k) Q_2(\zeta _k)\right] \rho (\zeta _k)\\ &{} &{} + \dfrac{1}{3} \text {Area}(\Delta ) \sum \limits _{\begin{array}{c} k=2\\ \text {k even} \end{array}}^{N-1} \left[ \sum \limits _{p=2}^{N-1} 2k(\zeta _i-\eta _{p}) Q_1(\eta _{p}) k(\eta _{p}-\zeta _k) Q_2(\zeta _k)\right. \\ &{} &{} + \left. \sum \limits _{p=1,N} k(\zeta _i-\eta _{p}) Q_1(\eta _{p}) k(\eta _{p}-\zeta _k) Q_2(\zeta _k) \right] \rho (\zeta _k). \end{array} \end{aligned}$$

(217)

The approximated eigenvalue $\lambda$ is then calculated as the dominant eigenvalue of matrix $A = (a_{ij})_{N\times N}$, where

$$\begin{aligned} a_{ij} = \left\{ \begin{array}{ll} \dfrac{1}{3} \text {Area}(\Delta )&{}\left[ \sum \limits _{p=1}^{\frac{N-1}{2}} k(\zeta _i-\eta _{2p}) Q_1(\eta _{2p}) k(\eta _{2p}-\zeta _k) Q_2(\zeta _k)\right] ,\, \\ &{}\text {if } j=1 \text {or} j=N, \\ \dfrac{1}{3} \text {Area}(\Delta )&{}\left[ \sum \limits _{p=1}^{\frac{N-1}{2}} 2k(\zeta _i-\eta _{2p}) Q_1(\eta _{2p}) k(\eta _{2p}-\zeta _k) Q_2(\zeta _k)\right] ,\, \\ &{} \text {if } j\ne 1 \text { or } j=N, j \text {odd}, \\ \dfrac{1}{3} \text {Area}(\Delta )&{}\left[ \sum \limits _{p=2}^{N-1} 2k(\zeta _i-\eta _{p}) Q_1(\eta _{p}) k(\eta _{p}-\zeta _k) Q_2(\zeta _k)\right. \\ &{}+ \left. \sum \limits _{p=1,N} k(\zeta _i-\eta _{p}) Q_1(\eta _{p}) k(\eta _{p}-\zeta _k) Q_2(\zeta _k)\right] ,\, \text {if j even}. \end{array}\right. \end{aligned}$$

1.1 Analytic example revisited

We tested the numerical scheme by comparing the numerical results with the analytic formula (41) for the “Flooding Pond Scenario”. Figure 9 illustrates the dependence of the dominant eigenvalue $\lambda$ on the seasonal variation $\epsilon$, where solid lines are numerical results and circles are analytical results calculated from formula (41). Numerical results match with analytic results well for most $\epsilon$ values, though they start to overestimate $\lambda$ when $\epsilon$ is near $\sigma ^2$. This is probably because $\sigma ^2$ is a singular point of the habitat quality function Q(y), and numerical evaluation of the function is challenging at singular points because it involves dividing by 0.

Fig. 9

Comparison of the numerical results with the analytic formula (41) for the “Flooding Pond” scenario. Solid lines are numerical results and circles are analytical results. Numerical results start to overestimate $\lambda$ when $\epsilon$ is near $\sigma ^2$, because $\sigma ^2$ is a singular point of the habitat suitability function. Here, $D = 3$, $\sigma = 2$, $f^{\prime }(0) = 2.5$