Mathematical modeling of lymphocytes selection in the germinal center

Abstract

Lymphocyte selection is a fundamental process of adaptive immunity. In order to produce B-lymphocytes with a target antigenic profile, mutation selection and division occur in the germinal center, a specific part of lymph nodes. We introduce in this article a simplified mathematical model of this phenomenon, taking into account the main mechanisms. This model is written as a non-linear, non-local, inhomogeneous second order partial differential equation, for which we develop a mathematical analysis. We assess, mathematically and numerically, in the case of piecewise-constant coefficients, the performance of the biological function by evaluating the duration of this production process as a function of several parameters such as the mutation rate or the selection profile, in various asymptotic regimes.

1 Introduction

Understanding the immune system is a key challenge in current biological, medical and pharmaceutical research, leading to revolutionary biomedical applications such as vaccination, immunotherapy or specific antibody production.

Adaptive immunity is responsible for the evolution of the antibody repertoire, a learning process necessary to identify and fight new foreign pathogens. This adaptation relies on a Darwinian process of Division-Mutation-Selection (DMS) occurring in the germinal centers (Kelsoe 1996), where an explosion of the mutation rate associated with B-cells division, called somatic hypermutation (Teng and Papavasiliou 2007), is observed, hence providing a unique example of an evolutionary process occurring within living organisms.

Although the general qualitative description of this process is well-established in the literature (Wabl et al. 1999; Neuberger et al. 1998; Diaz and Casali 2002), the quantitative assessment of this DMS process has remained largely unexplored experimentally, in particular due to the difficulty to gather precise phylogenetic data of the B-cell repertoire during the various phases (Dunn-Walters et al. 2002). Recently, several biological studies (Gitlin et al. 2014; Victora 2014; Tarlinton 2014) have provided new experimental insights about the microscopic features of B-cell dynamics in the germinal center. Moreover, several key questions remain highly debated, such as the recycling of selected B-cells (Kepler and Perelson 1993; Meyer-Hermann et al. 2001) or the neutrality of the mutation process. Over the last few years, this system has been studied using relatively detailed computational models and numerical simulations Swerdlin et al. (2008), Meyer-Hermann (2002), providing a method to investigate several hypothesis and phenomena such as B-cell migration in the lymph node or the impact of recycling.

The aim of this article is to introduce a simplified macroscopic mathematical model of this process, in order to establish rigorous mathematical foundations and to investigate theoretically the impact of a few key parameters, such as the mutation rate or the selection profile, on the performance of the B-cell production, characterized by the duration of the process or the final quality of the repertoire.

Mathematical modeling of population dynamics can be approached either from a microscopic agent-based point of view, considering the behavior of many individuals, leading to a stochastic system in high dimension, or from a macroscopic point of view, where global quantities such as the number of individuals in a given state are considered, leading to partial differential equations (PDE) or integro-differential equations. In this article, we focus on the latter approach, and introduce a PDE model describing a population of B-cells subject to division, mutation and selection. In our framework, the division and mutation features give rise to classical linear diffusion terms, whereas selection introduces an inhomogeneous term. When a sufficient amount of B-cell with desired properties has been selected, the overall process shall terminate, which is modeled through a feedback term. As a result, the proposed model is a non-linear, non-local and inhomogeneous elliptic PDE.

Several mathematical models of evolutionary dynamics with mutation and selection have been previously studied, especially in population dynamics (Perthame 2006; Bürger 2000; Nowak 2006), ranging from the early works of Fisher (1999) to advanced mathematical models of adaptive dynamics. The model we introduce in this article has the particularity to combine spatial inhomogeities (in the space of traits) with a non-linear global feedback, which give rises to a specific PDE, for which we establish general properties, as well as precise estimates describing the impact of relevant parameters. In particular, our aim is to understand how the interplay between the mutation rate and the selection function influence the characteristic time-scale of the B-cell production process.

We first start with existence and uniqueness results for solutions of our new model. This gives a precise meaning to the solution, its regularity under the more general hypotheses. From the mathematical point of view, the main difficulty is due to the stiff, non-linear and non-local source term. The non-local feature is expressed in time and in the trait space.

In a second step, we compute, for a birth rate that is piecewise constant, the production time, i.e, the time $t_{{\varrho _0}}$ for which ${\varrho _0}$, a threshold selected population, is reached. This is performed with respect to two parameters of the model: $\varepsilon$ the width of the selection window, and $\mu$ the mutation rate.

The results of this study lead to several conclusions:

• For a general traits-square-integrable initial population of B cells,

  • If $\varepsilon$ is small enough, and $\mu$ is greater than a threshold value, then $t_{{\varrho _0}}$ behaves as $|\log \varepsilon |$, and is independent on $\mu$,

  • For a fixed $\varepsilon$, if $\mu$ is small, we observe that $t_{{\varrho _0}}$ tends towards a constant that depends on the initial birth rate, $\varepsilon$ and initial conditions.

  • For a fixed $\varepsilon$, when the mutation rate becomes large, $t_{{\varrho _0}}$ tends to another finite value, still depending on the same parameters.

• For an initial datum which is a Dirac mass supported at a given trait z outside of the selection window:

  • If the domain is unbounded, we show that when $\mu$ tends to either 0 or $\infty$, $t_{{\varrho _0}}$ blows up,

  • On the other hand, when the domain is finite, $t_{{\varrho _0}}$ stays bounded for $\mu$ growing large.

  Intuitively these results can be interpreted by the paradigm: the larger the size of the repertoire, the more likely there should be an optimal mutation rate in terms of efficiency.

The distinction between different initial conditions comes from a debate in the literature, opposing supporters of mono-clonal germinal centers at the beginning of the process (Perelson and Weisbuch 1997) to authors trying to prove and measure oligo-clonal initial populations (Faro and Or-Guil 2013).

The article is organized as follows. In Sect. 2, we define mathematically our model and discuss its motivations, assumptions and limitations. In Sect. 3, we derive general results concerning existence and uniqueness of solutions, as well as their quantitative properties. To gain further understanding into the dynamical behavior of the system with respect to the data, we study in Sect. 4 the asymptotic behavior of $t_{{\varrho _0}}$ when $\varepsilon$ becomes small, whereas in 5 we consider for a fixed $\varepsilon$, the asymptotic regimes when $\mu$ is either large or small. This section focusses as well on different types of initial B-cell population. Throughout the paper, theoretical results are illustrated with numerical simulations.

2 Mathematical model

We consider the time evolution of a population of lymphocytes during the Division-Mutation-Selection process within the germinal center.

2.1 Biological background

In this first section, we provide an elementary summary of the relevant biological background to describe our modeling approach. For the interested reader, we refer to Abbas et al. (2012) for a more detailed account.

The immune response to an external pathogen (virus, bacteria, etc.,) involves many different types of cells and employs various strategies to eliminate the pathogenic sources.

One of the most important way to fight pathogens relies on the bonding between antigens and antibodies, which triggers an efficient immune response, recruiting many other agents such as macrophages or T-lymphocytes. Antibodies are macromolecular compounds, made of peptidic chains, and whose purpose is to bond with antigens, which are complementary molecules presented at the surface of pathogens. The antibody-antigens (A–A) bonding can be thought as putting a key in a lock, and is characterized by the concept of affinity, which quantifies the likelihood that this bonding occurs for a specific A–A pair.

The production of antibodies in the immune response is ensured by the B-type lymphocyte, which is an immune cell able to produce a single specific antibody. Therefore, it is essential for B-cells to be able to learn how to produce high affinity antibodies with respect to a given antigen. Studying this learning process is precisely the purpose of the present article.

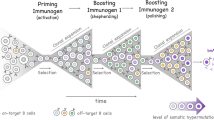
Once a new antigen, called the target, is detected by the immune system, it is captured by the follicular dendritic cells, and brought to the lymph nodes. A simplified vision of the process of affinity maturation in the germinal center, a specific part of the lymph node, can be summarized as follows:

• 1. An initial population of a few immature B-cells enters in the germinal center. The affinity between the initial antibodies carried by these B-cells is in general relatively low, although it is not known whether this initial choice of B-cells is generic, or is already somehow adapted to the target.

• 2. During the first three days, B-cells divide and the population increases, until it migrates to another part of the germinal center, called the light zone. Notice that this population of B-cells is only able to produce a few types of different antibodies, typically less than 10.

• 3. In the light zone, the B-cells are now subject to a full division-mutation-selection process, which is the focus of our model.

  • Division- Mutation: At each division, a single B-cell produces two cells, one of which has undergone a significant amount of mutations in the part of its DNA responsible for the production of the antibody peptide sequence. This process is called somatic hypermutation, since the mutation rate is now increased to extremely high levels, several orders of magnitude higher than in normal cell divisions.

  • Selection: follicular dendritic cells are in the light zone and present at their surface the target antigen. B-cells are also presenting their antibody at their surface and wander in a seemingly random manner in the light zone. Then, the affinity between the presented antibody and the target antigen determines the probability that a bonding occurs and lasts long enough. In that case, the B-cell is selected and receives a signal which enables the cell to escape from the germinal center. Otherwise, low affinity B-cells, which were not able to receive such a signal, die.

• 4. After selection, a B-cell might have several fates: either it transforms into a plasma cell, which is able to produce and release antibodies in order to fight the pathogen, or into a memory cell whose aim is to remember the antigen (therefore being able to produce quickly high affinity antibodies, in case the pathogen returns later). A third possible fate which is also discussed in the literature (Meyer-Hermann et al. 2001) is the possibility for the selected B-cell to come back inside the germinal center and to be subject a second time to the DMS process.

• 5. At some point, this affinity maturation terminates, and the precise biological mechanisms responsible for the determination of the stopping time remain unclear. However, it seems reasonable to consider that the process would stop as soon as a sufficient quantity of selected B-cell has escaped the germinal center.

2.2 Assumptions of the model

Of course, the above description is only a simplified and partial overview of a process which is in reality more complex and involves many different cell types, in particular T-cells. However, we think that it is neither possible nor wishful to take into account all the details of real biological processes into a mathematical model. Therefore, after running numerical simulations of various models (agent-based, stochastic models, PDE models with many variables), and motivated by the idea of introducing a simple, yet non-trivial, macroscopic mathematical model of the evolution of a population of B-cells during DMS phase, we have identified and selected what we consider to be the key parts of this complex process.

Space of traits: We consider that each B-cell is characterized by a trait corresponding to a specific antibody sequence. Instead of a discrete space of traits, composed with strings of amino-acids (as for instance in Balelli et al. 2016a, b), we view here the trait as an abstract property of the antibody and we therefore consider the space of traits to be made with real numbers, for instance the interval [0, 1].

Affinity and selection: The target antigen is also characterized by a trait $x_0$ in the same space, and if x denotes the trait associated with a B-cell, then we consider that the A-A affinity is given by a function $s(x) = F(x_0,x)$: the higher is s(x), the higher is the likelihood that the B-cell with trait x binds to the target. Since the affinity with the target summarizes the necessary information about a given B-cell to decide its fate, it seems reasonable to consider real trait x, directly translated into an affinity through the function F. However, this model does not address the difficult question of understanding how a small change in the DNA of the B-cell will result into a change in the peptide chain of the antibody and finally into a modification of the affinity.

Mutations: In our modeling approach, we consider that a mutation will change slightly the trait x to $x+dx$ in a diffusion manner, and that the affinity will also change slightly through the function F. This model of mutation does not take into account the possibility for a small mutation of the DNA to produce a large change in affinity. One way to overcome this difficulty would be to consider a non-local mutation kernel instead of a diffusion, but it seems relatively uneasy to us to make precise and justified assumptions on such a kernel.

Termination: We assume that the termination of the affinity maturation process is regulated by a measure of the number of selected B-cells. More precisely, we assume that the division rate is a decreasing function of the number of selected B-cells. Therefore, if this number reaches a certain value, the birth rate becomes lower than the death rate and the population inside the germinal center should extinct.

2.3 Mathematical model

We are now able to define precisely the mathematical model we will consider in this article. First, we introduce the following notations:

• 1. Parameters:

  • Cell division rate function $Q:\mathbb {R}\rightarrow \mathbb {R}_+$ is monotonic decreasing and $Q_1 \le Q(z) \le Q_0$

  • Cell death rate $d>0$

  • Affinity-dependent selection function s(.), peaked around $x_0$, the target.

  • Mutation rate $\mu >0$, which may either be a constant or a bounded function of the trait $\mu :{\mathbb {R}}\rightarrow {\mathbb {R}}_+^*$

• 2. Variables:

  • n(t, x) is the quantity of lymphocytes with a trait x

  • $\varrho (t)$ is the quantity of selected lymphocytes at time t and is given by:

    $$\begin{aligned} \varrho (t) := \int _0^t\int _{\mathbb {R}} s(x)n({\tilde{t}},x)dxd{\tilde{t}}\end{aligned}$$

The domain in the trait-space is denoted ${\varOmega }$ and could be practically seen as a distance to a specific target trait. We are now able to formulate the main evolution equation, for x in the trait space ${\varOmega }:=(0,1)$ and $t \ge 0$. It is an initial boundary value problem reading : find the function n solving

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _t n(t,x) = (Q(\varrho (t)) - d - s(x) )n(t,x) + \partial _x(\mu \partial _x n(t,x)) , &{} (t,x) \in {\mathcal {O}}_T:= (0,T)\times {\varOmega }, \\ \mu \partial _{{\mathfrak {\mathbf{n}}}} n(t,\cdot ) = 0,&{} (t,x) \in {\varSigma }_T := (0,T)\times \partial {\varOmega }, \\ n(0,x)=n_I(x),&{} \{ 0 \} \times {\varOmega }, \end{array} \right. \end{aligned}$$

(1)

where the second line is the homogeneous Neumann boundary condition ($\partial _{{\mathfrak {\mathbf{n}}}} n := \partial _x n \cdot {\mathfrak n}$), and the third one is the setting of initial data at time $t=0$. Notice that in the case where $\mu$ is a constant scalar, then the main equation simply reads:

$$\begin{aligned} \partial _t n(t,x) = (Q(\varrho (t)) - d - s(x) )n(t,x) + \mu \partial _{xx} n(t,x). \end{aligned}$$

3 General results

In this section, we establish general results of existence and uniqueness, as well as spectral decomposition, concerning system 1 under various assumptions on the coefficients.

3.1 Existence and uniqueness

Here, we present general existence and uniqueness results concerning system (1) (Theorem 1 for a Lipschitz continuous Q and Theorem 2 for a piecewise constant Q).

We consider the Banach space

$$\begin{aligned} X=C\big ([0,T];L^2({\varOmega })\big ),\quad \left\| m\right\| _X:=\sup _{0\le t \le T}||m(t)||_{L^2({\varOmega })}, \end{aligned}$$

for some T chosen later. Moreover we set

$$\begin{aligned} V({\mathcal {O}}_T) := L^\infty ((0,T);L^2({\varOmega })) \cap L^2((0,T)\times H^1({\varOmega })) \end{aligned}$$

and we define the form

$$\begin{aligned} \begin{aligned} I(t_1,n,\eta ) :=&\int _{{\varOmega }} n(t_1,x){~}\eta (t_1,x) dx - \int _0^{t_1}\int _{{\varOmega }} n(t,x)\partial _t\eta (t,x) dx dt \\&+ \int _0^{t_1}\int _{{\varOmega }} \mu \partial _x n (t,x)\cdot \partial _x \eta (t,x)+ (s(x) + d - Q(\varrho )) n(t,x){~}\eta (t,x) dx. \end{aligned} \end{aligned}$$

Definition 3.1

We call a weak solution of problem (1) any solution $n \in V({\mathcal {O}}_T)$ s.t.

$$\begin{aligned} I(T,n,\eta ) = 0 ,\quad \end{aligned}$$

(2)

for every function $\eta \in H^1({\mathcal {O}}_T)$ s.t. $\eta \equiv 0$ when $t=0$. We say moreover that the solution is consistent with the initial condition if

$$\begin{aligned} I(T,n,\eta )= \int _{\varOmega } n_I(x) \eta (0,x) dx, \quad \forall \eta \in H^1({\mathcal {O}}_T). \end{aligned}$$

the latter equation will be denoted as the variational formulation associated to the problem (1).

Hypotheses 3.1

Concerning the data, we assume

• (i) The initial data $n_I(x)$ belongs to $L^2({\varOmega })$ and is non-negative.

• (ii) The function Q is a globally Lipschitz with respect to $\varrho$, i.e. $Q \in W^{1,\infty }({\mathbb {R}})$.

• (iii) The selection function s is a bounded non-negative function of x.

• (iv) The mutation rate $\mu$ is a bounded positive definite function of x.

• (v) The death rate d is a non-negative constant.

Theorem 1

Under hypotheses 3.1, there exists a unique positive weak solution $n \in V({\mathcal {O}}_T)$ for any positive time T.

Proof

We suppose in a first step that the constant d is strictly positive. Then we prove the existence using the Banach fixed point theorem. We define A a closed subset of X

$$\begin{aligned} A=\{m\in X, m > 0, ||m||_X \le C_{\varPhi }\}, \end{aligned}$$

where $C_{\varPhi }$ is defined so that ${\left\| {n_I}\right\| }_{L^2({\varOmega })}^2 + {\left\| {Q}\right\| }_{L^\infty }^2 T C_{\varPhi }^2 / (4 d) < C_{\varPhi }^2$. We denote by $c_1 := {\left\| {Q}\right\| }_{L^\infty }^2 / (4 d)$. For each $m\in A$, let n be the weak solution associated to the problem:

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _t n(t,x)- \partial _x (\mu \partial _x n(t,x))+(d+s(x))n(t,x)=Q(\varrho (t)) m(t,x),&{}\quad (t,x) \in {\mathcal {O}}_T\\ \varrho (t)=\int _0^t \int _{{\varOmega }} s(x)m({\tilde{t}},x)dxd{\tilde{t}}, &{} \quad t \in (0,T),\\ {\partial _{{\mathfrak {\mathbf{n}}}}}n(t,x) = 0&{}\quad (t,x) \in {\varSigma }_T,\\ n(t=0,x)=n_I(x) > 0,&{}\quad t=0,x\in {\varOmega }. \end{array} \right. \end{aligned}$$

(3)

This system defines the operator ${\varPhi }: m\longmapsto n$. We prove that it admits a unique point in A.

• Existence: The solution $n \in V({\mathcal {O}}_T)$ exists uniquely by standard parabolic theory (Theorem 5.1 p. 170 chap. III Ladyženskaja et al. 1968) for any given $m \in L^\infty ({\mathcal {O}}_T)$. The $L^\infty$ bound follows the same way by Theorem 7.1 p. 181 (Ladyženskaja et al. 1968). Moreover by Theorem 4.2 p. 160 we know that

  $$\begin{aligned} \int _0^{T-h}{\left\| {n(t+h,\cdot )-n(t,\cdot ) }\right\| }_{L^2({\varOmega })}^2 dt = o(h). \end{aligned}$$

• Non-negativeness: We suppose that m is a positive function in $V({\mathcal {O}}_T)\cap L^\infty ({\mathcal {O}}_T)$. We follow results from p. 183 Ladyženskaja et al. (1968) and we choose $n_h^- := \min (n_h,0)$ as a test function in (2) where $n_h$ is the Steklov approximation of n i.e.

  $$\begin{aligned} n_h(t,x) = \frac{1}{h}\int _t^{t+h} n(\tau ,x) \, d\tau , \quad \forall (t,x) \in (0,T-h)\times {\varOmega }. \end{aligned}$$

  Applying such a test function is possible since $n_h^-$ actually does belong to $H^1({\mathcal {O}}_T)$. Passing to the limit with respect to the small parameter h then gives the identity

  $$\begin{aligned}&\frac{1}{2}\left[ \int _{{\varOmega }} (n^-)^2(\tau ,x) dx \right] ^{\tau =t_1}_{\tau = 0} + \int _0^{t_1} \int _{{\varOmega }} \left\{ \mu \partial _x n \partial _x n^- + (s(x)+ d) n n^- \right\} dx dt \\&\quad = \int _0^{t_1} \int _{{\varOmega }} Q m n^- dx dt. \end{aligned}$$

  But the support of $n^-$ is the set where $n\le 0$ thus one has due to the positivity of m and Q that

  $$\begin{aligned} \frac{1}{2}\left[ \int _{{\varOmega }} (n^-)^2(\tau ,x) dx \right] ^{\tau =t_1}_{\tau = 0} \le 0, \end{aligned}$$

  which gives that

  $$\begin{aligned} \int _{{\varOmega }} (n^-)^2(t_1 ,x) dx \le 0, \quad \forall t_1 \le T. \end{aligned}$$

  Since this integral is also non-negative, we deduce that the negative part of n vanishes, which proves the claimed non-negativeness property.

• The map ${\varPhi }$ is an endomorphism in X: By the same technique as above, we test by $n_h$ and pass to the limit with respect to h (for a more detailed explanation see p. 141-142 Ladyženskaja et al. 1968) in the weak formulation, which writes:

  $$\begin{aligned}&\frac{1}{2} \left[ \int _{{\varOmega }} n^2(\tau ,x) dx \right] ^{\tau =t_1}_{\tau =0} + \int _{{\mathcal {O}}_{t_1}} \{ \mu |\partial _x n |^2 + (d+s(x))n^2 \} dx dt \\&\quad = \int _{{\mathcal {O}}_{t_1}} Q(\varrho (t))\, m\, n \, dx dt, \end{aligned}$$

  and applying Cauchy-Schwarz and the Young inequalities on the right hand side gives

  $$\begin{aligned} \frac{1}{2} \left[ \int _{{\varOmega }} n^2(\tau ,x) dx \right] ^{\tau =t_1}_{\tau =0} \le \frac{{\left\| {Q}\right\| }_{L^\infty }T}{4d} {\left\| {m}\right\| }_{X}^2 \le \frac{{\left\| {Q}\right\| }_{L^\infty }T}{4d} C_{\varPhi }^2, \quad \forall t_1 < T. \end{aligned}$$

  Using the hypothesis on $C_{\varPhi }$ we then deduce that in turn

  $$\begin{aligned} \forall t \in [0,T],||n(t,\cdot ) ||_{L^2}\le C_{\varPhi }, \end{aligned}$$

  and thus $n\in A$.

• The map ${\varPhi }$ is a contraction: We denote $n_i = {\varPhi }(m_i)$ for $i \in \{1,2\}$ where $m_i$ are two given functions in A. Then we denote $\tilde{n}:= n_1 - n_2$ and $\tilde{m}:=m_1 - m_2$, and we have

  $$\begin{aligned}&\frac{1}{2} \left[ \int _{{\varOmega }} \tilde{n}^2(\tau ,x) dx \right] ^{\tau =t_1}_{\tau =0} + \int _{{\mathcal {O}}_{t_1}} \{ \mu |\partial _x \tilde{n} |^2 + (d+s(x))\tilde{n}^2 \} dx dt \\&\quad = \int _{{\mathcal {O}}_{t_1}} (Q(\varrho _1(t))m_1-Q(\varrho _2)m_2)\tilde{n}\, dx dt, \\&\quad \le \frac{1}{4d} \int _{{\mathcal {O}}_{t_1} }\big [Q(\varrho _1)m_1-Q(\varrho _2)m_2\big ]^2 dxdt + d \int _{{\mathcal {O}}_{t_1}}\tilde{n}^2 dx dt . \end{aligned}$$

  We establish a bound for the first term in the latter right hand side

  $$\begin{aligned} \begin{aligned} \frac{1}{4d} \int _{{\mathcal {O}}_{t_1} }\big [Q(\varrho _1)m_1-Q(\varrho _2)m_2\big ]^2 dxdt \le \frac{t_1{\left\| {Q}\right\| }_{L^\infty }^2}{2d}{\left\| {\tilde{m}}\right\| }_{X}^2 + \frac{{\left\| {m_2}\right\| }_{X}^2}{2d} \int _0^{t_1} |\tilde{Q}|^2 dt . \end{aligned} \end{aligned}$$

  The last term above can then be estimated using that

  $$\begin{aligned} \int _0^{t_1} |\tilde{Q}|^2 dt = \int _0^{t_1} |Q(\varrho _1)-Q(\varrho _2)|^2 dt \le {\left\| {Q}\right\| }_{\mathrm{Lip}}^2 {\left\| {s}\right\| }_{L^2({\varOmega })}^2 {\left\| {\tilde{m}}\right\| }_{X}^2 \frac{t_1^3}{3}, \end{aligned}$$

  which gives

  $$\begin{aligned} {\left\| {\tilde{n}(t_1,\cdot )}\right\| }_{L^2({\varOmega })}^2 \le t_1 (c_1 + t^2_1 C_{\varPhi }^2 c_2) {\left\| {\tilde{m}}\right\| }_{X}^2, \end{aligned}$$

  where

  $$\begin{aligned} c_2 = \frac{{\left\| {Q}\right\| }_{L^\infty }^2}{2d} \quad c_3 = \frac{{\left\| {Q}\right\| }_{\mathrm{Lip}}^2 {\left\| {s}\right\| }_{L^2({\varOmega })}^2 }{6d}. \end{aligned}$$

  This finally provides

  $$\begin{aligned} {\left\| {\tilde{n}}\right\| }_{X} \le \sqrt{T(c_2 + C_{\varPhi }^2 T^2c_3) } {\left\| {\tilde{m}}\right\| }_{X} \end{aligned}$$

  Choose T small enough so that the contraction holds. The local existence and uniqueness follow from the Banach-Picard theorem.

• Global existence Denote $S_k = \sum _{i=1}^{k} T_i$. By induction, we assume that existence and uniqueness of (1) hold until the time $S_k$ with the corresponding bound $C_k$. Now consider the time interval $[S_k,S_{k+1}]$, the new problem is the variational formulation corresponding to the system written in a strong form:

  $$\begin{aligned} \left\{ \begin{array}{ll} \partial _t \breve{n}_{in}(t,x)=\big [Q(\varrho _{out}(t))-d-s(x)\big ] \breve{n}_{in}(t,x)+\partial _x(\mu \partial _x \breve{n}_{in})(t,x),&{}\quad (t,x)\in (S_k,S_{k+1})\times {\varOmega },\\ \varrho _{out}(t)=\varrho _{out}(S_k)+\int _{[S_k,t]\times {\varOmega }} s(x)\breve{n}({\tilde{t}},x)dxd{\tilde{t}},&{}\quad t \in \left( S_k,S_{k+1}\right) ,\\ \breve{n}_{in}(t=S_k,x)=n(S_k,x),&{}\quad (t,x)\in ( \{ S_k \} \times {\varOmega }, \\ {\partial _{{\mathfrak {\mathbf{n}}}}}\breve{n}_{in}(t,0) = 0. &{}\quad (t,x)\in ((S_k,S_{k+1})\times \partial {\varOmega }. \end{array} \right. \end{aligned}$$

  Iterating the same argument as in the first and second steps, existence and uniqueness hold on this new time interval if there exist $(T_k,C_k)_{k\in \mathbb {N}}$ s.t.

  $$\begin{aligned} \left\{ \begin{aligned}&{\left\| {n(S_k,\cdot )}\right\| }_{L^2}^2 + c_1 T_{k+1} C_{k+1}^2< C_{k+1}^2,\\&\left( c_2 + C_{k+1}^2 T_{k+1}^2 c_3 \right) T_{k+1} < 1, \end{aligned} \right. \quad \forall k \in \mathbb {N}. \end{aligned}$$

  The first condition ensures that the map ${\varPhi }$ is an endomorphism while the second one insures that it is a contraction. Because ${\left\| {n(S_k,\cdot )}\right\| }_{L^2} \le C_k$, the first inequality holds if we suppose that

  $$\begin{aligned} C_k^2 + c_1T_{k+1} C_{k+1}^2 < C_{k+1}^2. \end{aligned}$$

  We choose $(T_k)$ and $(C_k)$ as

  $$\begin{aligned} T_k := \frac{1}{ 2 k \, c_1} ,\quad C_k := \alpha k, \end{aligned}$$

  where $\alpha$ is s.t.

  $$\begin{aligned} \alpha < \frac{c_1}{c_3}( 4 c_1 - c_2) =\frac{c_1}{2 c_3 d} {\left\| {Q}\right\| }_{L^\infty }^2 \end{aligned}$$

  the series $S_k = \sum _{i=1}^{k} T_i$ diverges. Thus global uniqueness and existence hold.

For a fixed positive constant d we proved the theorem: there exists a unique weak solution $n_d \in V({\mathcal {O}}_T)$, for any time T, solving

$$\begin{aligned} I_d(t_1,n_d,\eta )=0 ,\quad \forall \eta \in H^1({\mathcal {O}}_T) \quad \text { s.t. } \eta \equiv 0 \text { for } t=0. \end{aligned}$$

Testing again with an appropriate averaged test function and passing to the limit gives:

$$\begin{aligned} \frac{1}{2} \left[ \int _{{\varOmega }} n^2_d(\tau ,x) dx \right] ^{\tau =t_1}_{\tau =0} + \int _{{\mathcal {O}}_{t_1}} \{ \mu |\partial _x n_d |^2 + s(x)n^2_d \} dx dt \le \int _{{\mathcal {O}}_{t_1}} Q(\varrho _d(t))\, n_d^2 \, dx dt, \end{aligned}$$

which provides by standard techniques

$$\begin{aligned} {\left\| {n_d}\right\| }_{V({\mathcal {O}}_{t_1})} \le C e^{{\left\| {Q}\right\| }_{L^\infty }t_1} {\left\| {n_I}\right\| }_{L^2({\varOmega })}. \end{aligned}$$

This estimate is uniform with respect to d. By weak convergence, one passes to the limit when $d \rightarrow 0$. This proves the theorem in this specific case. $\square$

Hereafter we weaken the Lipschitz hypothesis made on Q and we define

Hypotheses 3.2

We suppose that Hypotheses 3.1 (i),(iv) hold, moreover we suppose that

• (ii)’ Q is a smooth function on ${\mathbb {R}}{\setminus } \{\varrho _0\}$, it admits two possibly different limits in the neighborhood of $\varrho _0\,Q_\pm := \lim _{\varrho \rightarrow \varrho _0^\pm } Q(\varrho )$.

• (iii)’ s is a positive definite function : $\inf _{x \in {\varOmega }} s(x) > 0$.

Theorem 2

Under Hypotheses 3.2, one has the same conclusions as in Theorem 1, except for uniqueness that holds until a time $t_0^-$ defined below.

Proof

We define $Q_\delta$ a regularized non-linear source term

$$\begin{aligned} Q_\delta (\varrho ) := {\left\{ \begin{array}{ll} Q(\varrho ) &{} \text { if } \varrho \in {\mathbb {R}}\setminus ]\varrho _0,\varrho _0+\delta [ ,\\ Q _- + \frac{Q(\varrho _0+\delta )-Q_-}{\delta } (\varrho -\varrho _0) &{} \text { otherwise}. \end{array}\right. } \end{aligned}$$

As $Q_\delta$ is now Lipschitz continuous, one applies Theorem 1, denoting $n_\delta$ the corresponding unique solution, it belongs to $V({\mathcal {O}}_T)$ for any time T, uniformly with respect to $\delta$. Moreover, one has also that $n_\delta \in C(0,T;L^2({\varOmega }))$ uniformly with respect to $\delta$. Thus, one might extract a subsequence denoted again $n_\delta$ that converges weakly in $L^2(0,T; H^1({\varOmega }))$ and weak star in $L^\infty (0,T;L^2({\varOmega }))$. For every fixed $t\ge 0$, $n_\delta (t,x)$ tends to n(t, x) in $L^2({\varOmega })$ weak. This shows that as $\delta \rightarrow 0$,

$$\begin{aligned} \begin{aligned}&\int _{\varOmega }n_\delta (t_1,x) \eta (t_1,x) dx \rightarrow \int _{\varOmega }n (t_1,x) \eta (t_1,x) dx, \\&\int _{{\mathcal {O}}_{t_1}} n_\delta (t,x) \partial _t\eta (t,x) dx dt \rightarrow \int _{{\mathcal {O}}_{t_1}} n(t,x) \partial _t\eta (t,x) dx dt ,\\&\int _{{\mathcal {O}}_{t_1}} \mu \partial _x n_\delta (t,x) \partial _x \eta (t,x)dx dt \rightarrow \int _{{\mathcal {O}}_{t_1}} \mu \partial _x n (t,x) \partial _x \eta (t,x) dx dt ,\\&\int _{{\mathcal {O}}_{t_1}} (s(x) + d) n_\delta (t,x) \eta (t,x) dx dt \rightarrow \int _{{\mathcal {O}}_{t_1}} (s(x)+d) n(t,x) \eta (t,x) dx dt. \\ \end{aligned} \end{aligned}$$

It remains to show that

$$\begin{aligned} \int _{{\mathcal {O}}_{t_1}} Q_\delta (\varrho _\delta ) n_\delta (t,x) \eta (t,x) dx dt \rightarrow \int _{{\mathcal {O}}_{t_1}} Q(\varrho ) n(t,x) \eta (t,x) dx dt . \end{aligned}$$

• $\varrho _\delta$ converges strongly to $\varrho$ in C(0, T). Indeed, because $s \in L^\infty ({\varOmega })$,

  $$\begin{aligned} \rho _\delta (t) = \int _0^t \int _{\varOmega }s(x) n_\delta (t,x)dx dt \rightarrow \int _0^t \int _{\varOmega }s(x) n(t,x) dx dt =: \rho (t). \end{aligned}$$

  and because s and n are non-negative functions $\varrho$ is a non-decreasing function.

• $\varrho _\delta$ is a strictly increasing In the weak formulation $I(t,n_\delta ,\eta )=0$, we set $\eta$ as a time dependent function independent on x that solves

  $$\begin{aligned} \left\{ \begin{array}{ll} \partial _t\eta = ({\left\| {s}\right\| }_{L^\infty ({\varOmega })} + d - Q(\varrho _\delta (t))) \eta , &{} \quad t \in (0,t_1) \\ \eta (0) = 1, &{} \quad t=0 \end{array} \right. \end{aligned}$$

  $\eta$ is then explicit and reads:

  $$\begin{aligned} \eta = \exp \left( \int _0^t ({\left\| {s}\right\| }_{L^\infty ({\varOmega })} + d - Q(\varrho _\delta (\tilde{t}))) d\tilde{t} \right) . \end{aligned}$$

  We denote hereafter $\overline{n}$ the average of n with respect to the trait variable :

  $$\begin{aligned} \overline{n}:= \int _{\varOmega }n(t,x) dx. \end{aligned}$$

  Finally one has that:

  $$\begin{aligned}&\overline{n}_\delta (t) \exp \left( \int _0^t ({\left\| {s}\right\| }_{L^\infty ({\varOmega })} + d - Q(\varrho _\delta (\tilde{t}))) d\tilde{t} \right) \\&\quad = \overline{n}_\delta (0) + \int _{{\mathcal {O}}_{t}} ({\left\| {s}\right\| }_{L^\infty } - s(x) ) n_\delta ({\tilde{t}}, x) \eta ({\tilde{t}}) dx \, d{\tilde{t}}\end{aligned}$$

  the latter term being non-negative, and because the initial condition does not depend on $\delta$, one concludes:

  $$\begin{aligned} \begin{aligned} \overline{n}_\delta (t)&\ge \overline{n}(0)\exp \left( \int _0^t ( Q(\varrho _\delta (\tilde{t}))-({\left\| {s}\right\| }_{L^\infty ({\varOmega })} + d )) d\tilde{t} \right) \\&\ge \exp \left( \left( \inf _{\varrho \in {\mathbb {R}}_+} Q(\varrho ) - ( {\left\| {s}\right\| }_{L^\infty } + d) \right) t\right) =:b(t) > 0 \end{aligned} \end{aligned}$$

  which is positive definite for every finite time and the bound from below is uniform with respect to $\delta$. Then one remarks that

  $$\begin{aligned} \partial _t\varrho _\delta \ge \inf _{x \in {\varOmega } } s(x) \overline{n}_\delta (t) \ge \inf _{x \in {\varOmega } } s(x) b(t) > 0 \end{aligned}$$

  which proves that $\varrho _\delta$ is strictly increasing for any fixed time uniformly with respect to $\delta$ provided condition (iii)’ of Hypotheses 3.2.

• Reaching $\varrho _0$: As $\varrho _\delta$ is an increasing function whose initial datum is zero, there are two possibilities

  • 1. Either $\varrho _\delta$ never reaches $\varrho _0$ i.e. $\varrho (t)<\varrho _0$ for every non negative $t \in {\mathbb {R}}$. Then for all times $Q_\delta (\varrho _\delta )=Q(\varrho _\delta )$ and Q is always regular thus uniqueness results from Theorem 1 imply that $n_\delta = n$ a.e. in $(0,\infty )\times {\varOmega }$. There is nothing to prove

  • 2. Or there exists a time $t_0$ s.t. $\varrho _\delta (t_0) = \varrho _0$. Again by uniqueness, one has that

    $$\begin{aligned} n_\delta (t,x) = n(t,x) \quad \text { a.e } (t,x) \in (0,t_0)\times {\varOmega }. \end{aligned}$$

    and thus this time $t_0$ is equal for every $\delta$. We fix a time $t_1 = 2 t_0$ and define $\underline{c}$ as

    $$\begin{aligned} \underline{c} := \inf _{t\in [0,t_1]} \overline{n}(0)\exp \left( \left( \inf _{\varrho \in {\mathbb {R}}_+} Q(\varrho ) - ( {\left\| {s}\right\| }_{L^\infty } + d) \right) t \right) > 0 \end{aligned}$$

    We deduce then that in the neighborhood of $t_0$ one can write

    $$\begin{aligned} \varrho _\delta (t_0+\omega ) - \varrho _0> \underline{c} \omega ,\quad \forall \omega >0. \end{aligned}$$

    Choosing then $\omega = \delta / \underline{c}$, one writes

    $$\begin{aligned}&\int _{{\mathcal {O}}_{t_1}} (Q_\delta (\varrho _\delta )n_\delta - Q(\varrho )n) \eta dx dt\\&\quad = \int _{((0,t_0)\cup (t_0+\omega ,t_1))\times {\varOmega }} (Q(\varrho _\delta )n_\delta - Q(\varrho )n)\eta dx dt \\&\qquad + \int _{ ((t_0,t_0+\omega ))\times {\varOmega }} (Q_\delta (\varrho _\delta )n_\delta - Q(\varrho )n)\eta dx dt =: R_1 + R_2 \end{aligned}$$

    As previously shown $n_\delta (t,x) \equiv n(t,x)$ everywhere on $(0,t_0)$ a.e. $x\in {\varOmega }$, thus $R_1$ reduces to

    $$\begin{aligned} R_1= & {} \int _{ ((t_0+\omega ,t_1))\times {\varOmega }} (Q(\varrho _\delta )n_\delta - Q(\varrho )n)\eta dx dt \\= & {} \int _{ ((t_0+\omega ,t_1))\times {\varOmega }} (Q(\varrho _\delta )n_\delta - Q(\varrho )n_\delta + Q(\varrho )n_\delta - Q(\varrho )n)\eta dx dt \\\le & {} c_1{\left\| {\varrho _\delta -\varrho }\right\| }_{L^\infty (0,t_1)}{\left\| {n_\delta }\right\| }_{L^\infty ((0,t_1);L^2({\varOmega }))} \\&+ \left| \int _{ ((t_0+\omega ,t_1))\times {\varOmega }} (n_\delta -n)Q(\varrho )\eta dx dt \right| \end{aligned}$$

    where $c_1 = {\left\| {Q}\right\| }_{W^{1,\infty }({\mathbb {R}}\setminus B({\varrho _0},\delta ))}$, the latter term tends to zero when $\delta \rightarrow 0$ thanks to weak convergence arguments on $n_\delta$. On the other hand,

    $$\begin{aligned} R_2 \le \sqrt{\omega }{\left\| {Q}\right\| }_{L^\infty } \left( {\left\| {n}\right\| }_{L^\infty (0,t_1;L^2({\varOmega }))}+{\left\| {n_\delta }\right\| }_{L^\infty (0,t_1;L^2({\varOmega }))}\right) {\left\| {\eta }\right\| }_{H^1({\mathcal {O}}_{t_1})} \end{aligned}$$

This proves existence of a weak solution $n \in V({\mathcal {O}}_{T})$ of (1). Uniqueness follows up to the time $t_0^-$. $\square$

We end this part with a time asymptotic result.

Proposition 1

Under hypotheses 3.1 and supposing that

$$\begin{aligned} d > \lim _{\varrho \rightarrow \infty }Q(\varrho ), \end{aligned}$$

the solution of (1) provides a monotone increasing function $\varrho (t)=\int _0^t \int _{{\varOmega }} s(x) n(\tilde{t},x) dx d\tilde{t}$ that satisfies

$$\begin{aligned} \varrho ^\infty := \lim _{t\rightarrow \infty } \varrho (t) < \infty \end{aligned}$$

Proof

One has

$$\begin{aligned} \frac{d}{dt}\varrho = \int _\mathbb {R} s(x)n(t,x)dx \ge 0, \end{aligned}$$

and thus $\varrho (t)$ is monotone increasing. By contradiction, assume that $\varrho (t)\rightarrow \infty$. Setting $\overline{n}(t) := \int _{{\varOmega }} n(t,x) dx$ and testing the weak formulation with 1 gives

$$\begin{aligned} \left[ \overline{n}(t)+\varrho (t) \right] ^{t=t_2}_{t=t_1} = \int _{t_1}^{t_2} \big [ Q(\varrho (t))-d\big ]\overline{n}(t) dt \end{aligned}$$

Since $d > \lim _{t\rightarrow \infty }Q(\varrho (t))$, for $t_1$ large enough, the right hand side becomes negative implying $\overline{n}(t)+\varrho (t)$ shall not increase any more. This contradicts the assumption $\varrho (t)\rightarrow \infty$. We conclude that $\varrho ^\infty < \infty$. $\square$

3.2 Spectral analysis

In this part, we investigate the spectral decomposition of the solution, in particular under the assumption of piecewise-linear coefficient Q(.).

3.2.1 Spectral decomposition

As it is usual in the field of parabolic equations (Dautray and Lions 1990), one shall try the variable separation. To this aim we consider the spectral problem in the trait-space ${\varOmega }$.

We denote $\mathcal {A}$ the operator defined by:

$$\begin{aligned} \mathcal {A} n(x) = - \mu \partial _{xx}^2 n(x) + s(x) n(x). \end{aligned}$$

Lemma 1

We suppose that s is a bounded function for almost every $x \in {\varOmega }$. We denote the eigenvalues ${\varLambda }_k$ (resp. the eigenvectors $V_k$) of $\mathcal {A}$ the solution of the following equation:

$$\begin{aligned} \left\{ \begin{aligned}&\mathcal {A} V_k = {\varLambda }_k V_k ,&\text { a.e. } x \in {\varOmega },\quad \forall k \in \mathbb {N}\\&\partial _x V_k(-1) = \partial _x V_k(1) = 0,&x \in \partial {\varOmega } \end{aligned} \right. \end{aligned}$$

(4)

All eigenvalues are simple. The sequence of eigenvalues $({\varLambda }_k)_{k\in \mathbb {N}}$ is monotone increasing and positive. The limit of ${\varLambda }_k$ when k goes to infinity is infinite. Moreover the sequence $(V_k)_{k\in \mathbb {N}}$ is an orthonormal basis of $L^2({\varOmega })$. One can bound the eigenvalues, setting $m:= \inf _{x\in {\varOmega }} \min ( \mu , s)$ and $M:= \sup _{x\in {\varOmega }} \max ( \mu ,s)$,

$$\begin{aligned} m \left( \left( \frac{ k \pi }{2} \right) ^2 + 1 \right) \le {\varLambda }_k \le M \left( \left( \frac{ k \pi }{2} \right) ^2 + 1 \right) . \end{aligned}$$

The eigenvector associated to the smallest eigenvalue is positive. The eigenvector associated to the $k^{\text {th}}$ eigenvalue ${\varLambda }_k$ has precisely k zeros on ${\varOmega }$.

Proof

The proof is standard (Coddington and Levinson 1955; Dautray and Lions 1990) and can be found for instance in Zettl (2005) Theorem 4.6.2 p. 87. $\square$

Then we project the initial data on the eigen-basis. The solution n of (1) shall be expressed as a time dependent superposition of modes:

$$\begin{aligned} n = \sum _{k \in \mathbb {N}} \alpha _k(t) V_k(x), \quad \forall (t,x) \in {\mathbb {R}}_+\times {\varOmega } \end{aligned}$$

where the $\alpha _k$ should satisfy

$$\begin{aligned} \left\{ \begin{aligned}&\partial _t\alpha _k + ({\varLambda }_k + d) \alpha _k = Q\left( \sum _k s_k \int _0^t \alpha _k(\tilde{t}) d\tilde{t}\right) \alpha _k ,&k\ge 1\\&s_k = \int _{{\varOmega }} V_k(x) s(x)dx = {\varLambda }_k \int _{{\varOmega }} V_k dx, \\&\alpha _k (0) = \int _{{\varOmega }} V_k(x) n_I(x)dx \end{aligned} \right. \end{aligned}$$

(5)

We now make the assumption that the non-linearity Q is piecewise-constant:

Assumption 3.1

The function Q(.) is piecewise-constant: $Q(\varrho )=Q_0$ for $\varrho \le {\varrho _0}$ and $Q(\varrho )=Q_1$ for $\varrho >{\varrho _0}$.

Under this assumption, and for a time small enough $t<t_0$, i.e before $\rho (t)$ reaches ${\varrho _0}$, one solves explicitly (5) which gives:

$$\begin{aligned} \left\{ \begin{aligned}&\alpha _k = \alpha _k(0) \exp \left( (Q_0 - d - {\varLambda }_k) t\right) ,&t \in [0,t_0[ \\&\alpha _k(0)= <V_k, n_I> \end{aligned} \right. \end{aligned}$$

where $<.,.>$ denotes the usual scalar product on $L^2({\varOmega })$. We denote by ${\varLambda }^0_k := b- {\varLambda }_k$ where $b:=Q_0-d$, so that we can write the solution as:

$$\begin{aligned} n(t,x) = \sum _{k=0}^\infty <n_I,V_k> e^{{\varLambda }^0_k t} V_k(x), \quad t \le t_{{\varrho _0}}\end{aligned}$$

(6)

Let us define:

$$\begin{aligned} t_{{\varrho _0}}= \inf \{t\ge 0;\ \varrho (t)={\varrho _0}\} \end{aligned}$$

(7)

Then, one estimates the value of $t_{{\varrho _0}}$, from the above expression, and solve the system for time greater than $t_{{\varrho _0}}$. To find the value of $t_{{\varrho _0}}$, one solves the non-linear equation ${\varrho _0}=\varrho (t_{{\varrho _0}})$, more precisely:

$$\begin{aligned} {\varrho _0}= \sum _k \phi _k \left( e^{{\varLambda }^0_k t_{{\varrho _0}}} -1 \right) \end{aligned}$$

(8)

with

$$\begin{aligned} \phi _k := \frac{<n_I,V_k> < V_k , s >}{{\varLambda }^0_k}. \end{aligned}$$

It appears relatively difficult to solve analytically (8). However, we will study in Sects. 4 and 5 several approaches to derive asymptotic estimates of this key quantity.

It remains to solve the system for time t larger than $t_{{\varrho _0}}$. The strategy is exactly the same, except that the new eigenvalues are now ${\varLambda }_k^1 = (Q_1-d)-{\varLambda }_k$, and that the new initial condition is $n(t_{{\varrho _0}},x)$, denoted $n_{t_{{\varrho _0}}}(x)$. Therefore, for $t>t_{{\varrho _0}}$:

$$\begin{aligned} n(t,x) = \sum _k <n_{t_{{\varrho _0}}},V_k> e^{{\varLambda }^1_k (t-t_{{\varrho _0}})} V_k(x) \end{aligned}$$

(9)

Since the spectrum of $\mathcal A$ is located on the positive real axis : if $d > Q_1$ then

$$\begin{aligned} \lim _{t\rightarrow \infty } n(t,x) = 0, \quad a.e. \, x \in {\varOmega } \end{aligned}$$

3.2.2 Spectral calculus

We now consider the problem of finding explicit expressions for the eigenvalues and eigenvectors associated with problem (4). To this end, we now make some more assumptions on Q, s and $\mu$:

Assumption 3.2

• 1. The function Q(.) is piecewise-constant: $Q(\varrho )=Q_0$ for $\varrho \le {\varrho _0}$ and $Q(\varrho )=Q_1$ for $\varrho >{\varrho _0}$

• 2. The function s(.) is piecewise-constant: $s(x)=s_\varepsilon (x)=1$ if $x\in [-\varepsilon ,\varepsilon ]\cap {\varOmega }$ and 0 otherwise.

• 3. The function $\mu (.)$ is constant $\mu (x)=\mu >0.$

Notice that $\varepsilon$ is a parameter in (0, 1] that we do not assume, here, to be small. We consider this limit in Sect. 4 instead.

We study the eigen-problem (4) under Assumptions 3.2. This means find the sequence $(V_k,{\varLambda }_k)$ solving

$$\begin{aligned} - \mu V_k'' + s_\varepsilon V_k = {\varLambda }_k V_k, \text { in } ]0,1[ , \quad V_k'(0)=V_k'(1)=0. \end{aligned}$$

On each part of the domain one has a constant coefficient problem that can be solved. Our goal is to construct by composition the complete eigenproblem in this particular case. Converting the second order problem into a first order system one has:

$$\begin{aligned} \left\{ \begin{aligned}&\partial _x{\mathbf {Y}}(x,{\varLambda })= M(x,{\varLambda }) {\mathbf {Y}}(x,{\varLambda }) ,&\text { in } ]0,1[ \\&Y_2(0,{\varLambda })=Y_2(1,{\varLambda })=0,&x \in \{0,1\} \end{aligned} \right. \end{aligned}$$

(10)

where ${{\mathbf {Y}}} = (V_k,\partial _x V_k)^T$. So the complete problem can be solved by piecewise exponentials:

$$\begin{aligned} {\mathbf {Y}}(x,{\varLambda })= {\varPhi } (x,{\varLambda }) {\mathbf {Y}}(0) , \quad {\varPhi } (x,{\varLambda }):= {\left\{ \begin{array}{ll} e^{M({\varLambda }-1) x} &{} \text { if } x < \varepsilon \\ e^{M({\varLambda }) (x-\varepsilon )} e^{M({\varLambda }-1) \varepsilon } &{} \text { if } x > \varepsilon \end{array}\right. }, \end{aligned}$$

and

$$\begin{aligned} M ({\varLambda }) = \begin{pmatrix} 0 &{}\quad 1 \\ - \omega _0^2({\varLambda }) &{}\quad 0 \end{pmatrix} \mathbbm {1}_{(0,\varepsilon )}(x) + \begin{pmatrix} 0 &{}\quad 1 \\ - \omega _1^2({\varLambda }) &{}\quad 0 \end{pmatrix} \mathbbm {1}_{(\varepsilon ,1)}(x) \end{aligned}$$

where $\omega _0^2 := -\frac{s_0-{\varLambda }}{\mu }$ and $\omega _1^2 := \frac{{\varLambda }}{\mu }$. The exponential matrices are then explicit:

$$\begin{aligned} e^{M ({\varLambda }) x}= & {} \begin{pmatrix} \cos (\omega _0 x ) &{} \sin (\omega _0 x ) / \omega _0 \\ -\omega _1 \sin (\omega _0 x ) &{} \cos (\omega _0 x) \end{pmatrix}\mathbbm {1}_{(0,\varepsilon )}(x) \\&+ \begin{pmatrix} \cos (\omega _1 x ) &{} \sin (\omega _1 x ) / \omega _1 \\ -\omega _1 \sin (\omega _1 x ) &{} \cos (\omega _1 x) \end{pmatrix}\mathbbm {1}_{(\varepsilon ,1)}(x). \end{aligned}$$

The boundary problem (10) can be rewritten in an algebraic form:

$$\begin{aligned} T {\mathbf {Y}}(0) = 0 ,\quad T := N_1 + N_2 {\varPhi }(1) , \quad N_1:= \begin{pmatrix} 0&{}\quad 1 \\ 0&{}\quad 0 \end{pmatrix} , \quad N_2:= \begin{pmatrix} 0&{}\quad 0\\ 0&{}\quad 1 \end{pmatrix}, \end{aligned}$$

that has a solution when $\det T = 0$ i.e.

$$\begin{aligned} \left| N_1 + N_2 e^{M({\varLambda })(1-\varepsilon )}e^{M({\varLambda }-1)\varepsilon } \right| =0 \end{aligned}$$

this leads to a simpler condition

$$\begin{aligned} \omega _0 \tan _0 + \omega _1\tan _1 = 0 \end{aligned}$$

where $\tan _j := \tan (\omega _j x_j)$, $j\in \{ 0,1\}$, $x_0=\varepsilon$ and $x_1=(1-\varepsilon )$. As a function of ${\varLambda }$ the latter equation becomes:

$$\begin{aligned} \sqrt{ {\varLambda } - 1} \tan \left( \delta \sqrt{ {\varLambda } - 1}{\mu } \right) + \sqrt{{\varLambda }} \tan ( (1-\delta ) \sqrt{{\varLambda }}) = 0. \end{aligned}$$

(11)

The corresponding eigenvector is

$$\begin{aligned} \begin{aligned} V(x) =\,&\mathbbm {1}_{x\le \varepsilon } \cos (x \omega _0 ) \\&+ \mathbbm {1}_{x\ge \varepsilon } \left\{ \cos (\varepsilon \omega _0) \cos (\omega _1 (x-\varepsilon )) - \sin (\varepsilon \omega _0) \sin (\omega _1(x-\varepsilon )) \frac{\omega _0 }{\omega _1} \right\} , \end{aligned} \end{aligned}$$

(12)

and one should simply take into account whether $\omega _0$ is a pure imaginary or real number in order to pass from hyperbolic to standard trigonometric functions. So there exists a sequence $({\varLambda }_k,V_k)_{k\in \mathbb {N}}$, s.t. for each $k\in \mathbb {N}$, ${\varLambda }_k$ solves (11) and $V_k$ writes as in (12). But, for a given set of data s(x) and $\mu$, ${\varLambda }_k$, the solution (11) is not explicit. In what follows we approximate it by a spectral asymptotic expansion.

4 Asymptotic analysis for narrow selection profiles

In this section, we focus our attention on the case of a narrow selection profile, namely considering that the selection function s(x) can be written as $s(x/\epsilon )$ where $\epsilon$ is a small parameter. In biological terms, this assumption means that selection is very specific, and that only B-cells with a trait very similar to the target are selected.

We first consider this asymptotic regime from the spectral point of view, and then construct an asymptotic expansion of the solution in $\epsilon$. These two approaches enable an asymptotic estimation of the time to threshold, characterizing the duration of the production process until a sufficient level of selected B-cell is reached.

4.1 Asymptotic spectral analysis

4.1.1 Spectrum of auto-adjoint operators with compact inverse

Because the Neumann problem admits a zero eigenvalue we shift the spectrum by adding the identity because then $-{\partial _{x^2}^2} + I$ has an auto-adjoint compact inverse and the spectral theory can be used. Since the shift is artificial and does not change any of the results presented below we omit it—in what follows we return to the original operator. Any time that we mention that the operator has a compact inverse, it is understand in the sense above (i.e., modulo a unit shift).

In a first step we study again problem (4) under assumptions 3.2. Since the operator $\mathcal A$ is auto-adjoint and has a compact inverse from $L^2(0,1)$ into itself $L^2(0,1)$ it admits (see Theorem 6. p. 38 Dautray and Lions 1990) a discrete spectrum that can be arranged into an increasing sequence of real eigenpairs denoted $({\varLambda }_{\varepsilon ,k},V_{\varepsilon ,k})$ for $k\in \mathbb {N}$.

4.1.2 An asymptotic Ansatz

We develop $V_{\varepsilon ,k}$ using an asymptotic expansion, to this purpose we approach $V_{\varepsilon ,k}$ by a series reading

$$\begin{aligned} {\mathcal {V}}_{\varepsilon ,k}(x,y) := v_{0,k}(x,y) + \varepsilon v_{1,k}(x,y) + \varepsilon ^2\pi _{\varepsilon ,2,k}(x,y) \end{aligned}$$

where x represents the slow variable ($x\in (0,1)$) and y the fast variable (typically $y=x/\varepsilon$). Replacing this expansion in the eigen-problem and gathering terms for each power of $\varepsilon$ provides equations at each scale. For instance, at the order $\varepsilon ^{-2}$ one recovers that $v_{0,k}$ does not depend on y, while at order $\varepsilon ^0$ it solves

$$\begin{aligned} \left\{ \begin{aligned}&- \mu v_{0,k}'' = \lambda _{0,k}v_{0,k}, \quad x \in (0,1), \\&v_{0,k}'(0)=v_{0,k}'(1)=0, \end{aligned} \right. \end{aligned}$$

(13)

the solution is explicit : $\lambda _{0,k}:= \mu (k \pi )^2$ for $k\in {\mathbb {Z}}$, whereas normalizing the eigenvectors gives:

$$\begin{aligned} v_{0,k}(x ) = {\left\{ \begin{array}{ll} 1, &{} \text { if } k = 0 \\ \sqrt{2} \cos ( k \pi x),&{} \text { otherwise} \end{array}\right. } \end{aligned}$$

Since $v_{0,k}$ does not solve the original equation, we correct it by adding a second order microscopic corrector $\pi _{\varepsilon ,2,k}(x):=\pi _{2}(x/\varepsilon ) v_{0,k}(x)$ where $\pi _{2}(y)$ solves

$$\begin{aligned} \left\{ \begin{aligned}&- \mu \partial _{y^2}^2 \pi _{2}+ s_0(y) = 0, \quad x \in (0,\infty ), \\&\partial _y\pi _{2}(0)=0. \end{aligned} \right. \end{aligned}$$

(14)

The solution is explicit:

$$\begin{aligned} \pi _{2}(y) = \pi _{2}(0)+ \frac{1}{\mu } \int _0^y \int _0^z s(\tilde{z}) d \tilde{z}d z. \end{aligned}$$

Since all the functions are defined up to a constant we omit them in the rest of the section. If we take the first order derivative of $\pi _{2,k}$ one has:

$$\begin{aligned} \partial _y\pi _{2,k}(y) = \frac{1}{\mu } {\left\{ \begin{array}{ll} \int _0^y s(z) dz &{} \text { if } y<1, \\ \overline{s} := \int _0^1 s(z) dz &{} \text { otherwise }. \end{array}\right. } \end{aligned}$$

In order to reduce the contribution of the growth at infinity of the latter microscopic boundary layer function, we introduce the first order spectral problem: $v_{1,k}$ solves

$$\begin{aligned} \left\{ \begin{array}{ll} - \mu v_{1,k}'' = \lambda _{0,k}v_{1,k}+ \lambda _{1,k}v_{0,k}+ 2 \overline{s} v_{0,k}' , &{}\quad x \in (0,1), \\ v_{1,k}'(0)=0,&{}\quad \text { if } x=0, \\ v_{1,k}'(1)= - \frac{\overline{s} }{\mu } v_{0,k}(1) ,&{}\quad \text { if } x=1. \end{array} \right. \end{aligned}$$

Because the operator $-\partial ^2_{x^2}-\lambda _{0,k}$ admits a kernel of dimension one and is auto-adjoint, the data of this problem should be polar to the kernel of this operator. Therefore, due to this latter condition:

$$\begin{aligned} \lambda _{1,k}:= \frac{ \overline{s} \; v_{0,k}^2 (0)}{{\left\| {v_{0,k}}\right\| }_{L^2(0,1)}^2} = {\left\{ \begin{array}{ll} 2 \overline{s} &{} \text { if } k \ne 0, \\ \overline{s} &{} \text { otherwise. } \end{array}\right. } \end{aligned}$$

Interestingly enough this first order eigen-contribution is independent on $\mu$. The solution of the latter problem then reads (modulo a multiple of $v_{0,k}$)

$$\begin{aligned} v_{1,k}= - \frac{\overline{s}}{\mu } \cdot {\left\{ \begin{array}{ll} x^2/2 &{} \text { if } k = 0, \\ (1-x)\frac{v_{0,k}'(x)}{(k\pi )^2} + x v_{0,k}(x)&{} \text { otherwise} \end{array}\right. } \end{aligned}$$

We compute the problem solved by ${\mathcal {V}}_{\varepsilon ,k}$:

$$\begin{aligned} \begin{aligned} - \mu {\mathcal {V}}_{\varepsilon ,k}'' + s_\varepsilon {\mathcal {V}}_{\varepsilon ,k}=&- \mu v_{0,k}'' + s_\varepsilon v_{0,k}- \varepsilon \mu v_{1,k}'' + \varepsilon s_\varepsilon v_{1,k}\\&- \varepsilon ^2 \mu \left( \frac{\partial ^2_{y^2}\pi _{2,k}(x/\varepsilon )}{\varepsilon ^2} v_{0,k}+ 2 \frac{\partial _y\pi _{2,k}(x/\varepsilon )}{\varepsilon } v_{0,k}' + \pi _{2,k}v_{0,k}''\right) \\&+ \varepsilon ^2 s_\varepsilon \pi _{\varepsilon ,2,k}\\ =&\, (\lambda _{0,k}+ \varepsilon \lambda _{1,k})( v_{0,k}+ \varepsilon v_{1,k}+ \varepsilon ^2 \pi _{\varepsilon ,2,k}) - \varepsilon ^2 ( \lambda _{1,k}v_{1,k}+ \varepsilon \pi _{\varepsilon ,2,k}) \\&+ \varepsilon s_\varepsilon (v_{1,k}+ \varepsilon \pi _{\varepsilon ,2,k}) + 2 \varepsilon \left( \int _x^\varepsilon s(z/\varepsilon ) dz \mathbbm {1}_{(0,\varepsilon )}(x) \right) v_{0,k}' \\ =&\,\lambda _{\varepsilon ,1,k} {\mathcal {V}}_{\varepsilon ,k}+ \varepsilon \left( s_\varepsilon v_{1,k}+ 2 \left( \int _x^\varepsilon s(z/\varepsilon ) dz \mathbbm {1}_{(0,\varepsilon )}(x) \right) v_{0,k}' \right) \\&+ O(\varepsilon ^2). \end{aligned} \end{aligned}$$

where we defined $\lambda _{\varepsilon ,1,k} := \lambda _{0,k}+ \varepsilon \lambda _{1,k}$. We define the bi-continuous bi-linear form associated to the elliptic operator above:

$$\begin{aligned} a_\varepsilon ( u,v) := \int _{{\varOmega }} u'(x) v'(x) dx + s_\varepsilon (x) u(x) v(x) dx \end{aligned}$$

which is coercive on $H^1({\varOmega })$ for any positive definite $\varepsilon$.

Theorem 3

Under the hypotheses on $s_\varepsilon$, and for $\varepsilon _0$ small enough, the tuple $(\lambda _{\varepsilon ,1,k},{\mathcal {V}}_{\varepsilon ,k})$ is a generalized eigen-pair, i.e., it verifies

$$\begin{aligned} \left| a_\varepsilon ({\mathcal {V}}_{\varepsilon ,k},v) - \lambda _{\varepsilon ,1,k} ( {\mathcal {V}}_{\varepsilon ,k},v) \right| \le C_1 (k+1) \pi \varepsilon ^{\frac{3}{2}} {\left\| {{\mathcal {V}}_{\varepsilon ,k}}\right\| }_{L^2(0,1)}{\left\| {v}\right\| }_{L^2(0,1)},\quad \forall v \!\in \! H^1(0,1), \end{aligned}$$

which implies that

$$\begin{aligned} \left| {\varLambda }_{\varepsilon ,k}- \lambda _{\varepsilon ,1,k} \right| \le C_2 (k+1) \pi \varepsilon ^{\frac{3}{2}}. \end{aligned}$$

The constants $C_1$ and $C_2$ depend on s, but not on $\mu$.

Proof

A simple triangular inequality shows that there exists a constant $c_0$ independent on $\varepsilon$ and on k s.t.

$$\begin{aligned} 0< c_0 \le {\left\| {{\mathcal {V}}_{\varepsilon ,k}}\right\| }_{L^2({\varOmega })},\quad \forall k \in \mathbb {N},\; \varepsilon \in (0,\varepsilon _0), \end{aligned}$$

for $\varepsilon _0$ small enough. Then ${\mathcal U}_{\varepsilon }$ being regular (typically ${\mathcal U}_{\varepsilon }\in H^2({\varOmega })$), the error estimates computed above hold as well in the weak formulation associated and lead to estimate from above:

$$\begin{aligned}&\varepsilon \left( \left( s_\varepsilon v_{1,k}+ 2 \left( \int _x^\varepsilon s(z/\varepsilon ) dz \mathbbm {1}_{(0,\varepsilon )}(x) \right) v_{0,k}' \right) ,v\right) _{L^2(0,1)} \\&\quad \le \varepsilon {\left\| {s_\varepsilon }\right\| }_{L^2(0,1)} {\left\| {v_{1,k}}\right\| }_{L^\infty (0,1)}{\left\| {v}\right\| }_{L^2(0,1)} \\&\qquad + 2 \varepsilon {\left\| {s_\varepsilon }\right\| }_{L^\infty } {\left\| {\mathbbm {1}_{0,\varepsilon }}\right\| }_{L^2(0,1)} {\left\| {v_{0,k}'}\right\| }_{L^\infty (0,1)} {\left\| {v}\right\| }_{L^2(0,1)} \\&\quad \le c_1 \varepsilon ^\frac{3}{2}(1 + k ) \pi {\left\| {{\mathcal {V}}_{\varepsilon ,k}}\right\| }_{L^2(0,1)}{\left\| {v}\right\| }_{L^2(0,1)} \end{aligned}$$

while higher order terms are bounded in the $L^\infty (0,1)$ norm with respect to $\varepsilon$ and independent on k. Then we apply Theorem 6 p. 38 in Dautray and Lions (1990), whose proof by contradiction, based on the spectral decomposition of $a_\varepsilon$, can be found in Bendali et al. (2009) and Bendali et al. (2008). $\square$

4.1.3 Numerical comparison

In Fig. 1, we compare the first order approximation of the eigenvalues for the first ten values of k and we display the numerical solution of the characteristic polynomial (11). We choose $\varepsilon =0.1$.

Fig. 1

Numerical comparison between asymptotic and numerical eigen-pairs. On the left the eigenvectors for $k\in \{0,1\}$ and $\varepsilon =0.1$, on the right the eigenvalues for $k\in \{0,\dots ,11\}$

4.1.4 Application: estimation of the time to threshold

We consider the non-linear equation:

$$\begin{aligned} {\varrho _0}= \sum _k {\varPhi }_{\varepsilon ,k} \left( e^{(b-{\varLambda }_{\varepsilon ,k}) t_{{\varrho _0}}} -1 \right) \end{aligned}$$

(15)

with

$$\begin{aligned} {\varPhi }_{\varepsilon ,k} := \frac{{<}n_I,V_{\varepsilon ,k}{>}{<}V_{\varepsilon ,k}, s{>}}{b-{\varLambda }_{\varepsilon ,k}}. \end{aligned}$$

There exists no analytical solution for $t_{{\varrho _0}}$ for the above equation. However, it is possible to obtain an asymptotic description of $t_{{\varrho _0}}$. In Sect. 3.2, we derived an asymptotic expansion of the eigenvalues ${\varLambda }_{\varepsilon ,k}$ and eigenvectors $V_{\varepsilon ,k}$ when $\epsilon \rightarrow 0$ in the form:

$$\begin{aligned} {\varLambda }_{\varepsilon ,k}= \sum _{l\ge 0} \lambda _{l,k} \epsilon ^l \quad \text{ and } \quad V_{\varepsilon ,k}= \sum _{l\ge 0}v_{l,k}\epsilon ^l \end{aligned}$$

(16)

We first show the following:

Lemma 2

Assuming that the following limits exists:

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0}\frac{1}{\varepsilon }\int s(x/\varepsilon ) v_{i,k}(x) dx = \underline{v}_{i,k} \end{aligned}$$

(17)

and that $\lambda _{0,k}\ne b$ for all $k\ge 0$, the coefficient ${\varPhi }_{\varepsilon ,k}$ can be approximated by: ${\varPhi }_{\varepsilon ,k} = \varepsilon \phi _{0,k} + O(\varepsilon ^2)$, with $\phi _{0,k} = \frac{{<}n_I,v_k^0{>}\underline{v}_k^0}{b-\lambda _{0,k}}$.

Proof

By definition,

$$\begin{aligned} {\varPhi }_{\varepsilon ,k} := \frac{{<}n_I,v^{\epsilon }_k{>}{<}s^{\epsilon } , v^{\epsilon }_k>}{b-{\varLambda }^{\epsilon }_k} \end{aligned}$$

(18)

From the asymptotic description of the spectrum, we know that:

$$\begin{aligned} {\varLambda }_{\varepsilon ,k}= & {} \lambda _{0,k} + \varepsilon \lambda _{1,k} + O(\varepsilon ^2) \end{aligned}$$

(19)

$$\begin{aligned} V_{\varepsilon ,k}= & {} v_{0,k} + \epsilon v_{1,k} + O(\varepsilon ^2) \end{aligned}$$

(20)

Therefore, assuming that the following limits exists:

$$\begin{aligned} \lim _{\epsilon \rightarrow 0}\frac{1}{\epsilon }\int s(x/\epsilon ) v_{i,k}(x) dx = \underline{v}_{i,k} \end{aligned}$$

(21)

we obtain:

$$\begin{aligned} {<}s_{\epsilon } , V_{\varepsilon ,k}{>} = \varepsilon \underline{v}_{0,k} + \epsilon ^2 \underline{v}_{1,k} + O(\epsilon ^3) \end{aligned}$$

(22)

Gathering the above estimates, we obtain the desired result. $\square$

An asymptotic description of $t_{{\varrho _0}}$ is given by the following result, which essentially assumes that only the first mode is growing (assumption (iii) below).

Lemma 3

If $t_{{\varrho _0}}$ is the solution of Eq. (15), with:

• (i) ${\varLambda }_{\varepsilon ,k}=\lambda _{0,k}+O(\epsilon )$

• (ii) ${\varPhi }_{\epsilon ,k}=\epsilon \phi _{0,k}+O(\epsilon ^2)$

• (iii) $b-\lambda _{0,0}>0$ and $b-\lambda _{0,k}<0$ for all $k>0$

Then $t_{{\varrho _0}}$ diverges to $+\infty$ when $\epsilon \rightarrow 0$ as:

$$\begin{aligned} t_{{\varrho _0}} = \frac{1}{b-\lambda _{0,0}} \ln \left( \frac{{\varrho _0}}{\phi _{0,0}}\frac{1}{\epsilon }+o\left( \frac{1}{\epsilon }\right) \right) \end{aligned}$$

(23)

Proof

We introduce $x=e^{t_{{\varrho _0}}}$ and look for an expansion of the form:

$$\begin{aligned} x=\frac{x_0}{\epsilon ^{\beta }} + o\left( \frac{1}{\epsilon ^{\beta }}\right) \end{aligned}$$

(24)

First, we write $x^{b-{\varLambda }_{\varepsilon ,k}} = C_{k,\epsilon }\left( \frac{x_0}{\epsilon ^{\beta }}\right) ^{b-\lambda _{0,k}}$ where $C_{k,\epsilon }\rightarrow 1$ when $\epsilon \rightarrow 0$. Furthermore, using assumption (iii), one controls the convergence of $x^{b-{\varLambda }_{\varepsilon ,k}}$ to 0 uniformly in k. Therefore,

$$\begin{aligned} \frac{{\varrho _0}}{\epsilon }= & {} {\varPhi }_{\epsilon ,0}C_{0,\epsilon }\left( \frac{x}{\epsilon ^{\beta }}\right) ^{b-\lambda _{0,0}}-\sum _{k\ge 0}{\varPhi }_{\epsilon ,k} + \sum _{k\ge 1} {\varPhi }_{\epsilon ,k}x^{b-{\varLambda }_{\varepsilon ,k}} \end{aligned}$$

(25)

$$\begin{aligned}= & {} \phi _{0,0} \left( \frac{x_0}{\epsilon ^{\beta }}\right) ^{b-\lambda _{0,0}} + O(1) \end{aligned}$$

(26)

We deduce that

$$\begin{aligned} \frac{{\varrho _0}}{\phi _{0,0} x^{b-\lambda _{0,0}}\epsilon }=\frac{1}{\epsilon ^{\beta (b-\lambda _{0,0})}} \end{aligned}$$

(27)

implying that $\beta =1/(b-\lambda _{0,0})$ and $x_0=({\varrho _0}/\phi _{0,0})^{1/(b-\lambda _{0,0})}$. $\square$

In terms of the original parameters of the model, we conclude that the time to produce an output quantity ${\varrho _0}$ is asymptotically given by:

$$\begin{aligned} t_{{\varrho _0}}=\frac{1}{Q_0-d}\ln \left( \frac{{\varrho _0}(Q_0-d)}{{<}n_I,v_{0,0}{>}\underline{v}_{0,0}}\frac{1}{\epsilon } + o\left( \frac{1}{\epsilon }\right) \right) \end{aligned}$$

(28)

This formula relates in a compact form the birth rate $Q_0$, the death rate d, the width of the selection function $\epsilon$, the mutation rate $\mu$ and the initial condition $n_I$ to the characteristic time-scale of the B-cell production process. Notice that this formula relies on the assumption that only the first mode grows, meaning that $\mu$ must be larger than $(Q_0-d)/\pi ^2$. Numerical comparison between the time $t_{{\varrho _0}}$ computed from the numerical solution of the PDE and this formula is displayed in Fig. 2. From the spectral decomposition, we learn that decreasing the mutation rate $\mu$ has the effect of recruiting further modes, whereas a large $\mu$ implies that the evolution of the solution forgets the other modes which were present in the initial condition.

Fig. 2

Time to threshold $t_{{\varrho _0}}$ as a function of the threshold parameter $\rho _0$ in log-scale. The crosses are obtained by a direct numerical simulations of the PDE model with constant birth-rate Q. The line is obtained by evaluating formula (28) at first order, i.e., discarding the terms of $o(1/\epsilon )$. Parameters: $b=Q-d=0.1$, $\epsilon =0.01$

4.2 Asymptotic expansion

4.2.1 Asymptotic expansion of the solution

When Q is piecewise constant, using the notation $b= Q_0 -d$, n(t, x), the solution of (1), solves as well the following linear problem, until $\rho (t)$ reaches $\rho _0$:

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _tn_\varepsilon - \mu {\partial _{x^2}^2} n_\varepsilon = (b-s_\varepsilon ) n_\varepsilon &{}\quad (t,x) \in {\mathcal {O}}_T,\\ \partial _xn_\varepsilon (t,x)= 0&{}\quad (t,x) \in {\varSigma }_T,\\ n_\varepsilon (0,x)=n_I(x)&{}\quad (t,x) \in \{ 0 \} \times {\varOmega }\\ \end{array} \right. \end{aligned}$$

(29)

Dropping the balance term between death and birth, we look for an approximation of the solution of:

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _t{\mathcal {N}}_\varepsilon - \mu {\partial _{x^2}^2} {\mathcal {N}}_\varepsilon +s_\varepsilon {\mathcal {N}}_\varepsilon = 0, &{}\quad (t,x) \in {\mathcal {O}}_T,\\ \partial _x{\mathcal {N}}_\varepsilon =0, &{}\quad (t,x) \in {\varSigma }_T,\\ {\mathcal {N}}_\varepsilon (0,x) = n_I(x),&{}\quad (t,x) \in \{ 0\} \times {\varOmega }. \end{array} \right. \end{aligned}$$

(30)

We make the Ansatz:

$$\begin{aligned} {\mathcal {N}}_\varepsilon = {\mathcal {N}}_0\left( t,x,\frac{x}{\varepsilon } \right) + \varepsilon {\mathcal {N}}_1\left( t,x,\frac{x}{\varepsilon } \right) + \cdots \end{aligned}$$

When we plug it in (30), it gives after separating orders of $\varepsilon$ that ${\mathcal {N}}_{0}(t,x,y)$ is independent of the fast variable y. Moreover, it solves the homogeneous equations:

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _t{\mathcal {N}}_0 - \mu {\partial _{x^2}^2} {\mathcal {N}}_0 = 0, &{} (t,x) \in {\mathcal {O}}_T\\ \partial _x{\mathcal {N}}_0 = 0,&{} (t,x) \in {\varSigma }_T\\ {\mathcal {N}}_0(0,x)= n_I(x) (t,x) \in \{ 0 \} \times {\varOmega }, \end{array} \right. \end{aligned}$$

(31)

and thus ${\mathcal {N}}_0(t,x) = \sum _{k \in \mathbb {N}} \overline{n}_I^k \exp (-\lambda _{0,k} t) v_k(x)$.

Proposition 2

If $n_I\in L^2({\varOmega }) \cap L^\infty ({\varOmega })$ then at zeroth order, one can approach $n_\varepsilon (t,x)$ solving (29) by $\exp (b t){\mathcal {N}}_0(t,x)$ and the error in the $L^\infty ((0,T); L^2({\varOmega }))$ norm is estimated as:

$$\begin{aligned} \sup _{t \in (0,T)}{\left\| {n_\varepsilon (t,\cdot ) - \exp (b t ){\mathcal {N}}_0(t,\cdot )}\right\| }_{L^2({\varOmega })} \le \varepsilon \exp (bT) T {\left\| {n_I}\right\| }_{L^\infty ({\varOmega })}. \end{aligned}$$

Proof

One defines the zero order error:

$$\begin{aligned} {\mathcal {E}}_0(t,x) := {\mathcal {N}}_\varepsilon (t,x) - {\mathcal {N}}_0(t,x) \end{aligned}$$

which solves in the strong sense

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _t{\mathcal {E}}_0- \mu {\partial _{x^2}^2} {\mathcal {E}}_0+ s {\mathcal {E}}_0= -s {\mathcal {N}}_0, &{}\quad (t,x) \in {\mathcal {O}}_T\\ \partial _x{\mathcal {E}}_0= 0,&{}\quad (t,x) \in {\varSigma }_T\\ {\mathcal {E}}_0(0,x)= 0, &{}\quad (t,x) \in \{ 0 \} \times {\varOmega }, \end{array} \right. \end{aligned}$$

using standard a priori estimates, one obtains that

$$\begin{aligned} \frac{1}{2}\partial _t{\left\| { {\mathcal {E}}_0(t,\cdot ) }\right\| }_{L^2({\varOmega })}^2 \le {\left\| { s {\mathcal {N}}_0 }\right\| }_{L^2({\varOmega })} {\left\| {{\mathcal {E}}_0}\right\| }_{L^2({\varOmega })} \end{aligned}$$

which then by dividing both sides by $\sqrt{{\left\| {{\mathcal {E}}_0}\right\| }_{L^2({\varOmega })}^2+ \delta }$ one gets:

$$\begin{aligned} \frac{1}{2}\partial _t\sqrt{ {\left\| { {\mathcal {E}}_0(t,\cdot ) }\right\| }_{L^2({\varOmega })}^2 + \delta } \le {\left\| { s {\mathcal {N}}_0 }\right\| }_{L^2({\varOmega })} . \end{aligned}$$

This, integrated in time, provides after passing to the limit $\delta \rightarrow 0$,

$$\begin{aligned} {\left\| { {\mathcal {E}}_0(t,\cdot ) }\right\| }_{L^2({\varOmega })} \le \int _0^t {\left\| { s(\cdot ) {\mathcal {N}}_0({\tilde{t}},\cdot ) }\right\| }_{L^2({\varOmega })} d{\tilde{t}}\le \varepsilon t {\left\| {{\mathcal {N}}_0}\right\| }_{L^\infty ((0,t)\times {\varOmega })} \le {\left\| {n_I}\right\| }_{L^\infty ({\varOmega })} \varepsilon t \end{aligned}$$

where we used the maximum principle in order to provide the $L^\infty$ bound on ${\mathcal {N}}_0$ and the result follows. $\square$

4.2.2 Estimation of the time to threshold

Using asymptotic expansions above, we estimate the time $t_{{\varrho _0}}$:

Theorem 4

If s satisfies hypotheses 3.2, and $\mu > b/\pi ^2$, then for every given ${\varrho _0}$ , there exists a time

$$\begin{aligned} t_{{\varrho _0}} := \frac{1}{b} \ln \left( 1+ \frac{ {\varrho _0}b}{\varepsilon \overline{n}_0} \right) , \end{aligned}$$

(32)

and a constant C independent on $t_{{\varrho _0}}$ s.t.

$$\begin{aligned} \left| {\varrho _0}- \varrho _\mathrm{out}(t_{{\varrho _0}}) \right| \le |\ln (\varepsilon )| \sqrt{\varepsilon } C(\mu ,n_I) \end{aligned}$$

Proof

The previous proposition allows to compute $\varrho _{\text { app}}$, an approximation of $\varrho _\mathrm{out}$ which reads:

$$\begin{aligned} \varrho _{\text { app}}(t):= & {} \int _0^t \int _{{\varOmega }} s(x) {\mathcal {N}}_0(t,x) \exp (b {\tilde{t}}) dx d{\tilde{t}}\\= & {} \frac{(\exp (b t) -1)}{b} \int _{{\varOmega }} n_I(x) dx \int _{{\varOmega }} s(\tilde{x}) d\tilde{x} + \sum _{k \in \mathbb {N}^*} \frac{\left( \exp ( (b-\lambda _k) t )-1 \right) }{(b-\lambda _k)} \\&\,\times {<}n_I,v_k{>} {<}s , v_k{>} \end{aligned}$$

where $(\lambda _k)_{k\in \mathbb {N}}$ denote eigenvalues associated to the homogeneous heat equation (31). Under hypotheses 3.2, the previous computation gives

$$\begin{aligned} \varrho _{\text { app}}(t) := \varepsilon \frac{(\exp (b t) -1)}{b}\overline{n}^0_I + \sum _{k \in \mathbb {N}^*} \frac{\left( \exp ( (b-\lambda _k) t )-1 \right) }{(b-\lambda _k)} {<}n_I,v_k{>} {<}s , v_k{>} \end{aligned}$$

Using Cauchy-Schwartz, one has that

$$\begin{aligned} \begin{aligned}&\left| \varrho _\mathrm{out}(t) - \varrho _{\text { app}}(t) \right| \le \int _0^t \int _{\varOmega } s | n(t,x) - \exp (b \,t) {\mathcal {N}}_0({\tilde{t}},x) | dx d{\tilde{t}}\\&\quad \le \int _0^t {\left\| {s}\right\| }_{L^2(\omega )} {\left\| {n(t,\cdot ) -\exp (b {\tilde{t}}) {\mathcal {N}}_0({\tilde{t}},\cdot )}\right\| }_{L^2({\varOmega })} d{\tilde{t}}\le \varepsilon ^{\frac{3}{2}} {\left\| {n_I}\right\| }_{L^\infty ({\varOmega })} \\&\qquad \times \int _0^t \exp (b {\tilde{t}}) {\tilde{t}}d{\tilde{t}}\le \varepsilon ^{\frac{3}{2}} {\left\| {n_I}\right\| }_{L^\infty ({\varOmega })} \frac{ t \exp (b t) }{b} \end{aligned} \end{aligned}$$

On the other hand using the explicit expression of $\varrho _{\text { app}}$ one writes:

$$\begin{aligned} \begin{aligned} \left| \varrho _{\text { app}}- \left( \frac{ \exp (bt)-1 }{b} \right) \overline{n}^0_I \overline{s} \right|&\le S(t) \sum _{k \in \mathbb {N}^*} | {<} n,v_k {>} {<}s, v_k{>} | \\&\le S(t) {\left\| {s}\right\| }_{L^2({\varOmega })} {\left\| {n_I}\right\| }_{L^2({\varOmega })} \le S(t) \sqrt{\varepsilon } {\left\| {n_I}\right\| }_{L^2({\varOmega })} \end{aligned} \end{aligned}$$

(33)

where we denoted $S(t):=\sup _{k \in \mathbb {N}^*} \left| \frac{ \exp ( (b -\lambda _k) t) -1 }{(b-\lambda _k)}\right|$. Then two cases occur:

• (i) either there exists $k_0$ s.t. $\lambda _{k_0} \le b \le \lambda _{k_0+1}$ and then

  $$\begin{aligned} S(t) \le \frac{ \exp ( (b-\mu \pi ^2) t) -1}{ b- \lambda _{k_0}}, \end{aligned}$$

• (ii) or $b<\lambda _1=\mu \pi ^2$ and thus

  $$\begin{aligned} S(t) \le \frac{2}{(\lambda _1-b)} = \frac{2}{(\mu \pi ^2 -b)}, \end{aligned}$$

  which justifies our hypothesis between b and $\mu$.

Using a triangular inequality gives:

$$\begin{aligned} | \varrho _\mathrm{out}(t_{{\varrho _0}}) - {\varrho _0}| \le \left| \varrho _\mathrm{out}(t_{{\varrho _0}}) - \varrho _{\text { app}}(t_{{\varrho _0}}) \right| + \left| \varrho _{\text { app}}(t_{{\varrho _0}}) - {\varrho _0}\right| \end{aligned}$$

which, because of the estimates ii) above, gives

$$\begin{aligned} | \varrho _\mathrm{out}(t_{{\varrho _0}}) - {\varrho _0}| \le C \left( \varepsilon ^{\frac{3}{2}} t_{{\varrho _0}} \exp (b t_{{\varrho _0}}) + \sqrt{\varepsilon } \right) \le C \sqrt{\varepsilon } | \ln (\varepsilon ) |. \end{aligned}$$

$\square$

Remark 1

In fact, if b is large enough [case (i) above], the previous estimate does not hold since in this case $S(t_{{\varrho _0}})$ blows as $1/\varepsilon$.

Remark 2

Due to (33), one can not, to our knowledge, improve the accuracy when computing $t_{{\varrho _0}}$ by increasing the order of the asymptotic expansion since the major source of error comes from this step, when integrating in the selection window the zero order term.

4.2.3 Numerical simulation

The parameters we choose are ${\varrho _0}=100, b=2$ together with a random initial condition $n_I$. We compute the error between $t_{{\varrho _0}}^{h,k}$, the time to reach ${\varrho _0}$ and the theoretical formula (32). The direct simulation is made using a P1-Finite Element Method with first order implicit Euler scheme for the time discretization. The same numerical tools are used for the rest of the paper. Results are displayed for various (small) values of $\varepsilon$. We plot, in Fig. 3, the error estimates for two values of $\mu$ corresponding to $\mu = b/((k+1/2)^2 \pi ^2$ for $k\in \{0,1\}$. When $k=0$ we are in the hypotheses of the latter theorem, whereas for $k=1$ the theoretical error is not uniform with respect to $\varepsilon$. For this specific test-case, the error is comparable in both cases, although greater as $\mu$ becomes smaller as expected. The numerical order of convergence is greater than what is predicted theoretically.

Fig. 3

Starting from a random initial condition, the difference between the numerical $t_{{\varrho _0}}^{h,k}$ and the limit time to reach $t_{{\varrho _0}}$ for various values of $\varepsilon$

5 Asymptotic analysis for small and large mutation rates

In this section, we focus on the regimes of small and large mutation rates. We first consider the case of initial conditions restricted to a single trait (Dirac initial data), deriving explicit solutions in this case, and providing asymptotics for the time to threshold. Then, we establish asymptotic expansions of the solution in the regimes $\mu \ll 1$ and $\mu \gg 1$.

5.1 The initial condition is a Dirac mass

5.1.1 The case of the whole space

When the size of the domain goes to infinity we face the problem

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _t{\mathcal G}_\varepsilon - \mu {\partial _{x^2}^2} {\mathcal G}_\varepsilon + s_\varepsilon {\mathcal G}_\varepsilon = b {\mathcal G}_\varepsilon ,&{}\quad (t,x)\in {\mathbb {R}}_+\times {\mathbb {R}}, \\ {\mathcal G}_\varepsilon (0,x)=\delta _z(x),&{}\quad x \in {\mathbb {R}}, \end{array} \right. \end{aligned}$$

(34)

Definition 5.1

We define a very weak solution of (34) the function ${\mathcal G}_\varepsilon \in L^2(0,T\times {\mathbb {R}})$ that solves:

$$\begin{aligned} \int _{(0,T)\times {\mathbb {R}}} {\mathcal G}_\varepsilon \left( - \partial _t- {\partial _{x^2}^2} +(s_\varepsilon (x)-b) \right) \varphi dx dt - \varphi (0,z) = 0 \end{aligned}$$

for every $\varphi \in C(0,T;H^1({\mathbb {R}})) \cap L^2(0,T;H^2({\mathbb {R}}))$ s.t. $\varphi (T,x)=0$, $\forall x \in (0,1)$.

Theorem 5

Providing $s_\varepsilon \in L^\infty ({\mathbb {R}})$ there exists a unique very weak function ${\mathcal G}_\varepsilon \in L^2((0,T)\times {\mathbb {R}})$ solving (34). Moreover one has the comparison principle:

$$\begin{aligned} \tilde{{\mathcal {G}}}_{b-s_\infty }(t,x,z) \le {\mathcal G}_\varepsilon (t,x,z) \le \tilde{{\mathcal {G}}}_{b} (t,x,z), \quad \text { a.e } (t,x) \in (0,T) \times {\mathbb {R}}\end{aligned}$$

where $\tilde{{\mathcal {G}}}_b$ is the fundamental solution of the heat equation and reads :

$$\begin{aligned} \tilde{{\mathcal {G}}}_b(t,x,z) = \frac{1}{\sqrt{ 4 \mu \pi t} }\exp \left( b t - \frac{ (x-z)^2 }{ 4 \mu t} \right) , \end{aligned}$$

and $s_\infty := {\left\| {s}\right\| }_{L^\infty ({\mathbb {R}})}$.

Proof

The proof of existence and uniqueness relies on duality arguments and the Riesz Theorem and is left to the reader for sake of conciseness. We detail the comparison principle. The maximum principle shows that if we define the backward equation :

$$\begin{aligned} \left\{ \begin{array}{ll} - \partial _t\varphi - {\partial _{x^2}^2} \varphi + {\mathfrak b} \varphi = {\varPsi }, &{} \quad (t,x) \in {\mathcal {O}}_T\\ \partial _x\varphi = 0, &{} \quad (t,x) \in {\varSigma }_T\\ \varphi (T,0) = 0, &{} \quad (t,x) \in \{T\} \times {\varOmega }\\ \end{array} \right. \end{aligned}$$

(35)

where ${\mathfrak b}$ is a bounded function in ${\mathcal {O}}_T$, ${\varPsi } \in \mathcal {D}({\mathcal {O}}_T)$ and ${\varPsi } (t,x) \ge 0$ for all $(t,x) \in {\mathcal {O}}_T$, then $\varphi (t,x) \ge 0$. Indeed, testing the forward expression of the previous equation in the weak form with $\varphi _h^- := \min (\varphi _h,0)$ where $\varphi _h$ is a Steklov approximation of $\varphi$ i.e.,

$$\begin{aligned} \varphi _h (t,x) = \frac{1}{h} \int _t^{t+h} \varphi (\tau ,x) d \tau \end{aligned}$$

and passing then to the limit with respect to h, one has

$$\begin{aligned}&\frac{1}{2}\left[ {\left\| {\varphi ^-(\tau ,\cdot )}\right\| }_{L^2({\varOmega })}^2 \right] _{\tau =0}^{\tau =T} + \int _{{\mathcal {O}}_T} {\mathfrak b}^+ \varphi \varphi ^- \, dx\, dt \le - \int _{{\mathcal {O}}_T} {\mathfrak b}^- \varphi \varphi ^- \\&\quad \le {\left\| {-{\mathfrak b}^-}\right\| }_{L^\infty ({\mathcal {O}}_T)} {\left\| {\varphi ^-}\right\| }_{L^2({\varOmega })}^2 \end{aligned}$$

by Gronwall, the result comes easily.

The difference between ${\mathcal G}_\varepsilon$ and $\tilde{{\mathcal {G}}}_{b-s_\infty }$ that we denote ${\hat{\mathcal {G}}}:= {\mathcal G}_\varepsilon -\tilde{{\mathcal {G}}}_{b-s_\infty }$ solves

$$\begin{aligned} \begin{aligned} \int _{{\mathcal {O}}_T} {\hat{\mathcal {G}}}\left\{ - \partial _t\varphi - \partial ^2_{x^2} \varphi + (s_\varepsilon -b) \varphi \right\} dx dt = \int _{{\mathcal {O}}_T} \left\{ s_\infty -s_\varepsilon \right\} \tilde{{\mathcal {G}}}_{b-s_\infty }(t,x) \varphi (t,x) dx dt \end{aligned} \end{aligned}$$

As $\tilde{{\mathcal {G}}}_{b-s_\infty }(t,x)$ is non-negative for a.e. $(t,x) \in (0,T)\times {\varOmega }$, and choosing ${\mathfrak b}:= (s_\varepsilon -b)$ in the dual problem (35), with ${\varPsi } \in \mathcal {D}({\mathcal {O}}_T)$ and ${\varPsi } \ge 0$, proves that ${\hat{\mathcal {G}}}$ is positive almost everywhere in ${\mathcal {O}}_T$. $\square$

Lemma 4

Suppose that $a \in {\mathbb {R}}_+$ and set $J_a(t) := \int _0^t \exp \left( a t -\frac{1}{t} \right) \frac{d{\tilde{t}}}{\sqrt{{\tilde{t}}}}$ then

$$\begin{aligned} J_a(t) \ge \frac{1}{ 2 e } \exp \left( - \frac{2}{t} \right) , \quad \forall t\ge 0. \end{aligned}$$

Proof

Using Jensen’s inequality one writes

$$\begin{aligned} \begin{aligned} J_a(t)&\ge \int _0^t \exp \left( - \frac{1}{{\tilde{t}}} \right) \frac{ d{\tilde{t}}}{\sqrt{{\tilde{t}}}} = \int _{1/t}^\infty \exp (- z) \frac{ d z}{z^{\frac{3}{2}}} \ge \left( \int _{1/t}^\infty \exp (-z) dz \right) \\&\quad \times \left( \frac{\int _{1/t}^\infty \exp (-z) z dz}{\int _{1/t}^\infty \exp (-z) dz} \right) ^{-\frac{3}{2}} \\&= \exp \left( - \frac{1}{t} \right) \left( \frac{t}{t+1} \right) ^{\frac{3}{2}} \ge \exp \left( - \frac{1}{t} \right) \frac{1}{2}\exp \left( - \frac{ t+1}{t} \right) = \frac{1}{2 e} \exp \left( - \frac{2}{t} \right) \end{aligned} \end{aligned}$$

The last inequality comes when estimating $t^\frac{3}{2}$ by an exponential, i.e. $\forall t \ge 0 , \quad \exp \left( - \frac{1}{t} \right) < 2 t^{\frac{3}{2}}$. $\square$

Theorem 6

We suppose that $s_\varepsilon$ is the characteristic function of the set $(-\varepsilon ,\varepsilon )$ and that $z > \varepsilon$. If we denote the time $t_{{\varrho _0}}$ s.t. $\rho _{\varepsilon }(t) := \int _0^t \int _{{\mathbb {R}}} s(x) {\mathcal G}_\varepsilon (t,x,z) dx dt$ reaches ${\varrho _0}$, one has that $t_{{\varrho _0}} \rightarrow \infty$ when either $\mu \rightarrow 0$ or $\mu \rightarrow \infty$. Moreover $t_{{\varrho _0}}$ does not grow faster than any polynomial with respect to $\mu$.

Proof

We shall provide a lower bound for $I_{\ell }(t) := 2 \varepsilon \int _0^t \tilde{{\mathcal {G}}}_{b-s_\infty }(t,-\varepsilon ,z) dt$ and un upper bound for $I_u(t) := 2 \varepsilon \int _0^t$ $\tilde{{\mathcal {G}}}_{b}(t,\varepsilon ,z) dt$. If there exists a time $t_u$ (resp. $t_{\ell }$) s.t. $I_{\ell }(t_u) \ge {\varrho _0}$ (resp. $I_u(t_{\ell }) \le {\varrho _0}$) then $t_{{\varrho _0}} \le t_u$ (resp. $t_{{\varrho _0}} \ge t_{\ell }$).

Because the lower bound from Lemma 4 is not accurate for large values of t, we distinguish two cases:

• Either $t<t_0 := (z+\varepsilon )/(2 \sqrt{(b+ s_\infty )\mu })$ and one uses Lemma 4:

  $$\begin{aligned} I_{\ell }(t) \ge \frac{\varepsilon (z+\varepsilon )}{4 \mu e\sqrt{\pi }} \exp \left( - \frac{ (z+\varepsilon )^2}{ 2 \mu t} \right) =: j_1(t). \end{aligned}$$

• Or $t>t_0$ and we split the integral $I_{\ell }$ in two parts : integrating first on $(0,t_0)$ and then on $(t_0,t)$. The first part is estimated thanks to Lemma 4 again, whereas for the latter integral one writes:

  $$\begin{aligned} \begin{aligned} I_{\ell }(t)&\ge j_1(t_0) + \frac{\exp (-(b-s_\infty ) t_0)}{\sqrt{ \mu \pi }} \int _{t_0}^t \exp ((b-s_\infty ) {\tilde{t}}) \frac{d{\tilde{t}}}{\sqrt{{\tilde{t}}}} \\&\ge j_1(t_0) + \frac{\exp (-(b-s_\infty ) t_0)}{\sqrt{ \mu \pi } k ! } \int _{t_0}^t (b-s_\infty )^k {\tilde{t}}^{k-\frac{1}{2}} d{\tilde{t}}\\&= j_1(t_0) + \frac{\exp (-(b-s_\infty ) t_0)}{\sqrt{ \mu \pi } k ! (k+\frac{1}{2})} (b-s_\infty )^k \left[ {\tilde{t}}^{k+\frac{1}{2}} \right] _{{\tilde{t}}= t_0}^{{\tilde{t}}= t} =:j_2(t). \end{aligned} \end{aligned}$$

  since for larger times the linear term $(b-s_\infty )\,t$ dominates $(z+\varepsilon )^2/(4\mu t)$ inside the exponential.

Inverting the latter piecewise formula, one obtains

$$\begin{aligned} t_u := {\left\{ \begin{array}{ll} j_1^{-1}( {\varrho _0}) &{} \text { if }{\varrho _0}< j(t_0), \\ j_2^{-1} ( {\varrho _0}) &{} \text { otherwise }, \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned} j_1^{-1} ( {\varrho _0}):= & {} \frac{ (z+\varepsilon )^2 }{-2 \ln \left( \frac{{\varrho _0}4 e\mu }{ \varepsilon (z + \varepsilon ) } \right) },\, \text { and } \, j_2^{-1} ( {\varrho _0}) \\:= & {} \left( \frac{( k + \frac{1}{2}) k! \sqrt{ \pi \mu } }{(b-s_\infty )^k} \exp ((b-s_\infty ) t_0) ({\varrho _0}- j_1(t_0)) + t_0^{k+\frac{1}{2}}\right) ^{\frac{1}{k + \frac{1}{2}}}. \end{aligned}$$

This proves the second part of the claim.

In order to provide a lower bound $t_{\ell }$, we estimate $\varrho _\mathrm{out}$ by $I_u$. Indeed we write:

$$\begin{aligned} I_u (t) \le \frac{2 \varepsilon }{\sqrt{ \mu \pi }} \exp \left( b t -\frac{(z-\varepsilon )^2}{4\mu t} \right) \sqrt{t} \le \frac{2 \varepsilon }{\sqrt{ \mu \pi }} \exp \left( (b+1) t -\frac{(z-\varepsilon )^2}{4\mu t} \right) \end{aligned}$$

this gives that

$$\begin{aligned} t_{\ell } := \frac{ \ln \omega + \sqrt{ \ln ^2 \omega + (z-\varepsilon )^2(b+1)/\mu } }{2 (b+1)} , \quad \omega :=\left( {\varrho _0}/2 \varepsilon \sqrt{ \pi } \right) \sqrt{\mu } \end{aligned}$$

which proves the first part of the claim. $\square$

In the previous proof the results remain identical if $z<-\varepsilon$ by symmetry. We plot in Fig. 4, left, the comparison between our bounds and numerical computations of the integrals $I_l$ and $I_u$ for a given set of data $(b,{\varrho _0},\varepsilon ,z)$ when $\mu$ varies : $t_{{\varrho _0}}$ is always between the $t_{I_u}$ and $t_{I_l}$ curves.

5.1.2 The case of a bounded domain

We consider the problem: find ${\mathcal G}_\varepsilon$ solution of

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _t{\mathcal G}_\varepsilon - \mu {\partial _{x^2}^2} {\mathcal G}_\varepsilon + s_\varepsilon {\mathcal G}_\varepsilon = b {\mathcal G}_\varepsilon ,&{}\quad (t,x)\in {\mathbb {R}}_+\times (0,1), \\ {\mathcal G}_\varepsilon '(t,0)={\mathcal G}_\varepsilon '(t,1)=0,&{}\quad t\in {\mathbb {R}}_+, \\ {\mathcal G}_\varepsilon (0,x)=\delta _z(x),&{}\quad x \in (0,1), \end{array} \right. \end{aligned}$$

(36)

where the support of the dirac mass is located in $z \in (0,1)$.

Theorem 7

If $s \in L^\infty (0,1)$ and $b\in {\mathbb {R}}$, there exists a unique very weak solution ${\mathcal G}_\varepsilon \in L^2({\mathcal {O}}_T)$ for every given positive T i.e.,

$$\begin{aligned} \int _{(0,T)\times {\mathbb {R}}} {\mathcal G}_\varepsilon \left( - \partial _t- {\partial _{x^2}^2} +(s(x)-b) \right) \varphi dx dt - \varphi (0,z) = 0 \end{aligned}$$

for every test function $\varphi \in C([0,T];H^1((0,1)))\cap L^2((0,T); H^2((0,1)))$. Moreover, one has for a.e. $(t,x)\in {\mathcal {O}}_T$:

$$\begin{aligned} \tilde{{\mathcal {G}}}_{b-s_{\infty }} (t,x,z) \le {\mathcal G}_\varepsilon (t,x,z) \le \tilde{{\mathcal {G}}}_b(t,x,z), \end{aligned}$$

the bounds being fundamental solutions of the heat equation with Neumann boundary conditions:

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _t\tilde{{\mathcal {G}}}_b- \mu {\partial _{x^2}^2} \tilde{{\mathcal {G}}}_b= b \tilde{{\mathcal {G}}}_b,&{}\quad (t,x)\in {\mathbb {R}}_+\times (0,1), \\ \tilde{{\mathcal {G}}}_b'(t,0)=\tilde{{\mathcal {G}}}_b'(t,1)=0,&{}\quad t\in {\mathbb {R}}_+, \\ \tilde{{\mathcal {G}}}_b(0,x)=\delta _z(x),&{}\quad x \in (0,1), \end{array} \right. \end{aligned}$$

(37)

given explicitly as series by the formula:

$$\begin{aligned} \tilde{{\mathcal {G}}}_b(t,x,z) := \frac{\exp (bt)}{\sqrt{4 \pi \mu t} }\sum _{n \in {\mathbb {Z}}} \left\{ \exp \left( {- \frac{(x-2n+z)^2}{4 \mu t}}\right) + \exp \left( {-\frac{ (x-2n-z)^2}{4 \mu t}}\right) \right\} . \end{aligned}$$

We need here two technical lemmas:

Lemma 5

If $x\in (0,\varepsilon )$ and $z\in (\varepsilon ,1)$ and $t\ge 0$ then

$$\begin{aligned} \tilde{{\mathcal {G}}}_b(t,x,z) \le \exp \left( bt - \frac{(z-\varepsilon )^2}{4\mu t}\right) \left( \frac{4}{\sqrt{4 \pi \mu t}} + \frac{2}{\sqrt{2 ( 1-\varepsilon )} }\right) . \end{aligned}$$

The proof uses an upper bound of the higher order terms ($|n|\ge 1$) in the expansion above, and is skipped for sake of conciseness.

Lemma 6

Setting

$$\begin{aligned} \tilde{\rho }_{b} (t,z) := \int _0^t \int _0^\varepsilon \tilde{{\mathcal {G}}}_b({\tilde{t}},x,z)dx d{\tilde{t}}, \end{aligned}$$

we fix $\varepsilon >0$, $z\in (\varepsilon ,1)$,

$$\begin{aligned} \tilde{\rho }_{b} (t,z) \le \varepsilon \frac{\exp \left( (b+1)t - \frac{(z-\varepsilon )^2}{4\mu t}\right) }{\sqrt{4 \mu \pi }} \left( 1 + \sqrt{\frac{2 \mu }{(1-\varepsilon )}} \right) , \end{aligned}$$

the time that $\tilde{\rho }_{b}$ reaches ${\varrho _0}$ is then greater than

$$\begin{aligned} t_0 := \frac{ \ln \omega + \sqrt{ \ln ^2 \omega + \frac{(z-\varepsilon )^2}{ \mu } } }{2 (b+1)}, \,\text { and }\, \omega := \frac{ 2 {\varrho _0}\sqrt{(1-\varepsilon )\mu \pi }}{ \varepsilon ( \sqrt{1-\varepsilon } + \sqrt{2 \mu } ) }. \end{aligned}$$

If $\mu$ is small then

$$\begin{aligned} t_0 \sim \frac{| z-\varepsilon | }{2 (b+1)} \frac{1}{\sqrt{\mu }}. \end{aligned}$$

When $\mu \rightarrow \infty$,

$$\begin{aligned} t_0 \rightarrow \frac{1}{(b+1)} \ln \left( \frac{{\varrho _0}\sqrt{2 \pi (1-\varepsilon )} }{\varepsilon }\right) . \end{aligned}$$

Proof

Thanks to the previous results there exists a $t_1$ s.t. $\tilde{\rho }_b(t_1) > {\varrho _0}$. This implies that $t_b$, the time such that $\tilde{\rho }_b(t) > {\varrho _0}$ for all $t>t_b$ is greater than $t_1$. As in turn $t_0\ge t_b$ this ends the proof. $\square$

Lemma 7

If $(x,z)\in (0,1)^2$, the fundamental solution can be estimated from below as:

$$\begin{aligned} \tilde{{\mathcal {G}}}_b(t,x,z) \ge \exp \left( b t - \frac{(x+z)^2}{4 \mu t}\right) \left\{ \frac{1}{\sqrt{4 \pi \mu t} }+ \frac{1}{4\sqrt{3}} \mathrm{erfc}\left( \sqrt{ \frac{ 3}{ \mu t } }\right) \right\} . \end{aligned}$$

Proof

We write simply that:

$$\begin{aligned}&\sum _{|n| \ge 1} \exp \left( bt - \frac{(x+z-2 n )^2}{4 \mu t}\right) \ge \exp \left( bt - \frac{(x+z )^2}{4 \mu t}\right) \\&\qquad \times \sum _{|n| \ge 1} \exp \left( - \frac{(x+z) |n| }{\mu t} - \frac{n^2}{\mu t} \right) \\&\quad \ge 2 \exp \left( bt - \frac{(x+z )^2}{4 \mu t}\right) \sum _{ n \ge 1 } \exp \left( - \frac{3 n^2}{\mu t} \right) \ge 2 \exp \left( bt - \frac{(x+z )^2}{4 \mu t}\right) \\&\quad \quad \times \int _{1}^\infty \exp \left( - \frac{3 s^2}{\mu t} \right) ds \end{aligned}$$

which ends the proof. $\square$

Again we can estimate the time $t_{{\varrho _0}}$ for which the selected population $\varrho _\mathrm{out}$ reaches the threshold value ${\varrho _0}$.

Theorem 8

We suppose that $s_\varepsilon$ is the characteristic function of the set $(0,\varepsilon )$ and that $z > \varepsilon$, $b \in {\mathbb {R}}_+$ s.t. $b>s_\infty :={\left\| {s}\right\| }_{L^\infty (0,1)}$ and $z>\varepsilon$, then if we denote $t_{{\varrho _0}}$ the time s.t. $\varrho _\mathrm{out}$ reaches ${\varrho _0}$, for large (resp. small) values of $\mu$ one has:

$$\begin{aligned} \lim _{ \mu \rightarrow 0 } t_{{\varrho _0}} = + \infty , \quad \left( \text { resp. } \lim _{ \mu \rightarrow \infty } t_{{\varrho _0}} \in (\underline{t}, \overline{t})\right) , \end{aligned}$$

where the interval $(\underline{t},\overline{t})$ depends only on the data set $({\varrho _0}, \varepsilon , z, b,s_\infty )$, and $0< \underline{t}< \overline{t} < \infty$.

Proof

When $x<\varepsilon <z$, the heat kernel $\tilde{{\mathcal {G}}}_b$ is monotone with respect to x. Firstly, we compute the lower bound $t_{\ell }$ which is provided estimating $I_u (t) := \varepsilon \int _0^t \tilde{{\mathcal {G}}}_b (t,\varepsilon ,z) dt$ from above. By Lemma 5, one has that

$$\begin{aligned} I_u(t) \le \varepsilon \frac{\exp \left( (b+1)t - \frac{(z-\varepsilon )^2}{4\mu t}\right) }{\sqrt{4 \mu \pi }} \left( 1 + \sqrt{\frac{2 \mu }{(1-\varepsilon )}} \right) \end{aligned}$$

and so the time that $I_u$ reaches ${\varrho _0}$ is then greater than

$$\begin{aligned} t_{\ell } := \frac{ \ln \omega + \sqrt{ \ln ^2 \omega + \frac{(z-\varepsilon )^2}{ \mu } } }{2 (b+1)},\, \text { and }\, \omega := \frac{ 2 {\varrho _0}\sqrt{(1-\varepsilon )\mu \pi }}{ \varepsilon ( \sqrt{1-\varepsilon } + \sqrt{2 \mu } ) }. \end{aligned}$$

If $\mu$ is small then

$$\begin{aligned} t_{\ell } \sim \frac{| z-\varepsilon | }{2 (b+1)} \frac{1}{\sqrt{\mu }}. \end{aligned}$$

Whereas if $\mu \rightarrow \infty$,

$$\begin{aligned} t_{\ell } \rightarrow \frac{1}{(b+1)} \ln \left( \frac{{\varrho _0}\sqrt{2 \pi (1-\varepsilon )} }{\varepsilon }\right) =: \underline{t}. \end{aligned}$$

For what concerns $t_u$, one has, thanks to Lemma 7,

$$\begin{aligned}&\tilde{{\mathcal {G}}}_{b-s_\infty } (t,x,z) \ge \tilde{{\mathcal {G}}}_{b-s_\infty } (t,0,z) \ge \exp \left( (b-s_\infty ) t - \frac{ z^2}{4 \mu t} \right) \\&\quad \left\{ \frac{1}{\sqrt{4 \pi \mu t}} + \frac{1}{4\sqrt{3}}\mathrm{erfc}\left( \sqrt{\frac{3}{\mu t}} \right) \right\} , \end{aligned}$$

which allows to write:

$$\begin{aligned} I_{\ell } (t) := \varepsilon \int _0^t \tilde{{\mathcal {G}}}_{b-s_\infty } (t,0,z) dt \ge I_1(t) + I_2(t), \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} I_1(t)&:= \frac{ \varepsilon }{2 \sqrt{\pi \mu }} \int _0^{\tilde{t}}\exp \left( (b-s_\infty ) {\tilde{t}}- \frac{ z^2}{4 \mu {\tilde{t}}} \right) \frac{d{\tilde{t}}}{\sqrt{{\tilde{t}}}}, \\ I_2(t)&:= \frac{\varepsilon }{4 \sqrt{3}} \int _0^t \exp \left( (b-s_\infty ) {\tilde{t}}- \frac{ z^2}{4 \mu {\tilde{t}}} \right) \mathrm{erfc}\left( \sqrt{\frac{3}{\mu {\tilde{t}}}} \right) d{\tilde{t}}, \end{aligned} \end{aligned}$$

and both functions are increasing with respect to t. This allows us to estimate $I_{\ell }$ as

$$\begin{aligned} I_{\ell }(t) \ge I_1(t) \mathbbm {1}_{(0,t_0)}(t) + \left\{ I_1(t_0) + I_2(t)-I_2(t_0) \right\} \mathbbm {1}_{(t_0,\infty )}(t) \end{aligned}$$

where, as in the unbounded case, $t_0$ represents the time at which the coefficient of the exponential function changes sign i.e. $t_0 := z/(2\sqrt{\mu (b-s_\infty )})$. As before, when $t< t_0$, the estimate follows the same from Lemma 4. Thus we re-define $j_1(t) := \varepsilon z /( 4 \mu e) \exp (-z^2/(2 \mu t))$. Instead when $t>t_0$, one writes:

$$\begin{aligned} I_{\ell }(t) \ge j_1(t_0) + \frac{\varepsilon }{4 \sqrt{3}} \int _{t_0}^t \exp ((b-s_\infty )(t - t_0)) \mathrm{erfc}\left( \sqrt{\frac{3}{\mu {\tilde{t}}}} \right) d{\tilde{t}}, \end{aligned}$$

but because $\mathrm{erfc}(\sqrt{3/(\mu t)})$ is a monotone increasing function with respect to t, one may estimate again the latter term as:

$$\begin{aligned} \begin{aligned} I_{\ell }(t)&\ge j_1(t_0) + \mathrm{erfc}\left( \sqrt{\frac{3}{\mu t_0}} \right) \frac{\varepsilon }{4 \sqrt{3}} \int _{t_0}^t \exp ((b-s_\infty )(t - t_0)) d{\tilde{t}}\\&= j_1(t_0) + \mathrm{erfc}\left( \sqrt{\frac{3}{\mu t_0}} \right) \frac{\varepsilon }{4 \sqrt{3}} \frac{ \left( \exp \left( (b-s_\infty ) (t-t_0) \right) -1 \right) }{(b-s_\infty )}, \end{aligned} \end{aligned}$$

which leads to the inverse function:

$$\begin{aligned} t_u := {\left\{ \begin{array}{ll} j_1^{-1}({\varrho _0}) &{} \text { if }{\varrho _0}< j_1(t_0) \\ t_0 + \frac{1}{(b-s_\infty )} \ln \left( 1 + \frac{ 4 \sqrt{3} (b-s_\infty ) }{\varepsilon \mathrm{erfc}\left( \sqrt{\frac{3}{\mu t_0}} \right) } \left( {\varrho _0}- j_1(t_0) \right) \right) &{} \text { otherwise. } \end{array}\right. } \end{aligned}$$

when studying the limit of the latter expression when $\mu \rightarrow \infty$ one concludes that $j_1(t_0) \rightarrow 0$ and $\overline{t} := t_0 + \ln (1 + 4\sqrt{3} (b-s_\infty ) {\varrho _0}/\varepsilon )$. $\square$

Corollary 1

Under hypotheses of Theorem 7, one might give another upper bound for $t_{\rho _0}$:

$$\begin{aligned} t_{\rho _0} \le t^\infty _u := {\left\{ \begin{array}{ll} j^{-1}_1 (\rho _0) &{} \text { if }\rho _0 < j_1(t_0), \\ j^{-1}_2 (\rho _0) &{} \text { otherwise}, \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned} t_0 = \frac{z}{ 2 \sqrt{b-s_\infty }}, \quad j_1(t_0) := \frac{\varepsilon z}{4 \mu e \sqrt{ \pi } } \exp \left( - \frac{z \sqrt{b-s_\infty }}{\sqrt{\mu }} \right) , \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} j_1^{-1} ( {\varrho _0})&:= \frac{ z^2 }{-2 \ln \left( \frac{{\varrho _0}4 e\mu }{ \varepsilon z } \right) }, \\ j_2^{-1} ( {\varrho _0})&:= \left( \frac{( k + \frac{1}{2}) k! \sqrt{ \pi \mu } }{(b-s_\infty )^k} \exp ((b-s_\infty ) t_0) ({\varrho _0}- j_1(t_0)) + t_0^{k+\frac{1}{2}}\right) ^{\frac{1}{k + \frac{1}{2}}}. \end{aligned} \end{aligned}$$

The proof simply takes into account that the Green function ${\mathcal {G}}_{b-s_\infty }$ in the bounded case is greater that the Green function in the case of the whole space, applying the same arguments as in Sect. 5.1.1 one concludes. These latter estimates shall improve the upper bound of $t_{{\varrho _0}}$ for $\mu$ small.

We plot in Fig. 4, right, the comparison between our bounds $t_u$, $t_u^\infty$ and $t_l$ and the direct numerical simulations of ${\mathcal G}_\varepsilon$ solving (36) for a given set of data $(b,{\varrho _0},\varepsilon ,z)$ when $\mu$ varies.

Fig. 4

The mutation rate $\mu$ is plotted in the log scale on the x-axis. The left (resp. right) figure displays the unbounded (resp. bounded) case. On the left side, one shows the upper and lower estimates of $t_{\rho _0}$, the time to reach ${\varrho _0}$, between these curves we computed numerically $t_{I_l}$ and $t_{I_u}$ in order to validate our estimates. On the right, one plots a numerical computation of ${\mathcal G}_\varepsilon$ solving (36) and the respective theoretical bounds

5.2 Asymptotic expansion for large mutation rates

5.2.1 The formal result

When $\mu$, the mutation rate dominates, one sets the decomposition :

$$\begin{aligned} {\mathcal {N}}_\mu (t,x) = {\mathcal {N}}_0(\mu t,x) + \frac{1}{\mu } {\mathcal {N}}_1( \mu t,x) + \cdots \end{aligned}$$

and one gathers powers of $1/\mu$, separating the scales this leads to solve:

• At zero order one obtains the equation:

  $$\begin{aligned} \partial _t{\mathcal {N}}_0 - {\partial _{x^2}^2} {\mathcal {N}}_0 = 0 \end{aligned}$$

• While at jth order one writes:

  $$\begin{aligned} \partial _t{\mathcal {N}}_j - {\partial _{x^2}^2} {\mathcal {N}}_j = (b-s) {\mathcal {N}}_{j-1}, \quad j \in \mathbb {N}^*. \end{aligned}$$

Using the spectral decomposition, one gets, for the zeroth order term, that it reads

$$\begin{aligned} {\mathcal {N}}_0 (t,x) := \sum _{k \in \mathbb {N}} \overline{n}^k_I v_k (x) \exp (-\lambda _{0,k} t),\quad \overline{n}^k_I := <n_I, v_k>, \end{aligned}$$

where the brackets denote the scalar product in $L^2((0,1))$, and the eigenvectors are those of the homogeneous problem (13). This expression leads to exponentially decreasing modes and a mean that remains constant.

Denoting ${\mathcal {N}}_j := \sum _{k \in \mathbb {N}} \gamma _{j,k}(t) v_k(x)$ and ${\varGamma }_j(t) := (\gamma _{j,k}(t))_{k\in \mathbb {N}}$ one can write the modal equivalent of the equation above:

$$\begin{aligned} \dot{{\varGamma }}_j + {{\mathrm{diag}}}(\lambda ) {\varGamma }_j = (b-{\mathcal {M}}) {\varGamma }_{j-1}, \quad ({\mathcal {M}})_{ik} := {<}s v_i,v_k{>}, \quad {\varGamma }_j(0)=0,\; \forall j\ge 1. \end{aligned}$$

(38)

where ${{\mathrm{diag}}}(\lambda ) := {{\mathrm{diag}}}(\lambda _{0,0},\dots ,\lambda _{0,k},\dots )$. As the dominant mode is the constant one, we prove below that

$$\begin{aligned} \gamma _{j,k} \sim {\left\{ \begin{array}{ll} \overline{n}^0_I \frac{(b-{\mathcal {M}}_{0,0})^{j} t^j }{j !} &{} \text { if }k = 0 \\ 0 &{} \text { otherwise } \end{array}\right. } + O( t^{j-1} ) \end{aligned}$$

when t is large. This gives the asymptotic limit:

$$\begin{aligned} {\mathcal {N}}_\mu \sim \overline{n}^0_I \sum _j \frac{(b-{\mathcal {M}}_{0,0})^{j} t^j }{j ! \mu ^j} + R_j t^{j-1} = \overline{n}^0_I \exp \left( \frac{ (b- {\mathcal {M}}_{0,0})t }{ \mu } \right) + \dots . \end{aligned}$$

Returning to the original variables and after integration in time this gives that the final formula shall be

$$\begin{aligned} t_{{\varrho _0}} := \frac{1}{b-{\mathcal {M}}_{0,0}} \ln \left( 1 + \frac{ \rho _0 \left( b- {\mathcal {M}}_{0,0}\right) }{\left( \int _0^1 s(x) dx\right) \overline{n}^0_I} \right) + O\left( \frac{1}{\mu } \right) . \end{aligned}$$

Assuming that s fulfills hypotheses 3.2 this provides

$$\begin{aligned} t_{{\varrho _0}} := \frac{1}{b-\varepsilon } \ln \left( 1 + \frac{ \rho _0 \left( b-\varepsilon \right) }{\varepsilon \overline{n}^0_I} \right) + O\left( \frac{1}{\mu } \right) . \end{aligned}$$

(39)

5.2.2 Numerical simulations

We display in Fig. 5 for various values of $\mu$, $t_{{\varrho _0}}$ computed using direct numerical simulations with a random initial data $n_I$, compared with the value given by (39). In this particular case, the convergence occurs for values of $\mu$ larger then 1.

Fig. 5

Time to reach ${\varrho _0}$ starting from a random initial condition, for various values of $\mu$ (in the logscale)

5.2.3 Mathematical proofs

Setting $\tilde{n}(t,x) := n(t,x) \exp (-(b-{\mathcal {M}}_{0,0})t) / \overline{n}^0_I$, with $\overline{n}^0_I := \int _{{\varOmega }} n_I(x) dx$, it is solution of

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _t\tilde{n}- \mu {\partial _{x^2}^2} \tilde{n}= ({\mathcal {M}}_{0,0}-s) \tilde{n}&{}\quad (t,x) \in {\mathcal {O}}_T,\\ \partial _x\tilde{n}(t,x)= 0&{}\quad (t,x) \in {\varSigma }_T,\\ \tilde{n}(0,x)=n_I(x)/\overline{n}^0_I&{}\quad (t,x) \in \{ 0 \} \times {\varOmega }\\ \end{array} \right. \end{aligned}$$

(40)

When $\mu$, the mutation rate dominates one sets the decomposition:

$$\begin{aligned} {\mathcal {N}}_\mu = {\mathcal {N}}_0 + \frac{1}{\mu } {\mathcal {N}}_1 + \cdots \end{aligned}$$

We suppose moreover that we focus on solutions for long times so that the time scaling should be

$$\begin{aligned} {\mathcal {N}}_{\mu } (\mu t,x) \sim \tilde{n}(t,x), \quad (t,x) \in {\mathbb {R}}_+\times (0,1). \end{aligned}$$

One then writes the asymptotic expansion of the equations with respect to $1/\mu$:

• ${\mathcal {O}}\left( \mu \right)$ terms provide:

  $$\begin{aligned} \left\{ \begin{array}{ll} \partial _t{\mathcal {N}}_0 - {\partial _{x^2}^2} {\mathcal {N}}_0 = 0, &{}\quad (t,x) \in {\mathcal {O}}_T, \\ \partial _x{\mathcal {N}}_0(t,x) = 0 , &{}\quad (t,x) \in {\varSigma }_T, \\ {\mathcal {N}}_0(0,x)=n_I(x)/\overline{n}^0_I, &{}\quad (t,x) \in \{0\}\times {\varOmega }. \end{array} \right. \end{aligned}$$

• while ${\mathcal {O}}\left( \frac{1}{\mu ^j}\right)$ terms give :

  $$\begin{aligned} \left\{ \begin{aligned}&\partial _t{\mathcal {N}}_j - {\partial _{x^2}^2} {\mathcal {N}}_j = ({\mathcal {M}}_{0,0}-s) {\mathcal {N}}_{j-1},&(t,x) \in {\mathcal {O}}_T, \\&\partial _x{\mathcal {N}}_j(t,x) = 0 ,&(t,x) \in {\varSigma }_T, \\&{\mathcal {N}}_j(0,x)= 0,&(t,x) \in \{0\}\times {\varOmega }, \end{aligned} \right. \end{aligned}$$

  for $j \in \mathbb {N}^*$.

Proposition 3

For any $n_I\in L^2({\varOmega })$, one has

• If $j = 0$

  $$\begin{aligned} {\left\| {{\mathcal {N}}_0(t,\cdot ) -1}\right\| }_{L^2(0,1)} \le c_0 \exp ( - \pi ^2 t) , \quad \forall t \ge 0 \end{aligned}$$

• If $j\ge 1$ then

  $$\begin{aligned} {\left\| {{\mathcal {N}}_j (t,\cdot )}\right\| }_{L^2(0,1)} \le c_j t^{j-1}, \quad \forall t \ge 0 \end{aligned}$$

  where the constant $c_j$ does not depend on t.

Proof

The proof follows in two steps

• If $j=0$ then the spectral decomposition gives directly the claim.

• For the second part we proceed by induction. If $j=1$, ${\mathcal {N}}_1$ solves

  $$\begin{aligned} \partial _t{\mathcal {N}}_1 - {\partial _{x^2}^2} {\mathcal {N}}_1 = ({\mathcal {M}}_{0,0}- s) {\mathcal {N}}_0 \end{aligned}$$

  complemented with homogeneous Neumann boundary and zero initial conditions. Integrating in space shows that $\overline{{\mathcal {N}}}_1(t) := \int _{{\varOmega }} {\mathcal {N}}_1(t,x) dx$ solves

  $$\begin{aligned} \partial _t\overline{{\mathcal {N}}}_1 = \overline{ ({\mathcal {M}}_{0,0}-s) {\mathcal {N}}_0} = \overline{ ({\mathcal {M}}_{0,0}-s) \sum _{k\in \mathbb {N}} \gamma _{0,k} v_k } = - \sum _{k\ne 0} {\mathcal {M}}_{0,k} \gamma _{0,k}, \end{aligned}$$

  but the functions $\gamma _{0,k}$ are explicit and read: $\gamma _{0,k} = \overline{n}^k_I \exp ( - \lambda _k t)$. Integrating in time and using Cauchy-Schwartz gives:

  $$\begin{aligned} | \overline{{\mathcal {N}}}_1 |^2 \le \left( \sup _{k \in \mathbb {N}} | {\mathcal {M}}_{0,k} | \right) ^2 \left| \sum _{k\ne 0} \overline{n}^k_I \left( \frac{ (1-\exp (-\lambda _k t) )}{\lambda _k} \right) \right| ^2 \le c {\left\| {s}\right\| }_{L^\infty (0,1)}^2 {\left\| {n_I}\right\| }_{L^2(0,1)}^2 . \end{aligned}$$

  For the rest, we set $\underline{{\mathcal {N}}}_1 := {\mathcal {N}}_1- \overline{{\mathcal {N}}}_1$, it solves

  $$\begin{aligned} \partial _t\underline{{\mathcal {N}}}_1 - {\partial _{x^2}^2} \underline{{\mathcal {N}}}_1 = ( {\mathcal {M}}_{0,0}-s){\mathcal {N}}_0 -\partial _t\overline{{\mathcal {N}}}_1, \end{aligned}$$

  which multiplied by $\underline{{\mathcal {N}}}_1$ and integrated with respect to x reads :

  $$\begin{aligned} \frac{1}{2}\partial _t{\left\| {\underline{{\mathcal {N}}}_1 }\right\| }_{L^2(0,1)}^2 + \lambda _1 {\left\| {\underline{{\mathcal {N}}}_1 }\right\| }_{L^2(0,1)}^2 \le c {\left\| {{\mathcal {N}}_0}\right\| }_{L^2(0,1)} {\left\| {\underline{{\mathcal {N}}}_1 }\right\| }_{L^2(0,1)}, \end{aligned}$$

  by Young’s inequality and Gronwall’s lemma, the second claim holds for $j=1$.

• We suppose now that for $\ell \le j-1$ the property is true. Again for the constant mode one has

  $$\begin{aligned} \partial _t\overline{{\mathcal {N}}}_j = \int _{{\varOmega }} ({\mathcal {M}}_{0,0}-s) {\mathcal {N}}_{j-1} dx \le {\left\| {{\mathcal {M}}_{0,0}-s}\right\| }_{L^2(0,1)}{\left\| {{\mathcal {N}}_{j-1}}\right\| }_{L^2(0,1)} \le c t^{j-2}, \end{aligned}$$

  where the last inequality comes from the induction hypothesis. Integrating the latter inequality in time provides the result for the zero mode. As above, one has

  $$\begin{aligned} \partial _t\underline{{\mathcal {N}}}_j - {\partial _{x^2}^2} \underline{{\mathcal {N}}}_j = ( {\mathcal {M}}_{0,0}-s ) {\mathcal {N}}_{j-1} - \partial _t\overline{{\mathcal {N}}}_j, \end{aligned}$$

  the latter term being constant in space and $\underline{{\mathcal {N}}}_j$ being of zero mean value provides after multiplication by $\underline{{\mathcal {N}}}_j$ and integration with respect to x that

  $$\begin{aligned} \frac{1}{2}\partial _t{\left\| {\underline{{\mathcal {N}}}_j}\right\| }_{L^2(0,1)}^2 + \lambda _1 {\left\| {\underline{{\mathcal {N}}}_j}\right\| }_{L^2(0,1)}^2 \le 2 {\left\| {s}\right\| }_{L^\infty (0,1)} {\left\| {{\mathcal {N}}_{j-1}}\right\| }_{L^2(0,1)}{\left\| {\underline{{\mathcal {N}}}_j}\right\| }_{L^2(0,1)}, \end{aligned}$$

  which again by Young inequality and Gronwall proves the second claim for $\ell =j$. This ends the induction argument.$\square$

5.2.4 Error estimates

We define the error ${\mathcal {E}}_N:= n(t,x) \exp (-bt) /\overline{n}^0_I - \exp (-{\mathcal {M}}_{0,0}t) {\mathcal {N}}_{\mu ,N}$ where ${\mathcal {N}}_{\mu ,N} := \sum _{j =0}^{j=N} \frac{1}{\mu ^j} {\mathcal {N}}_j(\mu t,x)$, it solves

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _t{\mathcal {E}}_N- \mu {\partial _{x^2}^2} {\mathcal {E}}_N+ s {\mathcal {E}}_N= \frac{({\mathcal {M}}_{0,0}-s)}{\mu ^N} {\mathcal {N}}_N(\mu t,x) \exp (-{\mathcal {M}}_{0,0}t), &{}\quad (t,x) \in {\mathcal {O}}_T, \\ \partial _x{\mathcal {E}}_N=0,&{}\quad (t,x) \in {\varSigma }_T,\\ {\mathcal {E}}_N(0,x)= 0, &{}\quad (t,x) \in \{ 0 \} \times {\varOmega }.\\ \end{array} \right. \end{aligned}$$

Theorem 9

If $n_I\in L^2({\varOmega })$ and s satisfies hypotheses 3.2, one has for any fixed time T that

$$\begin{aligned} {\left\| {{\mathcal {E}}_N(T,\cdot )}\right\| }_{L^2({\varOmega })} \le \frac{c }{\mu {\mathcal {M}}_{0,0}^N}, \end{aligned}$$

where the constant c is independent both on T and on $\mu$.

Proof

Multiplying the latter equation by ${\mathcal {E}}_N$ and integrating with respect to x, one has

$$\begin{aligned} \partial _t{\left\| {{\mathcal {E}}_N}\right\| }_{L^2({\varOmega })}^2 \le \frac{2 c}{\mu ^N} {\left\| {{\mathcal {N}}_N}\right\| }_{L^2({\varOmega })} {\left\| {{\mathcal {E}}_N}\right\| }_{L^2({\varOmega })} \exp (-{\mathcal {M}}_{0,0}t) \end{aligned}$$

dividing both sides by $\sqrt{{\left\| {{\mathcal {E}}_N}\right\| }_{L^2({\varOmega })}^2+ \delta }$, one gets:

$$\begin{aligned} \partial _t\sqrt{{\left\| {{\mathcal {E}}_N}\right\| }_{L^2({\varOmega })}^2+ \delta }\le & {} \frac{2 c}{\mu ^N} \frac{ {\left\| {{\mathcal {N}}_N}\right\| }_{L^2({\varOmega })} {\left\| {{\mathcal {E}}_N}\right\| }_{L^2({\varOmega })} }{\sqrt{{\left\| {{\mathcal {E}}_N}\right\| }_{L^2({\varOmega })}^2+ \delta }} \quad \exp (-{\mathcal {M}}_{0,0}t ) \\\le & {} \frac{2 c}{\mu ^N} {\left\| {{\mathcal {N}}_N(\mu t,\cdot )}\right\| }_{L^2({\varOmega })} \exp (-{\mathcal {M}}_{0,0}t ) \end{aligned}$$

here we use the estimates of Proposition 3 to conclude that

$$\begin{aligned} \sqrt{{\left\| {{\mathcal {E}}_N(t,\cdot )}\right\| }_{L^2({\varOmega })}^2+ \delta } \le \sqrt{\delta } + \frac{c}{\mu } \int _0^t s^{N-1} \exp (- {\mathcal {M}}_{0,0}s) ds \le \sqrt{\delta } + \frac{c }{\mu {\mathcal {M}}_{0,0}^N }, \end{aligned}$$

which finally gives the claim, since the result holds for any arbitrarily small $\delta >0$.

$\square$

Turning back to the original function n(t, x) solving (29), the consequence of results above is that

Corollary 2

$n_I\in L^2({\varOmega })$ and s satisfies hypotheses 3.2, one has for any fixed time t that

$$\begin{aligned} {\left\| {n(t,\cdot )-\overline{n}^0_I \exp ((b-{\mathcal {M}}_{0,0})t)}\right\| }_{L^2({\varOmega })} \le \frac{c |\overline{n}^0_I| }{\mu {\mathcal {M}}_{0,0}^N}\exp ( b t). \end{aligned}$$

where the constant c is independent both on t and on $\mu$.

Remark 3

These results show that it is possible to compute the limit of n when $\mu$ is large. Nevertheless, the approximation is only first order accurate with respect to $\mu$. An interesting and open question is whether one is able to construct a higher order approximation.

Theorem 10

If $n_I\in L^2({\varOmega })$ and s satisfies hypotheses 3.2, for any $\eta >0$, there exists a $\mu$ large enough, s.t. if

$$\begin{aligned} t_{{\varrho _0}}:= \frac{1}{b-{\mathcal {M}}_{0,0}} \ln \left( 1 + \frac{ \rho _0 \left( b- {\mathcal {M}}_{0,0}\right) }{\left( \int _0^1 s(x) dx\right) \overline{n}^0_I} \right) , \end{aligned}$$

then $\left| \varrho _\mathrm{out}(t_{{\varrho _0}}) - {\varrho _0}\right| \le \eta$.

5.3 Asymptotic expansion for small mutation rates

On the other hand, if we consider $\mu$ small, one can decompose the solution of (29)

$$\begin{aligned} n (t,x) \sim \sum _{j \in \mathbb {N}} \mu ^j {\mathcal {N}}_j(t,x) \end{aligned}$$

where the different terms ${\mathcal {N}}_j$ solve:

• if $j=0$

  $$\begin{aligned} \left\{ \begin{aligned}&\partial _t{\mathcal {N}}_0 = (b-s(x)) {\mathcal {N}}_0 ,&(t,x) \in {\mathcal {O}}_T,\\&{\mathcal {N}}_0(0,x)=n_I(x). \end{aligned} \right. \end{aligned}$$

  (41)

• if $j \ge 1$

  $$\begin{aligned} \left\{ \begin{aligned}&\partial _t{\mathcal {N}}_j = (b-s(x)) {\mathcal {N}}_j + {\partial _{x^2}^2} {\mathcal {N}}_{j-1},&(t,x) \in {\mathcal {O}}_T, \\&{\mathcal {N}}_j(0,x)=0 . \end{aligned} \right. \end{aligned}$$

  (42)

5.3.1 Formal computations

One can solve explicitly ${\mathcal {N}}_0$, which reads:

$$\begin{aligned} {\mathcal {N}}_0(t,x) = \exp ( (b-s(x)) t ) n_I(x). \end{aligned}$$

We compute a zero order approximation of $\varrho _\mathrm{out}$:

$$\begin{aligned} \varrho _\mathrm{out}\sim \int _0^t \int _{{\varOmega }} s (x) \exp ( (b-s(x)) {\tilde{t}}) n_I(x) dx d{\tilde{t}}=: \rho _\mathrm{app}(t). \end{aligned}$$

For the particular case when s satisfies hypotheses 3.2, one recovers

$$\begin{aligned} \rho _\mathrm{app}(t) = \frac{\exp ( (b -1)t) -1 }{(b-1)} \int _{{\varOmega }} s(x) n_I(x) dx, \end{aligned}$$

which gives then an explicit formula for $\mu$ small

$$\begin{aligned} t_{{\varrho _0}} := \frac{1}{(b-1)} \log \left( 1 + \frac{(b-1) {\varrho _0}}{\int _{{\varOmega }} s(x) n_I(x) dx }\right) . \end{aligned}$$

(43)

5.3.2 Numerical simulations

We display, in Fig. 6, $t_{{\varrho _0}}$, the time to reach ${\varrho _0}$, for various values of $\mu$ and for a given random initial data $n_I\in L^2({\varOmega })$.

Fig. 6

Time to reach ${\varrho _0}$ starting from a random initial condition, for various values of $\mu$, we use again the same code as in Fig. 5

5.3.3 Rigorous proofs

Lemma 8

We suppose that s satisfies the hypotheses 3.2. For any given ${\varPsi } \in L^2({\mathcal {O}}_T)$ there exists a unique solution $\varphi \in C((0,T);H^1({\varOmega }))\cap L^2((0,T);H^2({\varOmega }))$ solving

$$\begin{aligned} \left\{ \begin{array}{ll} \partial _t\varphi - \mu {\partial _{x^2}^2} \varphi + s \varphi = {\varPsi } (t,x), &{}\quad (t,x) \in {\mathcal {O}}_T\\ \partial _x\varphi (t,x) = 0,&{}\quad (t,x) \in {\varSigma }_T\\ \varphi (0,x)=0,&{}\quad (t,x)\in \{0\} \times {\varOmega }, \end{array} \right. \end{aligned}$$

(44)

and one has continuity with respect to the $L^2((0,T);H^2({\varOmega }))$ norm:

$$\begin{aligned} {\left\| { \varphi }\right\| }_{L^2((0,T);H^2({\varOmega }))} \le C {\left\| {{\varPsi }}\right\| }_{L^2({\mathcal {O}}_T)}. \end{aligned}$$

The proof, based on the Galerkin decomposition, is classical and can be found in Ladyženskaja et al. (1968) Chap III, Sect. 6, p. 172–178.

Theorem 11

If $n_I\in L^2({\varOmega })$ and s satisfies hypotheses 3.2, one has the $L^2({\mathcal {O}}_T)$-error estimates:

$$\begin{aligned} {\left\| { n - {\mathcal {N}}_0 }\right\| }_{L^2({\mathcal {O}}_T)} \le \mu \sqrt{ \frac{ \exp ( 2 b T ) -1}{2 b}} {\left\| {n_I}\right\| }_{L^2({\varOmega })} \end{aligned}$$

Proof

We rescale the problem (29) and the asymptotic expansion so to drop the damping term b, in the respective equations. Let define $Y:=C^0((0,T);H^1({\varOmega }))\cap L^2((0,T); H^2({\varOmega }))$. Considering (41), the equation is satisfied also in the weak sense namely, for any $\varphi \in Y$, one has

$$\begin{aligned} \left[ \int _{{\varOmega }} {\mathcal {N}}_0 (t,x) \varphi (t,x) dx \right] _{t=0}^{t=T} - \int _{{\mathcal {O}}_T} {\mathcal {N}}_0 (t,x) \left( \partial _t\varphi -s(x) \varphi \right) dx dt = 0. \end{aligned}$$

On the other hand, one has also that n solving (29), satisfies as well for any $\varphi \in Y$,

$$\begin{aligned} \left[ \int _{{\varOmega }} n (t,x) \varphi (t,x) dx \right] _{t=0}^{t=T} - \int _{{\mathcal {O}}_T} n (t,x) \left( \partial _t\varphi + \mu {\partial _{x^2}^2} \varphi -s(x) \varphi \right) dx dt = 0. \end{aligned}$$

This gives when setting ${\mathcal {E}}(t,x) := n(t,x) -{\mathcal {N}}_0(t,x)$, for any $\varphi \in Y$

$$\begin{aligned}&\left[ \int _{{\varOmega }} {\mathcal {E}}(t,x) \varphi (t,x) dx \right] _{t=0}^{t=T} - \int _{{\mathcal {O}}_T} {\mathcal {E}}(t,x) \left( \partial _t\varphi + \mu {\partial _{x^2}^2} \varphi -s(x) \varphi \right) dx dt \\&\quad = \mu \int _{{\mathcal {O}}_T} {\mathcal {N}}_0(t,x) {\partial _{x^2}^2} \varphi (t,x) dx dt . \end{aligned}$$

For any ${\varPsi } \in L^2({\mathcal {O}}_T)$, there exists $\varphi \in Y$, the forward form solving (44). Now let insert the backward expression of $\varphi$ in the latter weak form, this gives:

$$\begin{aligned} \int _{{\mathcal {O}}_T} {\mathcal {E}}(t,x) {\varPsi }(t,x) dx dt \le \mu {\left\| {{\mathcal {N}}_0}\right\| }_{L^2({\mathcal {O}}_T)} {\left\| {{\partial _{x^2}^2} \varphi }\right\| }_{L^2({\mathcal {O}}_T)} \le C \mu {\left\| {{\mathcal {N}}_0}\right\| }_{L^2({\mathcal {O}}_T)} {\left\| {{\varPsi }}\right\| }_{L^2({\mathcal {O}}_T)}, \end{aligned}$$

which holds for any ${\varPsi } \in L^2({\mathcal {O}}_T)$. Taking the supremum over all functions in this latter space provides the bound ${\left\| {{\mathcal {E}}}\right\| }_{L^2({\mathcal {O}}_T)} \le C \mu {\left\| {{\mathcal {N}}_0}\right\| }_{L^2({\mathcal {O}}_T)}$. Turning back to the correct scaling with respect to the damping term b, one recovers the claim. $\square$

Corollary 3

Under the same hypotheses as in Theorem (11), the time $t_{{\varrho _0}}$ being defined in (43), one has the error estimates : there exists a constant $C(s,n_I,b)>0$, independent of $\mu$, s.t.

$$\begin{aligned} \left| \varrho _\mathrm{out}(t_{{\varrho _0}}) - {\varrho _0}\right| \le \mu C(s,n_I,b) {\left\| {n_I}\right\| }_{L^2({\varOmega })} {\left\| {s}\right\| }_{L^2({\varOmega })}. \end{aligned}$$

The proof comes easily combining a triangular inequality as in the proof of Theorem 4, results above and the definition of $t_{{\varrho _0}}$. As the latter time does not depend on $\mu$, the claim follows straightforwardly.