2M₁ phlogopite–muscovite series minerals at increasing pressure to 9 GPa. I Atomic volumes and compressibilities

Abstract

Muscovite (Ms) and phlogopite (Phl) series mineral is studied in the 2M₁ polytype and modeled by the substitution of three Mg²⁺ cations in the three octahedral sites of Phl [KMg₃(Si₃Al)O₁₀(OH)₂] by two Al³⁺ and one vacancy, increasing the substitution up to reach the Ms [KAl₂□(Si₃Al)O₁₀(OH)₂]. The series was computationally examined at DFT using Quantum ESPRESSO, as a function of pressure from − 3 to 9 GPa. Crystal structure is calculated, and cell parameters, and geometry of atomic groups agree with experimental values. OH in the Mg²⁺ octahedrons are approximately perpendicular to the (001) plane, meanwhile when they are in Al³⁺, octahedral groups are approximately parallel to this plane. From Quantum Theory of Atoms in Molecules, the atomic basins are calculated as a function of the pressure, K⁺ and basal O show the largest volumes. The bulk excess volume (Vxs) and the excess atomic volumes are analyzed as a function of the composition and the pressure. K⁺, basal and apical O Vxs show a behavior similar to the bulk Vxs as a function of the composition, keeping qualitatively this behavior as a function of pressure; substituent atoms do not show a Vxs behavior similar to the bulk and their effect consequently is mostly translated to atoms in the interlayer space. Atomic compressibilities are also calculated. Atomic compressibilities are separated in the different sheets of the crystal cell. Atomic moduli of K and basal O are the lowest and the ones behaving as the bulk modulus of the series. The atomic bulk modulus of the H’s is different depending of their position with respect to the (001) plane.

Introduction

Micas are layer silicates and one of the most common minerals in crustal rocks (igneous, metamorphic, and sedimentary rocks). Micas are different series minerals which incorporate many different ions in their structures, which have wide chemical compositions, and consequently wide ranges of temperatures and pressures are possible for their formation and stability (Monier and Robert 1986; Robert 1976). So, pure end members are difficult to be found in natural minerals but ideal formulae could be considered as the end members of series minerals. Micas and phyllosilicates in general have a complex structure in which many different bonds [covalent, ionic, hydrogen bonds (HB) and non-covalent-interactions] are found in their structures; besides, many cations are tetra- and hexa-coordinate in the Tetrahedral (T)-Octahedral (O) - T (T-O-T) layers, and 12-coordinate in the interlayer spaces. Different polyhedrons and sheets are coexisting in the crystal cell, where diverse cation substitutions produce many different micas series minerals. All of them give especial properties to the minerals. These minerals are structurally formed by two T sheets sandwiching an O sheet, forming a layer (T-O-T). Layers are stacking ones over others with an interlayer space in-between. If the layer has a negative charge as consequence of the cation substitutions, other cations offset the charge in the interlayer space (···M^{+ δ−}T-O-T^δ− M^{+ δ−}T-O-T ^δ− M⁺···). It also leads to an increasement of the lateral dimensions of the tetrahedral sheet compared to the adjacent octahedral sheet, which is reduced by rotating adjacent tetrahedra of six-membered rings in opposite directions in the plane. Angle α is a measure of this rotation, necessary to relieve the misfit. The six-membered rings occurring in micas generate large structural voids, and so micas, together with clay minerals, are stable under surficial conditions and constitute the alteration products of more dense silicate minerals.

Phlogopite (Phl) and muscovite (Ms) belong to the trioctahedral and 2:1 dioctahedral layer silicates, whose ideal end members’ formulae are [KMg₃(Si₃Al)O₁₀(OH)₂] and [KAl₂□(Si₃Al)O₁₀(OH)₂], respectively. Phl and Ms members of the series can contain ^VIMg²⁺ and ^VIAl³⁺ in their octahedral (VI) sheets.¹ Both ^IVAl³⁺ and ^VIAl³⁺are coexisting in the layer but by simultaneous isomorphous substitutions, both Al³⁺ and Mg²⁺ and other different cations can also coexist in the structure. There are many works studying the extent of the series (Foster 1960; Monier and Robert 1986; Robert 1976; Rutherford 1973). Two mechanisms could be produced to incorporate Mg²⁺ in the octahedral sheet: (i) phengitic mechanism, in which the substitution preserves the dioctahedral nature of the octahedral sheet, by simultaneous substitution of ^VIAl³⁺ by ^VIMg²⁺ in the octahedral structure, and ^IVSi⁴⁺ by ^IVAl³⁺ in the tetrahedral sheet; and (ii) phlogopite substitution, in which the nature of the octahedral sheet changes from trioctahedral to dioctahedral, keeping unchanged the tetrahedral sheet, and the three Mg²⁺ are substituted by two ^VIAl³⁺and one octahedral vacant cavity (represented by a □ in the formulae) of the dioctahedral series, keeping the same charge than before in the octahedral sheet. Our title series belongs to the later substitution mechanism.

Micas incorporate atomic groups (OH) that can be transformed to water at special thermodynamics conditions: at 100 km Earth’s depth, these minerals can be dehydrated and water can be freed in subduction slabs which triggered off important melting processes in Earth crust (Huang and Wyllie 1973; Hwang et al. 2017). Micas along with serpentines can bring water even beyond the arc front depths (Schmidt and Poli 1998; Schmidt et al. 2004). These layer silicates can be stable to depths greater than 300 km, due to the low geothermal gradients observed in subduction zones and to the strong dependence on temperature for the dehydration reaction curves of mica-bearing rocks. These silicates can be used as geo-thermo-barometers (Fleet 2003).

Phl is considered to be stable up to 9 GPa (Yoder and Eugster 1954; Yoder and Kushitro 1969). A stability limit of 9–10 GPa at 1000 ℃ was found out (Trønnes 2002); and Phl was still recovered at 8 GPa and 1300 ℃ (Sato et al. 1997), and at 9.0 GPa and 1365 ℃ (Kushiro et al. 1967). In the decomposition products of Phl, this compound was still got back. From stability critical P–T curve, Phl is considered stable at room pressure at critical temperature of 1370 ℃, increasing 118 ℃ its critical temperature each 1 GPa of increasing pressure (Hazen 1977). Phl can undergo dehydroxylation reaction at approximately 200 km depths, but its stability is affected with Ms substitution (Hwang et al. 2017). In general, the thermodynamics stability of these trioctahedral compounds can be affected by the dioctahedral substitutions.

From experiments with diamond-anvil cell and X-ray diffraction, Ms was found stable at room temperature and approximately at 18 GPa, and Ms loses its long-range crystallinity and amorphizes at ~ 27 GPa; however, Ms is not stable at 800 ℃ from 1.8 GPa (Faust and Knittle 1994). Nonetheless, Ms was also considered stable at a pressure > 10 GPa (Sekine et al. 1991), considering Ms as one of the most stable minerals in subducted oceanic sediments (Huang and Wyllie 1973).

These complex substitution effects are not deeply known, and this work is an intend to start to understand it by studying the pressure–composition–coordination (P–X–C) space, although X and C go together, but the changes in composition bring the changes from trioctahedral to dioctahedral coordination. Besides, these crystals are very anisotropic due to their layered structure and compositions, and this anisotropy is suitable to be studied at the P–X space at the light of theoretical methods, which is going to yield complementary knowledge to the previous one (Brigatti and Guggenheim 2002; Mottana et al. 2002; Zanazzi and Pavese 2002).

Considering all these features, we study the mineral series at different concentration of Al³⁺ and Mg²⁺ with phlogopitic substitutions, trying to cover, in the most simplified way, the range of concentrations of both cations in the octahedral sheet. Besides, the systems will be subjected at different pressures, calculating and analyzing atom, bulk volumes, and bulk moduli.

On the other hand, important insights of mechanical properties of these minerals can be deeply obtained if suitable models are considered (Cosenza et al. 2023). Besides, the elastic properties of the clay minerals are difficult to be experimentally determined by their polycrystalline size, porosity, anisotropy, bending layers (Tunega and Zaoui 2020), water in their interlayer space, and the different experimental methods. There are two theoretical/computational methodologies at hand: (i) those where the crystal structure (inter-atomic distances, angles and crystal face tensions of the unit/super cell) is minimized; and (ii) those where the time is considered in the calculations, that is, the molecular dynamic (MD) methods. Both methodologies can be applied with force field (FF) and with density functional theory (DFT) methods. The former ones are very reliable for large systems and swelling minerals. Recently, Na-montmorillonite plus an increasing hydration in the interlayer space was submitted to uniaxial compression and unidirectional shearing (Yuan et al. 2023, and reference therein), indicating that lattice parameter and the number of molecules in the model influence the stress–strain relationship. The problem with this type of methodologies is the reliability of the FF, and results must be compared with experimental values to do them trustworthy. The quantum mechanics methodology of DFT methods are used for calculating electronic, crystal structure, and properties and they are reliable, although is depending on the correlation exchange functional (vide supra). Considering the degree of detail that the DFT methods can give, it is possible that many internal properties of the crystal cell can be calculated, such as bond lengths, bond angles, volumes of the internal polyhedral forms, the size of the internal sheets, and the interlayer space and elastics constants. All of them are reliably calculated with DFT methods, especially those of non-swelling clay minerals as Ms is (Cosenza et al. 2023, and reference therein). In effect, from the different data, experiments and methods these authors’ review match, we know the isotropic bulk and shear moduli, and mechanical properties in general, are calculated with large confidence from DFT methods. The degree of detail is so large that even the atomic volumes and their compressibilities can be obtained. Some of these information are not different of those coming from diamond-anvil high pressure cells and crystal X-Ray diffraction experiments. However, experiments would yield an average image, whereas the DFT calculation is a theoretical tool, at first principle calculations that give us detailed effects in precise atoms of precise crystal structure.

In a previous paper, the compressibility of this series was searched, reaching to carry out the solvus of the series and the effect of pressure on the solvus (Hernández-Laguna et al. 2019). The compressibility of the series was reliably obtained and the effect of the pressure on the solvus gave a deep insight on the series, but the effect of the pressure on the atoms was not investigated. This effect on the atoms can deeply shed light about how the addition of the substituents affects other atoms and whole crystal cell compressibility, and where are either the weakest or less compressible atoms of the crystal. In a previous paper, related with the Ms–paragonite series (Hernández-Haro et al. 2016), the compressibilities of the bonds and polyhedral structures components of the crystal cells were calculated, giving a clear insight of the compression mechanism of the series. In these previous articles, distances and atomic groups compressibilities were calculated as a function of the pressure, by calculating the distance and the volume variation. Nowadays, the DFT methods permit a much more detailed knowledge of the electron and crystal structure, even by searching the topology of the electron density, fundamental observable in DFT methods, using the Bader’s theory (Bader 1990). So, it is possible to give a step further and the crystal cell be separated in atomic basins, in such a way, that we can separate the compressibility of the crystal cell in atomic domains, i.e., atoms with a definite volume; and the atomic volumes can be studied as a function of pressure. For these facts, the compressibility can be brought to the atomic level.

Considering both ranges of pressure, both minerals are stable, especially Phl (9 GPa, Yoder and Eugster 1954; Yoder and Kushitro 1969), and the range of pressure considered in our previous work (0–9 GPa, Hernández-Laguna et al. 2019), the series minerals are calculated between 0 and 9 GPa.

Therefore, in this work, we explore a three-variable space (P-X-C), and the atomic volume research is a novel approach to study this space, which is multiplied at least by the number of different atoms, viewing the properties and structural arrangements at atomic level. All of this is important for increasing the knowledge of the thermodynamic stability of the series, which is part of the rock assemblages in particular and in earth and planetary sciences in general.

Finally, it is well known, one of the aims of Chemistry is to account for structure, properties, and reactivity at local level and even at atomic level if possible, trying to do them transferable from each other compounds. In effect, in our previous work (Hernández-Laguna et al. 2019), the compressibility of the Phl–Ms series was calculated at bulk level, but now, following the trend for analyzing bulk properties in term of local and atomic contributions, we aim to provide explanations for the atomic-level compressibility of the Phl–Ms series mineral and explore the transferability to other similar series minerals.

Methods

Models

The real crystals of natural samples of these minerals have very heterogeneous distributions of cation substitutions, and in this series, one mixed member has a mixed dioctahedral and trioctahedral composition, being difficult to separate its effects. Besides, most of experimental methods applied on natural samples get us an average image of these substitutions. For these reasons, model samples would be important to study, where the effect of both substitutions can be clearly separated and located. These crystal models can be studied by theoretical methods, fixing our choice in the Quantum Mechanical methods, particularly those methods coming from the DFT. Besides, large models cannot be designed because of the complexity of our DFT calculations.

The complex stoichiometry of the Ms–Phl series may be expressed by K_yAl_x□_x/2Mg_3-3x/2 (Si_4-yAl_y)O₁₀(OH)₂, where □ means the octahedral vacancy, x = 0 represents for Phl end member, and x = 2 represents for Ms end member. In the tetrahedral site, y = 1, so 3:1 for Si:Al relationship is the most frequent ratio, and therefore, K⁺ is the counter ion of choice for balancing the charge in the interlayer space. The substitutions of a cluster of three Mg²⁺ by two ^VIAl³⁺ and an empty cavity are progressively performing in different concentrations reaching to design the following five compositions: X(Ms) = Phl (0.0), 0.25, 0.50, 0.75, and Ms (1.0) where X(Ms) = ${\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}$ x, x being the subindex in the general chemical formulae of the Ms–Phl series. However, as Hernández-Laguna et al. (2019) calculated, the central concentration in these models is inside the gap of solubility of the solvus of this series mineral; nonetheless, all concentrations are reliable for knowing the effects of pressure on the volume and properties of the crystal cell on a progressive increasing concentration procedure. In this way, the series mineral means the increasing concentration in our model.

Our model is in the polytype 2M₁. This polytype is very frequent in Ms, but in Phl, 2M₁ and 3 T are not so frequent (Gatta et al. 2011; Scordari et al. 2012) but, anyway, the 2M₁ polytype is considered as one more between the different polytypes of Phl (Fleet 2003). Therefore, this polytype is kept in the series to preserve the structure of the model in the increasing concentration cell procedure and not change the compressibility of the model by polytype changing.

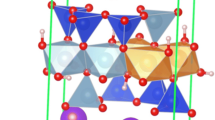
Our models have been designed being always the three Mg²⁺ cations cluster in the same octahedral cavity, for keeping the balance of charge in the octahedral sheet as localized as possible. The substitutions in different sheets are kept as far as possible. Full substitutions in one sheet and none in the other could be possibly considered as interstratified substitutions. The model has been well described by Hernández-Laguna et al. (2019); nonetheless, in order this article be self-consistent, in Fig. 1a, drawing of the model is given. All models of the Ms–Phl series were performed in the 2M₁ polytype. The unit cells considered in this study have 88 atoms for Phl end member [K₄Mg₁₂(Si₁₂Al₄)O₄₀(OH)₈] and 84 atoms for the Ms end member [K₄Al₈□₄(Si₁₂Al₄)O₄₀(OH)₈].

Fig. 1

Atomic volumes (au³) for Phl. Green, red, grey, light brown, purple, and white spheres mean Mg²⁺, O, Al³⁺, Si, K⁺, and H, respectively

Another feature of the natural samples of these minerals is the order–disorder substitutions; however, larger models are necessary for studying these substitutions, and consequently, this study is out of the scope of this work. Nonetheless, the low extension of our models lets us to obtain a model image of the octahedral/trioctahedral substitution in the structure, in such a way the properties can be viewed as pure properties.

Theoretical methods

All calculations were performed at the DFT level with Quantum ESPRESSO 5.4 (Giannozzi et al. 2009, 2017) with plane waves basis sets, PAW pseudopotentials (Blöchl 1994); being the PAW data sets generated from the pseudopotential library pslibrary (Dal Corso 2014). B86b exchange (Becke 1986) plus PBE (Perdew et al. 1996) correlation as exchange–correlation functional, and the exchange-hole dipole moment model (XDM) for dispersion forces (Becke and Johnson 2007; Otero de la Roza and Johnson 2012) are used in our calculations. This combination of functionals was suitable for describing weak interactions (Otero de la Roza and Johnson 2012). In a previous paper (Hernández-Laguna et al. 2019), this series minerals were studied at increasing pressure and the crystal structure and mixing properties were properly reproduced. Optimal plane-wave kinetic energy cutoff, density cutoff, and k-point grid were 110 Ry, 440 Ry, and 5 × 3 × 5, respectively. The convergence thresholds of forces and stresses were 0.001 Ry/Bohr and 0.05 GPa, respectively.

QTAIM atomic volumes

The topological analysis of the electron density $\rho (r)$ by the Quantum Theory of Atoms in Molecules (QTAIM, Bader 1990) offers an accurate mapping of the chemical objects, such as atoms, bonds, and particular structures, such as atomic groups (rings, cages). QTAIM provides a unique partitioning of the physical space of either a molecule or a solid in subsystems where any quantum chemical observable is univocally defined. Every subsystem (one electron basin, one atom) is bounded by the presence of zero-flux surfaces of the gradient of $\rho (r)$ which surrounds one local maxima of $\rho (r)$. The definition of an atom inside a molecule emerges when it is considered that the nuclear positions behave topologically as local maxima in $\rho (r)$. As a result, either in a molecule or solid property associated to a quantum chemical observable can be partitioned into atomic basins contributions using QTAIM. Therefore, the unit cell volume can be divided into atomic-like volumes:

$$V={\sum }_{i}{V}_{i}$$

(1)

Such atomic partition allows the analysis of the bulk properties of solids in terms of atomic contributions. In effect, the compressibility, β, and bulk modulus, K, of the system at constant temperature are

$$\beta =\frac{1}{K}=-\frac{1}{V}{\left(\frac{\partial V}{\partial P}\right)}_{T}$$

(2)

Introducing Eq. (1) into Eq. (2):

$$\beta =-\frac{1}{{\varvec{V}}}{\left(\frac{\partial \sum^{{\varvec{i}}}{{\varvec{V}}}_{{\varvec{i}}}}{\partial {\varvec{P}}}\right)}_{{\varvec{T}}}=-\frac{1}{{\varvec{V}}}\sum^{{\varvec{i}}}{\left(\frac{\partial {{\varvec{V}}}_{{\varvec{i}}}}{\partial {\varvec{P}}}\right)}_{{\varvec{T}}}=-\sum^{{\varvec{i}}}\frac{{{\varvec{V}}}_{{\varvec{i}}}}{{\varvec{V}}}\frac{1}{{{\varvec{V}}}_{{\varvec{i}}}}{\left(\frac{\partial {{\varvec{V}}}_{{\varvec{i}}}}{\partial {\varvec{P}}}\right)}_{{\varvec{T}}}$$

(3)

Therefore, the atomic compressibility is

$${\beta }_{i}=-\frac{1}{{V}_{i}}{\left(\frac{\partial {V}_{i}}{\partial P}\right)}_{T}$$

(4)

and the V_i/V relationship of Eq. (3) is the fractional volume occupancy of an atom in the crystal unit cell, such as:

$$\beta =\sum^{i}\frac{{V}_{i}}{V}{\beta }_{i}=\sum^{i}{f}_{i}{\beta }_{i}=\sum^{i}{f}_{i}\frac{1}{{K}_{i}}$$

(5)

In this last equation, bulk compressibility is analyzed in atomic compressibilities. This can be considered as a weighted addition of the atomic compressibilities. The weight is given by the fractional volume. This sum can be aggregated in atomic terms:

$$\upbeta =\sum^{\mathrm{i}}{\mathrm{f}}_{\mathrm{i}}{\beta }_{i}=\sum^{\mathrm{j}\in \mathrm{A}}{f}_{j}^{A}{\beta }_{j}^{A}+\cdot \cdot \cdot \cdot +\sum^{\mathrm{n}\in \mathrm{N}}{f}_{n}^{N}{\beta }_{n}^{N}$$

(6)

where A, B, … N are the atoms with the same atomic number, or those with the same atomic number being in a special place in the structure. j + ··· + n = number of atoms of the system. So, from each atomic addition, a weighted average atomic compressibility can be extracted:

$${\beta }_{av}^{A}=\frac{\sum^{\mathrm{j}\in \mathrm{A}}{f}_{j}^{A}{\beta }_{j}^{A}}{\sum^{\mathrm{j}\in \mathrm{A}}{f}_{j}^{A}}$$

(7)

The inverse of this last equation, an average atomic bulk modulus can also be extracted:

$${K}_{av}^{A}= \frac{1}{{\beta }_{av}^{A}}$$

(8)

These atomic volumes were calculated with the help of the CRITIC2 code (Otero-de-la-Roza et al. 2009, 2014; Pendás et al. 2000).

Equation of state

Crystal structures were calculated at the following tractions: − 3.0, − 2.0, − 1.5, − 1.2, − 1.0, − 0.9, − 0.6, − 0.3 GPa; and at a range of compressions from 0.0 to 9.0 GPa, with increments of 1.0 GPa. The pressure and volume results were fitted to a third-order Birch–Murnaghan (BM3) equation of state:

$$P=3{K}_{0}{f}_{v}{\left(1+2{f}_{v}\right)}^\frac{5}{2}\left[1+\frac{3}{2}\left({K}^{\prime}-4\right){f}_{v}\right]$$

(9)

f_v being the Eulerian finite strain

$${f}_{v}=\frac{{\left(\frac{{V}_{0}}{V}\right)}^\frac{3}{2}-1}{2}$$

An Eulerian finite strain will be also defined for atoms f_vi. K₀ in Eq. (9) is the bulk modulus at 0 GPa, and K′ $\left(=\frac{dK}{dP}\right)$.

The atomic volumes from Eq. (1) were also fitted with the same equation [Eq. (7)] as the crystal cell EOSFIT 7c program (Angel 2000; Angel et al. 2014; Milani et al. 2017) was used for fitting pressure to f_v and f_vi.

Mixing energy

The mixing Gibbs free energy, ΔG_mix, is given by:

$$\Delta {G}_{mix}=\Delta {G}_{ideal}+{G}_{xs}$$

(10)

where G_xs is the excess Gibbs free energy, which gives the deviation of a solution from the mechanical mixture. In this last model, the mixing free energy is a linear function of the composition. G_xs was calculated at a fixed pressure and temperature with the formalism:

$${G}_{xs,k}={G}_{k}-\sum_{l}{X}_{kl}{G}_{l}$$

(11)

where the index k is for an intermediate composition of the mixture, the index l represents end member of the series, and X_kl is the molar fraction of the l end member in the mixed-member k; ΔG_ideal is the free energy for the entropy change of the random mixing of cations. ${G}_{xs,k}$ can be described following a Redlich–Kister equation (Ganguly 2008; Guggenheim 1937; Redlich and Kister 1948):

$${G}_{xs}=X\left(1-X\right)[A+B\left(2X-1\right)+C(2X-1{)}^{2}+\dots ]$$

(12)

where X is the molar fraction of one component in the binary series, and each A, B, and C coefficients are dependent of temperature and pressure, and they can be resolved in enthalpy, entropy, and volume components as (Roux and Hovis 1996):

$$A={A}_{H}-{A}_{s}T+{A}_{V}P$$

(13)

where A_H, A_S, and A_V are terms depending on the enthalpy, the entropy, and the volume, respectively; similar equations can be written for B and C coefficients. In this work, volume terms will be calculated only.

The volume of a mixed composition has an excess equation similar to Eq. (11), such as:

$${V}_{xs,k}={V}_{k}-\sum_{l}{X}_{kl}{V}_{l}$$

(14)

Substituting Eq. (1) in (14), a separation of bulk excess volume in atomic excess volumes can be obtained:

$${V}_{xsk}=\sum_{i=1}^{nat}{V}_{ki}-\sum_{l}{X}_{kl}{\sum_{i=1}^{nat}{V}_{li}}= {V}_{xsk}^{A}+{V}_{xsk}^{B}+\cdot \cdot \cdot +{V}_{xsk}^{N}$$

(15)

V_xsk and ${V}_{xsk}^{A}$ are the bulk excess volumes of the mixed composition and atomic excess volume, respectively, of this mixed composition. These atomic excess volumes can be got together in atomic groups with the same atomic number (A, B,…N) or the same atomic number in an especial place of the structure (A₁, A₂, B, …. N), that is, basal oxygens in the interlayer space, oxygens in the OH groups, and oxygens in the apical positions are included in diverse groups.

Finally, Redlich–Kister equations [Eq. (12)] can be interpolated for the set of excess volumes of mixed compositions {V_xsk^A} at specific pressures, getting A^A, B^A, and C^A atomic coefficients of the expansion. This approximation gives us a landscape of the excess atomic volumes at different pressures.

Results and discussion

Crystal structure and atomic volumes at room pressure

Geometry of the crystal structure as a function of the composition

The crystal structures of the series were taken from Hernández-Laguna et al. (2019), which agree with the known experimental results. The table is given here for the sake of completeness (Table 1), including more structural details than Table 1 in Hernández-Laguna et al. (2019). Calculated cell parameters are in the range of known experimental values, although in some case, computational values are slightly different; nonetheless, the cell volumes agree with experimental values. The monoclinic symmetry is computationally kept in the optimization procedure. Cell parameters decrease as a function of the content of Ms:

• (i) The a axis decreases as a convex quadratic function (Table 2), where, from values larger than X(Ms) > 0.5, a has larger slope than the more phlogopitic compositions (X(Ms) < 0.5). In effect, this local increasing of charge into two octahedra provokes a decreasing of a axis in the structure.

• (ii) b linearly decreases also as a function of X(Ms), being the linear coefficient (Table 2) slightly larger than a.

• (iii) β shows a quadratic behavior, with a minimum at X(Ms) = 0.25, and from this value, β increases quadratically.

• (iv) ${\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}$·c·sinβ decreases linearly to X(Ms) = 0.5, and from this value, it irregularly increases.

• (v) Finally, the volume decreases from Phl to Ms linearly, with a slope of − 43.5 Å³ by unit of X(Ms).

Table 1 Cell parameters (Å and degrees), cell volumes (ų), and average atomic bond distances (Å) of meaningful atomic groups of the Ms–Phl series minerals at PB86b-PBE-XDM-PW level (Hernández-Laguna et al. 2019)

Table 2 Square polynomial and lineal functions fitting coefficients of cell parameters (Å, and degrees), square correlation coefficient and residual sum of squares for Phl–Ms as a function of increasing molar fraction of Ms

In Table 1, averaged ^IVX-O bond distances are also given, which agree with the range of the known values. ^IVAl-O_b are larger than that of Si-O_b. The same happens with ^IVAl-O_a and Si-O_a, being the bonds with the apical O’s larger than those with the basal O’s. The values are slightly larger than the known experimental values. Values of Mg-O_a and ^VIAl-O_a agree with the experimental values as well, and their values are also slightly larger than the experimental values, Mg-O_a being larger than ^VIAl-O_a, because of the increasing charge of the Al³⁺, the bond lengths with the O’s decrease. O–H distances are larger in the Mg²⁺ octahedrons than in the Al³⁺ octahedrons. Besides, O–H in the Mg²⁺ octahedra are approximately perpendicular to (001) plane, pointing to the interlayer cations, producing a H⁺···K⁺ repulsion (Comodi et al. 2004); but OH’s of the dioctahedral substitutions are approximately parallel to (001) plane. K···O_outer show slightly larger values than the experimental values. The same happens with K···O_inner, but the behavior is decreasing. These larger values in both distances will lead to a larger theoretical than experimental interlayer thicknesses. Δ = K···O_outer – K···O_inner shows an increasing quadratic behavior [Δ = 0.49 − 0.02X(Ms) + 0.18X(Ms)²] as a consequence of the increasing asymmetry of the substitution. Besides, this increasing/decreasing behavior of K⁺···O_outer/inner distances in the interlayer space also comes from the rotation of the tetrahedrons to fit the misfit between tetrahedral and octahedral sheets as a consequence of the composition of the crystal structure, which yield the α angle (Table 1, which comes from the deviation from the hexagonal symmetry to a ditrigonal symmetry of the tetrahedral crown). This α angle also produce a change of the coordination of the interlayer cation from twelve to six plus six (Ferraris and Ivaldi 2002), as the different K···O_outer and K···O_inner distances indicate. This α angles show slightly larger values than those found in the experimental literature², but the α increasing behavior (Fig. 1) is similar to the experimental values. This increasing behavior as a function of X(Ms) also comes from the asymmetric substitution of the increasing dioctahedral character in the structure. Following to Bailey (1984), cosα = b_obs/b_ideal, b_ideal being the b axis of the hexagonal tetrahedral sheet. This relationship gives the lateral reduction of the two axes, that, with our calculated values, the reduction from b_ideal to b_obs goes from 2.2% in Phl to 2.8% in Ms. The tetrahedral, octahedral, and interlayer thicknesses show values larger, but compatible with experimental values.

Atomic and groups volumes as a function of composition

All of these previous bond distances and atomic group geometrical parameters are calculated from the geometrical relationships between the points where the nuclei of the atoms are localized, which are obtained from the minimizing procedures of the forces, stresses, and energy of the crystal. However, nothing is said about the atomic volumes of the system, which can be also calculated following Bader’s theory (Bader 1990).

Let us start with the atomic volumes found at room pressure as a function of the composition. Bulk and atomic volumes as a function of the molar fraction (Table 3) of Ms have the following features:

• (i) The cell volumes calculated from cell parameters, Eq. (1), and average atomic volumes are quite close (Table 3). The bulk volume calculated from the cell parameters and from the addition of atomic volumes have an average difference of 0.268 Å³; and the bulk volume from the cell parameters and the bulk volume calculated from the addition of the average atomic volumes have an average difference of 0.045 Å³, which may come from the round errors in the numeric integration procedure of the atomic volumes. Total volumes as a function of X(Ms) are generally decreasing and agree with the experimental values (Hernández-Laguna et al. 2019).

• (ii) Most of the atomic volumes decrease as a function of the increasing Ms composition, following the trend of the bulk.

• (iii) In general, Mg²⁺ volumes increase as the composition augments, showing a maximum at the middle composition.

• (iv) Average atomic volumes laying in the interlayer space (K and O_b) have the largest atomic volumes. These atoms follow similar behavior as a function of the composition.

• (v) The O_b, O_a, and O_O(OH) atoms have different values depending on the position they have in the crystalline structure, O_a’s being the smallest, which are in the densest part of structure.

• (vi) The O_O(OH) and H atoms have quadratic behaviors as a function of composition, but the first one with a maximum and the second one with a minimum, which could be considered as complementary. If the average volumes of both atoms are added, a decreasing quadratic function is found (V_O(OH)+H = 17.67 + 0.007X(Ms) − 0.36X(Ms)²; R² = 0.98).

• (vii) The average atomic volume of Si is smaller than ^IVAl and they follow quadratic decreasing trends, but Si follows a much milder behavior.

• (viii) The ^IVAl³⁺ and ^VIAl³⁺ cations have approximately the same volumes at function of the concentration of Ms, indicating the atomic volumes of Al³⁺ are independent of their position in the crystalline structure; however, fittings show different coefficients because of the lack of the first term of ^VIAl³⁺ as a function of composition.

• (ix) The Si⁴⁺, ^VIAl³⁺, and Mg²⁺ cations are isoelectronic atoms. However, the volume of the more charged atoms is approximately between 1 and 1.5 Å³ smaller than the Mg²⁺ volume, indicating the volume contraction due to the increasing nuclear charge.

• (x) If the radius of K⁺ is extracted assuming this volume as spherical, we obtain a radius range between 1.675 and 1.689 Å, which are slightly larger than 1.64 Å, value given by Shannon (1976) for the effective ionic radius of K⁺ with a coordination number of 12, which agrees quite well with our values. However, if we apply the same procedure for the ^IVAl³⁺, ^VIAl³⁺, ^VIMg²⁺, and ^IVSi⁴⁺ cations, we obtain 0.97, 0.96, 1.04, and 0.921 Å, which are larger than the Shannon’s effective ionic radii with values of 0.39, 0.53, 0.72, and 0.26 Å, respectively. These differences are coming from the electron basins, the topology of the electron density in the crystal space, and the non-spherical shapes of atomic basins. All of this can indicate once again the non-completely ionic character of these ions in the micas crystal structure, where bonds in the crystal pertain to several types.

Table 3 Average atomic volumes (ų), total volumes (V_t)^a,b,c, and their coefficients from square polynomial equations fitted by means of the least square fitting method as a function of X(Ms) for the Phl–Ms series at room pressure

Therefore, in general, the atomic volumes at a function of the composition show a similar behavior as the total volume; however, the O_OH, H, and Mg²⁺ follow an extremal behavior approximately at the middle composition. The H atoms are at first sight dangling in the octahedral hole, but they have different configurations and hydrogen bonds (HB) with O_b and O_a and different lengths depending on composition in consequence.

From this view, a more general landscape can be accomplished if we fix our choice in the influence of the substituent’s atomic volumes in the bulk volume by studying the bulk and atomic excess volumes. Considering Eqs. (14) and (15) and interpolating excess volumes with Eq. (12), Fig. 2a can be depicted. The excess volume of the bulk as a function of X(Ms) shows two maximal curves and one minimum in-between calculated from Eq. (12) (Fig. 2a). The two maxima are at X(Ms) = 0.15 and 0.85, indicating the most important deviations of the volumes out of the normal mix are remarkably close to end members, that is, a few amounts of one of the substituents in either direction produce the largest distortion of volume, getting a smaller asymmetry between both maxima at X(Ms) = 0.5. The maximum excess volumes in nearby of the end members could come from the cation distribution models used in our calculations (Hernández-Laguna et al. 2019). In effect, our models with X(Ms) = 0.25 and 0.75 are interstratified cation distributions in the octahedral sheets: one sheet is merely Phl and other is mix of ^VIAl³⁺ and Mg²⁺ substitutions at X(Ms) = 0.25, meanwhile at X(Ms) = 0.75, one sheet is Ms and the other is a cation mixture. However, in the central composition, both octahedral sheets have the same concentration of both substituents. Therefore, the largest changes in the volume with respect to the mechanic mixture are produced for the interstratified compositions.

Fig. 2

Excess bulk and atomic volumes as a function of composition of the Phl–Ms series mineral at different pressures: a P = 0 GPa; b P = 3 GPa; c P = 7 GPa; and d P = 9 GPa

If analysis of excess atomic volumes is considered, the groups of atoms contributing to this bulk behaviour can be highlighted (Fig. 2a). In effect, the O_b, O_a, and ^VIAl³⁺ show excess volume curves with shapes like the bulk contour. Even the K⁺ curve shows a similar shape but with a very flat minimum at the central concentration. The most surprising behavior is related with ^VIAl³⁺ substituent, that, having the same curve shape than the bulk, it shows small deviations around Vxs = 0.0 J/molbar. Therefore, considering that this element is one of the substituents of the system, its excess volume should show larger values, which looks like to indicate that ^VIAl³⁺ substitution in the system has small deviations of the normal mixture, but its influence on other atoms of the system induces distortions similar to the whole behavior of the bulk, as it happens with O_b, O_a, and K. These three last atoms show the largest volumes of the system, especially O_b, which has the largest volume of the O’s in the system and along with K⁺ have a special role in the interlayer space and in the ditrigonal cavity. So, these atoms are very sensible to substitution in the octahedral sheet. Besides, K⁺ has a similar behavior to O_b. The opposite behavior is related with the other changing cation on the system: Mg²⁺, which shows a curve with a shape opposite to the bulk curve and with larger values than ^VIAl³⁺ curve, especially in the central composition, indicating that this cation influences the bulk Vxs in the opposite sense and with larger extension than ^VIAl³, compensating the effect of ^VIAl³⁺. So, the slight changes of volume of the substituents with respect to the mechanical mixture are transmitted and magnified to the locus of the structure easier to change, that is, the easy-to-deform interlayer space. The excess atomic volumes of Si⁴⁺, and ^IVAl³⁺ show values near of 0.0 J/molbar and with similar curve shapes; the substituents do not have any important influence on them. The H and O_OH atoms show complementary behaviors, that is, O_OH shows the largest positive deviation at the middle composition and H the largest negative deviation at the same composition. The complementary behavior of these groups yields a small contribution to the excess volume of the system.

From the average atomic volumes (Table 3), average bonds, bond angles, and polyhedral volumes are built by simple addition of the atomic volumes. These atomic group volumes can be considered as average volumes of the crystal. Therefore, once the atomic volumes are calculated, the average volumes of atomic groups can be easily studied. In Fig. 3a and Table 4, the bond and atomic group volumes as functions of the X(Ms) are depicted. Si/^IVAl-O_b and Si/^IVAl-O_a show quadratic and lineal functions decreasing as X(Ms) is increasing. Volumes of ^IVAl-O_b/a are larger than Si-O_b/a bonds, similar to the atomic distances. However, the volumes of the Si/^IVAl-O_b are larger than Si/^IVAl-O_a, which is opposite to that found for the bond distances. The bond distances are the distances between the points where the nuclei are located in the crystal cell. However, the basal oxygens, in the T sheet, are in the interlayer space, where the atomic electron basins have more room for expansion, and the limit of the electron basins is much more expanded than those of the oxygens in the apical position, which are narrowly closed by the coordination atoms. This fact put the question mark about the absolute volumes for the atoms, seeing from Bader’s analysis that the atomic volume in a crystal or a molecule is deeply related with the bond and position in the crystal. The behavior of all these bond volumes as a function of composition is parallel (Fig. 3a). Quadratic and linear fitting equations as a function of X(Ms) are written in the same figure. Quadratic equation fittings are found for the Si/^IVAl-O_b bond volumes and linear equations for the corresponding Si/^IVAl-O_a bond volumes. Coefficients of the fitting equations for the ^IVAl³⁺ are larger than for Si equations, indicating the effect of composition is more important for the ^IVAl-O bond volumes than for Si–O bond volumes.

Fig. 3

Bond and atomic group volumes from the average atomic groups: a Si/^IVAl-O_b/a bond volumes; b Mg²⁺/^VIAl³⁺-O_aO(OH); c tetrahedra of Si and ^IVAl³⁺

Atoms in octahedral sheet show different behavior (Fig. 3b and Table 4): Mg-O_a/O(OH) volumes are larger than ^VIAl³⁺-O_a/O(OH) volumes, being the volumes where the O_(OH) are involved the largest. ^VIAl³⁺-O_a have homogeneous decreasing behavior. The largest bond volumes for O_(OH) atoms could come from the octahedral vacant where they are located. The OH groups form HB with O_a/b atoms of different strength. The Mg²⁺-O_a bonds have a decreasing behavior (Fig. 3b and Table 4); with a maximum either at X(Ms) = 0.25; and Mg²⁺-O_O(OH) has also a maximum at 0.50. The coefficients of the equations for Mg²⁺ and ^VIAl, where apical O atoms are involved, have opposite signs.

The O–H volumes of the (Mg²⁺)O–H in Phl are larger than (^VIAl³⁺)O–H in Ms. Besides, (Mg²⁺)O–H shows a configuration perpendicular to the basal plane. However, those of Ms show an angular bond quasi parallel to the (001) plane. In effect, the average volume of the angular atomic group of Mg²⁺-O–H is 22.363 ų, while that of ^VIAl³⁺-O–H is 20.894 ų, which looks like to indicate that the perpendicular arrangement of the OH with respect to the basal plane in the octahedral vacant develops larger volumes than O–H closer to the basal plane.

Average K-O_b volumes are the largest volume bonds in the crystal, they show a clearly decreasing linear behavior (V_K-Ob = 37.60 − 0.69X(Ms); R² = 0.95).

The average volumes of the tetrahedrons of Si and ^IVAl³⁺ decrease with respect to the X(Ms) proportion following quadratic functions (Fig. 3c and Table 4), the ^IVAl³⁺ tetrahedron being the largest and the function the steepest.

Finally, the Mg²⁺ octahedral has a volume value of 92.513 ų in Phl, and the ^VIAl³⁺ octahedral has a volume of 90.228 Å³ in Ms. They have the largest volumes out-of-interlayer-space atomic groups in the crystal structure. Nonetheless, the polygons of K⁺ with the basal oxygens in the interlayer space have the largest volume, which also decrease at function of the Ms composition.

Crystal structure and atomic volumes at increasing pressure

Tractions and compressions from − 3 to 9 GPa are applied to our system. In general, the crystal structure, atomic volumes, atomic groups, polyhedron volumes, and atomic distances decrease when pressure is increasing. Variation of all these geometrical parameters as a function of pressure for this series mineral was studied by Hernández-Laguna et al. (2019). However, in this work, the atomic volumes are especially considered as a function of pressure.

In this system, the atomic volumes decrease as a function of P, and this relationship is given by the atomic bulk moduli (vide supra). Nonetheless, the evolution of the bulk and atomic excess volumes at different P as a function of X(Ms) can yield us an atomic mechanism landscapes of the compression of the system. In effect, at pressures of 3, 7 and 9 GPa bulk and atomic Vxs are depicted in Fig. 2b–d. Bulk Vxs from 0 to 7 GPa evolve decreasing the value of their maxima and minima, making the structure more lineal with respect to end members of the series. Minima change Vxs values from positive to negative values, increasing the negative value of the minimum with the increasing pressure. Besides, 3 GPa bulk excess volume shows the largest asymmetry between maxima; and the largest maximum being near X(Ms) = 1. This asymmetry is softened at 7 GPa, and the value of the maxima is the shortest. The effect of increasing P on the bulk Vxs is to make the mix more normal with respect to the end members. At a P = 9 GPa, the central minimum shows the most negative value, and the maxima increase their values and asymmetry with respect to the 7 GPa bulk Vxs. Therefore, the most general effect of the increasing P on the bulk Vxs is to change the sign of the excess volume, especially at the central member.

The atomic excess volumes follow the trend previously mentioned at pressure of 0 GPa, in general keeping the shape and decreasing their maxima and minimum values, especially O_b which follows bulk excess behavior quite faithfully. At 7 GPa, Vxs of K shows the same trend but with very flat values but increasing their maxima and minimum at 9 GPa. From 7 GPa, the Vxs of O_OH show an important asymmetry in the extreme values of X(Ms). The Vxs of the H atoms follow this trend with the opposite sign. Therefore, at high pressure, OH groups are affected in diverse ways at concentrations near the end members, when OH are approximately either perpendicular or parallel at the (001) plane. Si and ^IVAl³⁺ show maxima at the central concentration, small deviations from the origin of Vxs (0.0 J/molbar) and they have parallel behavior, with small separations between them at increasing P. The asymmetry of extremes, shape, and values of Mg and ^VIAl Vxs curves are kept with the increasing pressure. Therefore, the influence of these substituents is brought to interlayer space where the major changes of atomic Vxs are produced, especially in the basal O, which can be considered the building block of the excess bulk volume.

Bulk moduli of the series [the values are calculated from bulk volume and the atomic values, Eq. (5)] increase as a function of X(Ms), following the next fitting equation: K₀ = 46.8 + 6.7X(Ms); R² = 0.991. The substitution of three Mg²⁺ in the cell by two Al³⁺ plus an octahedral vacant address for increasing of the bulk modulus at 6.7 GPa at the pure Ms, which could come from by the larger charge concentration on two octahedra instead of to share the 6 + formal charges of the three Mg²⁺ in three octahedra. On the other hand, an empty cavity located in the Ms loci should make the octahedral sheet more compressible. However, three Mg²⁺ in Phl have a volume of 14.05–14.16 Å³ but two ^VIAl³⁺ have a volume between 7.41 and 7.16 Å³. The difference of volume between the 3 Mg²⁺ and 2 ^VIAl³⁺ is between 6.64 and 7.06 ų. At first, these differences could be approximately estimated to the volumes of the empty cavities, which, along with the different nature of the substituent cation and its influence on the rest of the structure, could be the origin of property changes along the series. The volume difference of the bulk along the series is between 9.96 and 11.73 Å³, indicating that, in terms of volume, the substitutions go further than the difference of volume between 3Mg²⁺ and 2^VIAl³⁺ volumes. So, with respect to the more spread/concentrated charge in the three Mg²⁺ of Phl/two ^VIAl³⁺ of Ms and the change of volume of no-empty-cavity in Phl/open-octahedral-cavity of Ms for the Phl/Ms loci, the system performs by decreasing/increasing bulk modulus.

In general, the atoms varying their atomic moduli in the same direction than the bulk moduli are the following: the O–H groups are located in the octahedral cavity, forming HB with the basal and apical O atoms. Besides, these O–H form mainly two types of angles as a function of the progression of the mineral series: approximately perpendicular or parallel to the basal plane in Phl and Ms substitutions, respectively. These orthogonal H’s present two different values of the atomic incompressibility modulus: around 24 (H_orto1 in Table 5) and around 19 GPa (H_orto2 in Table 5). The O–H bond distances and angles show slight differences between them. However, the angle of OH groups in the Al³⁺ octahedral cavity decreases to extremely low values, being approximately parallel to the basal plane with the progressing of Ms concentration. The atomic bulk modulus of these H’s increases to 57.7 GPa in the X(Ms) = 0.25 mixed member, meanwhile the orthogonal H’s keep on the previous two mentioned values. The high rigid H atoms associated with the low angle of the O–H are located close to the O_a’s, and at the compression process, they have less room and freedom for compressing consequently. Meanwhile, the H_ortho atoms pointing up to the tetrahedral cavity have more room and freedom in the compression process. At the end member of the series (X(MS) = 1), the atomic bulk modulus of the H_O-H atoms increases to 75 GPa, indicating clearly that H’s parallel to (001) are more rigid than H_O-H perpendicular to this plane. These facts could also have implications in the HB of the OH groups with the basal and apical O atoms. In Phl, the OH groups form HB with one donor O_b, meanwhile in Ms cavities, bifurcate HB are found doing interactions with three donor O (two apical and one basal O). So, they play a key role in the compression mechanism. Therefore, Ms’s H atoms, with their different configurations and bonds, are more resistant to pressure. The HB of the OH groups are so important that they control also the elastic constants and bulk modulus in kaolinite (Sato et al. 2005), decreasing the bulk modulus in a range between 21 and 55 GPa, following different experimental and theoretical methods. In effect, the HB’s between the OH groups of the octahedral sheet and the siloxane O atoms of the next sheet control the bulk modulus of kaolinite. In our case, the HB’s are internal HB’s, but in the trioctahedral substitutions, OH vectors point to K⁺, producing repulsion between H and K positively charged atoms.

The K⁺ cation shows the lowest values of the atomic bulk modulus of all atoms in these series minerals, except H_ortho2. The average atomic bulk modulus values of K⁺ increase as a function of the Ms composition and with the bulk moduli in the series: K_K = -0.79 + 0.51K₀, R² = 0.992. The slope of the fitting indicates that K_k is approximately half of K₀, so the other half must be determined by other atoms and locus of the crystal structure. This fact comes from the interlayer position of K⁺ in the interlayer space, being the locus where the weaker forces are interacting and, therefore, the place where the bulk modulus is determined. As also Comodi et al. (2004) suggest: “the interlayer cation strongly controls bulk mica compressibility”. The weakest “string” in the crystal structure clearly is the interlayer space, and the place where the structure collapses the easiest when pressure is applied. Furthermore, K⁺ atomic volumes are the largest (Table 3), and the weakest bonded, and the most compressible in consequence (Table 5). The atomic volume decreases as X(Ms) (Table 3) and K_K increases (Table 5).

Table 4 Average atomic group volumes (ų) as a function of X(Ms) at room pressure

Table 5 Weighted average atomic incompressibility moduli $\left[ {{\text{K}}_{{0{\text{i}}}} {\text{ and K}}_{0} \, \left( {K_{0} = \frac{1}{{\sum\nolimits_{{}}^{{\text{i}}} {{\text{f}}_{{\text{i}}} \beta_{i} } }}} \right){\text{ GPa}}} \right]$ as a function of X(Ms)

Previously analyzed atoms have constant concentrations in the different compositions; however, Mg²⁺ are decreasing with increasing X(Ms). The average atomic bulk moduli are one of the largest in the structure (141.7–168.5 GPa). The position they have in the crystal is very deep and tight by the apical O and O_OH atoms in the octahedral sheet.

^VIAl³⁺ is increasing along the series and shows larger K_0VIAl than K_0Mg, and K₀ increases in spite there are two Al³⁺ by three Mg²⁺. In general, K_VIAl increases along the series; however, at the middle concentration, the values reduce, like Mg²⁺. The decreasing of Mg²⁺ and the increasing Al³⁺ and one octahedral cavity all along the mineral series are the main differential features in our system; however, they do not show any regular nor functional behavior with K₀.

The Si⁴⁺ cation has a constant concentration in our system. The average atomic bulk modulus goes between 132.0 and 159.4 GPa. Although it shows an increasing behavior with respect to K₀, it does not follow any easy functional behavior. Maybe O_b atoms, which are bonded to Si, at the vertexes of the tetrahedral cavity and in the interlayer space absorb the highest strains in the compression process.

In general, atomic bulk modulus of ^IVAl³⁺’s show higher and lower values than ^VIAl³⁺, depending on the composition.

The O_a atoms have K_0Oa values lower than O_OH but both being of the same order. However, K_0Ob shows values about one tier of the previous ones. The position in the interlayer space of O_b, which gives them the largest volumes of the O atoms in the structure, determines the lowest atomic bulk modulus value of the O atoms, that, along with K⁺, shows the lowest incompressibility locus of the structure. This large compressibility at the interlayer space is related to the occurrence of six-membered ring of micas and phyllosilicates in general. Interconnection of six-member rings of tetrahedra provides a bond angle at O_b that approximates the tetrahedral angle in opposite to three- or four-membered rings (Burdett and McLarnan 1984). Thus, we consider that covalency of bonds at O_b determines the nature of interactions at the interlayer space. In fact, there is a reduction of this covalency of bonds at O_b in Ms with respect to Phl due to the inductive effect arising from the di–trioctahedral substitution in the studied micas (Al-O bonds are more covalent than Mg-O bond). According to it, atomic compressibility of O_b and the nature of the bond at O_b would determine the compressibility of the phyllosilicates. In addition, the largest volumes of the O_b atoms increase drastically their polarizabilities, and, as a consequence, the refractive index also increases (Bloss 1994). Thus, hexa-net defined by O_b atoms in the T sheet at the level of the interlayer space explains the major refraction index of phyllosilicates parallel to the (001) plane. The problem of bonding in this series will be accomplished in the next article about this subject.

Conclusion

DFT calculations are performed to 2M₁ Phl–Ms mineralogical series as a function of the composition. Crystal structure, bond distances, angles and volumes of atomic groups agree with known experimental results. OH of Mg²⁺ octahedra are approximately perpendicular to the (001) plane, and those of the ^VIAl³⁺ octahedra are approximately parallel to the (001) plane.

Atomic volumes are calculated from the atomic basins, which are found between the limits of the zero-flux surfaces of the gradient of $\rho (r)$ which surrounds one local maxima of $\rho \left(r\right)$. By the nature of these calculations, the volume of the crystal can be analyzed in terms of atomic volumes. This analysis gives us a detailed landscape of the crystal structure in terms of the building block of the atoms. Atomic volumes of the same atomic number present different values depending on the position they have in the crystal structure. The O_b atoms are the most highlighted example, having the largest volume between all O’s in the crystal. This large volume is determined by the interlayer space and the tetrahedral cavity in which O_b are placed. Besides, K⁺ shows the same features. Therefore, the Si – O_b is shorter than Si–O_a distances calculated from atomic positions of the nuclei; however, the opposite is true if calculations are made in terms of atomic volumes. The interlayer space lets atomic basins be more spreads than atoms in more compact places of the crystal structure.

Bulk excess volumes as a function of composition show a double maximum with a minimum in-between. The atomic excess volume of O_a, O_b, K⁺, and ^VIAl³⁺ shows curves with similar shapes than the bulk shape, but that of ^VIAl³⁺ is very much softer than the bulk curve. Mg²⁺ excess volume curve is opposite to the bulk curve. Therefore, substitution atoms transmit their effect to other atoms, especially those in the interlayer space.

At high pressures, excess bulk and atomic volumes tend to decrease their effect, being closer to normal mix, even passing on their positive effect to negative values, and showing some asymmetries between the maxima at the extreme compositions. Pressure highlights the differences between the interstratified compositions. In all cases, excess bulk volume curve is determined by the same set of atoms, especially by O_b.

Atomic bulk moduli also show differences depending on the nature of the atoms, so K⁺ have the lowest atomic bulk moduli, but also of the position that atoms occupy in the crystal structure, such as O_b having the lowest value between the majority of the atoms and the rest of O. Both atoms behave as the bulk modulus of the series. We conclude that the structural behavior of phyllosilicates under pressure may be monitored by the atomic bulk moduli of O_b. Finally, there are significant differences in the atomic bulk moduli between H coordinating to Mg²⁺ (H_ortho) and those coordinating to ^VIAl³⁺ (H_planar).