Introduction

Aluminium alloy is extensively used in aero-space area. The aluminum-rare earth intermetallic compounds with CsCl structure (B2 crystal structure) provide good performance with lower dense, good resistance to oxidation and corrosion, heat resistance and highly ordered. Therefore, the intermetallic compound (IMC) has caused wide concern (Morris et al. 2004; Tao et al. 2007a, b). In recent decades, some properties of aluminum-rare earth intermetallic compounds with B2 crystal structure such as mechanical properties, electronic property, crystal structure, elastic property and thermodynamic property are studied extensively (Farkas et al. 1995; Schroll et al. 1998; Vitek 1998; Ludwig and Gumbsch 1998; Gschneidner et al. 2003; Li et al. 2011; Lazar and Podloucky 2007; Pagare et al. 2011). B2-AlPr is one of the aluminum-rare earth intermetallic compounds and the lattice constant of AlPr 3.82 Å is discovered as early as 1965 (Buschow 1965). Then, the formation enthalpy of AlPr is obtained by Kober et al. (1983). Massalski (1990) points out that as they provide phase diagram of Al–Pr that AB component of AlPr possessing two structural phase, α-AlPr and β-AlPr, and α-AlPr perform stable state when the temperature is lower than 973 K. And in 973 K–1178 K, β-AlPr performed stable state, in which B2-AlPr is metastable phase.

Tao et al. (2007a, b) investigated the mechanical and thermodynamical properties of AlPr using projector augmented wave (PAW) method within generalized gradient approximation (GGA). Srivastava et al. (2008) calculated lattice parameters, bulk modulus, Debye temperature and Grüneisen constants. It performed a pressure-induced variation of Debye temperature and has found a decreasing in Debye temperature around 40 kbar in AlRE (RE = La, Ce, Pr) intermetallics. However, few studies have been conducted on the mechanical properties of AlPr.

Dislocation is one of the important factors which affects the plasticity of materials. Therefore, the study of dislocation and mobilities is very significant for B2 structure AlPr. This paper mainly focuses on the dislocation core structure of B2-AlPr and related Peierls stress using the truncated approximation method.

The dislocation core structure of AlPr

Dislocation equation and its truncated dislocation solution

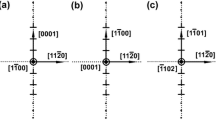
Generally, the natural coordinate system is adopted in dislocation theoretical analysis. One coordinate axis is set as dislocation line direction, and the other coordinate axis is perpendicular to dislocation line direction, where Burgers vector was involved in glide plane. In fact, it is reasonable that a coordinate is set as Burgers vector “b”. In commonly used dislocation coordinates, the dislocation line direction is defined as y-axis, the x-axis is parallel to edge dislocation, in which x–y plane, glide plane or misfit plane is determined by the dislocation line and the Burgers vector “b”. The intrinsic frame is determined by a set of orthogonal unit vector (\( e_{ \bot } ,e_{\parallel } \)), which is obtained by rotating the natural coordinate frame along with the y-axis (Wang et al. 2011). Figure 1 shows the intersection angle (\( \alpha \)) of Burgers vector and dislocation line.

Fig. 1
figure 1

The intrinsic frame

Full size image

In intrinsic frame, displacement field can be represented by \( u = u_{\parallel } + u_{ \bot } \), in which \( u_{\parallel } \) is the parallel component of Burgers vector, and \( u_{ \bot } \) is the normal component of the Burgers vector. The coordinate transformation of two frameworks can be represented by the following matrix:

$$ \left( {\begin{array}{*{20}c} {u_{\parallel } } \\ {u_{ \bot } } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\sin \alpha } \\ { - \cos \alpha } \\ \end{array} \begin{array}{*{20}c} {\cos \alpha } \\ {\sin \alpha } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {u_{x} } \\ {u_{y} } \\ \end{array} } \right) . $$
(1)

Besides, restoring force can be represented by the similar transformation relation:

$$ \left( {\begin{array}{*{20}c} {f_{\parallel } } \\ {f_{ \bot } } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\sin \alpha } \\ { - \cos \alpha } \\ \end{array} \begin{array}{*{20}c} {\cos \alpha } \\ {\sin \alpha } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {f_{x} } \\ {f_{y} } \\ \end{array} } \right) . $$
(2)

Meanwhile, the translation paralleled to the Burgers vector direction is the main part of the displacement, and the normal component is regarded as the perturbation in solving of the displacement of parallel component. The bounded path is similar to the following unidimensional equation:

$$ - \frac{1}{2}\beta_{\parallel } \sigma \frac{{d^{2} u_{\parallel } }}{{dx^{2} }} - \frac{{K_{\parallel } \sigma }}{2\pi }\int_{ - \infty }^{ + \infty } {\frac{dx'}{x' - x}} \left. {\left( {\frac{{du_{\parallel } }}{dx}} \right)} \right|_{x' = x} = f_{\parallel } , $$
(3)

where \( \sigma \) is the original cell area, \( \beta_{\parallel } \) is discrete lattice effect correction factor, \( K_{\parallel } \) the energy factor, \( u_{\parallel } \) is the displacement field, \( f_{\parallel } \) is the restoring force. As it is a second-order integral differential equation, the analytic solution is difficult to obtain.

To separate the dislocation core part from the displacement field, the displacement field \( u \) is resolved into two main parts:

$$ u = u^{0} + u^{c} , $$
(4)

where \( u^{0} \) is the dislocation shape, which stays away from the center of dislocation. \( u^{c} \) is the dislocation center section. In intrinsic frame:

$$ u{}_{\parallel }^{0} = \frac{b}{\pi }\arctan q + \frac{b}{2},u_{ \bot }^{0} = 0,q = \kappa x, $$
(5)

where \( \kappa \) is the structure factor determined by the asymptotic characteristic of dislocation and \( b \) is the Burgers vector. The \( u^{c} \) in the dislocation core part is represented as follows:

$$ u{}_{\parallel }^{c} = \frac{bq}{\pi }\left[ {c_{1}^{{^{\parallel } }} W_{1} (Y) + c_{2}^{{^{\parallel } }} W_{2} (Y) + \cdots } \right], $$
(6)

where \( Y = {1 \mathord{\left/ {\vphantom {1 {(1 + q^{2} )}}} \right. \kern-0pt} {(1 + q^{2} )}},W_{n} ,n = 1,2 \ldots ,W \) is the orthogonal polynomials defined in the interval (0,1) (Wang 2003).

$$ W_{n} (Y) = \sum\limits_{l = 1}^{n} {b_{l}^{n} Y^{l} } , $$
(7)
$$ b_{l}^{n} = \frac{{( - 1)^{n + l} (n + l)!}}{(l + 1)!(l - 1)!(n - l)!}, $$
(8)

\( c_{n}^{{^{\parallel } }} ,c_{n}^{ \bot } ,n = 1,2, \ldots \) are the core parameters need to confirm. The calculation formula of restoring force is as follows:

$$ f_{\parallel } = - \frac{{d\gamma_{\parallel } }}{{du_{\parallel } }}\sigma = - \frac{{\mu_{\gamma } \sigma b}}{2\pi d}\sin \left( {\frac{{2\pi u_{\parallel } }}{b}} \right)\left( {1 + 2\Delta_{1} \sin^{2} \frac{{\pi u_{\parallel } }}{b}} \right) . $$
(9)

The trial solution can be written integrity as:

$$ u{}_{\parallel } = \frac{b}{\pi }\left[ {\arctan q + c_{1}^{{^{\parallel } }} qW_{1} (Y) + c_{2}^{{^{\parallel } }} qW_{2} (Y) + \cdots } \right] + \frac{b}{2} . $$
(10)

For different dislocation core structures, the dislocation solution can be truncated at the appropriate place; so it is called truncated dislocation solution. The core structural parameters cn in trial solution can be obtained by introducing the material-related parameters; the dislocation core structure can be acquired later.

The dislocation core structure of AlPr

Because of the aeolotropism properties of B2-AlPr, the aeolotropism should to be considered, and the shear modulus and poisson ratio can be obtained by Voigt (1966):

$$ \mu = c_{44} - \frac{1}{5}H,\quad \nu = \frac{\lambda }{{2(\bar{\mu } + \lambda )}}, $$
(11)

in which the Lame constant is expressed as:

$$ \lambda = c_{12} - \frac{1}{5}H, $$
(12)

where H is the anisotropic factor,

$$ H = 2c_{44} + c_{12} - c_{11} , $$
(13)

\( K_{e} \) and \( K_{\text{s}} \) are the Energy factors shown as,

$$ K_{e} = \frac{\mu }{1 - \nu }\text{,}\quad K_{s} = \mu . $$
(14)

The equations of the discrete lattice effect correction factor are as follows:

$$ \beta_{s} \sigma = \frac{3}{4}\varOmega \mu \left[ {1 - \tan^{2} \theta \sin^{2} \phi } \right], $$
(15)
$$ \beta_{e} \sigma = \text{ }\frac{3}{4}\varOmega \mu \left[ {\frac{2(1 - \nu )}{(1 - 2\nu )} - \tan^{2} \theta \cos^{2} \phi } \right], $$
(16)

where

$$ \beta_{\parallel } = \beta_{e} \sin^{2} \alpha + \beta_{s} \cos^{2} \alpha ,\quad K_{\parallel } = K_{e} \sin^{2} \alpha + K_{s} \cos^{2} \alpha . $$
(17)

The restoring force on the equation right side is calculated by the section on the expression of generalized-stacking-fault energy (GSFE) (Li et al. 2011):

$$ f_{\parallel } = - \frac{{d\gamma_{\parallel } }}{{du_{\parallel } }}\sigma = - \frac{{\mu_{\gamma } \sigma b}}{2\pi d}\sin \left( {\frac{{2\pi u_{\parallel } }}{b}} \right)\left( {1 + 2\Delta_{1} \sin^{2} \frac{{\pi u_{\parallel } }}{b} + 3\Delta_{2} \sin^{4} \frac{{\pi u_{\parallel } }}{b}} \right), $$
(18)

where \( \mu_{\gamma } \) is the equivalent shear modulus obtained by the γ-surface. \( \sigma \) is the original cell area, \( d \) is the interlamellar spacing of upper and lower layers of atoms, \( b \) is the Burgers vector, and Δ is the correction factor of sine force law. In the {110} misfit plane of B2-AlPr, \( \tan \theta = 1 \) , \( \sin \phi = {1 \mathord{\left/ {\vphantom {1 {\sqrt 3 }}} \right. \kern-0pt} {\sqrt 3 }} \). \( \alpha \) is the intersection angle (\( \alpha \)) of Burgers vector and dislocation line.

In Table 1, \( \mu \) is the average value of shear modulus, and in Table 2, is the \( {{\mu_{\gamma } b^{2} } \mathord{\left/ {\vphantom {{\mu_{\gamma } b^{2} } {(4\pi^{2} d)}}} \right. \kern-0pt} {(4\pi^{2} d)}} \) coefficient of generalized stacking fault energy curve. \( \Delta_{1} \) and \( \Delta_{2} \) are the correction factor of sine force law curve. The previous generalized dislocations section images can conclude that there is no reverse boundary energy in < 100 > {110} and < 110 > {110} direction curve; therefore, only a corrected parameter could fit out perfect. In addition, antiphase boundary (APB) energy was existed in < 111 > {110} direction curve; two corrected parameter were needed to fit it out.

Table 1 The relational parameters in AlPr
Full size table
Table 2 The fitting parameters of {110} plane’s generalized-stacking-fault energy in B2-AlPr
Full size table

After substituting trial solution, the restoring force and the corresponding material parameters into dislocation equation, the corresponding expressions can be represented by the orthogonal polynomial, after which the algebraic equation related to the core structural parameters \( c_{n} ,n = 1,2, \ldots \) is acquired by subtracting the right and left sides of the equation. Then, the corresponding dislocation solution and core structural parameters can be obtained by calculating the algebraic equation.

The high symmetry line and the close line are easy to slide, on the B2 structure rare earth intermetallic compound of {110} surface, when the Burgers vector b = <100 > , \( \alpha = 0^{ \circ } \), \( \alpha = 54.7^{ \circ } \) and \( \alpha = 90^{ \circ } \); when the Burgers vector b = <110 > , maybe \( \alpha \) = \( 0^{ \circ } \), \( \alpha = 35.3^{ \circ } \) and \( \alpha = 90^{ \circ } \); when the Burgers vector b = <111 > , maybe \( \alpha = 0^{ \circ } \), \( \alpha = 35.3^{ \circ } \), \( \alpha = 54.7^{ \circ } \) and \( \alpha = 90^{ \circ } \). α angle is the intersection angle of Burgers vector and dislocation line.

Tables 3 and 4 display the B2-AlPr, core structural parameters \( c_{n} ,n = 1,2, \ldots \) core width ξ, decomposition width \( d_{\text{eq}} \), which is the distance between the two peaks in the superdislocation along the Burgers vector of b = <111 > or the balance distance between two parts of dislocation and shape factor S. According to the observation of generalized-stacking-fault energy curve, the paper forecasts that the dislocation core structure is not very complicated; thus, only the first four items in the expression of displacement are kept.

Table 3 The core parameters cn, n = 1; 2; 3; 4 and core width \( \xi \), with the Burgers vector b = <100 > and < 110 > in {110} plane of AlPr
Full size table
Table 4 The core parameters cn, n = 1; 2; 3; 4 sharp-factor \( \left| S \right| \) and dissociated width \( d_{\text{eq}} \), with the Burgers vector b = <111 > in {110} plane of AlPr
Full size table

The related parameter settings are shown in Tables 1 and 2. The trial solution and dislocation restoring force are provided by the Eqs. (3), (9) and (10). Tables 3 and 4 list the first four items, and the core structure parameters calculated by the Burgers vector along the < 100 >,  < 110 >, < 111 > directions on B2-AlPr of {110} surface and calculated dislocation width, decomposition width and shape factor in describing the decomposition dislocation shape.

Because the coordinates selected in this paper are intrinsic coordinate frames based on the Burgers vector, the following calculations are based on the Burgers vector as the reference unit. It could be seen from Table 3 that on the {110} surface of AlPr, the Burgers vector is the dislocation of < 100 > and < 110 > , and the values of c1, c2, c3 and c4 of any possible dislocation line decrease in order, indicating that the higher the dislocation, core parameters have less influence on the dislocation properties. For different dislocation lines, c1 gradually increases and c2, c3 and c4 gradually decrease with the increase of dislocation angle. In the Burgers vector of < 100 > direction, the dislocation core width is within the range of 1.33b–1.69b. In the dislocation of < 110 > direction, the dislocation core width is within the range of 1.13b–1.575b. In general, the core width of edge dislocation is the largest, the mixed dislocation is in the middle, and the screw dislocation is the smallest, which conforms to the basic law of dislocation.

The generalized fault energy curve in the direction of < 111 > {110} of AlPr has antiphase boundary (APB) energy, and the dislocation is decomposed two superpartial dislocations: superdislocation. In B2 structure, < 111 > {110} superdislocation is decomposed as follows (Lazar and Podloucky 2007):

$$ b\left\langle {111} \right\rangle \to b/2\left\langle {111} \right\rangle + APB + b/2\left\langle {111} \right\rangle , $$

where APB is the antiphase boundary between the two super partial dislocation and represents the antiphase boundary between two superpartial dislocations. Table 4 shows the related properties of AlPr’s < 111 > {110} superdislocation calculated in this paper. S is the shape factor and \( d_{\text{eq}} \) is the decomposition width of the dislocation. S is defined as the second derivative of the dislocation density of the partial superdislocation peak point (Wang et al. 2011):

$$ S = a^{2} \left. {\frac{{d^{2} \rho }}{{dx^{2} }}} \right|_{\text{peak}} . $$
(19)

In which a is the lattice constant, and \( \rho = {{du} \mathord{\left/ {\vphantom {{du} {dx}}} \right. \kern-0pt} {dx}} \) is the dislocation density, Shape factor S is similar to the dislocation width, which describes the decomposition of the width of the dislocation of partial dislocation. If the value of S is larger, part of the dislocation density of the image peak will be sharp, dislocation is narrower, and it is difficult to move in the crystal. On the contrary, if the value of S is relatively large, the peak of partial dislocation density image is relatively smooth and the dislocation is relatively wide, which means that it is easier to move in solids.

It can be obtained from Table 4 that in {110} surface of AlPr, the values of c1, c2, c3 and c4 of any possible dislocation along the Burgers vector of < 111 > direction decrease successively, indicating that the higher the dislocation core parameters, the less influence on the dislocation properties. And the correctness of truncated dislocation solution is also verified. For different dislocation lines, with the increase of dislocation angle, c1 and c4 gradually increase, c3 gradually decreases, c2 does not change regularly, and < 100 > , < 110 > directions are different. The value of the shape factor S, which describes the image of dislocation density, decreases with the increase of dislocation angle. The results in the Fig. 4 show that the larger the value of S, the sharper the peak of dislocation density graph and the narrower the width of partial dislocation. The edge dislocation has the largest decomposition width, the mixed dislocation is in the middle, and the screw dislocation is the smallest. In other words, the edge superdislocation with the Burgers vector < 111 > is the easiest to decompose.

Figures 2, 3, and 4 show that in the direction of the same Burgers vector, the larger the dislocation angle is, the wider the dislocation core width or decomposition width will be. The figure of dislocation density of screw dislocations with the Burgers vector < 100 > and < 111 > is obviously sharper than that of other dislocations, which proves that the core width and decomposition width of screw dislocations are much narrower than those of other dislocations, which are consistent with the numerical results given in Tables 3 and 4. By comparing the core width of < 100 > and < 110 > direction, it is not difficult to find that the core width of screw dislocation and edge dislocation with the Burgers vector < 100 > is wider than that of < 110 >. At the same time, the unstable-stacking-fault energy also exists the relationship of \( \gamma_{\text{us}} \langle 110\rangle > \gamma_{\text{us}} \langle 001\rangle \). So, for B2-AlPr, the unstable-stacking-fault energy is an important factor affecting the dislocation core width.

Fig. 2
figure 2

The dislocation profile and density in AlPr along the < 100 > direction in {110} plane

Full size image
Fig. 3
figure 3

The dislocation profile and density in AlPr alone < 110 > direction in {110} plane

Full size image
Fig. 4
figure 4

The dislocation profile and density in AlPr along < 111 > direction in {110} plane

Full size image

Peierls barrier and Peierls stress

The calculation method of Peierls barrier and Peierls stress in B2 structure

Peierls energy and Peierls stress are two key quantities that characterize dislocation mobility. Dislocation mobility determines the mechanical properties of materials. The existence of dislocation makes the crystal energy increase; this part of energy is called dislocation energy. To study the mobility of dislocation, a lot of studies have been conducted on dislocation energy (Peierls 1940; Nabarro 1967; Foreman et al. 1951; Kroupa and Lejcek 1972; Ohsawa et al. 1994; Wang 1996; Joós and Duesbery 1997; Wu et al. 2008). Peierls energy of dislocation is composed of two parts, (1) elastic strain energy of upper and lower half of infinite elastomer, and (2) the interaction energy of atoms on the sliding surface and the lower two layers is often called misfit energy (Wu et al. 2008). Since Peierls and Nabarro first advanced Peierls energy and Peierls stress, they have made theoretical improvements in various aspects (Peierls 1940; Nabarro 1967). Foreman has calculated Peierls stress under improved sinusoidal force law (Foreman et al. 1951). But there are two obvious contradictions: one is Peierls stress cycle that is half of the Burgers vector rather than the Burgers vector; the other is Peierls stress that slip surface atoms on both sides are aligned in different ways. Joos and Duesbery research show that Peierls stress is different mainly because of the different law of restoring force treated in semi-infinite crystal (Joós and Duesbery 1997). Lu believes that the latter contradiction is caused by the different calculation methods used to calculate the misfit energy (Lu et al. 2000).

It is well known that Peierls energy and Peierls stress are related to the discrete lattice. The key to all these questions lies in the different ways to calculate the discrete displacement field when Peierls energy and Peierls stress employed. In addition, P–N model only considers discrete and independent of misfit energy, while ignoring the elastic strain energy. In lattice theory, when calculating Peierls energy and Peierls stress, then with the contribution of elastic strain energy, the above argument is automatically eliminated. The study shows that the contribution of elastic strain energy to Peierls barrier is greater than the misfit energy. Therefore, to make accurate results, elastic strain material cannot be ignored; Peierls barrier should be the total energy misfit energy and elastic strain energy sum.

In the P–N theory, the Hamiltonian can be written as the sum of the following three parts (Wang 2006):

$$ H = H_{a} + H_{b} + H_{ab} , $$
(20)

where \( H_{a} \)(\( H_{b} \)) is the Hamiltonian of the semi-crystalline body above (below) the cutting surface, \( H_{ab} \) is the Hamiltonian of the interaction between two semi-crystals separated by the cutting surface. Each crystal can be approximately half of its atoms is considered by harmonic force interaction linking. Since the potential energy of deformation of semicrystalline is generated called elastic strain energy, the energy generated by the interaction between the two is called “a” semi-crystalline misfit energy. It can be shown when subjected to force size, semi-crystalline potential harmonic equilibrium is:

$$ H_{a} = \frac{1}{2}\sum\limits_{n = - \infty } {f_{n} \cdot u_{n} .} $$
(21)

The interaction is:

$$ H_{ab} = \sum\limits_{n \to \infty } {\gamma_{n} } (u) . $$
(22)

Sum covering all atoms with discontinuous forces is not equal to zero. Thus, the length of the dislocation, dislocation lines per unit length of elastic strain energy and energy misfit are:

$$ \begin{aligned} E_{e} \left( {x_{0} } \right) & = \frac{1}{l}\left( {H_{a} + H_{b} } \right) = \frac{{2H_{a} }}{l} \hfill \\ E_{m} \left( {x_{0} } \right) & = \frac{{H_{ab} }}{l} \hfill \\ \end{aligned} . $$
(23)

Since the two upper and lower semi-crystalline are equivalent, so \( H_{a} = H_{b} \). The misfit energy is related with generalized stacking fault energy. The expressions of elastic strain energy and misfit energy are different for different dislocation lines and misfit surfaces.

Figure 5 shows the projection diagram of B2-AlRE atoms in {110} plane. The hollow point represents the lower layer of atoms, and the solid point represents the projection of the upper layer of atoms. Different sizes represent different species of atoms. Taking the intermetallic compound of B2 structure < 110 > {110} as an example, as shown in Fig. 5, if the dislocation line < 110 > is set as axis y and the direction perpendicular to the dislocation line is set as direction x, then the position of atoms in {110} plane is:

Fig. 5
figure 5

The B2-AlRE atoms projection in the {110} plane, hollow points stand for below layer atoms, solid points stand for above layer atoms projection, different size means different kinds of atoms

Full size image
$$ R_{mn} = (m + n)\frac{\sqrt 2 a}{2}e_{y} + (m - n)\frac{a}{2}e_{x} , $$
(24)

\( e_{y} \) and \( e_{x} \) is the unit vector of y and x, \( m \) and \( n \) is the unit vector。All dislocations total atomic energy of external force energy is not zero sum, it can be expressed as follows:

$$ E = \sum\limits_{m = - \infty }^{ + \infty } {\sum\limits_{n = - \infty }^{ + \infty } {E\left[ {u\left( {R_{mn} - x_{0} } \right)} \right]} } , $$
(25)

\( x_{0} \) is the dislocation centre, \( m + n = n',m - n = m' \). For the same parallel to the dislocation line displacement, sum can only x direction, the direction becomes an y integral multiple,

$$ E = N\sum\limits_{m' = - \infty }^{ + \infty } {E[u(R_{m'} - x_{0} )]} . $$
(26)

For the final result is needed a unit of energy dislocation dislocation line, then there is:

$$ E = \frac{1}{l}\sum\limits_{m' = - \infty }^{ + \infty } {E[u(R_{m'} - x_{0} )]} , $$
(27)

\( l \) is the dislocation line direction of the cycle. Since different coordinate neighborhood along the < 110 > direction of the two rows of atoms, based on the principle of symmetry, \( E_{e} \left( {x_{0} } \right) \) and \( E_{m} \left( {x_{0} } \right) \) were in the structure of the intermetallic compound B2 < 110 > {110} expression slip system have the following forms:

$$ E_{e} \left( {x_{0} } \right) = \frac{\sigma }{\sqrt 2 a}\sum\limits_{n = - \infty }^{\infty } {\left\{ \begin{aligned} f\left\{ {u\left[ {\left( {n + \frac{1}{2}} \right)a - x_{0} } \right]} \right\}u\left[ {\left( {n + \frac{1}{2}} \right)a - x_{0} } \right] \hfill \\ + f[u(na - x_{0} )]u(na - x_{0} ) \hfill \\ \end{aligned} \right\}} , $$
(28)
$$ E_{m} \left( {x_{0} } \right) = \frac{\sigma }{\sqrt 2 a}\sum\limits_{n = - \infty }^{\infty } {\left\{ {\gamma \left\{ {u\left[ {\left( {n + \frac{1}{2}} \right)a - x_{0} } \right]} \right\} + \gamma [u(na - x_{0} )]} \right\},} $$
(29)

u is the relative displacement of the center of the dislocation, the length of the original cell basis vectors, the sum of all the atomic level cover-band width of the misfit in the face. Per unit length of the dislocation energy:

$$ E_{t} \left( {x_{0} } \right) = E_{m} \left( {x_{0} } \right) + E_{e} \left( {x_{0} } \right) . $$
(30)

\( E_{t} \) is the total energy. The same method can be concluded that the structure of the intermetallic B2 < 100 > {110} expression slip system compound has the following form:

$$ \begin{aligned} E_{e} \left( {x_{0} } \right) = \frac{\sigma }{a}\sum\limits_{n = - \infty }^{\infty } {\left\{ \begin{aligned} &f\left\{ {u\left[ {\left( {n + \frac{1}{2}} \right)\sqrt 2 a - x_{0} } \right]} \right\}\\&\quad u\left[ {\left( {n + \frac{1}{2}} \right)\sqrt 2 a - x_{0} } \right] \hfill \\&\quad + f[u(\sqrt 2 na - x_{0} )]u(\sqrt 2 na - x_{0} ) \hfill \\ \end{aligned} \right\},} \end{aligned} $$
(31)
$$ E_{m} \left( {x_{0} } \right) = \frac{\sigma }{a}\sum\limits_{n = - \infty }^{\infty } {\left\{ {\gamma \left\{ {u\left( {n + \frac{1}{2}} \right)\sqrt 2 a - x_{0} } \right\} + \gamma [u(\sqrt 2 na - x_{0} )]} \right\}} , $$
(32)
$$ \begin{aligned} E_{t} \left( {x_{0} } \right) &= \frac{\sigma }{{\frac{\sqrt 3 }{2}a}}\sum\limits_{n = - \infty }^{\infty } {\left\{ {\gamma \left\{ {u\left[ {\left( {n + \frac{1}{3}} \right)\sqrt 6 a - x_{0} } \right]} \right\}}\right.}\\&\quad {\left.{+ \gamma \left\{ {u\left[ {\left( {n + \frac{2}{3}} \right)\sqrt 6 a - x_{0} } \right]} \right\} + \gamma \left[ {u\left( {\sqrt 6 na - x_{0} } \right)} \right]} \right\}} . \end{aligned}$$
(33)

For different slip systems and different displacement, the specific values are substituted into the expressions the corresponding Peierls barrier could be obtained. Since the lattice symmetry, when the dislocation slip dislocations in the crystal energy periodically change.

$$ E(x_{0} + b) = E(x_{0} ), $$
(34)

where the shaft \( x \) is parallel to the direction of slip, b along the direction of the cycle slip. As a periodic function, the dislocation energy expanded into Fourier series form. Typically, the series to retain the following form:

$$ E(x_{0} ) = E_{0} + \frac{1}{2}E_{P} \cos \frac{{2\pi x_{0} }}{b}, $$
(35)

where \( E_{0} \) is related to the crystal and infinite divergence constant, \( E_{P} \) is the Peierls barrier which needs to climb when moving dislocations. Elastic strain energy and the misfit energy can be expressed in the same way. Since the lattice is discreteness, only the applied force exceeds the Peierls stress dislocation movement will be. So Peierls stress is defined as maximum stress overcome Peierls barrier required, or moving dislocations require a minimum of applied stress:

$$ \sigma_{P} = \hbox{max} \left| {\frac{1}{b}\frac{{dE_{P} (x_{0} )}}{dx}} \right| . $$
(36)

Dislocation energy includes the energy and the misfit strain energy contribution. In addition, the specific structure of B2-AlPr between misfit energy, elastic strain energy and total energy was calculated, and the corresponding stresses were also calculated..

Peierls energy and Peierls stress of AlPr

B2-AlPr lattice constant a = 3.759 Å (Li et al. 2011), the average shear modulus \( \mathop \mu \limits^{ - } \) = 31.516 GPa, \( \nu \) = 0.26, {110} planes of different pitch surfaces \( d = {{\sqrt 2 a} \mathord{\left/ {\vphantom {{\sqrt 2 a} 2}} \right. \kern-0pt} 2} \), different Burgers vectors dislocation angle core structure parameters cn have been given in detail at the previous section. Correlation coefficients and parameters of generalized stacking fault energy surface are given in Tables 1 and 2. Substitute the specific parameters and expressions into the Eqs. (28)–(35) to obtain the misfit energy, elastic strain energy, total energy of different dislocation angles of the different Burgers vector and the corresponding stress determined by them. Specific results are given in Tables 5, 6 and 7.

Table 5 The Peierls barriers and Peierls stress for various dislocations of the < 100 > {110} direction in B2-structure AlPr
Full size table
Table 6 The Peierls barriers and Peierls stress for various dislocations of the < 110 > {110} direction in B2-structure AlPr
Full size table
Table 7 The Peierls barriers and Peierls stress for various dislocations of the < 111 > {110} direction in B2-structure AlPr
Full size table

As shown in Tables 5 and 6, the slip system of the intermetallic compound B2-AlPr is < 100 > {110} and < 110 > {110}. The misfit energy, elastic strain energy, total energy and the corresponding stress are determined by dislocation angles. The results show that the misfit energy is always smaller than the elastic strain energy, maybe one or two orders of magnitude (Lu et al. 2000), and their phases are always opposite. For the same slip system, the misfit energy, elastic strain energy, total energy and the corresponding stress determined by them all decrease with the increase of dislocation angle. For the same dislocation angle, the energy and stress of the slip system < 100 > {110} are greater than that of < 110 > {110} direction.

Table 7 shows the misfit energy, elastic strain energy, total energy and the corresponding stress determined by the different dislocations of B2-AlPr with the Burgers vector < 111 > {110}. The easiest slip system of B2-AlPr is < 111 > {110}. In addition to the dislocation angle is 54.7° dislocation, misfit energy is always smaller than the elastic strain energy, and their phase is always opposite. But for the dislocation angle of 54.7° dislocation, misfit energy is larger than the elastic strain energy, and they have the same phase. For all dislocations on the < 111 > {110} slip system, with the increase of dislocation angle, misfit energy, elastic strain energy, total energy and the corresponding stress determined by them decrease in turn.

Figure 6 shows the total energy (Peierls barrier) of B2-AlPr as a function of dislocation angle. The unit of x-axis is Å, and that of the y-axis is \( E_{m} (10^{ - 20}\;{\text{J}}/{\AA}) \). It is transparent that the different dislocation angles of the slip system < 100 > {110}, < 110 > {110} and < 111 > {110} have a common rule. Peierls barrier gradually decreases with the increasing of dislocation angle. The potential barrier of the screw dislocation is much higher than that of the other dislocations, indicating that the screw dislocation is difficult to move.

Fig. 6
figure 6

The total energy (Peierls barrier)is the function of dislocation position in B2-AlPr. The Burgers vector are < 100 > {110}, < 110 > {110} and < 111 > {110} direction, respectively

Full size image

Conclusions

In this paper, the dislocation properties of B2-AlPr are studied by truncation dislocation method. The results show that the core width of < 100 > screw and edge dislocation are wider than that of < 110 > . Meanwhile, the unstable-stacking-fault energy is also exists the relationship of \( \gamma_{\text{us}} \langle 110\rangle > \gamma_{\text{us}} \langle 001\rangle \), which showing that the unstable-stacking-fault-energy is an important factor in B2-AlPr affecting the dislocation core width. The easiest slip system of B2-AlPr is < 111 > {110}. In addition to the dislocation angle of 54.7° dislocation, the misfit energy is always smaller than the elastic strain energy, and they have always opposite phases. But for the dislocation angle of 54.7° dislocation, the misfit energy is larger than the elastic strain energy, and both of them have same phase. For all dislocations on the < 111 > {110} slip system, with the dislocation angle increasing, the misfit energy, elastic strain energy, total energy and the corresponding stresses decrease in turn. Slip systems < 100 > {110}, < 110 > {110} and < 111 > {110} dislocations of different angles have a common law, that is, with the increase of the dislocation angle, Peierls barrier decreases, screw dislocation barrier is much higher than other dislocations, indicating that the screw dislocation is difficult to move.