40 years of mineral elasticity: a critical review and a new parameterisation of equations of state for mantle olivines and diamond inclusions

Abstract

Elasticity is a key property of materials, not only for predicting volumes and densities of minerals at the pressures and temperatures in the interior of the Earth, but also because it is a major factor in the energetics of structural phase transitions, surface energies, and defects within minerals. Over the 40 years of publication of Physics and Chemistry of Minerals, great progress has been made in the accuracy and precision of the measurements of both volumes and elastic tensors of minerals and in the pressures and temperatures at which the measurements are made. As an illustration of the state of the art, all available single-crystal data that constrain the elastic properties and pressure–volume–temperature equation of state (EoS) of mantle-composition olivine are reviewed. Single-crystal elasticity measurements clearly distinguish the Reuss and Voigt bulk moduli of olivine at all conditions. The consistency of volume and bulk modulus data is tested by fitting them simultaneously. Data collected at ambient pressure and data collected at ambient temperature up to 15 GPa are consistent with a Mie–Grünesien–Debye thermal-pressure EoS in combination with a third-order Birch–Murnaghan (BM) compressional EoS, the parameter V ₀ = 43.89 cm³ mol⁻¹, isothermal Reuss bulk modulus $K_{\text{TR,0}} = 126.3(2){\text{ GPa}}$, $K^{\prime}_{\text{TR,0}} = 4.54(6)$, a Debye temperature $\theta_{\text{D}} = 644(9)\;{\text{K}}$, and a Grüneisen parameter γ ₀ = 1.044(4), whose volume dependence is described by q = 1.9(2). High-pressure softening of the bulk modulus at room temperature, relative to this EoS, can be fit with a fourth-order BM EoS. However, recent high-P, T Brillouin measurements are incompatible with these EoS and the intrinsic physics implied by it, especially that $\left( {\frac{{\partial K^{\prime}_{\text{TR}} }}{\partial T}} \right)_{P} > 0$. We introduce a new parameterisation for isothermal-type EoS that scales both the Reuss isothermal bulk modulus and its pressure derivative at temperature by the volume, $K_{\text{TR}} (T,P = 0) = K_{\text{TR,0}} \left[ {\frac{{V_{0} }}{V(T)}} \right]^{{\delta_{\text{T}} }}$ and $K^{\prime}_{\text{TR}} (T,P = 0) = K^{\prime}_{\text{TR,0}} \left[ {\frac{V(T)}{{V_{0} }}} \right]^{{\delta^{\prime}}}$, to ensure thermodynamic correctness at low temperatures. This allows the elastic softening implied by the high-P, T Brillouin data for mantle olivine to be fit simultaneously and consistently with the same bulk moduli and pressure derivatives (at room temperature) as the MGD EoS, and with the additional parameters of α _V0 = 2.666(9) × 10⁻⁵ K⁻¹, $\theta_{\text{E}} = 484(6)$, $\delta_{\text{T}}$ = 5.77(8), and $\delta^{\prime}$ = −3.5(1.1). The effects of the differences between the two EoS on the calculated density, volume, and elastic properties of olivine at mantle conditions and on the calculation of entrapment conditions of olivine inclusions in diamonds are discussed, and approaches to resolve the current uncertainties are proposed.

Introduction

Elasticity is critical not only for predicting volumes and densities of minerals at the pressures and temperatures in the interior of the Earth, but also because it is a major factor in the energetics of structural phase transitions, surfaces, and defects within minerals. Elasticity is, therefore, a key property for describing the physics and chemistry of minerals. Over the last 40 years this journal has, therefore, published papers on the determination of equations of state (EoS), elastic tensors, and their applications as diverse as the orientation of the lamellae in e-plagioclase (Fleet 1981) and domain walls in albite (Salje et al. 1985), the first complete analysis of the coupled phase transitions in albite (Salje 1985) and the influence of deviatoric and coherency stress on the thermodynamics of reactions (Geilikman 1980), the last being an issue of the current major dispute in metamorphic petrology (see Wheeler 2014 and the subsequent discussion papers). Publications on the actual determination of elastic tensors in PCM are relatively sparse compared to other subjects, reflecting the very challenging nature of the measurements. Nonetheless, the papers that have been published in PCM reflect the incredible development of techniques in terms of pushing forward the boundaries in P and T at which elastic and diffraction measurements can be made, and the precision and accuracy of the data. The first report of an elastic tensor in PCM was the measurement of cubic MgF₂ at ambient P and to 650 K by ultrasonic wave velocity measurements on cm-sized single crystals (Jones 1977). At that time, high-pressure elastic measurements were limited by sample sizes to gas-pressure apparatus capable of obtaining 1.2 GPa at ambient temperature (Özkan and Jamieson 1978), or to 0.6 GPa for polycrystalline hot-pressed samples immersed in a hydrostatic pressure medium (Jackson et al. 1978). The first decade of publication of PCM then witnessed significant progress with elastic tensors determined at temperatures up to 1300 K (Sumino et al. 1983; Suzuki et al. 1983) and to pressures of 3 GPa (Webb et al. 1984). As this review paper will show, the precision and accuracy of these early measurements remain competitive with modern measurements and their data provide a basis for evaluating single-crystal diffraction (e.g., Zhang et al. 2017) and elasticity measurements (e.g., Trots et al. 2013; Mao et al. 2015; Zhang and Bass 2016) at the much more extreme conditions now attainable with much smaller samples within diamond-anvil pressure cells.

Inclusions in diamonds are a natural analogue of a diamond-anvil pressure cell experiment. These inclusions in diamonds are direct samples of the Earth from depths greater than 100 km. However, they can only be interpreted if we know the depths (i.e., P and T) at which they were trapped by the growing diamond. Diamond is essentially pure carbon and, therefore, carries no intrinsic signal that can be used to infer its formation conditions. The depths of formation of diamond can only be determined by characterizing the mineral inclusions that are found trapped inside 0.6–4% of diamonds (Stachel and Harris 2008). When the diamond is examined at room conditions, the inclusions exhibit high pressures, of 0.1–4 GPa. These remnant pressures are developed because the inclusions and the host diamond have different thermal expansion and compressibilities, and the inclusions are constrained by the diamond host to occupy a smaller volume than a free crystal in the air. The measured residual pressures in the inclusion can be used to determine a line in P–T space which represents possible conditions of entrapment and hence diamond growth (e.g., Graham and Cybriwsky 1981).

To determine the conditions at which a mineral inclusion was trapped it is therefore necessary to have accurate and precise knowledge of the elastic behaviour and EoS for both the diamond and the inclusion mineral. When fluids are also present in the inclusion, as is found for silicate inclusions in gem-quality lithospheric diamonds (Nimis et al. 2016), the EoS of the fluid is also required. EoS of minerals are conventionally used to calculate their volumes, densities, and elasticity at pressures for calculating phase equilibria or seismic wave velocities. For these applications, the EoS parameters at room conditions only serve as a useful reference point simply because many measurements of EoS are based on room conditions and then extend to either high P (as in compression measurements) or high T (as in measurements of thermal expansion) or to simultaneous P and T. However, it is not necessary, for example, for the volume, density, or bulk modulus of a mineral to be correct at room conditions to correctly predict its volume in a reaction at high-P–T metamorphic conditions. However, to interpret the remnant pressures in inclusions at room temperature, it is necessary to have EoS that are not only accurate at the P and T conditions of entrapment, but across the whole of P–T space down to room conditions. The study of host-inclusion systems, therefore, places far more stringent demands on the accuracy and precision of EoS than most other applications.

There is an additional complication for minerals trapped as inclusions in diamonds that is not normally considered when discussing EoS for applications to seismology or phase equilibria. If the inclusion includes a small proportion of fluid, as reported for silicate inclusions in diamonds (Nimis et al. 2016; Smith et al. 2016), then the stresses in the inclusion will be hydrostatic, just as the stresses on a crystal in a diamond-anvil cell are hydrostatic while the pressure medium remains liquid. However, if the inclusion is a fluid-free single crystal, it will not be subject to hydrostatic pressure. Instead, its size and shape will be constrained by the host diamond, which is cubic. The inclusion will, therefore, be forced by the diamond to expand and contract isotropically in response to changes in P and T. If the inclusion is an anisotropic single crystal of olivine, then the imposed isotropic strain obviously implies that the olivine develops anisotropic stresses. The EoS to describe the volume variation of the inclusion for these two cases, fluid-present and fluid-free, are different and correspond to the Reuss and Voigt bounds, respectively, on the bulk modulus of the inclusion phase. Note that as the difference between the internal inclusion pressure and the external pressure applied to the host diamond becomes larger, there is an additional relaxation of the system which reduces the pressure gradient which was ignored by Graham and Cybriwsky (1981). This relaxation cannot be simply modelled by an EoS and requires more careful analysis involving the full elastic tensors of both the host and inclusion (e.g., Zhang 1998; Angel et al. 2014b, 2015b). Therefore, host-inclusion systems are a rare example of a system in which both the P–V–T EoS and the full elastic tensor of the minerals must be used to interpret the behaviour. Indeed, the full solution for anisotropic inclusions remains an unsolved challenge for mineral physics.

Olivines form around 20% of the inclusion minerals found in diamonds identified as coming from the lithosphere (Stachel and Harris 2008). In this paper, we examine the available data that can be used to constrain the P–V–T equation of state of mantle-composition olivine (with compositional range 90–92% forsterite component, Fo90–Fo92) and develop EoS that are suitable for determining the formation conditions of olivine inclusions in diamond from the inclusion pressure measured while the inclusion is still trapped in the diamond at room temperature. At the same time, the data on olivine also serve as an example of the precision and accuracy of the several experimental methods to determine both the volume EoS and the full elastic tensor of minerals and the level of consistency between them. Our analysis points to the significant experimental challenges that remain to determine the high-temperature high-pressure elastic properties of even the most common mantle minerals such as olivine, and suggests approaches by which more accurate EoS for them might be obtained.

General issues

Elasticity and bulk moduli

The general relationship between the stresses applied to a crystal σ _j and the resulting strains ε _j can be expressed in Voigt matrix notation as ε _j  = s _ij σ _j , where s _ij is the elastic compliance matrix of the crystal (Nye 1957). The indices i and j run from 1 to 6, and the Einstein summation convention is applied.

The Reuss and Voigt bulk moduli are often described as being bounds on the volume response of a polycrystalline aggregate to applied stress. However, they also represent the specific and exact response of a single crystal to two different sets of applied stresses. The Reuss bulk modulus is the bulk modulus obtained when the crystal is subject to hydrostatic stress, P, a state in which all of the normal stresses applied to the crystal are equal, and there are no shear stresses. If we consider a small increment in pressure $\partial P$, and using the common convention that a positive pressure corresponds to negative (compressional) normal stress, we can write the three normal strains as

$$\begin{aligned} \varepsilon_{1} = & - \partial P(s_{11} + s_{12} + s_{13} ) \\ \varepsilon_{2} = & \, - \partial P(s_{21} + s_{22} + s_{23} ) \\ \varepsilon_{3} = & - \partial P(s_{31} + s_{32} + s_{33} ). \\ \end{aligned}$$

(1)

The volume strain of the crystal is just the sum of the three normal strains, so that the Reuss bulk modulus is, therefore, given exactly by a sum over some of the elements of the elastic compliance matrix of the crystal:

$$K_{\text{R}} = - {{V\delta P} \mathord{\left/ {\vphantom {{V\delta P} {\delta V}}} \right. \kern-0pt} {\delta V}} = \left[ {s_{11} + s_{22} + s_{33} + 2(s_{12} + s_{13} + s_{23} )} \right]^{ - 1} .$$

(2)

This is the bulk modulus determined by measuring the volume of a single crystal as a function of pressure by diffraction in a diamond-anvil cell, provided that the pressure medium remains hydrostatic. It is also, therefore, the bulk modulus for a single-crystal inclusion surrounded by a fluid in a diamond. If the crystal is not cubic, the change in shape of the crystal under hydrostatic compression will be anisotropic; the strains induced by the pressure change (Eq. 1) will be different in different directions. The stiffness of any direction in the crystal under hydrostatic stress can be described by linear moduli $M_{\text{R}} = - l\delta P/\delta l$. The linear moduli of the principal directions in the crystal can be derived from Eq. 1 as

$$\begin{aligned} M_{1} =\; & - \frac{\partial P}{{\varepsilon_{1} }} = (s_{11} + s_{12} + s_{13} )^{ - 1} \\ M_{2} =\; & - \frac{\partial P}{{\varepsilon_{2} }} = (s_{21} + s_{22} + s_{23} )^{ - 1} \\ M_{3} = \; & - \frac{\partial P}{{\varepsilon_{3} }} = (s_{31} + s_{32} + s_{33} ).^{ - 1} \\ \end{aligned}$$

(3)

Conversely, if the crystal is forced to undergo isotropic strain, then ε ₁ = ε ₂ = ε ₃ = ε and the three normal stresses are given by

$$\begin{aligned} \sigma_{1} = & c_{11} \varepsilon + c_{12} \varepsilon + c_{13} \varepsilon = (c_{11} + c_{12} + c_{13} )\varepsilon \\ \sigma_{2} = & c_{21} \varepsilon + c_{22} \varepsilon + c_{23} \varepsilon = (c_{21} + c_{22} + c_{23} )\varepsilon \\ \sigma_{3} = & c_{31} \varepsilon + c_{32} \varepsilon + c_{33} \varepsilon = (c_{31} + c_{32} + c_{33} )\varepsilon . \\ \end{aligned}$$

(4)

c _ij is the elastic modulus matrix of the crystal, the inverse of the matrix s _ij (Nye 1957). For a non-cubic crystal, Eq. 4 shows that isotropic strain produces $\sigma_{1} \ne \sigma_{2} \ne \sigma_{3}$ which means anisotropic stress in the crystal. The Voigt bulk modulus relates the volume response $\delta V/V = 3\varepsilon$ of the crystal to the mean of the normal stresses:

$$\begin{aligned} K_{\text{V}} = & - V\frac{{{\text{d}}P}}{{{\text{d}}V}} = \frac{{{{(\sigma_{1} + \sigma_{2} + \sigma_{3} )} \mathord{\left/ {\vphantom {{(\sigma_{1} + \sigma_{2} + \sigma_{3} )} 3}} \right. \kern-0pt} 3}}}{3\varepsilon } \\ K_{\text{V}} = & \frac{{(c_{11} + c_{22} + c_{33} + 2(c_{12} + c_{13} + c_{23} ))}}{9}. \\ \end{aligned}$$

(5)

The Voigt and Reuss bulk moduli are only identical for cubic crystals and elastically isotropic materials, because for them, an isotropic applied stress (hydrostatic pressure) gives rise to isotropic strain and vice versa. For anisotropic materials, $K_{\text{V}} > K_{\text{R}}$. Because the volume measurements of crystals are made under hydrostatic conditions, we use the Reuss bulk modulus calculated from the elastic matrices in the combined fits of volume and elasticity data. One additional difficulty is that direct measurements of the elastic tensor are normally adiabatic measurements, whereas measurements of volumes are isothermal. Thus, there are four distinct bulk moduli that must be considered for any non-cubic mineral. The notation used to distinguish them in this paper is summarised in Table 1.

Table 1 Notation for bulk moduli

We perform the adiabatic to isothermal conversion by applying the relationship $K_{\text{SR}} = (1 + \alpha_{\text{V}} \gamma T)K_{\text{TR}}$, where the value of volume thermal expansion (α _V) is taken from the current EoS at the pressure and temperature of interest. The Grüneisen parameter γ can be expressed in terms of measurable quantities, for example, $\gamma = \frac{{\alpha_{\text{V}} K_{\text{SR}} }}{{C_{\text{p}} }} = \frac{{\alpha_{\text{V}} K_{\text{TR}} }}{{C_{\text{V}} }}$. However, since heat capacity data are not available at elevated pressures, we use the simple approximation (e.g., Anderson 1995) that

$$\gamma (P,T) = \gamma_{0} \left( {\frac{V(P,T)}{{V_{0} }}} \right)^{q} ,$$

(6)

where V ₀ is the volume at reference conditions, and the value of q is believed to be close to 1 for ‘normal’ solids under modest P–T conditions (Boehler and Ramakrishnan 1980; Boehler 1982). It is clear from heat capacity measurements that this is an over-simplification of the behaviour of the Grüneisen parameter of olivine, and indeed, it decreases with increasing temperature (e.g., Isaak 1992; Kroll et al. 2012) contrary to the form used in (5) if q > 0. More complex formulations make only a small difference to the value of $K_{\text{TR}}$ derived from measurements of $K_{\text{SR}}$, often within the experimental uncertainties of the value of $K_{\text{SR}}$, even at high temperatures. Kroll et al. (2012) calculated $\gamma_{0} = 1.25$ for Fo90–Fo92 and an average value of $\gamma = 1.15$ for the temperature range 300–1500 K.

Fitting EoS

For the compressional part of the EoS at room temperature, we only use the Birch–Murnaghan EoS in its third- and fourth-order forms (Birch 1947) which we denote by BM3 and BM4. Essentially identical sets of parameters are obtained using a Tait EoS (Huang and Chow 1974; Holland and Powell 2011). We have used the EosFit7c program (Angel et al. 2014a) for all of the fits of EoS discussed in this paper. In the EosFit7 program suite, the observed material parameter (either the volume or the bulk modulus) is fit to the pressure (Milani et al. 2017), using the effective variance method (Orear 1982) to convert the experimental uncertainties in V or K, and T, into effective uncertainties in pressure that are then combined with the uncertainty in pressure to provide a weight for each datum in the least-squares process. Single-crystal diffraction data typically have fractional uncertainties in volumes of 1 part in 10,000 or better which translate into effective uncertainties in pressures $\sigma^{\prime}_{\text{P}} \approx K_{\text{TR}} \frac{{\sigma_{\text{V}} }}{V}$ or ~0.012 GPa for olivine at modest pressures. By contrast, the typical uncertainty in bulk moduli from Brillouin data is of the order of 1 GPa at room temperature and high pressure, and can be as large as 3 GPa at simultaneous high pressures and temperatures (e.g., Mao et al. 2015). The corresponding effective uncertainty in pressures from elastic moduli data is, therefore, $\sigma^{\prime}_{\text{P}} \approx \frac{{\sigma_{\text{K}} }}{{K^{\prime}_{\text{TR}} }}$ or 0.2–0.6 GPa, an order of magnitude greater than diffraction data. Therefore, if the uncertainties in pressure and temperature of the diffraction and elastic measurements made at similar conditions are similar, then the diffraction data are weighted significantly more in the least-squares process and can be more influential in constraining the parameters in the equation of state when both types of data are fit together. The advantage of simultaneous fitting of elastic and volume data comes from the reduction in the strong correlation between the refined values of K _TR,0 and $K^{\prime}_{\text{TR,0}}$ when only volume data are used (e.g., Angel 2000).

Data for mantle olivine

The elastic response of a crystal to changes in pressure or temperature depends on the stress state applied to the crystal. In polycrystalline samples, even of a single phase, each grain is not subject to the externally applied stress, but each grain is under the stress applied to it by the adjacent grains. In these conditions it is impossible to precisely define the stress state of any one single grain; the response of the polycrystalline aggregate to stress is estimated through average moduli which certainly do not represent the response of any one single-crystal grain in the sample. Furthermore, the stress state in powders almost certainly changes with P and T, and at high applied stresses there will be plastic deformation which potentially changes the intrinsic elastic properties of the mineral. In addition, the stress state leads to considerable uncertainties in pressure determined by diffraction in solid mixed-phase samples (e.g., Will et al. 1980). Therefore, we only consider single-crystal data collected from Fo90 to Fo92 olivine under hydrostatic conditions in our analysis.

We use the single-crystal high-pressure diffraction data at room temperature from Nestola et al. (2011). Since that paper was published, the quartz EoS used to determine the pressure from measured unit-cell volumes of a quartz crystal included with the sample in the diamond-anvil cell has been revised (Scheidl et al. 2016), so we have revised the pressure values accordingly. Thermal expansion data for the forsterite–fayalite solid solution were reviewed in detail by Kroll et al. (2012) and we follow their recommendation to use only the dilatometry data of Suzuki (1975) for Fo92.3 from the literature. There is no single-crystal variable-T diffraction data for mantle-composition olivines. But for loosely packed powders there are no significant inter-grain stress. Therefore we also use recent high-T powder diffraction data for an Fo92 olivine (Helbert et al. 2013). These two data sets are in good agreement with one another, and also with new low-temperature data for the same sample obtained by powder diffraction (Nestola et al. 2017). Each individual data set of volumes was scaled to its’ own determination of volume at room conditions prior to fitting the data together. For fitting the Mie–Grüneisen–Debye EoS, a molar volume for Fo92 olivine of 43.89 cm³ mol⁻¹ at room conditions was calculated from the molar volume of Fo100 and the trend of V with composition of Schwab and Küstner (1977). We are not aware of any volume measurements made on mantle-composition olivine single crystals made at simultaneous high P and T, except for those in Mao et al. (2015).

The full elastic tensor of Fo90–Fo92 olivine has been determined by a variety of different methods over the past five decades. Room-pressure values of the adiabatic Voigt and Reuss bulk moduli from the various measurement techniques (Table 2) show, for most of the data, agreement that is significantly better than expected from the measurement uncertainties. The one significant outlier among data more recent than the work of Webb (1989) is the Fo92.1 sample of Isaak (1992) which is systematically stiffer than the Fo90 sample measured in the same study. This cannot be correct in terms of the known variation of bulk moduli with the Mg/Fe ratio in the forsterite–fayalite solid solution (Speziale et al. 2004; Jacobsen et al. 2008). Because the room-temperature Fo90 measurements of Isaak (1992) are in better agreement with other determinations (Table 2), we use the high-temperature data from this sample in preference to their Fo92 data. Table 2 shows that the Reuss and Voigt adiabatic bulk moduli determined from the full elastic tensor of Fo90–Fo92 olivine at room conditions differ by 4.1 GPa, on average, or about 3% in the values of the bulk moduli. It is clear from the agreement in values from the different experiments listed in Table 2 that single-crystal elasticity measurements clearly distinguish the Reuss and Voigt bulk moduli of olivine at room conditions.

Table 2 Fo90–Fo92 olivine adiabatic bulk moduli at room conditions from single-crystal measurements

In our analysis, we used adiabatic Reuss bulk moduli recalculated from the c _ij values reported at high P by Abramson et al. (1997) at the four pressures where the data are complete, and the data of Zha et al. (1998), Mao et al. (2015), and Zhang and Bass (2016) (Table 3). These four sets of moduli are in excellent agreement with one another (Fig. 1) up to ~15 GPa and with the room-pressure measurements (Table 2) and the volume compression data of Nestola et al. (2011). A fit of a BM3 EoS to all of this high-pressure, room-temperature data yields $K_{\text{TR,0}} = 126.7(2){\text{ GPa}}$ and $K^{\prime}_{\text{TR,0}} = 4.43(6)$, corresponding to an adiabatic value room-pressure bulk modulus of $K_{\text{SR,0}} = 127.9(2){\text{ GPa}}$. Above 15 GPa, the Brillouin data show significant softening (Fig. 1) relative to the extrapolation of the BM3 EoS from lower pressures, and cannot be fit with a BM3 EoS within the data uncertainties. A fit of all of the room-temperature diffraction and bulk modulus data listed in Table 1 with a BM4 EoS yield parameters $K_{\text{TR,0}} = 126.0(3){\text{ GPa}}$ and $K^{\prime}_{\text{TR,0}} = 4.9(1)$ and $K^{\prime\prime}_{0} = - 0.133(15){\text{ GPa}}^{ - 1}$. The softening has been attributed to elastic instabilities in the olivine structure that lead to amorphisation at higher pressures (Andrault et al. 1995).

Table 3 Data sources

Fig. 1

Variation of the adiabatic Reuss bulk modulus $K_{\text{SR}}$ of Fo90–Fo92 olivine calculated by Eq. (2) from experimental high-pressure measurements of the elastic moduli. The red solid line is a Birch–Murnaghan third-order EoS fit to this data up to 15 GPa and the compression data of Nestola et al. (2011). The blue dashed line is a BM4 EoS fit to all of the data. This same colour coding is used in subsequent figures

The only in situ single-crystal measurements of the high P–T elastic moduli of mantle-composition olivine are by Mao et al. (2015) and Zhang and Bass (2016). When they are compared with the data from Isaak (1992), the Mao et al. (2015) data imply that $\left( {\frac{{\partial K_{\text{TR}}^{'} }}{\partial T}} \right)_{P}$ is slightly negative at room pressure (see their Fig. 5 which shows the slopes of $K_{\text{S}}$ against T becoming shallower at higher T) which has been explained as a pre-transition phenomenon associated with the transformation of olivine to wadsleyite (Mao et al. 2015, and references therein), although it is clear from the data that these effects occur at pressures and temperatures well-away from the stability field of wadsleyite. However, the bulk moduli obtained from the results of Mao et al. (2015) are inconsistent with the in situ diffraction measurements of volume made at the same time and reported in the same paper. This indicates that the data may include some systematic error from either the experiment (e.g., in pressure scale or in V ₀ measurements) or the data reduction process. We, therefore, only use these data in some EoS fits, as discussed below. Zhang and Bass (2016) report the full elastic tensor of mantle olivine at a series of five pressures from ambient to 12.8 GPa at a single temperature of 1300 K, which enabled them to infer the densities directly, without measurement, in a self-consistent manner from the Brillouin data.

Equations of state

All EoS are built on assumptions, some obvious, and some subtle (for an introduction to these issues, see Anderson 1995; Angel 2000). These assumptions can bias either the parameter values at room conditions (which are especially important for host-inclusion calculations) derived from the experimental data or the predicted volume and bulk modulus at simultaneous high P and T, where experimental data can be sparse or of lower accuracy. The major challenge in EoS calculations is how to handle the cross derivatives of the elastic parameters with respect to P and T, for example, how the bulk modulus changes with temperature or how the thermal expansion coefficient changes with pressure. There are two possible approaches: one based on isothermal EoS at high temperature and the other based on the concept of thermal pressure. We discuss examples of each approach applied to olivine in the next sections.

Conventional isothermal EoS

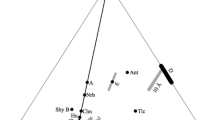
In this approach, the thermal expansion at room pressure is described, along with how the bulk modulus and its pressure derivatives change with temperature. Note that the model chosen for the specific variation of the bulk modulus with temperature also defines the change in thermal expansion coefficient with pressure, because $\left( {\frac{\partial \alpha }{\partial P}} \right)_{T} = \frac{1}{{K_{T}^{2} }}\left( {\frac{{\partial K_{T} }}{{{\text{d}}T}}} \right)_{P}$. The volume at high P and T is then calculated using V(P = 0, T), $K_{\text{TR}} (P = 0,T)$, and its pressure derivatives at high T and room P in an isothermal equation of state. The major advantages of this approach are that the variation of V and K can be determined directly from measurements at high temperatures and that the calculation follows a conceptually simple path in P–T space (Fig. 2). However, this conventional isothermal approach fails in two significant ways. First, although the experimental data for the bulk modulus of olivine above 300 K can be described with $(\partial K_{{{\text{TR}}}} /\partial T)_{P}$ constant, this is a non-physical approach, because there is a thermodynamic requirement that $(\partial K_{{{\text{TR}}}} /\partial T)_{P} = 0$ at T = 0. The failure to account for this with the linear model biases the room-T value of the bulk modulus $K_{\text{TR,0}}$. This is not obvious for olivine, but it is a serious problem for diamond, where $(\partial K_{{{\text{TR}}}} /\partial T)_{P}$ changes significantly below ~800 K (Fig. 3).

Fig. 2

P–T diagram showing the two different paths used in calculating the volume in a thermal-pressure EoS and an isothermal EoS. The isochor shown is calculated from the BM4–MGD EoS of Fo92 olivine

Fig. 3

Solid line is the variation of the isothermal bulk modulus of diamond as a function of temperature at room pressure, calculated from the EoS of Angel et al. (2015a). The dashed line is a linear extrapolation of the behaviour from high temperature and results in considerable error (arrow) in the value of the bulk modulus at room T

Second, it is also usually assumed that $K^{\prime}_{\text{TR}}$ does not change with increasing temperature, simply because there is little or no data to constrain this variation. However, it is clear that in the absence of phase transitions, $(\partial K^{\prime}_{\text{TR}} /\partial T)_{P}$ should be very slightly positive at high temperatures (e.g., Duffy and Anderson 1989; Anderson 1995). Hellfrich and Connolly (2009) showed that if $(\partial K^{\prime}_{\text{TR}} /\partial T)_{P}$ is assumed to be zero, and $K^{\prime}_{\text{TR}}$ is, therefore, invariant with temperature, then the volume thermal expansion coefficient always becomes zero and then negative at high P and T. The conventional isothermal EoS with $(\partial K_{\text{TR}} /\partial T)_{P}$ constant should, therefore, not be applied to calculate the elasticity of minerals to mantle P and T (Hellfrich and Connolly 2009).

Holland–Powell thermal-pressure EoS

The fundamental difference of thermal-pressure EoS models is that the volume is calculated over a different path in P–T space (Fig. 2) starting with an isothermal compression to the required volume at T ₀, followed by a path along an isochor to the final temperature. Then, the pressure at a given volume and temperature includes two parts:

$$P(V,T) = P(V,T_{0} ) + P_{\text{th}} (V,T).$$

(7)

The first term corresponds to the pressure calculated with the conventional EoS for compression at the reference temperature (usually room T), and the second term is the additional pressure generated by heating the material at constant volume, i.e. along an isochor. Because an isochor in P–T space has the slope $\left( {\frac{\partial P}{\partial T}} \right)_{V} = \alpha_{\text{V}} K_{\text{TR}}$, the thermal pressure induced by heating along the isochor is $P_{\text{th}} = \int_{T0}^{T} {\alpha_{\text{V}} K_{\text{TR}} \partial T}$. There is nothing theoretically superior about thermal-pressure EoS over the isothermal approach, because they also require assumptions to be made about the EoS parameters and behaviour: first along the isothermal compression path in exactly the same way as used in the isothermal approach and then also along the isochor. For example, one can assume that $\alpha_{\text{V}} K_{\text{TR}}$ is constant along the isochor, so that $P_{\text{th}} = \alpha_{\text{V}} K_{\text{TR}} (T - T_{0} )$, but this is clearly thermodynamically wrong, because it will still give $(\partial K_{\text{TR}} /\partial T)_{P}$ non-zero at low T.

The thermodynamic problems at low temperatures can be overcome using vibrational models for the thermal pressure, which then ensure that all of $\alpha_{\text{V}}$, $(\partial K_{\text{TR}} /\partial T)_{P}$ and $(\partial K^{\prime}_{\text{TR}} /\partial T)_{P}$ tend to zero as T approaches absolute zero. Holland and Powell (2011) introduced an empirical function to model thermal pressure with the motivation to provide realistic P–V–T EoS with the minimum number of additional parameters. The thermal-pressure part is (Holland and Powell 2011; Kroll et al. 2012)

$$\begin{aligned} P_{\text{th}} (V,T) = \;& \alpha_{\text{V,0}} K_{\text{TR,0}} \left( {\frac{{\theta_{\text{E}} }}{{\xi_{0} }}} \right)\left( {\frac{1}{{\exp (\theta_{\text{E}} /T) - 1}} - \frac{1}{{\exp (\theta_{\text{E}} /T_{0} ) - 1}}} \right), \\ \xi = & \frac{{(\theta_{\text{E}} /T)^{2} \exp ({{\theta_{\text{E}} } \mathord{\left/ {\vphantom {{\theta_{\text{E}} } T}} \right. \kern-0pt} T})}}{{\left( {\exp (\theta_{\text{E}} /T) - 1} \right)^{2} }}. \\ \end{aligned}$$

(8)

The parameter $\xi_{0}$ is the value of $\xi_{{}}$ at the reference temperature T ₀. The big advantage of this model is that the only additional parameter is a characteristic ‘Einstein’ temperature $\theta_{\text{E}}$ that can be estimated from entropy measurements (Holland and Powell 2011) or obtained by fitting V–T data. The remaining parameters $K_{\text{TR,0}}$ and $\alpha_{\text{V,0}}$ can be obtained from the conventional measurements of volume under compression and heating alone, so more difficult measurements at simultaneous P and T are not required. This model successfully fits the P–V–T data of diamond (Angel et al. 2015a), and both the P–V–T and bulk moduli data collected at both high P and at high T of grossular garnet (Milani et al. 2017).

However, it is not possible to simultaneously fit the P–V, T–V, and the T–K data for Fo92 (or Fo100) olivines with this model. The V–T data constrain $\alpha_{\text{V,0}} = 2.68(2) \, \times \, 10^{ - 5} \;{\text{K}}^{ - 1}$ and the Einstein temperature to be 497 ± 11 K (Fig. 4a), consistent with the estimate of 531 K for Fo100 from the measured entropy (Holland and Powell 2011) and the known decrease of characteristic temperatures with increasing iron content (Kroll et al. 2012). Figure 4b shows that with the values of $K_{\text{SR,0}} = 127.9(2){\text{ GPa}}$ and $K^{\prime}_{\text{TR,0}} = 4.43(6)$ determined from the fit of the high-pressure data at room temperature with a BM3 EoS, the adiabatic bulk modulus calculated from the EoS is significantly higher than the values measured by Isaak (1992) at high temperatures. The discrepancy is slightly reduced with the BM4 EoS which describes the high-P softening at room temperature, but a significantly higher value of $K^{\prime}_{\text{TR,0}} \sim 5.5 \;{\text{to}} \;5.7$ is required to obtain good agreement with the experimental data of Isaak (1992).

Fig. 4

a Volume data for Fo92 olivine (Table 3) at high temperature fit with a Holland–Powell thermal-pressure EoS (Eq. 8). The fits of the BM3 and BM4 EoS are indistinguishable. b Data points are the adiabatic Reuss bulk moduli, $K_{\text{SR}}$, calculated from the c _ij values of Isaak (1992). The lines are the prediction of Holland–Powell thermal-pressure EoS with the BM3, $K^{\prime}_{\text{TR}} = 4.4$, and the BM4 $K^{\prime}_{\text{TR}} = 4.9$. The black dashed line with the BM4 and $K^{\prime}_{\text{TR}} = 5.5$ agrees more closely with the data; a BM3 EoS requires $K^{\prime}_{\text{TR}} \sim 5.7$ to obtain the same values of $K_{\text{SR}}$. This illustrates the limitations of the Holland–Powell thermal-pressure model

The reason for this failure to fit the high-T bulk moduli data lies in a subtle intrinsic property of the Holland–Powell EoS, which can be understood as follows. The value of the Anderson–Grüneisen parameter, δ _T, determines the change in bulk modulus along an isochor (Anderson 1995):

$$(\partial K_{\text{TR}} /\partial T)_{\text{V}} = \alpha_{\text{V}} K_{\text{TR}} (\delta_{\text{T}} - K^{\prime}_{\text{TR}} ).$$

(9)

An intrinsic property of the Holland–Powell thermal-pressure EoS is that the isothermal bulk modulus is constant along an isochor, $(\partial K_{\text{TR}} /\partial T)_{\text{V}} = 0$ (Kroll et al. 2012). Equation (9) then implies that $\delta_{\text{T}} = K^{\prime}_{\text{TR}}$. However, Kroll et al. (2012) calculate that $(\partial K_{\text{TR}} /\partial T)_{\text{V}} \sim 0.004{\text{ GPa}}\;{\text{K}}^{ - 1}$ for olivines, so that $\delta_{\text{T}} \sim K^{\prime}_{\text{TR}} + 1$ ~5.5.

This explains why the high-T variation in bulk modulus can be only fit with the EoS by setting $\delta_{\text{T}} = K^{\prime}_{\text{TR}} \sim 5.5$ (Fig. 4b) in this EoS instead of ~4.5, although $K^{\prime}_{\text{TR}} \sim 5.5$ is completely inconsistent with the room-T elasticity data at high pressure (Fig. 1). Therefore, it is clear that the Holland–Powell thermal-pressure EoS involves insufficient independent parameters to accurately fit the available data for olivines and should only be used for materials such as diamond and garnet for which $K_{\text{TR}}$ appears to be constant along isochors, and thus, $\delta_{\text{T}} = K^{\prime}_{\text{TR}}$. For those materials, the Holland–Powell thermal-pressure EoS offers a robust, thermodynamically-valid EoS that can be used down to low temperatures, with a minimum number of parameters.

Mie–Grüneisen–Debye thermal-pressure EoS

This EoS is based on the idea that the spectrum of thermally-induced vibrations in the material can be described by the Debye model (Debye 1912), whose energy is represented by a characteristic temperature θ _D, the Debye temperature. The thermal energy then becomes

$$E_{\text{D}} = \frac{9nRT}{{(\theta_{\text{D}} /T)^{3} }}\int\limits_{0}^{{{{\theta_{D} } \mathord{\left/ {\vphantom {{\theta_{D} } T}} \right. \kern-0pt} T}}} {\frac{{x^{3} }}{{{\text{e}}^{x} - 1}}{\text{d}}x} ,$$

(10)

in which R is the gas constant, T is the absolute temperature, and n is the number of atoms per formula unit, 7 for olivine. The Debye temperature is explicitly assumed to be a function only of volume:

$$\theta_{\text{D}} (V) = \theta_{\text{D}} (V_{0} )\exp \left( {\frac{{\gamma_{0} - \gamma (V)}}{q}} \right),$$

(11)

where q is a constant, and γ is the same as the thermal Grüneisen parameter (e.g., Mulargi 1977; Anderson 1995; Jackson and Rigden 1996; Holzapfel 2001) defined in Eq. (6). This makes γ only a function of volume and not explicitly of T, so that γ is constant along an isochor.

The thermal pressure for the Mie–Grüneisen–Debye (MGD) EoS, relative to the isotherm at the reference temperature, is then given in terms of the thermal energies from the Debye model (Eq. 10) as

$$P_{\text{th}} (V,T) = \frac{\gamma (V)}{V}\left\{ {E_{\text{D}} (T,\theta_{\text{D}} (V)) - E_{\text{D}} (T_{0} ,\theta_{\text{D}} (V_{0} ))} \right\}.$$

(12)

The big advantage of the MGD EoS is that the parameters γ ₀ and q control the value of the Debye temperature θ _D through Eqs. (6) and (11), which means that V–T data provide constraints on the values of these parameters in addition to the constraints from the $K_{\text{SR}}$ data. In combination with the BM3 and BM4 EoS for room-temperature compression, the MGD EoS can fit all of the available data for mantle-composition olivine at high temperatures and ambient pressure (Fig. 5) with the parameters given in Table 4, which are quite similar to earlier fits of the MGD EoS (as summarised by Anderson 1995; Stixrude and Lithgow-Bertelloni 2005). The ambient temperature high-pressure data are also fit well, with the use of the high-temperature data changing the values of $K_{\text{TR,0}}$ and $K^{\prime}_{\text{TR,0}}$ by less than an esd from the fit to the high-pressure data alone. However, Fig. 6 shows that the $K_{\text{SR}}$ values determined from the high P–T data of Mao et al. (2015) and Zhang and Bass (2016) are systematically and significantly lower than the values calculated from both the BM3–MGD and the BM4–MGD EoS. For example, at 13.3 GPa and 900 K, both MGD EoS predict $K_{\text{SR}}$ = 174.6 GPa, whereas the measured value is 167(3) GPa. This misfit of the high P–T data is not reduced even if the data are included in the fits of the EoS parameters.

Fig. 5

a Thermal expansion and b bulk modulus $K_{\text{SR}}$ of Fo90–Fo92 olivine at room pressure predicted by the two BM–MGD EoS (Table 4). The two BM–isothermal EoS are identical to the corresponding order of BM–MGD EoS within uncertainties and, therefore, cannot be distinguished on this scale

Table 4 Best-fit Reuss EoS parameters for mantle-composition olivine

Fig. 6

Isothermal-pressure variation of the bulk modulus $K_{\text{SR}}$ at high temperatures. Data points from Mao et al. (2015) and Zhang and Bass (2016). The slopes of $K_{\text{SR}}$ with pressure predicted by the BM3–MGD and BM4–EoS slightly increase with increasing pressure, reflecting the intrinsic property of $\left( {\frac{{\partial K^{\prime}_{\text{R}} }}{\partial T}} \right)_{P} > 0$ of the MGD EoS, and cannot fit the data at higher temperatures at these pressures. In contrast, the isothermal EoS allows the softening in the high-temperature elastic moduli data to be represented; the slopes of $K_{\text{SR}}$ with pressure from the isothermal EoS decrease with increasing temperature. EoS parameters are given in Table 4. Room-temperature data and EoS are shown in Fig. 1

The big disadvantage of the MGD EoS is the need to use the molar volume V in Eq. (12) to convert the thermal energy into the thermal pressure (pressure having units of energy per unit volume). This makes the parameters of an MGD EoS specific to a single combination of specific volume and pressure scales, consistent with the units used for the bulk modulus. This limits the transferability and ease of use of the EoS and results in frequent calculation errors. This is not an intrinsic problem for all thermal-pressure EoS; for example, the Holland–Powell thermal-pressure EoS is scaled simply by the value of K _TR,0 (Eq. 8), so that the pressure scale of the thermal pressure is automatically the same as the pressure scale of the EoS at the reference temperature. The second disadvantage of the MGD EoS is that the parameters γ ₀, q, and θ _D are not directly measurable by experiment, in contrast to $\left( {\frac{{\partial K_{\text{T}} }}{\partial T}} \right)_{P}$ used in a conventional isothermal EoS. The third limitation of the MGD EoS is that it imposes the requirement that $\left( {\frac{{\partial K^{\prime}_{\text{TR}} }}{\partial T}} \right)_{P} > 0$, which is normal behaviour for materials, although this derivative is normally so small that it cannot normally be distinguished from being zero by experimental data. However, as noted by Zhang and Bass (2016), the elastic moduli reported at simultaneous high P and T by Mao et al. (2015) clearly imply that $\left( {\frac{{\partial K_{\text{TR}}^{'} }}{\partial T}} \right)_{P}$ is negative at room pressure (Fig. 6), and the MGD EoS cannot fit such variation, not even if a fourth-order Birch–Murnaghan EoS is used to fit the softening at high P and room T (Fig. 1).

New parameterisation of isothermal EoS

The preceding discussion of the thermal-pressure EoS shows that they do not provide sufficient flexibility to fit all of the available diffraction and elastic data for mantle-composition olivine and that the principle difficulty lies in fitting the data at simultaneous high P and T. We now present a new parameterisation of the isothermal approach that is thermodynamically correct, as are the thermal-pressure EoS, but provides the additional flexibility required to fit the high P–T elastic data for mantle-composition olivines.

In order for any ‘isothermal-type’ EoS to be thermodynamically correct, it must ensure that all of $\alpha_{\text{V}}$, $(\partial K_{\text{TR}} /\partial T)_{P}$, and $(\partial K^{\prime}_{\text{TR}} /\partial T)_{P}$ tend to zero as T approaches absolute zero. This precludes simple polynomial models for the volume as a function of T at room P, which have no such requirement. Kroll et al. (2012) reviewed a number of other models specifically in the context of olivine thermal expansion and found that the room-pressure thermal expansion equation implicit in the Holland–Powell thermal-pressure EoS fitted the experimental constraints as well as the best alternatives, whereas other models were deficient in one or more respects. We implement the Kroll et al. (2012) version of Holland–Powell thermal expansion, but we explicitly use the Anderson–Grüneisen (Anderson 1995) parameter $\delta_{\text{T}}$ in place of $(1 + K^{\prime}_{\text{TR}} )$. The expression for volume at temperature then becomes

$$\begin{aligned} V(T) = & \,V_{0} \left[ { - (\delta_{\text{T}} - 1) + \delta_{\text{T}} \left( {1 - \frac{{(\delta_{\text{T}}^{2} - 1)}}{{\delta_{\text{T}} }}A} \right)^{B} } \right], \\ A = \;& \alpha_{\text{V,0}} \left( {\frac{{\theta_{\text{E}} }}{{\xi_{0} }}} \right)\left( {\frac{1}{{\exp (\theta_{\text{E}} /T) - 1}} - \frac{1}{{\exp (\theta_{\text{E}} /T_{\text{ref}} ) - 1}}} \right), \\ B = \;& (\delta_{\text{T}}^{2} - 1)^{ - 1} . \\ \end{aligned}$$

(13)

The parameter $\xi_{0}$ was defined in Eq. (8). The use of $\delta_{\text{T}}$ and $K^{\prime}_{\text{TR}}$ as independent parameters allows data with any bulk modulus variation along an isochor (Eq. 9) to be fit. This approach also completely separates the thermal and baric parts of the EoS while maintaining a reasonable physical basis in the Einstein oscillator model; any description of the thermal expansion and temperature dependence of the bulk moduli $K$ is completely separated from the description of the isothermal compression. This also allows this thermal expansion equation to be combined with any isothermal equation of state for compression.

Hellfrich and Connolly (2009) used the definition of $\delta_{\text{T}}$ to propose an alternative description of the variation of bulk modulus with temperature:

$$K_{\text{TR}} (T,P = 0) = K_{\text{TR,0}} \exp \left[ { - \delta_{T} \int\limits_{{T_{0} }}^{T} {\alpha_{\text{V}} (T)} {\text{d}}T} \right],$$

(14)

which can be re-arranged as

$$K_{\text{TR}} (T,P = 0) = K_{\text{TR,0}} \left[ {\frac{{V_{0} }}{V(T)}} \right]^{{\delta_{\text{T}} }} .$$

(15)

This provides the correct behaviour of $K_{\text{TR}}$ at low temperatures, because $K_{\text{TR}}$ follows the volume variation and Eq. (13) ensures that $\alpha_{\text{V}}$ goes to zero as the temperature approaches absolute zero. There is no simple thermodynamic expression for the temperature variation of $K^{\prime}_{\text{TR}}$, because $\frac{{\partial^{2} K_{\text{TR}} }}{\partial P\partial T} = \left( {\frac{{\partial K^{\prime}_{\text{TR}} }}{\partial T}} \right)_{P} = \alpha \delta_{\text{T}} (\delta_{\text{T}} - K^{\prime}_{\text{TR}} + \kappa )$, where $\kappa = \frac{{\partial \ln \delta_{T} }}{{\partial (V/V_{0} )}}$ (Anderson 1995). Therefore, to avoid the thermal expansion becoming zero or negative at high pressures, which would be a consequence of $\left( {\frac{{\partial K^{\prime}_{\text{TR}} }}{\partial T}} \right)_{P} = 0$ (Hellfrich and Connolly 2009), we introduce a simple expression for the temperature variation of $K^{\prime}_{\text{TR}}$:

$$K^{\prime}_{\text{TR}} (T,P = 0) = K^{\prime}_{\text{TR,0}} \left[ {\frac{V(T)}{{V_{0} }}} \right]^{{\delta^{\prime}}} .$$

(16)

Equation (16) in combination with Eq. (13) ensures that $(\partial K^{\prime}_{\text{TR}} /\partial T)_{P}$ becomes zero at low temperatures in the same way as in the MGD and Holland–Powell thermal-pressure EoS.

Recommended Reuss EoS parameters for mantle olivine

The parameters for ‘best fits’ of EoS to the available single-crystal data of mantle-composition olivine are listed in Table 4, and are provided in the supplementary materials as ‘.eos’ files for use in the EosFit7 family of programs (Angel et al. 2014a; Gonzalez-Platas et al. 2016) to perform calculations of all EoS parameters at P and T.

The BM3–MGD EoS provides an accurate representation of all of the available single-crystal data for mantle-composition olivine, except for the room-pressure data above 15 GPa, and the simultaneous high P and T elasticity data of Mao et al. (2015) and the highest two pressure points at 1300 K from Zhang and Bass (2016), see Figs. 1 and 6. The BM4–MGD EoS also fits the softening relative to the BM3 EoS reported at pressures in excess of 15 GPa at room T (Zha et al. 1998). At high temperatures, for example at 1300 K, the BM3–MGD and BM4–MGD predict indistinguishable properties for olivine up to at least 19 GPa (Fig. 7). This is because the MGD EoS is a quasi-harmonic EoS and the change in bulk moduli along any isochor is small (Eq. 9), less than 1.3 GPa for olivine from 300 to 1300 K. Up to pressures of ~15 GPa at room T, the BM3 and BM4 EoS predict indistinguishable K _RS (Fig. 1). Since the BM4–MGD isochor through 15 GPa and 298 K reaches 18.9 GPa at 1300 K (Fig. 2), it is only above 19 GPa that the room-temperature softening (Fig. 1) contributes softening at 1300 K (Fig. 7). Isothermal-type EoS with $\delta^{\prime} = 1.0$ combined with BM3 and BM4 EoS for compression have EoS parameters and predict volumes, densities, and bulk moduli at P and T that cannot be distinguished within the uncertainties from those of the corresponding MGD EoS.

Fig. 7

Variation with pressure of the adiabatic bulk modulus $K_{\text{SR}}$ at 1300 K. Data points from Zhang and Bass (2016). The BM3–MGD and BM4–MGD EoS only diverge significantly above ~19 GPa, where the thermal pressure is ~4 GPa and the corresponding pressure on the isochor at 298 K is, therefore, 15 GPa, which is the pressure of divergence of the two EoS at 298 K (Fig. 1)

The high-temperature data of Mao et al. (2015) and Zhang and Bass (2016) represent elastic softening relative to the predicted moduli from both the BM–MGD EoS (Fig. 6), at pressures significantly below the pressures, where the room-T softening contributes to the value of K _RS (Fig. 7). Therefore, this softening cannot be fit with an MGD EoS. The softening can be fit simultaneously with the room-pressure data on bulk moduli and thermal expansion with the isothermal-type EoS by allowing the value of $\delta^{\prime}$ to become negative. While this does not violate thermodynamics at modest pressures, this implies that $\left( {\frac{{\partial K^{\prime}_{\text{TR}} }}{\partial T}} \right)_{P} < 0$ at finite temperatures, and will eventually lead to a prediction of negative thermal expansion at high pressures. Values of $\delta^{\prime}$ between −3 and −4 are obtained by least-squares fit to all of the data (Table 4) which fit all of the high-P, T elastic data within the uncertainties. As for the MGD EoS, the BM3–isothermal EoS does not fit the room-temperature softening, but this modelled by the BM4–isothermal EoS (Table 4).

The corresponding orders of BM–MGD and BM–isothermal EoS provide identical fits to the data at room T and high P and to the high-T data at room pressure (Fig. 5) and predict indistinguishable properties under these conditions. They also both show excellent agreement with the determinations of bulk moduli by elasticity measurements at room conditions (Table 2). The isothermal and MGD EoS of the same order (BM3 or BM4) are, therefore, only distinguished by the volumes, density, and elasticity (Figs. 6, 7) that they predict at simultaneous high P and T. The general trend is that the MGD EoS predict larger volumes, bulk moduli and thermal expansion coefficients, and lower densities, at all P and T. For example, at 900 K and 13.3 GPa, the most extreme point of Mao et al.’s (2015) data, the MGD EoS yields a density 0.2% lower than the isothermal EoS, bulk moduli about 6.5 GPa higher (Fig. 6) and $\alpha_{\text{V}}$ about 25% higher. The differences at P and T corresponding to depths of 410–420 km, at the stability limit of olivine, are ~1% in volume and density, ~10% in bulk modulus, and ~40% in thermal expansion coefficient. As far as we are aware, there are no diffraction data from mantle-composition olivines of sufficient precision to distinguish these two EoS. For example, at 8.2 and 1073 K, the powder diffraction data of Liu and Li (2006) yield V/V ₀ = 0.964(8). Both the MGD and the isothermal EoS predict compression ratios within the quoted uncertainty of this value.

Olivine inclusions in diamond

An olivine trapped inside a diamond at mantle temperatures and pressures is not free to expand and contract in response to changes in P and T as free olivine crystal would. Instead, it is constrained to expand and contract by the same amount as the host diamond. As a consequence, olivine inclusions in diamond exhibit positive pressures when measured in situ inside diamonds at room conditions (Izraeli et al. 1999; Nestola et al. 2011; Howell et al. 2012). If no other processes such as plastic flow or cracking of the diamond have occurred to modify the remnant pressure in the inclusion, its remnant pressure, P _inc, is comprised of two contributions. The constraint of the inclusion to the volume change of the host is termed the ‘thermodynamic’ pressure which can be calculated from the EoS of the host and the inclusion (e.g., Rosenfeld and Chase 1961; Graham and Cybriwsky 1981; Guiraud and Powell 2006; Angel et al. 2014b, 2015b). In addition to this P _thermo, the pressure difference between the internal pressure in the inclusion and the external pressure applied to the diamond is reduced by mutual elastic relaxation arising from the pressure difference. The relaxation can only be calculated exactly when the inclusion is perfectly spherical and when both the host and inclusion phases are elastically isotropic. Given that no single crystal can be elastically isotropic over any range of P and T, and olivine inclusions in diamond are not spherical but faceted, the calculation of this elastic relaxation becomes an approximation (Angel et al. 2014b, 2015b). The effects of non-spherical inclusion shape have been calculated by finite-element modelling to be small (Mazzucchelli et al. 2016) and of the order of the other uncertainties introduced into the calculation by the esd’s in EoS parameters. In this discussion, we use the isotropic spherical relaxation approximation to allow us to illustrate the consequences for the interpretation of residual inclusion pressures of using the different EoS of olivine (Table 4). The P–V–T EoS of diamond is well constrained and contributes relative little uncertainty to these calculations (Angel et al. 2015a).

Inclusions with fluids: the Reuss case

Olivine inclusions in diamonds are normally surrounded by a thin film of aqueous fluid (Nimis et al. 2016). The fluid film occupies only a few % of the total volume of the inclusion and its volume expansion will be similar to that of olivine from typical entrapment conditions to ambient conditions if it is dominated by water (Zhang and Duan 2005). The effect of the fluid film on the final inclusion pressures will, therefore, be small. For this discussion, we will ignore the effects of the hydrous fluid films except for the important point that if they completely surround the olivines, the films ensure hydrostatic conditions for the olivine, much like the pressure fluid in a diamond-anvil cell. Therefore, the Reuss EoS describes the P–V–T behaviour of the olivine component of the inclusions. Table 5 compares the expected P _thermo and the final inclusion pressures P _inc calculated for the limits of lithospheric entrapment conditions (between depths of 120 and 240 km) for a hot and cold craton geotherm (Pollack and Chapman 1977). Given that lithospheric pressures are significantly less than 19 GPa, there is no significant effect of the high-P and low-T elastic softening on calculated inclusion pressures; for example, the BM3–MGD and BM4–MGD EoS yield inclusion pressures that differ by less than 0.1 GPa, so we only compare the MGD and isothermal EoS in detail here.

Table 5 Diamond-olivine host-inclusion calculations

The BM3–MGD EoS consistently yields lower predicted P _thermo and P _inc for all entrapment conditions than the BM3–isothermal EoS that includes the elastic softening implied by the high P–T Brillouin data (Mao et al. 2015; Zhang and Bass 2016). For entrapment at shallow depths and, therefore, low pressures, the difference is less than 0.1 GPa, but this increases significantly to 0.4 GPa as the pressure of entrapment increases (Table 5). The consequences for the calculation of entrapment conditions from the measured P _inc can be visualised by performing the reverse calculation. An inclusion exhibiting P _inc of 0.241 GPa, for example, will be predicted to have P _trap of 4.134 GPa at 1060 °C (1330 K) by the BM3–MGD EoS, a difference of less than 0.2 GPa or 6 km in depth from the prediction of the BM3–isothermal EoS including the high-T elastic softening. The discrepancies are much more severe when P _inc is higher, corresponding to deeper entrapment. For the worst case example in Table 5, a residual P _inc = 2.234 GPa will lead with the MGD EoS to the calculation of an entrapment pressure 0.7 GPa higher than that predicted by the BM3–isothermal EoS, a difference in entrapment depth of the order of 20 km.

Solid inclusions: the Voigt case

If the inclusion is a single crystal without fluid, it will not be subject to hydrostatic pressure. Instead its size and shape will be directly constrained by the host diamond, which is cubic. Therefore, the olivine inclusion will be forced to expand and contract isotropically in response to changes in P and T. This imposed isotropic strain means that the stress state in the olivine inclusion becomes anisotropic (Eq. 4). In other words, the normal stresses in the inclusion will be different in different directions, and the term ‘pressure’ is used to mean the average of the normal stresses. The Voigt bulk modulus (Eq. 5), therefore, describes the volume variation of a 100% solid olivine inclusion in diamond, and a ‘Voigt EoS’ is needed to determine the average stress, or ‘pressure’, in the inclusion. Inclusions in cubic host minerals are, therefore, one of the very few cases that a Voigt EoS is applicable to non-cubic single crystals.

The Voigt EoS of olivine, which describes the volume response of the material under isotropic strain, is only constrained by direct measurements of the elastic tensor, and not by volume measurements under hydrostatic stress. Therefore, there are far fewer experimental data to constrain a Voigt EoS than a Reuss EoS. However, the available elastic tensor data at both room conditions (Table 1) and at non-ambient conditions (Table 3) yield an almost constant ratio of $K_{\text{SV}} /K_{\text{SR}} = 1.032(3)$. If we assume that this ratio is constant (it appears to increase to 1.036 at the highest temperatures, Isaak 1992), and also assume that the same ratio applies to the isothermal moduli, we can estimate an EoS for Voigt case of isothermal stress from the Reuss EoS by simply setting $K_{\text{TV,0}} = 1.032K_{\text{TR,0}}$ and $K^{\prime}_{\text{TV,0}} = 1.032K^{\prime}_{\text{TR,0}}$. For the well-defined case of compression at room temperature, the Voigt EoS provides bulk moduli that are higher than the corresponding Reuss EoS by about 3% over the pressure range 0–20 GPa, and consequently volumes that are up to 0.3% larger at 20 GPa. Extension of such an EoS from P–V behaviour to P–V–T is, however, dependent upon the assumption that the anisotropy of thermal expansion does not contribute to a change in the average stress, under the constraint of isotropic strain. For olivine, this is reasonable, because the available thermal expansion and elasticity data (Table 2) show that a change in temperature of 1000 K will contribute a shift in average normal stress or ‘pressure’ of less than 0.1 GPa from that calculated assuming that the thermal expansion is isotropic. Both these factors are small, and therefore, the remnant pressures calculated for olivine inclusions in diamond are very similar for the Reuss and Voigt EoS with the biggest differences in P _inc being of the order of 0.04 GPa (Table 5). When back-calculating entrapment conditions, the MGD Reuss and Voigt EoS yield maximum differences in entrapment pressures of ~0.06 GPa, which correspond to an uncertainty in depth from the calculation of about 2 km.

Discussion

EoS and elasticity of olivine: status quo

The steady improvement in precision of the determination of the full elastic tensors of olivine at room conditions and at high pressures clearly defines the difference between the Reuss and Voigt bulk moduli (Table 1). Similarly, at ambient pressure, the conversion between adiabatic and isothermal bulk moduli has also been well established for at least two decades (e.g., Isaak et al. 1989; Isaak 1992). Therefore, there is no reason to compare bulk moduli determined by diffraction and by Brillouin spectroscopy without making the appropriate well-defined conversions between the different types of moduli. We should note that the Voigt–Reuss–Hill bulk moduli, being an average of the Reuss and Voigt moduli, have no significance whatsoever in the context of the EoS of single crystals.

While the values of both the Reuss and the Voigt bulk moduli, and the difference between them, are well constrained by the Brillouin data, it is clear from Fig. 8 that the values of axial moduli (the inverse of the axial compressibilities, as defined in Eq. 3) determined in these measurements are often scattered by much more than the uncertainties estimated from the measurements. For a given data set at one pressure, there is a tendency for individual moduli to be shifted in opposite directions from the trend lines. This scatter in moduli is significantly greater when the velocity data have been collected on only one oriented single crystal (circles in Fig. 8) than when two or more different orientations have been used (square symbols in Fig. 8) indicating that it arises from covariance of the values of individual c _ij values because of inadequacy of coverage of different phonon propagation directions (e.g., Abramson et al. 1997; Kurnosov et al. 2017). As a consequence, even when the bulk moduli are well-constrained by the measured velocity data, the variation of the unit-cell parameters with P and T can be less well-constrained than the EoS of the material, and indicates that further experimental effort is needed to determine precisely the elastic anisotropy of mantle minerals.

Fig. 8

Adiabatic axial moduli from Brillouin experiments at room temperature show much greater scatter than the bulk moduli determined from the same data. The opposite shifts of individual moduli from the trend lines at a given pressure (e.g., arrowed) indicate that the scatter arises from covariance between individual c _ij values. The scatter is less when the wave velocity data are collected from multiple crystal orientations (square symbols). Further data up to 32 GPa (Zha et al. 1998) not shown for clarity, but exhibit greater scatter

The fact that the room-temperature bulk moduli and compressional data for mantle olivine are consistent with one another (Fig. 1) and that these are also consistent within the theory of the MGD EoS with the high-T data on thermal expansion and bulk modulus was established some years ago and is further confirmed by the addition of the new low-T data for olivine thermal expansion (Fig. 5). However, the MGD EoS has the disadvantage of portability issues in that it requires the volume to be molar because of the indirect relationship between parameter values and measured data. It also has the restriction that $\left( {\frac{{\partial K^{\prime}_{\text{TR}} }}{\partial T}} \right)_{P} > 0$, which means that it cannot be used to describe the elastic softening at high P and T implied by the data of Mao et al. (2015) and Zhang and Bass (2016), which require $\left( {\frac{{\partial K^{\prime}_{\text{TR}} }}{\partial T}} \right)_{P} < 0$. This requires that $\delta^{\prime} < 0$ which is possible in the new isothermal EoS that we have introduced, and a value of $\delta^{\prime}\sim - 3.5$ almost fits all of the available data within the experimental uncertainties. Both the MGD and the isothermal EoS give identical properties at room pressure and varying temperature (Fig. 5) and at high pressures at ambient temperatures, reflecting the consistency of all of the experimental data at these conditions. The difference between the two EoS is only at simultaneous high P and T, where they predict significantly different properties. Therefore, one accurate and precise measurement of V and K at P and T of the order of 15 GPa and 1300 K in a hydrostatic pressure medium would suffice to distinguish between the predictions of the MGD and isothermal EoS and the fundamentally different physics they imply for the behaviour of olivine. At these conditions, the predicted volumes from the two EoS differ by 0.5% and the bulk moduli by 16 GPa (Fig. 7). Such a measurement must necessarily be with a single crystal to avoid the stress uncertainties introduced by grain–grain contacts in a powder. To be useful, a measurement with a precision of about 1 part in 10,000 in volume and about 2 GPa in bulk modulus would be necessary, to allow for the additional uncertainties in the comparison that arise from the experimental uncertainties in P and T. Without such a measurement, it is still not possible to predict the volume, and hence the density, of mantle olivines to better than ~1% in volume and density, ~10% in bulk modulus, and ~20% in thermal expansion coefficient at P and T corresponding to the transformation of olivine to wadsleyite. Further experimental data are, therefore, essential to be able to draw robust conclusions about the structure and composition of the mantle from seismic data.

Olivine inclusions in diamond

Careful consideration of the stress state of the inclusion is important for back-calculating entrapment conditions from measured remnant inclusion pressures. If the inclusion contains fluid, then the stress state is hydrostatic, and the conventional EoS using the Reuss isothermal bulk modulus and its pressure derivatives is appropriate for the inclusion. However, the pressure of the inclusion even in the absence of cracks or defects will be modified by the presence of the fluid, and the effects depend on the contrast between fluid EoS and the solid component of the inclusion, and their volume proportions within the inclusions. On the other hand, a 100% solid inclusion in diamond is subject to uniform strain by the cubic diamond host, and is, therefore, under anisotropic stress. The variation of the inclusion pressure with changes in solely the external pressure is, therefore, determined not by the Reuss bulk modulus of the inclusion but by its isothermal Voigt bulk modulus and EoS. Only for cubic minerals are these two EoS identical. For olivine, although the difference between the Reuss and Voigt bulk modulus is 3% (Table 1), the difference in remnant pressures for lithospheric olivine inclusions is less than 0.1 GPa, leading to differences in inferred entrapment pressures of less than 0.1 GPa. For other, more elastically anisotropic minerals such as coesite (Weidner and Carleton 1977), the differences will be larger. Of more importance for olivine inclusions is the uncertainty about the high-P, T EoS, represented by the MGD EoS that describe it as a ‘normal solid’ and the isothermal EoS that describes elastic softening at high P and T. This uncertainty translates into uncertainties in entrapment depths of at least 20 km. This means that while olivines originating from shallow depths in cratons can clearly be distinguished from those trapped in diamonds grown at the base of the lithosphere, we cannot determine the absolute depths of entrapment to better than 20–30 km, equivalent to a pressure uncertainty of ~1 GPa.

EoS and elasticity: the future

Despite the impressive improvement over the last four decades, both in accuracy and precision, and in P and T that can be obtained in a controlled manner, in situ simultaneous P–T elasticity and volume measurements remain severely challenging. However, they are essential if one is to draw conclusions about the fundamental physics of the behaviour of minerals and similar materials and if one is to be able to draw robust conclusions about the structure, composition, and dynamics of the Earth from geophysical observations such as seismic wave velocities. While individual experiments and data sets can be internally consistent and, therefore, precise, their accuracy depends on questions of pressure and temperature determination, and especially the accuracy of high P–T pressure scales. The consequence is that the two sets of high P–T determinations of the elasticity of single-crystal mantle olivines (Mao et al. 2015; Zhang and Bass 2016) are on the margins of being mutually inconsistent (Fig. 6), and the elastic anisotropy of olivine at high pressures is poorly constrained (Fig. 8). Some of the discrepancies between data sets probably lie in the different complex assumptions built into the data reduction of elasticity data because of the need to determine densities to convert measured velocities into elastic moduli and in the handling of the adiabatic to isothermal corrections at high P and T. As a consequence, the EoS parameters obtained from a single, or a few, experiments often differ considerably. Furthermore, when EoS parameters obtained from fits to different data sets are compared, the origin of the discrepancies is not obvious, especially because they can be further obscured by the covariance of EoS parameters. Nor is it clear how one should combine the results of different fits of different EoS to different data sets into better constraints on the EoS parameters such as $K_{\text{TR,0}}$.

An alternative approach to data analysis has been presented in this paper, the simultaneous fitting of both volume and moduli data to a single EoS as previously advocated by, for example, Stixrude and Lithgow-Bertelloni (2005) and Kennett and Jackson (2009). This allows the mutual compatibility of very different data sets to be examined directly, by testing whether a single EoS and set of parameters can fit all of the data within their experimental uncertainties. As we have also demonstrated, this approach also allows the physical assumptions behind different EoS to be explored and the differences in the fundamental physical behaviour of the mineral implied by the use of the MGD and isothermal EoS (with $\delta^{\prime} < 0$) to be identified. This in turn has indicated the precision and accuracy that would be required in new experiments to distinguish the true behaviour of mantle olivines at mantle conditions.

In its current form, the approach of simultaneous fitting relies on the bulk modulus having been obtained from the measured wave velocities with the correct density and with the correct adiabatic to isothermal conversion. A further valuable development would be to use the primary data of the adiabatic wave velocities instead of the derived values of bulk moduli in the fit of the EoS parameters, as has been done for individual series of Brillouin measurements at high pressures (e.g., Kurnosov et al. 2017). This would have several benefits. First, it would use the raw unbiased data to constrain the bulk modulus in the same way that the volume data obtained by diffraction are raw and not biased by assumptions in data reduction. Then, the uncertainties in the refined EoS parameters would correctly reflect the true uncertainties in the underlying raw data, and not include the influence of choices made in data reduction. Second, this approach would also increase the value of the much more difficult P–T measurements of wave velocities by allowing them to be reduced to bulk moduli using densities in part constrained by the more precise measurements at ambient P and at ambient T. In addition, it would allow fundamental thermodynamic issues such as the variation of the Grüneisen parameter and q with temperature, pressure, and volume to be addressed and tested directly.