Non-Markovian Mean-Variance Portfolio Selection Problems via Closed-Loop Equilibrium Strategies

Abstract

In this article, a class of mean-variance portfolio selection problems with constant risk aversion is investigated by means of closed-loop equilibrium strategies. Thanks to the non-Markovian setting, two delicate kinds of equilibrium strategies are introduced and both of them obviously reduce to the existing counterpart in the Markovian case. To explicitly represent the equilibrium strategy, a class of backward stochastic Riccati system is introduced, and its solvability is carefully discussed for the first time in the literature. Different from the current literature, the spectacular role of random interest rates in the model is firstly indicated by several interesting phenomena, and the new deeper relations between closed-loop, open-loop equilibrium strategies are shown as well. Finally, numerical analysis via deep learning method is shown to illustrate the novel theoretical findings.

1 Introduction

The well-known Markowitz mean-variance portfolio selection problem established the foundation of modern investment portfolio theory. If one considers this financial problem in a multiperiod setting, the so-called time inconsistency issue is encountered. In other words, the strategy at one moment may not be optimal at the next moment, which implies that the strategy must be continuously updated to maintain optimality. Here it is worth mentioning that the pre-committed optimal solution is studied in, e.g., [1, 2]. However, it is optimal only when viewed at the initial time, and the restriction for the remaining time horizon is not optimal. Although such a static solution is of practical and theoretical importance, it actually does not fit well with the dynamic nature of the mean-variance portfolio selection problem, and may neglect the time-inconsistency character.

In addition to optimality, the time consistency of policies is also a basic requirement for rational decision-making in many situations. As far as we know, the time-consistent strategy was first introduced by Strotz in [3], where a class of consumption problems with non-exponential discount factors was carried out. Later, Strotz’s idea was interpreted in [4] in terms of game theory, and consistent planning was referred to as the game-theoretic approach. Thus, for the dynamic mean-variance portfolio selection problem, we adopt the notion of time-consistent equilibrium investment strategies, where the term equilibrium is borrowed from game theory. Recently, such strategies have attracted much attention. Basically, there are two types of equilibrium strategies along this line: open-loop equilibrium investment strategies (OLEISs), which admit certain linear closed-loop (or feedback) representations under proper conditions; and closed-loop equilibrium investment strategies (CLEISs). We first look at the former notion. For mean-variance problems with deterministic interest rate, OLEISs as well as their closed-loop representations were introduced and investigated carefully in [5, 6]. Later, [7] extended it into the general asset-liability management problem with full random coefficients. Other related topics can be found in [8,9,10,11], and the references therein. As to CLEISs, they were first investigated for dynamic mean-variance problem with deterministic coefficients in [12]. To improve the wealth-independent equilibrium strategies in [12], a class of state-dependent risk aversion strategies was introduced in [13], and the equilibrium strategies were derived via the extended Hamilton–Jacobi–Bellman (HJB) equations developed in [14]. We refer to [15,16,17,18,19,20], and [21] for other related topics.

In this paper we discuss the dynamic mean-variance problem by means of CLEISs when all the coefficients are random. Let us first explain the reasons of choosing CLEISs. In the first place, it is in general a different notion from the OLEIS, even under the Markovian framework, see e.g., [5, Section 5.4] or [19]. In the second place, we find that CLEISs share an advantage of optimality in time-inconsistent problems while OLEISs can not. For example, in the classical stochastic linear quadratic framework that is inherently related to the mean-variance problems, [17] showed that the open-loop equilibrium controls are fully characterized by first-order and second-order necessary optimality conditions, and are clearly not optimal in general, while the closed-loop equilibrium controls naturally reduce to closed-loop optimal controls. Now we show the motivations of working in the random coefficients setting. First, as far as we know, there is no study that treats the corresponding CLEISs in the same non-Markovian framework. Second, compared with the case of deterministic coefficients, this general scenario allows us to capture more features of risky asset prices, describe more accurate market models, and obtain improved investment strategies.

In comparison with the existing literature, we will encounter several new features and difficulties. First of all, to explicitly show the pre-committed optimal solution, one can introduce two backward stochastic differential equations (BSDEs) that are independent of each other (see [1]). However, here we need to solve two fully coupled backward stochastic Riccati systems that are correlated. These systems are highly nonlinear and very little is known about their direct solvability. Fortunately, stochastic Riccati systems have a certain ad hoc structure among different equations. We shall prove the existence of adapted solutions by some delicate analysis. The second difficulty comes from the essential gap between certain strong requirements in the definitions of CLEISs and the weak regularities of the second component of solutions to a stochastic Riccati system. Because of the requirement of random coefficients for interest rates, the martingale component of a BSDE, which does not appear in [5] or [6], is introduced here. To fulfill the definition of CLEISs, one must ensure such a martingale component to be well-defined for any $t\in [0,T)$, which is in general impossible. Notice that this situation is naturally avoided in the deterministic coefficient case. To solve this problem, we provide two approaches. On the one hand, by introducing proper Malliavin assumptions, we improve the property of the solutions to the stochastic Riccati system. On the other hand, we keep the low regularity of the martingale component. As a tradeoff, we introduce a slightly weaker notion that is proved to be equivalent to the original CLEISs in a Markovian setting.

From our study, we observe that the randomness of the coefficients yields several interesting phenomena. First, it is known that closed-loop equilibrium strategies in the Markovian setting does not depend on initial wealth ([13]). However, in our non-Markovian scenario, they are feedback forms of the equilibrium wealth process, and naturally rely on initial wealth, which makes our conclusion clearly meaningful. Second, for the mean-variance problems with constant risk aversion, we find that the obtained closed-loop equilibrium strategy and the existing closed-loop representation of an open-loop equilibrium strategy have the same feedback manner on the equilibrium wealth process, even when all the coefficients are random. If interest rates are deterministic, these two equilibrium strategies happen to equal if they exist.¹ Third, in [13] the state-dependent risk aversion was introduced to make the obtained equilibrium strategy rely on the initial state. In our opinion, if so, the original mean-variance problem essentially changed, and the new strategy surely can not recover the old one. However, from our study, owing to the randomness of interest rates, the equilibrium strategies are allowed to vary in terms of wealth level, and the previous mentioned issues obviously disappear. Fourth, in the existing paper it is taken for granted that the randomness of interest rates may not bring essential changes to the study. Therefore, it is usually supposed to be deterministic while the expected return and the volatility are allowed to be random. However, from our study we find that the random interest rates can also bring us interesting conclusions. These four facts do not appear in the deterministic coefficients (or Markovian) setting. More importantly, we further explain them by numerical study via deep learning method. To the best of our knowledge, the current paper is the first work to combine the deep learning approach with the closed-loop equilibrium strategy of dynamic mean-variance problem.

At this moment, we summarize the main contributions of the current article from three different viewpoints. Speaking of notions, the non-Markovian setting prompts us to introduce two delicate kinds of closed-loop equilibrium strategy, both of which naturally reduce to the Markovian case. Speaking of methodology, we explicitly solve the encountered backward stochastic Riccati system, and demonstrate the theoretical conclusions by numerical study via deep learning method. Both procedures appear for the first time in the literature. Speaking of conclusions, we find the spectacular role of random coefficients (especially the interest rates) and the deeper and clearer connections between closed-loop equilibrium strategies and open-loop equilibrium strategies.

The rest of this paper is organized as follows. In Sect. 2, some notations and spaces are introduced, and the mean-variance problem is formulated in detail. Section 3 includes five parts. In the first part, we provide sufficient conditions for the closed-loop equilibrium operators defined in Sect. 2. In the second part, we discuss the solvability of the introduced Riccati systems, and present the explicit form of the closed-loop equilibrium strategy. In the third part, we compare our results with the analogous study in the Markovian setting and reveal several new phenomena that arise. In the fourth part, we make detailed comparisons with the existing work of open-loop equilibrium strategies and list a few interesting conclusions. In the fifth part, we discuss the mean-variance problem with Vasiček’s stochastic interest rate. In Sect. 4, we demonstrate some numerical studies via deep learning method. Section 5 concludes the study.

2 Preliminary Notation and Model Formulation

Throughout this paper, let $(\Omega , {{{\mathcal {F}}}}, P, \mathbb {F})$ be the filtered probability space such that ${{{\mathcal {F}}}}_0$ contains all $\mathbb {P}$-null sets, and filtration $\mathbb {F}\buildrel \triangle \over =({{{\mathcal {F}}}}_t)_{t\in [0,T]}$, generated by a one-dimensional standard Brownian motion, satisfies the usual conditions. For $n, p\in \mathbb {N}, 0\le s<t\le T, L^2_{{{{\mathcal {F}}}}_t}(\Omega ;\mathbb {R}^n)$ is the set of ${{{\mathcal {F}}}}_t$-measurable mapping $X:\Omega \rightarrow \mathbb {R}^n$ such that $\mathbb {E}|X|^2<\infty , L^2_{\mathbb {F}}\big (\Omega ;C([s,t];\mathbb {R}^n)\big )$ is the set of measurable, $\mathbb {F}$-adapted continuous process $X:[s,t]\times \Omega \rightarrow \mathbb {R}^n$ such that $\mathbb {E}\sup \limits _{r\in [s,t]}|X(r)|^2<\infty , L^\infty _{\mathbb {F}}(\Omega ;C([s,t];\mathbb {R}^n))$ is the set of process $X\in L^2_{\mathbb {F}}\big (\Omega ;C([s,t];\mathbb {R}^n)\big )$ such that $~\mathop {\textrm{esssup}}\limits _{\omega \in \Omega }\sup \limits _{r\in [s,t]}|X(r)| <\infty , L^p_{\mathbb {F}}(\Omega ;L^1(s,t;\mathbb {R}^n))$ is the set of measurable, $\mathbb {F}$-adapted process $X:[s,t]\times \Omega$ such that $\mathbb {E}\left( \int _{s}^t|X(r)|dr\right) ^{ p }<\infty , L^p_{\mathbb {F}}(\Omega ;L^2(s,t;\mathbb {R}^n))$ is the set of process $X\in L^p_{\mathbb {F}}(\Omega ;L^1(s,t;\mathbb {R}^n))$ such that $\mathbb {E}\left( \int _{s}^t|X(r)|^2dr\right) ^{\frac{p}{2}}<\infty$. In particular, $L^2_{\mathbb {F}}(s,t;\mathbb {R}^n)=L^2_{\mathbb {F}}(\Omega ;L^2(s,t;\mathbb {R}^n))$.

We consider a financial market where the bond and the stock are traded continuously on [0, T]. In the following, r is the risk-free return (or interest rate); b is the expected return of the risky asset; and $\sigma$ is the corresponding volatility. The randomness of these coefficients comes from Brownian motion $W(\cdot )$ as above. Given initial capital $x>0$, risk premium $\beta :=b-r$, market price of risk $\theta =\frac{\beta }{\sigma }$, and the capital invested in the risky asset u, for $s\in [0,T]$, the investor’s wealth X(s) satisfies

$$\begin{aligned} \begin{array}{ll} \displaystyle X(s)=x+\int _0^s \left[ r(\tau ) X(\tau )+\beta (\tau ) u(\tau ) \right] d\tau +\int _0^s u(\tau )\sigma (\tau ) dW(\tau ). \end{array} \end{aligned}$$

(2.1)

(H0) Suppose $r, b, \sigma$ are one-dimensional $\mathbb {F}$-adapted bounded processes, and $|\sigma |^2 \ge \delta$ for constant $\delta >0$.

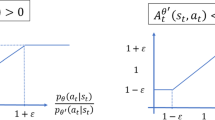
At time t, the objective of the mean-variance portfolio selection is to choose an investment strategy that minimizes $J(u(\cdot );t,X(t))=\text{ Var}_{t}\left[ X(T)\right] -\gamma \mathbb {E}_{t}\left[ X(T)\right] ,$ where $\mathbb {E}_{t}[\cdot ]:=\mathbb {E}[\cdot |{\mathcal {F}}_t],$ $\gamma$ is constant risk aversion, X(t) is the wealth at time t. Given $t\in [0,T], \varepsilon >0$, a pair of $(\Theta ^*,\varphi ^*)$ and bounded $v\in L^2_{{{{\mathcal {F}}}}_t}(\Omega ;\mathbb {R})$, let

$$\begin{aligned} \displaystyle u^{v,\varepsilon }:=\Theta ^* X^{v,\varepsilon }+\varphi ^*+ vI_{[t,t+\varepsilon ]}, \quad u^{*}:=\Theta ^* X^{*}+\varphi ^*, \end{aligned}$$

(2.2)

where $X^{v,\varepsilon }(\cdot )$ and $X^*(\cdot )$ satisfy (2.1) associated with $u^{v,\varepsilon }(\cdot )$ and $u^*(\cdot )$, respectively. For simplicity, here and next we omit the dependence of $u^{v,\varepsilon }, X^{v,\varepsilon }$ on time t. We point out that the affine feedback representation in (2.2) is inspired by the existing literature (e.g., [5,6,7, 13, 14, 16, 17]).

Definition 2.1

A pair of $(\Theta ^*(\cdot ),\varphi ^*(\cdot ))\in L^p_{\mathbb {F}}(\Omega ;L^2(0,T;\mathbb {R}))\times L^2_{\mathbb {F}}(0,T;\mathbb {R})$ is called a closed-loop equilibrium operator if for any positive sequence $\varepsilon _n\rightarrow 0, x\in \mathbb {R}$, and $v\in L^2_{{{{\mathcal {F}}}}_t}(\Omega ;\mathbb {R})$, one has $u^*, u^{v,\varepsilon _n}\in L^2_{\mathbb {F}}(0,T;\mathbb {R})$, and

$$\begin{aligned} \lim _{\overline{\varepsilon _n\rightarrow 0}} {J(u^{v,\varepsilon _n}(\cdot );t,X^*(t))-J\big (u^*(\cdot );t,X^*(t)\big ) \over \varepsilon _n}\ge 0,\quad \forall t\in [0,T), \ \ a.s.\nonumber \\ \end{aligned}$$

(2.3)

where $u^*$ and $X^*$ are the (linear) closed-loop equilibrium investment strategy, and the closed-loop equilibrium wealth process, respectively.

Remark 2.1

We explain the meaning of “closed-loop,” “equilibrium,” and “operators” one by one. First, the term “closed-loop” comes from the feedback relation between $u^{v,\varepsilon }$ and $X^{v,\varepsilon }$, and $u^*$ and $X^*$ in (2.2). It is different from that that of open-loop equilibrium strategy (Remark 3.5). Second, as is stated in the Introduction, the term “equilibrium” comes from game theory. The word “operator” is borrowed from [22], where the characterization of closed-loop optimal operators for stochastic linear quadratic problems with random coefficients is obtained. This operator indicates the linear feedback relationship between the equilibrium strategy and equilibrium wealth.

Remark 2.2

For time-inconsistent optimal control problem with either nonlinear state or nonlinear cost functional, a generalization of (2.2) is $u^{v,\varepsilon }(\cdot ):=F(\cdot , X^{v,\varepsilon }(\cdot ))+ vI_{[t,t+\varepsilon ]}(\cdot ),$ $u^{*}(\cdot ):=F(\cdot ,X^{*}(\cdot )),$ for some function F (e.g., [14, 23]). Here we restrict ourselves to (2.2) due to the linear-quadratic structure of our problem, as well as the ansatz technique to seek the Riccati system.

Remark 2.3

Due to the randomness of coefficients, the limit in (2.3) is taken with any sequence $\{\varepsilon _n\}$ tending to 0, not $\varepsilon \in \mathbb {R}$ tending to 0, see e.g. [23]. In fact, in the non-Markovian framework, the difference quotient in (2.3) with $\varepsilon _n$ replaced by $\varepsilon$ is well-defined in a full measure with respect to $\omega$. Due to the uncountable property of $\varepsilon >0$, the limit in (2.3) may not be well-defined and this is the reason of using $\{\varepsilon _n\}$ instead. However, in the Markovian setting (e.g. [12, 13, 16]) one can avoid this issue and replace $\{\varepsilon _n\}$ by arbitrarily small $\varepsilon >0$. In this case, our definition is in the essentially similar spirit as theirs.

In the sequel, K is a generic constant that varies in different contexts.

3 Equilibrium Strategies in Mean-Variance Problems

3.1 Sufficient Condition for the Closed-Loop Equilibrium Operator

To show the sufficient conditions for the existence of closed-loop equilibrium operator, we state the following hypothesis which will be verified in the next subsection.

(H1) Suppose there exists $(\Theta ^*,\varphi ^*)\in L^p_{\mathbb {F}}(\Omega ;L^2(0,T;\mathbb {R}))\times L^2_{\mathbb {F}}(0,T;\mathbb {R})$ such that for any $x\in \mathbb {R}, u^*, u^{v,\varepsilon }\in L^2_{\mathbb {F}} (0,T;\mathbb {R})$, where $u^*$ and $u^{v,\varepsilon }$ are defined in (2.2).

Under (H1), we have $X^*, X^{v,\varepsilon }\in L^2_{\mathbb {F}}(\Omega ;C([0,T];\mathbb {R})), J(u^*;t,X^*(t)),$ $J(u^{v,\varepsilon } ;t,X^*(t)), t\in [0,T)$ are well defined. We define $X_1^{v,\varepsilon }(\cdot ):=X^{v,\varepsilon } (\cdot )-X^*(\cdot )$ which satisfies

$$\begin{aligned} \left\{ \begin{aligned} \displaystyle dX_1^{v,\varepsilon }(s)&=\big \{ [r (s)+\beta (s)\Theta ^*(s)] X_1^{v,\varepsilon }(s) +\beta (s) vI_{[t,t+\varepsilon ]}(s) \big \}ds\\&\quad + \sigma (s)\left[ \Theta ^*(s) X_1^{v,\varepsilon }(s)+ vI_{[t,t+\varepsilon ]} (s) \right] dW(s),\ \ s\in [0,T], \\ X^{v,\varepsilon }_1(0)&=0. \end{aligned}\right. \end{aligned}$$

(3.1)

From the definition of $u^{v,\varepsilon }$ in (2.2), a direct calculation implies that

$$\begin{aligned} \begin{aligned}&\displaystyle J(u^{v,\varepsilon }(\cdot );t,X^*(t))-J(u^*(\cdot );t,X^*(t)) \\&\quad \displaystyle \ge \mathbb {E}_t\left\{ \left[ 2X^*(T)- 2\mathbb {E}_t\left[ X^*(T)\right] - \gamma \right] X_1^{v,\varepsilon }(T)\right\} . \end{aligned} \end{aligned}$$

(3.2)

To deal with the right-hand term, for $t\in [0,T]$, we introduce (e.g., [16, 17])

$$\begin{aligned} \left\{ \begin{aligned} \displaystyle dY^*(s,t)&= -\big \{[r(s)+\beta (s)\Theta ^*(s)]Y ^*(s,t)+\Theta ^*(s) \sigma (s) Z^*(s,t)\big \}ds\\&\quad \displaystyle +Z^*(s,t)dW(s),\ \ s\in [t,T],\\ \displaystyle Y^*(T,t)&=2X^*(T)- 2\mathbb {E}_t\left[ X^*(T)\right] -\gamma . \end{aligned}\right. \end{aligned}$$

(3.3)

Suppose that (3.3) is solvable. Then by applying Itô’s formula to $Y^*(\cdot ,t)X_1^{v,\varepsilon }(\cdot )$,

$$\begin{aligned} \begin{aligned}&\displaystyle \mathbb {E}_t\left\{ \left[ 2X^*(T)- 2\mathbb {E}_t\left[ X^*(T)\right] -\gamma \right] X_1^{v,\varepsilon }(T)\right\} \\&\quad \displaystyle =v \mathbb {E}_t \int _t^{t+\varepsilon }[\beta (s)Y^*(s,t)+\sigma (s)Z^*(s,t)]ds. \end{aligned} \end{aligned}$$

(3.4)

Therefore, from the above (3.2),

$$\begin{aligned} \begin{aligned} \displaystyle \frac{J(u^{v,\varepsilon }(\cdot );t,X^*(t))-J(u^*(\cdot );t,X^*(t))}{\varepsilon } \ge \frac{v}{\varepsilon }\mathbb {E}_t \int _t^{t+\varepsilon }[\beta (s)Y^*(s,t)+\sigma (s)Z^*(s,t)]ds. \end{aligned} \end{aligned}$$

If there exists proper $(\Theta ^*,\varphi ^*)$ such that for any positive $\varepsilon _n\rightarrow 0$,

$$\begin{aligned} \begin{aligned} \displaystyle \lim _{\varepsilon _n\rightarrow 0} \frac{1}{\varepsilon _n}\mathbb {E}_t \int _t^{t+\varepsilon _n}[\beta (s)Y^*(s,t)+\sigma (s)Z^*(s,t)]ds=0, \end{aligned} \end{aligned}$$

(3.5)

then according to Definition 2.1, $(\Theta ^*,\varphi ^*)$ will be the desired closed-loop equilibrium operator. This motivates us to explore the appropriate property of $(Y^*,Z^*)$. Therefore, we return to the solvability of (3.3). If $\Theta ^*$ in (H1) is deterministic ( [16, 17]), for any $t\in [0,T]$, it is easy to see that there exists a unique pair of $(Y^*(\cdot ,t),Z^*(\cdot ,t))\in L^2_{\mathbb {F}}(\Omega ;C([t,T];\mathbb {R}))\times L^2_{\mathbb {F}}(t,T;\mathbb {R})$ satisfying (3.3). However, in our framework, it becomes hard to directly deal with the well-posedness of (3.3). Note that $(X^*,Y^*,Z^*)$ satisfy a decoupled linear forward-backward stochastic differential equation (FBSDE). Therefore, we use the decoupling ideas to establish a connection between (3.3) and a new class of backward stochastic Riccati system (BSRS). Then we discuss the solvability of (3.3) via the introduced BSRS. To this end, we first suppose that

$$\begin{aligned} \begin{aligned} \displaystyle Y^*(s,t)= P_1^*(s)X^*(s)-2P_2^*(s)\mathbb {E}_t\left[ P_3^*(s)X^* (s)+P_4^*(s)\right] +P_{5}^*(s). \end{aligned} \end{aligned}$$

(3.6)

Here and next, for $s\in [t,T]$, let $(P_i^*(\cdot ),\Lambda ^*(\cdot ))$ satisfy BSDE

$$\begin{aligned} \left\{ \begin{aligned} \displaystyle dP_i^*(s)&=\Pi _{i}(s)ds+\Lambda _i^*(s) dW(s),\ \ s\in [0,T],\ \ i=1,2,3,4,5,\\ \displaystyle P_1^*(T)&=2,\ \ P_2^*(T)=1,\ \ P_3^*(T)=1,\ \ P_4^*(T)=0,\ \ P_5^*(T)=-\gamma , \end{aligned}\right. \end{aligned}$$

where $\Pi _i(\cdot )$ is defined as:

$$\begin{aligned} \begin{aligned} \displaystyle \Pi _1&=-\Big [2P_1^* (r+\beta \Theta ^*)+2\Lambda _1^* \sigma \Theta ^* +|\Theta ^*|^2\sigma ^2P_1^*\Big ],\\ \displaystyle \Pi _2&=-\Big [(r +\beta \Theta ^* )P_2^*+\Theta ^*\sigma \Lambda _2^*\Big ],\\ \displaystyle \Pi _3&=-\Big [P_3^*r +(P_3^*\beta + \Lambda _3^* \sigma )\Theta ^* \Big ],\\ \displaystyle \Pi _4&=-(P_3^*\beta +\Lambda _3^*\sigma )\varphi ^*,\\ \displaystyle \Pi _5&=-\Big [(r +\beta \Theta ^* )P_5^*+ \Theta ^*\sigma \Lambda _5^*+(P_1^*\beta +\Lambda _1^*\sigma +\Theta ^*\sigma ^2P_1^*)\varphi ^* \Big ]. \end{aligned} \end{aligned}$$

(3.7)

Next let us explain the way to obtain the above (3.7). First, by Itô’s formula, we have

$$\begin{aligned} \left\{ \begin{aligned} \displaystyle d \left[ P_1^*X^*\right]&=\left[ P_1^* (r+\beta \Theta ^*)+\Pi _1+\Lambda _1^* \sigma \Theta ^* \right] X^* ds\\&\quad +(P_1^*\beta +\Lambda _1^*\sigma )\varphi ^* ds + [P_1^*( \sigma \Theta ^* X^*+ \sigma \varphi ^*)+\Lambda _1^*X^*] dW(s),\\ \displaystyle d\left\{ P_2^*\mathbb {E}_t[ P_3^*X^* ]\right\}&=\left\{ \Pi _2\mathbb {E}_t[ P_3^*X^* ]+P_2^*\left\{ \mathbb {E}_t\left[ (P_3^*r+P_3^*\beta \Theta ^* + \Pi _3+\negthinspace \Lambda _3^* \sigma \Theta ^*)X^* \right] \right. \right. \\&\left. \left. \quad +\mathbb {E}_t\left[ (P_3^*\beta +\Lambda _3^*\sigma )\varphi ^* \right] \right\} \right\} ds+\Lambda _2^* \mathbb {E}_t[P_3^*X^*]dW(s),\\ \displaystyle d\Big [ P_2^*\mathbb {E}_t \left[ P_4^*\right] \Big ]&= \left[ \Pi _2\mathbb {E}_t P_4^*+P_2^* \mathbb {E}_t \Pi _4 \right] ds+\Lambda _2^* \mathbb {E}_t P_4^* dW(s). \end{aligned}\right. \end{aligned}$$

Therefore,

$$\begin{aligned} \begin{aligned}&\displaystyle d\left\{ P_1^*X^*-2P_2^*\mathbb {E}_t\left[ P_3^*X^*+P_4^*\right] + P_{5}^*\right\} \\&\quad \displaystyle =\left\{ \left[ P_1^* (r+\beta \Theta ^*)+\Pi _1+\Lambda _1^* \sigma \Theta ^* \right] X^*+ (P_1^*\beta +\Lambda _1^*\sigma )\varphi ^*+\Pi _5-2\Pi _2\mathbb {E}_t[ P_3^*X^*+P_4^* ]\right. \\&\left. \qquad \displaystyle -2P_2^*\left\{ \mathbb {E}_t\left[ (P_3^*r+P_3^*\beta \Theta ^* + \Pi _3+\negthinspace \Lambda _3^* \sigma \Theta ^*)X^* \right] \right. \right. \\&\left. \left. \qquad +\mathbb {E}_t\left[ (P_3^*\beta +\Lambda _3^*\sigma )\varphi ^* +\Pi _4 \right] \right\} \right\} ds\\&\qquad \displaystyle +\left\{ P_1^*[ \sigma \Theta ^* X^*+ \sigma \varphi ^*]+ \Lambda _1^*X^*-2\Lambda _2^* \mathbb {E}_t[P_3^*X^*+P_4^*]+\Lambda _5^*\right\} dW(s)\\&\quad \displaystyle = -\left\{ (r +\beta \Theta ^* )[ P_1^*X^*-2P_2^*\mathbb {E}_t\left[ P_3^*X^*+P_4^*\right] + P_{5}^*]+\Theta ^* \sigma Z^* \right\} ds+Z^* dW(s). \end{aligned} \end{aligned}$$

By identifying the terms w.r.t. ds and dW(s), respectively, we see that

$$\begin{aligned} \begin{aligned} \displaystyle Z^*(\cdot ,t)= P_1^*[ \sigma \Theta ^* X^*+ \sigma \varphi ^*]+ \Lambda _1^*X^*-2\Lambda _2^* \mathbb {E}_t[P_3^*X^*+P_4^*]+\Lambda _5^*. \end{aligned} \end{aligned}$$

(3.8)

Consequently,

$$\begin{aligned} \begin{aligned}&\displaystyle (r +\beta \Theta ^* )[ P_1^*X^*-2P_2^*\mathbb {E}_t\left[ P_3^*X^*+P_4^*\right] + P_{5}^*]+\Theta ^* \sigma Z^*\\&\quad \displaystyle = \Big [ (r +\beta \Theta ^* )P_1^*+ |\Theta ^*|^2\sigma ^2P_1^*+ \Theta ^*\sigma \Lambda _1^* \Big ]X^*\\&\qquad +(r +\beta \Theta ^* )P_5^*+ \Theta ^*\sigma ^2P_1^*\varphi ^*+\Theta ^*\sigma \Lambda _5^* \\&\qquad \displaystyle -2\Big [(r +\beta \Theta ^* )P_2^*+\Theta ^*\sigma \Lambda _2^*\Big ]\mathbb {E}_t\left[ P_3^*X^*+P_4^*\right] . \end{aligned} \end{aligned}$$

Comparing the ds terms in the previous expressions, we obtain a system of BSDEs, the generators of which are shown in (3.7).

A careful look at (3.7) indicates that $\Pi _2=\Pi _3$. Hence, $P_2^*=P_3^*$ if they exist. As a result, for notational simplicity, we keep the labels $P_1^*, P_2^*$, and replace $P_3^*, P_4^*, P_5^*$ by $P_2^*, P_3^*, P_4^*$. To summarize, given an undetermined process $(\Theta ^*,\varphi ^*)$, we arrive at a system of BSDEs:

$$\begin{aligned} \left\{ \begin{aligned} \displaystyle dP^*_1&=-\Big [2P_1^* (r+\beta \Theta ^*)+2\Lambda _1^* \sigma \Theta ^* +|\Theta ^*|^2\sigma ^2P_1^*\Big ]ds+\Lambda _1^*dW(s),\\ \displaystyle dP^*_2&=-\Big [(r +\beta \Theta ^* )P_2^*+\Theta ^*\sigma \Lambda _2^*\Big ]ds+\Lambda _2^*dW(s),\\ \displaystyle dP^*_3&=-(P_2^*\beta +\Lambda _2^*\sigma )\varphi ^*ds+\Lambda _3^*dW(s),\\ \displaystyle dP^*_4&=-\Big [(r +\beta \Theta ^* )P_4^*+ \Theta ^*\sigma \Lambda _4^*+ (P_1^*\beta +\Lambda _1^*\sigma +\Theta ^*\sigma ^2P_1^*)\varphi ^*\Big ]ds+\Lambda _4^*dW(s),\\ \displaystyle P_1^*(T)&=2, \ \ P_2^*(T)=1, \ \ P_3^*(T)=0,\ \ P_4^*(T)=-\gamma . \end{aligned} \right. \end{aligned}$$

(3.9)

Remark 3.1

Recently, [23] also studied dynamic mean-variance portfolio selection problem by closed-loop equilibrium strategy in the non-Markovian setting. However, to obtain the backward stochastic Riccati system, they used the backward stochastic PDEs while here we rely on FBSDEs and decoupling method. More importantly, the solvability of the backward stochastic Riccati system was not touched in [23] while in the following subsection we give a detailed discussion.

In the following, we define

$$\begin{aligned} \left\{ \begin{aligned} \displaystyle \Theta ^*&:=-\frac{\beta (P_1^*- 2|P_2^*|^2)+\sigma (\Lambda _1^*- 2\Lambda _2^*P_2^*) }{\sigma ^2 P_1^*},\\ \displaystyle \varphi ^*&:= -\frac{\beta ( P_4^*-2P_2^*P_3^*)+\sigma ( \Lambda _4^*-2\Lambda _2^*P_3^*)}{\sigma ^2P_1^*}. \end{aligned}\right. \end{aligned}$$

(3.10)

We will explain the reason for defining $(\Theta ^*,\varphi ^*)$ in this way via Remark 3.2. Plugging these into the first two equations in (3.9), we obtain a coupled BSDEs system:

$$\begin{aligned} \left\{ \begin{aligned} \displaystyle dP^*_1&=-\left\{ 2rP_1^* -\frac{\left[ \beta (P_1^*-2|P_2^*|^2) +\sigma (\Lambda _1^*-2\Lambda _2^*P_2^*)\right] }{\sigma ^2 P_1^*}\right. \\&\left. \quad \displaystyle \cdot \left[ \beta (P_1^*+2|P_2^*|^2)+\sigma (\Lambda _1^*+2\Lambda _2^*P_2^*) \right] \right\} ds+\Lambda _1^*dW(s),\\ \displaystyle dP^*_2&=-\left\{ rP_2^*-\frac{(\beta P_2^*+\sigma \Lambda _2^*)\left[ \beta (P_1^* -2|P_2^*|^2)+\sigma (\Lambda _1^*-2\Lambda _2^*P_2^*)\right] }{\sigma ^2P_1^*} \right\} ds\\&\quad \displaystyle +\Lambda _2^*dW(s),\\ \displaystyle P_1^*(T)&=2, \ \ P_2^*(T)=1. \end{aligned} \right. \nonumber \\ \end{aligned}$$

(3.11)

Once $(P_1^*,\Lambda _1^*)$ $(P_2^*,\Lambda _2^*)$ are given, we obtain the coupled system for $(P_3^*,P_4^*)$ as follows:

$$\begin{aligned} \left\{ \begin{aligned} \displaystyle dP^*_3&= (P_2^*\beta +\Lambda _2^*\sigma ) \frac{\beta (P_4^*-2P_2^*P_3^*)+\sigma ( \Lambda _4^*-2\Lambda _2^*P_3^*)}{\sigma ^2P_1^*}ds+\Lambda _3^*dW(s),\\ \displaystyle dP^*_4&=-\Big [(r +\beta \Theta ^* )P_4^*+ \Theta ^*\sigma \Lambda _4^*- (P_1^*\beta +\Lambda _1^*\sigma +\Theta ^*\sigma ^2P_1^*)\\&\quad \displaystyle \cdot \frac{\beta (P_4^*-2P_2^*P_3^*)+\sigma ( \Lambda _4^*-2\Lambda _2^*P_3^*)}{\sigma ^2P_1^*}\Big ]ds+\Lambda _4^*dW(s),\\ \displaystyle P_3^*(T)&=0,\ \ P_4^*(T)=-\gamma . \end{aligned} \right. \end{aligned}$$

(3.12)

Because the equation of $(P_1^*,\Lambda ^*_1)$ is analogous to the classical backward stochastic Riccati equation, we label the previous BSDE system (3.11)–(3.12) as a backward stochastic Riccati system for our mean-variance portfolio selection problem.

By imposing appropriate assumptions on $(P_i^*,\Lambda _i^*)$, in the next theorem we obtain the desired regularities of $(Y^*,Z^*)$, from which (using (3.5)) we further prove that $(\Theta ^*,\varphi ^*)$ in (3.10) is a closed-loop equilibrium operator. We leave the verification of these assumptions of $(P_i^*,\Lambda _i^*)$ to the next subsection.

Theorem 3.1

Suppose (H0) holds, and there exist four pairs of $(P_i^*,\Lambda _i^*)$ satisfying system (3.11)–(3.12), where $P_1^*(\cdot )>\delta >0,$ $\delta$ is a constant. Moreover, (H1) holds, and for any $p>2$,

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle (P_i^*,\Lambda _i^*)\in L^{\infty }_{\mathbb {F}}(\Omega ;C([0,T];\mathbb {R})) \times L^{p}_{\mathbb {F}}(\Omega ;L^2(0,T;\mathbb {R})),\ \ i:=1,2, \\ \displaystyle (P_j^*,\Lambda _j^*)\in L^{p}_{\mathbb {F}}(\Omega ;C([0,T];\mathbb {R})) \times L^{p}_{\mathbb {F}}(\Omega ;L^2(0,T;\mathbb {R})),\ \ j:=3,4,\\ \displaystyle \qquad \qquad \qquad \sup _{s\in [t,T]}\mathbb {E}_t|\Lambda _2^*(s)|^2<\infty ,\ \ a.s.\ \ t\in [0,T]. \end{array}\right. \end{aligned}$$

(3.13)

Then, $(\Theta ^*,\varphi ^*)$ as defined in (3.10) is a closed-loop equilibrium operator.

Proof

Given $(P_i^*,\Lambda _i^*), i=1,2,3,4$, satisfying system (3.11)–(3.12), and any $(s,t)\in [0,T]$, we define

$$\begin{aligned} \begin{aligned} \displaystyle Y^*(s,t)&:=P_1^*(s)X^*(s)-2P_2^*(s)\mathbb {E}_t\left[ P_2^*(s)X^*(s)+P_3^*(s)\right] + P_{4}^*(s),\\ \displaystyle Z^*(s,t)&:= P_1^*(s)[ \sigma (s)\Theta ^*(s) X^*(s)+ \sigma (s)\varphi ^*(s)]+ \Lambda _1^*(s)X^*(s)\\&\qquad \displaystyle -2\Lambda _2^*(s) \mathbb {E}_t[P_2^*(s)X^*(s)+P_3^*(s)]+\Lambda _4^*(s). \end{aligned} \end{aligned}$$

Hence,

$$\begin{aligned} \begin{aligned}&\displaystyle \beta (s) Y^*(s,t)+\sigma (s) Z^*(s,t)\\&\quad \displaystyle =\left[ \beta (s) P_1^*(s)+ \sigma (s)(P_1^*(s)\sigma (s)\Theta ^*(s)+\Lambda _1^*(s))\right] X^*(s)\\&\qquad \displaystyle + \sigma ^2(s) P_1^*(s)\varphi ^*(s) +(\beta (s)P_4^*(s)+\sigma (s)\Lambda _4^*(s))\\&\qquad \displaystyle -2\left[ \beta (s) P_2^*(s)+\sigma (s)\Lambda _2^*(s)\right] \mathbb {E}_t(P_2^*(s) X^*(s)+P_3^*(s)). \end{aligned} \end{aligned}$$

(3.14)

From the arguments between (3.6) and (3.9), for $t\in [0,T]$, it is easy to check that $(Y^*,Z^*)$ satisfy BSDE (3.3) on [t, T]. In addition, by (3.13), for some $q\in (1,2)$, we have $(Y^*(\cdot ,t),Z^*(\cdot ,t))\in L^q_{\mathbb {F}}(\Omega ;C([t,T];\mathbb {R}))\times L^q_{\mathbb {F}}( t,T ;\mathbb {R}).$

Note that in the above definitions of $(Y^*,Z^*)$, time variable s, t are defined independently. Hence by letting $t=s$, we see that $(\mathbb {Y}^*(s),\mathbb {Z}^*(s)):=(Y^*(s,s),Z^*(s,s)),$ $s\in [0,T],$ are well-defined. By the definition of $(\Theta ^*,\varphi ^*)$ in (3.10), for almost all $s\in [0,T]$, from (3.14),

$$\begin{aligned} \begin{aligned} \displaystyle 0&=\beta (s) \mathbb {Y}^*(s)+\sigma (s)\mathbb {Z}^*(s)=\beta (s) Y^*(s,s)+\sigma (s)Z^*(s,s)\\ \displaystyle&= \left\{ \beta (s)[P_1^*(s)-2|P_2^*(s)|^2]+ P_1^* \sigma ^2\Theta ^*+ \sigma (\Lambda _1^*- 2\Lambda _2^* P_2^*)\right\} X^*(s)\\ \displaystyle&\quad - \beta (s) [2P_2^*(s) P_3^*(s)- P_{4}^*(s)]+\sigma (s)\left[ P_1^*(s) \sigma (s)\varphi ^*(s)-2\Lambda _2^*(s)P_3^*(s) +\Lambda _4^*(s)\right] . \end{aligned} \end{aligned}$$

In order to obtain (3.5), it is sufficient to prove

$$\begin{aligned} \begin{aligned} \displaystyle \lim _{\varepsilon _n\downarrow 0}\mathbb {E}_t\int _t^{t+\varepsilon _n}\frac{\left[ \beta (s) (Y^*(s,t)-Y^*(s,s))+\sigma (s)(Z^*(s,t)-Z^*(s,s))\right] }{\varepsilon _n}ds=0. \end{aligned}\nonumber \\ \end{aligned}$$

(3.15)

In fact, we first have

$$\begin{aligned} \begin{aligned} \displaystyle \mathbb {E}_t\left[ \beta Y^*(\cdot ,t)+\sigma Z^*(\cdot ,t)\right] = \mathbb {E}_t\left[ \beta \mathbb {Y}^* +\sigma \mathbb {Z}^*\right] -2\mathbb {E}_t\Big [{\mathscr {G}}^*(\cdot ,X^*) (\beta P_2^*+\sigma \Lambda _2^*)\Big ], \end{aligned}\nonumber \\ \end{aligned}$$

(3.16)

where

$$\begin{aligned} \displaystyle {\mathscr {G}}^*(\cdot ,X^*):=\mathbb {E}_t( P_2^*X^*+P_3^*)-P_2^*X^*-P_3^*. \end{aligned}$$

(3.17)

From (3.13) and dominated convergence theorem, $\lim \limits _{\varepsilon _n\downarrow 0}\mathbb {E}_t\sup \limits _{s\in [t,t+\varepsilon _n]}\big |{\mathscr {G}}^*(s,X^*(s))\big | =0.$ a.s. Then, as $\varepsilon _n\downarrow 0$, we obtain

$$\begin{aligned} \begin{aligned}&\displaystyle \frac{1}{\varepsilon _n} \mathbb {E}_t\int _t^{t+\varepsilon _n}\big |\Lambda _2^*(s) {\mathscr {G}}^*(s,X^*(s))\big |ds\\&\quad \displaystyle \le \sup _{s\in [t,T]}\left[ \mathbb {E}_t |\Lambda _2^*(s)|^2 \right] ^{\frac{1}{2}}\Big [\mathbb {E}_t\sup _{s\in [t,t+\varepsilon _n]}\big |{\mathscr {G}}^*(s,X^*(s))\big |^2\Big ] ^{\frac{1}{2}}\rightarrow 0. \end{aligned} \end{aligned}$$

(3.18)

Similarly, by the imposed regularity of $P_2^*$,

$$\begin{aligned} \begin{aligned} \displaystyle \frac{1}{\varepsilon _n} \mathbb {E}_t\int _t^{t+\varepsilon _n}\big |P_2^*(s) {\mathscr {G}}^*(s,X^*(s)) \big |ds\rightarrow 0,\ \ \varepsilon _n\downarrow 0. \end{aligned} \end{aligned}$$

(3.19)

Putting (3.18) and (3.19) back into (3.16), we get the desired conclusion (3.15). $\square$

Remark 3.2

We point out two useful facts by the above proof. First, the pointwise integrability of $\Lambda _2(\cdot )$ in (3.13) plays an important role, even though it is stronger than the conventional square integrability. We will verify this assumption in the next subsection. Second, the reason of defining $(\Theta ^*,\varphi ^*)$ in (3.10) lies in the requirement of $\beta (s)Y^*(s,s)+\sigma (s) Z^*(s,s)=0, s\in [0,T].$ a.e. The equality is crucial for the sufficiency of closed-loop equilibrium operators.

In the remaining part of this subsection, we drop the pointwise assumption of $\Lambda _2^*$ in (3.13). As a tradeoff, we introduce a slightly weak notion as follows.

Definition 3.1

The pair $(\Theta ^*(\cdot ),\varphi ^*(\cdot ))$ is called a relaxed closed-loop equilibrium operator if for any $x\in \mathbb {R}$, $v\in L^2_{{{{\mathcal {F}}}}_t}(\Omega ;\mathbb {R})$, and any positive sequence $\{\varepsilon _n\}$ approaching to zero, there exists a subsequence $\{\varepsilon '_n\}$ such that $u^*, u^{v,{\varepsilon '_n}}\in L^2_{\mathbb {F}}(0,T;\mathbb {R}),$ and

$$\begin{aligned} \begin{array}{ll} \displaystyle \ \ \lim _{\overline{\varepsilon '_n\rightarrow 0}} { J(u^{v,{\varepsilon '_n}}(\cdot );t,X^*(t))- J\big (u^*(\cdot );t,X^*(t)\big ) \over \varepsilon _n'}\ge 0.\ \ a.e. \ \ a.s. \end{array} \end{aligned}$$

(3.20)

Here, $u^*$ (resp. $X^*$) is a relaxed closed-loop equilibrium investment strategy (resp. wealth process).

If $(\Theta ^*,\varphi ^*)$ is a closed-loop equilibrium operator in the sense of Definition 2.1, then for any positive sequence $\{\varepsilon _n\}$ tending to zero, there exists a subsequence $\{\varepsilon '_n\}$ such that (3.20) holds for any $t\in [0,T)$. This is stronger than that of Definition 3.1. Hence $(\Theta ^*,\varphi ^*)$ is also a relaxed closed-loop equilibrium operator. Conversely, we give the positive answer in the deterministic coefficients case.

Lemma 3.1

Suppose that the coefficients in (H0) are deterministic, $(\Theta ^*,\varphi ^*)\in L^2(0,T;\mathbb {R}^2)$ is a relaxed closed-loop equilibrium operator. Then $(\Theta ^*,\varphi ^*)$ is also a closed-loop equilibrium operator.

Proof

Given $(\Theta ^*,\varphi ^*)$, it is easy to see the solvability of the following system:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle dP^*_1=- \Big [2(r+\beta \Theta ^*) +|\Theta ^*|^2\sigma ^2\Big ]P_1^*ds,\\ \displaystyle dP^*_2=- (r +\beta \Theta ^* )P_2^* ds,\\ \displaystyle dP^*_3=-P_2^*\beta \varphi ^*ds,\\ \displaystyle dP^*_4=-\Big [(r +\beta \Theta ^* )P_4^* + (P_1^*\beta +\Theta ^*\sigma ^2P_1^*)\varphi ^*\Big ]ds,\\ \displaystyle P_1^*(T)=2, \ \ P_2^*(T)=1, \ \ P_3^*(T)=0,\ \ P_4^*(T)=-\gamma . \end{array} \right. \end{aligned}$$

In addition, $P_1^*(\cdot )\ge \delta >0$ for some constant $\delta$. We observe that the following $(Y^*,Z^*)$ satisfies (3.3) with deterministic $(\Theta ^*,\varphi ^*)$:

$$\begin{aligned} \begin{array}{ll} \displaystyle Y^*(\cdot ,t)= P_1^*X^*-2P_2^*\mathbb {E}_t\left[ P_2^*X^*+P_3^*\right] +P_{4}^*,\ \ Z^*(\cdot ,t)= P_1^*\sigma [\Theta ^* X^*+\varphi ^*]. \end{array} \end{aligned}$$

It follows from (3.4) that

$$\begin{aligned} \begin{aligned} \displaystyle \mathbb {E}_t\left\{ \left[ 2X^*(T)- 2\mathbb {E}_tX^*(T)-\gamma \right] X_1^{v,\varepsilon }(T)\right\} =\mathbb {E}_t\int _t^{t+\varepsilon }\Big [{\mathscr {H}}_1(s)X^*(s) +{\mathscr {H}}_2(s)\Big ]ds v, \end{aligned} \end{aligned}$$

where ${\mathscr {H}}_i(\cdot )$ are deterministic and are defined as

$$\begin{aligned} \begin{aligned} \displaystyle {\mathscr {H}}_1(t)&:=\beta (t)[P_1^*(t)-2|P_2^*(t)|^2]+\sigma ^2(t)P_1^*(t)\Theta ^*(t),\\ \displaystyle {\mathscr {H}}_2(t)&:=\beta (t)[P_4^*(t)-2P_2^*(t)P_3^*(t)]+\sigma ^2(t) P_1^*(t)\varphi ^*(t). \end{aligned} \end{aligned}$$

For almost all $t\in [0,T]$, we see that

$$\begin{aligned} \begin{aligned} \displaystyle \lim _{\varepsilon \rightarrow 0}\frac{1}{\varepsilon }\mathbb {E}_t\left\{ \left[ 2X^*(T)- 2\mathbb {E}_tX^*(T)-\gamma \right] X_1^{v,\varepsilon }(T)\right\} =\Big [ {\mathscr {H}}_1(t)X^*(t)+{\mathscr {H}}_2(t)\Big ]v. \end{aligned} \end{aligned}$$

From Lemma 3.4 in [16], we have

$$\begin{aligned} \begin{aligned} \displaystyle \lim _{\varepsilon \rightarrow 0}\frac{1}{\varepsilon }\mathbb {E}_t \left\{ [ X_1^{v,\varepsilon }(T)- \mathbb {E}_tX_1^{v,\varepsilon }(T)]X_1^{v,\varepsilon }(T)\right\} =\frac{1}{2} \sigma ^2(t) P_1^*(t) v^2. \ \ dt\otimes d\mathbb {P}\end{aligned} \end{aligned}$$

Therefore, it follows from the equality in (3.2) and Definition 3.1 that there exists subsequence $\{\varepsilon _n'\}$ such that

$$\begin{aligned} \begin{aligned} \displaystyle 0&\le \lim _{\varepsilon _n'\rightarrow 0}\frac{1}{ \varepsilon _n'}\Big [J(u^{v,\varepsilon _n'}(\cdot );t,X^*(t))-J(u^*(\cdot );t,X^*(t)) \Big ]\\ \displaystyle&=\Big [ {\mathscr {H}}_1(t)X^*(t)+{\mathscr {H}}_2(t)\Big ]v+\frac{1}{2} \sigma ^2(t) P_1^*(t) v^2. \ \ \end{aligned} \end{aligned}$$

By the arbitrariness of v, we have ${\mathscr {H}}_1(t)=0$ and ${\mathscr {H}}_2(t)=0$, which implies that

$$\begin{aligned} \begin{aligned} \displaystyle \Theta ^*=-\frac{\beta (P_1^*- 2|P_2^*|^2) }{\sigma ^2 P_1^*},\ \ \varphi ^*= -\frac{\beta ( P_4^*-2P_2^*P_3^*)}{\sigma ^2P_1^*}. \end{aligned} \end{aligned}$$

(3.21)

We note that (H1) holds naturally for $(\Theta ^*,\varphi ^*)$ in (3.21). Therefore, according to Theorem 3.1, $(\Theta ^*,\varphi ^*)$ is a closed-loop equilibrium operator. $\square$

The following result gives a sufficient condition for a relaxed closed-loop equilibrium operator without imposing the pointwise assumption on $\Lambda _2^*$.

Theorem 3.2

Suppose (H0) holds, and there exist four pairs of $(P_i^*,\Lambda _i^*)$ satisfying system (3.11)–(3.12), where $P_1^*>\delta >0, \delta$ is a constant. Moreover, (H1) holds, and for any $p>2$,

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle (P_i^*,\Lambda _i^*)\in L^{\infty }_{\mathbb {F}}(\Omega ;C([0,T];\mathbb {R}))\times L^{p}_{\mathbb {F}}(\Omega ;L^2(0,T;\mathbb {R})),&{}\quad i:=1,2, \\ \displaystyle (P_j^*,\Lambda _j^*)\in L^{p}_{\mathbb {F}}(\Omega ;C([0,T];\mathbb {R}))\times L^{p}_{\mathbb {F}}(\Omega ;L^2(0,T;\mathbb {R})),&{}\quad j:=3,4.\ \end{array}\right. \end{aligned}$$

Then $(\Theta ^*,\varphi ^*)$ defined in (3.10) is a relaxed closed-loop equilibrium operator.

Proof

By the proof of Theorem 3.1, for any sequence $\{\varepsilon _n\}\downarrow 0$, it is sufficient to show that there exists a subsequence $\{\varepsilon '_n\}$ such that for almost every $t\in [0,T)$,

$$\begin{aligned} \displaystyle \lim _{\varepsilon '_n\downarrow 0}\frac{1}{\varepsilon '_n}\mathbb {E}_t\int _t^{t+{\varepsilon '_n}}\big | \Lambda _2^*(s){\mathscr {G}}^*(s,X^*(s))\big |ds=0. \ \ a.s. \end{aligned}$$

(3.22)

Here, ${\mathscr {G}}^*(\cdot ,X^*(\cdot ))$ is defined in (3.17). For later usefulness, we extend the involved functions on [0, 2T] as,

$$\begin{aligned} \displaystyle \widetilde{f}^*(s):= & {} f^*(s) I_{[0,T]}(s), \ \ f:=P_2,\ P_3,\ X, \ \Lambda _2, \\ \displaystyle \widetilde{\mathscr {G}}^*(s,\widetilde{X}^*(s)):= & {} \mathbb {E}_t \left[ \widetilde{P}_2^*(s) \widetilde{X}^*(s)+\widetilde{P}_3(s)\right] -\widetilde{P}_2^*(s) \widetilde{X}^*(s)-\widetilde{P}_3(s). \end{aligned}$$

As a result, for almost $t\in [0,T)$,

$$\begin{aligned} \begin{aligned} \displaystyle \lim _{\varepsilon _n'\downarrow 0}\frac{1}{\varepsilon _n'}\mathbb {E}_t\int _t^{t+{\varepsilon '_n}}\Big [\big | \Lambda _2^*(s){\mathscr {G}}^*(s,X^*(s))\big |-\big | \widetilde{\Lambda }_2^*(s)\widetilde{\mathscr {G}}^*(s, \widetilde{X}^*(s))\big |\Big ]ds=0. \end{aligned} \nonumber \\ \end{aligned}$$

(3.23)

Using Hölder inequality, we obtain that

$$\begin{aligned} \begin{aligned}&\displaystyle \mathbb {E}\int _0^{T }\frac{1}{\varepsilon }\int _t^{t+\varepsilon }\big |\widetilde{\Lambda }_2^*(s)\widetilde{\mathscr {G}}^*(s,\widetilde{X}^*(s))\big |dsdt\\&\quad \displaystyle \le \Big [\frac{1}{\varepsilon }\mathbb {E}\int _0^{T }\int _t^{t+\varepsilon } |\widetilde{\Lambda }_2^*(s)|^2ds dt \Big ]^{\frac{1}{2}}\left[ \mathbb {E}\int _0^{T } \sup _{s\in [t,t+\varepsilon ]}\big |\widetilde{\mathscr {G}}^*(s,\widetilde{X}^*(s))\big |^2dt\right] ^{\frac{1}{2}}. \end{aligned} \end{aligned}$$

As for the first term,

$$\begin{aligned} \begin{aligned} \displaystyle \lim _{\varepsilon \rightarrow 0}\frac{1}{\varepsilon }\mathbb {E}\int _0^{T }\int _t^{t+\varepsilon } |\widetilde{\Lambda }_2^*(s)|^2ds dt&=\lim _{\varepsilon \rightarrow 0}\frac{1}{\varepsilon }\mathbb {E}\int _0^\varepsilon \int _{s}^{T +s}|\widetilde{\Lambda }^*_2(r)|^2drds\\&=\mathbb {E}\int _0^{T }|\widetilde{\Lambda }_2^*(r)|^2dr. \end{aligned} \end{aligned}$$

Notice that

$$\begin{aligned} \begin{aligned}&\displaystyle \sup _{s\in [t,t+\varepsilon ]}|\widetilde{\mathscr {G}}^*(s,\widetilde{X}^*(s))|^2\\&\quad \displaystyle \le K\mathbb {E}_t\sup _{s\in [t,T]}|\widetilde{P}_2^*(s)\widetilde{X}^*(s)+\widetilde{P}_3^*(s)|^2 +K\sup _{s\in [t,T]}|\widetilde{P}_2^*(s)\widetilde{X}^*(s)+\widetilde{P}_3^*(s)|^2. \end{aligned} \end{aligned}$$

It then follows from the dominated convergence theorem that

$$\begin{aligned} \begin{aligned} \displaystyle \lim _{\varepsilon \downarrow 0}\mathbb {E}\int _0^{T } \sup _{s\in [t,t+\varepsilon ]}\big |\widetilde{\mathscr {G}}^*(s,\widetilde{X}^*(s))\big |^2dt=0. \end{aligned} \end{aligned}$$

To sum up, we have

$$\begin{aligned} \begin{aligned} \displaystyle \lim _{\varepsilon \downarrow 0}\frac{1}{\varepsilon }\mathbb {E}\int _0^{T }\int _t^{t+\varepsilon }\big | \widetilde{\Lambda }_2^*(s)\widetilde{\mathscr {G}}^*(s,\widetilde{X}^*(s))\big |dsdt=0. \end{aligned} \end{aligned}$$

As a result, for any sequence $\{\varepsilon _n\}\downarrow 0$, there exists $\{\varepsilon '_n\}$ such that

$$\begin{aligned} \begin{aligned} \displaystyle \lim _{\varepsilon '_n\downarrow 0}\frac{1}{\varepsilon '_n}\mathbb {E}_t\int _t^{t+{\varepsilon '_n}}\big | \widetilde{\Lambda }_2^*(s)\widetilde{\mathscr {G}}^*(s,\widetilde{X}^*(s))\big |ds=0,\ \ t\in [0,T], \ \ dt\otimes d\mathbb {P}. \end{aligned} \end{aligned}$$

From (3.23), we see that (3.22) holds true for almost every $t\in [0,T)$. $\square$

3.2 Explicit Expressions for Closed-Loop Equilibrium Strategy

In this subsection, we present the explicit forms of closed-loop equilibrium strategies for mean-variance portfolio selection problems with random coefficients.

We make some intuitive arguments on the solvability of Riccati systems. First, let us look at system (3.11), which is fully coupled. We cook up some techniques to decouple them from each other. Given $P_2^*$ in (3.9), by Itô’s formula,

$$\begin{aligned} \begin{aligned} \displaystyle d|P_2^*|^2=-\Big [2r|P_2^*|^2+2P_2^*(\beta P_2^*+\sigma \Lambda _2^*)\Theta ^*-|\Lambda _2^*|^2\Big ]ds+2P_2^*\Lambda _2^*dW(s). \end{aligned} \end{aligned}$$

Recalling $P_1^*$ in (3.9), we denote $M^*:=P_1^*-2|P_2^*|^2,$ $N^*:=\Lambda _1^*-4P_2^*\Lambda _2^*.$ Then we can describe $(M^*,N^*)$ as

$$\begin{aligned} \left\{ \begin{aligned} \displaystyle dM^*&=-\Big [ -\frac{(\beta M^*+\sigma N^*)^2+4\sigma P_2^*\Lambda _2^*(\beta M^*+\sigma N^*)}{\sigma ^2 P_1^*}\\&\quad \displaystyle +2\left( r +\frac{|\Lambda _2^*|^2}{P_1^*}\right) M^*\Big ]ds+N^* dW(s),\\ \displaystyle M^*(T)&=0. \end{aligned}\right. \end{aligned}$$

(3.24)

Of course, $M^*(\cdot )=N^*(\cdot )=0$ is a solution, which leads to $P_1^*=2|P_2^*|^2, \Lambda _1^*=4P_2^*\Lambda _2^*$. Recall (3.10), we further have $\Theta ^*=-\frac{2\Lambda _2^*P_2^*}{\sigma P_1^*}$. Therefore,

$$\begin{aligned} \begin{aligned} 2(P_1^* \beta +\Lambda _1^* \sigma )\Theta ^*+|\Theta ^*|^2\sigma ^2P_1^* =- \frac{ \beta \Lambda _1^*}{\sigma } -\frac{3|\Lambda _1^*|^2}{4P_1^*}. \end{aligned} \end{aligned}$$

(3.25)

Hence, the first equation in (3.9)) reduces to

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle dP_1^*=-\left( 2r P_1^* - \frac{\beta \Lambda _1^*}{\sigma } -\frac{3|\Lambda _1^*|^2}{4P_1^*} \right) ds+\Lambda _1 ^*dW(s),\ \ s\in [0,T],\\ \displaystyle P_1^*(T)=2, \end{array}\right. \end{aligned}$$

(3.26)

which does not rely on $(P_2^*,\Lambda _2^*)$. Similarly, one obtains the case of $(P_2^*,\Lambda _2^*)$.

Once $(P_1^*,\Lambda _1^*)$ and $(P_2^*,\Lambda _2^*)$ are obtained, we continue to look at the system (3.12). Notice that

$$\begin{aligned} \displaystyle d(-2P_2^*P_3^*)= & {} -\Big [-2P_2^*(P_2^*\beta +\Lambda _2^*\sigma )\varphi ^* -2(r+\beta \Theta ^*)P_2^*P_3^*-2P_3^*\Theta ^* \sigma \Lambda _2^* \nonumber \\{} & {} \quad \displaystyle +2\Lambda _2^*\Lambda _3^*\Big ]ds-(2P_2^*\Lambda _3^*+2P_3^*\Lambda _2^*)dW(s). \end{aligned}$$

(3.27)

Recalling $(P_4^*,\Lambda _4^*)$ in (3.12), we define $\Phi :=P_4^*-2P_2^*P_3^*, \Psi :=\Lambda _4^*-2\Lambda _2^*P_3^*-2\Lambda _3^*P_2^*.$ Then it follows from some basic calculations that

$$\begin{aligned} \left\{ \begin{aligned} \displaystyle d\Phi&=-\Big [(r+\beta \Theta ^*)\Phi +\Theta ^*\sigma \Psi \Big ]ds+\Psi dW(s),\\ \displaystyle \Phi (T)&=-\gamma , \end{aligned}\right. \end{aligned}$$

(3.28)

and $\varphi ^*:=-\frac{2P_2^*\Lambda _3^*}{\sigma P_1^*}-\frac{(\beta \Phi +\sigma \Psi )}{\sigma ^2 P_1^*}$. Plugging $\varphi ^*$ into the first equation in (3.12), we obtain

$$\begin{aligned} \left\{ \begin{aligned} \displaystyle dP_3^*&=\Big [\frac{2(P_2^*\beta +\Lambda _2^*\sigma ) P_2^*}{\sigma P_1^*}\Lambda _3^*+\frac{(P_2^*\beta +\Lambda _2^* \sigma )(\beta \Phi +\sigma \Psi )}{\sigma ^2 P_1^*} \Big ]ds+\Lambda _3^*dW(s),\ \\ \displaystyle P_3^*(T)&=0, \end{aligned}\right. \nonumber \\ \end{aligned}$$

(3.29)

which depends only on the given $(P_1^*,\Lambda _1^*), (P_2^*,\Lambda _2^*), (\Phi ,\Psi )$. Similarly, one can obtain the case of $(P_4^*,\Lambda _4^*)$.

In the following, we make the above procedures rigorous and construct the solutions of system (3.11)–(3.12) explicitly. To do so, we need the next hypothesis, the verification of which is provided in Remark 3.4.

(H2) For $s\in [0,T], r(s), \frac{\beta (s)}{\sigma (s)}$ are Malliavin differentiable, and there exists a constant $K>0$ such that $\big |D_{\nu }r(s)\big |+\big |D_{\nu }\left[ \frac{\beta (s)}{\sigma (s)}\right] \big |\le K,$ $\nu , s\in [0,T]$.

Theorem 3.3

Suppose that (H0) and (H2) hold. Then (H1) holds true, and there exist four pairs of $(P_i^*,\Lambda _i^*)$ satisfying system (3.11)–(3.12) with $P_1^*(\cdot )>\delta >0$ and (3.13) being true with any $p>2$. In addition, we have the following relation between $(P_1^*,\Lambda _1^*)$ and $(P_2^*,\Lambda _2^*)$:

$$\begin{aligned} P_1^*=2|P_2^*|^2,\ \ \ \Lambda _1^*=4P_2^*\Lambda _2^*, \end{aligned}$$

and (3.10) is rewritten as (with $(\Psi ,\Phi )$ in (3.28)),

$$\begin{aligned} \begin{aligned} \displaystyle \Theta ^*=-\frac{\Lambda _2^*}{\sigma P_2^*},\quad \varphi ^*=-\frac{2P_2^*\Lambda _3^*}{\sigma P_1^*}-\frac{\beta \Phi +\sigma \Psi }{\sigma ^2 P_1^*} \in L^p_{\mathbb {F}}(\Omega ;L^2(0,T;\mathbb {R})),\quad p>2. \end{aligned} \nonumber \\ \end{aligned}$$

(3.30)

Proof

Step 1. We prove that (3.11) and (3.12) is solvable, (3.13) holds true.

First, we consider

$$\begin{aligned} \left\{ \begin{aligned} \displaystyle dM&=\big (r M+\frac{\beta }{\sigma }N\big )ds+ N dW(s),\ \ s\in [0,T],\\ \displaystyle M(T)&=-\sqrt{2}. \end{aligned}\right. \end{aligned}$$

(3.31)

It is easy to see that M is bounded and that $\int _0^{\cdot }N(s)dW(s)$ is a BMO-martingale.

By defining $P_1^*:=\frac{4}{M^2},$ $\Lambda _1^*:=-\frac{8N}{M^3}$, we see that $(P_1^*,\Lambda _1^*)$ satisfies the above equation (3.26). Notice that M is bounded, $\int _0^{\cdot }\Lambda _1(s)dW(s)$ is a bounded mean oscillation (BMO)-martingale. We define $(P_2^*,\Lambda _2^*)$ as $P_2^*:=\sqrt{\frac{P_1^*}{2} },$ $\Lambda _2^*:=\frac{\Lambda _1^*}{4P_2^*}.$ Therefore, the desired relations among $P_1^*, P_2^*, \Lambda _1^*, \Lambda _2^*$ are derived and the expression of $\Theta ^*$ in (3.10) becomes $\Theta ^*=-\frac{2\sigma \Lambda _2^*P_2^*}{\sigma ^2 P_1^*}=-\frac{\Lambda _2^*}{\sigma P_2^*}$. Moreover, $\int _0^{\cdot }\Lambda _2^*(s)dW(s), \int _0^{\cdot }\Theta ^*(s)dW(s)$ are BMO martingales and the above (3.25) holds. As a result, we can rewrite (3.26) as the first equation in (3.9), and $(P_1^*,\Lambda _1^*)$ is a solution to the first equation in (3.11).

To prove that $(P_2^*,\Lambda _2^*)$ satisfies the second equation in (3.11), by Itô’s formula,

$$\begin{aligned} \begin{aligned} \displaystyle d\left[ \frac{P_1^*}{2}\right] ^{\frac{1}{2}} =\Big [ -r\left( \frac{P_1^*}{2}\right) ^{\frac{1}{2}}+ \frac{\beta \Lambda _1^*}{2^{\frac{3}{2}}|P_1^*|^{\frac{1}{2}}\sigma }+ \frac{|\Lambda _1^*|^2}{2^{\frac{5}{2}}|P_1^*|^{\frac{3}{2}}}\Big ]ds+ \frac{\Lambda _1^*}{2^{\frac{3}{2}}|P_1^*|^{\frac{1}{2}}} dW(s). \end{aligned} \nonumber \\ \end{aligned}$$

(3.32)

With $\Theta ^*=-\frac{\Lambda _2^*}{\sigma P_2^*}$, we observe that

$$\begin{aligned} (\beta P_2^*+\sigma \Lambda _2^*)\Theta ^*= & {} -\left[ \beta \left( \frac{P_1^*}{2}\right) ^{\frac{1}{2}}+\frac{\sigma \Lambda _1^*}{4P_2^*}\right] \frac{\Lambda _1^*}{2\sigma P_1^*}\\= & {} -\left( 2^{-\frac{3}{2}}|P_1^*|^{-\frac{1}{2}}\frac{\beta }{\sigma }\Lambda _1^*+2^{-\frac{5}{2}}|P_1^*|^{-\frac{3}{2}}|\Lambda _1^*|^2\right) . \end{aligned}$$

Since $P_2^*(T)=1$, we can rewrite (3.32) into the second equation in (3.9), which indicates the desired conclusion of $(P_2^*,\Lambda _2^*)$. It should be noted that the regularity of $(P_i^*,\Lambda _i^*), i=1,2$ in (3.13) is obvious.

We continue to investigate $(P_3^*,\Lambda _3^*), (P_4^*,\Lambda _4^*)$. Because $\int _0^{\cdot }\Theta ^*(s)dW(s)$ is BMO-martingale, for any $p>2$, by [24, Theorem 10], (3.28) admits a unique pair of $(\Phi ,\Psi )\in L^p_{\mathbb {F}}(\Omega ;C([0,T];\mathbb {R}))\times L^p_{\mathbb {F}}(\Omega ;L^2(0,T;\mathbb {R})).$ By the integrability of $(P_2^*,\Lambda _2^*), (\Phi ,\Psi )$, for any $p>2$, it follows from [24, Theorem 10] that (3.29) admits the unique pair $(P_3^*,\Lambda _3^*)$ with the corresponding regularity in (3.13). We define $\varphi ^*:=-\frac{2P_2^*\Lambda _3^*}{\sigma P_1^*}-\frac{\beta \Phi +\sigma \Psi }{\sigma ^2 P_1^*}.$ The result of $\varphi ^*\in L^p_{\mathbb {F}}(\Omega ;L^2(0,T;\mathbb {R}))$ is easy to obtain. Moreover, we can transform (3.29) into the third equation in (3.9). Keeping this in mind, by Itô’s formula, we obtain the above (3.27). Let $P_4^*:=\Phi +2P_2^*P_3^*,$ $\Lambda _4^*:=\Psi +2\Lambda _2^*P_3^*+2\Lambda _3^*P_2^*.$ We can rewrite the definition of $\varphi ^*$ as the second expression in (3.10). Therefore, $(P_3^*,\Lambda _3^*)$ is the solution to the first equation of (3.12). In addition, it is a direct calculation that

$$\begin{aligned} \left\{ \begin{aligned} \displaystyle dP_4^*&=-\left[ (r+\Theta ^*\beta )P_4^*+\Theta ^*\sigma \Lambda _4^*-2\Theta ^*\sigma P_2^*\Lambda _3^*+2P_2^*( P_2^*\beta +\Lambda _2^*\sigma )\varphi ^* \right. \\&\left. \quad \displaystyle -2\Lambda _2^*\Lambda _3^*\right] ds+\Lambda _4^* dW(s),\\ \displaystyle P_4^*(T)&=-\gamma . \end{aligned}\right. \end{aligned}$$

(3.33)

By the definition of $(P_2^*,\Lambda _2^*)$, we observe that $\Theta ^*=-\frac{\Lambda _2^*}{\sigma P_2^*},$ $\Theta ^*\sigma P_2^*\Lambda _3^*+\Lambda _2^*\Lambda _3^*=0,$ $\Lambda _1^*+\Theta ^*\sigma P_1^*=2P_2^*\Lambda _2^*.$ Consequently,

$$\begin{aligned} \displaystyle -2 \Theta ^*\sigma P_2^*\Lambda _3^*-2\Lambda _2^*\Lambda _3^* +2P_2^*( P_2^*\beta +\Lambda _2^*\sigma )\varphi ^* =P_1^*\beta \varphi ^*+(\Lambda _1^*\sigma +\Theta ^*\sigma ^2 P_1^*)\sigma \varphi ^*. \end{aligned}$$

Plugging it back into (3.33), we obtain the fourth equation in (3.9), and $(P_4^*,\Lambda _4^*)$ satisfies the first equation of (3.12). The regularity of $(P_4^*,\Lambda _4^*)$ in (3.13) is obvious.

Step 2. In this step, we prove the integrability of $\Lambda _2^*$.

Given $\tau \in [0,T],$ $\nu \in [\tau ,T]$, by (H2) and [25, Proposition 5.3], the Malliavin derivatives $(D_\nu M(s),D_\nu N(s))$ exist, $s\in [0,T]$, and a version is given by

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle (D_\nu M(t),D_\nu N(t))=(0,0),\ \ a.s. \ a.e., \ \ t\in [0,\nu ),\\ \displaystyle D_\nu M(t)=-\int _t^T\left\{ D_\nu r(s) \cdot M(s) +D_\nu \left[ \frac{\beta (s)}{\sigma (s)}\right] \cdot N(s)+r(s) D_\nu M(s)\right. \\ \left. \displaystyle \qquad \qquad \quad +\frac{\beta (s)}{\sigma (s)} D_\nu N(s)\right\} ds-\int _t^TD_\nu N(s)dW(s),\ \ t\in [\nu ,T]. \end{array}\right. \end{aligned}$$

By the classical estimate of BSDEs, for $\nu \in [\tau ,T]$,

$$\begin{aligned} \begin{aligned}&\displaystyle \mathbb {E}_\tau \sup _{t\in [\nu ,T]}|D_\nu M(t)|^2+\mathbb {E}_\tau \int _\nu ^T |D_\nu N(s)|^2ds\\&\quad \displaystyle \le K\mathbb {E}_\tau \left\{ \int _\nu ^T\left[ |D_\nu r(s)||M(s)|+|D_\nu \left[ \frac{\beta (s)}{\sigma (s)}\right] | |N(s)|\right] ds\right\} ^2.\ \ a.s. \end{aligned} \end{aligned}$$

According to (H3), for $\tau \in [0,T]$, we arrive at

$$\begin{aligned} \begin{aligned} \displaystyle \sup _{\nu \in [\tau ,T]}\mathbb {E}_\tau |D_\nu M(\nu )|^2\le K\sup _{\nu \in [\tau ,T]}\mathbb {E}_\tau \left\{ \int _\nu ^T\left[ |M(s)|+ |N(s)|\right] ds\right\} ^2<\infty . \end{aligned} \end{aligned}$$

Therefore, $\sup \limits _{t\in [\tau ,T]}\mathbb {E}_\tau |N(t)|^2=\sup \limits _{t\in [\tau ,T]}\mathbb {E}_\tau |D_{t}M(t)|^2<\infty .$ a.s. Our conclusion follows from the definition of $\Lambda _1^*,$ and $(P_2^*,\Lambda _2^*)$.

Step 3. We verify the assumptions in (H1).

First, let us look at the case of $(u^*,X^*)$. For $t\in [0,T]$, recall that

$$\begin{aligned} \left\{ \begin{aligned} \displaystyle dX^*(s)&=\left[ (r+\beta \Theta ^*)X^* +\beta \varphi ^*\right] ds +\left[ \sigma \Theta ^* X^*+ \sigma \varphi ^*\right] dW(s),\\ \displaystyle X^*(0)&=x. \end{aligned}\right. \end{aligned}$$

We introduce $\Xi (\cdot )$ satisfying $\Xi (0)=1$, and

$$\begin{aligned} \displaystyle d\Xi (s)=\Xi ( r+\beta \Theta ^*)ds+ \sigma \Theta ^*\Xi dW(s),\quad s\in [0,T]. \end{aligned}$$

It is easy to check

$$\begin{aligned} \displaystyle d\Xi ^{-1}=\Xi ^{-1}\left[ \sigma ^2|\Theta ^*|^2-r-\beta \Theta ^*\right] ds-\Xi ^{-1}\sigma \Theta ^*dW(s). \end{aligned}$$

Applying Itô’s formula to $\Xi ^{-1}X^*$, for $t\in [0,T]$ we have

$$\begin{aligned} \begin{aligned} \displaystyle X^*(t)&=\Xi (t)x+\Xi (t)\int _0^t\frac{\varphi ^*(\beta -\sigma ^2\Theta ^*)}{\Xi } ds +\Xi (t)\int _0^t \frac{\sigma \varphi ^*}{\Xi }dW(s). \end{aligned} \end{aligned}$$

(3.34)

By the integrability of $(\Theta ^*,\varphi ^*)$ in (3.30), for any $p>2, p', q'>1, \frac{1}{p'}+\frac{1}{q'}=1$,

$$\begin{aligned} \begin{aligned}&\displaystyle \mathbb {E}\Big |\int _0^T|\varphi ^* ||\beta -\sigma ^2\Theta ^* |ds\Big |^{p}\\&\quad \displaystyle \le \mathbb {E}\left\{ \Big [\int _0^T|\varphi ^* |^2ds\Big ]^{\frac{p}{2}} \Big [\int _0^T|\beta -\sigma ^2\Theta ^* |^2ds\Big ]^{\frac{p}{2}}\right\} \\&\quad \displaystyle \le \left\{ \mathbb {E}\Big [\int _0^T|\varphi ^* |^2ds\Big ]^{\frac{p p'}{2}}\right\} ^{\frac{1}{p'}} \left\{ \mathbb {E}\Big [\int _0^T|\beta -\sigma ^2\Theta ^* |^2ds\Big ]^{\frac{pq'}{ 2}}\right\} ^{\frac{1}{q'}}<\infty . \end{aligned} \end{aligned}$$

(3.35)

We claim that $\Xi (\cdot )=\frac{P_2^*(0)}{P_2^*(\cdot )}$, and thus $\Xi$ is bounded. In fact,

$$\begin{aligned} \begin{aligned} \displaystyle \Xi (t)=\exp \left[ \int _0^t\left( r-\frac{\beta \Lambda _2^*}{\sigma P_2^*}-\frac{|\Lambda _2^*|^2}{2|P_2^*|^2}\right) ds-\int _0^t \frac{\Lambda _2^*}{P_2^*}dW(s)\right] ,\ \ t\in [0,T]. \end{aligned} \end{aligned}$$

By Itô’s formula to $\ln (P_2^*)$, we have

$$\begin{aligned} \begin{aligned} \displaystyle d(\ln P_2^*)=\left( -r+\frac{\beta \Lambda _2^*}{\sigma P_2^*}+\frac{|\Lambda _2^*|^2}{2|P_2^*|^2}\right) ds+\frac{\Lambda _2^*}{P_2^*}dW(s). \end{aligned} \end{aligned}$$

The above expression of $\Xi$ is obvious. Combining this result with (3.34) and (3.35), we conclude that for any $p>2, \mathbb {E}\sup \limits _{t\in [0,T]}|X^*(t)|^p<\infty$. Using again the integrability of $(\Theta ^*,\varphi ^*)$ in (3.30), we have

$$\begin{aligned} \begin{aligned} \displaystyle \mathbb {E}\int _0^T|u^*(s)|^2ds\le \mathbb {E}\Big [\sup _{s\in [0,T]}|X^*(s)|^2\int _0^T|\Theta ^*(s)|^2 ds\Big ]+\mathbb {E}\int _0^T|\varphi ^*(s)|^2ds<\infty . \end{aligned} \end{aligned}$$

Similarly, we have

$$\begin{aligned} \begin{aligned} \displaystyle \mathbb {E}\sup \limits _{t\in [0,T]}|X^{v,\varepsilon }(t)|^p<\infty ,\ \ p>2,\ \ \mathbb {E}\int _0^T|u^{v,\varepsilon }(s)|^2ds<\infty . \end{aligned} \end{aligned}$$

The conclusion is easy to see. $\square$

Remark 3.3

If we introduce $(\widetilde{M},\widetilde{N})$ as

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle d\widetilde{M}=\left( r \widetilde{M}+\frac{\beta }{\sigma }\widetilde{N}\right) ds+ \widetilde{N} dW(s),\ \ s\in [0,T],\\ \displaystyle \widetilde{M}(T)=1, \end{array}\right. \end{aligned}$$

(3.36)

then for (M, N) satisfying (3.31), we have $(M,N)=-\sqrt{2} (\widetilde{M},\widetilde{N})$. If $r(\cdot )$ is deterministic, then $\widetilde{M}(\cdot )$ is the common discount factor. When $r(\cdot )$ is random, for a financial claim with unit terminal payoff, $\widetilde{M}(\cdot )$ and $\sigma ^{-1}(\cdot )\widetilde{N}(\cdot )$ can be considered as the price process and the replicating portfolio, respectively. According to [1], $\widetilde{M}(\cdot )$ is referred to as the risk-adjusted discount factor. From the above proof of Theorem 3.3, we see that $P_2^*=\frac{1}{\widetilde{M}},$ $\Lambda _2^*=-\frac{\widetilde{N}}{|\widetilde{M}|^2},$ $\Theta ^*=\frac{\widetilde{N}}{\widetilde{M} \sigma }.$ In other words, the first component $\Theta ^*(\cdot )$ of the equilibrium operator is explicitly shown by the risk-adjusted discount factor and the replicating portfolio.

Remark 3.4

For the solvability of (3.11)–(3.12), there is no need to impose assumption (H2) which is only used to verify the pointwise integrability of $\Lambda _2^*$. For example, let $r(\cdot ):=f_1(W(\cdot )), \frac{\beta (\cdot )}{\sigma (\cdot )}:=f_2(W(\cdot ))$, where both function $f_i$ and derivative function $f_i'$ are bounded, $i=1,2.$ In this case, (H2) is obvious.

From Theorem 3.3, in order to represent $(\Theta ^*,\varphi ^*)$, we only need $(P_2^*,\Lambda _2^*), (\Phi ,\Psi ), (P_3^*,\Lambda _3^*)$. For notational consistency, in the following we replace these by $({\mathscr {P}}_1^*,{\mathscr {L}}_1^*), ({\mathscr {P}}_2^*,{\mathscr {L}}_2^*), ({\mathscr {P}}_3^*,{\mathscr {L}}_3^*)$, respectively, where

$$\begin{aligned} \left\{ \begin{aligned} \displaystyle d {\mathscr {P}}_1^*&=- \left[ r {\mathscr {P}}_1^* -\frac{{\mathscr {L}}_1^*}{\sigma {\mathscr {P}}_1^*}( \beta {\mathscr {P}}_1^* +\sigma {\mathscr {L}}_1^*) \right] ds+ {\mathscr {L}}_1^* dW(s),\\ \displaystyle d{\mathscr {P}}_2^*&=-\Big [(r-\frac{\beta {\mathscr {L}}_1^*}{\sigma {\mathscr {P}}_1^*}){\mathscr {P}}_2^*-\frac{{\mathscr {L}}_1^*}{{\mathscr {P}}_1^*} {\mathscr {L}}_2^*\Big ]ds+{\mathscr {L}}_2^* dW(s),\\ \displaystyle d{\mathscr {P}}_3^*&= \frac{({\mathscr {P}}_1^* \beta +{\mathscr {L}}_1^*\sigma )(2{\mathscr {P}}_1^*{\mathscr {L}}_3^*\sigma +\beta {\mathscr {P}}_2^*+\sigma {\mathscr {L}}_2^*)}{2\sigma ^2 |{\mathscr {P}}_1^*|^2} ds+{\mathscr {L}}_3^*dW(s),\\ \displaystyle {\mathscr {P}}_1^*(T)&=1, \ \ {\mathscr {P}}_2^*(T)=-\gamma , \ \ {\mathscr {P}}_3^*(T)=0. \end{aligned}\right. \end{aligned}$$

(3.37)

Moreover, the above (3.30) can be rewritten as

$$\begin{aligned} \begin{array}{ll} \displaystyle \ \ \Theta ^*=-\frac{{\mathscr {L}}_1^*}{\sigma {\mathscr {P}}_1^*},\ \ \varphi ^*=-\frac{2{\mathscr {P}}_1^*{\mathscr {L}}_3^*\sigma +\beta {\mathscr {P}}_2^*+\sigma {\mathscr {L}}^*_2}{2\sigma ^2|{\mathscr {P}}_1^*|^2}. \end{array} \end{aligned}$$

(3.38)

The following result is a concise combination of Theorem 3.1 and Theorem 3.3.

Theorem 3.4

Suppose that (H0), (H2) hold. Then there exist $({\mathscr {P}}_i^*,{\mathscr {L}}_i^*), i=1,2,3$, satisfying (3.37). In addition, $(\Theta ^*,\varphi ^*)$ in (3.38) is a closed-loop equilibrium operator, $u^*:=\Theta ^* X^*+\varphi ^*$ is a closed-loop equilibrium investment strategy,

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \sup _{s\in [t,T]}\mathbb {E}_t|\Theta ^*(s)|^2<\infty ,\ \ a.s.\ \ t\in [0,T],\\ \displaystyle \varphi ^* \in L^p_{\mathbb {F}}(\Omega ;L^2(0,T;\mathbb {R})), \ \ p>2. \end{array}\right. \end{aligned}$$

(3.39)

We have the following corollary, which is useful in Sect. 3.3.

Corollary 3.1

Suppose that (H0) and (H2) hold, and the closed-loop equilibrium operator is given in (3.38). Then, for any $t\in [0,T]$, we have

$$\begin{aligned} \begin{aligned}&\displaystyle \mathbb {E}_t\left[ X^*(T)\right] ={\mathscr {P}}_1^*(t) X^*(t)+{\mathscr {P}}_3^*(t),\\&\displaystyle \mathbb {E}_t\left[ X^*(T)-\mathbb {E}_t X^*(T)\right] ^2=\mathbb {E}_t\int _t^T\Big [{\mathscr {P}}_1^*\sigma (\Theta ^* X^*+\varphi ^*)+{\mathscr {L}}_3^*\Big ]^2ds. \end{aligned} \end{aligned}$$

(3.40)

Proof

By Itô’s formula to ${\mathscr {P}}_1^* X^*+{\mathscr {P}}_3^*$, we have

$$\begin{aligned} \begin{aligned} \displaystyle X^*(T)={\mathscr {P}}_1^*(t) X^*(t)+{\mathscr {P}}_3^*(t)-\int _t^T\Big [{\mathscr {P}}_1^*\sigma (\Theta ^* X^*+\varphi ^*)+{\mathscr {L}}_3^*\Big ] dW(s). \end{aligned} \end{aligned}$$

According to Theorem 3.3, we have ${\mathscr {P}}_1^*\in L^{\infty }_{\mathbb {F}}(\Omega ;C([0,T];\mathbb {R})),$ $u^*:=\Theta ^*X^*+\varphi ^* \in L^2_{\mathbb {F}}(0,T;\mathbb {R}).$ Therefore, (3.40) is easy to see. $\square$

3.3 New Phenomena in the Non-Markovian Framework

In this subsection, we present several interesting facts due to the randomness of the coefficients.

If only r is deterministic, then $({\mathscr {L}}_1^*,{\mathscr {L}}_2^*)=(0,0)$, and

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle d {\mathscr {P}}_i^* =- r {\mathscr {P}}_i^* ds,\ \ s\in [0,T],\ \ i:=1,2,\\ \displaystyle d{\mathscr {P}}_3^* = \left( \frac{\beta }{\sigma }{\mathscr {L}}_3^*-\frac{\gamma \beta ^2}{2\sigma ^2 }\right) ds+{\mathscr {L}}_3^*dW(s),\\ \displaystyle {\mathscr {P}}_1^*(T)=1, \ \ {\mathscr {P}}_2^*(T)=-\gamma , \ \ {\mathscr {P}}_3^*(T)=0. \end{array}\right. \end{aligned}$$

In this case, $\Theta ^*=0,$ $\varphi ^*=\left( \frac{\beta \gamma }{2\sigma ^2} -\frac{{\mathscr {L}}_3^*}{\sigma }\right) e^{-\int _{\cdot }^Tr(s)ds}.$ If both $\beta$ and $\sigma$ become deterministic, then ${\mathscr {L}}_3^*=0, \varphi ^*=\frac{\gamma \beta }{2|\sigma |^2}e^{-\int _{\cdot }^T r(s)ds}$, which coincides with that in [12, 13, 16]. In other words, the randomness effect of $\beta , \sigma$ induces the non-zero term ${\mathscr {L}}_3^*$. Notice that ${\mathscr {P}}_1^*(t)=e^{\int _t^Tr(s)ds}$. According to [12, pp.2979] and Corollary 3.1 above, $\mathbb {E}_t X^*(T)-X^*(t){\mathscr {P}}_1^*(t)={\mathscr {P}}_3^*(t)$ represents the expected total gain or loss from the optimal stock investment during time duration [t, T]. This gives the financial interpretation of ${\mathscr {P}}_3^*(\cdot )$. By defining $\frac{d\mathbb {Q}}{d\mathbb {P}}=\exp \big \{-\int _0^T\frac{\beta (s)}{\sigma (s)}dW(s)-\frac{1}{2} \int _0^T \frac{ \beta ^2(s)}{ \sigma ^2(s) }ds\big \}$, we can rewrite ${\mathscr {P}}_3^*(\cdot )$ as ${\mathscr {P}}_3^*(t)=\mathbb {E}^{\mathbb {Q}}_t\int _t^T\frac{\gamma \beta ^2(s)}{2\sigma ^2(s)}ds$. Here, $\mathbb {Q}$ is the risk-neutral measure, which coincides with the hedge-neutral measure in [12].

We present several interesting facts that have not been discussed elsewhere. Recall that $(\Theta ^*,\varphi ^*)$ is the equilibrium operator that does not depend on x, and $u^*:=\Theta ^* X^*+\varphi ^*$ is the equilibrium strategy.

• Fact 1) When r is a deterministic function, $\beta ,$ and $\sigma$ are random, and by Remark 3.3 we have $\Theta ^*=0, u^*=\varphi ^*$. This means that the investment does not depend on the initial wealth. Of course, this does not make sense from the viewpoint of economics. However, if r is random, we have $\Theta ^*\ne 0$, even though $\beta , \sigma$ become deterministic. This means that the feedback dependence of equilibrium strategy on the wealth level comes back, a big advantage of random interest rates.

• Fact 2) For the pre-committed optimal strategy (e.g. [1]), it is common sense that $\Theta ^*$ is used to hedge the risk/uncertainty of the risk premium $\beta$, the volatility $\sigma$, and the interest rate r in the non-Markovian setting. Even when $\beta , \sigma$, and r are deterministic, they still affect the value of $\Theta ^*$. However, for an investor seeking the above equilibrium strategy, he/she will not use $\Theta ^*$ to hedge the uncertainty of $\beta$ and $\sigma$ if r is deterministic. In other words, the interesting roles of b and $\sigma$ become clear only if r is random, which is an essential difference from the pre-committed solution.

• Fact 3) To make the equilibrium strategy depend on initial wealth and become economically meaningful, state-dependent risk aversion is introduced in [13]. However, this obviously changed the original structure of mean-variance portfolio selection problem. Therefore, is it possible to achieve the following two goals simultaneously: keeping the original constant risk aversion mean-variance problem, providing state dependent equilibrium strategies? In our paper we give an affirmative answer to this question.

• Fact 4) Suppose the volatility $\sigma$ is random and the risk premium $\beta =0$. If the interest rate r is deterministic, then $\varphi ^*=0, \Theta ^*=0$, and equilibrium strategy $u^*=0$; while if r is random, then in general $\Theta ^*\ne 0, \varphi ^*\ne 0$, and thus $u^*\ne 0$. These conclusions indicate that the randomness of r is more essential than that of $\sigma$. The financial interpretation is as follows. If the expected rate of return of the stock equals the deterministic interest rate of the bond, then there is no need to put money into the risky asset. However, if the interest rate is random, then the investor should put the proper investment in stock to hedge the risk of the interest rate.

3.4 Comparisons With Open-Loop Equilibrium Strategy

Recall that for the closed-loop equilibrium strategy, we start with the closed-loop equilibrium operator and then continue to construct the equilibrium strategy in a linear manner. As for open-loop equilibrium strategies, it turns out to be the other way around. In the literature ([5,6,7, 9, 10]) the equilibrium strategies are introduced, and then a particular class that is represented as linear feedback system is sought.

In the following, we compare our closed-loop equilibrium strategies with closed-loop representations of open-loop equilibrium strategies. To this end, given $({{\bar{\Theta }}},{{\bar{\varphi }}})$, we define $u^{v,\varepsilon }_1:={{\bar{\Theta }}}{{\bar{X}}}+{{\bar{\varphi }}}+vI_{[t,t+\varepsilon ]},$ ${{\bar{u}}}:={{\bar{\Theta }}}{{\bar{X}}}+{{\bar{\varphi }}},$ where ${{\bar{X}}}$ satisfies (2.1) associated with ${{\bar{u}}}$. A pair of processes $({{\bar{\Theta }}}(\cdot ),{{\bar{\varphi }}}(\cdot ))$ is called an open-loop equilibrium operator if for any $x\in \mathbb {R}$, and any $\varepsilon _n\downarrow 0$, we have ${{\bar{u}}}\in L^2_{\mathbb {F}}(0,T;\mathbb {R})$, and

$$\begin{aligned} \lim _{\overline{\varepsilon _n\rightarrow 0}} {J(u^{v,\varepsilon _n}_1(\cdot );t,{{\bar{X}}}(t))-J \big ({{\bar{u}}}(\cdot );t,{{\bar{X}}}(t)\big ) \over \varepsilon _n}\ge 0. \end{aligned}$$

(3.41)

Here, ${{\bar{u}}}$ is an open-loop equilibrium investment strategy that admits a closed-loop representation, and $({{\bar{\Theta }}},{{\bar{\varphi }}})$ is independent of x. Similar notions are discussed in [17] (also see [5, 6, 9, 10], and [7]).

Remark 3.5

For the above $u^{v,\varepsilon }_1$ and ${{\bar{u}}}$, both of them depend on equilibrium wealth process ${{\bar{X}}}$. However, $u^{v,\varepsilon }$ and $u^*$ in (2.2), depend on two different processes $X^{v,\varepsilon }$ and $X^*$, respectively. This implies that $u^{v,\varepsilon }$ has the true feedback form with respect to the corresponding state process, while $u^{v,\varepsilon }_1$ does not. Moreover, this also indicates that for an open-loop equilibrium operator, one only needs to verify ${{\bar{u}}}\in L^2_{\mathbb {F}}(0,T;\mathbb {R})$, while for our closed-loop equilibrium operator, one has to check that $u^*,\ u^{v,\varepsilon } \in L^2_{\mathbb {F}}(0,T;\mathbb {R})$.

To obtain the explicit forms of the open-loop equilibrium operator, we consider the following system of equations in [0, T]:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle d{{\bar{{{{\mathcal {P}}}}}}}_1=- \Big [ r {{\bar{{{{\mathcal {P}}}}}}}_1-({{\bar{{{{\mathcal {P}}}}}}}_1\beta +{{\bar{{{{\mathcal {L}}}}}}}_1\sigma )\frac{{{\bar{{{{\mathcal {L}}}}}}}_1}{\sigma {{\bar{{{{\mathcal {P}}}}}}}_1}\Big ]ds+ {{\bar{{{{\mathcal {L}}}}}}}_1dW(s),\\ \displaystyle d{{\bar{{{{\mathcal {P}}}}}}}_2=-r{{\bar{{{{\mathcal {P}}}}}}}_2 ds+{{\bar{{{{\mathcal {L}}}}}}}_2 dW(s),\\ \displaystyle d {{\bar{{{{\mathcal {P}}}}}}}_3 =-\Big [\left( r-\frac{\beta {{\bar{{{{\mathcal {L}}}}}}}_2}{\sigma {{\bar{{{{\mathcal {P}}}}}}}_2}\right) {{\bar{{{{\mathcal {P}}}}}}}_3-\frac{{{\bar{{{{\mathcal {L}}}}}}}_2}{{{\bar{{{{\mathcal {P}}}}}}}_2}{{\bar{{{{\mathcal {L}}}}}}}_3\Big ] ds+{{\bar{{{{\mathcal {L}}}}}}}_3dW(s),\\ \displaystyle d{{\bar{{{{\mathcal {P}}}}}}}_4=- \big ({{\bar{{{{\mathcal {P}}}}}}}_1\beta +{{\bar{{{{\mathcal {L}}}}}}}_1\sigma \big )\left( \frac{\beta {{\bar{{{{\mathcal {P}}}}}}}_3+\sigma {{\bar{{{{\mathcal {L}}}}}}}_3}{\sigma ^2{{\bar{{{{\mathcal {P}}}}}}}_2{{\bar{{{{\mathcal {P}}}}}}}_1}-\frac{{{\bar{{{{\mathcal {L}}}}}}}_4}{\sigma {{\bar{{{{\mathcal {P}}}}}}}_1}\right) ds+{{\bar{{{{\mathcal {L}}}}}}}_4dW(s),\\ \displaystyle {{\bar{{{{\mathcal {P}}}}}}}_1(T)=1,\ \ {{\bar{{{{\mathcal {P}}}}}}}_2(T)=-2, \ \ {{\bar{{{{\mathcal {P}}}}}}}_3(T)=-\gamma , \ \ {{\bar{{{{\mathcal {P}}}}}}}_4(T)=0.\ \ \end{array}\right. \end{aligned}$$

(3.42)

The above system (3.42) is derived by the following BSDE with parameter t:

$$\begin{aligned} \begin{aligned} \displaystyle \widehat{Y}(\tau ,t)&=2\widehat{X}(T)- 2\mathbb {E}_t\widehat{X}(T)-\gamma +\int _\tau ^T r(s)\widehat{Y}(s,t) ds\\&\quad -\int _\tau ^T \widehat{Z}(s,t)dW(s),\ \ \tau \in [t,T]. \end{aligned} \end{aligned}$$

(3.43)

It is the analogue version of our BSDE (3.3) in the open-loop case with simpler form. By [7], we see that (3.42) is solvable, from which we define

$$\begin{aligned} \begin{aligned} \displaystyle {{\bar{\Theta }}}:=-\frac{{{\bar{{{{\mathcal {L}}}}}}}_1}{\sigma {{\bar{{{{\mathcal {P}}}}}}}_1},\ \ \ {{\bar{\varphi }}}:=\frac{\beta {{\bar{{{{\mathcal {P}}}}}}}_3+\sigma {{\bar{{{{\mathcal {L}}}}}}}_3}{\sigma ^2 {{\bar{{{{\mathcal {P}}}}}}}_2{{\bar{{{{\mathcal {P}}}}}}}_1}-\frac{{{\bar{{{{\mathcal {L}}}}}}}_4}{\sigma {{\bar{{{{\mathcal {P}}}}}}}_1}.\ \ \end{aligned} \end{aligned}$$

(3.44)

For $\nu ,s\in [0,T]$, suppose that the Malliavin derivative $D_\nu r(s)$ exists and $\big |D_\nu r(s)\big |\le K$. Using [7, Proposition 3.9], ${{\bar{u}}}:={{\bar{\Theta }}} {{\bar{X}}}+{{\bar{\varphi }}}$ is an open-loop equilibrium strategy, $({{\bar{\Theta }}},{{\bar{\varphi }}})$ is an open-loop equilibrium operator in sense of (3.41).

If r is deterministic, then ${{\bar{{{{\mathcal {L}}}}}}}_i=0,$ $i=1,2,3$, and

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle d{{\bar{{{{\mathcal {P}}}}}}}_i=- r {{\bar{{{{\mathcal {P}}}}}}}_i ds, \ \ i:=1,2,3,\\ \displaystyle d{{\bar{{{{\mathcal {P}}}}}}}_4=\left( \frac{\beta }{\sigma }{{\bar{{{{\mathcal {L}}}}}}}_4-\frac{\beta ^2\gamma }{2\sigma ^2}\right) ds+{{\bar{{{{\mathcal {L}}}}}}}_4dW(s),\\ \displaystyle {{\bar{{{{\mathcal {P}}}}}}}_1(T)=1,\ \ {{\bar{{{{\mathcal {P}}}}}}}_2(T)=-2, \ \ {{\bar{{{{\mathcal {P}}}}}}}_3(T)=-\gamma , \ \ {{\bar{{{{\mathcal {P}}}}}}}_4(T)=0. \end{array}\right. \end{aligned}$$

In this case, ${{\bar{\Theta }}}=0,\ {{\bar{\varphi }}}=\left( \frac{\beta \gamma }{2\sigma ^2}-\frac{{{\bar{{{{\mathcal {L}}}}}}}_4}{\sigma {{\bar{{{{\mathcal {P}}}}}}}_1}\right) e^{-\int _{\cdot }^Tr(s)ds}.$

The following conclusions are pointed out for the first time in the literature.

• Fact 5) If the interest rate r is random, system (3.42) includes four BSDEs, while system (3.37) only contains three BSDEs. Because the expression of $\varphi ^*$ in (3.38) is different from ${{\bar{\varphi }}}$ in (3.44), in general, the resulting closed-loop equilibrium strategy $\Theta ^* X^*+\varphi ^*$ is not equal to the open-loop equilibrium strategy ${{\bar{\Theta }}}{{\bar{X}}}+{{\bar{\varphi }}}$.

• Fact 6) If we look carefully at $\Theta ^*$ in (3.38) and ${{\bar{\Theta }}}$ in (3.44), we find that they are equal, even when $(r,\beta ,\sigma )$ are random. In other words, both closed-loop equilibrium strategies and open-loop equilibrium strategies have the same feedback coefficient on the equilibrium wealth process, and thus initial wealth. Similarly, one can also obtain the same dependence between closed-loop equilibrium wealth process and open-loop equilibrium wealth process on the initial wealth.

• Fact 7) If r is deterministic, we have further equality between $\varphi ^*$ and ${{\bar{\varphi }}}$, even when $(\beta ,\sigma )$ are random. This means that the mean-variance portfolio selection problem admits a pair of closed-loop and open-loop equilibrium strategies that coincide.

• Fact 8) The above two equality conclusions indicate the distinctive role of constant risk aversion, since they do not occur in the same framework with state-dependent risk aversion ([5]).

3.5 Mean-Variance Problem With Vasiček’s Stochastic Interest Rate

In this subsection, we look at an interesting case when the bounded assumption of stochastic interest rate $r(\cdot )$ in (H0) is not fulfilled. We will show that the previous approach still works and the existence of closed-loop equilibrium strategy can be obtained as well. Moreover, the investigation also closely relates to the numerical study in Sect. 4.

Suppose $b(\cdot )$ and $\sigma (\cdot )$ are deterministic functions, while the interest rate $r(\cdot )$ is described by the Vasiček model as

$$\begin{aligned} \left\{ \begin{aligned} \displaystyle d r(s)&=\big (\zeta -\xi r(s)\big )ds+\rho dW(s),\ \ \ s\in [0,T],\\ \displaystyle r(0)&=r_0, \end{aligned}\right. \end{aligned}$$

(3.45)

where $\zeta , \xi >0, \rho \in \mathbb {R}$. For any $p\ge 0$, by e.g., [7, Lemma 4.1], $\mathbb {E}\left[ \sup \limits _{t\in [0,T]}e^{p|r(t)|}\right] <\infty$.

For $t\in [0,T]$, we define $g(t):=\frac{1}{\xi }\left[ 1-e^{-\xi (T-t)}\right]$, and

$$\begin{aligned} \left\{ \begin{aligned} \displaystyle G_1(t)&=\exp \left\{ \int _t^T g(s)\left[ \zeta -\frac{\beta (s)}{\sigma (s)}\rho -\frac{1}{2} g(s)\rho ^2\right] ds\right\} ,\\ \displaystyle G_2(t)&=\int _t^T \frac{\gamma (\beta (s)+\rho \sigma (s) g(s))^2}{2\sigma ^2(s)}ds. \end{aligned}\right. \end{aligned}$$

For $t\in [0,T],$ it is easy to check that $({\mathscr {P}}_3^*(t),{\mathscr {L}}_3^*(t)):=(G_2(t),0),$

$$\begin{aligned} \begin{aligned} \displaystyle ({\mathscr {P}}_1^*(t),{\mathscr {L}}_1^*(t))&:=(G_1(t)e^{g(t)r(t)},\rho g(t)G_1(t)e^{g(t)r(t)}),\ \ \\ \displaystyle ({\mathscr {P}}_2^*(t),{\mathscr {L}}_2^*(t))&:=(-\gamma G_1(t)e^{g(t)r(t)},\gamma \rho g(t)G_1(t)e^{g(t)r(t)}) \end{aligned} \end{aligned}$$

satisfy the BSDE system (3.37). Based on these $({\mathscr {P}}_i^*,{\mathscr {L}}_i^*)$, we know that

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \big ( P_2^*,\Lambda _2^*\big ):=\big ({\mathscr {P}}_1^*,{\mathscr {L}}_1^*\big ),\ \ \big (P_3^*,\Lambda _3^*\big ):=\big ({\mathscr {P}}_3^*,{\mathscr {L}}_3^*\big ),\ \\ \displaystyle \big (P_4^*,\Lambda _4^*\big ):=\big (2{\mathscr {P}}_1^*{\mathscr {P}}_3^*+{\mathscr {P}}_2^*, {\mathscr {L}}_2^*+2{\mathscr {L}}_1^* {\mathscr {P}}_3^*+2{\mathscr {L}}_3^*{\mathscr {P}}_1^*\big ), \\ \displaystyle \big ( P_1^*,\Lambda _1^*\big ):=(2|{\mathscr {P}}_1^*|^2,4{\mathscr {P}}_1^*{\mathscr {L}}_1^*), \end{array}\right. \end{aligned}$$

(3.46)

is furthermore a solution to (3.9) with

$$\begin{aligned} \begin{aligned} \displaystyle \Theta ^*(t):=-\frac{\rho g(t)}{\sigma (t)},\ \ \varphi ^*(t)=\gamma \frac{\beta (t)+\sigma (t)\rho g(t)}{2\sigma ^2(t)G_1(t)}e^{-g(t)r(t)}. \end{aligned} \end{aligned}$$

(3.47)

Here $P_3^*(\cdot )\in C([0,T];\mathbb {R}), (P_i^*(\cdot ),\Lambda _i^*(\cdot ))\in L^p_{\mathbb {F}}(\Omega ;C([0,T];\mathbb {R}^2)), i=1,2,4.$ By the explicit form of $\Lambda ^*_2$ in (3.46), the above (H2) is not needed anymore.

We observe that the stochastic interest rate $r(\cdot )$ given by (3.45) violates the boundedness assumption given in (H0). As a result, we need to check the previous arguments point by point. Notice that $\Theta ^*(\cdot )$ is bounded, and for any $p>1, \varphi ^*(\cdot )\in L^p_{\mathbb {F}}(0,T;\mathbb {R})$ ([7, Lemma 4.1]). It is direct calculation that (H1) is satisfied with the above $(\Theta ^*(\cdot ),\varphi ^*(\cdot ))$, where $X^*(\cdot ) \in L^p_{\mathbb {F}}(\Omega ;C([0,T];\mathbb {R})),$ $\forall p>1,$ $u^*(\cdot ):=\Theta ^*(\cdot ) X^*(\cdot )+\varphi ^*(\cdot )\in L^p_{\mathbb {F}}(0,T;\mathbb {R}).$ For any $p>1$, one has $X_1^{v,\varepsilon }(\cdot )\in L^p_{\mathbb {F}}(\Omega ;C([0,T];\mathbb {R})), (Y^*(\cdot ,t),Z^*(\cdot ,t)) \in L^{p}_{\mathbb {F}}(\Omega ;C([t,T];\mathbb {R}))\times L^{p}_{\mathbb {F}}(\Omega ;L^2(t,T;\mathbb {R})).$ Even though $(P_1^*(\cdot ),P_2^*(\cdot ),P_3^*(\cdot ))$ do not have the boundedness as in (3.13), the above Theorem 3.1 is still valid. To sum up the above arguments, we present the following conclusion.

Lemma 3.2

Suppose (H0) holds with bounded assumption of $r(\cdot )$ replaced by (3.45), and $(\Theta ^*,\varphi ^* )$ is defined in (3.47). Then $u^* :=\Theta ^* X^* +\varphi ^*$ is the a closed-loop equilibrium strategy.

Remark 3.6

There are references on closed-loop equilibrium strategies for mean-variance problems under stochastic interest rate model. In [12, Subsection 3.3], the mean-variance criterion is explored over terminal wealth in units of bond price, and thus the equilibrium strategy is independent of wealth. However, the strategy given by Lemma 3.2 is a linear feedback of wealth. In this respect, our result is in line with [26], which considers a mean-variance reinsurance and investment problem under stochastic interest rate and inflation risk. But the two results do not include each other since the formualtion of financial markets considered in both papers is different.

4 Some Numerical Study via Deep Learning Method

This section devotes to explaining the interesting facts in the Sects. 3.3 and 3.4 in the numerical way. More precisely, we numerically solve the backward stochastic Riccati systems (3.37), (3.42), that characterize the closed-loop and open-loop equilibrium strategies, respectively, and use the deep neural network as function approximator ( [27]) for these two equilibrium strategies. The time interval from 0 to T is discretized into 20 time steps. At each time step, we approximate the solution ${\mathscr {L}}_i^*, {{\bar{{{{\mathcal {L}}}}}}}_j, i=1,2,3, j=1,2,3,4$ of the Riccati system by a residual network (ResNet) [28] of 6 layers with 2048 hidden units for each layer. Each neural network takes the Brownian path history as input, and outputs ${\mathscr {L}}^*= ({\mathscr {L}}^*_i)_{i \in \{1, 2, 3\}}$ in case of closed-loop strategy, and ${{\bar{{{{\mathcal {L}}}}}}}= ({{\bar{{{{\mathcal {L}}}}}}}_j)_{j \in \{1, 2, 3, 4\}}$ in case of open-loop strategy. The initial value of P(0) is treated as a learnable variable in the optimization scheme to minimize the empirical $L^2$ loss between the simulated and the target terminal condition for the Riccati system.

In the following, let the interest rate $r(\cdot )$ be described by the following Ornstein-Uhlenbeck (OU) process,

$$\begin{aligned} \left\{ \begin{aligned} \displaystyle dr(t)&= - \kappa (r(t) - {\bar{r}}) dt + \sigma dW(t),\ \ t\in [0,T]\\ \displaystyle r(0)&=r_0. \end{aligned}\right. \end{aligned}$$

(4.1)

Apparently, it is special case of (3.45) with ${{\bar{r}}}=\frac{\zeta }{\xi }, \kappa =\xi ,$ $\sigma =\rho$. We compute the closed-loop equilibrium operator and open-loop equilibrium operator, denoted by $(\Theta _c,\varphi _c)$ and $(\Theta _o,\varphi _o)$, respectively, and then represent the corresponding equilibrium strategies as $u_c= \Theta _c X_c + \varphi _c , u_o= \Theta _o X_o + \varphi _o$, where $X_c, X_o$ are the closed-loop, open-loop equilibrium wealth, respectively. In the following, let $b=0.09, \sigma = 0.2, \gamma = 0.5$ with $b, \sigma$ being the expected return, volatility of the risky asset, and the investor’s risk aversion, respectively. The investment horizon is supposed to be $T = 0.5$ year.

Figure 1 shows three sample paths of closed-loop, open-loop equilibrium (investment) strategy when the initial wealth is supposed to be 1, and the interest rate is random, deterministic, respectively. From the figures, we find that with random $r(\cdot )$, these two equilibrium strategy are different from each other, while with deterministic interest rate, they coincide with each other. This point was mentioned in the Fact 5), Fact 7) of Sect. 3.4.

Fig. 1

Simulated sample paths of two equilibrium strategies with random interest rate, deterministic interest rate, respectively. OL and CL stands for open-loop and closed-loop equilibrium strategy, respectively. Black dashed lines, blue dashed lines show the case of closed-loop, open-loop equilibrium strategy with random $r(\cdot )$, respectively. Here the interest rate is described by the OU process (4.1) with $\kappa = 8 , \sigma _r = 0.05$ and ${\bar{r}} = 0.03$, and initial condition $r(0) = 0.03$. The red dashed lines show the benchmark case for these two equilibrium strategies with deterministic interest rate $r(\cdot ) = 0.03$  (Color figure online)

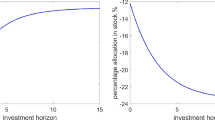
Figure 2 exhibits the hypothetical closed-loop equilibrium strategies. In the left panel, the interest rate is constant, in which case $\Theta _c = 0$ and the strategy $u_c$ is independent of wealth. This is consistent with Fact 1) in Sect. 3.3. We also find that the investment strategy is increasing in time, which is consistent with the above conclusion (3.47) with $\rho =0, \beta , \sigma$ being positive constants. Right panel exhibits the strategy $u(t,\omega )= \Theta (t,\omega ) x + \varphi (t,\omega )$ for a random Brownian sample $\omega$ with $x \in [0, 10]$ at time $t = 0.1, 0.2, 0.3$ and 0.4, respectively. These figures indicates that the closed-loop equilibrium strategy is a linear function of the equilibrium wealth with slopes $\Theta (\cdot )$ and intercepts $\varphi (\cdot )$. Moreover, the slopes do not reduce to zero, and both slopes and intercepts depend on time variable. These conclusions are consistent with Fact 1) in Sect. 3.3. Even though the risk aversion $\gamma =0.5$, the equilibrium strategy still depends on the wealth process or initial wealth. Such conclusion was pointed out in Fact 3) of Sect. 3.3.

Fig. 2

Closed-loop equilibrium strategy as a linear function of current wealth $X(\cdot )$ at four different times. The left panel shows the case of deterministic $r(\cdot ) = 0.03$, while the right panel represents the case when $r(\cdot )$ is described by OU process with $\kappa = 8 , \sigma = 0.05 , {\bar{r}} = 0.03$, and the initial condition $r(0) = 0.03$

Figure 3 describes the sample paths of equilibrium investment strategies and the corresponding wealth processes under closed-loop and open-loop framework respectively. The rightmost figure at the top (resp. bottom) row, numerically demonstrate the result that at any given time t, the difference of equilibrium wealth processes (resp. the two equilibrium strategies) does not depend on the initial wealth. It is shown by the figures that they are almost the same among initial wealth level 1, 10 and 20 for two simulations of Brownian sample paths. Recall that both the wealth processes and equilibrium strategies are linear functions of initial wealth $X_0$, these two independence of the difference on the initial wealth indicates that the closed-loop, and open-loop equilibrium strategy/wealth processes have the same dependence on initial wealth. These conclusions are consistent with Fact 6) of Sect. 3.4.

Fig. 3

Sample paths of equilibrium strategies and the corresponding wealth process on the top and bottom row, respectively. The interest rate follows OU process with the same parameter as Figure 1. Initial wealth $X_0$ is supposed to be 1, 10, 20 for the first, second and third figure from the left. In the top row, the red lines, and the blue lines show the equilibrium wealth processes generated from Brownian sample 1, Brownian sample 2, respectively. Dashed line represents the sample path for the closed-loop equilibrium strategy, while the dotted line shows the analogue case for the open-loop equilibrium strategy. The fourth figure on the right shows the differences of the two equilibrium wealth processes for both Brownian samples. In the bottome row, the red lines, the blue lines, the dashed line, the dotted line has the similar meanings associated with equilibrium strategies (Color figure online)

In the above, the decoupled structure of the Riccati system facilitates the numerical solution by the deep neural network. Next, we investigate the distribution of terminal wealth of two equilibrium strategies with different levels of initial wealth by numerical simulation. We choose to focus on the terminal wealth because it closely relates to the mean-variance criterion corresponding to the equilibrium strategies. Figure 4 shows the distribution of terminal wealth X(T) by simulation. Let the initial wealth level vary from 1, 10, 20 and 100 as shown from the left to right panel on each row. For each level of initial wealth, we generate 2048 Brownian paths and compute the terminal wealth under the closed-loop case (top row) and the open-loop case (bottom row) respectively. The red vertical line in each figure shows the average of simulated terminal wealth in each sub-figures. By the previous theoretical discussion, the difference of equilibrium terminal wealths $X_c(T)-X_o(T)$ is independent of the initial wealth X(0), even when the interest rate is random. Therefore, the ratio $\frac{X_c(T)-X_o(T)}{X(0)}$ shrinks to zero as X(0) increases. This phenomenon can be demonstrated from Fig. 4. Comparing the top and bottom rows, we can see both the mean of the terminal wealth and the distributions become indifferent of the control type (i.e., open-loop or closed-loop) as the initial wealth level increases.

Fig. 4

Distribution of the terminal wealth associated with equilibrium strategies. The top row, the bottom row, shows distribution for the closed-loop equilibrium strategy, open-loop equilibrium strategy, respectively. On each row, the initial wealth level is supposed to be 1, 10, 20 and 100 from the left to right

5 Concluding Remark

In this study, we discussed the dynamic mean-variance portfolio selection problem with random coefficients, and a class of systems of backward stochastic Riccati equations was introduced and discussed for the first time. As a result of the non-Markovian setting, several interesting phenomena, which are absent in existing literature with deterministic coefficients, have been shown here for the first time. Without further essential difficulties, our investigation also works when investment strategies, as well as Brownian motion, are multidimensional. The uniqueness of closed-loop equilibrium strategies is left for future research.