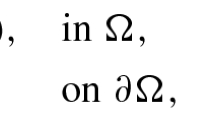A Double Phase Problem Involving Hardy Potentials

Abstract

In this paper, we deal with the following double phase problem

$$\begin{aligned} \left\{ \begin{array}{lll} -\text{ div }\left( |\nabla u|^{p-2}\nabla u+a(x)|\nabla u|^{q-2}\nabla u\right) =&{} \gamma \left( \displaystyle \frac{|u|^{p-2}u}{|x|^p}+a(x)\displaystyle \frac{|u|^{q-2}u}{|x|^q}\right) \\ &{}+f(x,u) &{} \text{ in } \Omega ,\\ u=0&{} &{} \text{ in } \partial \Omega , \end{array} \right. \end{aligned}$$

where $\Omega \subset {\mathbb {R}}^N$ is an open, bounded set with Lipschitz boundary, $0\in \Omega$, $N\ge 2$, $1<p<q<N$, weight $a(\cdot )\ge 0$, $\gamma$ is a real parameter and f is a subcritical function. By variational method, we provide the existence of a non-trivial weak solution on the Musielak-Orlicz-Sobolev space $W^{1,{\mathcal {H}}}_0(\Omega )$, with modular function ${\mathcal {H}}(t,x)=t^p+a(x)t^q$. For this, we first introduce the Hardy inequalities for space $W^{1,{\mathcal {H}}}_0(\Omega )$, under suitable assumptions on $a(\cdot )$.

1 Introduction

In the present paper, we study the following problem

$$\begin{aligned} \left\{ \begin{array}{lll} -\text{ div }\left( |\nabla u|^{p-2}\nabla u+a(x)|\nabla u|^{q-2}\nabla u\right) = &{}\gamma \left( \displaystyle \frac{|u|^{p-2}u}{|x|^p}+a(x)\displaystyle \frac{|u|^{q-2}u}{|x|^q}\right) \\ &{}+f(x,u) &{} \text{ in } \Omega ,\\ u=0&{} &{} \text{ in } \partial \Omega , \end{array} \right. \end{aligned}$$

(1.1)

where $\Omega \subset {\mathbb {R}}^N$ is an open, bounded set with Lipschitz boundary, $0\in \Omega$, $N\ge 2$, $\gamma$ is a real parameter, $1<p<q<N$ and

$$\begin{aligned} \frac{q}{p}<1+\frac{1}{N},\quad a:{\overline{\Omega }}\rightarrow [0,\infty ){ \text{ is } \text{ Lipschitz } \text{ continuous. }} \end{aligned}$$

(1.2)

Here, we assume that $f:\Omega \times {\mathbb {R}}\rightarrow {\mathbb {R}}$ is a Carathéodory function verifying

$(f_1)$:

there exists an exponent $r\in (q,p^*)$, with the critical Sobolev exponent $p^*=Np/(N-p)$, such that for any $\varepsilon >0$ there exists $\delta _\varepsilon =\delta (\varepsilon )>0$ and

$$\begin{aligned} |f(x,t)|\le q\varepsilon \left| t\right| ^{q-1} +r\delta _\varepsilon \left| t\right| ^{r-1} \end{aligned}$$

holds for a.e. $x\in \Omega$ and any $t\in {\mathbb {R}}$;

$(f_2)$:

there exist $\theta \in (q,p^*)$, $c>0$ and $t_0\ge 0$ such that

$$\begin{aligned} c\le \theta F(x,t)\le tf(x,t) \end{aligned}$$

for a.e. $x\in \Omega$ and any $|t|\ge t_0$, where $F(x,t)=\displaystyle \int ^{t}_{0}f(x,\tau )d\tau$.

The existence of r in $(f_1)$ is assured by (1.2) and $q>1$, which yield $N(q-p)<p<qp$ so that $q<p^*$. The function $f(x,t)=\phi (x)\left( \theta t^{\theta -1}+r t^{r-1}\right)$, with $\phi \in L^\infty (\Omega )$ and $\phi >0$ a.e. in $\Omega$, verifies all assumptions $(f_1)-(f_2)$.

Problem (1.1) is driven by the so-called double phase operator, which switches between two different types of elliptic rates, according to the modulating function $a(\cdot )$. The functionals with double phase were introduced by Zhikov in [29,30,31,32] in order to describe models for strongly anisotropic materials and provide examples of Lavrentiev’s phenomenon. Other physical applications can be found for instance on transonic flow [2], quantum physics [4] and reaction diffusion systems [8]. Also, (1.1) falls into the class of problems driven by operators with non-standard growth conditions, according to Marcellini’s definition given in [18, 19]. Following this direction, Mingione et al. prove different regularity results for minimizers of double phase functionals in [3, 10, 11]. See also [7, 25] for regularity results in more generalized situations. In [9], Colasuonno and Squassina analyze the eigenvalue problem with Dirichlet boundary condition of the double phase operator. In particular, in [9, Sect. 2] they provide the basic tools to solve variational problems like (1.1), introducing the standard condition (1.2). Recently, Mizuta and Shimomura study Hardy–Sobolev inequalities in the unit ball for double phase functionals in [20]. Concerning nonlinear problems driven by the double phase operator, we refer to [13, 16, 17, 22, 24] where existence and multiplicity results are provided via variational techniques. While, in [15, 27, 28] the double phase operator interacts with a convection term depending on the gradient of the solution, causing a non-variational characterization of the problem.

Inspired by the above papers, we provide an existence result for (1.1) by variational method. The main novelty, as well as the main difficulty, of problem (1.1) is the presence of a double phase Hardy potential. Indeed, such term is responsible of the lack of compactness of the Euler-Lagrange functional related to (1.1). In order to handle the double phase potential in (1.1), our weight function $a:{\overline{\Omega }}\rightarrow [0,\infty )$ satisfies

(a):

$a(\lambda x)\le a(x)$ for any $\lambda \in (0,1]$ and any $x\in {\overline{\Omega }}$.

A simple example of Lipschitz continuous function verifying (a) is given by $a(x)=|x|$. Also, we control parameter $\gamma$ with the Hardy constants

$$\begin{aligned} H_m:=\left( \frac{m}{N-m}\right) ^{-m}, \end{aligned}$$

(1.3)

when $m=p$ and $m=q$. Thus, we are ready to introduce the main result of the paper.

Theorem 1.1

Let $\Omega \subset {\mathbb {R}}^N$ be an open, bounded set with Lipschitz boundary, $0\in \Omega$ and $N\ge 2$. Let $1<p<q<N$ and $a(\cdot )$ satisfy (1.2) and (a). Let $(f_1)-(f_2)$ hold true. Then, for any $\gamma \in (-\infty ,\min \{H_p,H_q\})$ problem (1.1) admits a non-trivial weak solution.

The proof of Theorem 1.1 is based on the application of the classical mountain pass theorem, see for example [23]. Also, Theorem 1.1 generalizes [17, Theorem 1.3], where the authors consider problem (1.1) with $\gamma =0$. However, our situation with $\gamma \ne 0$ is much more delicate than [17], because of the lack of compactness, as well explained in Remark 3.1.

The paper is organized as follows. In Sect. 2, we introduce the basic properties of the Musielak–Orlicz and Musielak–Orlicz–Sobolev spaces, including also the new Hardy inequalities, and we set the variational structure of problem (1.1). In Sect. 3, we prove Theorem 1.1.

2 Preliminaries

The function ${\mathcal {H}}:\Omega \times [0,\infty )\rightarrow [0,\infty )$ defined as

$$\begin{aligned} {\mathcal {H}}(x,t):=t^p+a(x)t^q,\quad \text{ for } \text{ a.e. } x\in \Omega \text{ and } \text{ for } \text{ any } t\in [0,\infty ), \end{aligned}$$

with $1<p<q$ and $0\le a(\cdot )\in L^1(\Omega )$, is a generalized N-function (N stands for nice), according to the definition in [12, 21], and satisfies the so called $(\Delta _2)$ condition, that is

$$\begin{aligned} {\mathcal {H}}(x,2t)\le t^q{\mathcal {H}}(x,t),\quad \text{ for } \text{ a.e. } x\in \Omega \text{ and } \text{ for } \text{ any } t\in [0,\infty ). \end{aligned}$$

Therefore, by [21] we can define the Musielak–Orlicz space $L^{{\mathcal {H}}}(\Omega )$ as

$$\begin{aligned} L^{{\mathcal {H}}}(\Omega ):=\left\{ u:\Omega \rightarrow {\mathbb {R}} \text{ measurable }:\,\,\varrho _{{\mathcal {H}}}(u)<\infty \right\} , \end{aligned}$$

endowed with the Luxemburg norm

$$\begin{aligned} \Vert u\Vert _{{\mathcal {H}}}:=\inf \left\{ \lambda >0:\,\,\varrho _{{\mathcal {H}}}\left( \frac{u}{\lambda }\right) \le 1\right\} , \end{aligned}$$

where $\varrho _{{\mathcal {H}}}$ denotes the ${\mathcal {H}}$-modular function, set as

$$\begin{aligned} \varrho _{{\mathcal {H}}}(u):=\int _\Omega {\mathcal {H}}(x,|u|)dx=\int _\Omega \left( |u|^p+a(x)|u|^q\right) dx. \end{aligned}$$

(2.1)

By [9, 12], the space $L^{{\mathcal {H}}}(\Omega )$ is a separable, uniformly convex, Banach space. While, by [17, Proposition 2.1] we have the following relation between the norm $\Vert \cdot \Vert _{{\mathcal {H}}}$ and the ${\mathcal {H}}$-modular.

Proposition 2.1

Assume that $u\in L^{{\mathcal {H}}}(\Omega )$, $\{u_j\}_j\subset L^{{\mathcal {H}}}(\Omega )$ and $c>0$. Then

(i):

for $u\ne 0$, $\Vert u\Vert _{{\mathcal {H}}}=c\Leftrightarrow \varrho _{{\mathcal {H}}}\left( \frac{u}{c}\right) =1$;

(ii):

$\Vert u\Vert _{{\mathcal {H}}}<1$ $(resp.=1,\,>1)$ $\Leftrightarrow \varrho _{{\mathcal {H}}}(u)<1$ $(resp.=1,\,>1)$;

(iii):

$\Vert u\Vert _{{\mathcal {H}}}<1\Rightarrow \Vert u\Vert _{{\mathcal {H}}}^q\le \varrho _{{\mathcal {H}}}(u)\le \Vert u\Vert _{{\mathcal {H}}}^p$;

(iv):

$\Vert u\Vert _{{\mathcal {H}}}>1\Rightarrow \Vert u\Vert _{{\mathcal {H}}}^p\le \varrho _{{\mathcal {H}}}(u)\le \Vert u\Vert _{{\mathcal {H}}}^q$;

(v):

$\displaystyle \lim _{j\rightarrow \infty }\Vert u_j\Vert _{\mathcal H}=0\,(\infty )\Leftrightarrow \lim \limits _{j\rightarrow \infty }\varrho _{{\mathcal {H}}}(u_j)=0\,(\infty )$.

The related Sobolev space $W^{1,{\mathcal {H}}}(\Omega )$ is defined by

$$\begin{aligned} W^{1,{\mathcal {H}}}(\Omega ):=\left\{ u\in L^{{\mathcal {H}}}(\Omega ):\,\,|\nabla u|\in L^{{\mathcal {H}}}(\Omega )\right\} , \end{aligned}$$

endowed with the norm

$$\begin{aligned} \Vert u\Vert _{1,{\mathcal {H}}}:=\Vert u\Vert _{{\mathcal {H}}}+\Vert \nabla u\Vert _{{\mathcal {H}}}, \end{aligned}$$

(2.2)

where we write $\Vert \nabla u\Vert _{{\mathcal {H}}}=\Vert |\nabla u|\Vert _{{\mathcal {H}}}$ to simplify the notation. We denote by $W^{1,{\mathcal {H}}}_0(\Omega )$ the completion of $C^\infty _0(\Omega )$ in $W^{1,{\mathcal {H}}}(\Omega )$ which can be endowed with the norm

$$\begin{aligned} \Vert u\Vert :=\Vert \nabla u\Vert _{{\mathcal {H}}}, \end{aligned}$$

equivalent to the norm set in (2.2), thanks to [9, Proposition 2.18(iv)] whenever (1.2) holds true.

For any $m\in [1,\infty )$ we indicate with $L^m(\Omega )$ the usual Lebesgue space equipped with the norm $\Vert \cdot \Vert _m$. Then, by [9, Proposition 2.15(ii)-(iii)] we have the following embeddings.

Proposition 2.2

Let (1.2) holds true. For any $m\in [1,p^*]$ there exists $C_m=C(N,p,q,m,\Omega )>0$ such that

$$\begin{aligned}\Vert u\Vert _m^m\le C_m\Vert u\Vert ^m \end{aligned}$$

for any $u\in W^{1,{\mathcal {H}}}_0(\Omega )$. Moreover, the embedding $W^{1,{\mathcal {H}}}_0(\Omega )\hookrightarrow L^m(\Omega )$ is compact for any $m\in [1,p^*)$.

We denote by $L^q_a(\Omega )$ the weighted space of all measurable functions $u:\Omega \rightarrow {\mathbb {R}}$ with the seminorm

$$\begin{aligned} \Vert u\Vert _{q,a}:=\left( \int _\Omega a(x)|u|^q dx\right) ^{1/q}<\infty . \end{aligned}$$

Using this further notation, in the next result we provide the Hardy inequalities for space $W^{1,{\mathcal {H}}}_0(\Omega )$. The proof of the lemma is inspired by [14, Lemma 2.1].

Lemma 2.1

Let (1.2) and (a) hold true. Then, for any $u\in W^{1,{\mathcal {H}}}_0(\Omega )$ we have

$$\begin{aligned} \begin{aligned}&H_p\Vert u\Vert _{H_p}^p\le \Vert \nabla u\Vert _p^p, \qquad \quad \text{ with } \,\,\Vert u\Vert _{H_p}:=\int _\Omega \frac{|u|^p}{|x|^p}dx\\&H_q\Vert u\Vert _{H_{q,a}}^q\le \Vert \nabla u\Vert _{q,a}^q, \quad \text{ with } \,\,\Vert u\Vert _{H_{q,a}}:=\int _\Omega a(x)\frac{|u|^q}{|x|^q}dx, \end{aligned} \end{aligned}$$

where $H_p$ and $H_q$ are given in (1.3).

Proof

By [14, Lemma 2.1], (2.1) and Proposition 2.1, we know that

$$\begin{aligned} \Vert u\Vert _{H_p}^p\le \left( \frac{p}{N-p}\right) ^p\Vert \nabla u\Vert _p^p, \end{aligned}$$

for any $u\in W^{1,{\mathcal {H}}}_0(\Omega )$. Now, taking inspiration from [14, Lemma 2.1], let $u\in C^\infty _0(\Omega )$. Then, we have

$$\begin{aligned} |u(x)|^q=-\int _1^\infty \frac{d}{d\lambda }|u(\lambda x)|^qd\lambda =-q\int _1^\infty |u(\lambda x)|^{q-2}u(\lambda x)\nabla u(\lambda x)\cdot x\,d\lambda \end{aligned}$$

a.e. in ${\mathbb {R}}^N$. Hence, by Hölder inequality, (a) and trivially extending $a(\cdot )$ in the whole space ${\mathbb {R}}^N$

$$\begin{aligned} \begin{aligned} \int _\Omega a(x)\frac{|u(x)|^q}{|x|^q}dx&=\int _{{\mathbb {R}}^N}a(x)\frac{|u(x)|^q}{|x|^q}dx\\&=-q\int _1^\infty \int _{{\mathbb {R}}^N}a(x)\frac{|u(\lambda x)|^{q-2}u(\lambda x)}{|x|^{q-1}}\nabla u(\lambda x)\cdot \frac{x}{|x|}dx\,d\lambda \\&=-q\int _1^\infty \int _{{\mathbb {R}}^N}\frac{1}{\lambda ^{N+1-q}}\,a\left( \frac{y}{\lambda }\right) \frac{|u(y)|^{q-2}u(y)}{|y|^{q-1}}\nabla u(y)\cdot \frac{y}{|y|}dy\,d\lambda \\&\le q\int _1^\infty \frac{d\lambda }{\lambda ^{N+1-q}}\int _{{\mathbb {R}}^N}a(y)\frac{|u(y)|^{q-1}}{|y|^{q-1}}|\nabla u(y)|dy\\&\le \frac{q}{N-q}\left( \int _\Omega a(y)\frac{|u(y)|^q}{|y|^q}dy\right) ^{(q-1)/q}\left( \int _\Omega a(y)|\nabla u(y)|^qdy\right) ^{1/q}. \end{aligned} \end{aligned}$$

From this, we obtain

$$\begin{aligned} \Vert u\Vert _{H_{q,a}}^q\le \left( \frac{q}{N-q}\right) ^q\Vert \nabla u\Vert _{q,a}^q, \end{aligned}$$

which holds true for any $u\in W^{1,{\mathcal {H}}}_0(\Omega )$ by density, (2.1) and Proposition 2.1. $\square$

We are now ready to introduce the variational setting for problem (1.1). We say that a function $u\in W^{1,{\mathcal {H}}}_0(\Omega )$ is a weak solution of (1.1) if

$$\begin{aligned}&\int _\Omega \left( |\nabla u|^{p-2}+a(x)|\nabla u|^{q-2}\right) \nabla u\cdot \nabla \varphi dx \\&\quad =\gamma \int _\Omega \left( \frac{|u|^{p-2}u}{|x|^p}+a(x)\frac{|u|^{q-2}u}{|x|^q}\right) \varphi dx+\int _\Omega f(x,u)\varphi dx, \end{aligned}$$

for any $\varphi \in W^{1,{\mathcal {H}}}_0(\Omega )$. Clearly, the weak solutions of (1.1) are exactly the critical points of the Euler-Lagrange functional $J_\gamma :W^{1,{\mathcal {H}}}_0(\Omega )\rightarrow {\mathbb {R}}$, given by

$$\begin{aligned} J_\gamma (u):=\frac{1}{p}\Vert \nabla u\Vert _p^p+\frac{1}{q}\Vert \nabla u\Vert _{q,a}^q -\gamma \left( \frac{1}{p}\Vert u\Vert _{H_p}^p+\frac{1}{q}\Vert u\Vert _{H_{q,a}}^q\right) -\int _\Omega F(x,u)dx, \end{aligned}$$

which is well defined and of class $C^{1}$ on $W^{1,{\mathcal {H}}}_0(\Omega )$.

3 Proof of Theorem 1.1

Throughout the section we assume that $\Omega \subset {\mathbb {R}}^N$ is an open, bounded set with Lipschitz boundary, $0\in \Omega$, $N\ge 2$, $1<p<q<N$, (1.2) and (a) hold true, without further mentioning. Also, we denote with $t^+=\max \{t,0\}$ and $t^-=\max \{-t,0\}$ respectively the positive and negative parts of a number $t\in {\mathbb {R}}$.

We recall that functional $J_\gamma :W^{1,{\mathcal {H}}}_0(\Omega )\rightarrow {\mathbb {R}}$ fulfills the Palais-Smale condition (PS) if any sequence $\{u_j\}_j\subset W^{1,{\mathcal {H}}}_0(\Omega )$ satisfying

$$\begin{aligned} \{J_\gamma (u_j)\}_j \text{ is } \text{ bounded } \text{ and } J'_\gamma (u_j)\rightarrow 0 \text{ in } \left( W^{1,{\mathcal {H}}}_0(\Omega )\right) ^{*} \text{ as } j\rightarrow \infty , \end{aligned}$$

(3.1)

possesses a convergent subsequence in $W^{1,{\mathcal {H}}}_0(\Omega )$.

The verification of the (PS) condition for $J_\gamma$ is fairly delicate, considering the contribution of the double phase Hardy potential. Indeed, even if $W^{1,\mathcal H}_0(\Omega )\hookrightarrow L^p(\Omega ,|x|^{-p}) \text{ and } W^{1,\mathcal H}_0(\Omega )\hookrightarrow L^q(\Omega ,a(x)|x|^{-q})$ by Lemma 2.1, these embeddings are not compact. For this, we exploit a suitable tricky step analysis combined with the celebrated Brézis and Lieb lemma in [6, Theorem 1], which can be applied in $W^{1,{\mathcal {H}}}_0(\Omega )$ if we first prove the convergence $\nabla u_j(x)\rightarrow \nabla u(x)$ a.e. in $\Omega$, as $j\rightarrow \infty$.

Proposition 3.1

Let $(f_1)-(f_2)$ hold true. Then, for any $\gamma \in (-\infty ,\min \{H_p,H_q\})$ the functional $J_\gamma$ verifies the (PS) condition.

Proof

Let us fix $\gamma \in (-\infty ,\min \{H_p,H_q\})$ and let $\{u_j\}_j\subset W^{1,{\mathcal {H}}}_0(\Omega )$ be a sequence satisfying (3.1).

We first show that $\{u_j\}_j$ is bounded in $W^{1,{\mathcal {H}}}_0(\Omega )$, arguing by contradiction. Then, going to a subsequence, still denoted by $\{u_j\}_j$, we have $\lim \limits _{j\rightarrow \infty }\Vert u_j\Vert =\infty$ and $\Vert u_j\Vert \ge 1$ for any $j\ge n$, with $n\in {\mathbb {N}}$ sufficiently large. Thus, according to $(f_2)$ and Lemma 2.1, we get

$$\begin{aligned} J_\gamma (u_j)-\frac{1}{\theta }\langle J^{\prime }_\gamma (u_j), u_j\rangle&=\left( \frac{1}{p}-\frac{1}{\theta }\right) \Vert \nabla u_j\Vert _p^p +\left( \frac{1}{q}-\frac{1}{\theta }\right) \Vert \nabla u_j\Vert _{q,a}^q -\gamma \left( \frac{1}{p}-\frac{1}{\theta }\right) \Vert u_j\Vert _{H_p}^p \nonumber \\&\quad -\gamma \left( \frac{1}{q}-\frac{1}{\theta }\right) \Vert u_j\Vert _{H_{q,a}}^q -\int _{\Omega }\left[ F(x,u_j)-\frac{1}{\theta }f(x,u_j)u_j\right] dx\nonumber \\&\ge \left( \frac{1}{p}-\frac{1}{\theta }\right) \left( 1-\frac{\gamma ^+}{H_p}\right) \Vert \nabla u_j\Vert _p^p +\left( \frac{1}{q}-\frac{1}{\theta }\right) \left( 1-\frac{\gamma ^+}{H_q}\right) \Vert \nabla u_j\Vert _{q,a}^q\nonumber \\&\quad -\int _{\Omega _{t_0}}\left[ F(x,u_j)-\frac{1}{\theta }f(x,u_j)u_j\right] ^+dx\nonumber \\&\ge \left( \frac{1}{q}-\frac{1}{\theta }\right) \left( 1-\frac{\gamma ^+}{\min \{H_p,H_q\}}\right) \varrho _{{\mathcal {H}}}(\nabla u_j) -D,\nonumber \\ \end{aligned}$$

(3.2)

since $\theta>q>p$ by $(f_2)$, where

$$\begin{aligned} \Omega _{t_0}=\left\{ x\in \Omega :\,\,|u_j(x)|\le t_0\right\} \quad \text{ and } \quad D=|\Omega |\sup _{x\in \Omega ,|t|\le t_0}\left[ F(x,t)-\frac{1}{\theta }f(x,t)t\right] ^+<\infty , \end{aligned}$$

with the last inequality which is consequence of $(f_1)$. Thus, by (3.1) there exist $c_1$, $c_2>0$ such that (3.2) and Proposition 2.1 yield at once that as $j\rightarrow \infty$,

$$\begin{aligned} c_1+c_2\Vert u_j\Vert +o(1)\ge \left( \frac{1}{q}-\frac{1}{\theta }\right) \left( 1-\frac{\gamma ^+}{\min \{H_p,H_q\}}\right) \Vert u_j\Vert ^p -D \end{aligned}$$

giving the desired contradiction, since $\theta>q>p>1$ and $\gamma <\min \{H_p,H_q\}$.

Hence, $\{u_j\}_j$ is bounded in $W^{1,{\mathcal {H}}}_0(\Omega )$. By Propositions 2.1–2.2, Lemma 2.1, [5, Theorem 4.9] and the reflexivity of $W^{1,{\mathcal {H}}}_0(\Omega )$, there exist a subsequence, still denoted by $\{u_j\}_j$, and $u\in W^{1,{\mathcal {H}}}_0(\Omega )$ such that

$$\begin{aligned} u_j\rightharpoonup u \text{ in } W^{1,\mathcal H}_0(\Omega ),\qquad \nabla u_j\rightharpoonup \nabla u \text{ in } \left[ L^{\mathcal H}(\Omega )\right] ^N,\nonumber \\ u_j\rightharpoonup u \text{ in } L^p(\Omega ,|x|^{-p}),\quad u_j\rightharpoonup u \text{ in } L^q(\Omega \setminus A,a(x)|x|^{-q}),\nonumber \\ \Vert u_j-u\Vert _{H_p}^p+\Vert u_j-u\Vert _{H_{q,a}}^q\rightarrow \ell ,\quad u_j\rightarrow u \text{ in } L^m(\Omega ),\nonumber \\u_j(x)\rightarrow u(x) \text{ a.e. } \text{ in } \Omega , \quad |u_j(x)|\le h(x) \text{ a.e. } \text{ in } \Omega , \end{aligned}$$

(3.3)

as $j\rightarrow \infty$, with $m\in [1,p^*)$, $h\in L^q(\Omega )$ and A is the nodal set of weight $a(\cdot )$, given by

$$\begin{aligned} A:=\left\{ x\in \Omega :\,\,a(x)=0\right\} . \end{aligned}$$

Indeed, since $a(\cdot )$ is a Lipschitz continuous function by (1.2), then $\Omega \setminus A$ is an open subset of ${\mathbb {R}}^N$. Also, $h\in L^q(\Omega )$ by Proposition 2.2 and [5, Theorem 4.9], since $q<p^*$ by (1.2).

Now, we claim that

$$\begin{aligned} \nabla u_j(x)\rightarrow \nabla u(x) \text{ a.e. } \text{ in } \Omega , \text{ as } j\rightarrow \infty . \end{aligned}$$

(3.4)

Let $\varphi \in C^\infty ({\mathbb {R}}^N)$ be a cut-off function with $0\le \varphi \le 1$, $\varphi \equiv 1$ in B(0, 1/2) and $\varphi \equiv 0$ in B(0, 1). Then, we define $\psi _R(x)=1-\varphi (x/R)$ for any $R>0$, so that $\psi _R\in C^\infty ({\mathbb {R}}^N)$ with $0\le \psi _R\le 1$, $\psi _R\equiv 1$ in ${\mathbb {R}}^N\setminus B(0,R)$, $\psi _R\equiv 0$ in B(0, R/2) and the sequence $\{\psi _R u_j\}_j$ is bounded in $W^{1,{\mathcal {H}}}_0(\Omega )$, thanks to Proposition 2.1. By simple calculation, for any $j\in {\mathbb {N}}$ we have

$$\begin{aligned} \begin{aligned} \langle J^{\prime }_\gamma (u_j),\psi _R(u_j-u)\rangle&= \int _\Omega \psi _R\left( |\nabla u_j|^{p-2}\nabla u_j+a(x)|\nabla u_j|^{q-2}\nabla u_j\right) \cdot (\nabla u_j-\nabla u)dx\\&\quad +\int _\Omega \left( |\nabla u_j|^{p-2}\nabla u_j+a(x)|\nabla u_j|^{q-2}\nabla u_j\right) \cdot \nabla \psi _R(u_j-u) dx\\&\quad -\gamma \int _\Omega \psi _R\left( \frac{|u_j|^{p-2}u_j}{|x|^p}+a(x)\frac{|u_j|^{q-2}u_j}{|x|^q}\right) (u_j-u)dx\\&\quad -\int _\Omega \psi _R f(x,u_j)(u_j-u)dx. \end{aligned}\nonumber \\ \end{aligned}$$

(3.5)

Of course, all integrals in (3.5) are zero whenever ${\overline{\Omega }}\subset B(0,R/2)$, since $\psi _R\equiv 0$ in B(0, R/2). Thus, let us consider $R>0$ sufficiently small such that

$$\begin{aligned} \left[ {\mathbb {R}}^N\setminus B(0,R/2)\right] \cap {\overline{\Omega }}\ne \emptyset . \end{aligned}$$

(3.6)

By Hölder inequality, (3.3), the facts that $\psi _R\in C^\infty ({\mathbb {R}}^N)$, $a(\cdot )$ is continuous in ${\overline{\Omega }}$ and $\{u_j\}_j$ is bounded in $W^{1,{\mathcal {H}}}_0(\Omega )$, we get

$$\begin{aligned} \begin{aligned}&\int _\Omega \left( |\nabla u_j|^{p-2}\nabla u_j+a(x)|\nabla u_j|^{q-2}\nabla u_j\right) \cdot \nabla \psi _R(u_j-u)dx\\&\quad \le C\left( \Vert \nabla u_j\Vert _p^{p-1}\Vert u_j-u\Vert _p+\Vert \nabla u_j\Vert _{q,a}^{q-1}\Vert u_j-u\Vert _{q,a}\right) \le {\widetilde{C}}\left( \Vert u_j-u\Vert _p+\Vert u_j-u\Vert _q\right) \rightarrow 0, \end{aligned} \end{aligned}$$

(3.7)

as $j\rightarrow \infty$, for suitable C, ${\widetilde{C}}>0$. Similarly, by considering also $(f_1)$ with $\varepsilon =1$, we obtain

$$\begin{aligned} \begin{aligned} \left| \int _\Omega \psi _R f(x,u_j)(u_j-u)dx\right|&\le \int _\Omega \left( q|u_j|^{q-1}+r\delta _1|u_j|^{r-1}\right) |u_j-u|dx\\&\le C\left( \Vert u_j-u\Vert _q+\Vert u_j-u\Vert _r\right) \rightarrow 0 \end{aligned} \end{aligned}$$

(3.8)

as $j\rightarrow \infty$, for a suitable $C>0$. Furthermore, by (3.3) and [1, Proposition A.8], considering that $a(\cdot )>0$ in $\Omega \setminus A$, we have

$$\begin{aligned}&|u_j|^{p-2}u_j\rightharpoonup |u|^{p-2}u\, \text{ in } \,L^{p'}(\Omega ,|x|^{-p}),\\&|u_j|^{q-2}u_j\rightharpoonup |u|^{q-2}u\, \text{ in } \,L^{q'}(\Omega \setminus A,a(x)|x|^{-q}) \end{aligned}$$

so that

$$\begin{aligned} \begin{aligned} \lim _{j\rightarrow \infty }\int _\Omega \psi _R\frac{|u_j|^{p-2}u_j}{|x|^p}u dx&= \int _\Omega \psi _R\frac{|u|^p}{|x|^p}dx,\\ \lim _{j\rightarrow \infty }\int _\Omega \psi _R\, a(x)\frac{|u_j|^{q-2}u_j}{|x|^q}u dx&= \lim _{j\rightarrow \infty }\int _{\Omega \setminus A}\psi _R\, a(x)\frac{|u_j|^{q-2}u_j}{|x|^q}u dx\\&=\int _{\Omega \setminus A}\psi _R\,a(x)\frac{|u|^q}{|x|^q}dx\\&=\int _\Omega \psi _R\,a(x)\frac{|u|^q}{|x|^q}dx. \end{aligned} \end{aligned}$$

(3.9)

While, by (3.3) it follows that

$$\begin{aligned} \psi _R(x)\frac{|u_j(x)|^p}{|x|^p}\le \left( \frac{2}{p}\right) ^{p}|u_j(x)|^p\le \left( \frac{2}{p}\right) ^{p}h^p(x) \quad \text{ a.e } \text{ in } \Omega \setminus B(0,R/2), \end{aligned}$$

so that, since $\psi _R\equiv 0$ in B(0, R/2), the dominated convergence theorem gives

$$\begin{aligned} \lim _{j\rightarrow \infty }\int _\Omega \psi _R\frac{|u_j|^p}{|x|^p}dx= & {} \lim _{j\rightarrow \infty }\int _{\Omega \setminus B(0,R/2)}\psi _R\frac{|u_j|^p}{|x|^p}dx =\int _{\Omega \setminus B(0,R/2)}\psi _R\frac{|u|^p}{|x|^p}dx \nonumber \\= & {} \int _\Omega \psi _R\frac{|u|^p}{|x|^p}dx. \end{aligned}$$

(3.10)

Similarly, by using also (1.2), for a suitable constant $L>0$ we get

$$\begin{aligned} \psi _R(x)a(x)\frac{|u_j(x)|^q}{|x|^q}\le L\left( \frac{2}{q}\right) ^{q}h^q(x) \quad \text{ a.e } \text{ in } \Omega \setminus B(0,R/2), \end{aligned}$$

which yields joint with the dominated convergence theorem

$$\begin{aligned} \lim _{j\rightarrow \infty }\int _\Omega \psi _R\,a(x)\frac{|u_j|^q}{|x|^q}dx =\int _\Omega \psi _R\,a(x)\frac{|u|^q}{|x|^q}dx. \end{aligned}$$

(3.11)

Thus, by (3.1), (3.5), (3.7)–(3.11), we obtain

$$\begin{aligned} \lim _{j\rightarrow \infty }\int _\Omega \psi _R\left( |\nabla u_j|^{p-2}\nabla u_j+a(x)|\nabla u_j|^{q-2}\nabla u_j\right) \cdot (\nabla u_j-\nabla u)dx=0. \end{aligned}$$

By Hölder inequality and being $\psi _R\le 1$, we see that functional

$$\begin{aligned} G:g\in \left[ L^{{\mathcal {H}}}(\Omega )\right] ^N\mapsto \int _\Omega \psi _R\left( |\nabla u|^{p-2}\nabla u+a(x)|\nabla u|^{q-2}\nabla u\right) \cdot g\,dx \end{aligned}$$

is linear and bounded. Hence, by (3.3) we have

$$\begin{aligned} \lim _{j\rightarrow \infty }\int _\Omega \psi _R\left( |\nabla u|^{p-2}\nabla u+a(x)|\nabla u|^{q-2}\nabla u\right) \cdot (\nabla u_j-\nabla u)dx=0, \end{aligned}$$

so that, denoting $\Omega _R:=\left\{ x\in \Omega :\,\,|x|>R\right\}$ for any $R>0$, we get

$$\begin{aligned} \begin{aligned}&\lim _{j\rightarrow \infty }\int _{\Omega _R}\left[ |\nabla u_j|^{p-2}\nabla u_j-|\nabla u|^{p-2}\nabla u \right. \\&\qquad \left. +a(x)\left( |\nabla u_j|^{q-2}\nabla u_j-|\nabla u|^{q-2}\nabla u\right) \right] \!\cdot \!(\nabla u_j-\nabla u)dx\\&\quad \le \lim _{j\rightarrow \infty }\int _\Omega \psi _R\left[ |\nabla u_j|^{p-2}\nabla u_j-|\nabla u|^{p-2}\nabla u\right. \\&\qquad \left. +a(x)\left( |\nabla u_j|^{q-2}\nabla u_j-|\nabla u|^{q-2}\nabla u\right) \right] \!\cdot \!(\nabla u_j-\nabla u)dx\\&\quad =0 \end{aligned} \end{aligned}$$

(3.12)

since $\psi _R\equiv 1$ in ${\mathbb {R}}^N\setminus B(0,R)$. Now, we recall the well known Simon inequalities, see [26], such that

$$\begin{aligned} |\xi -\eta |^m\le {\left\{ \begin{array}{ll} \kappa _m\,(|\xi |^{m-2}\xi -|\eta |^{m-2}\eta )\cdot (\xi -\eta ),\quad \text{ if } m\ge 2,\\ \kappa _m\left[ (|\xi |^{m-2}\xi -|\eta |^{m-2}\eta )\cdot (\xi -\eta )\right] ^{m/2}\left( |\xi |^m+|\eta |^m\right) ^{(2-m)/2}, \quad \text{ if } \\ 1<m<2, \end{array}\right. }\nonumber \\ \end{aligned}$$

(3.13)

for any $\xi$, $\eta \in {\mathbb {R}}^N$, with $\kappa _m>0$ a suitable constant. Therefore, if $p\ge 2$ by (3.13) we have

$$\begin{aligned}&\int _{\Omega _R}|\nabla u_j-\nabla u|^pdx \nonumber \\&\quad \le \kappa _p\int _{\Omega _R}\left( |\nabla u_j|^{p-2}\nabla u_j-|\nabla u|^{p-2}\nabla u\right) \cdot (\nabla u_j-\nabla u)dx. \end{aligned}$$

(3.14)

While, if $1<p<2$ by (3.13) and the Hölder inequality we obtain

$$\begin{aligned} \begin{aligned}&\int _{\Omega _R}|\nabla u_j-\nabla u|^pdx\\&\quad \le \kappa _p \int _{\Omega _R}\left[ \left( |\nabla u_j|^{p-2}\nabla u_j-|\nabla u|^{p-2}\nabla u\right) \cdot (\nabla u_j-\nabla u)\right] ^{p/2} \left( |\nabla u_j|^p+|\nabla u|^p\right) ^{(2-p)/2}dx\\&\quad \le \kappa _p \left[ \int _{\Omega _R}\left( |\nabla u_j|^{p-2}\nabla u_j-|\nabla u|^{p-2}\nabla u\right) \cdot (\nabla u_j-\nabla u)dx\right] ^{p/2} \left( \Vert \nabla u_j\Vert _p^p+\Vert \nabla u\Vert _p^p\right) ^{(2-p)/2}\\&\quad \le \widetilde{\kappa _p} \left[ \int _{\Omega _R}\left( |\nabla u_j|^{p-2}\nabla u_j-|\nabla u|^{p-2}\nabla u\right) \cdot (\nabla u_j-\nabla u)dx\right] ^{p/2} \end{aligned} \end{aligned}$$

(3.15)

where the last inequality follows by the boundedness of $\{u_j\}_j$ in $W^{1,{\mathcal {H}}}_0(\Omega )$ and Proposition 2.1, with a suitable new $\widetilde{\kappa _p}>0$. Also, by convexity and since $a(x)\ge 0$ a.e. in $\Omega$ by (1.2), we have

$$\begin{aligned} a(x)\left( |\nabla u_j|^{q-2}\nabla u_j-|\nabla u|^{q-2}\nabla u\right) \cdot (\nabla u_j-\nabla u) \ge 0 \text{ a.e. } \text{ in } \Omega . \end{aligned}$$

(3.16)

Thus, combining (3.12), (3.14)–(3.16) we prove that $\nabla u_j\rightarrow \nabla u$ in $[L^p(\Omega _R)]^N$ as $j\rightarrow \infty$, whenever $R>0$ satisfies (3.6). However, when ${\overline{\Omega }}\subset B(0,R/2)$ we have $\Omega _R=\emptyset$. Thus, for any $R>0$ the sequence $\nabla u_j\rightarrow \nabla u$ in $[L^p(\Omega _R)]^N$ as $j\rightarrow \infty$, and by diagonalization we prove claim (3.4).

Since the sequence $\{|\nabla u_j|^{p-2}\nabla u_j\}_j$ is bounded in $L^{p^{\prime }}(\Omega )$, by (3.4) we get

$$\begin{aligned} \lim _{j\rightarrow \infty }\int _\Omega |\nabla u_j|^{p-2}\nabla u_j\cdot \nabla u\,dx=\Vert \nabla u\Vert _p^p. \end{aligned}$$

(3.17)

While, since $\{|\nabla u_j|^{q-2}\nabla u_j\}_j$ is bounded in $L^{q^{\prime }}(\Omega \setminus A,a(x))$, by (3.4) and [1, Proposition A.8]

$$\begin{aligned} \lim _{j\rightarrow \infty }\int _\Omega a(x)|\nabla u_j|^{q-2}\nabla u_j\cdot \nabla u\,dx= & {} \lim _{j\rightarrow \infty }\int _{\Omega \setminus A} a(x)|\nabla u_j|^{q-2}\nabla u_j\cdot \nabla u\,dx\nonumber \\= & {} \Vert \nabla u\Vert _{q,a}^q. \end{aligned}$$

(3.18)

Also, arguing as in (3.8) and (3.9), we can prove

$$\begin{aligned} \begin{aligned}&\lim _{j\rightarrow \infty }\int _\Omega f(x,u_j)(u_j-u)dx=0,\\&\lim _{j\rightarrow \infty }\int _\Omega \left( \frac{|u_j|^{p-2}u_j}{|x|^p}u+a(x)\frac{|u_j|^{q-2}u_j}{|x|^q}u\right) dx= \Vert u\Vert _{H_p}^p+\Vert u\Vert _{H_{q,a}}^q. \end{aligned} \end{aligned}$$

(3.19)

Furthermore, using (3.3), (3.4) and the Brézis and Lieb lemma in [6, Theorem 1], we obtain

$$\begin{aligned} \begin{aligned}&\Vert \nabla u_j\Vert _p^p-\Vert \nabla u_j-\nabla u\Vert _p^p=\Vert \nabla u\Vert _p^p+o(1),\\&\Vert \nabla u_j\Vert _{q,a}^q-\Vert \nabla u_j-\nabla u\Vert _{q,a}^q=\Vert \nabla u\Vert _{q,a}^q+o(1),\\&\Vert u_j\Vert _{H_p}^p-\Vert u_j-u\Vert _{H_p}^p=\Vert u\Vert _{H_p}^p+o(1),\\&\Vert u_j\Vert _{H_{q,a}}^q-\Vert u_j-u\Vert _{H_{q,a}}^q=\Vert u\Vert _{H_{q,a}}^q+o(1) \end{aligned} \end{aligned}$$

(3.20)

as $j\rightarrow \infty$. Thus, by (3.1), (3.17), (3.18) and (3.19), we get

$$\begin{aligned} \begin{aligned} o(1){=}\left\langle J^{\prime }_\gamma (u_j),u_j-u\right\rangle&= \int _\Omega \left( |\nabla u_j|^{p-2}\nabla u_j{+}a(x)|\nabla u_j|^{q-2}\nabla u_j\right) \cdot (\nabla u_j{-}\nabla u)dx\\&\quad -\gamma \int _\Omega \left( \frac{|u_j|^{p-2}u_j}{|x|^p}+a(x)\frac{|u_j|^{q-2}u_j}{|x|^q}\right) (u_j-u)dx\\&\quad -\int _\Omega f(x,u_j)(u_j-u)dx\\&=\Vert \nabla u_j\Vert _p^p-\Vert \nabla u\Vert _p^p +\Vert \nabla u_j\Vert _{q,a}^p-\Vert \nabla u\Vert _{q,a}^p\\&\quad -\gamma \left( \Vert u_j\Vert _{H_p}^p-\Vert u\Vert _{H_p}^p+\Vert u_j\Vert _{H_{q,a}}^q-\Vert u\Vert _{H_{q,a}}^q\right) +o(1) \end{aligned} \end{aligned}$$

(3.21)

as $j\rightarrow \infty$. Hence, by (3.20) it follows that

$$\begin{aligned} \Vert \nabla u_j-\nabla u\Vert _p^p+\Vert \nabla u_j-\nabla u\Vert _{q,a}^q= & {} \gamma \left( \Vert u_j-u\Vert _{H_p}^p+\Vert u_j-u\Vert _{H_{q,a}}^q\right) +o(1)\nonumber \\= & {} \gamma \ell +o(1) \end{aligned}$$

(3.22)

as $j\rightarrow \infty$. Now, assume for contradiction that $\ell >0$. Then, from Lemma 2.1, (3.22) and the fact that $\gamma <\min \{H_p,H_q\}$, we have

$$\begin{aligned} \begin{aligned}&\lim _{j\rightarrow \infty }\Vert \nabla u_j-\nabla u\Vert _p^p+\lim _{j\rightarrow \infty }\Vert \nabla u_j-\nabla u\Vert _{q,a}^q\\&\quad \le \gamma ^+\left( \lim _{j\rightarrow \infty }\Vert u_j-u\Vert _{H_p}^p+\lim _{j\rightarrow \infty }\Vert u_j-u\Vert _{H_{q,a}}^q\right) \\&\quad <\min \{H_p,H_q\}\left( \lim _{j\rightarrow \infty }\Vert u_j-u\Vert _{H_p}^p+\lim _{j\rightarrow \infty }\Vert u_j-u\Vert _{H_{q,a}}^q\right) \\&\quad \le \lim _{j\rightarrow \infty }\Vert \nabla u_j-\nabla u\Vert _p^p+\lim _{j\rightarrow \infty }\Vert \nabla u_j-\nabla u\Vert _{q,a}^q \end{aligned} \end{aligned}$$

which is impossible. Therefore $\ell =0$, so that by (3.22) we have $\nabla u_j\rightarrow \nabla u$ in $\left[ L^p(\Omega )\cap L_a^q(\Omega )\right] ^N$ as $j\rightarrow \infty$, implying that $u_j\rightarrow u$ in $W^{1,{\mathcal {H}}}_0(\Omega )$ thanks to (2.1) and Proposition 2.1. This concludes the proof.

$\square$

Now, we complete the proof of Theorem 1.1, proving first that functional $J_\gamma$ satisfies the geometric features of the mountain pass theorem.

Lemma 3.1

Let $(f_1)$ holds true. Then, for any $\gamma \in (-\infty ,\min \{H_p,H_q\})$ there exist $\rho =\rho (\gamma )\in (0,1]$ and $\alpha =\alpha (\rho )>0$ such that $J_\gamma (u)\ge \alpha$ for any $u\in W^{1,{\mathcal {H}}}_0(\Omega )$, with $\Vert u\Vert =\rho$.

Proof

Let us fix $\gamma \in (-\infty ,\min \{H_p,H_q\})$. By $(f_1)$, for any $\varepsilon >0$ we have a $\delta _\varepsilon >0$ such that

$$\begin{aligned} |F(x,t)|\le \varepsilon |t|^q+\delta _\varepsilon |t|^r,\quad \text{ for } \text{ a.e. } x\in \Omega \text{ and } \text{ any } t\in {\mathbb {R}}. \end{aligned}$$

(3.23)

Thus, by (3.23), Lemma 2.1, Propositions 2.1 and 2.2, for any $u\in W^{1,{\mathcal {H}}}_0(\Omega )$ with $\Vert u\Vert \le 1$, we obtain

$$\begin{aligned} J_\gamma (u)&\ge \frac{1}{p}\left( 1-\frac{\gamma ^+}{H_p}\right) \Vert \nabla u\Vert _p^p +\frac{1}{q}\left( 1-\frac{\gamma ^+}{H_q}\right) \Vert \nabla u\Vert _{q,a}^q -\varepsilon \Vert u\Vert _q^q-\delta _\varepsilon \Vert u\Vert _r^r\\&\ge \frac{1}{q}\left( 1-\frac{\gamma ^+}{\min \{H_p,H_q\}}\right) \varrho _{{\mathcal {H}}}(\nabla u) -\varepsilon C_q\Vert u\Vert ^q-\delta _\varepsilon C_r\Vert u\Vert ^r\\&\ge \left[ \frac{1}{q}\left( 1-\frac{\gamma ^+}{\min \{H_p,H_q\}}\right) -\varepsilon C_q\right] \Vert u\Vert ^q-\delta _\varepsilon C_r\Vert u\Vert ^r, \end{aligned}$$

since $q>p$ and $\gamma <\min \{H_p,H_q\}$. Therefore, choosing $\varepsilon >0$ sufficiently small so that

$$\begin{aligned} \sigma _\varepsilon =\frac{1}{q}\left( 1-\frac{\gamma ^+}{\min \{H_p,H_q\}}\right) -\varepsilon C_q>0, \end{aligned}$$

for any $u\in W^{1,{\mathcal {H}}}_0(\Omega )$ with $\Vert u\Vert =\rho \in \big (0,\min \{1,[\sigma _\varepsilon /(2\delta _\varepsilon C_r)]^{1/(r-q)}\}\big ]$, we get

$$\begin{aligned} J_\gamma (u)\ge \left( \sigma _\varepsilon -\delta _\varepsilon C_r\rho ^{r-q}\right) \rho ^q:=\alpha >0. \end{aligned}$$

This completes the proof. $\square$

Lemma 3.2

Let $(f_1)-(f_2)$ hold true. Then, for any $\gamma \in {\mathbb {R}}$ there exists $e\in W^{1,{\mathcal {H}}}_0(\Omega )$ such that $J_\gamma (e)<0$ and $\Vert e\Vert >1$.

Proof

Let us fix $\gamma \in {\mathbb {R}}$. By $(f_1)$ and $(f_2)$, there exist $d_1>0$ and $d_2\ge 0$ such that

$$\begin{aligned} F(x,t)\ge d_1|t|^\theta -d_2\quad \text{ for } \text{ a.e. } x\in \Omega \text{ and } \text{ any } t\in {\mathbb {R}}. \end{aligned}$$

(3.24)

Thus, if $\varphi \in W^{1,{\mathcal {H}}}_0(\Omega )$ with $\Vert \varphi \Vert =1$, then by Proposition 2.1 also $\varrho _{{\mathcal {H}}}(\nabla \varphi )=1$, so that by (3.24), for any $t\ge 1$ we have

$$\begin{aligned} J_\gamma (t\varphi )\le \frac{t^q}{p}-t^p\frac{\gamma ^-}{p}\Vert \varphi \Vert _{H_p}^p-t^q\frac{\gamma ^-}{q}\Vert \varphi \Vert _{H_{q,a}}^q -t^\theta d_1\Vert \varphi \Vert _\theta ^\theta -d_2|\Omega |. \end{aligned}$$

Since $\theta>q>p$ by $(f_2)$, passing to the limit as $t\rightarrow \infty$ we get $J_\gamma (t\varphi )\rightarrow -\infty$. Thus, the assertion follows by taking $e=t_{\infty }\varphi$, with $t_{\infty }$ sufficiently large. $\square$

Proof of Theorem 1.1

Since $J_\gamma (0)=0$, by Proposition 3.1, Lemmas 3.1–3.2 and the mountain pass theorem, we prove the existence of a non-trivial weak solution of (1.1). $\square$

We conclude this section with a result of independent interest, which shows how (3.4) allows us to cover the complete situation in Theorem 1.1, with $1<p<q<N$ and $\gamma \in (-\infty ,\min \{H_p,H_q\})$. For this, let $L_\gamma :W^{1,\mathcal H}_0(\Omega )\rightarrow \left( W^{1,\mathcal H}_0(\Omega )\right) ^*$ be an operator such that

$$\begin{aligned} \langle L_\gamma (u),v\rangle&:=\int _\Omega \left( |\nabla u|^{p-2}+a(x)|\nabla u|^{q-2}\right) \nabla u\cdot \nabla v dx \\&\quad -\gamma \int _\Omega \left( \frac{|u|^{p-2}u}{|x|^p}v+a(x)\frac{|u|^{q-2}u}{|x|^q}v\right) dx, \end{aligned}$$

for any u, $v\in W^{1,{\mathcal {H}}}_0(\Omega )$.

Lemma 3.3

Let $2\le p<q<N$ and $\gamma \in (-\infty ,\min \{H_p,H_q\}/\max \{\kappa _p,\kappa _q\})$, with $\kappa _p$ and $\kappa _q$ given by (3.13). Then, the operator $L_\gamma$ is a mapping of (S) type, that is if $u_j\rightharpoonup u$ in $W^{1,{\mathcal {H}}}_0(\Omega )$ and

$$\begin{aligned} \lim \limits _{j\rightarrow \infty }\langle L_\gamma (u_j)-L_\gamma (u),u_j-u\rangle =0, \end{aligned}$$

(3.25)

then $u_j\rightarrow u$ in $W^{1,{\mathcal {H}}}_0(\Omega )$.

Proof

Let us fix $2\le p<q<N$ and $\gamma \in (-\infty ,\min \{H_p,H_q\}/\max \{\kappa _p,\kappa _q\})$. Let $\{u_j\}_j$ be a sequence in $W^{1,{\mathcal {H}}}_0(\Omega )$ such that $u_j\rightharpoonup u$ in $W^{1,{\mathcal {H}}}_0(\Omega )$ and (3.25) holds true. Then, up to a subsequence $\{u_j\}_j$ is bounded in $W^{1,{\mathcal {H}}}_0(\Omega )$ and by Lemma 2.1 and [5, Theorem 4.9], we obtain

$$\begin{aligned} \Vert u_j-u\Vert _{H_p}^p+\Vert u_j-u\Vert _{H_{q,a}}^q\rightarrow \ell , \qquad u_j(x)\rightarrow u(x) \text{ a.e. } \text{ in } \Omega , \end{aligned}$$

as $j\rightarrow \infty$. Thus, by [6, Theorem 1] we get

$$\begin{aligned}&\Vert u_j\Vert _{H_p}^p-\Vert u_j-u\Vert _{H_p}^p=\Vert u\Vert _{H_p}^p+o(1),\nonumber \\&\Vert u_j\Vert _{H_{q,a}}^q-\Vert u_j-u\Vert _{H_{q,a}}^q=\Vert u\Vert _{H_{q,a}}^q+o(1) \end{aligned}$$

(3.26)

as $j\rightarrow \infty$. While, by (3.13) we have

$$\begin{aligned}&\int _{\Omega }\left[ \left( |\nabla u_j|^{p-2}\nabla u_j-|\nabla u|^{p-2}\nabla u\right) +a(x)\left( |\nabla u_j|^{q-2}\nabla u_j-|\nabla u|^{q-2}\nabla u\right) \right] \cdot (\nabla u_j-\nabla u)dx\nonumber \\&\quad \ge \frac{1}{\max \{\kappa _p,\kappa _q\}}\left( \Vert u_j-u\Vert _p^p+\Vert u_j-u\Vert _{q,a}^q\right) \end{aligned}$$

(3.27)

for any $j\in {\mathbb {N}}$. Hence, combining (3.25)–(3.27), as $j\rightarrow \infty$

$$\begin{aligned}&\frac{1}{\max \{\kappa _p,\kappa _q\}}\Vert \nabla u_j-\nabla u\Vert _p^p+\Vert \nabla u_j-\nabla u\Vert _{q,a}^q \\&\quad =\gamma \left( \Vert u_j-u\Vert _{H_p}^p+\Vert u_j-u\Vert _{H_{q,a}}^q\right) +o(1)=\gamma \ell +o(1), \end{aligned}$$

which recalls (3.22), up to a constant. From this point, we can argue as in the end of the proof of Proposition 3.1, proving that $u_j\rightarrow u$ in $W^{1,{\mathcal {H}}}_0(\Omega )$. $\square$

Remark 3.1

When $2\le p<q<N$ and $\gamma \in (-\infty ,K_{p,q}\min \{H_p,H_q\})$, with

$$\begin{aligned} K_{p,q}:=\min \left\{ 1,\frac{1}{\max \{\kappa _p,\kappa _q\}}\right\} , \end{aligned}$$

we can prove Proposition 3.1 arguing as in [17, Lemma 5.1] and using Lemma 3.3 instead of (3.4).