Abstract
We consider some repulsive multimarginal optimal transportation problems which include, as a particular case, the Coulomb cost. We prove a regularity property of the minimizers (optimal transportation plan) from which we deduce existence and some basic regularity of a maximizer for the dual problem (Kantorovich potential). This is then applied to obtain some estimates of the cost and to the study of continuity properties.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This paper deals with the following variational problem. Let \(\rho \in \mathcal P(\mathbb R^d)\) be a probability measure, let \(N>1\) be an integer and let
with \(\phi :(0,+\infty ) \rightarrow \mathbb R\) satisfying the assumptions which will be described in the next section; in particular for \(\phi (t)=1/t\) we have the usual Coulomb repulsive cost. Consider the set of probabilities on \(\mathbb R^{Nd}\)
where \(\pi ^i\) denotes the projection on the ith copy of \(\mathbb R^d\) and \(\pi ^i_\sharp P\) is the push-forward measure. We aim to minimize the total transportation cost
This problem is called a multimarginal optimal transportation problem and elements of \(\Pi (\rho )\) are called transportation plans for \(\rho \). Some general results about multimarginal optimal transportation problems are available in [3, 17, 22,23,24]. Results for particular cost functions are available, for example in [11] for the quadratic cost, with some generalization in [15], and in [4] for the determinant cost function.
Optimization problems for the cost function \(C(\rho )\) in (1.1) intervene in the so-called Density Functional Theory (DFT), we refer to [16, 18] for the basic theory of DFT and to [13, 14, 25,26,27] for recent development which are of interest for us. Some new applications are emerging for example in [12]. In the particular case of the Coulomb cost there are also many other open questions related to the applications. Recent results on the topic are contained in [2, 5,6,7, 10, 20] and some of them will be better described in the subsequent sections. For more general repulsive costs we refer to the recent survey [9]. The literature quoted so far is not at all exhaustive and we refer the reader to the bibliographies of the cited papers for a more detailed picture.
Since the functions \(\phi \) we consider are lower semicontinuous, the functional \(\rho \mapsto C(\rho )\) above is naturally lower semicontinuous on the space of probability measures equipped with the tight convergence. In general it is not continuous as the following example shows. Take \(N=2\), \(\phi (t)=t^{-s}\) for some \(s>0\), and
with \(x\ne y\), which gives
In the last section of the paper we show that the functional \(C(\rho )\) is continuous or even Lipschitz on suitable subsets of \(\mathcal P(\mathbb R^d)\) which are relevant for the applications.
Problem (1.1) admits the following Kantorovich dual formulation.
Theorem 1.1
(Proposition 2.6 in [17]) The equality
holds, where \(\mathcal I_ \rho \) denotes the set of \(\rho \)-integrable functions and the pointwise inequality is satisfied everywhere.
Thanks to the symmetries of the problem we also have that the right-hand side of (1.2) coincides with
In fact, the supremum in (1.3) is a priori larger than the one in (1.2); however, since for any admissible N-tuple \((u_1,\dots ,u_N)\) the function
is admissible in (1.2), equality holds.
Definition 1.2
A function u will be called a Kantorovich potential if it is a maximizer for the right-hand-side of (1.2).
The paper [17] contains a general approach to the duality theory for multimarginal optimal transportation problems. A different approach which make use of a weaker definition of the dual problem (two marginals case) is introduced in [1] and may be applied to this situation too [2]. Existence of Kantorovich potentials is the topic of Theorem 2.21 of [17]. That theorem requires that there exist \(h_1, \dots , h_N \in L^1_\rho \) such that
and so it does not apply to the costs we consider in this paper, as for example the costs of Coulomb type. For Coulomb type costs, the existence of a Kantorovich potential is proved in [8] under the additional assumption that \(\rho \) is absolutely continuous with respect to the Lebesgue measure in \(\mathbb R^d\). As a consequence of our main estimate, here we extend the existence result to a larger class of probability measures \(\rho \). We then use the Kantorovich potentials as a tool.
We adopt the notation \(\mathbf{x}=(x_1,\dots ,x_N)\in \mathbb R^{Nd}\) so that \(x_i\in \mathbb R^d\) for each \(i\in \{1,\dots ,N\}\). Also, we denote the cost of a transport plan \(P\in \Pi (\rho )\) by
Finally, for \(\alpha >0\) we may also introduce the natural truncation of the cost
with the natural notation \(\phi _\alpha (t):=\min \big \{\phi (t),\phi (\alpha )\big \}\) and the corresponding transportation costs \(C_\alpha (\rho )\) and \(\mathbf{\mathfrak {C}}_\alpha (P)\).
2 Results
We assume that \(\phi \) satisfies the following properties:
-
(1)
\(\phi \) is continuous from \((0,+\infty )\) to \([0,+\infty )\).
-
(2)
\(\lim _{t\rightarrow 0^+}\phi (t)=+\infty \);
-
(3)
\(\phi \) is strictly decreasing;
Remark 2.1
A careful attention to the present work shows that all our results also hold when (3) is replaced by the weaker hypothesis :
(3\(^{\prime }\)) \(\phi \) is bounded at \(+\infty \), that is \(\sup \{ | \phi (t) | : t \ge 1 \} <+\infty \);
Under this assumption, one has to replace \(\phi \) and \(\phi ^{-1}\) in the statements respectively by \(\Phi (t) = \sup \{\phi (s) : s \ge t \}\) and \(\Phi ^{-1}(t) = \inf \{s : \phi (s)=t \}\). For example in Theorem 2.4 the number \(\alpha \) should be chosen lower than \(\Phi ^{-1}\big (\frac{N^2(N-1)}{2}\Phi (\beta )\big )\). Even if less general, we believe that the present form and stronger hypothesis (3) makes our approach and arguments more clear.
Definition 2.2
For every \(\rho \in \mathcal P(\mathbb R^d)\) the measure of concentration of \(\rho \) at scale r is defined as
In particular, if \(\rho \in L^1(\mathbb R^d)\) we have \(\mu _\rho (r)=o(1)\) as \(r\rightarrow 0\), and more generally
The main role of the measures of concentration is played in the following assumption.
Assumption (A)
We say that \(\rho \) has small concentration with respect to N if
For \(\alpha >0\) we denote by
the open strip around the singular set where at least two of the \(x_i\) coincide. Finally, we denote by \(\mathbb R^{d(N-1)}\otimes _i A\) the Cartesian product on N factors the ith of which is A while all the others are copies of \(\mathbb R^d\).
Lemma 2.3
Assume that \(\rho \) satisfies assumption (A). Let \(\mathbf{x}:=\mathbf{x}^1\in \mathbb R^{dN}\) and let \(\beta \) be such that
Then for every \(P\in \Pi (\rho )\) there exist \(\mathbf{x}^2,\dots ,\mathbf{x}^N\in {{\mathrm{spt}}}P\) such that
Proof
By definition of marginals and by the choice of \(\beta \) we have
for all indices \(\alpha ,i,k\). Then for any \(j\in \{2,\dots ,N\}\)
and, since P is a probability measure, this allows us to choose
It is easy to verify that the \(\mathbf{x}^j\) above satisfy the desired property (2.1). \(\square \)
2.1 Estimates for the Optimal Transport Plans
Theorem 2.4
Let \(\rho \in \mathcal P(\mathbb R^d)\) and assume that \(\rho \) satisfies assumption (A). Let \(P\in \Pi (\rho )\) be a minimizer for the transportation cost \(C(\rho )\) (or \(C_\alpha (\rho )\)) and let \(\beta \) be such that
Then
Proof
We make the proof for the case where P is a minimizer for \(C(\rho )\), the argument being the same for \(C_\alpha (\rho )\). Take \(\alpha \) as in the statement and \(\delta \in (0,\alpha )\). Note from the hypotheses on \(\phi \) that \(\alpha < \beta \). Assume that \(\mathbf{x}^1=(x^1_1,\dots ,x^1_N)\in D_{\delta } \cap {{\mathrm{spt}}}P\) and choose points \(\mathbf{x}^2,\dots ,\mathbf{x}^N\) in \({{\mathrm{spt}}}P\) as in Lemma 2.3. Let k be large enough so that \(\delta +2\beta /k < \alpha \). Since all the chosen points belong to \({{\mathrm{spt}}}P\), we have
where \(Q(\mathbf{x}^i,\beta /k) = \Pi _{j=1}^N B(\mathbf{x}^i_j,\beta /k)\). Denote by \(P_i=P_{\big |Q(\mathbf{x}^i,\frac{\beta }{k})}\) and choose constants \(\lambda _i\in (0,1]\) such that
where \(|P_i|\) denotes the mass of the measure \(P_i\). We then write
and we estimate from below the cost of P as follows:
where we used the fact that \(\mathbf{x}^1 \in D_\delta \) and \(\delta +2\beta /k < \alpha \). We consider now the marginals \(\nu ^i_1,\dots ,\nu ^i_N\) of \(\lambda _i P_i\) and build the new local plans
To write the estimates from above it is convenient to remark that we may also write
where we consider the upper index (mod N). Consider now the transport plan
it is straightforward to check that the marginals of \(\tilde{P}\) are the same as the marginals of P. Moreover \(|\tilde{P}_i|= \lambda _i |P_i|\). So we can estimate the cost of \(\tilde{P}\) from above using the distance between the coordinates of the centers of the cubes established in Lemma 2.3, and we obtain
Then if
we have that
thus contradicting the minimality of P. It follows that the strip \(D_{\alpha _1}\) and \({{\mathrm{spt}}}P\) do not intersect if \(\alpha \) satisfies the inequality above and since k may be arbitrarily large and \(\phi \) is continuous we obtain the conclusion for any \(\alpha _1 \in (0,\alpha )\), which concludes the proof. \(\square \)
The Theorem above allows us to estimate the costs in term of \(\beta \).
Proposition 2.5
Let \(\rho \in \mathcal P(\mathbb R^d)\) and assume that \(\rho \) satisfies assumption (A). Then if \(\beta \) is such that
we have
Moreover,
Proof
Let P be an optimal transport plan for the cost C. According to Theorem 2.4, if \(\alpha \) is as in the statement then the support of P may intersect only the boundary of \(D_\alpha \) and this means that \(c\le \frac{N(N-1)}{2}\phi (\alpha )\) on the support of P. Then
and, taking the largest admissible \(\alpha \) we obtain
which is the desired estimate. Let now \(P_\alpha \) be an optimal plan for the cost \(C_\alpha \), then also \({{\mathrm{spt}}}P_\alpha \subset \mathbb R^{Nd}\setminus D_\alpha \) so that \(c=c_\alpha \) on \({{\mathrm{spt}}}P_\alpha \). It follows that
and since the opposite inequality is always true we conclude the proof. \(\square \)
As a consequence of Proposition 2.5 above, Proposition 2.6 of [17] and Theorem 2.21 of [17] we also obtain an extension of the duality theorem of [8] to a wider set of \(\rho \).
Theorem 2.6
Let \(\rho \in \mathcal P(\mathbb R^d)\) and assume that \(\rho \) satisfies assumption (A). Then
Moreover, whenever \(\alpha \le \phi ^{-1}\Big (\frac{N^2(N-1)}{2}\phi (\beta )\Big )\), any Kantorovich potential \(u_\alpha \) for \(C_\alpha \) is also a Kantorovich potential for C.
Proof
By monotonicity of the integral the left-hand side of (2.2) is always larger than the right-hand side. Proposition 2.6 and Theorem 2.21 of [17] may be applied to the cost \(c_\alpha \) to obtain
Since \(\rho \) satisfies assumption (A), by Proposition 2.5 for \(\alpha \) sufficiently small we have that there exists \(u_\alpha \in \mathcal I_\rho \) such that
and
as required. \(\square \)
Remark 2.7
Note that if u is a Kantorovich potential for C and P is optimal for C then \(u(x_1)+\ldots +u(x_N)=c(x_1,\ldots ,x_N)\) holds P-almost everywhere.
3 Applications
3.1 Estimates for the Cost
Since the parameter \(\beta \) in the previous section is naturally related to the summability of \(\rho \), we can obtain some estimate of the cost \(C(\rho )\) in term of the available norms of \(\rho \).
Proposition 3.1
Let \(\rho \in \mathcal P(\mathbb R^d)\cap L^p(\mathbb R^d)\) for some \(p>1\). Then, if \(P\in \Pi (\rho )\) is optimal for the transportation cost \(C(\rho )\), we have
where \(\omega _d\) denotes the Lebesgue measure of the ball of radius 1 in \(\mathbb R^d\) and \(p'\) the conjugate exponent of p. It follows that
Proof
Let
By Hölder inequality we have
so that
The desired inequality (3.1) now follows by Theorem 2.5. \(\square \)
Remark 3.2
The Coulomb type costs \(\phi (t)=t^{-s}\) for \(s>0\) play a relevant role in several applications.
-
1.
For \(\phi (t)=t^{-s}\) estimate (3.1) above takes the form
$$\begin{aligned} C(\rho )\le \frac{N^3(N-1)^2}{4}\bigg (\omega _d\big (N(N-1)^2\big )^{p'}\Vert \rho \Vert _p^{p'}\bigg )^{s/d}. \end{aligned}$$ -
2.
In dimension \(d=3\) and for \(s=1\) the set
$$\begin{aligned} {\mathcal H}:=\Big \{\rho \in L^1(\mathbb R^3)\ :\ \rho \ge 0,\ \sqrt{\rho }\in H^1(\mathbb R^3),\ \int \rho \,dx=1\Big \} \end{aligned}$$plays an important role in the Density Functionals Theory. In fact, Lieb in [19] proved that \(\rho \in {\mathcal H}\) if and only if there exists a wave function \(\psi \in H^1(\mathbb R^{3N})\) such that
$$\begin{aligned} \pi ^i_\sharp |\psi |^2dx=\rho ,\qquad \text{ for } i=1,\dots ,N. \end{aligned}$$Taking \(s=1\), \(d=3\), \(p=3\) in Proposition 3.1 gives
$$\begin{aligned} C(\rho )\le C N^{7/2} (N-1)^3\Vert \rho \Vert _3^{1/2}=C N^{7/2} (N-1)^3\Vert \sqrt{\rho }\Vert _6\le C N^{7/2} (N-1)^3\Vert \sqrt{\rho }\Vert _{H^1}.\end{aligned}$$
3.2 Estimates for Kantorovich Potentials
In general, a Kantorovich potential u is a \(\rho \)-integrable function which can be more or less freely modified outside a relevant set. In this section we show the existence of Kantorovich potentials which are more regular.
Lemma 3.3
Let u be a Kantorovich potential; then there exists a Kantorovich potential \(\tilde{u}\) which satisfies
and
Proof
We first define
then we consider
Since \(u(x)\le \overline{u}(x)\) we have also \(u(x)\le \hat{u}(x)\) ; moreover it is straightforward to check that
Notice that if u does not satisfy (3.2) at some x then \(u(x) < \hat{u}(x)\). We then consider
with the partial ordering \(v_1 \le v_2\) if \(v_1(x) \le v_2(x)\) for all x. With this partial ordering, every chain (totally ordered subset) of \({\mathcal A}\) admits an upper bound, given by the pointwise \(\sup \). As in the proof of Theorem 1.4 in [21], we conclude from Zorn’s Lemma that \({\mathcal A}\) contains at least one maximal element \(\tilde{u}\), which satisfies all the required properties : otherwise, by the discussion above, we would have \(\tilde{u}\le \hat{\tilde{u}}\) and \(\tilde{u}\ne \hat{\tilde{u}}\) which contradicts maximality. \(\square \)
Taking some constant \(\alpha _1,\dots ,\alpha _N\) such that \(\sum \alpha _i=0\) we may define \(u_i(x)=\tilde{u}(x)+\alpha _i\) and we obtain an N-tuple of functions which is optimal for problem (1.3) and satisfies
The choice of the constants \(\alpha _i\) can be made so that the functions \(u_i\) take specific and admissible values at some points. A final, elementary, remark is that \(\tilde{u}\) is the arithmetic mean of the \(u_i\)s.
Theorem 3.4
Let \(\rho \in \mathcal P(\mathbb R^d)\). Assume that \(\rho \) satisfies assumption (A), and let \(\beta \) be such that \(\mu _\rho (\beta )\le \frac{1}{N(N-1)^2}\). Let u be a Kantorovich potential which satisfies
Then for any choice of \(\alpha \) as in Theorem 2.4 it holds
Proof
Let P be an optimal transport plan for C, let \(\alpha \) be as in Theorem 2.4 and take \(\overline{\mathbf{x}} \in {{\mathrm{spt}}}P\), then \(|\overline{\mathbf{x}}_i-\overline{\mathbf{x}}_j|\ge \alpha \) for \(i\ne j\). From Remark 2.7 we can assume that \(u(\overline{\mathbf{x}}_1)+\ldots +u(\overline{\mathbf{x}}_N) = c(\overline{\mathbf{x}}_1,\dots ,\overline{\mathbf{x}}_N)\). From the above discussion we may consider a Kantorovich N-tuple \((u_1,\dots ,u_N)\) obtained from u which is optimal for (1.3) and satisfies
and \(u_i(\overline{\mathbf{x}}_i)=\frac{1}{N}c(\overline{\mathbf{x}}_1,\dots ,\overline{\mathbf{x}}_N) \ge 0\) for all i. If \(x\notin \cup _{i=2}^N B(\overline{\mathbf{x}}_i,\frac{\alpha }{2})\) it holds:
Taking \(\mathbf{x}^1 = \overline{\mathbf{x}}\), we apply Lemma 2.3 and obtain a point \(\mathbf{x}^2 \in {{\mathrm{spt}}}P \setminus D_\alpha \) such that \(|\mathbf{x}^2_j - \overline{\mathbf{x}}_\sigma | \ge \beta \ge \alpha \) for all j and \(\sigma \), and from Remark 2.7 we may assume that
where we used \(\mathbf{x}^2_1 \notin \cup _{j \ge 2} B(\overline{\mathbf{x}}_j,\alpha )\). Fix \(i \ge 2\), it follows that if \(x\in B(\overline{\mathbf{x}}_i,\frac{\alpha }{2})\) then \(|x - \mathbf{x}^2_j| \ge \frac{\alpha }{2}\) for all \(j \ge 2\) so that
This concludes the estimate from above for \(u_1\) on \(\mathbb R^d\), and analogously for all \(u_i\). The formula above now allows us to find an estimate from below which, again, we write for \(u_1\) as
Then for all i one has
and analogously for \(u=\frac{1}{N}\sum _i u_i\) the same estimate holds. \(\square \)
Remark 3.5
Theorem 3.4 above applies to all costs considered in this paper including \(c_\alpha \) obtained replacing the function \(\phi \) by its truncation \(\phi _\alpha \).
The next theorem shows that under the usual assumptions on \(\rho \) and some additional assumptions on \(\phi \) there exists a Kantorovich potential which is Lipschitz and semiconcave with Lipschitz and semiconcavity constants depending on the concentration of \(\rho \). In the next statement we denote by Sc(u) the semiconcavity constant, that is the lowest nonnegative constant K such that \(u-K|\cdot |^2\) is concave.
Theorem 3.6
Let \(\rho \in \mathcal P(\mathbb R^d)\). Assume that \(\rho \) satisfies assumption (A), and let \(\beta \) be such that \(\mu _\rho (\beta )\le \frac{1}{N(N-1)^2}\).
-
If \(\phi \) is of class \(\mathcal C^1\) and for all \(t>0\) there exists a constant
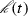 such that
such that  (3.4)
(3.4)then there exists a Kantorovich potential u for problem (1.2) such that
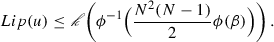
-
If \(\phi \) is of class \(\mathcal C^2\) and for all \(t>0\) there exists a constant
 such that
such that 
then there exists a Kantorovich potential u for problem (1.2) such that

Proof
According to Proposition 2.5 and Theorem 2.6 for \(\alpha \le \phi ^{-1}\Big (\frac{N^2(N-1)}{2}\phi (\beta )\Big )\) any Kantorovich potential \(u_\alpha \) for the cost \(\mathbf{\mathfrak {C}}_\alpha \) is also a potential for \(\mathbf{\mathfrak {C}}\). According to Lemma 3.3 above we choose a potential \(u_\alpha \) satisfying
Since the infimum of uniformly Lipschitz (resp. uniformly semiconcave) functions is still Lipschitz (resp. semiconcave) with the same constant, it is enough to show that the functions
are uniformly Lipschitz and semiconcave. To check that it is enough to compute the gradient and the Hessian matrix of these functions and use the respective properties of the pointwise cost \(\phi \). \(\square \)
Remark 3.7
The above Theorem 3.6 applies to the Coulomb cost \(\phi (t)=1/t\) and more generally to the costs \(\phi (t)=t^{-s}\) for \(s>0\).
3.3 Continuity Properties of the Cost
In this subsection we study some conditions that imply the continuity of the transportation cost \(C(\rho )\) with respect to the tight convergence on the marginal variable \(\rho \).
Lemma 3.8
Let \(\{\rho _n\}\subset \mathcal P(\mathbb R^d)\) be such that \(\rho _n\mathop {\rightharpoonup }\limits ^{*}\rho \) and assume that \(\rho \) satisfies assumption (A). Let \(\beta \) be such that
Then for all \(\delta \in (0,1)\) there exists \(k\in \mathbb N\) such that for all \(n>k\)
Proof
We argue by contradiction assuming that there exists a sequence \(\{x_n\}\) such that
Since the sequence \(\{\rho _n\}\) is uniformly tight there exists K such that \(|x_n|<K\). Up to subsequences we may assume that \(x_n\rightarrow \tilde{x}\) for a suitable \(\tilde{x}\). Let \(\delta ' \in (\delta ,1)\). Then, for n large enough, \(\overline{B(x_n,\delta \beta )}\subset B(\tilde{x},\delta ' \beta )\) and since
and
we obtain
which is a contradiction. \(\square \)
Theorem 3.9
Let \(\{\rho _n\}\subset \mathcal P(\mathbb R^d)\) be such that \(\rho _n\mathop {\rightharpoonup }\limits ^{*}\rho \) with \(\rho \) satisfying assumption (A). Assume that the cost function \(\phi \) satisfies assumption (3.4). Then
Proof
We first note that the theorem above holds for the costs \(c_\alpha \) since they are continuous and bounded in \(\mathbb R^d\), and from the fact that whenever \(P \in \Pi (\rho )\) there exists \(P_n \in \Pi (\rho _n)\) such that \(P_n\mathop {\rightharpoonup }\limits ^{*} P\), so that \(C_\alpha \) is continuous with respect to weak convergence.
Thanks to Lemma 3.8 and Theorem 2.4 we infer that there exists \(k>0\) and \(\alpha >0\) such that the optimal transport plans for \(C(\rho )\) and \(C(\rho _n)\) all supported in \(\mathbb R^{Nd} \setminus D_\alpha \) for \(n \ge k\). But then the functionals C and \(C_\alpha \) coincide on \(\{\rho \}\cup \{\rho _n\}_{n \ge k}\) and the thesis follows form the continuity of \(C_\alpha \). \(\square \)
Remark 3.10
Under the hypothesis (3.4) on \(\phi \) we may propose the following alternative proof for Theorem 3.9 above. Since the pointwise cost c is lower semicontinuous, by the dual formulation (1.2) the functional C is lower semicontinuous too. Then we only need to prove the inequality \(\limsup _{n\rightarrow \infty }C(\rho _n)\le C(\rho )\). By Theorems 3.4 and 3.6 and Lemma 3.8 above, there exists a constant K and an integer \(\nu \) such that for \(n\ge \nu \) we can choose a Kantorovich potential \(u_n\) for \(\rho _n\) and the cost C which is K-Lipschitz and bounded by K. Up to subsequences we may assume that \(u_n\rightarrow u\) uniformly on compact sets, so u is K-Lipschitz and satisfies
It follows that
as required.
Theorem 3.11
Let \(\rho _1,\rho _2\in \mathcal P(\mathbb R^d)\) be such that
for a suitable \(\beta >0\). Then for every \(\alpha \) as in Theorem 2.4 we have
Proof
Without loss of generality we may assume that \(C(\rho _2) \le C(\rho _1)\). Let \(u_1\) and \(u_2\) be Kantorovich potentials which satisfy the estimate of Theorem 3.4 respectively for \(\rho _1\) and \(\rho _2\) . We have
By the optimality of \(u_1\) and \(u_2\)
and the conclusion now follows by estimate (3.3). \(\square \)
Corollary 3.12
The functional \(C(\rho )\) is Lipschitz continuous on any bounded subset of \(L^p(\mathbb R^d)\) for \(p>1\) and in particular on any bounded subset of the space \({\mathcal H}\).
References
Beiglböck, M., Léonard, C., Schachermayer, W.: A general duality theorem for the Monge-Kantorovich transport problem. Studia Math. 209, 2 (2012)
Buttazzo, G., De Pascale, L., Gori-Giorgi, P.: Optimal-transport formulation of electronic density-functional theory. Phys. Rev. A 85(6), 062502 (2012)
Carlier, G.: On a class of multidimensional optimal transportation problems. J. Convex Anal. 10(2), 517–530 (2003)
Carlier, G., Nazaret, B.: Optimal transportation for the determinant. ESAIM Control Optim. Calc. Var. 14(04), 678–698 (2008)
Colombo, M., De Pascale, L., Di Marino, S.: Multimarginal optimal transport maps for 1-dimensional repulsive costs. Can. J. Math. 54, 717 (2013)
Colombo, M., Di Marino, S.: Equality between Monge and Kantorovich multimarginal problems with Coulomb cost. Ann. Math. Pura Appl., 1–14 (2013)
Cotar, C., Friesecke, G., Klüppelberg, C.: Density functional theory and optimal transportation with Coulomb cost. Commun. Pure Appl. Math. 66(4), 548–599 (2013)
De Pascale, L.: Optimal transport with Coulomb cost. Approximation and duality. ESAIM Math. Model. Numer. Anal. 49(6), 1643–1657 (2015)
Di Marino, S., Gerolin, A., Nenna. L.: Optimal transportation theory with repulsive costs. arXiv:1506.04565
Friesecke, G., Mendl, C.B., Pass, B., Cotar, C., Klüppelberg, C.: N-density representability and the optimal transport limit of the Hohenberg-Kohn functional. J. Chem. Phys. 139(16), 164109 (2013)
Gangbo, W., Swiech, A.: Optimal maps for the multidimensional Monge-Kantorovich problem. Commun. Pure Appl. Math. 51(1), 23–45 (1998)
Ghoussoub, N., Moameni, A.: A self-dual polar factorization for vector fields. Commun. Pure Appl. Math. 66(6), 905–933 (2013)
Gori-Giorgi, P., Seidl, M.: Density functional theory for strongly-interacting electrons: perspectives for physics and chemistry. Phys. Chem. Chem. Phys. 12(43), 14405–14419 (2010)
Gori-Giorgi, P., Seidl, M., Vignale, G.: Density-functional theory for strongly interacting electrons. Phys. Rev. Lett. 103(16), 166402 (2009)
Heinich, H.: Problème de Monge pour \(n\) probabilités. C. R. Math. Acad. Sci. Paris 334(9), 793–795 (2002)
Hohenberg, P., Kohn, W.: Inhomogeneous electron gas. Phys. Rev. 136(3B), B864 (1964)
Kellerer, H.G.: Duality theorems for marginal problems. Probab. Theory Relat. Fields 67(4), 399–432 (1984)
Kohn, W., Sham, L.J.: Self-consistent equations including exchange and correlation effects. Phys. Rev. 140(4A), A1133 (1965)
Lieb, E.H.: Density functionals for coulomb systems. Int. J. Quantum Chem. 24(3), 243–277 (1983)
Mendl, C.B., Lin, L.: Kantorovich dual solution for strictly correlated electrons in atoms and molecules. Phys. Rev. B 87(12), 125106 (2013)
Moameni, A.: Invariance properties of the Monge-Kantorovich mass transport problem. Discret. Contin. Dyn. Syst. 36(5), 2653–2671 (2016)
Pass, B.: Uniqueness and monge solutions in the multimarginal optimal transportation problem. SIAM J. Math. Anal. 43(6), 2758–2775 (2011)
Pass, B.: On the local structure of optimal measures in the multi-marginal optimal transportation problem. Calc. Var. Partial. Differ. Equat. 43(3–4), 529–536 (2012)
Rachev, S.T., Rüschendorf, L.: Mass Transportation Problems. Vol. I: Theory (Probability and Its Applications ). Springer, New York (1998)
Seidl, M.: Strong-interaction limit of density-functional theory. Phys. Rev. A 60(6), 4387 (1999)
Seidl, M., Gori-Giorgi, P., Savin, A.: Strictly correlated electrons in density-functional theory: a general formulation with applications to spherical densities. Phys. Rev. A 75(4), 042511 (2007)
Seidl, M., Perdew, J.P., Levy, M.: Strictly correlated electrons in density-functional theory. Phys. Rev. A 59(1), 51 (1999)
Acknowledgements
This paper has been written during some visits of the authors at the Department of Mathematics of University of Pisa and at the Laboratoire IMATH of University of Toulon. The authors gratefully acknowledge the warm hospitality of both institutions. The research of the first and third authors is part of the project 2010A2TFX2 Calcolo delle Variazioni funded by the Italian Ministry of Research and is partially financed by the “Fondi di ricerca di ateneo” of the University of Pisa. The authors also would like to thank the anonymous referees for their valuable comments and suggestions to improve the paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Buttazzo, G., Champion, T. & De Pascale, L. Continuity and Estimates for Multimarginal Optimal Transportation Problems with Singular Costs. Appl Math Optim 78, 185–200 (2018). https://doi.org/10.1007/s00245-017-9403-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00245-017-9403-7



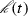 such that
such that 
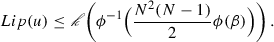
 such that
such that 
