Abstract
We propose a calculus for concurrent reversible multiparty sessions, equipped with a flexible choice operator allowing for different sets of participants in each branch. This operator is inspired by the notion of connecting action recently introduced by Hu and Yoshida to describe protocols with optional participants. We argue that this choice operator allows for a natural description of typical communication protocols. Our calculus also supports a compact representation of the history of processes and types, which facilitates the definition of rollback. Moreover, it implements a fine-tuned strategy for backward computation. We present a session type system for the calculus and show that it enforces the expected properties of session fidelity, forward progress and backward progress.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Session types are a simple but expressive type formalism that specifies the structure of interactions. Traditionally, session types have been used to ensure safety properties of interactions, such as absence of communication errors, deadlock freedom and race freedom.
Reversibility is a means to improve system flexibility and reliability. Reversing a computation may be defined as the act of undoing some suffix of the computation, in order to return to a previously visited state. In a nondeterministic computation, this possibility may be used to return to a previous branching point, in case the chosen branch has led to an unsuccessful state.
In the setting of structured communications, reversibility has been first studied for contracts [2, 3] and transactions [11, 12, 21]. More recently, it has started to be investigated also for session calculi, both binary [24, 34] and multiparty [14, 26, 28, 35] (see Sect. 6 for more discussion on related work).
When reversing a structured interaction, one has to preserve the consistency of the global state: if one partner triggers a rollback, then all its communicating partners should roll back accordingly. Session types turn out to be very useful here, since they specify both the functionality of communications (sender, receiver and type of message), and the order in which they should occur.
We present a calculus for concurrent reversible multiparty sessions, whose distinctive feature is a flexible choice operator, allowing for different sets of participants in its branches. The only participant which is required to occur in all branches is the one which solves the choice, henceforth called the choice leader.
Our choice operator is inspired by the notion of connecting action recently introduced by Hu and Yoshida to describe protocols with optional participants [20]. The intuition behind connecting actions is that in some parts of the protocol, delimited by a choice construct, some participants are required to take part in the interaction while some others may be optional. Connecting actions are used to invite optional participants to join the interaction along some branches of the choice. For instance, in a PC meeting, it could happen that in case of divergent views about a paper, the PC chair launches a discussion among the concerned PC members, but also invites some additional PC members to join the discussion. These additional members are optional in the sense that they are not required to discuss on that particular paper, but they may be invited to do so in some cases.
Here we shall make a more permissive use of connecting actions than in [20].
The differences between our connecting actions and those in [20] are discussed in Sect. 6.
Compared to the standard choice operator of multiparty session calculi, our flexible choice allows for a more natural description of typical communication protocols, such as the one mentioned above. Another example is the vacation protocol discussed below, where Alice has to decide between two destinations, and depending on her decision she will wish to contact either an airline or a railway company but not both. This will be modelled by a choice between two connecting actions, one with the airline and one with the railway company.
Another notable feature of our calculus is that it gives a compact representation of the history of processes and types, which facilitates the definition of rollback. It also implements a fine-tuned strategy for backward computation, which is geared towards achieving compliance. In essence, a backward move can only return to a past choice point, and it can only be triggered by the leader of that choice; moreover, the past choice state is restored without the already explored branch, thus forcing the choice leader to engage into a different branch.
The main contributions of our paper may be summarised as follows:
-
the introduction of a flexible choice operator based on connecting actions in a reversible multiparty session framework;
-
a fine-tuned strategy for rollback to checkpointed choices, whereby rollback can only be triggered by choice leaders in predefined states of the computation, leading back to the choice state stripped off the unsuccessful path.
This work builds on our previous papers [8, 14]. As regards the treatment of reversibility in multiparty sessions, the general principles and the use of checkpoints for return points are taken from [14], while the formalisation of histories and the specific rollback mechanism are borrowed from [8]. The formalisation of histories is pushed a little further here than in [8], including notions of causality and conflict for communication occurrences. On the other hand, the use of connecting actions is new with respect to [8, 14], and so is the study of their interplay with reversible computations. This interplay is not entirely trivial, as it requires revisiting the definition of projection of a global type onto its participants. A relevant new notion to this purpose is that of affecting choice for a participant: intuitively, a choice specified by a global type affects a participant if the whole choice is needed to determine the projection on that participant. By definition, a choice affects all its required participants while it does not affect optional participants which appear in only one branch. If we ignore connecting actions, the expressive power of our calculus is comprised between that of [14] and that of [8]. Indeed, [8] allows for both parallel and sequential composition within processes and types, yielding a powerful but somewhat complex calculus. Here we decided to stick to a more standard syntax, in order to be able to focus on the main topic of the paper, namely backward computation in the presence of connecting actions.
Vacation protocol example
To illustrate our approach, we present a simple protocol involving five parties, Alice, Bob, Carol, the airline company Alitalia and the railway company Trenitalia. This protocol, henceforth called the vacation protocol, will serve as our running example throughout the paper.
For Easter holidays, Alice receives two independent invitations from Bob and Carol. Bob proposes to Alice to visit him in Paris, while Carol offers to host her in her seaside house in Amalfi. Since Alice lives in Rome, depending on her decision she will need to book a flight to go to Paris or a train to reach Amalfi. To do so, Alice will either contact Alitalia or Trenitalia to buy a ticket, and then inform both Bob and Carol of her decision. In case of a plane or train strike, Alice is allowed to change her mind. Letting \(\textsf {a} , \textsf {b} , \textsf {c} , \textsf {f} , \textsf {t} \) denote respectively Alice, Bob, Carol, Alitalia and Trenitalia, a global type describing this communication protocol is:
where \(_C{\boxplus }\) is a choice with checkpoint label C, meaning that the choice leader (i.e. the participant who makes the choice, Alice in this case) can rollback to take a different branch of the choice. The communications between Alice and Alitalia/Trenitalia are connecting communications (represented by messages of the form \({\mathop {\leftrightarrow }\limits ^{\lambda }}\)). This means that there is no assurance for Alitalia and Trenitalia that they will receive a message from Alice. With standard global types, Alitalia and Trenitalia should receive a message from Alice in both branches of the choice, and this is clearly not realistic. A different way out would be to use three global types instead of one, respectively with sets of participants {Alice, Bob, Carol}, {Alice, Alitalia} and {Alice, Trenitalia}. The drawback of the latter solution is that, in the presence of more than one global type, a simple session type system is not sufficient to ensure progress, and one needs to recourse to more refined type systems [29].
Thanks to connecting actions, the vacation protocol may be described by a single global type, without the constraints of standard global types.
Outline The rest of the paper is organised as follows. In Sect. 2 we define the syntax and operational semantics—both forward and backward—of our calculus. In Sect. 3 we introduce our syntax for global types and session types and we establish well-formedness conditions for global types. In Sect. 4 we present our type system and prove some preliminary properties. In Sect. 5 we prove the soundness of our type system, namely that it ensures the expected semantic properties of session fidelity and forward and backward progress. We conclude in Sect. 6 with some discussion on related and future work. The Appendix proves the correctness of a possible implementation of backward reduction.
2 Calculus
We assume the following base sets: simple messages, ranged over by \(\lambda ,\lambda ',\dots \) and forming the set \(\textsf {Msg} \); connecting messages, ranged over by \({\mathop {\leftrightarrow }\limits ^{\lambda }},{\mathop {\leftrightarrow }\limits ^{\lambda '}},\dots \) and forming the set \(\textsf {CMsg} \); checkpoint labels, ranged over by \(C, C'\) and forming the set \(\textsf {ChLa} \); and session participants, ranged over by \(\textsf {p} ,\textsf {q} ,\textsf {r} \) and forming the set \(\textsf {Part} \). We use \(\varLambda \) to range over both simple messages and connecting messages.
We use \(\textstyle {\varDelta }\) to range over sets of checkpoint labels, and \(\overline{\gamma }\) to stand for either the empty set or a singleton consisting of an overlined checkpoint label (curly brackets will be omitted around singletons):
Sets \(\textstyle {\varDelta }\) and \(\overline{\gamma }\) are associated with choices in processes. More precisely, a set \(\textstyle {\varDelta }\) is associated with an external choice and said to be passive, while a set \(\overline{\gamma }\) is associated with an internal choice and said to be active. Intuitively, an overlined label \(\overline{C}\) is the handle for a backward move: a participant who crossed an internal choice (henceforth called the choice leader) with checkpoint label \(\overline{C}\), and then proceeded in the computation, may decide to return to that choice whenever she has the ability to send a message. Within a network, this backward move of the choice leader will have to be matched by backward moves of all the participants who did some action after crossing the matching external choice, whose checkpoint set contains label \(C\). The asymmetry between \(\textstyle {\varDelta }\) and \(\overline{\gamma }\) is justified by the fact that there is only one choice leader who can send messages to various participants.
Let \(\pi \in \{ \textsf {p} ?\varLambda , \textsf {p} !\varLambda ~|~\textsf {p} \in \textsf {Part} , \varLambda \in \textsf {Msg} \cup \textsf {CMsg} \}\) denote an atomic action, namely a simple input/output action or an input/output action establishing a connection. As in [20], connecting inputs may be dangling forever, whereas simple inputs will eventually take place. This gives a natural freedom in the definition of communication protocols as illustrated in the examples of the introduction. An atomic action can bear a hat, in which case it represents an already executed action. We use \(\widetilde{\pi }\) to stand for either \(\pi \) or \(\widehat{\pi }\). External choices and internal choices are denoted by \(\sum \) and \(\bigoplus \), respectively.
Definition 1
(Processes) Processes are defined by:
where in both kinds of choice the pairs \((\textsf {p} _i,\varLambda _i)\) are assumed to be all distinct. Moreover, for external choices we also assume that the \(\varLambda _i\)’s are either all simple or all connecting messages. This condition allows us to distinguish between simple and connecting external choices according to the kind of their inputs. This is essential for requiring that at least one of the inputs in a simple external choice will eventually be matched by a message. Instead all inputs in a connecting external choice can wait forever. Processes without hats are called user processes and the others are runtime processes.
We will omit empty sets of checkpoint labels, choice symbols in one-branch choices, and trailing \({\textsf {end} } \) processes.
External and internal choices are assumed to be associative, commutative, and non-empty (except when combined with binary choices). A prefixed process may be either an input process or an output process. We require recursion to be guarded. Processes are treated equi-recursively, i.e. they are identified with their generated tree [33]. In other words, we consider processes up to the standard structural equivalence of processes.
The typing rules of Sect. 4 will ensure that in a choice, at most one of the first atomic actions bears a hat. This condition expresses the fact that executing a choice amounts to executing one of its branches.
In a full-fledged calculus, messages would carry values, namely they would be of the form \(\varLambda (v)\). Here, for simplicity we consider only pure messages.
Networks are parallel compositions of pairs \(\textsf {p} \llbracket \,P\,\rrbracket \), where participant \(\textsf {p} \) has behaviour \(P\).
Definition 2
(Networks) Networks are defined by: \(\qquad \mathbb {N}\quad \,{:}{:}{=}\, \quad \textsf {p} \llbracket \,P\,\rrbracket ~~~\mathbf {|\!|}~ ~~\mathbb {N}\mathrel {\Vert }\mathbb {N}\)
The operator \(\mathrel {\Vert }\) is associative and commutative, with neutral element \(\textsf {p} \llbracket \,{\textsf {end} } \,\rrbracket \) for each \(\textsf {p} \). These laws, together with the structural equivalence of processes, give the structural equivalence of networks.
Example 1
(Networks) A network for the vacation example of Sect. 1 is as follows:
where
\(P^{\textsf {a} }{=}\textsf {b} ?{ iP}{\mathrel {;}\,}\textsf {c} ?{ iA}{\mathrel {;}\,}(P_1^{\textsf {a} }\ {}_{{\overline{C}}}\oplus \ P_2^{\textsf {a} })\,\) with \(P_1^{\textsf {a} }{=}\textsf {f} !{\mathop {\leftrightarrow }\limits ^{{ tk}}}{\mathrel {;}\,}\textsf {b} !{ yes}{\mathrel {;}\,}\textsf {c} !{ no}\,\) and \(P_2^{\textsf {a} }=\textsf {t} !{\mathop {\leftrightarrow }\limits ^{{ tk}}}{\mathrel {;}\,}\textsf {b} !{ no}{\mathrel {;}\,}\textsf {c} !{ yes}\)
\(P^{\textsf {b} }=\textsf {a} !{ iP}{\mathrel {;}\,}(\textsf {a} ?{ yes}\ {}_{ {{C}}}+\ \textsf {a} ?{ no})\,\) \(P^{\textsf {c} }=\textsf {a} !{ iA}{\mathrel {;}\,}(\textsf {a} ?{ no}\ {}_{ {{C}}}+\ \textsf {a} ?{ yes})\) \(P^{\textsf {f} }=P^{\textsf {t} }={}_{ {{C}}}\textsf {a} ?{\mathop {\leftrightarrow }\limits ^{{ tk}}}\)
The operational semantics is given by two LTSs, one for processes and one for networks. In the LTS for processes, forward transitions have the form  and backward transitions have the form
and backward transitions have the form  or
or  . We define \(P\downarrow _{out}\) if
. We define \(P\downarrow _{out}\) if  for some \(\textsf {p} , \varLambda , P'\). In the LTS for networks, forward and backward transitions have respectively the form
for some \(\textsf {p} , \varLambda , P'\). In the LTS for networks, forward and backward transitions have respectively the form  and
and  .
.
The LTSs for processes and networks are given in Fig. 1. Rules \({\textsc {[ExtCh]}}\) and \({\textsc {[IntCh]}}\) allow an action to be extracted from one of the summands, as usual, but instead of discarding the other summands they record the fact that the choice has been crossed by marking the executed action with a hat. With this technique, inspired by [6] and already used for reversible computations in [8, 26], all the dynamic operators are turned into static operators and nothing is lost of the original user process. Notice that when \(I=\{j\}\) these rules become  . Rule \({\textsc {[BackA]}}\) is the main backward rule: it applies to a past internal choice in which one branch has been partially executed, and it allows the process to roll back to the original choice where the executed branch is removed.Footnote 1 For this to be possible, the choice must have at least one alternative branch \(P_i\) and an overlined label \(\overline{C}\), which will label the back transition. This is essential to ensure (by means of typing) that the choice leader will be the only participant habilitated to trigger a rollback to this choice. The condition \(P\downarrow _{out}\) means that in order to trigger a rollback, the process \(P\) must be “in lead”, namely able to do an output. In this way, rolling back acts as an alternative to one of its possible outputs.
. Rule \({\textsc {[BackA]}}\) is the main backward rule: it applies to a past internal choice in which one branch has been partially executed, and it allows the process to roll back to the original choice where the executed branch is removed.Footnote 1 For this to be possible, the choice must have at least one alternative branch \(P_i\) and an overlined label \(\overline{C}\), which will label the back transition. This is essential to ensure (by means of typing) that the choice leader will be the only participant habilitated to trigger a rollback to this choice. The condition \(P\downarrow _{out}\) means that in order to trigger a rollback, the process \(P\) must be “in lead”, namely able to do an output. In this way, rolling back acts as an alternative to one of its possible outputs.
Rule \({\textsc {[BackP]}}\) is needed to allow the remaining participants to roll back. The mapping  erases hats from processes, yielding user processes, i.e.
erases hats from processes, yielding user processes, i.e.

and  acts homomorphically otherwise. Note that the rollback rules can only be applied to processes that are not user processes: in particular, one branch can be erased only if at least one of its actions has been executed.
acts homomorphically otherwise. Note that the rollback rules can only be applied to processes that are not user processes: in particular, one branch can be erased only if at least one of its actions has been executed.
Evaluation contexts are as expected.
Definition 3
(Evaluation contexts) Evaluation contexts\(\mathcal {E}\) are defined by:
An evaluation context \(\mathcal {E}\) is \(\textsf {ok} \) for \(C\) (\(\overline{C}\)) if \(C\not \in \textstyle {\varDelta }\) (\(\overline{C}\not =\overline{\gamma }\)) whenever \(\mathcal {E}\) has a sub-context of the shape \({}_{\textstyle {\varDelta }}(\sum _{h\in H}P_h~+~\widehat{\pi }{\mathrel {;}\,}\mathcal {E}')\) (\({}_{{}_{{\scriptstyle {\overline{\gamma }}}}}(\bigoplus _{h\in H}P_h~\oplus ~\widehat{\pi }{\mathrel {;}\,}\mathcal {E}')\)). We use this condition in rules \({\textsc {[CtBA]}}\) and \({\textsc {[CtBP]}}\) to assure that all participants involved in a recursion go back to the same checkpoint, namely to the outermost one, as in [28]. This is needed to assure subject reduction, see Example 6.
Rule \({\textsc {[Com]}}\) is standard and deals with both simple and connecting messages. We write  if Rule \({\textsc {[CtBP]}}\) (with label \(C\)) cannot be applied to \(P\). This means that \(C\) can only occur in user processes within \(P\). In other words, \(P\) does not contain an executed \({}_{\textstyle {\varDelta }}+\) with \(C\in \textstyle {\varDelta }\). In a well-typed network, Rule \({\textsc {[Back]}}\) will make participant \(\textsf {p} \) roll back to an internal choice and moreover, all participants that can roll back to corresponding external choices will do so in the same step. This will be the basis for our soundness result in Sect. 5. Notice that the only requirements of rule \({\textsc {[Back]}}\) concern process \(P\), since it is easy to verify that either
if Rule \({\textsc {[CtBP]}}\) (with label \(C\)) cannot be applied to \(P\). This means that \(C\) can only occur in user processes within \(P\). In other words, \(P\) does not contain an executed \({}_{\textstyle {\varDelta }}+\) with \(C\in \textstyle {\varDelta }\). In a well-typed network, Rule \({\textsc {[Back]}}\) will make participant \(\textsf {p} \) roll back to an internal choice and moreover, all participants that can roll back to corresponding external choices will do so in the same step. This will be the basis for our soundness result in Sect. 5. Notice that the only requirements of rule \({\textsc {[Back]}}\) concern process \(P\), since it is easy to verify that either  or
or  for any other process \(Q\). Note that a direct implementation of rule \({\textsc {[Back]}}\) would be unrealistic. We discuss a possible asynchronous implementation of this rule at the end of the section.
for any other process \(Q\). Note that a direct implementation of rule \({\textsc {[Back]}}\) would be unrealistic. We discuss a possible asynchronous implementation of this rule at the end of the section.
When the labels of transitions are not relevant, we write them simply as \(\longrightarrow \) and  . In this case, we use \(\longrightarrow ^* \) to denote the reflexive and transitive closure of \(\longrightarrow \) and
. In this case, we use \(\longrightarrow ^* \) to denote the reflexive and transitive closure of \(\longrightarrow \) and  to denote the reflexive and transitive closure of
to denote the reflexive and transitive closure of  .
.
Example 2
(Reduction of networks) We describe the evolution of the network \(\mathbb {N}\) of Example 1. At each step we only show the participants that are modified by the reduction.

The last rollback is triggered by a \({[\textsc {BackA}]}\) move of Alice synchronised with \({[\textsc {BackP}]}\) moves of Bob and Alitalia.
In the rest of this section we discuss a possible implementation of rule \({\textsc {[Back]}}\), which decomposes the simultaneous rollback of a set of participants into a sequence of backward moves, one for each participant in the set. The first move of the sequence is always that of the choice leader.
We introduce states to define systems, which are pairs of networks and states.
States are defined by \(\sigma := \langle c,\mathbb {P}_1,\mathbb {P}_2\rangle \), where \(c\) denotes either a checkpoint label \(C\) or ‘−’, and \(\mathbb {P}_1, \mathbb {P}_2\) form a partition on the set of network participants. In a state of the form \(\langle -,\mathbb {P}_1,\mathbb {P}_2\rangle \), the set \(\mathbb {P}_2\) is always \(\emptyset \). A state is ready if it is of the shape \(\langle -,\mathbb {P},\emptyset \rangle \). A communication can only take place in a ready state, yielding a ready state again. Similarly, the starting move of a rollback can only take place in a ready state, but it gives rise to a state of the form \(\langle C,\mathbb {P}_1,\mathbb {P}_2\rangle \). In a state \(\langle C,\mathbb {P}_1,\mathbb {P}_2\rangle \), a rollback is underway: the participants in \(\mathbb {P}_1\) have already contributed to the rollback, while the participants in \(\mathbb {P}_2\) still need to respond to the rollback “call” from the choice leader.
Systems have the form \(\mathbb {N}\between \langle c,\mathbb {P}_1,\mathbb {P}_2\rangle \), where \(\mathbb {P}_1\cup \mathbb {P}_2\) is the participant set of \(\mathbb {N}\). A system \(\mathbb {N}\between \sigma \) is ready if the state \(\sigma \) is ready. Figure 2 gives the LTS for systems. We use the labelled double arrows  and the labelled curly arrows
and the labelled curly arrows  ,
,  ,
,  ,
,  for communication and backward moves of systems, respectively. In this way the labelled arrows for networks and systems are disjoint.
for communication and backward moves of systems, respectively. In this way the labelled arrows for networks and systems are disjoint.
The reverse rule [Back] of Fig. 1 splits into four rules for systems:
-
rule [BackS] allows the choice leader \(\textsf {p} \) to start a rollback: the new state contains the checkpoint label and all participants but \(\textsf {p} \) are required to roll back, if possible;
-
rule [BackY] allows participant \(\textsf {p} \) to roll back to the checkpoint label memorised in the state: the new state records the rollback of \(\textsf {p} \);
-
rule [BackN] modifies the state recording that participant \(\textsf {p} \) cannot roll back with the current checkpoint label;
-
rule [BackE] ends the rollback by erasing from the state the current checkpoint label when all participants have become aware of the rollback.
The participants different from the choice leader are split into those that may roll back and those that may not.
The first ones reduce by rule [BackY] and the second ones reduce by rule [BackN].
In “Appendix A” we prove the equivalence between the LTS of Fig. 1 and the one of Fig. 2.
Example 3
(Reduction of systems) We show now how the rules of Fig. 2 may be used to simulate the execution of the network \(\mathbb {N}\) in Example 2. First observe that, since the initial state is \(\sigma =\,\)\(\langle -,\{\textsf {a} ,\textsf {b} ,\textsf {c} ,\textsf {f} ,\textsf {t} \},\emptyset \rangle \), the first four communications of the system can be derived by rule [ComS], leaving the state \(\sigma \) unchanged and yielding the same network as in Example 2 (fourth line), namely \(\mathbb {N}'= \mathbb {N}_1\mathrel {\Vert }\mathbb {N}_2\) where:
Then, an application of rule [BackS] starts the rollback and a possible evolution of the system \(\mathbb {N}'\between \sigma \) is the following:

The application of rule [BackE] closes the rollback and brings the system back to the ready state \(\sigma \). Note that the [BackN] and [BackY] moves can be performed in any order as long as they follow the [BackS] move by Alice. The network \(\mathbb {N}\) is typable in the system of Sect. 4 by the global type given in the Introduction. By the Subject Reduction Theorem (Theorem 1) also the network \(\mathbb {N}'\) is typable. This example shows that the four back rules of Fig. 2 are all used for reducing typable networks.
3 Global types and session types
According to [18, 19], a multiparty session is a series of communications among participants [20], which follows a predefined protocol specified by a global type. Global types are built from choices among communications with the same sender, possibly using recursion. The choices are required to be non-ambiguous, i.e. to have either different receivers or different messages. As in processes, choices in global types have checkpoint labels which mark them as return points for rollbacks, and the executed part is highlighted with hats. For consistency, when a communication has a hat, then also all the communications that cause it (see Definition 7) must have a hat. This condition is expressed by Definition 8.
The inputs/outputs of each participant are determined by her session type, which is obtained by projecting the global type of the whole conversation. To define session types we start with the syntax of session pre-types (Definition 9) and then we single out session types (Definition 11) using the projection of global types (Fig. 5). The crucial point in the definition of projection is to determine when a participant which is not the choice leader of a choice may be realised by an external choice of processes. To this aim we define a meet operation on session pre-types (Definition 10).
We use \(\gamma \) to denote either the empty set or a singleton made of a checkpoint label:
Sets \(\gamma \) will be associated with choices in global types.
Let \(\alpha ^{\textsf {p} } \in \{ \textsf {p} \xrightarrow {\varLambda }\textsf {q} ~|~\textsf {q} \in \textsf {Part} , \varLambda \in \textsf {Msg} \cup \textsf {CMsg} \}\) denote an atomic communication with sender \(\textsf {p} \). The communication \(\textsf {p} \xrightarrow {\lambda }\textsf {q} \) is simple, while the communication \(\textsf {p} \xrightarrow {{\mathop {\leftrightarrow }\limits ^{\lambda }}}\textsf {q} \) is connecting. An atomic communication can bear a hat, in notation \(\widehat{\alpha ^{\textsf {p} }}\), in which case it represents a past or executed communication. The symbol \(\widetilde{\alpha ^{\textsf {p} }}\) stands for either \(\alpha ^{\textsf {p} }\) or \(\widehat{\alpha ^{\textsf {p} }}\). We write \(\widetilde{\alpha }\) instead of \(\widetilde{\alpha ^{\textsf {p} }}\) when the sender is not relevant. Given a communication \(\alpha =\textsf {p} \xrightarrow {\varLambda }\textsf {q} \), we define the sender and receiver of \(\alpha \) to be \(\textsf {sender} (\alpha )=\textsf {p} \) and \(\textsf {recv} (\alpha )=\textsf {q} \). Moreover, we denote by \(\textsf {part} (\alpha )=\{\textsf {recv} (\alpha ), \textsf {sender} (\alpha )\}\) the participants of the communication \(\alpha \).
A global type \(\textsf {K} \) specifies an interaction that is still to start. A general global type \(\textsf {G} \) specifies a partially executed interaction, whose parts that have been discarded in choices or remain to be executed are specified by subterms \(\textsf {K} \). By \(|I|\) we denote the cardinality of the set I.
Definition 4
(Global types) Global types\(\textsf {G} \) are defined by:
where \(|J|>1\), \(|I|>0\) and all atomic communications in a choice are different. I.e. \(\alpha ^\textsf {p} _h\ne \alpha ^\textsf {p} _k\) for all \(h\ne k\in J\) in a choice \({}_{\gamma }{\boxplus }_{j\in J}\,\alpha ^{\textsf {p} }_{j}{\mathrel {;}\,}\textsf {K} _j\), and \(\alpha ^\textsf {p} _h\ne \alpha ^\textsf {p} _k\) for all \(h\ne k\in I\) and \(\alpha ^\textsf {p} _h\ne \alpha ^\textsf {p} \) for all \(h\in I\) in a partially executed choice \({}_{\gamma }({\boxplus }_{i\in I}\,\alpha ^{\textsf {p} }_{i}{\mathrel {;}\,}\textsf {K} _i\mathrel {\boxplus }\widehat{\alpha ^{\textsf {p} }}\mathrel {;}\,\textsf {G} )\).
The type \({}_{\gamma }\widetilde{\alpha }{\mathrel {;}\,}\textsf {G} \) represents a prefixing communication. The choice operator \({\boxplus }\) is n-ary (\(n\ge 2\)) and commutative, and “;” has higher precedence than \({\boxplus }\). The notation \({}_{\gamma }({\boxplus }_{i\in I}\,\alpha ^{\textsf {p} }_{i}{\mathrel {;}\,}\textsf {K} _i\mathrel {\boxplus }\widehat{\alpha ^{\textsf {p} }}\mathrel {;}\,\textsf {G} )\) stands for a choice where the branch initiating with \(\widehat{\alpha ^{\textsf {p} }}\) has started to be executed, while the other branches have been discarded.
By abuse of notation, we will write \({}_{\gamma }\boxplus _{j\in J}\,\widetilde{\alpha ^{\textsf {p} }_{j}}{\mathrel {;}\,}\textsf {G} _j\) for either \({}_{\gamma }{\boxplus }_{j\in J}\,\alpha ^{\textsf {p} }_{j}{\mathrel {;}\,}\textsf {G} _j\) or \({}_{\gamma }({\boxplus }_{j\in J\setminus \{k\}}\,\alpha ^{\textsf {p} }_{j}{\mathrel {;}\,}\textsf {G} _j\mathrel {\boxplus }\widehat{\alpha ^{\textsf {p} }_k}\mathrel {;}\,\textsf {G} _k)\). In the examples we will write \(\widetilde{\alpha ^{\textsf {p} }_1}{\mathrel {;}\,}\textsf {G} _1{\;}_\gamma \mathrel {\textstyle {{\boxplus }}}\widetilde{\alpha ^{\textsf {p} }_2}{\mathrel {;}\,}\textsf {G} _2\) and \({}_{\gamma }(\widetilde{\alpha ^{\textsf {p} }_1}{\mathrel {;}\,}\textsf {G} _1\mathrel {\textstyle {{\boxplus }}}\ldots \mathrel {\textstyle {{\boxplus }}}\widetilde{\alpha ^{\textsf {p} }_n}{\mathrel {;}\,}\textsf {G} _n)\). (Note however that only one of the \(\widetilde{\alpha ^{\textsf {p} }_i}\) may have a hat.)
We use \({}_{\gamma }\boxdot _{i\in I}\,\widetilde{\alpha ^{\textsf {p} }_{i}}{\mathrel {;}\,}\textsf {G} _i\) to stand for \({}_{\gamma }\,\widetilde{\alpha ^\textsf {p} }{\mathrel {;}\,}\textsf {G} \) when I is a singleton and for \({}_{\gamma }\boxplus _{i\in I}\,\widetilde{\alpha ^{\textsf {p} }_{i}}{\mathrel {;}\,}\textsf {G} _i\) otherwise. Moreover, \({}_{\gamma }(\boxdot _{h\in H}\,{\alpha ^{\textsf {p} }_{h}}{\mathrel {;}\,}\textsf {G} _h{\textstyle {\boxdot }}\widehat{\alpha ^{\textsf {p} }}\mathrel {;}\,\textsf {G} ){}\) stands for \({}_{\gamma }\widehat{\alpha ^{\textsf {p} }}{\mathrel {;}\,}\textsf {G} \) when \(H=\emptyset \). We write \({}_{\gamma }(\boxdot _{j\in J\setminus \{k\}}\,\widetilde{\alpha ^{\textsf {p} }_{j}}{\mathrel {;}\,}\textsf {G} _j{\textstyle {\boxdot }}\widetilde{\alpha ^{\textsf {p} }_k}{\mathrel {;}\,}\textsf {G} _k)\) when we want to emphasise the branch \(\widetilde{\alpha ^{\textsf {p} }_k}{\mathrel {;}\,}\textsf {G} _k\).
When the checkpoint set \(\gamma \) associated with a choice is empty, we omit it. We call rooted interaction a subterm \(\widetilde{\alpha }{\mathrel {;}\,}\textsf {G} \). So \(\widetilde{\alpha ^{}}{\mathrel {;}\,}\textsf {G} \) can denote either a rooted interaction or a prefixing communication (the context will disambiguate if needed). A type \({}_{\gamma }\boxplus _{j\in J}\,\widetilde{\alpha ^{}_{j}}{\mathrel {;}\,}\textsf {G} _j\) is a choice among more than one rooted interaction with the same sender, at most one of which bears a hat. Recursion must be guarded and it is treated equi-recursively.
We use \(\textsf {part} (\textsf {G} )\) to denote the set of participants of\(\textsf {G} \), as defined in Fig. 3.
We represent global types as trees, with \({}_{\gamma }\boxplus \) or \({}_{\gamma }{\mathrel {;}\,}\) on internal nodes, atomic communications on the branches, and \({\textsf {End} } \) on the leaves. For simplicity we assume that each index set I, J, H is of the form \(\{1,\ldots ,n\}\), where n is its cardinality. The jth branch of a \({}_{\gamma }\boxplus \) node is labelled by \(\widetilde{\alpha ^{}_j}\), and the unique branch of a \({}_{\gamma }{\mathrel {;}\,}\) node, called 0th branch to distinguish it from proper choice branches, is labelled by the corresponding communication. In case the global type has some recursive subtype, the tree is an infinite (regular) tree.
Example 4
(Trees) Figure 4 shows the tree representing the global type
where \(\alpha _i\) denotes the communication with message \(\varLambda _i = \lambda _i\) or \(\varLambda _i = \,{\mathop {\leftrightarrow }\limits ^{\lambda _i}}\,\) for \(i=0,\ldots ,4\).
We introduce now a notation to distinguish different occurrences of the same communication \(\widetilde{\alpha }\) within a type \(\textsf {G} \).
Communication occurrences in \(\textsf {G} \), denoted by \(\xi , \xi '\), have the form \(\sigma \tilde{\alpha }\), where \(\tilde{\alpha }\) is a possibly hatted communication and \(\sigma \) is a finite string over \({\textsf {Nat} } \), which represents the path leading to that particular occurrence of \(\alpha \) in the tree of \(\textsf {G} \). Formally, the path \(\sigma \) records the branch chosen at each \({}_{\gamma }\boxplus \) or \({}_{\gamma }{\mathrel {;}\,}\) node in \(\textsf {G} \). In particular, the last element of \(\sigma \) specifies the branch labelled by the communication \(\tilde{\alpha }\). (Note that in \(\sigma \tilde{\alpha }\) the path \(\sigma \) is not empty since it contains at least the index of the branch labelled by \(\tilde{\alpha }\).) We use \(\sqsubseteq \) (\(\sqsubset \)) to denote the prefix ordering (strict prefix ordering) between strings of naturals.
For instance, the two shown occurrences of \(\alpha _2\) in the tree of Fig. 4 are identified by \(010\alpha _2\) and \(01010\alpha _2\).
Definition 5
(Occurrences) The set of communication occurrences of \(\textsf {G} \), written Occ(\(\textsf {G} \)), is defined by:
-
\({ Occ}({\textsf {End} })=\emptyset \quad \quad { Occ}(\mu \mathbf t .\textsf {K} )={ Occ}(\textsf {K} \{\mu \mathbf t .\textsf {K} /\mathbf t \})\)
-
\( { Occ}({}_{\gamma }\,\widetilde{\alpha }{\mathrel {;}\,}\textsf {G} )=\{0\widetilde{\alpha }\}\cup \{0\xi \mid \ \xi \in { Occ}(\textsf {G} )\}\)
-
\({ Occ}({}_{\gamma }\boxplus _{j\in J}\,\widetilde{\alpha ^{}_{j}}{\mathrel {;}\,}\textsf {G} _j)=\{j\widetilde{\alpha _j}\mid \ j\in J\} \cup \{j\xi \mid \ j\in J \, \text { and }\, \xi \in { Occ}(\textsf {G} _j) \} \)
In the following, communication occurrences will be simply referred to as occurrences. Given an occurrence \(\xi =\sigma \widetilde{\alpha }\) of \(\textsf {G} \), we define the path of \(\xi \) in \(\textsf {G} \) to be \(\textsf {path} (\xi )=\sigma \), the communication of \(\xi \) to be \(\textsf {comm} (\xi )=\widetilde{\alpha }\) and the participants of \(\xi \) to be \(\textsf {part} (\xi )=\textsf {part} (\alpha )\).
An occurrence \(\xi \) is executed in \(\textsf {G} \) if \(\textsf {comm} (\xi )\) bears a hat. We define \({ ExOcc}(\textsf {G} )\), the set of executed occurrences of\(\textsf {G} \), as follows:
The relation of conflict on occurrences is handy. Intuitively, two occurrences are in conflict if they mutually exclude each other in any computation.
Definition 6
(Conflict) The conflict relation in \(\textsf {G} \), denoted by \(\#_\textsf {G} \), is the symmetric irreflexive relation on \({ Occ}(\textsf {G} )\) defined by: \(\, \xi \,\,\#_\textsf {G} \,\xi '\) if there exist \(\sigma _0, \sigma _1, \sigma _2\) such that \(\textsf {path} (\xi ) = \sigma _0 i \sigma _1 \) and \(\textsf {path} (\xi ') = \sigma _0 j \sigma _2 \) with \(i \ne j\).
Two conflicting occurrences have paths that diverge at some choice node of the tree. Since the syntax of global types does not allow hats on more than one branch of a choice, this implies that two conflicting occurrences can never be both executed.
We now formalise the notion of causality on occurrences by defining the set of causes of a given occurrence. Intuitively, the set of causes of \(\xi \) in \(\textsf {G} \) is the set of occurrences in \(\textsf {G} \) on which \(\xi \) depends, namely those that need to be executed before \(\xi \) in any computation allowed by \(\textsf {G} \).
Definition 7
(Causes)
Given an occurrence \(\xi \in { Occ}(\textsf {G} )\), the set of causes of\(\xi \)in\(\textsf {G} \), written \({ Causes}(\textsf {G} ,\xi )\), is the smallest set that contains an occurrence \(\xi '\) if:
-
either \(\textsf {path} (\xi ')\sqsubset \textsf {path} (\xi )\) and \(\textsf {part} (\xi ')\cap \textsf {part} (\xi )\ne \emptyset \);
-
or \(\xi '\in { Causes}(\textsf {G} ,\xi '')\,\) and \(\,\xi ''\in { Causes}(\textsf {G} ,\xi )\) for some \(\xi ''\).
Our notions of conflict and causality are similar to those defined in [37] for Prime Event Structures (although simpler, since we only deal with trees here).
We require global types to respect causality of occurrences, as formalised in the following definition.
Definition 8
(Causally correct global type) A global type \(\textsf {G} \) is causally correct if, whenever an occurrence \(\xi \) is executed in \(\textsf {G} \), then every occurrence in \({ Causes}(\textsf {G} ,\xi )\) is executed in \(\textsf {G} \), namely if \(\xi \in { ExOcc}(\textsf {G} )\) implies \({ Causes}(\textsf {G} ,\xi )\subseteq { ExOcc}(\textsf {G} )\).
The conflict relation is hereditary, namely if \(\xi \,\#_G\, \xi '\) and \(\xi '\in { Causes}(\textsf {G} ,\xi '')\), then \(\xi \, \#_G\, \xi ''\). To show this property (which is an axiom in Prime Event Structures), it is enough to observe that if \(\textsf {path} (\xi ) = \sigma _0 i \sigma _1\) and \(\, \textsf {path} (\xi ') = \sigma _0 j \sigma _2\), then \(\sigma _0 j \sigma _2\sqsubset \textsf {path} (\xi '')\) implies \(\textsf {path} (\xi '')= \sigma _0 j \sigma _2 \sigma _3\) for some \(\sigma _3\).
Session types are projections of global types onto participants. They represent the contributions of individual participants to the session. The projection of a choice yields a union for the choice leader and intersections for the receivers. Checkpoint labels of global types are preserved by the projection onto session types, and the checkpoint label of the choice leader is distinguished by overlining it.
We now define session pre-types, which are a superset of session types. Session types will be session pre-types which are projections of global types. Session pre-types are obtained from processes by replacing external and internal choices with intersections and unions, X with \(\mathbf t \) and \({\textsf {end} } \) with \({\textsf {End} } \), with similar conventions.
Definition 9
(Session pre-types) Session pre-types are defined by:
As for processes, we assume that intersections and unions are not ambiguous, i.e. that the pairs \((\textsf {p} _i,\varLambda _i)\) (\(i\in I\)) are all distinct and the \(\varLambda _i\)’s in intersections are either all simple or all connecting messages.
We want projection to ensure that in a global choice, the choice leader makes the decision and all the other participants act accordingly. We do so by requiring that, for any participant except the choice leader, the set of projections of the choice branches on that participant, say \(\{\textsf {T} _i\ |\ i\in I\}\), be consistent, i.e., the meet of the types in the set,\(\sqcap _{i\in I}\textsf {T} _i\), be defined.
The meet \(\sqcap _{i\in I}\textsf {T} _i\) is a partial operator, which checks that the \(\textsf {T} _i\)’s are compatible behaviours and then combines them into a single session type. Intuitively, \(\sqcap _{i\in I}\textsf {T} _i\) is defined if the concerned participant receives a message that “notifies” her about the chosen \(\textsf {T} _i\). If one of the \(\textsf {T} _i\)’s is an intersection of simple inputs, then so must be all the other \(\textsf {T} _i\)’s. Instead, intersections of connecting inputs can be combined with \({\textsf {End} } \).
To build the meet of intersection types, we define an auxiliary operator \(\Cap \), which takes an intersection \(\bigwedge _{i \in I}\widetilde{\textsf {p} _i?\varLambda _i}{\mathrel {;}\,}\textsf {T} _i\) and an input type (after removing checkpoint labels in both of them) and combines them, if possible:
To define \(\Cap \) on two intersection types, we just iterate the above definition on the members of one of the intersections. In a similar way, we can extend \(\Cap \) to a set of types. Using \(\Cap \) we are able to build meets.
Definition 10
(Meet) The meet of a set of session pre-types is defined by:
If possible we combine the \(\textsf {T} _i\) with \(\Cap \) as explained above. The set of checkpoint labels of the resulting intersection is the union of the corresponding sets for the \(\textsf {T} _i\)’s. If some \(\textsf {T} _i\) is \({\textsf {End} } \), it means that the participant terminates in the branch \(\textsf {T} _i\). Then it must terminate or be connecting in all the other branches.
We do not need to define the meet when the arguments are recursive types, since we consider recursion equi-recursively. The meet is not defined in all other cases, i.e. between intersections and unions, between unions etc.
To define projection we need one last auxiliary operator, the labelling of a session pre-type \(\textsf {T} \) by a set \(\gamma \) of at most one checkpoint label (notation \(\gamma \lfloor \textsf {T} \rfloor \)), defined by:
Labelling adds \(\gamma \) to the first (possibly empty) set \(\textstyle {\varDelta }\) found in \(\textsf {T} \). Intuitively, the checkpoint labels that are spread along successive choices in the global type may get grouped together on a single local choice represented by an intersection when projected on participants. Labelling of union and recursive types is not defined since this operator is only used with types resulting from the application of the meet.
The projection of global types uses the projections of rooted interactions, see the first line of Fig. 5, where the projection operator “\(\, \upharpoonright \,\,\)” has higher precedence than “ ; ”. The projection of a choice is a union for the sending participant, and it is otherwise computed as the meet of the projections on the branches. By abuse of notation, in Fig. 5\(\,\overline{\gamma }\) means \(\overline{C}\) if \(\gamma =C\) and \(\emptyset \) if \(\gamma =\emptyset \). The meet operation can be undefined, and therefore also the projection of global types can be undefined. The definition of projection does not ensure that all the branches of a choice \({}_{\gamma }\boxplus _{i\in I}\,\widetilde{\alpha ^{\textsf {p} }_{i}}{\mathrel {;}\,}\textsf {G} _i\) have the same participants. They can differ for participants whose first communication is a connecting input. Notice that projection respects hats and checkpoint labels (transforming \(C\) to \(\overline{C}\) for the leader of a \(C\)-labelled choice).
Example 5
(Projection) Let us see our notion of projection at work on a few examples.
-
1.
If \(\textsf {G} \) is the global type shown in Example 4 we get
$$\begin{aligned} \begin{array}{lll}\textsf {G} \upharpoonright \textsf {p} \,=\widehat{\textsf {q} !\lambda _0}{\mathrel {;}\,}\mu \mathbf t . (\textsf {r} ?\lambda _2{\mathrel {;}\,}\mathbf t \,_C\wedge \textsf {q} ?\lambda _3{\mathrel {;}\,}\textsf {q} !\lambda _4) &{}\qquad &{} \textsf {G} \upharpoonright \textsf {r} \,=\mu \mathbf t ._C\textsf {q} ?{\mathop {\leftrightarrow }\limits ^{\lambda _1}}{\mathrel {;}\,}\textsf {p} !\lambda _2{\mathrel {;}\,}\mathbf t \\ \textsf {G} \upharpoonright \textsf {q} \,=\widehat{\textsf {p} ?\lambda _0}{\mathrel {;}\,}\mu \mathbf t . (\textsf {r} !{\mathop {\leftrightarrow }\limits ^{\lambda _1}}{\mathrel {;}\,}\mathbf t \,_{\overline{C}}\vee \textsf {p} !\lambda _3{\mathrel {;}\,}\textsf {p} ?\lambda _4) \end{array} \end{aligned}$$ -
2.
An example showing how projections can decorate intersections by more checkpoint labels is \(\textsf {G} =\textsf {p} \xrightarrow {\lambda _1}\textsf {q} {\mathrel {;}\,}(\textsf {p} \xrightarrow {{\mathop {\leftrightarrow }\limits ^{\lambda _2}}}\textsf {r} _{C_1}{\boxplus }\,\textsf {p} \xrightarrow {{\mathop {\leftrightarrow }\limits ^{\lambda _3}}}\textsf {s} )\,{\boxplus }\textsf {p} \xrightarrow {\lambda _4}\textsf {q} {\mathrel {;}\,}(\textsf {q} \xrightarrow {{\mathop {\leftrightarrow }\limits ^{\lambda _5}}}\textsf {r} _{C_2}{\boxplus }\,\textsf {q} \xrightarrow {{\mathop {\leftrightarrow }\limits ^{\lambda _6}}}\textsf {s} )\) where \(\textsf {G} \upharpoonright \textsf {r} \,=\textsf {p} ?{\mathop {\leftrightarrow }\limits ^{\lambda _2}}_{\{C_1,C_2\}}\wedge \, \textsf {q} ?{\mathop {\leftrightarrow }\limits ^{\lambda _5}}\).
-
3.
Let \(\textsf {G} =\mu \mathbf t . (\textsf {p} \xrightarrow {\lambda _1}\textsf {q} {\mathrel {;}\,}\mathbf t \,{\boxplus }\textsf {p} \xrightarrow {\lambda _2}\textsf {q} )\) and \(\textsf {G} '=\textsf {p} \xrightarrow {\lambda _1}\textsf {q} {\mathrel {;}\,}\textsf {G} {\boxplus }\textsf {p} \xrightarrow {\lambda _2}\textsf {q} \). Then \(\textsf {G} \upharpoonright \textsf {q} \,= \mu \mathbf t . (\textsf {p} ?\lambda _1{\mathrel {;}\,}\mathbf t \wedge \textsf {p} ?\lambda _2)\) and \(\textsf {G} ' \upharpoonright \textsf {q} \,=\textsf {p} ?\lambda _1{\mathrel {;}\,}\textsf {G} \upharpoonright \textsf {q} \,\wedge \textsf {p} ?\lambda _2\).
In the following we will consider only causally correct and projectable global types. The Subject Reduction Theorem (Theorem 1) shows that these conditions are preserved by reducing networks that can be typed using the rules introduced in the next section.
We end this section by defining session types.
Definition 11
(Session types) A session pre-type \(\textsf {T} \) is a session type if \(\textsf {T} =\textsf {G} \upharpoonright \textsf {p} \,\) for some global type \(\textsf {G} \) and some participant \(\textsf {p} \).
4 Type system
In this section we define our type system and prove some initial results about it. The shape of typing judgements is \(\varGamma \vdash P :\textsf {T} \), where the environment \(\varGamma \) associates process variables with session types: \(\varGamma \,{:}{:}{=}\, \emptyset ~\mathbf {|\!|}~ \varGamma , X:\textsf {T} \). Process typing exploits the correspondence between external choices and intersections, internal choices and unions. The typing rules for both processes and networks are given in Fig. 6. Typing respects hats: in rules \({\textsc {[t-ExtCh]}}\), and \({\textsc {[t-IntCh]}}\), the hats in processes and types are exactly on the same actions.
Figure 7 gives the subtyping rules, where the double line indicates that the rules are interpreted coinductively [33] (Chapter 21). Subtyping takes into account the rules for intersection and union and preserves hats. Rule \({\textsc {[Sub-In-Skip]}}\) reflects the fact that connecting inputs can be added without causing problems. Rule \({\textsc {[t-Net]}}\) is the only rule for typing networks: it requires that the types of all processes be subtypes of the projections of a unique global type. The condition \(\textsf {part} (\textsf {G} )\subseteq \{\textsf {p} _1,\ldots ,\textsf {p} _n\}\) ensures the presence of all session participants and allows the typing of sessions containing \(\textsf {p} \llbracket \,{\textsf {end} } \,\rrbracket \) for any \(\textsf {p} \), a property needed to guarantee invariance of types under structural equivalence of networks. Clearly, typing imposes constraints on the way hats and checkpoint labels are placed within processes.
Example 6
(\(\textsf {ok} \)condition on evaluation contexts) The following example shows the need of the \(\textsf {ok} \) condition in reduction rules to assure subject reduction. Let \(P=\mu X. (\textsf {q} !\lambda _1{\mathrel {;}\,}\textsf {r} !\lambda _2{\mathrel {;}\,}X\mathrel {_{ C}\oplus }\textsf {q} !\lambda _3{\mathrel {;}\,}\textsf {r} !\lambda _4{\mathrel {;}\,}X)\) and \(Q=\mu Y. (\textsf {p} ?\lambda _1{\mathrel {;}\,}Y\mathrel { _{ C}+}\textsf {p} ?\lambda _3{\mathrel {;}\,}Y)\) and \(R=\mu Z. (\textsf {p} ?\lambda _2{\mathrel {;}\,}Z\, _{ C}+\,\textsf {p} ?\lambda _4{\mathrel {;}\,}Z)\). The network \(\textsf {p} \llbracket \,P\,\rrbracket \mathrel {\Vert }\textsf {q} \llbracket \,Q\,\rrbracket \mathrel {\Vert }\textsf {r} \llbracket \,R\,\rrbracket \) reduces by forward reductions to \(\textsf {p} \llbracket \,P'\,\rrbracket \mathrel {\Vert }\textsf {q} \llbracket \,Q'\,\rrbracket \mathrel {\Vert }\textsf {r} \llbracket \,R'\,\rrbracket \) where
\(P'=\widehat{\textsf {q} !\lambda _1}{\mathrel {;}\,}\widehat{\textsf {r} !\lambda _2}{\mathrel {;}\,}(\textsf {q} !\lambda _1{\mathrel {;}\,}\textsf {r} !\lambda _2{\mathrel {;}\,}P\mathrel { _{ C}\oplus }\widehat{\textsf {q} !\lambda _3}{\mathrel {;}\,}\textsf {r} !\lambda _4{\mathrel {;}\,}P) \mathrel {_{ C}\oplus }\textsf {q} !\lambda _3{\mathrel {;}\,}\textsf {r} !\lambda _4{\mathrel {;}\,}P\) and
\(Q'=\widehat{\textsf {p} ?\lambda _1}{\mathrel {;}\,}(\textsf {p} ?\lambda _1{\mathrel {;}\,}Q\mathrel { _{ C}+}\widehat{\textsf {p} ?\lambda _3}{\mathrel {;}\,}Q)_{ C}+\,\textsf {p} ?\lambda _3{\mathrel {;}\,}Q\) and \(R'=\widehat{\textsf {p} ?\lambda _2}{\mathrel {;}\,}R\mathrel {_{ C}+}\textsf {p} ?\lambda _4{\mathrel {;}\,}R\). By rule \({\textsc {[Back]}}\),  where \(P''=\textsf {q} !\lambda _3{\mathrel {;}\,}\textsf {r} !\lambda _4{\mathrel {;}\,}P\). Without the condition \(\mathcal {E}~\textsf {ok} \text { for } \overline{C}\) on rule \({\textsc {[CtBA]}}\), we could have also the backward move:
where \(P''=\textsf {q} !\lambda _3{\mathrel {;}\,}\textsf {r} !\lambda _4{\mathrel {;}\,}P\). Without the condition \(\mathcal {E}~\textsf {ok} \text { for } \overline{C}\) on rule \({\textsc {[CtBA]}}\), we could have also the backward move:
 , where
, where
\(P'''=(\widehat{{\textsf {q} !\lambda _1}}{\mathrel {;}\,}\widehat{{\textsf {r} !\lambda _2}}{\mathrel {;}\,}\textsf {q} !\lambda _1{\mathrel {;}\,}\textsf {r} !\lambda _2{\mathrel {;}\,}P)\, _{ C}\oplus \,\textsf {q} !\lambda _3{\mathrel {;}\,}\textsf {r} !\lambda _4{\mathrel {;}\,}P\) and \(Q''=\widehat{\textsf {p} ?\lambda _1}{\mathrel {;}\,}Q\mathrel {_{ C}+}\textsf {p} ?\lambda _3{\mathrel {;}\,}Q\). Then Subject Reduction would fail, since the network \(\textsf {p} \llbracket \,P\,\rrbracket \mathrel {\Vert }\textsf {q} \llbracket \,Q\,\rrbracket \mathrel {\Vert }\textsf {r} \llbracket \,R\,\rrbracket \) is typable with the global type \(\mu \mathbf t . \textsf {p} \xrightarrow {\lambda _1}\textsf {q} {\mathrel {;}\,} \textsf {p} \xrightarrow {\lambda _2}\textsf {r} {\mathrel {;}\,}\mathbf t \,_C{\boxplus }\, \textsf {p} \xrightarrow {\lambda _3}\textsf {q} {\mathrel {;}\,} \textsf {p} \xrightarrow {\lambda _4}\textsf {r} {\mathrel {;}\,}\mathbf t \), while \(\textsf {p} \llbracket \,P'''\,\rrbracket \mathrel {\Vert }\textsf {q} \llbracket \,Q''\,\rrbracket \mathrel {\Vert }\textsf {r} \llbracket \,R\,\rrbracket \) is not typable. In fact the output \(\textsf {r} !\lambda _2\) has a hat in the session type of \(P'''\), while the corresponding input \(\textsf {p} ?\lambda _2\) does not have a hat in the session type of R. This example shows also why it would not be possible to roll back to the innernost checkpoints in recursive processes, since they could be different for different participants.
In the remainder of this section we prove some properties of our type system which will be used to show the soundness results in the next section. The reader not interested in proofs can go directly to Sect. 5. We start with the classical lemmas of inversion and canonical forms.
Lemma 1
(Inversion Lemma)
-
1.
If \(\varGamma \vdash {}_{\textstyle {\varDelta }}\sum _{i\in I}\widetilde{\pi _i}{\mathrel {;}\,}P_{i} :\textsf {T} \), then \(\textsf {T} ={}_{\textstyle {\varDelta }}\bigwedge _{i \in I}\widetilde{\pi _i}{\mathrel {;}\,}\textsf {T} _{i}\) and \(\varGamma \vdash P_i :\textsf {T} _i\) for \(i\in I\).
-
2.
If \(\varGamma \vdash {}_{{}_{{\scriptstyle {\overline{\gamma }}}}}\bigoplus _{i\in I}\widetilde{\pi _i}{\mathrel {;}\,}P_{i} :\textsf {T} \), then \(\textsf {T} ={}_{{}_{{\scriptstyle {\overline{\gamma }}}}}\bigvee _{i \in I}\widetilde{\pi _i}{\mathrel {;}\,}\textsf {T} _{i}\) and \(\varGamma \vdash P_i :\textsf {T} _i\) for \(i\in I\).
-
3.
If \(\varGamma \vdash \mu X.P :\textsf {T} \), then \(\textsf {T} =\mu \mathbf t .\textsf {T} '\) and \(\varGamma , X:\mathbf t \vdash P :\textsf {T} '\).
-
4.
If \(\varGamma \vdash X :\textsf {T} \), then \(\textsf {T} =\mathbf t \) and \(\varGamma =\varGamma ', X:\mathbf t \).
-
5.
If \(\varGamma \vdash {\textsf {end} } :\textsf {T} \), then \(\textsf {T} ={\textsf {End} } \).
-
6.
If \(\vdash \textsf {p} _1\llbracket \,P_1\,\rrbracket \mathrel {\Vert }\cdots \mathrel {\Vert }\textsf {p} _n\llbracket \,P_n\,\rrbracket :\textsf {G} \), then \( \vdash P_i :\textsf {T} _i\) and \(\textsf {T} _i\leqslant \textsf {G} \upharpoonright \textsf {p} _i\,\) for \(1\le i\le n\) and \(\textsf {part} (\textsf {G} )\subseteq \{\textsf {p} _1,\ldots ,\textsf {p} _n\}\).
Lemma 2
(Canonical Form Lemma)
-
1.
If \(\varGamma \vdash P :{}_{\textstyle {\varDelta }}\bigwedge _{i \in I}\widetilde{\pi _i}{\mathrel {;}\,}\textsf {T} _{i}\), then \(P={}_{\textstyle {\varDelta }}\sum _{i\in I}\widetilde{\pi _i}{\mathrel {;}\,}P_{i}\) and \(\varGamma \vdash P_i :\textsf {T} _i\) for \(i\in I\).
-
2.
If \(\varGamma \vdash P :{}_{{}_{{\scriptstyle {\overline{\gamma }}}}}\bigvee _{i \in I}\widetilde{\pi _i}{\mathrel {;}\,}\textsf {T} _{i}\), then \(P={}_{{}_{{\scriptstyle {\overline{\gamma }}}}}\bigoplus _{i\in I}\widetilde{\pi _i}{\mathrel {;}\,}P_{i}\) and \(\varGamma \vdash P_i :\textsf {T} _i\) for \(i\in I\).
-
3.
If \(\varGamma \vdash P :\mu \mathbf t .\textsf {T} \), then \(P=\mu X. Q\) and \(\varGamma , X:\mathbf t \vdash Q :\textsf {T} \).
-
4.
If \(\varGamma \vdash P :\mathbf t \), then \(P=X\) and \(\varGamma =\varGamma ', X:\mathbf t \).
-
5.
If \(\varGamma \vdash P :{\textsf {End} } \), then \(P={\textsf {end} } \).
-
6.
If \(\vdash \mathbb {N} :\textsf {G} \) and \(\textsf {part} (\textsf {G} )=\{\textsf {p} _1,\ldots ,\textsf {p} _n\}\), then \(N \equiv p_1\llbracket \,P_1\,\rrbracket \mathrel {\Vert }\cdots \mathrel {\Vert }\textsf {p} _n\llbracket \,P_n\,\rrbracket \) and \( \vdash P_i :\textsf {T} _i\) and \(\textsf {T} _i\leqslant \textsf {G} \upharpoonright \textsf {p} _i\,\) for \(1\le i\le n\) .
The mapping  defined at page 7 for processes may be extended in the obvious way to session types. As expected, this mapping preserves typing.
defined at page 7 for processes may be extended in the obvious way to session types. As expected, this mapping preserves typing.
Lemma 3
If \( \vdash P :\textsf {T} \), then  .
.
Another classical lemma we need for proving Subject Reduction is the following, which retrieves the shape of processes and networks from their labelled transitions.
Lemma 4
-
1.
If
 , then \(P=\mathcal {E}[{}_{\textstyle {\varDelta }}\textstyle {\sum _{i\in I}\pi _i{\mathrel {;}\,}P_i}]\), where \(\pi _j=\textsf {p} ?\varLambda \) for some \(j\in I\), and \(P'=\mathcal {E}[{}_{\textstyle {\varDelta }}(\textstyle {\sum _{i\in I\setminus \{j\}}\pi _i{\mathrel {;}\,}P_i ~+ ~ \widehat{\pi _j}{\mathrel {;}\,}P_j)}]\).
, then \(P=\mathcal {E}[{}_{\textstyle {\varDelta }}\textstyle {\sum _{i\in I}\pi _i{\mathrel {;}\,}P_i}]\), where \(\pi _j=\textsf {p} ?\varLambda \) for some \(j\in I\), and \(P'=\mathcal {E}[{}_{\textstyle {\varDelta }}(\textstyle {\sum _{i\in I\setminus \{j\}}\pi _i{\mathrel {;}\,}P_i ~+ ~ \widehat{\pi _j}{\mathrel {;}\,}P_j)}]\). -
2.
If
 , then \(P=\mathcal {E}[{}_{\overline{\gamma }}\textstyle {\bigoplus _{i\in I}\pi _i{\mathrel {;}\,}P_i}]\), where \(\pi _j=\textsf {p} !\varLambda \) for some \(j\in I\), and \(P'=\mathcal {E}[{}_{\overline{\gamma }}(\textstyle {\bigoplus _{i\in I\setminus \{j\}}\pi _i{\mathrel {;}\,}P_i ~\oplus ~ \widehat{\pi _j}{\mathrel {;}\,}P_j)}]\).
, then \(P=\mathcal {E}[{}_{\overline{\gamma }}\textstyle {\bigoplus _{i\in I}\pi _i{\mathrel {;}\,}P_i}]\), where \(\pi _j=\textsf {p} !\varLambda \) for some \(j\in I\), and \(P'=\mathcal {E}[{}_{\overline{\gamma }}(\textstyle {\bigoplus _{i\in I\setminus \{j\}}\pi _i{\mathrel {;}\,}P_i ~\oplus ~ \widehat{\pi _j}{\mathrel {;}\,}P_j)}]\). -
3.
If
 , then \(P=\mathcal {E}[{}_{{}_{\overline{C}}}\textstyle {(\bigoplus _{i\in I}\pi _i{\mathrel {;}\,}Q_i~\oplus ~\widehat{\pi }{\mathrel {;}\,}Q)}]\) and \(Q\downarrow _{out} \) and \(I \ne \emptyset \) and \(\mathcal {E}~\textsf {ok} \text { for } \overline{C}\) and \(P'=\mathcal {E}[{}_{{}_{\overline{C}}}\bigoplus _{i\in I}\pi _i{\mathrel {;}\,}Q_i]\).
, then \(P=\mathcal {E}[{}_{{}_{\overline{C}}}\textstyle {(\bigoplus _{i\in I}\pi _i{\mathrel {;}\,}Q_i~\oplus ~\widehat{\pi }{\mathrel {;}\,}Q)}]\) and \(Q\downarrow _{out} \) and \(I \ne \emptyset \) and \(\mathcal {E}~\textsf {ok} \text { for } \overline{C}\) and \(P'=\mathcal {E}[{}_{{}_{\overline{C}}}\bigoplus _{i\in I}\pi _i{\mathrel {;}\,}Q_i]\). -
4.
If
 , then \(P=\mathcal {E}[{}_{\textstyle {\varDelta }}\sum _{i\in I}P_{i}]\) and \(C\in \textstyle {\varDelta }\) and \(\mathcal {E}~\textsf {ok} \text { for } C\) and
, then \(P=\mathcal {E}[{}_{\textstyle {\varDelta }}\sum _{i\in I}P_{i}]\) and \(C\in \textstyle {\varDelta }\) and \(\mathcal {E}~\textsf {ok} \text { for } C\) and  .
. -
5.
If
 , then \(P\) does not contain an executed external choice with checkpoint label \(\textstyle {\varDelta }\) and \(C\in \textstyle {\varDelta }\).
, then \(P\) does not contain an executed external choice with checkpoint label \(\textstyle {\varDelta }\) and \(C\in \textstyle {\varDelta }\). -
6.
If
 , then \(\mathbb {N}=\textsf {p} \llbracket \,P\,\rrbracket \mathrel {\Vert }\textsf {q} \llbracket \,Q\,\rrbracket \mathrel {\Vert }\mathbb {N}_0\) and
, then \(\mathbb {N}=\textsf {p} \llbracket \,P\,\rrbracket \mathrel {\Vert }\textsf {q} \llbracket \,Q\,\rrbracket \mathrel {\Vert }\mathbb {N}_0\) and  and
and  and \(\mathbb {N}'=\textsf {p} \llbracket \,P'\,\rrbracket \mathrel {\Vert }\textsf {q} \llbracket \,Q'\,\rrbracket \mathrel {\Vert }\mathbb {N}_0\).
and \(\mathbb {N}'=\textsf {p} \llbracket \,P'\,\rrbracket \mathrel {\Vert }\textsf {q} \llbracket \,Q'\,\rrbracket \mathrel {\Vert }\mathbb {N}_0\). -
7.
If
 , then \(\mathbb {N}=\textsf {p} \llbracket \,P\,\rrbracket \mathrel {\Vert }\varPi _{h\in H}\textsf {p} _h\llbracket \,P_h\,\rrbracket \mathrel {\Vert }\varPi _{k\in K}\textsf {p} _k\llbracket \,P_k\,\rrbracket \) and
, then \(\mathbb {N}=\textsf {p} \llbracket \,P\,\rrbracket \mathrel {\Vert }\varPi _{h\in H}\textsf {p} _h\llbracket \,P_h\,\rrbracket \mathrel {\Vert }\varPi _{k\in K}\textsf {p} _k\llbracket \,P_k\,\rrbracket \) and  and
and  for all \(h\in H\) and
for all \(h\in H\) and  for all \(k\in K\) and $$\begin{aligned} \mathbb {N}'=\textsf {p} \llbracket \,P'\,\rrbracket \mathrel {\Vert }\varPi _{h\in H}\textsf {p} _h\llbracket \,P'_h\,\rrbracket \mathrel {\Vert }\varPi _{k\in K}\textsf {p} _k\llbracket \,P_k\,\rrbracket \end{aligned}$$
for all \(k\in K\) and $$\begin{aligned} \mathbb {N}'=\textsf {p} \llbracket \,P'\,\rrbracket \mathrel {\Vert }\varPi _{h\in H}\textsf {p} _h\llbracket \,P'_h\,\rrbracket \mathrel {\Vert }\varPi _{k\in K}\textsf {p} _k\llbracket \,P_k\,\rrbracket \end{aligned}$$
We now introduce some notions that are specific to the present type system, and prove some results about them. More precisely:
-
we define session contexts (Definition 12) and we show that they correspond to evaluation contexts (Lemma 5);
-
by extending the definition of meet to session contexts (Definition 14), we show how session contexts may be retrieved as projections of global contexts (Definition 13);
-
we show that the maximal hatted path in the tree of a global type splits the global type into a global context and the global type filling the hole (Definition 15);
-
the main result is Lemma 6: it devises the shape of global types starting from one of its projections. It uses the notion of “global type affecting a participant” (Definition 16).
We start by defining session contexts, which mirror process evaluation contexts (Definition 3):
Definition 12
(Session contexts) Session contexts are defined by:
We generalise typing, subtyping, and the definitions of \(\textsf {ok} \) for \(C\) (\( \overline{C}\)) to session contexts. We omit these definitions, which are trivial due to the correspondence between process evaluation contexts and session contexts.
The following lemma gives easy relations between contexts and typing/subtyping.
Lemma 5
-
1.
If \(\mathcal {T}\,\,[\textsf {T} ]\leqslant \textsf {T} '\) and \(\textsf {T} '\not ={\textsf {End} } \), then \(\textsf {T} '=\mathcal {T}\,\,'\,[\textsf {T} '']\) and \(\mathcal {T}\leqslant \mathcal {T}\,\,'\) and \(\textsf {T} \leqslant \textsf {T} ''\). Moreover if \(\mathcal {T}\) is \(\textsf {ok} \) for \(C\) (\( \overline{C}\)), then \(\mathcal {T}\,\,'\) is \(\textsf {ok} \) for \(C\) (\( \overline{C}\)).
-
2.
If \(\textsf {T} \leqslant \mathcal {T}\;[\textsf {T} ']\), then \(\textsf {T} =\mathcal {T}\,\,'[\textsf {T} '']\) and \(\mathcal {T}\,\,'\leqslant \mathcal {T}\) and \(\textsf {T} ''\leqslant \textsf {T} '\). Moreover if \(\mathcal {T}\) is \(\textsf {ok} \) for \(C\) (\( \overline{C}\)), then \(\mathcal {T}\,\,'\) is \(\textsf {ok} \) for \(C\) (\( \overline{C}\)).
-
3.
If \(\varGamma \vdash \mathcal {E}[P] :\textsf {T} \), then \(\textsf {T} =\mathcal {T}\;[\textsf {T} ']\) and \(\varGamma \vdash \mathcal {E} :\mathcal {T}\) and \(\varGamma \vdash P :\textsf {T} '\). Moreover if \(\mathcal {E}\) is \(\textsf {ok} \) for \(C\) (\( \overline{C}\)), then \(\mathcal {T}\) is \(\textsf {ok} \) for \(C\) (\( \overline{C}\)).
-
4.
If \(\varGamma \vdash \mathcal {E} :\mathcal {T}\) and \(\varGamma \vdash P :\textsf {T} \) and \(\mathcal {T}\;[\textsf {T} ]\) is a type, then \(\varGamma \vdash \mathcal {E}[P] :\mathcal {T}\;[\textsf {T} ]\).
-
5.
If \(\varGamma \vdash P :\mathcal {T}\;[\textsf {T} ]\), then \(P=\mathcal {E}[Q]\) and \(\varGamma \vdash \mathcal {E} :\mathcal {T}\) and \(\varGamma \vdash Q :\textsf {T} \). Moreover if \(\mathcal {T}\) is \(\textsf {ok} \) for \(C\) (\( \overline{C}\)), then \(\mathcal {E}\) is \(\textsf {ok} \) for \(C\) (\( \overline{C}\)).
Proof
By induction on contexts.
We define now global contexts, which identify subtypes of global types which do not occur in discarded branches.
Definition 13
(Global contexts) Global contexts are defined by:
We extend to session contexts the labelling defined at page 14 by \(\gamma \lfloor [\;]{} \rfloor =[\;]{}\). This allows us to define projections of global contexts into session contexts using \([\;] \upharpoonright \,\textsf {p} =[\;]{}\) and generalising the definition of the meet operator as follows:
Definition 14
(Meet with contexts) The meet of session contexts and session types is defined by:
Projections of global contexts define session contexts only for a subset of participants. A simple example is \(\mathcal {G}=\textsf {p} \xrightarrow {\lambda }\textsf {q} {\mathrel {;}\,}[\;]{}\), whose projections on all \(\textsf {r} \ne \textsf {p} ,\textsf {q} \) is \(\mathcal {G} \upharpoonright \textsf {r} \,=[\;]{}\). However, \(\mathcal {G} \upharpoonright \textsf {p} \,=\textsf {q} !\lambda {\mathrel {;}\,}[\;]{}\) and \(\mathcal {G} \upharpoonright \textsf {q} \,=\textsf {p} ?\lambda {\mathrel {;}\,}[\;]{}\) are not session contexts because the actions before the hole are not hatted. A more interesting example is the ternary choice:
In fact \(\mathcal {G}' \upharpoonright \textsf {p} \,=\textsf {q} !{\mathop {\leftrightarrow }\limits ^{\lambda _1}}\vee \,\textsf {r} !{\mathop {\leftrightarrow }\limits ^{\lambda _2}}{\vee }\,\widehat{\textsf {q} !{\mathop {\leftrightarrow }\limits ^{\lambda _3}}}{\mathrel {;}\,}[\;]{}\) and \(\mathcal {G}' \upharpoonright \textsf {q} \,=\textsf {p} ?{\mathop {\leftrightarrow }\limits ^{\lambda _1}}{\wedge }\,\widehat{\textsf {p} ?{\mathop {\leftrightarrow }\limits ^{\lambda _3}}}{\mathrel {;}\,}[\;]{}\) are session contexts, while \(\mathcal {G}' \upharpoonright \textsf {r} \,=\textsf {p} ?{\mathop {\leftrightarrow }\limits ^{\lambda _2}}{\wedge }\,[\;]{}\) is not. Notice that without connecting communications such kind of example would be longer, since the participants \(\textsf {q} \) and \(\textsf {r} \) would have to occur in all branches of the choice.
The paths that are not on discarded branches in the tree representation of a global type \(\textsf {G} \) may be used to split \(\textsf {G} \) between a global context and the subtype filling the hole. This is formalised in the following definition.
Definition 15
(Contexts and subtypes determined by paths) Let \({\sigma }\) be a path in a global type \(\textsf {G} \).
-
1.
The context determined by\(\sigma \), \({ Ctx}(\textsf {G} ,\sigma )\), is defined by:
-
\({ Ctx}(\textsf {G} ,\epsilon )=[\;]\)
-
\({ Ctx}({}_{\gamma }\,\widetilde{\alpha }{\mathrel {;}\,}\textsf {G} ',0\sigma )={}_{\gamma }\,\widetilde{\alpha }{\mathrel {;}\,}{ Ctx}(\textsf {G} ',\sigma )\)
-
\({ Ctx}({}_{\gamma }({\boxplus }_{j\in {J\setminus \{k\}}}\,\alpha ^{}_{j}{\mathrel {;}\,}\textsf {K} _j\mathrel {\textstyle {{\boxplus }}}\widetilde{\alpha _{k}}{\mathrel {;}\,}\textsf {G} _k){},k\sigma )={}_{\gamma }({\boxplus }_{j\in {J\setminus \{k\}}}\,\alpha ^{}_{j}{\mathrel {;}\,}\textsf {K} _j\mathrel {\textstyle {{\boxplus }}}\widetilde{\alpha _{k}}{\mathrel {;}\,}{ Ctx}(\textsf {G} _k,\sigma )){}\)
-
\({ Ctx}(\mu \mathbf t .\textsf {K} ,\sigma )={ Ctx}(\textsf {K} \{\mu \mathbf t .\textsf {K} /\mathbf t \},\sigma ) \)
-
-
2.
The subtype determined by\(\sigma \), \({ SubT}(\textsf {G} ,\sigma )\), is defined by:
-
\({ SubT}(\textsf {G} ,\epsilon )=\textsf {G} \)
-
\({ SubT}({}_{\gamma }\,\widetilde{\alpha }{\mathrel {;}\,}\textsf {G} ',0\sigma )={ SubT}(\textsf {G} ',\sigma )\)
-
\({ SubT}({}_{\gamma }({\boxplus }_{j\in {J\setminus \{k\}}}\,\alpha ^{}_{j}{\mathrel {;}\,}\textsf {K} _j\mathrel {\textstyle {{\boxplus }}}\widetilde{\alpha _{k}}{\mathrel {;}\,}\textsf {G} _k),k\sigma )={ SubT}(\textsf {G} _k,\sigma )\)
-
\({ SubT}(\mu \mathbf t .\textsf {K} ,\sigma )={ SubT}(\textsf {K} \{\mu \mathbf t .\textsf {K} /\mathbf t \},\sigma )\)
-
Note that \({ Ctx}(\textsf {G} ,\sigma )\) and \({ SubT}(\textsf {G} ,\sigma )\) are defined if and only if the occurrences on \(\sigma \) are not in conflict with executed occurrences, in other words if all \(\xi \in { ExOcc}(\textsf {G} )\) are such that \(\textsf {path} (\xi )\sqsubseteq \sigma \) or \(\sigma \sqsubset \textsf {path} (\xi )\).
It is easy to verify that \(\textsf {G} ={ Ctx}(\textsf {G} ,\sigma )[{ SubT}(\textsf {G} ,\sigma )]\) whenever \({ Ctx}(\textsf {G} ,\sigma )\) is defined.
The properties of our calculus mainly depend on the possibility of deriving information on the shape of a global type from its projections on participants. A useful notion is that of global type “affecting” a participant, which essentially means that the whole type is needed in order to obtain the projection on that participant. A global type \(\textsf {G} \) affects \(\textsf {p} \) if:
-
either there is one branch of \(\textsf {G} \) whose first communication has participant \(\textsf {p} \)
-
or there are two branches of \(\textsf {G} \) whose projections on \(\textsf {p} \) are both different from \({\textsf {End} } \).
Definition 16
(Affecting global types) A global type\({}_{\gamma }\boxdot _{i\in I}\,\widetilde{\alpha _{i}}{\mathrel {;}\,}\textsf {G} _i\)affects participant\(\textsf {p} \) if one of the following holds:
-
\(\textsf {p} \in \textsf {part} (\alpha _{i})\) for some \(i\in I\);
-
\(|\{ i\in I \mid \widetilde{\alpha _{i}}{\mathrel {;}\,}\textsf {G} _i \upharpoonright \textsf {p} \,\ne {\textsf {End} } \}|>1\).
For instance, if \(\textsf {G} \) is the global type of Example 4, then \(\textsf {G} \) affects participants \(\textsf {p} \) and \(\textsf {q} \) but it does not affect participant \(\textsf {r} \), as shown by their projections given in Example 5(1).
In the projection of a global type \(\textsf {G} \) on \(\textsf {p} \), the intersections have sets of checkpoint labels. We know that at most one of these checkpoint labels is the label of the subtype of \(\textsf {G} \) which affects \(\textsf {p} \). But which one? The projection does not give us enough information to decide. We overcome this problem by means of an equality relation on session types which disregards the sets of checkpoint labels decorating intersections.
We say that two session types \(\textsf {T} \) and \(\textsf {T} '\) are equal up to intersection labelling, dubbed \(\textsf {T} \mathrel {\doteq }\textsf {T} '\), if they are equal (\(\textsf {T} =\textsf {T} '\)) or they are the same intersection with different sets of checkpoint labels (\(\textsf {T} ={}_{\textstyle {\varDelta }}\textsf {T} ''\), \(\textsf {T} '={}_{\textstyle {\varDelta }'}\textsf {T} ''\) for some \(\textsf {T} ''\)).
We have now enough machinery to prove that if the projection of \(\textsf {G} \) on \(\textsf {p} \) is split into a session context and a session type \(\textsf {T} \) which is either a union or an intersection of simple inputs, then this is mirrored by a splitting of \(\textsf {G} \) into a global context and a subtype which affects \(\textsf {p} \). Moreover, if the session context is a hole, then all the choices along the path leading to the hole in \(\textsf {G} \) must be unary choices. Distinguishing the two shapes of \(\textsf {T} \) we can also show that:
-
if \(\textsf {T} \) is a union type, then the subtype of \(\textsf {G} \) is a choice with leader \(\textsf {p} \);
-
if \(\textsf {T} \) is an intersection of simple inputs, then each “long enough” path in \(\textsf {G} \) leads to a communication that projects onto one of these inputs.
Lemma 6
-
1.
If \(\textsf {G} \upharpoonright \textsf {p} \,=\mathcal {T}\,\,[{}_{{}_{{\scriptstyle {\overline{\gamma }}}}}\bigvee _{i \in I}\textsf {T} _{i}]\), then there is a unique path \(\sigma \) in \(\textsf {G} \) such that \({ SubT}(\textsf {G} ,\sigma )={}_{\gamma }\boxdot _{i\in I}\,\widetilde{\alpha ^{\textsf {p} }_{i}}{\mathrel {;}\,}\textsf {G} _i\) affects \(\textsf {p} \) and
$$\begin{aligned} {{ Ctx}(\textsf {G} ,\sigma ) \upharpoonright \textsf {p} \,} = {\mathcal {T}}\hbox { and } {{ SubT}(\textsf {G} ,\sigma ) \upharpoonright \textsf {p} \,} = {}_{{}_{{\scriptstyle {\overline{\gamma }}}}}\bigvee _{i \in I}\textsf {T} _{i}. \end{aligned}$$ -
2.
If \(\textsf {G} \upharpoonright \textsf {p} \,=\mathcal {T}\;[{}_{\textstyle {\varDelta }}\bigwedge _{i \in I}\widetilde{\textsf {q} _i?\lambda _i}{\mathrel {;}\,}\textsf {T} _i]\), then there is a unique path \(\sigma \) in \(\textsf {G} \) such that \({ SubT}(\textsf {G} ,\sigma )\) affects \(\textsf {p} \) and
$$\begin{aligned} { Ctx}(\textsf {G} ,\sigma ) \upharpoonright \textsf {p} \,\mathrel {=}\mathcal {T}\hbox { and } \,{ SubT}(\textsf {G} ,\sigma ) \upharpoonright \textsf {p} \,\mathrel {\doteq }{}_{\textstyle {\varDelta }}\bigwedge _{i \in I}\widetilde{\textsf {q} _i?\lambda _i}{\mathrel {;}\,}\textsf {T} _i. \end{aligned}$$Moreover for each path \(\sigma '\) in \({ SubT}(\textsf {G} ,\sigma )\) there are \(j\in I\) and \(\sigma _j\) such that
$$\begin{aligned} \sigma \sigma _j\widetilde{\textsf {q} _j\xrightarrow {\lambda _j}\textsf {p} }\in { Occ}(\textsf {G} ) \hbox { and either }\sigma _j\sqsubseteq \sigma '\hbox { or }\sigma '\sqsubset \sigma _j. \end{aligned}$$
In both cases if \(\mathcal {T}\) is the hole, then \(\sigma \) is a possibly empty string of 0’s.
Proof
(1) By induction on session type contexts. If \(\mathcal {T}=[\;]{}\), then \(\textsf {G} \upharpoonright \textsf {p} \,={}_{{}_{{\scriptstyle {\overline{\gamma }}}}}\bigvee _{i \in I}\textsf {T} _{i}\) and by definition of projection \(\textsf {G} ={}_{\gamma }\boxdot _{i\in I}\,\widetilde{\alpha ^{\textsf {p} }_{i}}{\mathrel {;}\,}\textsf {G} _i\), so \(\textsf {G} \) affects \(\textsf {p} \). In this case \(\sigma =\epsilon \) is the required path, since \({ SubT}(\textsf {G} ,\epsilon )=\textsf {G} \) affects \(\textsf {p} \) and \({{ Ctx}(\textsf {G} ,\epsilon )} \upharpoonright \textsf {p} \,=[\;] \upharpoonright \textsf {p} \, =[\;]\) and \({ SubT}(\textsf {G} ,\epsilon ) \upharpoonright \textsf {p} \, = \textsf {G} \upharpoonright \textsf {p} \, = {}_{{}_{{\scriptstyle {\overline{\gamma }}}}}\bigvee _{i \in I}\textsf {T} _{i}\).
Moreover, \(\sigma \) is unique because for any path \(\sigma '\ne \epsilon \) the first communication along \(\sigma '\) would be an output from \(\textsf {p} \), which would imply \({ Ctx}(\textsf {G} ,\sigma ') \upharpoonright \textsf {p} \, \ne [\;]\) whenever \({ Ctx}(\textsf {G} ,\sigma ') \upharpoonright \textsf {p} \,\) is defined.
If \(\mathcal {T}={}_{\textstyle {\varDelta }}(\bigwedge _{i \in I}\textsf {T} _{i}{\wedge }\widehat{\textsf {q} ?\varLambda }{\mathrel {;}\,}\mathcal {T}\,\,')\), then \(\widehat{\textsf {q} \xrightarrow {\varLambda }\textsf {p} }\) occurs in \(\textsf {G} \) by definition of projection. This means that there exists \(\xi \in { Occ}(\textsf {G} )\) such that \(\xi = \sigma '\, \widehat{\textsf {q} \xrightarrow {\varLambda }\textsf {p} }\) and there does not exist \(\xi ' \in { Occ}(\textsf {G} )\) such that \(\textsf {path} (\xi ') \sqsubset \sigma '\) and \(\textsf {p} \in \textsf {part} (\xi ')\). The definition of meet implies that there is no \(j\in I\) such that \(\textsf {T} _j\) starts by \(\textsf {q} ?\varLambda \). Let \(\textsf {G} '={ SubT}(\textsf {G} ,\sigma ')\). By construction \(\textsf {G} ' \upharpoonright \textsf {p} \,=\mathcal {T}\,\,'[ {}_{{}_{{\scriptstyle {\overline{\gamma }}}}}\bigvee _{i \in I}\textsf {T} _{i}]\). By induction hypothesis on \(\mathcal {T}\,\,'\) there is a unique path \(\sigma ''\) such that \({ SubT}(\textsf {G} ',\sigma '')\) affects \(\textsf {p} \) and \({ Ctx}(\textsf {G} ',\sigma '') \upharpoonright \textsf {p} \,\mathrel {=}\mathcal {T}\,\,'\) and \({ SubT}(\textsf {G} ',\sigma '') \upharpoonright \textsf {p} \,\mathrel {=} {}_{{}_{{\scriptstyle {\overline{\gamma }}}}}\bigvee _{i \in I}\textsf {T} _{i}\). We can then choose \(\sigma =\sigma '\sigma ''\). The proof of the other inductive case is similar.
(2) By induction on session type contexts. Let \(\textsf {T} ={}_{\textstyle {\varDelta }}\bigwedge _{i \in I}\widetilde{\textsf {q} _i?\lambda _i}{\mathrel {;}\,}\textsf {T} _i\). If \(\mathcal {T}=[\;]{}\) the proof proceeds by an inner induction on the path \(\textsf {ap} (\textsf {p} ,\textsf {G} )\) defined by:
Intuitively, \(\textsf {ap} (\textsf {p} ,\textsf {G} )\) represents the access path to the first choice affecting \(\textsf {p} \) in \(\textsf {G} \). Let \(\sigma =\textsf {ap} (\textsf {p} ,\textsf {G} )\). If \(\sigma =\epsilon \), then \(\textsf {G} ={}_{\gamma }\boxdot _{h\in H}\,\widetilde{\alpha _{h}}{\mathrel {;}\,}\textsf {G} _h\) must satisfy either \(|H|>1\) or \(\textsf {p} \in \textsf {part} (\alpha _j)\) for the unique \(j \in H\). In the latter case, \(\textsf {G} \) trivially affects \(\textsf {p} \). If \(|H|>1\), then by definition of projection and the fact that all inputs are simple, there are two branches whose projections on \(\textsf {p} \) are different from \({\textsf {End} } \). Therefore \(\textsf {G} \) affects \(\textsf {p} \). In both cases we have \({{ Ctx}(\textsf {G} ,\epsilon )} \upharpoonright \textsf {p} \,=[\;] \upharpoonright \textsf {p} \, =[\;]\) and \({ SubT}(\textsf {G} ,\epsilon ) \upharpoonright \textsf {p} \, = \textsf {G} \upharpoonright \textsf {p} \, = \textsf {T} \).
We show that \(\sigma \) is unique. Let \(\sigma '= j \sigma ''\) for some \(j \in H\) and suppose that \({ Ctx}(\textsf {G} ,\sigma ') \upharpoonright \textsf {p} \,\) is defined. If \(\textsf {p} \in \textsf {part} (\alpha _j)\), then clearly \({ Ctx}(\textsf {G} ,\sigma ') \upharpoonright \textsf {p} \,\ne [\;]{}\). If \(|H|>1\), then \({ Ctx}(\textsf {G} ,\sigma ') \upharpoonright \textsf {p} \,\) contains the projection on \(\textsf {p} \) of all the paths of \(\textsf {G} \) starting with a branch different from the jth one. Since \(\textsf {p} \) appears as receiver along all these paths as shown below, this again implies \({ Ctx}(\textsf {G} ,\sigma ') \upharpoonright \textsf {p} \,\ne [\;]{}\).
If \(\sigma =0\,\sigma '\) where \(\sigma '=\textsf {ap} (\textsf {p} ,\textsf {G} ')\) and \(\textsf {G} =\widetilde{\alpha }{\mathrel {;}\,}\textsf {G} '\), then by inductive hypothesis on \(\sigma '\) we have that \({ SubT}(\textsf {G} ',\sigma ')\) affects \(\textsf {p} \) and \({ Ctx}(\textsf {G} ',\sigma ') \upharpoonright \textsf {p} \,\mathrel {=}[\;]\) and \({ SubT}(\textsf {G} ',\sigma ') \upharpoonright \textsf {p} \,\mathrel {=}\textsf {T} \). Therefore, \({ SubT}(\textsf {G} ,0 \sigma ')\) affects \(\textsf {p} \) and \({ Ctx}(\textsf {G} ,0\sigma ') \upharpoonright \textsf {p} \,\mathrel {=}[\;]\) and \({ SubT}(\textsf {G} ,0 \sigma ') \upharpoonright \textsf {p} \,\mathrel {=}\textsf {T} \). By induction hypothesis \(\sigma '\) is unique and so is \(\sigma \).
The proof for \(\mathcal {T}\ne [\;]{}\) is as in (1).
In the remaining we prove that for each path \(\sigma '\) in \({ SubT}(\textsf {G} ,\sigma )\) there are \(\sigma ''\) and \(j\in I\) such that \(\sigma \sigma ''\widetilde{\textsf {q} _j\xrightarrow {\lambda _j}\textsf {p} }\in { Occ}(\textsf {G} )\) and either \(\sigma ''\sqsubseteq \sigma '\) or \(\sigma '\sqsubset \sigma ''\). The path \(\sigma '\) crosses different choices. By the assumption that all inputs are simple and by the definition of \(\Cap \), the projections of the branches of these choices on \(\textsf {p} \) must be intersections of types starting with inputs with different senders or messages, namely \(\widetilde{\textsf {q} _j?\lambda _j}\) (\(j\in I'\subseteq I\)). Moreover, the corresponding communications \(\widetilde{\textsf {q} _j\xrightarrow {\lambda _j}\textsf {p} }\) (\(j \in I'\)) must be the first communications involving \(\textsf {p} \) in paths of \({ SubT}(\textsf {G} ,\sigma )\). Therefore, given \(\sigma '\) in \({ SubT}(\textsf {G} ,\sigma )\) there are \(\sigma ''\) and \(\alpha \) such that \(\xi =\sigma \sigma ''\widetilde{\alpha }\in { Occ}(\textsf {G} )\) and \(\xi \) is the first occurrence with \(\textsf {p} \in \textsf {part} (\xi )\) and either \(\sigma ''\sqsubseteq \sigma '\) or \(\sigma '\sqsubset \sigma ''\). The definition of projection implies \(\widetilde{\alpha }=\widetilde{\textsf {q} _j\xrightarrow {\lambda _j}\textsf {p} }\) for some \(j\in I'\). \(\square \)
5 Soundness
This section is devoted to the formulation and the proof of the properties of our calculus, i.e. subject reduction, session fidelity and progress. These proofs are not trivial due to the presence of both reverse computations and connecting communications.
Lemma 7 deals with subtypes of global contexts. It uses the notions of “alive” and “enabled” for communication occurrences. An occurrence of a communication is alive if it can be executed in the future, and it is enabled if it can be immediately executed. We also define the notions of “alive” and “enabled” for checkpoint labels as they are needed for session fidelity. A checkpoint label is alive if it can be the target of a rollback in the future, and it is enabled if the next action of the choice leader is an output, possibly triggering a backward reduction of the network.
Definition 17
(Alive and enabled)
-
1.
An occurrence\(\xi \)is alive in\(\textsf {G} \) if \(\xi \in { Occ}(\textsf {G} ){\setminus }{ ExOcc}(\textsf {G} )\) and there is no \(\xi ' \in { ExOcc}(\textsf {G} )\) such that \( \xi '\#_\textsf {G} \,\xi \).
-
2.
An occurrence\(\xi \)is enabled in\(\textsf {G} \) if it is alive in \(\textsf {G} \) and \({ Causes}(\textsf {G} ,\xi ) \subseteq { ExOcc}(\textsf {G} )\).
-
3.
A path\(\sigma \)is\(\textsf {ok} \) for the checkpoint labelCin \(\textsf {G} \) if C does not occur along the path \(\sigma \) in the tree of \(\textsf {G} \).
-
4.
A checkpoint label\(C\)is alive in\(\textsf {G} \) if for some path \(\sigma \)\(\textsf {ok} \) for \(C\) (in \(\textsf {G} \))
$$\begin{aligned} { SubT}(\textsf {G} ,\sigma )={}_{C}({\boxplus }_{j\in J{\setminus }\{k\}}\,\alpha ^{\textsf {p} }_{j}{\mathrel {;}\,}\textsf {K} _j{\boxplus }\widehat{\alpha ^{\textsf {p} }_k}{\mathrel {;}\,}\textsf {G} _k) \end{aligned}$$and \(|J|>1\) and there are \(\sigma '\) and \(\alpha ^{\textsf {p} }\) such that \(\sigma {k\sigma '}\alpha ^{\textsf {p} }\in { Occ}(\textsf {G} )\) is alive in \(\textsf {G} \).
-
5.
A checkpoint label\(C\)is enabled in\(\textsf {G} \) if it is alive in \(\textsf {G} \) and \(\sigma {k\sigma '}\alpha ^{\textsf {p} }\) is enabled in \(\textsf {G} \), where \(\sigma \), k, \(\sigma '\) and \(\alpha ^{\textsf {p} }\) are as in (3).
For instance in the global type of Example 4 the occurrence \(01\alpha _1\) is enabled and the occurrence \(0101\alpha _1\) is alive but not enabled. The checkpoint label C is enabled for the path \(\epsilon \) in the global type \(\textsf {p} \xrightarrow {\lambda _1}\textsf {q} \,_C{\boxplus }\, \widehat{\textsf {p} \xrightarrow {\lambda _2}\textsf {q} }{\mathrel {;}\,}\textsf {p} \xrightarrow {{\mathop {\leftrightarrow }\limits ^{\lambda _3}}}\textsf {r} \), since the occurrence \(20\textsf {p} \xrightarrow {{\mathop {\leftrightarrow }\limits ^{\lambda _3}}}\textsf {r} \) is enabled in G. The checkpoint label C is alive but not enabled for the path \(\epsilon \) in the global type \(\textsf {p} \xrightarrow {\lambda _1}\textsf {q} \,_C{\boxplus }\, \widehat{\textsf {p} \xrightarrow {\lambda _2}\textsf {q} }{\mathrel {;}\,}\textsf {q} \xrightarrow {\lambda _3}\textsf {p} {\mathrel {;}\,}\textsf {p} \xrightarrow {{\mathop {\leftrightarrow }\limits ^{\lambda _4}}}\textsf {r} \), since the occurrence \(200{\textsf {p} \xrightarrow {{\mathop {\leftrightarrow }\limits ^{\lambda _4}}}\textsf {r} }\) is alive, but not enabled in \(\textsf {G} \).
Lemma 7
-
1.
If \(\sigma j\alpha \) is enabled in \(\textsf {G} \) and \(\textsf {p} \in \textsf {part} (\alpha )\), then \({ Ctx}(\textsf {G} ,\sigma ) \upharpoonright \textsf {p} \,\) is a session context.
-
2.
If \({ SubT}(\textsf {G} ,\sigma )={}_{\gamma }\boxdot _{i\in I}\,{\alpha ^{}_{i}}{\mathrel {;}\,}\textsf {G} _i\), then \(\sigma i\alpha ^{}_i\) is alive in \(\textsf {G} \) for all \(i\in I\).
-
3.
If \({ SubT}(\textsf {G} ,\sigma )={}_{\gamma }(\boxdot _{i\in I\setminus \{j\}}\,{\alpha ^{\textsf {p} }_{i}}{\mathrel {;}\,}\textsf {K} _i\boxdot \alpha _j^\textsf {p} {\mathrel {;}\,}\textsf {G} _j)\) and \(\textsf {recv} (\alpha _j^\textsf {p} )=\textsf {q} \) and both \({ Ctx}(\textsf {G} ,\sigma ) \upharpoonright \textsf {p} \,\) and \({ Ctx}(\textsf {G} ,\sigma ) \upharpoonright \textsf {q} \,\) are session contexts, then \(\sigma j\alpha ^{\textsf {p} }_j\) is enabled in \(\textsf {G} \).
Proof
(1) If \(\sigma j\alpha \) is enabled in \(\textsf {G} \), then \({ Causes}(\textsf {G} ,\sigma j\alpha ) \subseteq { ExOcc}(\textsf {G} )\) and \(\xi \in { ExOcc}(\textsf {G} )\) implies \(\textsf {path} (\xi ) \sqsubseteq \sigma \). Hence \({ Ctx}(\textsf {G} ,\sigma )\) is defined. If \(\textsf {p} \in \textsf {part} (\alpha )\), define \({ Causes}_{\textsf {p} }(\textsf {G} ,\sigma j\alpha ) = { Causes}(\textsf {G} ,\sigma j\alpha ) \cap \{ \xi \in { Occ}(\textsf {G} )\mid \textsf {p} \in \textsf {part} (\xi )\}\). Since the projection of \({ Ctx}(\textsf {G} ,\sigma )\) on \(\textsf {p} \) retains only \({ Causes}_{\textsf {p} }(\textsf {G} ,\sigma j\alpha )\) and forgets everything else on the path \(\sigma \), and moreover it preserves and reflects hats, \({ Ctx}(\textsf {G} ,\sigma ) \upharpoonright \textsf {p} \,\) is a session context.
(2) From \({ SubT}(\textsf {G} ,\sigma )={}_{\gamma }\boxdot _{i\in I}\,{\alpha ^{}_{i}}{\mathrel {;}\,}\textsf {G} _i\) it follows that \(\sigma i\alpha ^{}_i\in { Occ}(\textsf {G} )\backslash { ExOcc}(\textsf {G} )\). Moreover, since \({ SubT}(\textsf {G} ,\sigma )\) is defined, the path \(\sigma \) must follow the executed branches of \(\textsf {G} \), if any, thus \(\xi \in { Causes}(\textsf {G} ,\sigma i\alpha ^{}_i) \) implies \(\textsf {path} (\xi ) \sqsubseteq \sigma \). Hence \(\sigma i\alpha ^{}_i\) is alive in \(\textsf {G} \).
(3) By (2) \(\sigma j\alpha ^{\textsf {p} }_j\) is alive in \(\textsf {G} \). We prove that \({ Causes}(\textsf {G} ,\sigma j\alpha ^{\textsf {p} }_j) \subseteq { ExOcc}(\textsf {G} )\) by induction on the definition of \({ Causes}\). If \(\xi \in { Causes}(\textsf {G} ,\sigma j\alpha ^{\textsf {p} }_j)\) because \(\textsf {part} (\xi )\cap \{\textsf {p} ,\textsf {q} \}\not =\emptyset \), then it must be \(\xi \in { ExOcc}(\textsf {G} )\), otherwise the projection of the communication of \(\xi \) would appear unhatted in \({ Ctx}(\textsf {G} ,\sigma ) \upharpoonright \textsf {p} \,\) or in \({ Ctx}(\textsf {G} ,\sigma ) \upharpoonright \textsf {q} \,\). Suppose now that \(\xi \in { Causes}(\textsf {G} ,\sigma j\alpha ^{\textsf {p} }_j)\) because \(\xi \in { Causes}(\textsf {G} ,\xi ')\) and \(\xi '\in { Causes}(\textsf {G} ,\sigma j\alpha ^{\textsf {p} }_j)\). By induction hypothesis \(\xi ' \in { ExOcc}(\textsf {G} )\), hence by causal correctness of \(\textsf {G} \) also \(\xi \in { ExOcc}(\textsf {G} )\). \(\square \)
Theorem 1
(Subject reduction) If \(\vdash \mathbb {N} :\textsf {G} \) and  , then \(\vdash \mathbb {N}' :\textsf {G} '\) for some \(\textsf {G} '\).
, then \(\vdash \mathbb {N}' :\textsf {G} '\) for some \(\textsf {G} '\).
Proof
By case analysis on the reduction rules for networks. Since the case of structural equivalence is trivial, there are only two rules to consider, Rule \({\textsc {[Com]}}\) and Rule \({\textsc {[Back]}}\). Let the applied rule be \({\textsc {[Com]}}\), then

By Lemma 4(2) \(P=\mathcal {E}[{}_{\overline{\gamma }}\textstyle {\bigoplus _{i\in I}\pi _i{\mathrel {;}\,}P_i}]\), where \(\pi _j=\textsf {p} !\varLambda \) for some \(j\in I\), and \(P'=\mathcal {E}[{}_{\overline{\gamma }}(\textstyle {\bigoplus _{i\in I\setminus \{j\}}\pi _i{\mathrel {;}\,}P_i ~\oplus ~ \widehat{\pi _j}{\mathrel {;}\,}P_j)}]\). By Lemma 4(1) \(Q=\mathcal {E}'[{}_{\textstyle {\varDelta }}\textstyle {\sum _{h\in H}\pi '_h{\mathrel {;}\,}Q_h}]\), where \(\pi '_k=\textsf {p} ?\varLambda \) for some \(k\in H\), and \(Q'=\mathcal {E}'[{}_{\textstyle {\varDelta }}(\textstyle {\sum _{h\in H\setminus \{k\}}\pi '_h{\mathrel {;}\,}Q_h ~+ ~ \widehat{\pi '_k}{\mathrel {;}\,}Q_k)}]\).
By Lemma 1(6) \( \vdash P :\textsf {T} \) and \( \vdash Q :\textsf {S} \) and \(\textsf {T} \leqslant \textsf {G} \upharpoonright \textsf {p} \,\) and \(\textsf {S} \leqslant \textsf {G} \upharpoonright \textsf {q} \,\). By Lemma 5(3) \(\textsf {T} =\mathcal {T}\,\,[\textsf {T} ']\) and \( \vdash \mathcal {E} :\mathcal {T}\) and \( \vdash {}_{\overline{\gamma }}\textstyle {\bigoplus _{i\in I}\pi _i{\mathrel {;}\,}P_i} :\textsf {T} '\) and \(\textsf {S} =\mathcal {T}\,\,'[\textsf {S} ']\) and \( \vdash \mathcal {E}' :\mathcal {T}\,\,'\) and \( \vdash {}_{\textstyle {\varDelta }}\textstyle {\sum _{h\in H}\pi '_h{\mathrel {;}\,}Q_h} :\textsf {S} '\). By Lemma 1(2) and (1) \(\textsf {T} '={}_{\overline{\gamma }}\bigvee _{i \in I}\pi _i{\mathrel {;}\,}\textsf {T} _i\) and \(\textsf {S} '={}_{\textstyle {\varDelta }}\bigwedge _{h \in H}\pi '_h{\mathrel {;}\,}\textsf {S} _h\).
By Lemma 5(1) \(\textsf {G} \upharpoonright \textsf {p} \,=\mathcal {T}_0[\textsf {T} '']\) and \(\mathcal {T}\leqslant \mathcal {T}_0\) and \({}_{\overline{\gamma }}\bigvee _{i \in I}\pi _i{\mathrel {;}\,}\textsf {T} _i\leqslant \textsf {T} ''\) and \(\textsf {G} \upharpoonright \textsf {q} \,=\mathcal {T}\,\,'_0[\textsf {S} '']\) and \(\mathcal {T}\,\,'\leqslant \mathcal {T}\,\,'_0\) and \({}_{\textstyle {\varDelta }}\bigwedge _{h \in H}\pi '_h{\mathrel {;}\,}\textsf {S} _h\leqslant \textsf {S} ''\). By definition of \(\leqslant \) we get \(\textsf {T} ''={}_{\overline{\gamma }}\bigvee _{i \in I}\pi _i{\mathrel {;}\,}\textsf {T} '_i\) with \(\textsf {T} _i\leqslant \textsf {T} '_i\) for \(i\in I\) and \(\textsf {S} ''={}_{\textstyle {\varDelta }}\bigwedge _{h \in H'}\pi '_h{\mathrel {;}\,}\textsf {S} '_h\) with \(H\supseteq H'\) and \(\textsf {S} _h\leqslant \textsf {S} '_h\) for \(h\in H'\).
From \(\textsf {G} \upharpoonright \textsf {p} \,=\mathcal {T}_0[{}_{\overline{\gamma }}\bigvee _{i \in I}\pi _i{\mathrel {;}\,}\textsf {T} '_i]\) it follows by Lemma 6(1) that there is a unique path \(\sigma \) of \(\textsf {G} \) such that \({ SubT}(\textsf {G} ,\sigma )={}_{\gamma }\boxdot _{i\in I}\,{\alpha ^{\textsf {p} }_{i}}{\mathrel {;}\,}\textsf {G} _i\) affects \(\textsf {p} \) and \({ Ctx}(\textsf {G} ,\sigma ) \upharpoonright \textsf {p} \,\mathrel {=}\mathcal {T}_0\) and \({ SubT}(\textsf {G} ,\sigma ) \upharpoonright \textsf {p} \,\mathrel {=}{}_{\overline{\gamma }}\bigvee _{i \in I}\pi _i{\mathrel {;}\,}\textsf {T} '_i\). Since \(\pi _j=\textsf {q} !\varLambda \), we have \(\alpha ^{\textsf {p} }_j= \textsf {p} \xrightarrow {\varLambda }\textsf {q} \). Consider now the projection \({ SubT}(\textsf {G} ,\sigma ) \upharpoonright \textsf {q} \,= ({}_{\gamma }\boxdot _{i\in I}\,{\alpha ^{\textsf {p} }_{i}}{\mathrel {;}\,}\textsf {G} _i) \upharpoonright \textsf {q} \,\). It must be \({ SubT}(\textsf {G} ,\sigma ) \upharpoonright \textsf {q} \, ={\gamma \lfloor \sqcap _{i\in I}(\ \alpha ^{\textsf {p} }_i{\mathrel {;}\,}\textsf {G} _i\ ) \upharpoonright \textsf {q} \, \rfloor }\mathrel {\doteq } {}_{\textstyle {\varDelta }}(\bigwedge _{h \in H'\setminus \{k\}}\pi '_h{\mathrel {;}\,}\textsf {S} '_h\wedge \pi '_k{\mathrel {;}\,}\textsf {S} '_k) = \textsf {S} ''\), where \(\gamma \in \textstyle {\varDelta }\) and \(\pi '_k=\textsf {p} ?\varLambda \).
By definition we have \(\textsf {G} = { Ctx}(\textsf {G} ,\sigma )[{ SubT}(\textsf {G} ,\sigma )]\). Then we can choose \(\textsf {G} '= { Ctx}(\textsf {G} ,\sigma )[{}_{\gamma }(\boxdot _{i\in I\setminus \{j\}}\,{\alpha ^{\textsf {p} }_{i}}{\mathrel {;}\,}\textsf {K} _i{}{}{\textstyle {\boxdot }}\widehat{\alpha ^{\textsf {p} }_j}{\mathrel {;}\,}\textsf {K} _j)]\). Indeed \(\textsf {G} ' \upharpoonright \textsf {p} \,=\mathcal {T}_0[\textsf {T} _0]\) and \(\textsf {G} ' \upharpoonright \textsf {q} \,=\mathcal {T}\,\,'_0[ \textsf {S} _0]\), where \(\textsf {T} _0={}_{\overline{\gamma }}(\bigvee _{i \in I\setminus \{j\}}\pi _i{\mathrel {;}\,}\textsf {T} _i{\vee }\widehat{\pi _j}{\mathrel {;}\,}\textsf {T} _j)\) and \(\textsf {S} _0= {}_{\textstyle {\varDelta }}(\bigwedge _{h \in H'\setminus \{k\}}\pi _h{\mathrel {;}\,}\textsf {S} _h{\wedge }\widehat{\pi '_k}{\mathrel {;}\,}\textsf {S} '_k)\), while \(\textsf {G} ' \upharpoonright \textsf {r} \,=\textsf {G} \upharpoonright \textsf {r} \,\) for \(\textsf {r} \not =\textsf {p} ,\textsf {q} \). By Lemma 5(4) \( \vdash P' :\mathcal {T}\;[\textsf {T} _0]\) and \( \vdash Q' :\mathcal {T}\,\,'[\textsf {S} _0]\). Since \(\mathcal {T}\;[\textsf {T} _0]\leqslant \textsf {G} ' \upharpoonright \textsf {p} \,\) and \(\mathcal {T}\,\,'[\textsf {S} _0]\leqslant \textsf {G} ' \upharpoonright \textsf {q} \,\) we can derive \(\vdash \textsf {p} \llbracket \,P'\,\rrbracket \mathrel {\Vert }\textsf {q} \llbracket \,Q'\,\rrbracket \mathrel {\Vert }\mathbb {N} :\textsf {G} '\). By Lemma 7(3) \(\sigma j \alpha _j^\textsf {p} \) is enabled in \(\textsf {G} \), being both \({ Ctx}(\textsf {G} ,\sigma ) \upharpoonright \textsf {p} \,\) and \({ Ctx}(\textsf {G} ,\sigma ) \upharpoonright \textsf {q} \,\) session contexts. This implies the causal correctness of \(\textsf {G} '\). The projectability of \(\textsf {G} '\) is immediate.
Let now the applied reduction rule be \({\textsc {[Back]}}\), then:

By Lemma 4(3) \(P=\mathcal {E}[{}_{{}_{\overline{C}}}\textstyle {(\bigoplus _{i\in I}\pi _i{\mathrel {;}\,}Q_i~\oplus ~ \widehat{\pi }{\mathrel {;}\,}Q)}]\) and \(Q\downarrow _{out} \) and \(I \ne \emptyset \) and \(\mathcal {E}~\textsf {ok} \text { for } \overline{C}\) and \(P'=\mathcal {E}[{}_{{}_{\overline{C}}}\bigoplus _{i\in I}\pi _i{\mathrel {;}\,}Q_i]\). By Lemma 4(4) \(P_h=\mathcal {E}_h[S_h]\), and  , where \(S_h = {}_{\textstyle {\varDelta }_{h}}\sum _{\ell \in L_h}R_{\ell } \) and \(C\in \textstyle {\varDelta }_h\) and \(\mathcal {E}_h~\textsf {ok} \text { for } C\) with \(h\in H\). By Lemma 4(5), in a \(P_k\) with \(k\in K\) there cannot be executed external choices whose checkpoint labels contain \(C\).
, where \(S_h = {}_{\textstyle {\varDelta }_{h}}\sum _{\ell \in L_h}R_{\ell } \) and \(C\in \textstyle {\varDelta }_h\) and \(\mathcal {E}_h~\textsf {ok} \text { for } C\) with \(h\in H\). By Lemma 4(5), in a \(P_k\) with \(k\in K\) there cannot be executed external choices whose checkpoint labels contain \(C\).
By Lemma 1(6) \( \vdash P :\textsf {T} \) for some \(\textsf {T} \leqslant \textsf {G} \upharpoonright \textsf {p} \,\), and \( \vdash P_j :\textsf {T} _j\) for some \(\textsf {T} _j\leqslant \textsf {G} \upharpoonright \textsf {p} _j\,\) for each \(j\in H\cup K\). By Lemma 1(1), in a \(\textsf {T} _k\) with \(k\in K\) there cannot be executed intersections whose checkpoint labels contain \(C\).
By Lemma 5(3) \(\textsf {T} =\mathcal {T}\;[\textsf {T} ']\), where \( \vdash \mathcal {E} :\mathcal {T}\) and \(\mathcal {T}\)\(\textsf {ok} \) for \(\overline{C}\) and
and \(\textsf {T} _h=\mathcal {T}_h[\textsf {S} _h]\), where \( \vdash \mathcal {E}_h :\mathcal {T}_h\) and \(\mathcal {T}_h\)\(\textsf {ok} \) for \(C\) and \( \vdash S_h :\textsf {S} _h\) for each \(h\in H\). By Lemma 1(2) \(\textsf {T} '={}_{{}_{\overline{C}}}(\bigvee _{i \in I}\pi _i{\mathrel {;}\,}\textsf {T} _i {\vee }\widehat{\pi }{\mathrel {;}\,}\textsf {T} _Q)\) and by Lemma 1(1) \(\textsf {S} _h\) is an intersection with \(\varDelta _h\) as set of checkpoint labels (\(h \in H\)).
By Lemma 5(1) \(\textsf {G} \upharpoonright \textsf {p} \,=\mathcal {T}\,\,'[\textsf {T} '']\) and \(\mathcal {T}\leqslant \mathcal {T}\,\,'\) and \(\mathcal {T}\,\,'\)\(\textsf {ok} \) for \(\overline{C}\) and
and \(\textsf {G} \upharpoonright \textsf {p} _h\,=\mathcal {T}\,\,'_h[\textsf {S} _h']\) and \(\mathcal {T}_h\leqslant \mathcal {T}\,\,_h'\) and \(\mathcal {T}\,\,'_h\)\(\textsf {ok} \) for \(C\) and \(\textsf {S} _h\leqslant \textsf {S} _h'\) for \(h\in H\). By definition of \(\leqslant \) we get \(\textsf {T} ''={}_{{}_{\overline{C}}}(\bigvee _{i \in I}\pi _i{\mathrel {;}\,}\textsf {T} '_i {\vee }\widehat{\pi }{\mathrel {;}\,}\textsf {T} '_Q)\) with \(\textsf {T} _i\leqslant \textsf {T} '_i\) for \(i\in I\) and \(\textsf {T} _Q\leqslant \textsf {T} '_Q\) and \(\textsf {S} '_h\) is an intersection with \(\varDelta _h\) as set of checkpoint labels (\(h \in H\)).
By Lemma 6(1), from \(\textsf {G} \upharpoonright \textsf {p} \,=\mathcal {T}\,\,'[{}_{{}_{\overline{C}}}(\bigvee _{i \in I}\pi _i{\mathrel {;}\,}\textsf {T} '_i {\vee }\widehat{\pi }{\mathrel {;}\,}\textsf {T} '_Q)]\) it follows that there is a unique path \(\sigma \) of \(\textsf {G} \) such that \({ SubT}(\textsf {G} ,\sigma )= {}_{C}({\boxplus }_{i\in I}\,\alpha ^{\textsf {p} }_{i}{\mathrel {;}\,}\textsf {K} _i\,{\boxplus }\, \widehat{\alpha ^{\textsf {p} }}{\mathrel {;}\,}\textsf {G} _Q)\) affects \(\textsf {p} \) and \({ Ctx}(\textsf {G} ,\sigma ) \upharpoonright \textsf {p} \,\mathrel {=}\mathcal {T}\,\,'\) and \({ SubT}(\textsf {G} ,\sigma ) \upharpoonright \textsf {p} \,\mathrel {=}{}_{{}_{\overline{C}}}(\bigvee _{i \in I}\pi _i{\mathrel {;}\,}\textsf {T} '_i {\vee }\widehat{\pi }{\mathrel {;}\,}\textsf {T} '_Q)\). The conditions \(\mathcal {T}\,\,'\)\(\textsf {ok} \) for \(\overline{C}\) and \(\mathcal {T}_h\)\(\textsf {ok} \) for \(C\)\((h\in H)\) and \(\textsf {T} _k\) without executed intersections whose checkpoint labels contain \(C\) (\(k\in K\)) assure that the path \(\sigma \) is \(\textsf {ok} \) for \(C\), i.e. that \({ Ctx}(\textsf {G} ,\sigma )\) does not contain occurrences of \(C\). Therefore the occurrence of C in \({ SubT}(\textsf {G} ,\sigma )\) is the outermost one and it is projected on the checkpoint labels of \(\textsf {T} ''\) and \(\textsf {S} _h\) for \(h\in H\). Then we can choose \(\textsf {G} '= { Ctx}(\textsf {G} ,\sigma )[{}_{C}({\boxplus }_{i\in I}\,\alpha ^{\textsf {p} }_{i}{\mathrel {;}\,}\textsf {K} _i)]\). In fact \({\textsf {G} ' \upharpoonright \textsf {p} \,}={\mathcal {T}\,\,'[{}_{{}_{\overline{C}}}\bigvee _{i \in I}\pi _i{\mathrel {;}\,}\textsf {T} '_i]}\) and  for \(h\in H\) and \(\textsf {G} ' \upharpoonright \textsf {p} _k\,=\textsf {G} \upharpoonright \textsf {p} _k\,\) for \(k\in K\). We can derive \( \vdash P' :\mathcal {T}\;[{}_{{}_{\overline{C}}}\bigvee _{i \in I}\pi _i{\mathrel {;}\,}\textsf {T} _i]\) by Lemma 5(4) and
for \(h\in H\) and \(\textsf {G} ' \upharpoonright \textsf {p} _k\,=\textsf {G} \upharpoonright \textsf {p} _k\,\) for \(k\in K\). We can derive \( \vdash P' :\mathcal {T}\;[{}_{{}_{\overline{C}}}\bigvee _{i \in I}\pi _i{\mathrel {;}\,}\textsf {T} _i]\) by Lemma 5(4) and  for \(h\in H\) by Lemma 3. Since \({\mathcal {T}\;[{}_{{}_{\overline{C}}}\bigvee _{i \in I}\pi _i{\mathrel {;}\,}\textsf {T} _i]}\leqslant \textsf {G} ' \upharpoonright \textsf {p} \,\) and
for \(h\in H\) by Lemma 3. Since \({\mathcal {T}\;[{}_{{}_{\overline{C}}}\bigvee _{i \in I}\pi _i{\mathrel {;}\,}\textsf {T} _i]}\leqslant \textsf {G} ' \upharpoonright \textsf {p} \,\) and  for \(h\in H\) we may conclude that \(\vdash \textsf {p} \llbracket \,P'\,\rrbracket \mathrel {\Vert }\varPi _{h\in H}\textsf {p} _h\llbracket \,P'_h\,\rrbracket \mathrel {\Vert }\varPi _{k\in K}\textsf {p} _k\llbracket \,P_k\,\rrbracket :\textsf {G} '\). The causal correctness of \(\textsf {G} \) implies the causal correctness of \(\textsf {G} '\) since \(\textsf {G} '\) is obtained from \(\textsf {G} \) by erasing one branch in a choice. The projectability of \(\textsf {G} '\) is immediate. \(\square \)
for \(h\in H\) we may conclude that \(\vdash \textsf {p} \llbracket \,P'\,\rrbracket \mathrel {\Vert }\varPi _{h\in H}\textsf {p} _h\llbracket \,P'_h\,\rrbracket \mathrel {\Vert }\varPi _{k\in K}\textsf {p} _k\llbracket \,P_k\,\rrbracket :\textsf {G} '\). The causal correctness of \(\textsf {G} \) implies the causal correctness of \(\textsf {G} '\) since \(\textsf {G} '\) is obtained from \(\textsf {G} \) by erasing one branch in a choice. The projectability of \(\textsf {G} '\) is immediate. \(\square \)
A standard property enforced by session types is session fidelity: all communications occur as specified by global types. In our case this applies also to backward reductions. The proof relies on the proof of subject reduction.
Theorem 2
(Session fidelity) Let \(\vdash \mathbb {N} :\textsf {G} \).
-
1.
If \(\sigma \textsf {p} \xrightarrow {\varLambda }\textsf {q} \) is enabled in \(\textsf {G} \), then
 .
. -
2.
If
 , then \(\sigma \textsf {p} \xrightarrow {\varLambda }\textsf {q} \) is enabled in \(\textsf {G} \) for some \(\sigma \).
, then \(\sigma \textsf {p} \xrightarrow {\varLambda }\textsf {q} \) is enabled in \(\textsf {G} \) for some \(\sigma \). -
3.
If \(C\) is enabled in \(\textsf {G} \), then
 .
. -
4.
If
 , then \(C\) is enabled in \(\textsf {G} \).
, then \(C\) is enabled in \(\textsf {G} \).
Proof
(1) Let \(\sigma =\sigma 'j\). Since \(\sigma ' j\textsf {p} \xrightarrow {\varLambda }\textsf {q} \) is enabled in \(\textsf {G} \), from Lemma 7(1) for some session contexts \(\mathcal {T}\) and \(\mathcal {T}\,\,'\) we have \(\mathcal {T}\mathrel {=}{ Ctx}(\textsf {G} ,\sigma ') \upharpoonright \textsf {p} \,\) and \(\mathcal {T}\,\,'\mathrel {=}{ Ctx}(\textsf {G} ,\sigma ') \upharpoonright \textsf {q} \,\). Therefore the projections of \(\textsf {G} \) on \(\textsf {p} \) and \(\textsf {q} \) may be written as \(\textsf {G} \upharpoonright \textsf {p} \,=\mathcal {T}\,\,[{}_{{}_{{\scriptstyle {\overline{\gamma }}}}}(\textstyle {\bigvee _{i \in I{\setminus }\{j\}}\pi _i{\mathrel {;}\,}\textsf {T} _i}\vee \textsf {q} !\varLambda {\mathrel {;}\,}\textsf {T} _j)]\) and \(\textsf {G} \upharpoonright \textsf {q} \,=\mathcal {T}\,\,'[{}_{\textstyle {\varDelta }}(\textstyle {\bigwedge _{h \in H\setminus \{k\}}\pi '_h{\mathrel {;}\,}\textsf {S} _h}\wedge \textsf {p} ?\varLambda {\mathrel {;}\,}\textsf {S} _{k})]\).
By Lemma 2(6) \(\mathbb {N}=\textsf {p} \llbracket \,P\,\rrbracket \mathrel {\Vert }\textsf {q} \llbracket \,Q\,\rrbracket \mathrel {\Vert }\mathbb {N}''\) and \( \vdash P :\textsf {T} \) and \( \vdash Q :\textsf {S} \) and \(\textsf {T} \leqslant \textsf {G} \upharpoonright \textsf {p} \,\) and \(\textsf {S} \leqslant \textsf {G} \upharpoonright \textsf {q} \,\). By Lemma 5(2) and the definition of \(\leqslant \) we have :
-
\(\textsf {T} =\mathcal {T}_1[{}_{{}_{{\scriptstyle {\overline{\gamma }}}}}\textstyle {\bigvee _{i \in I}\pi _i{\mathrel {;}\,}\textsf {T} '_i}]\) where \(\pi _j={\textsf {q} !\varLambda }\) with \(j\in I\) and \(\textsf {T} '_i\leqslant \textsf {T} _i\) (\(i\in I\)) and \(\mathcal {T}\leqslant \mathcal {T}_1\)
-
\(\textsf {S} =\mathcal {T}_2[{}_{\textstyle {\varDelta }}\textstyle {\bigwedge _{h \in H'}\pi '_h{\mathrel {;}\,}\textsf {S} '_h}]\) where \(\pi _k=\textsf {p} ?\varLambda \) with \(k\in H\) and \(H'\supseteq H\) and \(\textsf {S} '_h\leqslant \textsf {S} _h\) (\(h\in H\)) and \(\mathcal {T}\,\,'\leqslant \mathcal {T}_2\).
By Lemma 5(5) we get \(P=\mathcal {E}[P']\) and \( \vdash \mathcal {E} :\mathcal {T}_1\) and \( \vdash P' :{}_{{}_{{\scriptstyle {\overline{\gamma }}}}}\textstyle {\bigvee _{i \in I}\pi _i{\mathrel {;}\,}\textsf {T} '_i}\) and \(Q=\mathcal {E}'[Q']\) and \( \vdash \mathcal {E}' :\mathcal {T}_2\) and \( \vdash Q' :{}_{\textstyle {\varDelta }}\textstyle {\bigwedge _{h \in H'}\pi '_h{\mathrel {;}\,}\textsf {S} '_h}\). By Lemma 2(2) \(P'={}_{\overline{\gamma }}\textstyle {\bigoplus _{i\in I}\pi _i{\mathrel {;}\,}P_i}\) and by Lemma 2(1) \(Q'={}_{\textstyle {\varDelta }}\textstyle {\sum _{h\in H'}\pi '_h{\mathrel {;}\,}Q_h}\). Therefore

and

which imply  .
.
(2) By Lemma 4(6) \(\mathbb {N}=\textsf {p} \llbracket \,P\,\rrbracket \mathrel {\Vert }\textsf {q} \llbracket \,Q\,\rrbracket \mathrel {\Vert }\mathbb {N}_0\) and  and
and  . Therefore rule \({\textsc {[Com]}}\) has been applied and from the proof of Theorem 1 we know that \(\sigma \textsf {p} \xrightarrow {\varLambda }\textsf {q} \) is enabled in \(\textsf {G} \) for some \(\sigma \).
. Therefore rule \({\textsc {[Com]}}\) has been applied and from the proof of Theorem 1 we know that \(\sigma \textsf {p} \xrightarrow {\varLambda }\textsf {q} \) is enabled in \(\textsf {G} \) for some \(\sigma \).
(3) From Definition 17(4) we know that there exists a path \(\sigma \)\(\textsf {ok} \) for \(C\) such that \({ SubT}(\textsf {G} ,\sigma )={}_{C}({\boxplus }_{j\in J{\setminus }\{k\}}\,\alpha ^{\textsf {p} }_{j}{\mathrel {;}\,}\textsf {K} _j{\boxplus }\widehat{\alpha ^{\textsf {p} }_k}{\mathrel {;}\,}\textsf {G} _k)\). Since \(\textsf {G} ={ Ctx}(\textsf {G} ,\sigma )[{ SubT}(\textsf {G} ,\sigma )]\) is causally correct all the communications involving \(\textsf {p} \) in \({ Ctx}(\textsf {G} ,\sigma )\) are executed communications. This implies that \(\mathcal {T}\mathrel {=}{ Ctx}(\textsf {G} ,\sigma ) \upharpoonright \textsf {p} \,\) is a session context and thus the projection of \(\textsf {G} \) on \(\textsf {p} \) may be written as \({\textsf {G} \upharpoonright \textsf {p} \,}={\mathcal {T}\,\,[{}_{{}_{{\scriptstyle {\overline{\gamma }}}}}(\textstyle {\bigvee _{j \in J{\setminus }\{k\}}\pi _j{\mathrel {;}\,}\textsf {T} _j}\vee \widehat{\pi _k}{\mathrel {;}\,}\textsf {T} )]}\). Therefore \(\mathcal {T}\) is \(\textsf {ok} \) for \(C\) and \((\alpha ^{\textsf {p} }_j{\mathrel {;}\,}\textsf {K} _j) \upharpoonright \textsf {p} \,=\pi _j{\mathrel {;}\,}\textsf {T} _j\) for \(j\in J{\setminus }\{k\}\) and \((\widehat{\alpha ^{\textsf {p} }_k}{\mathrel {;}\,}\textsf {G} _k) \upharpoonright \textsf {p} \,=\widehat{\pi _k}{\mathrel {;}\,}\textsf {T} \). By Lemma 2(6) \(\mathbb {N}=\textsf {p} \llbracket \,P\,\rrbracket \mathrel {\Vert }\mathbb {N}''\) and \( \vdash P :\textsf {T} '\) and \(\textsf {T} '\leqslant \textsf {G} \upharpoonright \textsf {p} \,\). By Lemma 5(2) \(\textsf {T} '=\mathcal {T}\,\,'[{}_{{}_{{\scriptstyle {\overline{\gamma }}}}}(\textstyle {\bigvee _{j \in J{\setminus }\{k\}}{\textsf {S} _i}}\vee \widehat{\pi _k}{\mathrel {;}\,}\textsf {S} )]\) and \(\mathcal {T}\,\,'\leqslant \mathcal {T}\) and \(\pi _j{\mathrel {;}\,}\textsf {S} _j\leqslant \pi _j{\mathrel {;}\,}\textsf {T} _j\) for \(j\in J{\setminus }\{k\}\) and \(\widehat{\pi _k}{\mathrel {;}\,}\textsf {S} \leqslant \widehat{\pi _k}{\mathrel {;}\,}\textsf {T} \).
By Lemma 5(5) \(P=\mathcal {E}[P']\) and \( \vdash \mathcal {E} :\mathcal {T}\,\,'\) and \( \vdash P' :{}_{{}_{{\scriptstyle {\overline{\gamma }}}}}(\textstyle {\bigvee _{j \in J{\setminus }\{k\}}\pi _j{\mathrel {;}\,}\textsf {S} _j}\vee \widehat{\pi _k}{\mathrel {;}\,}\textsf {S} )\). By Lemma 2(2) \(P'=\mathcal {E}[{}_{\overline{\gamma }}\textstyle {(\bigoplus _{j\in J\setminus \{k\}}\pi _j{\mathrel {;}\,}Q_j~\oplus ~\widehat{\pi _k}{\mathrel {;}\,}Q)}]\) and \( \vdash \widehat{\pi _k}{\mathrel {;}\,}Q :\widehat{\pi _k}{\mathrel {;}\,}\textsf {S} \). Let \(\sigma '\) and h be such that \(\sigma k\sigma 'h\alpha ^{\textsf {p} }\in { Occ}(\textsf {G} )\) is enabled in \(\textsf {G} \). Then \({ SubT}(\textsf {G} ,\sigma k\sigma ')={}_{\gamma '}\boxdot _{i\in I}\,{\alpha ^{\textsf {p} }_{i}}{\mathrel {;}\,}\textsf {K} _i\) with \(h\in I\) and \(\alpha _h^\textsf {p} =\alpha ^{\textsf {p} }\) and for some \(\mathcal {T}\,\,''\) we have that \(\textsf {T} =\mathcal {T}\,\,''[{}_{{}_{{\scriptstyle {\overline{\gamma }}}'}}(\textstyle {\bigvee _{i \in I}\textsf {T} '_i})]\). By Lemma 5(2) \(\textsf {S} =\mathcal {T}\,\,'''[{}_{{}_{{\scriptstyle {\overline{\gamma }}}'}}(\textstyle {\bigvee _{i \in I}\textsf {S} '_i})]\) for some \(\mathcal {T}\,\,'''\). By Lemma 2(2) \(Q=\mathcal {E}'[{}_{{}_{{\scriptstyle {\overline{\gamma }}}'}}\textstyle {\bigoplus _{i\in I}Q_i'}]\), which implies \(Q\downarrow _{out}\). Then  and
and  , since all processes in \(\mathbb {N}\) may contain or may not contain executed internal choices labelled \(C\).
, since all processes in \(\mathbb {N}\) may contain or may not contain executed internal choices labelled \(C\).
(4) By Lemma 4(7) \(\mathbb {N}=\textsf {p} \llbracket \,P\,\rrbracket \mathrel {\Vert }\varPi _{h\in H}\textsf {p} _h\llbracket \,P_h\,\rrbracket \mathrel {\Vert }\varPi _{k\in K}\textsf {p} _k\llbracket \,P_k\,\rrbracket \) and  and
and  for all \(h\in H\) and
for all \(h\in H\) and  for all \(k\in K\) and
for all \(k\in K\) and
Therefore rule \({\textsc {[Back]}}\) has been applied and from the proof of Theorem 1 we know that:
-
\(P=\mathcal {E}[{}_{{}_{\overline{C}}}\textstyle {(\bigoplus _{i\in I}\pi _i{\mathrel {;}\,}Q_i~\oplus ~\widehat{\pi }{\mathrel {;}\,}Q)}]\) and \(Q\downarrow _{out} \) and \(I \ne \emptyset \) and \(\mathcal {E}~\textsf {ok} \text { for } C\)
-
\({ SubT}(\textsf {G} ,\sigma )= {}_{C}({\boxplus }_{i\in I}\,\alpha ^{\textsf {p} }_{i}{\mathrel {;}\,}\textsf {K} _i\,{\boxplus }\, \widehat{\alpha ^{\textsf {p} }}{\mathrel {;}\,}\textsf {G} _Q)\) and \(\sigma \) is \(\textsf {ok} \) for C
-
\( \vdash P :\textsf {T} \) and \(\textsf {T} \leqslant \textsf {G} \upharpoonright \textsf {p} \,\) and \( \vdash Q :\textsf {T} _Q\) and \(\textsf {T} _Q\leqslant \textsf {G} _Q \upharpoonright \textsf {p} \,\)
-
\(\textsf {G} \upharpoonright \textsf {p} \,=\mathcal {T}\,\,'[{}_{{}_{\overline{C}}}(\bigvee _{i \in I}\pi _i{\mathrel {;}\,}\textsf {T} '_i {\vee }\widehat{\pi }{\mathrel {;}\,}\textsf {T} '_Q)]\) and \(\textsf {T} _Q\leqslant \textsf {T} '_Q\).
Let \(\widehat{\alpha ^\textsf {p} }{\mathrel {;}\,}\textsf {G} _Q\) be the \(\ell \)th branch in \({ SubT}(\textsf {G} ,\sigma )\). By definition \(Q\downarrow _{out}\) implies \(Q=\mathcal {E}'[{}_{{}_{{\scriptstyle {\overline{\gamma }}}'}}\textstyle {\bigoplus _{j\in I'}Q'_j}]\).
From \( \vdash Q :\textsf {T} _Q\) and Lemma 5(3) \(\textsf {T} _Q=\mathcal {T}_Q[\textsf {S} _Q]\) and \( \vdash {}_{{}_{{\scriptstyle {\overline{\gamma }}}'}}\textstyle {\bigoplus _{j\in I'}Q'_j} :\textsf {S} _Q\). By Lemma 1(2) \(\textsf {S} _Q={}_{{}_{{\scriptstyle {\overline{\gamma }}}'}}\bigvee _{j \in I'}\textsf {S} _j{}\), which together with \(\textsf {T} _Q\leqslant \textsf {T} '_Q\) imply \(\textsf {T} '_Q=\mathcal {T}\,\,'_Q[{}_{{}_{{\scriptstyle {\overline{\gamma }}}'}}\bigvee _{j \in I'}\textsf {S} '_j{}]\) by Lemma 5(1). Let \(\mathcal {T}\,\,''=\mathcal {T}\,\,'[{}_{{}_{\overline{C}}}(\bigvee _{i \in I}\pi _i{\mathrel {;}\,}\textsf {T} '_i {\vee }\widehat{\pi }{\mathrel {;}\,}\mathcal {T}\,\,'_Q)]\), then \(\textsf {G} \upharpoonright \textsf {p} \,=\mathcal {T}\,\,''[{}_{{}_{{\scriptstyle {\overline{\gamma }}}'}}\bigvee _{j \in I'}\textsf {S} '_j{}]\). By Lemma 6(1) there is \(\sigma '\) such that \({ SubT}(\textsf {G} ,\sigma \ell \sigma ')={}_{{}_{{\scriptstyle {\overline{\gamma }}}'}}\boxdot _{j\in I'}\,{\beta ^{\textsf {p} }_{j}}{\mathrel {;}\,}\textsf {K} '_j\) affects \(\textsf {p} \) and \({ Ctx}(\textsf {G} ,\sigma \ell \sigma ') \upharpoonright \textsf {p} \,=\mathcal {T}\,\,''\) and \({ SubT}(\textsf {G} ,\sigma \ell \sigma ') \upharpoonright \textsf {p} \,={}_{{}_{{\scriptstyle {\overline{\gamma }}}'}}\bigvee _{j \in I'}\textsf {S} '_j{}\). From Lemma 7(2) \(\sigma \ell \sigma ' j\beta ^{\textsf {p} }_j\) is alive in \(\textsf {G} \) for all \(j\in I'\) and then \(C\) is alive in \(\textsf {G} \). We finally conclude that \(C\) is enabled in \(\textsf {G} \), since \({ Ctx}(\textsf {G} ,\sigma \ell \sigma ') \upharpoonright \textsf {p} \,\) is a session context, and this implies that \(\sigma \ell \sigma ' j\beta ^{\textsf {p} }_j\) is enabled in \(\textsf {G} \) for all \(j\in I'\). \(\square \)
The remainder of this section is devoted to the proof of forward and backward progress.
For forward progress we first show that a communication which is alive in a global type has at least one enabled cause, and will eventually become enabled.
Lemma 8
-
1.
If \(\xi \in { Occ}(\textsf {G} )\) is alive in \(\textsf {G} \), then either \(\xi \) is enabled in \(\textsf {G} \) or there is some occurrence in \({ Causes}(\textsf {G} ,\xi )\) which is enabled in \(\textsf {G} \).
-
2.
If \(\vdash \mathbb {N} :\textsf {G} \) and \(\xi \in { Occ}(\textsf {G} )\) is alive in \(\textsf {G} \), then \(\mathbb {N}\longrightarrow ^* \mathbb {N}'\) with \(\vdash \mathbb {N}' :\textsf {G} '\) and \(\xi \) is enabled in \(\textsf {G} '\).
Proof
(1) By induction on the cardinality of the set of non executed occurrences in \({ Causes}(\textsf {G} ,\xi )\), namely on \(n = |{ Causes}(\textsf {G} ,\xi )\backslash { ExOcc}(\textsf {G} )|\). If \(n = 0\), then \(\xi \) is enabled in \(\textsf {G} \) by definition. Let \(n > 0\). Note that every \(\xi ' \in { Causes}(\textsf {G} ,\xi )\backslash { ExOcc}(\textsf {G} )\) must be alive, because otherwise there would exist an executed \(\xi ''\) such that \(\xi '' \#_\textsf {G} \xi '\), which by conflict heredity would imply \(\xi '' \#_\textsf {G} \xi \), contradicting the assumption that \(\xi \) is alive. So, let us choose a non executed \(\xi '\in { Causes}(\textsf {G} ,\xi )\). If \(\xi '\) is enabled we are done, otherwise, since \(\xi '\) is alive and \({ Causes}(\textsf {G} ,\xi ')\subset { Causes}(\textsf {G} ,\xi )\), by inductive hypothesis there is \(\xi ''\) in \({ Causes}(\textsf {G} ,\xi ')\) which is enabled in \(\textsf {G} \).
(2) Again, we proceed by induction on \(n = |{ Causes}(\textsf {G} ,\xi )\backslash { ExOcc}(\textsf {G} )|\). If \(n = 0\), then \(\xi \) is enabled in \(\textsf {G} \) and the result is immediate by Theorem 2(1). Let now \(n > 0\). By (1) there exists \(\xi '\) in \({ Causes}(\textsf {G} ,\xi )\) which is enabled in \(\textsf {G} \). If \(\xi '=\sigma \textsf {p} \xrightarrow {\varLambda }\textsf {q} \), by Theorem 2(1) we have  and then by Theorem 1 we have \(\vdash \mathbb {N}'' :\textsf {G} ''\). Let \(\xi '' =\sigma \widehat{\textsf {p} \xrightarrow {\varLambda }\textsf {q} }\). Since \({ Causes}(\textsf {G} '',\xi ) = { Causes}(\textsf {G} ,\xi )\setminus \{\xi '\}\cup \{\xi ''\}\) and \({ ExOcc}(\textsf {G} '') = { ExOcc}(\textsf {G} )\cup \xi ''\), we have \({ Causes}(\textsf {G} '',\xi )\backslash { ExOcc}(\textsf {G} '') \subset { Causes}(\textsf {G} ,\xi )\backslash { ExOcc}(\textsf {G} )\). Then by induction \(\mathbb {N}''\longrightarrow ^* \mathbb {N}'\) (whence \(\mathbb {N}\longrightarrow ^* \mathbb {N}'\)) with \(\vdash \mathbb {N}' :\textsf {G} '\) and \(\xi \) is enabled in \(\textsf {G} '\). \(\square \)
and then by Theorem 1 we have \(\vdash \mathbb {N}'' :\textsf {G} ''\). Let \(\xi '' =\sigma \widehat{\textsf {p} \xrightarrow {\varLambda }\textsf {q} }\). Since \({ Causes}(\textsf {G} '',\xi ) = { Causes}(\textsf {G} ,\xi )\setminus \{\xi '\}\cup \{\xi ''\}\) and \({ ExOcc}(\textsf {G} '') = { ExOcc}(\textsf {G} )\cup \xi ''\), we have \({ Causes}(\textsf {G} '',\xi )\backslash { ExOcc}(\textsf {G} '') \subset { Causes}(\textsf {G} ,\xi )\backslash { ExOcc}(\textsf {G} )\). Then by induction \(\mathbb {N}''\longrightarrow ^* \mathbb {N}'\) (whence \(\mathbb {N}\longrightarrow ^* \mathbb {N}'\)) with \(\vdash \mathbb {N}' :\textsf {G} '\) and \(\xi \) is enabled in \(\textsf {G} '\). \(\square \)
Connecting communications cause the failure of the standard progress property, since a participant offering an external choice between connecting communications can wait forever. Instead, processes offering outputs or simple inputs can always communicate.
Theorem 3
(Forward progress)
-
1.
If \(\vdash \textsf {p} \llbracket \,\mathcal {E}[{}_{{}_{{\scriptstyle {\overline{\gamma }}}}}\textstyle {\bigoplus _{i\in I}\pi _i{\mathrel {;}\,}P_i}]\,\rrbracket \mathrel {\Vert }\mathbb {N} :\textsf {G} \), then for every \(j\in I\) there exists an \(\mathbb {N}_j\) such that \(\textsf {p} \llbracket \,\mathcal {E}[{}_{{}_{{\scriptstyle {\overline{\gamma }}}}}\textstyle {\bigoplus _{i\in I}\pi _i{\mathrel {;}\,}P_i}]\,\rrbracket \mathrel {\Vert }\mathbb {N}\longrightarrow ^* \textsf {p} \llbracket \,\mathcal {E}[{}_{{}_{{\scriptstyle {\overline{\gamma }}}}}(\textstyle {\bigoplus _{i\in I\setminus \{j\}}\pi _i{\mathrel {;}\,}P_i~\oplus ~\widehat{\pi _j}{\mathrel {;}\,}P_j})]\,\rrbracket \mathrel {\Vert }\mathbb {N}_j\).
-
2.
If \(\vdash \textsf {p} \llbracket \,\mathcal {E}[{}_{\textstyle {\varDelta }}\textstyle {\sum _{i\in I}\pi _i{\mathrel {;}\,}P_i}]\,\rrbracket \mathrel {\Vert }\mathbb {N} :\textsf {G} \) and all \(\pi _i\) are simple inputs, then there is \(\mathbb {N}'\) such that \(\textsf {p} \llbracket \,\mathcal {E}[{}_{\textstyle {\varDelta }}\textstyle {\sum _{i\in I}\pi _i{\mathrel {;}\,}P_i}]\,\rrbracket \mathrel {\Vert }\mathbb {N}\longrightarrow ^* \textsf {p} \llbracket \,\mathcal {E}[ {}_{\textstyle {\varDelta }}(\textstyle {\sum _{i\in I\setminus \{j\}}\pi _i{\mathrel {;}\,}P_i~+~\widehat{\pi _j}{\mathrel {;}\,}P_j})]\,\rrbracket \mathrel {\Vert }\mathbb {N}'\) for some \(j\in I\).
Proof
(1) Let \(P=\mathcal {E}[{}_{{}_{{\scriptstyle {\overline{\gamma }}}}}\textstyle {\bigoplus _{i\in I}\pi _i{\mathrel {;}\,}P_i}]\), by Lemma 1(6) \( \vdash P :\textsf {T} \) and \(\textsf {T} \leqslant \textsf {G} \upharpoonright \textsf {p} \,\). By Lemma 5(3) \(\textsf {T} =\mathcal {T}\;[\textsf {T} ']\) and \( \vdash \mathcal {E} :\mathcal {T}\) and \( \vdash {}_{\overline{\gamma }}\textstyle {\bigoplus _{i\in I}\pi _i{\mathrel {;}\,}P_i} :\textsf {T} '\). By Lemma 1(2) \(\textsf {T} '={}_{\overline{\gamma }}\bigvee _{i \in I}\pi _i{\mathrel {;}\,}\textsf {T} _i\). By Lemma 5(1) \(\textsf {G} \upharpoonright \textsf {p} \,=\mathcal {T}\,\,'[\textsf {T} '']\) and \(\mathcal {T}\leqslant \mathcal {T}\,\,'\) and \({}_{\overline{\gamma }}\bigvee _{i \in I}\pi _i{\mathrel {;}\,}\textsf {T} _i\leqslant \textsf {T} ''\). By definition of \(\leqslant \) we get \(\textsf {T} ''={}_{{}_{{\scriptstyle {\overline{\gamma }}}}}\bigvee _{i \in I}\pi _i{\mathrel {;}\,}\textsf {T} '_i\) with \(\textsf {T} _i\leqslant \textsf {T} '_i\) for \(i\in I\). Therefore \(\textsf {G} \upharpoonright \textsf {p} \,=\mathcal {T}\,\,'[{}_{\overline{\gamma }}\bigvee _{i \in I}\pi _i{\mathrel {;}\,}\textsf {T} _i']\).
From Lemma 6(1), for some \(\sigma \) we have that \({ SubT}(\textsf {G} ,\sigma )={}_{\gamma }\boxdot _{i\in I}\,{\alpha ^{\textsf {p} }_{i}}{\mathrel {;}\,}\textsf {K} _i\) and \({ Ctx}(\textsf {G} ,\sigma ) \upharpoonright \textsf {p} \, = \mathcal {T}\,\,'\) and \({{ SubT}(\textsf {G} ,\sigma ) \upharpoonright \textsf {p} \,} ={}_{\overline{\gamma }}\bigvee _{i \in I}\pi _i{\mathrel {;}\,}\textsf {T} '_i \). This implies, by Lemma 7(2), that \(\sigma j\alpha ^{\textsf {p} }_j\) is alive in \(\textsf {G} \). Therefore from Lemma 8(2) we get that
with \(\vdash \textsf {p} \llbracket \,\mathcal {E}[{}_{{}_{{\scriptstyle {\overline{\gamma }}}}}\textstyle {\bigoplus _{i\in I}\pi _i{\mathrel {;}\,}P_i}]\,\rrbracket \mathrel {\Vert }\mathbb {N}_j' :\textsf {G} '\) and \(\sigma j\alpha ^{\textsf {p} }_j\) enabled in \(\textsf {G} '\). From Theorem 2(1) we conclude  .
.
(2) Let \(P=\mathcal {E}[{}_{\textstyle {\varDelta }}\textstyle {\sum _{i\in I}\pi _i{\mathrel {;}\,}P_i}]\), by Lemma 1(6) \( \vdash P :\textsf {T} \) and \(\textsf {T} \leqslant \textsf {G} \upharpoonright \textsf {p} \,\). By Lemma 5(3) \(\textsf {T} =\mathcal {T}\,\,[\textsf {T} ']\) and \( \vdash \mathcal {E} :\mathcal {T}\) and \( \vdash {}_{\textstyle {\varDelta }}\textstyle {\sum _{i\in I}\pi _i{\mathrel {;}\,}P_i} :\textsf {T} '\). By Lemma 1(1) \(\textsf {T} '={}_{\textstyle {\varDelta }}\bigwedge _{i \in I}\pi _i{\mathrel {;}\,}\textsf {T} _i\). By Lemma 5(1) \(\textsf {G} \upharpoonright \textsf {p} \,=\mathcal {T}\,\,'[\textsf {T} '']\) and \(\mathcal {T}\leqslant \mathcal {T}\,\,'\) and \({}_{\textstyle {\varDelta }}\bigwedge _{i \in I}\pi _i{\mathrel {;}\,}\textsf {T} _i\leqslant \textsf {T} ''\). By definition of \(\leqslant \) we get and \(\textsf {T} ''={}_{\textstyle {\varDelta }}\bigwedge _{i \in I'}\pi _i{\mathrel {;}\,}\textsf {T} '_i\) with \(I\supseteq I'\) and \(\textsf {T} _i\leqslant \textsf {T} '_i\) for \(i\in I'\). Therefore \(\textsf {G} \upharpoonright \textsf {p} \,=\mathcal {T}\,\,'[{}_{\textstyle {\varDelta }}\bigwedge _{i \in I'}\pi _i{\mathrel {;}\,}\textsf {T} '_i]\). From Lemma 6(2) we have that there is \(\sigma \) such that \({ SubT}(\textsf {G} ,\sigma )\) affects \(\textsf {p} \) and \({ Ctx}(\textsf {G} ,\sigma ) \upharpoonright \textsf {p} \,= \mathcal {T}\,\,'\) and \({ SubT}(\textsf {G} ,\sigma ) \upharpoonright \textsf {p} \,\mathrel {\doteq }{}_{\textstyle {\varDelta }}\bigwedge _{i \in I'}\pi _i{\mathrel {;}\,}\textsf {T} '_i\). For each \(i\in I'\), the action \(\pi _i\) must have the form \(\pi _{i}=\textsf {q} _{i}?\lambda _{i}\) and be obtained projecting a communication \(\alpha _i=\textsf {q} _{i}\xrightarrow {\lambda _{i}}\textsf {p} \). We consider two cases: either \({ SubT}(\textsf {G} ,\sigma )\) is an executed choice, or it is either a non executed choice or a sequence starting with a non executed communication.
-
If \({ SubT}(\textsf {G} ,\sigma )={}_{\gamma }(\boxdot _{h\in H{\setminus }\{k\}}\,{\beta {}_{h}}{\mathrel {;}\,}\textsf {K} _h\ {\boxdot }\ \widehat{\beta }_k{\mathrel {;}\,}\textsf {G} _k)\), then let \(\sigma _k\) be the longest path in \({ SubT}(\textsf {G} ,\sigma )\) such that \(k\sqsubseteq \sigma _k \) and \(\sigma \sigma _k = \textsf {path} (\xi )\) for some \(\xi \in { ExOcc}(\textsf {G} )\). By Lemma 6(2) there are \(\sigma '\) and \(j\in I'\) such that \(\sigma \sigma '{\alpha _j}\in { Occ}(\textsf {G} )\) and either \(\sigma '\sqsubseteq \sigma _k\) or \(\sigma _k\sqsubset \sigma '\). Since \(\xi '\in { ExOcc}(\textsf {G} )\) implies \(\textsf {path} _{}(\xi ') \sqsubseteq \sigma \sigma _k\), then \(\xi '\) is not in conflict with \(\sigma \sigma '{\alpha _j}\). Therefore \(\sigma \sigma '{\alpha _j}\) is alive in \(\textsf {G} \).
-
If \({ SubT}(\textsf {G} ,\sigma )={}_{\gamma }\boxdot _{h\in H}\,{\beta ^{}_{h}}{\mathrel {;}\,}\textsf {G} _h\), then \(\sigma h\beta _h\) is alive in \(\textsf {G} \) for all \(h\in H\) by Lemma 7(2). Then by Lemma 6(2) for any \(h\in H\) we can find \(\sigma _h\) such that \(\sigma {\sigma _h\alpha _j}\) is alive in \(\textsf {G} \) for some \(j\in I'\).
In both cases there is \(\sigma _\textsf {p} \) such that \(\sigma _\textsf {p} \alpha _j\) is alive in \(\textsf {G} \) for some \(j\in I'\). Lemma 8(2) implies
and \(\vdash \textsf {p} \llbracket \,\mathcal {E}[{}_{\textstyle {\varDelta }}\textstyle {\sum _{i\in I}\pi _i{\mathrel {;}\,}P_i}]\,\rrbracket \mathrel {\Vert }\mathbb {N}_j' :\textsf {G} '\) with \(\sigma _\textsf {p} \alpha _j\) enabled in \(\textsf {G} '\). From Theorem 2(1) we conclude  . \(\square \)
. \(\square \)
Notice that the standard formulation of progress [13], which requires that each simple input and each output that is persistently offered be eventually consumed, is an easy consequence of this theorem.
Theorem 4
(Backward progress) If \(\vdash \mathbb {N} :\textsf {G} \) and C is alive in \(\textsf {G} \), then there is \(\mathbb {N}'\) such that \(\mathbb {N}\longrightarrow ^* \mathbb {N}'\) and  .
.
Proof
By definition \(\textsf {G} ={ Ctx}(\textsf {G} ,\sigma )[{}_{C}({\boxplus }_{j\in J{\setminus }\{k\}}\,\alpha ^{\textsf {p} }_{j}{\mathrel {;}\,}\textsf {K} _j{\boxplus }\widehat{\alpha ^{\textsf {p} }_k}{\mathrel {;}\,}\textsf {G} _k)]\) and \(|J| >1\) and \(\sigma \) is \(\textsf {ok} \) for \(C\) (in \(\textsf {G} \)) and there are \(\sigma '\) and \(\alpha ^{\textsf {p} }\) such that \(\sigma k\sigma '\alpha ^{\textsf {p} }\in { Occ}(\textsf {G} )\) is alive in \(\textsf {G} \). Lemma 8(2) implies that \(\mathbb {N}\longrightarrow ^* \mathbb {N}'\) and \(\vdash \mathbb {N} :\textsf {G} '\) with \(\sigma k\sigma '\alpha ^{\textsf {p} }\) enabled in \(\textsf {G} '\).
This implies that \(C\) is enabled in \(\textsf {G} \). We conclude  by Theorem 2(3). \(\square \)
by Theorem 2(3). \(\square \)
To sum up, our calculus enjoys:
-
subject reduction for both forward and backward computations;
-
session fidelity for enabled communications and for rollbacks to enabled checkpoint labels;
-
forward progress, assuring the absence of dangling actions but for connecting inputs;
-
backward progress for alive checkpoint labels.
We end this section with a remark on causal consistency and the loop lemma [10]. Causal consistency states that a cause cannot be reversed without first reversing its effects. Clearly, our calculus enjoys causal consistency since a rollback to a checkpointed choice removes all communications that were done after that checkpoint. The loop lemma prescribes that each transition has an inverse. The loop lemma does not hold for our calculus, since a reverse computation can only go back to a checkpointed choice whose leader currently offers an output.
6 Related work and conclusion
Since the seminal work by Danos and Krivine on reversible CCS [10], reversible computation has been widely studied in process calculi. In [31], Phillips and Ulidowski proposed a method for reversing process operators defined in a general SOS format, and noted that thread identifiers and histories were needed to record the past of computations. In [30] the authors use a cursor to mark past actions, thus avoiding the use of extra memory information as in [10].
In [23], Lanese et al. extended the approach of Danos and Krivine by defining a reversible variant of the higher-order \(\pi \)-calculus, using tags to identify threads, and explicit memory processes. This calculus was enriched with a fine-grained rollback primitive in [22]. In [9], Cristescu et al. proposed a causal semantic model for the reversible \(\pi \)-calculus.
Reversibility for structured communications was first studied in [11, 12, 21], where transactions with rollback and coordinated checkpoints were modelled in an extended CCS. More recently, reversibility has been incorporated into contracts [1, 4] and session calculi [17, 18]. In [2, 3], the authors investigated the notions of compliance and sub-behaviour for contracts with checkpoints. While rollbacks are forgetful in [2], in [3] they are used as a strategy to achieve compliance: in this case, after a rollback a process cannot engage again in the previously explored branch, presumably unsuccessful. We used a similar idea for defining our rollback here.
Our backward mechanism is most closely related to the recent proposals [24,25,26, 34, 35]. Tiezzi and Yoshida [34] use tags and memories to allow full reversibility of binary sessions with delegation. In [35], two forms of reversibility are considered: either a session is completely reversed in a single backward step, or any intermediate state is restored. Mezzina and Pérez [24, 25] use monitors as memories for reversing binary sessions. A key novelty of this work is the use of session types with present and past. In [26], this approach is generalised to multiparty sessions, asynchronous higher-order communications, and decoupled rollbacks.
In [28], Neykova and Yoshida provide an algorithm to analyse and extract causal dependencies from a given multiparty global type, and use it to ensure that communicating processes are safely recovered from consistent states in the presence of a failure. In [27], Mezzina and Tuosto propose a semantic control of reversibility: a computation along a branch is reversed according to the guards on the current configuration. A feature of [27] is that inputs are potentially irreversible actions, unless they appear within a loop.
Our work builds on our previous papers [8, 14]. In [14] we introduced a multiparty session calculus in which choices could be labelled with checkpoints. Participants could revert to one of these checkpointed choices in order to make a different choice. Global types were used to control reversibility, and shown to enforce the properties of fidelity and progress (both forward and backward). In [8] we enriched the syntax for types and processes with parallel and sequential composition, and used a more compact representation for past communications and a more refined strategy for backward moves. The current work borrows ideas and techniques from both papers while sticking to a simpler syntax than [8], and improves on both of them by allowing connecting communications.
As regards dynamic participants, in [13, 15] global types prescribe the behaviours of fixed roles, and each role includes an arbitrary number of participants, which can dynamically join and leave roles. Instead, in the Conversation Calculus [7, 36] the protocols describe communications between participants which can dynamically join and leave conversations. The model based on conversation contexts and labelled message-passing primitives is quite different from multiparty session types and this makes it difficult to adapt their approach to our setting.
The paper [20] has been our inspiration for connecting messages, but our calculus is more permissive than the original one. In fact, in [20] a connecting message can be exchanged only between two participants that did not communicate before, unless they have been disconnected by an ad hoc primitive. This means for example that \(\textsf {p} \xrightarrow {{\mathop {\leftrightarrow }\limits ^{\lambda _1}}}\textsf {q} {\mathrel {;}\,}\textsf {q} \xrightarrow {{\mathop {\leftrightarrow }\limits ^{\lambda _2}}}\textsf {p} \) is not allowed. Another difference of [20] with respect to our calculus is that in a choice, the first message received by a participant must be a connecting message, which forbids for instance \(\textsf {p} \xrightarrow {\lambda _1}\textsf {q} \,{\boxplus }\,\textsf {p} \xrightarrow {\lambda _2}\textsf {r} \). A further restriction is that all the inputs in an external choice must have the same sender. A final major difference is that communication in [20] is asynchronous.
The properties of our calculus are standard for reversible session calculi, but their proofs require some ingenuity due to the presence of connecting communications and to the specificity of our rollback mechanism. As argued already in Sect. 3, connecting communications may be used to avoid the use of multiple global types. They could also be useful for incorporating delegation into global types. For example, a seller could delegate a bank to receive a credit card number only when the client wants to buy an item, otherwise the bank is not involved in the transaction (so delegation would appear in one branch of a choice but not in the others). This is a topic we plan to investigate. As regards the conditions for reversing a computation, a current limitation of our work is that the starting points of rollbacks are statically determined. By contrast, these points are determined dynamically in [27], offering a more realistic solution. We plan to introduce similar runtime conditions for rollback in our calculus.
Finally, we would like to study the interpretation of global types into a model of Event Structures, for which reversible variants have already been proposed [16, 32]. We plan to explore a reversible variant of Flow Event Structures [5], a model that has already been used to interpret CCS processes with past in [6].
Notes
We could also leave the executed branch, just erasing its hats. This change would preserve all the properties of the calculus. We prefer the current formulation, since it avoids the possibility of going back and fourth several times along the same branch (which could yield a livelock).
References
Barbanera, F., de’ Liguoro, U.: Sub-behaviour relations for session-based client/server systems. Math. Struct. Comput. Sci. 25(6), 1339–1381 (2015)
Barbanera, F., Dezani-Ciancaglini, M., de’Liguoro, U.: Reversible client/server interactions. Form. Asp. Comput. 28(4), 697–722 (2016)
Barbanera, F., Dezani-Ciancaglini, M., Lanese, I., de’ Liguoro, U.: Retractable contracts. In: PLACES, volume 203 of EPTCS, pp. 61–72 (2016)
Bernardi, G., Hennessy, M.: Modelling session types using contracts. Math. Struct. Comput. Sci. 26(3), 510–560 (2016)
Boudol, G., Castellani, I.: Permutation of transitions: an event structure semantics for CCS and SCCS. In: REX School, volume 354 of LNCS, pp. 411–427. Springer (1988)
Boudol, G., Castellani, I.: Flow models of distributed computations: three equivalent semantics for CCS. Inf. Comput. 114(2), 247–314 (1994)
Caires, L., Vieira, H.T.: Analysis of service oriented software systems with the conversation calculus. In: FACS, volume 6921 of LNCS, pp. 6–33. Springer (2010)
Castellani, I., Dezani-Ciancaglini, M., Giannini, P.: Concurrent reversible sessions. In: CONCUR, volume 85 of LIPIcs, pp. 30:1–30:17. Schloss Dagstuhl (2017)
Cristescu, I., Krivine, J., Varacca, D.: Rigid families for the reversible \(\pi \)-calculus. In: RC, volume 9720 of LNCS, pp. 3–19. Springer (2016)
Danos, V., Krivine, J.: Reversible communicating systems. In: CONCUR, volume 3170 of LNCS, pp. 292–307. Springer (2004)
de Vries, E., Koutavas, V., Hennessy, M.: Communicating transactions—(extended abstract). In: CONCUR, volume 6269 of LNCS, pp. 569–583. Springer (2010)
de Vries, E., Koutavas, V., Hennessy, M.: Liveness of communicating transactions—(extended abstract). In: APLAS, volume 6461 of LNCS, pp. 392–407. Springer (2010)
Deniélou, P.-M., Yoshida, N.: Dynamic multirole session types. In: POPL, pp. 435–446. ACM Press (2011)
Dezani-Ciancaglini, M., Giannini, P.: Reversible multiparty sessions with checkpoints. In: EXPRESS/SOS, volume 222 of EPTCS, pp. 60–74 (2016)
Giachino, E., Sackman, M., Drossopoulou, S., Eisenbach, S.: Softly safely spoken: Role playing for session types. In: PLACES (2009)
Graversen, E., Phillips, I., Yoshida, N.: Towards a categorical representation of reversible event structures. In: PLACES, volume 246 of EPTCS, pp. 49–60 (2017)
Honda, K., Vasconcelos, V.T., Kubo, M.: Language primitives and type disciplines for structured communication-based programming. In: ESOP, volume 1381 of LNCS, pp. 22–138. Springer (1998)
Honda, K., Yoshida, N., Carbone, M.: Multiparty asynchronous session types. In: POPL, pp. 273–284. ACM Press (2008)
Honda, K., Yoshida, N., Carbone, M.: Multiparty asynchronous session types. J. ACM 63(1), 9 (2016)
Hu, R., Yoshida, N.: Explicit connection actions in multiparty session types. In: Fundamental Approaches to Software Engineering, volume 10202 of LNCS, pp. 116–133. Springer (2017)
Koutavas, V., Spaccasassi, C., Hennessy, M.: Bisimulations for communicating transactions—(extended abstract). In: FOSSACS, volume 8412 of LNCS, pp. 320–334. Springer (2014)
Lanese, I., Mezzina, C.A., Schmitt, A., Stefani, J.-B.: Controlling reversibility in higher-order pi. In: CONCUR, volume 6901 of LNCS, pp. 297–311. Springer (2011)
Lanese, I., Mezzina, C.A., Stefani, J.-B.: Reversing higher-order pi. In: CONCUR, volume 6269 of LNCS, pp. 478–493. Springer (2010)
Mezzina, C.A., Pérez, J.A.: Reversible semantics in session-based concurrency. In: ICTCS, volume 1720 of CEUR, pp. 221–226 (2016). CEUR-WS.org
Mezzina, C.A., Pérez, J.A.: Reversible sessions using monitors. In: PLACES, volume 211 of EPTCS, pp. 56–64 (2016)
Mezzina, C.A., Pérez, J.A.: Causally consistent reversible choreographies: a monitors-as-memories approach. In: PPDP, pp. 127–138. ACM Press (2017)
Mezzina, C.A., Tuosto, E.: Choreographies for automatic recovery (2017). CoRR, arXiv:1705.09525
Neykova, R., Yoshida, N.: Let it recover: multiparty protocol-induced recovery. In: CC, pp. 98–108. ACM Press (2017)
Padovani, L.: Type reconstruction for the linear \(\pi \)-calculus with composite regular types. Log. Methods Comput. Sci. 11(4), 1–23 (2015)
Phillips, I., Ulidowski, I.: Operational semantics of reversibility in process algebra. In: APC, volume 162 of ENTCS, pp. 281–286 (2006)
Phillips, I., Ulidowski, I.: Reversing algebraic process calculi. J. Log. Algebr. Methods Program. 73(1–2), 70–96 (2007)
Phillips, I., Ulidowski, I.: Reversibility and asymmetric conflict in event structures. J. Log. Algebr. Methods Program. 84(6), 781–805 (2015)
Pierce, B.C.: Types and Programming Languages. MIT Press, Cambridge (2002)
Tiezzi, F., Yoshida, N.: Reversible session-based pi-calculus. J. Log. Algebr. Methods Program. 84(5), 684–707 (2015)
Tiezzi, F., Yoshida, N.: Reversing single sessions. In: RC, volume 9720 of LNCS, pp. 52–69. Springer (2016)
Vieira, H.T., Caires, L., Seco, J.C.: The conversation calculus: a model of service-oriented computation. In: ESOP, volume 4960 of LNCS, pp. 269–283. Springer (2008)
Winskel, G.: Events in Computation. PhD thesis, Department of Computer Science, University of Edinburgh (1980)
Acknowledgements
We would like to thank the anonymous referees for their helpful comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Mariangiola Dezani-Ciancaglini: Partially supported by EU H2020-644235 Rephrase project, EU H2020-644298 HyVar project, IC1402 ARVI and Ateneo/CSP project RunVar. Paola Giannini: This original research has the financial support of the Università del Piemonte Orientale. The authors acknowledge a partial support of COST Action IC1405 on Reversible Computation—extending horizons of computing.
A: Reductions of networks and systems
A: Reductions of networks and systems
It is easy to define a bijection between networks and initial systems:
where \(\mathbb {P}\) is the set of participants in \(\mathbb {N}\).
We establish now an operational correspondence between networks and their associated systems. More precisely we prove the following:
-
Communication preservation and reflection: every network communication is simulated by a communication in the associated system and vice-versa;
-
Rollback preservation: every network rollback is simulated by a sequence of backward moves in the associated system, initiating with a starting backward move and terminating with an ending backward move;
-
Rollback reflection: every starting backward move in a system can be extended to a complete sequence of backward moves such that the resulting system is the image of a rollback in the source network.
In the following theorem we denote  transitive closure of
transitive closure of  and
and  .
.
Theorem 5
-
1.
If
 , then
, then  .
. -
2.
If
 , then
, then  .
. -
3.
If
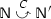 , then
, then  .
. -
4.
If
 , then
, then 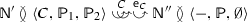 and
and  .
.
Proof
(1) and (2). The result is immediate since Rule [Com] of Fig. 1 and Rule [ComS] of Fig. 2 have the same antecedents.
(3). If  , then the applied rule is
, then the applied rule is

where
Then \({\mathcal {S}}(\mathbb {N})=\mathbb {N}\between \sigma \) and \({\mathcal {S}}(\mathbb {N}')=\mathbb {N}'\between \sigma \) with \(\sigma =\langle -,\{\textsf {p} \}\cup \{\textsf {p} _i\mid 1\le i \le n\},\emptyset \rangle \). We get

(4). If  , then Rule [BackS] has been applied, so
, then Rule [BackS] has been applied, so

Since \(\mathbb {P}_2\) can be split in two subsets of participants, according to whether the associated processes satisfy the premise of Rule [BackY] or of Rule [BackN] in Fig. 2, we may assume without loss of generality that
where for all i, \(1\le i\le n\),  if \(i\le m\) and
if \(i\le m\) and  otherwise. With a sequence of reductions as in the proof of point (3), we then obtain for some network \(\mathbb {N}''\):
otherwise. With a sequence of reductions as in the proof of point (3), we then obtain for some network \(\mathbb {N}''\):

Since \(P\) and all the \(P_i\) for \(1\le i\le n\) satisfy the premises of Rule [Back] in Fig. 1, we may apply this rule to \(\mathbb {N}\) to conclude  , as required. \(\square \)
, as required. \(\square \)
Rights and permissions
About this article
Cite this article
Castellani, I., Dezani-Ciancaglini, M. & Giannini, P. Reversible sessions with flexible choices. Acta Informatica 56, 553–583 (2019). https://doi.org/10.1007/s00236-019-00332-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00236-019-00332-y












 , then
, then  , then
, then  , then
, then 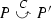 , then
, then  .
. , then
, then  , then
, then  and
and  and
and  , then
, then 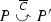 and
and  for all
for all  for all
for all  .
.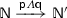 , then
, then 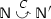 .
. , then
, then 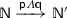 , then
, then  .
. , then
, then 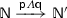 .
. , then
, then  .
. , then
, then 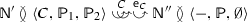 and
and  .
.